First-Year Development of Modules and Hubs in Infant Brain Functional Networks

Abstract

The human brain develops rapidly in the first postnatal year, in which rewired functional brain networks could shape later behavioral and cognitive performance. Resting-state functional magnetic resonances imaging (rs-fMRI) and complex network analysis have been widely used for characterizing the developmental brain functional connectome. Yet, such studies focusing on the first year of postnatal life are still very limited. Leveraging normally developing longitudinal infant rs-fMRI scans from neonate to one year of age, we investigated how brain functional networks develop at a fine temporal scale (every 3 months). Considering challenges in the infant fMRI-based network analysis, we developed a novel algorithm to construct the robust, temporally consistent and modular structure augmented group-level network based on which functional modules were detected at each age. Our study reveals that the brain functional network is gradually subdivided into an increasing number of functional modules accompanied by the strengthened intra- and inter-modular connectivities. Based on the developing modules, we found connector hubs (the high-centrality regions connecting different modules) emerging and increasing, while provincial hubs (the high-centrality regions connecting regions in the same module) diminishing. Further region-wise longitudinal analysis validates that different hubs have distinct developmental trajectories of the intra- and inter-modular connections suggesting different types of role transitions in network, such as non-hubs to hubs or provincial hubs to connector hubs et al. All findings indicate that functional segregation and integration are both increased in the first year of postnatal life. The module reorganization and hub transition lead to more efficient brain networks, featuring increasingly segregated modular structure and more connector hubs. This study provides the first comprehensive report of the development of functional brain networks at three month intervals throughout the first postnatal year of life, which provides essential information to the future neurodevelopmental and developmental disorder studies.

1. Introduction

In the first postnatal year, the human brain undergoes the most dramatic growth with its total volume expanding up to double its size (Knickmeyer et al., 2008; Tau and Peterson, 2010; Gao et al., 2016; Li et al., 2018). Concurrently, remarkable functional brain milestones are achieved during this period, including not only the improved vision (Courage and Adams, 1990) and body manipulation, but also a number of higher-order cognitive functions, such as self-awareness (Amsterdam, 1972), spatial attention (Haith et al., 1988), and working memory (Reznick, 2009). These dramatic changes greatly shape subsequent cognitive and behavioral development and lay foundations for the essential skills in later life. Thus, it is critical to improve our limited understandings of developmental patterns and mechanisms of the human brain in the first postnatal year.

In recent years, resting-state functional magnetic resonance imaging (rs-fMRI) has been emerging for probing functional brain development (Gao et al., 2009; Smyser et al., 2010; Fransson et al., 2011; Gao et al., 2011; Smyser et al., 2011; Barrett and Satpute, 2013; Alcauter et al., 2014; Damaraju et al., 2014; De Asis-Cruz et al., 2015; Gao et al., 2015a; Gao et al., 2015b; van den Heuvel et al., 2015; Cao et al., 2016a). However, only a few studies have focused on the longitudinal aspects of functional brain development in this most important period, i.e., the first stages of postnatal life. In a large-scale longitudinal study, Gao et al. delineates the developmental trajectories of nine brain functional sub-networks every three months from neonate to one year of age. It reveals that different brain sub-networks have distinct growth trajectories following a sequence from the primary to higher-order functional systems (Gao et al., 2015a). This finding investigates the developmental functional segregation in the brain, but largely neglects the development of functional integration (i.e., the functional interactions among different brain regions or different functional systems). It is worth noting that studying the development of functional integration is essential in the developmental neuroscience, due to that matter, the functional interactions are believed to mediate more complex cognitive functions (Barrett and Satpute, 2013; Behrmann and Plaut, 2013; Friederici and Gierhan, 2013; Sporns, 2013; Gao et al., 2015a; Cohen and D’Esposito, 2016).

The spatiotemporal characteristics of developing large-scale functional brain networks could deepen our understanding on how the human brain develops well-coordinated functional systems that mirror cognitive milestones at such a pivotal age. To this end, it is highly required to have more sophisticated and fine-grained network modeling and topological analyses. The most popular method is to represent the inter-regional functional interactions as a complex network that consists of all brain regions as nodes linked by functional connectivity (FC) as edges. In the network, the edge strength is usually measured by the temporal synchronization of regional blood-oxygen level-dependent (BOLD) rs-fMRI signals (Friston, 2011). Graph theory analyses can help uncover the details of the topological properties of such a complex network. Abundant evidence indicates that matured adult brain networks follow a small-world property with both high local and global efficiencies to facilitate the efficient information exchange (Watts and Strogatz, 1998; Liao et al., 2017). From another viewpoint, this efficient organization also suggests well-balanced functional segregation (supporting intra-functional-system information exchange to process single-modal information) and functional integration (enabling inter-functional-system collaboration to process multimodal information and support higher-level functions) with limited wiring resources (Sporns, 2013). Such properties have been observed in many other age groups, such as infants (Gao et al., 2011; De Asis-Cruz et al., 2015; van den Heuvel et al., 2015; Cao et al., 2016a), older children (Fair et al., 2009), adolescents (Smyser et al., 2011), and the elderly (Onoda and Yamaguchi, 2013). Despite the well-observed global network properties, the detailed rewiring processes, i.e., the longitudinal development of the localized nodes and edges, have not currently been investigated, although they could be more important and helpful to understand the developing brain.

It has been hypothesized that the developmental brain network continuously reconfigures with a small amount of connections rewired to drive the entire network toward a more efficient organization (both globally and locally), while keeping the whole system relatively stable (Fair et al., 2009; Supekar et al., 2009; Gao et al., 2011; Uddin et al., 2011; Chen et al., 2013; Huang et al., 2013; Damaraju et al., 2014; Thomason et al., 2015; Zhao et al., 2015; Cao et al., 2016a; Cao et al., 2017). However, most evidences come from the age groups spanning from late childhood (~ five years of age) to early adolescence (~12 years of age). Based on these studies, a few key connections that link different functional systems are prone to rewire in order to achieve enhanced functional integration/segregation, as well as increased local and global efficiencies (Fair et al., 2009; Supekar et al., 2009; Dosenbach et al., 2010; Wu et al., 2013; Cao et al., 2014). From neonate to early childhood, a similar developmental trend was suggested, but it came from only one study on the large-scale functional brain networks of the infants at three-week, one-year and two-years of age (Gao et al., 2011), which revealed increasing local and global efficiency, as well as the increasingly uniform spatial distribution of “hub” regions (the nodes with significantly more connections or higher degrees). While the study is still lacking for the first postnatal year, a bold hypothesis has been proposed, which assumes more rapid changes in functional integration/segregation (Cao et al., 2016a; Cao et al., 2017). Therefore, it is highly important and necessary to fill this gap and test such a hypothesis by characterizing fine-grained, month-to-month spatiotemporal developmental trajectories of the brains functional networks and its topological structures.

In this paper, leveraging a large longitudinal rs-fMRI dataset from normally developing infants with each having multiple dense scans (at every three months from birth), we aim to (1) delineate the fine-grained developmental trajectories of the large-scale functional brain networks in the first postnatal year, and (2) explore the possible driving forces of such a dynamic evolution with explicit evidences from network topological analysis. Instead of using global network metrics (e.g., local/global efficiency), we focus on a group of densely interconnected brain regions, i.e., communities or modules (Rubinov and Sporns, 2010), which are suggested to be relevant to specific cognitive/behavioral functions (Bertolero et al., 2015). Based on the modular structure, we further investigated the longitudinal reconfiguration and rewiring involving a small set of “hub” regions. In this sense, the functional segregation and integration can be assessed by quantifying the modular structures and hubs (Hwang et al., 2012; Huang et al., 2013; van den Heuvel and Sporns, 2013; Bertolero et al., 2015). Based on different topological roles of hubs, we investigate and identify the longitudinally sensitive spatial location changes of both provincial hubs (for integrating the nodes within a module) and connector hubs (for integrating the nodes belonging to different modules) (van den Heuvel and Sporns, 2013; Bertolero et al., 2015). We hypothesize that from neonate to one year of age, (1) the number of functional brain modules will gradually increase, driven by the increasingly strengthened within-module FC (i.e., functional segregation); (2) the number of connector hubs will increase, driven by strengthened inter-modular FC (i.e., functional integration); and (3) the spatial distribution of different types of hubs are continuously changing, which represents different maturation order for different functional systems.

2. Materials and Methods

2.1. Subject Information

Images were obtained from subjects enrolled in the “Multi-visit Advanced Pediatric brain imaging study for characterizing structural and functional development (MAP Study)”. Fifty-one typically developing infants with 158 longitudinal rs-fMRI scans, i.e., 0 month (n = 33), 3 months (n = 29), 6 months (n = 31), 9 months (n = 30), and 12 months (n = 35), in the first postnatal year were used in this study. Fig. S1 in Supplementary Materials presents a distribution of age for all the included subjects whose image quality passed the quality control (QC). The percentages of the subjects who completed each of the five scans are 19.61%, 19.61%, 13.73%, 25.49%, and 21.57%, respectively. All subjects were in a natural sleeping state during rs-fMRI acquisition. For the detailed inclusion and exclusion criteria for infants, please see our previous study (Gao et al., 2015a). Informed written consent was obtained from the parents of all participants and all study protocols were approved by the University of North Carolina at Chapel Hill Institutional Review Board.

2.2. Data Acquisition

All images were acquired with a Siemens 3T MRI scanner. Rs-fMRI was acquired using a T2-weighted EPI sequence. The imaging parameters were as follows: TR = 2 s, TE = 32 ms, 33 slices, voxel size = 4×4×4 mm³, total volumes = 150 (five minutes). In order to provide an anatomical reference, structural images were also acquired using a 3D MP-RAGE sequence with the following parameters: TR = 1820 ms, TE = 4.38 ms, inversion time = 1100 ms, voxel size of 1×1×1 mm³.

2.3. Imaging Preprocessing

Allowing for the equilibration of the magnetic field, the first 10 volumes were discarded. The remaining data were pre-processed using FSL (http://www.fmrib.ox.ac.uk/fsl). It includes the following procedures: slice-timing correction, head motion correction, spatial smoothing (6-mm full width at half maximum Gaussian kernel), low-pass temporal filtering (<0.08 Hz), and mean signal removal (including white matter, cerebrospinal fluid (CSF), whole-brain averaged signal and six head motion parameters) by using a linear regression model. To further reduce head motion effects, we conducted data “scrubbing”, which removed one volume before and two volumes after each bad frame to control the global measure of signal change (DVARS < 0.5%) and frame-wise displacement (FD < 0.5 mm) (Power et al., 2012). After scrubbing, subjects with less than 90 volumes were excluded, and twenty rs-fMRI scans were removed from further analysis. No significant differences were found in terms of mean FD (p = 0.538) and the number of censored frames (p = 0.923) among all the age groups by using Kruskal-Wallis test. No correlations were observed between the mean FD (r = −0.112, p = 0.164) and the number of censored frames (r = −0.144, p = 0.072) with age. Additionally, three benchmark metrics, including QC-FC correlation, QC-FC distance dependence and the loss of temporal degrees of freedom (tDOF-loss), were reported in Fig. S2 in Supplementary Materials to further evaluate the effectiveness of the head motion control in our study (Parkes et al., 2018).

To improve registration accuracy, we used structural tissue-labeled images derived by a learning-based multi-source integration framework (LINKS) (Wang et al., 2015) for longitudinal and cross-sectional image registration. In the labeled images, the voxels were labeled as gray matter, white matter and cerebrospinal fluid, rather than their original intensity. Specifically, for each subject at each age, the first volume of the rs-fMRI data was affine registered to the corresponding structural images. We then adopted a group-wise registration method using GLIRT (Wu et al., 2012) to implement within-subject longitudinal registration, thus aligning different structural images of the same subject scanned at different ages. After that, we registered the mean image of each subject to a standard symmetric Montreal Neurological Institute (MNI-152 adult) template by using Demons (Thirion, 1998). By combing the linear transformation matrix and the deformation fields from the above steps, we obtained a final deformation field of each subject at each scan from its native space to the MNI space.

2.4. Individual-Level Brain Functional Network Construction

We parcellated the whole brain into 200 regions by using the atlas provided by Craddock et al. (Craddock et al., 2012). As cerebellum registration is difficult for infants due to its small size and weak contrast, we excluded 20 cerebellar regions and only used 180 regions. For each subject, we warped the atlas back to each subject’s native space by using the inverted deformation field obtained from the registration, and then extracted the averaged rs-fMRI time series in each brain region. We calculated pairwise Pearson’s correlation between each pair of the nodes (i.e., regions), thus generating a weighted brain functional network for each subject at each age. Only the positive connections were kept and all negative values were set as zeros, as the anti-correlations are still biologically unclear (Garrison et al., 2015). Of note, all the following experiments were based on the weighted networks.

2.5. Module-Guided Group-level Network Construction

To detect robust functional brain modules for each age group, one widely-adopted strategy is to generate a group-level weighted FC matrix by averaging all individual-level FC matrices of the same age and detect the modular structure based on it. However, this strategy bears two limitations. First, the potential image noises could lead to spurious individual-level FC matrices that might dominate the group-level result. Second, the resultant averaged FC matrix is usually over-blurred, making the following module and hub detection difficult and biased. Such problems could be magnified in the neonate/infant study due to the increased noise and artifact in infants’ fMRI data (Zhang et al., 2018b). To generate robust group-level networks, we proposed a novel method called “Module-Guided Group-Level Network Construction”, which leverages the information of the modular structure detected at the individual level and utilizes it as the anatomical prior to guide the group-level FC network construction.

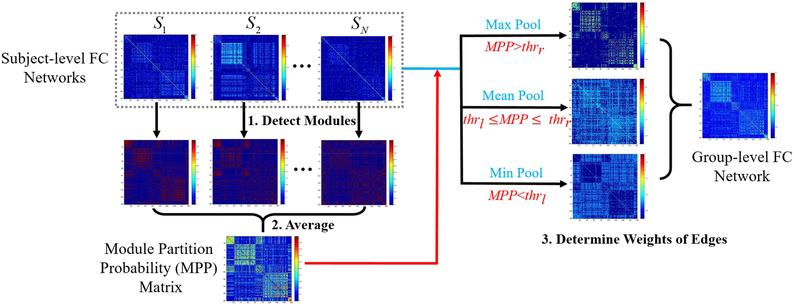
The flowchart of our method is illustrated in Fig. 1, consisting of three steps. First, for each subject, we kept top 10% strongest positive connections to ensure the sparsity of FC networks and to remove weak connections (Power et al., 2012; Cole et al., 2013; Yeo et al., 2014; Najafi et al., 2016). We then detected corresponding modular structure for each individual FC matrix by maximizing modularity (Q) with a widely-used toolbox (Radtools, deim.urv.cat/~sergio.gomez/radatools.php). It allows to use multiple searching algorithms in an iterative manner and output the best partition with the highest Q. We combined tabu search (Arenas et al., 2008), extremal optimization (Duch and Arenas, 2005), fast heuristics (Newman, 2004), and spectral optimization (Newman, 2006) as recommended by Radtools developers. For each individual-level network, the module detection was repeated for 100 times and the modular structure obtained from each run was converted to a “modular partition matrix”, where the element with two nodes assigned to the same module has a value of one; otherwise, zero. We then averaged 100 module partition matrices to obtain an individual-level “modular partition probability” (MPP) matrix. Second, by averaging individual-level MPP matrices across all subjects of the same age group, we generated a group-level MPP matrix, where each element represents the probability of assigning a pair of nodes to the same module. Third, we generated a MPP-guided group-level FC network. The edges with higher MPPs are more likely to be intra-modular connections with strong FC, while those with lower MPPs are more probably inter-modular connections with weak FC. Therefore, we divided the MPPs of all edges into three categories using two cutoffs, i.e., thr_l and thr_h, which respectively represent the low and high thresholds for MPPs. We set the final weight of a group-level FC edge to be the mean of the five highest individual-level FC of the same edge across all subjects, if the MPP of this edge is larger than thr_h (i.e., max Pool). Similarly, we set it to be the mean of the five weakest individual-level FC across all subjects, if this edge has an MPP lower than thr_l (i.e., min Pool). For the edges in-between of thr_l and thr_h, we treated them as uncertain modular partition and set their final weights to the mean FC of all subjects (i.e., mean Pool). The values of thr_l and thr_h were set to 0.1 and 0.5 in the following experiments. Other settings for thr_l and thr_h are discussed in Section 4.5.3.

Fig. 1.

Flowchart of the proposed Module-Guided Group-Level Network Construction method. First, based on each subject-level FC network, we detected the subject-level modular structure of FC network for each subject and represented such modular structure as a matrix. In such a matrix, if two nodes were assigned to the same module, the corresponding value was set to one; otherwise, zero. Second, we averaged modular partition matrices across all subjects in each age group to generate the group-level “possibility matrix”, i.e., “Module Partition Possibility” (MPP) matrix. In the MPP matrix, each element represents the probability of assigning a pair of nodes to the same module. Third, we determined the final weights of edges in the group-level FC network guided by the MPP matrix. For each edge, if its MPP is larger than thr_h, the edge weight is set to the mean of the five highest individual-level FC of the same edge across all subjects (i.e., max Pool). If the MPP is smaller than thr_l, the edge weight is the mean of the five weakest individual-level FC across all subjects (i.e., min Pool); otherwise, the weight is the average value across all subjects (i.e., mean Pool).

Rather than calculating the MPP matrix independently for each age group, we added an extra step, i.e., temporal smoothness, during the MPP calculation to adjust it and to ensure its temporal consistency across ages (Li et al., 2012; Wang et al., 2012; Yan et al., 2017). We assume that the neighboring age groups share similar brain network architectures to certain extent. In light of this, we let each element in the adjusted MPP matrix at each time point shares the information from its temporal neighborhood. Specifically, for an edge (i, j) in the r-th time point, the adjusted MPP_r(i, j) was calculated as the weighted sum of the original MPP _t(i, j) (t = 1, …, T) as follows:

$${\text{MPP}}_r^{\text{adjust}}(i,j)={\sum }_{t=1}^T{w}_t^r\mathrm{M}\mathrm{P}{\mathrm{P}}_t^{\text{orig}}(i,j)$$ (1)

where T is the total number of the age time points, and $w_t^r$ is the contribution ratio of the t-th time point (t = 1, …, T) to the r-th time point, as defined below:

$$w_t^r=\frac{1}{\sqrt{2\pi }\delta }\exp (-\frac{{(t-r)}^2}{2{\delta }^2})/{\sum }_{t=1}^T{w}_t^r$$ (2)

where δ is the standard deviation of the Gaussian function to control the “temporal smoothness”, which is set to 1.5 in this study (please see the further discussion on the choice of this parameter in Section 4.5.2). According to Sections 2.4–2.5, we generated “augmented” group-level FC networks for each age group by both enhancing the modular structure and making them temporally consistent for following longitudinal module detection (Section 2.6) and hub assessment (Sections 2.7–2.8).

2.6. Module Detection from Augmented Group-Level FC Networks

Based on the “augmented” group-level FC networks, we detected the modular structures for each age separately using Radtools with the same sparsity (10%) as used for individual-level module detection (Power et al., 2012; Cole et al., 2013; Yeo et al., 2014; Najafi et al., 2016). For each group-level network, we repeated the module detection for 100 times and used a consensus clustering method (Bassett et al., 2013) to obtain the consistent modules. The modular structure for the age-specific FC networks was compared across different ages (0-, 3-, 6-, 9-, and 12-months of age). Based on the detected modular structures, we further calculated mean intra- and inter-modular connectivities across all modules for each subject at all age groups for quantitative assessment of the developmental changes in the FC network segregation and integration. The mean intra-modular connectivity (reflecting functional segregation) was defined as the averaged FC strength across all the within-modular connections. The mean inter-modular connectivity (measuring functional integration) was calculated as the averaged FC strength across all the edges that linked different modules. All the positive connections were used, and the negative connections were not counted. As the intra- and inter-modular connectivities were calculated using whole-brain FC links, they provide direct measurement for the whole-brain functional segregation/integration changes.

After obtaining the mean intra- and inter-modular connectivities of each subject at all age groups, we adopted a linear mixed-effect regression (LMER) model to delineate the developmental trajectories of intra- and inter-modular connectivities. The LMER model was used due to its ability to handle missing data for the longitudinal study (Verbeke and Molenberghs 2000). Specifically, both a linear model (using age as a fixed-effect variable to test for a linear change) and a log-linear model (using log(age) as a fixed-effect variable to test for a nonlinear change) were built. The log-linear model has been widely used in the previous brain development studies (Gao et al., 2015a, 2015b). Random intercept and subject effects were included to characterize the temporal correlation. The Akaike information criterion (AIC) was adopted for model selection between the linear and nonlinear models. For all models, the significance was defined as p < 0.05. Next, we identified and characterized key brain regions (i.e., hubs) that contributed to the developing functional segregation/integration.

2.7. Provincial and Connector Hub Detection

Instead of investigating hubs as a whole, we step further to classify hubs into provincial and connector hubs based on their topological roles in the modular partitions measured by within-module degree (WD) and participation coefficient (P) (Guimera and Amaral, 2005; Meunier et al., 2009; Meunier et al., 2010; Bertolero et al., 2015). WD measures how well-connected a node is in the same module that this node belongs to (Guimera and Amaral, 2005). P measures distribution of nodes’ connections among different modules (Guimera and Amaral, 2005). In other words, WD evaluates the importance of a region to its module and P characterizes the importance of a region in connecting with different modules. Specifically, suppose a modular partition is M = {m_c | c = 1, …, C}. For a node i in module m_c, WD_i and P_i were respectively calculated by:

$$W{D}_i=\frac{{\kappa }_{m_c}^i-\overline{{\kappa }_{m_{\text{c}}}}}{{\delta }_{{\kappa }_{m_c}}},$$ (3)

$$P_i=1-{\sum }_{c=1}^C(\frac{{\kappa }_{m_c}^i}{k_i}),$$ (4)

where ${\kappa }_{m_c}^i$ is the total FC strength between node i and the other nodes in module $m_c.\overline{{\kappa }_{m_c}}$ and ${\sigma }_{{\kappa }_m{}_{{}_c}}$ represent the average and standard deviation (SD) of ${\kappa }_{m_c}^i$ across all nodes in module m_c, respectively. k_i is the sum of FC strength connecting node i.

Provincial hubs provide structures within the local module, and connector hubs mediate connections between multiple modules (Guimera and Amaral, 2005; van den Heuvel and Sporns, 2013). Thus, provincial hubs should have high WD but low P, while connector hubs have both high WD and P. By setting thresholds for within-module degree (thr_WD) and participation coefficient (thr_P), we detected provincial and connector hubs from each age-specific group-level FC network. For node i, it is categorized to a provincial hub if WD_i > thr_WD and P_i < thr_P, or to a connector hub when WD_i > thr_WD and P_i > thr_P. In the experimental results, we only showed the detected hubs when thr_WD and thr_P were set to 1.0 and 0.6, respectively. The other settings for WD_thr and P_thr are discussed in Section 4.5.6.

2.8. Characterization of Regional Developmental Trajectories of WD and P

Besides investigating hubs at each age in a cross-sectional manner, we further used LMER model to characterize developmental trajectories of the regional WD and P to delineate how a brain region evolves to be a provincial/connector hub. We thus selected hub regions detected in 12-months-old as regions of interest (ROIs) and assessed their WD and P values at all age groups in the first postnatal year. In each LMER, the ROI’s WD or P was modeled as the dependent variable, and age or log(age) in days was entered as the independent variable. Random intercept and subject effects were included to characterize the temporal correlation. The Akaike information criterion (AIC) was adopted for model selection between age and log(age). For all models, significance was defined as p < 0.001 after false discovery rate (FDR) correction.

3. Results

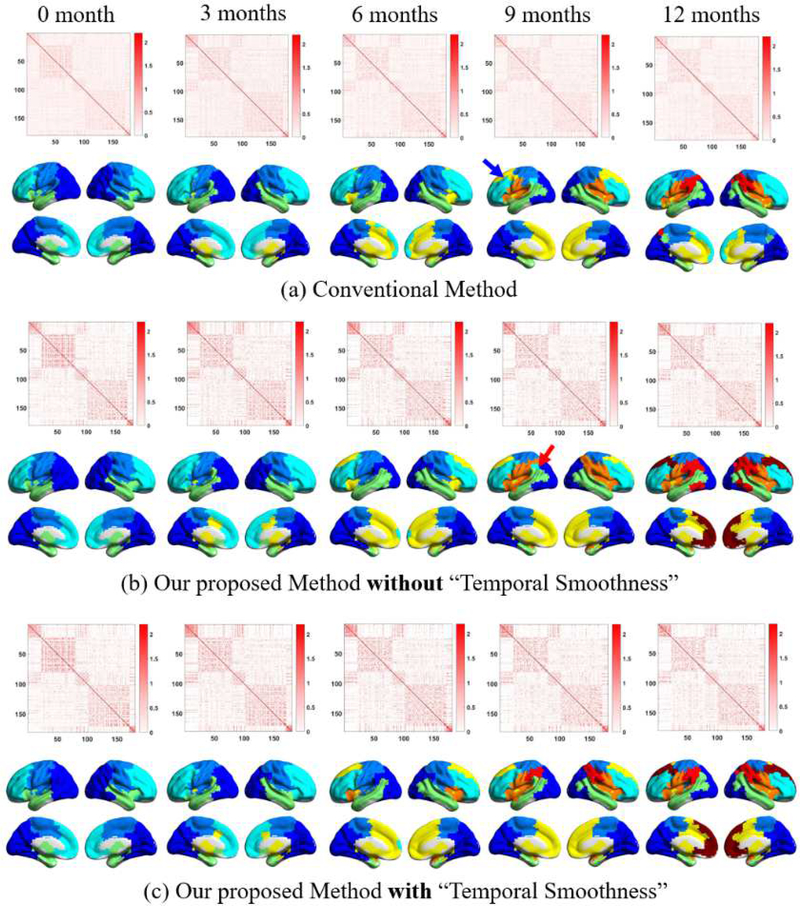
We evaluated the effectiveness of our proposed group-level network construction method by comparing the generated group-level FC matrix at each age group with those derived from the conventional (i.e., average-based) method. After the group-level networks were constructed, we used the same algorithm as described in Section 2.6 to detect modular structures and compared results between two methods. Of note, the proposed “temporal smoothness” constraint could not be easily applied to the conventional method as it should be applied to the MPP matrices (see Section 2.5). For unbiased comparisons, we also generated the module-guided group-level networks without adding the step of “temporal smoothness”. The three results are shown in Fig. 2.

Fig. 2.

Comparisons of the constructed group-level FC networks and their corresponding modular structures obtained by (a) conventional method, (b) our proposed method without “temporal smoothness”, and (c) our method with “temporal smoothness”. In each subplot, the upper row shows the group-level FC matrices after rearranging rows and columns according to the modular structure obtained on adults. The lower row shows modular structure (different modules in different colors). The arrows highlight the inconsistent module detection results.

As expected, the group-level FC network matrices obtained from the conventional method (Fig. 2a) are much more blurred than those from our method either with or without “temporal smoothness” for all age groups (Figs. 2b and 2c). Such results were also supported by higher modularity (Q) values of the networks derived from our methods than those from the conventional method (Fig. S5 in Supplementary Materials), because Q measures the degree of modular structure in a network, with a larger Q indicating a clearer modular structure. The blurred FC matrices increase the difficulty in module detection and further result in inconsistent modular structures across ages. Comparisons of the detected modular structures show that, even without additional “temporal smoothness”, the modules derived from our method are still consistent across ages compared to the conventional method. For example, the conventional method leads to an additional dorsal frontal module at nine months of age compared to other ages (see the blue arrow in Fig. 2a). In contrast, from our proposed method, the frontal area is consistently and smoothly partitioned into three modules during the development in the first postnatal year. We also find that the introduction of “temporal smoothness” in the MPP prior calculation could further improve the temporal consistency of modular structures. As shown in Fig. 2b, without “temporal smoothness”, a small region in the inferior parietal cortex is singled out from the main parietal modules (see the red arrow in Fig. 2b), but such a result does not exist at neighboring ages. With the method of integrating “temporal smoothness”, such inconsistent results can be avoided. We also evaluated the effectiveness of our method on an adult dataset. For detailed information, please see Supplementary Materials.

3.1. Development of Modular Structures in Infant Functional Brain Networks

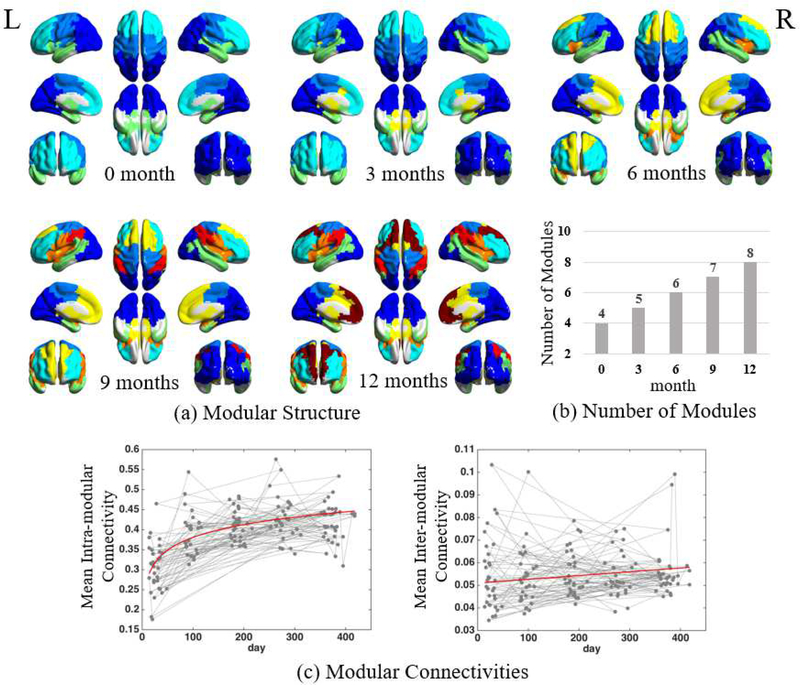
The full views of the detected modules from neonates to 12 months of age are visualized in Fig. 3a. Asides from the temporally consistent modular patterns across ages, we find that the brain is gradually divided into more and more modules, from 4 modules at neonate to 8 after 12 months of maturation (Fig. 3b). Table 1 summarizes how these new modules emerge by splitting from or merging to the existing modules at previous ages. Specifically, the quantity of modules increases with the emergence of new modules in spatially-independent brain regions at different ages, which seems to follow a particular order as described below.

Fig. 3.

Developmental changes in functional brain networks in the first postnatal year, including (a) developing modular structure, (b) continuously increasing modular quantity, and (c) longitudinal developmental trajectories of the mean intra-modular and mean inter-modular FC connectivities.

Table 1.

Development of modules from 0- to 12-months of age.

0 mo.	* [a] Visual cortex	[b] Temporal lobes, subcortical areas, anterior insula		[c] Frontal areas			[d] Central areas, posterior insula
3 mo.	Visual cortex	Temporal lobes	Subcortical areas	Frontal areas			Central areas, posterior insula
6 mo.	Visual cortex	Temporal lobes	Subcortical areas, medial prefrontal areas		Inferior/middle frontal cortices	Inferior prefrontal gyrus (triangularis), anterior insula	Central areas, posterior insula
9 mo.	Visual cortex	Temporal lobes	Subcortical areas, medial prefrontal areas		Inferior/middle frontal cortices	Inferior prefrontal gyrus (triangularis), central areas (ventral part), insula	Central areas (dorsal)	Inferior parietal lobule
12 mo.	# [1] Visual cortex	[2] Temporal lobes	[3] Subcortical areas, middle cingulate cortex	[4] Superior frontal, medial prefrontal areas	[5] Inferior/ middle frontal cortices	[6] Inferior prefrontal gyrus (triangularis), central areas (ventral part), insula	[7] Central areas (dorsal)	[8] Inferior parietal lobule

^*[a-d] Modules a-d at the neonatal stage;

^#[1–8] Modules 1–8 at 1 year of age; Merged and split columns indicate module merging and splitting; Italic words show the most significant modular structure change at each age period.

In neonates, the brain is separated into four modules: neonatal-module a (mainly covering the visual cortex in the occipital lobe), neonatal-module b (encompassing the temporal lobe and subcortical regions), neonatal-module c (in the frontal area), and neonatal-module d (located at central areas for sensorimotor function, i.e., pre- and post-central gyrus). With development, all modules are gradually reshaped or divided and new modules emerge. Compared to other three modules, the spatial pattern of the neonatal-module a has less change from neonates to one year of age.

At three months of age, the neonatal-module b is divided into two modules: one at subcortical regions and the other covering the temporal area.

At six months of age, the neonatal-module c is divided into medial and lateral parts, with the lateral part further dividing into a larger dorsal module (covering major part of the inferior and middle frontal gyrus) and a smaller ventral module (covering the triangular part of the inferior prefrontal gyrus and the anterior insula). The new medial prefrontal module (i.e., the medial part of the neonatal-module c) further combines with another module in the sub-cortical regions that was separated three months ago.

At nine months of age, the parietal part of the neonatal-module a continues to shrink, and finally incorporates the bilateral superior parietal lobules separated out as a new module. Such changes occur in parallel with shrinking neonatal-module d, with its recessed area occupied by the expending triangular prefrontal/anterior insular module (now covering the whole insula and the ventral part of the central area).

At 12 months of age, the medial prefrontal module that belongs to the neonatal-module c is divided into the anterior and posterior portions, with the posterior part covering subcortical regions, middle cingulate cortex, and supplementary motor area.

In this manner, by one year of age, the number of modules doubles, with eight modules formed: visual module, temporal module, subcortical and middle cingulate module, medial prefrontal module, lateral prefrontal module, ventral central and perisylvian module, dorsal central module, and parietal module. During the first year of development, we find the module generation and splitting roughly follows a general anatomical order that from inferior to superior, from lateral to medial, from subcortical to cortical, from primary to higher-level function-related areas. Anatomically, the development of the lobes roughly follows an (not strict) order of occipital, temporal, parietal and frontal lobes.

With the increasing module quantity, we further find that the mean intra- and inter-modular FC are also both increased (Fig. 3c), but with diverse developmental trajectories. The averaged intra-modular FC has a nonlinear developmental trajectory with the largest enhancement at the first three months, but a much flatter curve thereafter. In contrast, the averaged inter-module FC shows a growth curve with the consistent increasing speed.

3.2. Development of Hubs in Infant Functional Brain Networks

3.3.1. Hub Location and Quantity Changes

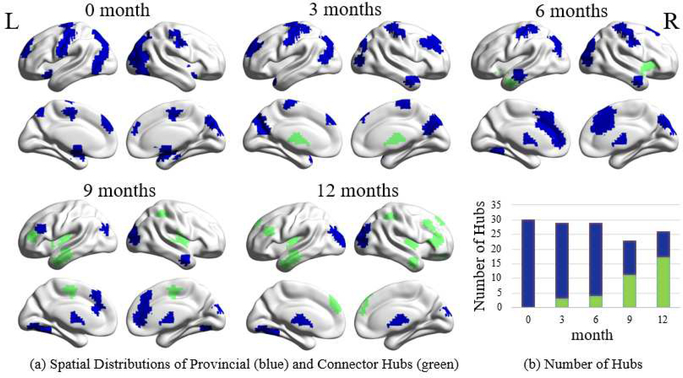
Figure 4a visualizes the spatial distributions of the detected functional hubs (both provincial and connector hubs) for all age groups. The total number of hubs firstly decreases a little bit at nine months of age and increases thereafter (Fig. 4b). Meanwhile, the spatial distribution of hubs is dramatically changed (Fig. 4a). Specifically, for neonate and three months of age, the hubs are mainly located in the sensorimotor, visual areas, and the superior frontal cortex. Starting at the age of six months, the hubs are spatially expanded with a shrinking number at the primary areas and newly emerging hubs, mostly in the cingulate cortex, temporal area and thalamus. After nine months of age, the hubs emerge in the higher cognition-related areas, including the lateral prefrontal areas, insula, posterior superior temporal gyrus, and superior parietal lobules.

Fig. 4.

Developmental changes in spatial distribution and quantity of different types of hubs. (a) Spatial distributions of provincial (blue) and connector hubs (green) in the first postnatal year. (b) The numbers of provincial (blue) and connector hubs (green) at all age groups in the first postnatal year.

Although the total number of hubs does not change a lot, the ratio between the quantity of the provincial hubs and that of the connector hubs gradually decreases (Fig. 4b), with continuously increasing connector hubs and decreasing provincial hubs. From neonate to one year of age, the spatial distribution of the provincial hubs gradually shrinks. In contrast, the connector hubs gradually expand to the temporal (at 6 months of age), frontal (at 9 months of age), and parietal association areas (at 12 months of age). The increasing connector hubs further support increasing mean inter-modular FC (Fig. 3d) and could be related to more integrated functional brain networks.

3.3.2. Hub Connection Property Changes

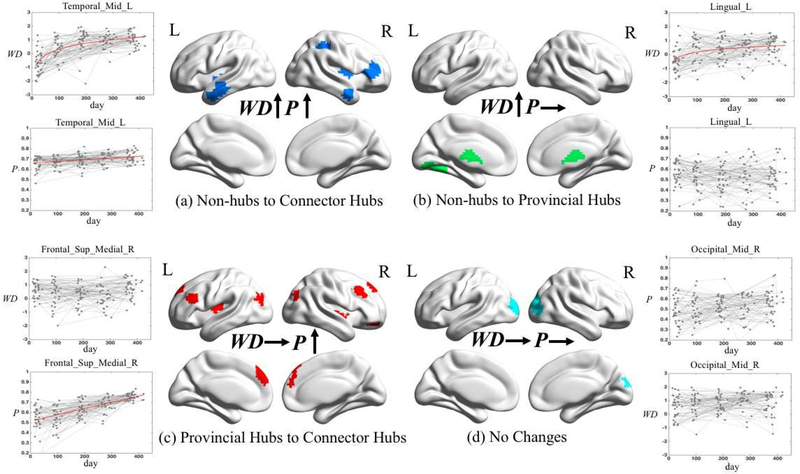
In addition to the above cross-sectional hub detection results, we further measured the longitudinal change of each hub during development by delineating the developmental trajectories of within-module degree (WD) and participation coefficient (P), which are two key properties that characterize hubs regarding to their positions in the network modular topology. Intuitively, one can detect several different scenarios based on WD and P developmental trajectories, each of which may represent a certain type of role transitions of brain regions along development. For example, the ROIs with both significantly increased WD and P are more likely converting from non-hubs to connector hubs because connector hubs generally have high WD and P. The ROIs with significantly increased WD only may gradually convert from non-hubs to provincial hubs because provincial hubs have large WD but small P. For the ROIs with significantly increased P only, they might convert from provincial hubs to connector hubs because connector hubs have high P and WD while the unchanged high WD might suggest that they were the provincial hubs at the beginning. Finally, the ROIs with no significant change in either WD or P could already be provincial hubs or connector hubs in neonates. Based on these intuitive thoughts, we classified the ROIs into four categories: 1) both WD and P are significantly increased (Fig. 5(a)), 2) only WD is significantly increased (Fig. 5(b)), 3) only P is significantly increased (Fig. 5(c)), and 4) both WD and P show no significant changes (Fig. 5(d)). The fitted curves from LMER on four categories are respectively showed in Figs. S7, S8, S9 and S10 in Supplementary Materials.

Fig. 5.

The spatial distributions of hubs with (a) both within-module degree (WD) and participation coefficient (P) significantly increased (p<0.001 FDR corrected); (b) only WD significantly increased (p<0.001 FDR corrected); (c) only P significantly increased (p<0.001 FDR corrected); (d) both WD and P having no significant changes (p<0.001 FDR corrected). For each category, we select one brain region and plot its developmental trajectories of WD and P. Statistically significant increasing curves are fitted with the red lines.

Of all 26 ROIs, eight (31%) have both significantly increased WD and P along growth (the first category), which indicates these nine regions are gaining importance with respect to their within-modular connections and inter-modular connections. With growth in the first year, these regions could become (or have potentials to become) connector hubs, thus are quite important to the brain functional network development. They mainly locate in the anterior middle temporal gyrus and posterior insula of both sides, as well as right inferior frontal areas, right inferior parietal areas, and posterior part of the middle temporal gyrus (Fig. 5a). Interestingly, none of them constitutes any initial hub regions in neonates.

As shown in Fig. 5b, 4 (15%) regions out of all 26 ROIs have a tendency towards growing from non-hub regions into provincial hubs (i.e., with increasing WD but constant P, the second category). They sit in the left lingual, as well as the thalamus and caudate. Of note, all these regions show exponential increases in the WD (i.e., fitting better with a log-linear regression model).

The third category of developing trends consists of the most regions (11, 42%), which shows significant linear growth in P but constant WD. Combing with Fig. 4a, many regions in this category have already been provincial hubs in the neonatal stage, which can also be reflected by a relatively high level of WD developmental curves (larger intercept in Table 2). Therefore, many of these regions are probably transforming from provincial hubs in the earlier months to connector hubs in the later months of the first year of life. The majority of them are located in the frontal association or high-level cognitive function-related areas, some of which are left lateralized, such as Broca’s area. The other regions are located in the occipital association areas (Fig. 5c).

Table 2.

Fitted Developmental Curves of Within-module Degree and Participation Coefficient of Selected Hubs in the First Year of Life

Brain Regions	Within-module Degree						Participation Coefficient
	Model	Intercept	Slope	P (Slope)	AIC (Linear)	AIC (Log-linear)	Model	Intercept	Slope	P (Slope)	AIC (Linear)	AIC (Log-linear)
A. Both within-module degree and participation coefficient significantly increased with age (p<0.001 FDR corrected)
Insula_L	Linear	−0.6777	0.0028	3.89E-06	436.56	4.46E+02	Log-linear	0.5014	0.0458	9.48E-23	−480.74	−491.72
Parietal_Inf_R	Log-linear	−1.0005	0.0058	1.32E-18	399.46	4.35E+02	Linear	0.5943	0.0006	1.74E-32	−427.91	−384.70
Frontal_Mid_R	Log-linear	−0.1109	0.0022	2.26E-05	376.92	3.78E+02	Linear	0.5688	0.0005	1.81E-15	−315.08	−296.85
Frontal_Inf_Tri_R	Linear	−1.3895	0.3310	5.60E-05	408.63	4.08E+02	Linear	0.6176	0.0004	7.69E-12	−337.32	−320.38
Insula_R	Linear	0.0440	0.0022	1.37E-05	382.75	3.93E+02	Linear	0.06385	0.0003	2.34E-19	−459.68	−449.53
Temporal_Mid_R	Linear	−1.0655	0.3646	1.14E-06	347.98	3.43E+02	Linear	0.6500	0.0002	1.20E-07	−455.04	−452.71
Temporal_Inf_L	Linear	−2.3270	0.5727	1.63E-14	396.61	3.65E+02	Linear	0.6580	0.0002	3.14E-06	−446.38	−438.51
Temporal_Mid_L	Log-linear	−2.5666	0.6291	1.47E-20	376.12	3.48E+02	Linear	0.6607	0.0002	1.88E-06	−456.65	−455.74
B. Within-module degree significantly increased with age (p<0.001 FDR corrected)
Caudate Head	Log-linear	−0.5115	0.2412	3.79E-04	347.33	333.97	Linear	0.60151	0.0001	1.02E-02	−300.17	−296.73
Thalamus_L	Log-linear	−0.5618	0.2251	1.03E-04	336.86	333.07	Linear	0.6265	0.0000	9.28E-02	−330.60	−328.81
Lingual_L	Log-linear	−0.3697	0.2078	3.83E-04	361.86	360.47	Linear	0.5318	0.0000	3.74E-01	−198.52	−196.14
Lingual_L	Log-linear	−1.3538	0.3348	1.36E-07	388.86	381.24	Log-linear	0.6051	−0.0130	1.64E-01	−202.60	−205.06
C. Participation coefficient significantly increased with age (p<0.001 FDR corrected)
Insula_R	Linear	0.1248	0.0005	3.78E-01	436.68	437.07	Log-linear	0.5186	0.0426	2.37E-23	−505.88	−526.20
Frontal_Sup_Medial_L	Log-linear	0.2951	0.0974	1.69E-01	373.59	372.32	Linear	0.4932	0.0007	4.37E-20	−310.50	−275.26
Frontal_Sup_Medial_L	Log-linear	1.01948	−0.1050	1.09E-01	392.31	390.67	Linear	0.5169	0.0007	3.38E-24	−356.76	−321.78
Frontal_Mid_R	Log-linear	0.5278	−0.0007	1.22E-01	361.41	363.11	Linear	0.5459	0.0006	2.01E-23	−316.69	−285.33
Frontal_Sup_Medial_R	Log-linear	0.4109	0.0002	6.19E-01	370.72	370.92	Linear	0.5160	0.0006	6.27E-21	−335.44	−302.49
Frontal_Inf_Tri_L	Linear	−0.7318	0.2146	1.59E-03	410.38	407.03	Linear	0.5767	0.0005	6.28E-21	−357.27	−320.15
Frontal_Sup_Orb_R	Linear	−0.3724	0.0016	4.22E-03	413.83	418.21	Linear	0.5982	0.0005	8.54E-16	−345.12	−327.82
Rolandic_Oper_L	Log-linear	0.5917	0.0009	2.79E-02	324.53	325.54	Linear	0.5958	0.0004	1.73E-16	−360.02	−341.34
Occipital_Mid_R	Linear	1.0949	−0.0935	1.72E-01	372.00	371.15	Linear	0.5051	0.0004	2.15E-08	−249.06	−244.81
Occipital_Mid_L	Linear	1.0553	−0.0320	5.92E-01	351.33	351.17	Linear	0.4747	0.0004	1.09E-05	−232.68	−229.48
Pallidum_R	Log-linear	1.2645	−0.1973	3.21E-03	395.1144575	386.0104807	Linear	0.6498	0.0002	7.18E-07	−404.74	−397.96
D. Both within-module degree and participation coefficient had no significant changes with age (p<0.001 FDR corrected)
Occipital_Mid_R	Log-linear	0.2093	0.1180	6.43E-02	352.43	350.21	Linear	0.4760	0.0002	1.16E-03	−217.84	−214.43
Occipital_Sup_R	Log-linear	0.0184	0.1115	8.42E-02	330.32	322.45	Linear	0.5140	0.0001	6.33E-02	−208.04	−206.82
Occipital_Mid_L	Linear	0.1741	0.0018	5.25E-04	384.96	386.63	Linear	0.5046	0.0001	1.61E-01	−176.43	−173.10

Note: The same brain region names in the table represent the different parts of the corresponding brain areas. Statistically significant increase of within-module degree or participation coefficient with age are in bold.

The fourth category only includes three ROIs in the visual areas (Fig. 5d) with non-significant WD or P growth. Considering these two regions are identified as provincial hubs at 12 months of age, they could be acting similarly as provincial hubs in the previous ages and did not change their roles in the brain network during development.

4. Discussion

In this paper, we, for the first time, provide a comprehensive report of the development of functional brain networks in the first postnatal year by investigating two important network measures, i.e., modules and hubs (including provincial and connector hubs). Particularly, we developed a novel algorithm for generating robust, temporally consistent and modular structure-enhanced group-level FC networks for infants’ longitudinal rs-fMRI data. We find during the first year of development, the brain network is gradually subdivided into more modules accompanied by the strengthening intra- and inter-modular connections. Based on the developing modules, hubs are spatiotemporally rewired with connector hubs emerging and increasing, but provincial hubs diminishing and decreasing. All the findings suggest that functional segregation and integration are both enhanced in the first postnatal year. The reorganizations of modules and hubs drive the functional brain networks to become more efficient with both higher intra- and inter-modular information transmission at the low wiring cost. Additionally, the systematic ROI-wise analysis of within-module degree and participation coefficient further characterized different developmental trajectories for brain regions evolved to be provincial or connector hubs.

4.1. Enhanced Functional Segregation and Integration

To the best of our knowledge, this is the first study to characterize the development of the infants’ functional brain networks by detecting modular structures. Previous studies generally adopted seed-based correlations (Gao et al., 2015a) or ICA (Gao et al., 2015b) to detect brain functional systems. However, seed-based correlations limit the study only on a specific functional system, other than multiple functional systems and their interactions as a whole. Although ICA could simultaneously detect multiple functional systems, the results of within-component FC and inter-component FC are not quite straightforward to interpret, and a component-based network-wise FC analysis lose the spatial specificity across ages (Sporns and Betzel, 2016). By building region-wise FC networks and detecting modular structures at each age, we could systematically delineate when and how each functional subsystem develops with large-scale metrics (i.e., modular quantity, intra/inter-modular FC), meso-scale metrics (i.e., single module) and local metrics (i.e., hubs, nodal WD and nodal P).

By investigating modules and hubs of functional brain networks, we found: 1) gradually increasing modular quantity (Fig. 3b), 2) both increasing intra- and inter-modular FC (Fig. 3b), and 3) increasing quantity of connector hubs and decreasing number of provincial hubs (Fig. 4b) in the first postnatal year. The increasing modular quantity and tightening intra-modular connectivity indicate the enhanced functional segregation, and the tightening inter-modular connectivity suggests the increasing functional integration. The increasing number of connector hubs provides additional support to the enhanced functional integration since those regions are mostly responsible for integrating inter-modular information. Although the number of provincial hubs decreases, it is not likely to be an indicator of decreasing functional segregation, due to the globally increased FC, the connections could be less concentrated, making it more challenging to detect hubs. The increasing functional segregation could be due to the improved primary brain functions in the first postnatal year (Courage and Adams, 1990). During this period, the high-level cognitive function-related regions, such as the temporal, frontal, and parietal association regions, also show rapid development (Amsterdam, 1972; Haith et al., 1988; Reznick, 2009), which facilitates the increase of functional integration. The development of these association regions could mirror increasingly prominent functions in the coordination of different functional systems and the integration of different unimodal information (Bertolero et al., 2015).

Comparing our findings with a few previous early brain development studies, we found that increasing functional segregation and integration is still quite controversial. Several previous whole brain and graph-theory-based studies using local efficiency and global efficiency suggested increasing functional segregation and integration in the first two years of life (Gao et al., 2011). While they did not use module-derived metrics as we used, their interpretations are consistent with ours. However, in Gao et al. (2015b), ICA was adopted to extract different brain networks and both intra- and inter-network FC were respectively computed as within-network FC values and between-network synchronization of the component-associated time courses. While they reported increasing intra-network FC for various functional networks, the inter-network FC was observed to be decreasing along ages. The same method was used in another study but led to decreased intra-network FC and increased inter-network FC from 4- to 9-months of age (Damaraju et al., 2014).

It is thus highly needed to have more future studies using different metrics and different networks to comprehensively investigate the developmental trajectories of functional segregation and integration.

4.2. More Efficient Network Information Processing

Brain function has been conceptualized as a balance between modular and integrative processing (Bertolero et al., 2015). In such a theory, each module functions autonomously with strong ability of local information processing. Meanwhile, highly efficient global information communication requires cooperation among different modules, and such cooperation could be mainly mediated by connector hubs that are located between different modules. During development, the functional brain networks are dynamically rewired (van den Heuvel et al., 2015; Cao et al., 2016b), and the modular structure is continuously changing (the quantity of modules is increasing during the infant developmental stage). Due to the fact that building inter-modular (often long-range) connections requires enormous energy consumption, such a rewiring could lead to inter-modular connections concentrated into a small number of brain regions (i.e., connector hubs). This could keep each module function largely autonomous, while facilitating the efficiency of inter-modular information processing at the low wiring cost. Taken together, the reconfiguration of the functional brain networks during development could feature with more efficient information exchange with the increasing number of connector hubs.

4.3. Different Developmental Patterns for Provincial and Connector Hubs

In this study, based on the regional-wise longitudinal analysis of intra- and inter-modular connections, we identified four subtypes of hubs with distinct developmental trajectories. Among four categories, the second category of brain regions with the significant increase in WD (within-modular degree, characterizing intra-modular connections) displayed non-linear (exponential) trajectories (Table 2), with more rapid changes in the earlier months than the later months in the first year of postnatal life. These regions are mainly located at the primary visual areas and thalamus (Fig. 5b). The third category of brain regions with significant increase in P (participation coefficient, characterizing the ability of inter-modular connections) had linear trajectories (Table 2). They are mainly located at frontal areas, high-order motor areas, and higher-order visual areas (Fig. 5c). Such a difference in developmental trajectories reflects the distinct growth rates that provincial hubs gain more connections in the earlier stages, while connector hubs gain connections in whole ages, of the first year of life. Such finding imply that the intra-modular connections may saturate much faster, but the inter-modular connections could have protracted development into later ages.

Combining the first and the third categories (both with P significantly increased), we found that the involved brain regions are mainly located in the temporal association areas and inferior parietal lobules, part of the default mode network (Fig. 5a), as well as regions in frontal task executive control network, and high-order motor/visual areas (Fig. 5c). Such findings suggest hubs in the high-level functional networks could be maturing rapidly, which could help the functional and anatomical maturation of the high-level functional networks in later ages (Cao et al., 2017). These hub regions should be further studied due to their essential roles in the normative and abnormal development of the high-level functions, because the hubs are the most important regions in the network, and any targeted attack on them could lead to major disruption of the network (Gao et al., 2011).

4.4. Module-guided Group-level Network Construction

Our proposed module-guided group-level network construction method addresses two issues in the conventional averaging-based strategy. First, the possible outliers of individual-level FC matrices could exert significant influence on the traditional average-based group-level network, especially for the infant study with severer noise and artifacts (Zhang et al., 2018b). In our method, we determine the group-level FC based on the modular assignment probability (i.e., MPP matrix) calculated across all subjects. Therefore, each subject has the same contribution during the MPP calculation, thereby avoiding the effects of the outliers with extreme FC strength. Second, we use different strategies to determine weights of edges based on the corresponding MPPs (module partition probability) to avoid making group-level FC matrix over-blurred, which is better for the subsequent group-level module and hub detection. The decision of choosing the group-averaging method from max/mean/min pool is based on the useful prior information of node-to-modular assignment probability. In such a way, both individual FC strength and the topological consistency of individual-level modular structure across all subjects are considered to form the group-level FC matrix. This is similar to “robust mean” (Fair et al., 2009; Meunier et al., 2009; Lynall et al., 2010) that derives more robust group means by removing outliers. Our method-derived group-level FC could thus be treated as an augmented, or de-noised result. Whilst useful for other options, such as “robust mean”, our method could be more suitable for the subsequent group-level module detection.

Additionally, the introduction of the MPP in our proposed method helps generate temporally consistent group-level FC networks and longitudinally smooth modular structure changes for the brain functional development studies. According to the MPP matrix, we could improve the temporal consistency of group-level networks across age groups, but do not touch individual FCs.

4.5. Method Robustness Evaluation

Our study has several parameters to be determined. In the group-level network construction, our model introduces four parameters, i.e., a density threshold for sparsifying individual-level networks (thr_i), a parameter δ for controlling “temporal smoothness”, and an upper (thr_h) threshold and a lower (thr_l) threshold for group-level MPP matrix. Additionally, the threshold for sparsifying group-level network (thr_g) and the atlas for brain parcellation may also affect the detected modular structure. In the hub detection, thresholds for within-module degree (thr_WD) and participation coefficient (thr_P) may influence the categorization of provincial and connector hubs. We discuss the effect of each parameter below. Of note, when one parameter was varied, the others were fixed to be the values used in the main experiments.

4.5.1. Density Threshold for Sparsifying Individual-level Networks

The parameter thr_i may affect individual-level module detection and further affect the generated group-level MPP matrices and networks. To evaluate such influences, we changed thr_i from 0.05 to 0.15 in a step of 0.01. At each setting, we constructed a corresponding group-level MPP matrix and compared its cumulative distribution of probability values with the one adopted in our main analysis (i.e., the MPP matrix with thr_i = 0.1) by using Kolmogorov-Smirnov test. As shown in Fig. S11 in Supplementary Materials, most of the thr_i settings led to similar MPP distributions for all age groups (p > 0.05), except very small or very large thr_i settings mainly lying at the start and end of the range (p < 0.05). We further picked thr_i = 0.05 and 0.15 and visualized their corresponding group-level modules of all age groups in Fig. S12 in Supplementary Materials. We found different settings of thr_i generated very similar results regarding the modular structures (Fig. S12a) and the intra-/inter-modular connectivities (Fig. S12b), suggesting that thr_i may have little effect on the results.

4.5.2. Temporal Smoothness Applied to the Group-level MPP Matrix

The parameter δ controls the temporal smoothness of MPP matrices for improvement of the consistency of group-level networks across ages. No golden standard can be found from the previous studies for δ selection. We decide to use temporal smoothness of Q curves as an evaluation index to select δ because the motivation of introducing temporal smoothness is mainly to improve modular consistence across ages. We set δ to multiple values (i.e., 0, 0.5, 1, 1.2, 1.4, 1.5, 1.6, 1.8, and 2) and evaluated the temporal consistency of the networks’ Q values at each setting. As shown in Fig. S13a in Supplementary Materials, with the increase of δ, the modular structure gradually became smoother along development. When δ is smaller than 1.5, the development curves are less smooth, where a large dip at 3 months of age can be spotted, which seems not biologically meaningful. When δ was set to 2, there was an over-smoothed Q curve, which could also be suboptimal. We chose δ = 1.5 because it located at a turning point of the temporal smoothness. We also compared the modular detection results with δ = 0 and 1.5 and found that the introduction of temporal smoothness did not significantly change the modular structure of each age group (Fig. S13b in Supplementary Materials) and also the developmental patterns of intra- and inter-modular connectivities (Fig. S13c in Supplementary Materials), while removed several inconsistent modular affiliations at certain ages and smoothed the developmental trajectories.

4.5.3. Upper and Lower Thresholds for Group-level MPP Matrix

The parameters thr_l and thr_r are lower and upper thresholds for MPP matrices, respectively, which affect the distribution of FC strength in the group-level network. To investigate their effects on the results, we changed thr_l from 0.05 to 0.25 and thr_h from 0.45 to 0.65. For different combinations, we re-generated multiple networks for each age group and compared the detected modular structures with the one generated with thr_l = 0.1 and thr_h = 0.5 in the main result. Normalized mutual information (NMI) and modularity difference were used as evaluation indexes for the comparison.

As shown in Fig. S14 in Supplementary Materials, the changes induced by thr_l and thr_r are quite small at all age groups.

4.5.4. Density Threshold for Sparsifying Group-level Networks

Before group-level module detection, a threshold (thr_g) was used for sparsifying the group-level networks. To investigate its influence on the result, we changed thr_g from 0.05 to 0.15 in the step of 0.01. At each setting, we detected the corresponding modular structure and calculated its similarity to the result in our main analysis (thr_g = 0.1) by using NMI. As shown in Fig. S15 in Supplementary Materials, most of NMI values were greater than 0.8, suggesting high similarities of modular structures between different settings of thr_g. We then picked thr_g = 0.05 and 0.15 and visualized their corresponding group-level modular structures at all age groups and the developmental trajectories of intra- and inter-modular connectivities to make the further comparison with our main results (thr_g = 0.1). We found that the main findings did not change regarding thr_g that 1) the brain network is gradually subdivided into more and more modules from neonates to 1 year of age (Fig. S16a in Supplementary Materials), and 2) both mean intra- and inter-modular connectivies increase with age (Fig. S16b in Supplementary Materials).

4.5.5. Brain Parcellation Scheme

To test whether different brain parcellation schemes could lead to different results, we repeated the analysis with a new brain atlas, which includes 1024 ROIs of the same size obtained by a random parcellation method (Zalesky et al., 2010). After individual-level FC networks were determined by using the new atlas, we adopted the same methods and parameters as described in Sections 2.5 and 2.6 to construct the group-level networks and then detect modular structure for each age group. As shown in Fig. S17 in Supplementary Materials, the modules derived from new atlas were similar to our main results, where the brain functional network is gradually subdivided into an increasing number of functional modules (Figs. S17a and S17b) accompanied by both strengthened intra- and inter-modular connectivities (Fig. S17c).

4.5.6. Thresholds for Determinations of Provincial and Connector Hubs

In the hub detection, thr_WD (influencing the hub determination) and thr_P (influencing the hub classification) have effects on the hub classification. We thus conducted the following experiments to evaluate the influence of setting such thresholds. By fixing thr_P to 0.6 and increasing thr_WD from 0.8 to 1.1 with 0.1 as an increment, we tested the effects of thr_WD on hub assessment. As shown in Fig. S18 in Supplementary Materials, the detected cortical hubs in each age group did not change a lot in spatial distribution or in quantity. All thr_WD settings show similar developmental patterns of hubs. On the other hand, by fixing thr_WD to 1.0 and varying thr_P from 0.50 to 0.65 with a step of 0.05, we investigated the possible influence of thr_P on the categorization of provincial and connector hubs. Despite decreased number of brain regions being classified as connector hubs as thr_P increased, both provincial and connector hubs show similar developmental patterns to the main results (Fig. S19 in Supplementary Materials), i.e., the quantity of connector hubs is increased and the number of provincial hubs is decreased.

4.6. Technical Considerations and Future Works

Several technical considerations should be discussed. First, the large voxel size may worsen the partial volume effect for studies of neonates and infants who have relatively smaller brains. Previous infant studies (Gao et al., 2015a, 2015b) adopted adaptive spatial smoothing that adjusts the Gaussian kernel proportionally to the actual size of the brain to alleviate this issue. An alternative is to improve the spatial resolution of the fMRI data. For example, in an ongoing Baby Connectome Project (BCP)¹, fMRI data was collected with a high spatial resolution (voxel size = 2×2×2 mm³) by using a multiband echo-planar imaging (EPI) sequence (Howell et al., 2018; Zhang et al., 2018a). Second, the smaller and quickly developing brain during infancy poses a great challenge in infant brain fMRI registration for aligning the data at each age to a standard MNI space. If using the conventional registration algorithms, the registration accuracy cannot be guaranteed because a large and varying “distance” exists between a moving image (source) and a fixed image (target). To address this issue, one may choose a set of specified neonate/infant atlases corresponding to different ages instead of using a single adult-based atlas to reduce the distance of images and improve registration quality (Zhang et al., 2018a). An alternative we used is to perform advanced registration with dedicated algorithms that can handle a large variability of brain size and image appearance as used in previous studies (Zhang et al., 2017a, 2017b, 2018b). Third, head motion is another issue for fMRI analysis. It is recommended to evaluate motion quality control (QC) by reporting several benchmarks metrics, including QC-FC correlation, QC-FC distance dependence and the loss of temporal degrees of freedom (tDOF-loss) (Parkes et al., 2018). In addition to providing the QC benchmarks, we also repeated the analysis by using two different thresholds for data scrubbing. The one that we used in our main analysis is FD < 0.5 and DVARS< 0.5% (Figs. 2 and 3), and the results using the other threshold (FD < 0.25 and DVARS < 0.5%) were reported in Supplementary Materials. The similar results of both modules and hubs derived from the two thresholds indicate that our findings are less likely affected by head motion (Figs. S20 and S21). Finally, in this paper, the adopted module detection method limits each node can only be assigned to one module. Such constraint may lead to our resultant functional brain network (i.e., module) showing different spatial configurations with those derived from seed-based correlation or ICA-based method, which allows each node to belong to multiple functional networks. For example, Gao et al. (2015a) found matured default mode network (DMN) at 9 months of age by using a voxel-wise seed-based correlation method, which fails to be detected in our study. Such inconsistent findings may be due to Gao et al., (2015a) assigned posterior DMN (pDMN) (including posterior cingulate cortex and bilateral inferior parietal cortex) to both visual network and DMN, while we only assigned it to the visual module. In future, we could use a certain algorithm that can detect modules with overlapping brain regions (Wen et al., 2016).

5. Conclusions

In this study, we provided the first comprehensive report of the early development of large-scale functional brain networks at a fine temporal scale (every three months). We proposed a novel modular information-guided method to combine individual-level FC networks to form a robust, temporally consistent, and modular structure-enhanced group-level network at each age. We found that the functional brain networks were gradually subdivided with strengthening intra- and inter-modular connectivities, indicating the enhancement of functional segregation and integration in the first postnatal year. Meanwhile, the rewiring could drive the hubs to be more and more spatially uniform, with increasing connector hubs and increasing intra- and/or inter-modular FCs, towards more efficient information exchanges. These findings unravel detailed spatiotemporal changes of large-scale functional brain networks, which paves a road for the future works for better understanding of infant brain development.