Brain Active Trans-Membrane Water Cycling Measured by MR Is Associated with Neuronal Activity

Abstract

Purpose:

Functional magnetic resonance imaging (fMRI) is widely used to study brain activity. Unfortunately, conventional fMRI methods assess neuronal activity only indirectly, through hemodynamic coupling. Here, we show that active, steady-state transmembrane water cycling (AWC) could serve as a basis for a potential fMRI mechanism for direct neuronal activity detection.

Methods:

AWC and neuronal actitivity in rat organotypic cortical cultures were simultaneously measured with a hybrid MR-fluorescence system. Perfusion with a paramagnetic MRI contrast agent, Gadoteridol, allows NMR determination of the kinetics of transcytolemmal water exchange. Changes in intracellular calcium concentration, [Ca_i²⁺] were used as a proxy of neuronal activity and were monitored by fluorescence imaging.

Results:

When we alter neuronal activity by titrating with extracellular [K⁺] near the normal value, we see an AWC response resembling Na⁺-K⁺-ATPase (NKA) Michaelis-Menten behavior. When we treat with the voltage-gated sodium channel inhibitor, or with an excitatory postsynaptic inhibitor cocktail we see AWC decrease by up to 71%. AWC was found also to be positively correlated with the basal level of spontaneous activity, which varies in different cultures.

Conclusions:

These results suggest that AWC is associated with neuronal activity and NKA activity as a major contributor in coupling AWC to neuronal activity. Though AWC comprises steady-state, homeostatic transmembrane water exchange, our analysis also yields a simultaneous measure of the average cell volume, which reports any, slower net transmembrane water transport.

Introduction

Functional magnetic resonance imaging (fMRI) has been widely used in the cognitive neurosciences since its discovery in the 1990s (1–3). The most common fMRI method, Blood Oxygenation-Level Dependent (BOLD) MRI, assesses neuronal activity indirectly, using brain hemodynamic changes as a proxy for metabolic activity (4). Furthermore, the generally assumed hemodynamic dominance in conventional fMRI limits both its spatial and temporal resolution (5,6). Alternate fMRI methods that detect neuronal activity more directly are needed to overcome confounds in BOLD fMRI measurements and to improve their spatial and temporal resolution. Alternative to BOLD fMRI have been proposed (7,8): most notable are functional diffusion MRI (9), detection of neuronal electromagnetic fields (10), and molecular imaging of neural metabolites or signaling species (11). However, there has been considerable debate about the sensitivity and specificity of the first two methods in their ability to directly detect neuronal activity (12–14), while the molecular imaging methods suffer from the need to inject contrast agents (CA) capable of crossing the blood-brain barrier (15). None of these newer fMRI methods is currently deemed superior to conventional BOLD-based fMRI. Accordingly, progress in this area would improve our understanding of normal brain function and, in a clinical setting, would advance the study of normal and abnormal brain function, or surgical outcomes.

Here we propose active water cycling (AWC) as a novel mechanism with potential to directly monitor neuronal metabolic activity. AWC is a physiological process measurable by water proton (¹H₂O) MRI in vivo (16,17). Unlike the slow water net influx or efflux (on the time scale of seconds or minutes) during cell swelling or shrinking in response, respectively, to an osmotic gradient (18), the steady-state water exchange across the cell membrane is a much faster process (on the time scale of milliseconds), and may have a different molecular mechanism (19). Recent studies demonstrate fast transcytolemmal water exchange exists in both neurons and astrocytes (20,21). In general, homeostatic transcytolemmal water exchange has long been thought to be a passive, diffusion-dominated process. More recently, however, it has been suggested that there is an additional contribution from an AWC process, schematized in (Figure 1), (16,17,20,22) which is present in both neurons and astrocytes, as abbreviated in (Figure 2 and Table 1) (20,21). AWC is largely driven by cell plasma membrane Na⁺-K⁺-ATPase pump (NKA) ion cycling activity via an obligate, concomitant trans-membrane water transport that employs secondary active water co-transporters (I and IV in Fig. 1, left), such as the Na⁺-K⁺-Cl⁻ cotransporter (NKCC) and the sodium-dependent glucose cotransporter (SGLT) (16,17,20,23,24). A review of potential water co-transporters is found in (24) and, by definition, these water co-transporter kinetics are rate-limited by NKA activity. In fact, our recent studies suggest that this NKA-driven component of AWC might account for half of the homeostatic basal trans-membrane water exchange in brain tissue (20). This paper focuses on the steady-state AWC phenomenon. However, our analysis also yields a simultaneous measure of the intracellular water mole fraction. This is proportional to the mean cell volume, and reflects the slower net water in- or efflux. Some invasive optical techniques may measure such changes during neuronal activity (25–27). Although aquaporin (AQP) alone is passive, it has been found to sometimes co-localize with other membrane transporters, such as NKA (28). This might, for example, enable an NKA/AQP complex to function as an active water co-transporter, though this has not been proven.

Figure 1.

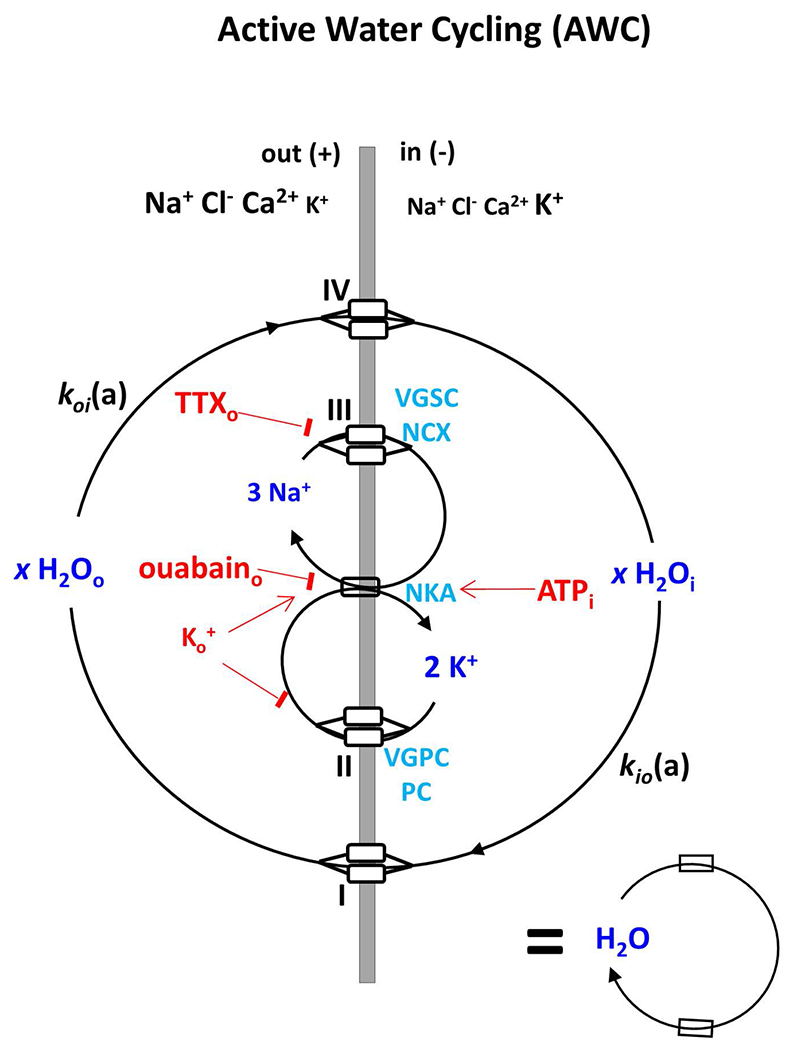
A cartoon illustrating the active water cycling (AWC) system as a Na⁺-K⁺-ATPase pump (NKA) driven process, adapted from (20). k_io(a) and k_oi(a) are the active steady-state cellular water efflux and influx rate constant, respectively. I and IV represent secondary active water co-transporters for water to exit and enter cells (out, + potential; in, − potential), respectively. II and III are transporters for K⁺ to re-exit and Na⁺ to re-enter exit the cell, respectively. In this work, we find III to almost certainly include voltage-gated sodium channels (VGSC), and II voltage-gated potassium channels (VGPC), and potassium channels (PC) in neurons. Extracellular ouabain is a specific NKA inhibitor. Note, the simplified AWC system symbol at the bottom right is used in Figure 2. AWC perturbations employed in this study are indicated in red.

Figure 2.

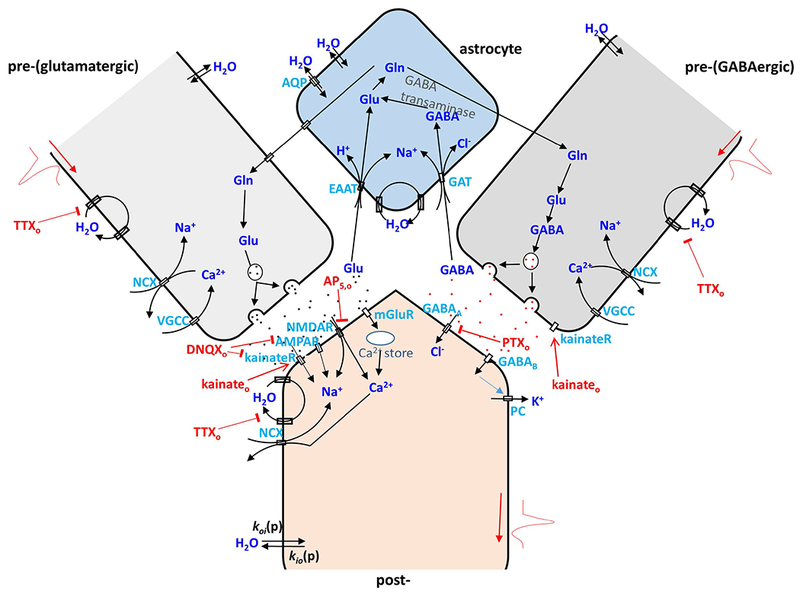
A cartoon illustrating cycling pathways for water, ions and neurotransmitters in a glutamatergic (left) and a GABAergic (right) pre- and post-synaptic neuron pair with an associated astrocyte. In pre-synaptic glutamatergic and GABAergic neurons, action potentials involve serial Na⁺ influx, K⁺ efflux, and Ca²⁺ influx via VGSC, VGPC, and voltage-gated calcium channels (VGCC). After release of pre-synaptic vesicular glutamate (Glu), it binds to post-synaptic ionotropic glutamate receptors (kainateR, AMPAR, NMDAR) or metabotropic glutamate receptors (mGlu), which trigger subsequent Na⁺ and Ca²⁺ influx or Ca²⁺ release from intracellular storage. In contrast, GABA binding leads to a post-synaptic Cl⁻ influx and K⁺ efflux. Glu and GABA are recycled through astrocyte membrane glutamate transports (EAAT) and GABA transporters (GAT) utilizing a Na⁺ gradient via an intermediate glutamine (Gln) step. NKA is the essential enzyme to restore ion gradients in all the processes mentioned above and in all cell compartments. In addition, passive, diffusion-driven components (k_io(p) and k_oi(p)) for water crossing all cell compartment membranes are present (20). As in Fig. 1, AWC perturbations employed in this study are indicated in red. They include extracellular: K⁺ (K_o⁺), TTX_o, DNQX_o plus AP_5,o, kainate_o, PTX_o, and ouabain_o (in (20)). This cartoon is inspired by (60). The abbreviations, definitions and actions of the drugs used are given in Table 1.

Table 1.

Abbreviations for agents, symbols, and acronyms.

Agents and Expected Effects
agent	name / molecular interaction / expected effect
AP5	(2R)-amino-5-phosphonovaleric acid / glutamate receptors (NMDA receptors) antagonist / reduce postsynaptic excitation activity and spontaneous neuronal firing rate
DNQX	6,7-dinitroquinoxaline-2,3-dione / glutamate receptors (kainate and AMPA receptors) antagonist / reduce postsynaptic excitation activity and spontaneous neuronal firing rate
[Ko+]	extracellular K+ concentration / NKA substrate, PC product / alter NKA and PC kinetics and neuronal spontaneous activity: at low [Ko+] values, < ~ 10 mM, spontaneous neuronal firing rate increase with increasing [Ko+]; at high [Ko+] values, induce prolonged depolarization and decrease spontaneous neuronal firing rate
kainate	neurotransmitter amino acid agonist / enhance glutamate receptor function and increase postsynaptic excitation activity [kainateo] = 1 μM / increase spontaneous neuronal firing rate but decrease neuronal firing synchronization [kainateo] = 100 μM / induce prolonged depolarization with spontaneous neuronal firing suppression
PH	Gadoteridol (ProHance) / extracellular T1 contrast agent (CA) / reduce extracellular water magnetization T1
PTX	picrotoxin (picrotoxinin/picrotin mixture) / GABAA receptor antagonists / reduce postsynaptic inhibition activity, decrease spontaneous neuronal firing rate but increase its synchronization
TTX	tetrodotoxin / voltage-gated sodium channel (VGSC) inhibitor / reduce Na+ influx, and then reduce the neuronal action potential generation and spontaneous neuronal firing rate
Symbols and Acronyms
2SX	two-site-exchange
AWC	active water cycling
[H2Oi]	intracellular water concentration
A	mean cell surface area
ACSF	artificial cerebrospinal fluid
AMPAR	AMPA receptor
CA	contrast agent
cMRNKA	cellular metabolic rate of NKA
EAAT	excitatory amino acid transporter
F	fluorescence signal intensity of the entire tissue
GABAA	ionotropic GABA receptor
GABAB	metabotropic GABA receptor
GAT	GABA transporter
Glu	glutamate
kainateR	kainate receptor
kio	steady-state cellular water efflux rate constant
kio(a)	active kio contribution
kio(p)	passive kio contribution
KM	Michaelis constant in Michaelis–Menten Model
koi	steady-state cellular water influx rate constant
koi(a)	active koi contribution
koi(p)	passive koi contribution
M-M	Michaelis–Menten
mGlu	metabotropic glutamate receptor
MRgly	metabolic rate of oxidative glycolysis
MRO2	O2 uptake rate
MRoxphos	metabolic rate of oxidative phosphorylation
n	number of measurements
NKA	Na+-K+-ATPase
NMDAR	NMDA receptor
OCC	organotypic cortical culture
PC	potassium channel
pi	intracellular water mole fraction
PW(p)	passive membrane water permeability coefficient
R1	longitudinal relaxation rate constant
SR	saturation recovery
V	the average cell volume
VGCC	voltage-gated calcium channels
VGPC	voltage-gated potassium channel
VGSC	voltage-gated sodium channel
x	water stoichiometric coefficient of NKA activity

It is well established that neuronal activity is a metabolically demanding process that involves both ion and neurotransmitter transport and recycling, which consume as much as 40% to 50% of the total energetic budget of the central nervous system (29,30). Studies have demonstrated a direct coupling between neuronal and metabolic activity in the brain (29,31,32). Specifically, Na⁺, K⁺, Cl⁻, Ca²⁺ and other key ions must be maintained in non-equilibrium concentration gradients across the plasma membrane for neurons to initiate action potentials followed by synaptic transmission (Fig. 2). The key protein involved in the maintenance and restoration of these steady-state ion concentration differences is NKA—the master driver of the cell membrane (33). Moreover, the glutamate transporter, which recycles the brain’s main excitatory neurotransmitter, is coupled to and regulated by NKA activity: the two transporters appear to form a membrane inter-protein complex (34). The central role of NKA in action potential firing and excitatory synaptic transmission points to NKA activity as a potentially less confounded fMRI biomarker, if there is a MR way to measure NKA activity.

Here we demonstrate AWC positively correlates with neuronal activity, suggesting that AWC could provide a direct physical indicator or measure of neuronal activity. This feature was found with the spontaneous neuronal activity of organotypic cortical cultures under basal conditions, and by using bath application of small molecules known to change neuronal activity (indicated in red on Fig. 2; as activators (arrowheads) or inhibitors (flatheads)). Since these cultures do not have a vascular systems, there are no confounds from drug extravasation kinetics or potential hemodynamic and respiratory complications commoly encountered in vivo. We simultaneously measured AWC and neuronal actitivity changes, respectively, with a tandem MR-optical imaging system capable of simultanous ¹H MR acquisition and intracellular Ca²⁺ fluorescence imaging on the whole rat organotypic cortical culture (OCC)— a live brain cortical tissue model (35). This setup was well described in (20) and allows us to directly correlate changes in neuronal activity with AWC. To demonstrate the NKA contribution to this AWC/neuronal activity coupling, small molecule perturbations known to directly affect NKA activity were also performed here, as well as literature results summarized (Table 1 and Fig. 2).

Methods

Organotypic cortical cultures

Organotypic brain tissue cultures were prepared from acute coronal somatosensory cortex slices of newborn rats (postnatal day 1–3, Sprague Dawley), with a protocol approved by the National Institute of Mental Health Animal Care and Use Committee. For each study, two acute slices (350 μm thickness each) were attached to a #1 coverslip by using a plasma-thrombin mixture, submerged in culture medium and incubated at 35.0 (± 0.5) °C. Cultures were grown for 12 to 20 days before being used in experiments (for details see (36,37)). The cultures were incubated with 50 μM Oregon Green 488 BAPTA-1 (OGB; Life Technologies, NY, USA) for 1–2 hrs before the experiments were performed.

Simultaneous measurement of water cycling kinetics and neuronal activity

The measurement was achieved by using a hybrid optical-MR system that enables simultaneous fluorescence imaging and MR measurements. Details of the setup are provided in (20,35) and briefly described as follows. It combines a single-sided NMR system and a wide-field fluorescence microscope with an objective lens having a long working distance. Transcytolemmal water cycling and water compartmentation were measured by longitudinal MR relaxometry with an extracellular gadolinium-based MR relaxation contrast agent (CA), Gadoteridol (ProHance (PH), Bracco Diagnostics, Princeton, NJ, USA). The CA was used to distinguish intracellular and extracellular water magnetization signals by increasing the extracellular water resonance’s longitudinal relaxation rate constant (R₁). A saturation-recovery (SR) MR sequence with 21 recovery times (t₁) was used to measure exchange-modified ¹H₂O R₁ values at a single CA concentration (5.0 mM) in the perfusing medium. Because [CA] was constant and there was no tissue vasculature, there are no complications from CA pharmacokinetics (20). A two-site-exchange [2SX] model was used to determine the homeostatic cellular water efflux rate constant (k_io) and the sample intracellular water mole fraction (p_i), which is related to the average cell volume (V). Details on the experimental setup and model fitting have been reported (20).

Neuronal activity was monitored with intracellular calcium fluorescence imaging, simultaneously acquired with MR measurements. A GFP fluorescence filter unit (Olympus America Inc., USA) and a color CCD camera (ProgRes^® CF scan, Jenoptik, Inc., Germany) were used to acquire the real-time fluorescence images with 1 × magnification, (8.8 × 6.6) mm² field of view, 680 × 512 pixels, exposure of 100 ms, at 10 frames per second. The percentage change in the normalized, temporal integral of the fluorescence signal intensity (F) of the entire tissue, ∆F/F₀ (%), was used as a measure of neuronal activity. Detailed fluorescence signal processing is provided below and in (35).

Experimental protocol

In these experiments, the OCC was maintained in an environmental chamber with constant and slow perfusion (30 mL/h) of oxygenated (95% O₂ + 5% CO₂) artificial cerebrospinal fluid (ACSF, 124 mM NaCl, 3.5 mM KCl, 10 mM glucose, 26.2 mM NaHCO₃, 0.3 mM NaH₂PO₄, 1.2 mM CaCl₂ and 1 mM MgSO₄). The perfusing media temperature was kept constant at 34.0 (± 1.0) ^°C. A total of 172 OCC samples were scanned, but 40 OCC samples were abandoned due to their low cellularity (p_i < 0.04) in the basal condition (i.e., before perturbation).

The CA PH, with or without other small molecules known to modulate neuronal activity, was added directly to the perfusing medium with the NaCl concentration adjusted to maintain constant ACSF osmolality. In all experiments, [PH] was maintained at 5 mM. The general experimental protocol for adding neuro-active drugs (AP₅ plus DNQX, TTX, KCl, kainate, and PTX, Table 1) was as follows: (1) the basal condition was established, with two SR NMR acquisitions (scan time ~26 min); (2) switch to ACSF containing neuro-active drug and wait for ~13min; (3) two SR NMR acquisitions, for the “perturbed” condition; (4) switch back to normal ACSF and wait for ~13 min; (5) two SR NMR acquisitions, for the “wash out” condition. Throughout these perturbations, calcium fluorescence imaging was simultaneously performed to assess real-time neuronal activity and the effects of each neuro-active drug. In each condition, the two SR acquisitions were averaged to improve the SNR.

Active and passive water cycling

As shown in Fig. 1, k_io has two components:

$$k_{\mathit{io}}=k_{\mathit{io}}(\text{a})+k_{\mathit{io}}(\text{p})$$ (1)

which can be elaborated from first principles of chemical kinetics

$$k_{\mathit{io}}=\{x∕([{\text{H}}_2{\text{O}}_i]\cdot \langle V\rangle ){\}}^{\text{c}}{\text{MR}}_{\text{NKA}}+\langle A∕V\rangle \cdot P_{\text{w}}(\text{p})$$ (2)

The first term represents the active, NKA-driven component (k_io(a)), and the second term represents the passive, diffusion-driven component (k_io(p)). The active rate constant depends on the cellular metabolic rate of NKA, ^cMR_NKA (e.g., fmol(ATP)/s/cell), and the water stoichiometric coefficient, x. The x value is 500 to 1000 per co-transporter (I, IV in Fig. 1) involved (24), and is estimated near 5000 H₂O/ATP in brain gray matter (17,23). [H₂O_i] is the intracellular water concentration and should be constant (conventional wisdom is that V changes to maintain [H₂O_i]). The passive rate constant depends on the mean cell surface area/volume ratio, 〈A/V〉, and the passive membrane water permeability coefficient, P_W(p) (16,17,22).

Calcium fluorescence signal processing

For each sample, the raw fluorescence intensity from a tissue-free background region [F_back] was subtracted from that of the entire tissue within the chamber [F_tis] to overcome potential excitation light intensity changes, as follows: F = F_tis – F_back. Then we subtracted the averaged F during the inter-spike baseline periods, F_0, from F to overcome fluorescence photo-bleaching effects, as follows:

$$\Delta F∕F_0=(F-F_0)∕F_0$$ (3)

Michaelis–Menten (M-M) model

The k_io data as [K_o⁺] were varied from 1 to 6.25 mM and further fitted with the Michaelis–Menten (M-M) model, by using three independent parameters:

$$k_{\mathit{io}}=k_{\mathit{io}}(\text{a})+k_{\mathit{io}}(\text{p})=k_{\mathit{io}}(\text{a}{)}_{\text{max}}\frac{[K_o^{+}]}{[K_o^{+}]+K_{\text{M}}}+k_{\mathit{io}}(\text{p})$$ (4)

the maximum k_io(a), k_io(a)_max; the constant k_io(p); and the Michaelis constant, K_M. Non-negative constraints were set for the three parameters within the non-linear least square model fitting paradigm. The M-M fitting (shown in Fig. 2C, middle) returned: k_io(a)_max = 4.5 (±1.6) s⁻¹, k_io(p) = 0 (±0.8) s⁻¹, and K_M = 4.5 (±6.1) mM.

Statistics

Paired Student’s t tests were performed between the “perturbed” conditions and the basal conditions. In all experiments, the sample mean value was calculated with a trimmed mean (10% at each side was discarded) to reduce potential bias from outliers. In the (extracellular potassium and kainate) concentration dependence experiments, the results were further scaled by their corresponding group basal values (n = 132).

Results

Extracellular potassium concentration, [K_o⁺], dependence

Under normal conditions, cultures exhibited brief (0.5 – 3 s) and irregular periods of spontaneous neuronal excitation separated by longer ~10 s periods of low activity (Figure 3A) as reported previously (38). Titrating with K_o⁺ over the normal concentration range (up to 6.3 mM), <∆F/F₀>_n, the sample-averaged calcium fluorescence signal percent change, was found to increase linearly with [K_o⁺] (R = 0.99; Fig. 3B). This reflects both greater event amplitude and frequency (Fig. 3A). However, 〈k_io〉_n shows a hyperbolic [K_o⁺]-dependence (Fig. 3C) in this range. The change in k_io for [K_o⁺] between 1 and 6.3 mM is well described by a Michaelis-Menten (M-M) equation (red, in Fig. 3C) with Michaelis constant, K_M = 4.5 mM, and k_io(a)_max = 4.5 s⁻¹. When [K_o⁺] is increased well above the physiological range, to 30 mM, neuronal firing quenching and calcium influx is observed (Fig. 3A). There is also a non-significant ~35% k_io decrease (Fig. 3C). The results in Fig. 3C bear a remarkable similarity with the [K_o⁺]-dependence of O₂ uptake reported for isolated rat brain synaptosomes, Fig. 3E (Fig. 1A from (29)). The latter was an early study of NKA activity in ex vivo tissue. This agreement, and the M-M parameters themselves, provide strong support that k_io changes at normal [K_o⁺] values reflect NKA activity being influenced by K_o⁺ in its role as NKA substrate. Thus, it has an arrowhead in Fig. 1. However, at [K_o⁺] = 30 mM (n = 8), there is a significant 67% p_i increase (Fig. 3D). The latter surely reflects a V increase (see Discussion). At this high concentration, K_o⁺ likely decreases K⁺ efflux through the potassium channel (PC) [hypo-polarization]. The fact that k_io decreases suggests that, in neurons, PC is one of the II transporters in Fig. 1. Thus, K_o⁺ is also given a flathead in Fig. 1: it has two roles; NKA substrate, and PC inhibitor.

Figure 3.

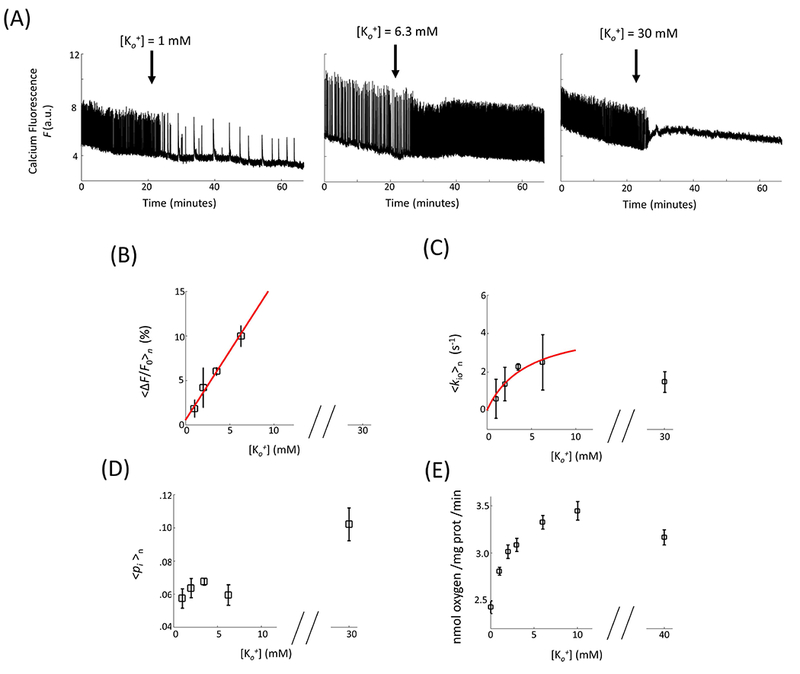
[K_o⁺]-dependences. (A) Representative neuronal activity in OCC in response to change (arrow) in [K_o⁺] from 3.5 mM to 1 mM (left), 6.3 mM (middle), and 30 mM (right). (B - D) The statistical results of mean neuronal activity (B), cellular water efflux rate constant (C), and intracellular water mole fraction (D) as a function of [K_o⁺] (n = 12, 8, 132, 12, and 8 for [K_o⁺] = 1, 2, 3.5, 6.3, and 30 mM, respectively). (ΔF is the temporal F integral in a 30 s moving time window. F₀ is the baseline fluorescence signal between neuronal activity events. 〈〉_n indicates sample mean.) The red, continuous lines result from linear regression (B) and Michaelis–Menten [M-M] model (C) fittings. The M-M fitting is elaborated in Methods and the parameter values given in the text. (E) is literature (29) data for O₂ consumption in isolated rat brain synaptosomes. The points represent means (± standard error of the mean).

The mismatch between the linear <∆F/F₀>_n increase (Fig. 3B) and hyperbolic 〈k_io〉_n increase (Fig. 3C) and O₂ uptake (Fig. 3E) with low [K_o⁺] is intriguing. We will consider this further in the Discussion section.

Blocking neuronal action potential firing with extracellular TTX significantly decreases AWC

The low [K_o⁺] results above add to the evidence that direct NKA perturbations affect k_io(a) (16,17,20). The high [K_o⁺] result begins to suggest perturbations of other transporters necessarily coupled to NKA can also affect k_io(a). Our hypothesis is that AWC [k_io(a)] is sensitive to neuronal spiking activity. Thus, we applied a perturbation known to affect a transporter essential to actuation of the spikes. The voltage-gated sodium channel (VGSC) was blocked by adding extracellular tetrodotoxin (TTX_o, 0.2 μM), a specific inhibitor, to the perfusing medium. In Figure 4A, full suppression of spontaneous neuronal activity is observed during TTX perfusion followed by recovery, at a somewhat reduced frequency, during washout with normal ACSF. Averaged over 13 samples, <∆F/F₀>_n was reduced from 4.9 (±2.87) % to 0.6 (±0.6) % (p = 3 x 10⁻⁵) (Fig. 4B, left), 〈k_io〉_n was significantly reduced by 63%, from 2.05 (± 1.67) s⁻¹ to 0.75 (± 1.13) s⁻¹ (p = 0.03), concomitant with a 〈p_i〉_n reduction from 0.070 (± 0.018) to 0.057 (± 0.015) (p = 8 × 10⁻⁴) (Fig. 4B). As implied in the high [K_o⁺] interpretation above, the 〈p_i〉_n decrease suggests a k_io(p) increase (more on this below). Thus, it is most likely that k_io(a) is decreased by even more than 63% during TTX_o application (as required by Eq. 1). The fact that k_io decreases with TTX_o suggests that, in neurons, VGSC is one of the III transporters in Fig. 1. Thus, TTX_o is given a flathead in Fig. 1

Figure 4.

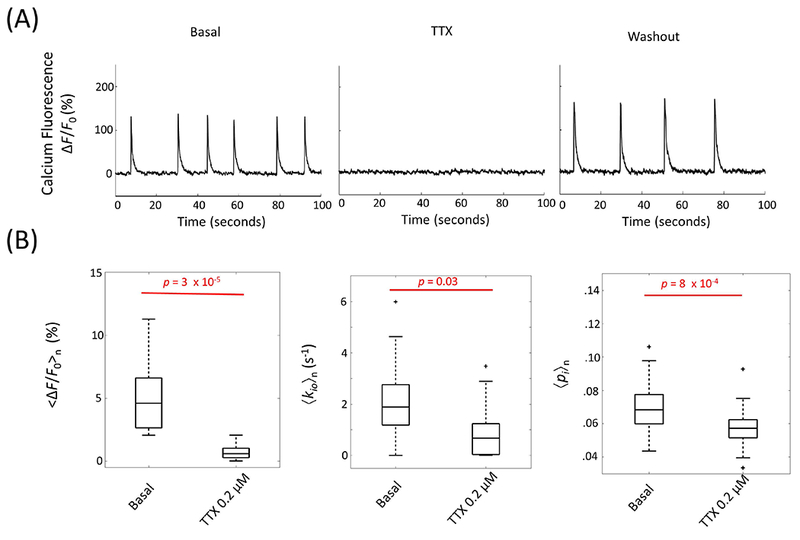
Blocking neuronal spike activity with extracellular TTX_o (0.2 μM) reduces AWC. (A) Time courses of representative continuous population calcium fluorescence signal before TTX perfusion, during TTX perfusion, and during washout with normal ACSF. (B) Significant decreases in mean neuronal activity (left), cellular water efflux rate constant k_io (middle), and intracellular water mole fraction p_i (right) in the presence of TTX_o (n = 13). In the boxplots, box edges represent 25^th and 75^th percentiles, the middle line is the median, and whisker length is 1.5 times the box length.

Blocking post-synaptic glutamate receptors significantly slows AWC

Figure 5A shows transient bath-application of extracellular glutamate receptor antagonists (10 μM 6,7-dinitroquinoxaline-2,3-dione (DNQX_o) and 50 μM (2R)-amino-5-phosphonovaleric acid (AP_5,o)) reduced the spontaneous activity, followed by a rebound upon washout with normal ACSF. Accordingly, the time- and sample-averaged fluorescent signal, <∆F/F₀>_n, was reduced from 5.2 (± 3.4) % to 0.4 (± 0.6) % (p = 8 × 10⁻⁴, n = 10 cultures), and fully recovered to 5.3 (± 3.5) % (n = 7, p = 0.8) after 13-min washout (Fig. 5B, left). Importantly, a concomitant 71% decrease in sample mean k_io, 〈k_io〉_n, [2.19 (± 0.96) s⁻¹ to 0.64 (± 1.39) s⁻¹; n = 10, p = 8 × 10⁻³], which partially recovered to 1.37 (± 1.65) s⁻¹ (n = 7, p = 0.27) following washout, was observed (Fig. 5B,center). Similarly, the sample mean p_i, 〈p_i〉_n, decreased from 0.082 (± 0.031) to 0.064 (± 0.019) (n = 10, p = 6 × 10⁻³) and recovered to 0.089 (± 0.036) (n = 7, p = 0.5) (Fig. 5B, right). The k_io(p) term has an inverse dependence on cell volume [proportional to p_i] by theory (Eq. 2), which suggests k_io(p) increases with DNQX_o and AP_5,o. Thus, it is likely that k_io(a) decreases by even more than 71% during post-synaptic glutamate receptor blockage.

Figure 5.

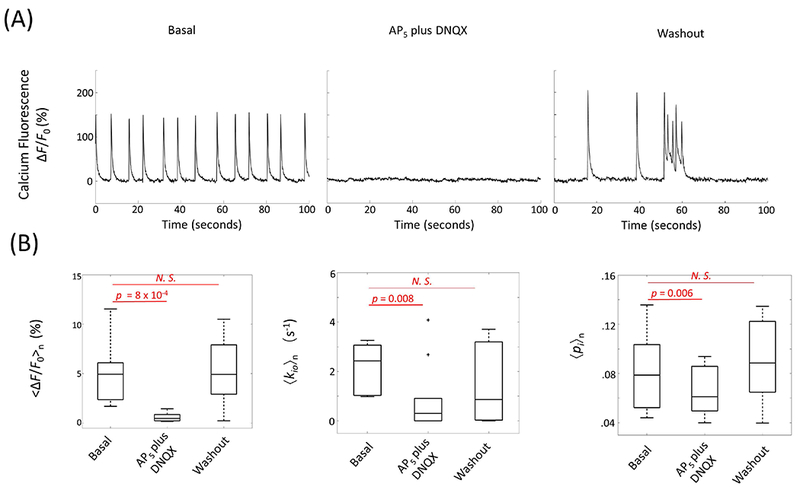
Bath-application of extracellular ionotropic glutamate receptor antagonists blocks spontaneous neuronal activity and decreases AWC. (A) Spontaneous neuronal excitation (basal) is blocked by 10 μM DNQX_o plus 50 μM AP_5,o, and recovers after washout. Time-courses of representative continuous population calcium fluorescence signals in response to AP₅ plus DNQX and washout with normal ACSF. (B) Significant decreases in mean fluorescent activity <∆F/F₀>_n, (left), mean cellular water efflux rate constant 〈k_io〉_n (middle), and intracellular water mole fraction 〈p_i〉_n (right) when spontaneous activity is blocked. Basal (n = 10), AP₅ plus DNQX perfusion (n = 10), and washout with normal ACSF (n = 7). In the boxplots, box edges represent 25^th and 75^th percentiles, the middle line is the median, and whisker length is 1.5 times the box length. N. S. represents non-significant with p ≥ 0.05.

Correlation of k_io and neuronal activity in the basal condition

Given the intriguing correlations between AWC and neuronal activity during the direct and indirect NKA perturbations reported above, it is natural to inquire whether a quantitative correlation exists between k_io and our direct neuronal activity measure even without perturbation – under basal conditions. As shown in Figure 6A, considerable spontaneous neuronal activity variability is observed in the basal condition, due to neuronal excitability, network formation, cell population, or other variations across samples. Some OCCs exhibited high neuronal population activity with larger amplitude and higher frequency responses, while others showed low neuronal population activity with smaller amplitudes and lower frequencies. Here, 132 OCCs were measured, and the time-averaged <∆F/F₀>_t in each OCC varied from 0.5% to 19.5% (only one OCC lay outside this range) with the mean (± one standard deviation) equal to 6.0 (± 5.2)%. Effort was expended to correct for potential F variations from photo bleaching, dye loading efficiency, etc. (see Methods). A hyperbolic dependence of the time-averaged, cellular water efflux rate constant, <k_io>_t on the time-averaged fluorescence change <∆F/F₀>_t is seen (Fig. 6B). The overall correlation coefficient, R, is positive, 0.23 (p = 0.007) with Pearson’s linear correlation, and 0.18 (p = 0.003) with Spearman’s rank correlation test. Interestingly, Pearson’s R can be as large as 0.43 (p = 0.006) if we include only the OCCs with <∆F/F₀>_t less than 3.2%. No significant correlations were found between <p_i>_t and <∆F/F₀>_t (Pearson p = 0.41 and Spearman p = 0.13) (Fig. 6C) or <k_io>_t and <p_i>_t (Pearson p = 0.12 and Spearman p = 0.09) (Fig. 6D). The latter indicates the Fig. 6B <k_io>_t dependence on <∆F/F₀>_t is not from cell density (ρ, to which p_i is proportional) but must almost certainly arise from the neuronal activity variations. It is important to note that, averaged over a myriad of neuronal events, there is no significant change in p_i (Fig. 6C), and thus no significant change in the average cell volume, V, in the sample [see Discussion Section].

Figure 6.

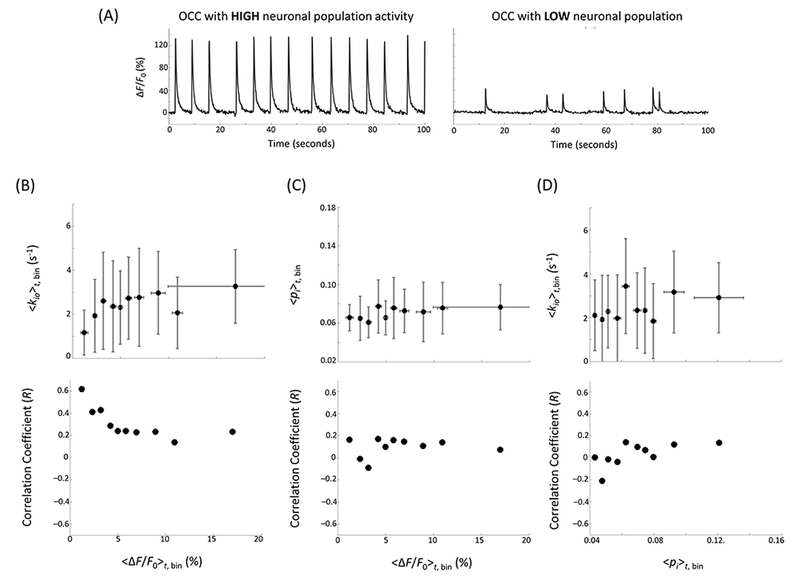
(A) Representative OCC calcium fluorescence percentage signal changes with high (left) and low (right) basal neuronal population activity, i.e., during normal ACSF perfusion. (B - D), Upper: mean (± 1 standard deviation) bin-averaged, time-averaged: (B) <k_io>_t,bin vs. <∆F/F₀>_t,bin, (C) <p_i>_t,bin vs. <∆F/F₀>_t,bin, and (D) <k_io>_t,bin vs. <p_i>_t,bin. Ten bins were created on the <ΔF/F₀ >_t axis (B, C) and <p_i >_t axis (D), with 13 consecutive OCCs in each bin (15 in the last). Lower: correlation coefficient between: (B) 〈k_io〉_t and 〈∆F/F₀〉_t, (C) 〈p_i〉_t and 〈∆F/F₀〉_t, and (D) 〈k_io 〉_t and 〈p_i〉_t, as a function of x axis threshold. The correlation coefficients were calculated for all data points with <∆F/F₀>_t (B, C) or <p_i>_t (D) below the x axis threshold marked with the filled black circle, with Pearson’s linear correlation test.

The large 〈k_io〉_n error bars in Fig. 6B stem from low MR signal due to our small magnetic field strength, and from the low tissue filling factor of our experiment (typical p_i values ~0.07 (Fig. 6C)) (20). Fortunately, these unavoidable aspects affect precision more than accuracy: with enough samples, the mean values are reasonably trustworthy (20). [For in vivo studies, magnetic field strength and p_i are each typically an order of magnitude larger.] At the same time, the smaller Fig. 6B <∆F/F₀>_t,bin error bars mainly reflect the sizes of the <∆F/F₀>_t bins necessary to see the correlation. Given all the factors affecting F listed above, actual <∆F/F₀>_t uncertainties are much larger.

Bathing with kainate, a glutamate receptor activator

Neuronal activity is a balance of excitatory and inhibitory processes. To further probe AWC sensitivity to neuronal activity subtypes, OCC spontaneous neuronal activity was perturbed by addition of extracellular kainate, a potent neuroexcitatory amino acid agonist that enhances glutamate receptor function. Bath application of 1 μM kainate increased neuronal event frequency while reducing event amplitudes (Figure 7A, left). <∆F/F₀>_n was increased by 36% (n = 8) (Fig. 7B, left), while 〈k_io〉_n and 〈p_i〉_n remained relatively unaltered (Fig. 7B, center). The mismatch between the <∆F/F₀>_n increase (7B, left) and 〈k_io〉_n constancy (7B, middle) is reminiscent of Figs. 3B and 3C. We will consider this further below. At 100 μM kainate, prolonged activity quenching was observed, along with Ca²⁺ influx (Fig. 7A, right), again with no changes in 〈k_io〉_n, but with a significant 95% 〈p_i〉_n increase (Fig. 7B, right). The latter is reminiscent of the large 〈p_i〉_n increase at high K_o⁺ (Fig. 3D).

Figure 7.

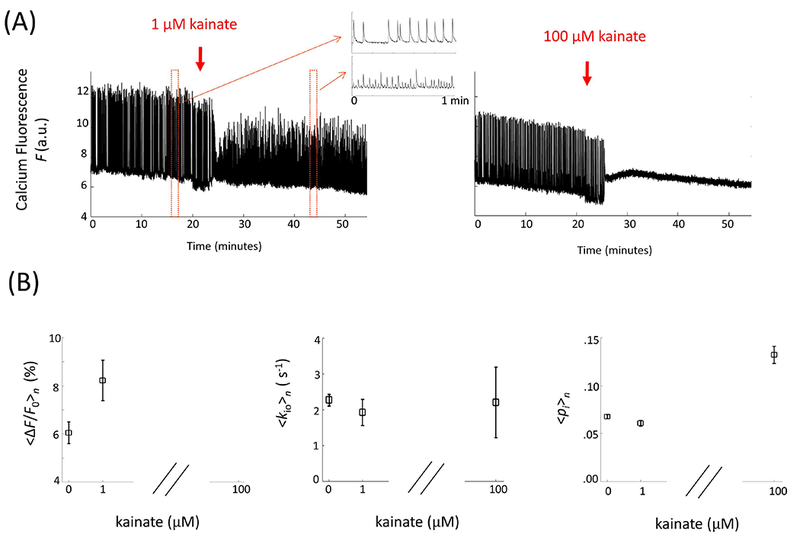
Bathing with low kainate concentration increases 〈ΔF/F₀〉_n without affecting steady state water efflux and cell volume. (A) Changes of representative spontaneous neuronal activity in OCCs upon bath application of 1 μM (left, n = 8) and 100 μM (right, n = 6) kainate. (B) Statistical results for the 〈ΔF/F₀〉_n (left), 〈k_io〉_n (middle), and 〈p_i〉_n (right) kainate concentration dependences; the data are displayed as the mean (± standard error of the mean).

Bathing with picrotoxin, a GABA_A receptor antagonist

Here we tested the sensitivity of AWC to neuronal inhibition activity by perfusion with a post(inhibitory) receptor blocker, picrotoxin (PTX). Reducing inhibitory synaptic transmission could enhance neuronal spiking activity. Bath application of the GABA_A receptor antagonist, PTX (5 μM), slightly increased spontaneous population events with enhanced synchronization (Figure 8A) and increased <∆F/F₀>_n by 31% (n = 10, p = 0.03, Fig. 8B). No significant change was observed in either 〈k_io〉_n or 〈p_i〉_n (Fig. 8B). Once again, there is a disconnect between <∆F/F₀>_n and 〈k_io〉_n.

Figure 8.

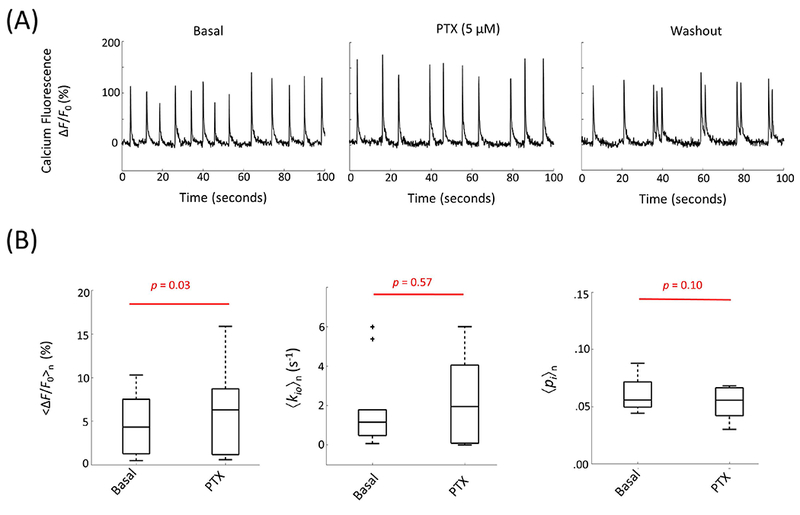
(A) Representative calcium fluorescence signal response to picrotoxin, PTX (5 μM), perfusion and subsequent washout with normal ACSF. (B) The results for 〈ΔF/F₀〉_n (left), 〈k_io〉_n (middle), and 〈p_i〉_n (right) are shown in two phases: basal and PTX perfusion (n = 10).

Discussion

Noninvasive, accurate detection of neuronal activity throughout the brain, with high spatial and temporal resolution, is a desideratum in both neuroscience and medicine. To achieve this goal, novel fMRI contrast mechanisms that can detect neuronal activity more directly, precisely, and accurately than conventional hemodynamic-based fMRI methods need to be developed. The hypothesis tested here is that active trans-membrane water cycling (AWC) could be such a mechanism. AWC can be detected by ¹H₂O MRI, which can measure k_io. The k_io(a) term of Eq. (1) embodies AWC, and contains a factor for the metabolic rate of NKA activity, ^cMR_NKA, explicit in Eq. (2). Since NKA metabolic activity is an integral part of neuronal activity, we hypothesize that k_io(a) is key.

First, we show how our findings confirm the existence of the k_io(a) term. Our new results, along with those from the pertinent literature, are summarized in the Figure 9 bar graph, which displays all known k_io measurements with perturbations that do not directly affect NKA. The ordinate is percentage change. Each perturbation has three bars measuring the k_io change (red), the provisional k_io(p) change (blue), and the provisional k_io(a) change (green). We can determine the provisional changes by taking advantage of our independently measured p_i parameter, which is proportional to V,

$$p_i=(\rho V-f_{\text{M}})∕(1-f_{\text{M}})$$ (5)

where ρ is the sample cell density and f_M is the sample volume fraction inaccessible to mobile aqueous solutes (17). The perturbations in this study change neither ρ nor f_M, thus fractional changes in V can be estimated from fractional changes in p_i with proper estimation of f_M, which is small here (20). Then, the percentage change in k_io(p) (blue bars) can be estimated from the % change of 1/V^1/3, provided there is no change in P_W(p) or gross cell shape (Eq. (2)). These are both good approximations, particularly the former. The % 1/V change is proportional to the percentage change in k_io(a) (green bars) provided there is no change in [H₂O_i], x, and ^cMR_NKA (Eq. (2)). The former is a good assumption, and the latter is precisely what we want to disprove. (All bars in Fig. 9 use the mean parameter value).

Figure 9.

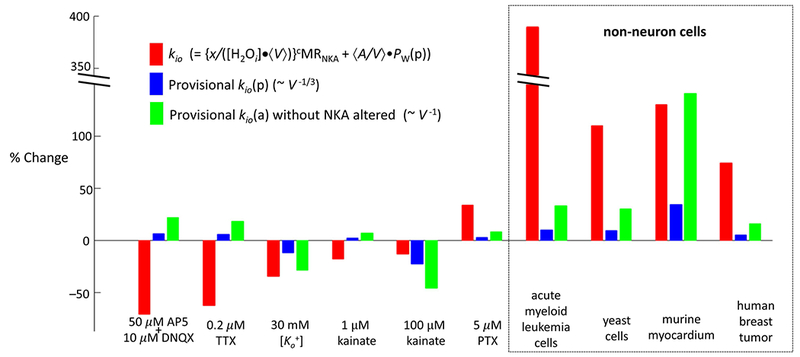
Measured percentage changes in the cellular water efflux rate constant (k_io, red bars) and the estimated provisional percentage changes in the passive k_io (k_io(p), blue bars) and active k_io (k_io(a), green bars) terms. Four perturbations of non-neuronal systems from the literature are given on the right. Details and references are given in the text.

The results in Fig. 9 comprise ten disparate perturbations from five different laboratories: the six on the left are from the present work. The non-neuronal Fig. 9 perturbations on the right include the addition of the therapeutic drug cisplatin to a cancer cell suspension, the switch from N₂ to O₂ bubbling of a yeast cell suspension, the release from hypertension of murine heart tissue in vivo, and intra-tumor variation within a human breast tumor in vivo (all from (16), and referenced there). No perturbations shown in Fig. 9 have red and blue bars of equal length: the red bar is always larger, usually considerably. Moreover, in three of the entries from the current work (AP_5,o plus DNQX_o, TTX_o, 1 μM kainate_o), the direction of the blue bar is opposite to that of the red bar. Thus, a k_io(p) change (blue) cannot explain any measured k_io change (red): these findings confirm the conclusion that there must be a k_io(a) term in k_io. Furthermore, almost no perturbations shown in Fig. 9 have red and green bars of equal length: in most cases here also, the red bar is always larger. Moreover, in some of the entries from the current work (AP_5,o plus DNQX_o, TTX_o, PTX_o), the direction of the green bar is opposite to that of the red bar. Thus, a change in the k_io(a) term with constant x^cMR_NKA (green bar) cannot explain the measured k_io change (red). These findings point to the conclusion that there must be a change in the k_io(a) x^cMR_NKA factor in every perturbation. We cannot say that the algebraic subtraction of the green bar from the red bar gives the percentage change of the x^cMR_NKA factor because we do not know the proportions of k_io(a) and k_io(p) before the perturbation. We cannot discriminate changes in x from changes in ^cMR_NKA, or changes in both. However, any of the latter three possibilities is important.

Here we have shown that AWC — an intrinsic property of cells and detectable by ¹H MRI — correlates with neuronal activity in neuronal cultures by simultaneously measuring neuronal activity and water cycling using a tandem calcium fluorescence optical/MR imaging system. In this study, we found: (1) AWC decreased (up to 71%) when either synaptic glutamatergic transmission or neuronal spiking activity was reduced (Figs. 4, 5); (2) AWC positively correlated with [K_o⁺] as [K_o⁺] was adjusted from 1 to 6.3 mM (Fig. 3); (3) AWC positively correlated with the basal level of spontaneous activity in cultures (Fig. 6). These results demonstrate a positive relationship between AWC and neuronal activity, and suggest that AWC could be a potential novel contrast mechanism for functional brain imaging and mapping.

The underlying connection between AWC and neuronal activity is the associated NKA metabolic process (Fig. 2). Neuronal activity involves altering the transmembrane transport of inorganic ions: Na⁺, K⁺, Ca²⁺, and Cl⁻. These include the re-establishment of the basal (resting) state after an action potential event, the re-uptake of synaptic glutamate into the neuronal cytoplasm (for the dominant glutamatergic synapses), and the concentration of cytoplasmic glutamate into neuronal vesicles. It is almost certain that NKA activity is required for each of these steps. There is a growing body of evidence that the AWC, k_io(a) term is driven by NKA (16,20,22,23). Studies of several different systems with perturbations known to directly affect NKA always change k_io in the direction expected. These perturbations include ouabain_o, K_o⁺, and ATP_i (shown in red in Fig. 1). They are reviewed and tabulated in (16). Our subsequent study of brain tissue with ouabain perfusion (20) and the K_o⁺ titration here (Fig. 3) extended this evidence.

Particularly strong, both k_io and independently measured NKA enzyme activity (29) show very similar extracellular potassium concentration-dependence (Fig. 3C vs. Fig. 3E). Up to [K_o⁺] = 6.3 mM, both are well described by the Michaelis-Menten model of enzyme kinetics. The facts that our K_M is similar to that reported by Erecinska and Dagani (29), and close to the normal [K_o⁺] value, are important to note. It indicates that, in the normal concentration range, K_o⁺ serves mainly to modify NKA activity. As [K_o⁺] reaches 30 mM or above, both k_io and the NKA enzyme activity show small decreases (Fig. 3 and (29)). This phenomenon suggest the potentially dual role of K_o⁺ as both an NKA substrate (“reactant”, well described by M-M model) and a ”product” of K⁺ channel (PC) transport (Fig. 1). When [K_o⁺] is increased by a factor of five above 6 mM, it is likely its role as a PC product takes over. Normally, K⁺ efflux through PCs dominates the membrane potential. But when the K_o⁺ concentration increases sufficiently, there could be “product inhibition” of PC by K_o⁺, to at least reduce K⁺ efflux (and thus depolarize the cell): PCs can transport K⁺ outward or inward. At a high enough concentration, K_o⁺ could lower K⁺ efflux (39) sufficiently to increase [K_i⁺] and reduce NKA activity. Along with the prolonged at high [K_o⁺] perfusion is the reduction of spontaneous neuronal activity. This could be another potential source of the k_io and NKA enzyme activity reduction due to the fact that decrease in both synaptic activity and action potential generation rate could reduce NKA activity and AWC, as discussed above. Reduced NKA activity can also lead to intracellular Na⁺ and Ca²⁺ build-up, and V increase (Fig. 3) (20,40). [K_o⁺]-sensitivity of NKA activity is important. Due to the constrained nature of brain interstitial space, [K_o⁺] can be readily altered (41). This may be a major mechanism of paracrine communication in the brain (23). Aspects of [kainate_o]-dependent experiments in Fig. 7 bear a striking resemblance to [K_o⁺]-dependent experiments. A [kainate_o] value of 100 μM produces similar F and 〈p_i〉_n changes as 30 mM K_o⁺ (Fig. 3). Perhaps high stimulation of glutamate receptor activity, at 100 μM kainate_o, induces molecular consequences similar as 30 mM K_o⁺ (hypothesized above).

AP_5,o plus DNQX_o and TTX_o are known to affect neuronal synaptic activity or firing even though they do not directly affect NKA (shown in red in Fig. 2). In both cases (Figs. 5 and 4), k_io shows a large decrease (>60%). This result is expected because NKA activity must also be reduced as neuronal activity is suppressed, as illustrated in Fig. 2. Interestingly, TTX_o is known to specifically inhibit VGSC, and the latter plays perhaps its most important role in actuating a neuronal event, and in other excitable cells. The suppression by TTX_o of k_io suggests that VGSC or other sodium channels/transporters involved in neuronal firing constitute several (or the majors) of the III transporters (Na⁺ influx transporters) in the AWC system (Fig. 1) of the neuron (Fig. 2). In other words, VGSC inhibition slows neuronal firing, metabolic transmembrane Na⁺/K⁺ cycling, and also AWC.

In this study, our simultaneous measurement of k_io and mean cell volume V (derived from p_i) enabled us to ascertain the k_io(a) and k_io(p) contributions to the observed k_io changes. The MR methods have been carefully validated in our previous work (20). Ideally, we would like to perturb only AWC without altering the passive pathway (cell size determined, Eq. 2). However, simultaneous changes (e.g., in cell morphology, volume) likely occur for any perturbation of membrane water transport. Experiments with long-term neuronal activity suppression (AP_5,o plus DNQX_o, TTX_o, and low [K_o⁺]) showed significant cell volume reduction, which might be caused by the reduction in neuronal and glial cell swelling associated with neuronal activity (42–47). From Eq. (2), k_io(p) is inversely proportional to cell diameter (assuming the cell shape is little changed and P_W(p) is constant). Thus, k_io(p) should increase in our neuronal activity suppression experiments, that is, the observed decreases in k_io must be induced by a greater reduction in k_io(a). From Eq. 2, the reduction in k_io(a) must come from a reduction in NKA activity (x^cMR_NKA) since V decreases: there is surely no change in [H₂O_i].

Thus, we can state with confidence that k_io detects x^cMR_NKA decreases with treatment of brain tissue with high [K_o⁺], AP_5,o plus DNQX_o, and TTX_o. It is encouraging that interventions that are expected to and do, in fact, decrease neuronal activity also decrease k_io because of decreased x^cMR_NKA. This phenomenon could be due to decreased x, decreased ^cMR_NKA, or both. Whatever the cause, it is clear that ^cMR_NKA is involved. We can also state with confidence that k_io detects x^cMR_NKA increases caused by cisplatin treatment of acute myeloid leukemia cells, relief from hypertension of myocardium, in certain regions within the human breast tumor, and x^cMR_Pma1 increases with oxygenation of yeast cells P_ma1 plays the NKA role in yeast (22).

Neuronal activity includes both excitation and inhibition. In the basal condition, both excitatory and inhibitory activity might contribute to the measured AWC. In the bath application of AP₅ and DNQX, the excitatory signaling pathway was blocked while a significant AWC reduction was observed. This result demonstrates a significant excitatory contribution to AWC. Picrotoxin (PTX) is known to inhibit the inhibitory neuronal system (Fig. 2). Thus, one might expect postsynaptic neuronal firing, to increase. Increase in <∆F/F₀>_n with little changes in 〈k_io〉_n was observed during the bath application of 5 μM PTX (Fig. 7). This suggests inhibitory activity are present in the basal state and might contribute to k_io, i.e., potential cancellation between inhibitory activity and neuronal firing in k_io. Kainate is known to enhance excitatory activity by binding to the kainateR receptor. However, it is has also been shown that kainate is a double agent and can also excite GABAergic neurons and increase inhibition (48), and then might even reduce the net neuronal firing in the postsynaptic neurons. The unchanged k_io with bath perfusion of 1 mM kainate might reflect more complicated compensation between excitatory and inhibitory activity.

We have noted a number of instances of “mismatch” [i.e., nonlinearity] between <∆F/F₀>_n and 〈k_io〉_n. There are a number of possible explanations. An ultimate goal would be to measure MR_NKA, perhaps even absolutely (17). As often in the literature, Erecinska and Dagani (29) measure O₂ uptake (i.e., ^tMR_O2) with the presumption it may be proportional to ^tMR_NKA. Indeed, O₂ is consumed to produce ATP both by oxidative phosphorylation (MR_oxphos) and by oxidative glycolysis (MR_gly), with a large stoichiometric weighting for the former, and NKA is the largest ATP consumer (17). The relationship between MR_O2 and MR_NKA might be linear, but it need not be [there could be a switch between MR_oxphos and MR_gly]. Thus, the observed nonlinearity between <∆F/F₀>_n (Fig. 3B) and ^tMR_O2 (Fig. 3E) might or might not signify a nonlinearity between <∆F/F₀>_n and MR_NKA. The nonlinearity between <∆F/F₀>_n (Fig. 3B) and 〈k_io〉_n Fig. 3C) could be attributed to either. Equation (2) indicates k_io would be linear in ^cMR_NKA only if x, [H₂O_i], V, and k_io(p) are constant. Neurons and astrocytes have different k_io values (21), and presumably different x and ^cMR_NKA values. During any particular dependence, the proportion of (excitatory and/or inhibitory) neuronal and astrocytic activity could change. Also x values could vary if cells change mechanisms [e.g., switching to different I and/or IV transporters (Fig. 1)]. There is nonlinearity between <∆F/F₀>_n and 〈k_io〉_n in the basal condition (Fig. 6B), and in the [kainate_o]- (Figs. 7B, left, middle) and [PTX_o]- (Figs. 8A,B) dependences. These are all important and interesting issues to pursue.

In this study, we propose a novel functional MRI mechanism and suggest that the existence of AWC could lead to a more direct and accurate indicator of neuronal activity — one based on concomitant metabolic changes. Organotypic tissue cultures constitute a well-characterized biological model of neuronal activity free of hemodynamic, respiratory, and other physiological confounds. Not only is the in vivo cortical cytoarchitecture largely preserved (including cortical layers and cortical cell types), but neuronal activity in these cultures exhibit bursts of spontaneous neuronal avalanches grouped into so-called up-states, separated by periods of low activity (49–52), resembling resting neuronal activity in vivo (38,53,54). We therefore conclude that AWC MRI could also be sensitive enough to capture neuronal activity in vivo.

Studies are still needed to further test and vet this new fMRI mechanism and consider its use in pre-clinical and possibly clinical applications in vivo. Additional research is needed, for example, to gather more temporal information about the AWC response under stimulations, and to develop reliable MRI methods to measure AWC noninvasively, particularly without use of contrast agents. In this study, a high concentration of an extracellular MRI CA was used to quantitatively measure k_io. This same experiment is not feasible for in vivo human application for many reasons. For example, in vivo the CA is administered vascularly, but it does not sufficiently cross the normal blood-brain-barrier and enter the brain interstitium. Even if it could, the interstitial concentration used here is unachievable. In addition to these technical challenges, there are serious, looming safety and environmental issues that challenge all further CA use in humans (17). Encouraging developments in MRI methods suggest it may be possible to use non-invasive diffusion-based exchange MRI to measure and map k_io in the brain, as well as in other tissues (17,55–59). In addition, k_io measurement in vivo should be much less noisy than our in vitro measurement, for the reasons given above (20). In this study, the k_io from glial cells was not emphasized due to the low population of glia in this OCC preparation (35). Fast water exchange was observed in glial cells (21), and the glial cell contribution to k_io should also be considered in in vivo studies.