Exploring Folding Patterns of Infant Cerebral Cortex Based on Multi-view Curvature Features: Methods and Applications

Abstract

The highly convoluted cortical folding of the human brain is intriguingly complex and variable across individuals. Exploring the underlying representative patterns of cortical folding is of great importance for many neuroimaging studies. At term birth, all major cortical folds are established and are minimally affected by the complicated postnatal environments; hence, neonates are the ideal candidates for exploring early postnatal cortical folding patterns, which yet remain largely unexplored. In this paper, we propose a novel method for exploring the representative regional folding patterns of infant brains. Specifically, first, multi-view curvature features are constructed to comprehensively characterize the complex characteristics of cortical folding. Second, for each view of curvature features, a similarity matrix is computed to measure the similarity of cortical folding in a specific region between any pair of subjects. Next, a similarity network fusion method is adopted to nonlinearly and adaptively fuse all the similarity matrices into a single one for retaining both shared and complementary similarity information of the multiple characteristics of cortical folding. Finally, based on the fused similarity matrix and a hierarchical affinity propagation clustering approach, all subjects are automatically grouped into several clusters to obtain the representative folding patterns. To show the applications, we have applied the proposed method to a large-scale dataset with 595 normal neonates and discovered representative folding patterns in several cortical regions, i.e., the superior temporal gyrus (STG), inferior frontal gyrus (IFG), precuneus, and cingulate cortex. Meanwhile, we have revealed sex difference in STG, IFG, and cingulate cortex, as well as hemispheric asymmetries in STG and cingulate cortex in terms of cortical folding patterns. Moreover, we have also validated the proposed method on a public adult dataset, i.e., the Human Connectome Project (HCP), and revealed that certain major cortical folding patterns of adults are largely established at term birth.

1. Introduction

The cerebral cortex of the human brain is a convoluted structure with highly complex and variable folding patterns across individuals. Many neurodevelopmental and neuropsychiatric disorders are associated with abnormal cortical folding morphology, which is likely the consequence of the abnormality in the dynamic folding development during perinatal brain development. During the last trimester of human pregnancy, the cortex develops rapidly from a smooth lissencephalic structure to an extremely folded one with notable increases in terms of many measures, e.g., brain volume, cortical surface area, sulcal depth, and curvature (Kapellou et al., 2006; Dubois et al., 2007; Dubois et al., 2008; Studholme, 2011; Orasanu et al., 2016). Meanwhile, the hemispheric asymmetries of cortical folding emerge in several regions during this period, e.g., the Heschl’s gyrus, planum temporale, and superior temporal sulcus (Dubois et al., 2010; Habas et al., 2011; Orasanu et al., 2016; Shimony et al., 2016). At term birth, neonates have already developed all the primary and secondary cortical folds and presented sex difference and hemispheric asymmetries (Chi et al., 1977; Awate et al., 2010; Hill et al., 2010; Li et al., 2014b), largely resembling the complex cortical folding morphology of adults (Li et al., 2014d; Li et al., 2018). Therefore, studying the morphology of neonatal cortical folding could provide important insights into normal early brain development and neurodevelopmental and neuropsychiatric disorders.

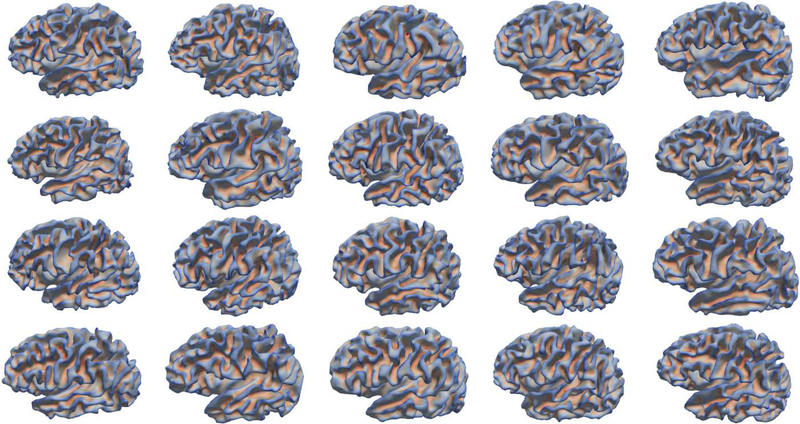
However, noticing the remarkable inter-subject variability of cortical folding in neonates (Fig. 1), it is still unclear on what are the representative normal neonatal folding patterns in each cortical region. Discovering the underlying representative patterns of cortical folding in neonatal brains is of great importance for neuroimaging studies of early brain development. As this will help: 1) provide important insights into early cortical folding variability across individuals and better understanding of the possible relationship between folding patterns and behavioral/cognitive functions (Klyachko and Stevens, 2003; Choe et al., 2012; Sun et al., 2012; Im et al., 2015; Cachia et al., 2016); 2) build multiple infant cortical surface atlases based on cortical folding patterns for enabling better spatial normalization and registration of cortical surfaces across infants; 3) identify the abnormal cortical folding patterns that could potentially associate with brain disorders during infancy; 4) explore possible sex differences as well as hemispheric asymmetries in relation to cortical folding patterns (Paus et al., 1996; Awate et al., 2010; Dubois et al., 2010; Li et al., 2014d; Li et al., 2015a; Fish et al., 2016); and 5) investigate the latent relationships of cortical folding patterns between the developing neonatal brains and the matured adult brains.

Fig. 1.

Large variability of cortical folding patterns across 20 neonates, which are randomly selected from our dataset with 595 neonates. Cortical surfaces are color-coded by mean curvature, with the red denoting the sulci and the blue denoting the gyri.

Several pioneer studies of cortical folding patterns have been conducted based on visual inspection of adult brains. For example, the classic textbook “Atlas of Sulci” (Ono et al., 1990) comprehensively describes sulcal patterns of various regions, by visual examination of 25 autopsy specimen brains. Relying on MR imaging, Ebeling et al. classified the cortical folding of the inferior frontal gyrus into four types, and Clark and Plante further refined this classification (Ebeling et al., 1989; Clark and Plante, 1998; Tomaiuolo et al., 1999). Yucel et al. classified the cortical folding of the anterior cingulate cortex into three types by identifying the presence of the paracingulate sulcus (Yücel et al., 2001). Pereira-Pedro et al. classified the cortical folding of the precuneus into three categories by checking sulcal connections and sulcal shape patterns (Pereira-Pedro and Bruner, 2016; Bruner et al., 2017). However, visual inspection is very subjective, error-prone and time consuming, and thus is not capable of fully capturing inter-subject variability of cortical folding in the modern large-scale MRI datasets.

To address this issue, several computational methods were proposed for automatically and objectively discovering cortical folding patterns (Sun et al., 2007; Sun et al., 2009; Coulon et al., 2012; Meng et al., 2016). Sun et al. leveraged 3D moment invariants as shape descriptors of sulci to explore the folding patterns of the cingulate cortex, and successfully identified three patterns (Sun et al., 2007). As the 3D moment invariants may not be sufficient to capture the complexity of cortical folding, Sun et al. further combined the Iterative Closest Point (ICP) registration method and the Isomap algorithms to better explore the folding patterns in the superior temporal sulcus (STS), cingulate cortex, and inferior frontal region (Sun et al., 2009). This method led to the discovery of an additional parallel cingulate pattern, which indeed occupies a big percentage in large populations (Ono et al., 1990; Cachia et al., 2016; Meng et al., 2016). Coulon et al. proposed a template-based method to extract features for encoding the presence and orientation of sulcal regions and revealed five patterns of the left inferior frontal sulcus (IFS) (Coulon et al., 2012). As the averaging-based template missed lots of specific folding information of individual subjects, these features still cannot comprehensively characterize cortical folding.

Although the above studies identified several meaningful folding patterns of specific cortical regions, they were only applied to adult datasets with relatively small or moderate sample sizes, where many representative cortical folding patterns might have been missed. Moreover, the existing discovered cortical folding patterns of adults might not be representative of that of neonates, due to the remarkable postnatal development and environmental influence. To date, the prenatal developmental mechanisms and postnatal origins of representative cortical folding patterns are not clearly underpinned. Therefore, Meng et al. devised a method to discover the sulcal folding patterns using a large neonatal dataset (Meng et al., 2016). Specifically, they characterized sulcal folding based on the spatial distribution of sulcal pits (i.e., deep sulcal landmarks) and their relational graphs, and revealed several typical folding patterns in the central sulcus, STS and cingulate sulcus. For example, three and four sulcal folding patterns were discovered in STS and cingulate cortex, respectively. However, since the folding patterns were characterized based on sulcal pits, which are only applicable for deep sulci, this method is not suitable for mining gyral folding patterns. Indeed, sulci and gyri have distinct cortical properties, structural/functional connections, and developmental mechanisms (Van Essen, 1997; Nie et al., 2011; Li et al., 2015a; Li et al., 2015b).

In this paper, we propose a novel computational method for exploring the representative folding patterns in local regions (especially for gyri) of the infant cerebral cortex based on multi-view curvature features, by leveraging a large-scale neonatal dataset with 595 healthy subjects. Specifically, first we devise multi-view curvature features to comprehensively characterize the complex and multi-scale nature of cortical folding. Then, for each feature in a local cortical region, we build a similarity matrix to measure the affinity of cortical folding between any pair of subjects. Third, we nonlinearly fuse the similarity matrices from all features into a single matrix to retain both shared and complementary similarity information of multi-view features. Finally, based on the fused similarity matrix, we apply a hierarchical affinity propagation clustering approach to group subjects into several clusters, each with a representative folding pattern of the specific region. To show the applications of the proposed method, we explore the representative folding patterns in four cortical regions, including the superior temporal gyrus, inferior frontal gyrus, precuneus, and cingulate cortex. The motivation of choosing these regions is that most of them have shown notably variable folding patterns in previous adult studies, thus we can easily compare our discovered neonatal folding patterns with those discovered adult folding patterns. Meanwhile, we also analyze the sex effects and hemispheric asymmetries of our discovered folding patterns of these regions. Importantly, we also validate the proposed method on an adult dataset, i.e., the Human Connectome Project (HCP), and compare the cortical folding patterns as well as their hemispheric asymmetries between infant and adult brains.

2. Materials and Methods

2.1. Subjects and MR Image Acquisition

The Institutional Review Board of the University of North Carolina (UNC) School of Medicine approved this study. The dataset includes both healthy singletons and twin infants and is part of a large prospective study of early brain development. The UNC hospitals recruited the pregnant mothers during their second trimester of pregnancy. Parents of each recruited subject provided written informed consents. Infants with abnormalities on fetal ultrasound as well as mothers with major medical or psychotic illness were excluded from the study. None of infants in this study cohort suffered from congenital anomalies, metabolic disease, and focal lesions (Gilmore et al., 2012).

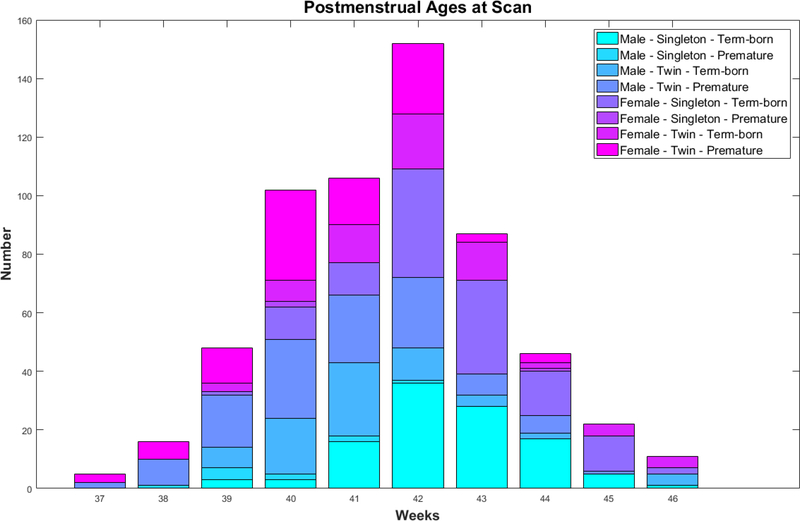
MR images were acquired from 595 healthy neonates in this study, including 308 males (119 singletons and 189 twin children) and 287 females (124 singletons and 163 twin children). All infants were scanned unsedated. Before MRI scanning, infants were fed, swaddled, and fitted with ear protection. No significant difference was found in the gestational ages (GA) at birth and postmenstrual ages (PA) at MRI scan between male and female subjects. Demographic information of the infant cohort is shown in Table 1. The histogram of PA at MRI scan of infants in 8 sub-groups (related to male/female, singleton/twin and term-born/premature) is displayed in Fig. 2.

Table 1.

Demographic information of the infant cohort. (GA: gestational age, PA: postmenstrual age. The range in the bracket denotes the age range of each group. All the ages are measured in ‘weeks’.)

	All	Male	Female
Subjects	595	308	287
GA at birth	37.2 ± 2.8 (28.6 – 42.1)	37.4 ± 2.8 (28.9 – 41.7)	37.1 ± 2.7 (28.6 – 42.1)
PA at scan	41.6 ± 1.8 (36.7 – 46.5)	41.8 ± 1.9 (36.7 – 46.4)	41.4 ± 1.7 (37.4 – 46.5)
Singleton - Term-born	230	109	121
GA at birth	39.6 ± 1.1 (37.0 – 42.1)	39.6 ± 1.0 (37.0 – 41.7)	39.6 ± 1.2 (37.0 – 42.1)
PA at scan	42.6 ± 1.4 (38.9 – 46.1)	42.5 ± 1.3 (38.9 – 46.1)	42.6 ± 1.5 (39.1 – 45.7)
Singleton - Premature	13	10	3
GA at birth	35.8 ± 0.6 (34.4 – 36.4)	35.7 ± 0.7 (34.4 – 36.3)	36.0 ± 0.4 (35.6 – 36.4)
PA at scan	40.2 ± 1.8 (37.9 – 44.4)	39.8 ± 1.4 (37.9 – 42.3)	41.7 ± 2.4 (40.3 – 44.4)
Twin - Term-born	137	72	65
GA at birth	37.8 ± 0.5 (37.0 – 39.9)	37.6 ± 0.5 (37.0 – 39.9)	37.9 ± 0.6 (37.0 – 39.0)
PA at scan	41.8 ± 1.9 (38.6 – 46.5)	41.3 ± 1.6 (38.6 – 46.4)	42.3 ± 2.1 (39.2 – 46.5)
Twin - Premature	215	117	98
GA at birth	34.4 ± 2.2 (28.6 – 36.9)	34.5 ± 2.3 (28.9 – 36.9)	34.2 ± 2.2 (28.6 – 36.9)
PA at scan	40.6 ± 1.5 (36.7 – 44.9)	40.7 ± 1.6 (36.7 – 44.9)	40.5 ± 1.4 (37.4 – 44.1)

Fig. 2.

Histogram of postmenstrual ages at MRI scan of our dataset.

T1-weighted and T2-weighted brain MR images were acquired on a Siemens head-only 3T scanner with a circular polarized head coil (Allegra, Siemens Medical System, Erlangen, Germany). T1-weighted images (160 sagittal slices) were acquired with a 3D magnetization-prepared rapid gradient echo (MPRAGE) sequence (TR = 1820 ms, TE = 4.38 ms, inversion time = 1100 ms, flip angle = 7º, and resolution = 1×1×1 mm³). T2-weighted images (70 transverse slices) were acquired with the turbo spinecho (TSE) sequences (TR = 7380 ms, TE = 119 ms, flip angle = 150º, and resolution = 1.25×1.25×1.95 mm³).

2.2. Image Processing and Cortical Surface Mapping

All T1-weighted and T2-weighted MR images were processed using the UNC Infant Pipeline (Li et al., 2015c), which has been validated on >2000 infant MRI scans. Concretely, for image preprocessing, this pipeline includes the following main steps: 1) stripping the non-cerebral tissues through a learning-based method (Shi et al., 2012); 2) removing the cerebellum and brain stem by the HAMMER registration method (Shen and Davatzikos, 2002); 3) correcting the intensity inhomogeneity using N3 algorithm (Sled et al., 1998); 4) segmenting the brain tissue into gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF) through an infant-specific level set based method (Wang et al., 2013; Wang et al., 2014b); 5) masking the non-cortical structures (i.e., lateral ventricles and subcortical structures) and filling these regions, and then dividing each brain into left and right hemispheres.

Cortical surfaces of each hemisphere for each subject were reconstructed by a deformable surface method (Li et al., 2012b; Li et al., 2014a) based on the segmented tissues. Specifically, first, topology defects were corrected based on a learning-based method (Hao et al., 2016), thus ensuring a spherical topology for each hemisphere. Then, the corrected white matter was tessellated as a triangular mesh and further deformed by preserving its initial topology to reconstruct the inner and outer cortical surfaces. Each inner cortical surface was further smoothed, inflated and mapped onto a standard sphere (Fischl et al., 1999). Each spherical cortical surface was aligned onto the UNC 4D Infant Cortical Surface Atlas¹ (Li et al., 2015c) using Spherical Demons (Yeo et al., 2010), thus establishing the vertex-to-vertex cortical correspondences across all subjects. All cortical surfaces were finally resampled to the same standardmesh tessellation with 163,842 vertices.

2.3. Discovering Cortical Folding Patterns

The proposed method for exploring the representative cortical folding patterns of infants is shown in Fig. 3. Specifically, given the mean curvature map on the inner surface of each subject (Fig. 3-a), we first derive two kinds of curvature-related features: 1) decomposed curvature maps at multiple spatial-frequency scales (Fig. 3-b); and 2) gyral crest curves (Fig. 3-c) extracted from the mean curvature map. These “multi-view” curvature features lead to a comprehensive characterization of cortical folding. Second, to better measure the similarity among subjects on multi-view features in a specific cortical region of interest (ROI), the folding difference between any pairs of subjects was firstly computed for each feature, thus obtaining multiple inter-subject distance matrices (Fig. 3-d), which were further converted as similarity matrices (Fig. 3-e). Third, leveraging the similarity matrix fusion (SNF) method (Wang et al., 2014a), these multiple similarity matrices were adaptively and nonlinearly fused together as a single comprehensive similarity matrix (Fig. 3-f) to carry both shared and complementary information across multi-view features. Ultimately, all subjects were clustered into several groups based on this fused similarity matrix, with each group representing a typical cortical folding pattern in the specific cortical region (Fig. 3-g). We detail each of these steps in the following sections.

Fig. 3.

Pipeline of the proposed computational framework for exploring cortical folding patterns. (a) The original mean curvature maps on inner cortical surfaces of all the subjects. Here, N=595 is the total number of subjects in the dataset. (b) The decomposed curvature maps at multiple scales using overcomplete spherical wavelets. (c) The extracted gyral crest curves based on the original mean curvature maps. (d) The six distance/dissimilarity matrices based on curvature-derived features for measuring the folding difference between any pair of subjects in a specific cortical ROI. (e) The six corresponding similarity matrices. (f) The fused similarity matrix by nonlinear fusion of six similarity matrices using SNF. (g) The discovered cortical folding patterns in a specific region (herein the superior temporal gyrus) using clustering.

2.3.1. Computing Multi-View Curvature-based Features

Cortical folding can be characterized at multiple scales and aspects (Li et al., 2010b; Mangin et al., 2010; Duan et al., 2017a; Duan et al., 2017b). For instance, the mean curvature has been extensively used to study the fine-scale features of cortical folding, as it is informative in the highly-bended regions, such as gyral crests and sulcal bottoms. Sulcal depth has been used to explore the relatively coarse scale features of cortical folding, as it can capture the gradual slopes of gyri and sulci. However, both curvature and sulcal depth can only characterize cortical folding to some extent, and their intrinsic relationships remain unclear. To this end, we leveraged over-complete spherical wavelet transformation to decompose the mean curvature map of the cortical surface into multiple spatial-frequency scales for a natural multi-scale characterization of cortical folding. Meanwhile, we further extracted the gyral crest curves based on the curvature map as high-level characteristics. Thus, we obtain multi-view curvature features to comprehensively characterize the infant cortical folding.

Multi-scale Decomposition of Curvature Map

First, we computed the mean curvature map of the inner cortical surface (with a spherical topology) for each subject (Fig. 4-a) and further decomposed the mean curvature map into multiple complementary spatial-frequency scales (Fig. 4-b), by using over-complete spherical wavelets (Yeo et al., 2006; Yeo et al., 2008). Of note, the conventional spherical wavelets (e.g., orthogonal/bi-orthogonal wavelet transforms) would fail to meet our purpose, since they suffer from sampling aliasing and thus lack translational and rotational invariance in surface parameterization (Yu et al., 2007). In contrast, over-complete spherical wavelets address this issue by guaranteeing that each scale is sufficiently sampled, and thus are much more robust and accurate in characterizing cortical folding.

Fig. 4.

Decomposed multi-scale curvature maps based on over-complete spherical wavelets. (a) The original mean curvature map of the inner cortical surface. (b) The decomposed curvature maps at levels 17. As we can see, at coarser levels, the wavelet coefficients encode the larger scale folding information; while at finer levels, the wavelet coefficients capture the smaller scale folding information.

Let c be an input mean curvature map mapped onto a spherical cortical surface, and ${\left\{{\tilde{\mathit{h}}}_l\right\}}_{l=1}^L$ be the spherical analysis filters at L frequency levels. By convolving each filter ${\tilde{\mathit{h}}}_l$ with c in the spherical domain, we can obtain a set of wavelet coefficients ρ_l at multiple spatial-frequency scales as:${\mathit{\rho }}_l=\mathit{c}*{\tilde{\mathit{h}}}_l$, which can thus encode multi-scale information of the original surface characteristics (Fig. 4). Herein, the analysis filter is defined as:${\tilde{\mathit{h}}}_l=Q_l\mathit{\psi }$, where Q_l is a nonlinear dilation operator and l is the frequency level (with a larger l corresponding to a narrower filter). ψ denotes the mother wavelet filter, which is defined as a Laplacian-of-Gaussian filter in our application.

To ensure the shape analysis is rotation-invariant, we over-sampled the wavelet coefficients with 163,842 vertices on the spherical surface. As the underlying wavelet basis functions have local supports in both space and frequency, multi-scale wavelet coefficients encode rich information of cortical folding at different levels. As shown in Fig. 4, the original mean curvature map of one subject was decomposed into 7 frequency levels, thus generating a natural multi-scale characterization of cortical folding. Specifically, at coarser levels, the wavelet coefficients encode larger scale folding information, while at finer levels, the wavelet coefficients capture smaller scale folding information. These 7 levels are sufficient to capture multi-scale folding information, since the level 7 already mainly contains less useful high-frequency noises.

Extraction of Gyral Crest Curves

Gyral crest curves are high-level features of cortical folding and thus can be used as reliable landmarks for characterizing the inter-subject variability of cortical folding. To extract gyral crest curves, first, we partitioned the original mean curvature map of each surface into small patches, called supervertices (Li et al., 2012a). Herein, the boundaries of supervertices aligned well with the gyral crest curves and sulcal fundi in the highly bended cortical regions. Next, we automatically linked boundaries of these supervertices to form gyral crest curves. The flowchart of extraction of gyral crest curves is shown in Fig. 5.

Fig. 5.

Extraction of gyral crest curves. (a) The original mean curvature surface with initial seeds of supervertices. (b) The boundaries of partitioned supervertices. (c) The results of supervertices partition, where different colors indicate different supervertices. (d) The extracted gyral crest curves.

The supervertices partition of the cortical surface was formulated as a labeling problem, i.e., assigning a supervertex label to each vertex by taking into account the spatial contextual information. First, a total of 1280 seeds, which were relatively uniformly distributed on the cortical surface (Fig. 5-a), were initialized as the seeds of supervertices (Li et al., 2012a). Next, the label of each vertex belonging to a supervertex was determined based on geometric information by minimizing the following energy function:

$$E={\sum }_x^{}(1-\exp (-\alpha |g_{s_x}(x)|))+\lambda {\sum }_{\{x,y\}\in \mathcal{N}}^{}w(x,y)\cdot (1-\delta (|s_x-s_y|))$$ (1)

where the first term is a data term, the second term is a spatial smoothness term, and λ is a weight determining the tradeoff between these two terms. Specifically, the data term was determined by the curvature-weighted geodesic distance $g_{s_x}(x)$ between each vertex x and each seed representing a supervertex label s_x. The $g_{s_x}(x)$ was computed by the fast marching method on triangular meshes (Kimmel and Sethian, 1998; Li et al., 2010a), with a marching speed setting as exp(−β|c(x)|), where c(x) denotes the mean curvature of a vertex x. Herein, we set λ = 0.1, α = 0.2, and β = 0.3, as suggested in (Li et al., 2012a). Intuitively, given the seed of a supervetex, if a geodesic path connecting the supervertex seed and another vertex passes through regions with large magnitudes of curvature, typically corresponding to sulcal bottoms or gyral crests, their weighted geodesic distance will be large. Thus the cost of labeling this vertex as the current supervertex is large.

In the smoothness term, w(x, y) was a spatially-adaptive weight between a pair of vertices in the neighborhood $\mathcal{N}$ on the cortical surface, defined as:

$$w(x,y)=\frac{1}{4}(\exp (-|c(x)|)+\exp (-|c(y)|))\cdot (1+\mathit{n}(x)\cdot \mathit{n}(y))$$ (2)

where n represents the normal direction. Accordingly, the cost of labeling two neighboring vertices x and y is small at flat regions, but large at highly-bended regions, i.e., sulcal bottoms or gyral crests, especially for two vertices on the same sulcal bank. Hence, the above energy function encourages the boundaries of supervertices to align well with sulcal fundi or gyral crest curves at highly bended regions. This energy minimization problem was efficiently solved by alpha-expansion graph cuts method (Boykov et al., 2001). An example of supervertices partition is shown in Fig. 5-b and 5-c.

Based on supervertices partition, we extracted the gyral crest curves using a two-step threshold method. Note that the mean curvatures of the vertices on gyral crest curves are negative values on the cortical surface with inward-oriented normal vector field. First, we marked the boundaries with the average mean curvature smaller than a low threshold T_low as ‘strict’ segments of gyral crest curves, and marked those with the average mean curvature smaller than a high threshold T_high as ‘candidate’ segments. We empirically set T_low ⁼ −0.3 and T_{high =} −0.2, as suggested in (Li et al., 2012a). Then, from each strict segment, we performed curve linking by adding the adjacent strict or candidate segments with the minimum transition angle between them, thus obtaining the linked gyral crest curves, as shown in Fig. 5-d. Of note, if we set the thresholds as positive values, we can extract the sulcal fundi. Thus, the whole framework is applicable to discover folding patterns for both gyri and sulci as needed.

2.3.2. Computing Similarity Matrices of Multi-view Features

To integrate the high-dimensional multi-view features of a specific cortical region for clustering, a simple way is to first concatenate them together and then calculate a similarity matrix. However, it is very difficult to define appropriate weights for different features and also difficult to leverage their complementary and common information. To address this issue, we first computed the similarity matrix of each feature and then adaptively and nonlinearly integrated all similarity matrices together, by leveraging an effective similarity network fusion (SNF) method (Wang et al., 2014a). To this end, for each feature we first devised a distance matrix for measuring inter-subject dissimilarity of cortical folding in a specific region, and then converted it as a similarity matrix.

For the multi-scale curvature features obtained via over-complete spherical wavelets, we only leveraged the levels 2 to 6 for our task. This is because level 1 only captures very large scale information that is highly similar across individuals, thus only containing the indistinctive information. As for level 7, it mainly contains useless high frequency noises, as shown in Fig. 4, making the results unreliable and unstable. Thus, both level 1 and level 7 were not useful for mining folding patterns. Given a specific cortical ROI, its distance matrices for decomposed curvature levels 2 to 6 were calculated as:

$${\mathit{D}}_l(i,j)={\sum }_x{({\mathit{\rho }}_l^i(x)-{\mathit{\rho }}_l^j(x))}^2,l\in \{2,3,4,5,6\}$$ (3)

where i and j indicate the i-th subject and the j-th subject, respectively, l is the decomposed level, and x represents a vertex in the specific cortical ROI. Thus, we obtained five distance matrices {D₂, … , D₆} for all subjects.

As for the gyral crest curves on each surface, we first calculated their geodesic distance map on the aligned spherical cortical surface, with each vertex value denoting the geodesic distance between itself and its nearest gyral crest curve. For any pair of subjects i and j, given their gyral crest curves C_i and C_j in a specific cortical ROI, a point on C_i is denoted as a, a point on C_j as b, the corresponding closest point of a as aˊ on C_j, and the corresponding closest point of b as bˊ on C_i. The distance matrix of the specific cortical region was defined as:

$${\mathit{D}}_{Crest}(i,j)=\frac{1}{2}\left(\frac{1}{v_i}{\sum }_{a\in {\mathit{C}}_i}^{}dist(a,a^{\prime })+\frac{1}{V_j}{\sum }_{b\in {\mathit{C}}_j}^{}dist(b,b^{\prime })\right)$$ (4)

where dist(∙) defines the geodesic distance between two points on the aligned spherical cortical surface. V_i and V_j are the total numbers of points on gyral crest curves C_i and C_j in the specific ROI, respectively.

After calculating the distance matrices, we converted them into similarity matrices through a scaled exponential kernel (Wang et al., 2014a), defined as:

$${\mathit{W}}_f(i,j)=\exp \left(-\frac{{\mathit{D}}_f^2(i,j)}{\mu {\epsilon }_{i,j}}\right)$$ (5)

where D_f is one of the distance matrices: {D₂, … , D₆} and D_Crest. μ is a hyperparameter of the kernel function, and set as 0.8 as recommended in (Wang et al., 2014a). ε_i,j is defined as:

$${\epsilon }_{i,j}=\frac{mean({\mathit{D}}_f(i,R_i))+mean({\mathit{D}}_f(j,R_j))+{\mathit{D}}_f(i,j)}{3}$$ (6)

where mean $({\mathit{D}}_f(i,R_i))$ denotes the average distance between i-th subject and its K nearest neighbors. Herein, we empirically set K = 30. We thus obtained six similarity matrices W_f :{W₂, … , W₆} and W_Crest, for comprehensively measuring inter-subject similarities of cortical folding in a specific region.

2.3.3. Fusing Similarity Matrices of Multi-view Features

As mentioned above, to properly integrate the similarity matrices of multi-view curvature features, we leveraged the effective SNF method (Wang et al., 2014a). Specifically, SNF nonlinearly fuses these similarity matrices together by propagating reliable information across them, thus capturing both shared and complementary information for effectively discovering folding patterns. For each similarity matrix W_f, two corresponding matrices were derived: 1) P_f, which contains the full similarity information of each subject to all others; 2) S_f, which only carries the important sparse similarity information of each subject with its K nearest neighbors. The matrix P_f was obtained by normalizing the similarity matrix W_f as:

$${\mathit{P}}_f(i,j)=\{\begin{array}{ll}\frac{{\mathit{W}}_f(i,j)}{2{\sum }_{k\ne i}^{}{\mathit{W}}_f(i,k)}\hfill & ,j\ne i\hfill \\ \frac{1}{2},\hfill & j=i\hfill \end{array}$$ (7)

By setting ${\mathit{P}}_f(i,i)=\frac{1}{2}$, the normalized matrix will be numerically stable, since the self-similarities on the diagonal entries of W_f were excluded. Let R_i denote the subject i’s K nearest neighbors including i. The sparse similarity matrix is defined as:

$${\mathit{S}}_f(i,j)=\{\begin{array}{c}\frac{{\mathit{W}}_f(i,j)}{{\sum }_{k\in {\mathit{R}}_i}^{}{\mathit{W}}_f(i,k)},j\in {\mathit{R}}_i\\ 0,\text{otherwise}\end{array}$$ (8)

Through this equation, only the K highest values in each row of W_f were normalized, and all elements with low similarity were set to zero. This is based on the assumption that elements with higher similarity values carry the most important information for pattern discovery, while those with low similarity values carry less useful information. By setting ${\mathit{P}}_f^{t=0}={\mathit{P}}_f$, these matrices were iteratively updated using the following equation:

$${\mathit{P}}_f^{t+1}={\mathit{S}}_f\times \left(\frac{{\sum }_{k\ne f}^{}{\mathit{P}}_k^t}{5}\right)\times {({\mathit{S}}_f)}^T$$ (9)

where ${\mathit{P}}_f^{t+1}$ was the status matrix of f-th feature after t iterations and was normalized after each iteration based on Eq. 7. Thus, the isolated weak similarities disappeared, while the strong similarities were added to others. Meanwhile, the weak similarities supported by all matrices were retained, depending on their neighborhood connections across features. After convergence at t^∗ iterations, the fused full similarity matrix was defined as the average of all ${\mathit{P}}_f^{t*}$, which are typically similar to each other. In our experiments, this procedure typically converged in 20 iterations.

2.3.4. Clustering of Folding Patterns based on the Fused Similarity Matrix

To discover the representative patterns of cortical folding, a proper data-driven clustering method is needed to identify the groups of similar subjects. The majority of existing clustering methods require to predefine the number of clusters. However, there is no universally best method to choose a good cluster number, although there are many kinds of clustering quality measures, which typically lead to different results. As an exploratory study without prior knowledge on how many patterns existing in each region, we should choose one clustering method which decides the cluster number automatically based on the underlying characteristics of data. Thus we leveraged the widely used AP clustering method (Frey and Dueck, 2007), which doesn’t need to define cluster number. Moreover, since AP treats all the data points as potential exemplars in the beginning, it is more robust and unbiased by initialization. In AP, the real-valued information ‘responsibility’ and ‘availability’ propagate between data points until the final exemplars and corresponding clusters emerge.

However, since cortical folding is typically complex and highly variable across subjects, too many clusters unexpectedly emerged in our study. To discover the most representative patterns of cortical folding, we further clustered the identified exemplars in a hierarchical way until the final cluster number was in a moderate range. Specifically, after performing the AP clustering, we obtained the subjects’ cluster map (i.e., assigned cluster labels to each subject) and exemplars. First, we constructed a new similarity matrix among these exemplars. Second, we performed the AP based on this new similarity matrix and obtained the exemplars’ cluster map (i.e., assigned cluster labels to each exemplar of previous hierarchy) and new exemplars. Third, we modified the subjects’ cluster map according to the exemplar’s cluster map obtained in the second step. We repeated these three steps to reduce the cluster number hierarchically. After several iterations, the resulted cluster number decreased to a moderate value, e.g., no more than M. For a compact inspection of major patterns, we set M = 5 in this study, since the number of major folding patterns in some stable regions (e.g., the cingulate cortex, central sulcus, and superior temporal sulcus) are typically no more than 5 in most adult studies (Yücel et al., 2001; Sun et al., 2009; Pereira-Pedro and Bruner, 2016; Bruner et al., 2017). Of note, the proposed framework is generic for discovering folding patterns at other desired numbers.

3. Experiments and Results

We evaluated our method using a large-scale dataset including 595 healthy neonates. Specifically, we discovered representative cortical folding patterns independently in each of our selected four representative cortical regions, including the superior temporal gyrus (STG), inferior frontal gyrus (IFG), precuneus, and cingulate cortex, which were automatically labeled by the method in (Li et al., 2014c) based on the protocol in (Desikan et al., 2006). Then, we investigated the sex difference as well as hemispheric asymmetries in our identified infant folding patterns of these four regions. We also further validated our method on the public Human Connectome Project (HCP) dataset (Van Essen et al., 2013) (500 release version) with 511 healthy adults, and compared the discovered folding patterns as well as their hemispheric asymmetries between infant and adult cortical surfaces.

3.1. Validation on the Superior Temporal Gyrus

As a novel exploratory study with absence of ground truth, we validated our method on STG by the following manners: 1) to visually validate the discovered patterns, we displayed the discovered cortical folding patterns as well as included examples of each pattern in representative individuals; 2) to show that the proposed method can capture much richer information and identify more representative folding patterns, we compared the discovered patterns by our method based on multi-view curvatures and those by the original mean curvatures and gyral crest curves separately; 3) to evaluate the reproducibility of the identified patterns and the effectiveness of cluster number selection, we used two different clustering methods (i.e., hierarchical AP and spectral clustering); 4) to validate the reproducibility and scalability of the proposed method, we performed an additional 2-fold cross-validation, as conventionally adopted in exploratory neuroscientific studies; and 5) to validate the reliability of the proposed method, we further applied our method on simulated datasets.

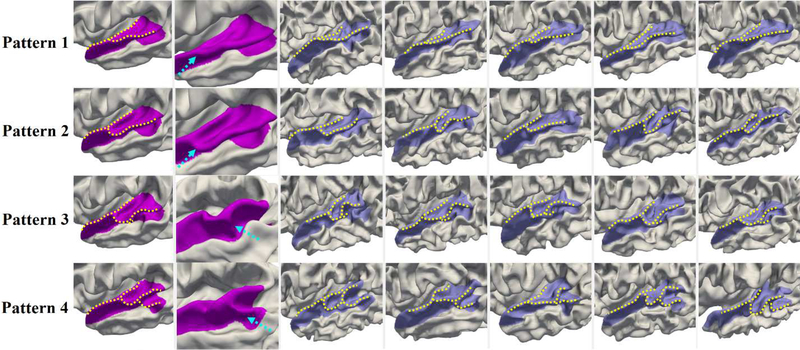
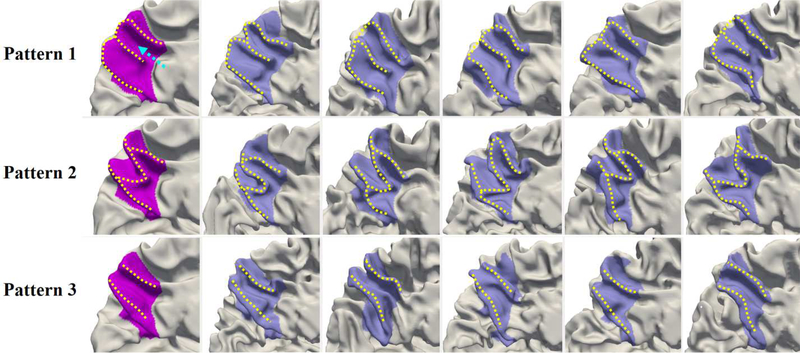
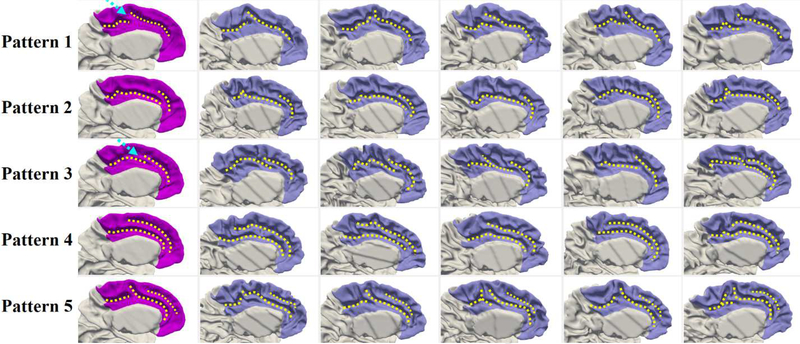
Fig. 6 shows the four discovered representative patterns of STG by the proposed method and representative individuals in each pattern, where we note the high intra-pattern similarity and low inter-pattern similarity. Herein, STG includes the cortical regions with labels of STG, transverse temporal cortex (Heschl’s gyrus), and banks of the superior temporal sulcus (STS) in the Desikan cortical parcellation (Desikan et al., 2006). In pattern 1, STG is relatively straight, and its posterior region is flat as shown in the close-up view (second column of Fig. 6). In pattern 2, STG slightly bends around its posterior region. Compared with pattern 2, pattern 3 is even more curved in the posterior part, with a small gyral fold in the anterior bank, as highlighted by a dashed arrow in the close-up view of pattern 3. Pattern 4 is the most bended pattern with a notable gyral branch in the posterior part. In 595 neonates, the percentage of each of the four identified patterns is 36.3%, 25.0%, 18.5%, and 20.2%, respectively.

Fig. 6.

Representative patterns of the superior temporal gyrus (STG). The first column displays the four discovered patterns. The second column presents the close-up views of distinct parts. The dashed arrows in patterns 1 and 2 point to the flat and bended posterior regions of STG, while in patterns 3 and 4 they point to the distinct gyral folds. Columns 3–7 display five typical individuals in each pattern, which indeed demonstrated that our discovered patterns exist in the dataset.

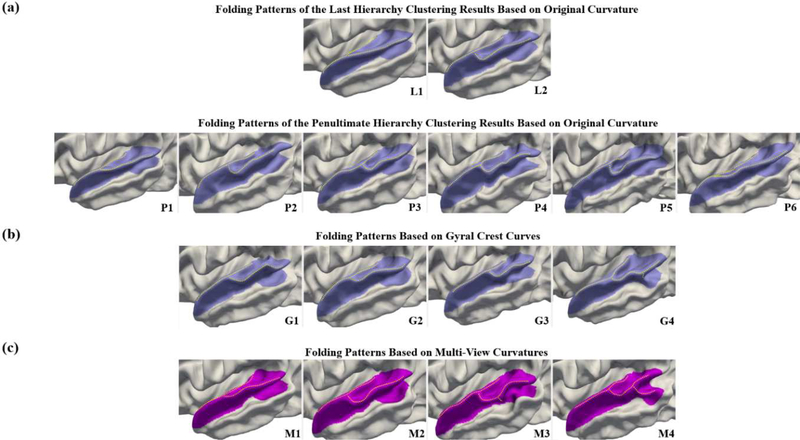
We compare the results by our proposed multi-view curvature features with those of using the original mean curvature map and gyral crest curves separately. We display in Fig. 7 the identified patterns by using the original mean curvature map (Fig. 7(a)), gyral crest curves (Fig. 7(b)), and the proposed multi-view curvature features (Fig. 7(c)). Note that, in our hierarchical AP, the resulting cluster number decreases from the earlier hierarchy to the later hierarchy. Based on the original mean curvature map, only 2 patterns (L1 and L2) emerge in the clustering result of the last hierarchy. Hence, we further display the clustering results of the penultimate hierarchy, which revealed 6 patterns (P1-P6). However, compared with the results (M1 to M4) by the proposed multi-view curvatures, all the patterns including L1 to L2 and P1 to P6 discovered based on the original mean curvature map can be actually grouped into two patterns M1 and M2. Notably, patterns M3 and M4 have not been identified based on the original mean curvature map, due to its limited capability in characterization of cortical folding. In addition, we compared the identified patterns by using gyral crest curves (G1 to G4) with our results (M1 to M4). As we can see, the patterns G1 and G3 are similar to our pattern M2, and the pattern G4 is similar to pattern M3. However, the pattern G2 is a transition state of the flat pattern M1 and the bended pattern M2. And the bended pattern M4 with a notable gyral branch is missing, indicating that gyral crest curves alone are also not able to comprehensively characterize cortical folding. In contrast, our proposed multi-view curvature features are able to better capture the complexity of cortical folding, and thus are more capable of revealing the diverse representative folding patterns.

Fig. 7.

Comparison of discovered patterns of the superior temporal gyrus by using (a) the original mean curvature map (L1 to P6), (b) the gyral crest curves (G1 to G4), and (c) the proposed multi-view curvature features (M1 to M4). Herein, patterns L1 to L2 and patterns P1 to P6 are the last hierarchy and penultimate hierarchy clustering results of using the original curvature feature, respectively. As we can see, the proposed method discovered four distinctive folding patterns, while using the original curvature feature or gyral crest curves essentially only discovered two or three distinct patterns, as several patterns are similar among their discovered folding patterns.

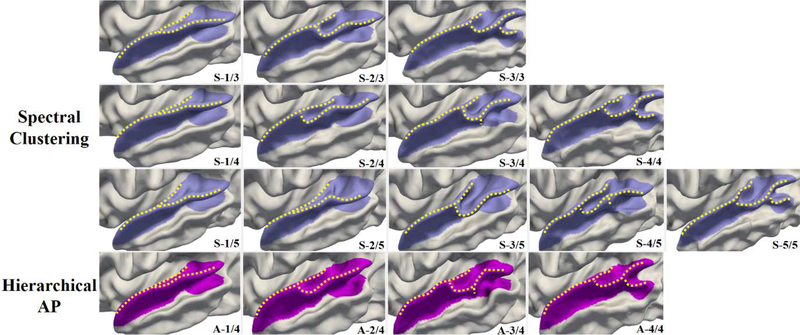
To evaluate the reproducibility of our results and the effectiveness of cluster number choosing, we compare our hierarchical AP method with an alternative clustering method: spectral clustering method (Ng et al., 2002; Von Luxburg, 2007), based on our fused similarity matrix. The results of spectral clustering with cluster number M = 3, 4 and 5 are shown in the first three rows in Fig. 8. As we can see, when the cluster number was set to M = 4, which is identical to the automatically determined cluster number by hierarchical AP, both clustering methods revealed very similar patterns. However, when M = 3, the third pattern A-3/4 by hierarchical AP has not been captured in the discovered patterns S-1/3 to S3/3 (corresponding to patterns A-1/4, A-2/4 and A-4/4, respectively) by spectral clustering. When M = 5, the first two patterns S-1/5 and S-2/5 discovered by spectral clustering actually can be summarized in one pattern similar to the pattern A-1/4, and the remaining patterns S-3/5 to S-5/5 correspond to patterns A2/4 to A-4/4. These results indicate that our hierarchical AP is able to automatically discover a proper number of distinctive folding patterns and also that our findings are reproducible using a different clustering approach.

Fig. 8.

Comparison of discovered patterns of the superior temporal gyrus by using spectral clustering (top rows) and hierarchical AP (bottom row). For spectral clustering, the cluster number M is predefined as 3, 4 and 5, and the corresponding discovered folding patterns are shown in the first three rows, respectively. While for the hierarchical AP, the four patterns A-1/4 to A-4/4 automatically emerge without predefining the cluster number.

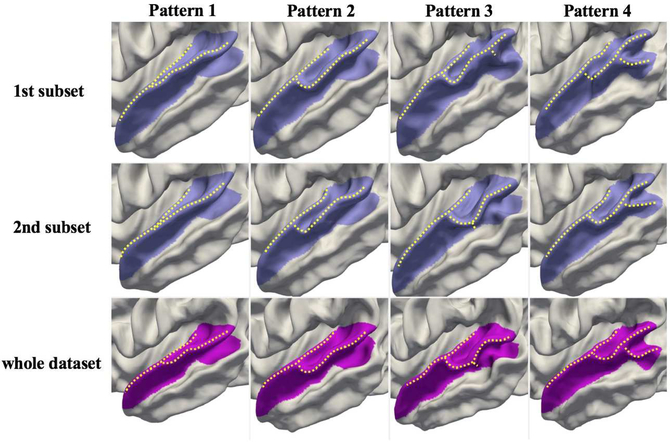
To further validate the reproducibility and scalability of the proposed method, we use 2-fold cross-validation to examine the differences of the revealed cortical folding patterns in these two sub-populations (Fig. 9), which were obtained by randomly and equally dividing the whole dataset. The first two rows in Fig. 9 display the discovered folding patterns of STG in the first and second sub-populations and the third row displays the folding patterns based on the whole dataset. As can be seen, the four folding patterns identified using both sub-populations are highly consistent and also similar to those identified using the whole dataset, indicating that our method can obtain reproducible and scalable results.

Fig. 9.

Comparison of discovered patterns of the superior temporal gyrus using 2-fold cross-validation (rows 1–2) vs. the whole dataset (bottom row). The identified folding patterns are similar across different sub-populations and also consistent with patterns discovered using the whole dataset, indicating that our results are reproducible, scalable, and reliable.

To further validate the proposed method, we apply it on simulated datasets, which are generated based on the simulated deformation of our discovered folding patterns in real neonatal dataset. The details of generation of the simulated datasets are described in Eq. 1 in Supplementary Materials. To simulate different degrees of deformation, we set the deformation ‘rate’ to 0.1, 0.2, 0.3, 0.4 and 0.5, respectively. Several surfaces simulated with typical deformation rates 0.3 and 0.5 are shown in Fig. S1 in Supplementary Materials. The discovered folding patterns of these two simulated datasets are shown in Fig. S2. As we can see, the discovered folding patterns in the simulated datasets are largely consistent with the folding patterns discovered in our neonatal dataset. The average discovery accuracies of correctly clustering the simulated surfaces into their corresponding patterns in the five simulated datasets with deformation rates 0.1, 0.2, 0.3, 0.4 and 0.5 are 100%, 100%, 100%, 93.5% and 85.2%, respectively. These results indicate that the proposed method is reliable and effective for cortical folding discovery.

3.2. Discovered Folding Patterns in Other Cortical Regions

For the precuneus, we discovered three typical patterns shown in Fig. 10. Specifically, in pattern 1, the precuneal gyrus shows a lowercase ‘m’ shape, with the precuneal sulcus (highlighted by the dashed arrow) reaching the edge of the precuneus. In pattern 2, the precuneal gyrus is similar to a capital ‘M’ shape. The precuneal sulcus does not reach the edge of the precuneus, while one additional sulcus branch shows in the middle of the dorsal peaks of the ‘M’ shape. As for pattern 3, compared to the first two patterns, we note the absence of the gyral structure right in the middle part of the precuneus and the presence of a long deep sulcus, thus exhibiting as an ‘II’ shape. The three discovered patterns occupy 47.7%, 27.1%, and 25.2% of our dataset, respectively.

Fig. 10.

Representative patterns of the precuneus. The first column displays the three discovered patterns. The dashed arrow highlights the precuneal sulcus, which reaches the edge of precuneus in patterns 1 and 3. Columns 2–6 display five typical individuals for each pattern.

In the inferior frontal gyrus (IFG), four representative folding patterns are discovered as shown in Fig. 11. Of note, IFG includes the pars opercularis, pars triangularis and pars orbitalis in the parcellation protocol in (Desikan et al., 2006). Pattern 1 resembles a slightly deformed capital ‘N’ shape, with an additional sulcus in the pars opercularis, as indicated by the dashed arrow. Pattern 2 has two continuous bended turns, showing as a lowercase ‘m’ shape slightly flattened around the middle. Compared with pattern 2, pattern 3 becomes more bended and is interrupted by a sulcus (highlighted by a dashed arrow) in the middle, thus morphing into a capital ‘M’ shape. As for pattern 4, it appears as a combination of pattern 2 or 3 with pattern 1 to some extent, as its anterior part is similar to that of patterns 2 or 3, while its posterior part is similar to that of pattern 1 with an additional sulcus in the pars opercularis (highlighted by a dashed arrow). These IFG patterns represent 25.2%, 29.6%, 30.8%, and 14.4% of our dataset, respectively.

Fig. 11.

Representative patterns of the inferior frontal gyrus. The first column displays the four discovered patterns. The dashed arrows point to the additional sulci. Columns 2–6 display five typical individuals for each pattern.

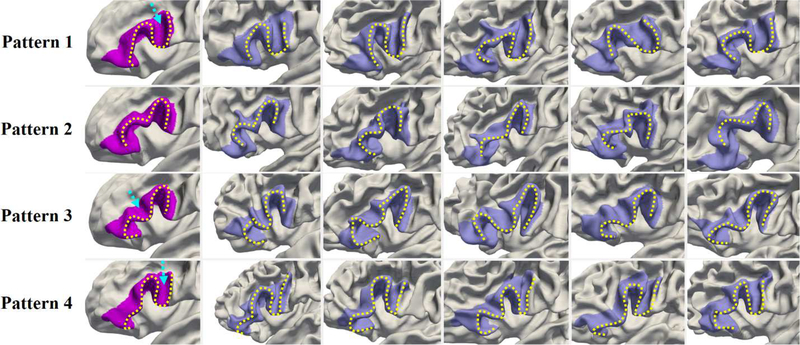
For the cingulate cortex, we found that the individual variability mainly locates in sulci rather than in gyri. Since the cingulate sulcus is spatially interlaced with the superior frontal gyrus, we examined a relatively large region, including the posterior cingulate cortex, caudal anterior-cingulate cortex, rostral anterior cingulate cortex, medial orbital frontal cortex, paracentral lobule, and medial superior frontal gyrus in the Desikan parecellation (Desikan et al., 2006). Five typical folding patterns were identified in the cingulate cortex, as shown in Fig. 12. Specifically, pattern 1 shows a long cingulate sulcus interrupted by a narrow gyrus in the posterior part. Pattern 2 shows a long continuous cingulate sulcus with a set of small folds topping its anterior part. The cingulate sulcus in pattern 3 is interrupted in the middle part, while pattern 4 contains two long parallel sulci. Pattern 5 can be seen as a representation of pattern 1 with an additional shallow parallel sulcus in the anterior part. The percentage of each pattern in our dataset is 19.8%, 16.6%, 18.7%, 23.0%, and 21.9%, respectively.

Fig. 12.

Representative patterns of the cingulate cortex. The first column displays the five discovered patterns. Columns 2–6 show five typical individuals for each pattern. In pattern 1 and pattern 3, the dashed arrows point to the locations, where the posterior and middle parts of the cingulate are interrupted.

3.3. Sex Differences of Cortical Folding Patterns

Our dataset contains 595 healthy neonates, and the numbers of males and females are relatively balanced, i.e., 308 males (51.8%) and 287 females (48.2%). However, in each discovered pattern, the male percentage is not always similar to the female percentage. To examine the possible association between folding patterns and sex, cross tabulation and Pearson chi-square test were performed in each region (Table 2). According to the results of our statistical analysis, sex difference in folding patterns was observed in the STG, IFG and cingulate cortex, but not in the precuneus. Moreover, the proportions of male/female infants listed in Table 2 for different patterns in four cortical regions were displayed in Fig. T1 in Supplementary Materials, in which the patterns with significantly different proportions between male and female infants were marked based on Two-Proportions Z-Test.

Table 2.

The folding patterns * sex cross tabulation and chi-square test results. ‘%’ is the percentage within patterns. ‘p-value’ denotes the 2-sided asymptotic significance of Pearson chi-square test. The significance value highlighted in bold means that sex difference (p-value < 0.05) was observed in the corresponding region. (Each percentage in the bracket denotes the ratio of the number of male (female) infants in each pattern to the total number of male (female) infants.)

Region	Pattern	Male (%)	Female (%)	Total	p-value
Superior Temporal Gyrus	Pattern 1	108 (35.1%)	108 (37.6%)	216	0.001
	Pattern 2	72 (23.4%)	77 (26.8%)	149
	Pattern 3	47 (15.2%)	63 (22.0%)	110
	Pattern 4	81 (26.3%)	39 (13.6%)	120
Precuneus	Pattern 1	137 (44.5%)	147(51.2%)	284	0.154
	Pattern 2	93 (30.2%)	68 (23.7%)	161
	Pattern 3	78 (25.3%)	72 (25.1%)	150
Inferior Frontal Gyrus	Pattern 1	83 (26.9%)	67 (23.3%)	150	0.022
	Pattern 2	88 (28.6%)	88 (30.7%)	176
	Pattern 3	82 (26.6%)	101 (35.2%)	183
	Pattern 4	55 (17.9%)	31 (10.8%)	86
Cingulate Cortex	Pattern 1	47 (15.3%)	71 (24.7%)	118	0.015
	Pattern 2	52 (16.9%)	47 (16.4%)	99
	Pattern 3	53 (17.2%)	58 (20.2%)	111
	Pattern 4	79 (25.6%)	58 (20.2%)	137
	Pattern 5	77 (25.0%)	53 (18.5%)	130

In Table 2, the p-value obtained by the Pearson chi-square test for STG is 0.001, which suggests that the folding patterns of STG are significantly associated with sex. We also note that pattern 3 is significantly less associated with males (15.2%) than females (22.0%), while pattern 4 is significantly more associated with males (26.3%) than females (13.6%), as marked in Fig. T1. As for patterns 1 and 2, they were largely evenly associated with both males and females. In IFG, the folding patterns are also significantly associated with sex with p-value = 0.022 given by Pearson chi-square test. From Fig. T1, we clearly see that pattern 3 contains significantly fewer males (26.6%) than females (35.2%), while pattern 4 contains significantly more males (17.9%) compared with females (10.8%). Another region with folding patterns significantly associated with sex is the cingulate cortex (p-value = 0.015), in which pattern 1 contains significantly fewer males (15.3%) than females (24.7%) as marked in Fig. T1. However, we did not observe significant sex difference in the precuneus (p-value = 0.154). In addition, we further performed two-sample t-test for testing the statistical dependence of sex distribution between different folding pattern pairs as shown in Table S1 in Supplementary Materials. According to Table S1, significant differences (p<0.05) of sex distributions were found between certain pairs of cortical folding patterns in STG, IFG and cingulate cortex, except for Precuneus. These results indicate that the sex differences of cortical folding patterns present in STG, IFG and cingulate cortex. Additionally, since sex is related to brain size, we investigated whether the folding patterns are related to brain volume using one-way analysis of variance (ANOVA). The corresponding results in Table S2 and corresponding brain volume distributions in Fig. T2 in Supplementary Materials show that the folding patterns are not related to brain volume in most cortical regions: STG, precuneus and cingulate cortex. However, brain volumes in different folding patterns of IFG significantly differ.

3.4. Hemispheric Asymmetries of Cortical Folding Patterns

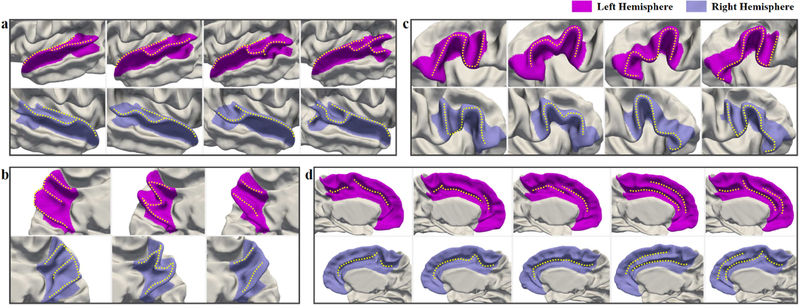
As all the above presented results are from the left hemisphere, to explore the left-right hemispheric asymmetries of infant cortical folding patterns, we further apply the proposed method onto the corresponding regions in the right hemispheres. The comparisons of discovered cortical folding patterns on both hemispheres are shown in Fig. 13, in which the most similar patterns are placed in the same column in each region. Besides, the percentages of each discovered infant folding pattern in the left and right hemispheres in four cortical regions are displayed in Table S6 in Supplementary Materials. As we can see, significant asymmetries are observed in STG, and slight asymmetries are observed in the cingulate cortex, while no hemispheric asymmetry is observed in IFG and precuneus.

Fig. 13.

Comparisons of the discovered infant folding patterns in the left and right hemispheres. (a) Superior Temporal Gyrus; (b) Precuneus; (c) Inferior Frontal Gyrus; (d) Cingulate Cortex.

In STG, the first two patterns in the right hemisphere are more curved than the corresponding first two patterns in the left hemisphere, thus no flat STG pattern is found in the right hemisphere. And the third pattern in the right hemisphere is much shorter than that of the left hemisphere and also no small gyral fold is found in the anterior bank of STS as shown in the close-up view of Fig. 6. Moreover, the most asymmetric pattern is the fourth pattern. Unlike the corresponding pattern with a notable gyral branch in the posterior part in the left hemisphere, there is only a small gyral fold in the inferior-posterior region of the banks of STS on the right hemisphere. As for the cingulate cortex, we found that most cortical folding patterns are similar on both hemispheres except the second and third patterns. Different from the corresponding patterns in the left hemisphere, the second pattern shows a cingulate sulcus without a set of small folds in the anterior part, and the third pattern shows a long smooth sulcus without interruption in the middle part in the right hemisphere.

3.5. Other Confounding Factors

Considering other confounding factors which may affect folding patterns, we further analyze the effects of postmenstrual ages (PA) at scan, twins, and preterm birth in our discovered folding patterns (see Supplementary Materials). To investigate whether the discovered folding patterns are related to PA at scan, one-way ANOVA is performed as shown in Table S3, and the distributions of PA at scan in different patterns of four regions are shown in Fig. T3. We can see that the folding patterns are not related to PA at scan in all regions except for the cingulate cortex. As for the other two factors, we firstly apply the proposed method on the subsets with either only singletons or only term-born neonates, respectively, to visually examine whether the discovered folding patterns are influenced by twins or premature neonates. The comparison of the discovered cortical folding patterns of the whole dataset and the singleton subset is shown in Fig. S3, and the comparison with the term-born neonate subset is shown in Fig. S4. These two figures indicate that the majority folding patterns are not influenced by the factors of twin and premature infants. Besides, to statistically analyze the independence of the cortical folding patterns with singleton/twin infants, the Pearson chi-square test is performed in each region as shown in Table S4. The proportions of singleton/twin infants in each pattern are displayed in Fig. T4, in which the patterns with significantly different proportions between singleton and twin infants are marked based on Two-Proportions Z-Test. Similarly, the results for studying the independence of folding patterns with term-born/premature infants are displayed in Table S5, and the corresponding plot is shown in Fig. T5. Moreover, since subjects overlapped in singleton/twin and term-born/premature groups, the Pearson chisquare test is further performed to analyze the independence of discovered cortical folding patterns and four subject groups (i.e., Singleton - Term-born, Twins - Term-born, Singletons - Premature, and Twins - Premature) in specific regions, as shown in Table S8. These tables and figures indicate that the folding patterns are independent of the factors singleton/twin, term-born/premature, and their combinations. In conclusion, all these results suggest that the majority of our discovered folding patterns cannot be significantly influenced by these confounding factors. (see Supplementary Materials for more details).

3.6. Validation on Adults

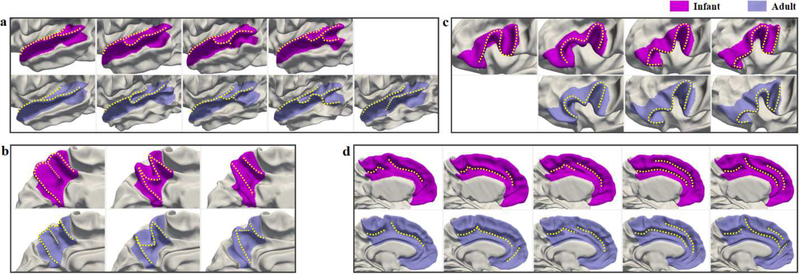
To investigate the applicability of our method to adult data, and more importantly, to compare the infant and adult folding patterns more intuitively and reveal their underlying relations, we apply the proposed method on a widely used adult dataset, i.e., the Human Connectome Project (HCP) (Van Essen et al., 2013). Herein, the HCP 500 Subjects + MEG2 Data Release² is adopted. Our experiment uses 511 young adults’ cortical surfaces, which are obtained through the HCP structural preprocessing pipeline and HCP FreeSurfer pipeline (Glasser et al., 2013). We extract the cortical features and discover the folding patterns using the same steps detailed in Section 2. Similarly, we explore the same four cortical regions in our infant study, including the left STG, precuneus, IFG, and cingulate cortex. Fig. 14 shows the comparisons of the discovered infant and adult cortical folding patterns. The majority of folding patterns discovered in the four cortical regions of adult brains are largely consistent with those of infant brains, indicating that our method is reliable and applicable to both infant and adult datasets. However, in STG, an extra pattern emerges in adult brains, which shows a notable gyral branch occupying the middle STS; as for IFG, pattern 1 discovered in the infant brain disappears in the adult brain.

Fig. 14.

Comparisons of the discovered folding patterns in infant and adult brains. (a) Superior Temporal Gyrus; (b) Precuneus; (c) Inferior Frontal Gyrus; (d) Cingulate Cortex.

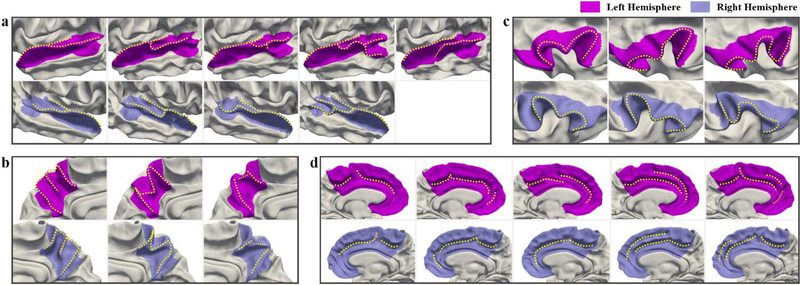
To explore the left-right hemispheric asymmetries of adult cortical folding patterns, and reveal the relations of the hemispheric asymmetries of infants and adults, we further apply the proposed method on the right hemispheres in HCP dataset. The comparisons of the discovered adult folding patterns in left and right hemispheres are shown in Fig. 15. The percentages of each discovered adult folding pattern in both hemispheres in four cortical regions are displayed in Table S7 in Supplementary Materials. As we can see, most of the discovered cortical folding patterns of adults in the four regions are largely symmetric on two hemispheres, while the hemispheric asymmetries are observed in STG and cingulate cortex. In STG, the posterior part of the third pattern in the right hemisphere is more bended and shorter than that in the left hemisphere, and no small gyral fold is found in the anterior bank of STS in the right hemisphere. Moreover, the most notable asymmetric pattern is the extra pattern presenting in the left hemisphere but absenting in the right hemisphere. As for the cingulate cortex, the asymmetric pattern is observed in the third pattern, which shows a long smooth sulcus in the right hemisphere, but shows a sulcus with an interruption in the middle part in the left hemisphere.

Fig. 15.

Comparisons of the discovered adult folding patterns in the left and right hemispheres. (a) Superior Temporal Gyrus; (b) Precuneus; (c) Inferior Frontal Gyrus; (d) Cingulate Cortex.

4. Discussion

4.1. Computational Method

One main contribution of this paper is that we have developed a novel computational framework based on multi-view curvature features for discovering the representative patterns of cortical folding in large-scale datasets. Our proposed method has several appealing aspects. First, we leveraged multi-view curvature features, i.e., the decomposed curvature maps at multiple spatial-frequency scales and high-level gyral crest curves, to comprehensively characterize the cortical folding. Indeed, the proposed multi-view features are able to identify the most representative patterns of cortical folding, a few of which were not depicted when using the original curvature map or gyral crest curves (Fig. 7). Second, we showed that our framework is robust to the clustering methods and that the identified patterns using affinity propagation clustering methods are reproducible when using an alternative clustering method (i.e., spectral clustering). Third, the proposed framework can easily integrate more geometric features, such as local gyrification (Luders et al., 2006; Schaer et al., 2008; Li et al., 2014d) and sulcal depth (Im et al., 2006b; Fornito et al., 2008) through the adaptive nonlinear fusion procedure. Fourth, it is generic and can be easily applied to any cortical region or even the whole cortex. Noting that most existing studies in this field generally group the folding patterns based on visual inspection (Ono et al., 1990; Borst et al., 2014; Garrison et al., 2015; Pereira-Pedro and Bruner, 2016; Bruner et al., 2017), the proposed method greatly contributes to neuroimaging research with a sharp focus on folding morphology analysis of specific cortical regions.

4.2. Comparison of Infant and Adult Folding Patterns

Another main contribution of this paper consists in unravelling the distinctive representative folding patterns of four typical cortical regions: STG, IFG, precuneus, and cingulate cortex, in both infant and adult brains. STG plays an important role in higher-order auditory processing, language processing and social perception (Buchsbaum et al., 2001; Bigler et al., 2007; Leff et al., 2009; Chang et al., 2010; Jou et al., 2010). Current evidence indicates that STG is structurally and functionally altered in many neurodevelopmental disorders, e.g., schizophrenia and autism (Delisi et al., 1994; Keshavan et al., 1998; De Bellis et al., 2002; Kasai et al., 2003; Bigler et al., 2007; Lee et al., 2007; Takahashi et al., 2009). Hence, discovering the typical folding patterns of STG might help spot atypical changes due to specific neurodevelopmental disorders. Herein, we discovered four typical folding patterns of STG in infants, which display similar morphologies to a large extent with the first four patterns discovered in HCP adult dataset, while an extra fifth folding pattern with a notable gyral branch occupying the middle STS is shown in the discovered adult patterns (Fig. 14-a). As for the fifth pattern, the reason for its absence in infants and existence in adults is unclear. It might emerge with postnatal neurodevelopment, since STG develops rapidly in folding degree during infancy (Li et al., 2014d). However, this needs to be further investigated in future studies. To the best of our knowledge, no previous studies have explored typical folding patterns of STG. Only a few studies explored the folding patterns of STS (Sun et al., 2009; Meng et al., 2016; Le Guen et al., 2018), which overlaps with the STG, thus providing meaningful information to our discovery. For instance, Le Guen et al. found the sulcal interruption (equal to the gyral branch in our study), named plis de passage (PP), in STS on the average surface of a subset from HCP. In particular, two types of PPs were found respectively in the posterior STS and in the middle STS. These findings are consistent with our discovered fourth pattern in both datasets and the fifth pattern in adult dataset, respectively. These also indirectly demonstrate the reliability of our discovered STG folding patterns. For the first time, we revealed representative neonatal folding patterns of STG in a large-scale dataset. These could be employed as references for the future comparative studies of normal and abnormal folding patterns of STG.

Precuneus is an important region involved in visuo-spatial integration, self-awareness, egocentric memory, motor imagery and autonoesis (Cavanna and Trimble, 2006; Bruner et al., 2017). In our experiment, the discovered folding patterns in precuneus of infant brains are largely consistent with that of adult brains, as shown in Fig. 14-b, which are also similar to other discoveries in the related existing adult studies. For instance, through multiple times of visual examination on a dataset with 50 adult specimens (Pereira-Pedro and Bruner, 2016; Bruner et al., 2017), Pereira-Pedro et al. classified the precuneus into three categories, totally 14 types, based on different sulcal connections and sulcal shape patterns. Among these types, their identified patterns B2, B3 and C3 are actually very similar to our discovered patterns 1, 2 and 3, respectively. Notably, they indicated that in B category, patterns B2 and B3 account for 88% of their whole dataset; while in C category, pattern C3 is the most frequent type. These findings on adults are largely in line with our results on neonates, and further emphasize that the three patterns discovered by our method are prevalent since early postnatal brain development.

IFG is critical for motor control (Swann et al., 2009; Hampshire et al., 2010; Swann et al., 2012) and language processing, including word comprehension and production (Indefrey and Levelt, 2000; Costafreda et al., 2006). In addition, IFG is the core structure of emotional empathy, involved in emotional contagion and emotion recognition (Schulte-Rüther et al., 2007; Shamay-Tsoory et al., 2009). Several studies have focused on studying the folding patterns of IFG in adults through visual inspection (Ebeling et al., 1989; Clark and Plante, 1998; Tomaiuolo et al., 1999). Ebeling et al. classified IFG folding patterns into four types, and Clark et al. further classified the third type into four subtypes. In our study, we discovered four distinct folding patterns in infants, among which, the last three folding patterns ‘mirrored’ the discovered adult folding patterns in HCP dataset, as shown in Fig. 14-c. Based on our qualitative comparison with previous studies, we found that the infant folding patterns 1 and 4 (Fig. 11) correspond to the subtypes of ‘TYPE III’ in (Clark and Plante, 1998), which show an additional sulcus in the posterior IFG. Furthermore, both pattern 2 and the bended pattern 3 ( a small extra sulcus presents in its middle part), correspond to the ‘TYPE I’ in (Clark and Plante, 1998). Since Clark et al. classified IFG folding patterns based on the structural connections of its surrounded sulci, they did not identify the gradual folding we discovered in patterns 2 and 3 with the same type of surrounded sulci. Overall, patterns ‘TYPE I’ and ‘TYPE III’, which have corresponding folding patterns in our results, are most prevalent (Clark and Plante, 1998) to represent 93.9% of their depicted 7 IFG patterns in adults. This indicates that our proposed method can discover the most representative folding patterns of IFG, and also suggests that the adult folding patterns in IFG are largely established at term birth.

As for the cingulate cortex, existing studies have reported that the anterior cingulate cortex is involved in emotional processing and performance monitoring of cognitive control (Devinsky et al., 1995; Rainville et al., 1997; Carter et al., 1998; Bush et al., 2000; MacDonald et al., 2000; Critchley et al., 2003; Botvinick et al., 2004; Kerns et al., 2004). The morphological differences in the cingulate cortex could associate with hallucinations and inhibitory control (Borst et al., 2014; Garrison et al., 2015). Herein, we discovered five typical folding patterns of infants, including both single sulcus types and parallel sulci types, which are largely consistent with our discovered patterns of adults in HCP dataset (Fig. 14-d), and are also in line with the discoveries in previous studies in adults and infants (Ono et al., 1990; Sun et al., 2009; Cachia et al., 2016; Meng et al., 2016). Specifically, the four types of the cingulate cortex patterns in adults (Sun et al., 2009) correspond to our neonatal patterns 4, 2, 3 and 5, respectively, while the four neonatal patterns identified in (Meng et al., 2016) correspond to our patterns 1, 4, 3 and 5, respectively. Thus, compared to both studies, our proposed method is able to identify an additional representative folding pattern, which represents more than 15% of subjects in the whole dataset, indicating the advantage of our method.

4.3. Sex Difference of Cortical Folding Patterns

The influence of sex on the cortical folding patterns is still largely unknown. To fill this knowledge gap, for the first time, we explored the sex difference in our discovered cortical folding patterns in the STG, IFG, cingulate cortex, and precuneus. As shown in Table 2, sex is significantly associated with cortical folding patterns in STG, IFG, and cingulate cortex, but not in precuneus. This indicates that some typical folding patterns may present male or female dominant trends. Some studies on older children and adults showed gender differences in cortical folding (Awate et al., 2010; Li et al., 2014d; Takerkart et al., 2017). For instance, Takerkart et al. found the gender differences in the spatial organization of sulcal pits in parts of the frontal cortex (overlapped with IFG) and the cingulate cortex, which are partially consistent with our results. In addition to cortical folding, many studies found gender differences in the STG, IFG and cingulate cortex in terms of cortical morphology (e.g., cortical volume, cortical thickness, and surface area) and functional activations (Blanton et al., 2004; Schirmer et al., 2004; Hofer et al., 2006; Im et al., 2006a; Koch et al., 2007; Wang et al., 2007; Schulte-Rüther et al., 2008; Brun et al., 2009; Li et al., 2014d; Meng et al., 2014). Specifically, the cortical volume of IFG, the cortical thickness of IFG and STG, and the surface areas of auditory structure (parts of the STG) and cingulate region, are larger in females than in males, which might be related to the general higher language skills in females (Blanton et al., 2004; Im et al., 2006a; Brun et al., 2009). These studies show that structural and functional gender differences exist in the STG, IFG and cingulate region, which might also be related to cortical folding morphology as highlighted by our findings.

4.4. Hemispheric Asymmetries of Cortical Folding Patterns

Human brain exhibits hemispheric asymmetries in terms of structure and function (Toga and Thompson, 2003). In existing infant studies, cortical hemispheric asymmetries, which appear before term birth and largely preserve during postnatal brain development, have been observed in various cortical measurements, e.g., surface area, sulcal depth, cortical thickness, vertex position, as well as sulcal pits distribution (Hill et al., 2010; Li et al., 2014d; Meng et al., 2014; Li et al., 2015a; Le Guen et al., 2017; Takerkart et al., 2017; Im and Grant, 2018). Herein, we found hemispheric asymmetries present in STG and cingulate cortex by comparing our discovered cortical folding patterns in left and right hemispheres of both infant and adult brains. Consistent with a number of studies in infants (Hill et al., 2010; Glasel et al., 2011; Li et al., 2014b; Li et al., 2014d; Meng et al., 2014; Leroy et al., 2015; Li et al., 2015a) as well as adults (Im et al., 2009; Leroy et al., 2015; Maingault et al., 2016; Le Guen et al., 2018), we found that the most significant hemispheric asymmetries of cortical folding are in STG, which might be related to the lateralization of language functions and the asymmetric genetic programs. Specifically, in infants, the most asymmetric folding pattern of STG exists an obvious gyral branch in the banks of STS on the left hemisphere, while no such gyral branch is found on the right hemisphere, as shown in Fig. 13. Interestingly, in adults, this folding pattern is present in the right hemisphere, occupying a small percentage in the HCP. The most asymmetric folding pattern in adults is the extra folding pattern with a notable gyral branch in the middle STS, which is only present in the left hemisphere, as displayed in Fig. 15. Recently, it has been shown that STS is the most asymmetric sulcus in both children and adults, and the asymmetry of STS is associated with more frequent sulcal interruptions, i.e., PPs, shown in the left hemisphere (Leroy et al., 2015; Le Guen et al., 2018). This is consistent with our discovered fourth pattern in both datasets and the fifth pattern in HCP in the left hemisphere. Le Guen et al. also found that when the PPs are present in the right hemisphere, they are mostly located at the junction between the STS main horizontal branch and its caudal branch, and the pattern with this kind of PPs occupies a small percentage (11.2%) in their dataset. This supports our finding that the fourth pattern with gyral branch in the posterior STG exists in the right hemisphere, and it also occupies a small percentage (11.7%, see Table S7 in Supplementary Materials). Moreover, we also found that the posterior temporal region of third and fourth patterns in the right hemisphere is much shorter than those in the left hemisphere, which is in line with previous findings that the right Sylvian fissure is shorter than the left one (LeMay, 1984) and the left hemisphere presents a larger planum temporale (Geschwind and Levitsky, 1968; Glasel et al., 2011). As for the cingulate cortex, slightly asymmetric patterns are found based on the presence and extension of the paracingulate sulcus. From Tables S6 and S7, and Fig. 13and 15, we clearly see that the paracingulate sulcus occur more pronounced and more often in the ACC of the left hemisphere (patterns 2, 4, and 5) as compared to that of the right hemisphere in both infant and adult datasets, in line with a previous study in adults (Huster et al., 2007). More importantly, from Tables S6 and S7, we can see that in precuneus, IFG, and cingulate cortex, the percentages of most of the corresponding patterns in the left and right hemispheres are largely similar, while the percentages in STG with significant hemispheric asymmetries are quite different. This further indicates that the discovered folding patterns presenting hemispheric asymmetries are reliable. In summary, our findings suggest that hemispheric asymmetries of cortical folding patterns in adults are likely present in neonates.

4.5 Limitations and Future Work

This work has several limitations. First, in our current method, we only leveraged curvature-derived multi-view features for discovering cortical folding patterns. One can also use the proposed generic framework to incorporate more cortical features, e.g., local gyrification and sulcal depth, to examine the possible relevance of other features. Second, although the most representative cortical folding patterns discovered in each region are largely consistent when applying the method on different sub-datasets, the cluster number automatically determined by hierarchical AP is not always very stable and the appearance of a few folding patterns could slightly change. As shown in Fig. S3 and Fig. S4 in Supplementary Materials, several folding patterns occupying small percentages in the whole dataset may not be discovered when using small sub-datasets, but the major cortical folding patterns are consistently present. Third, although we found that the discovered cortical folding patterns of neonates are largely in line with our discovered adult patterns in HCP and reported visual examination results in related studies, we also found few STG and IFG patterns differed between infants and adults. The mechanisms driving such differences are still unclear, but it may relate to rapid development of cortical folding in STG and IFG during infancy (Li et al., 2014d). Further studies are needed to give more insights into these findings. Last, we also note that little is known about the underlying mechanisms of forming these variable folding patterns from a smooth neuronal tube during prenatal brain development. As white matter fiber connectivity is thought to be a major driving force of cortical folding formation (Van Essen, 1997; Nie et al., 2011; Li et al., 2015b), it would be interesting to investigate the relationship between these discovered folding patterns and the underlying fiber connectivity using diffusion tensor imaging. In our future work, we will further apply our proposed method to fetal datasets at different gestational ages to examine when these major folding patterns emerge, and apply it to toddler and also other adult datasets. These findings will thus reveal the evolution of cortical folding patterns during prenatal and postnatal brain development. Moreover, we will investigate the identified cortical folding patterns in relation to genetics, cognitive scores, and early neurodevelopmental disorders.

5. Conclusion

We have presented a novel computational method to automatically explore the most representative folding patterns of the cerebral cortex in a large-scale dataset of neonates. Leveraging the multi-view curvature-derived representations, our method is capable of comprehensively capturing the complexity and variability of cortical folding patterns. We unprecedentedly identified in neonatal brains the representative distinct folding patterns of the superior temporal gyrus (STG), inferior frontal gyrus (IFG), precuneus, and cingulate cortex. On one hand, most of the folding patterns in the infant cortex are in line with those in the adult cortex discovered through our method, and also in line with previous reports in adult studies largely based on laborious and time-consuming visual inspection, suggesting that the variability of folding patterns has been largely established at term birth. On the other hand, our results revealed a few new folding patterns of specific cortical regions that were absent in the state-of-the-art studies. Moreover, for the first time, we found sex differences of neonatal folding patterns in the STG, IFG and cingulate cortex, as well as hemispheric asymmetries of folding patterns in the STG and cingulate cortex. Our method can be widely applied to automatically identify cortical folding patterns and study their possible relationships with cognition, function, connectivity, and brain disorders. (Li et al., 2015c)

Highlights:

1. A novel method for exploring representative folding patterns of human brains;

2. Applications to discover representative folding patterns in several cortical regions;

3. Folding patterns show region-specific sex differences and hemispheric asymmetries;

4. Certain major cortical folding patterns of adults are largely established at term birth.