Theoretical analysis of spectral precision in spectroscopic single-molecule localization microscopy

Abstract

Spectroscopic single-molecule localization microscopy (sSMLM) is a novel super-resolution imaging technology, which simultaneously records the nanoscopic location and the corresponding full emission spectrum of every stochastic single-molecule emission event. This spectroscopic imaging capability of sSMLM necessitates the establishment of a theoretical foundation of the newly introduced spectral precision and to guide the system design and optimization. Based on numerical simulation and analytical solution, we introduced such a theoretical model to analyze spectral precision by considering the main system parameters, including signal and background shot noises, readout noise, and the spectral calibration procedure. Using this model, we demonstrated the delicate balance among these parameters in achieving the optimal spectral precision and discovered that the best spectral precision can only be achieved at a particular system spectral dispersion. For example, with a given signal of 3000 photons and a readout noise of 2 e-, a system spectral dispersion of 1.6 nm/pixel is required for sSMLM to achieve the highest spectral precision of 1.31 nm.

I. INTRODUCTION

We¹ and several other research groups^2–4 recently reported a new class of photon localization microscopy, which captures and analyzes the full emission spectrum of every stochastic single-molecule emission and simultaneously reveals their spatial localizations with nanoscale precision. Here we refer to this class as spectroscopic single-molecule localization microscopy (sSMLM). Its ability to acquire spectroscopic signatures enables specific identification of different types of individual molecules and, therefore, the number of different molecules that can be imaged simultaneously is no longer constrained by the discrete color channels in existing multi-color super-resolution microscopy methods.^1–3 In addition, resolving minute spectroscopic variations in fluorescence emission associated with molecular compositional and conformational heterogeneities at the single-molecule level enables studying inter-molecular and intra-molecular interactions.^4,5 Furthermore, its potential can be extended for chemical recognitions by probing chemical reactions at the single-molecule level.^6–9 Ultimately, sSMLM may allow better understanding of properties of single molecules rather than average properties of a large molecule population in current spectroscopy, which will benefit cell and molecular biology studies. Motivated by its great promise, sSMLM has been implemented by multiple groups with diverse optical designs and imaging parameters, which signifies the need for a unified theoretical framework to correlate key system parameters and their contributions to the performance of sSMLM, especially the newly introduced spectral precision.

sSMLM simultaneously records the diffraction-limited spatial images of stochastically emitting fluorescent molecules and the spectrally dispersed images (spectral images) resulting from the convolution of diffraction-limited point-spread-function (PSF) and the linearly spread spectral signature distinct to individual molecules. While researchers have developed theoretical models for localizing molecules from the spatial images with the highest spatial precision,^10–14 spectral precision in extracting molecules’ spectroscopic signatures from the spectral image is yet to be fully understood. Since sSMLM’s goal is to obtain the optimal precisions from both the diffraction-limited spatial and spectral images, we introduced a theoretical model with numerical simulation and analytical solution to analyze spectral precision with contributions from all key system parameters. We further quantitatively evaluated the contributions from image noises and the spectral calibration procedure with respect to the system’s spectral dispersion to provide a guideline in optimizing the sSMLM system.

II. METHODS

A. Working principle of sSMLM

Building upon SMLM, sSMLM can be realized by inserting a dispersive optical element, such as a prism or a diffraction grating. Using the dispersive element, we can divide the emitted photons from every stochastic single-molecule emission event into two groups, which, respectively, form one spatial image and one spectral image.^1,2 Thus, every recorded sSMLM image frame consists of simultaneously acquired spatial and spectral images of all the stochastic emission events that happened during the exposure time of the image frame. We used the spatial image to localize the positions of individual emission events and further to establish the reference point for analyzing the spectroscopic signatures in the spectral image.^1–4

B. Spectral precision

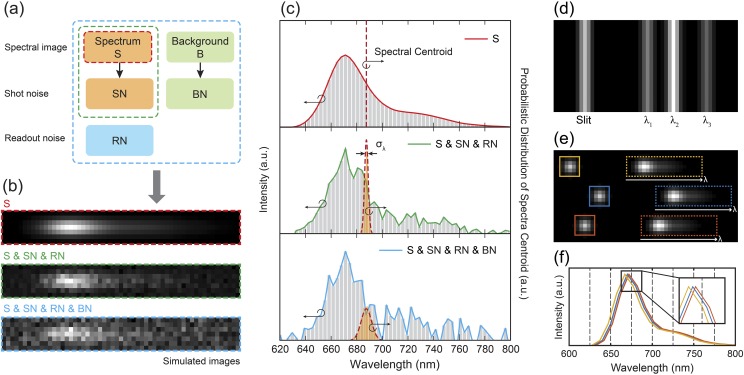
As illustrated in Fig. 1(a), the recorded spectral images comprise an emission spectrum and the background, which are governed by the intrinsic characteristics of the samples. Image noises, including shot noise from both the emission spectrum and background, and the readout noise collectively contribute to the fluctuations in the spectral images [Figs. 1(a) and 1(b)]. Among several estimators that have been tested in SMLM, including least-square fitting and maximum-likelihood fitting,^15,16 we use the commonly accepted weighted centroid method to represent the emission spectrum.^17,18 The spectral centroid wavelength can be obtained via the weighted centroid method (as the weighted mean) defined by

$${\lambda }_c=\frac{{\sum }_i{\lambda }_i{S}_i}{{\sum }_i{S}_i},$$ (1)

where λ_i is the wavelength determined by the calibration process at pixel i and S_i is the signal intensity at each pixel i after the background subtraction. Spectral precision is described by the standard deviation of the centroid wavelength distribution, which is typically a Gaussian distribution since it reflects the distribution of statistical errors in experimental measurements.

FIG. 1.

(a) Summary of the different image noises. (b) Simulated spectral images illustrate the contributions of different image noises. The ideal spectral image (S) shown in the red box. Image noises, including SN and RN, were added to the ideal spectral image (in the green box). When background (B) is presented (20 000 photons in total), BN further increases the fluctuation of the spectral image (in the blue box). (c) Spectra (left vertical-axis) of the three simulated spectral images shown in (b) and their spectral precisions. To emphasize the influence of different image noises, we first subtracted the background and visualized the spectral image in (b) and the spectra in (c). (d) Simulated reference image for spectral calibration. (e) An ideal sSMLM image, which contains three emission events, recorded in a single camera frame. Every recorded sSMLM image frame consists of simultaneously acquired spatial and spectral images. (f) The pixelated emission spectra from (e). The inset shows the magnified view of the black box in (f) to illustrate the spectral-shift error. a.u.: arbitrary units.

C. Image noise model

To investigate the influence of various noise sources on the spectral precision, we established the camera noise model using the electron multiplying charge-coupled device (EMCCD) camera (iXon897, Andor). Given the electron multiplication (EM) gain process, the noise model can be expressed as¹⁴

$$Y_{i,j}=\left(S_{i,j}+B_{px,i,j}\right)+F_{EM}\left(S{N}_{i,j}+B{N}_{i,j}\right)+R{N}_{i,j},$$ (2)

where S_i,j is the emission signal of single-molecule fluorescence emitters at the pixel (i, j), Y_i,j is the EMCCD output signal of S_i,j, B_px,i,j is the background per pixel, $F_{EM}\left(=\sqrt{2}\right)$ is the excess noise factor generated by the EM process,¹⁰ SN_i,j is the shot noise, BN_i,j is the background noise, and RN_i,j is the readout noise. Note that (S_i,j + SN_i,j) and (B_px,i,j + BN_i,j) follow Poisson distributions with mean values of S_i,j and B_px,i,j, respectively, and RN_i,j follows Gaussian distribution with a zero mean and a standard deviation equaling to the rms readout noise. The dark noise is negligible for a deeply cooled EMCCD camera with a fast acquisition time (∼10 ms).¹⁴

D. Numerical simulation

We implemented numerical simulation by generating the noise-added spectral images of a single-molecule fluorescence emitter. To simulate the emission spectrum of single-molecule fluorescence emitters, a spatial image was first produced. The PSF was modeled as a two-dimensional (2D) Gaussian function and the full-width-at-half-maximum (FWHM) of PSF was set to be 2.57 pixels, which represents the PSF acquired by an EMCCD with a pixel size of 16 µm using a 100× Nikon TIRF objective lens (NA = 1.49) and a 1.5× tube lens (f = 300 mm) at the emission wavelength of 670 nm. Using the generated PSF, an ideal spectral image was calculated at a certain spectral dispersion as a result of the convolution of the PSF and the emission spectra of a single fluorescent molecule (Alexa Fluor 647). The spectral dispersion of the simulated spectral images was defined as the wavelength range per individual pixel. Assuming the spectral dispersion is linear in a given sSMLM system, it can be expressed that Δλ = W_p × R_d (nm/pixel), where W_p is the width of the camera pixel (μm) and R_d is the reciprocal linear dispersion and shows the separation of wavelength (nm) per interval distance (μm). The representative images of the simulated spectral image of a single fluorescence molecule at the spectral dispersion of 3.2 nm/pixel with and without image noises are illustrated in Fig. 1(b). All key characteristic parameters of the EMCCD camera used in simulations are listed in Table I.

TABLE I.

List of camera parameters used in simulations.

	Pixel	QEa	EM			ADU
Camera	size	at 670 nm	gainb	RNc	FEMd	gaine
iXon 897	16 µm	92.5%	100	2 e-	$\sqrt{2}$	14.2 e-/count

^aQE is the quantum efficiency.

^bEM gain is the electron multiplication gain.

^cRN is the readout noise.

^dF_EM is the excess noise factor.

^eADU gain is the analog-to-digital unit.

Considering that the total amount of background presented in the entire spectral image is a constant, the number of photons from the background allocated to each camera pixel is inversely proportional to the spectral dispersion. Therefore, the photon number of the background recorded by each pixel can be defined as

$$B_{px}=\frac{B}{N_{\lambda }{N}_y}=\frac{B}{\left(W_{\lambda }/\mathrm{\Delta }\lambda \right)N_y},$$ (3)

where B_px is the background per pixel, B is the total background, N_y and N_λ are the number of pixels along the y-axis and spectral-axis, respectively, W_λ is the wavelength range used in spectral analysis, and Δλ is the spectral dispersion (nm/pixel). For instance, when the y-axis contains 7 pixels and the wavelength range is 160 nm, the total background of 5600 photons assigns 20 photons per pixel at the spectral dispersion of 4 nm/pixel.

Finally, we generated 10 000 noise-added spectral images at different B according to the noise model defined in Eq. (3). We then obtained the emission spectra by binning the 7 pixels along the y-axis. In this study, we used a wavelength range of 160 nm (620 nm–780 nm) for spectral analysis using the weighted centroid method.

E. Spectral calibration procedure

In order to convert the recorded spectral images in the spatial domain into the emission spectrum in the wavelength domain, a spectral calibration procedure is required to establish the spatial-wavelength mapping, which is specific to individual sSMLM systems. Unique to sSMLM, the spectral calibration procedure refers to not only the acquisition of the reference image for the conventional spectral calibration (Step 1) but also the conversion of the recorded spectral images into emission spectrum in the wavelength domain (Step 2).

In step 1, we first recorded a reference image using a narrow slit illuminated by using a spectrometer wavelength calibration light source, as illustrated by Fig. 1(d). A single line corresponds to the slit position in the spatial image, whereas the multiple spectral lines in the spectral image correspond to the emissions centered at λ₁, λ₂, and λ₃ of the calibration source. Then, the pixel positions and wavelengths of these spectral lines were fitted by a linear polynomial function using a customized MATLAB code. We used the fitted function to determine the conventional spectral calibration between the spatial image and the spectral image.

In step 2, we converted the recorded spectral images of individual stochastic radiation events from pixel position to wavelength, as illustrated in Figs. 1(e) and 1(f). Here, the spatial images of the radiation events were used as the reference location for the spectral analysis. Accordingly, spectral windows with the same wavelength range can be determined by the spectral calibration obtained in step 1, shown as the colored boxes in Fig. 1(e). Therefore, by integrating the spectral images along the y-axis, we can obtain the emission spectra, as depicted in Fig. 1(f).

F. Spectral-shift error

Unique to sSMLM, the spectral calibration procedure (step 2) introduces a systematic error in converting the recorded spectral images in the spatial domain into the emission spectrum in the wavelength domain. This leads to a sub-pixel level spectral shift in calculating the spectral centroid, which is defined as the spectral-shift error. The spectral-shift error becomes more significant for the system featuring lower spectral dispersion. As an example, an ideal sSMLM image of three emission events at system a spectral dispersion of 10 nm/pixel is illustrated in Fig. 1(e). After the spectral analysis, the pixelated emission spectra of each event are plotted in Fig. 1(f). The inset shows the magnified view of the black boxed region, illustrating the spectral-shift error. Notably, the spectral analysis contains two types of uncertainties: the localization uncertainty and the spectral-shift error, which are induced by the localization analysis and the spectral calibration procedure, respectively. Since the localization precision is typically at a deep-sub-pixel level, we assume that its influence on the spectra-shift error is negligible.

G. Analytical solution

To better understand the underlying principle, we further established the analytical solution of the spectral precision. To simplify the analytical model, here we assume that the spectral image consists of the emission spectrum described as a 2D Gaussian function,^10–12

$$S\left(\lambda ,y\right)=N\frac{1}{\sqrt{2\pi s_{\lambda }^2}}{e}^{-\frac{{\left(\lambda -{\lambda }_c\right)}^2}{2s_{\lambda }^2}}\frac{1}{\sqrt{2\pi s_y^2}}{e}^{-\frac{{\left(y-y_c\right)}^2}{2s_y^2}},$$ (4)

where N is the total number of photons of the emission signal acquired in the spectral image, s_y and s_λ are the standard deviations of the Gaussian function along the y-axis and spectral-axis, respectively, and y_c and λ_c are the weighted centroids of the Gaussian function along the y-axis and spectral-axis, respectively.

Since the spectral images are recorded using a pixelated senor array, the spectral centroid can be expressed in the discretized form as

$${\lambda }_c=\frac{{\sum }_{i,j}\left[\left(S_{i,j}+R_{i,j}\right){\lambda }_{i,j}\right]}{{\sum }_{i,j}\left(S_{i,j}+R_{i,j}\right)},$$ (5)

where i, j are the pixel coordinates in the spectral image and R is a noise contribution due to various sources, including the shot noise (n_s,i,j) of the emission spectrum, the shot noise of the background (n_bg), and the readout noise (n_ro). In the analytical solution, we assume that n_s,i,j and n_bg follow Poisson distributions with the mean values of S_i,j and B_px, respectively, whereas n_ro follows Gaussian distribution with a zero mean. Given the main noise sources, r_i,j (the standard deviation of R_i,j) can be written as $r_{i,j}^2=n_{s,i,j}^2+n_{bg}^2+n_{ro}^2$. Therefore, the spectral precision, σ_λ, can be described using propagation of error assuming that the errors are uncorrelated,^11,19–21

$$\begin{array}{ccc}\hfill {\sigma }_{\lambda }^2& =\hfill & \frac{{\sum }_{i,j}{\left({\lambda }_{i,j}-{\lambda }_c\right)}^2{n}_{s,i,j}^2}{N^2}+\frac{n_{bg}^2{\sum }_{i,j}{\left({\lambda }_{i,j}-{\lambda }_c\right)}^2}{N^2}\hfill \\ \hfill & \hfill & +\frac{n_{ro}^2{\sum }_{i,j}{\left({\lambda }_{i,j}-{\lambda }_c\right)}^2}{N^2}.\hfill \end{array}$$ (6)

In Eq. (6), the first term represents the contribution of shot noise from the emission spectrum (σ_s). In a similar way to calculate its contribution in localization precision,^11,13 σ_s along the spectral-axis can be written as ${\sigma }_s^2=s_{\lambda }^2/N$. Note that we ignored the pixelation noise to simplify the analytical solution as its influence is less than 5% under our experimental condition (when spectral dispersion <10 nm/pixel).¹³

The second term in Eq. (6) represents the contribution of shot noise from the background σ_bg and here we have

$$\begin{array}{ccc}\hfill {\sigma }_{bg}^2& =\hfill & \frac{n_{bg}^2}{N^2}\sum _{i,j}{\left({\lambda }_{i,j}-{\lambda }_c\right)}^2\hfill \\ \hfill & =\hfill & \frac{n_{bg}^2}{\mathrm{\Delta }\lambda \mathrm{\Delta }y{N}^2}\int {\int }_{-\infty }^{+\infty }{\left({\lambda }_{i,j}-{\lambda }_c\right)}^{2}d\lambda dy,\hfill \end{array}$$ (7)

where Δλ is the spectral dispersion (nm/pixel) and Δy is the image pixel size along the y-axis (nm). The size of the kernel used in our analytical model was set to be [−4s_y, 4s_y] along the y-axis and [−4s_λ, 4s_λ] along the spectral-axis, respectively, around the weighted centroid (λ_c, y_c) in order to cover the area corresponding to 99.9% of the signal in the spectral image. Thus

$$\begin{array}{ccc}\hfill {\sigma }_{bg}^2& =\hfill & \frac{n_{bg}^2}{\mathrm{\Delta }\lambda N^2}{\int }_{-4s_{\lambda }}^{+4s_{\lambda }}{\left({\lambda }_i-{\lambda }_c\right)}^{2}d\lambda \frac{1}{\mathrm{\Delta }y}{\int }_{-4s_y}^{+4s_y}dy\hfill \\ \hfill & =\hfill & \frac{1024n_{bg}^2{s_{\lambda }}^3{s}_y}{3\mathrm{\Delta }\lambda \mathrm{\Delta }\lambda N^2},\hfill \end{array}$$ (8)

where $n_{bg}^2=B_{px}=\frac{B}{\left(8s_{\lambda }/\mathrm{\Delta }\lambda \right)\left(8s_y/\mathrm{\Delta }y\right)}=\frac{B\mathrm{\Delta }\lambda \mathrm{\Delta }y}{64s_{\lambda }{s}_y}$ since background noise is determined by the background per pixel. Therefore, we have

$${\sigma }_{bg}^2=\left(\frac{B\mathrm{\Delta }\lambda \mathrm{\Delta }y}{64s_{\lambda }{s}_y}\right)\frac{1024s_{\lambda }^3{s}_y}{3\mathrm{\Delta }\lambda \mathrm{\Delta }y{N}^2}=\frac{16B{s}_{\lambda }^2}{3N^2}.$$ (9)

The third term in Eq. (6) represents the contribution of readout noise (σ_ro). Since readout noise is constant for each pixel, we have

$$\begin{array}{ccc}\hfill {\sigma }_{ro}^2& =\hfill & \frac{n_{ro}^2}{N^2}\sum _{i,j}{\left({\lambda }_{i,j}-{\lambda }_c\right)}^2=\frac{n_{ro}^2}{\mathrm{\Delta }\lambda \mathrm{\Delta }y{N}^2}\int {\int }_{-\infty }^{+\infty }{\left({\lambda }_{i,j}-{\lambda }_c\right)}^{2}d\lambda dy\hfill \\ \hfill & =\hfill & \frac{1024n_{ro}^2{s}_{\lambda }^3{s}_y}{3\mathrm{\Delta }\lambda \mathrm{\Delta }y{N}^2}.\hfill \end{array}$$ (10)

Additionally, the uncertainty of the spectral-shift error, σ_sse, is linearly proportional to Δλ. As the spectral-shift error follows a top-hat distribution, σ_sse can be quantitatively expressed as¹³

$${\sigma }_{sse}^2=\frac{\mathrm{\Delta }{\lambda }^2}{12}.$$ (11)

In conclusion, by adding a factor of the EM process to the shot noise in the case of the EMCCD camera,¹¹ the overall spectral precision is expressed as

$$\begin{array}{ccc}\hfill {\sigma }_{\lambda }^2& =\hfill & F_{EM}^2\left({\sigma }_s^2+{\sigma }_{bg}^2\right)+{\sigma }_{ro}^2+{\sigma }_{sse}^2\hfill \\ \hfill & =\hfill & F_{EM}^2\left(\frac{s_{\lambda }^2}{N}+\frac{16B{s}_{\lambda }^2}{3N^2}\right)+\frac{1024n_{ro}^2{s}_{\lambda }^3{s}_y}{3\mathrm{\Delta }\lambda \mathrm{\Delta }y{N}^2}+\frac{\mathrm{\Delta }{\lambda }^2}{12},\hfill \end{array}$$ (12)

where F_EM is approximately $\sqrt{2}$ due to the EM gain when the EMCCD camera is used for image acquisition.¹⁰

III. RESULTS

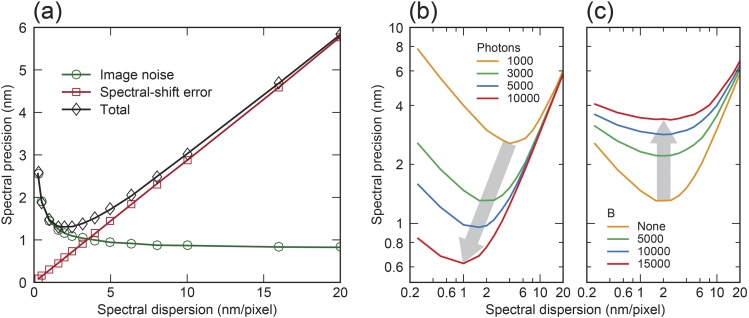
Only considering the contributions from the three aforementioned primary forms of image noises, the overall characteristic scaling behavior of spectral precision with respect to spectral dispersion was calculated as the green curve in Fig. 2(a). By contrast, the spectral-shift error is linearly proportional to the pixel size and, thus, can be significant in a system with lower spectral dispersion [the red curve in Fig. 2(a)]. Considering the competing contributions from image noises and spectral-shift error, our numerical models predicted the optimal spectral dispersion in order to achieve the best spectral precision [the black curve in Fig. 2(a)]. For example, the best spectral precision of 1.31 nm can be achieved by designing the optical system with a spectral dispersion of 1.6 nm/pixel for a blinking event with 3000 photons.

FIG. 2.

(a) Spectral precision as a function of spectral dispersion when considering image noises (green circles), spectral-shift error (red squares), and their overall contributions (black diamonds). (b) Dependence of spectral precision on spectral dispersion under different photon numbers without the background. (c) Dependence of spectral precision on spectral dispersion with different background levels when the spectral signal contains 3000 photons. Note that the iteration number of numerical simulations is 10 000.

Our model further enables quantitative evaluation of all experimental conditions. Using the photon number as an example, while one would anticipate that increasing photon number will favorably improve the spectral precision, our study suggests that the best spectral precision can only be achieved with a matching spectral dispersion at a given photon number, as shown in Fig. 2(b). Taking 20-nm/pixel spectral dispersion as an example of a non-optimal condition, increasing photon number from 1000 to 10 000 will marginally improve the spectral precision from 6.02 nm to 5.79 nm. By contrast, respectively matching optimal spectral dispersions of 4 and 1 nm/pixel with 1000 and 10 000 photons, the spectral precision improves from 2.56 nm to 0.62 nm. We showed that while higher background noise reduces the overall spectral precision, background noise negligibly impacts the optimal spectral dispersion required to achieve the best spectral precision [Fig. 2(c)].

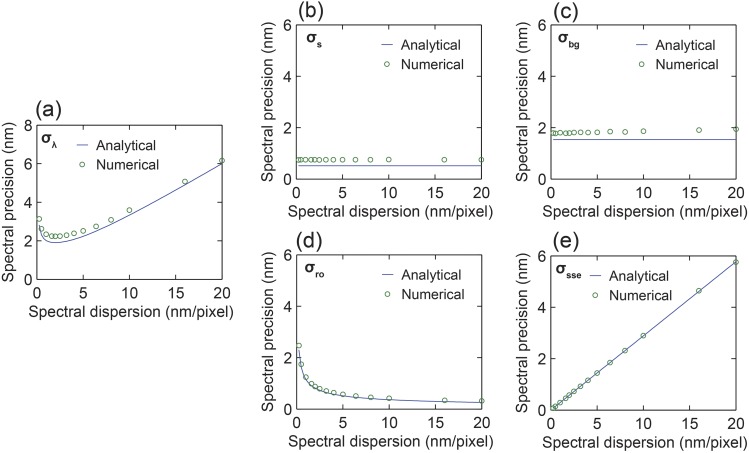
As illustrated in Fig. 3(a), we confirmed an excellent agreement between the numerical simulation and the analytical solution of the overall spectral precision with respect to spectral dispersion when considering the contribution from all system parameters, as listed in Table II. We also confirmed that σ_s and σ_bg are constant and independent of the spectral dispersion, whereas σ_ro is inversely proportional to the square root of the spectral dispersion, as illustrated in Figs. 3(b)–3(d). Additionally, σ_sse is linearly proportional to ∆λ as the spectral-shift error follows a top-hat distribution, as visualized in Fig. 3(e). Note that the emission spectrum of the fluorescent dye molecule used in the numerical simulation does not perfectly follow a Gaussian distribution. Nevertheless, our results suggested the analytical solution assuming that the Gaussian distribution of the emission spectrum can be used as a relatively accurate guideline to estimate the spectral precision.

FIG. 3.

Comparison of spectral precisions obtained by numerical simulation and analytical solution. The spectral signal contains 3000 photons, and the total background has 5000 photons. (a) Overall spectral precision and spectral precision when only considering the contribution of (b) the shot noise from the emission spectrum, (c) the shot noise from the background, (d) the readout noise, and (e) the spectral-shift error with respect to spectral dispersion.

TABLE II.

List of parameters used in the analytical solution.

N (photons)	B (photons)	∆y (nm)a	nro (e-)	sy (nm)	sλ (nm)
3000	5000	106.67	2	116.47	20

^a∆y is the image pixel size along the y-axis on the objective plane, which is determined by the EMCCD camera pixel size (16 µm, shown in Table I) divided by the magnification of the imaging system, which includes 100× from the objective lens and 1.5× from the matching tube lens being used.

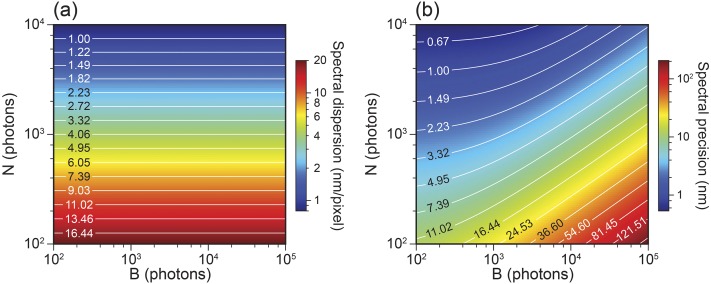
We further calculated the optimal spectral dispersion and the corresponding spectral precision with respect to the photon numbers of the recorded emission spectrum and the background. In the simulation, the photon number of the emission spectrum was increased from 100 to 10 000 and the background was increased from 100 to 100 000, approximating the practical conditions used in experiments. First, the spectral precision under each condition was calculated as a function of the spectral dispersion from 0.1 to 20 nm/pixel. The optimal spectral dispersion and the corresponding spectral precision were found and shown as the 2D contour plot in Fig. 4. Interestingly, the spectral dispersion of the sSMLM system used to achieve the best spectral precision solely depends on the photon number of the spectra image, as indicated by Fig. 4(a). By contrast, spectral precision further depends on the total background. When the total background increases, spectral precision decreases, as indicated by Fig. 4(b).

FIG. 4.

(a) 2D contour plot of the optimal spectral dispersion of sSMLM to achieve the best spectral precision. (b) 2D contour plot of the corresponding spectral precision with respect to the photon number of the emission spectrum and the background.

IV. DISCUSSION AND CONCLUSION

When the localization uncertainty is relatively less significant than the spectral-shift error in actual experiments, we could reduce the spectral-shift error by taking the localized position of individual molecules in the spatial images as a reference for the spectral analysis. This localized position at the sub-pixel level allows one to approximately estimate the sub-pixel level spectral shift between the emission spectra of individual molecules. Thus, we could potentially minimize the influence of the spectral-shift error by compensating for the estimated sub-pixel level spectral shift.

In conclusion, we introduced a theoretical model with numerical simulation and analytical solution to analyze the spectral precision influenced by the spectral calibration procedure and contributions from all key system parameters. Our study suggests that the best spectral precision can only be achieved with a particular system spectral dispersion. These findings reveal the delicate balance among key imaging parameters for achieving the optimal spectral precision, which provide a unified guidance for developing and optimizing sSMLM technologies.