Abstract
The goal of this study was to find the most robust algorithm for a phase-sensitive coil combination of 3D single-cycle and lactate-edited, multi-channel H-1 point-resolved spectroscopy (PRESS) localized echo planar spectroscopic imaging (EPSI) data for clinical applications in the brain.
Data were acquired over 5–10 minutes at 3T using 8- or 32-channel array coils. Peak referencing with residual water and N-acetyl-aspartate, first-point phasing, generalized least squared (GLS) and whitened singular-value decomposition (WSVD) combination algorithms were evaluated relative to unsuppressed water with data from a phantom, six volunteers and 55 patients with brain tumors. Comparison metrics were signal-to-noise ratio, coefficient of variance and percent signal increase.
Where residual water was present, using it as a reference peak for phasing and weighting factors from an imaging calibration scan gave the best overall performance. Greater improvement was seen for large selected volumes (> 720 cm3) and for the 32-channel array (25%) compared with the 8-channel array (19%). Applying voxel-by-voxel phase corrections produced a larger increase in performance for the 32- versus 8-channel coil.
We conclude that, for clinically relevant 3D H-1 PRESS localized EPSI studies, the most robust technique employed individual phase maps generated from high residual water and individual amplitude maps generated from calibration scans.
Keywords: coil combination techniques, first-point phasing, GLS, lactate editing, multichannel EPSI, peak referencing, PRESS localization, WSVD
1 |. INTRODUCTION
The power of in vivo H-1 magnetic resonance spectroscopic imaging (MRSI) is to obtain non-invasively biologically relevant information for assessing underlying disease mechanisms and monitoring response to therapy. This is especially true for applications to patients with brain tumors, where parameters derived from 3D single-cycle and lactate-edited H-1 spectroscopic imaging are relevant for defining target volumes for focal therapy1–5 and predicting the outcome.6–11 Constraints on scan time and signal-to-noise ratio (SNR) are primary factors in designing protocols for clinical applications. The use of echo planar spatial encoding and phased array coils can alleviate these limitations, but new challenges arise in combining data from different receive channels in an efficient manner.
Several strategies have been proposed for producing phase-sensitive coil combinations, with the majority focusing on signals from single-voxel H-1 MR spectra.12–27 The general approach is to form a linear combination of spectra with complex-valued weights that provide constructive addition of the signals and give higher emphasis to coil elements with higher signal. The most common method has been the acquisition of a separate water reference scan.26,28–32 This provides spatially dependent weights with relatively high precision if there is little discrepancy between the spatial distribution of water and the metabolites of interest, but requires longer overall acquisition times. Although some investigators27,33 have proposed acquiring H-1 MRSI without water suppression and using the unsuppressed water signal as a reference, our experience is that water side-bands can be as large as metabolite concentrations and, as a result, interfere in their qualification. Another possibility is to use reference peaks from residual water or individual metabolites. For in vivo datasets, this is limited by the SNR of data from individual channels. Other methods such as first-point phasing (FPphasing) and whitened singular-value decomposition (WSVD)15,20,21 are less dependent on individual peaks, but may be more susceptible to spectral artifacts.
The purpose of this study was to compare coil combination strategies in order to find the most robust technique for evaluating conventional single-cycle 3D H-1 point-resolved spectroscopy (PRESS) echo planar spectroscopic imaging (EPSI) data and two-cycle 3D H-1 lactate-edited PRESS EPSI for clinically relevant acquisition schemes of 5–10 minutes in length. Methods considered were implemented and tested in phantoms and normal volunteers for commercially available 8- and 32-channel head coils. Simulations were applied to test the limitations on SNR for each approach. The robustness and practical application of the most relevant methodologies were evaluated by analyzing datasets from a large population of patients with brain tumors.
2 |. METHODS
2.1 |. Experiments
3D H-1 PRESS localized EPSI data were acquired from a commercially available MR spectroscopy phantom, 6 healthy volunteers and 55 patients with glioma (30 males, 25 females, 25–71 years old). Volunteers and patients provided informed consent as approved by the Institutional Review Board. Data were obtained with a 3T scanner (GE Medical Systems, Milwaukee, WI) using body coil transmit and commercially available 8- (MRI Devices, Gainesville, FL) or 32-channel (Nova Medical, Wilmington, MA) phased-array receive coils.
2.1.1 |. Phantom data
The head phantom comprised 3mM choline, 10 mM creatine, 12.5 mM N-acetyl-aspartate (NAA), 12.5 mM glutamate, 7.5 mM myo-Inositol and 5 mM lactate. Calibration and 3D volumetric T1-weighted images were also obtained. The 3D PRESS localized EPSI data were obtained as described previously34 with a flyback echo planar readout in the superior-inferior direction that provided 712 dwell points and 988 Hz bandwidth. The selected volume was prescribed as 120×120×60 mm3, but utilized over-PRESS factors of 1.5 in all three spatial dimensions (TR/TE = 1500/144 ms, field of view (FOV) = 18 × 18 × 16 cm3, nominal voxel size = 1cm3). Very spatially selective (VSS) pulses were applied to remove signal from the voxels on the edge of the over-PRESS region and hence eliminate chemical-shift artifacts.35 The acquisition included an unsuppressed water scan, a single-cycle scan with CHESS water suppression and a two-cycle lactate-edited scan with BASING and CHESS water suppression.34 The latter had one cycle with low residual water (the editing pulse was placed at 4.7 ppm) and one with much higher residual water.
2.1.2 |. Volunteer studies
Three healthy volunteers received two MR exams on different days within a period of two weeks with the 8-channel coil, automatic MRSI prescription (PRESS box and saturation bands)36 and the 3D PRESS localized EPSI sequence described above.37,38 An additional three volunteers received two exams, one with the 8-channel and the other with the 32-channel head coil. Each exam included 3D PRESS localized EPSI acquisitions prescribed from similar regions based on an atlas definition39 single-cycle without CHESS water suppression, single-cycle with CHESS and lactate-edited with CHESS,34 with the same residual water scheme as described for the phantom experiments. These datasets were prescribed with excited volumes of 150 × 180 × 60 mm3 (TR/TE = 1140/144 ms, FOV = 18 × 18 × 16 cm3, nominal voxel size = 1cm3) and over-PRESS factors of 1.2, 1.2 and 1.5, respectively, with automatically generated VSS bands.37
2.1.3 |. Patient studies
A total of 105 MR exams were acquired from 55 patients. The scan protocol included low-resolution calibration images for estimating coil element profiles, T2-weighted FLAIR images, pre- and post-contrast T1-weighted images, 3D lactate-edited PRESS localized H-1 EPSI data with TE = 144ms, TR = 1104–1500 ms, spectral array = 16 × 16 × 16 or 18 × 18 × 16, nominal voxel size = 1cm3 and effective spatial resolution = 1.014 or 1.013 cc, depending on the sampling pattern (Tacq = 4.7–8.1 min). The selected volume (prior to applying over-PRESS factors of 1.2, 1.2 and 1.5) varied from 192–1512 cm3.
2.1.4 |. Simulations
The performance of the combination algorithms was tested with the phantom data by simulating spectra with different SNRs. The noise level was estimated from the average standard deviation of 75 points at the end of free induction decay (FID) (σ). Statistically uncorrelated complex-valued Gaussian distributed noise with zero mean and finite variance λσ was added to the raw data because, when examining the noise correlation matrix shown in Figure 1A, very little noise correlation was found among channels in either coil set-up, hence the correlation matrix was approximated by an identity matrix. The resulting noise levels of λσ, where λ = 1, 1.2, 1.4, … 8, 10, … , 16, were generated to approximate the covariance matrix, where each diagonal element value was λσ. For volunteer data, the impact of the magnitude of the residual water on the reliability of the coil combination was assessed using weighted sums of lactate-edited cycles. The cycle with residual water was added with weight levels of 0, 5, 10, 15, … , 100% to produce datasets with residual water peaks from 0 to 18-fold higher than NAA.
FIGURE 1.
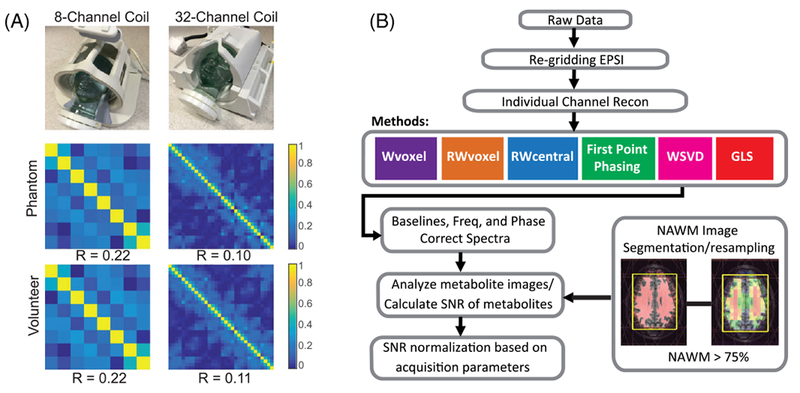
A, Noise correlation levels among channels for both head-coil arrays for phantom and in vivo data. The noise correlation matrices were estimated by calculating the correlation matrix of the noise of the data acquired with RF excitation disabled, demonstrating low noise correlation among the coil elements, with mean values of off-diagonal correlation coefficients being 0.22 for 8-channel and 0.11 for 32-channel. The 32-channel case shows smaller noise correlation compared with the 8-channel one for both phantom and in vivo experiments. B, 3D MRSI processing diagram. The steps used to process the data included reconstruction of individual channel spectral arrays, coil combination and post-processing to perform baseline subtraction, removal of residual phase variations in the metabolite peaks and quantification of peak intensities
2.2 |. Data processing
Steps used to process the data are represented in Figure 1B. The raw data were reconfigured and linearly phased for the echo planner sampling. The individual channels were reconstructed by zero-filling and apodization in the time domain, followed by Fourier-transforming in time and space to produce a 3D spatial array of spectra. The combination techniques were then used to create separate amplitude and phase estimates to combine the individual channels. The input to the coil combination algorithms comprised spatial arrays of spectra, with 1 array per channel for unsuppressed water or single-cycle data and 2 arrays per channel for lactate-edited data. Additional frequency, phase and baseline subtraction were performed. Maps of metabolite peak intensity were determined from the phase-sensitive, baseline-subtracted data.40 To examine the effect of poor lipid suppression and its impact on the WSVD method, four patients with the worst performance using WSVD were pre-processed using non-iterative time-domain fitting with the Lanczos-based version of HSVD to filter out lipid signals from 1.8 to −1.0 ppm.41
2.2.1 |. Evaluation of phase variations among channels between coils
The phase in voxels from each channel includes contributions due to field inhomogeneity, applied gradients, sequence encoding and coil receiver phase offset (ϕc). It was assumed that the phases from datasets with unsuppressed water represented the ground truth. Phase maps were generated by subtracting the average phase (θc) from the central eight (2×2×2) voxels for each element, with the remaining net phase difference (Ψc) depending only on the geometry of the coil (Equation 1).
| (1) |
The between-channel variation in phase maps was assessed by taking the standard deviation of phase values as follows:
| (2) |
2.2.2 |. Coil combination
The pre-processed spectrum for channel c is a function of voxel location x and frequency f as described by Equation 3,
| (3) |
where is the spectrum from voxel X with between-channel phase offsets corrected and is the independent and identically distributed (i.i.d.) complex (Gaussian) normal () noise with zero mean and channel-dependent variance (σc), i.e. . is the differential amplitude factor representing the receive profile of channel c and is the phase offset for each coil. To obtain a combined spectrum (Equation 4), the phase offsets must first be removed and spectra from individual channels weighted to account for differences in amplitude factors.
| (4) |
Data from individual channels were combined using a weighting function that divides by the square root of the sum of squares of amplitudes of the individual coil weights. This is preferred for initial analysis and for viewing the data, because it maintains similar noise levels in each spectrum. Direct comparison of metabolite levels between voxels must also take into account the spatial weighting of signals inindividual voxels due to non-uniformity of the combined coil reception profiles.
2.2.3 |. Combination methods
The algorithms considered are summarized in Table 1. The first seven strategies are characterized by using a reference peak to estimate relevant parameters. The Wvoxel method uses the water peak from a separate dataset acquired without water suppression to provide the phase reference. Amplitude-weighting factors were obtained from either the height of the reference water peak or proton-density-weighted gradient-echo images acquired using the manufacturer-provided coil-sensitivity calibration sequence for parallel imaging (CAL images). The RWvoxel and NAAvoxel methods used similar strategies, but phase estimates were obtained from the residual water or NAA peaks, the latter of which was chosen because it has the largest signal in normal-appearing white matter. If this is not the case in a different population, creatine or another high-concentration metabolite could be selected instead to minimize noise variation. For voxels with reference peaks having SNR less than 5, phase estimates were obtained by interpolation from surrounding voxels. The RWcentral and NAAcentral methods used similar amplitude weighting, but assumed that there was a constant phase offset between channels that was estimated from reference peaks in the central eight voxels of the spectral array.
TABLE 1.
Summary of the coil combination methods that were evaluated
| Method | Abbrevation | Phase Estimation | Amplitude Weights |
|---|---|---|---|
| Unsuppressed water peak from separate dataset | Wvoxel | voxel-by-voxel | reference peak hight or calibration images |
| Residual water peak from same dataset | RWvoxel | voxel-by-voxel | reference peak height or calibration images |
| Residual water peak from same dataset | RWcentral | constant offset | reference peak height or calibration images |
| Generalized least squares using residual water peak | GLSRW | direct estimation from peak region | |
| NAA peak from same dataset | NAAvoxel | voxel-by-voxel | reference peak height or calibration images |
| NAA peak from same dataset | NAAcentral | constant offset | reference peak height or calibration images |
| Generalized least squares using NAA peak | GLSNAA | direct estimation from peak region | |
| First-point FID phasing | FPphasing | voxel-by-voxel | first FID point height or calibration images |
| Whitened singular valued decomposition | WSVD | direct estimation from spectra | |
For the WSVD method, the phase and amplitude estimations are intrinsic to the calculation itself. The first step is to whiten the noise contribution using an additional noise prescan as described by Rodgers and Robson.20 For cases in which noise acquisition was not available, the covariance matrix was estimated from a region of the spectra between −0.4 and −1.0 ppm that contained 75 noise samples. The multi-channel data were decomposed into a series of contributions of increasing rank and the best rank-1 decomposition in terms of the complex coil sensitivities and combined signals was selected. This is represented by first expressing the relationship in Equation 3 in vector format:
| (5) |
where P and N are c × k matrices of the spectrum and noise, respectively, with c being the total number of coil elements and k being the number of digitized MRS data points in the FIDs; s is the complex-valued c-element column vector of coil sensitivities and m is a k-element row vector of the underlying signals. In Equation 6, the rows of Pc×k are scalar multiples of the signal vector m and therefore P is a rank-1 matrix and the SVD of P computes the maximum-likelihood combined spectrum,
| (6) |
where Uc×c and Vk×k are orthonormal singular vector matrices and Σc×k is a diagonal matrix that contains the singular values in descending order. The first singular vectors of Uc,1 and Vk,1 corresponding to the largest singular value Σ1,1 give the maximum-likelihood coil sensitivities and combined spectrum, respectively, as shown by Rodgers and Robson.20,21 From this, w can be calculated using Equations 7 and 8.
| (7) |
| (8) |
where w are complex coil sensitivities and λ is an arbitrary amplitude/phase term for each voxel. The amplitude and phase were calculated implicitly from w for individual coils as described in Equations 9 and 10.
| (9) |
| (10) |
The GLS algorithms used the complex integral of the spectra over the reference peak (residual water or NAA) to estimate coil sensitivity maps. The combined spectrum was calculated according to sensitivity encoding (SENSE) reconstruction, as described by Equation 11.22
| (11) |
where the receiver noise matrix is Ψ = NNH. The phase and amplitude estimations are in the complex term (sHΨ−1s)−1sHΨ−1.
The other two methods (FPphasing and WSVD) apply corrections to each voxel independently, but make use of information from the entire frequency range. As its name suggests, the FPhasing strategy applies a correction based on the phase from the first point of the FID of each voxel. If one considers the properties of the discrete Fourier transform, it can be appreciated that this is equivalent to averaging the signals from the real and imaginary parts of the spectrum and then using them to provide the phase estimate.
2.2.4|. Image processing
Spectral data from volunteers and patients were referenced to the 3D anatomic T1-weighted images, assuming that there was no movement of subjects between the image and spectra acquisitions. FLAIR images were aligned with the corresponding 3D T1-weighted images using FSL’s linear registration tool (FLIRT).42 Segmentation of the brain was performed automatically using a program based on a Markov random field model.43 A white matter (WM) mask was then used to identify spectral voxels with at least 75% normal-appearing white matter (NAWM). Metrics considered were the average SNR of NAA and the coefficient of variance (CV) of the SNR of NAA.
2.2.5 |. Post-processing
The spectral arrays were processed as described previously.40 For the lactate-edited data, the two cycles of data were summed to produce a 3D spectral array containing choline, creatine, NAA and lipid and subtracted to provide an array containing only lactate. Quantification of peak intensities included additional frequency phase and baseline correction on a voxel-by-voxel basis. This was necessary because, although the spectra from different channels had been correctly phased relative to each other, the phases of the metabolite peaks and reference peak in the combined spectra were not always identical. Maps of metabolite peak intensity were determined from the phase-sensitive, baseline-subtracted data. In each case, a region of 75 spectral points without metabolite signal was selected to estimate the standard deviation (SD) of the noise for each voxel in the selected volume in order to calculate SNR on a voxel-by-voxel basis. The individual SNR values for each voxel were then averaged to obtain a single normalization factor for each subject.
For the patient data, corrected SNRs were calculated according to Equation 12 to account for differences in (i) acquisition and repetition times using the relaxation constant44 for individual metabolites and (ii) k-space sampling pattern (i.e. traditional versus ellipsoidal) by estimating the effective spatial resolution ():45
| (12) |
Metabolite peaks were considered detectable if they had a measured SNR value greater than 5. Lipid peaks were considered detectable if they had a peak height greater than 25% of the mean NAA peak in NAWM. Voxels in the volunteers and patients that contained a detectable lipid peak were considered to have lipid contamination. Voxels with measured SNR greater than the mean NAA in NAWM were considered to have extreme lipid contamination.
3 |. RESULTS
3.1 |. Analysis of phantom data
The spectra obtained using the lactate-edited sequence have two cycles, one with high residual water and one with very low residual water, as shown in Figure 2A. The average SNRs of the residual water and NAA peak in the combined spectra from the lactate-edited cycle with high residual water were 5500 and 70; those from the cycle with low residual water were 44 and 75. Note the differences in phase between the metabolites and residual water peaks, as well as the elevated baseline caused by the tail of the residual water peak. Spectra from the center four voxels for the lactate-edited 8-channel head coil data with various noise levels are shown in Figure 2B.
FIGURE 2.
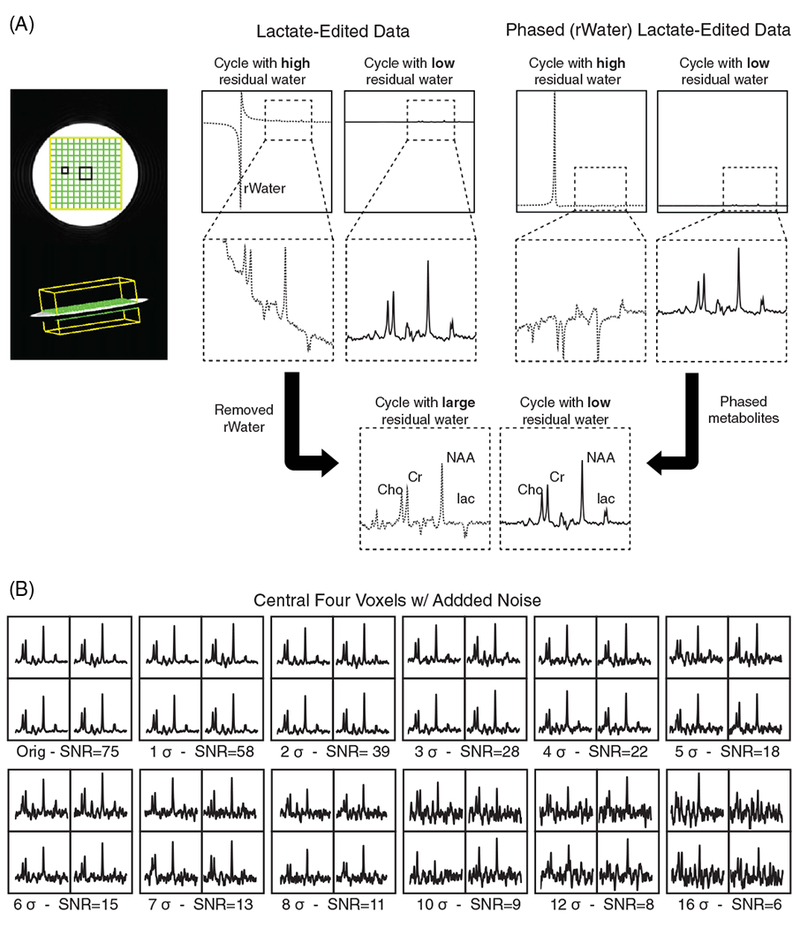
Phantom data and simulated noise levels using the lactate-edited 3D MRSI sequence. A, Comparison of one voxel for two cycles of lactate-edited 3D MRSI sequence. Spectra from the cycle with high residual water (rWater) are indicated by the dashed line, while spectra from the cycle with very low residual water are denoted with solid lines. The differences in phase between metabolites and residual water peaks are illustrated, as well as the baseline caused by the tail of the residual water peak. B, The central four voxels of the combined spectra of the phantom used to test the performance of different combination algorithms are shown with additional simulated noise levels. The noise level for patient data was typically between 5σ and 7σ
Table 2 summarizes the SNR and the percent signal increase relative to the Wvoxel method in phantom for all algorithms. There was a 25% increase in SNR across all techniques for the 32-versus the 8-channel coil. This was less than for the volunteer data (see Table 3:40%) because the phantom was smaller than an average human head.46 When using the cycle with high residual water to estimate parameters for combination, the performance of the relevant techniques was similar for all except the RWcentral method, which was 13% and 19% worse than the standard Wvoxel method for the 8- and 32-channel coils respectively For the cycle with very low residual water, NAA was used as the reference peak. In this case, the performance of NAAvoxel, FPphasing and WSVD methods were similar to Wvoxel, but worse for GLSNAA (6%/16% lower for 8-/32-channel coils) and NAAcentral (15%/19% lower for 8-/32-channel coils) was worse.
TABLE 2.
Raw SNR and percent change compared with Wvoxel values for all techniques for NAA in a phantom*
| 8-channel | ||||||
|---|---|---|---|---|---|---|
| Cycle with residual water | Cycle without residual water | |||||
| Methods | SNR | % | Methods | SNR | % | |
| Wvoxel | 69.4 | – | Wvoxel | 74.6 | – | |
| RWvoxel | 69.7 | < 1% | NAAvoxel | 75.0 | < 1% | |
| GLSrw | 67.2 | −3% | GLSNAA | 70.0 | −6% | |
| FPphasing | 69.6 | < 1% | FPphasing | 74.4 | < 1% | |
| WSVD | 70.1 | < 1% | WSVD | 75.0 | < 1% | |
| RWcentral | 60.2 | −13% | NAAcentral | 63.6 | −15% | |
| 32-channel | ||||||
| Wvoxel | 86.8 | – | Wvoxel | 93.6 | – | |
| RWvoxel | 86.6 | < 1% | NAAvoxel | 94.3 | < 1% | |
| GLSRW | 83.8 | −4% | GLSNAA | 78.7 | −16% | |
| FPphasing | 86.2 | < 1% | FPphasing | 92.8 | < 1% | |
| WSVD | 87.5 | < 1% | WSVD | 94.3 | < 1% | |
| RWcentral | 70.9 | −19% | NAAcentral | 75.8 | −19% | |
| +25% | +25% | |||||
Data acquired using lactate-edited 3D MRSI sequence.
TABLE 3.
Mean raw SNR, mean corrected SNR (CSNR: cm−3 min−1/2) and percent change compared with Wvoxel values for all techniques for NAA in NAWM in three volunteers.* CSNR values were calculated according to Equation 12 to account for differences in acquisition and repetition times and the effective spatial resolution
| 8-channel | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cycle with residual water | Cycle without residual water | |||||||
| Methods | SNR | % | CSNR | Methods | SNR | % | CSNR | |
| Wvoxel | 17.2±1.9 | – | 9.9±1.1 | Wvoxel | 18.1±1.3 | – | 10.4±0.8 | |
| RWvoxel | 17.5±1.9 | +2% | 10.1±1.1 | NAAvoxel | 17.7±1.6 | −2% | 10.5±0.9 | |
| GLSRW | 16.0±1.7 | −7% | 9.3±1.0 | GLSNAA | 9.2±1.2 | −49% | 5.3±0.7 | |
| FPphasing | 17.5±1.9 | +2% | 10.1±1.1 | FPphasing | 17.±1.1 | −2% | 10.2±0.6 | |
| WSVD | 16.9±1.9 | −1% | 9.8 ±1.1 | WSVD | 17.3±1.5 | −5% | 9.9±0.9 | |
| RWcentral | 15.0±1.9 | −13% | 8.7±1.1 | NAAcentral | 15.9±1.4 | −12% | 9.2±0.8 | |
| 32-channel | ||||||||
| Wvoxel | 24.1±2 | – | 13.9±1.2 | Wvoxel | 25.3±2 | – | 14.6±1.2 | |
| RWvoxel | 24.5±2 | +2% | 14.1±1.3 | NAAvoxel | 24.8±2 | −2% | 14.3±1.4 | |
| GLSRW | 22.6±3 | −6% | 13.0±1.5 | GLSNAA | 14.2±4 | −44% | 8.2±2.6 | |
| FPphasing | 24.4±2 | +2% | 14.1±1.3 | FPphasing | 23.1±1 | −8% | 13.3±0.6 | |
| WSVD | 23.9±2 | −1% | 13.8±1.3 | WSVD | 24.4±2 | −3% | 14.1±1.0 | |
| RWcentral | 19.8±1 | −18% | 11.4±0.9 | NAAcentral | 20.6±2 | −19% | 11.9±1.1 | |
| +40% | +40% | |||||||
Standard deviation between the 3 volunteers is shown as mean ± SD. Data acquired using lactate-edited 3D MRSI sequence.
Figure 3 summarizes the behavior of synthetic data in three measures: the average combined signal (SNR) of the NAA peak, the coefficient of variance (CV) of SNR of the NAA peak and the percent signal increase (PI) of the NAA peak relative to the Wvoxel method. The performance of all techniques remained strong for the cycle with high residual water but degraded rapidly for the cycle where NAA was used as a reference peak (Figure 3A, D). All of the methods became unstable as the SNR decreased, especially when a strong reference peak did not exist. It is important to note that, although these data-driven methods failed at different SNR values, it is difficult to determine which algorithm performed best in the absence of a strong water peak. At lower SNRs, the RWvoxel and FPphasing combination methods were comparable to WSVD in terms of SNR, CV and PI (e.g. at 12σ, SNR = 5.5, 5.5 and 5.7; CV = 0.38, 0.39 and 0.31; PI = 0.2, −0.3 and 3.8), while the GLSRW method performed poorly (SNR = 4.8, CV = 0.52, PI = −13.9 at 12σ) and the RWcentral method performed the worst.
FIGURE 3.
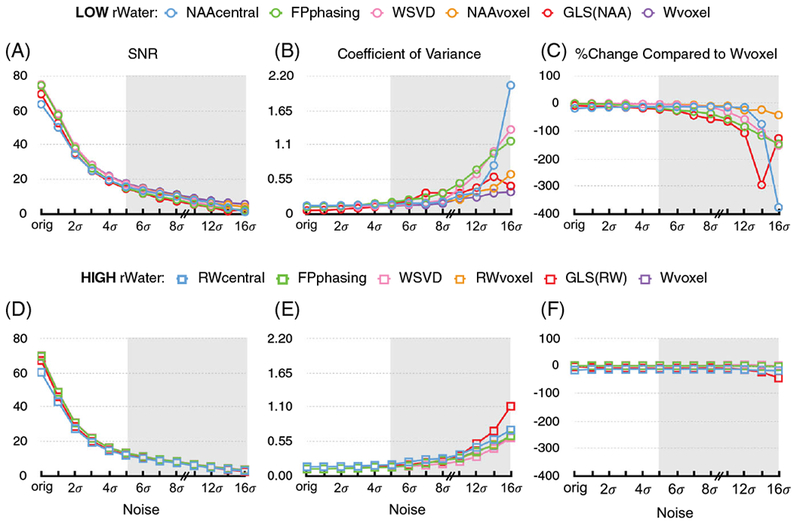
Summary of coil combination performance as a function of SNR in synthetic phantom data using the lactate-edited 3D MRSI sequence. A-C and D-F present results from the cycles with low and high residual water respectively Three measures are compared: A,D, the average combined SNR of the NAA peak, B,E, the coefficient of variance (CV) of the SNR of NAA peak and C,F the percent change of SNR of the NAA peak of all techniques relative to the gold standard (Wvoxel). The behavior of the combination algorithms is presented at several noise levels. When additional random noise was added (Figure 2), the performance of all techniques remained strong and similar when there was residual water but degraded rapidly when NAA was used as a reference peak. The performance of the Wvoxel method was unchanged because it uses the data from a reference scan to compute values for phase and amplitude. All of the other methods broke down as the SNR decreased, the effects being exacerbated when a strong reference peak did not exist
3.2 |. Amplitude factors and phase offsets for volunteer data
Combined amplitude-factor maps for calibration images, non-suppressed water, residual water and NAA peaks for 8- and 32-channel data are shown in Figure 4. Observed differences are due to variations in the SNR of the reference peaks, the longer T2 of water in cerebrospinal fluid (CSF) and the spatial distribution of NAA. The SNR of the NAA peak was too low to be reliable in weighting data from different channels. Weighting by the reference peak intensity or first FID intensity is an option and we have performed the analysis on our volunteer data using both that option and the calibration image intensities. We found that using the calibration image intensities gave results either similar to or better than the reference peak intensities (Figure 5).
FIGURE 4.
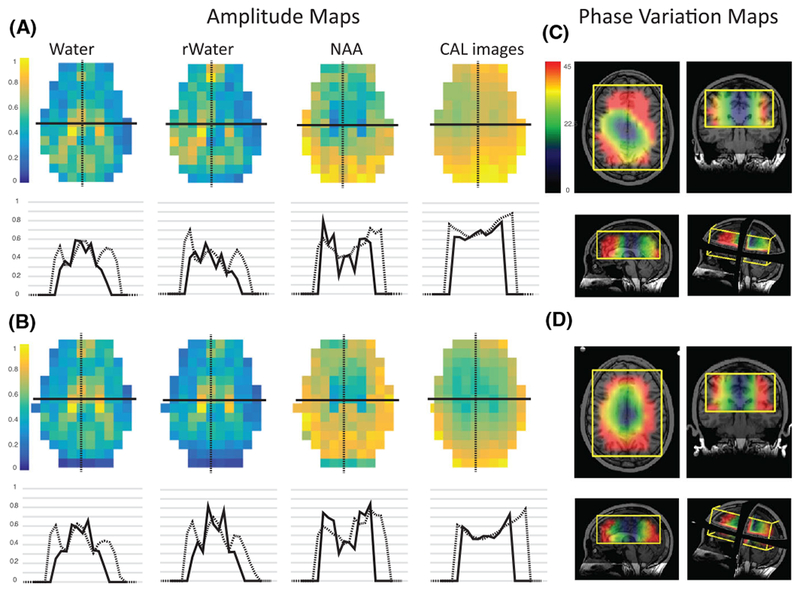
Amplitude factors and phase offsets for volunteer data. A,B, Amplitude maps with cross-sectional plots for a volunteer with 8- and 32-channel head coils respectively The differences observed in the combined amplitude maps for non-suppressed water, residual water, NAA peaks and calibration images are due not only to variations in SNR in the reference peaks, but also the longer T2 of water in cerebrospinal fluid (CSF) and the distribution of NAA. C,D, Phase variation maps using Equation 2 in axial, coronal, sagittal and 3D view for the same volunteer. Large phase variations among coil elements were observed, due to the geometry and possibly the number of elements. These phase variations were more severe in locations closer to the coils than the center of the selected volume and were larger for the 32- versus the 8-channel coil
FIGURE 5.
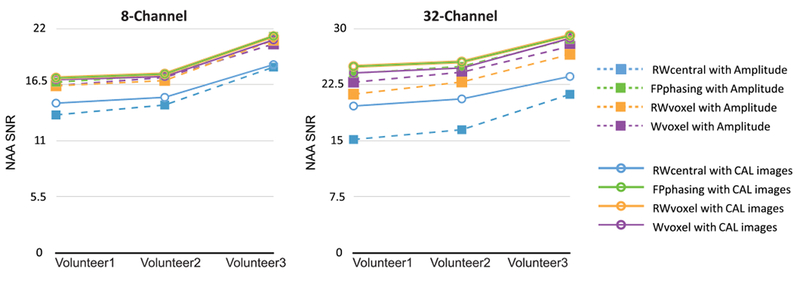
Average SNR of the NAA peak for the three volunteers, comparing amplitude and calibration image weighting for each combination method. The conventional versions of these algorithms use the amplitude of the reference peak or first FID point intensity for weighting, in contrast to the proposed approach using the calibration image intensities. Using the calibration image intensities gave results either similar to or better than the amplitude of the reference peak intensity
The impact of different coil geometries is represented in the phase-offset deviation maps from non-suppressed water acquisition. In the center of the selected volume, the offsets were relatively constant, but the between-channel deviation increased for voxels closer to the edge, up to an average of 94°–89°, and was larger for the 32- versus the 8-channel coil. The net phase difference for each channel was calculated by relating the phase of each voxel to an arbitrarily designated reference channel. The mean offsets varied substantially between acquisitions, by 10°–40° for the 8-channel coil and 5°–30° for the 32-channel coil, and followed no clear pattern. The presence of such large variations implies that phase-offset values could not be pre-calculated and stored for reconstructing similar datasets.
3.3 |. Comparison of combination methods for volunteer data
The differences between methods for 8- versus 32-channel coil spectral arrays with high residual water are represented in Figure 6A. The RWvoxel combination gave 19% and 25% higher NAA SNR for these coils compared with the RWcentral method, with the 32-channel coil having 40% and 25% increases in NAA SNR over the 8-channel coil for RWvoxel and RWcentral methods, respectively. The performance of the other methods showed similar trends between these two extremes. The techniques incorporating the assumption of spatially varying phase outperform the RWcentral method, which assumes constant phase variation among channels. These same techniques result in greater increases in SNR with a larger number of coil elements.
FIGURE 6.
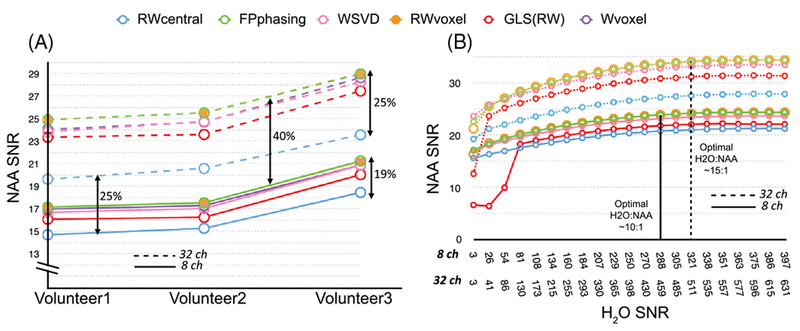
Summary of the differences in SNR performance of data acquired using the lactate-edited 3D MRSI sequence for both 8- (solid line) and 32- (dashed line) channel coils. A, Comparison between the combination algorithms in three volunteers using the cycle with sufficient residual water. The techniques that incorporated the assumption of spatially varying phase outperformed the RWcentral method, which assumes a constant phase variation among channels. Going from 8 to 32 channels, techniques with spatially varying phase produced a 40% increase in performance, compared with a 25% increase with constant phase variation, suggesting that voxel-by-voxel phase correction is crucial to reach the optimal combination and becomes more apparent in the 32-channel coil. B, Comparison between combination algorithms in one volunteer using the cycle with minimal residual water with different simulated levels of residual water. Modifying the sequence to leave residual water 10–15 fold higher than NAA obviated the need for a reference scan for both head coils and stabilized the performance of the techniques
For the data that were acquired using lactate-edited PRESS MRSI, we evaluated the combination methods for the two cycles individually by choosing residual water as a reference when the cycle had high residual water and NAA as a reference when the editing cycle had low residual water. Table 3 shows mean raw SNR, mean CSNR (mean±SD) and the percent signal increase relative to the Wvoxel method in three volunteers. Between 98 and 100% of all voxels outside the ventricles had a detectable NAA peak (SNR > 5) for all techniques except GLSNAA (88%), suggesting that the phasing and amplitude weighting steps have performed sub-optimally. The percentage of voxels with lipid peaks greater than 25% of the mean NAA signal from NAWM for both 8- and 32-channel head coils was presented for the Wvoxel, RWcentral, RWvoxel, GLS RW, FPphasing and WSVD methods, in order to demonstrate the effects of aliased lipid, which can influence the result of WSVD and FPphasing combination significantly if the lipid concentration is high enough. Since no voxels in the volunteers had lipid peaks equal to or greater than the mean NAA SNR in NAWM for either cycle, the WSVD and FPphasing still performed well in both cycles, despite the presence of some lipid. While the RWvoxel and FPphasing had maximum SNR and RWcentral was the only method with significantly lower performance in the cycles with high residual water, the Wvoxel combination outperformed all others in cycles with low residual water. The NAAcentral and GLSNAA methods both performed poorly.
3.4 |. Impact of the magnitude of residual water
Given that the lactate-edited data had one cycle with high residual water and one cycle with very low residual water, it was possible to simulate single-cycle datasets with intermediate residual water peaks by adding different combinations of the cycles together. Figure 6B shows the impact of the amount of residual water on the NAA SNR for the RWvoxel, RWcentral, GLSRW, FPphasing and WSVD methods for both head-coil arrays, as well as the minimum relative intensity required for each combination not to break down. Having sufficient residual water would not only obviate the need for a reference scan for both head coils, but also help to stabilize the performance of the techniques.
3.5 |. Application to patients with brain tumors
Table 4 summarizes the performance for voxels from NAWM for 105 datasets obtained from 55 patients with brain tumors (Figure 7) and demonstrates the impact of lipid contamination on each method’s performance. For the peak referencing methods, for lactate-edited datasets, combination parameters were estimated from the cycle with the higher residual water. Overall, the performance was similar to that in normal volunteers, even though a wide range of selected volumes, patient ages and disease states was included. The improvement in SNR of RWvoxel relative to the RWcentral method was more noticeable for volumes larger than 720 cc, with a 4% increase at 200 cc, 10% increase at 700 cc and 14% increase at 1500 cc. Figure 8 shows an example of 16 voxels of lactate-edited data from a region of T2-hyperintensity for the various combination techniques in a patient with a brain tumor. Although the choline is significantly increased relative to creatine and NAA in these voxels, all methods that used the residual water for coil combination produced similar average metabolite ratios.
TABLE4.
Mean corrected SNR (CSNR: cm−3 min−1/2) values and percentage of voxels with detectable lipid for all combination techniques for NAA in NAWM in patients.* CSNR values were calculated according to Equation 12 to account for differences in acquisition and repetition times and the effective spatial resolution. Voxels were considered to have either ‘low to moderate’ aliased lipid if the lipid SNR was greater than 25% of the mean NAA SNR in NAWM or an ‘extreme’ amount of aliased lipid as defined by a lipid SNR equal to or greater than the mean NAA SNR in NAWM. The extreme lipid case negatively influences the result of the WSVD and FPphasing combination, causing this to fail to combine signals from contaminated voxels properly†
| Cycle with residual water | Cycle without residual water | ||||||
|---|---|---|---|---|---|---|---|
| Methods | CSNR | %voxels (Lip>25%NAA) | % voxels (Lip≥NAA) | Methods | CSNR | % voxels (Lip>NAA) | % voxels (Lip≥NAA) |
| RWvoxel | 8.0±1.5 | 25.4±19.9 | 1.4±3.7 | NAAvoxel | – | – | – |
| GLSRW | 7.8±1.5 | 26.1±20.4 | 1.2±3.5 | GLSNAA | – | – | – |
| FPphasing | 8.0±1.5 | 25.4±20.0 | 1.4±3.9 | FPphasing | 8.2±1.7 | 31.3±21.8 | 2.4±6.3 |
| WSVD | 7.7±1.4 | 25.5±19.4 | 1.5±3.9 | WSVD | 8.0±1.8 | 33.5±23.8 | 4.3±2.7 |
| RWcentral | 7.3±1.3 | 26.1±19.2 | 1.1±3.2 | NAAcentral | – | – | – |
| RWvoxel‡ | 8.6±1.6 | 28.8±20.9 | 1.0±2.8 | ||||
Standard deviations between scans are shown as mean±SD. N = 105 exams, 51 patients.
30% of all patients had extreme lipid contamination.
Combination parameters estimated from the other cycle.
FIGURE 7.
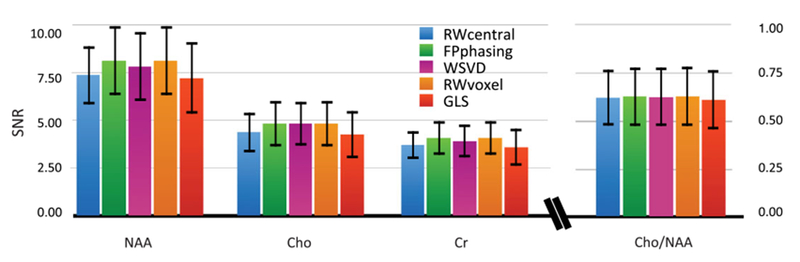
Summary of performance of the methods in 55 patients (105 exams). The average SNRs of three main metabolites and their ratios in normal-appearing white matter from 55 patients with gliomas are shown with different color bars representing each technique. SNR corrections were made for variation in Tacq, TR and spatial resolution for all exams. Although the RWvoxel method produced the best overall SNR, all methods produced consistent metabolite ratios.
FIGURE 8.
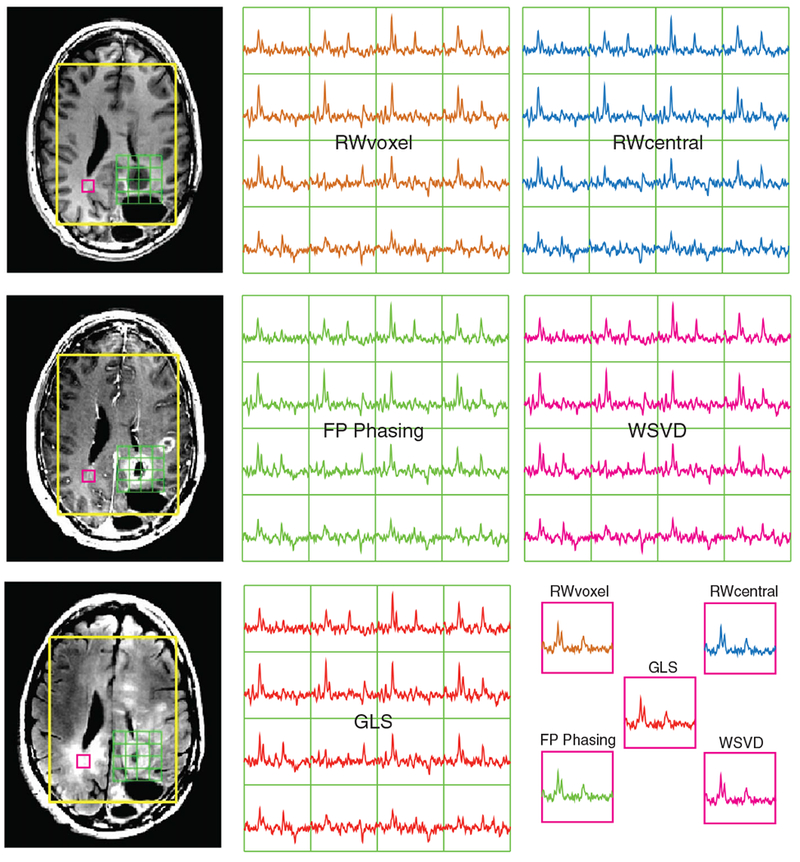
Representative voxels of combined spectra and corresponding anatomical imaging from a patient with a grade IV glioma. The combined spectra from each technique for 16 voxels around the tumor region are displayed with an additional voxel from the contralateral region. In the presence of sufficient residual water, all methods produced consistent metabolite levels and ratios
An added complication for patient data is the increased likelihood of lipid artifacts, due to the lesion being in a location that is difficult to cover using PRESS volume selection. Figure 9 demonstrates the influence of lipid contamination on the quality of the WSVD algorithm when there is low residual water. Even when the HSVD lipid removal algorithm was applied,41 it did not perform well and some voxels ended up with higher lipid in the original data. Figure 10 shows that adding sufficient residual water to recover some of the missing signals in these voxels makes both WSVD and FPphasing less sensitive to these lipid artifacts.
FIGURE 9.
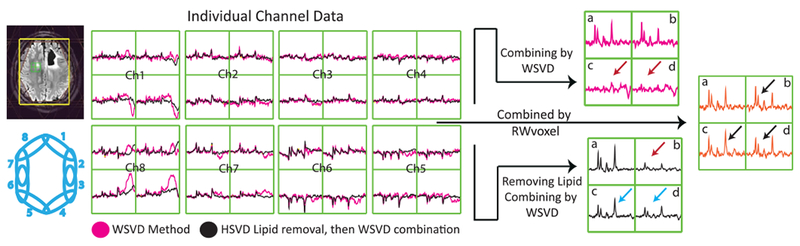
Impact of lipid contamination on WSVD combination. Left: the individual channel data are shown before (in magenta) and after (in black) HSVD lipid removal. Large lipid signals are observed in channels 1and 8 of the uncombined spectra that will impact the overall combination on the right. The HSVD lipid removal algorithm clearly failed for the top right voxel in channels 1 and 8, such that it ends up with higher lipid levels than are present in the original data. Right: the combined spectra using the WSVD alone and WSVD in addition to lipid removal. When combining the spectra using WSVD alone (magenta), voxels a and b have good SNR but voxels c and d lack any signal. Incorporating lipid removal (black spectra) improves voxels c and d at the expense of voxel b
FIGURE 10.
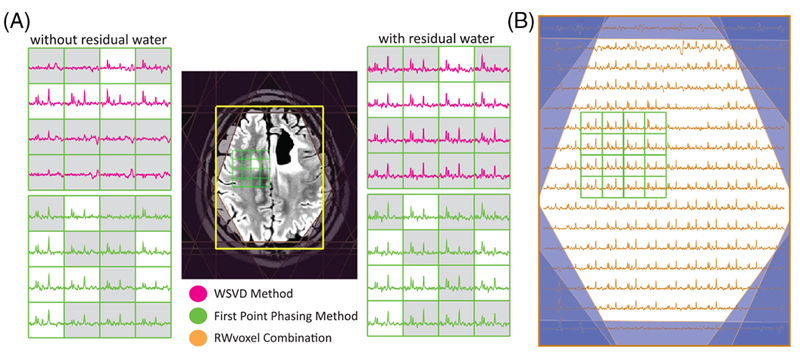
Outcome of the WSVD and FPphasing on patients with large lipid contamination. A, Several spectra from near the lesion are shown for the WSVD and FP phasing algorithms with and without sufficient residual water. The presence of large lipid signals results in a lack of metabolite signals in the combined spectra in some voxels (highlighted in gray) where there was an absence of a high reference peak. This was improved when sufficient residual water was added, in which case the RWcentral method performed well across the entire imaging volume, as shown in B
In the 30% of patient datasets from Table 4 that had extreme lipid contamination in 1–87% of their voxels, the percentages of voxels with ’extreme’ lipid peaks (equal to or greater than the mean NAA SNR in NAWM) for WSVD and FPphasing methods were 15.1%±20.2 and 8.3%±9.7, with 78.2%±20.5 and 80.3%±13.00 of these having quantifiable NAA (SNR greater than 5) within the voxel, respectively If combination parameters were estimated from the cycles with high residual water (RWvoxel method), the lipid contamination decreased to an average of 3.6%±4.2 and there was higher NAA peak detection (88%±10). For the cycles with high residual water, 6.3%±5.3, 5.5%±5.9 and 5.8%±5.3 of voxels had extreme lipid peaks for WSVD, FPphasing and RWvoxel methods, with more of them having quantifiable NAA (83.4%±11.3, 85.6%±9.6 and 85.6%±9.4, respectively). This indicates that the effects of lipid contamination are more detrimental with less residual water present in these techniques.
4 |. DISCUSSION AND CONCLUSION
The study presented here addresses the performance of different coil combination methods for 3D single-cycle and lactate-edited multi-channel H-1 PRESS localized EPSI studies from large regions of the brain that are independent of the acquisition method. Critical requirements are that these methods are robust across various locations, can be used for a wide variety of selected volumes and can cope with voxels with relatively low SNR. While it is clear that obtaining a separate non-water suppressed scan is a viable method for estimating amplitude factors and phase offsets (Wvoxel), there are many circumstances where limitations on acquisition time make it preferable to perform the combination without obtaining an additional scan. Several strategies for achieving this were evaluated, including those that use residual water and NAA peaks as a reference (RWcentral, RWvoxel, GLSRW, NAAvoxel, NAA central, GLSNAA,22 FPphasing15 and WSVD algorithms).20,21
In a previous study Rodgers et al.20 showed that using WSVD, FPphasing and Wvoxel gave good results for analysis of single voxel spectroscopy data obtained from a normal volunteer with a 3T scanner with 12 receiver elements, but WSVD gave the best overall performance. In a subsequent study, An et al.22 demonstrated, for data obtained with a 7T scanner and 32-channel RF coil, that the WSVD method was more sensitive than the GLS method to baseline errors from water or lipid signals from outside the voxels of interest. This resulted in the GLS method outperforming the WSVD method with respect to the coefficient of variance. It is important to note that NAA was used as the reference peak in that case. The results obtained from our analysis of multi-voxel data from a phantom that had no lipid contamination and different simulated noise levels were consistent with these findings. When any amount of lipid was present, however, the performance of this method degraded significantly.
In another recent study Abdoli et al.31 used a volumetric spin-echo EPSI acquisition with interleaved water-reference data (TR = 1.71s, TE = 70 ms and Tacq = 26 min) to evaluate amplitude weighting and combination strategies for data from normal volunteers. They reported that using the signal, signal-to-noise and signal-to-noise squared weighting from the water reference scan performed similarly and gave better results than the SVD, WSVD and GLS combination methods. For the normal volunteers considered in our study, we found that using calibration image intensities to estimate amplitude weighting factors gave results similar to or better than the non-suppressed water (Wvoxel) or high residual water (RWvoxel) reference peak intensities and the intensities from the FPphasing algorithm. This is likely due to the CAL images approximating the true coil sensitivity map more accurately as shown in Figure 4. The SNRs obtained from our large patient cohort verified that the RWvoxel methods consistently had maximum metabolite SNR.
For the in vivo analysis of 3D MRSI including tumor voxels with very little to no NAA and some lipid contamination for voxels within the selected volume, a residual water peak 10–15 times higher than the NAA in NAWM was found to give robust estimates of phase and amplitude parameters. We were able to achieve this level of residual water routinely in all acquisitions through optimizing the flip angles and separation ofthe CHESS water suppression pulses, along with higher order shimming and an overpress factor of 1.5 to avoid chemical shift artifacts and spatial variations in the residual water peak on the edge ofthe selected volume. This meant that there was a residual water peak in almost every voxel ofthe 3D array for the cycle without the editing pulse. Other methods have since been introduced to control amplitude-reduced residual water more accurately, such as the dual-band spectral–spatial excitation scheme with additional phase-modulation by Schricker et al.47 With sufficient residual water, however achieved, the RWvoxel combination method was the most robust and accurate method, with low computational complexity. Although the response of these methods to baseline/signal artifacts was variable, their overall performance was similar when the largest peak in the spectrum was the residual water.
For in vivo data, techniques that incorporated spatially varying phase offsets outperformed the RWcentral and NAAcentral methods. Voxel-by-voxel phase correction was especially important for coils with higher numbers of elements and for larger excitation volumes. Among the voxel-by-voxel correction techniques, the RWvoxel and FPphasing methods performed better than the WSVD and GLSRW methods. This behavior was consistent among all volunteer exams, but different from that obtained for the phantom study due mainly to baseline errors and lipid contamination. In the absence of a strong residual water peak, the WSVD and FPphasing methods suffered for voxels with large lipid signals from outside the voxel of interest.
The impact of different coil geometries on the spatial variation of phase offsets was studied using deviation maps calculated from the non-suppressed water acquisition. In the center ofthe selected volume these offsets were relatively constant, but the between-channel deviation increased for voxels nearer to the coils and was larger for the 32-versus the 8-channel coil. One way to compare the methods is to look at the consistency of the phases and weights in different datasets compared with the unsuppressed water reference scan. By adding sufficiently high levels of residual water, these maps were seen to be very similar to those calculated from the unsuppressed water scan reference. To test the sensitivity of the maps to differences in coil loading, results from three volunteer scans were compared and showed that the amplitude varied by factors of 2–10, while the phase varied from 5°−40°. This suggests that between-subject variations in coil loading are significant and extrapolating from phantom or other previously acquired data may be unreliable.
Even with conservative acquisition strategies, it was observed that unsuppressed residual lipid resonances were present in some of the voxels from the 3D array of patient data. In some cases this was due to the point-spread function (PSF) of the phase-encoding method and in other cases to artifacts from the surgical cavity Lipid contamination from signals outside the prescribed voxel resulted in suboptimal combination for both the WSVD and FPphasing methods. Although previous studies have proposed a number of methods for reducing unwanted lipid by post-processing approaches such as time-domain fitting,48 data extrapolation49 or using the sensitivity information of the 8-channel phased array coil and SENSE to unalias the lipid resonances50 and non-iterative time-domain fitting with the Lanczos-based version of the HSVD method was employed to reduce the outer volume lipid signals,41 the WSVD algorithm could not combine channels robustly when the unwanted lipid signal was at a level comparable in magnitude to the true metabolite signals. Although Rodgers et al.21 recently suggested that this could be avoided by either reducing the acquisition bandwidth so the contaminating signals are not recorded or zeroing the signal for chemical shifts around the contaminated signal before applying the WSVD combination method, this is not a practical solution for brain tumors, as the presence of high lipid can provide evidence for apoptosis or necrosis and it is important to be able to detect these peaks within the tumor. Modifying the acquisition parameters to leave sufficient residual water was a more effective solution.
In summary, results obtained in volunteers and from a large cohort of patients with brain tumors indicated that the method that employed high residual water peaks to estimate voxel-by-voxel phase offsets for each channel was able to outperform other, more sophisticated algorithms. Although WSVD was shown to be a viable technique for analyzing spectra with small selected volumes and limited lipid contamination, it was not a robust choice for evaluating multi-voxel spectra from larger regions of the brain. While the GLS method was less sensitive to these issues and performed well in terms of the coefficient of variance, it provided a lower average SNR. These results can inform the design of future robust acquisition and processing strategies for routine clinical MRSI applications.
ACKNOWLEDGEMENTS
We thank Yan Li for her advice and discussion and Angela Jakary for her help in data acquisition and proof reading. This work has been presented in part at the Annual Meeting of the International Society for Magnetic Resonance in Medicine, Toronto, Canada, June 2015 and was supported by NIH grants R01 CA127612 and P01 CA118816.
Funding information
NIH, Grant/Award Number: R01 CA127612 and P01 CA118816
Abbreviations used:
- CV
coefficient of variance
- EPSI
echo planar spectroscopic imaging
- FID
free induction decay
- FLIRT
FSL’s linear registration tool
- FOV
field of view
- FPphasing
first-point phasing
- GLS
generalized least squares
- i.i.d.
independent and identically distributed
- MRSI
magnetic resonance spectroscopic imaging
- NAWM
normal-appearing white matter
- PI
percent signal increase
- PRESS
point-resolved spectroscopy
- PSF
point-spread function
- SD
standard deviation
- SENSE
sensitivity encoding
- SNR
signal-to-noise ratio
- VSS
Very spatially selective
- WM
white matter
- WSVD
whitened singular-value decomposition
REFERENCES
- 1.Park I,Tamai G, Lee MC, et al. Patterns of recurrence analysis in newly diagnosed glioblastoma multiforme after three-dimensional conformal radiation therapy with respect to pre-radiation therapy magnetic resonance spectroscopic findings. Int J Radiat Oncol Biol Phys. 2007;69:381–389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Laprie A, Catalaa I, Cassol E, et al. Proton magnetic resonance spectroscopic imaging in newly diagnosed glioblastoma: Predictive value for the site of postradiotherapy relapse in a prospective longitudinal study. Int J Rad Oncol Biol Phys. 2008;70:773–781. [DOI] [PubMed] [Google Scholar]
- 3.Wei B, Khayal IS, Lupo JM, et al. Multiparametric characterization of Grade 2 glioma subtypes using magnetic resonance spectroscopic, perfusion, and diffusion imaging. Transl Oncol. 2009;2:271–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nelson SJ. Assessment of therapeutic response and treatment planning for brain tumors using metabolic and physiological MRI. NMR Biomed. 2011;24:734–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ozturk-Isik E, Pirzkall A, Lamborn KR, Cha S, Chang SM, Nelson SJ. Spatial characteristics of newly diagnosed Grade 3 glioma assessed by magnetic resonance metabolic and diffusion tensor imaging. Transl Oncol.2012;5:10–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nelson SJ. Multivoxel magnetic resonance spectroscopy of brain tumors. Mol Cancer Ther. 2003;2:497–507. [PubMed] [Google Scholar]
- 7.Li X, Jin H, Lu Y, Oh J, Chang S, Nelson SJ. Identification of MRI and 1H MRSI parameters that may predict survival for patients with malignant gliomas. NMR Biomed. 2004;17:10–20. [DOI] [PubMed] [Google Scholar]
- 8.Oh J, Henry RG, Pirzkall A, et al. Survival analysis in patients with glioblastoma multiforme: Predictive value of choline-to-n-acetylaspartate index, apparent diffusion coefficient, and relative cerebral blood volume. J Magn Reson Imaging. 2004;19:546–554. [DOI] [PubMed] [Google Scholar]
- 9.McKnight TR, Noworolski SM, Vigneron DB, Nelson SJ. An automated technique for the quantitative assessment of 3D-MRSI data from patients with glioma. J Magn Reson Imaging. 2000;13:167–177. [DOI] [PubMed] [Google Scholar]
- 10.Muruganandham M, Clerkin PP, Smith BJ, et al. 3-dimensional magnetic resonance spectroscopic imaging at 3 Tesla for early response assessment of glioblastoma patients during external beam radiation therapy. Radiat Oncol Biol. 2014;90:181–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li Y, Lupo JM, Parvataneni R, et al. Survival analysis in patients with newly diagnosed glioblastoma using pre- and postradiotherapy MR spectroscopic imaging. Neuro Oncol. 2013;15:607–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wright SM, Wald LL. Theory and application of array coils in MR spectroscopy. NMR Biomed. 1997;10:394–410. [DOI] [PubMed] [Google Scholar]
- 13.Wald LL, Moyher SE, Day MR, Nelson SJ, Vigneron DB. Proton spectroscopic imaging of the human brain using phased-array detectors. Magn Reson Med. 1995;34:440–445. [DOI] [PubMed] [Google Scholar]
- 14.Schaffter T, Bornert P, Leussler C, Carlsen IC, Leibfritz D. Fast H-1 spectroscopic imaging using a multi-element head-coil array. Magn Reson Med. 1998;40:185–193. [DOI] [PubMed] [Google Scholar]
- 15.Brown MA. Time-domain combination of MR spectroscopy data acquired using phased-array coils. Magn Reson Med. 2004;52:1207–1213. [DOI] [PubMed] [Google Scholar]
- 16.Debbins JP, Felmlee JP, Riederer SJ. Phase alignment of multiple surface coil data for reduced bandwidth and reconstruction requirements. Magn Reson Med. 1997;38:1003–1011. [DOI] [PubMed] [Google Scholar]
- 17.Sandgren N, Stoica P, Frigo FJ, Selén Y. Spectral analysis of multichannel MRS data. J Magn Reson. 2005;175:79–91. [DOI] [PubMed] [Google Scholar]
- 18.Bydder M, Hamilton G, Yokoo T, Sirlin CB. Optimal phased-array combination for spectroscopy. Magn Reson Imaging. 2008;26:847–850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Martini N, Santarelli MF, Giovannetti G, et al. Noise correlations and SNR in phased-array MRS. NMR Biomed. 2010;23:66–73. [DOI] [PubMed] [Google Scholar]
- 20.Rodgers CT, Robson MD. Receive array magnetic resonance spectroscopy: Whitened singular value decomposition (WSVD) gives optimal Bayesian solution. Magn Reson Med. 2010;63:881–891. [DOI] [PubMed] [Google Scholar]
- 21.Rodgers CT, Robson MD. Coil combination for receive array spectroscopy: Are data-driven methods superior to methods using computed field maps? Magn Reson Med. 2015;75:473–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.An L, Veen J, Li S, Thomasson DM, Shen J. Combination of multichannel single-voxel MRS signals using generalized least squares. J Magn Reson Imaging. 2012;37:1445–1450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hall EL, Stephenson MC, Price D, Morris PG. Methodology for improved detection of low concentration metabolites in MRS: Optimised combination of signals from multi-element coil arrays. NeuroImage. 2014;86:35–42. [DOI] [PubMed] [Google Scholar]
- 24.Natt O, Bezkorovaynyy V, Michaelis T, Frahm J. Use of phased array coils for a determination of absolute metabolite concentrations. Magn Reson Med. 2004;53:3–8. [DOI] [PubMed] [Google Scholar]
- 25.Wijtenburg SA, Knight-Scott J. Reconstructing very short TE phase rotation spectral data collected with multichannel phased-array coils at 3 T. Magn Reson Imaging. 2011;29:937–942. [DOI] [PubMed] [Google Scholar]
- 26.Avdievich NI, Pan JW, Baehring JM, Spencer DD, Hetherington HP. Short echo spectroscopic imaging of the human brain at 7T using transceiver arrays. Magn Reson Med. 2009;62:17–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dong Z. Proton MRS and MRSI of the brain without water suppression. Progr Nucl Magn Reson Spectrosc. 2015;86–87:65–79. [DOI] [PubMed] [Google Scholar]
- 28.Maudsley AA, Domenig C, Govind V, et al. Mapping of brain metabolite distributions by volumetric proton MR spectroscopic imaging (MRSI). Magn Reson Med. 2009;61:548–559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gasparovic C, Song T, Devier D, et al. Use of tissue water as a concentration reference for proton spectroscopic imaging. Magn Reson Med. 2006;55:1219–1226. [DOI] [PubMed] [Google Scholar]
- 30.Maril N, Lenkinski RE. An automated algorithm for combining multivoxel MRS data acquired with phased-array coils. J Magn Reson Imaging. 2005;21:317–322. [DOI] [PubMed] [Google Scholar]
- 31.Abdoli A, Maudsley AA. Phased-array combination for MR spectroscopic imaging using a water reference. Magn Reson Med. 2015;76:733–741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fang L, Wu M, Ke H, Kumar A, Yang S. Adaptively optimized combination (AOC) of magnetic resonance spectroscopy data from phased array coils. Magn Reson Med. 2015;75:2235–2244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dong Z, Peterson B. The rapid and automatic combination of proton MRSI data using multi-channel coils without water suppression. Magn Reson Imaging. 2007;25:1148–1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Park I, Chen AP, Zierhut ML, Ozturk-Isik E, Vigneron DB, Nelson SJ. Implementation of 3 T lactate-edited 3D 1H MR spectroscopic imaging with flyback echo-planar readout for gliomas patients. Ann Biomed Eng. 2010;39:193–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Li Y, Osorio JA, Ozturk-Isik E, et al. Considerations in applying 3D PRESS H-1 brain MRSI with an eight-channel phased-array coil at 3 T. Magn Reson Imaging. 2006;24:1295–1302. [DOI] [PubMed] [Google Scholar]
- 36.Ozhinsky E Automated acquisition of brain MRSI data. [PhD thesis] San Francisco: University of California;2012. [Google Scholar]
- 37.Ozhinsky E, Vigneron DB, Chang SM, Nelson SJ. Automated prescription of oblique brain 3D magnetic resonance spectroscopic imaging. Magn Reson Med. 2012;69:920–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ozhinsky E, Vigneron DB, Nelson SJ. Improved spatial coverage for brain 3D PRESS MRSI by automatic placement of outer-volume suppression saturation bands. J Magn Reson Imaging. 2011;33:792–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bian W, Li Y, Crane JC, Nelson SJ. Towards robust reproducibility study for MRSI via fully automated reproducible imaging positioning. In: Proc 23rd Scientific Meeting & Exhibition (ISMRM); 2015; San Francisco, CA:1. [Google Scholar]
- 40.Nelson SJ. Analysis of volume MRI and MR spectroscopic imaging data for the evaluation of patients with brain tumors. Magn Reson Med. 2001;46:228–239. [DOI] [PubMed] [Google Scholar]
- 41.Pijnappel WWF, Boogaart A, DeBeer R, Van Ormondt D. SVD-based quantification of magnetic resonance signals. J Magn Reson. 1992;97:122–134. [Google Scholar]
- 42.Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17:825–841. [DOI] [PubMed] [Google Scholar]
- 43.Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20:45–57. [DOI] [PubMed] [Google Scholar]
- 44.Li Y, Srinivasan R, Ratiney H, Lu Y, Chang SM, Nelson SJ. Comparison of T1 and T2 metabolite relaxation times in glioma and normal brain at 3T. J Magn Reson Imaging. 2008;28:342–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zierhut ML, Ozturk-Isik E, Chen AP, Park I, Vigneron DB, Nelson SJ. 1H spectroscopic imaging of human brain at 3 Tesla: Comparison of fast three-dimensional magnetic resonance spectroscopic imaging techniques. J Magn Reson Imaging. 2009;30:473–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wiggins GC, Polimeni JR, Potthast A, Schmitt M,Alagappan V, Wald LL. 96-channel receive-only head coil for 3 Tesla: Design optimization and evaluation. Magn Reson Med. 2009;62:754–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schricker AA, Pauly JM, Kurhanewicz J, Swanson MG, Vigneron DB. Dualband spectral-spatial RF pulses for prostate MR spectroscopic imaging. Magn Reson Med. 2001;46:1079–1087. [DOI] [PubMed] [Google Scholar]
- 48.DeBeer R, Michels F, Van Ormondt D, Van Tongeren BPO, Luyten PR, Van Vroonhoven H. Reduced lipid contamination in in-vivo H-1 MRSI using time-domain fitting and neural-network classification. Magn Reson Imaging. 1993;11:1019–1026. [DOI] [PubMed] [Google Scholar]
- 49.Schuff N, Weiner MW, Maudsley AA. Removal of lipid artifacts in 1H spectroscopic imaging by data extrapolation. Magn Reson Med. 1996;35(5):678–687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ozturk-Isik E, Crane JC, Cha S, Chang SM, Berger MS, Nelson SJ. Unaliasing lipid contamination for MR spectroscopic imaging of gliomas at 3T using sensitivity encoding (SENSE). Magn Reson Med. 2006;55:1164–1169. [DOI] [PubMed] [Google Scholar]


