Modeling Sex Differences in the Renin Angiotensin System and the Efficacy of Antihypertensive Therapies

Abstract

The renin angiotensin system is a major regulator of blood pressure and a target for many anti-hypertensive therapies; yet the efficacy of these treatments varies between the sexes. We use published data for systemic RAS hormones to build separate models for four groups of rats: male normotensive, male hypertensive, female normotensive, and female hypertensive rats. We found that plasma renin activity, angiotensinogen production rate, angiotensin converting enzyme activity, and neutral endopeptidase activity differ significantly among the four groups of rats. Model results indicate that angiotensin converting enzyme inhibitors and angiotensin receptor blockers induce similar percentage decreases in angiotensin I and II between groups, but substantially different absolute decreases. We further propose that a major difference between the male and female RAS may be the strength of the feedback mechanism, by which receptor bound angiotensin II impacts the production of renin.

1. Introduction

The renin angiotensin system (RAS) is an important regulator of blood pressure. The RAS consists of an enzymatic cascade that produces the bioactive peptide angiotensin II (Ang II)[1]. The cascade starts with angiotensinogen (AGT), which is cleaved by renin and later angiotensin converting enzyme (ACE) and neutral endopeptidase (NEP) into different forms of angiotensin (see Figure 1) [1, 2, 3]. The enzyme renin catalyzes the first reaction in the RAS and is often thought as the driving force in the cascade. The products of the RAS are major biologically active products includes angiotensin (1–7) (Ang (1–7)) and Ang II. These bind to receptors and impact the brain, heart, kidney, vasculature, and immune system [1]. Ang II has two different types of receptors. When bound to angiotensin II type 1 receptor (AT1R), Ang II stimulates renal vasoconstriction, raises sodium reabsorption, and promotes inflammation and fibrosis [2]. When bound to angiotensin II type 2 receptor (AT2R), Ang II induces vasodilation and natriuresis. Ang (1–7) binds to the angiotensin type 7 receptor (AT7R), also known as the MAS receptor, to cause vasodilation and natriuresis and increase production of nitric oxide to reduce inflammation and fibrosis [2, 3].

Figure 1.

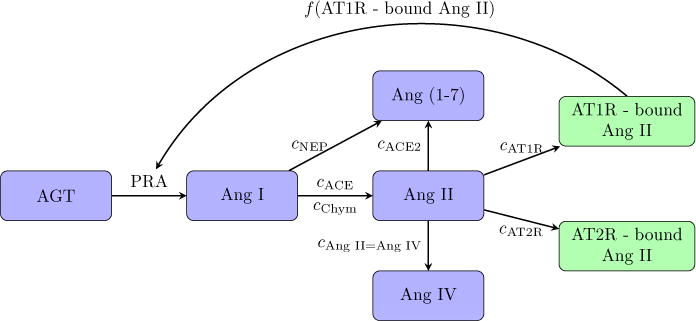
Schematic diagram depicting the RAS reaction cascade.

AT1R-bound Ang II regulates overall blood pressure via its effects on the kidney. The kidney is responsible for filtering blood into urine to remove waste from the body. Through the glomerulus, blood is filtered leaving all proteins, such as hemoglobin, behind in the body. Attached to the glomerulus is the nephron, which is the kidney’s functional unit and is responsible for reabsorption and secretion. As the filtrate travels through the nephrons, essential solutes and water are reabsorbed or secreted. In particular, the reabsorption of sodium by the nephron is critical for blood pressure regulation [4]. AT1R-bound Ang II regulates blood pressure by increasing sodium and fluid reabsorption in the proximal tubule, which is a key segment of nephron that normally reabsorbs about 2/3 of the filtered salt and water [1].

The relation between the RAS and the kidney is two-way with the kidney influencing the RAS by providing the first two essential components of the RAS: AGT and renin. The proximal tubule, as well as the liver, are the primary places of production for AGT, whereas renin is produced in the juxtaglomerular apparatus, a microscopic structure in the kidney. When blood pressure is low, renal blood flow decreases and kidney function may become impaired. To compensate, the kidney elevates renin production, causing an increase in AT1R-bound Ang II, which raises blood pressure.

Because of its central role in fluid homeostasis, the RAS, in particular ACE and AT1R, are often targeted in hypertensive treatments. Given that AT1R-bound Ang II causes vasoconstriction and higher blood pressure, antihypertensive drug treatments seek to lower the amount of Ang II bound to AT1R. Given also that ACE converts Ang I into Ang II, by lowering the level of ACE activity through ACE inhibitors (ACEI), the total amount of Ang II that is available to bind to AT1R can be reduced. Angiotensin receptor blockers (ARB) are AT1R antagonists that reduce vasoconstriction by preventing the binding of vasoactive peptides (i.e. Ang II).

The RAS is similar in mammals, as are the sex differences. Females have been shown to have lower blood pressure than males in humans, rats, dogs, and birds [5]. Major sex differences in the RAS have been identified, including how much substrate is produced and how angiotensin interacts with receptors. For example, in both rats and humans, females have greater circulating levels of AGT [6], causing an overall greater amount of angiotensin to be flowing through the system. Also, male rats have been shown to have greater Ang II levels [5] while female rats have greater levels of Ang (1–7) [7]. However, a greater level of ACE2 activity (which converts Ang II to Ang (1–7)) has been measured in male rats [7].

Interestingly, males and females exhibit differing responses to Ang II. Changes in Ang II levels produce smaller changes in blood pressure in female rats [5, 6]. That discrepancy may be attributed to differences in receptor expression, inasmuch as male rats have greater AT1R expression and lower AT2R expression than female rats [5, 7, 8]. Estrogen also reduces the half life of AT1R-bound Ang II [9].

Given the above observations, it should come as no surprise that males and females respond differently to antihypertensive treatments that target the RAS. In one study, women who were prescribed ARBs had better survival rates than women prescribed ACEIs, while the opposite was true in men [10]. Studies have provided evidence that the effectiveness of ACEIs in women decreases over time and offers less benefit to women as determined by total mortality [10]. While these trends have been observed in multiple studies, the underlying mechanisms are not well understood. Thus, the goal of this study is to obtain a better understanding of the RAS of the rat and the functional implications of the sex differences. To achieve that goal, we develop mathematical models of the RAS for four groups of rats: normotensive male, normotensive female, hypertensive male, and hypertensive female rats. The models are formulated using ordinary differential equations based on a published RAS model for normotensive humans, presumably males [11]. Other studies have modeled the RAS within the larger context of the circulatory system, but none of these have looked into how sex differences within the RAS affects the circulatory system and blood pressure [12, 13, 14]. A goal of this study is to identify individual parameter sets that correspond to the different types of rats (normotensive and hypertensive rats, male and female). Our focus on the rat is motivated by its role as one of the most commonly used animal models in experiments and drug trials. Following the successful determination of the model parameters, we apply the models to elucidate the mechanisms by which the known differences between the sexes contribute to the sex-specific responses to anti-hypertensive therapies. Since the rat and human share many of the known sex differences in the RAS, conclusions from this study should be applicable to humans.

2. Methods

2.1. Model equations

A schematic diagram that depicts the RAS reaction cascade can be found in Figure 1. As previously discussed, AGT is catalytically cleaved by renin to produce Ang I. The rate of change of [AGT] is given by the production rate k_AGT, the conversion to Ang I catalyzed by renin, and the decay based on its half life h_AGT:

$$\frac{\mathrm{d}[\mathrm{AGT}]}{\mathrm{d}t}=k_{\mathrm{AGT}}-\mathrm{PRA}-\frac{\ln (2)}{h_{\mathrm{AGT}}}[\mathrm{AGT}]$$ (1)

where PRA denotes plasma renin activity. PRA is assumed to follow Michaelis-Menton kinetics, characterized by the maximum rate V_max [11]. The Michaelis constant is taken to be the [AGT] value at which PRA reaches half of its maximum value (denoted [AGT]_EQ). PRA also depends on the feedback effect of AT1R-bound Ang II [12].

$$\mathrm{PRA}=\frac{V_{max}[\mathrm{AGT}]}{[\mathrm{AGT}]+{[\mathrm{AGT}]}_{EQ}}\ast f([\text{AT}1\text{R-bound}\text{Ang}\text{II}])$$ (2)

$$f={\left(\frac{{\left[\text{AT}1\text{R-bound}\text{Ang}\text{II}\right]}_{EQ}}{\left[\text{AT}1\text{R-bound}\text{Ang}\text{II}\right]}\right)}^{B_{AT1}}$$ (3)

Because the exponent B_AT1 is taken to be positive (0.95), when [AT1R-bound Ang II] is above its equilibrium value ([AT1R-bound Ang II]_EQ), PRA decreases.

Ang I is converted into other forms through ACE, chymase, and NEP; the respective reaction rate constants are denoted c_ACE, c_Chym, and c_NEP. The rate of change of [Ang I] is given by

$$\frac{d[\text{Ang}\mathrm{I}]}{\mathrm{d}t}=\mathrm{PRA}-(c_{\text{ACE}}+c_{\text{Chym}}+c_{\text{NEP}})[\text{Ang}\mathrm{I}]-\frac{\ln (2)}{h_{\text{Ang}\mathrm{I}}}[\text{Ang}\mathrm{I}]$$ (4)

where h_Ang I denotes the half-life of Ang I.

Ang II is converted from Ang I through ACE and chymase and then converted into Ang (1–7) through ACE2 with the rate constant c_ACE2. Ang II also binds to the AT1R and AT2R with rate constants c_AT1R and c_AT2R, respectively. We assume that Ang II has a half life of h_Ang II. With this notation the rate of change of [Ang II] is

$$\frac{\mathrm{d}[\text{Ang}\text{II}]}{\mathrm{d}t}=(c_{\text{ACE}}+c_{\text{chym}})[\text{Ang}\mathrm{I}]-(c_{\text{ACE}2}+c_{\text{Ang}\text{II}=\text{Ang}\text{IV}}+c_{\text{AT}1\mathrm{R}}+c_{\text{AT}2\mathrm{R}})\times [\text{Ang}\text{II}]-\frac{\ln (2)}{h_{\text{Ang}\text{II}}}[\text{Ang}\text{II}]$$ (5)

Ang II binds to AT1R with rate constant c_AT1R to produce AT1R-bound Ang II. AT1R-bound Ang II decays with a half life of h_AT1R, giving the rate of change of [AT1R-bound Ang II] as

$$\frac{\mathrm{d}[\text{AT}1\text{R-bound}\text{Ang II}]}{\mathrm{d}t}=c_{\text{AT}1\mathrm{R}}[\text{Ang}\text{II}]-\frac{\ln (2)}{h_{\text{AT1R}}}[\text{AT}1\text{R-bound}\text{Ang}\text{II}]$$ (6)

Ang II binds to the AT2R with rate constant c_AT2R to produce AT2R-bound Ang II. AT2R-bound Ang II decays with a half life of h_AT2R, giving the rate of change of [AT2R-bound Ang II] as

$$\frac{d[\text{AT2R-bound}\text{Ang}\text{II}]}{\mathrm{d}t}=c_{\text{AT}2\mathrm{R}}[\text{Ang}\text{II}]-\frac{\ln (2)}{h_{\text{AT}2\mathrm{R}}}[\text{AT2R-bound}\text{Ang}\text{II}]$$ (7)

Ang (1–7) is converted by NEP from Ang I and by ACE2 from Ang II, and it decays with a half life of h_Ang (1–7). Thus the rate of change of [Ang (1–7)] is

$$\frac{\mathrm{d}[\text{Ang}(1-7)]}{\mathrm{d}t}=c_{\text{NEP}}[\text{Ang}\mathrm{I}]+c_{\text{ACE}2}[\text{Ang}\text{II}]-\frac{\ln (2)}{h_{\text{Ang}(1-7)}}[\text{Ang}(1-7)]$$ (8)

Ang IV is converted from Ang II with the rate constant c_Ang II=Ang IV and decays with a half life of h_Ang IV, giving the rate of change of [Ang IV] as

$$\frac{d[\text{Ang IV}]}{\mathrm{d}t}=c_{\text{Ang}\text{II}=\text{Ang}\text{IV}}[\text{Ang II}]-\frac{\ln (2)}{h_{\text{Ang}\text{IV}}}[\text{Ang}\text{IV}]$$ (9)

2.2. Model parameters

As previously noted, the goal of this study is to identify model parameters that characterize the RAS system in a normotensive male rat, a hypertensive male rat, a normotensive female rat, and a hypertensive female rat. To that end, we seek to identify parameters that yield hormone levels that are known to differ among these four types of rats. Notably, Ang I and Ang II levels have been observed to be substantially elevated in hypertensive males [15]. We seek parameter sets such that at steady state, Eqs. (1)–(9) yield the desired hormone levels for each type of rats, as follows:

1. We substitute the known hormone concentrations (shown in Table 1) into the steady-state formulation of the model equations (i.e., Eqs. (1), (4)–(9) with the time derivatives set to zero).

2. Half lives for each form of angiotensin, the steady state AGT and Ang IV concentrations, and the feedback function fitting constant B_AT1 are assumed the same for all groups of rats. Half lives and B_AT1 were assumed to be constant over time. The value for B_AT1 is taken to be 0.95 [12].

3. AT1R-bound Ang II levels are determined from the measured [Ang II] in rats [15] and the ratio of [AT1R-bound Ang II] to [Ang II] in Ref. [11]. Similarly, AT2R-bound Ang II levels are determined from the measured [Ang II] in rats [15] and the ratio of [AT2R-bound Ang II] to [Ang II] in Ref. [11].

4. At steady state, [AGT] = [AGT]_EQ, and [AT1R-bound Ang II] = [AT1R-bound Ang II]_EQ. From Eq. (2), f = 1 and PRA = V_max/2.

5. Given these assumptions, the unknowns are PRA, k_AGT, c_ACE, c_Chym, c_NEP, c_ACE2, c_Ang II=Ang IV, cAT1R, and c_AT2R. This gives 7 linear equations (Eqs. (2) and (3) do not give additional constraints) and 9 unknowns.

6. To achieve a fully determined system of equations, we impose two additional constraints. One relates the reaction rate constant of ACE to chymase, since ACE is responsible for over 90% of the Ang I that is converted into Ang II [11].

Table 1.

Hormone levels and enzymatic activity. Values from Ref. [15] are for normotensive Lewis rats and hypertensive mRen(2). Lewis rats and were estimated from figures therein. Values from Ref. [16] are for Sprague-Dawley rats. Human values from Ref. [11] are applied to the rat when rodent data are not available.

		Normotensive		Hypertensive
Hormone	Unit	Male	Female	Male	Female	Reference
AGT	fmol/ml	576000	576000	576000	576000	[16]
Ang I	fmol/ml	90	75	200	61	[15]
Ang II	fmol/ml	6	6	47	20	[15]
Ang 1–7	fmol/ml	50	25	31	162	[15]
Ang IV	fmol/ml	1.29	1.29	1.29	1.29	[11]
AT1R - bound Ang II	fmol/ml	20.46	20.46	160.29	68.21
AT2R - bound Ang II	fmol/ml	6.82	6.82	53.43	22.74
Enzyme Activity
ACE2	fmol/mg/min	87.5	55	69	41	[15]
NEP	fmol/mg/min	412.5	975	300	920	[15]

$$c_{\text{ACE}}=9c_{\text{Chym}}$$ (10)

The second relates c_ACE2 and c_NEP by

$$c_{\text{ACE}2}={\alpha }_{\text{ACE}2,\text{NEP}}{c}_{\text{NEP}}$$ (11)

where α_ACE2,NEP is given by the experimentally determined enzymatic activity for ACE2 and NEP for the different types of rats (Table 1).

Given the above assumptions, we can formulate a linear system Ax = b where

$$A=\left[\begin{array}{ccccccccc}\hfill -1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill -[\text{Ang}\mathrm{I}]\hfill & \hfill -[\text{Ang}\mathrm{I}]\hfill & \hfill -[\text{Ang}\mathrm{I}]\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill [\text{Ang}\mathrm{I}]\hfill & \hfill [\text{Ang}\mathrm{I}]\hfill & \hfill 0\hfill & \hfill -[\text{Ang}\text{II}]\hfill & \hfill -[\text{Ang}\text{II}]\hfill & \hfill -[\text{Ang}\text{II}]\hfill & \hfill -[\text{Ang}\text{II}]\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill [\text{Ang}\mathrm{I}]\hfill & \hfill [\text{Ang}\text{II}]\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill [\text{Ang}\text{II}]\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill [\text{Ang}\text{II}]\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill [\text{Ang}\text{II}]\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill -9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_{\text{ACE}2,\text{NEP}}\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$$ (12)

$$x=\left[\begin{array}{c}\hfill \mathit{PRA}\hfill \\ \hfill k_{\mathrm{AGT}}\hfill \\ \hfill c_{\text{ACE}}\hfill \\ \hfill c_{\text{Chym}}\hfill \\ \hfill c_{\text{NEP}}\hfill \\ \hfill c_{\text{ACE}2}\hfill \\ \hfill c_{\text{Ang}\text{II}=\text{Ang}\text{IV}}\hfill \\ \hfill c_{\text{AT}1\mathrm{R}}\hfill \\ \hfill c_{\text{AT}2\mathrm{R}}\hfill \end{array}\right]b=\left[\begin{array}{c}\hfill \frac{\ln (2)}{h_{\mathrm{AGT}}}[\mathrm{AGT}]\hfill \\ \hfill \frac{\ln (2)}{h_{\text{Ang I}}}\ast [\text{Ang I}]\hfill \\ \hfill \frac{\ln (2)}{h_{\text{Ang II}}}\ast [\text{Ang II}]\hfill \\ \hfill \frac{\ln (2)}{h_{\text{Ang}(1-7)}}\ast [\text{Ang}(1-7)]\hfill \\ \hfill \frac{\ln (2)}{h_{\text{Ang IV}}}\ast [\text{Ang IV}]\hfill \\ \hfill \frac{\ln (2)}{h_{\text{AT}1\mathrm{R}}}\ast [\text{AT}1\mathrm{R}-\text{bound Ang II}]\hfill \\ \hfill \frac{\ln (2)}{h_{\text{AT}2\mathrm{R}}}\ast [\text{AT}2\mathrm{R}-\text{bound Ang II}]\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$$ (13)

3. Model results

3.1. Parameter identification

By solving the system Ax = b (Eqs. 12, 13), we obtain model parameters for normo/hypertensive male/female rats. Results are shown in Table 2. A notable difference between the reaction rate constants computed for the normotensive and hypertensive rats are the much higher c_ACE and lower c_Ang II=Ang IV in the latter, for both male and female rats. This implies a higher Ang I-to-Ang II conversion rate and a lower Ang II-to-Ang IV conversion rate, which explains the substantially higher [Ang II] in hypertensive rats (Table 1).

Table 2.

Calculated kinetic parameters for four cohorts of rats.

		Normotensive		Hypertensive
Parameter	Unit	Male	Female	Male	Female
Vmax	fmol/ml/h	16270.4	13705.8	40976	13962.4
PRA	fmol/ml/h	8135.2	6852.9	20488	6981.2
kAGT	fmol/ml/h	48061	46778	60413	46906
cACE	1/h	5.81	6.96	17.15	24.88
cChym	1/h	0.65	0.77	1.91	2.76
cNEP	1/h	0.76	0.46	0.20	3.63
cACE2	1/h	0.16	0.026	0.047	0.16
cAng II=Ang IV	1/h	17.88	17.88	2.28	5.37
cAT1R	1/h	11.82	11.82	11.82	11.82
cAT2R	1/h	3.94	3.94	3.94	3.94

Additionally, the model predicts substantial sex differences among hypertensive rats in c_ACE, c_Chym, c_NEP, and c_ACE2. In contrast, sex differences for these reaction rate constants are much smaller among normotensive rats. This result should be expected, given the more substantial sex differences in hormone levels among hypertensive rats (Table 1). Model results indicate that hypertensive females have an especially high level of NEP activity (3.63, compared to 0.2 and 0.76 for hypertensive and normotensive male). That, combined with their higher ACE2 rate constant compared to hypertensive male, means that much more angiotensin is being converted into Ang (1–7). These higher rate constants can explain the high Ang (1–7) levels observed experimentally. Similarly, the relatively lower ACE2 and NEP activities predicted for hypertensive male rats slows the conversion of Ang II and explains the higher Ang II levels seen in these rats.

3.2. Parameter sensitivity study

In the next set of simulations, we sought to assess the stability of the system and to determine the extent to which a perturbation in each parameter can affect model results. To achieve these goals, we conducted a local sensitivity analysis in which we varied each parameter by 10% and recalculated the steady state hormone levels by solving for the root of the nonlinear system. In addition, we assessed the impact of the feedback system (Eq. 3) by conducting the parameter sensitivity study with and without feedback (f = 1 in the latter). Tables 3–6 show the results for the four groups of rats, given as the percentage changes in key hormone levels in response to a given parameter variation. Values in parentheses are for the system without feedback.

Table 3.

Percent change in response to parameter perturbation for male normotensive rats. Values in parentheses are from the system without feedback function f.

	AGT	Ang I	Ang II	Ang (1–7)	Ang IV	AT1R-bound Ang II	AT2R-bound Ang II	PRA
Vmax + 10%	−0.97 (−1.83)	4.75 (8.98)	4.75 (8.98)	4.75 (8.98)	4.75 (8.98)	4.75 (8.98)	4.75 (8.98)	4.75 (8.98)
Vmax − 10%	1.02 (1.87)	−5.01 (−9.17)	−5.01 (−9.17)	−5.01 (−9.17)	−5.01 (−9.17)	−5.01 (−9.17)	−5.01 (−9.17)	−5.01 (−9.17)
[AGT]EQ + 10%	0.48 (0.88)	−2.35 (−4.32)	−2.35 (−4.32)	−2.35 (−4.32)	−2.35 (−4.32)	−2.35 (−4.32)	−2.35 (−4.32)	−2.35 (−4.32)
[AGT]EQ−10%	−0.52 (−0.97)	2.54 (4.78)	2.54 (4.78)	2.54 (4.78)	2.54 (4.78)	2.54 (4.78)	2.54 (4.78)	2.54 (4.78)
[AT1R-bound Ang II]EQ + 10%	−0.92 (0)	4.50 (0)	4.50 (0)	4.50 (0)	4.50 (0)	4.50 (0)	4.50 (0)	4.50 (0)
[AT1R-bound Ang II]EQ − 10%	0.97 (0)	−4.77 (0)	−4.77 (0)	−4.77 (0)	−4.77 (0)	−4.77 (0)	−4.77 (0)	−4.77 (0)
kAGT + 10%	11.48 (10.98)	2.75 (5.20)	2.75 (5.20)	2.75 (5.20)	2.75 (5.20)	2.75 (5.20)	2.75 (5.20)	2.75 (5.20)
kAGT − 10%	−11.40 (−10.87)	−3.15 (−5.75)	−3.15 (−5.75)	−3.15 (−5.75)	−3.15 (−5.75)	−3.15 (−5.75)	−3.15 (−5.75)	−3.15 (−5.75)
cACE + 10%	0.74 (0)	−4.25 (−0.64)	4.37 (8.30)	−4.13 (−0.51)	4.37 (8.30)	4.37 (8.30)	4.37 (8.30)	−3.63 (0)
cACE−10%	−0.84 (0)	4.82 (0.65)	−4.61 (−8.41)	4.69 (0.52)	−4.61 (−8.41)	−4.61 (−8.41)	−4.61 (−8.41)	4.15 (0)
cChym + 10%	0.09 (0)	−0.50 (−0.07)	0.50 (0.93)	−0.48 (−0.06)	0.50 (0.93)	0.50 (0.93)	0.50 (0.93)	−0.43 (0)
cChym − 10%	−0.09 (0)	0.50 (0.07)	−0.50 (−0.93)	0.49 (0.06)	−0.50 (−0.93)	−0.50 (−0.93)	−0.50 (−0.93)	0.43 (0)
cNEP + 10%	−0.01 (0)	−0.05 (−0.08)	−0.05 (−0.08)	9.81 (9.77)	−0.05 (−0.08)	−0.05 (−0.08)	−0.05 (−0.08)	0.04 (0)
cNEP − 10%	0.01 (0)	0.05 (0.08)	0.05 (0.08)	−9.82 (−9.78)	0.05 (0.08)	0.05 (0.08)	0.05 (0.08)	−0.04 (0)
cACE2 + 10%	0 (0)	0.01 (0)	−0.01 (−0.02)	0.15 (0.14)	−0.01 (−0.02)	−0.01 (−0.02)	−0.01 (−0.02)	0.01 (0)
cACE2 − 10%	0 (0)	−0.01 (0)	0.01 (0.02)	−0.15 (−0.14)	0.01 (0.02)	0.01 (0.02)	0.01 (0.02)	−0.01 (0)
cAngII=AngIV + 10%	−0.17 (0)	0.85 (0)	−0.98 (−1.81)	0.83 (−0.03)	8.92 (8.01)	−0.98 (−1.81)	−0.98 (−1.81)	0.85 (0)
cAngII=AngIV − 10%	0.18 (0)	−0.86 (0)	1.01 (1.88)	−0.83 (0.03)	−9.09 (−8.31)	1.01 (1.88)	1.01 (1.88)	−0.86 (0)
cAT1R + 10%	0.77 (0)	−3.78 (0)	−4.94 (−1.21)	−3.80 (−0.02)	−4.94 (−1.21)	4.56 (8.67)	−4.94 (−1.21)	−3.78 (0)
cAT1R − 10%	−0.90 (0)	4.40 (0)	5.69 (1.24)	4.42 (0.02)	5.69 (1.24)	−4.88 (−8.89)	5.69 (1.24)	4.40 (0)
CAT2R + 10%	−0.04 (0)	0.19 (0)	−0.22 (−0.41)	0.18(−0.01)	−0.22 (−0.41)	−0.22 (−0.41)	9.76 (9.55)	0.19 (0)
CAT2R − 10%	0.04 (0)	−0.19 (0)	0.22 (0.41)	−0.18 (0.01)	0.22 (0.41)	0.22 (0.41)	−9.80 (−9.63)	−0.19 (0)

Table 6.

Percent change in response to parameter perturbation for female hypertensive rats. Values in parentheses are from the system without feedback function f.

	AGT	Ang I	Ang II	Ang (1–7)	Ang IV	AT1R-bound Ang II	AT2R-bound Ang II	PRA
Vmax + 10%	−0.84 (−1.59)	4.78 (9.12)	4.78 (9.12)	4.78 (9.12)	4.78 (9.12)	4.78 (9.12)	4.78 (9.12)	4.78 (9.12)
Vmax − 10%	0.88 (1.62)	−5.05 (−9.28)	−5.05 (−9.28)	−5.05 (−9.28)	−5.05 (−9.28)	−5.05 (−9.28)	−5.05 (−9.28)	−5.05 (−9.28)
[AGT]EQ + 10%	0.41 (0.77)	−2.36 (−4.38)	−2.36 (−4.38)	−2.36 (−4.38)	−2.36 (−4.38)	−2.36 (−4.38)	−2.36 (−4.38)	−2.36 (−4.38)
[AGT]EQ − 10%	−0.45 (−0.85)	2.55 (4.84)	2.55 (4.84)	2.55 (4.84)	2.55 (4.84)	2.55 (4.84)	2.55 (4.84)	2.55 (4.84)
[AT1R-bound Ang II]EQ + 10%	−0.79 (0)	4.54 (0)	4.54 (0)	4.54 (0)	4.54 (0)	4.54 (0)	4.54 (0)	4.54 (0)
[AT1R-bound Ang II]EQ − 10%	0.84 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)
kAGT + 10%	11.28 (10.85)	2.70 (5.15)	2.70 (5.15)	2.70 (5.15)	2.70 (5.15)	2.70 (5.15)	2.70 (5.15)	2.70 (5.15)
kAGT − 10%	−11.21 (−10.75)	−3.09 (−5.68)	−3.09 (−5.68)	−3.09 (−5.68)	−3.09 (−5.68)	−3.09 (−5.68)	−3.09 (−5.68)	−3.09 (−5.68)
cACE+10%	0.52 (0)	−5.04 (−2.13)	3.51 (6.68)	−4.91 (−2.00)	3.51 (6.68)	3.51 (6.68)	3.51 (6.68)	−2.97 (0)
cACE − 10%	−0.60 (0)	5.73 (2.22)	−3.79 (−6.98)	5.59 (2.09)	−3.79 (−6.98)	−3.79 (−6.98)	−3.79 (−6.98)	3.43 (0)
cChym + 10%	0.06 (0)	−0.59 (−0.24)	0.40 (0.76)	−0.58 (−0.23)	0.40 (0.76)	0.40 (0.76)	0.40 (0.76)	−0.35 (0)
cChym − 10%	−0.06 (0)	0.60 (0.24)	−0.41 (−0.76)	0.58 (0.23)	−0.41 (−0.76)	−0.41 (−0.76)	−0.41 (−0.76)	0.36 (0)
cNEP + 10%	−0.03 (0)	−0.17 (−0.32)	−0.17 (−0.32)	9.67 (9.51)	−0.17 (−0.32)	−0.17 (−0.32)	−0.17 (−0.32)	0.15 (0)
cNEP−10%	0.03 (0)	0.17 (0.32)	0.17 (0.32)	−9.70 (−9.57)	0.17 (0.32)	0.17 (0.32)	0.17 (0.32)	−0.15 (0)
cACE2+10%	0 (0)	0.01 (0)	−0.01 (−0.02)	0.15 (0.14)	−0.01 (−0.02)	−0.01 (−0.02)	−0.01 (−0.02)	0.01 (0)
cACE2 − 10%	0 (0)	−0.01 (0)	0.01 (0.02)	−0.15 (−0.14)	0.01 (0.02)	0.01 (0.02)	0.01 (0.02)	−0.01 (0)
cAngII=AngIV + 10%	−0.05 (0)	0.30 (0)	−0.34 (−0.63)	0.29 (−0.01)	9.63 (9.30)	−0.34 (−0.63)	−0.34 (−0.63)	0.30 (0)
cAngII=AngIV − 10%	0.05 (0)	−0.30 (0)	0.34 (0.64)	−0.29 (0.01)	−9.69 (−9.42)	0.34 (0.64)	0.34 (0.64)	−0.30 (0)
cAT1R + 10%	0.65 (0)	−3.73 (0)	−5.06 (−1.38)	−3.75 (−0.02)	−5.06 (−1.38)	4.44 (8.48)	−5.06 (−1.38)	−3.73 (0)
cAT1R − 10%	−0.76 (0)	4.34 (0)	5.82 (1.42)	4.36 (0.02)	5.82 (1.42)	−4.76 (−8.72)	5.82 (1.42)	4.34 (0)
cAT2R + 10%	−0.04 (0)	0.22 (0)	−0.25 (−0.47)	0.21 (−0.01)	−0.25 (−0.47)	−0.25 (−0.47)	9.73 (9.49)	0.22 (0)
cAT2R − 10%	0.04 (0)	−0.22 (0)	0.25 (0.47)	−0.21 (0.01)	0.25 (0.47)	0.25 (0.47)	−9.77 (−9.58)	−0.22 (0)

An overall observation is that adjusting a parameter causes each hormone to change in the same direction (albeit by different amounts) in all rats. In other words, the four rats behave qualitatively similarly, which is to be expected. In addition, with and without feedback, increasing a parameter by 10% causes the opposite response as decreasing it by 10%. Without feedback, each reaction rate constant is positively correlated with hormones downstream of it. For example, k_AGT is positively correlated with all variables while c_AT1R is only positively correlated with AT1R-bound Ang II. The hormone that is directly upstream of the reaction rate constant is negatively correlated, while hormones farther upstream are not effected. Hormones that are part of an alternate path than the path defined by the reaction rate constant are negatively correlated with the perturbed reaction rate constant, but have a much smaller effect size. With feedback some noise is introduced but the same patterns hold.

Our model supports the common description of PRA as the driving force of the RAS. V_max, [AGT]_EQ, and [AT1R-bound Ang II]_EQ determine PRA and have strong effects on all hormones.

In the absence of feedback, V_max is the strongest determinant of all hormone levels, through its effect on PRA. c_ACE is the second strongest determinant of all downstream hormone levels except for Ang (1–7). With feedback, c_ACE is a strong effector of all hormones save AGT. With or without feedback, Ang (1–7), Ang IV, AT1R-bound Ang II, and AT2R-bound Ang II are more strongly effected by c_NEP, c_Ang II=Ang IV, cAT1R, and c_AT2R, respectively. A clinical implication of these results is that ACEIs (which reduce c_ACE) have a potential for strongly influencing most RAS components and for regulating blood pressure via its effects on the concentration of AT1R-bound Ang II. However, blood pressure is positively influenced by Ang (1–7) and AT2R-bound Ang II, which ACEIs suppress. AT2R-bound Ang II has been shown to have a greater influence in females, so this may explain why ACEI are less effective in females.

Without feedback, c_AT1R has a strong effect on [AT1R-bound Ang II], a smaller effect on [Ang II], [Ang IV], and [AT2R-bound Ang II], and a weak effect on other hormones. With feedback, c_AT1R has a weaker effect on [AT1R-bound Ang II], but a strong effect on other hormone levels. [Ang I] and [Ang (1–7)] exhibit the same percentage change as PRA, a results that suggests that their changes are driven by PRA. [Ang II], [Ang IV], and [AT2R-bound Ang II] change by a larger percentage than PRA, meaning that their change is driven by PRA and by the blockage or increase of flow from the change in c_AT1R. Taken together, these results indicate that the feedback stabilizes [AT1R-bound Ang II], i.e., the feedback mechanism keeps [AT1R-bound Ang II] close to its equilibrium value. A clinical implication of this result is that ARBs may regulate blood pressure by both lowering [AT1R-bound Ang II] and by adjusting the levels of other hormones such as AT2R-bound Ang II.

Except for the cases of c_NEP and c_ACE2, [Ang I] and [Ang (1–7)] change by similar percentages. But notably, [Ang (1–7)] changes by a larger amount in female hypertensive rats relative to all other rats, while in all other rats [Ang I] increases by a larger amount. This is due to female hypertensive rats having a much higher baseline [Ang (1–7)] and the lowest [Ang I]: female hypertensive [Ang (1–7)] is more than triple that of the next highest (male normotensive) (Table 1). As neither ACEIs nor ARBs, the two drug treatments considered in this study, change c_NEP and c_ACE2, we can expect [Ang I] and [Ang (1–7)] to behave similarly in all drug simulations.

Except for the cases of c_AT1R and k_AGT, [AT1R-bound Ang II] changes by a similar percentage in all rats but by a much larger amount in male hypertensive rats, followed by female hypertensive rats, whereas normotensive rats show the least response and do not show a significant sex difference. This result stems from the fact that in our model the male hypertensive rat is assumed to have a much larger baseline [AT1R-bound Ang II], meaning that a given percentage change has a larger absolute effect.

3.3. ACE inhibitors

As previously noted, a major goal of this study is to better understand the mechanisms by which animals exhibit sex differences in their responses to pharmaceutical drugs used in the treatment for hypertension and congestive heart failure. We first considered ACEIs. To simulate their effects, we reduce c_ACE by a target level γ_ACE:

$$c_{\text{ACE}}=c_{\text{ACE}}^0\ast (1-{\gamma }_{\text{ACE}})$$ (14)

We modeled 50% and 90% inhibition of ACE (i.e., γ_ACE = 0.5 and 0.9) and assessed any sex differences in the responses of hypertensive rats. Results are shown in Figure 2. The model predicted that a 90% reduction in c_ACE resulted in 60.0% and 54.5% reduction in [Ang II] in male and female hypertensive rats, respectively. This corresponds to a drop from 47 fmol/ml to 18.8 fmol/ml in male hypertensive rats and a drop from 20 fmol/ml to 9.1 fmol/ml in female hypertensive rats. Model predictions are consistent with experiments by Campbell et al., who found in male hypertensive rats that Ang II drops by 65.9% [16]. A 50% reduction in ACE resulted in a 25.7% and 22.8% reduction in [Ang II] in male and female hypertensive rats, respectively (Figure 2d). While the percentages are similar, in male hypertensive rats exhibited a larger absolute reduction in [Ang II] (from 47 fmol/ml to 34.9 fmol/ml) than its female counterpart (from 20 fmol/ml to 15.4 fmol/ml). Taken together, our model predicted a moderately larger percentage decrease and a much larger absolute decrease in male hypertensive Ang II levels than it does for female hypertensive rats. This result suggests that ACEIs may be more effective in lowering [Ang II] in males compared to females. Under ACE inhibition, [Ang IV], [AT1R-bound Ang II], and [AT2R-bound Ang II] all directly scale with [Ang II] in our model.

Figure 2.

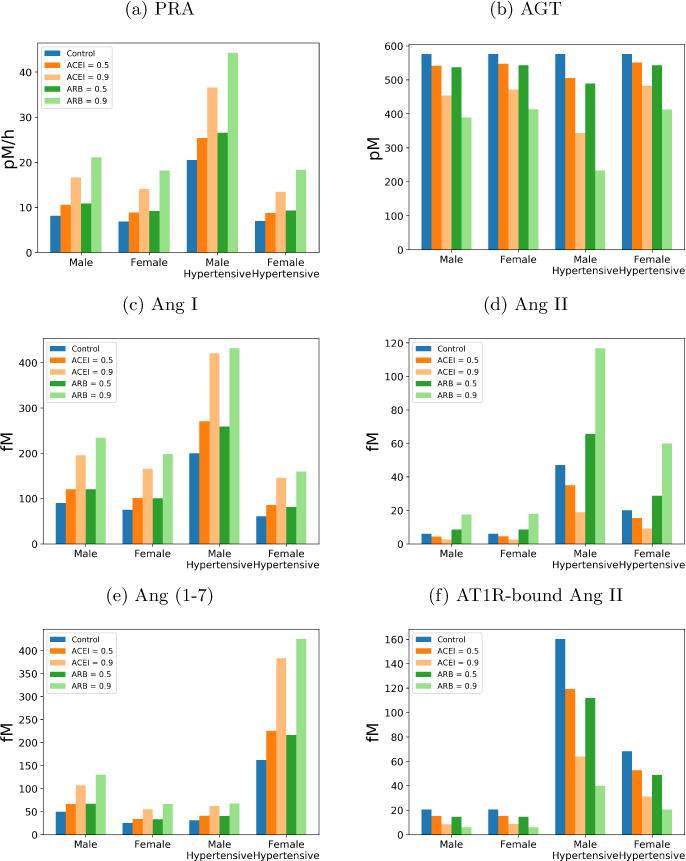
Simulated hormone concentrations after angiotensin converting enzyme inhibitors (ACEI) or angiotensin receptor blockers (ARB) treatment for virtual normotensive and hypertensive rats.

With 90% ACE inhibition our model predicted a 110.3% and a 139.5% increase in [Ang I] in male and female hypertensive rats, respectively (Figure 2c). In male hypertensive rats, [Ang I] increased from 200 fmol/ml to 420.6 fmol/ml, whereas in females [Ang I] increased from 61 fmol/ml to 146.1 fmol/ml. A 50% reduction shows a smaller but qualitatively similar response for both sexes.

The model predicted that ACE inhibition induces similar percentage increases in [Ang (1–7)] between the two sexes. With 90% ACE inhibition, our model predicted a 101.6% and 136.7% increase in [Ang (1–7)] levels in male and female hypertensive rats, respectively. Due to their higher baseline [Ang (1–7)], the absolute increase is higher in female hypertensive rats than males (Figure 2e). The larger increase in females may be explained, in part, by their higher c_NEP. Thus, as [Ang I] rises, more of the Ang I is converted by NEP to Ang (1–7) in females.

Model male hypertensive rats have a higher level of PRA, compared to females, with and without ACE inhibition. However, ACE inhibition results in a larger percentage increase in female hypertensive rats (Figure 2a). With 90% ACE inhibition, male hypertensive rat’s PRA increases by 78.6% while PRA increases by 92.6% in female hypertensive rats. This difference in PRA drives the sexes’ different responses in AGT concentration. Since the production rate of AGT is constant in our model, an increase in PRA decreases the AGT concentration. In male hypertensive rats we predict a drop of 40.3% while in female hypertensive rats we predict a drop of 16.2% (Figure 2b).

3.4. Angiotensin receptor blockers

In the next set of simulations, we studied the effect of ARBs. To simulate their effects, we reduce c_AT1R by a target level γ_ARB:

$$c_{\text{AT}1\mathrm{R}}=c_{\text{AT}1\mathrm{R}}^0\ast (1-{\gamma }_{\text{ARB}})$$ (15)

We modeled 50% and 90% blockage of angiotensin receptors, i.e., γ_ARB = 0.5 and 0.9. Model results are summarized in Figure 2. With 50% inhibition of c_AT1R, our model predicted essentially the same percentage decreases (30.2% and 28.4%) in [AT1R-bound Ang II] in male and female hypertensive rats respectively (Figure 2f). These percentage reductions correspond to an absolute decrease from 160.3 fmol/ml to 111.8 fmol/ml in hypertensive males, and a smaller decrease from 68.2 fmol/ml to 48.85 fmol/ml in hypertensive females. With 90% inhibition of c_AT1R, the model predicted a 75.13% and 70.01% decrease in [AT1R-bound Ang II] in male and female, respectively. In this case, [AT1R-bound Ang II] in male hypertensive rats decreased from 160.3 fmol/ml to 39.9 fmol/ml, and in female hypertensive rats, it decreased from 68.2 fmol/ml to 20.5 fmol/ml.

The lowered conversion rate to AT1R-bound Ang II elevated the concentrations of its precursors. Larger fractional increases in [Ang I] and [Ang II] were predicted in female hypertensive rats (162.1 and 199.9%, respectively) than in male hypertensive rats (116.1 and 148.7%, respectively), although male hypertensive rats had higher levels overall. In females, [Ang I] increased from 61 fmol/ml to 159.9 fmol/ml, and [Ang II] from 20 fmol/ml to 60 fmol/ml. In males, [Ang I] increased from 200 fmol/ml to 432.1 fmol/ml, and [Ang II] increased from 47 fmol/ml to 116.9 fmol/ml. Since Ang (1–7) is derived from Ang I and Ang II, its dynamics follow similar trends.

3.5. Effect of feedback

Our current model shows a 110.3% and 101.6% increase in Ang I and Ang (1–7), respectively, in male hypertensive rats in response to 90% ACE inhibition. These predicted changes are substantially smaller compared to the 766% and 1120% increases observed experimentally [16]. As discussed above (Sect. 3.2), through its action on PRA (Eq. 3), V_max is one of the strongest effectors of RAS hormone levels. Thus, we hypothesize that increasing the sensitivity of the feedback function, f, would more acutely increase PRA during ACE inhibition, which would elevate Ang I level and may yield model results that accurately replicate experimental observed changes in Ang I and Ang (1–7). To test this hypothesis, we simulated drug treatments with 10 different values for B_AT1 between 0 and 2 (baseline B_AT1 = 0.95). Results are shown in Figure 3. Values obtained without feedback (B_AT1 = 0) are indicated by bars.

Figure 3.

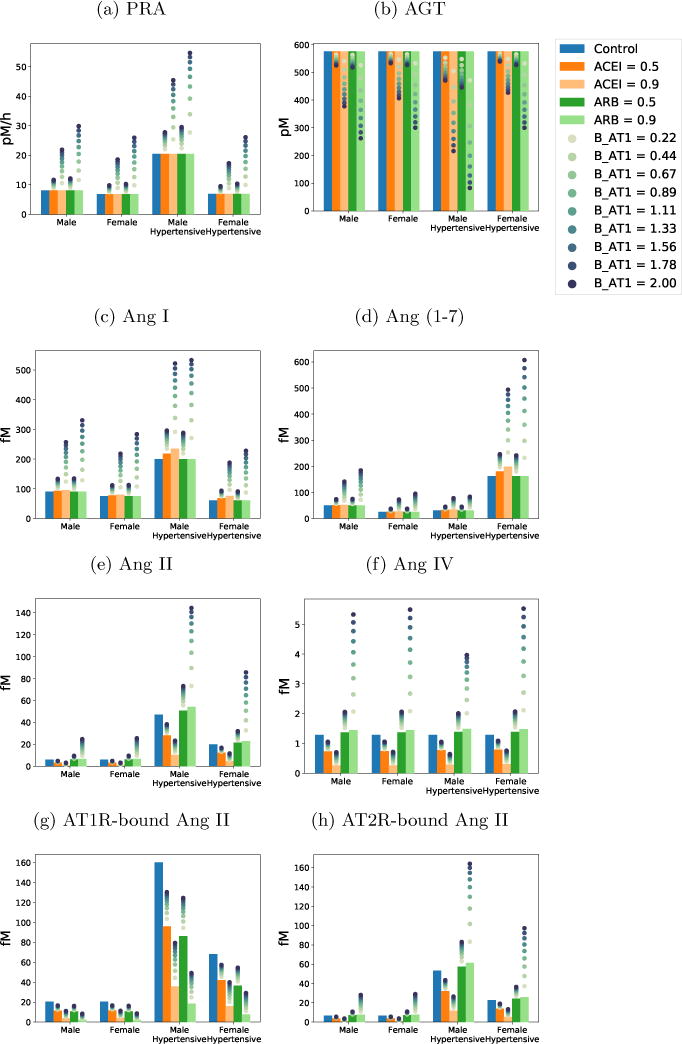
Hormone levels after drug treatment simulation with varying levels of feedback. Bars show the system with no feedback (B_AT1 = 0).

For both ACEI and ARB, a stronger feedback gain (i.e., larger B_AT1) keeps [AT1R-bound Ang II] closer to its equilibrium value shown in the blue bar (Figure 3g). This result can be explained by the observation that with a larger B_AT1, a reduction in [AT1R-bound Ang II] would increase PRA by a larger amount. This negative feedback increases [Ang I], [Ang II], and thus [AT1R-bound Ang II].

As noted above, with ACE inhibition, PRA is higher when feedback is represented. Thus, more AGT is being converted into Ang I, but, with lower ACE, less Ang I is being converted into Ang II. Consequently, a higher B_AT1 yields a higher [Ang I] (Figure 3c); [Ang (1–7)] has a response similar to [Ang I]. Taken together, the competing factors of a higher [Ang I] and a slower conversion rate (with ACE inhibition) result in smaller reductions in downstream peptides [Ang II], [Ang IV], and [AT2R-bound Ang II] when feedback is stronger (larger B_AT1) (Figure 3e).

When ARBs are administered in the absence of feedback, upstream peptides [Ang I] and [Ang (1–7)] are unaffected, whereas [Ang II], [Ang IV], and [AT2R-bound Ang II] increase. With feedback, all peptides except [AGT] monotonically increase with B_AT1.

4. Discussion

The goal of this study is to seek insights into the sex differences in the RAS of the rat, an animal that plays a major role in many experimental and clinical studies. To accomplish that goal, we have applied a previously published human RAS model [11], and identified parameter sets to simulate the RAS in normotensive and hypertensive rats, both male and female. In particular, we identified different parameter sets for the four types of rats to recapitulate the higher [Ang II] in hypertensive rats, especially in males. Analysis of model results suggests that the observed difference in hormone levels among the four types of rats may be attributable to the differing key reaction rate constants that characterize the conversion from Ang I to Ang II (see Table 2). For example, our model identified much higher k_AGT in male hypertensive rats than in any other group (k_AGT in male hypertensive rat is 28.8% higher than female). Similarly, PRA in male hypertensive rat is 193.5% higher than female. k_AGT and PRA are key players in the first reactions in this pathway and control the overall amount of angiotensin circulating through the system. Indeed, one reason male hypertensive rats can support a higher Ang II and AT1R-bound Ang II levels is simply because there is more angiotensin circulating through the system. The higher k_AGT and PRA values mean that male hypertensive rats can support more Ang II even when female hypertensive rats have higher ACE activity and thus a faster Ang I-to-Ang II conversion rate (a c_ACE level of 24.88 1/h in female hypertensive rats as compared to 17.15 1/h in male hypertensive rats).

Another of goal of this study is to better understand the sex-specific responses to anti-hypertensive treatments. To that end, we applied the model to simulate the effects of two major classes of hypertensive drugs: ACEIs and ARBs. Following ACE inhibition, the model predicts a significantly larger absolute decrease in [Ang II] in male hypertensive rats, relative to females. Given that Ang II induces vasoconstriction and raises blood pressure, our model result suggests that ACE inhibition may be more effective in lowering blood pressure in males than in females. That result is consistent with findings by Reckelhoff et al., who measured blood pressure in male and female spontaneously hypertensive rats (SHR) after treatment with ACEIs [17]. They found that the ACEIs reduced blood pressure in both genders of hypertensive rats but significantly more so in male SHR than females (63% versus 40–45%) [17].

Model simulation of ACE inhibition yielded changes that are in general agreement with experimental data [16, 17]. Nonetheless, some discrepancies can be noted. Campbell et al. reports that [Ang I] and [Ang (1–7)] increase by 766% and 1120%, respectively, in male normotensive rats following ACE inhibition. Those observed increases are many folds higher than our model’s predicted increases of 110.3%. and 101.6%. To reconcile that discrepancy, we increased the strength of the feedback function (Eq. (3)). That has the effect of enhancing the model’s response to ACE inhibition, a result that suggests the feedback in the male normotensive rat may be stronger than the model’s baseline assumption. Alternatively, the fact that our model underestimates the changes in [Ang I] and [Ang (1–7)] may imply that the some of the animal’s responses to the drug treatment may be missing from the model.

Model simulation of ARBs indicates similar percentage decreases in [AT1R-bound Ang II] in hypertensive male and female rats, with a larger absolute decrease predicted in hypertensive males. To our knowledge, sex differences in the response of AT1R-bound Ang II to ARB treatment have not been well characterized in experiments. Thus, we instead compare model predictions to measured blood pressure responses, assuming that high [AT1R-bound Ang II] corresponds to higher blood pressure. Yanes et al. found that following ARB treatment male SHR exhibit a larger blood pressure reduction than female (51.5% versus 39%) [18]. In contrast, Rodrigues et al. reported similar decreases in both sexes after 24 hours of ARB treatment [19]. The discrepancy may be attributed to differences in strains and experimental protocols. Also, comparing [AT1R-bound Ang II] to blood pressure does not take into account the vasodilatory effects of [AT2R-bound Ang II].

The feedback parameter B_AT1 has a substantial impact on the animal’s predicted response to drug treatment. A stronger feedback parameter lowers the percentage change of [AT1R-bound Ang II], indicating a potentially smaller blood pressure response (Figure 3g). However, ACEIs and ARBs have different effects on AT2R-bound Ang II that are changed by varying B_AT1. This is worth noting as AT1R-bound Ang II and AT2R-bound Ang II are known to have opposing effects on the body, with AT1R-bound Ang II increasing blood pressure and AT2R-bound Ang II decreasing blood pressure. A stronger feedback function causes AT2R-bound Ang II to decrease less with ACEI and to increase more with ARB while a weaker feedback function causes AT2R-bound Ang II to decrease more with ACEI and to increase less with ARB. This suggests that the feedback function determines the balance in receptor responses to drug treatment. Since AT1R and AT2R receptors have opposing effects on the body, the balance between them could determine the difference between the animal’s responses to ARB.

We offer two possible explanations for why ARBs may be more effective in women than ACEIs [20]. First, AT2R-bound Ang II may have a stronger effect on the body in women than in men. AT2R-bound Ang II causes vasodilation and ACEIs decrease [AT2R-bound Ang II] by a similar percentage in hypertensive males and females but by a larger amount in hypertensive males. In both sexes the benefit from a drop in [AT1R-bound Ang II] outweighs the harm from a drop in [AT2R-bound Ang II] but more so in males than in females. Since we see a greater blood pressure reduction yet a larger absolute drop in [AT2R-bound Ang II] from ACEI in males, the difference must be in how the body responds to a drop in [AT2R-bound Ang II] in each sex. Second, women may have a stronger feedback loop than men. This would cause ACEIs to reduce [AT1R-bound Ang II] less in women than in men and thus cause less vasodilation (Figure 3g). A stronger feedback loop in women would also mean that ARBs increase [AT2R-bound Ang II] in women more than in men (Figure 3h). Thus women would have a stronger vasodilatory response. Both factors provide adequate explanation for why ARBs may be more effective in women than ACEIs while the opposite is true for men [10].

A limitation of the present model is that there is not sufficient data to fully characterize the system. For instance, because AT1R-bound Ang II and AT2R-bound Ang II levels have not been determined, the present model assumes that their values are proportional to the corresponding Ang II level. One consequence of this assumption is that c_AT1R and c_AT2R are identical among all groups of rats. However, normotensive females have been shown to have higher levels of AT2 receptors than normotensive males [7, 21] while hypertensive male have higher levels of AT1 receptors and a similar level of AT2R than hypertensive females [22]. Also, the present model predicts a higher c_ACE2 (conversion from Ang II to Ang (1–7)) in hypertensive females compared to hypertensive males. However, experimental results point to higher ACE2 activity in normotensive and hypertensive males as compared to females [7]. Despite this discrepancy, our model still supports the higher expression of Ang (1–7) found in females [21] by predicting a much higher c_ACE in females (Table 2).

This model is not a complete diagram of the RAS. Instead it limits the number of model parameters (and the inevitable degree of uncertainty) by focusing on the more well studied components. The model does not include the conversion of Ang I to Ang (1–9) by ACE2 [23], Ang (1–7) to Ang (1–5) by ACE, or the binding of Ang (1–7) to its receptor. Our model contains a simplified conversion of Ang II to Ang IV by skipping the intermediate form of Ang III [2]. Despite not representing the influence of these reactions and hormones on blood pressure, our model still captures the actions and responses of the two major vasoactive hormones, Ang II and Ang (1–7), to anti-hypertensive treatment. Expanding our model to include Ang (1–7) receptors could be useful to explore other options for anti-hypertensive therapies. Ang (1–7) stimulation of vasodilation through the production of nitric oxide [2] suggests that drug treatments targeting NEP activity, ACE2 activity or Ang (1–7) receptors may be particularly effective for females in which Ang (1–7) is expressed at higher levels.

Table 4.

Percent change in response to parameter perturbation for female normotensive rats. Values in parentheses are from the system without feedback function f.

	AGT	Ang I	Ang II	Ang (1–7)	Ang IV	AT1R-bound Ang II	AT2R-bound Ang II	PRA
Vmax + 10%	−0.82 (−1.57)	4.79 (9.13)	4.79 (9.13)	4.79 (9.13)	4.79 (9.13)	4.79 (9.13)	4.79 (9.13)	4.79 (9.13)
Vmax − 10%	0.87 (1.59)	−5.05 (−9.29)	−5.05 (−9.29)	−5.05 (−9.29)	−5.05 (−9.29)	−5.05 (−9.29)	−5.05 (−9.29)	−5.05 (−9.29)
[AGT]EQ + 10%	0.41 (0.75)	−2.36 (−4.39)	−2.36 (−4.39)	−2.36 (−4.39)	−2.36 (−4.39)	−2.36 (−4.39)	−2.36 (−4.39)	−2.36 (−4.39)
[AGT]EQ − 10%	−0.44 (−0.83)	2.56 (4.85)	2.56 (4.85)	2.56 (4.85)	2.56 (4.85)	2.56 (4.85)	2.56 (4.85)	2.56 (4.85)
[AT1R-bound Ang II]EQ + 10%	−0.78 (0)	4.54 (0)	4.54 (0)	4.54 (0)	4.54 (0)	4.54 (0)	4.54 (0)	4.54 (0)
[AT1R-bound Ang II]EQ − 10%	0.82 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)	−4.80 (0)
kAGT + 10%	11.25 (10.83)	2.70 (5.14)	2.70 (5.14)	2.70 (5.14)	2.70 (5.14)	2.70 (5.14)	2.70 (5.14)	2.70 (5.14)
kAGT − 10%	−11.19 (−10.74)	−3.08 (−5.68)	−3.08 (−5.68)	−3.08 (−5.68)	−3.08 (−5.68)	−3.08 (−5.68)	−3.08 (−5.68)	−3.08 (−5.68)
cACE + 10%	0.62 (0)	−4.33 (−0.76)	4.28 (8.18)	−4.29 (−0.72)	4.28 (8.18)	4.28 (8.18)	4.28 (8.18)	−3.60 (0)
cACE − 10%	−0.71 (0)	4.92 (0.77)	−4.52 (−8.30)	4.88 (0.73)	−4.52 (−8.30)	−4.52 (−8.30)	−4.52 (−8.30)	4.12 (0)
cChym + 10%	0.07 (0)	−0.51 (−0.08)	0.49 (0.91)	−0.50 (−0.08)	0.49 (0.91)	0.49 (0.91)	0.49 (0.91)	−0.42 (0)
cChym − 10%	−0.07 (0)	0.52 (0.08)	−0.49 (−0.92)	0.51 (0.08)	−0.49 (−0.92)	−0.49 (−0.92)	−0.49 (−0.92)	0.43 (0)
cNEP + 10%	0 (0)	−0.03 (−0.05)	−0.03 (−0.05)	9.93 (9.90)	−0.03 (−0.05)	−0.03 (−0.05)	−0.03 (−0.05)	0.02 (0)
cNEP − 10%	0 (0)	0.03 (0.05)	0.03 (0.05)	−9.93 (−9.91)	0.03 (0.05)	0.03 (0.05)	0.03 (0.05)	−0.02 (0)
cACE2 + 10%	0 (0)	0 (0)	0 (0)	0.05 (0.04)	0 (0)	0 (0)	0 (0)	0 (0)
cACE2 − 10%	0 (0)	0 (0)	0 (0)	−0.05 (−0.04)	0 (0)	0 (0)	0 (0)	0 (0)
cAngII=AngIV + 10%	−0.15 (0)	0.86 (0)	−0.97 (−1.82)	0.85 (−0.01)	8.93 (8.00)	−0.97 (−1.82)	−0.97 (−1.82)	0.86 (0)
cAngII=AngIV − 10%	0.15 (0)	−0.87 (0)	1.00 (1.88)	−0.86 (0.01)	−9.10 (−8.30)	1.00 (1.88)	1.00 (1.88)	−0.87 (0)
cAT1R + 10%	0.65 (0)	−3.81 (0)	−4.97 (−1.21)	−3.82 (−0.01)	−4.97 (−1.21)	4.53 (8.67)	−4.97 (−1.21)	−3.81 (0)
cAT1R − 10%	−0.76 (0)	4.43 (0)	5.73 (1.24)	4.44 (0.01)	5.73 (1.24)	−4.85 (−8.89)	5.73 (1.24)	4.43 (0)
cAT2R + 10%	−0.03 (0)	0.19 (0)	−0.22 (−0.41)	0.19 (0)	−0.22 (−0.41)	−0.22 (−0.41)	9.76 (9.55)	0.19 (0)
cAT2R − 10%	0.03 (0)	−0.19 (0)	0.22 (0.41)	−0.19 (0)	0.22 (0.41)	0.22 (0.41)	−9.80 (−9.63)	−0.19 (0)

Table 5.

Percent change in response to parameter perturbation for male hypertensive rats. Values in parentheses are from the system without feedback function f.

	AGT	Ang I	Ang II	Ang (1–7)	Ang IV	AT1R-bound Ang II	AT2R-bound Ang II	PRA
Vmax + 10%	−2.25 (−3.98)	4.39 (7.76)	4.39 (7.76)	4.39 (7.76)	4.39 (7.76)	4.39 (7.76)	4.39 (7.76)	4.39 (7.76)
Vmax − 10%	2.40 (4.18)	−4.68 (−8.16)	−4.68 (−8.16)	−4.68 (−8.16)	−4.68 (−8.16)	−4.68 (−8.16)	−4.68 (−8.16)	−4.68 (−8.16)
[AGT]EQ + 10%	1.12 (1.95)	−2.18 (−3.80)	−2.18 (−3.80)	−2.18 (−3.80)	−2.18 (−3.80)	−2.18 (−3.80)	−2.18 (−3.80)	−2.18 (−3.80)
[AGT]EQ − 10%	−1.21 (−2.15)	2.36 (4.18)	2.36 (4.18)	2.36 (4.18)	2.36 (4.18)	2.36 (4.18)	2.36 (4.18)	2.36 (4.18)
[AT1R-bound Ang II]EQ + 10%	−2.14 (0)	4.17 (0)	4.17 (0)	4.17 (0)	4.17 (0)	4.17 (0)	4.17 (0)	4.17 (0)
[AT1R-bound. Ang II]EQ − 10%	2.29 (0)	−4.45 (0)	−4.45 (0)	−4.45 (0)	−4.45 (0)	−4.45 (0)	−4.45 (0)	−4.45 (0)
kAGT + 10%	13.49 (12.18)	3.19 (5.74)	3.19 (5.74)	3.19 (5.74)	3.19 (5.74)	3.19 (5.74)	3.19 (5.74)	3.19 (5.74)
kAGT − 10%	−13.23 (−11.89)	−3.70 (−6.32)	−3.70 (−6.32)	−3.70 (−6.32)	−3.70 (−6.32)	−3.70 (−6.32)	−3.70 (−6.32)	−3.70 (−6.32)
cACE+10%	1.52 (0)	−4.56 (−1.65)	4.03 (7.20)	−4.12 (−1.19)	4.03 (7.20)	4.03 (7.20)	4.03 (7.20)	−2.96 (0)
cACE − 10%	−1.73 (0)	5.14 (1.70)	−4.32 (−7.45)	4.65 (1.23)	−4.32 (−7.45)	−4.32 (−7.45)	−4.32 (−7.45)	3.38 (0)
cChym + 10%	0.18 (0)	−0.53 (−0.19)	0.46 (0.81)	−0.48 (−0.13)	0.46 (0.81)	0.46 (0.81)	0.46 (0.81)	−0.35 (0)
cChym − 10%	−0.18 (0)	0.54 (0.19)	−0.47 (−0.82)	0.49 (0.14)	−0.47 (−0.82)	−0.47 (−0.82)	−0.47 (−0.82)	0.35 (0)
cNEP + 10%	0 (0)	−0.01 (−0.02)	−0.01 (−0.02)	9.47 (9.47)	−0.01 (−0.02)	−0.01 (−0.02)	−0.01 (−0.02)	0.01 (0)
cNEP − 10%	0 (0)	0.01 (0.02)	0.01 (0.02)	−9.48 (−9.47)	0.01 (0.02)	0.01 (0.02)	0.01 (0.02)	−0.01 (0)
cACE2+10%	0 (0)	0 (0)	0 (−0.01)	0.51 (0.51)	0 (−0.01)	0 (−0.01)	0 (−0.01)	0 (0)
cACE2 − 10%	0 (0)	0 (0)	0 (0.01)	−0.51 (−0.51)	0 (0.01)	0 (0.01)	0 (0.01)	0 (0)
cAngII=AngIV + 10%	−0.06 (0)	0.12 (0)	−0.16 (−0.28)	0.11 (−0.01)	9.82 (9.69)	−0.16 (−0.28)	−0.16 (−0.28)	0.12 (0)
cAngII=AngIV − 10%	0.06 (0)	−0.12 (0)	0.16 (0.28)	−0.11 (0.01)	−9.86 (−9.75)	0.16 (0.28)	0.16 (0.28)	−0.12 (0)
cAT1R+10%	1.76 (0)	−3.43 (0)	−4.82 (−1.44)	−3.50 (−0.07)	−4.82 (−1.44)	4.70 (8.42)	−4.82 (−1.44)	−3.43 (0)
cAT1R − 10%	−2.03 (0)	3.96 (0)	5.50 (1.48)	4.04 (0.08)	5.50 (1.48)	−5.05 (−8.67)	5.50 (1.48)	3.96 (0)
cAT2R+10%	−0.11 (0)	0.21 (0)	−0.28 (−0.48)	0.18 (−0.02)	−0.28 (−0.48)	−0.28 (−0.48)	9.70 (9.47)	0.21 (0)
cAT2R − 10%	0.11 (0)	−0.21 (0)	0.28 (0.49)	−0.18 (0.03)	0.28 (0.49)	0.28 (0.49)	−9.75 (−9.56)	−0.21 (0)

Highlights.

• An ordinary differential equations model of the renin angiotensin system is fitted to experimental systemic hormone levels for male normotensive, male hypertensive, female normotensive, and female hypertensive rats.

• Plasma renin activity, angiotensinogen production rate, angiotensin converting enzyme activity, and neutral endopeptidase activity differ significantly among the four groups of rats.

• Anti-hypertensive therapies show similar percentage changes in each group while absolute changes differ.

• We propose that drug treatment efficacy varies between the sexes because the strength of the feedback mechanism, by which receptor bound angiotensin II effects plasma renin activity, varies between the sexes.