An empirical approach to determine a threshold for assessing overdispersion in Poisson and negative binomial models for count data

Abstract

Overdispersion is a problem encountered in the analysis of count data that can lead to invalid inference if unaddressed. Decision about whether data are overdispersed is often reached by checking whether the ratio of the Pearson chi-square statistic to its degrees of freedom is greater than one; however, there is currently no fixed threshold for declaring the need for statistical intervention. We consider simulated cross-sectional and longitudinal datasets containing varying magnitudes of overdispersion caused by outliers or zero inflation, as well as real datasets, to determine an appropriate threshold value of this statistic which indicates when overdispersion should be addressed.

1. Introduction

The assumption of Poisson regression that the conditional mean must be equal to the conditional variance often fails in real data situations. Overdispersion occurs when data have greater conditional variance than is assumed under the Poisson model (Cox 1983), which may result from population heterogeneity, correlation, omission of important covariates in the model, the presence of outliers, zero inflation, or other reasons (Hardin and Hilbe 2007; Rigby and Stasinopoulos 2008). A Poisson model estimated on overdispersed data can include underestimated standard errors of the parameter estimates. As a consequence, the hypotheses on the regression parameters may be rejected more often than they should be (Breslow 1990; Faddy and Smith 2011; Hilbe 2011; McCullagh and Nelder 1989). Payne et al. previously examined overdispersion occurring in real and simulated datasets resulting from outliers, omission of key predictors, and omission of necessary random effects (2015). The authors compared six different scaling and modeling methods of analysis via goodness-of-fit and error statistics. The results showed that negative binomial regression and negative binomial generalized linear mixed models were preferred for dealing with overdispersion resulting from the sources they considered. Scaling methods and unadjusted Poisson regression were less reliable and often produced larger or smaller standard errors than expected.

The two most commonly used estimators of dispersion in the literature are the ratio of the model deviance to its corresponding degrees of freedom and the ratio of the Pearson χ² statistic to its corresponding degrees of freedom (McCullagh and Nelder 1989). For a study with sample n and p predictors, the degrees of freedom are typically given by n − p. This ratio will equal one when the Poisson assumption or, equivalently, the assumption that the conditional mean and variance are equal, holds. Relative to the model, the data are considered overdispersed if this ratio is greater than one, with greater magnitudes of overdispersion corresponding to higher Pearson χ² statistics.

A likelihood ratio test may be used to test the difference of the simple Poisson and more complex models such as negative binomial regression to assess whether the simpler model should be rejected (Cameron and Trivedi 1986). The Wald statistic associated with a test of the dispersion parameter in the more complex model may also be used for this assessment (Molla and Muniswamy 2012). Score tests for determining the presence of extra-Poisson variation are also available in many case-specific variations (Breslow 1990; Collings and Margolin 1985; Dean and Lawless 1989; Gurmu 1991; Lee et al. 2007), and may be more appropriate than Wald or likelihood ratio tests since the score test requires only an estimation of the simpler model and provides greater power (Yang et al. 2007). In addition, hypothesis testing of the ratios of negative binomial and Poisson regression log-likelihoods may rely on asymptotic distributions which underestimate the evidence against the base model and thereby provide results which are misleading (Cameron and Trivedi 1998; Dean 1992; Lawless 1987). O’Hara Hines provides an overview of numerous score tests which have been developed to test for overdispersion (O’Hara Hines 1997). Molla and Muniswamy recently demonstrated the superior power of the score test compared to likelihood ratio and Wald tests via an extensive Monte Carlo simulation study (2012).

Currently, one of the most commonly used estimators of overdispersion in the literature is the goodness-of-fit ratio of the Pearson χ² statistic to its corresponding degrees of freedom. A decision about whether data are overdispersed is made by checking whether this ratio is greater than one. The relative variance is defined as the ratio of the variance to the mean and is theoretically comparable to the Pearson χ² ratio with its degrees of freedom. One possible rule of thumb suggests that if the relative variance is greater than two, then the data may be considered overdispersed and require statistical intervention (Cameron and Trivedi 1990). In this case, the average of the covariate-pattern specific ratio of the conditional variance to conditional mean of the count outcome is more than two, contradicting the Poisson model. Smaller values in the average of the ratios of conditional variance to conditional mean may still point to an overdispersed model which underestimates the parameter standard errors and requires a more complex modeling strategy than simple Poisson regression (Rodriguez 2015). In some cases, relative variance tests and curves may be more effective in identifying the presence of overdispersion than score tests (Lambert and Roeder 1995).

In this paper, we examine count outcomes containing overdispersion represented by varying magnitudes of Pearson χ² ratios in cross-sectional and longitudinal datasets, to determine the threshold over one (ratio > 1) at which overdispersion may be considered detrimental to data analysis if ignored. We examine scenarios in which overdispersion is the result of either outliers or zero inflation in the count outcome. Results from two real case studies containing varying magnitudes of overdispersion are also considered. This paper is organized in the following manner. Subsequent to the introduction, a description of the statistical models as well as measures and tests of overdispersion is given in Section 2. Section 3 provides information about the design of the simulation study. Section 4 provides the results of the simulation study. Section 5 gives a description and results from our real datasets. Section 6 gives a conclusion and discussion based on all results.

2. Statistical models and estimation

2.1. Models

For cross-sectional data, let vector Y = (Y₁, … , Y_n)′ be a response vector with independent and identically Poisson distributed random Y values. The variance function is Var(Y_i) = μ_i and the probability mass function for the quasi-Poisson is given by

$$f(y_i|{\mu }_i)=\frac{{\mu }_i{}^{yi}{e}^{-\mu i}}{y_i!}$$ (1)

with 0 ≤ y_i < ∞ and positive conditional mean parameter μ_i. The conditional variance as a function of the conditional mean is given in general form by ϕμ, with dispersion parameter ϕ. There is equidispersion in the dataset when ϕ = 1, while if ϕ < 1 there is under-dispersion, and if ϕ > 1 there is overdispersion. The Poisson can be extended to define the generalized Poisson regression model including covariates for which the conditional mean is $E(Y_i)={\mu }_i=exp(X_i\prime \beta )$ via the following format (Yang et al. 2009):

$$\mathrm{Pr}(Y_i|x_i,\beta ,\phi )={\left(\frac{{\mu }_i}{1+\phi {\mu }_i}\right)}^{y_i}{\frac{\left(1+\phi y_i\right)}{y_i!}}^{y_i-1}\exp \left(-\frac{{\mu }_i\left(1+\phi y_i\right)}{1+\phi {\mu }_i}\right)$$ (2)

with 0 ≤ y_i < ∞ and constant scale parameter φ. This parameterization indicates that the variance is $Var(Y_i)={\mu }_i{(1+\phi {\mu }_i)}^2$ such that a value of φ = 0 will reduce to the simple Poisson. A score test may then be used to assess the scale parameter φ to determine whether the conditional variance exceeds the conditional mean (refer to Section 2.2). If $Y|\theta ~Pois(\theta )$ and θ is a random variable such that E(θ) = μ and Var(θ) = σ², then E(Y) = μ and $Var(Y)=\mu +{\sigma }^2$, indicating greater variance compared to the mean. If θ is assumed to be distributed gamma, then Y follows a negative binomial distribution with $E(Y)=\frac{k}{\lambda }=\mu$ and $Var(Y)=\mu +\frac{{\mu }^2}{k}$ (Payne et al. 2015).

Random effects may also be included to deal with overdispersion. For response vector (Y_i) and vectors of fixed effect (X_i) and random effect (Z_i) for explanatory variables (i = 1, … , n) the generalized linear mixed model (GLMM) family is given by,

$$E(Y_i|X_i,Z_i)=g^{-1}(X_i\beta +Z_i{b}_i)={\mu }_i$$ (3)

Here, β is a vector of p fixed coefficients, g is a monotone link function, and b_t is a vector of unobserved normally-distributed random deviations with zero mean for which the variance will be estimated. The conditional variance for this model is given by $Var(Y_i)={\mu }_i+k{\mu }_i{}^2$. The negative binomial GLMM allows for greater conditional variance than assumed by the Poisson GLMM. It has previously been shown that negative binomial and negative binomial GLMM are superior for dealing with overdispersion compared to other models in various scenarios, jointly considering the specified criteria (Payne et al. 2015).

We also consider a generalized linear model setup for longitudinal scenarios with a general set of predictor variables. Let Y_ij be a response, while vector X_ij contains m covariates of interest (X_1ij, … , X_mij) at the jth repeated measure for the ith subject (i = 1, … , n, j = 0, … , T_i). Let q_i denote the random effects for each individual i which could be assumed to have a normal distribution with zero mean and covariance G. Let (β₁, … , β_m) be the regression coefficients corresponding to respective covariates (X₁, … , X_m) which gives

$${\eta }_{ij}=q_i+{\displaystyle \sum _{p=1}^m{X}_{pij}{\beta }_p}$$ (4)

We can rewrite this in vector form as for the cross-sectional GLMM above:

$${\eta }_i=Z_i{b}_i+X_i\beta$$ (5)

Where $X_i=(X_{1ij},\mathrm{...},X_{mij})\prime ,{\eta }_i=g(E[Y_{ij}|q_i,\beta ]),\beta =({\beta }_1,\mathrm{...},{\beta }_m)$, g is a monotone link function, Z_i is the random effects design matrix and b_i is the random effects vector for each individual i.

In this paper we address overdispersion resulting from the presence of outliers or zero inflation in the count outcome in both cross-sectional and longitudinal datasets. We consider four methods for analyzing cross-sectional data: unadjusted Poisson regression (Poisson), negative binomial regression (NB), and two GLMM with random intercept, log link, and compound symmetry covariance, with outcomes distributed as Poisson and negative binomial (Poisson-GLMM, NB-GLMM, respectively) (Payne et al. 2015). In the longitudinal scenario, we consider GLMM with random intercept to account for individual variability with outcomes distributed as either Poisson or negative binomial (Poisson-GLMM, NB-GLMM, respectively). SAS 9.4 was utilized in all analyses, particularly the Proc GENMOD and Proc GLIMMIX packages.

2.2. Tests and measures of overdispersion

A variety of score, Wald, and likelihood ratio tests have been considered to determine when overdispersion is statistically significant. One such score statistic (Yang et al. 2009) for testing whether the dispersion parameter indicates extra-Poisson variation H₀ : φ = 0 vs. H₁ : φ > 0 is given by

$$S_1(\widehat{\beta })={\left({\displaystyle \sum _{i=1}^{n}2{\widehat{\mu }}_i^2}\right)}^{-1}{\left({\displaystyle \sum _{i=1}^n\left({\left(y_i-{\widehat{\mu }}_i\right)}^2-y_i\right)}\right)}^2$$ (6)

Under the null hypothesis that overdispersion is not present and the data follow an unadjusted Poisson model, the score statistic is distributed according to the χ₁² distribution with one degree of freedom. We can also write this score statistic as

$$S_2(\widehat{\beta })={\left(\sqrt{2{\displaystyle \sum _{i=1}^n{\widehat{\mu }}_i^2}}\right)}^{-1}{\displaystyle \sum _{i=1}^n\left({\left(y_i-{\widehat{\mu }}_i\right)}^2-y_i\right)}$$ (7)

which is asymptotically distributed as a standard normal. It is clear from the structure of this statistic that greater variability between observed and predicted values will increase the magnitude of the score statistic, which implies overdispersion resulting from data heterogeneity or other factors. According to this statistic, we can reject the assumption of equidispersion at a significance level of 0.05 via a one-sided test if score statistic $S_2(\widehat{\beta })$ is greater than the 95th percentile of the N(0, 1) distribution. This gives us a score statistic cutoff of 1.65 for declaring the presence of overdispersion in large samples. Though this is a useful paradigm, our interest is in determining a general threshold for declaring the presence of overdispersion across datasets using the commonly considered Pearson χ² ratio to its degrees of freedom. We will provide a crossover comparison of rejection via score test at each of our Pearson χ² ratio values under consideration.

Using our notation, the Pearson χ² statistic is defined for the Poisson distribution within the context of GLMs as below (Morel and Neerchal 2012):

$${\chi }^2={{\displaystyle \sum _{i=1}^n\frac{\left(y_i-{\widehat{\mu }}_i\right)}{{\widehat{\mu }}_i}}}^2$$ (8)

This statistic is commonly utilized to analyze model goodness-of-fit, and is approximately distributed χ_df² (Morel and Neerchal 2012). For a study with sample n and p predictors, the degrees of freedom are typically given by n − p. The dispersion statistic σ_p is therefore defined as the ratio of the Pearson χ² to its degrees of freedom and is a common method used to estimate overdispersion (Rodriguez 2015). It is approximately unbiased (Ruoyan 2004) and can be given as follows:

$${\sigma }_p=\frac{{\chi }^2}{n-p}$$ (9)

The dispersion statistic σ_p will equal approximately one where the Poisson model assumption of equal mean and variance holds. Our goal is to determine if there is an appropriate threshold for declaring outlier or zero inflation dependent overdispersion requiring statistical intervention via the proposed method. This value may also be used to determine the presence of underdispersion in datasets, though this is a less common scenario when working with clinical data.

3. Simulation

3.1. Design

We simulated 200 cross-sectional datasets each with a sample size of 100 random observations, to include a Poisson count outcome and m = 2 binary predictor variables X₁ and X₂ according to the model $\log (E(Y_{im}=y|X_{im}))=\alpha +{\displaystyle {\sum }_{m-1}^2{\beta }_m{X}_{im}}$ where β is the collection of parameters (β₁, β₂) and α = 1.0. Outcome count Y for the i^th individual was determined by exp $(\alpha +{\displaystyle {\sum }_{m=1}^2{\beta }_m{X}_{im}})$. We alternated assigning true parameter value β₁ = [0.01, 0.41, 0.92] to yield rate ratios of 1.0, 1.5, and 2.5, respectively, and assigned true parameter value β₂ = 0.69 to yield a rate ratio of 2.0 as a potential confounder.

We then created overdispersion relative to Poisson via the addition of outliers to the count outcome Y. Overdispersion magnitudes of σ_p = [1.0, 1.2, 1.3, 1.4, 1.5, 2.0, 2.5, 5.0, 10.0] were achieved via increasing a random sample of 10% of the Y outcomes such that running unadjusted Poisson regression gave each desired value of σ_p. We created a second scenario in which the unadjusted Poisson gave overdispersion magnitudes of σ_p = [1.0, 1.2, 1.3, 1.4, 1.5, 2.0, 2.5, 5.0] by setting various percentages of the Y outcome variable to zero to achieve the desired values of σ_p (we could not achieve a value of 10.0 in this scenario).

Recall our discussion of a score test statistic (Yang et al. 2009) to test H₀ : φ = 0 vs. H₁ : φ > 0 presented in Section 2.2. The frequency of rejection of H₀ : φ = 0 via this score test for both outlier and zero inflation dependent overdispersion of all magnitudes is given in Table 1. Higher percentages of rejection via the score test statistic in simulations indicate overdispersion in the dataset at the given level of σ_p, suggesting that statistical intervention is necessary for valid analysis. From this table we can see that values of 1.5 ≤ σ_p ≤ 2.0 result in a percentage of rejection close to the nominal 95% depending on the effect size of β₁, indicating rejection of H₀ : φ = 0 and conclusion that the data are overdispersed according to the score test. Values of σ_p < 1.5 result in lower rejection percentages under both scenarios and therefore do not reject the null hypothesis of equidispersion. Higher effect sizes give slightly more conservative results. At values of σ_p ≥ 2.5, equidispersion is rejected in 100% of cases.

Table 1.

Percent of simulations at varying levels of overdispersion in which the score test did in fact reject the null hypothesis and affirm the presence of overdispersion in the dataset.

σp	Outlier Dependent			Zero Inflation
	β1 = 0.01	β1 = 0.41	β1 = 0.92	β1 = 0.01	β1 = 0.41	β1 = 0.92
1.0	6.50	6.50	6.50	6.50	6.50	6.50
1.2	55.50	50.50	28.50	46.50	43.50	51.50
1.3	71.50	53.00	47.00	63.50	64.00	56.50
1.4	79.00	71.50	68.00	74.50	77.00	69.00
1.5	95.50	88.00	87.50	90.00	90.00	85.00
2.0	99.50	99.50	98.50	100.00	100.00	99.00
2.5	100.00	100.00	100.00	100.00	100.00	100.00
5.0	100.00	100.00	100.00	100.00	100.00	100.00
10.0	100.00	100.00	100.00	—	—	—

σ_p is defined as the ratio of the Pearson χ² to its degrees of freedom

We further simulated 200 longitudinal datasets of the same initial sample size of 100 to include the time-varying Poisson count outcome and two time-varying binary predictor variables according to the model $\log (E(Y_{ijm}=y|X_{ijm}))=\alpha +{\displaystyle {\sum }_{m=1}^2{\beta }_m{X}_{ijm}}$ with data now taken at five continuous time points j = 1, 2, … , 5. Again, β is the collection of parameters (β₁,β₂) and α = 1.0. Outcome count Y for the i^th individual was now generated using a mean exp $(\alpha +{\displaystyle {\sum }_{m-1}^2{\beta }_m{X}_{ijm})}$. The overdispersion magnitudes of interest were achieved via data manipulation at baseline similar to that utilized in the cross-sectional examples, such that running Poisson-GLMM resulted in each of the desired values of σ_p.

Comparison among models in all scenarios was then made using Type I and II errors, as well as coverage probabilities of β₁. Type I error is determined via the percentage of simulations in which the effect of β₁ is detected though not present, i.e. the percentage of false positives; here we consider datasets with a true β₁ value of 0.01. Type II error is determined via the percentage of simulations in which the effect of β₁ is not detected though present, i.e. the percentage of false negatives. These errors are observed for both true β₁ values of 0.41 and 0.92. Coverage probabilities are considered for all values of β₁ = [0.01, 0.41, 0.92] and are the percentage of simulations in which parameter 95% confidence intervals contain the true β₁.

4. Results

4.1. Cross-sectional results

Poisson and negative binomial results for both cross-sectional scenarios are given in Tables 2 and 3, respectively, and illustrated in Figures 1a-b and 2a-b by model type and value of β₁ at all values of σ_p. Increases in magnitude of both outlier and zero inflation dependent overdispersion result in increases in Type I and II errors of the β₁ estimates as well as a decrease in coverage probabilities. Not surprisingly, the Type II error and coverage probabilities decrease with the higher effect size (Figure 2a-b). Given the Type I error results shown in Figure 1a-b, the unadjusted Poisson regression model and Poisson-GLMM perform fairly well for both scenarios with low overdispersion magnitude, particularly when σ_p ≤ 1.2. The corresponding Type II error results and coverage probabilities in Figure 2a-b give consistent results. The negative binomial regression models have higher tolerance for extra variability considering all criteria, performing well in both scenarios up to about σ_p ≤ 1.5. Furthermore, the NB-GLMM gives acceptable results in some cases up to σ_p ≤ 5.0, particularly considering Type I error and coverage probabilities. Based on these results it would appear the simple Poisson model may be utilized in cross-sectional cases where σ_p ≤ 1.2. Furthermore, negative binomial regression should be utilized if 1.2 < σ_p ≤ 1.5 while NB-GLMM should be utilized for higher values up to σ_p ≤ 5.0.

Table 2.

Percentage of simulations with Χ₁ Type I and II errors and in which parameter coverage included the true parameter given true values of 0.01, 0.41, and 0.92 for the cross-sectional scenario using the unadjusted Poisson model and Poisson GLMM.

σp	Outlier Dependent Unadjusted Poisson						Zero Inflation Unadjusted Poisson
	β1 = 0.01		β1 = 0.41		β1 = 0.92		β1 = 0.01		β1 = 0.41		β1 = 0.92
	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage(%)
1.0	3.50	95.50	0.50	92.50	0.00	91.50	3.50	95.50	0.50	92.50	0.00	91.50
1.2	5.00	95.00	1.50	88.50	0.00	81.50	4.50	94.50	1.00	89.50	0.00	89.50
1.3	6.00	94.00	1.50	87.50	0.00	76.00	7.00	93.00	2.00	91.00	0.00	88.50
1.4	8.50	91.50	1.50	86.50	0.00	77.00	8.50	91.50	3.00	86.00	0.00	89.00
1.5	11.00	87.00	2.00	83.50	0.00	66.00	10.00	90.50	6.00	83.50	0.00	86.50
2.0	15.50	85.00	6.50	72.00	0.00	59.00	14.50	85.00	11.00	79.50	0.00	86.50
2.5	19.50	81.00	8.50	71.00	0.00	52.50	29.00	71.50	14.50	74.00	0.00	82.00
5.0	43.50	57.00	21.00	53.00	0.00	29.00	36.00	64.00	43.00	56.50	0.00	63.50
10.0	59.50	39.50	23.00	42.50	1.00	23.00	—	—	—	—	—	—

σp	Poisson GLMM						Poisson GLMM
	β1 = 0.01		β1 = 0.41		β1 = 0.92		β1 = 0.01		β1 = 0.41		β1 = 0.92
	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)
1.0	3.00	95.50	1.00	93.50	0.00	92.00	3.00	95.50	1.00	93.50	0.00	92.00
1.2	4.50	95.00	2.00	89.50	0.00	81.50	7.00	93.50	2.00	91.50	0.00	90.00
1.3	6.00	93.50	2.50	89.00	0.00	77.50	8.50	91.50	2.50	91.50	0.00	90.50
1.4	8.00	91.50	1.50	87.00	0.00	78.00	6.00	94.00	2.50	90.50	0.00	89.50
1.5	11.00	90.00	2.50	84.00	0.00	67.50	10.00	90.00	4.00	86.50	0.00	89.00
2.0	14.50	85.50	7.50	74.00	0.00	61.50	22.50	79.00	8.50	83.50	0.00	80.50
2.5	18.00	82.00	8.50	71.50	0.00	52.50	20.00	80.00	8.50	78.50	0.00	82.00
5.0	43.00	57.00	22.00	54.00	0.00	30.00	31.50	69.00	53.50	60.50	1.00	65.50
10.0	59.00	39.00	24.00	42.50	1.50	23.50	—	—	—	—	—	—

σ_p is defined as the ratio of the Pearson χ² to its degrees of freedom

Table 3.

Percentage of simulations with Χ₁ Type I and II errors and in which parameter coverage included the true parameter given true values of 0.01, 0.41, and 0.92 for the cross-sectional scenario using the negative binomial regression model and negative binomial GLMM.

σp	Outlier Dependent Negative Binomial						Zero Inflation Negative Binomial
	β1 = 0.01		β1 = 0.41		β1 = 0.92		β1 = 0.01		β1 = 0.41		β1 = 0.92
	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)
1.0	3.00	95.50	0.50	93.00	0.00	91.50	3.00	95.50	0.50	93.00	0.00	91.50
1.2	3.50	95.00	3.00	90.00	0.00	82.00	3.50	96.50	4.50	92.50	0.00	94.00
1.3	3.00	97.50	3.50	91.00	0.00	79.00	5.00	94.50	5.50	93.00	0.00	92.50
1.4	6.00	93.00	3.00	89.50	0.00	80.50	6.00	94.50	8.50	96.00	0.00	93.50
1.5	7.00	94.50	5.50	90.50	0.00	77.50	5.00	94.00	10.00	95.00	0.00	93.50
2.0	6.00	94.00	17.50	85.50	0.00	73.00	3.00	97.50	33.50	97.50	0.00	96.00
2.5	7.50	93.50	24.00	85.00	0.00	67.50	2.00	98.50	60.50	99.00	0.00	95.00
5.0	15.50	84.00	46.50	80.50	0.00	59.00	5.00	95.00	93.00	97.50	34.50	98.50
10.0	22.50	78.00	61.00	77.50	11.00	54.50	—	—	—	—	—	—

σp	Negative Binomial GLMM						Negative Binomial GLMM
	β1 = 0.01		β1 = 0.41		β1 = 0.92		β1 = 0.01		β1 = 0.41		β1 = 0.92
	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)
1.0	0.52	99.48	7.33	97.38	0.00	96.88	0.52	99.48	7.33	97.38	0.00	96.88
1.2	0.51	99.49	8.59	96.46	0.00	91.96	1.52	98.99	11.00	96.00	0.00	97.47
1.3	0.50	99.50	12.63	95.96	0.00	91.96	1.02	97.46	12.56	98.49	0.00	97.50
1.4	2.00	98.00	13.50	98.50	0.00	89.95	3.02	97.49	13.00	95.50	0.00	96.97
1.5	0.50	99.50	21.00	96.00	0.00	86.93	0.50	99.50	19.00	98.50	0.00	96.00
2.0	2.00	98.00	30.50	93.50	0.00	84.50	2.00	99.00	43.00	96.50	0.00	97.50
2.5	1.00	98.50	38.50	92.00	0.00	80.00	2.00	98.50	59.50	98.00	0.00	96.00
5.0	7.50	93.00	62.00	89.50	3.00	73.50	5.03	94.97	88.94	96.48	18.00	98.50
10.0	13.50	88.00	79.00	91.00	23.00	67.50	—	—	—	—	—	—

σ_p is defined as the ratio of the Pearson χ² to its degrees of freedom

Figures 1.

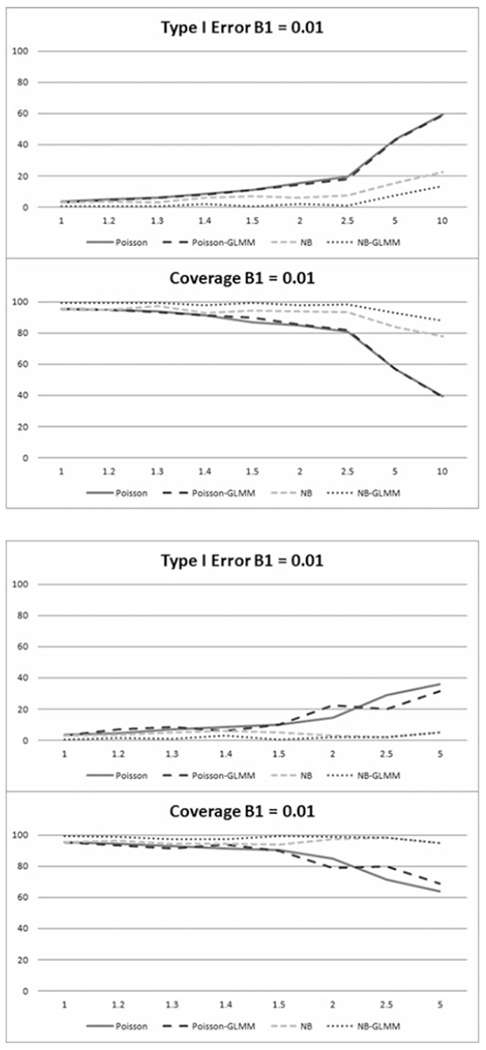
a-b. Percentage of simulations with Type I errors and in which parameter coverage included the true parameter given a true parameter value of 0.01 in the cross-sectional scenario, for a.) outlier dependent overdispersion and b.) overdispersion caused by zero inflation.

Figures 2.

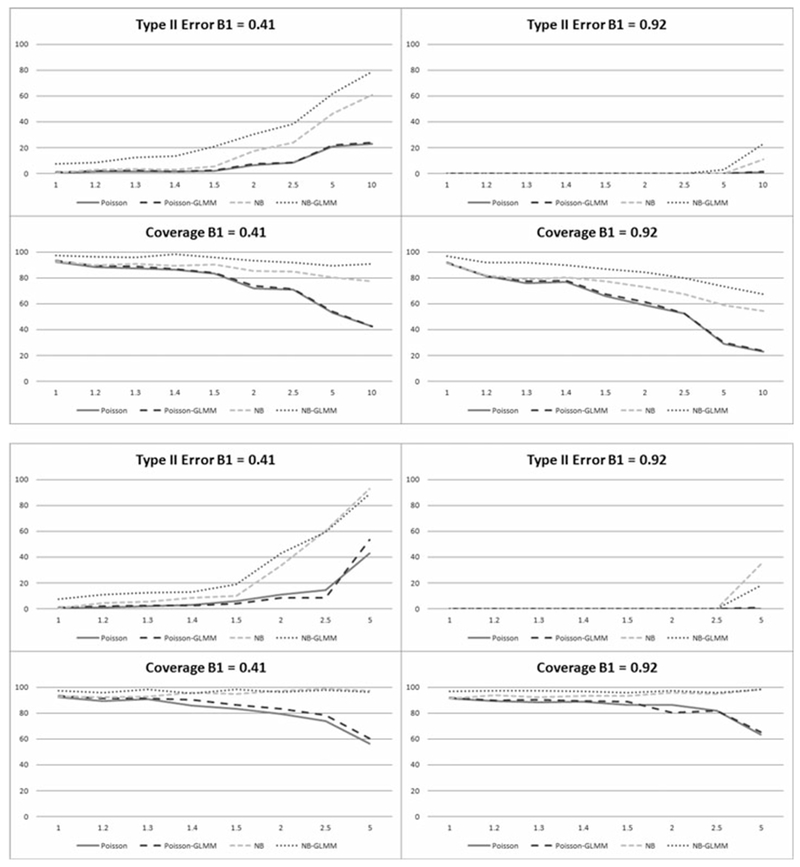
a-b. Percentage of simulations with Type II errors and in which parameter coverage included the true parameter given true parameter values of 0.41 and 0.92 in the cross-sectional scenario, for a.) outlier dependent overdispersion and b.) overdispersion caused by zero inflation.

There is clearly an effect of overdispersion on the models for values of σ_p lower than those picked up by the score test. NB-GLMM also results in the highest Type II error of all considered models, suggesting that negative binomial regression may be sufficient in some cases to address overdispersion of higher magnitude in these scenarios. The contrast between negative binomial and Poisson distribution models becomes more obvious as the magnitude of σ_p increases.

4.2. Longitudinal results

Results for both longitudinal scenarios are given in Table 4 and illustrated in Figures 3a-b and 4a-b for all considered values of σ_p, calculated under the Poisson-GLMM model. Longitudinal results are similar to those for the cross-sectional analysis. Given the percentage values of the Type I errors and coverage probabilities shown in Figure 3a-b, and the corresponding Type II error results and coverage probabilities in Figure 4a-b, the Poisson-GLMM again performs fairly well in addressing both outlier and zero inflation dependent overdispersion when σ_p ≤ 1.2. For larger magnitudes of overdispersion up to σ_p ≤ 2.5, NB-GLMM performs well in both scenarios when considering all criteria. NB-GLMM results in considerably lower Type I errors and higher coverage probabilities and comparable Type II errors compared to Poisson-GLMM. As the magnitude of σ_p increases, the superiority of the NB-GLMM model becomes more apparent as the difference in errors and coverage increases compared to the Poisson-GLMM. Not surprisingly, results become overall much less reliable when σ_p ≥ 5.0 for the Poisson-GLMM given the very low coverage probabilities at all effect sizes shown in both figures.

Table 4.

Percentage of simulations with Χ₁ Type I and II errors and in which parameter coverage included the true parameter given true values of 0.01, 0.41, and 0.92 for the longitudinal scenario using Poisson and negative binomial GLMM.

σp	Outlier Dependent Poisson GLMM						Zero Inflation Poisson GLMM
	β1 = 0.01		β1 = 0.41		β1 = 0.92		β1 = 0.01		β1 = 0.41		β1 = 0.92
	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)
1.0	3.50	98.00	0.00	97.50	0.00	98.00	3.50	98.00	0.00	97.50	0.00	98.00
1.2	7.00	94.00	0.00	93.50	0.00	89.00	3.50	96.00	0.00	93.00	0.00	90.00
1.3	9.00	95.00	0.00	85.50	0.00	85.50	10.50	90.00	0.00	93.50	0.00	90.00
1.4	8.50	92.00	0.00	88.00	0.00	81.50	6.00	94.50	0.00	86.50	0.00	88.50
1.5	14.00	86.00	0.00	85.50	0.00	77.50	7.00	93.50	0.00	86.50	0.00	89.00
2.0	25.50	77.00	0.00	73.00	0.00	55.00	15.00	84.50	0.00	84.00	0.00	80.50
2.5	31.50	70.00	0.00	61.00	0.00	46.50	27.00	72.50	0.00	68.00	0.00	75.50
5.0	63.50	38.50	2.50	38.00	0.00	27.00	38.50	62.00	8.00	66.00	0.00	56.50
10.0	86.00	15.00	12.00	18.50	0.50	15.50	—	—	—	—	—	—

σp	Negative Binomial GLMM						Negative Binomial GLMM
	β1 = 0.01		β1 = 0.41		β1 = 0.92		β1 = 0.01		β1 = 0.41		β1 = 0.92
	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)	Type I (%)	Coverage (%)	Type II (%)	Coverage (%)	Type II (%)	Coverage (%)
1.0	3.55	98.82	0.00	100.00	0.00	97.48	3.55	98.82	0.00	100.00	0.00	97.48
1.2	4.02	95.98	0.00	94.44	0.00	90.86	3.00	97.50	0.00	96.00	0.00	92.46
1.3	5.00	95.50	0.00	90.95	0.00	88.38	3.50	97.00	0.00	97.50	0.00	96.00
1.4	4.50	95.50	0.00	90.95	0.00	86.00	1.00	99.50	0.00	97.00	0.00	97.50
1.5	5.00	94.00	0.00	92.00	0.00	86.00	1.50	99.00	0.00	94.50	0.00	98.50
2.0	9.00	91.50	0.00	90.50	0.00	71.00	1.50	99.50	0.00	99.00	0.00	99.50
2.5	9.50	91.00	0.00	86.50	0.00	67.00	1.00	99.50	3.50	98.50	0.00	99.50
5.0	19.00	83.00	0.50	81.50	0.00	72.50	0.00	100.00	75.00	99.50	0.00	100.00
10.0	18.50	83.00	3.50	86.50	0.00	81.00	—	—	—	—	—	—

σ_p is defined as the ratio of the Pearson χ² to its degrees of freedom

Figures 3.

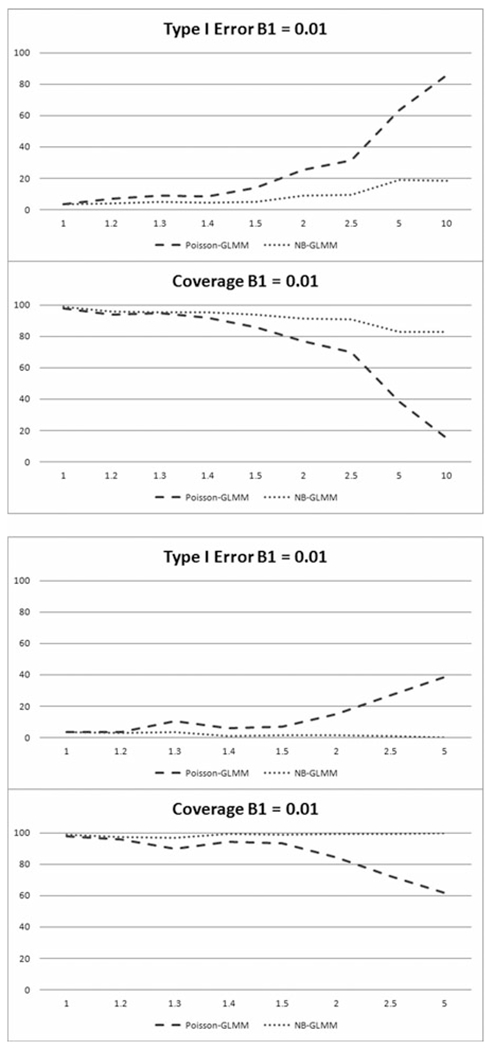
a-b. Percentage of simulations with Type I errors and in which parameter coverage included the true parameter given a true parameter value of 0.01 in the longitudinal scenario, for a.) outlier dependent overdispersion and b.) overdispersion caused by zero inflation.

Figure 4.

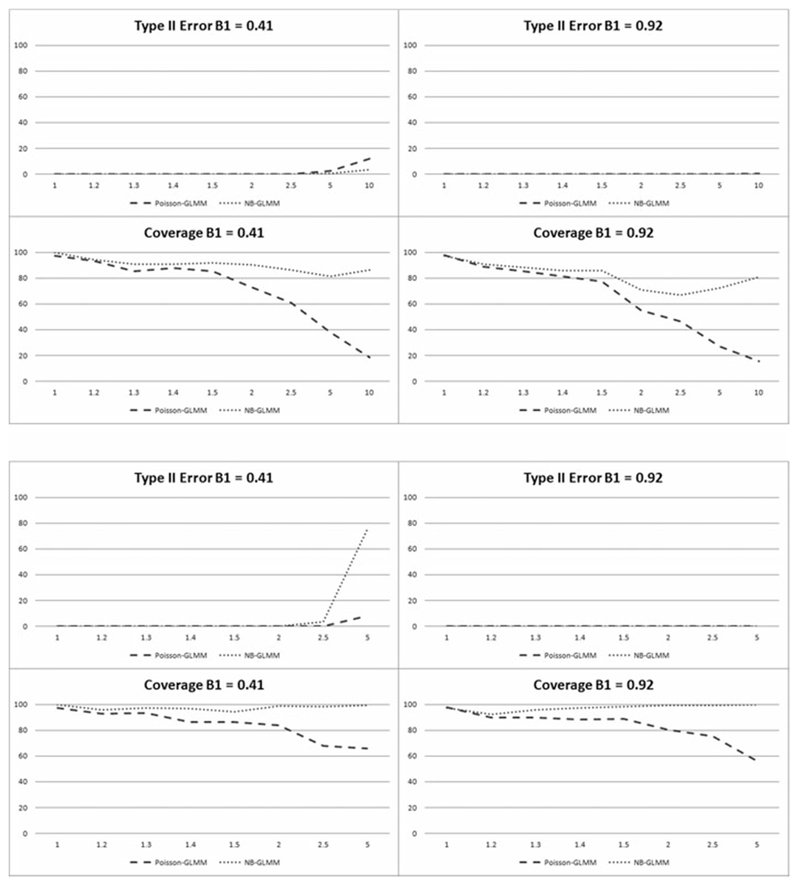
a-b. Percentage of simulations with Type II errors and in which parameter coverage included the true parameter given true parameter values of 0.41 and 0.92 in the longitudinal scenario.

5. Motivating real datasets

5.1. Description

We utilize two real datasets to examine model performance at varying magnitudes of overdispersion. We modify the datasets in order to produce samples with different levels of overdispersion present when the data is modeled using unadjusted Poisson regression. The National Lung Screening Trial (NLST) (Aberle and Adams 2011) randomized 50,263 non-Hispanic white (NHW) and non-Hispanic black (NHB) patients to compare lung cancer mortality rates between those screened via low-dose CT screening and those given chest radiography. We consider the relationship between patient race predictor (NHB versus NHW) and comorbidity burden count outcome (with possible range from 0 to 31) and adjusted for assigned treatment group. The sample dispersion statistic σ_p for the whole cohort is 1.30. When we look into gender based subgroups, the dispersion statistic values for comorbidity burden are 1.25 and 1.36 for male and female patients, respectively.

The second example is the classic Ames Salmonella dataset that is known for its highly overdispersed count data (Mortelmans and Zeiger 2000). This classic dataset includes a count outcome of bacterial colonies by six levels of medication dose on three different plates and results in a much greater magnitude of overdispersion. The dispersion statistic σ_p for the whole cohort is 5.33. Here, we examine the relationship between bacterial colony count outcome and log medication dose predictor.

5.2. Results

All model results are given in Table 5, including rate ratios, AIC goodness-of-fit statistics, standard error of the beta parameters, and parameter p-values. We observe that the negative binomial regression model results in moderately adjusted standard error values and low AIC goodness-of-fit statistics in each of the NLST datasets, with respective dispersion magnitudes of 1.25 (male patients), 1.30 (whole cohort), and 1.36 (female patients). The standard errors resulting from the NB model for these dispersion magnitudes are, respectively, 12.00%, 17.65%, and 20.83% higher than those resulting from the simple unadjusted Poisson model. The percent increase in standard error produced by the NB here clearly increases with the level of overdispersion in the dataset. The NB-GLMM also performs well based on the goodness-of-fit and standard error criteria. The Poisson-GLMM results are comparable with the unadjusted Poisson by these criteria.

Table 5.

Standard error and rate ratio by overdispersion magnitude for NLST and Salmonella datasets.

NLST
Description	Model	σp	AIC	RR	SE	P-Value
Male Patients	Poisson	1.25	86772.4	1.127	0.025	<0.0001
	Poisson-GLMM		86499.0	1.102	0.025	0.0001
	NB		86070.3	1.127	0.028	<0.0001
	NB-GLMM		85861.2	1.200	0.020	0.0005
Whole Cohort	Poisson	1.30	151861.2	1.211	0.017	<0.0001
	Poisson-GLMM		151314.1	1.190	0.018	<0.0001
	NB		150147.2	1.211	0.020	<0.0001
	NB-GLMM		149741.7	1.190	0.021	<0.0001
Female Patients	Poisson	1.36	64958.8	1.296	0.024	<0.0001
	Poisson-GLMM		64709.1	1.279	0.025	<0.0001
	NB		63952.0	1.296	0.029	<0.0001
	NB-GLMM		63787.5	1.279	0.030	<0.0001

Salmonella
Description	Model	σp	AIC	RR	SE	P-Value
Whole Cohort	Poisson	5.33	171.77	1.119	0.027	<0.0001
	Poisson-GLMM		152.85	1.119	0.027	0.0009
	NB		140.43	1.134	0.057	0.0275
	NB-GLMM		141.02	1.132	0.047	0.0194

In the Salmonella dataset, the standard error resulting from the NB model for dispersion magnitude of 5.33 is 111.11% higher than that resulting from the simple unadjusted Poisson model. The NB-GLMM gives a more moderate increase of 74.07% compared to the unadjusted Poisson and may be preferable here. Again, the percent increase in standard error appears to correspond with the increase in overdispersion magnitude occurring in this sample when the data is modeled using unadjusted Poisson regression. The goodness-of-fit statistics further confirm the better fit of the negative binomial models to the data.

6. Conclusion

We assessed threshold for overdispersion under Poisson and negative binomial models via simulation study. We considered cross-sectional and longitudinal datasets with two binary predictors and count outcome containing overdispersion due to either the addition of outliers or zero inflation. Magnitude of overdispersion was measured by dispersion statistic σ_p, defined as the ratio of the Pearson χ² value to its corresponding degrees of freedom n − p. Comparison among models was made using Type I error with a true β₁ value of 0.01, Type II errors using true β₁ values of 0.41 or 0.92, 95% CI, and coverage probability of β₁ for all effect sizes of β₁.

Results of our simulations demonstrate that the unadjusted Poisson regression and Poisson-GLMM perform fairly well for cross-sectional scenarios when there is low overdispersion magnitude, particularly when σ_p ≤ 1.2. The negative binomial regression model performs well at higher magnitudes of overdispersion under both outlier and zero inflation dependent scenarios, up to about σ_p ≤ 1.5. The NB-GLMM gives acceptable results at high magnitudes of overdispersion in some cases up to about σ_p ≤ 5.0. Both the Poisson-GLMM and NB-GLMM resulted in more conservative Type I errors than their corresponding regression models. The Type II errors are higher for negative binomial regression and NB-GLMM compared to the unadjusted Poisson and Poisson-GLMM. The Type II error and coverage probability also decreased for higher β₁ effect sizes. NB-GLMM resulted in the highest Type II errors overall, so negative binomial regression appears to be sufficient to address the overdispersion in many of the cross-sectional datasets. Further statistical intervention would be required under the most extreme outlier or zero inflation dependent overdispersion scenario when σ_p ≥ 10.0, as our results demonstrate that none of our models would likely give reliable results in these cases.

Longitudinal datasets appeared to be somewhat less tolerant of the more moderate levels of overdispersion. NB-GLMM gave more conservative Type I errors and higher coverage probabilities than Poisson-GLMM, as well as generally comparable Type II errors. Again, the Poisson-GLMM performs well in addressing both outlier and zero inflation dependent overdispersion when σ_p ≤ 1.2. For larger magnitudes of overdispersion, up to about σ_p ≤ 2.5, NB-GLMM performs well. The superiority of the NB-GLMM model became more apparent as the overdispersion in the dataset increased. Once again, further statistical intervention may be required when σ_p ≥ 5.0 in longitudinal analysis. Our models addressing both outlier and zero inflation dependent overdispersion are less reliable in these cases. In a clinical setting, the covariates included in the model should be reexamined for errors leading to faulty models beyond the issue of overdispersion.

Based on these simulations, it would appear that a general threshold for relying on the simple Poisson model for cross-sectional and longitudinal datasets is in cases where σ_p ≤ 1.2. For cross-sectional datasets, the negative binomial distribution via NB or NB-GLMM should be utilized if 1.2 < σ_p ≤ 1.5. For higher values of σ_ρ in these scenarios, NB-GLMM should be utilized up to about σ_p ≤ 5.0. However, if σ_p ≥ 5.0 for longitudinal datasets or if σ_ρ ≥ 10.0 for cross-sectional datasets, the model may not be reliable based on adjustment for overdispersion and should be checked for additional modeling errors.

We also utilized two real cross-sectional datasets to produce varying magnitudes of overdispersion for analysis. We used data from the National Lung Screening Trial (NLST) (Aberle and Adams 2011) to examine the relationship between comorbidity count and patient race (NHB to NHW), adjusting for assigned treatment group. The σ_p value for the whole cohort was 1.30, and stratifying by gender gave dispersion values of 1.25 and 1.36 for male and female patient subgroups, respectively. According to our simulation results, these levels of σ_p would require statistical intervention via negative binomial regression or NB-GLMM. This was confirmed by decreased goodness-of-fit statistics and moderately adjusted standard errors compared to the unadjusted Poisson model. We also considered a higher magnitude of overdispersion using the Ames Salmonella dataset (Mortelmans and Zeiger 2000), which is a classic example of overdispersion in a dataset and includes measures of medication dose by plate and a count of Salmonella bacterial colonies. The σ_p value was 5.33 for the whole cohort. Our results indicate that this high level of overdispersion requires adjustment via the NB or the NB-GLMM, which is also supported by our analysis. The percent increase in standard errors resulting from the negative binomial models compared to the unadjusted Poisson models increased in correspondence with higher magnitudes of overdispersion for both real datasets.

We discussed a score test for overdispersion in Section 2.2 of H₀ : φ = 0 vs. H₁ : φ > 0 in which the score statistic has a standard normal distribution under the null hypothesis. This score test suggests that a dataset which results in a score statistic greater than or equal to 1.65 allows us to reject the assumption of equidispersion at a significance level less than or equal to 0.05. In our simulations, this translated into a level of overdispersion given by a value of σ_p at about 1.5 ≤ σ_p ≤ 2.0 for both overdispersion scenarios dependent on effect size, as demonstrated by the nominal 95% rejection of equidispersion by the score test at these levels. It is clear from our simulations, however, that the presence of overdispersion is harmful to our analyses and should be addressed at even lower values of σ_p, particularly at σ_p > 1.2, although the assumption of equidispersion may not be rejected at these levels by the score test. Lastly, it should be noted that these results may not be applicable in all clinical cases where overdispersion is present. Additional simulation studies and real data analyses are required to make further generalizations.