External validation of cerebral aneurysm rupture probability model with data from two patient cohorts

Abstract

Background:

For a treatment decision of unruptured cerebral aneurysms, physicians and patients need to weigh the risk of treatment against the risk of hemorrhagic stroke caused by aneurysm rupture. The aim of this study was to externally evaluate a recently developed statistical aneurysm rupture probability model, which could potentially support such treatment decisions.

Methods:

Segmented image data and patient information obtained from two patient cohorts including 203 patients with 249 aneurysms were used for patient-specific computational fluid dynamics simulations and subsequent evaluation of the statistical model in terms of accuracy, discrimination, and goodness of fit. The model’s performance was further compared to a similaritybased approach for rupture assessment by identifying aneurysms in the training cohort that were similar in terms of hemodynamics and shape compared to a given aneurysm from the external cohorts.

Results:

When applied to the external data, the model achieved a good discrimination and goodness of fit (area under the receiver operating characteristic curve AUC=0.82), which was only slightly reduced compared to the optimism-corrected AUC in the training population (AUC=0.84). The accuracy metrics indicated a small decrease in accuracy compared to the training data (misclassification error of 0.24 vs. 0.21). The model’s prediction accuracy was improved when combined with the similarity approach (misclassification error of 0.14).

Conclusions:

The model’s performance measures indicated a good generalizability for data acquired at different clinical institutions. Combining the model-based and similarity-based approach could further improve the assessment and interpretation of new cases, demonstrating its potential use for clinical risk assessment.

Introduction

Intracranial aneurysms [IAs] are a common vascular disease occurring in about 2–3 percent of the population [25, 33]. Whereas most IAs remain asymptomatic and never rupture, the event of aneurysm rupture results in hemorrhagic stroke, which is related to high mortality, morbidity, and, consequently, a notable economic burden [26, 34]. Nowadays, IAs are increasingly diagnosed incidentally [11]. In these cases, physicians need to weigh the natural risk of aneurysm rupture, which is relatively low at 1% per year [17, 31, 36], against the risks of treatment and their complications when deciding on a treatment strategy.

Several risk factors for IA rupture have previously been identified, including molecular, genetic, morphological, and hemodynamic parameters [18]. While these findings indicate the importance of considering various types of risk factors for rupture risk assessment, current treatment decisions are mainly based on aneurysm size, location in the cerebral vasculature, and patient-related factors [13, 28, 29].

We recently developed a probability model for aneurysm rupture combining morphological, hemodynamic, and patient-related parameters [10]. The internal validation of the model with 1,631 IAs that were used for model training indicated a good predictive performance. As a subsequent step, the aim of the current study was to externally validate the model with 249 aneurysms from two different patient cohorts. The probability model-based approach was further compared to rupture assessment by identifying “similar cases” in terms of aneurysm location, morphology and flow characteristics in the training dataset.

Methods

Patient and image data

The rupture probability model has been previously developed using cross-sectional image and patient data from 1,061 patients with 1,631 aneurysms obtained from hospitals in the US, Japan, and Colombia [10]. For the external evaluation of this model, cross-sectional data of two patient cohorts, the AneuRisk dataset¹ [27] and datasets from the AneuX project, which had not been used for model training, were used. Both datasets included segmented 3D geometries that had been derived from 3D rotational angiography (3DRA) images as well as patient data of patients who underwent cerebral angiography for cerebral aneurysm assessment in the Neuroradiology Division of the Niguarda Ca’ Granda Hospital in Milan (AneuRisk) and at the Geneva University Hospitals (HUG, Hôpitaux Universitaires Genève, AneuX)². In total, 203 patients with 249 IAs (66 ruptured, 183 unruptured) were included. Multiple aneurysms were present in 35 patients (17.2%).

Tab. 1 summarizes the patient characteristics for both external patient cohorts and the cohort used for training the model. The mean age of the patients in the three cohorts was 56, 54, and 55 years for the training data, AneuRisk, and AneuX, respectively (p=0.314, ANOVA). Both for the training population and the AneuRisk data, the majority of the aneurysms was located at the internal carotid artery (ICA, 39% and 32%, respectively), whereas most of the AneuX IAs were located at the middle cerebral artery (MCA, 32%). Fig. 1 shows the relative distribution of IAs by aneurysm location for the three cohorts.

Table 1.

Comparison of patient cohorts used for model training and model evaluation. ACA=Anterior cerebral artery, ACOM=anterior communicating artery, BA=basilar artery, ICA=internal carotid artery, MCA=middle cerebral artery, PCOM=posterior communicating artery, VA=vertebral artery; R and U refer to the number of ruptured and unruptured aneurysms, respectively

		Training population	AneuRisk	AneuX
Number of patients		1061	99	104
Number of aneurysms (ruptured/unruptured)		1631 (492R/1139U)	113 (44R/69U)	136 (22R/114U)
Patient age (mean ± sd) (of 1065 patients with known age)		56.25 ± 13.77	54.36 ± 13.58	54.99 ± 13.70
Patients with multiple aneurysms		328	13	22
Number of patients with SAH		490	44	22
Distribution by location	ACA	57 (3.49%) 20R/37U	1 (0.89%) 1R/0U	4 (2.94%) 1R/3U
	ACOM	226 (13.86%) 148R/78U	23 (20.35%) 17R/6U	22 (16.18%) 6R/16U
	BA	106 (6.50%) 35R/71U	7 (6.19%) 4R/3U	7 (5.15%) 3R/4U
	ICA	636 (38.99%) 64R/572U	36 (31.86%) 3R/33U	41 (30.15%) 2R/39U
	MCA	310 (19.01%) 82R/228U	28 (24.78%) 9R/19U	43 (31.62%) 5R/38U
	PCOM	260 (15.94%) 127R/133U	18 (15.93%) 10R/8U	15 (11.03%) 4R/11U
	VA	36 (2.21%) 16R/20U	0 (0%) 0R/0U	4 (2.94%) 1R/3U
Gender		802 F, 259 M	62F, 37M	82F, 22M

Fig. 1.

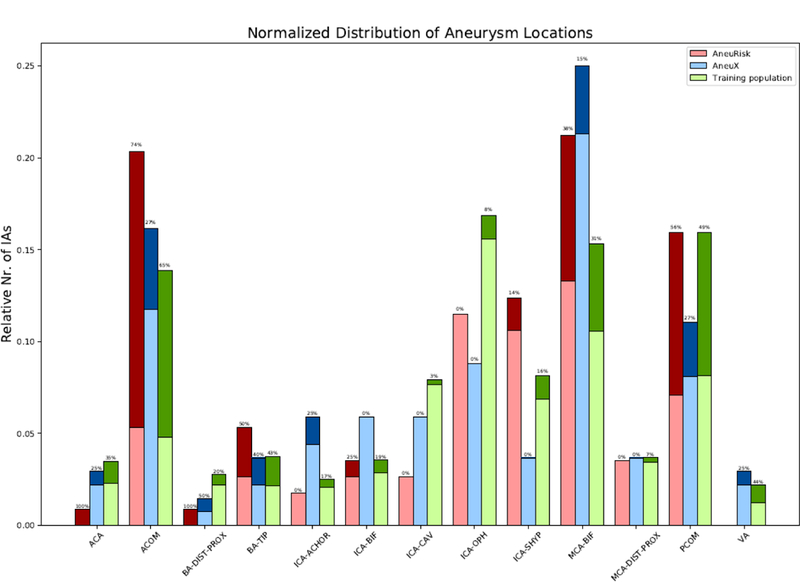
Distribution ruptured (dark colors) and unruptured (light colors) aneurysms by location and patient cohort. To facilitate a comparison between the different cohorts, all absolute numbers of aneurysms per location were normalized by the total number of aneurysms of the respective cohort. The shown percentages refer to the rupture rates for each location. For the definition of the aneurysm locations see the description of the model’s parameters in [7]

Hemodynamic modeling and shape characterization

Computational fluid dynamics (CFD) simulations and the quantitative characterization of aneurysm morphology require 3D geometries of the cerebral aneurysm(s) and surrounding vasculature that are extracted from 3D medical imaging data by means of vessel lumen segmentation. The images of the training data had been segmented using in-house software with a thresholding-based approach [10]. The AneuRisk data were segmented using the “Vascular Modeling ToolKit” (VMTK) with a gradientdriven level-set approach [23]. For the AneuX data, a geodesic active regions method [14] integrated in the @neuFuse software [32] as well as a level-set based approach implemented in Matlab were applied.

Using the segmented 3D aneurysm geometries, we performed CFD simulations as previously described for the training data [10]. Briefly, unstructured grids were automatically generated using tetrahedral elements with a maximum element size of 0.2 mm. For numerically solving the unsteady Navier-Stokes equations, an in-house finite element solver with a fully implicit scheme was used [3]. Vessel walls were modeled as rigid and blood was represented as a Newtonian fluid with a density of 1.0 g/cm^³ and viscosity of 0.04 Poise. For the inflow boundary conditions, a flow waveform obtained from a healthy subject was scaled to the area of the inflow artery using a power law [4]. Outflow boundary conditions were set as pressure and flow outlets. Two cardiac cycles with 100 time steps per cycle, assuming a heart rate of 60 beats per minute were computed and the results of the second cycle were used for subsequent hemodynamic characterization.

Next, the hemodynamic and morphological parameters of the aneurysm rupture probability model were automatically computed based on the CFD solutions as well as the 3D geometries as previously described [10].

Model evaluation

The aneurysm rupture probability model had been developed using logistic group lasso regression [10]. To evaluate it, the linear predictors and predicted probabilities of being ruptured were computed for the AneuRisk and AneuX IAs (test IAs) based on the model coefficients [10]. Subsequently, the model’s discrimination as well as goodness of fit were assessed by the area under the receiver operating characteristic (ROC) curve (AUC) and calibration plots. For the latter, a loess smoother with a span parameter of 0.75 was used as part of the visualization [1]. Confidence intervals of the AUC were estimated based on 1,000 bootstrap repetitions. To assess the accuracy of the model in terms of true positive rate (TPR), false positive rate (FPR), positive predictive value (PPV or precision), and NPV (negative predictive value), a threshold for classification of an IA as ruptured was selected as the probability corresponding to the point on the ROC curve with the minimum distance to the point (0,1). For all AneuRisk and AneuX cases, information for all variables of the model was available (no missing data). All statistical analyses were performed with scripts written in the R language [24].

Rupture prediction based on similarities between aneurysms

We compared the accuracy of the rupture model in the external data to a more directly data-based approach that uses aneurysms from the training cohort with similar characteristics compared to the test IAs. For this alternative approach, the rupture status of the test IAs was defined as the most frequent rupture status (“majority vote”) of all “similar” aneurysms selected from the training data set. Here, aneurysms situated at the same location in the cerebral vasculature as well as having comparable values of non-sphericity index (NSI), maximum oscillatory shear index (OSImax), and aneurysm size were considered as similar. The first three parameters (location, NSI, OSImax) capture anatomic, morphologic, and hemodynamic characteristics of the aneurysm and were identified as important variables for identifying an aneurysm’s rupture status in our previous study [10]. We further included aneurysm size as a selection criterion to identify aneurysms that are at a similar phase of their evolution. Starting with a threshold of 5%, aneurysms at the same location and having a value of the selected variables within a deviation of this threshold were defined as matching cases. If no similar case was identified, the deviation threshold was increased in steps of 5% until reaching a maximum of 200% (10%, 15%, 20%, … , 200%). If for a test IA and a specific threshold, the number of identified similar ruptured IAs was identical to the number of similar unruptured IAs (ties), the rupture status of the test IA was defined as the one of the similar case with the closest value of aneurysm size. The scheme of this “similarity-based approach” is illustrated in Fig. 2.

Fig. 2.

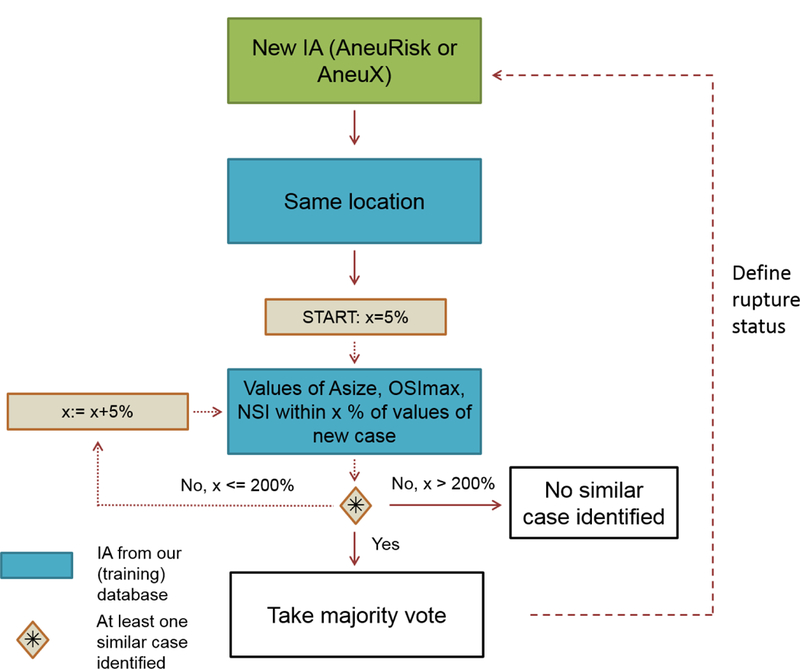
Scheme of the similarity-based approach for estimating an aneurysm’s rupture status. For a new case, aneurysms from our database with the same location and values of aneurysm size (Asize), maximum OSI (OSImax) and non-sphericity index (NSI) within a five percent range of the values of the new case were selected. If no aneurysms fulfilling these criteria were identified, the range was increased by five percentage points until at least one aneurysm was found or the percent range reached 200 %. If more than one aneurysm was identified for a specific range, the majority vote was taken. In case of the same number of ruptured and unruptured IAs, the rupture status of the aneurysm with the closest aneurysm size was selected

Results

Model evaluation

When applying the model to the test data (AneuRisk and AneuX combined), the AUC was 0.82 (mean and 95% bootstrap confidence interval 0.8245, [0.8227, 0.8263], see Fig. 3, left for the ROC curve). Evaluated separately in the two test cohorts, the AUC for the AneuRisk data was 0.82 and for AneuX 0.86 (mean and confidence intervals of 0.8202 [0.8177, 0.8227] and 0.8666 [0.8645, 0.8686]). The calibration plot (Fig. 3, right) indicates an appropriate goodness of fit of the model both in the training and testing population quantified by a calibration slope and intercept of 1.12 and −0.11, respectively, for the testing data. Based on the ROC curve, a threshold of 0.316 was selected to classify the IAs of the testing population as ruptured. For this threshold, the TPR, FPR, and PPV were 0.77, 0.24, and 0.54, respectively (see Tab. 2). The relative number of misclassified IAs was 0.24. When applying the threshold that was determined based on the training data to the test data (0.323), the TPR, FPR, and misclassification error were slightly decreased to 0.76, 0.23 and 0.23, whereas the PPV remained constant at 0.54 (see Tab. 2). The ROC curves, calibration plots, and accuracy metrics for the AneuRisk and AneuX data separately are shown in Fig. 1 and Tab. 1 in the Suppl. Data.

Fig. 3.

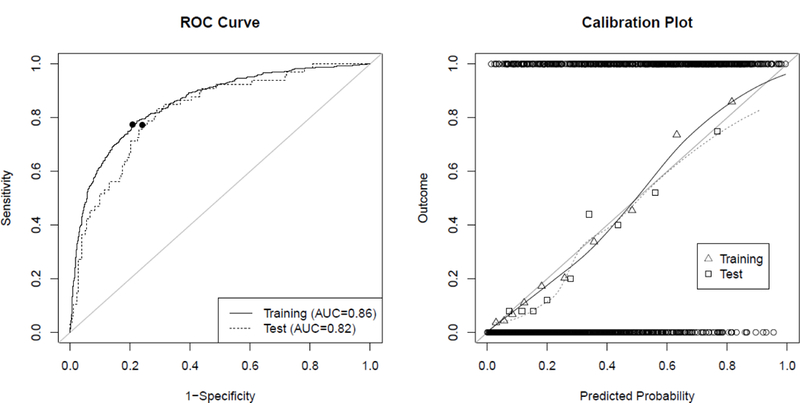
ROC-curves and calibration plots for the training data (solid line) and combined AneuX and AneuRisk data (“test”, dotted line). (Left) ROC curves visualize the discriminative ability of the model. The filled circles on the ROC curve indicate the values corresponding to the “optimal threshold” determined for the respective data. (Right) Calibration plots allow to assess the goodness-of-fit of the model. The circles at the top and bottom show the observed data. The triangles and squares show the observed outcomes of the training and test populations grouped by deciles, which are also represented by the loess smoother with the solid and dotted line. For a perfectly calibrated fit, all triangles/squares and the loess smoother would lie on the 45°-line

Table 2.

Accuracy measures for the model applied to the training and testing populations for given threshold (thresholds marked with an asterisk indicate are “optimal threshold” based on the ROC curve of the given dataset) as well as for the similarity-based approach. TPR=ratio of true to all positives (=sensitivity), FPR = ratio of false positives to all negatives (= 1-specificity), PPV (positive predictive value=precision) = ratio of true positives to number of true and false positives, NPV (negative predictive value) = ratio of true negatives to number of true and false negatives, misclassification error = number of incorrect classifications divided by the sample size

	Data	Threshold	TPR	FPR	PPV	NPV	Misclassification error
Model	Training	0.323*	0.77	0.21	0.62	0.89	0.21
	Test	0.316*	0.77	0.24	0.54	0.90	0.24
	Test	0.323	0.76	0.23	0.54	0.90	0.23
Similar Cases	Test	-	0.55	0.18	0.52	0.83	0.25
Model + Similar Cases	176 IAs of test population	0.323	0.79	0.12	0.61	0.95	0.14

Similar cases based on selected variables

For all 249 IAs of the test cohorts, “similar IAs” were identified in the training population within a range of 115% of deviation of the values for aneurysm size, NSI, and OSImax. Using the stepwise approach described above (increasing the deviation threshold until matching cases are found), on average 1.79 similar IAs in the training cohort per queried IA were selected. Based on the majority vote, the rupture status of 186 of the 249 IAs was correctly classified (74.7%). The TPR, FPR, and PPV for this approach were 0.55, 0.18, and 0.52 (see Tab. 2).

Combination of model and similarity based approach

To evaluate whether combining the predictions of the model and the approach based on the similar cases could improve the overall accuracy of the predictions, the subset of 176 IAs with the same predicted rupture status based on the majority vote of the similar cases and classification with the model was further analyzed. Here, for determining the rupture status based on the model, the “optimal threshold” determined in the training data of 0.323 was used. Of those 176 cases, 152 were correctly classified (86.4%). The TPR, FPR, and PPV were 0.79, 0.12, and 0.61 (see Tab. 2).

Discussion

The treatment decision of incidental IAs poses a challenge to physicians and patients since the risk of a devastating hemorrhagic stroke needs to be weighed against the risk of treatment. A statistical rupture prediction model could potentially support decision making for these cases. Recently, we presented a rupture probability model based on a large patient-cohort including patient-related, hemodynamic, and morphological information [10]. The model showed good discrimination and calibration in the training data (internal validation). Our current study assessed the model’s performance with data of aneurysms that have not been used for model training (external validation). The results showed a good predictive performance of the model in the external data, indicating that the model remains valid with new data.

Model performance

In this external validation, the model’s discrimination in terms of AUC was reduced to 0.82 compared to the AUC of 0.86 in the training data. The AUC was only slightly lower than the AUC in the training data after correction for the estimated optimism of 0.84, indicating reasonable optimism estimation. The further reduction of the AUC could potentially be explained by differences in the patient populations in the training compared to the test data. Interestingly, the AUC was higher when applying the model to the AneuX data (AUC=0.86) compared to both the AneuRisk (0.82) and the combined data (0.82). The model’s calibration was also only slightly poorer for the test data as illustrated by the larger deviation of the loess smoother from the 45° line in the calibration plot (see Fig. 3).

With respect to the model’s accuracy, when using the “optimal threshold” based on the ROC curve of the test data for classifying an IA as ruptured or unruptured, the TPR remained the same compared to the TPR for the training data (0.77) whereas the PPV slightly decreased and the FPR and misclassification error increased. Since for a new case it would not be possible to determine an “optimal threshold” based on the new case’s “population”, we also applied the threshold computed based on the training data (0.323) to the test data. The accuracy measures remained mainly the same, indicating that this threshold could also be applied for classifying new IAs. Overall, the presented measures indicated a reasonable accuracy of the model. At the same time, it is important to bear in mind that the predicted probability at which a physician decides to treat the patient depends on various factors related to the patient and treating physician. Therefore, accuracy measures based on fixed thresholds (like the “optimal” one based on the ROC curve) provide only approximate information on the model’s predictive performance in terms of (mis-)classification of cases in a clinical setting.

The PHASES score [13] uses patient specific information, aneurysm size, and aneurysm location to estimate a patient’s 5-year aneurysm rupture risk. Its internal and external validation resulted in a AUCs of 0.82 and 0.66, respectively [2, 13]. Our results indicate that incorporating hemodynamic and morphological information can potentially improve aneurysm risk assessment. The lack of some patient-related information used in the PHASES score (population, hypertension, and earlier SAH from another aneurysm) for the data used in the presented study did not allow for a direct comparison of the performances of our model and the PHASES score, which is therefore planned for future work.

To enable and encourage an evaluation of our model by other research groups as well as a comparison of the results with the findings presented here, this study follows the TRIPOD statement [9].

Data-driven risk assessment

Our results indicate that applying the statistical model can potentially provide guidance for physicians who need to decide whether to treat an aneurysm or conservatively observe it. Nevertheless, the interpretation of such a model can be difficult. Therefore, we implemented a datadriven “similarity based” approach to provide visual support for interpreting the model’s results as well as to compare the performance of this approach with the performance of the model. For each test IA, we identified IAs in our (training) data with the same location and similar values of NSI, OSImax, and aneurysm size. Our results showed that when using this approach for rupture prediction, its performance was only slightly worse compared to applying the rupture probability model in terms of the misclassification error (0.25 vs. 0.24). This indicates that the important variables as identified based on cross-validation in the training data can be used to identify similar aneurysms with identical rupture status.

A total of 176 IAs were classified as either ruptured or unruptured by both the statistical model and the similarity-based approach. Of those 176 cases, only 24 were misclassified (13.64%, see Tab. 2) compared to 24% of misclassification obtained for all the 249 cases when using the model alone. Hence, the similarity-based approach could be used to provide additional information about a case and facilitate the interpretation of the given parameters by visualizing the identified similar IA.

Of the 24 misclassified cases, 7 aneurysms were ruptured, but misclassified as unruptured. In these cases, the model clearly failed to identify the correct rupture status. The remaining 17 cases were unruptured, but misclassified as ruptured. It is possible that these unruptured aneurysms were at higher risk of future rupture, but no data was available to evaluate this hypothesis. Two examples of misclassified IAs are illustrated in Fig. 2 and Tab. 2 in the Suppl. Data.

The shape and hemodynamic environment of four example IAs from the AneuRisk and AneuX data and their identified similar IAs from the training population are illustrated in Fig. 4 and 5. The IAs in Fig. 4 are ruptured and have – in accordance with their rupture status – high predicted probabilities of being ruptured (>91% for the test cases, >89% for the corresponding similar IAs). Furthermore, they are similar in shape and exposed to a comparable flow environment (indicated by their wall shear stress distribution and stream lines). This also holds for the four IAs illustrated in Fig. 5, which are unruptured aneurysms with low predicted probabilities (<3% for the test cases, <8% for the corresponding training IAs).

Fig. 4.

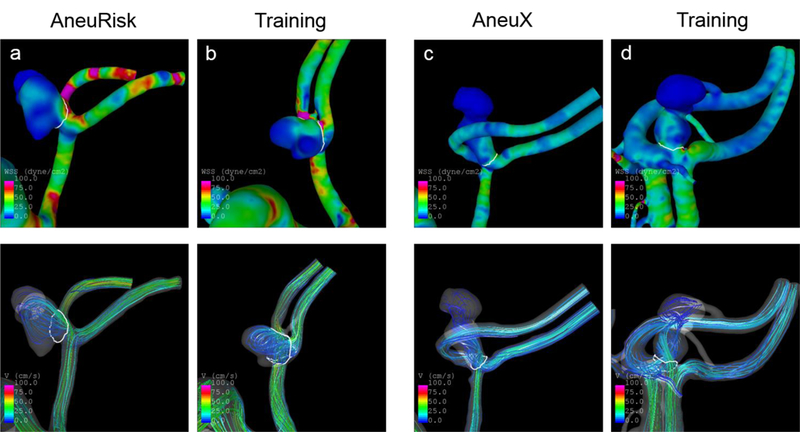
Wall shear stress distribution (top panel) and streamlines (bottom) at half of the cardiac cycle of four ruptured IAs with high probabilities of being ruptured based on the model. The shown IAs from training data were identified as similar cases for the respective AneuRisk or AneuX case. The predicted probabilities and values of selected variables for these cases are shown in Tab. 3

Fig. 5.

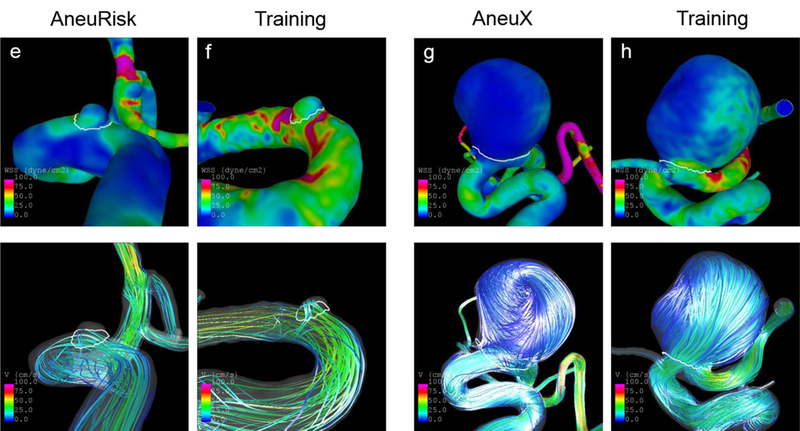
Wall shear stress distribution (top panel) and streamlines (bottom) at half of the cardiac cycle of four unruptured IAs with low probabilities of being ruptured based on the model. The shown IAs from training data were identified as similar cases for the respective AneuRisk or AneuX case. The predicted probabilities and values of selected variables for these cases are shown in Tab. 3

For the classification of new IAs purely using the similarity-based approach, the TPR was relatively low (0.55). Moreover, the identification of similar cases might not be possible for all future IAs given their specific shape, size or hemodynamic environment. Therefore, we suggest using primarily the statistical rupture probability model for rupture risk assessment and the identification of similar cases to obtain additional information (e.g. confirm a high rupture risk if all the similar IAs are ruptured) as well as to illustrate the case and facilitate the interpretation of the predicted risk.

Clinical considerations

The characterization of an IA in terms of shape and hemodynamic environment based on angiographic images requires as a first step the segmentation of the IA and the surrounding vasculature in the image. In the presented study, the segmentation of the IAs from the external populations (AneuRisk and AneuX) was performed by independent researchers using different segmentation tools compared to the segmentation of the training data. The good performance of our model in the two test cohorts indicates that the results of applying the model do not strongly depend on the image segmentation step. This aspect is important since image segmentation typically involves manual work and hence (depending on the amount of required manual work by the specific tool/algorithm) is to some extent user-dependent. The subsequent CFD simulations necessary for a hemodynamic characterization can be largely automatized. Hence, our results suggest that the model could be applied in a clinical setting even if segmentation requires some manual input and is performed by different users.

Particularly for follow-up observations, IAs are routinely assessed by means of MR angiography (MRA) or CT angiography (CTA). Whereas the training and test datasets for the presented study were based on 3DRA data, segmentation of IAs from CTA and MRA images is feasible as well [37, 38]. Hence, the model could also be applied for those cases. Moreover, fully automated image segmentation for IA assessment will likely be possible in future, thus facilitating the model’s application in a clinical setting [38].

When applying the statistical model for aneurysm risk assessment in clinical practice, it is important to consider that the current model was developed using cross-sectional data. Therefore, it gives the probability of being ruptured of a given aneurysm. However, based on the assumption that high risk aneurysms resemble those that have already ruptured [8], this model could also be useful for aneurysm rupture risk assessment. To evaluate the validity of the model for this application, the assessment of the model’s performance with longitudinal data is an essential next step and is planned for future work.

Current treatment decisions of incidental aneurysms are largely influenced by the aneurysm size [28, 29]. Whereas small aneurysms (< 5mm) are candidates for conservative follow-up observations, larger aneurysms often get treated [12]. Our statistical model might therefore be of use especially for assessment of small aneurysms. The model was developed using aneurysms within a large size range (1.1 mm – 39.3 mm). A model considering only small aneurysms could potentially improve risk assessment for this subgroup of IAs. At the same time, the “general model” could be applied to larger aneurysms as well, aiming at identifying larger low-risk aneurysms that do not require treatment and thus potentially reducing overtreatment [15].

Besides the parameters included in the aneurysm rupture probability model, several other risk factors have been associated with aneurysm rupture. As external risk factors, smoking, hypertension, and a previous SAH have been related to an increased aneurysm rupture risk [13, 19–21]. Considering these factors could further improve the risk assessment. Moreover, the presence of multiple aneurysms is often considered as a risk factor, although currently this association is not clear in the literature [16]. Irregular shape and particularly the presence of blebs are related to a higher risk of rupture [22]. While the evaluated model does not use the presence of blebs as a parameter, the combination of various shape indexes provides information about the irregularity of the aneurysm shape and potentially also indirectly about the presence of blebs.

Finally, it is important to mention that remodeling of the aneurysm wall eventually leads to its rupture. Especially the infiltration of the wall with inflammatory cells, particularly macrophages, seems to play an important role in aneurysm growth and rupture [7, 30]. Those aspects were not directly included in the evaluated risk assessment tool and should be taken into account when assessing an aneurysm’s rupture risk. At the same time, flow parameters are associated with changes in the vessel wall [5]. Besides, the presence of blebs might provide information about the wall properties [6]. Hence, aneurysm wall properties could be reflected to some extent in the computed hemodynamic and morphological parameters.

Limitations

In the present study, we used aneurysm data collected from two European hospitals to evaluate our model that had been developed using data mainly from hospitals in the US. Some studies indicate that Finish and Japanese populations have a higher risk of IA rupture compared to other populations [13, 35]. Consequently, the model’s performance could be different in test data coming from these two populations. Future work therefore will aim at evaluating the model with such data.

The external data that were used for model evaluation are subject to the same selection bias as for the training population [10]. Only patients that underwent cerebral angiography for aneurysm assessment were considered, whereas patients that deceased before reaching the hospital and those who only underwent CT or MR angiography could not be included in this study. It is planned to extend the database and thus the population for model training based on MRA and CTA data in future to address this limitation.

Conclusion

The developed aneurysm rupture probability model demonstrated a good predictive performance in two external patient cohorts, indicating the potential for its application to new clinical aneurysm cases. The model’s prediction and interpretation could further be improved by implementing an approach based on identifying similar IAs from the training database. Future work will include a validation of the model with longitudinal data and translating the risk assessment approach to the clinical practice.

Table 3.

Values of selected variables and predicted probabilities of being ruptured based on the statistical model for the IAs illustrated in Fig. 4 and 5. ACOM = anterior communicating artery, ICACAV = cavernous sinus of the internal carotid artery, ICA-OPH = ophthalmic segment of the internal carotid artery

Case	Population	Asize [cm]	Location	NSI	OSImax	Pred. Prob	Rupture Status
a	Test	1.0383	ACOM	0.3924	0.3391	0.9121	R
b	Training	0.9753	ACOM	0.3471	0.3752	0.8752	R
c	Test	1.2542	ACOM	0.3574	0.2705	0.9126	R
d	Training	0.9589	ACOM	0.3484	0.2694	0.9122	R
e	Test	0.3302	ICA-CAV	0.1871	0.0372	0.0227	U
f	Training	0.2965	ICA-CAV	0.2097	0.0373	0.0738	U
g	Test	1.6820	ICA-OPH	0.1871	0.4206	0.0154	U
h	Training	1.5441	ICA-OPH	0.1947	0.4021	0.0562	U