Abstract
Acoustic streaming has been widely used in microfluidics to manipulate various micro-/nano-objects. In this work, acoustic streaming activated by interdigital transducers (IDT) immersed in highly viscous oil is studied numerically and experimentally. In particular, we developed a modeling strategy termed the “slip velocity method” that enables a 3D simulation of surface acoustic wave microfluidics in a large domain (4×4×2 mm3) and at a high frequency (23.9 MHz). The experimental and numerical results both show that on top of the oil, all the acoustic streamlines converge at two horizontal stagnation points above the two symmetric sides of the IDT. At these two stagnation points, water droplets floating on the oil can be trapped. Based on these characteristics of the acoustic streaming field, we designed a surface acoustic wave microfluidic device with an integrated IDT array fabricated on a 128°YX LiNbO3 substrate to perform programmable, contactless droplet manipulation. By activating IDTs accordingly, the water droplets on the oil can be moved to the corresponding traps. With its excellent capability for manipulating droplets in a highly programmable, controllable manner, our surface acoustic wave microfluidic devices are valuable for on-chip contactless sample handling and chemical reactions.
Graphical Abstract
Graphic Content Entry: We investigated the 3D acoustic streaming activated by the IDT immersed in the oil by experimental investigation and numerical simulation using the modeling strategy termed “slip velocity method”.
1. Introduction
Acoustic streaming is the steady flow induced by acoustic waves. The acoustic streaming in small domains, such as channels,1–6 chambers,7 or droplets,8–14 has been extensively studied for various microfluidic applications15,16 such as mixing,1,2 pumping,3 and particle manipulation.4,7,17–21 Numerical simulation has also been applied to predict acoustic streaming in many studies.1,4,7,8,10–12,22 In most of the numerical schemes solving acoustic streaming, a perturbation approach22 is applied to separate the governing equations into first-order and second-order equations which are then solved for the acoustic field and the acoustic streaming, respectively. Based on these numerical schemes, several 2D numerical simulations have been carried out to analyze the acoustic streaming induced by bulk acoustic waves (BAW) or surface acoustic waves (SAW) in limited, narrow fluid domains.1,4,7,8,10–12,22
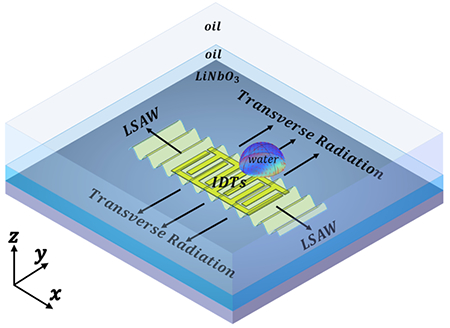
In studies considering BAW or SAW generated outside the transducer area,1,3,4,7,22,23 a simplified 2D simulation is suitable for predicting the real 3D, multi-domain coupled acoustic streaming problem in the liquid domain. The acoustic field in these cases are nearly uniform along a direction normal to the simulated 2D plane, and the actuation boundary condition can be represented by some formulas. However, there is a rare case where an IDT is immersed in the unconfined bulk liquid (Fig. 1(a)) in which the 2D simplification is no longer suitable for solving the acoustic streaming. In this case, the IDT on the substrate not only generates SAW which propagate normal to the IDT fingers inside and outside the IDT area, but also possibly some transverse radiation and oblique radiation waves.24–27 These waves, which cannot be approximated by existing formulas, will leak into the liquid loaded upon the IDT substrate and contribute to the acoustic streaming in a 3D butterfly pattern.9 Hence, the rarity of 3D substrate vibration, wave propagation and acoustic streaming pattern in this case demands a 3D simulation model that can systematically analyze IDT-induced substrate vibration and the resulting acoustic streaming pattern.
Fig. 1.
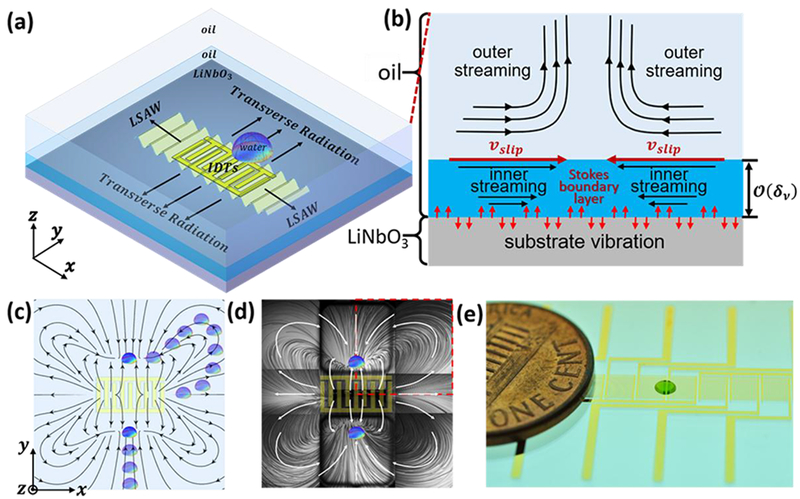
Illustration of the contactless droplet manipulation via boundary-driven streaming activated by an IDT. (a) Schematic of the mechanism of the acoustic streaming induced by a single IDT-activated vibration on the substrate. The IDT is fabricated on the 128° Y-X cut LiNbO3 substrate and immersed in the 2 mm-thick oil. The IDT, when activated, initiates 3D substrate vibration and thus generates the leaky acoustic wave in the loading oil. The leaky wave induces acoustic streaming in the oil because of the viscous attenuation, and thus it creates two “stagnation points” for trapping objects at the oil-air interface. (b) Schematic of the mechanism of boundary-driven streaming theory. The boundary-driven streaming induced by the substrate vibration mainly confines within the viscous boundary layer. The “outer streaming” (so-called “Rayleigh streaming”) is caused by the “inner streaming” (so-called “Schlichting streaming”) via a steady “slip velocity” at the top of the viscous boundary layer. (c) Simulated acoustic streaming pattern on the oil-air interface showing two symmetryic stagnation points on the two sides of the IDT, where objects floating on the oil would be trapped. Because of the induced acoustic streaming, randomly distributed objects gradually move towards the stagnation points. (d) Stacked image showing the streaming pattern on the oil-air interface. The streaming pattern forms the two stagnation points as indicated by two water droplets. The result shows that the streaming in this domain is roughly axial symmetric about both x-axis and y-axis. As such, a numerical model for this case can be simplified to simulate the area, as depicted by red dashed lines. (e) Image of a device with a 1×10 IDT array for contactless droplet manipulation. The green sphere is a drop of dyed water floating on the loading oil.
Performing 3D simulation in SAW microfluidics is not a straightforward task.28 For example, when we considered the size of the solution liquid domain in the above-mentioned case, we solved a targeted solution domain with 20 pairs of IDTs (Fig. 1(a)). The IDT area on the horizontal calculation plane would have a side length 20 times more than the acoustic wavelength. If the liquid thickness is in the millimeter range, the computation for 3D simulation in the liquid solution domain would be massive, considering the requirement of mesh resolution to solve an acoustic field: at least six elements (we used second-order Lagrange polynomials for the velocity solution) are needed for one wavelength in the wave-propagating direction.29 Hence, careful model simplification is required to conduct this 3D simulation in a bulk fluid domain.
The theory of boundary-driven streaming, a major type of acoustic streaming in microfluidic devices, is the basis for a solution to this problem.30 Based on this mechanism, boundary-driven streaming is generated from the friction between a vibrating solid boundary and the attached fluid domain. This mechanism mainly confines within a thin viscous boundary layer adjacent to the solid-fluid interface. This layer is equivalent to the Stokes boundary layer with a thickness of , where and are the kinematic viscosity of the fluid and angular frequency of the acoustic wave.31 Here, the wavelength of the acoustic wave is greater than the thickness of the boundary layer. Due to the significant viscous dissipation within the viscous boundary layer, a steady acoustic streaming called Schlichting streaming or inner streaming will be driven in the layer.15,30–32 The inner streaming causes a steady “slip velocity” at the top of the boundary layer and then drives the outer streaming, the so-called Rayleigh streaming, in the bulk fluid upon the boundary layer (Fig. 1(b)). Based on the above-mentioned mechanism of boundary-driven streaming theory, if the “slip velocity” is known, one can solve the outer streaming without solving the 1st-order and 2nd-order acoustic streaming governing equations7,12 outside the viscous boundary layer. In this regard, a 3D simulation has been performed to predict the BAW-induced streaming pattern in the microfluidic channels.33,34 Manor et al. deduced formulas for the 2D “slip velocity” activated by the SAW outside the IDT area decomposed into two components perpendicular to IDT fingers and perpendicular to the substrate.35 However, the SAW propagation in the area containing IDT area needs to account for wave reflection among electrodes and a third vibration component along the IDT fingers because of the transverse and oblique radiations.24–27 Due to this complicated substrate vibration mode in the area involving the IDT, deducing formulas for the “slip velocity” induced by the SAW propagating in and around the IDT in SAW microfluidics is not feasible.
In this work, we present a novel numerical simulation strategy – the “slip velocity method” – to analyze in three dimensions the acoustic streaming activated by an IDT immersed in bulk liquid. By using this numerical simulation method, we can predict the “slip velocity” based on the simulated IDT-induced substrate vibration and the resultant outer acoustic streaming motion in the bulk liquid. The results show that the streaming around the IDT forms two symmetric “stagnation points” at the oil-air interface, where objects floating on the oil could be trapped in a stable fashion, as indicated by solid blue dots on the sides of the IDT in Fig. 1(c). To validate this discovery, we experimentally characterized the flow field and droplet trajectories in the same case as shown in Fig. 1(d). Furthermore, we demonstrate that the IDT-activated acoustic streaming in oil can be an alternative approach of using ultrasound to control the location of an object on an interface,36–39 as well as transporting droplets based on the flow motion in thin oil films activated by other mechanisms such as heat convection40,41 and dielectrophoretic force.42 With this approach, we could manipulate droplets on the surface of an inert, massy fluorinated oil (loading liquid) in a programmable, contactless manner.43 Our numerical simulation strategy, the “slip velocity method”, produces simulation results that are in excellent agreement with the experiment results, indicating that our “slip velocity method” is amenable and reliable. Built upon the simulation and experimental results presented in this article, the performance of the SAW microfluidic devices can be predicted by the “slip velocity method” and tailored for various biological, biochemical, or biomedical applications involving liquid handling.
2. Theory and numerical model
As shown in Fig. 1(a), an IDT fabricated on a 128° Y-X cut LiNbO3 substrate was immersed in the oil. The oil layer was 2mm in depth from the top of the substrate to the oil-air interface. Upon the application of a RF signal to the IDTs, the substrate vibrated because of the piezoelectric effect, which in turn produced SAW in Rayleigh form propagating on the substrate in multiple directions (longitudinal, transverse, and oblique radiations24–26). The resulting leaky acoustic waves drove acoustic streaming in the oil. This section presents the theory and 3D numerical model for the phenomena of IDT-activated acoustic streaming near the IDTs.
2.1. Vibration on surface
The 128° Y-X cut LiNbO3 substrate is a piezoelectric material in which a solid can be strained by applying an electric signal. In piezoelectric materials, the mechanical vibration is governed by the momentum equations for solid mechanics, and the electrical behavior is governed by the charge conservation equation. The coupling relationship between stress, strain, electrical displacement field, and the electric field of a piezoelectric crystal is governed by the following constructive equations in the stress-charge form:
| (1) |
| (2) |
where is the stress vector, is the strain vector, is the electrical displacement, is the electric field, is the elasticity matrix ( is the piezoelectric matrix (), and is the permittivity matrix (). The parameters of the 128° Y-X cut LiNbO3 substrate are listed in the supplementary material.44
2.2. Acoustic streaming in the oil
In this work, the oil is considered to be a compressible linear viscous fluid. The dynamics of the oil, which is a viscous compressible fluid, are governed by the continuity and the compressible Navier-Stokes equations:
| (3) |
| (4) |
where , and are the mass density, dynamic shear viscosity, and dynamic bulk viscosity of fluid, respectively; and are velocity and pressure in the fluid, respectively. By assuming a linear relation between pressure and density, the constitutive relation between and can be written as:12
| (5) |
where is the speed of sound in the fluid. The acoustic waves and resulting fluid motion in our device are driven by the substrate vibration at the frequency of 23.9 MHz, which corresponds to a period of 0.042 μs. The steady streaming observed in our experiments, by contrast, is on a much-slower time scale. Therefore, the fluid motion can be composed of two components: (1) the fast time-scale component with a period equal to the substrate vibration, and (2) the slow time-scale component induced by the viscous dissipation that can be considered as the steady acoustic streaming12. Using Nyborg’s perturbation assumption, the fluid velocity, pressure, and density can be expanded:
| (6) |
| (7) |
| (8) |
Among Eqs. (6)-(8), the variables with subscript refer to the ith order, i.e., ~ O(), where is a small dimensionless parameter:
| (9) |
| (10) |
Since no background flow velocity is present in the fluid domain, the 0th order velocity () is set to be zero in this study. By substituting Eqs. (6)-(10) into the governing equations and only collecting the first-order terms O(), the 1st-order equations that govern the harmonic acoustic field () in the fluid can be obtained as
| (11) |
| (12) |
where j is the imaginary unit, j2 = −1. By repeating the above process, the 2nd-order equations that govern the acoustic streaming in the fluid can be obtained by only retaining and averaging the second-order terms O( ):
| (13) |
| (14) |
where represents the time-averaged variable during an oscillation time period. The mass source term () and the force sources terms () on the right sides of these two equations embody the 1st-order result’s effect on the 2nd-order problem.
2.3. “Slip velocity method” and validation
According to Eqs. (13) and (14), the 1st-order pressure () and 1st-order velocity () are needed to solve the 2nd-order problem. In this work, the driving frequency of the device is 23.9 MHz such that the wavelength in the substrate is around . To meet the requirement for solving the acoustic field (>6 elements per wavelength in the wave-propagating direction),29 the fluid domain ( in Fig.2(a)) of dimensions needs to be divided into at least ~1 million meshes, which leads to an extremely large computational cost. The boundary- driven streaming theory that dominates the IDT-induced acoustic streaming provides an approach to reduce the computational cost.
Fig. 2.
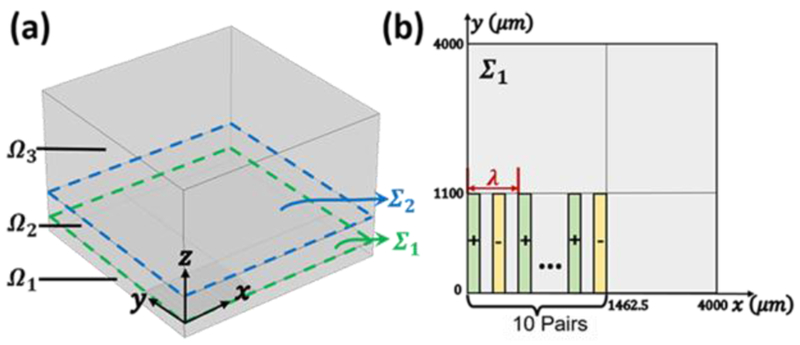
Sketch of the computational domain in our SAW microfluidic device. (a) The geometry and coordinate system created in the simulation modelillustratesthe physics in the domain upon and under a quarter of IDT. Ω1 is the substrate domain 0.5 mm in depth, Ω2 is the inner streaming domain 4δν in depth, and Ω3 is the outer streaming domain 2 mm-4δν in depth. The top view of Ω1, Ω2 and Ω3 is a square with the size of 4×4 mm2. Σ1 and Σ2 indicate the interfaces between Ω1 and Ω2, and Ω2 and Ω3, respectively. (b) Geometry of IDT fingers on the top surface of solid ( Σ1 ). 10 pairs of IDT fingers are distributed on this surface. The finger height, finger width, and the gap between two fingers are 1100 μm, 37.5 μm, and 37.5 μm, respectively, such that the
As shown in Fig. 1(b), the oil domain can be divided into two parts: a thin viscous boundary layer corresponding to the “Stokes boundary layer” (), and the rest of the oil domain outside the thin layer (). The viscous boundary layer with a thickness several times that of , which relates the ratio between the kinematic viscosity of the liquid () and the angular frequency of the SAW (). This is a liquid domain where the viscous dissipation of the leaky SAWs is extremely high due to the non-slipping boundary of the vibrating surface. As given in the second-order equations, Eqs. (13) and (14), the viscous dissipation generates mass and force sources confined mainly within the thin layer and drives a flow called Schlichting streaming or inner streaming inside the layer.30,31 On the other hand, the streaming outside that thin layer in the rest of liquid domain, named Rayleigh streaming or outer streaming, can be considered as driven by the inner streaming because of the continuity of the streaming velocity from the boundary layer to the outside domain.
Using this approximation, the computation of this 3D model can be significantly reduced by solving the acoustic field (1st-order problem) and the inner streaming (2rd-order problem) within the viscous boundary layer. For the oil at 23.9 MHz, the value of is ~405 nm, which is 2.025×104 times thinner than that of the whole oil domain of thickness 2,000 μm. The inner streaming velocity distribution on the top of the viscous boundary layer is captured as the “slip velocity”, which has been conventionally defined in microfluidics as the relative velocity between the fluid and the solid boundary.45,46 The outer streaming can be obtained by solving the original continuity and Navier-Stokes equations, i.e., Eqs. (3) and (4), in the outer streaming domain () and applying the “slip velocity” as the boundary condition at the bottom of this domain. This computation-reduction strategy is called the “slip velocity method”, and the details of the model which employ this strategy are given in the following section.
To validate that the “slip velocity method” can provide a reliable solution, a simple 2D problem (as shown in Fig. S1 in the Supporting Information) is solved by both the “slip velocity method” and the traditional approach. The latter method solves the 1st- and 2rd-order problems in the whole fluid domain. The physics and settings of the 2D simulation are almost the same as those in the work of Guo et al.7 except that the channel width is different. Based on the traditional solution, the horizontal component of the streaming velocity, with a gradient in the vertical direction, dominates the streaming patterns in the viscous boundary layer. The streaming velocity increases from the bottom and reaches a maximum at the top of this layer (Figs. S2(a)-(c) in the Supporting Information). The variation of the normalized value of the horizontal line averages (Eq. S3 in the Supporting Information) of the solutions shows that the horizontal mass source and the curl of the force source are mainly distributed in a layer of thickness near the substrate (Fig. S2(d) in the Supporting Information). Through the convergence analysis comparing the solution from the “slip velocity method” with the traditional solution, we confirmed that the “slip velocity method” yields a solution comparable to the traditional approach while saving the computation time by 53%. According to the parameter sweep for the thickness of the inner streaming domain, — at which the convergence functions (Eq. S4 in the Supporting Information) of the outer streaming velocity reaches a minimum of order 10−2 — is found to be the optimal inner streaming domain thickness for the “slip velocity method” (Fig. S3 in the Supporting Information). The detailed process, results, and discussion of this 2D validation of the “slip velocity” method are stated in Part 1 of the Supplementary Information.
2.4. Numerical model
Fig. 2(a) shows the domain established for the numerical simulation. To reduce the computational effort, we only solved a quarter of the domain as shown in Fig. 1(a) because the IDTs’ vibration is symmetrical in both the x- and y-directions. Domains , and are referred to as the substrate, inner streaming domain, and outer streaming domain, respectively, and have thicknesses of 500 μm, 1.62 μm (), and 2,000 μm, respectively. Boundaries , and are between substrate (solid) and oil (liquid), between inner streaming and outer streaming domains, and the top surface of oil (the interface between oil and air), respectively. The IDT fingers are set on the surface of the substrate (). Based on the above-mentioned approach of boundary-driven streaming, the solution of the “slip velocity method” is in three steps: (a) solving the coupled interaction between substrate vibration in and the acoustic field (1st-order problem) in ; (b) solving the 2nd-order problem in based on the 1st-order result from the former step and obtaining the “slip velocity”; and (c) solving the original governing equations in and applying the “slip velocity” at as the boundary condition to obtain the outer streaming.
COMSOL 5.2a (the COMSOL Group) was employed for the calculation according to the above-mentioned steps. In step (a), the predefined “Solid Mechanics” and the “Electrostatics” physics were used to calculate the piezoelectric substrate’s vibration governed by Eqs. (1) and (2) in . The positive and negative electric potential boundary conditions were applied to, respectively, the green fingers and yellow fingers as shown in Fig. 2(b). The “Thermoviscous Acoustics” physics was used to solve the acoustic field (1st-order problem) governed by Eqs. (11) and (12) in the inner streaming domain . A “Symmetry” boundary condition, which confines the normal component of the 1st-order velocity on the boundary to be zero, was applied to the x-0-z and 0-y-z planes. To eliminate wave reflection, other peripheral boundaries and (oil-oil interfaces) of were set as the “normal impedance” equal to that of the fluid in . A velocity continuity boundary condition was applied to to constrain the two-way coupled interaction between the physics of “Solid Mechanics” and “Thermoviscous Acoustics”. Based on these settings, a “Frequency Domain” solver was used to solve all the above-mentioned physics together at the driving frequency (23.9 MHz). In step (b), the “Laminar Flow” physics was used to solve the 2nd-order problem governed by Eqs. (13) and (14) in . The mass and force source terms were imposed by adding “weak contribution” and “volume force” conditions, respectively. Similarly, a “Symmetry” boundary condition confined the normal 2nd-order velocity at x-0-z and 0-y-z planes to be zero. And an “outlet” boundary condition, which indicates no pressure difference on the two sides of a boundary, was imposed to the oil-oil interfaces, i.e. and the other two peripheral boundaries. This physics is solved via a “Stationary” solver by using the 1st-order solution of the previously mentioned “Frequency Domain” solver. After acquiring the 2nd-order solution, the time-averaged 2nd-order velocity on was obtained as the “slip velocity”. As the last step, the normal continuity and the Navier-Stokes equations (Eqs. (3) and (4)) were calculated in another “Laminar Flow” solver to simulate the outer streaming in . The “slip velocity” found in the former step is applied as the motivation at the bottom of . Meanwhile, a “slip wall” condition, where no normal velocity component exists, is applied to the top of (oil-air interface), and an “outlet” condition was applied to the periphery of (oil-oil interfaces). The last step was to use another “Stationary” solver to solve the “Laminar Flow” physics, ultimately achieving the solution of outer streaming.
3. Materials and methods
The IDTs were fabricated using standard lithography. Five nm chromium and 50 nm gold were deposited on a 128° Y-X cut lithium niobate wafer (Precision Micro-Optics, USA) using Semicore (Kurt J. Lesker Co., PA, USA). The IDT fingers had a 45° intersection angle with the X-axis of the material’s coordinate system to ensure equal wave speed in two orthogonal directions. Silver epoxy was used to connect the wires with fingers on the wafer. The operation frequency was chosen to be 23.9 MHz, which was the resonant frequency of the IDTs with both finger width and finger interval 37.5 μm. The IDT section was 2,925 μm long and 2,200 μm wide. For the integrated SAW microfluidic device shown in Fig. 1(e), the distance between each IDT was 2.8 mm.
A 23.9 MHz sinusoidal AC signal was generated (DG 3012C, Teletronics Technology Corporation, PA, USA), amplified (25A250A, Amplifier Research, USA), and then applied to the IDTs. A relay array (USB24Mx, EasyDAQ, UK) was used to control the power input for individual IDTs. The controlling program was written in Visual C++ (Microsoft Corp., USA).
The wafer with IDTs was immersed in a carrier oil of thickness 2,000 μm. Fluorinert FC-70 oil (Hampton Research Corp., CA, USA) was chosen to be the carrier oil due to its inertness and high viscosity (24×10−3 Pa·s). Additionally, the density and the speed of sound in the oil were set as 1,940 kg/m3 and 640 m/s in this work, respectively. Teflon AF1600 (Dupont Co., DE, USA) was dissolved in the carrier oil to enhance the stability of the droplet trapped in FC-70.
The device was mounted on the stage of an inverted microscope (Eclipse TiU, Nikon, Japan). To visualize the streaming pattern, tracking beads of 30 μm were added into the oil. The motion of the tracking beads was recorded by a high-speed camera at a frame rate of 500 frames per second (fps). The trajectories of the tracking beads, which were considered as the streaming lines of the oil domain, were presented by stacking frames of the recorded videos using ImageJ.
4. Results and discussion
The following sections present numerical and experimental results regarding the substrate vibration, acoustic field, and acoustic streaming in the substrate as well as the oil domain shown in Fig. 2(a). All of the studies were conducted using the resonance frequency of the IDTs (23.9 MHz). Moreover, the droplet trajectories on the oil-air interface were studied, while the dependence of droplet trapping position and oil thickness are also discussed. Finally, a device with IDT arrays was tested for multistep contactless droplet manipulation.
4.1. Substrate vibration and physics in the boundary layer
The substrate vibration in , acoustic field, and inner streaming in the inner streaming domain () were solved together in Step (a). Fig. 3(a) shows the numerical displacement of the substrate at the frequency of 23.9 MHz and input peak-to-peak voltage of 40 V. Under this condition, the peak value of displacement reached ~3.5 nm, and the vibration originating from the IDTs area propagated in the x and y directions. Fig. 3(b) shows the distribution of displacement amplitude and the three decomposed components , and along the x, y, and z axes, respectively, along a cut line (y=100 μm) on the surface of the substrate. As displayed in these curves, the amplitude of , the displacement component along the IDTs fingers which is typically ignored in 2D analysis, is comparable to and . This suggests that its effect on the acoustic streaming motion in the y direction would be non-negligible in this problem.
Fig. 3.
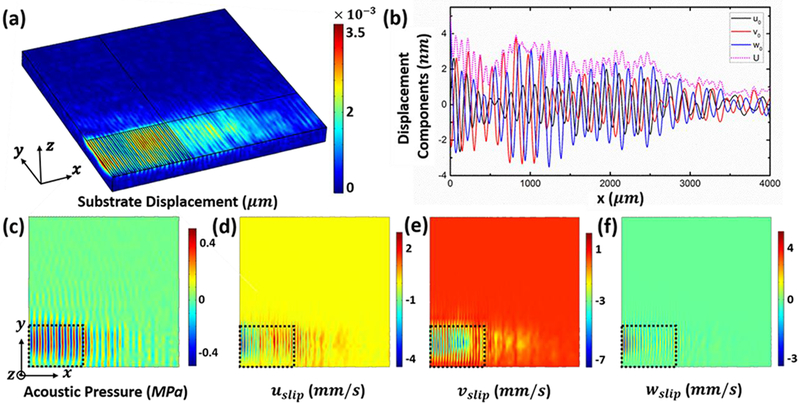
Simulation results in the substrate (Ω1) and inner streaming domain (Ω1) when the IDT was activated at the frequency of 23.9 MHz and the voltage of 40 Vpp. The calculation area is quarter of the IDT area using the symmetry boundary condition. (a) The amplitude of substrate displacement. (b) Distribution of displacement components on a line (y=100 μm) on the floor of the substrate (Σ1). U, u0, v0, and w0 are the amplitude, x component, y component, and z component of displacement, respectively. The value of y displacement component along the fingers (v0) is comparable to other components. (c) Acoustic pressure distribution on the floor of substrate. The acoustic energy is mainly concentrated in the IDT area and propagates along both x and y directions. (d)-(f) The decomposed “slip velocity” in x, y, and z directions on the top of the inner streaming domain (Σ2). The dotted boxes in (c)-(f) indicate the IDT area.
At the substrate-oil interface, the velocity continuity boundary condition was provided to couple the physics in the substrate and oil. Together with this boundary condition, the 1st-order equations (Eqs. (11) and (12)) were solved within the viscous boundary layer to obtain the acoustic pressure. In Fig. 3(c), the acoustic pressure distribution on the substrate-oil interface shows that at the resonance frequency, the acoustic pressure amplitude in the IDT area reached ~0.4 MPa, which was much stronger than the waves propagating outward in the x and y directions. The vibrating fingers generated SAW that leaked into the loading oil as leaky SAW that propagated upwards into the oil. Since each pair of IDT fingers generated SAW propagating in the +x and −x directions simultaneously, there were standing SAWs in the IDTs area and traveling SAWs outside the IDT area that decayed exponentially with the propagation distance. Additionally, the up-and-down vibration of the IDT fingers could also produce a component of BAW directly into the loading oil. Thus, the BAW and standing leaky SAW in the oil upon the IDT area and the traveling leaky SAW in the oil outside the IDT area collectively resulted in a higher acoustic pressure inside the IDTs area than outside the IDTs.
Based on the 1st-order results, the 2nd-order equations were solved in the viscous boundary layer. The 2nd-order velocity on the top of the viscous boundary layer () was the “slip velocity”. Fig.3(d)-(f) show the decomposed “slip velocity” in which , and represent the velocity components in the x, y, and z directions, respectively. Similar to the acoustic pressure distribution, the “slip velocity” in the area above the IDTs was faster than elsewhere. As shown in Fig. 3(d), near the right boundary of the IDTs area was almost positive, while it is mostly negative on the left side of this area. Because of the symmetric boundary condition on the left boundary (), the oil in the outer streaming domain () could be pumped towards +x. As shown in Fig. 3(e), the magnitude of the negative appeared in the IDTs area periodically and reached about −7 mm/s, which was much larger than its maximum positive value (~1 mm/s). As dominated the y component of the outer streaming, the oil in the outer streaming domain was attracted in the −y direction toward the IDT. This phenomenon could be the key to the formation of the counter vortex in the outer streaming domain.
4.2. Streaming around an IDT
By setting the velocity at the bottom () equal to the “slip velocity”, the outer streaming in the oil domain () was obtained by solving Eqs. (3) and (4). Fig. 4(a) shows the numerical result of the 3D outer streaming field. Red streamlines and black arrows indicate streaming velocity distribution and direction, respectively. The streaming in the x-0-z, 0-y-z and x-y-2000 μm planes is plotted to illustrate the intuitive formation of 3D outer acoustic streaming as shown in Figs. 4(g), (e), and (b), respectively. Figs. 4(g), (e), and (c) show the corresponding streamlines of recorded beads (1.9 g/cm3, 30 μm in diameter) on these three planes, which is obtained by stacking a series of frames.
Fig. 4.
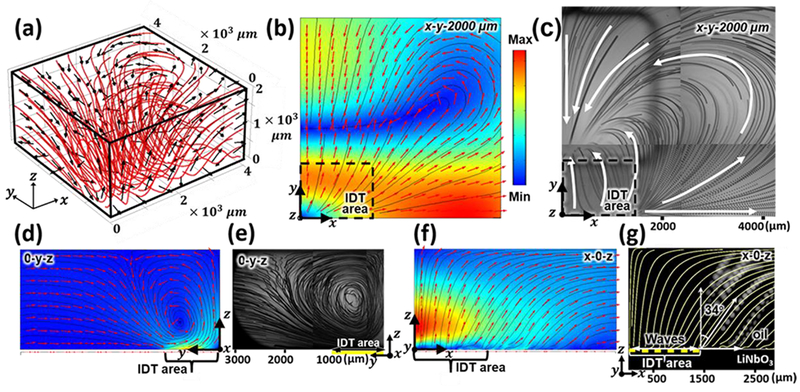
Numerical and experimental results of acoustic streaming in an outer oil domain (Ω3) in our SAW microfluidic device.. (a) Numerical results showing outer streaming pattern in the 3D domain. The streaming patterns on three typical planes, i.e., (b) x-y-2000 μm, (d) 0-y-z, and (f) x-0-z planes, are plotted for illustration. Experimental images showing streamlines on (c) the x-y-2000 μm plane and (e) the 0-y-z plane. A counter flow agrees with the numerical results. (g) Experimental image showing streamlines on the x-0-z plane visualized using 105-μm fluorescent particles (white dotted lines), which matches with the corresponding numerical streamlines (yellow solid lines). The result shows that the direction of the pumped flow is at an angle of 34° to z-axis.
As predicted in the previous section, the outer streaming on x-0-z (Figs. 4(f) and (g)) was drawn to flow in the +x direction by the . The mechanism is that the IDT-activated SAW propagating in x direction leaked into the oil and pumped out the loading oil upon it. As can be seen in Fig. 4(g), the numerical streamline (yellow) was captured from the streaming patterns in Fig. 4(f). Theseoverlapped with the experimentally measured flow directions from a side view (the trajectories of the white beads). Both the experimental and simulated results indicate that the flow direction of the pumped-out oil flow had a 34° angle with the z direction. This angle is much larger than the Rayleigh angle (10° for incidence from LiNbO3 to oil), which is the angle of the leaky wave propagation and initial streaming direction when the SAW first met liquid outside the IDT area.47 Considering that the SAW begins to leak into the liquid at its initial position, each IDT actually serves as a line source that keeps generating the cylindrical waves. These waves interfere with the leaky waves based on the Huygens-Fresnel principle.48 Thus, the interferential waves have a larger angle compared to the individual leaky waves on the edge of IDTs area. From the prediction, on the 0-y-z plane, the oil was drawn in the -y direction towards the IDTs area by . Due to the symmetric motion of the IDT, the oil was ejected to the oil-air surface near the x=0 boundary and flowed to the +y direction. On the oil-air boundary, the flow in the +y direction inside the IDT area blocked the flow in the opposite direction outside the IDT area and surged towards the substrate together. As a result, a “counter flow” formed, and this result matched well with the measured streamline shown in Fig. 4(e). As seen from the x-y-2000 μm plane, the counter flow obstructed the backflow in the -y direction, thereby forming a “stagnation point”, i.e., the hydrodynamic trap for floating objects at the side of the IDTs. This phenomenon was also confirmed experimentally where the particle trajectories in the first quadrant on the oil-air surface were recorded and stacked (Fig. 4(c)). The stacked image shows that the streamlines on the oil-air interface ended at the “stagnation point” on the sides of the IDTs, and this experimental observation agrees with the simulated streamlines. In addition, streamlines at 100 μm and 1,000 μm oil depth further confirm the consistency between simulation and experiment (Fig. S5 in the Supporting Information). The measured oil-air surface streamline driven by a whole IDT was also obtained as shown in Fig. 1(d). From the streamlines in the four quadrants, we found that the streamlines were distributed almost symmetrically about both the x-axis and y-axis. The main reason for not having strict symmetric distribution may be the uneven distribution of the tracking beads in the oil. The IDTs pumped the loading oil in the +x and −x directions and created two counter flows in the +y and −y planes, and thereby generated two symmetric stagnation points. With these two points, the object afloat on the oil may have been trapped on either side of the IDTs depending on its initial position. Experiments were carried out to confirm the prediction. The result is discussed in the next section.
4.3. Droplet trajectory around an IDT
On the basis of the acoustic streaming velocity distribution on the oil-air surface, we numerically estimated the trajectories of droplets floating on this 2D plane. If considering a tiny particle immersed in the liquid, the drag force, which is proportional to the relative velocity between the particle velocity and streaming velocity, can be simply modeled as7
| (15) |
where is the dynamic viscosity of the oil, is the radius of the particle, is the streaming velocity, and is the particle velocity. Since the physics behind the relative movement between the droplets and the incompatible liquid is complicated and is not the main target of this work, Eq. (15) was used to approximate the drag force of the droplet floating on the loading liquid. In this way, the droplet trajectory was approximated by the COMSOL interface “Particle tracing for fluid flow” and solved by a “Time Dependent” study. 100 water droplets with 5 μL in volume were released from initial positions in a 2D area, as shown in Fig. 5(a). The simulation results show that all of the droplets floating on the oil gradually concentrated to the trap (Fig. 5(a)). From the droplets’ trajectories, we found that the droplets at the left side of the domain moved faster towards the trap positions because the drag force at this area was greater.
Fig. 5.
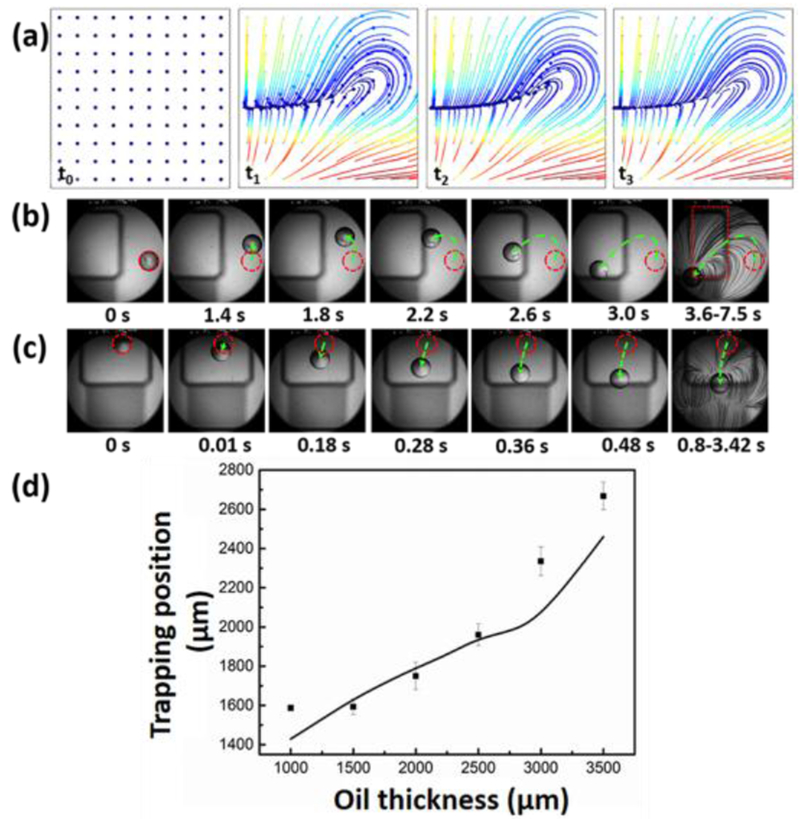
Droplet tracing in our SAW microfluidic device. (a) Numerical results showing droplets’ trajectories over time driven by the 2D streaming pattern in the x-y-2000 μm plane shown in Fig. 4(b). Each dot represents the center of a droplet, and their initial positions are indicated as shown in Fig. 5(a-t0). The results show that all the droplets moved towards the trap in the presence of the streaming. Experimental images show the trajectory of a droplet released (b) at the right side of the IDT and (c) at the top side of the IDT. The red dashed circles indicate the initial positions in each case and the green lines indicate the trajectories of the droplet from the initial position to the position shown on each figure. (d) Plot showing the dependence of the trapping position (stagnation point) on the oil thickness measured by experiment (spots and error bars) and simulation (line). The position is defined by the distance from the droplet center to the IDT center.
In an experiment, we measured the trajectories of two droplets (5 μL) released initially at two different positions. One droplet was first released at an initial position as shown in Fig. 5(b); in the presence of the acoustic streaming, it was gradually pushed away from the IDT in the +x direction, then drawn back to the side of IDTs by the backflow, and finally blocked by the counter flow to stop at the “stagnation point.” In this case, the device took 3.6 seconds to move the droplet from the initial position to the “stagnation point.” Afterwards, the droplet stabilized as shown in the rightmost panel of Fig. 5(b). The results indicate that the droplet stabilized at the “stagnation point” even when the IDTs kept generating streaming in the loading oil. As a comparison, the other droplet was released on the side of the IDT as shown in Fig. 5(c). Since the x-coordinate of the initial droplet position was close to the coordinate at the trap, this droplet was drawn immediately towards the “stagnation point” and only took 0.8 s to stabilize. Dynamic processes showing Figs. 5(a)-(c) can be seen in the Supplemental Movies S1–S3, respectively.
Compared with the droplets at the other initial positions, the droplet released at the lateral side of the IDT (the case in Fig. 5(c)) had moved less than that released far away from the IDT. Therefore, we chose the lateral side of the IDT, as the initial position for multi-step, contactless droplet manipulation. To optimize the device’s design for subsequent droplet manipulation, we quantitatively characterized the trapping behavior of the device. Fig. 5(d) shows the change of trapping positions as a function of oil thickness. The trapping position was defined as the y-coordinate of the trapped droplet center, according to the coordinate system shown in Fig. 1(d). As the oil thickness was increased from 1,000 μm to 3,500 μm, the “stagnation point” for hydrodynamically trapping of droplets moved further from the IDTs, which suggests that the oil thickness should be as thin as possible if the trap is intended to be closer to the IDTs. However, if the oil thickness is too thin, the droplet might attach to and be stuck at the substrate since the droplet immerses partly in the oil. Through the experimental characterization, 2,000 μm was found to be the optimal oil thickness for the device used in this work.
4.4. Droplet manipulation by IDT array
Since each IDT can create two symmetric “stagnation points” as hydrodynamic traps for droplet manipulation, a well-designed IDT array could contain multiple traps. As shown in Fig. 1(e), we designed a device where the IDTs were arranged as a 1×10 array on a 128°Y-X cut LiNbO3 wafer. The IDT fingers were inclined at 45° relative to the X-axis of the material’s coordinates. The red arrows in Fig. 6 indicate that the IDTs were being activated in every step. By activating the IDT following the order as shown in Fig. 6, we moved the green droplet up and down on the oil surface, which demonstrates on-demand droplet manipulation. The result shows that our device moves droplets on the oil surface in a controllable manner by alternating the IDTs in an array in a given order. This movement will enable various biological and biomedical applications where on-demand liquid handling is necessary.
Fig. 6.

Droplet manipulation achieved using a SAW microfluidic device with 1×10 IDT arrays. The red arrows and dotted boxes point out the single IDT that is being activated to manipulate the green droplet in every step. Depending on its initial position, the green droplet will be trapped at either side of the activated IDT closer to the droplet.
5. Conclusions
In this article, we developed a “slip velocity method” which performs 3D analysis in SAW microfluidics and significantly reduces the computation time of the 3D acoustic field solution. In particular, we solved the 1st-order and 2nd-order equations in the viscous boundary layer with the substrate displacement solved together as the actuation at the solid-liquid boundary. The 2nd-order velocity on the top of the boundary layer was captured as the “slip velocity” which was used as an actuation to calculate the outer streaming. Experiments showed acoustic streaming on several typical planes to verify the simulation results. It was found that the prediction of the simulation agreed with the experimental results. Further, we discussed the effects of some parameters on the trapping velocity and trap position based on the simulation and experimental results. On the strength of these findings, we fabricated a SAW microfluidic device with integrated IDT arrays to demonstrate stable, contactless droplet manipulation.
Besides the acoustic streaming in the oil, we also discovered streaming motion inside the droplet due to the relative movement of the loading oil and droplet. This discovery indicates that this non-contact droplet handling system has potential for on-chip sample handling. After reaching the “stagnation point,” the droplet stops moving but the oil still streams. The oil flows below the droplet and drives the streaming inside the droplet. The shape and immersion depth of the droplet depends on many factors, such as the surface tension at the droplet interface, the size of the droplet, and the original vertical distance between the position of the droplet to the oil-air interface.
Supplementary Material
Acknowledgements
We acknowledge support from the National Institutes of Health (R01HD086325, R44GM125439, and R33CA223908), the National Science Foundation (ECCS-1807601), and the National Natural Science Foundation of China (Grant Nos. 11774166 and 11474161).
Footnotes
Conflicts of interest
There are no conflicts to declare.
References
- 1.Nama N, Huang P-H, Huang TJ and Costanzo F, Lab Chip, 2014, 14, 2824–2836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ahmed D, Mao X, Juluri BK and Huang TJ, Microfluid. Nanofluidics, 2009, 7, 727–731. [Google Scholar]
- 3.Huang P-H, Nama N, Mao Z, Li P, Rufo J, Chen Y, Xie Y, Wei C-H, Wang L and Huang TJ, Lab Chip, 2014, 14, 4319–4323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mao Z, Li P, Wu M, Bachman H, Mesyngier N, Guo X, Liu S, Costanzo F and Huang TJ, ACS Nano, 2017, 11, 603–612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Collins DJ, Khoo BL, Ma Z, Winkler A, Weser R, Schmidt H, Han J and Ai Y, Lab Chip, 2017, 17, 1769–1777. [DOI] [PubMed] [Google Scholar]
- 6.Collins DJ, Ma Z and Ai Y, Anal. Chem, 2016, 88, 5513–5522. [DOI] [PubMed] [Google Scholar]
- 7.Guo F, Mao Z, Chen Y, Xie Z, Lata JP, Li P, Ren L, Liu J, Yang J, Dao M, Suresh S and Huang TJ, Proc. Natl. Acad. Sci, 2016, 113, 1522–1527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yeo LY and Friend JR, Biomicrofluidics, 2009, 3, 012002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Du XY, Swanwick ME, Fu YQ, Luo JK, Flewitt AJ, Lee DS, Maeng S and Milne WI, J. Micromechanics Microengineering, 2009, 19, 035016. [Google Scholar]
- 10.Shilton RJ, Travagliati M, Beltram F and Cecchini M, Adv. Mater, 2014, 26, 4941–4946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Alghane M, Fu YQ, Chen BX, Li Y, Desmulliez MPY and Walton AJ, J. Appl. Phys, 2012, 112, 084902. [DOI] [PubMed] [Google Scholar]
- 12.Nama N, Barnkob R, Mao Z, Kähler CJ, Costanzo F and Huang TJ, Lab Chip, 2015, 15, 2700–2709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fu C, Quan AJ, Luo JT, Pang HF, Guo YJ, Wu Q, Ng WP, Zu XT and Fu YQ, Appl. Phys. Lett, 2017, 110, 173501. [Google Scholar]
- 14.Meacham JM, Varady MJ, Degertekin FL and Fedorov AG, Phys. Fluids, , DOI:10.1063/1.1921249. [Google Scholar]
- 15.Wiklund M, Green R and Ohlin M, Lab Chip, 2012, 12, 2438–2451. [DOI] [PubMed] [Google Scholar]
- 16.Fu YQ, Luo JK, Nguyen NT, Walton AJ, Flewitt AJ, Zu XT, Li Y, McHale G, Matthews A, Iborra E, Du H and Milne WI, Prog. Mater. Sci, 2017, 31–91. [Google Scholar]
- 17.Meacham JM, Durvasula K, Degertekin FL and Fedorov AG, Sci. Rep, 2018, 8, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ahmed D, Ozcelik A, Bojanala N, Nama N, Upadhyay A, Chen Y, Hanna-Rose W and Huang TJ, Nat. Commun, 2016, 7, 11085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ren L, Chen Y, Li P, Mao Z, Huang P-H, Rufo J, Guo F, Wang L, McCoy JP and Levine SJ, Lab Chip, 2015, 15, 3870–3879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ren L, Yang S, Zhang P, Qu Z, Mao Z, Huang P, Chen Y, Wu M, Wang L and Li P, Small, 2018, 1801996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wu M, Ouyang Y, Wang Z, Zhang R, Huang P-H, Chen C, Li H, Li P, Quinn D, Dao M, Suresh S, Sadovsky Y and Huang TJ, Proc. Natl. Acad. Sci, 2017, 114, 10584–10589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Muller PB, Barnkob R, Jensen MJH and Bruus H, Lab Chip, 2012, 12, 4617–4627. [DOI] [PubMed] [Google Scholar]
- 23.Muller PB and Bruus H, Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys., 2015, 92, 1–13. [DOI] [PubMed] [Google Scholar]
- 24.Koskela J, Knuuttila JV, Makkonen T, Plessky VP and Salomaa MM, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2001, 48, 1517–1526. [DOI] [PubMed] [Google Scholar]
- 25.Inoue S, Nakamura K, Nakazawa H, Tsutsumi J, Ueda M and Satoh Y, IEEE Int. Ultrason. Symp. IUS, 2013, 1953–1956. [Google Scholar]
- 26.Holmgren O, Makkonen T, Knuutila JV, Kalo M, Plessky VP and Steichen W, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2007, 54, 861–869. [DOI] [PubMed] [Google Scholar]
- 27.Salim ZT, Hashim U and Arshad MKM, IEEE ICSE Proc, 2016, 5–8. [Google Scholar]
- 28.Kiebert F, Wege S, Massing J, König J, Cierpka C, Weser R and Schmidt H, Lab Chip, 2017, 17, 2104–2114. [DOI] [PubMed] [Google Scholar]
- 29.Łodygowski T and Sumelka W, J. Theor. Appl. …, 2006, 849–865. [Google Scholar]
- 30.Sadhal SS, Lab Chip, 2012, 12, 2292–2300. [DOI] [PubMed] [Google Scholar]
- 31.Manor O, Yeo LY and Friend JR, J. Fluid Mech, 2012, 707, 482–495. [Google Scholar]
- 32.Rayleigh Lord, Philos. Trans. R. Soc. London, 1884, 175, 1–21. [Google Scholar]
- 33.Lei J, Hill M and Glynne-Jones P, Lab Chip, 2014, 14, 532–41. [DOI] [PubMed] [Google Scholar]
- 34.Lei J, Glynne-Jones P and Hill M, Phys. Fluids, 2016, 28, 012004. [Google Scholar]
- 35.Manor O, Yeo LY and Friend JR, J. Fluid Mech, 2012, 707, 482–495. [Google Scholar]
- 36.Melde K, Mark AG, Qiu T and Fischer P, Nature, 2016, 537, 518–522. [DOI] [PubMed] [Google Scholar]
- 37.Li H, Friend JR and Yeo LY, Phys. Rev. Lett, 2008, 101, 1–4. [DOI] [PubMed] [Google Scholar]
- 38.Rogers P, Gralinski I, Galtry C and Neild A, Microfluid. Nanofluidics, 2013, 14, 469–477. [Google Scholar]
- 39.Zhou Q, Sariola V, Latifi K and Liimatainen V, Nat. Commun, 2016, 7, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Davanlou A, Cho HJ and Kumar R, Microfluid. Nanofluidics, 2016, 20, 1–10. [Google Scholar]
- 41.Basu AS and Gianchandani YB, J. Microelectromechanical Syst, 2009, 18, 1163–1172. [Google Scholar]
- 42.Velev OD, Prevo BG and Bhatt KH, Nature, 2003, 426, 515–516. [DOI] [PubMed] [Google Scholar]
- 43.Zhang SP, Lata J, Chen C, Mai J, Guo F, Tian Z, Ren L, Mao Z, Huang P-H and Li P, Nat. Commun. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kannan T, Dr. Diss, 2006, 1–115. [Google Scholar]
- 45.Li B and Kwok DY, Phys. Rev. Lett, 2003, 90, 4. [DOI] [PubMed] [Google Scholar]
- 46.Lu G, Duan YY and Wang XD, Colloids Surfaces A Physicochem. Eng. Asp, 2015, 486, 6–13. [Google Scholar]
- 47.Frommelt T, Gogel D, Kostur M, Talkner P, Hänggi P and Wixforth A, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2008, 55, 2298–2305. [DOI] [PubMed] [Google Scholar]
- 48.Devendran C, Collins DJ, Ai Y and Neild A, Phys. Rev. Lett, 2017, 118, 1–6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


