Connectivity in fMRI: Blind Spots and Breakthroughs

Abstract

In recent years, driven by scientific and clinical concerns, there has been an increased interest in the analysis of functional brain networks. The goal of these analyses is to better understand how brain regions interact, how this depends upon experimental conditions and behavioral measures and how anomalies (disease) can be recognized. In this work we provide, firstly, a brief review of some of the main existing methods of functional brain network analysis. But rather than compare them, as a traditional review would do, instead, we draw attention to their significant limitations and blind spots. Then, secondly, relevant experts, sketch a number of emerging methods, which can break through these limitations. In particular we discuss five such methods. The first two, stochastic block models and exponential random graph models, provide an inferential basis for network analysis lacking in the exploratory graph analysis methods. The other three address: network comparison via persistent homology, time-varying connectivity that distinguishes sample fluctuations from neural fluctuations and, network system identification that draws inferential strength from temporal autocorrelation.

I. Introduction

In the last two decades, interest has surged in network (NW) analysis across a wide range of disciplines. In fact modern network studies have a long history, stretching back at least 5 decades ¹ in a number of disciplines, with the best known being perhaps, Physics [1] and Sociology [2]; but others include: Economics (diffusion of innovations), Epidemiology (disease transmission), Electrical Engineering (power grids), Civil Engineering (transport), and still others.

Several factors have led to the recent widespread interest. The most obvious is that network data has become readily available to almost all disciplines due to advances in sensing and measurement technologies and storage. This has led to a demand for deeper understanding of NWs which in turn has led to advances such as: graphical analysis of network architecture e.g. small world NWs [3], methods of study of network dynamics [4]; and ultimately to the emergence of a network science [5] aimed at understanding network structure and function.

In neuroimaging, brain network study has been dominated by resting-state functional magnetic resonance imaging (rs-fMRI), where blood oxygen level dependent (BOLD) signals are measured in subjects at rest. A number of such rs-studies have found spontaneous activity that is highly correlated between multiple brain regions (e.g. [102], [103]). Because of this, the study of functional connectivity, or the undirected association between two or more fMRI time series, has come to the forefront of research efforts in the field. Here the time series can be obtained from individual voxels, [104], [105], [106], averaged over pre-specified regions of interest [107], or estimated using independent component analysis [108].

Thus network literature is then, in the midst of a classic exponential explosion in volume and it is not possible for any scholar or lab or even subdiscipline of scholars to keep up with it. How then to proceed? The classic leakage (‘diffusion of innovations [6]’) ² mechanism between disciplines ensures that significant new approaches will slowly make their way to other knowledge territories [8]. This paper is meant to be an example of, as well as to hopefully hasten, that process.

This short review paper has two major objectives. Firstly to briefly review some of the major current approaches in brain connectivity with the aim of highlighting significant blind spots; issues that are holding up development but being ignored. And secondly to sketch some emerging techniques that can break through these blind spots.

A. What is a Functional Network?

But before we get to this we must address the fundamental question of definition. This is necessary because unfortunately some current language is misleading if not confused. What then is a NW? What is the difference between a system and a NW? What is network structure? What is network function? What is network dynamics? What is the difference between ‘time-varying’, ‘dynamic’ and fluctuating?

We follow a terminology, more than half a century old, developed in areas such as Mathematical System Theory, Control Engineering, Statistical Signal Processing and Physics. We are also informed by the long running concern in the neurosciences with structure versus function.

A network consists of nodes connected by links ³. For simplicity, in a brain activity network, we take a node to be an anatomical parcel carrying a scalar or vector time series (see [9] for a more detailed discussion). This definition implies an underlying architecture showing how the nodes are connected. But it says nothing about interactions between nodes. Now let us now recall the following definition: a system is a set of interacting components forming a complex whole. Joining these two we get what we will call a functional network (fNW): a set of interacting nodes. A particular task may involve only a subset of connected nodes so a single network will be capable of performing many different functions.

There are then two aspects to a fNW: the ‘map’ or architecture showing how nodes are connected and the dynamics (time-lagged interaction) between the nodes, which shows how the fNW is used, namely its function. We prefer to use ‘structure’ solely for anatomical NWs. So anatomical NWs only have architecture while fNWs have both architecture and dynamics. The architecture of the fNW will vary with the task and in general be a subset of the architecture of the whole NW.

To understand the function of a fNW (carrying out a particular task) we thus need to understand the architecture and the dynamics. Clearly the architecture will constrain the dynamics in various ways, but just knowing the architecture is not enough to understand the function. This is why graph analysis methods, which only deal with architecture, cannot provide a complete understanding of fNW function.

Three pairs of words are used to distinguish between constancy versus change with time: time-invariant versus time-varying (TV); static versus dynamic; stationary versus non-stationary. In everyday language the first of each pair are used interchangeably as are the second of each pair and this has led to more than just semantic confusion because their technical uses are not interchangeable.

We need to describe time change for: nodal signals, network architecture, network function. The following mutually exclusive terminology is standard in the disciplines referred to above. For general discussion we say that nodal signals, architecture, and dynamics, may fluctuate over time. Specific terminology is as follows: nodal signals may be statistically stationary ⁴ or statistically non-stationary; architecture may be time-invariant or time-varying; network function can be static or dynamic and the dynamics may be statistically stationary or statistically non-stationary. Again note that ‘dynamics’ refers to the time-lagged interaction between nodal signals.

Unfortunately, it seems that in incorrectly using the term ‘dynamic’ connectivity for TV connectivity, the research community thinks it is treating dynamics whereas it has been ignoring it, i.e. failing to deal with time-lagged nodal interaction.

B. Constructing Functional Networks

To provide some context for the paper we sketch a standard approach to constructing a network model from rs-fMRI data, which broadly involves four steps:

1. Define the network nodes: Divide the brain into regions of interest (parcels representing network nodes) and collate the data within to give a single representative time series at each node.

2. Construct the network: Estimate whether the link between each pair of nodes is active (architecture), and the strength of link if it is active (dynamics).

3. Network Interpretation: Analyze the network architecture and dynamics within each individual network.

4. Network Comparison: Assess similarity and differences in architecture and dynamics between individual networks.

We note the crucial need in steps 1, 2, to deal comprehensively with potential artefacts [16],[17].

As explained below, Sections II,III deal with step 3. Sections IV,VI deal with step 2. Section V deals with step 4.

C. Omissions

Omitted areas include those already well surveyed or those whose blind spots have not been tackled. Graph analysis⁵ methods are well surveyed e.g. see [12]. Those badly in need of (whole paper) reviews include: Granger causality, see [10] and the critique in [11]; multi-modal methods, see [15]; software, a starting point is the recent controversy over major fMRI software ‘bugs’ as discussed in [14].

D. Blind Spots and Breakthroughs

The remainder of the paper splits naturally into two parts. In part I, consisting of section II,III, it is assumed that link strengths are given. In part II, consisting of sections IV,V,VI link strengths are estimated from the nodal time series data. We now introduce each section briefly.

While graph analysis methods have received intense attention in fNW modeling they are only exploratory, whereas for scientific and clinical use one needs to do inference, a problem that has been poorly addressed. Both stochastic block models (section II) and statistical network models (section III) provide an inferential basis for structural modeling.

Although time-varying connectivity has rapidly gained attention, early warnings of the need to find ways to distinguish sampling fluctuation from neural fluctuation [107] have been ignored. This can only be done from a principled inferential basis. Such methods are surveyed in section IV. Network comparison is fundamental for distinguishing abnormal from normal. Graph analysis methods may be able to do that if the networks have the same number of nodes and links. But what has been ignored, is that in practice, the networks to be compared have differing numbers of nodes and links as well as spatial and temporal resolutions. Standard graph analysis methods cannot handle this. But Persistent Homology (section V) can. As discussed above, function is intimately concerned with inter-nodal interaction and hence with nodal memory i.e. dynamics. But the current linear correlation-based connectivity analysis cannot deal with this. To do so one must take autocorrelation into account and until recently it has been ignored. Emerging approaches that include it, are discussed in section VI. Section VII contains conclusions.

II. Stochastic Block Models

A. A Short History

Stochastic block models (SBMs) originate from the social science objects called "sociograms" [18]. These social networks were later modeled by adjacency matrices. The representation of block models came with the idea that within a network, nodes could be grouped in communities, or clusters or blocks, and the nodes belonging to the same group would have similar structure or pattern of connections with the nodes of another community. [19] defined a block as a set of nodes which share a common "equivalence structure" with nodes in another block. In stochastic block models randomness is introduced, and this pattern of connections or equivalence structure is "stochastic", therefore providing a more flexible definition. The pattern of connections is represented by a probability of connections with other groups: given that two nodes e.g. i and j are from blocks A and B, the presence of a link between the nodes is governed by the probability : p_AB. SBMs initially proposed by Snijders and Nowicki [20] are today ubiquitous in many network characteristics estimation and analysis tasks, including community detection (see section II-C). The classical model generates simple non weighted networks and only allows a node to be assigned to a single block, but extensions have been developed (see below).

B. Definitions and Overview

The SBM is a generative model for graphs that takes as inputs n nodes, a partition of the nodes into B non overlapping blocks (or communities) C = C₁, C₂, ⋯,C_B, and a B × B matrix of probability P_kl specifying the probability of connection between nodes in C_k and C_l.

This model has the advantages of a link generative model, making assumptions explicit, clarifying interpretation of the parameters, and permitting the use of statistical techniques such as likelihood scores for model comparison: given a SBM M and some observed graph G, one can compute P(G∣M). However, estimation of the model from data can be costly.

Note that if P_kl = p for all k, l, the graphs generated are Erdös-Rényi random graphs. If P_kk ≥ P_kl for k ≠ l, then the model generates assortative communities, otherwise the communities are dissortative.

Figure 1 illustrates the type of graph obtained from a SBM model with five blocks.

Figure 1.

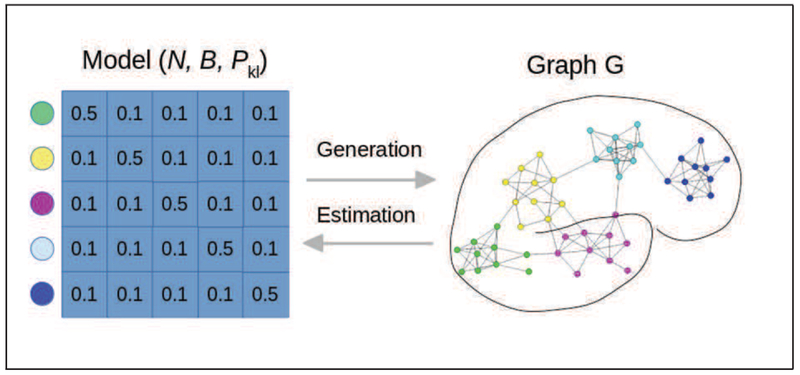
Stochastic Block Model: the model allows the generation of assortative communities, for example here the probability of connection is 0.5 within communities (i.e. blocks), and 0.1 across communities. The model consists of the number of nodes N, the partition of the nodes B, and the matrix of connection probability P_kl. normalsize

C. Use of SBMs for Community Detection

There are many deterministic algorithms to detect communities (or equivalently clusters) of the nodes of the graph (minimum cut, hierarchical clustering, Girvan-Newman algorithm [21], modularity maximization). Loosely speaking most algorithms attempt to maximize the number of connections within clusters and minimize it across clusters. Modularity (such as Newman and Girvan’s [21]) measures quantify the quality of the separation of the communities and are used as objective functions to estimate the clustering. The choice of the number of clusters (communities) is a critical element of any community detection attempt and algorithms often require this number to be fixed. The Spectral [22] and Fast Louvain [23] are two widely used examples of estimating this number.

Because SBMs can generate a wide range of networks, they are useful statistical models for community detection when the parameters of the model can be sufficiently accurately estimated. The estimation generally relies on maximum likelihood techniques [20], optimized with variational Bayes in the work of [24]. The number of blocks can be estimated with a number of techniques such as AIC and BIC, but the Integrated Classification Likelihood is well adapted in this context [24].

While these techniques have already shown their usefulness, it is worth noting the limitations of SBMs for the recovery of graph structure. Because SBMs are simple they may not necessarily provide a good and/or insightful model of actual fMRI data, and technically may not be able to recover fully or partially the true nodal partition [25]. We discuss below whether these models can be useful specifically for fMRI network detection given the characteristics of these signals.

D. Current use in fMRI Studies

The use of SBMs is only emerging in fMRI, and only a few studies have so far used this aproach for estimation of communities and of graph characteristics, despite the fact that SBMs are a widespread fundamental graph statistical tool. The reasons for this limited use are likely due to:

• the difficulty of estimation in particular for a large number of nodes and communities, and the competition of established deterministic approaches,

• the lack of well-documented libraries adapted for estimation on fMRI data,

• the limitations of the original model to unweighted graphs and non-overlapping communities, making this tool better adapted to anatomical connectivity [26]

Nevertheless SBMs are now being investigated by some authors for brain functional data. For instance, Pavlovic’s work extends the original SBM from Snijders and Nowicki [20] and from Daudin and colleagues [24], to multi-subject and repeated measure analyses where a common group level network is estimated while allowing inter-subject variations, as well as providing statistical tests for inference between populations. In a recent study, Rajapakse and colleagues [27] used the Human Connectome Project resting state data and show that SBM and degree corrected SBM (dc-SBM) have higher likelihood measures compared to power law and exponential networks. It should be noted that these works may need to be further pursue and replicated to better assess the usefulness of SBMs. These techniques are unlikely to be widely used until the methods are included into well maintained and well tested libraries (see for instance [28]. In addition, it is unclear how these methods will be able to scale if the number of region of interests is larger than the few hundreds tested for instance in [27], or to adapt to more complex temporal structure that may be needed for instance in longitudinal studies.

E. Future use in fMRI

Because SBMs are being extended in several ways, in particular to weighted graphs, degree corrected, and overlapping communities, its usefulness for fMRI data is likely to grow in the future. In the long term, the benefit of a formal statistical link generative model will outweigh the cost of additional computation implied by the use of these models. This however will only take place if well-documented, well-tested and efficient software libraries are developed and released, and if the theoretical limitations are clearly communicated to and understood by the brain imaging community. Finally, as with other models, there is a critical need to develop the validation frameworks for SBM and extensions, both with simulated data and more importantly with the convergence of biological results in specific neuroscience questions. Further use of SBMs also needs much tighter collaborations with cognitive neuroscientists, demonstrating their usefulness in providing answers to neuroscience or cognitive neuroscience questions that current methods cannot.

III. Statistical Network Models

Following the discussion in the introduction brain NW analysis necessitates a holistic multivariate modeling framework that allows assessing the effects of multiple variables of interest and topological NW features on the overall NW structure. That is, if we have

$$\text{Data}\{\begin{array}{c}{Y}_i:\text{network of participant}i\hfill \\ X_i:\text{covariate information (metrics, demographics,}\dots )\hfill \end{array}\phantom{\}}$$

we want the ability to model the probability density function of the network given the covariates P (Y_i∣X_i, θ_i), where θ_i are the parameters that relate the covariates to the NW structure. Strides in developing such a framework have been made both with exponential random graph models (ERGMs) [29],[30],[31],[32] and mixed models [33], but more work is needed on refining these approaches, and developing new ones.

We briefly delineate these two analytical approaches for brain NW analysis in sections III.A and III.B.

A. Exponential Random Graph Models (ERGMs)

ERGMs have the form of the regular exponential family given below:

$$P_{\theta }(Y=y\mid X)=\kappa (\theta {)}^{-1}\text{exp}\left\{{\theta }^{\mathrm{T}}\mathrm{g}(y,X)\right\}.$$ (1)

Here Y is an n × n (n nodes) random symmetric adjacency matrix representing a brain network from a particular class of NWs, with Y_ij = 1 if a link exists between nodes i and j and Y_ij = 0 otherwise. The probability mass function (pmf) (P_θ (Y = y∣X)) of this class of NWs is a function of the prespecified network features defined by g(y, X). This vector of prespecified explanatory metrics can consist of covariates that are functions of the network y (e.g., number of paths of length two) and nodal covariates (X) (e.g., brain location of the node). The parameter vector θ, associated with g(y, X), quantifies the relative significance of the network features in explaining the structure of the network after accounting for the contribution of all other network features in the model. More specifically, θ indicates the change in the log odds of a link existing for each unit increase in the corresponding explanatory metric. If the θ value corresponding to a given metric is large and positive, then that metric plays a considerable role in explaining the network architecture and is more prevalent than in the null model (random network with the probability of a link existing (p)= 0.5). Conversely, if the θ value is large and negative, then that metric still plays a considerable role in explaining the network architecture but is less prevalent than in the null model. Consequently, inferences can be made about whether certain local features/substructures are observed in the network more than would be expected by chance [34], enabling hypothesis development regarding the biological processes that produce these structural properties. The normalizing constant κ (θ) ensures that the probabilities sum to one. This approach allows representing the global brain NW structure by locally specified explanatory metrics, thus providing a means to examine the nature of NWs that are likely to emerge from these effects.

ERGMs provide a powerful approach for modeling, analyzing and simulating functional [29],[30] and structural [32] brain NWs while controlling for confounding that arises from NW metric dependencies. For example, as a proof of concept, [29] applied them to (task-free) fMRI connectivity NWs from 10 normal participants aged 20-35 and found they provided a good fit to the data as evidenced by the goodness-of-fit (GOF) plots and simulations. Additionally, the analysis found NW level difference between the five younger (aged 20-26) and five slightly older (aged 29-35) participants. Namely, that if two brain regions are not functionally connected, they are more likely to have shared connections with other regions in the brain NWs of the older group. Though speculative, this could be the result of older brains maintaining indirect connections between areas that have lost their direct connections. ERGMs also show utility in producing group-based "representative" NWs [30]. Simply averaging the connectivity matrices, and thresholding the resulting matrix, fails to produce an accurate “summary” brain NW [30],[35]. The need for these representative NWs is well documented [36],[37],[38],[39],[40],[41],[42],[43]. Using the same fMRI connectivity data discussed above, [30] simulated representative NWs from the pmf employing the average (mean and median) parameter estimates from the ERGM fits to each participant. Figure 3 exhibits the nodal distributions for path length, clustering coefficient, global efficiency, and local efficiency for the 10 participants’ NWs, mean and median correlation NWs (from averaging the connectivity matrices), and the most representative (mean and median) simulated ERGM NWs. The ERGM-based NWs more accurately capture both the average of the NW properties across the participants and distributions of those properties than the mean and median correlation NWs.

Figure 3.

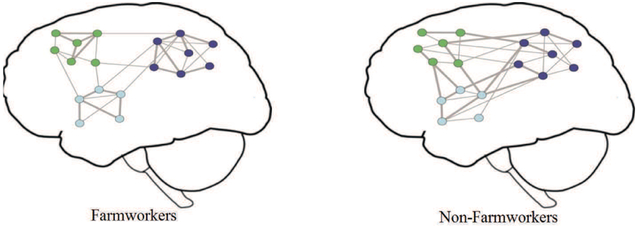
Cartoon model of important differences found between the NWs of farmworkers and non-farmworkers. Each network node represents a brain region and the lines represent functional connections. The node color indicates the module membership and the edge thickness represents connection strength. The average connection probability (density) and strength are the same between farmworkers and non-farmworkers. However, brain NWs of farmworkers are more modularly organized and have higher functional specificity and lower inter-modular integrity when compared to non-farmworkers (stronger connections are shown with thicker edges). Reproduced from [56]. normalsize

Despite the utility of the ERGM framework for brain Networks, important limitations remain. Multiple-participant comparisons can pose problems given that these models were originally developed for the modelling of one NW at a time [29]. Additionally, the programming work load increases linearly with the number of participants since ERGMs must be fitted and assessed for each participant individually [30]. Incorporating novel metrics (perhaps more rooted in brain biology) may be difficult due to degeneracy issues that may arise [44],[45]. MCMC MLE fits of ERGMs can be computationally intensive and may fail to converge with more spatially resolved NWs than the 90 ROI ones used in previous analyses. Model fits with this approach have been shown to handle NWs of several thousand nodes [55]; however, convergence properties are more dependent on the number and topological structure of the edges than the node count [55]. Further work is needed to more precisely assess the scalability of ERGMs in the brain NW context. While well-suited for substructural assessments, link-level examinations remain difficult with these models. Moreover, most ERGM developments have been for binary NWs; approaches for weighted NWs have been developed [46],[47], but have yet to be ported into the brain NW context.

Addressing the ERGM limitations directly provides an avenue for further inquiry; however, a mixed modeling approach may provide a more flexible, complementary method [48]. As with ERGMs, mixed modeling approaches for NW data have mostly been developed for analyzing an individual NW [48],[49],[50]. Simpson and Laurienti [33] provided the first attempt to adapt this framework to the multi-NW neuroimaging context, addressing many of the ERGM drawbacks: mixed models are well-suited for link-level examinations and multiple participant comparisons; novel metrics can be easily incorporated; and they are easily adaptable to weighted and longitudinal NWs.

B. Mixed-Effects Models

Mixed models have served as a complementary approach to ERGMs in the social NW literature [48],[49],[50],[51] and were recently ported into the brain NW context [33],[56]. Given the standard convention of having positively weighted NWs, with negative weights removed (i.e., set to 0 indicating no connection) due to the lack of metrics defined for negative values [52],[53], Simpson et al. [33] define the following two-part mixed-effects modeling framework to model both the probability of a connection (presence/absence) and the strength of a connection if it exists. Let Y_ijk represent the strength of the connection (quantified as the correlation in our case) and R_ijk indicate whether a connection is present (presence variable) between node j and node k for the i^th participant. Thus, R_ijk = 0 if Y_ijk = 0, and R_ijk = 1 if Y_ijk > 0 with conditional probabilities

$$P(R_{ijk}=r_{ijk}\mid {\beta }_r;b_{ri})=\{\begin{array}{cc}1-p_{ijk}({\beta }_r;b_{ri})\hfill & \text{if}{r}_{ijk}=0\hfill \\ p_{ijk}({\beta }_r;b_{ri})\hfill & \text{if}{r}_{ijk}=1\hfill \end{array}\phantom{\}}$$ (2)

where β_r is a vector of population parameters (fixed effects) that relate the probability of a connection to a set of covariates (X_ijk) for each participant and nodal pair (dyad), and b_ri is a vector of participant- and node-specific parameters (random effects) that capture how this relationship varies about the population average (β_r) by participant and node (Z_ijk). Here Z_ijk is the design matrix for participant i that contains the covariate values corresponding to the respective random effects b_ri (i.e., it is analogous to X_ijk for the fixed effects β_r). Hence, p_ijk (β_r; b_ri) is the probability of a connection between nodes j and k for participant i, and the logistic mixed model (part I model) for the probability of this connection follows:

$$logit(p_{ijk}({\beta }_r;b_{ri}))=X_{ijk}^{\prime }{\beta }_r+Z_{ijk}^{\prime }{b}_{ri}.$$ (3)

For the part II model, which aims to model the strength of a connection given that there is one, let S_ijk = [Y_ijk∣R_ijk = 1] and FZT denote Fisher’s Z-transform. In this case, the S_ijk will be the values of the correlation coefficients between nodes j and k for participant i. The mixed model for the strength of a connection (part II model) is

$$FZT(S_{ijk}({\beta }_s;b_{si}))=X_{ijk}^{\prime }{\beta }_s+Z_{ijk}^{\prime }{b}_{si}+e_{ijk},$$ (4)

where β_s is a vector of population parameters that relate the strength of a connection to the same set of covariates (X_ijk) for each participant and nodal pair (dyad), b_si is a vector of participant- and node-specific parameters that capture how this relationship varies about the population average (β_s) by participant and node (Z_ijk), and e_ijk accounts for the random noise in the connection strength of nodes j and k for participant i. Again Z_ijk is the design matrix for participant i that contains the covariate values corresponding to the respective random effects b_si. This framework enables quantifying the relationship between phenotype and brain connectivity patterns while reducing spurious correlations through inclusion of confounders, predicting phenotype based on connectivity structure, simulating NWs to establish normal ranges of topological variability, and thresholding individual NWs leveraging group information. Further details of the approach can be found in [33]. This approach was recently applied to examine the impacts of pesticide and nicotine exposures on the (task-free) functional brain NWs of Latino immigrant farmworkers [56]. Figure 4 (from [56]) presents a cartoon model of important differences found between the NWs of farmworkers (n = 48) and non-farmworkers (n = 26). Farmworkers tended to have more modularly organized brain NWs with higher functional segregation and lower inter-modular integrity. This suggests that farmworkers may have more segregated neural processing and less global integration of information.

Figure 4.

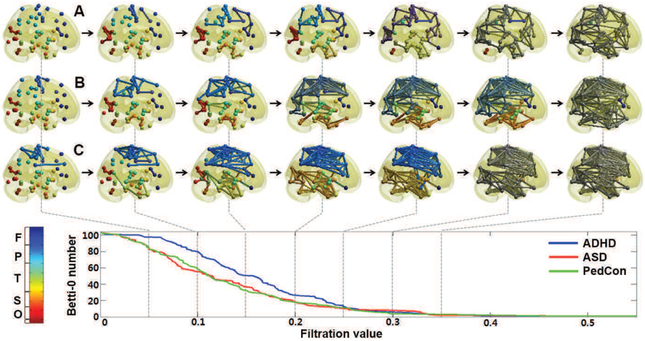
Graph filtration of: (a) attention-deficit hyperactivity disorder (ADHD); (b) autism spectrum disorder (ASD); (c) pediatric controls (Ped-Con). As the filtration value on the horizontal axis increases the NW connections in each panel increase. Reprinted from [72]. normalsize

While mixed modeling frameworks such as this one show promise, they remain in their infancy for the brain NW context. Additionally, while they can handle NWs on the order of a hundred nodes, scaling to larger NWs will require dimension reduction methods.

IV. Network Comparison using Persistent Homology

A. Why we need Persistent Homology?

There are many statistical methods of comparing NWs [57] including matrix norms of the difference between connectivity matrices [57], [58], [59]. However, the element-wise differences simply ignore the topology of the NWs failing to capture higher order similarity such as relations between pairs of columns or rows [58]. Further, matrix norms are sensitive to outliers. Since links are equally weighted a few extreme weights may severely affect the norms. Additionally norms may fail to recognize topological structures such as the connected components or cycles in the NW.

Thus it is necessary to develop comparison methods that recognize topology.

In graph analysis approaches, NW comparisons are based on features such as assortativity, betweenness centrality, smallworldness and NW homogeneity [60], [61], [62]. Comparison of such features appears to reveal changes of structural connectivity associated with different clinical populations [61]. Since weighted brain NWs are difficult to interpret and visualize, they are often turned into binary NWs by thresholding link weights [63]. The choice of threshold will impact the NW topology. To deal with this issue, a multiple comparison correction over every possible link has been proposed [64]. But now the underlying p–value impacts the topology. Another approach is to control the sparsity of links [65], [66], [63], [67]. But now one must threshold sparse parameters. Thus existing methods for binarizing weighted NWs have not escaped the threshold choice problem. Since it seems clear that the threshold must depend on cognitive conditions and clinical populations [68], a different approach is called for. A new multiscale hierarchical NW modeling framework based on persistent homology provides such an approach [69], [70], [71], [72].

B. What is Persistent Homology?

Persistent homology, a technique of computational topology [73], [74], provides a more coherent mathematical framework for comparing NWs. Instead of looking at NWs at a fixed scale, persistent homology charts the changes in topological network features over multiple resolutions and scales [74], [75], [76]. In doing so, it reveals the most ‘persistent’ topological features i.e. those that are robust to noise. This scale robustness is crucial since most NW distances are parameter and scale dependent.

Homology is an algebraic formalism to associate a sequence of objects with a topological space [74]. In persistent homology, homology usually refers to homology groups which are often built on top of a simplical complex for point cloud and NW data [77]. A simplical complex is a collection of points (0-simplex), lines (1-simplex), triangles (2-simplex) and higher dimensional counter parts. We build a vector space C_k using the set of k-simplices as a basis. The vector spaces C_k, C_k−1, C_k−2, ⋯ are then sequentially nested by boundary operator ∂_k [74]:

$$\cdots \stackrel{{\partial }_{k+1}}{\to }{C}_k\stackrel{{\partial }_k}{\to }{C}_{k-1}\stackrel{{\partial }_{k-1}}{\to }{C}_{k-2}\stackrel{{\partial }_{k-2}}{\to }\cdots .$$

Let B_k be a collection of boundaries obtained as the image of ∂_k. Let Z_k be a collection of cycles obtained as the kernel of ∂_k. We have B_k ⊂ Z_k and quotient space H_k = Z_k∣B_k, which is called the k-th homology group. The rank of H_k is the k-th Betti number.

In persistent homological NW analysis as established in [71], [72], instead of analyzing NWs at one fixed threshold, we build the collection of nested NWs over every possible threshold using a graph filtration, a persistent homological construct [69], [72]. The graph filtration is a threshold-free framework for analyzing a family of graphs but requires hierarchically building specific nested subgraph structures. The proposed method shares some similarities to existing multithresholding or multi-resolution NW models that use many different arbitrary thresholds or scales [78], [63], [79], [72]. However such approaches are exploratory, being mainly used to visualize graph feature changes over different thresholds without quantification. Persistent homology, on the other hand, quantifies such feature changes in a coherent way.

C. What is Graph Filtration?

In persistent homology, NWs are modeled as a metric space χ = (V, ρ) consisting of a node set V and link weight function ρ which satisfies the metric properties of: nonnegativity, identity, symmetry and the triangle inequality

$${\rho }_{i,j}\ge 0,{\rho }_{ii}=0{\rho }_{ij}={\rho }_{ji},{\rho }_{ij}\le {\rho }_{ik}+{\rho }_{kj}.$$

The most common such metric is $\sqrt{1-\text{linear correlation}}$. Using inter-nodal distances that are true metrics makes the comparison of brain NWs vastly easier due to the triangle inequality. Many NW distances are in fact metric or ultrametric [72].

Persistent homological NW analysis begins with the construction of the graph filtration. We threshold the weighted network χ = (V, ρ) at level ϵ to obtain a binary network denoted as ${\mathcal{B}}_{∊}(\chi )$. Then any graph X = (V, ρ) with up to r distinct link weights 0 < ρ_u(1) < ρ_u(2) < ⋯ < ρ_u(r) can be uniquely decomposed as a sequence of nested multiscale graph structures called the graph filtration [71], [72], [70]:

$${\mathcal{B}}_0(\chi )\supset {\mathcal{B}}_{{\rho }_{u(1)}}(\chi )\supset \cdots \supset {\mathcal{B}}_{{\rho }_{u(r)}}(\chi ).$$ (5)

For any ϵ ≥ 0, ${\mathcal{B}}_{∊}(\chi )$ is in one of the binary NWs of the filtration (5). In this sense, the representation (5) is unique.

D. What Persistent Homological Features are Used?

As the threshold level in a graph filtration increases, homologies in the homology group appear (are ’born’) and disappear (’die’). The NW topology can then be represented by the ’birth’ and ’death’ of homologies in the persistent homology. The zeroth and first homologies are a set of connected components and cycles, respectively. If a homology appears at the threshold ξ and disappears at τ, it can be encoded into a point, (ξ, τ) (0 ≤ ξ ≤ τ < ∞) in ${\mathbb{R}}^2$. If m homologies appear during the filtration of a NW χ = (V, ρ), the homology group can be represented by a point set $\mathcal{P}(\chi )=\left\{({\xi }_1,{\tau }_1),\dots ,({\xi }_m,{\tau }_m)\right\}$. This scatter plot is called the persistence diagram [88]. The premise of persistent homology is that a homology with a longer ’duration’ is a feature of the topological space and shown as points away from the diagonal line i.e. ξ = τ in persistent diagrams while homology with a shorter ’duration’ is noise and shown as points close to the diagonal line.

Aside from the persistence diagram, various persistent homological features such as barcodes [89] and persistent landscapes [90] are available. Unfortunately, statistical inference on these nonstandard and nonlinear features turns out to be nontrivial and so mostly relies on resampling techniques such as the jackknife and permutation tests [69], [70], [91]. A simpler and possibly more effective approach is to quantify the changes in NW topology using monotonic topological features such as the number of connected components, which is called the zeroth Betti number [69], [70], [80] (Fig. 4):

$$f\circ {\mathcal{B}}_0(\chi )\le f\circ {\mathcal{B}}_{u(1)}(\chi )\le \cdots \le f\circ {\mathcal{B}}_{u(r)}(\chi ).$$ (6)

The size of the largest cluster satisfies a similar but opposite relation of monotonic increase. Many graph theoretic features such as node degree will be also monotonic. In [80], the slope of the linear regression line is fitted in scatter plot $({\rho }_{u(j)},f\circ {\mathcal{B}}_{{\rho }_{u(j)}}(\chi ){)}_{1\le j\le q}$ and used to differentiate different clinical populations. In [70], integral ${\int }_0^{\infty }f\circ {\mathcal{B}}_{∊}(\chi )dϵ$ is used as the summary statistic instead of the vector (6).

E. Measuring Topological Distance Between NWs

Instead of using topological features that summarize each NW, one can directly compare NWs by computing a distance between NWs. The bottleneck distance is perhaps the most widely used distance measure in persistent homology [88], [74]. It is defined through the distance between corresponding persistence diagrams (PDs). Points in different PDs do not naturally correspond as a bijection. Thus, the computation of the distances between PDs is not straightforward and often requires bipartite graph matching algorithms [88] [92].

[93] bypassed the problem of comparing PDs by comparing the density of points in a square grid via kernel smoothing. Motivated by [93], later methods have used kernel distances [94], [95], [96]. Thus [95] introduced the persistent scale space (PSS) kernel, which is the inner product between heat diffusions with the PD-points as the initial heat sources. PSS was extended to multiple PSS kernels in determining the changes in brain NW distances in aging [96].

Gromov-Hausdorff (GH) distance is a popular NW distance, which measures the distance between the respective dendrograms of the NWs [73], [97]. Single linkage distance between two nodes is the shortest distance between two connected components that contain the nodes. GH-distance is the maximum of the single linkage distance differences [72]. It was applied to brain NWs in [71], [72]. It has been shown that the computation of GH-distance can be reduced to computing differences in single linkage matrices thus making a connection with hierarchical clustering [73], [72].

F. Computational Complexity

Persistent homology does not scale well with NW size. The computational complexity of the k-th Betti number depends on the number m of k-simplices [98]. For n nodes, m ≤ O(n^k+1). The homology computation requires Gaussian elimination, which often runs in O(m³). Thus, the overall worst case computational complexity is O(n^3k+3). As n increases, the computational bottleneck can be severe.

So resampling based statistical inference may not be feasible for very large-scale NWs. We need faster inference procedures that do not rely on resampling techniques [81].

G. Statistical Inference in network Distances

Given two NWs χ¹ = (V, ρ¹) and χ² = (V, ρ²), we are interested in testing the null hypothesis H₀ of equivalence: H₀ : χ¹ = χ². In persistent homology, this inference problem is mainly addressed by comparing a topological feature between NWs or computing a distance between NWs. Unfortunately, all the standard topological features or between NW distances do not have known probability distributions, which makes statistical inference difficult. Unless we are dealing with a ‘large’ number of observed NWs and so can appeal to the central limit theorem [90], statistical inference has to be done using resampling techniques such as jackknife, bootstrap or permutation methods [72], [91], [70], which causes computational bottlenecks for large scale NWs.

To bypass the computational bottleneck, the Kolmogorov-Smirnov (KS) distance was proposed in [69], [70], [91], [81]. KS-distance is motivated by the two-sample Kolmogorov-Smirnov (KS) test [99], [69], [100], which is a nonparametric test for determining the equivalence of two cumulative distribution functions (CDFs). The curve ${(ϵ,f\circ {\mathcal{B}}_{∊}(\chi ))}_{ϵ\ge 0}$ looks exactly like a CDF if it is properly normalized. KS-distance is the maximum differences between the two curves. The number of connected components and the size of the largest connected component can be used as monotonic features f.

The advantage of the KS-distance is its simple interpretation compared to other distances. It is possible to enumerate the sample space combinatorially and determine its probability distribution exactly [81]. Simulation based comparisons between different network distances are given in [101].

V. Time-varying Functional Connectivity

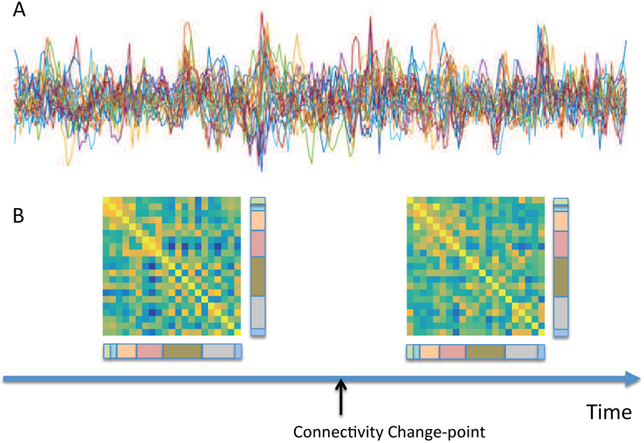
Recently, focus in the brain connectivity has begun to shift from evaluating static functional connectivity over the length of a scanning session, to analyzing time-varying (TV) functional connectivity ([105]). Here the goal is to study changes in functional connectivity on the time-scale of seconds to minutes, and classify the brain into distinct connectivity patterns (i.e. ‘brain states’) to which subjects tend to move between during the course of the scan. This is illustrated in Fig.5.

Figure 5.

Figure legend: (A) Resting-state fMRI time series from 21 regions of the brain from a single subject. (B) The results of a change point analysis ([109]) show a connectivity change point roughly half way through the scanning session. The two correlation matrices represent the brain state before and after the change point. Edges between visual components (color-coded as pink) and both cognitive control (olive green) and default mode (grey) components appear to be particularly variable. normalsize

Results have demonstrated that while the patterns of connectivity describing each state are reliable across groups and individuals [110], other characteristics such as the amount of time spent in specific states and the number of transitions between states can vary as a function of individual differences such as age [111] or disease status [112], [113].

A. Sliding Windows

To date, the most widely used strategy for detecting TV functional connectivity has been the so-called sliding window technique, where a linear (aka Pearson) correlation matrix is computed over a fixed-length time window of the fMRI time series. The window is thereafter moved step-wise across time, providing a TV measure of the linear correlation between brain regions. Observations within the fixed-length window can be given equal weight, or allowed to gradually enter and exit the window as it is shifted across time [108]. Potential pitfalls of the family of sliding-window methods include using arbitrarily fixed-length windows, ignoring all values outside of the windows, and an inability to handle abrupt changes in connectivity patterns.

B. Beyond Sliding Windows

To circumvent some of these shortcomings, we now point to a number of more advanced methods.

Multivariate time series methods (e.g., Dynamic Conditional Correlations [114]) that directly model the conditional correlation between fMRI time courses have recently been introduced to the neuroimaging field [115]. These techniques have been shown to be less susceptible to noise-induced temporal variability in correlations compared to the sliding-window based approaches. However, compared to sliding-window techniques there are increased computational costs involved with using these methods, which can become substantial as the number of regions of interest increases.

Another alternative is to use time-frequency analysis (e.g., wavelet transform coherence) to examine temporal variability in the relationship between time series from different regions [107]. This allows for the estimation of the coherence and phase lag between two time series as a function of both time and frequency. This technique has provided evidence of considerable modulation of coherence across the time-frequency plane, and that significant coherence is focal in time. However, a shortcoming of this type of analysis is that it tends to produce large amounts of information, presenting particular computational challenges when analyzing multiple subjects and brain regions.

Analysis is further complicated by the fact that, in contrast to many other statistical methods that reduce the dimensionality of the data, TV functional connectivity methods tend to substantially increase the number of data points. For example, a T × d (time-by-region) input matrix becomes a d × d × T array after application of sliding-window methods. Therefore, the ability to find meaningful measures that reliably summarize TV functional connectivity is of utmost importance. One approach is to compute basic summary statistics, such as the mean and variance of the TV functional connectivity across time. Another involves the estimation of “brain states", which are defined as recurring whole-brain connectivity profiles that are reliable across subjects throughout the course of the resting state scan [116]. A common approach to determining the presence of such coherent states across subjects is to perform k-means clustering on the set of correlation matrices measured across time. States can then be defined as the patterns of connectivity at each centroid, and additional summary metrics such as the amount of time each subject spends in a given state (i.e., dwell time) and the number of transitions between states can be computed.

A crucial observation here, is that the traditional k-means clustering procedures are time-invariant, since permutation of the correlation matrices (across time) give rise to equivalent results. Hence, alternative methods that incorporate lagged temporal information will almost certainly provide better results. One such alternative uses techniques from change point analysis (e.g., [117], [118], [109]). Here time courses from multiple regions are partitioned into distinct segments, within which the data follow a multivariate Gaussian distribution with a different covariance (or inverse covariance) matrix from its neighboring segments; see Fig.5 for an illustration. A number of different algorithms have been proposed that primarily differ in the manner in which change points are determined, and the network structures are identified. Yet another promising approach is the application of Hidden Markov Models [123],[124]. Here it is assumed that the time series data can be described using a sequence of a finite number of latent states, with each state characterized by a unique covariance matrix.

As the number of regions/components included in the analysis increases, the scalability of the different methods becomes critical. Here the sliding-window approaches tend to scale better than model based approaches. The latter can becomes particularly cumbersome if a separate model is fit to each bivariate connection. Of the model based approaches the DCD approach [109] was specifically designed with scalability in mind and thus tends to work better at high-dimensions than its counterparts.

C. Comments and controversies

The problem of estimating TV connectivity is difficult in practice. A major issue is related to the relatively few degrees of freedom availabale in the data, which in turn increases the statistical difficulty in estimating the correlation matrices. This is due to a number of factors, including: (i) the use of narrow window sizes when using sliding window approaches; (ii) the inherent autocorrelation present in the data; and (iii) the fact that a number of ‘nuisance’ effects (e.g., motion, low-frequency drift, and physiological measurements) are removed from the signal prior to analysis. Together this loss in degrees of freedom will contribute to increased variation (across time) in the TV correlation, which could lead to noise being interpreted as important signal. These problems are amplified if one seeks to study TV changes in partial-correlation. Here the resulting covariance matrices risk being ill-conditioned necessitating the inclusion of potentially severe penalization terms.

In addition, it should be noted that the existence of TV functional connectivity has not been without controversy [119], [120]. For example, a recent paper by [120] made the case that much of the observed ‘dynamics’ during rest is actually attributable to sampling variability, head motion, and fluctuating sleep state. Thus, they argue a single correlation matrix is sufficient to describe the resting state as measured by BOLD fMRI.

Clearly much work remains to gain a proper understanding of TV brain architecture. To achieve this goal it is critical that proper statistics and signal processing play an important role, as there remain multiple methodological shortcomings in the regularly applied approaches (e.g. there is a pressing need for confidence intervals on ‘curves’ to measure the significance of TV fluctuations [107]; see [121] for some initial work), making it difficult to determine whether observed fluctuations in connectivity should be attributed to neuronal activity, non-neural biological signals, or noise [104], [122].

VI. Functional Network System Identification

Our point of takeoff from the introduction is problems relating to step 2 in the NW construction.

Most rs-fMRI functional connectivity studies construct the NW (Step 2) using linear correlation (LC) as a measure of functional association between brain regions [125], [126]. But LC ignores various important issues in NW construction. Chiefly it only measures indirect association between nodal or regional time series whereas neuroscientific theories can only be built from measures of direct association [127]. Thus many of the common interpretations of functional connectivity networks (Steps 3 and 4) are implicitly invalidated if the NWs are constructed using indirect measures such as LC. Instead, we describe recent advances in NW system identification using concepts from statistical signal processing, to estimate the direct (i.e. conditional or partial) relationships between brain regions from rs-fMRI data thus defining fNW architecture and dynamics.

A. Conditional Independence

Partialling (out all other nodes) or conditioning (on all other nodes) is the basic method used to compute direct measures of association between nodes from indirect ones. This underlies the construction of conditional independence graphical models (CI-GMs), where a missing link between a particular pair of nodes implies those nodes are conditionally independent given the other nodes [128], [129], [130]. Then graph analysis concepts such as path length and node degree have a clearly defined and interpretable meaning being now applied to direct association measures.

CI (i.e. direct) interactions are difficult to estimate [131], especially for a large network as for fMRI [132]. In contrast, marginal (indirect) interactions are computationally easier to obtain, e.g. via a pairwise LC, but are uninterpretable because they are dominated by indirect relations. One further benefit which emerges during the construction of a CI graph is the implicit removal of NW-wide confounding signals from the estimation of each link strength. When estimating functional brain NWs, common physiological or scanner-induced noise, uncorrected motion artifact, or other uninteresting signal present among the set of nodal signals will be accounted for during the estimation of CI links. One approach to obtain CI NW link strengths in the Gaussian setting is to replace marginal LC with partial correlation [143], [144], [145], which can be computed via the regularized inverse of the data covariance matrix.

But partial correlation is not sufficient to deal with real time series such as from rs-fMRI data, as we also need to: i) overcome the ‘curse of dimensionality’, especially when there is an equal or greater number of parameters to estimate than the number of samples within the data, and ii) account for serial temporal autocorrelations within and between nodal time series.

B. Data Dimensionality Effects

The data dimensionality issue concerns both the relatively large number of spatial links to estimate from fewer temporal data points, and particularly for fMRI, the strong collinearity between many of the voxel signals. The problem is compounded for rs-fMRI data since brain activity can only be assumed to be stationary over a relatively short time interval, typically a few minutes at best; also it is not necessarily practical to collect more temporal data over a longer scanning session. If not dealt with, these problems cause estimated NWs to be so noisy that artefacts are consistently mistaken for structure. The problem is not confined to rs-fMRI data, as spurious structure emerges even from empirical covariance matrices constructed from white noise processes (i.e. null NWs) as studied in Random Matrix Theory (RMT) [133], [134]. Spurious structure emerging from null correlation NWs has been described previously in the rs-fMRI literature [135], but the link to data dimensionality and RMT has not yet been widely explored [127], [136]. The dimensionality problem can be dealt with in part by massive parameter dimension reduction, e.g. by collating local spatial collections of voxel time series into regions to represent NW nodes and summarizing these regions by a single representative time series at each node, collating data across subjects [144], and also by sparsity regularization [137]

C. Serial Correlations

Dealing with serial or lagged temporal correlations within data is crucial, as hemodynamics induce a strong spatially-varying temporal autocorrelation profile within the data. Fig. 6 demonstrates the increase in rs-fMRI data complexity caused by temporal correlations as the temporal sampling rate is increased. These serial correlations can be dealt with by using partial coherences instead of partial correlations [138], [139] to quantify the association between each pair of nodes. The link strength is then expressed as a function of frequency, giving a separate NW at each frequency. However, attempting to analyze NWs at each frequency is challenging and would still leave unanswered the question of producing a single summary NW; to do that one needs an overall measure of link strength. That issue was addressed in [127] by using sparse conditional trajectory (frequency domain) Mutual Information (SCoTMI).

Figure 6.

Univariate autoregressive model order estimated at each voxel of example rs-fMRI datasets; Human Connectome Project data having TR=0.72s (left), temporally down-sampled and anti-aliased HCP data with TR≈2.2s (centre), and standard quality data with TR=2s (right). normalsize

D. Sparse Conditional Trajectory Mutual Information

Let x_t = [x_(d),t], be a jointly stationary network time series at nodes d = 1, …, D and time points t = 1, …, T. Partitioning the data as [x_(a),t, x_(b),t, x_(z),t] where a and b are two nodes of interest, then as T → ∞ the frequency domain conditional Mutual Information is

$$\frac{1}{T}I(x_a;x_b\mid x_z)\to -\frac{1}{2}{\int }_{-\pi }^{\pi }\text{ln}\left(1-\mid {\rho }_{ab\mid z}(\omega {)}^2\mid \right)\frac{d\omega }{2\pi }$$

where ρ_ab∣z (ω) is the partial coherence at frequency ω between nodes a and b given other nodes z. For SCoTMI the partial coherence is estimated parametrically via the conditional spectra F(ω) of a vector ℓ₀-sparse penalized vector autoregression model as ${\rho }_{ab\mid z}=\frac{F_{ab\mid z}(\omega )}{\sqrt{F_{a\mid z}(\omega )F_{b\mid z}(\omega )}}$. Estimating ρ_ab∣z (ω) alternatively using a non-parametric estimate directly from the DFT of the data as done by [140], [141] leads to extremely noisy estimates when applied to real rs-fMRI time series [127].

The VAR model of order p is separable at each node, and the model to fit at node d is $y_{(d),t}={\sum }_i{X}_{(i),t}^T{\alpha }_{(d),i}+{∊}_t;$; where $X_t={\left[X_{(1),t}^T,\dots ,X_{(D),t}^T\right]}^T$, X_(d),t = [y_(d),t−1, …,y_(d),t−p]^T. The model is penalized to be sparse within each node by minimizing the cost function

$$J({\alpha }_{(d)})=\sum _{t=1}^T\frac{1}{T}\Vert y_{(d),t}-X_t^T{\alpha }_{(d)}{\Vert }^2+h\sum _{i\ne d}I(\Vert {\alpha }_{(d),i}\Vert \ne 0)$$

and h is a tuning parameter determining the degree of sparsity. An empirical significance threshold is estimated using null (unconnected) NW simulations; NW links above the threshold are kept and links below the threshold are discarded. Implementation and details to compute F(ω) from the VAR parameters are in [127].

The SCoTMI model fitting is trivially parallelized due to the separability per node, and can easily handle NWs of hundreds or thousands of nodes if there are sufficiently many samples in the time series.

E. Example Results

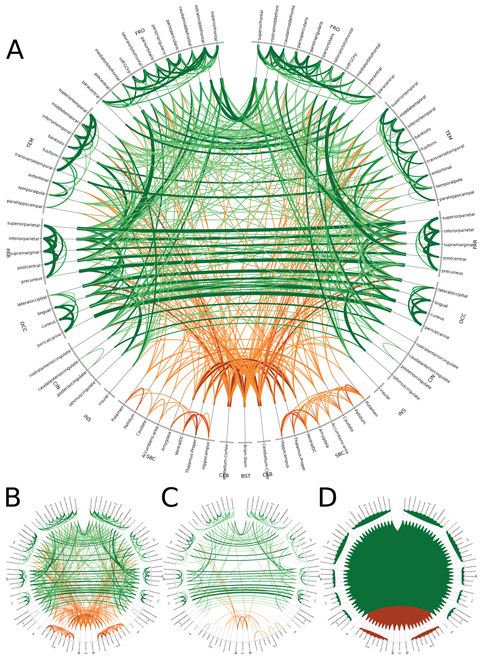
We show an example of SCoTMI NWs [127] using rs-fMRI data from the Human Connectome Project. Fig. 7 shows the repeatability of detecting SCoTMI NW links across 80 individual datasets (20 subjects with 4 scanning runs each). We see here the NW architecture is qualitatively similar between SCoTMI, sparse partial correlation and partial correlation; the quantitative superiority of SCoTMI over those approaches is documented in [127].

Figure 7.

Circos diagram of the repeated link detection from 80 SCoTMI NWs (A), using an 87 node Freesurfer parcellation of grey matter regions. Line width is proportional to the number of subjects with repeated detection of a particular link. Cortical links are green, subcortical links are orange. Comparison methods include sparse partial correlation (B), partial correlation (C), and linear correlation (D). normalsize

VII. Conclusions

In the introduction we cleared up confusion surrounding definitions including possible blind spots that had been thus generated. In the reviews we pointed to significant blind spots of some of the major current methods of studying fNWs and then sketched five emerging methods drawn from other disciplines that have already proved able to address various of these blind spots.

Stochastic block models treat the nodal links stochastically. This provides a powerful framework not just for for modeling/pruning the fNW, but also for inferring the (overlapping) clustering of functional regions. This promises a rich description of the functional subnetworks which current methods provide only in a very crude way.

While graph analysis has been very useful it has not proceeded beyond the exploratory stage. ERGMs (and mixed modeling approaches) provide a modeling framework in which to embed the graph analysis methods and so provide a means of confirmatory analysis.

For TV connectivity simple exploratory sliding window methodology has reached its limits having lead to overinterpretation of the estimated fluctuations and much more sophisticated confirmatory methods, particularly involving modeling autocorrelation are needed to dig out the true time-varying fluctuations if any.

In practical neuroimaging one needs to compare NWs with differing number of nodes and links and differing spatial and temporal resolutions. Graph analysis methods cannot do this but the emrging technique of persistent homology can.

Linear correlation has dominated fNW modeling. But it only measures indirect interactions and to get at direct interaction one needs to use measures such as partial correlation. The neuroimaging community has struggled to understand this fundamental issue. Further real dynamics requires analysis of serial correlation which has been ignored. NW system identification techniques being developed in the statistical signal processing and control engineering comunities can address this kind of issue and their preliminary extension and application to neuroimaging is already providing superior results.

Certainly each of these methods has a long way to go. They each address some blind spots but not all. Thus SBMs and ERGMs so far have not addressed the issue of autocorrelation. TV connectivity has not addressed the serial correaltion problem while the ScoTMI technique has not addressed the TV connectivity problem. And persistent homology needs to be embedded in a confirmatory framework to handle multisubject inference properly.

To sum up, fNW analysis has reached a cross-roads wherein current methods have reached their limits and some new tools are needed. In fact there are an array of powerful new methods beginning to be applied to neuroimaging connectivity, that are capable of answering practical fNW questions arising in clinical and scientific application.

Figure 2.

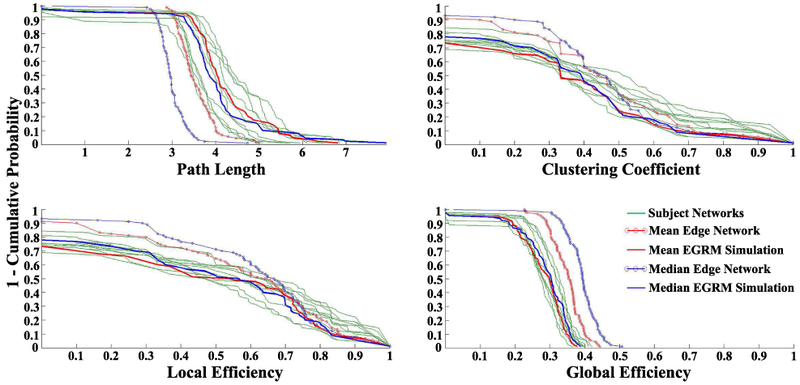
Nodal distributions of path length, clustering coefficient, global efficiency, and local efficiency for the 10 participants NWs, mean and median correlation NWs, and most representative (mean and median) ERGM-based NWs. Reproduced from [30]. normalsize