Abstract
The bipartite network representation of the drug–target interactions (DTIs) in a biosystem enhances understanding of the drugs’ multifaceted action modes, suggests therapeutic switching for approved drugs and unveils possible side effects. As experimental testing of DTIs is costly and time-consuming, computational predictors are of great aid. Here, for the first time, state-of-the-art DTI supervised predictors custom-made in network biology were compared—using standard and innovative validation frameworks—with unsupervised pure topological-based models designed for general-purpose link prediction in bipartite networks. Surprisingly, our results show that the bipartite topology alone, if adequately exploited by means of the recently proposed local-community-paradigm (LCP) theory—initially detected in brain-network topological self-organization and afterwards generalized to any complex network—is able to suggest highly reliable predictions, with comparable performance with the state-of-the-art-supervised methods that exploit additional (non-topological, for instance biochemical) DTI knowledge. Furthermore, a detailed analysis of the novel predictions revealed that each class of methods prioritizes distinct true interactions; hence, combining methodologies based on diverse principles represents a promising strategy to improve drug–target discovery. To conclude, this study promotes the power of bio-inspired computing, demonstrating that simple unsupervised rules inspired by principles of topological self-organization and adaptiveness arising during learning in living intelligent systems (like the brain) can efficiently equal perform complicated algorithms based on advanced, supervised and knowledge-based engineering.
Keywords: local-community-paradigm theory, unsupervised link prediction, drug–target interaction, bipartite complex networks, network topology, bio-inspired computing
Introduction
Modern drug development is facing a constant increase in costs, recently estimated to be above 1 billion US$ for each new drug reaching the market [1], while the number of new approved drugs per year is declining [2]. Drug repositioning is a promising solution to this problem [3], aiming at identifying new uses for old drugs. However, a prerequisite for drug repositioning is the identification of possible new targets for known drugs. For this reason, a plethora of methods and data sets has been proposed and applied to the drug–target interaction (DTI) prediction problem in the past years. Such methods can be divided into two main categories: supervised network inference or unsupervised/model-based approaches.
In 2008, the DTI inference problem has been formalized as a supervised learning task in bipartite graphs. Given a known graph—which is however incomplete—and information about its nodes, the aim is to predict the unknown part of the graph [4]. Following this strategy, Yamanishi and Bleakley [5] authored a groundbreaking paper in which they proposed the bipartite local model (BLM) as a supervised graph inference method and applied it to DTI prediction. This model has been used as a reference in several works, as well as the four gold standard networks released in the same publication [5, 6]. Related studies proposed after BLM include the semi-supervised drug–protein interaction predictions [7], the Gaussian profile kernel [8] and neighborhood regularized matrix factorization techniques [9]. More recently, improved methods to predict and account for distinct types of DTIs have been proposed [10]. Supervised methods are generally bound to one or more biological measures as prior knowledge. Thus, some limits are present because of incompleteness of biological data [11] or noise in the experimentally measured similarities. Moreover, the combination of extra biological information results in increased complexity and higher computational costs but might result in better prediction performance, thanks to problem-specific tuning. However, it has been pointed out that bias in their performance evaluation can be because of the small size of the data sets and fine-tuned machine learning methods. This results in lack of generality [12] and in the risk of performance overestimation because of simplified settings [13].
An alternative to supervised learning is the application of unsupervised techniques or topology-based models, which rely only on network structure to infer novel links. Contrary to supervised methods, there is no model learning based on external knowledge; therefore, such methods do not require additional biological measures and are less prone to overfitting. However, unsupervised methods accept only the bipartite network of the known DTIs as data input; hence, the incompleteness and noise in such topological data influence the network structure. For instance, a severe limitation of unsupervised topology-based methods is the difficulty to predict interactions involving new drugs or targets for which there are no known network interactions (i.e. ‘orphan’ nodes [14] isolated out of the network), or to predict interactions between drugs or targets that are located in two disconnected parts of the network. Supervised methods overcome these limitations (which originate from the missing network connectivity) by exploiting additional and external biological knowledge that is independent of the network structure.
Under an unsupervised setting, the task of DTI prediction can be generalized as a link prediction problem [15] in bipartite networks, and many strategies have been proposed in various fields.
Algebraic link prediction methods like collaborative filtering (CF) [16] or matrix factorization (MF) techniques [17] are popular approaches for online personal recommendation. Evolutionary models, such as the preferential attachment (PA) model [18], have been successfully used to make predictions in various domains, involving both monopartite and bipartite networks. Moreover, a previous analysis of many real bipartite networks [19] showed that PA has generally better performance than various MF methods. Topological measures based on node neighbourhood similarity—such as common neighbour (CN) [20] or Jaccard coefficient (JC) [21]—are powerful topology-based link prediction methods in monopartite networks. However, such methods are based on the triadic closure principle [22], therefore not applicable to bipartite networks [19] because of the specific properties of these networks [23] where the triadic closure is not anymore valid. To overcome this theoretical limitation, Zhou et al. [24] proposed a method called network-based inference (NBI) for topological link prediction in bipartite networks. This method decomposes the original bipartite topology in two separated monopartite topologies between nodes of the same class. However, in this manner, the original content of the bipartite structure is downgraded in two monopartite projections, which have been demonstrated to be always less informative than the original network [25]. Despite that, NBI was shown to outperform PA and CF in the personal recommendation task [24]. More recently, Cheng et al. [26] applied NBI for DTI prediction in previously used networks [5, 6] and in networks of the Food and Drug Administration-approved and experimental drugs, showing that such topology-based method outperformed biological measures based on either drug or target similarity. Many improvements of the method have been also proposed [9, 27–29]. However, as already mentioned, each of the topology-based methods described above relies on the projection of a bipartite network into its two monopartite topologies.
To overcome this limitation and apply topological measures based on node neighbourhood similarity directly in the bipartite topology, we recently proposed a definition of CN in bipartite networks [30]. This definition originates from the observation that the generally accepted notion of CNs as emerging from the triadic closure rule is misleading. The triadic closure seems the generative rule of common neighbours only as a specific case valid in particular for monopartite network topology. In fact, in bipartite networks, CNs between nodes of different classes are associated to the quadratic closure rule and, more in general, the definition of CNs between two seed nodes should be given as: the nodes touched by all the possible shortest paths of the minimum length allowed by a given topology between two seed nodes (see ‘Methods’ subsection on ‘Model-based methods’ for details). Consequently, having defined the notion of CN in bipartite networks, we could also translate and extend to these types of networks a novel theory named the local-community-paradigm (LCP) theory [31]. Initially detected in brain-network self-organization topology and afterwards extended to any monopartite complex network, the LCP theory derives from a purely topological-inspired interpretation of a local learning rule of neuronal networks named Hebbian learning rule [31]. A thoughtful discussion of the fundaments that advocate this theory is offered in a dedicated paragraph of the next section. At this point, we just need to report that one of the corollary of the LCP theory suggests that neighbourhood-based (local-based) topological link prediction should complement the information content related with CN nodes using also the topological knowledge emerging from the cross-interactions between them. Accurate tests on several real networks in both monopartite [31–36] and bipartite topologies [30] confirmed the theory’s validity. In fact, the LCP-based variations of the standard CN-based link predictors showed in general a significant improvement.
Here, we apply the LCP theory in the context of drug–target bipartite networks and thoroughly compare the prediction performance of 24 variations of six state-of-the-art methods (included LCP-based): three unsupervised and three supervised. In addition, we propose three diverse evaluation frameworks. The first evaluation strategy serves as comparison with reference methods and is identical to the one applied in previous works [37], where the ability of prediction methods is judged by their ability to highly score existing links in the considered networks. The second is based on random removal and re-prediction of DTIs [38]; thus, it is less prone to overfitting the existing network structure, and it aims at estimating the prediction performance under more general settings. To complement these evaluation strategies, we add a comprehensive external and independent validation set by integrating bioactivity assays and drug activity data from various resources. Using such data, predicted links are classified into active [i.e. true-positive (TP) predictions], inactive [i.e. false positives (FPs)] or candidate interactions (i.e. unknown). Having positive and negative information allows not only to evaluate a method for its ability to recover true interactions but also the estimation of how precise a method is in respect to its prioritization of active versus inactive interactions. In this manner, we can circumvent the problem of underestimating a method’s precision caused by considering all newly predicted interactions that are not included in the positive independent set as FPs, although they might be valuable candidates. Finally, we provide a detailed analysis that compares the novel predictions from the representative methods, one for each distinct class that offers high performance, and discuss their differences in detail.
Results
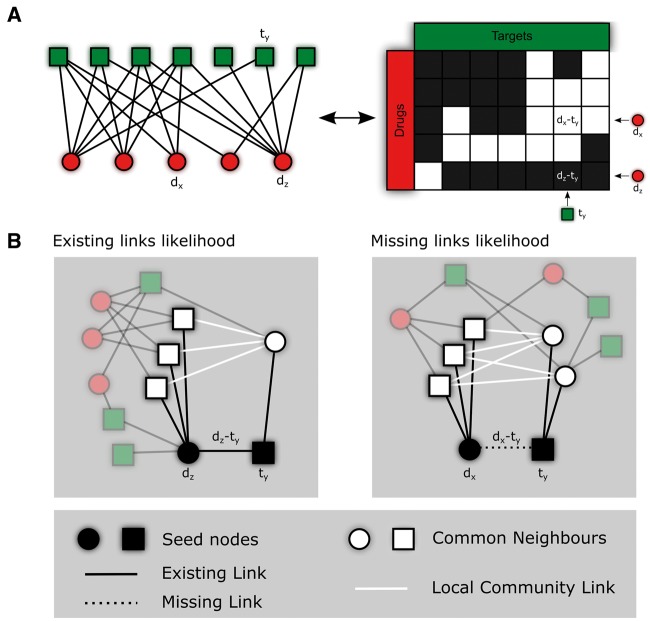
Interactions between drugs and their targets can be represented as bipartite networks, where two types of nodes are present, and only connections between distinct types of nodes might be present (Figure 1A, left). An equivalent representation of such networks are rectangular matrices (Figure 1A, right), with the number of drugs as the first dimension and the number of targets as the second. In this form, observed and missing interactions are labelled following a binary schema, or assigning real numbers and/or labels if data such as chemical affinity or type of interaction are known [10]. Similarly to many biological networks, DTIs are highly incomplete [39], and thus, several computational methods, which exploit known interactions to predict putative ones, have been proposed.
Figure 1.
CNs and quadrangular closure in bipartite networks. (A) A bipartite network of targets (t, dark green squares) and drugs (d, red circles) and its equivalent matrix representation. (B) Four CNs (white nodes) together with three LCLs (white links) as defined by Daminelli et al. [30] are used to calculate the interaction likelihood of the two seed nodes dz and ty (black nodes) of the existing link dz-ty (left). Similarly, five CNs and five LCLs are used to predict the likelihood of the missing dx-ty interaction (right) .
Generally, such approaches are either supervised or unsupervised. In this article, we compare 24 variations of the state-of-the-art methods (Table 1), which are either mere link predictors exploiting only the topology (unsupervised) or advanced methods exploiting not only topology but also additional biological information (supervised), to assign the likelihood of any possible missing DTI in the network.
Table 1.
Overview of the compared methods and their respective class
| Class | Method | Method or formula | |
|---|---|---|---|
| Supervised (SVM) | BLMdt [37] | SVM+chemical and sequence similarity | |
| BLMd [37] | SVM+drug chemical similarity | ||
| BLMt [37] | SVM+target sequence similarity | ||
| Supervised (GR+MF) | GRMFdt [14] | GR+MF+chemical and sequence similarity | |
| GRMFd [14] | GR+MF+chemical and sequence similarity | ||
| GRMFt [14] | GR+MF+chemical and sequence similarity | ||
| Supervised (WKNKN+GR+MF) | wGRMFdt [14] | WKNKN+GR+MF+chemical and sequence similarity | |
| wGRMFd [14] | WKNKN+GR+MF+chemical and sequence similarity | ||
| wGRMFt [14] | WKNKN+GR+MF+chemical and sequence similarity | ||
| Unsupervised (MF) | MF [14] | MF | |
| MFm | MF mean score CV | ||
| MFb | MF best score CV | ||
| MFw | MF weight score CV | ||
| Unsupervised (Projection) | BPR [40] | Random walk | |
| NBI [41] | RA | ||
| Jac [40] | Jac similarity | ||
| Euc [40] | Euclidean distance | ||
| Cos [40] | Cosine similarity | ||
| Pea [40] | Pearson correlation | ||
| Unsupervised (LCP) | CAR [30] | ||
| CJC [30] | |||
| CPA [30] | |||
| CAA [30] | |||
| CRA [30] |
Note. N(dx) indicates the first neighbours of the drug dx. CN(dx; ty) are the CNs of drug dx and target ty, respectively, and LCL(dx; ty) are their local community links. In respect to the (dx; ty) link, eN(dx) and eN(ty) represent the neighbours of drug dx and target ty, respectively, which do not belong to the set of CN(dx; ty), thus indicated as external neighbours. γ(s) are the neighbours of s, which are also CN(dx; ty), while N(s) are all the neighbours of s. SVM: Support Vector Machine; GR: Graph Regularization; MF: Matrix Factorization; MFb: best Matrix Factorization; MFm: mean Matrix Factorization; MFw: weighted Matrix Factorization; WKNKN: Weighted K Nearest Known Neighbours; BLM: Bipartite Local Model; GRMF: Graph Regularized Matrix Factorization; BPR: Bipartite Projection via Random-walk; NBI: Network-Based Inference; Jac: Jaccard; Euc: Euclidean; Cos: Cosine; Pea: Pearson; CAR: Cannistraci-Alanis-Ravasi; CJC: Cannistraci-Jaccard; CPA: Cannistraci-Preferential-Attachment; CAA: Cannistraci-Adamic-Adar; CRA: Cannistraci-Resource-Allocation.
The main unsupervised methods are the projection-based and the LCP-based, which are regarded, respectively, the old and new state of the art for general-purpose link prediction in complex networks. In particular, we consider five recent LCP-based topological models for link prediction, which directly exploit the bipartite nature of those networks. They assign a likelihood to any observed or missing interaction based on the local information of the neighbourhood of the two involved nodes. These measures—which were already applied for link prediction on monopartite networks [31]—are derived from a recent generalization of both the CN concept and the LCP to the bipartite domain [30]. Starting from the toy network in Figure 1A, Figure 1B gives emphasis to the neighbourhood information of two seed nodes, which is exploited by LCP-based measures to assign the likelihood of an existing interaction dz-ty (Figure 1B, left), and a missing interaction dx-ty (Figure 1B, right). Finally, a third type of unsupervised method, which is MF-based, was included and used as a reference in respect to the supervised version that we will discuss hereafter.
The first supervised method is the bipartite local model (BLM), which is based on support vector machine (SVM) [6]. It was the state-of-the-art until recently, and is still considered an important reference for supervised methods that, together with the network topology, exploit the biological information given by the chemical and sequence similarity of the molecules. The second supervised method was recently proposed, in 2016, and it is an advanced predictor named graph regularized matrix factorization (GRMF).The graph regularization (GR) boosts the performance because it prevents overfitting by facilitating the learning of a non-linear manifold on which the network is assumed to lie. Same strategies have been used in the past also to improve prediction in protein interaction networks [42, 43].The third supervised method is named weighted-K-nearest-known-neighbour (WKNKN) + GRMF, but here for brevity, we will call it wGRMF. In practice, it consists of GRMF applied on a pre-adjusted drug–target adjacency matrix by means of a preprocessing named WKNKN, which transforms all the 0’s (missing values rather than confirmed non-interactions) in the original drug–target adjacency matrix into interaction likelihood values in the range 0–1. Essentially, WKNKN can be interpreted as a method for pre-weighting the missing interactions according to the biological information of the known neighbours. Both GRMF and wGRMF demonstrated to improve results dramatically, therefore represent the new state-of-the-art methods that exploit the chemical and sequence similarity of the molecules as biological information to guide the supervised learning.
As described in the ‘Methods’ section, any observed/missing interaction was ranked by their likelihood, and the prediction performance of each method in Table 1 was evaluated by calculating the area under the precision–recall curves (AUPR) for the distinct evaluation frameworks. To compare the performance across different networks, each AUPR was normalized (nAUPR) against the random predictor.
| (1) |
The original values of AUPR are reported for reference in the Supplementary Information 2.
A set of well-established and widely used gold standard DTI networks [4, 37]—including four distinct protein classes: enzymes, ion channels, G-protein-coupled receptors (GPCRs) and nuclear receptors (NRs)—was used as a benchmark for the predictions. In addition, to verify whether the same topology-based principles work also when applied to a more diverse target space, the same prediction methods were compared on a high-quality heterogeneous drug–target network [44]. The additional biological knowledge to compute the features needed for the supervised methods is not available, and thus, the supervised methods cannot be applied to this fifth network.
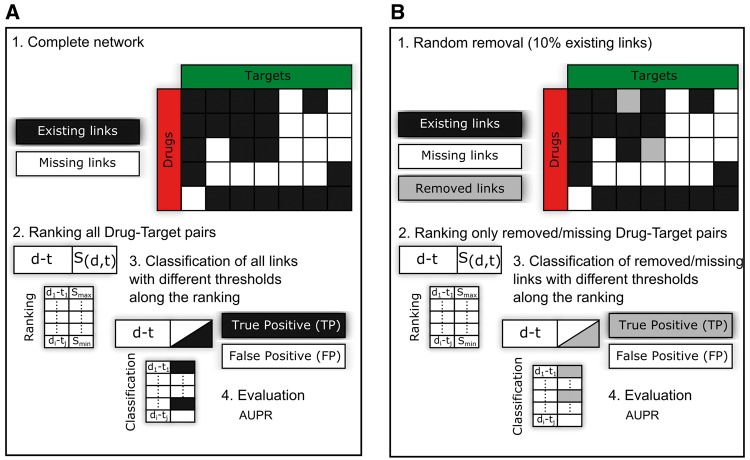
Further, we considered three different evaluations frameworks. First, we compared the performance following the strategy in Figure 2A, which is a commonly applied evaluation [5] that relies on the complete network topology. The prediction performance is quantified by how well a predictor is able to highly rank existing interactions over missing ones. However, this approach has been criticized, as the set of used interactions and the one used for the evaluation are the same, thus increasing the risk of overestimating the real performance because of overfitting [13]. Nevertheless, we report the prediction performance using previously applied settings, and analyse the behaviour of our topological-based methods versus state-of-the-art-supervised approaches in these evaluation frameworks. Afterwards, we summarize the results from the removal and re-prediction framework (Figure 2B) in which a certain percentage of interactions is removed (10%), while the topological information of the remaining 90% is used. In this case, the performance is evaluated by how well a prediction method is able to highly rank the removed interactions, which were not existing in the network used to assign the prediction likelihood, compared with all the other possible missing interactions. Finally, we investigate how each method performs exploiting an independent data set of DTIs, which are not present in the original data sets. Moreover, we consider experimental evidences and chemical affinities to define both true-active (positives) and true-inactive (negative) predictions to provide a better estimation of predictive power. To conclude, we report a comparison of predictions by each class’ representative method to shed light on differences in predictions from a network perspective.
Figure 2.
Existing and removal re-prediction evaluation frameworks. (A) Existing link evaluation framework. Every possible link (black and white squares) is left out one time and re-predicted (B) Removal and re-prediction evaluation framework. Ten percent of the network (gray squares) are randomly removed and re-predicted.
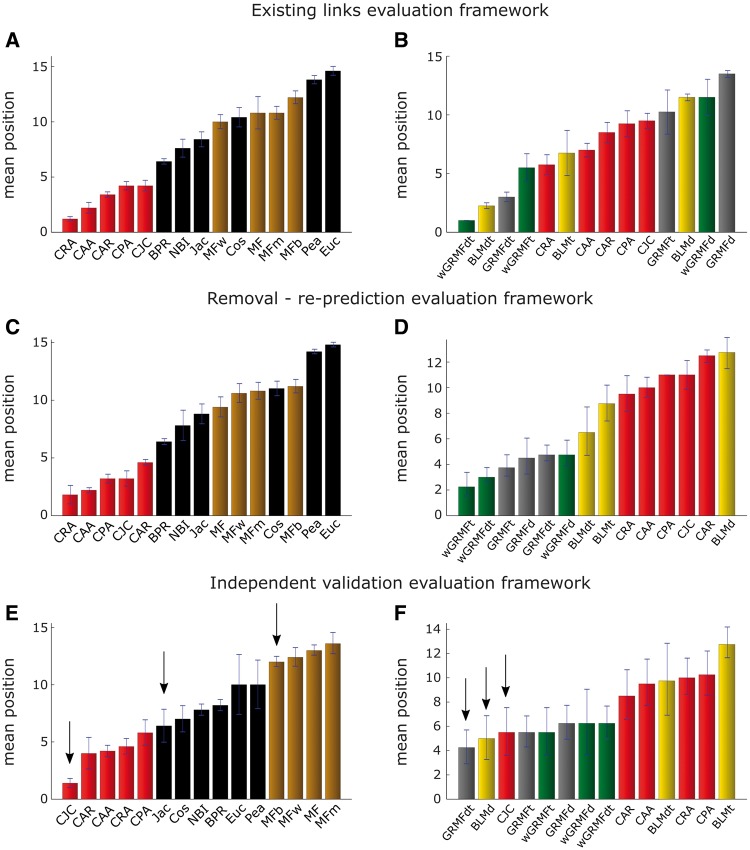
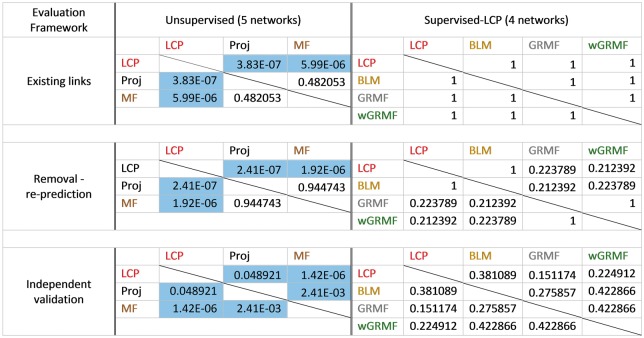
Finally, a procedure that summarizes the general performance of each method within each evaluation framework helps to conclude about the general prediction power of each method for each framework. The common sense of creating an evaluator by the mean or median nAUPR across all the networks inside a given evaluation framework could turn into a biased procedure. In fact, the magnitude of the nAUPRs of the methods for each network might be sensitive to the topological properties of a specific network, favouring some methods and disfavouring others. To this aim, we apply a procedure already adopted with success in two recent link prediction studies [36, 45], which takes the name of position ranking. Here, the methods are ranked for each network by decreasing performance. The mean method’s position in the ranking over all the networks within an evaluation framework represents the final evaluation score. Figure 7 reports these values.
Figure 7.
Mean position ranking on drug–target prediction across all networks within the three evaluation frameworks. Mean position for each method in each evaluation framework over all networks. Each bar in the plot is ordered from the best (left) to the worst (right) method. On the left (A, C and E), comparison of three types of unsupervised methods: LCP-based, projection-based and MF-based. On the right (B, D and F), comparison of three types of supervised methods: BLM, GRMF and wGRMF with unsupervised LCP-based methods. The arrows point the methods selected for the comparison of drug–target prioritization in the first percentile.
What is and how works the LCP theory
In 1949, Donald Olding Hebb [46] advanced a local learning rule in neuronal networks that can be summarized in the following: neurons that fire together wire together. In practice, the Hebbian learning theory assumes that different engrams (memory traces) are memorized by the differing neurons’ cohorts that are co-activated within a given network. Yet, the concept of wiring together was not further specified and could be interpreted in two different ways. The first interpretation is that the connectivity already present, between neurons that fire together, is reinforced, whereas the second interpretation is the emergence and formation of new connectivity between non-interacting neurons already embedded in a interacting cohort.
The first interpretation has been demonstrated in several neuroscientific studies, where it was proven that certain forms of learning consist of synaptic modifications, while the number of neurons remains basically unaltered [47–49]. A first mathematical model of this learning process was implemented in the Hopfield’s model of associative memory, where neuron -assemblies are shaped during engram formation by a re-tuning of the strengths of all the adjacent connections in the network [50]. It is important to specify that neuronal networks are oversimplified models, and between two nodes (that represent two neurons), only one unique connection, which is deceptively called ‘synapsis’, is allowed. This unique artificial synapsis is a network link with a weight (or strength) and abstractly represents in a unique connectivity all the multitude of synapses that can occur between two real neurons in a brain tissue. For non-computational readers, we stress that the word ‘synapsis’ used in computational modelling of artificial neural networks might be misleading for neurobiologists, and should be intended as a mere link between two nodes of a network that comprehensively symbolize the strength of all the real biological synapses connecting two neurons. Here, and in the reminder of this paragraph, we will refer only to this artificial neural network model where a link between two nodes (neurons) indicates an abstract interaction between them. In fact, although this artificial network model is based on evident simplifications, it demonstrated to be a powerful tool to simulate learning processes of intelligent systems [50, 51].
Surprisingly, the second possible interpretation of the Hebbian learning—a cohort of interacting neurons that fire together and give rise to new connections between non-interacting neurons in the cohort—to the best of our knowledge was never formalized as a general paradigm of learning, and therefore, it was never used with success to modify the architecture of abstract neural networks to simulate pure topological learning. We acknowledge the existence of studies that investigate how neuronal morphology predicts connectivity [52]. For instance, Peters’ rule predicts connectivity among neuron types based on the anatomical colocation of their axonal and dendritic arbors, providing a statistical summary of neural circuitry at mesoscopic resolution [52]. However, no paradigms were proposed to explain the extent to which new connections between non-interacting neurons could be predicted in function of their likelihood to be collectively co-activated (by firing together) on the already existing network architecture. This likelihood of localized functional interactions on the existing neural network can be influenced by external factors such as the temporal co-occurrence of the firing activity on a certain cohort of neurons, and by other factors that are intrinsic to the network architecture such as, among the most important, the network topology.
In 2013, Cannistraci et al. noticed that considering only the network topology, the second interpretation of the Hebbian learning could be formalized as a mere problem of topological link prediction in complex networks. The rationale is the following. The network topology plays a crucial role in isolating cohorts of neurons in functional communities that naturally and preferentially—by virtue of this predetermined local-community topological organization—can perform local processing. In practice, the local-community organization of the network topology creates a physical and structural ‘energy barrier’ that allows the neurons to preferentially fire together within a certain community and therefore to add links inside that community, implementing a type of local topological learning. In few words: the local-community organization influences (by increasing) the likelihood that a cohort of neurons fires together because they are confined in the same local community, and, consequently, also the likelihood that they will create new connections inside the community is increased by the mere structure of the network topology. Inspired by this intuition, Cannistraci et al. called this local topological learning theory epitopological learning, which stems from the second interpretation of the Hebbian leaning. The definition was not clearly given in the first article [31] that was immature, and therefore, we now provide an elucidation of the concepts behind this theory by offering new definitions. Epitopological learning occurs when cohorts of neurons tend to be preferentially co-activated because they are topologically restricted in a local community, and therefore, they tend to facilitate learning of new network features by forming new connections instead of merely re-tuning the weights of existing connections. As a key intuition, Cannistraci et al. postulated also that the identification of this form of learning in neuronal networks was only a special case; hence, the epitopological learning and the associated LCP were proposed as local rules of learning, organization and link growth valid in general for topological link prediction in any complex network with LCP architecture [31]. On the basis of these ideas, they proposed a new class of link predictors that demonstrated—also in following studies of other authors—to outperform many state-of-the-art local-based link predictors [31–36, 45, 80] both in brain connectomes and in other types of complex networks (such as social, biological, economical, etc.). In addition, they proposed that the LCP is a necessary paradigm of network organization to trigger epitopological learning in any type of complex network, and that LCP-corr is a measure to quantitatively evaluate the extent to which a given complex network is organized according to the LCP. In conclusion, the LCP originated from the initial idea to explain how the network topology indirectly influences the process of learning a memory by adding new connections in a network of neurons, and consequently generalized to advocate mechanistic modelling of topological growth and self-organization in real monopartite [31] and bipartite [30] complex networks. This explains the title of this article and justifies the theoretical fundaments behind our results.
Evaluation on existing links
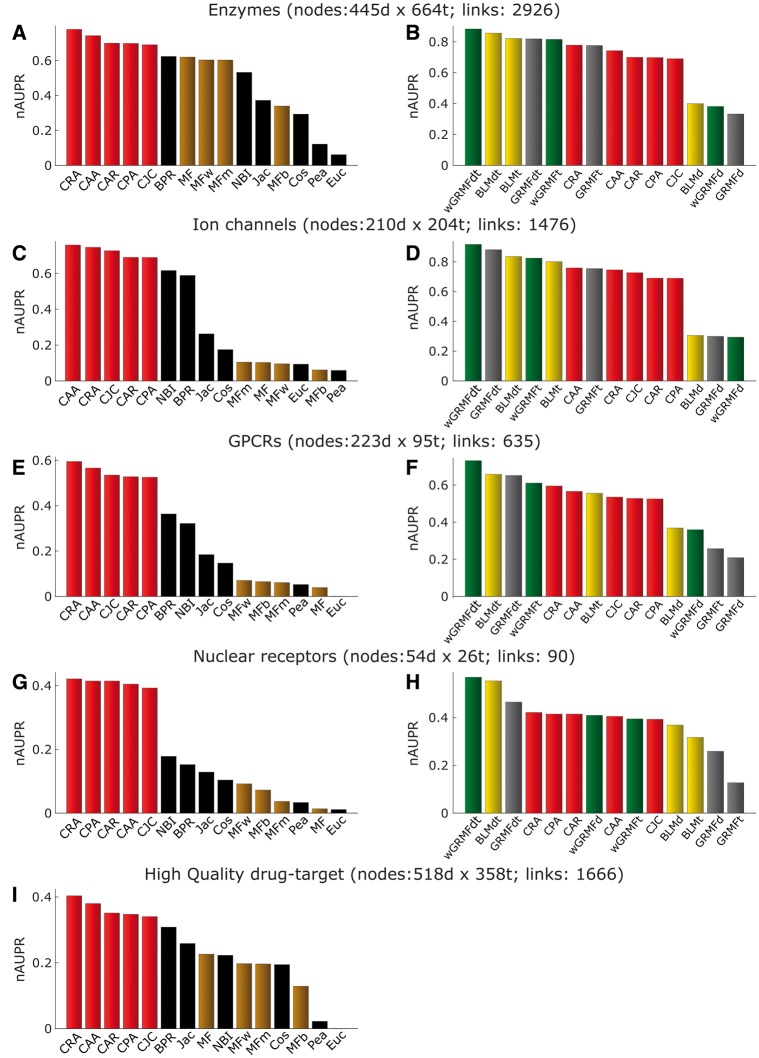
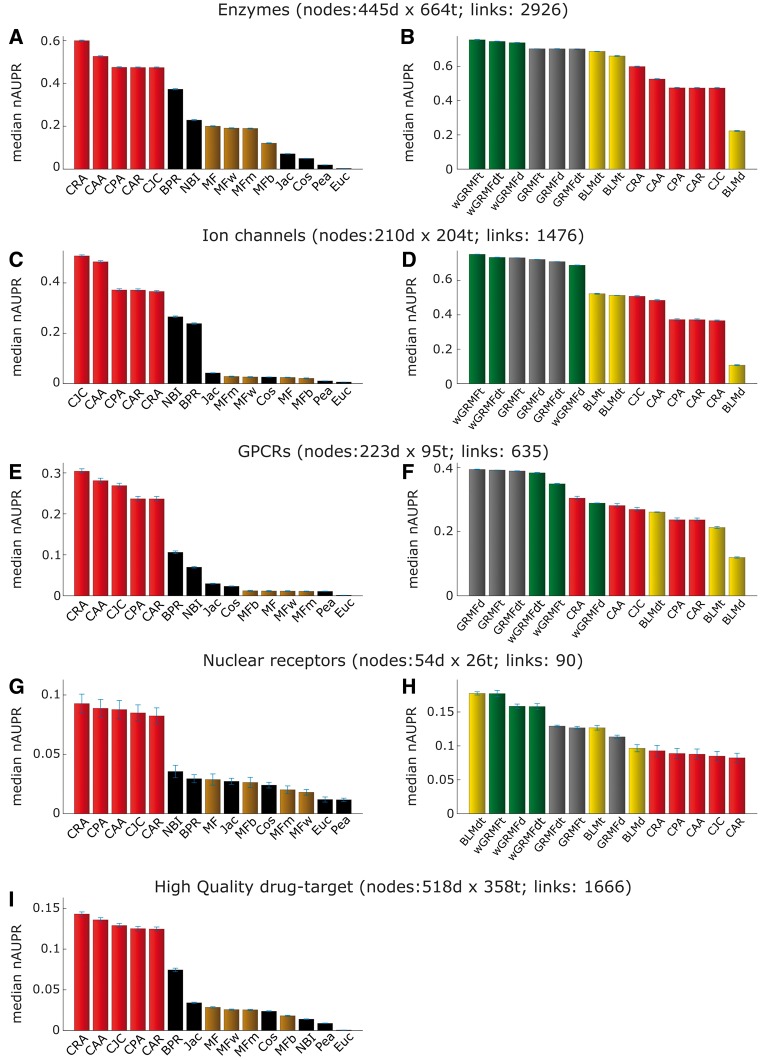
In the first evaluation framework (see ‘Methods’ section and Figure 2A for details), we considered the same settings used in previous publications [4, 37]. In particular in Figure 3A–H, we replicated the same analysis as described by Bleakley and Yamanishi [37] on their four data sets. In the left part of Figure 3, we compared the prediction performances of the unsupervised methods, while on the right part of Figure 3, we compared the prediction performance of supervised and LCP-based methods. In every network, the computed values of nAUPR for the three versions of the BLM approach show the reproducibility of previously reported AUPR values from the original work (Figure 3, right). This means that the AUPrandom has negligible values, and the nAUPR is close to the AUPR. Interestingly, in general, the supervised methods wGRMFdt and BLMdt, which exploit additional biological knowledge from both perspectives (chemical similarity for drugs and protein sequence similarity for targets) achieve the best results. However, it is clear that the two components have different impact, as the prediction performance of wGRMFt and BLMt is generally outperforming wGRMFd and BLMd. Despite it is not completely fair to compare supervised with unsupervised methods, it is surprising that LCP-based measures exploiting only topological features achieve prediction performances comparable with the supervised methods (Figure 3, right). This is confirmed because, considering the overall performance across all the networks (Figure 7B) and their respective AUPR, there is no significant difference between wGRMF, BLM and LCP methods (Figure 8). Conversely, the overall performance of LCP methods, if compared with the other unsupervised methods, is significantly higher (the P-values in Figure 8 are < 0.05). Finally, looking at the Precision-Recall (PR)-curves in Supplementary Figure S1—where the results of all the best-class methods are reported for each network—it is evident that in three networks (ion channels, GPCRs and NRs), the best LCP method overcomes the best BLM one in the first part of the ranking (in this case, until about recall <0.2). Remarkably, considering always the prioritization in the first part of the ranking, in GPCRs network, the best LCP method offers a performance even higher than the best wGRMF method, while in the NR network, the best LCP method offers a performance even higher than the best GRMF.
Figure 3.
Performance comparison in the existing links evaluation framework. Normalized AUPR values considering all existing links as TP as described in Figure 2A. On the left (A, C, E, G and I), comparison of three types of unsupervised methods: LCP-based, projection-based and MF-based. On the right (B, D, F, and H), comparison of three types of supervised: BLM, GRMF and wGRMF with unsupervised LCP-based methods.
Figure 8.
Statistical comparison for the classes of supervised and unsupervised methods. P-values computed by the non-parametric Mann–Whitney test and adjusted by Bonferroni’s correction for the classes of supervised and unsupervised methods in the three evaluation frameworks. Significant differences between classes of methods are highlighted in blue. On the left, comparison between three types of unsupervised methods: LCP-based, projection-based and MF-based. On the right, comparison of three types of supervised methods: BLM, GRMF and wGRMF with unsupervised LCP-based methods.
Removal and re-prediction
In this framework (Figure 2B), we aim to evaluate how well a method is able to generalize, trying to minimize the risk of overfitting to the known existing topology. The median AUPR results over 100 realizations are shown in Figure 4 as described for the removal and re-prediction evaluation framework. Every method behaves similarly as in the previous evaluation framework. However, few important differences are present and provide valuable information regarding each prediction strategy. First, each method’s performance is lower across all the networks (compare Figure 3B, D, F, and H versus Figure 4B, D, F, and H). This could be either because of a general overestimation of the performance in the first framework, or it could be because of information loss caused by the removal of a certain percentage of interactions. However, an interesting outcome of this evaluation is that although the difference between supervised and LCP-based methods is larger (notice that the respective P-values in Figure 8 are lower), it remains still not significant, and in the case of the GPCR network, three LCP-based measures perform better than the BLM-supervised method (Figure 4F). This result confirms that also in this framework, the performance of LCP-based methods is comparable with the one of supervised predictors (Figure 8, right panel, P-values >0.05) and, on the other side, LCP methods perform again significantly better than the other unsupervised methods (the respective P-values in Figure 8, left panel, are <0.05). Furthermore, considering the overall performance across all the networks (Figure 7C), the position of LCP and BLM methods is clearly in the same range.
Figure 4.
Performance comparison in the removal and re-prediction evaluation framework. Median of normalized AUPR values (over 100 repetitions) from the removal and re-prediction evaluation framework described in Figure 1D. On the left (A, C, E, G and I), comparison of three types of unsupervised methods: LCP-based, projection-based and MF-based. On the right (B, D, F and H), comparison of three types of supervised methods: BLM, GRMF and wGRMF with unsupervised LCP-based methods.
We note also that the NRs’ network has a different behaviour (all the methods perform lower) compared with the other data sets. However, this data set has a small dimension (only 90 interactions); therefore, both the topological information and the biological knowledge are limited and not so reliable as already noted in the original analysis [37]. To provide more details regarding the performance in the first part of the ranking, which is the most important for real applications, in Supplementary Figure S2, we show the PR curves of all the best-class methods for each network. Again, in the same three networks (ion channels, GPCRs and NRs), the best LCP method largely overcomes the best BLM one for prioritization of correctly predicted links in the first part of the ranking (recall <0.2). It is also confirmed that, considering the first part of the ranking, in GPCRs network, the best LCP method outperforms even the best wGRMF one, while in the NR network, the best LCP method offers a performance even higher than the best GRMF.
Interestingly, in the high-quality network (Figure 4I), all unsupervised methods, except the Euclidean (Euc) distance, show a significant improvement versus the random predictor, suggesting that even in complex scenarios with a variety of drug and target categories, the network topology offers enough information content for high-quality link prediction.
Validation with an integrated independent benchmark set
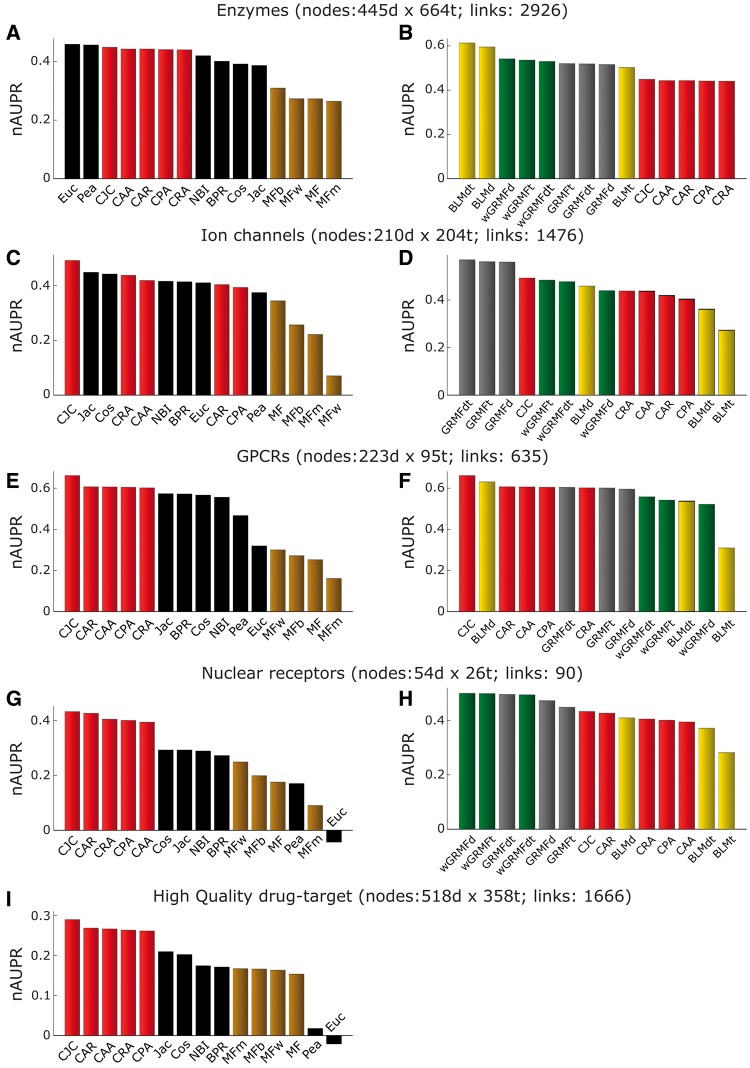
The validation of novel DTIs is generally a time-consuming and expensive endeavour. However, we can profit from the newly experimentally verified interactions, summarized in Supplementary Table S1, that have been discovered in the years following the publication of the original networks [37, 44]. Moreover, here, we tackle the known problem of missing drug–target data, by defining a reasonable chemical affinity range to consider a DTI as active or inactive. Thanks to the definition of both positive and negative interactions, it is not only possible to identify novel TP prediction but also to discriminate inactive interactions, i.e. FPs, from predictions for which no data are available (i.e. unknown). In this way, we can reliably estimate both precision and recall of each method as described in the ‘Methods’ section. Indeed, similar evaluation strategies have been proven beneficial for model generation and better performance estimation in previous analyses [39]. To compare the prediction power of different methods in each network, we report the nAUPR values in Figure 5. Additionally, after ordering each list of predictions by the specific method ranking, the respective 1st (Supplementary Table S2), 5th (Supplementary Table S3) and 10th (Supplementary Table S4) percentile of interactions has been selected and thoroughly evaluated against the independent set of novel positive or negative DTIs.
Figure 5.
Performance comparison in the independent validation evaluation framework. Normalized AUPR values considering the independent validation evaluation framework as described in the ‘Methods’ section. On the left (A, C, E, G and I), comparison of three types of unsupervised methods: LCP-based, projection-based and MF-based. On the right (B, D, F and H), comparison of three types of supervised methods: BLM, GRMF and wGRMF with unsupervised LCP-based methods.
Surprisingly, in contrast to the previous evaluation frameworks, where BLM-supervised methods offered a comparable (Figure 8, right panel, P-value >0.05: difference not significant) but generally higher AUPR than LCP methods (Figure 4B, D and H), here in three of four networks (Figure 5D, F and H), the AUPR of LCP methods is higher. This is evident also from the overall performance across all the networks provided in Figure 7F. With this third type of evaluation, we have a further evidence that also in this framework, the performance of LCP-based methods is comparable with the one of supervised predictors (Figure 8, right panel, P-values >0.05). On the other side, we have a final confirmation that the LCP methods perform significantly better than the other unsupervised methods (the respective P-values in Figure 8, left panel, are<0.05). However, it is important to notice that both for LCP and projection methods, the best approach was always a variation of the Jaccard (Jac) measure. In fact, the best LCP method was the Cannistraci–Jaccard variation (CJC), and the best projection method was the Jac similarity applied after one-mode projection of the bipartite network.
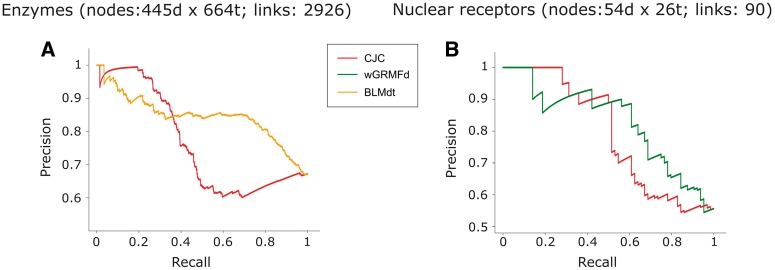
Interestingly, if we analyse the results singularly for each network, we notice that there is not a real overall predictor winner. BLMdt achieves the best performance in the enzyme network, GRMFdt is the best in ion channels, CJC is the best in GPCRs and wGRMFd is the best in NRs. Furthermore, many projection-based spatial distance (such as Jac and Euc) methods, which offered a lower performance in the previous validation frameworks, show in the independent validation a predictive power close (but still significantly inferior, Figure 8, P-value <0.05) to supervised and LCP-based methods. We speculate that the reasons for this behaviour might reside in an experimental bias, as classical spatial distances have been used to identify novel interactions in drug discovery for longer time, while LCP-based or bipartite projection via random-walk (BPR) are recent models. On the other side, the complete picture of all possible DTIs is still unclear; thus, those results could also suggest that different methods are indeed all able to retrieve true interactions, which might be associated to different topological properties. For this purpose, in the next section, we will investigate how similar are the first percentile predictions retrieved by the different classes of approaches. Finally, to investigate the performance in the first part of the ranking (the most important for real applications), Figure 6 emphasizes that CJC (the best LCP method) offers in enzymes and NRs (two of four networks) even a better prioritization (recall <0.2) than the BLMdt and wGRMFd, which, respectively, provide the best nAUPR in each of these networks. For completeness, the best-class methods for all networks are reported in Supplementary Figure S3.
Figure 6.
Precision–recall curves of the independent validation evaluation framework. For each class of prediction methods, the best method in enzymes and NR network was compared with the best LCP-based method: LCP-based (red), BLM (yellow) and wGRMF (green). (A) Precision–recall curves in enzyme network, LCP-based (CJC) versus BLM (BLMdt). (B) Precision–recall curves in NR network, LCP-based (CJC) versus wGRMF (wGRMFd).
Comparison of novel predicted interactions
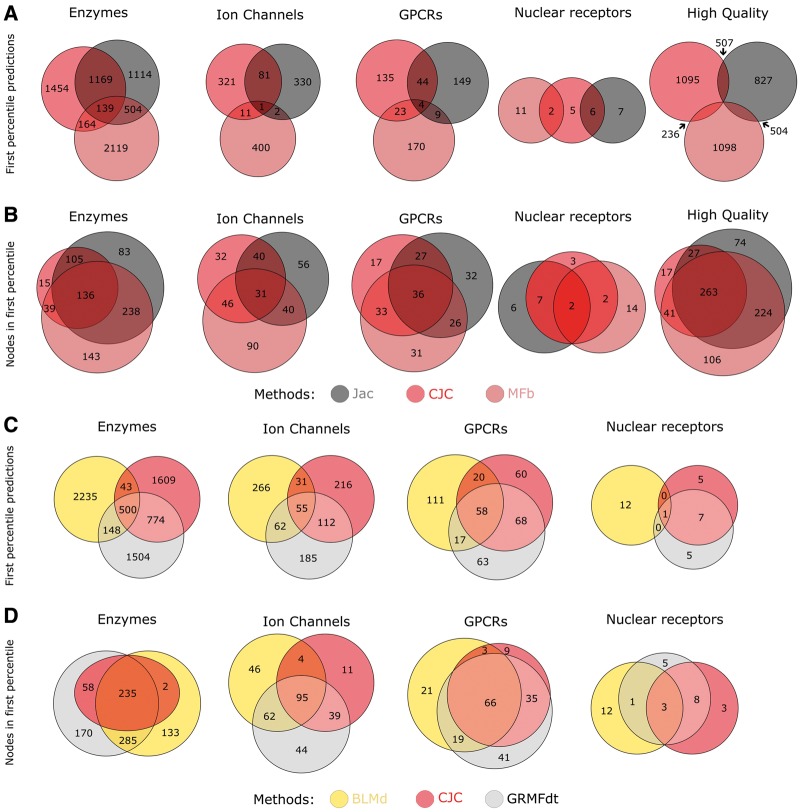
In this section, we will shed light on the differences in drug–target prioritization between the distinct approaches considering the overall performance displayed in Figure 7E and F for the independent validation framework. We selected the first three best-class methods in the unsupervised comparison [Figure 7E, pointed by an arrow: CJC, Jac and best matrix factorization (MFb)] and in the supervised comparison (Figure 7F, pointed by an arrow: GRMFdt, BLMd and CJC) and analysed whether they prioritize similar interactions in the first percentile of their ranking. Instead, an overview that reports the comparison between all the methods is offered in Supplementary Figure S5.
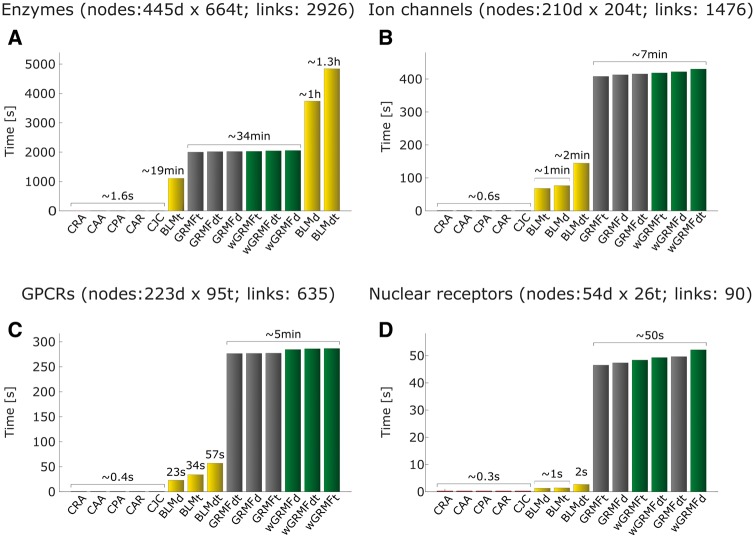
As clearly visible, for each network in Figure 9A and C, a small percentage of predictions is shared by all the three methods in the unsupervised and supervised comparison. In the unsupervised prediction comparison, the projection-based predictor shows higher mutual overlap with the LCP-based predictor than with the MF-based method. Notably, in the comparison with supervised methods, GRMFdt has higher mutual overlap with the LCP-based method CJC than with the BLM one. A similar trend is observed also considering the predictions identified as TPs or FPs in the independent validation, which are only partially shared by the methods (Supplementary Figure S4). As supervised methods rely on additional similarity measures other than network structural properties, it is not surprising that they tend to predict different DTIs compared with unsupervised topology-based methods. However, we expected that supervised methods tend to share more similar predictions between them than with unsupervised ones. Instead, surprisingly, we found that GRMFdt (which is the more computationally expensive method, Figure 10) tends to prioritize interactions more similar to the ones predicted by the unsupervised LCP method CJC (which is the less computational demanding, Figure 10) than to BLMd.
Figure 9.
Comparison of novel predicted interactions. (A) Overlap of the first percentile predictions in five networks for unsupervised methods, considering the representative method of each class: MFb (MF-based), Jac (projection-based) and CJC (LCP-based). (B) Overlap of the nodes (drugs and targets) involved in the first percentile predictions for the unsupervised methods. (C) Overlap of the first percentile predictions in four networks for supervised and LCP-based methods, considering the representative method of each class: BLMd (supervised), GRMFdt (supervised) and CJC (LCP-based). (D) Overlap of the nodes (drugs and targets) involved in the first percentile predictions for the previous methods.
Figure 10.
Comparison of computational time between supervised and LCP-based methods. Comparison of computational time on supervised and LCP-based methods for one simulation attempt. (A) Enzyme network, (B) ion channel network, (C) GPCR network, (D) NR network.
For instance, considering the biggest network, enzymes, only around 5% of the predictions in the respective first percentile (139 of 2926) are common to all three unsupervised methodologies; however, around 45% of the novel predicted links are shared between the projection-based Jac and LCP-based method CJC (which are both local approaches), and around 10% between MF-based and LCP-based method. This could be because of the fact that MF is the only global approach between the unsupervised, while LCP is the one that stresses more local topology prediction. In the comparison with supervised methods, around 17% (500 of 2926) of the predicted interactions are commonly shared, while around 22% of the predicted interactions are shared between both supervised methods, and impressively, around 44% are shared between the GRMF-based and LCP-based ones. This last result could be interpreted if we recall the theory behind GRMF. Although GRMF methods are global (because they use MF for inference), they adopt a GR to prevent overfitting. In the GR step, the similarity matrices are sparsified beforehand by keeping only the similarity values to the nearest neighbours for each drug/target [14]. By doing so, the GR is able to learn a manifold on which (or near to which) the data are assumed to lie [14]. In practice, the type of GR used by GRMF methods is based on nearest neighbours; therefore, it is a local-based adjustment, which could explain why GRMF prioritization is more similar to LCP than to BLM one.
Similar trends can be observed in the other networks. In general, the small number of shared predictions between all the methods can be explained by the fact that each class of predictors exploits different properties of the networks. However, considering the perspective of the number of diverse drugs and targets included in the respective first percentile predictions, the supervised methods includes, in general, a higher number of nodes, suggesting their ability to prioritize interactions across more diverse nodes. Such result is expected, as supervised methods rely on biological knowledge. Instead, topology-based methods (CJC, Jac and MFb) tend to obtain nodes and prioritize interactions involving a smaller set of drugs and targets limited by the network topology. In conclusion, meaningful predictions are proposed by each method, even though different sets of interactions are prioritized. Those results suggest that an ensemble algorithm based on a combination of methodologies could improve the prediction performance of any single approach.
Discussion
This study deals with the complex problem of drug repositioning and network-based DTI prediction. For this purpose, three evaluation frameworks were proposed, in which the performance of distinct predictors revealed how classical validation strategies might lead to over-optimistic results. In particular, we investigated the limits of different evaluation frameworks by comparing 24 variations of six state-of-the-art prediction methods applicable with bipartite drug–target networks, belonging to two main classes: unsupervised (among which we considered the new LCP-based techniques) and supervised. Precisely, the unsupervised methods rely only on the network topology, therefore are general-purpose methods for link prediction in bipartite networks that in the context of this study were applied to drug–target networks. On the other side, the supervised methods adopt both the network topology and the biological information, therefore are tailored only for applications in drug–target networks.
The first important result of this study is that LCP topological similarities represent ‘next generation’ unsupervised methods for network-based DTI prediction because they significantly outperform the previous state-of-the-art ones, in all the evaluation frameworks (Figure 8, left panel). The second key result, which is also surprising, is that LCP topological similarities perform comparably with the state-of-the-art supervised methods because their performance is not significantly different from the supervised approaches (Figure 8, right panel).
For application of these methods in real scenario, we could consider two crucial aspects: the computational time-consumption and the prioritization of true drug–targets offered by each singly method in the first part of their ranking. For the time-consumption, in Figure 10, we show that LCP-based methods, although have comparable results (Figure 8, right panel, P-values >0.05) with supervised methods, require only seconds (Figure 10A) or even fraction of seconds (Figure 10B–D) to issue predictions, while supervised methods require from seconds to hours depending on the size of the network. Note that the time reported in Figure 10 was calculated just for one attempt of the method per network. It means that in the case of the removal and re-prediction evaluation framework, the required computational time for the simulation was ∼100 times bigger. On the other hand, regarding the prioritization in the first part of the ranking, the LCP-methods tend to offer a performance often superior to many supervised ones for recall <0.2, and this is an impressive result. For instance, in the independent validation framework, for two of four networks, the same LCP method (named CJC) unexpectedly offers a better precision in prioritization (recall <0.2) of true DTIs, than the best supervised ones, respectively, in each network (Figure 6). In general, across the different evaluation frameworks, LCP predictors surpass the performance of BLM ones in the prioritization of true correct predictions. However, the fact that the performance of LCP-methods starts to drop down for recall >0.2 is because of the fact that, while LCP predictors are local methods (they offer prediction only for links with CNs), the other techniques not only are supervised but also global. In fact, global methods exploit the entire network topology, and not only the CNs’ topology, for making inference. As the performance in the first part of the ranking is crucial for suggesting truthful candidate DTIs in real applications, the good results attained by LCP methods in this task represent the third key finding of this study.
In practice, the three important results previously discussed point by point, taken together, suggest that the local topology (neighbourhood connectivity) alone, if adequately squeezed out by means of the LCP theory, contains yet enough information to achieve a prediction performance comparable with the current and more sophisticated supervised methods, which in turn exploit additional biological information. From the biological point of view, this result is reasonable, as the underlying modular and community-based structure of the drug–target network has been extensively described [28]. In general, the drugs’ and targets’ ability to bind a small cohort of partners is an accepted property, although the motivations behind drug promiscuity are not yet fully understood [53]. The LCP theory—which was initially formalized in brain-network self-organization topology and afterwards generalized to any complex network—and the derived LCP topological similarities exploit this modular- and community-based structure of the drug–target networks. In practice, the local-community organization of the network topology creates a physical and structural energy barrier that allows the DTIs to preferentially appear within a certain reduced number of communities, enabling local topological learning of new links in the complex network. Nevertheless, we expect that creating a geometrical version of the LCP predictors—for instance, taking into account the biological information as link weights (node distances)—might boost the performance of the existing ones that are indeed merely based on the network topology. On the other hand, also the computational strategy of current supervised methods might be modified to exploit the topology related with the local community links (LCLs) as the LCP theory suggests. An idea could be, for instance, the integration of such more complex LCP-based topological measures as features for the supervised classification. Finally—and this represents the forth key finding of our study—a detailed analysis of the novel drug–target predictions revealed that each class of methods prioritizes distinct true interactions; hence, combining methodologies based on diverse principles, by using consensus modelling, represents a promising strategy to improve drug–target discovery. Herewith, a clarification is necessary. This study was focused on the investigation of the main classes of unsupervised topological-based models. In addition, the LCP methods, which largely outperformed the other unsupervised methods, were compared with three important state-of-the-art-supervised models, two of which (GRMF and wGRMF) are recent. However, the research of drug–target prediction methods is ‘feverish’ and rich of diverse and multifaceted approaches [9, 10, 27, 54–60] that either are specialized on particular types of targets or are able to integrate different types of biological knowledge. We leave to future studies the mission to compare the diversity of the drug–target predictions possibly offered by the multitude of presently available supervised methods.
The results here provided indicate that the definitions of CNs and LCP theory in complex bipartite networks, and their particular application in drug–target ones, are not only an interesting theoretical innovation in the field of complex networks but also a practical contribution to enhance performance in drug repositioning by means of network-based drug–target prediction. On the other side, we should notice that the problem of evaluation and validation is still an important open problem in this field. We suggest that future studies involving drug–target prediction methods should include more general evaluation frameworks to prevent over-optimistic estimations caused by the overfitting to the known network topology. Finally, this study does not endorse the idea of finding the best drug–target prediction method or of opposing different methods’ categories. Instead, we advocate a new vision in which the evaluation and the integration of different strategies in ensemble algorithms or composite models represent the real improvement towards more reliable predictions. From the applicative perspective, further investigation of the validity of the novel DTIs predicted here or the application of such methodologies to large-scale data sets, bares a high potential for drug discovery and repositioning.
To conclude, previous studies demonstrated how bio-inspired modelling can capture the basic dynamics of network adaptability through iteration of local rules, and produce in few hours of computing solutions with properties comparable with or better than those of real-world infrastructure networks, which would require many months of designing by teams of engineers [61]. Similarly, this article aims to promote bio-inspired computing, demonstrating that simple unsupervised rules that emulate principles of network self-organization and adaptiveness arising during learning in living intelligent systems (like the brain) can in few seconds offer results comparable with complicated algorithms based on advanced, supervised and knowledge-based engineering, which require hours of computing when applied on large networks.
Methods
We applied 24 variations of six state-of-the-art methods to five distinct DTI networks. The methods are summarized in Table 1, and can be subdivided into approaches belonging to two main categories: supervised methods and unsupervised topology-based methods.
Network data sets and biological similarity measures
A set of well-established and widely used gold standard DTI networks [4, 37]—including four distinct protein classes: enzymes, ion channels, GPCRs and NRs—was used as a basis for this work. These four networks from publication [37] were assembled from the following data banks: Kyoto Encyclopedia of Genes and Genomes (KEGG) BRITE [62], BRENDA [63], SuperTarget [64] and DrugBank [65], where cofactors are not included except when they are annotated as regulators in BRENDA database. Compounds with molecular weights <100 were removed also. The networks have the following composition:
Enzymes: 445 drugs, 664 targets, 2926 existing and 292 554 missing interactions.
Ion channels: 210 drugs, 204 targets, 1476 existing and 41 364 missing interactions.
GPCRs: 223 drugs, 95 targets, 635 existing and 20 550 missing interactions.
NR: 54 drugs, 26 targets, 90 existing and 1314 missing interactions.
Moreover, for each of those data sets, in the supervised setting, relevant biological knowledge such as the compound chemical similarity and the protein sequence similarity is considered. We use those networks and biological measures as provided by the authors (http://web.kuicr.kyoto-u.ac.jp/supp/yoshi/drugtarget/) and as described in the original paper [37].
Additionally, we considered a recent drug–target network of high-confidence activity data [44], which comprises interactions from ChEMBL [66] and DrugBank [65]. This network was carefully constructed selecting only compounds, targets and their interactions having high-quality experimental evidences and consistently reported in different data sources:
HQ drug–target network: 518 drugs, 358 targets, 1666 existing and 183 778 missing interactions.
Supervised methods for DTI prediction
The supervised method named BLM [37] is generally reported as an established state-of-the-art approach for DTI prediction. Table 1 indicates the three versions of the BLMs (BLMdt, BLMt and BLMd) that are considered in this work. The computation of predictions from each BLM version is performed using the MATLAB implementation (http://cbio.ensmp.fr/∼yyamanishi/bipartitelocal/) provided by the authors [37].
On the other hand, we considered also two recent advanced supervised approaches for DTI prediction that are confirmed to perform better than many previous ones [14]. The first is known as GRMF. The second is named WKNKN + GRMF, but here for brevity, we will call it wGRMF. In practice, it consists of GRMF applied on a pre-adjusted drug–target adjacency matrix by means of a preprocessing named WKNKN. Table 1 indicates the three versions [which include the dt (drug–target), d (drug) and t (target) variants] for each of these two methods for six variations. The computation of predictions for GRMF and wGRMF was performed using the MATLAB implementation provided by the authors [14].
Unsupervised drug–target prediction methods
For predictions of novel interactions in bipartite networks, unsupervised methods can be divided into projection-based, MF-based and model-based methods.
Projection-based methods
It has been shown that any bipartite network can be projected into its two monopartite networks by bipartite network projection [24]. Various methods have been proposed, which exploit one or both monopartite layers obtained from a bipartite network to infer new links. Conceptually, two ways of calculating scores for novel links are applied on the projected network: similarity measures [e.g. Pearson (Pea) correlation [16]] or model based on physical processes [e.g. resource allocation (RA) [24], or random walk [40]]. Based on the vectorial representation of the two one-mode projections, we applied the following models with a drug-centric perspective: NBI [24] and BPR [40], and calculated four spatial distance similarities: Jac, Euc, cosine (Cos) and Pea. All those measures have been computed as described by Coscia et al. [40], using the authors’ python implementation (www.michelecoscia.com). For every drug d and target t not already interacting, the predicted likelihood is computed as the sum (NBI and BPR) or the average (Jac, Euc, Cos and Pea) of each similarity of t to all the known targets of d, where the t-t similarity is defined by the above topology-based metrics.
MF-based methods
A subset of singular value decomposition (SVD)-based methods (using the MATLAB SVD function and the largest singular values) were extrapolated following the mechanism of GRMF. We adapted the supervised method to work in an unsupervised (without information on chemical and sequence similarities) environment. Thus, four versions of MF methods were created using the SVD function: MF, MFb, mean matrix factorization (MFm) and weighted matrix factorization (MFw). The differences are in the exploitation of the cross-validations (CVs) to obtain the final link scores. MF does not use CV at all, and its computation is given by the following MATLAB code:
Where x is the original bipartite network adjacency matrix (which is not squared because the drugs and targets are in different numbers), and y is its low-rank approximation that contains the scores, which represent the likelihood for each observed and non-observed link.
The other three methods work in the following way. In the CV step, the original network is sampled at random to generate 10 different CV networks with 90% of the original network in it. The SVD function is used to generate the scores for the interaction ranking, and an evaluation function is used in each CV to calculate the AUPR of the current used CV network. MFb uses the scores of the CV network that obtained the best AUPR in the evaluation, MFm uses the mean among all the scores calculated and MFw uses weighted scores given by the calculated AUPRs as:
Where is the number of CVs (10 rounds in our case), is the AUPR in, are the scores of the subnetwork in and is the summation of all the AUPRs obtained.
Model-based methods
In many previous works from disparate fields, it has been shown that node neighbourhood topological information can be exploited for link prediction. In particular, classical measures such as CNs [20], JC [21], Adamic and Adar [67] and RA [24] are powerful measures to estimate the likelihood of an interaction between two nodes in monopartite networks. Similarly, the PA model [18] can be generalized to assign the likelihood of appearing interactions in growing networks.
While the PA model has been already applied for link prediction in bipartite networks [19], a reformulation of CN has been just recently proposed [30] for its application to bipartite networks. Here, we report the explicit formulation of CNs for calculating the likelihood of any possible interaction in undirected bipartite networks between a drug dx and a target ty:
| (2) |
where N(dx) and N(ty) indicate the first-layer neighbours, and N(N(dx)) and N(N(ty)) represent the second-layer neighbours of the drug dx and target ty, respectively.
Figure 1B shows, for a missing interaction dx-ty (right) or an existing interaction dz-ty (left), the respective set of CNs (Equation (2)), which are accounted to calculate the likelihood of the interaction in consideration. As a matter of fact, the commonly accepted notion that CNs are emerging from the triadic closure rule was demonstrated to be misleading by Daminelli et al. [30]. Instead, according to their definition [30], CNs between two nodes of different classes are all the nodes touched by all the possible shortest paths of the minimum length allowed by a given topology between these two nodes. For instance, in a monopartite network, the minimum length shortest path allowed by the topology is two steps, and therefore, it coincides with the triadic closure, which is only a specific geometrical transfiguration of the general rule. In fact, in a bipartite network, the minimum length shortest path allowed by the topology between different-class nodes is three steps; hence, the generative rule coincides with the quadratic closure. Instead, the minimum length shortest path allowed by the bipartite topology between same-class nodes is two steps; hence, the generative rule coincides with the triadic closure [68].
Local community-based methods
The LCP theory was developed in the theoretical framework of undirected monopartite complex networks [31] and recently extended to the bipartite domain [30] on the basis of the definition of CNs in bipartite networks discussed in the previous chapter. An exhaustive clarification of this theory was given in a dedicated subsection of the ‘Results’. Here, we only need to report that in both monopartite and bipartite topologies, the application of the LCP theory significantly improved the link prediction power of classical CN-based methods. Therefore, in this study, we decided to consider five LCP-based methods (also known as Cannistraci formulations [30]) adapted to bipartite networks: Cannistraci–Alanis–Ravasi (CAR), CJC, Cannistraci preferential attachment (CPA), Cannistraci–Adamic–Adar (CAA) and Cannistraci resource allocation (CRA). In each of those methods, the information content of a drug and a target neighbourhood is complemented with the topological information of the interactions (LCLs) between the cohort of their CNs (calculated as in Equation (2)), as depicted in Figure 1B. The formulation of CAR, CJC, CPA, CAA and CRA used to compute an interaction likelihood is reported in Table 1. The computation of any LCP-based method has been performed with the MATLAB code (available at: https://sites.google.com/site/carlovittoriocannistraci/5-datasets-and-matlab-code/bipartite-link-predictors) released in a previous publication [30].
Evaluation frameworks
Three evaluation frameworks have been considered to compare the performance of each prediction method: a complete leave one-out CV, a 10% removal and re-prediction evaluation (repeated 100 times) and an independent validation set. In each framework, we applied the topological models or the supervised methods described above to calculate an interaction likelihood for each possible combination of drugs and targets (Figure 2A and B). Afterwards, the complete list of interactions is ranked based on the given likelihood. However, in the first validation, the complete network is considered to calculate for each possible link (existing or missing) a likelihood; thus, the set of TPs is equivalent to all existing links (Figure 2A).
In the supervised methods, as a model needs to be built, the specific label of the considered link is left out. A model is built considering all the other interactions, which then is applied to give a likelihood to the single left out interaction. In the unsupervised methods, each link is assigned a likelihood based on the respective metric calculated on the entire topology (all existing links) minus the considered link. After having a likelihood for all possible drug–target pairs, the ranked links are given a class based on increasing thresholds, which are then compared with the original class in the complete network to calculate precision and recall values. Finally, a value of AUPR is given for each method, indicating how good a method is recovering the existing knowledge in the original network.
Such an analysis is the reference approach used for testing drug–target predictions [37]. To make our analysis comparable with previous analyses, we used the identical settings described in the paper by Bleakley and Yamanishi [37], in which they also proposed the reference supervised methods (the BLMs). Instead, in the second evaluation (Figure 2B), a random set of 10% of the interactions is excluded; thus, the likelihood calculation is based only on the topology of the remaining 90% of the links. The performance is evaluated like in the previous framework, but in this case, the set of TPs is only the excluded 10%, while the 90% existing links are not considered [9].
In the first two frameworks, assigning a positive or negative label for each interaction at different thresholds, we calculated the AUPR values for each method. In the second procedure, we repeated the random removal 100 times; thus, the AUPR values are reported as the median over 100 repetitions. The choice of such measure is motivated by the type of data we are considering, as only positive examples are available, and the data are assumed to be highly incomplete [11]. In fact, the AUPR has been reported to be more appropriate to compare the predictor performance in data sets were true-negative examples are missing [5, 69, 70]. Here, precision and recall are calculated at each point in the list, using unitary steps (single new link predicted). Using the values of precision and recall over the ranked prediction list, the AUPR summarizes how good a predictor is able to highly rank the correct predictions as well as its ability to recover all relevant interactions. The random predictor assigns an equal likelihood to any existing, missing or removed DTIs; thus, a list of all possible drug–target combinations is given an independent randomized order in each repetition. In each figure, error bars represent the standard error, calculated as the SD divided by the square root of the sample set dimension.
Independent validation
External validation is vital for assessing the performance of the analysed target prediction algorithms. To this end, millions of drug–target activity data from BindingDB and ChEMBL, binding structural evidences from the Protein Data Bank (PDB) and manually curated interactions from the Therapeutic Target Database (TTD) [71] were integrated into an in-house drug–target database. This resource was already used in previous studies [53, 72, 73], and here, it was used to screen for experimentally validated links, which have been discovered in the past years and are missing in the five original network data sets. The enzymes, ion channels, GPCRs and NR networks [4, 37] are built on KEGG drug and gene ids. Using the KEGG Application Programming Interface (KEGG API) [74], drugs and targets ids were mapped to PubChem Compound Identifiers (CIDs) via Substance Identifiers (SIDs) [75] and Uniprot accession numbers, respectively. Instead, the high-quality drug–target network [76] is based on ChEMBL target ids and Drugbank drug ids. These were mapped to Uniprot accession numbers using the ChEMBL API and to PubChem CIDs using the UniChem [77] mapping, respectively. A drug was considered active against a target if their interaction was reported either in PDB, TTD or in BindingDB with an activity value at least in the mM range (i.e. Ki, Half Maximal (50) Inhibitory Concentration (IC50), Half Maximal (50) Effective Concentration (EC50), Kon or Koff ≤1 mM). Consequently, all pairs with activity values >1 mM were regarded inactive. To complement these data, activity information from ChEMBL assays was added as follows. PubChem CIDs were mapped to ChEMBL compounds using UniChem. For each ChEMBL compound, all available ChEMBL assays were processed and filtered by UniProt accession number using the ChEMBL API. The Python package Pint by Hernan E. Grecco was used for parsing and converting the extracted activity data. Again, a drug was considered active against a specific target if an activity value ≤1 mM was found and inactive if >1 mM. Finally, a manually validated updated network of drug–target pairs recently published by Yamanishi et al. [78] was integrated and considered as active interactions. For each network, the number of originally known and the newly identified interactions (i.e. the independent set), which are missing in the complete network data sets, is reported in Supplementary Table S1. Overall, such an integrated data set including chemical affinity values allows for the definition not only of new positive interactions (active) but also of new negative interactions (inactive). In the independent validation, we considered the ranking of all missing interactions from each complete network. Additionally, as our benchmark set includes both positive and negative evidences, we are able to better estimate each method’s precision. In fact, the vast majority of predictions are neither in the independent positive nor negative set, therefore putative candidates (or unknown).
Statistical comparison between classes of predictor methods
To compare the AUPR values for each method class (projection-based, MF-based, LCP-based, BLM, GRMF and wGRMF), a non-parametric statistical test called Mann–Whitney [79] (which is a test based also on position ranking) was applied in each of the evaluation frameworks. The comparison was performed in two separate manners. For the unsupervised approaches, LCP-based, MF-based and projection-based classes, five networks were statistically compared. While for the supervised approaches, BLM, GRMF, wGRMF and LCP-based classes, four networks were statistically compared. All the P-values shown in Figure 8 were adjusted by Bonferroni’s correction [81] considering multiple testing inside each evaluation framework.
Key Points
The new class of proposed approaches—based on LCP theory—for unsupervised network-based drug–target prediction can achieve comparable performance with more sophisticated supervised methods.
Current evaluation methods of drug–target prediction can lead to over-optimistic results; therefore, we also propose novel evaluation frameworks.
Unsupervised and supervised methods predict almost mutual exclusive sets of interactions; thus, we encourage future studies to combine both classes of algorithms.
The application of the LCP theory on the prediction of DTIs can provide a novel surprising proof of efficiency in support of bio-inspired computing.
Supplementary Material
Acknowledgements
The authors kindly acknowledge Michele Coscia for providing the python implementation to compute the projection-based measures. The authors thank Alexander Mestiashvili and the BIOTEC System Administrators for their IT support, Claudia Matthes for the administrative assistance and the Centre for Information Services and High-performance Computing [Zentrum für Informationsdienste und Hochleistungsrechnen (ZIH)] of the TUD. C.V.C. thanks: Giancarlo Ferrigno for suggesting him (during the Master course in Intelligent Systems at the Polytechnic of Milano) the question on how the arise of new connections could implement a learning rule in artificial neural networks; Antonio Malgaroli for introducing him to the basic notions of neurobiology of learning; Pierre Julius Magistretti for the precious suggestions and the valuable lectures he personally gave him on neurobiology of learning and much more; Corrado Calì for introducing him to the Peters' rule; Hubert Fumelli for suggesting to clarify the idea of connectivity and synapsis in artificial models; Petra Vertes and Edward Bullmore for suggesting to clarify the idea of LCP and epitopological learning in neuronal networks; Saket Navlakha for the interesting discussions on the difference between LCP theory and clustering in complex network; Maksim Kitsak for the useful discussion on the definition of CNs in bipartite topology; Timothy Ravasi for encouraging and supporting in the past his research, giving him the freedom to invent and develop the LCP theory; Peter Csermely for his interest and support to the Local-community-paradigm theory.
Funding
The Technische Universität Dresden (TUD). For C.V.C. The Independent Group Leader starting grant of the BIOTEC, TUD (to C.V.C.). The Klaus Tschira Stiftung gGmbH, Germany, grant name:00.285.2016 (to C.V.C. laboratory).
Biographies
Claudio Durán is a Doctoral Student of the Biomedical Cybernetics group at TUD. His research interests include machine learning, network science and systems biomedicine.
Simone Daminelli is a Postdoctoral Researcher of the Bioinformatics group at TUD. His research interests include network bioinformatics and drug repositioning.
Josephine Thomas is a Doctoral Student of the Biomedical Cybernetics group at TUD. Her research interests include complex network theory.
V. Joachim Haupt is a Postdoctoral Researcher of the Bioinformatics group at TUD. His research interests include drug repositioning.
Michael Schroeder is Professor of Bioinformatics and Group Leader of the Bioinformatics group at TUD. His research interests include bioinformatics and text mining.
Carlo Vittorio Cannistraci is a Theoretical Engineer, Group Leader of the Biomedical Cybernetics group and Young Investigator of the Department of Physics at TUD. His research interests include subjects at the interface between physics of complex systems, complex networks and machine learning theory.
References
- 1. Paul SM, Mytelka DS, Dunwiddie CT, et al.How to improve R&D productivity: the pharmaceutical industry’s grand challenge. Nat Rev Drug Discov 2010;9(3):203–14. [DOI] [PubMed] [Google Scholar]
- 2. Munos B. Lessons from 60 years of pharmaceutical innovation. Nat Rev Drug Discov 2009;8(12):959–68. [DOI] [PubMed] [Google Scholar]
- 3. O’Connor KA, Roth BL.. Finding new tricks for old drugs: an efficient route for public-sector drug discovery. Nat Rev Drug Discov 2005;4(12):1005–14. [DOI] [PubMed] [Google Scholar]
- 4. Yamanishi Y. Supervised Bipartite Graph Inference. NIPS, 2008, 1841–1848. MIT press, Cambridge, USA. [Google Scholar]
- 5. Bleakley K, Biau G, Vert J-P.. Supervised reconstruction of biological networks with local models. Bioinformatics 2007;23(13):i57–65. [DOI] [PubMed] [Google Scholar]
- 6. Yamanishi Y, Araki M, Gutteridge A, et al.Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics 2008;24(13):232–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Xia Z, Wu L-Y, Zhou X, et al.Semi-supervised drug-protein interaction prediction from heterogeneous biological spaces. BMC Syst Biol 2010;4(S6):S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. van Laarhoven T, Nabuurs SB, Marchiori E.. Gaussian interaction profile kernels for predicting drug-target interaction. Bioinformatics 2011;27(21):3036–43. [DOI] [PubMed] [Google Scholar]
- 9. Liu Y, Wu M, Miao C, et al.Neighborhood Regularized Logistic Matrix Factorization for Drug-Target Interaction Prediction. PLoS Comput Biol 2016;12(2). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Wang Y, Zeng J.. Predicting drug-target interactions using restricted Boltzmann machines. Bioinformatics 2013;29(13): i126–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Mestres J, Gregori-Puigjané E, Valverde S, et al.Data completeness—the Achilles heel of drug-target networks. Nat Biotechnol 2008;26(9):983–4. [DOI] [PubMed] [Google Scholar]
- 12. Park Y, Marcotte EM.. Revisiting the negative example sampling problem for predicting protein-protein interactions. Bioinformatics 2011;27(21):3024–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Pahikkala T, Airola A, Pietilä AS, et al.Toward more realistic drug-target interaction predictions. Brief Bioinform 2014;16:325–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Ezzat A, Zhao P, Wu PM, et al.Drug-target interaction prediction with graph regularized matrix factorization. IEEE/ACM Trans Comput Biol Bioinform 2016, in press. [DOI] [PubMed] [Google Scholar]
- 15. Liben-Nowell D, Kleinberg J.. The link-prediction problem for social networks. J Am Soc Inf Sci Technol 2007;58(7):1019–1031. [Google Scholar]
- 16. Breese JS, Heckerman D, Kadie C. Empirical analysis of predictive algorithms for collaborative filtering. In: Proceedings of 14th Annual Conference on Uncertain Artificial Intelligence, 1998, 43–52. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA.
- 17. Koren Y, Bell R, Volinsky C.. Matrix factorization techniques for recommender systems. Computer 2009;42(8):42–49. [Google Scholar]
- 18. Barabási A-L, Albert R.. Emergence of scaling in random networks. Science 1999;286(5439):509–512. [DOI] [PubMed] [Google Scholar]
- 19. Kunegis J, Luca EWD, Albayrak S.. The link prediction problem in bipartite networks In: Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 6178 LNAI, 2010, 380–9. Springer Nature, LNAI, London, UK. [Google Scholar]
- 20. Newman ME. Clustering and preferential attachment in growing networks. Phys Rev E Stat Nonlin Soft Matter Phys 2001;64(2 Pt 2):25102. [DOI] [PubMed] [Google Scholar]
- 21. Jaccard P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull Soc Vaudoise Des Sci Nat 1901;37:241–272. [Google Scholar]
- 22. Easley D, Kleinberg J.. Strong and weak ties In: Networks, Crowds, and Markets: Reasoning about a Highly Connected World. Cambridge University Press, Cambridge, UK, 2010, 47–84. [Google Scholar]
- 23. Nacher JC, Akutsu T.. Structural controllability of unidirectional bipartite networks. Sci Rep 2013;3:1647.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Zhou T, Lü L, Zhang Y-C.. Predicting missing links via local information. Eur Phys J B 2009;71(4):623–630. [Google Scholar]
- 25. Latapy M, Magnien C, Del Vecchio N.. Basic notions for the analysis of large two-mode networks. Soc Netw 2008;30(1):31–48. [Google Scholar]
- 26. Cheng F, Liu C, Jiang J, et al.Prediction of drug-target interactions and drug repositioning via network-based inference. PLoS Comput Biol 2012;8(5):e1002503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Alaimo S, Pulvirenti A, Giugno R, et al.Drug-target interaction prediction through domain-tuned network-based inference. Bioinformatics 2013;29(16):2004–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Yildirim MA, Goh K-I, Cusick ME, et al.Drug-target network. Nat Biotechnol 2007;25(10):1119–26. [DOI] [PubMed] [Google Scholar]
- 29. Zhou T, Kuscsik Z, Liu J-G, et al.Solving the apparent diversity-accuracy dilemma of recommender systems. Proc Natl Acad Sci USA 2010;107(10):4511–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Daminelli S, Thomas JM, Durán C, et al.Common neighbours and the local-community-paradigm for topological link prediction in bipartite networks. N J Phys 2015;17(11):113037. [Google Scholar]
- 31. Cannistraci CV, Alanis-Lobato G, Ravasi T.. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks. Sci Rep 2013;3:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Liu Z, He JL, Kapoor K, et al.Correlations between community structure and link formation in complex networks. PLoS One 2013;8:9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Pan L-M, Zhou T, Lü L, et al.Predicting missing links and identifying spurious links via likelihood analysis. Sci Rep 2016;6:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Tan F, Xia Y, Zhu B.. Link prediction in complex networks: a mutual information perspective. PLoS One 2014;9(9). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Wang T, Wang H, Wang X.. CD-Based indices for link prediction in complex network. PLoS One 2016;11(1):5–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Wang W, Cai F, Jiao P, et al.A perturbation-based framework for link prediction via non-negative matrix factorization. Sci Rep 2016;6:38938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Bleakley K, Yamanishi Y.. Supervised prediction of drug-target interactions using bipartite local models. Bioinformatics 2009;25(18):2397–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Liu T, Lin Y, Wen X, et al.BindingDB: a web-accessible database of experimentally determined protein-ligand binding affinities. Nucleic Acids Res 2007;35:D198–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Mervin LH, Afzal AM, Drakakis G, et al.Target prediction utilising negative bioactivity data covering large chemical space. J Cheminform 2015;7:51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Yildirim MA, Coscia M.. Using random walks to generate associations between objects. PLoS One 2014;9(8):e104813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Zhou T, Ren J, Medo M, et al.Bipartite network projection and personal recommendation. Phys Rev E 2007;76:46115. [DOI] [PubMed] [Google Scholar]
- 42. Kuchaiev O, Rašajski M, Higham DJ, et al.Geometric de-noising of protein-protein interaction networks. PLoS Comput Biol 2009;5(8):e1000454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Cannistraci CV, Alanis-Lobato G, Ravasi T.. Minimum curvilinearity to enhance topological prediction of protein interactions by network embedding. Bioinformatics 2013;29(13):199–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Hu Y, Bajorath J.. Monitoring drug promiscuity over time [v1; ref status: indexed]. F1000Res 2014;3:218.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Pech R, Hao D, Pan L, et al.Link Prediction via Matrix Completion epl journal, IOP science, France, 2016;117(3): 1–7. [Google Scholar]
- 46. Hebb DO. The Organization of Behavior, Vol. 911. John Wiley and Sons Inc., Hoboken, NJ, USA, 1949.
- 47. Corti V, Sanchez-Ruiz Y, Piccoli G, et al.Protein fingerprints of cultured CA3-CA1 hippocampal neurons: comparative analysis of the distribution of synaptosomal and cytosolic proteins. BMC Neurosci 2008;9(1):36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Ziv NE, Ahissar E.. Neuroscience: new tricks and old spines. Nature 2009;462:859–61. [DOI] [PubMed] [Google Scholar]
- 49. Ansermet F, Magistretti PJ.. Biology of Freedom: Neural Plasticity, Experience, and the Unconscious. Karnac Books, London, UK, 2007. [Google Scholar]
- 50. Baldi P, Sadowski P.. A theory of local learning, the learning channel, and the optimality of backpropagation. Neural Netw 2016;83:51–74. [DOI] [PubMed] [Google Scholar]
- 51. Baldassi C, Borgs C, Chayes JT, et al.Unreasonable effectiveness of learning neural networks: from accessible states and robust ensembles to basic algorithmic schemes. Proc Natl Acad Sci USA 2016;113(48):E7655–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Rees CL, Moradi K, Ascoli GA.. Weighing the evidence in peters’ rule: does neuronal morphology predict connectivity? Trends Neurosci 2017;40(2):63–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Haupt VJ, Daminelli S, Schroeder M.. Drug promiscuity in PDB: protein binding site similarity is key. PLoS One 2013;8:6.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Mousavian Z, Khakabimamaghani S, Kavousi K, et al.Drug-target interaction prediction from PSSM based evolutionary information. J Pharmacol Toxicol Methods 2016;78:42–51. [DOI] [PubMed] [Google Scholar]
- 55. Emig D, Ivliev A, Pustovalova O, et al.Drug target prediction and repositioning using an integrated network-based approach. PLoS One 2013;8(4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Cobanoglu MC, Liu C, Hu F, et al.Predicting drug-target interactions using probabilistic matrix factorization. J Chem Inf Model 2013;53(12):3399–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Chen X, Liu M-X, Yan G-Y, et al.Drug–target interaction prediction by random walk on the heterogeneous network. Mol Biosyst 2012;8(7):1970. [DOI] [PubMed] [Google Scholar]
- 58. He Z, Zhang J, Shi XH, et al.Predicting drug-target interaction networks based on functional groups and biological features. PLoS One 2010;5(3):e9603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Ba-Alawi W, Soufan O, Essack M, et al.DASPfind: new efficient method to predict drug-target interactions. J Cheminform 2016;8(1):1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Guney E, Menche J, Vidal M, et al.Network-based in silico drug efficacy screening. Nat Commun 2015;7:10331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Tero A, Takagi S, Ito K, et al.Rules for biologically inspired adaptive network design. Science 2010;327:439–42. [DOI] [PubMed] [Google Scholar]
- 62. Hattori M, Okuno Y, Goto S, et al.Development of a chemical structure comparison method for integrated analysis of chemical and genomic information in the metabolic pathways. J Am Chem Soc 2003;125(39):11853–65. [DOI] [PubMed] [Google Scholar]
- 63. Schomburg I, Chang A, Ebeling C, et al.BRENDA, the enzyme database: updates and major new developments. Nucleic Acids Res 2004;32:D431–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Günther S, Kuhn S, Dunkel MM, et al.Super target and matador: resources for exploring drug-target relationships. Nucleic Acids Res 2008;36:D191–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Law V, Knox C, Djoumbou Y, et al.DrugBank 4.0: shedding new light on drug metabolism. Nucleic Acids Res 2014;42(D1):D1091–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Gaulton A, Bellis LJ, Bento AP, et al.ChEMBL: a large-scale bioactivity database for drug discovery. Nucleic Acids Res 2012;40(D1):D1100–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Adamic LA, Adar E.. Friends and neighbors on the Web. Soc Netw 2003;25(3):211–230. [Google Scholar]
- 68. Kitsak M, Papadopoulos F, Krioukov D.. Latent geometry of bipartite networks. Phys Rev E 2017;95(3):032309. American Physical Society, Ridge, NY, USA. [DOI] [PubMed] [Google Scholar]
- 69. Yang Y, Lichtenwalter RN, Chawla NV, et al.Evaluating link prediction methods. Knowl Inf Syst 2015;45:751–82. [Google Scholar]
- 70. Davis J, Goadrich M. The relationship between precision-recall and ROC curves. In: Proceedings of 23rd International Conference on Machine Learning–ICML’06, 2006, 233–40. ACM, New York, NY, USA.
- 71. Qin C, Zhang C, Zhu F, et al.Therapeutic target database update 2014: A resource for targeted therapeutics. Nucleic Acids Res 2014;42(D1):D1118–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Daminelli S, Haupt VJ, Reimann M, et al.Drug repositioning through incomplete bi-cliques in an integrated drug–target–disease network. Integr Biol 2012;4(7):778. [DOI] [PubMed] [Google Scholar]
- 73. Isik Z, Baldow C, Cannistraci CV, et al.Drug target prioritization by perturbed gene expression and network information. Sci Rep 2015;5:17417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Kanehisa M, Goto S, Sato Y, et al.Data, information, knowledge and principle: Back to metabolism in KEGG. Nucleic Acids Res 2014;42(D1):D199–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Kim S, Thiessen PA, Bolton EE, et al.PubChem substance and compound databases. Nucleic Acids Res 2016;44(D1):D1202–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Hu Y, Bajorath J.. Monitoring drug promiscuity over time. F1000Res 2014;218(0):1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Chambers J, Davies M, Gaulton A, et al.UniChem: a unified chemical structure cross-referencing and identifier tracking system. J Cheminform 2013;5:3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Yamanishi Y, Kotera M, Moriya Y, et al.DINIES: drug-target interaction network inference engine based on supervised analysis. Nucleic Acids Res 2014;42(W1):W39–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Mann HB, Whitney D.. On a test whether one of two random variables is stochastically larger than the other. Ann Math Stat 1947;18:50–60. [Google Scholar]
- 80. Shakibian H, Charkari NM.. Mutual information model for link prediction in heterogeneous complex networks. Scientific Reportss 7 (Sci Rep) 2017;18; doi:10.1038/srep44981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Bonferroni CE. Teoria statistica delle classi e calcolo delle probabilità. Publ R Ist. Super Sci Econ Commer Firenze 1936;8:3–62. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.