Using Odds Ratios to Detect Differential Item Functioning

Abstract

Differential item functioning (DIF) makes test scores incomparable and substantially threatens test validity. Although conventional approaches, such as the logistic regression (LR) and the Mantel–Haenszel (MH) methods, have worked well, they are vulnerable to high percentages of DIF items in a test and missing data. This study developed a simple but effective method to detect DIF using the odds ratio (OR) of two groups’ responses to a studied item. The OR method uses all available information from examinees’ responses, and it can eliminate the potential influence of bias in the total scores. Through a series of simulation studies in which the DIF pattern, impact, sample size (equal/unequal), purification procedure (with/without), percentages of DIF items, and proportions of missing data were manipulated, the performance of the OR method was evaluated and compared with the LR and MH methods. The results showed that the OR method without a purification procedure outperformed the LR and MH methods in controlling false positive rates and yielding high true positive rates when tests had a high percentage of DIF items favoring the same group. In addition, only the OR method was feasible when tests adopted the item matrix sampling design. The effectiveness of the OR method with an empirical example was illustrated.

The presence of differential item functioning (DIF) violates the assumption of measurement invariance and makes test scores incomparable across different groups of participants. In DIF assessments, participants from different groups (e.g., gender or ethnicity groups) are placed on the same metric via a matching variable, and the performances of a focal group (e.g., minority) and a reference group (e.g., majority) on the studied item are compared. The performance on the studied item is conditional on participants’ ability levels, which serves as a foundation to distinguish differences in the item functioning and ability level. When matched participants from different groups demonstrate disparate probabilities of endorsing or accurately answering the studied item, the studied item is deemed as having DIF. The present study addresses the drawbacks of two standard methods that rely on a matching variable and proposes a new, robust method to detect DIF items for practical use.

Several approaches have been developed to detect DIF items, and these methods can be classified as item response theory (IRT)–based and non-IRT-based approaches (Magis, Béland, Tuerlinckx, & De Boeck, 2010). Approaches based on IRT, such as the likelihood ratio test (Cohen, Kim, & Wollack, 1996), Lord’s chi-square test (Lord, 1980), and Raju’s (1988) signed area method, are implemented to compare item parameters (or derived item characteristic curves) among different groups. Once the parameter estimates of an item are significantly different between groups, this item is flagged as a DIF item. Although IRT-based approaches function well in DIF detection, their applications are somewhat challenging for practitioners who are not familiar with IRT models.

Non-IRT-based approaches to DIF assessment include the Mantel–Haenszel (MH; Holland & Thayer, 1988), logistic regression (LR; Rogers & Swaminathan, 1993), delta (Angoff & Ford, 1973), standardization (Dorans & Kulick, 1986), and Simultaneous Item Bias Test (SIBTEST) methods (Shealy & Stout, 1993). These procedures require neither specific forms of item response functions nor large sample sizes (Narayanon & Swaminathan, 1996) and demonstrate computational simplicity. Among these approaches, the MH and LR methods function well when the percentage of DIF items in a test is not high and there is no impact (no mean ability difference) between groups (French & Maller, 2007; Narayanon & Swaminathan, 1996). Moreover, these two methods are readily available in most commercial (e.g., SPSS, STATA, and SAS) or free statistical software (e.g., R).

In the MH method, examinees or participants are stratified by test scores, and item performance is compared for two groups across all strata. Suppose there are two groups of participants (e.g., boys and girls) and items are scored dichotomously (i.e., 0 and 1). A 2 × 2 contingency table can be created for each test score stratum on the studied item i. In stratum k$(k=1,\dots ,K)$, T_ik denotes the total number of examinees who answered item i. The number of examinees in the reference group who answered item i correctly and incorrectly are denoted as t_R1ik and t_R0ik, respectively, and t_F1ik and n_F0ik denote the numbers of examinees in the focal group who answered item i correctly and incorrectly, respectively. Accordingly, the null hypothesis that item i does not have DIF is tested by computing the following odds ratio (OR) across the strata for item i:

$${\alpha }_i=\frac{\sum _k(t_{\mathrm{R}1\mathrm{ik}}{t}_{\mathrm{F}0\mathrm{ik}}/T_{\mathrm{ik}})}{\sum _k(t_{\mathrm{F}1\mathrm{ik}}{t}_{\mathrm{R}0\mathrm{ik}}/T_{\mathrm{ik}})},$$

which indicates the general association between the grouping variable and the item response in a series of contingency tables. To test the null hypothesis (e.g., α_i = 1), the MH chi-square statistic is computed as follows:

$${\mathrm{\chi }}_1^2=\frac{{\{\sum _k[t_{\mathrm{R}1\mathrm{ik}}-E\left(t_{\mathrm{R}1\mathrm{ik}}\right)]-0.5\}}^2}{\sum _k\mathrm{Var}\left(t_{\mathrm{R}1\mathrm{ik}}\right)},$$

where

$$E\left(t_{\mathrm{R}1\mathrm{ik}}\right)=\frac{(t_{\mathrm{R}1\mathrm{ik}}+t_{\mathrm{R}0\mathrm{ik}})\times (t_{\mathrm{R}1\mathrm{ik}}+t_{\mathrm{F}1\mathrm{ik}})}{T_{\mathrm{ik}}},$$

$$\mathrm{Var}\left(t_{\mathrm{R}1\mathrm{ik}}\right)=\frac{(t_{\mathrm{R}1\mathrm{ik}}+t_{\mathrm{R}0\mathrm{ik}})\times (t_{\mathrm{R}1\mathrm{ik}}+t_{\mathrm{F}1\mathrm{ik}})\times (t_{\mathrm{F}1\mathrm{ik}}+t_{\mathrm{F}0\mathrm{ik}})\times (t_{\mathrm{R}0\mathrm{ik}}+t_{\mathrm{F}0\mathrm{ik}})}{T_{\mathrm{ik}}^2(T_{\mathrm{ik}}^2-1)}.$$

When the null hypothesis of no DIF on the studied item holds, the MH chi-square statistic will follow the chi-square distribution with one degree of freedom asymptotically. Consequently, item i is flagged as having DIF if the chi-square statistic is statistically significant.

In practice, all items in a studied test should be assessed for DIF, as we do not know which one is DIF-free. Holland and Thayer (1988) observed a special relationship between the MH method and the Rasch model–based DIF detection method (Rasch, 1960), in that the hypothesis of the MH method is equivalent to that of the Rasch model–based method when (a) the matching score includes the studied item, (b) all items but the studied item are DIF-free, and (c) both the reference and focal groups are random samples. In other words, when the Rasch model fits the data and the three conditions are met, the MH method will be the best way to detect DIF compared with other non-IRT-based approaches.

In the LR method, the test score X and the binary grouping variable G (e.g., G = 0 for the reference group and G = 1 for the focal group) are used to predict the log-odds of success over failure on the studied item i as follows:

$$\log \left(\frac{P_{i1}}{P_{i0}}\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}X+{\mathrm{\beta }}_{2}G+{\mathrm{\beta }}_3\mathrm{XG},$$

where P_i1 and P_i0 are the probabilities of success and failure on item i, respectively; β₁ corresponds to the influence of observed test scores on the studied item; and β₂ and β₃ refer to the group difference and the interaction between the observed test score and group membership, respectively. The studied item is deemed as having uniform DIF if β₂≠ 0 and β₃ = 0, while it has nonuniform DIF if β₃≠ 0 (regardless of whether β₂ = 0).

Both the MH and the LR methods are promising in detecting uniform DIF in dichotomous items when tests do not contain too many DIF items (e.g., less than 15%) and DIF magnitudes are large (Narayanon & Swaminathan, 1996; Rogers & Swaminathan, 1993). The LR method outperforms the MH method in detecting nonuniform DIF (Hidalgo & López-Pina, 2004) and/or small magnitude of DIF (Hidalgo & López-Pina, 2004). The power of the MH and LR methods increases as the sample size or DIF magnitude increases (Narayanon & Swaminathan, 1996).

A common feature of the MH and the LR methods is that different groups of examinees are placed on the same metric based on the test score. Ideally, a matching variable should consist of exclusively DIF-free items so that the matching is correct. Prior studies have shown that a test score can serve as a matching variable to yield satisfactory DIF detection only if the test score is a sufficient statistic for latent ability or is highly related to latent ability and the group ability distribution across groups are identical or extremely similar (Magis & De Boeck, 2014). In other words, the use of a matching variable is critical for DIF detection (Kopf, Zeileis, & Strobl, 2015). If a contaminated matching variable (i.e., consisting of DIF items) is used, examinees with the same ability levels will not be matched, and the subsequent DIF detection will be biased (Clauser, Mazor, & Hambleton, 1993). It has been found that the MH or LR method loses control of false positive rates (FPRs) in DIF detection when the matching variable (i.e., test score) consists of many DIF items (French & Maller, 2007).

It is challenging to identify a set of DIF-free items to serve as a clean matching variable. Various scale purification procedures have been proposed (Holland & Thayer, 1988; Kopf et al., 2015; Wang & Su, 2004); however, if the percentage of DIF items in a test is not low (e.g., more than 20%) and the DIF magnitude is large, scale purification procedures often fail, and the resulting FPRs are severely inflated (French & Maller, 2007). Even if the percentage is low, conducting scale purification procedures makes DIF assessment tedious, especially for practitioners (Magis & De Boeck, 2012, 2014). It is desirable to develop DIF detection methods that do not require specification of DIF-free items to serve as a matching variable and that can yield well-controlled FPRs and high true positive rates (TPRs), even when a test consists of a high percentage of DIF items (e.g., 30% or higher), which is the major goal of this study.

Recent developments in the outlier approach appear promising for addressing some limitations in non-IRT-based DIF detection. In the outlier approach, each item has its own value on a DIF statistic, and those items with extreme values on this statistic (termed outliers) are deemed to have DIF (Magis & De Boeck, 2012, 2014). Given the assumption that a well-constructed test should have fewer DIF items than DIF-free items, it seems reasonable to declare the outliers with DIF. For instance, Magis and De Boeck (2012) transformed the MH statistics across items into standardized z scores and classified items with extreme z scores as outliers with DIF. Because real tests usually have multiple DIF items, the sample median will be a better indicator for representing the central tendency than the sample mean, with which the outliers are identified; this method is called the robust MH method (Magis and De Boeck, 2012). It has been found that the robust MH method outperforms the conventional MH method when tests consist of DIF items.

The robust MH method is not widely used by many practitioners because it is relatively new, and the concept and computation of the MH statistic are complex. To facilitate robust DIF detection methods, a statistic that is much easier to understand and compute than the MH statistic is needed. In this study, the ORs of the reference and focal groups were proposed. Because, in practice, uniform DIF is more of concern than nonuniform DIF, and the MH method is more appropriate in detecting uniform DIF than nonuniform DIF, the authors focus on uniform DIF in this study. The study proceeds as follows: an introduction to the OR method is provided; three simulation studies are described, which were conducted to evaluate the performance of the OR method under various conditions; an empirical example is given to demonstrate the feasibility and advantages of the robust method; and conclusions and suggestions for future study are provided.

The OR Method

Conventionally, item difficulty (easiness) is defined as the passing rate for a group of examinees on an item. Let n_R1i and n_R0i be the number of examinees in the reference group who answer item i correctly and incorrectly, respectively, and n_F1i and n_F0i be the number of examinees in the focal group who answer item i correctly and incorrectly, respectively. The passing rate of item i is $n_{R1i}/(n_{R0i}+n_{R1i})$ for the reference group and $n_{F1i}/(n_{F0i}+n_{F1i})$ for the focal group. The passing rate can be also represented as the odds of success, $n_{R1i}/n_{R0i}$ and $n_{F1i}/n_{F0i}$, for the reference group and the focal group, respectively. Let ${\hat{\lambda }}_i$ denote the logarithm of the OR of success over failure on item i for the reference group and the focal group:

$${\hat{\lambda }}_i=\log \left(\frac{n_{\mathrm{R}1i}/n_{\mathrm{R}0i}}{n_{\mathrm{F}1i}/n_{\mathrm{F}0i}}\right),$$

which follows a normal distribution asymptotically (Agresti, 2002), with a mean of λ and standard deviation of

$$\sigma \left({\hat{\lambda }}_i\right)={(n_{\mathrm{R}1i}^{-1}+n_{\mathrm{R}0i}^{-1}+n_{\mathrm{F}1i}^{-1}+n_{\mathrm{F}0i}^{-1})}^{1/2}.$$

When data follow the Rasch model and there is no DIF in the test, λ represents the mean ability difference between the reference and focal groups (often referred to as impact). A positive λ indicates that the reference group has a higher mean than the focal group, and a negative λ indicates the reverse.

When tests are perfect (not containing any DIF item), every ${\hat{\lambda }}_i$$(i=1,\dots ,I)$ is an unbiased estimator of λ. The sample mean $\overline{\hat{\lambda }}=\sum _{i=1}^I{\hat{\lambda }}_i/I$ is more efficient than individual ${\hat{\lambda }}_i$ values in estimating λ because its sampling variance is smaller. When item i has DIF, the expected value of ${\hat{\lambda }}_i$ will not be equal to λ. In other words, if ${\hat{\lambda }}_i$ is far away from λ, item i is deemed as having DIF. Because λ is unknown in reality, the sample mean $\overline{\hat{\lambda }}$ was used instead. If ${\hat{\lambda }}_i\pm z_{\alpha /2}\times \sigma ({\hat{\lambda }}_i)$ does not contain $\overline{\hat{\lambda }}$, item i will be deemed as having DIF. If the studied item is the only item that might have DIF, this approach will be appropriate; however, tests are not always perfect, and they usually contain multiple DIF items, such that the sample mean $\overline{\hat{\lambda }}$ is no longer an unbiased estimator of λ. The sample median $\tilde{\hat{\lambda }}$ was used then to replace the sample mean $\overline{\hat{\lambda }}$ to estimate λ, which is more resistant to multiple DIF items. Specifically, if ${\hat{\lambda }}_i\pm z_{\alpha /2}\times \sigma ({\hat{\lambda }}_i)$ does not include $\tilde{\hat{\lambda }}$, item i will be deemed as having DIF.

As an example, a dataset was generated with 100 examinees in each of the reference and focal group, and they answered 10 dichotomous items. Items 1 to 7 were generated as non-DIF items, and Items 8, 9, and 10 were DIF items, which favors the reference group by 1 logit. There was no impact (i.e., mean ability difference) between the two groups. For Item 1, Examinees 21 and 28 in the reference and focal groups had a correct answer, respectively. According to Equations 6 and 7, the authors found that

$${\hat{\lambda }}_1=\log \left(\frac{n_{\mathrm{R}11}/n_{\mathrm{R}01}}{n_{\mathrm{F}11}/n_{\mathrm{F}01}}\right)=\log \left(\frac{21/79}{28/72}\right)=-0.380,$$

$$\sigma \left({\hat{\lambda }}_1\right)={(n_{\mathrm{R}11}^{-1}+n_{\mathrm{R}01}^{-1}+n_{\mathrm{F}11}^{-1}+n_{\mathrm{F}01}^{-1})}^{1/2}={({21}^{-1}+{79}^{-1}+{28}^{-1}+{72}^{-1})}^{1/2}=0.331.$$

$${\hat{\lambda }}_1\pm 1.96\times \sigma \left({\hat{\lambda }}_1\right)=-1.029,0.269.$$

${\hat{\lambda }}_i$, $\sigma ({\hat{\lambda }}_i)$, and ${\hat{\lambda }}_i\pm z_{\alpha /2}\times \sigma ({\hat{\lambda }}_i)$ were computed for the other items, and the sample median $\tilde{\hat{\lambda }}$ (the mean of ${\hat{\lambda }}_2$ and ${\hat{\lambda }}_7$) was 0.022. When α = .05, if an item’s 95% confidence interval does not cover 0.022, the corresponding item was deemed as having DIF. Finally, Items 8, 9, and 10 are successfully flagged as DIF (favoring the reference group; see Table 1 for details).

Table 1.

An Example of the OR Method Where Items 8, 9, and 10 of the 10 Items Favor the Reference Group.

Items	Reference group		Focal group		OR statistics
	Success	Fail	Success	Fail	${\hat{\lambda }}_i$	$\sigma ({\hat{\lambda }}_i)$	${\hat{\lambda }}_i\pm z_{\alpha /2}\times \sigma ({\hat{\lambda }}_i)$
1	21	79	28	72	−0.380	0.331	−1.029, 0.269
2	28	72	28	72	0.000	0.315	−0.617, 0.617
3	74	26	80	20	−0.340	0.338	−1.002, 0.322
4	52	48	63	37	−0.452	0.288	−1.016, 0.112
5	18	82	13	87	0.385	0.395	−0.389, 1.159
6	33	67	35	65	−0.089	0.299	−0.675, 0.497
7	35	65	34	66	0.044	0.298	−0.540, 0.628
8	42	58	12	88	1.670	0.368	0.948, 2.392
9	71	29	52	48	0.851	0.298	0.232, 1.399
10	58	42	16	84	1.981	0.340	1.315, 2.647

Note. α = .05. OR = odds ratio.

If the DIF detection is based on the sample mean, the accurate classification rate was reduced. In this case, the sample mean was 0.363. Items 1, 3, 4, 8, and 10 had a 95% confidence interval not covering 0.363; thus, they were deemed as having DIF, and the other items were deemed as non-DIF. Only six out of 10 items were correctly classified, and the correct classification rate was 60%. It is noticeable that using the median over the mean is not salient under the balanced DIF conditions, in which some DIF items favor the reference group and the other items favor the focal group; thus, the DIF effects are canceled out between groups. No matter how test developers try to balance the effects of potential DIF items, it is unlikely that the DIF effects will be canceled out completely between groups.

The OR method is easy to understand and implement; there is no need to identify DIF-free items. The performance of the OR method especially depends on two conditions. First, a long test is required to justify the OR method. The longer the test, the smaller the sampling variation in $\tilde{\hat{\lambda }}$, making the OR method more reliable. Second, as a basic concept of outliers, the number of DIF items should not exceed the number of DIF-free items; otherwise, the classification of outliers becomes tricky.

The OR method has two distinct features that differentiate it from the conventional MH and robust MH methods. The first is with regard to stratification. The OR method does not require stratification, and the log OR is directly computed for all items (see Equation 6). In contrast, both the conventional and robust MH methods assign examinees to strata based on examinees’ test scores, calculate an OR in each stratum, and generate a composite OR across strata (see Equation 1). The second feature is the principle of identifying DIF items. In the conventional MH method, an item is flagged as having DIF if its OR significantly deviates from 1 (or equivalently, the MH chi-square statistic is statistically significant). In the OR method, an item whose log OR is an outlier is deemed as having DIF. Therefore, although both methods use ORs to detect DIF, they differ in nature.

The OR method has several advantages. First, it is easy and simple for practitioners. The computation task in the OR method is minimized, and it can easily be implemented with a portable calculator. What is more, interpreting its result is intuitive and does not require any advanced statistical knowledge or techniques. Second, unlike conventional DIF assessment approaches, the OR method does not require matching variables; thus, there is no need for the identification of DIF-free items. The OR method uses the median of the log ORs of all items as the reference point for DIF detection. In contrast, the MH and LR methods rely on test scores to match examinees, which is biased when tests have multiple DIF items. Even if tests do not contain any DIF items, test scores cannot match examinees well when the impact is large (Narayanon & Swaminathan, 1996). Third, the OR method can accommodate missing data much more easily than the conventional or robust MH method. When there are missing data, the test score is usually no longer a valid matching variable, so the conventional or robust MH method will be adversely affected (Robitzsch & Rupp, 2009). In contrast, the OR method does not rely on test score and will be less affected by missingness. Fourth, scale purification procedures can easily be incorporated into the OR method; all that is necessary is the precomputation of the sample median based on presumably DIF-free items. Take a test with 20 items as an example. Suppose Items 1 to 5 are classified as having DIF by the OR method; a new sample median $\tilde{\hat{\lambda }}$ can be computed then based on Items 6 to 20. Again, for each item, the authors checked whether ${\hat{\lambda }}_i\pm z_{\alpha /2}\times \sigma ({\hat{\lambda }}_i)$ contains the new $\tilde{\hat{\lambda }}$. If not, the corresponding item is deemed as having DIF. Suppose that, this time, Items 1 to 4 are classified as having DIF; a new $\tilde{\hat{\lambda }}$ based was computed on Items 5 to 20, and for each item the authors checked whether ${\hat{\lambda }}_i\pm z_{\alpha /2}\times \sigma ({\hat{\lambda }}_i)$ contains the new $\tilde{\hat{\lambda }}$. Again, suppose that the same set of items (Items 1 to 4) is classified as having DIF. In this case, the scale purification stops; otherwise, a new $\tilde{\hat{\lambda }}$ will be computed, and the DIF detection continues until either the same set of items is classified as having DIF in two successive iterations or the maximum number of iterations is reached. These arguments are verified by the simulations below.

Simulation Study 1

Design

Study 1 concerned the performance of the OR method for complete data. A total of 1,000 examinees answered 20 dichotomous items. Five factors were manipulated as follows: (a) equal and unequal sample sizes of the reference and focal groups: 500/500 and 800/200; (b) percentages of DIF items: 0%, 10%, 20%, 30%, and 40%; (c) DIF patterns: balanced and unbalanced; (d) impact: 0 and 1; and (e) purification procedure: with or without. Item responses were generated from the Rasch model. Item difficulties were generated from a uniform distribution between −1.5 and 1.5. The abilities of the reference group were generated from N(0, 1). When impact = 0, the abilities of the focal group were also generated from N(0, 1); when impact = 1, they were generated from N(−1, 1). The differences in the item difficulty for DIF items were set at a constant of 0.5 logits. Under the unbalanced DIF conditions, all DIF items were set to favor the reference group; under the balanced DIF conditions, half of the DIF items favored the reference group and the other half favored the focal group. It has been shown that the MH and LR methods perform well under balanced DIF conditions because the DIF effects are canceled out between groups, as if there are no DIF items in the test. In contrast, they perform poorly under unbalanced DIF conditions because the test score is seriously contaminated (Wang & Su, 2004). Because the OR method does not rely on test scores to match examinees, it was anticipated that the OR method would not suffer much from unbalanced DIF patterns.

As in other DIF studies, the nominal level was set at .05. For completeness, scale purification procedures were also implemented on the three methods. Unlike the scale purification procedures for the MH and LR methods, which involve intensive computation and are often implemented in specific computer programs, the scale purification procedure for the OR method involves only recalculation of the sample median and can be easily implemented using portable calculators.

A total of 100 replications were carried out under each condition. The performance of the OR method was evaluated and compared with the performances of the MH and LR methods in terms of the FPR, in which a DIF-free item was misclassified as having DIF, and the TPR, in which a DIF item was correctly classified as having DIF. The MH and LR methods were implemented via the difMH and difLogistic functions in the difR package (Magis et al., 2010), and the OR method was implemented in R version 3.2.5 (R Core Team, 2016) and is available upon request.

Results

Due to space constraints, the FPR and TPR for individual items were not shown; rather, the averaged FPR across DIF-free items and averaged the TPR across DIF items were computed. Table 2 shows the averaged FPRs and TPRs under all conditions when impact = 0. As expected, all methods yielded well-controlled FPRs under the no-DIF and balanced DIF conditions, although the OR and MH methods were slightly conservative. Under the unbalanced DIF conditions, the MH and LR methods yielded inflated FPRs when tests had 20% or more DIF items; fortunately, the scale purification procedures could bring the inflation back to normal if the DIF items represented no more than 30%. The scale purification did not work in the MH and the LR approaches when a test included 40% or more DIF items. In contrast, the OR method yielded slightly inflated FPRs only when tests had 40% or more DIF items, and the inflation was back to normal when the scale purification procedure was incorporated.

Table 2.

Averaged FPR and TPR (%) Under the Conditions With Impact = 0 in Simulation 1.

	FPR						TPR
	500/500			800/200			500/500			800/200
	OR	LR	MH	OR	LR	MH	OR	LR	MH	OR	LR	MH
0%	3.20	4.75	4.10	3.55	4.70	3.50	—	—	—	—	—	—
	(3.45)	(3.75)	(3.80)	(3.70)	(4.90)	(3.65)	—	—	—	—	—	—
Balanced DIF
10%	3.33	5.05	4.17	3.50	5.28	4.06	87.50	94.50	94.00	79.00	85.50	84.50
	(3.50)	(4.56)	(4.06)	(3.44)	(5.06)	(4.17)	(87.50)	(91.50)	(89.50)	(78.50)	(83.00)	(79.50)
20%	3.25	4.81	3.94	3.56	5.19	4.00	87.75	92.25	91.75	68.75	79.75	74.75
	(4.00)	(4.63)	(4.06)	(3.69)	(5.06)	(3.63)	(87.25)	(89.25)	(88.50)	(70.00)	(76.00)	(70.75)
30%	3.14	5.50	4.14	2.86	4.71	3.93	83.50	89.33	87.50	70.67	78.33	77.00
	(3.57)	(5.21)	(4.00)	(3.29)	(4.93)	(4.00)	(82.50)	(85.67)	(82.33)	(70.50)	(75.17)	(71.83)
40%	3.00	4.25	3.67	2.58	4.58	3.17	87.50	93.75	91.63	74.75	82.88	80.50
	(3.58)	(4.83)	(3.67)	(3.08)	(5.08)	(3.42)	(86.75)	(90.38)	(88.50)	(74.38)	(76.75)	(73.38)
Unbalanced DIF
10%	3.22	6.39	5.22	4.28	6.33	5.00	86.00	88.50	84.50	75.50	76.00	72.50
	(3.11)	(4.50)	(3.78)	(4.50)	(5.78)	(4.89)	(87.00)	(90.50)	(88.50)	(77.00)	(81.50)	(78.00)
20%	4.44	11.00	9.44	4.75	8.50	7.63	80.50	80.25	74.50	61.00	60.75	56.25
	(4.25)	(5.31)	(4.56)	(4.31)	(6.13)	(4.25)	(83.75)	(89.25)	(85.00)	(65.50)	(69.50)	(67.75)
30%	6.29	17.50	15.57	5.93	12.21	10.07	73.00	66.50	63.33	47.83	48.17	42.50
	(5.14)	(6.14)	(5.43)	(5.93)	(7.58)	(6.71)	(82.00)	(85.17)	(82.33)	(54.83)	(58.17)	(52.50)
40%	10.75	26.08	22.42	11.17	20.75	18.42	59.88	54.63	50.88	34.75	36.75	31.50
	(7.42)	(10.17)	(8.00)	(11.00)	(16.75)	(13.58)	(72.75)	(74.50)	(73.13)	(42.50)	(43.88)	(38.63)

Note. The values in parentheses are obtained with the purification procedure. Inflated FPRs (≥7.5%) are marked in bold. FPR = false positive rate; TPR = true positive rate; OR = odds ratio; LR = logistic regression; MH = Mantel–Haenszel; DIF = differential item functioning.

When the FPRs for all methods were well controlled, as under the no-DIF and balanced DIF conditions, in general, the TPRs were slightly higher in the LR method than in the MH and OR methods. Under the unbalanced DIF conditions, the FPRs were inflated and the TPRs were deflated for the MH and LR methods, while the TPRs were lower than those for the OR method. In other words, once the FPRs were inflated, the TPRs were reduced, and the MH and LR methods suffered a greater loss in TPRs than the OR method did. In addition, the TPRs were higher in equal sample sizes than in unequal sample sizes given the fixed total sample size.

Table 3 summarizes the averaged FPRs and TPRs when impact = 1. The findings were comparable with those in Table 2 when impact = 0, except that the inflation of FPRs and deflation of TPRs in the MH and LR methods under the unbalanced DIF conditions became worse when impact = 1 than when impact = 0.

Table 3.

Averaged FPR and TPR (%) Under the Conditions With Impact = 1 in Simulation 1.

	FPR						TPR
	500/500			800/200			500/500			800/200
	OR	LR	MH	OR	LR	MH	OR	LR	MH	OR	LR	MH
0%	2.70	4.50	3.40	2.75	4.60	3.65	—	—	—	—	—	—
	(2.80)	(4.50)	(3.30)	(3.15)	(4.90)	(3.60)	—	—	—	—	—	—
Balanced DIF
10%	3.72	5.67	4.56	3.56	4.56	3.17	85.00	89.00	86.50	73.00	79.50	74.50
	(4.11)	(5.33)	(4.50)	(3.78)	(4.56)	(3.00)	(84.50)	(84.00)	(83.00)	(73.00)	(75.50)	(71.00)
20%	3.25	4.69	3.81	3.13	5.19	4.31	83.50	86.75	85.50	66.00	70.00	65.00
	(3.56)	(4.81)	(3.63)	(3.44)	(5.50)	(4.13)	(83.25)	(83.25)	(81.25)	(65.75)	(66.25)	(61.00)
30%	3.93	5.29	4.29	3.14	5.36	3.79	90.83	92.83	91.83	69.17	77.50	72.67
	(4.36)	(5.50)	(4.43)	(4.14)	(6.29)	(3.71)	(90.50)	(87.83)	(86.50)	(68.33)	(71.33)	(66.83)
40%	3.42	4.92	4.08	3.33	5.67	4.00	87.63	90.25	88.00	70.50	77.13	71.50
	(4.17)	(4.75)	(3.83)	(4.17)	(6.42)	(5.00)	(86.13)	(86.50)	(84.50)	(69.75)	(69.38)	(64.88)
Unbalanced DIF
10%	3.56	5.78	4.94	3.50	7.33	5.11	84.50	82.50	80.00	69.00	71.50	67.50
	(3.50)	(4.83)	(3.83)	(4.44)	(6.22)	(4.56)	(85.00)	(83.00)	(83.50)	(71.50)	(73.00)	(69.00)
20%	5.19	10.63	8.31	3.88	8.19	5.56	76.75	69.00	67.50	58.50	53.00	48.50
	(4.56)	(5.69)	(4.00)	(4.44)	(6.00)	(4.13)	(82.00)	(78.75)	(79.25)	(61.25)	(56.25)	(53.75)
30%	7.86	17.86	13.57	6.79	14.14	10.79	69.50	58.67	56.00	49.00	46.83	42.50
	(5.57)	(8.86)	(6.00)	(6.64)	(9.00)	(7.35)	(76.33)	(75.83)	(75.17)	(56.83)	(59.50)	(53.83)
40%	11.92	25.17	20.25	11.00	20.92	14.25	56.50	45.88	43.25	36.75	33.25	30.75
	(8.17)	(12.42)	(9.00)	(9.58)	(17.08)	(10.25)	(68.25)	(64.25)	(62.38)	(45.25)	(38.75)	(39.75)

Note. Values in the parentheses are obtained with the purification procedures. Inflated FPRs (≥7.5%) are marked in bold. FPR = false positive rate; TPR = true positive rate; OR = odds ratio; LR = logistic regression; MH = Mantel–Haenszel; DIF = differential item functioning.

Simulation Study 2

Design

Study 2 mimicked a horizontal equating design and aimed to demonstrate the advantages of the OR method over the MH and LR methods in accommodating missing data by design. There were 30 items in two 20-item booklets. The first booklet contained Items 1 to 20, and the second booklet contained Items 1 to 10 and 21 to 30. Thus, Items 1 to 10 were common between the two booklets. There were 600 examinees each in the reference and focal groups. In each group, half of the examinees received the first booklet, and the other half received the second booklet. Each examinee answered only 20 out of 30 items, so the missing rate was 33% by design. The data generation procedures and the three manipulated factors, including percentage of DIF items, impact, and purification procedure, were the same as those in Study 1. For example, in the condition of 10% DIF items, Items 10, 20, and 30 had DIF, so that each booklet included two DIF items and 18 DIF-free items. The DIF magnitude was set at 0.5 logits, and all DIF items favored the reference group. An examinee’s test score on his or her booklet (ranging from 0-20) was used as the matching variable in the MH and LR methods. A total of 100 replications were carried out under each condition. FPRs and TPRs were the outcome variables.

Results

Table 4 summarizes the averaged FPRs and TPRs. As in Simulation Study 1, the OR method yielded acceptable FPRs and satisfactory TPRs when tests had 30% or fewer DIF items, but it had lower TPRs in assessing the unique items than the common items because the number of examinees answering the unique items was only half the number of examinees answering the common items. The LR method yielded significantly inflated FPRs for both the common and unique items, but the purification procedure reduced the inflation. The MH method yielded FPRs close to zero under all conditions, which might be because the difMH function did not handle missing data properly. Thus, using the MH method was not recommended when data are missing by design. In sum, the OR method is quite robust to missing data in yielding well-controlled FPRs and high TPRs.

Table 4.

Averaged FPR and TPR (%) in Study 2.

	FPR						TPR
	Common items			Unique items			Common items			Unique items
	OR	LR	MH	OR	LR	MH	OR	LR	MH	OR	LR	MH
Impact = 0
0%	3.70	5.80	4.60	4.65	5.45	0.00	—	—	—	—	—	—
	(4.10)	(5.30)	(4.90)	(4.85)	(5.50)	(0.00)	—	—	—	—	—	—
10%	3.78	6.67	5.56	4.00	5.72	0.00	83.00	86.00	86.00	62.00	65.00	3.00
	(4.22)	(5.44)	(4.78)	(4.11)	(5.28)	(0.00)	(84.00)	(87.00)	(85.00)	(63.00)	(64.50)	(3.00)
20%	4.63	12.75	11.50	6.06	9.19	0.00	87.50	87.00	86.50	61.00	61.00	0.25
	(4.63)	(5.00)	(6.63)	(5.50)	(5.38)	(0.00)	(90.50)	(91.50)	(87.50)	(65.50)	(71.25)	(0.75)
30%	7.71	21.00	19.51	5.79	12.36	0.00	81.00	77.33	73.33	49.00	48.00	0.33
	(8.14)	(6.71)	(12.29)	(5.57)	(5.36)	(0.00)	(86.00)	(89.67)	(78.67)	(57.33)	(64.83)	(0.50)
40%	15.17	31.17	27.50	9.92	17.58	0.00	63.75	58.50	56.25	34.25	35.00	0.13
	(11.17)	(13.17)	(20.00)	(7.92)	(10.33)	(0.00)	(73.75)	(76.50)	(60.00)	(49.13)	(51.38)	(0.38)
Impact = 1
0%	3.90	5.20	4.20	3.45	5.45	0.00	—	—	—	—	—	—
	(4.20)	(4.80)	(4.10)	(3.50)	(5.50)	(0.00)	—	—	—	—	—	—
10%	5.33	7.56	6.56	4.50	5.67	0.00	93.00	88.00	87.00	57.00	51.50	2.50
	(5.22)	(6.56)	(5.67)	(4.33)	(4.89)	(0.00)	(95.00)	(89.00)	(85.00)	(59.50)	(53.50)	(2.00)
20%	8.00	13.25	10.63	5.94	8.06	0.06	84.50	80.00	78.50	53.25	49.75	0.75
	(7.25)	(7.00)	(8.88)	(5.69)	(6.94)	(0.31)	(86.50)	(86.00)	(78.50)	(57.75)	(59.00)	(1.50)
30%	10.59	16.56	13.29	7.50	11.86	0.50	78.00	72.33	71.33	47.67	41.67	1.83
	(7.57)	(7.00)	(8.71)	(5.79)	(5.79)	(0.21)	(85.67)	(89.67)	(74.67)	(56.83)	(59.17)	(3.17)
40%	20.00	30.00	25.00	10.33	16.33	0.08	56.75	50.75	47.25	34.63	28.88	0.00
	(17.67)	(14.00)	(20.50)	(10.00)	(9.33)	(0.00)	(64.50)	(72.25)	(49.00)	(43.13)	(43.25)	(0.13)

Note. Values in the parentheses are obtained with the purification procedure. Inflated FPRs (≥7.5%) are marked in bold. FPR = false positive rate; TPR = true positive rate; OR = odds ratio; LR = logistic regression; MH = Mantel–Haenszel.

The test score of the common items (ranging from 0-10) was also used as the matching variable in the LR method, which resulted in slightly better control of FPRs than using the booklet test score as the matching variable. Nevertheless, this matching method may not always be applicable, as common items across booklets are not always available in practice. For instance, large-scale assessments often adopt a matrix sampling design of booklets, so that examinees answer a subset of items and there is no common item across all examinees (please see “Simulation Study 3” section for details).

Simulation Study 3

In large-scale tests, such as the Program for International Student Assessment (PISA) and Trends in International Mathematics and Science Study (TIMSS), the matrix sampling design is often adopted to assemble multiple booklets. Simulation Study 3 mimicked such a design and evaluated how the three methods would perform. A total of 30 items were grouped into three item blocks as follows: Items 1 to 8 in Block 1, Items 9 to 18 in Block 2, and Items 19 to 30 in Block 3. The first booklet was composed of Blocks 1 and 2, the second booklet was composed of Blocks 2 and 3, and the third booklet was composed of Blocks 1 and 3. This matrix sampling had two features: (a) there was no item common to all three booklets, and (b) the numbers of items were different for different booklets. Both the reference group and the focal group had 600 examinees, in which one third of the examinees took each of the three booklets. The procedure for data generation and the three manipulated factors, including percentage of DIF items, impact, and purification procedure, were identical to those in Simulation Study 2. Each item block contained zero to four DIF items. The DIF magnitude was set at 0.5 logits, and all DIF items favored the reference group. Because no items common to all three booklets were available, an examinee’s test score on his or her booklet was used as the matching variable in the MH and LR methods. A total of 100 replications were carried out under each condition. FPRs and TPRs were the outcome variables.

Results

Table 5 summarizes the averaged FPRs and TPRs for all conditions in Simulation Study 3. As in the findings for Simulation Study 2, the OR method yielded acceptable FPRs and satisfactory TPRs when tests had 30% DIF items or less, and the scale purification procedure was helpful in reducing FPRs when tests had 40% or more DIF items. The LR method yielded inflated FPRs when tests had 20% or more DIF items, and the scale purification procedure could not bring FPRs back to the 5% nominal level when impact = 1. Compared with the OR and LR methods, the MH method performed extremely poor, which may have been due to the problem in handling missing data in the difMH function. Overall, the findings were in alignment with those of Simulation Study 2, showing that the OR method was efficient in detecting DIF when data were missing by design.

Table 5.

Averaged FPR and TPR (%) in Study 3.

	FPR			TPR
	OR	LR	MH	OR	LR	MH
Impact = 0
0%	3.70	4.77	0.00	—	—	—
	(3.90)	(4.97)	(0.00)	—	—	—
10%	4.48	6.93	0.11	77.67	82.67	21.67
	(4.67)	(5.48)	(0.04)	(80.00)	(85.00)	(23.67)
20%	4.54	8.25	0.13	71.83	74.67	15.50
	(4.17)	(5.04)	(0.08)	(77.17)	(84.83)	(16.83)
30%	6.71	13.10	0.19	67.00	63.11	8.44
	(4.90)	(5.14)	(0.19)	(77.22)	(79.78)	(9.56)
40%	12.59	21.83	0.61	46.67	47.25	4.67
	(9.94)	(8.88)	(0.50)	(59.33)	(67.58)	(4.92)
Impact = 1
0%	3.93	6.13	3.10	—	—	—
	(3.93)	(8.93)	(2.60)	—	—	—
10%	4.07	4.89	4.96	70.33	79.67	28.67
	(4.11)	(7.11)	(3.74)	(72.00)	(83.00)	(33.00)
20%	5.04	7.71	3.67	70.83	71.50	18.83
	(4.46)	(8.38)	(2.33)	(75.67)	(82.50)	(21.50)
30%	7.19	9.43	1.90	57.78	49.11	10.44
	(6.38)	(8.09)	(1.52)	(66.33)	(74.22)	(13.00)
40%	12.00	10.78	15.44	45.67	55.00	27.25
	(9.94)	(49.67)	(9.00)	(54.25)	(84.92)	(28.08)

Note. The values in parentheses were obtained with the purification procedure. Inflated FPRs (≥7.5%) are marked in bold. FPR = false positive rate; TPR = true positive rate; OR = odds ratio; LR = logistic regression; MH = Mantel–Haenszel.

An Empirical Example of PISA 2015

The PISA is a large-scale assessment of students’ performance in science (the major domain in 2015), reading, and mathematics (the two minor domains). Items in the three domains are assembled into several blocks, and each booklet is composed of four item blocks. This study used data from a sample of 14,530 Australian students (50.7% boys and 49.3% girls) taking the computer-based assessment (CBA) from PISA 2015. In the CBA design, a student is assigned to one of 66 booklets. The data matrix is rather sparse, as on average, 2,000 scores were observed for each item.

Only responses to the dichotomous items were analyzed. There were 46, 50, and 121 dichotomous items in the reading, mathematics, and science tests, respectively. For boys, the average rates of accuracy were 57.3%, 51.5%, and 56.2% for the three subjects, respectively; for girls, they were 60.9%, 49.7%, and 54.7%, respectively. At face value, the results suggest that boys outperformed girls in mathematics and science, while girls outperformed boys in reading.

The MH, LR, and OR methods with scale purification procedures were utilized to investigate gender DIF in the three subjects. Boys and girls were treated as the focal and reference groups, respectively, in the DIF analysis. Note that the number of items varied among the booklets. For example, in the reading test, the number of items in the 66 booklets was between 0 and 20. This implied that using the test score as the matching variable in the MH or LR method would be problematic.

The MH method yielded different results from those found using the LR and OR approaches. The MH, LR, and OR methods identified zero, 13, and 13 DIF items, respectively, in the reading test; zero, 16, and 15 DIF items, respectively, in the mathematics test; and zero, 52, and 59 DIF items, respectively, in the science test. In accordance with the findings in Simulation Studies 2 and 3, the MH method performed extremely poorly when there were missing data. Comparing the results from the LR and OR methods, coincidently, both methods detected gender DIF in five, seven, and 45 items in the reading, mathematics, and science tests, respectively. Below, the results of the OR method were focused.

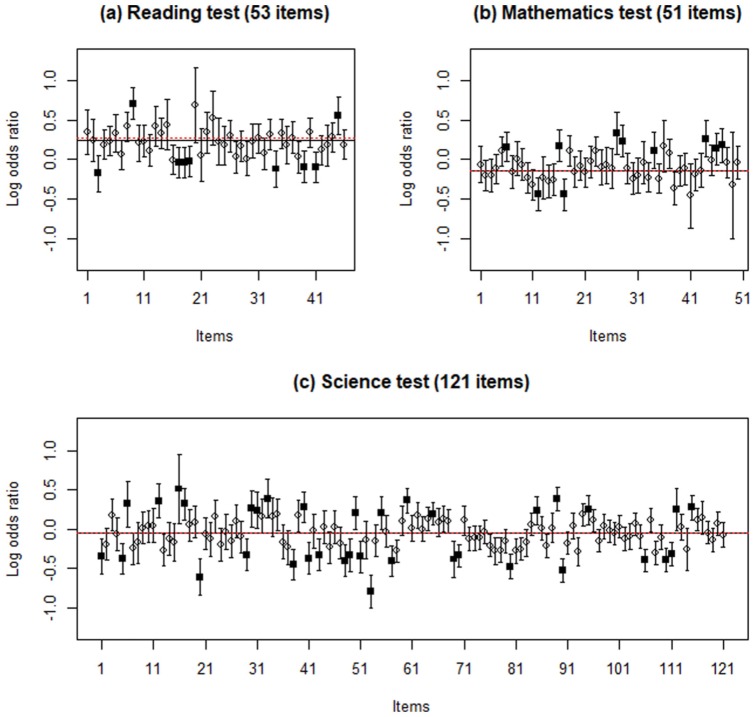
Because of the large sample size, a trivial DIF could be statistically significant. Le’s (2009) criteria were adopted in this analysis, in which an item is ultimately flagged as having substantial DIF when two conditions are jointly satisfied: (a) ${\hat{\lambda }}_i$ is significant at the .05 nominal level, and (b) the DIF size (i.e., $|{\hat{\lambda }}_i-\tilde{\hat{\lambda }}|$) is larger than 0.25 logits. There were nine, 10, and 36 items exhibiting substantial gender DIF in the reading, mathematics, and science tests, respectively. The results of DIF detection with scale purification are presented in Figure 1. Extreme $\hat{\lambda }$ values were bilaterally distributed in all tests, and the means and medians of $\hat{\lambda }$ for non-DIF items approximately overlapped. Specifically, seven, two, and 19 items in the reading, mathematics, and science tests favored boys, whereas two, eight, and 17 items favored girls, respectively.

Figure 1.

Log odds ratios and 95% confidence intervals for three tests in the PISA 2015.

Note. Circles and squares refer to non-DIF and DIF items, respectively; solid and dotted lines are the medians and means across non-DIF items, respectively. PISA = Program for International Student Assessment; DIF = differential item functioning.

Discussion and Conclusion

The MH and LR methods use test scores to match examinees from different groups for DIF detection. However, test scores cannot represent examinees’ ability levels properly when tests have DIF items or the impact is large. Solutions to this predicament include scale purification procedures and identification of a set of DIF-free items to serve as a matching variable (Kopf et al., 2015). Scale purification and identification of DIF-free items, however, may be rather inconvenient and challenging for practitioners. In this study, a simple solution that does not rely on a matching variable was provided. In the newly proposed OR method, the log OR of two groups of examinees on their responses to each item is computed, and an item is deemed as having DIF when its log OR is an outlier against the sample median. If a practitioner knows how to compute the log OR (Equation 6), its standard error (Equation 7), and the sample median, the OR method can be easily implemented. The scale purification is also straightforward. All we need to do is recalculate the sample median from those items identified as DIF-free in the previous step.

The findings from a series of simulation studies show that the OR method yielded satisfactory FPRs and high TPRs when tests had 30% or fewer DIF items, and the scale purification procedure could reduce the inflated FPRs when tests had 40% or more DIF items. In contrast, the MH and LR methods were vulnerable to high percentages of DIF items and missingness. Thus, the OR method is recommended because of its high effectiveness and feasibility in DIF detection.

A distinct advantage of the OR method is its robustness to missing data. Missing responses weaken the relationship between an examinee’s test score and latent ability level, such that standard DIF detection methods become thorny (Robitzsch & Rupp, 2009). Bank (2015) reviewed nine studies that examined DIF detection in missing data and recommended the use of deletion (including analysis-wise and listwise) and imputation. Although deleting cases with missing responses is simple, it may lead to a substantial loss of samples and, consequently, a lower power of DIF assessment (Finch, 2011). In addition, deletion is not always feasible when missing data are formulated by design, such as in booklets in large-scale assessments (e.g., the PISA). Although imputation, an advanced approach for treating missing data, may be more effective than deletion (Finch, 2011; Robitzsch & Rupp, 2009), selecting an imputation algorithm to add unsubstantial information into observed data is somewhat arbitrary and may fabricate the result of DIF assessment. Seemingly, deletion inevitably sacrifices some information, while imputation exaggerates the limited information.

Unlike deletion and imputation, the OR method utilizes information by employing observed data and considering the incompleteness of item responses to identify DIF items. As in Equation 7, a small number of valid responses would result in a large error variance of ${\hat{\lambda }}_i$. Conditional on the value of the log ORs, the more the missing data, the larger the error variance. This feature ensures that the OR method is not vulnerable to missing data, as the error variance for statistical testing will not be overestimated due to deletion or underestimated due to imputation.

The robust OR method is rather robust to missing data, and it might be applicable in detecting DIF in computerized adaptive testing (CAT). Because many responses are missing at random in CAT, existing DIF detection methods require a tedious procedure to obtain the ability estimate (or expected score over the entire item pool) as a matching variable to detect DIF in new items (Lei, Chen, & Yu, 2006). The robust OR method can be an alternative in such cases, but its performance needs further investigation.

Although the OR method was developed to detect DIF between two groups, it can be used to detect DIF in more than two groups. For example, once the reference group is identified, each focal group can be compared with the reference group individually (Finch, 2016). Like the MH method, the OR approach is effective in detecting uniform DIF when the data follow the Rasch model. It was suspected that the OR method will not perform well when data follow the two- or three-parameter logistic model or the DIF is nonuniform, which should be verified in future research. In recent years, polytomous items have been widely used in educational and psychological tests. It is important for future study to extend the OR method to detect DIF in polytomous items.