Abstract
Reproduction efficiency is a major factor in the profitability of the beef cattle industry. Genomic selection (GS) is a promising tool that may improve the predictive accuracy and genetic gain of fertility traits. There is a wide range of traits used to measure fertility in dairy and beef cattle including continuous (days open), discrete (pregnancy status), and count (number of inseminations) responses. In this study, a joint analysis of age of puberty (AOP), age at first calving (AOC), and the heifer pregnancy status (HPS) was performed. Data used in this study consisted of records from 1,365 Composite Gene Combination (CGC; 50% Red Angus, 25% Charolais, 25% Tarentaise) first parity females born between 2002 and 2011. The pedigree file included 5,374 animals. A total of 3,902 animals were genotyped with different density SNP chips (3K to 50K SNP). Animals genotyped with low-density arrays were imputed to higher density (BovineSNP50 BeadChip) using FImpute. Data were analyzed using univariate and multivariate classical quantitative models (pedigree based) and univariate genomic approaches. For the latter, 3 different Bayesian methods (BayesA, BayesB, and BayesCπ) were implemented and compared. Estimates of heritabilities using univariate and multivariate analyses based on pedigree relationships ranged between 0.03 (for AOC) to 0.2 (AOP). Heritability of pregnancy status was 0.15 and 0.09 using the univariate and multivariate analyses, respectively. Genetic correlation between pregnancy status and the other 2 traits was low being 0.08 with age at puberty and -0.10 with age at first calving. Heritability estimates were slightly higher using genomic rather than average additive relationships. The accuracy of genomic prediction was similar across the 3 Bayesian methods with higher accuracies for age of puberty than the age at first calving likely due to the higher heritability of the former. The prediction of the binary pregnancy status measured using the area under the curve increased by 27% to 29% compared to a random classifier. Due to the small size of the data, all estimates have large posterior standard deviations and results should be interpreted with caution.
Keywords: beef, fertility, genomic prediction, joint analysis
INTRODUCTION
Fertility is the most economically important trait in beef production. Selection for production traits has led to decay in fertility (Berry et al., 2014). Pedigree-based genetic improvement programs for reproduction performance had limited success due to several reasons including lack of uniformity in fertility traits, phenotyping difficulties, and low heritabilities (Dekkers, 2010; Thornton, 2010; Biscarini et al., 2015). Heritability estimates for fertility traits especially discrete responses are in the 10% range (VanRaden et al., 2004; Cammack et al., 2009). Availability of genomic information has provided an unprecedented opportunity to enhance the efficiency of selection, especially for lowly heritable traits.
Although genomic technologies have been successfully adopted in other species, their success in the beef sector is still relatively limited. Adoption of genomic selection (GS) in beef cattle is more challenging than other intensive livestock species due to the existence of multiple breeds and crosses, more diverse environments, the sparseness of phenotyping, the relatively limited use of AI, and the genotyping cost which hinders the availability of large samples (Berry et al., 2016).
For traits like AOP, the amount of information available is often limited, leading to imprecise estimates. Some of these traits are censored with non-negligible impact on the results. In fact, estimates of genetic parameters for AOP are all over the place. For genomic studies or for estimation of genetic parameters, informative priors are often needed. Even if a single study estimates are imprecise, the average over a large number of studies will have much less variation. Given the high quality of the data used in this study, our estimates will provide an additional source of information to be used in future research. The objectives of this study are to estimate genetic parameters of 3 fertility traits and to compare the genomic prediction accuracy of different Bayesian GS procedures for 2 continuous and 1 binary fertility traits using data from a composite beef cattle breed.
MATERIAL AND METHODS
Phenotypes
Data for this study consisted of records from 1,365 first parity cows from a Composite Gene Combination breed (CGC; 50% Red Angus, 25% Charolais, 25% Tarentaise; Newman et al. 1993a, 1993b) born between 2002 and 2011 at USDA-ARS, Fort Keogh Livestock and Range Research Laboratory, Miles City, MT. The pedigree file consisted of 5,374 animals including 128 sires and 1,723 dams. Fertility phenotypes consisted of age of puberty (AOP), age of first calving (AOC), and heifer pregnancy status (HPS). AOP was predicted as described by Roberts et al. (2009) and is subject to be left and right censored (animal reached puberty before testing date or animal did not reach puberty at testing date). Rate of censoring increases with the increase in the age at first evaluation. In our study, age at first evaluation for puberty ranged between 301 and 354 d. Right censoring will not be an issue in the multivariate analyses as nonobserved phenotypes will be imputed based on the observed other correlated traits. However, left censoring could be more problematic as it is hard to account for through the statistical model because it is seldom the case that the exact AOP is known. The first 2 traits (AOP and AOC) were treated as continuous responses, and HPS was treated as binary. Missing AOP records are largely due to right censoring. In fact, left and right censoring for AOP were 10% and 34%, respectively. A summary description of the data is presented in Table 1. Further information concerning management and production records on the population are given in Roberts et al. (2016)
Table 1.
Summary of descriptive statistics for age at first calving (AOC), age of puberty (AOP), and pregnancy status (HPS) of CGC1 heifers
| Trait2 | Records3 | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| AOC | 1,117 | 722.16 | 21.71 | 651 | 782 |
| AOP | 890 | 385.57 | 32.12 | 304 | 454 |
| HPS | 1,365 | 0.86 | 0.34 | 0 | 1 |
CGC = composite gene combination breed (50% Red Angus, 25% Charolais, 25% Tarentaise).
AOC and AOP were expressed as continuous traits in days; otherwise, HPS was treated as binary trait where 1 was pregnant and 0 not pregnant after the first breeding season.
Number of animal with records for each trait.
Marker Genotypes
A total of 4,457 CGC animals born between 2001 and 2015 were genotyped with a mixture of different density SNP arrays (Table 2). Across the different arrays, SNP with call rate smaller than 0.90, minor allele frequency (MAF) less than 0.05, and heterozygous deviation greater than 15% from Hardy-Weinberg Equilibrium (HWE) were removed. In addition, animals with a call rate less than 0.90 were also discarded. Number of animals and SNP remaining after quality control (QC) edits are presented in Table 2.
Table 2.
Description of total genotyped animals with a mixture of different density SNP arrays before and after the quality control (QC) procedure
| Raw Data1 | QC Data2 | ||||
|---|---|---|---|---|---|
| # Animals | # SNP | # Animals | #Animals_HPS3 | # SNP | |
| 50K SNP array | 64 | 54,166 | 88 | 0 | 42,264 |
| 24 | 54,209 | ||||
| 27K SNP array | 380 | 25,856 | 790 | 1 | 8,126 |
| 14 | 25,948 | ||||
| 96 | 25,890 | ||||
| 326 | 25,887 | ||||
| 20K SNP array | 396 | 19,642 | 379 | 0 | 7,945 |
| 9K SNP array | 391 | 8,727 | 909 | 226 | 6,754 |
| 185 | 8,781 | ||||
| 344 | 8,777 | ||||
| 3K SNP array | 1,944 | 2,866 | 1,739 | 925 | 2,727 |
| 197 | 2,877 | ||||
| 96 | 2,882 | ||||
Total number of genotyped animals (4,457) before the QC procedure.
Final number of genotyped animals (3,902) after the QC procedure.
Number of animals with HPS records genotyped with the different arrays after QC procedure.
Animals genotyped with low-density (LD) arrays were imputed to the 50K SNP array using FImpute software (Sargolzaei et al., 2011) where population and pedigree information were used simultaneously. FImpute was implemented using default parameters in all imputation analyses. Each group of animals that was genotyped with different density arrays was imputed separately. In all cases, animals genotyped with the 50K SNP array were used as reference. Furthermore, SNP markers present in LD arrays but not in the 50K SNP array were removed. After imputation, the same QC process indicated before was reapplied resulting in a dataset of 3,902 animals (1,387 males and 2,516 females) with genotype information on 41,694 SNP.
Variance Component and Data Analysis
Multivariate Analysis Using Pedigree Data
A threshold-linear model was performed to jointly analyze the 3 traits. In matrix notation, the model equation is
where y = (y1,l)´ is the vector of continuous responses (AOC and AOP) and liabilities (l) for the binary trait (HPS), β is the vector of systematic effects, u is the vector of breeding values, and e is the vector of error terms. X and Z are two known incidence matrices with the appropriate dimensions.
Systematic effects consisted of 55 contemporary groups (pen or feeding lot) feed treatment (2 classes), year-month of birth (30 classes), and the covariates of age of the dam. To avoid extreme case classes for the binary trait, the year-month of birth contemporary group was replaced by the effects of year (10 classes) and month (3 classes) of birth. Due to model identification requirements, the residual variance of the binary response set fixed to one.
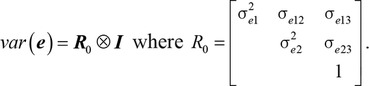 |
For the position parameters, the following priors were adopted:
where A is an expected additive relationship matrix, R0, and  is the Kroneker product. R0 and G0 are 3 × 3 residual and genetic covariance matrices, respectively.
is the Kroneker product. R0 and G0 are 3 × 3 residual and genetic covariance matrices, respectively.
Due to the size of the data used in this study, an informative conjugate prior was assumed for where the scaling parameters were obtained from single-trait analyses for the variances and literature values for covariances:
where IW(v,Σ)~ is a scaled inverted Wishart distribution with v = 5 degree of belief and scaling matrix.
 |
Because of the restrictions on the residual (co)variance matrix, the direct sampling of R0 is not feasible. To overcome this problem, the methods developed by Rekaya et al. (2013) were used. It is based on the ability of the Bayesian approach implemented via MCMC methods to be performed on unidentifiable models. Furthermore, the parameters of the identifiable model could be obtained through the appropriate postsampling transformation. In this study, the unidentifiable model with a nonrestricted residual (co)variance matrix was implemented first followed by a transformation using a diagonal matrix with elements equal to 1 for the continuous traits and the square root of the unrestricted variance for the binary response. Further information about the method is given in Albert and Chib (1993), Sorensen et al. (1995), and Rekaya et al. (2013).
To complete the Bayesian formulation, a prior for the nonrestricted residual covariance matrix was specified and consisted of U [0,105] for the diagonal elements and U 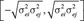 for (i ≠ j = 1,2,3) for the off-diagonal elements resulting in residual correlations ranging between −1 and 1, a priori. The resulting full conditional distributions needed for the implementation of Gibbs sampling for the systematic and random effects, liabilities, and genetic and residual (co)variance matrices were in closed form being normal, truncated normal, and scaled inverted Wishart, respectively. A unique chain of 200,000 samples was implemented where the first 100,000 samples were discarded as burn-in period based on visual inspection of the behavior of the chain. After each iteration, appropriate transformations were applied to generate samples from the identifiable model. The computer software developed by Rekaya et al. (2013) was used for analysis.
for (i ≠ j = 1,2,3) for the off-diagonal elements resulting in residual correlations ranging between −1 and 1, a priori. The resulting full conditional distributions needed for the implementation of Gibbs sampling for the systematic and random effects, liabilities, and genetic and residual (co)variance matrices were in closed form being normal, truncated normal, and scaled inverted Wishart, respectively. A unique chain of 200,000 samples was implemented where the first 100,000 samples were discarded as burn-in period based on visual inspection of the behavior of the chain. After each iteration, appropriate transformations were applied to generate samples from the identifiable model. The computer software developed by Rekaya et al. (2013) was used for analysis.
Univariate Analyses
Univariate analyses were implemented using either the average (A) or the genomic (G) additive relationships. A standard univariate linear model and a threshold model were used for the 2 continuous traits and the binary response, respectively. The same sets of systematic effects included in the multivariate analysis were used. For the position parameters, the following prior distributions were assumed:
where 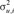 is the genetic variance for trait i(i = 1,2,3). For all genetic and residual variances, except the residual variance of HPS that was fixed to 1, flat uniform priors U[0, 105] were assumed. As with the multivariate scenario, a unique chain of 200,000 samples was implemented where the first 100,000 samples were discarded as burn-in period.
is the genetic variance for trait i(i = 1,2,3). For all genetic and residual variances, except the residual variance of HPS that was fixed to 1, flat uniform priors U[0, 105] were assumed. As with the multivariate scenario, a unique chain of 200,000 samples was implemented where the first 100,000 samples were discarded as burn-in period.
Genome-wide Prediction Models: Bayesian Estimation Methods
Several methods have been proposed for genome-wide predictions (Meuwissen et al., 2001; VanRaden, 2008; Habier et al., 2011; de los Campos et al., 2013); although they have different assumptions about the data-generating process and the complexity of implementation, they tend in general to give similar results. However, in small data sets, differences could be significant. In this study, 3 methods (BayesA, BayesB, and BayesC) were implemented and compared. For all 3 methods, the following association model was assumed for each trait separately:
where yi is the observed phenotype for the continuous traits or the liability for the binary response for cow i, β is the vector of systematic effect indicated in model [1], xi is an incidence vector relating the observation to the systematic effects, aj is the effect of SNP j = (1,2,3,…, p), zij is the genotype of cow i for SNP j (zij = 0,1, or 2), gjis an indicator variable taking the value of 1 for BayesA method and 1 (if the SNP is included in the model) or 0 (if the SNP is excluded) for BayesB and BayesCπ methods, and ei is the residual term.
The main difference between the 3 methods consists of the prior information assumed for the SNP effects that specified the number of markers to be included in the association model as well as their associated variance (Meuwissen et al., 2001; Habier et al., 2011).
A fivefold cross-validation was performed where 80% and 20% of the data were randomly assigned to the training and validation sets, respectively. Although assignment of validation animals could have been performed based on their relationships with animals in the training set, accuracy will depend on the pedigree structure. All analyses were implemented in R using the BGLR package (Pérez and de Los Campos, 2014). Point estimates of the SNP effects were used to compute the genomic prediction of animals in the validation set as
where 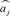 is the estimated effect of SNP j
is the estimated effect of SNP j
For the continuous traits, accuracy was calculated based on the correlation between the estimated genomic breeding values and the observed phenotypes adjusted for the systematic effects. For the binary response (HPS), the correct classification of observation within their true observed classes was used to access the model adequacy. The area under the curve (AUC) calculated using the true- and false-positive rates at different probability cutoff points was used. AUC has a value between 0 and 1. A value of 0.5 indicates the binary status is predicted at random. Obviously, AUC will have a different magnitude and interpretation than the correlation coefficient.
RESULTS AND DISCUSSIONS
Variance Components Estimation
Estimates of variance components and heritabilities of the 3 fertility traits using univariate and multivariate analyses based on pedigree relationship are presented in Table 3. Heritability estimates ranged from 0.03 for age at first calving to 0.191 for age at puberty. Heritability estimate for AOC (0.03) is in the lower end of reported estimates for this parameter. Although our estimate is similar to the result reported by Bourdon and Brinks (1982), it is much smaller than the 0.24 and 0.28 estimates reported by Frazier et al. (1999) and Minick Bormann and Wilson (2010), respectively. These differences could be in part due to whether the trait was recorded in days or months if rounding up was used. If the trait is rounded up when measured in months that could reduce the residual variance leading to an increase in heritability. Additionally, due to the small sample size our estimates have a large posterior standard deviation as indicated in Table 3. Reported estimates of heritability of AOP had an ample range (0.10 to 0.68). Such high variability in reported estimates is very likely due in part to the degree of left and right censoring in the trait. Our estimate (0.191) was greater than those reported by Smith et al. (1989), Morris et al. (1993), and Morris and Hickey (2004). However, it is much smaller than the 0.61 and 0.43 estimates reported by MacNeil et al. (1984) and Splan et al. (1998), respectively. At the liability scale, heritability of pregnancy status was 0.146 ± 0.072. It is much higher than the close to zero estimates reported by Morris et al. (1987) and Mathiews et al. (1995) or the 0.07 estimate reported by MacNeil et al. (2006). It is slightly higher than the estimates reported by Bormann et al. (2006). However, higher estimates exceeding 0.20 were reported by Doyle et al. (2000). Heritability estimates for AOC and AOP using multivariate approach were very similar to those obtained using the univariate analyses. However, the heritability of HPS was much smaller in the multivariate analysis (0.087 vs. 0.146). This could be due to culling females in the herd for purposes other than pregnancy status. In fact, all animals with nonpregnant status have a missing AOC phenotype.
Table 3.
Posterior means and posterior standard deviations (SD) for variance components1 and heritability (h2) of fertility traits using univariate and multivariate analyses based on pedigree relationships
| Univariate analysis | Multivariate analysis | ||||||
|---|---|---|---|---|---|---|---|
| Trait2 | # Animal 3 |
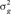 (SD) (SD) |
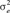 (SD) (SD) |
h2(SD) |
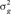 (SD) (SD) |
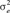 (SD) (SD) |
h2(SD) |
| AOC | 1117 | 9.95 (7.67) | 238.55 (12.26) | 0.039 (0.03) | 7.784 (5.26) | 240.76 (11.15) | 0.031 (0.01) |
| AOP | 890 | 169.17 (61.34) | 593.05 (60.10) | 0.221 (0.08) | 145.83 (46.39) | 589.3 (47.52) | 0.198 (0.06) |
| HPS | 1365 | 0.180 (0.11) | 1 (0.0) | 0.146 (0.07) | 0.096 (0.04) | 1 (0.0) | 0.087 (0.03) |
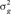 : additive genetic variance;.: residual variance.
: additive genetic variance;.: residual variance.
AOC: age at first calving (d); AOP: age of puberty (d); HPS: heifer pregnancy status (pregnant = 1, nonpregnant = 0).
Number of animals with phenotypic record for each trait.
Genetic and residual (co)variances between the 3 fertility traits are presented in Table 4. The favorable genetic correlation of 0.332 ± 0.195 between AOC and AOP found in this study suggests that selecting for an earlier age at puberty of heifers would result in a younger AOC. This moderate relationship is expected because the earlier the heifer reaches reproductive maturity, the more likely that it will become pregnant early in the breeding season. However, an early puberty does not necessarily mean a younger AOC if repeated inseminations are required for pregnancy or pregnancy does not occur or is lost prior to calving. Inconsistent results were found in the literature for the genetic correlation between AOC and AOP. Although our estimates agreed with those found by Smith et al. (1989), using data from several breeds of beef cattle, they are much larger than the near-zero estimates reported by Martínez-Velázquez et al. (2003), using 12 Bos taurus breeds at the Meat Animal Research Center (USDA). In a predefined breeding season system, these correlations are influenced by birth date of the animal, start of the breeding season, length of breeding season, and gestation length. The genetic correlation between AOC and HPS was -0.102 ± 0.165 indicating, as expected, that more fertile heifers will have a shorter AOC interval. Berry et al. (2013) reported a similar pattern, but a greater favorable genetic relationship between the 2 traits (-0.41 ± 0.129) using Holstein-Friesian in Ireland. A similar favorable estimate was reported (-0.38 ± 0.17) in Australian Holstein cows (Haile-Mariam and Pryce, 2011). Additionally, a meta-analysis across dairy populations conducted by Berry et al. (2014) reported high favorable relationships between AOC and pregnancy rate to first service (-0.27 ± 0.05) and AOC and pregnancy rate within an opportune time period (-0.41 ± 0.13). A small positive genetic correlation was found between HPS and AOP (0.077 ± 0.171). This point estimate is in the opposite direction of the majority of previously reported results. Other than the study by Martínez-Velázquez et al. (2003) that reported a near-zero estimate, several reports showed a favorable genetic correlation between AOP and pregnancy rate. A higher pregnancy rate in 2-yr-old New Zealand Angus cattle was reported to be associated with an earlier standardized age at first behavioral oestrus (-0.29 ± 0.30) as indicated by Morris et al. (2000). Similar favorable correlations of -0.30 ± 0.26 and -0.28 were reported by Morris and Cullen (1994) and Gargantini et al. (2005), respectively. Moreover, a high genetic correlation of heifer AOP and pregnancy rate of -0.71 ± 0.11 was reported in tropical beef cattle in Australia (Johnston et al., 2014). Similar patterns were reported for the genetic relationship between AOP and lifetime pregnancy rate (a good proxy for heifer pregnancy rate given their genetic correlation of 0.97). In fact, correlations of -0.21 and -0.29 were reported in Canadian composite cattle (Mwansa et al., 2000) and in New Zealand beef cattle (Morris and Cullen, 1994), respectively. The unfavorable genetic correlation between AOP and HPS found in this study could be due to the 36% missing records for AOP and the small size of the data set. Furthermore, left censoring (heifer reached puberty before testing date) that is intrinsically inherited in the way AOP is calculated penalizes heifers that reach puberty very early and could explain part of the unfavorable genetic correlation. In fact, in our study as well as in the majority of others reported in the literature, estimates of genetic parameters associated with the 3 fertility traits have large posterior standard deviations (due to small sample size).
Table 4.
Genetic and residual correlations using multivariate analysis between pairwise fertility traits
| Pairwise trait1 | Correlations | ||
|---|---|---|---|
| Genetic SD | Residual SD | ||
| (AOC, AOP) | 0.332 ± 0.195 | 0.054 ± 0.042 | |
| (AOC, HPS) | -0.102 ± 0.165 | 0.071 ± 0.126 | |
| (HPS, AOP) | 0.077 ± 0.171 | 0.028 ± 0.051 | |
AOC: age at first calving (day); AOP: age of puberty (day); HPS: heifer pregnancy status (pregnant = 1, nonpregnant = 0).
Table 5 presents the estimates of variance components and heritabilities of the 3 fertility traits using univariate analysis based on genomic relationships. Heritability estimates for AOP and AOC were 14% and 15% higher compared to pedigree relationships (Table 3). These increases in heritabilities are largely due to an increase in the estimated genetic variances using genomic information. The heritability estimate for HPS using genomic relationships was 8% lower than the estimate obtained using pedigree information. However, these differences between estimates of heritability are not statistically significant due to the large associated posterior standard deviations.
Table 5.
Posterior means and posterior standard deviations of variance components1 and heritability (h2) of fertility traits using univariate analyses based on genomic relationships.
| Trait2 | #Animals3 | (SD) | (SD) | h2(SD) |
|---|---|---|---|---|
| AOC | 958 | 11.07 (11.89) | 235.22 (15.59) | 0.045 (0.048) |
| AOP | 733 | 187.84 (64.64) | 567.33 (57.50) | 0.249 (0.079) |
| HPS | 1152 | 0.155 (0.10) | 1 (0.0) | 0.134 (0.069) |
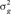 : additive genetic variance;
: additive genetic variance; 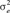 : residual variance.
: residual variance.
AOC: age at first calving (d); AOP: age of puberty (d); HPS: heifer pregnancy status (pregnant = 1, nonpregnant = 0).
Number of animals with SNP genotypes for each trait.
Accuracy of Genomic Predictions
Table 6 presents the accuracy of genomic breeding values for the 2 continuous traits measured by the correlation between estimates of genomic values and the phenotypes adjusted for the systematic effects and the predictability for the binary trait. The latter was measured by the AUC. Note that AUC will be equal to 0.5 if a random classifier was used. Accuracies were low due to the small sample size, low heritabilities, and the limited size of the reference population used for the imputation of missing SNP genotypes. Across the different methods used, higher accuracies were observed for AOP than AOC due to a higher heritability. For HPS, the AUC increased by 26% to 29% across the different methods compared to a random classifier (Table 6).
Table 6.
Correlation between estimated breeding values and adjusted phenotypes for AOC and AOP and the area under the curve (AUC) for HPS and their standard errors (between parentheses) using different statistical models and a fivefold cross validation.
| Models | |||||
|---|---|---|---|---|---|
| BayesB | |||||
| Trait1 | BayesA | π = 0.99 | π = 0.95 | π = 0.90 | BayesCπ |
| AOC | 0.148 (0.020) | 0.143 (0.020) | 0.154 (0.015) | 0.146 (0.020) | 0.150 (0.018) |
| AOP | 0.237 (0.014) | 0.188 (0.020) | 0.235 (0.014) | 0.242 (0.016) | 0.226 (0.014) |
| HPS | 0.637 (0.024) | 0.643 (0.024) | 0.639 (0.024) | 0.634 (0.024) | 0.639 (0.024) |
Continuous fertility traits, AOC: age at first calving (in d), AOP: age of puberty (in d); Binary fertility trait, HPS: heifer pregnancy status (pregnant = 1, nonpregnant = 0).
Although the BayesCπ method had similar results compared to the other methods, the portion of SNP not included in the association model (π) was 0.74, 0.52, and 0.45 for AOC, AOP, and HPS, respectively. The differences between methods across the 2 continuous traits are partly indicative of the genetic architecture of the traits as it relates to the number of causative loci and the distribution of their effects. Accuracies of genomic prediction for AOC obtained from our study were substantially lower than those observed in the literature. Boddhireddy et al. (2014b) reported an accuracy of 0.64 for AOC (measured in months) using BayesC (π = 0.90). Their data consisted of 1,496 Nelore animals genotyped with the 50K SNP array. Zhang et al. (2014) using the GBLUP model reported accuracies of 0.23 and 0.35 for AOP in tropical composite (1,097 genotyped animals) and Brahman cattle (996 genotyped animals) in Australia, respectively. Their accuracies were calculated as the correlation between GEBV and phenotypes adjusted for systematic effects divided by square root of heritability. More recently, Farah et al. (2016) reported accuracies of 0.14 and 0.34 for the same 2 breeds using the GBLUP method. Using high-density SNP array and GBLUP, Kramer et al. (2014) found an accuracy of 0.12 for days to first heat in Brown Swiss dairy cattle.
Figure 1 illustrates the AUC using different genomic evaluation models. HPS predictably ranged between 0.634 and 0.643, indicating that the assumed association model enhanced the prediction of the binary phenotype by 27% to 29% compared to a random classifier. Boddhireddy et al. (2014a), using U.S. Angus data and BayesC (π = 0.95), obtained accuracies between 0.54 and 0.57 adopting either the estimated breeding values or deregressed breeding values as dependent variables, respectively. Using 1,496 genotyped Nelore cattle in Brazil, Boddhireddy et al. (2014b) reported an accuracy of 0.64. Lower accuracy (0.27) for heifer pregnancy using 698 genotyped U.S. Angus beef cattle was reported by Saatchi et al. (2011). Using dairy cattle data, Sun et al. (2014) reported accuracies of 0.16 and 0.09 for Holstein and Jersey daughter pregnancy rate, respectively. Their reported accuracy results are based on the correlation between predicted breeding values and phenotypes. Although higher values of correlation coefficients and AUC indicate a higher degree of adequacy of the association model, they are not directly comparable.
Figure 1.
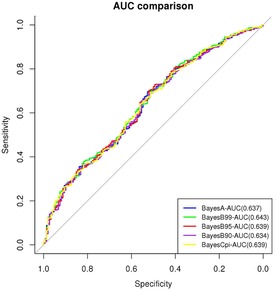
Area under curve (AUC) for the prediction of HPS using different genomic evaluation models. The solid line indicates the AUC using a random classifier.
Although comparison between studies is difficult due to the variations in the definition of reproductive related traits, the small size of the data used in several studies, and even the measure of accuracy itself, it is safe to say that prediction accuracies of fertility traits are generally in the lower end of the spectrum. This is largely due to the small heritability and limited size data sets. This does not imply the lack of usefulness of genomic information for the traits considered in this study. For AOP where phenotypic information is often limited or not available, a small improvement using genomic information is better than nothing as long as it is economically justifiable.
Conclusions
Fertility traits are of crucial importance to beef cattle production efficiency. Due to their low heritability and sometimes the logistics associated with their collection, genomic information could play an important role in the improvement of these traits. Two of the traits analyzed in this study (AOP and HPS) showed sufficient genetic variation to respond to selection that could be enhanced by genomic information. However, AOC had very low heritability, contrary to some literature reports. The latter is often measured in months, which substantially could have reduced the residual variance and artificially increased heritability within a breeding season. Results of this study, as well others referenced, should be interpreted with caution given the small size of the data sets used and the large uncertainty associated with the reported estimates. Multitrait genomic evaluation for fertility traits will likely enhance the accuracy of selection; however, it requires the joint analysis of continuous and discrete responses which often complicates the statistical analyses.
LITERATURE CITED
- Albert J. H., Chib S. 1993. Bayesian analysis of binary and polychotomous response data. J. Am. Stat. Assoc. 88:669–679. doi: 10.1080/01621459.1993.10476321 [DOI] [Google Scholar]
- Berry D., Garcia J., Garrick D. 2016. Development and implementation of genomic predictions in beef cattle. Anim. Front. 6:32–38. doi: 10.2527/af.2016-0005 [DOI] [Google Scholar]
- Berry D., Wall E., Pryce J. 2014. Genetics and genomics of reproductive performance in dairy and beef cattle. Animal 8:105–121. doi: 10.1017/S1751731114000743 [DOI] [PubMed] [Google Scholar]
- Berry D. P., Kearney J. F., Twomey K., Evans R. D. 2013. Genetics of reproductive performance in seasonal calving dairy cattle production systems. Ir. J. Agric. Food Res. 52:1–16. [Google Scholar]
- Biscarini F., Nicolazzi E. L., Stella A., Boettcher P. J., Gandini G. 2015. Challenges and opportunities in genetic improvement of local livestock breeds. Front. Genet. 6:1–7. doi: 10.3389/fgene.2015.00033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boddhireddy P., Kelly M. J., Northcutt S., Prayaga K. C., Rumph J., DeNise S. 2014a. Genomic predictions in Angus cattle: Comparisons of sample size, response variables, and clustering methods for cross-validation. J. Anim. Sci. 92:485–497. doi: 10.2527/jas.2013-6757. [DOI] [PubMed] [Google Scholar]
- Boddhireddy P., Prayaga K., Barros P., Lôbo R., DeNise S. 2014b. Genomic predictions of economically important traits in Nelore cattle of Brazil. In: 10th World Congr. Genet. Appl. Livest. Prod., Vancouver, BC, Canada. [Google Scholar]
- Bormann J. M., Totir L., Kachman S. D., Fernando R., Wilson D. 2006. Pregnancy rate and first-service conception rate in Angus heifers. J. Anim. Sci. 84:2022–2025. doi: 10.2527/jas.2005-615 [DOI] [PubMed] [Google Scholar]
- Bourdon R. M., Brinks J. S. 1982. Genetic, environmental and phenotypic relationships among gestation length, birth weight, growth traits and age at first calving in beef cattle. J. Anim. Sci. 55:543–553. doi: 10.2527/jas1982.553543x [DOI] [PubMed] [Google Scholar]
- Cammack K., Thomas M., Enns R. 2009. Reproductive traits and their heritabilities in beef cattle. Prof. Anim. Sci. 25:517–528. doi: 10.15232/S1080-7446(15)30753-1. [DOI] [Google Scholar]
- de los Campos G., Hickey J. M., Pong-Wong R., Daetwyler H. D., Calus M. P. 2013. Whole-genome regression and prediction methods applied to plant and animal breeding. Genetics 193:327–345. doi: 10.1534/genetics.112.143313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekkers J. C. M. 2010. Use of high-density marker genotyping for genetic improvement of livestock by genomic selection. CABI Anim. Sci. Rev. 2010:197–210. [Google Scholar]
- Doyle S., Golden B., Green R., Brinks J. 2000. Additive genetic parameter estimates for heifer pregnancy and subsequent reproduction in Angus females. J. Anim. Sci. 78:2091–2098. doi: 10.2527/2000.7882091x [DOI] [PubMed] [Google Scholar]
- Farah M., Swan A. A., Fortes M. R. S., Fonseca R., Moore S. S., Kelly M. J. 2016. Accuracy of genomic selection for age at puberty in a multi-breed population of tropically adapted beef cattle. Anim. Genet. 47:3–11. doi: 10.1111/age.12362 [DOI] [PubMed] [Google Scholar]
- Frazier E. L., Sprott L. R., Saunders J. O., Dahm P. F., Crouch J. R., Turner J. W. 1999. Sire marbling score expected progeny difference and weaning weight maternal expected progeny difference associations with age at first calving and calving interval in Angus beef cattle. J. Anim. Sci. 77:1322–1328. doi: 10.2527/1999.7761322x [DOI] [PubMed] [Google Scholar]
- Gargantini G., Cundiff L., Lunstra D., Van Vleck L. 2005. Genetic relationships between male and female reproductive traits in beef cattle. Prof. Anim. Sci. 21:195–199. [Google Scholar]
- Habier D., Fernando R. L., Kizilkaya K., Garrick D. J. 2011. Extension of the Bayesian alphabet for genomic selection. BMC Bioinf. 12:186. doi: 10.1186/1471-2105-12-186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haile-Mariam M., Pryce J.E. 2011. Age at first calving and its relationship with other dairy traits in Holstein cattle in Australian herds. Proc. Assoc. Adv. Anim. Breed. Genet, Armidale, Australia: p. 199–202. [Google Scholar]
- Johnston D., Corbet N., Barwick S., Wolcott M., Holroyd R. 2014. Genetic correlations of young bull reproductive traits and heifer puberty traits with female reproductive performance in two tropical beef genotypes in northern Australia. Anim. Prod. Sci. 54:74–84. doi: 10.1071/AN13044 [DOI] [Google Scholar]
- Kramer M., Erbe M., Seefried F.R., Gredler B., Bapst B., Bieber A., Simianer H. 2014. Accuracy of direct genomic values for functional traits in Brown Swiss cattle. J. Dairy Sci. 97:1774–1781. doi: 10.3168/jds.2013-7054 [DOI] [PubMed] [Google Scholar]
- MacNeil M. D., Cundiff L. V., Dinkel C. A., Koch R. M. 1984. Genetic correlations among sex-limited traits in beef cattle. J. Anim. Sci. 58:1171–1180. doi: 10.2527/jas1984.5851171x [DOI] [PubMed] [Google Scholar]
- MacNeil M. D., Geary T. W., Perry G. A., Roberts A. J., Alexander L. J. 2006. Genetic partitioning of variation in ovulatory follicle size and probability of pregnancy in beef cattle. J. Anim. Sci. 84:1646–1650. doi: 10.2527/jas.2005-698 [DOI] [PubMed] [Google Scholar]
- Martínez-Velázquez G., Gregory K. E., Bennett G. L., Van Vleck L. D. 2003. Genetic relationships between scrotal circumference and female reproductive traits. J. Anim. Sci. 81:395–401. doi: 10.2527/2003.812395x [DOI] [PubMed] [Google Scholar]
- Mathiews G., Green R. D., Brinks J. S., Golden B. L., Enns R. M., LeFever D. G. 1995. Genetic parameters for conception rate to synchronized breeding in Angus cattle. Proc. West. Sec. Am. Soc. Anim. Sci. 46:217–219. [Google Scholar]
- Meuwissen T. H., Hayes B. J., Goddard M. E. 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157:1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minick Bormann J., Wilson D. E. 2010. Calving day and age at first calving in Angus heifers. J. Anim. Sci. 88:1947–1956. doi: 10.2527/jas.2009-2249 [DOI] [PubMed] [Google Scholar]
- Morris C. A., Hickey S. M. 2004. Heritability of puberty traits in dairy heifers in commercial herds. In: Proc. N. Z. Soc. Anim. Prod., Hamilton: p. 115–117. [Google Scholar]
- Morris C. A., Baker R. L., Hickey S. M., Johnson D. L. 1993. Evidence of genotype by environment interaction for reproductive and maternal traits in beef cattle. Anim. Prod. 56:69–83. doi: 10.1017/S0003356100006176 [DOI] [Google Scholar]
- Morris C., Cullen N. 1994. A note on genetic correlations between pubertal traits of males or females and lifetime pregnancy rate in beef cattle. Livest. Prod. Sci. 39:291–297. doi: 10.1016/0301-6226(94)90291-7 [DOI] [Google Scholar]
- Morris C. A., Wilson J. A., Bennett G. L., Cullen N. G., Hickey S. M., Hunter J. C. 2000. Genetic parameters for growth, puberty, and beef cow reproductive traits in a puberty selection experiment. N. Z. J. Agric. Res. 43:83–91. doi: 10.1080/00288233.2000.9513411 [DOI] [Google Scholar]
- Morris C. A., Baker R. L., Johnson D. L., Carter A. H., Hunter J. C. 1987. Reciprocal crossbreeding of Angus and Hereford cattle 3. Cow weight, reproduction, maternal performance, and lifetime production. N. Z. J. Agric. Res. 30:453–467. doi: 10.1080/00288233.1987.10417957 [DOI] [Google Scholar]
- Mwansa P. B., Kemp R. A., Crews D. H., Jr, Kastelic J. P., Bailey D. R. C., Coulter G. H. 2000. Selection for cow lifetime pregnancy rate using bull and heifer growth and reproductive traits in composite cattle. Can. J. Anim. Sci. 80:507–510. doi: 10.4141/A99-135 [DOI] [Google Scholar]
- Newman S., MacNeil M., Reynolds W., Knapp B., Urick J. 1993a. Fixed effects in the formation of a composite line of beef cattle: I. Experimental design and reproductive performance. J. Anim. Sci. 71:2026–2032. doi: 10.2527/1993.7182026x [DOI] [PubMed] [Google Scholar]
- Newman S., MacNeil M., Reynolds W., Knapp B., Urick J. 1993b. Fixed effects in the formation of a composite line of beef cattle: II. Pre- and postweaning growth and carcass composition. J. Anim. Sci. 71:2033–2039. doi: 10.2527/1993.7182033x [DOI] [PubMed] [Google Scholar]
- Pérez P., de Los Campos G. 2014. Genome-wide regression and prediction with the BGLR statistical package. Genetics 198:483–495. doi: 10.1534/genetics.114.164442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rekaya R., Sapp R. L., Wing T., Aggrey S. E. 2013. Genetic evaluation for growth, body composition, feed efficiency, and leg soundness. Poultry Sci. 92:923–929. doi: 10.3382/ps.2012-02649. [DOI] [PubMed] [Google Scholar]
- Roberts A. J., Funston R. N., Grings E. E., Petersen M. K. 2016. TRIENNIAL REPRODUCTION SYMPOSIUM: Beef heifer development and lifetime productivity in rangeland-based production systems. J. Anim. Sci. 94:2705–2715. doi: 10.2527/jas.2016-0435. [DOI] [PubMed] [Google Scholar]
- Roberts A. J., Geary T. W., Grings E. E., Waterman R. C., MacNeil M. D. 2009. Reproductive performance of heifers offered ad libitum or restricted access to feed for a one hundred forty-day period after weaning. J. Anim. Sci. 87:3043–3052. doi: 10.2527/jas.2008-1476. [DOI] [PubMed] [Google Scholar]
- Saatchi M., McClure M. C., McKay S. D., Rolf M. M., W Kim J., Decker J. E., Taxis T. M., Chapple R. H., Ramey H. R., Northcutt S. L., Bauck S., Woodward B., Dekkers J. C. M., Fernando R. L., Schnabel R. D., Garrick D. J., Taylor J. F. 2011. Accuracies of genomic breeding values in American Angus beef cattle using K-means clustering for cross-validation. Genet. Sel. Evol. 43:40. doi: 10.1186/1297-9686-43-40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolzaei M., Chesnais J., Schenkel F. 2011. FImpute- An efficient imputation algorithm for dairy cattle populations. J. Dairy Sci. 94(E-Suppl. 1): 421. [Google Scholar]
- Smith B.A., Brinks J.S., Richardson G.V. 1989. Estimation of Genetic Parameters among Reproductive and Growth Traits in Yearling Heifers. J. Anim. Sci. 67:2881–2885. [PubMed] [Google Scholar]
- Sorensen D., Andersen S., Gianola D., Korsgaard I. 1995. Bayesian inference in threshold models using Gibbs sampling. Genet. Sel. Evol. 27:229–249. doi: 10.1186/1297-9686-27-3-229 [DOI] [Google Scholar]
- Splan R. K., Cundiff L. V., Van Vleck L. D. 1998. Genetic parameters for sex-specific traits in beef cattle. J. Anim. Sci. 76:2272–2278. doi: 10.2527/1998.7692272x [DOI] [PubMed] [Google Scholar]
- Sun C., VanRaden P. M., Cole J. B., O'Connell J. R. 2014. Improvement of prediction ability for genomic selection of dairy cattle by including dominance effects. PLoS ONE 9:e103934. doi: 10.1371/journal.pone.0103934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton P. K. 2010. Livestock production: Recent trends, future prospects. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 365:2853–2867. doi: 10.1098/rstb.2010.0134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanRaden P. M., Sanders A. H., Tooker M. E., Miller R. H., Norman H. D., Kuhn M. T., Wiggans G. R. 2004. Development of a national genetic evaluation for cow fertility. J. Dairy Sci. 87:2285–2292. doi: 10.3168/jds.S0022-0302(04)70049-1 [DOI] [PubMed] [Google Scholar]
- VanRaden P. M. 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91:4414–4423. doi: 10.3168/jds.2007-0980. [DOI] [PubMed] [Google Scholar]
- Zhang Y., Johnston D., Bolormaa S., Hawken R., Tier B. 2014. Genomic selection for female reproduction in Australian tropically adapted beef cattle. Anim. Prod. Sci. 54:16–24. doi: 10.1071/AN13016 [DOI] [Google Scholar]


