Abstract
Vascular patterning is a key process during development and disease. The diffusive decoy receptor sVEGFR1 (sFlt1) is a known regulator of endothelial cell behavior, yet the mechanism by which it controls vascular structure is little understood. We propose computational models to shed light on how vascular patterning is guided by self-organized gradients of the VEGF/sVEGFR1 factors. We demonstrate that a diffusive inhibitor can generate structures with a dense branching morphology in models where the activator elicits directed growth. Inadequate presence of the inhibitor leads to compact growth, while excessive production of the inhibitor blocks expansion and stabilizes existing structures. Model predictions were compared with time-resolved experimental data obtained from endothelial sprout kinetics in fibrin gels. In the presence of inhibitory antibodies against VEGFR1 vascular sprout density increases while the speed of sprout expansion remains unchanged. Thus, the rate of secretion and stability of extracellular sVEGFR1 can modulate vascular sprout density.
Keywords: VEGF, vasculature, pattern formation, reaction-diffusion
1. Introduction
Diffusion-limited growth can create various branching patterns, from snowflakes to bacterial colonies and epithelial structures [1, 2]. While these processes are highly diverse in physical details, each share the following common mechanism. A moving boundary, for example the surface of a crystal, interacts with a diffusive field, like the temperature. The dynamics of the field and the boundary is mutually interdependent as the expansion alters the surrounding field, while the field at the boundary determines the speed of expansion. This interdependent dynamics can give rise to the Mullins-Sekerka instability: steep gradients develop in the field around a protruding tip and promote its further extension. In this process, branching structures can be generated by progressive splitting of growing tips.
Vascular networks are also established by a series of branching events. Each vascular segment extends autonomously and contains several endothelial cells. While vascular patterning likely utilizes a variety of guidance mechanisms [3, 4, 5], one of the best established regulator of vascular growth is the response of endothelial cells to growth factors within the tissue environment, in particular to vascular endothelial growth factor type A (VEGF) [6, 7, 8, 9, 10]. In cultured endothelial cells, VEGF induces cell motility [11, 12], proliferation [13, 14] and directed movement (chemotaxis) [13, 15]. The chemotactic response is a sustained bias towards the growth factor gradient in the otherwise randomly directed cell movements [16]. While growth factors readily diffuse in culture, in a tissue environment growth factors are sequestered within the extracellular matrix – restricting both their diffusion and availability [17, 18].
Endothelial cells can be guided by a VEGF pre-pattern in the extracellular environment [17, 18]. Vasculogenesis in fish, where major vessels assemble directly (i.e. without forming an intermediate vascular plexus) also seems to be guided by a genetic pre-pattern, as specific vascular malformations are correlated with genetic defects [19]. However, a VEGF pre-pattern, similar to the one in the retina, has not been demonstrated in the ECM associated with the lateral plate mesoderm in avian embryos [20]. Furthermore, endothelial cells can self-assemble vascular networks in artificial culture environment [21, 22], an important factor in recent tissue engineering reports [23]. Thus, there is a biological interest to explore potential self-organization principles of vascular patterns.
Recent experiments demonstrated that secreted type 1 VEGF receptors (sVEGFR1 or sFlt1) can modulate vascular patterns. In particular, biochemical data indicates that sVEGFR1 can function as a “decoy receptor” by binding and inactivating VEGF within the tissue microenvironment [24, 25, 26, 27]. While the absence of sVEGFR1 does not fully eliminate vascular sprouts within mouse embryonic stem cell-derived embryoid bodies, the direction of and distance between the sprouts becomes irregular when endothelial cells are deficient in expressing sVEGFR1. Re-introduction of sVEGFR1 expression into deficient cells restored normal vascular morphology [26, 28]. Furthermore, vascular sprouts elongate faster when endothelial cells immediately adjacent to the sprouts express more sVEGFR1. In summary, the following patterning mechanism is consistent with the available experimental data: when endothelial cells secrete sVEGFR1, the diffusing decoy receptors antagonize the pre-existing VEGF within the tissue microenvironment. Interestingly, in this guidance mechanism the concentration of active (not antagonized) VEGF forms a gradient pointing away from endothelial cells. This patterning mechanism therefore operates with a functional VEGF gradient that is the opposite of what was predicted by previous models aimed to explain vascular patterning [29, 30, 31].
While the biological foundation of sVEGFR1-related vascular guidance is well explored, less is known how these processes modulate vascular patterns. Expansion of the cells is a simple consequence of cells being programmed to follow an outward directed gradient. However, could such a mechanism in itself promote sprouting (self-organized branching), and how does the pattern change when parameters such as the lifetime or the affinity of the diffusive inhibitor changes? To understand the connection between the multicellular-scale organization and the molecular signaling mechanism, we investigated computational models of the core patterning process. In particular, we considered sVEGFR1 to be a diffusive inhibitor of VEGF, which promotes the expansion of the vasculature. While sVEGFR1 is secreted by endothelial cells, most of the VEGF is produced by other cell types and sequestered in the ECM environment [32, 33, 34, 9].
To represent a biological system, a typical mathematical model makes several – often implicit – assumptions. Most of these modeling choices are thought to be irrelevant and not driving the behavior emerging within the model. To demarcate the relevant and irrelevant model details, one can use multiple complementary modeling approaches: the same biological mechanism, thought to be relevant, can be represented by distinct models that can differ greatly in several modeling choices [35]. When the complementary models yield the same behavior, the particular hidden or implicit assumptions in each model are thus likely irrelevant. In this paper we explore if and when a specific, sVEGFR1-like diffusive inhibitor can generate branching patterns. We introduce two, complimentary computational models to study the reaction-diffusion guided patterning process. One is a simple lattice model where cells can expand in discrete steps. The second represents the vascular structure by a continuous phase-field variable and associated partial differential equations to describe its growth. For various research questions we use either the lattice model or the phase-field model based on practical considerations. Computer simulations of both models as well as analytical dissection of conditions for boundary propagation reveal three modes of behavior: (i) arrested growth, (ii) formation of branching patterns and (iii) uniform expansion. The emerging patterning mechanism was found to be similar, but not equivalent to the Mullins-Sekerka type diffusion limited growth. We conclude that tissue vascularization (number of blood vessels in a unit volume) can thus be effectively controlled by the secretion rate of a diffusing inhibitor. Model predictions 65 were validated by morphometric analysis of time-lapse recordings in a 3D vascular sprout assay.
2. Materials and methods
2.1. Cell culture
Human umbilical vein endothelial cells (HUVEC, Lonza) were maintained in EGM-2 medium (Lonza) under normal cell culture conditions: 37oC with a humidified 5% CO2 atmosphere. HUVEC aggregates and sprouts were studied in an assay medium prepared by supplementing EGM-2 with 80 nM PMA (Merck), 40 ng/ml bFGF (Pierce), 40 ng/ml VEGF-A165 (Pierce) and 50 μg/ml ascorbic acid (Sigma). Cells were fixed with 4% paraformaldehyde for 30 minutes at room temperature. Fixed cultures were stained with 0.25 mg/ml toluidine blue solution in phosphate buffered saline (PBS, pH 7.4).
2.2. VEGFR1 inhibitor
Anti-VEGFR1 antibody [AP-MAB0702, Abcam] was used to sequester soluble isoform of VEGFR1. This antibody is directed against the extracellular domain of recombinant human VEGFR1. Based on earlier data [36], 20 μg/ml of final concentration was used in the assay medium to sequester the soluble receptors.
2.3. Spheroid formation
Cell aggregation chambers were made by casting liquid 2% agarose (Invitrogen) in a PDMS micromold (3D Petri Dish, Microtissues) and allowing it to gelate. The micromold contains 35 pillars that define 35 wells with a diameter and depth of 800 μm. After removing the agarose gel from the micromold and placing it into a 35 mm culture dish (Greiner), the wells were equilibrated with cell culture medium for 2 hours before transferring the cells.
Cell suspensions were obtained by incubation of the cell monolayer with trypsin-EDTA (Sigma) for 2 minutes and washing the cells off. Cell suspensions were transferred into the wells formed by non-adherent agarose walls. An average of 3000 cells were transferred into each well and the agarose chamber was filled up with EGM-2 medium and kept under normal cell culture conditions. In 24 hours HUVEC cells formed a single spheroid (aggregate) within each well.
2.4. Sprouting assay
HUVEC spheroid aggregates were embedded in fibrin gels. Fibrin gels were prepared using fibrinogen (Sigma), aprotinin (Sigma), human Factor XIII (gift from Dr. Balazs Dome, National Koranyi Institute for TB and Pulmonology, Budapest, Hungary) and thrombin (Sigma) following the protocol of Helm et al. [37, 38]. Briefly, fibrinogen solution (3 mg/ml) containing aprotinin and Factor XIII was made and transformed into fibrin gel by supplementing thrombin enzyme. Before gelation, HUVEC aggregates were added to the fibrinogen solution and the mixture was transferred into 6 mm diameter circular wells. Three of such polylactic acid (PLA) wells were fused filament deposition- (3D-) printed into tissue culture dishes (Greiner) using a suitably modified Ultimaker Original printer. After gelation, fibrin gels filling the circular wells were covered with assay medium and kept under normal cell culture conditions within a microscope stage-top incubator.
2.5. Time lapse imaging
Time-lapse recordings of the fibrin gel-embedded HUVEC aggregates were performed on a Zeiss Axio Observer Z1 inverted microscope with 10× Plan Neofluar objective. The microscope was equipped with a Zeiss Axiocam MRM CCD camera and a Marzhauser SCAN-IM powered stage. Cultures within tissue culture Petri dishes (Greiner) were kept in a stage-mounted incubator providing 37oC and a humidified 5% CO2 atmosphere. Stage positioning, focusing and image collection were controlled by Zeiss Axiovision 4.8 software and a custom experiment manager software module. Phase contrast images were collected every hour from each microscopic field for durations up to 72 hours.
2.6. Image analysis
Images recorded by time-lapse microscopy were analyzed by a custom-made segmentation algorithm using the NumPy [39], Scipy [40, 41, 42], Scikit-Image [43] and OpenCV [44] modules of Python 2.7. To identify the initial spheroid aggregates, the first frame of each image sequence was segmented by one of the following four methods: (i) Otsu’s thresholding, (ii) manual thresholding, (iii) Hough Circle Transform, (iv) adaptive thresholding. After segmentation, aggregates were reconstructed by using basic morphological operations and removal of small connected components. To detect sprout formation, images were preprocessed by extracting the background using a Gaussian mixture-based background segmentation algorithm [45, 46]. The resulting foreground image was blended with the reconstructed image of the initial aggregate, then basic morphological operations and small object removal were applied to reduce noise and to remove sprouts belonging to other aggregates. The sprouting spheroid was identified as the largest cluster of connected pixels. The image processing tools are available at https://github.com/doraelakatos/sprout-density-analyzer.git. All data files are available from the Open Science Framework database (https://osf.io/5e4px/).
2.7. Sprout density
To quantify sprout density around the spheroids, we calculated the radial density profile ρ0(r,t) for each frame as:
| (1) |
where r+δr and r−δr are the outer and inner radii of a ring, respectively. The area of the ring is Aring = 4πrδr. Within this ring, at a certain time t the area occupied by sprouts is denoted by Asprout(r + δr,r − δr,t). The ring has the same center as the minimal enclosing circle of the initial spheroid aggregate, and we choose δr = 5 μm. To eliminate differences due to the initial conditions, we normalized the radial density profiles as
| (2) |
where ρ0(r, t0) is the density profile of the first frame.
The cumulative density profile of a sprout can be calculated at a certain time point as
| (3) |
where Asprout(r) is the area occupied by the sprouts within a circle of radius r.
3. Models
3.1. Reaction-diffusion
For simplicity, we consider only a single VEGF isoform, VEGF-A165, that readily binds the extracellular matrix (ECM) [47, 48, 3]. We investigate a scenario in which a vascular sprout invades an area where VEGF is immobilized by the ECM, its concentration is spatially uniform (V0), and its availability as an extracellular signaling ligand is limited only by binding cell-secreted sVEGFR1 molecules. In our model VEGF can be either active (V ) or inactivated by forming a complex with sVEGFR1 (Rb), thus
| (4) |
holds. Active VEGF concentration (V ) is determined by the local concentrations of free (Rf) and bound (Rb) sVEGFR1 according to the following reaction-diffusion dynamics:
| (5) |
| (6) |
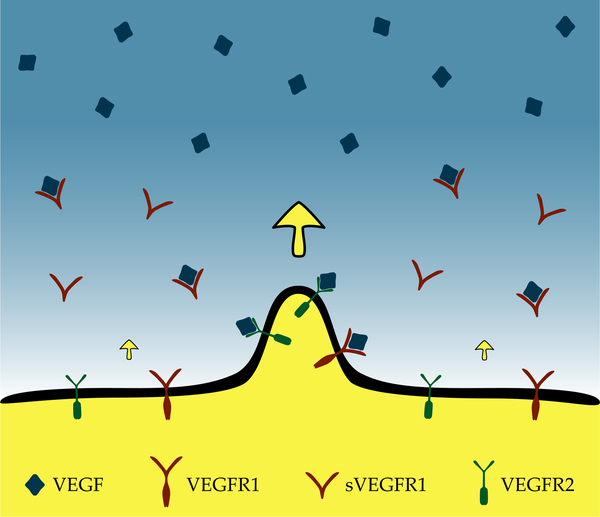
where kon and koff are the association and dissociation rates of the VEGF-sVEGFR1 complex, and DR, γ and Γ denote the diffusivity, degradation and the local secretion rate of sVEGFR1, respectively, and ∂t represents the partial derivative with respect to time. For simplicity we assume that the degradation rate of sVEGFR1 is the same irrespective of forming a complex with VEGF, and its secretion rate is uniform Γ* in areas occupied by cells and zero elsewhere (Fig. 1).
Fig. 1:
Model of sVEGFR1 driven vascular pattern formation. The concentration of VEGF (blue), immobilized by the ECM, is considered to be spatially uniform in the vicinity of the endothelial cell-covered area (yellow). The motility and proliferation of endothelial cells are promoted by the locally available VEGF via their cell surface receptors, VEGFR2 (green). Endothelial cells secrete a diffusive repressor, sVEGFR1 (red), that binds and inactivates VEGF. Thus, the concentration of active VEGF forms a gradient pointing away from endothelial cells (yellow arrow). As a protruding tip senses higher concentration and steeper gradients of active VEGF, it expands more rapidly, and further enhances its extension.
As the kinetics of receptor-ligand binding and complex dissociation is much faster than changes in the total amount of the protein, we apply quasi steady state approximation (QSSA, see Appendix A) for Eqs. (5) and (6). The concentration of bound sVEGFR1, Rb, can be expressed as a function of the concentration of free sVEGFR1, Rf, as
| (7) |
where the equilibrium constant K denotes
| (8) |
Subtracting Eq. (5) from Eq. (6) and replacing Rb by expression (7) yields the QSSA dynamics of the inhibitory receptor as
| (9) |
We couple the dynamics of sVEGFR1, Eq. (9), to vascular patterning by the following assumptions. First, the secretion rate of sVEGFR1 is uniform for each cell. Second, the extension of the cell-covered area is promoted – by a combination of chemotaxis, increased motility and proliferation of endothelial cells – by the locally available VEGF. According to Eqs. (4) and (7), the VEGF concentration can be determined as the function of unbound inhibitor:
| (10) |
By introducing the total receptor concentration (R) as
| (11) |
and substituting it into Eq. (7), the VEGF concentration can be expressed as a function of R, after solving the quadratic equation for Rb(R) (see Appendix A):
| (12) |
The binding affinity, 1/K, between VEGF and the decoy receptor sVEGFR1 is in the range of 2–30 pM [24, 49, 50, 51]. Accordingly, we set our concentration unit as c0 = 20 pM, and explored 1/K values between 6 − 20 pM. The steady-state sVEGFR1 concentration in culture media conditioned by a monolayer of HUVEC cells was reported in the range of 100 − 200 pM, i.e., 5–10 c0 [32, 52]. Our choice of simulation time unit, which must be much smaller than the time scale of patterning, is t0 = 10 s. We set the parameter γ characterizing spontaneous protein degradation in the range 4·10−5/t0 to 10−3/t0, corresponding to a lifetime range between 3 h and 3 days. The lifetime of most proteins falls in this range [53] and is also consistent with data characterizing the accumulation of sVEGFR1 in HUVEC culture [32, 52]. In a spatially homogeneous steady-state environment (Γ = Γ*) lacking binding partners or cellular uptake, Eq. (6) yields γ = Γ*/Rf. We selected the production rate Γ* in the range of 10−3 − 10−2c0/t0, corresponding to 7 – 70 pM/h. The experimental estimate for HUVEC monolayers is Γ* = 5 − 15 pM/h [32, 52]. Our choice of Γ* and γ parameters thus yields steady-state inhibitor concentrations in the range of 3 − 7 c0, comparable with experimental data (5–10 c0 [32, 52]).
The diffusion parameter of sVEGFR1 is not known in dense gels or tissues. As the molecule exhibits heparin binding sites [54, 55, 56, 57], we expect that it can bind to the extracellular matrix environment, and thus assumed rather low diffusivity. We used DR in the range of 10−8 − 10−7 mm2/s, the value reported for bFGF diffusion in basement membrane ECM [58] and three-four orders of magnitude less than diffusion coefficients of proteins in aqueous solutions. These values reflect that the diffusion of sVEGFR1 involves repeated binding and unbinding events which substantially restrict the molecule’s free diffusion [59]. The natural length scale of our simulation is that of the cells, thus we choose . This choice leads to , when expressed using the natural units of our simulations. The commonly used minimal concentration of exogenous recombinant VEGF to elucidate motility or proliferative effects on endothelial cells is 5 ng/ml = 100 pM = 5 c0 (R&D Systems, Catalog # 293-VE/CF). ECM-bound VEGF, however is much more potent [17, 60] – exerting signaling activity at concentrations as low as 0.1 ng/ml = 2.5 pM = 0.1 c0. The initial, spatially uniform, VEGF concentration was therefore chosen in our simulations as V0 = c0 = 20 pM.
3.2. Lattice model
To express the interdependence of vascular growth and sVEGFR1 diffusion, we augmented a simple lattice model with the reaction-diffusion equations (9) and (10). In this model the state σ of each lattice site can be either empty () or occupied by cells (). The inhibitor, sVEGFR1, is produced with a rate Γ* at lattice sites occupied by cells:
| (13) |
In the model, cells spread by the following mechanism. In each elementary step of the stochastic simulation, two neighbor sites and are selected randomly. If is occupied by cells, they can spread to (by leaving also occupied) with a probability p. The spreading process represents both VEGF-induced proliferation and motility. During a sufficiently short time period dt, the spreading probability is a linear function of χ(V ), the VEGF sensitivity function as
| (14) |
Where
| (15) |
Parameter ν characterizes the strength of VEGF response, both proliferative and motogenic. As in a single elementary step (of duration t0) the interface advances a lattice unit , Eq. (14) gives rise to a propagation speed of
| (16) |
Eq. (15) assumes a simple linear behavior above a threshold V*. The existence of a threshold is a crude approximation of the nonlinear behavior of binding between VEGF and its main cell surface receptor, VEGFR2, its neuropilin co-receptors, and subsequent dimerization of the receptors to initiate intracellular signal transduction reactions [14, 61]. In our simulations we used the threshold V* = c0/2, approximately corresponding to a 10 pM affinity between VEGF and its cell surface receptor complex. Our choice of ν = 0.025/c0 corresponds to a typical spreading speed of – similar to the typical speed of endothelial cell motility observed in culture [62, 63, 64].
3.3. Phase-field model
In the phase-field formulation the discrete state variable σ is replaced by a density-like variable, ϕ(x, t). Cell-free and cell-occupied areas are distinguished by the values ϕ = 0 and ϕ = 1, respectively. Instead of a sharp boundary separating these values, however, phase-field models operate with transition zones where the phase value changes gradually between the two extremes. We expect that the boundary is stationary except when it responds to a local driving force, a biological signal in the problem considered here. Thus, we require the propagation speed of the boundary, v, to be a monotonically increasing function of the local free VEGF concentration, VX:
| (17) |
where h(0) = 0.
To generate such a model, we consider the simplest, commonly used [65, 66, 67] equation determining the time evolution of the phase-field ϕ as
| (18) |
where F is a functional, analogous to the free energy of a physical system, written in the form of
| (19) |
Integration in Eq. (19) encompasses the entire system and the free energy density function f(ϕ, …) encodes the relative stability of the two phases for various values of external parameters [68, 69, 70, 71]. The parameter Dϕ needs to provide a microscopic dynamics compatible with the time and length scales of the patterning process. Thus, gradients in ϕ need to be orders of magnitude steeper than those characteristic for the external field, hence we have chosen Dϕ = 5 · 10−3DR.
To describe VEGF-induced vascular growth, we cast f in the form of
| (20) |
where τ sets the characteristic time scale of changes within the phase-field and parameter μ is analogous to ν, the parameter characterizing VEGF sensitivity in the lattice model.
The double-well potential
| (21) |
exhibits two minima at ϕ = 0 and ϕ = 1. The expression μχ(V )p(ϕ) modulates the minima of g and thus characterize – in the presence of VEGF – the preference of the cell-covered state over the cell-free state. The interpolating function p(ϕ) satisfies p(0) = 0 and p(1) = 1, and its usual choice [68, 70] is
| (22) |
Substitution of Eqs. (21 - 22) into the free energy density function Eq. (20) and derivation with respect to ϕ yields the phase-field equation for expanding endothelial cells:
| (23) |
Parameters τ and Dϕ are taken from the literature (Table 1) [72]. To set the parameter μ of the phase-field model, we consider a simpler, one dimensional version of the problem – the steady-state propagation of a straight interface with a velocity v. In this scenario the phase-field satisfies the advection equation
| (24) |
and replacing the time derivative of Eq. (18) with Eq. (24) yields
| (25) |
Table 1:
Parameters and emergent properties.
| Parameter | experimental value | reference | value in lattice model | value in phase-field model | ||
|---|---|---|---|---|---|---|
| sVEGFRl parameters | ||||||
| diffusivity (DR) | 10−7 mm2/s | [58] | 1 ℓo2/to | = 10 7 mm2/s | 0.25 io2/to | = 2.5 · 10−8 mm2/s |
| binding affinity to VEGF (1/K) | 2 – 30 pM | [24, 49, 50, 51] | 1 co | = 20 pM | 0.333 co | = 6.67 pM |
| secretion rate (Γ*) | 5 – 15 pM/h | [32, 52] | 10−2 co/to | = 72 pM/h | 10−3 co/to | = 7.2 pM/h |
| degradation rate (γ) | 0.03 – 0.8 1/h | [53] | 10−3 1 /to | = 0.36 1/h | 4 · 10−5 1/to | = 0.01 1/h |
| steady state concentration | 100 – 200 pM | [32, 52] | 3.5 co | = 70 pM | 7 co | = 140 pM |
| VEGF parameters | ||||||
| cellular sensitivity (ν, μ) | 10−2 1/co | 26.67 1/co | ||||
| threshold concentration (V*) | 2.5 pM < | [60, 75, 76] | 0.5 co | = 10 pM | 0.5 co | = 10 pM |
| other simulation parameters | ||||||
| phase-field diffusivity (Όφ) | 5 · 10−3 ℓo2/to | |||||
| characteristic time scale (t) | 200 to | |||||
| time step (Δί) | 0.1 to | 0.1 to | ||||
| mesh spacing (Δχ) | 1 ℓo | 0.5 ℓo | ||||
| emergent properties | ||||||
| branch width | 10.6 – 29.2 μm | * | 5.8 – 13.7 ℓo | = 5.8 – 13.7 μm | 13.2 – 37.2 ℓo | = 13.2 – 37.2 μm |
| branch growth speed | 3.05 ± 0.52 μm/h | * | 4.8 · 10−3 ± 13% ℓo/to | = 1.73 ± 0.22 μm/h | 9.6 · 10−3 ± 5% ℓo/to | = 3.46 ± 0.16 μm/h |
| VEGF gradient | 50 pM/mm < | [74, 77] | 7 · 10−3 ± 10% co/io | = 140 ± 14 pM/mm | 1.2 · 10−2 ± 10% co/io | = 240 ± 24 pM/mm |
time unit: to = 10 s, length unit: ℓo = 1 μm, concentration unit: co = 20 pM
Mvegf = 40 kDa, Msvegfri = 100 kDa,
: experimental values obtained in this study
Next we examine how the speed of propagation, v, depends on a pre-determined uniform VEGF response parameter μχ(x,t) = χ0. Close to the interface () the derivative ∂ϕf is dominated by the VEGF response term of Eq. (23) as
| (26) |
We rescale our variables by a positive factor s as
| (27) |
and define the rescaled field as
| (28) |
Expressing Eq. (25) in terms of the rescaled variables and using the approximation (26), we obtain
| (29) |
Thus, if is a solution of Eq. (29) with velocity and VEGF response , then is also a solution with velocity and VEGF response . Thus,
| (30) |
yielding Eq. (17)
| (31) |
To validate and calibrate the scaling relationship (31), we performed simulations of the phase-field model equation (23) with a fixed, spatially uniform VEGF response χ0. The initial condition corresponds to the setting considered in our analysis as
| (32) |
where is the step function: for x > 0 and zero otherwise. The boundary position, X, was defined as ϕ(X,0) = 1/2. In agreement with Eq. (31), the velocity v of the advancing front for our choice of Dϕ and τ could be well fitted as
| (33) |
for a wide range of the prescribed driving force 0 1/c0 ≤ χ0 ≤ 16 1/c0 with a = (7.6 ⋅ 10−3 ± 1%) μm/h. To obtain spreading speeds similar to that of the lattice model (10 μm/h) at typical VEGF concentrations V − V* = c0, we set μ = 13.3 1/c0. Substitution of Eq. (15) into Eq. (33) then yields the propagation speed of the boundary as a function of VX, the concentration of VEGF at the boundary:
| (34) |
4. Results
4.1. Endothelial sprouting modulated by VEGFR1
To obtain time-resolved quantitative data about the role of sVEGFR1 in vascular sprouting, we performed two independent sets of experiments with human umbilical cord vein endothelial cells (HUVECs) and commercially available function blocking antibodies that bind both the soluble and membrane-bound form of VEGFR1. Our sprouting assay consisted of HUVEC aggregates embedded in fibrin gel and supplemented with exogenous VEGF. During a time course of a day, endothelial cells left the aggregates in multicellular sprouts and created a vascular structure (Fig. 2A, Supplemental Movie C.1). Physical cross sections revealed lumen-forming vessels with a diameter comparable to the size of an individual endothelial cell, within the range of 10 − 30 μm. While most vascular segments grew straight during our one day long time-lapse observation period, some formed branched structures. After six days in culture, however, a branching network is more prominent (Supplemental Fig. B.1).
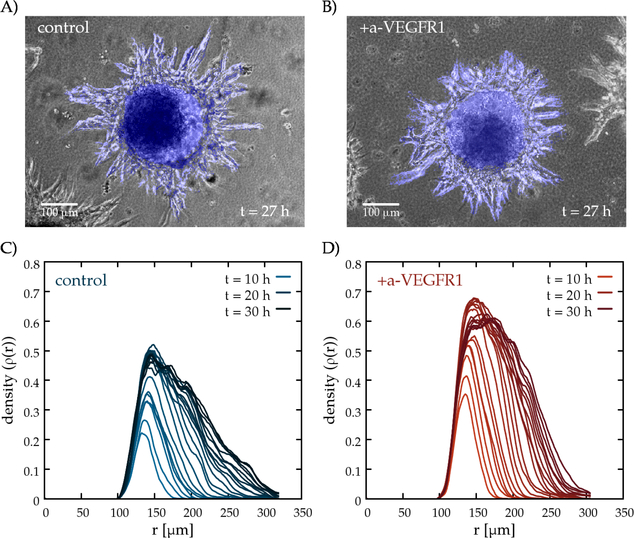
Fig. 2:
Sprouting assay using HUVEC spheroids in fibrin gel. Representative phase-contrast images from time-lapse recordings (Supplemental Movie C.1) of untreated control cultures (A), and of cultures exposed to function blocking antibodies against VEGFR1 at a concentration of 20 μg/ml (B). Exposure to the antibody reduces the interbranch distance and yields denser sprouts. Vascular components recognized by the image analysis algorithm are colored blue. Representative radial density profiles, ρ(r,t) are shown as a function of radius, for untreated (C) and a-VEGFR1 treated (D) sprout structures. The color saturation of the lines indicates the in vitro age of the culture between 10 and 30 hours, plotted for each frame.
Vascular sprouts grown in the presence of function blocking VEGFR1 antibodies were denser (exhibited more sprouts per unit volume) than those grown in control cultures (Fig. 2B). To quantitatively characterize vascular sprouting in this experimental model system, we segmented the area covered by cells by an image processing algorithm (Supplemental Movie C.2). The segmented image sequence was evaluated in terms of normalized radial density profiles ρ(r,t): for a sequence of concentric rings with various radii r, we determined the fraction of cell covered area within each ring (Fig. 2C-D). To focus on sprouts, density profiles were normalized by removing the contribution of the original aggregate. The time-dependent radial density profiles reveal that irrespective of the presence of antibodies, the sprouts expanded with a steady rate of 70 μm/day= 3 μm/h (Fig. 3B), which is substantially slower than the speed of individual endothelial cells in culture (10–20 μm/h, [62, 63, 64]). The density of vascular branches, however, is higher in the presence of function blocking VEGFR1 antibodies. To quantitatively characterize this phenomena, we determined ρmax(t), the maximal value of ρ(r,t), for each time-lapse frame t. For untreated cultures, vascular sprouts cover 40–50% of the area close to the aggregate. In contrast, the presence of VEGFR1 antibodies increases the maximal coverage to 60%. The density difference between treated and untreated cultures is visualized in Fig. 3A, by subtracting the population average of control cultures from the population average of treated cultures for each time point t. Data pooled from 19 distinct sprout networks supports the observation that the sprout network is denser in the presence of function blocking VEGFR1 antibodies throughout the entire recorded time period. The cumulative distribution function of normalized sprout densities within each sprout systems is shown in Supplemental Fig. B.2A. Statistical significance of the differences were established by t-tests (p < 0.05).
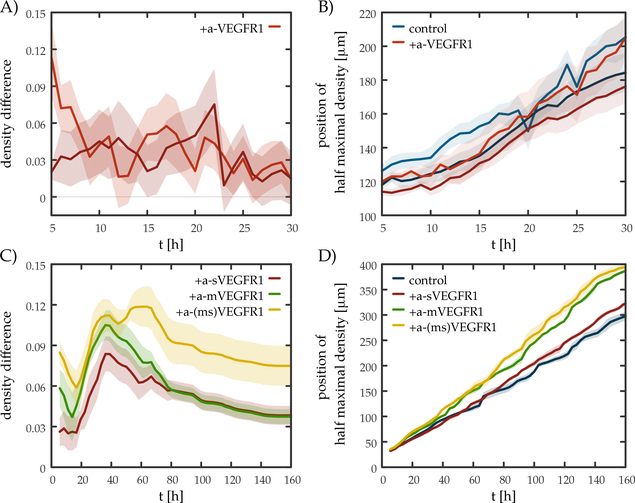
Fig. 3:
Soluble VEGFR1 increases sprout density both in experiments and in simulations. A) Density difference values demonstrate that cultures where VEGFR1 was blocked develop a denser sprout network than untreated cultures do. The lines show the average difference in density as a function of the age of culture t – obtained from two distinct experiments containing n = 8 and n = 11 HUVEC spheroids. B) Sprout expansion in experiments is insensitive to the presence of VEGFR1 antibodies. Sprout extent was established from normalized radial density profiles (ρ(r,t), see Fig. 2) as the radius R where ρ(R,t) is the half of the maximal density ρmax(t). Blue and red lines represent control and a-VEGFR1 treated cultures, respectively from two distinct experiments. Irrespective of the presence of antibodies, the sprouts expanded at similar rates: 3.13 ± 0.15 μm/h and 2.97 ± 0.09 μm/h (control), 3.43 ± 0.14 μm/h and 2.82 ± 0.09 μm/h (treated) in the two experiments respectively. C) Density difference in lattice simulations where soluble (red), membrane-bound (green) or both (yellow) population of VEGFR1 was blocked, according to Eqs. (35), (36) or both, respectively. In the simulations a 10% increase in the degradation rate (Eq. 35) represents the presence of a-sVEGFR1 antibodies, and a 10% shift in the VEGF response curve (Eq. 36) represents the inhibition of cell surface receptors. Each line indicates mean values obtained from n = 4 distinct simulations. D) Sprout expansion in lattice simulations was calculated by the same method used to evaluate experimental results. Expansion speed baseline (blue): 1.7±0.01 μm/h, sVEGFR1-blocked (red): 1.9±0.01 μm/h, mVEGFR1-blocked (green): 2.4±0.02 μm/h, both population blocked (yellow): 2.49±0.02 μm/h. Shaded areas represent the standard error of the mean, calculated from individual spheroids treated in identical manner (A, B) and distinct simulations (C, D). Expansion speed was obtained by fitting the position of half of the maximal density as a linear function of time.
4.2. Simulations
To explore the reaction-diffusion guided patterning mechanism formulated in our models, we performed computer simulations in two dimensions. The reaction-diffusion equation Eq. (9) was coupled to either the phase-field equation (Eq. (23)) or to the spreading probability (Eq. (14)) in the lattice model. Discretized equations were solved on a uniform, N × N grid by employing the forward Euler method. The lattice size was and in the lattice and the phase-field simulations, respectively. To avoid numerical instabilities, the time step Δt = 0.1 t0 was chosen in accordance with stability conditions. In case of the lattice model, the continuous variables were updated after N2 elementary steps. To suppress the inherent anisotropy of the square lattice in phase-field simulations, we introduced a multiplicative “quenched” noise with unit mean and standard deviation in the chemotactic sensitivity as [73].
As experimental data leave a substantial uncertainty about the parameter values, here we present results obtained with distinct choices (see Table 1) for the lattice and phase-field simulations. Despite using different parameter sets and different mathematical model formulations, the reaction-diffusion mechanism can produce branching patterns in a robust manner (Figs. 4, 5). Moreover, using the same set of parameters yields similar patterns in both implementations (Supplemental Fig. B.3).
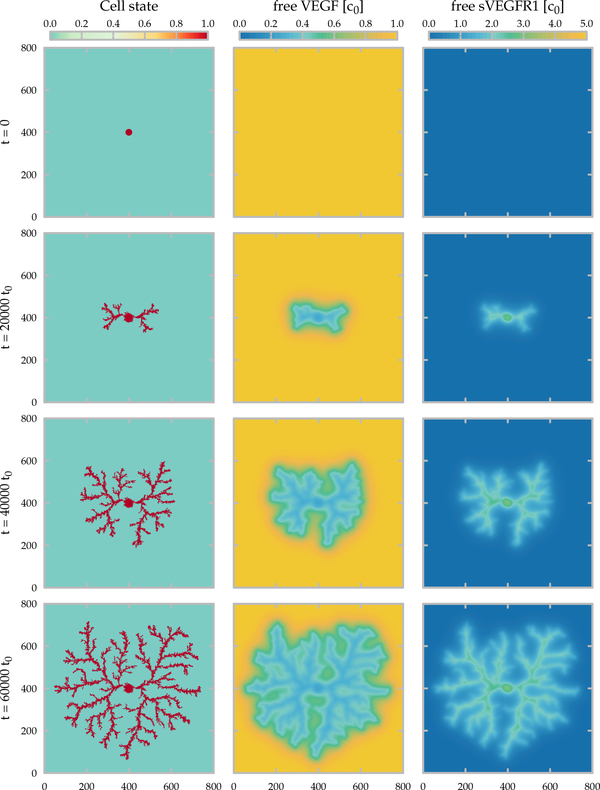
Fig. 4:
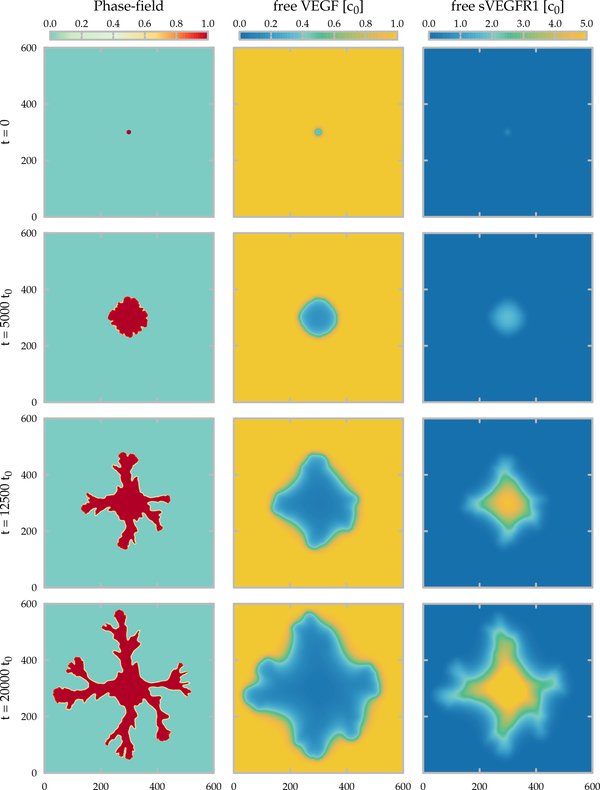
Time development of the lattice model. The area occupied by the cells and the concentration fields of the free growth factor (VEGF) and of the inhibitor (sVEGFR1) are shown in the left, middle and right columns, respectively. The state of the simulation is shown at the beginning (top) and after 20000, 40000 and 60000 (bottom) time units, corresponding approximately to 2, 4.5 and 7 days in culture. Parameters of the 800×800 lattice simulation are summarized in Table 1.
Fig. 5:
Time development of the phase-field model. As in Fig. 4, the area occupied by the cells and the concentration fields of the free growth factor (VEGF) and of the inhibitor (sVEGFR1) are shown in the left, middle and right columns, respectively. The state of the simulation is shown at the beginning (top) and after 5000, 12500 and 20000 (bottom) time units, corresponding approximately to 14, 35 and 55 hours of development. Parameters of the 1200 × 1200 lattice simulation with mesh spacing are summarized in Table 1.
Thus, model simulations indicate the presence of tip-splitting instability as the initial cluster of cells expands into a branching pattern (phase-field model results shown in Fig. 6). The secretion of sVEGFR1 inactivates the VEGF in the vicinity of the sprouts, and the threshold condition Eq. (15) is required to freeze those boundaries which are behind the expanding envelope of the branch tips. When the threshold concentration V* is not substantial enough (i.e., V* ⪡ c0), vascular segments continue to widen even far behind the branch tips and thus create a compact structure.
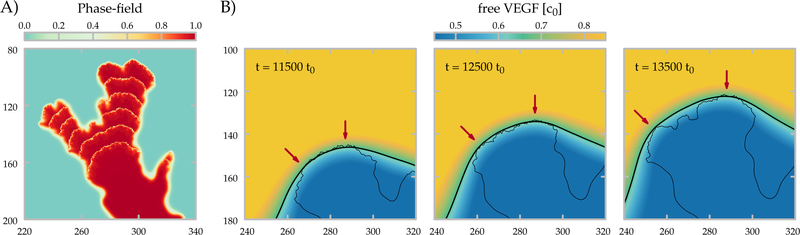
Fig. 6:
Tip-splitting event in the phase-field model. A) The area occupied by the cells are shown at every 1000 t0 simulation steps (∼ 2.7 h) of a representative tip splitting event. B) The concentration field of the free activator (VEGF) is shown at three different time points. The thicker and the thinner black lines correspond to a VEGF contour (V = 0.65c0) and to the boundary of the vasculature (ϕ = 0.65) respectively. Red arrows point to sites of future branches: border segments that experience especially high VEGF concentrations.
The profile of the self-generated VEGF gradient was determined – along the longitudinal direction – at selected branch tips of the phase-field model (Supplemental Fig. B.4). We also determined the profiles corresponding to the Mullins-Sekerka system, in which an external diffusive field (i.e., VEGF) drives the propagation of the boundary [72] (Supplemental Fig. B.5). The obtained profiles indicate that the gradient is 2–3 times steeper in the reaction-diffusion system than in the Mullins-Sekerka system with comparable parameters.
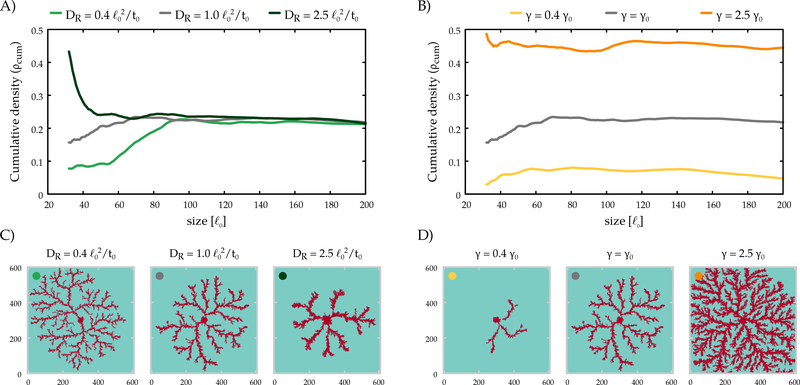
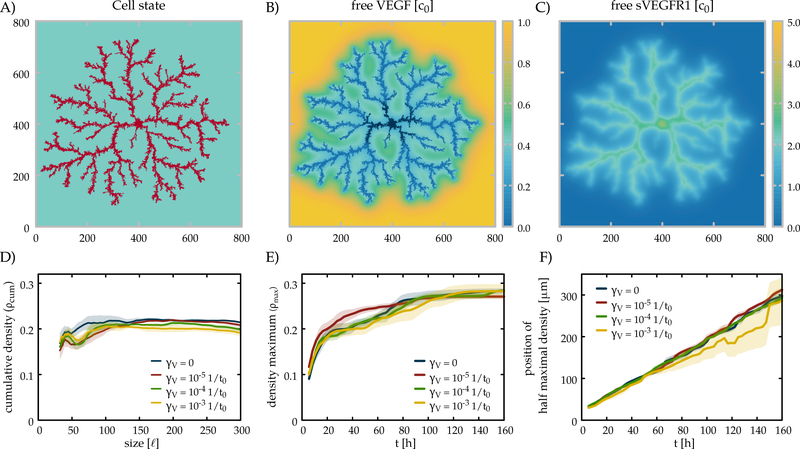
The typical branch width of the simulations is in the range of 10–30 μm, in accord with the experimentally observed values. Branches expand with a speed of 4.8 ⋅ 10−2 − 9.6 ⋅ 10−2, values close to the experimental observations (3 μm/h). The interbranch distance as well as the diffusion length of sVEGFR1 are both ~ 80, consistent with the theoretical estimate . Indeed, both increasing DR and decreasing γ leads to sparser branches as shown in Fig. 7 for the lattice model (parameter dependency of branching in both models are shown in Supplemental Figs B.6-7). The typical magnitude of VEGF gradients that develop in the model is pM/mm = 5–10 ng/(ml mm) – the same magnitude that the endothelial cells are able to detect in cell culture experiments [74].
Fig. 7:
The lattice model yields a dense branching morphology. The cumulative radial density (A, B) reaches a steady value, indicating a space-filling structure with a fractal dimension of 2. Morphologies are shown for three values of the diffusivity (C) and the degradation rate (D) of the inhibitor. The radial density profiles in panels (A,B) can be matched by the color code to the morphologies in panels (C,D). γ0 = 10−3 1/t0.
Our parameter choice yields an average cell coverage of 20% in the lattice model – which can be increased by faster sVEGFR1 degradation, but is unaffected by changing its diffusivity DR. In general, our simulations suggest that when parameters favor expansion (decreased threshold concentration, increased chemotactic response, etc) the branches are wider, and eventually they merge into a smooth propagating front. When parameters are less conductive to cell expansion, branches became thinner, and below a threshold, expansion ceases in both models (Supplemental Figs B.6–7).
4.3. Model validation
We validated our model by comparing it to experimental sprouting data obtained in the presence and absence of VEGFR1-blocking antibodies. These antibodies are thought to block both the membrane-bound and diffusive form of the inhibitor. As we detail below, the computational model can predict the consequences of blocking either form of the receptor.
To represent in our models the experimental perturbation of function blocking antibodies interacting with the soluble receptor, we altered the VEGFR1 degradation rate parameter γ as VEGFR1 can be inactivated both by degradation and by dimerization with a high affinity antibody. Since in the experiments antibodies were given in large excess, its concentration is approximately constant, A. Thus, inactivation of sVEGFR1 is given by
| (35) |
where is the association rate of the sVEGFR1-antibody complex and γ′ is the increased degradation rate (γ′ > γ). In agreement with experimental observations, when γ is increased to γ′ both the lattice and the phase-field model predicts denser sprouts (Fig. 3A, C and Supplemental Fig. B.8). While both model implementations predict a slight (less than 10%) increase in expansion speed (shown for the lattice model in Fig. 3D), this was not observed in experiments (Fig. 3B).
To represent antibody binding to cell surface receptors, we shift the VEGF-response curve (15) by a factor α as
| (36) |
Thus, we assume that competitive binding at the cell surface changes the EC-50 value of the VEGF dose-response curve. As the antibodies remove an inhibitory effect, we expect α > 1. Again, simulations predict an increase in vascular density, with a larger increase in the speed of pattern propagation (lattice model results shown in Fig. 3D).
The experimental findings and simulation results are thus in reasonable agreement. As in the experiments the increase in sprout growth speed is smaller than the increase in vascular density, we suggest that the effect of the antibodies are mainly exerted through their association with the diffusive form of VEGFR1.
4.4. Analysis of front propagation
4.4.1. Concentration profile generated by a moving front
To better understand the simulation results, we need to connect the self-organized concentration profile of the inhibitor and the expansion speed of the pattern. In particular, we would like to understand the three regimes: compact, branching, and arrested expansion. We consider a plane boundary propagating according to the locally available VEGF concentration. First, we determine the steady state concentration profile of the diffusive repressor field when the boundary propagates with a steady speed v. In order to solve our reactiondiffusion system analytically, we simplify our problem and assume that (i) the inhibitor diffuses irrespectively whether it is in a complex or not, and (ii) the boundary is sharp. Under these assumptions the total receptor concentration satisfies
| (37) |
Reflecting a sharp boundary located at x = X0(t), the secretion rate is given by
| (38) |
To calculate the stationary planar front solutions of Eq. (37), translating with a steady velocity v, we introduce the co-moving coordinate ξ = x − vt. The boundary position and the secretion rate then change to X = X0(t) − vt and , respectively. With appropriate choice of t, we can set the position of the planar front to X(t) = 0. The new spatial variable ξ transforms the partial time derivative as . Hence, in this scenario the total receptor concentration r0 and secretion rate Γ0(ξ) can be written as
| (39) |
and
| (40) |
respectively.
Since the front has a stationary profile in the co-moving frame, the time derivative vanishes and Eq. (37) reduces to an ordinary differential equation for r0:
| (41) |
It is convenient to construct r0 from two distinct spatial components as
| (42) |
By solving the corresponding homogeneous differential equations, we obtain the eigenvalues of the characteristic equation as:
| (43) |
For a front propagating from left to right, the boundary and continuity conditions are
| (44) |
respectively. Conditions (44) allow to fully specify the solution for Eq. (41):
| (45) |
The concentration of the inhibitor at the interface, rX, can be expressed as a function of the front velocity v as
| (46) |
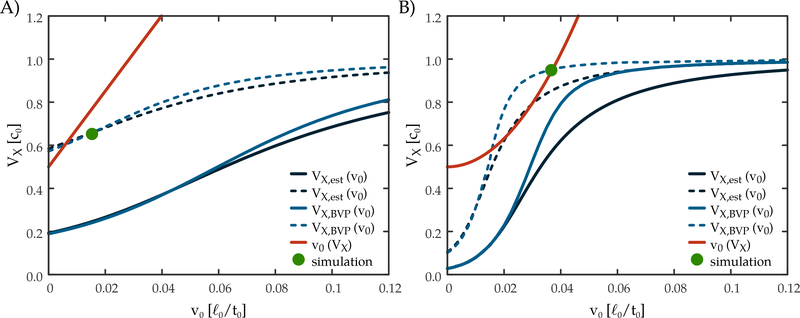
Substitution of rX(v) into Eq. (12) yields an analytic estimate for the VEGF concentration at the interface as a function of v (Fig. 8) as
| (47) |
Fig. 8:
Velocity selection in the lattice (A) and phase-field (B) models. The red curves represent the expected propagation speed of the boundary for a prescribed value (VX) of VEGF at the interface. The black and blue curves show the calculated (blue) and analytically estimated (black) VX values for a pre-determined propagation speed of the boundary (v0). Intersection of the red and blue curves determine the emergent propagation speed in the full model. In the absence of intersections, a planar front cannot propagate. By forming branches, the effective secretion rate of the inhibitor is decreased (dotted curves) allowing for the propagation of the leading tips of dense branching morphologies. VX,est(v0): analytic solution for V as the function of the propagation speed obtained from the differential equation of the simplified system; VX,BV P(v0): numerical solution of the reaction-diffusion equation of the free repressor in a co-moving frame with BVP solver; v0(VX): propagation speed of the boundary as the function of V obtained from simulation of the phase-field equation with uniform driving force; simulation: operating point obtained from the simulation of the full differential equation system.
To verify the correctness of the above picture, we also obtained VX(v) from the full reaction-diffusion equations, i.e., without the simplifications of Eq. (37). In the co-moving frame the stationary profile of the free sVEGFR1 repressor satisfies
| (48) |
The boundary conditions for Rf
| (49) |
| (50) |
specify a boundary value problem (BVP) for Eq. (48). The BVP was solved numerically for several v values and the free VEGF concentration at the boundary was obtained using Eq. (10). The resulting VX, BV P(v) curves (Fig. 8) exhibit very similar behavior to our analytic estimate Eq. (47).
4.4.2. Velocity selection
The velocity of the front and the concentration profile are mutually interdependent: The velocity of the front is determined by the concentration value at the boundary. On the other hand, the concentration profile is determined by Eq. (47), which depends on the propagation velocity. Thus, a front propagating in a steady state needs to satisfy both Eq. (47) and Eq. (34) for the phase-field model or Eq. (16) for the lattice model. These are equations for two unknowns, v and VX. As Fig. 8 demonstrates, the v(VX) and VX(v) functions may or may not have intersections.
When intersection points exists, their v and VX values specify possible steady states of moving fronts. However, when two intersection points are present, we expect the first one, i.e. the one corresponding to the smaller velocity, to be unstable. When VEGF concentration is slightly increased at the interface, this perturbation speeds up the advancement of the boundary. In the vicinity of the first fixed point faster propagation further increases the VEGF concentration, thus the front will accelerate and reach the second, stable fixed point.
If there are no intersections of the v(VX) and VX(v) functions, propagating steady state fronts cannot arise in the system. Branching, however, allows a steady expansion of the vascular sprouts even under such conditions. As the inhibitor can diffuse away from the branches in the lateral directions, its concentration is reduced at the branch tips. The crude approximation of infinitely efficient azimuthal diffusive transport across the branches yields the previously analyzed planar front problem where the envelope of branch tips form the expanding boundary. The propagation of this coarse-grained sprout system is then subject to the same velocity selection conditions Eq. (47) and Eq. (34). However, as the inhibitor is produced only at a fraction (ρ) of the surface, we need to scale its spatially uniform production factor as Γ′ = Γ/ρ. Indeed, simulations performed using the full set of equations (23), (9) and (10) and started from an initial condition consistent with boundary conditions Eq. (50), confirm that our analysis correctly provides the selected velocity and VEGF concentration at the boundary (Fig. 8). Hence, when a compact front cannot propagate, branching can be seen as an effective way to reduce inhibitor production and restore the possibility of growth. The approximation of an infinitely efficient azimuthal transport cannot hold when the sprout structure is so sparse that the characteristic distance between the branches is larger than the diffusion length. At this point the inhibitor concentration at the tip of the branches cannot be lowered further by increased distance between the branches, hence for high enough inhibitor 410 secretion branching structures will not be able to grow.
4.5. Generalizations of the model
The above results establish that a diffusing inhibitor (sVEGFR1) secreted by the cells can generate gradients of an activator (VEGF). The interplay between the diffusive fields and the moving source of the inhibitor can generate tip-splitting instabilities, reminescent of the multicellular sprouting behavior of endothelial cells in culture. Our simplified model, however, does not take into account several known aspects of endothelial biology. There is good evidence that the endothelial cells are not uniform: one can distinguish a population of leader cells with specific molecular and functional features [78, 79, 80] including the difference in sVEGFR1 secretion [28]. Endothelial cells are also known to internalize and eliminate VEGF [81, 82, 83], thereby altering the reaction-diffusion system considered in this work. To explore how these effects may change the basic patterning 420 mechanism, we augmented our model with two sets of rules.
4.5.1. Spatial variation in sVEGFR1 secretion
Without explicitly representing the tip cell selection process in our models, we introduced spatial inhomogeneity by restricting inhibitor secretion in areas recently occupied by the cells in the lattice model. Thus, we modify Eq. (13) to describe inhibitor secretion at time t as
| (51) |
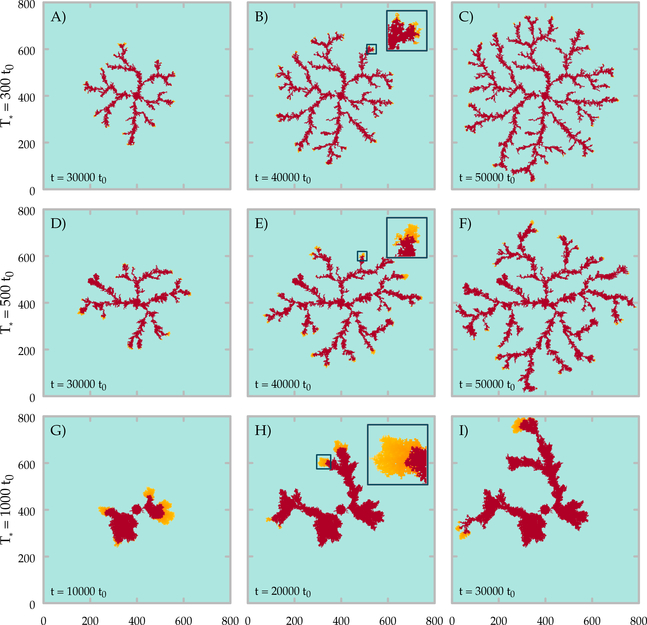
where t0 denotes the time lattice site was occupied, and the T* ≥ 0 threshold is an adjustable parameter. For T* = 0 we recover our original model. Increasing T* excludes secretion from increasingly larger areas beyond the leading edge of the sprouts, thus represents an increasing fraction of tip cell phenotypes at the branch tips. Simulations with a small excluded area (T* = 300 t0) does not alter the dynamics substantially (Fig. 9A-C).
Fig. 9:
Time development of the lattice model with heterogeneous sVEGFR1 secretion. The inhibitor is not produced at the branch tips: cells that were occupied less than T* time ago. Cell-occupied areas are shown for different values of T* ( A-C: T* = 300 t0, D-F: T* = 500 t0, G-I: T* = 1000 t0) at three snapshots of the simulations. Insets show branch tips at higher magnification (1 : 4.2). Orange colors indicate areas where the inhibitor is not produced, i.e., the presumed location of tip cells.
Simulations with T* = 500 t0 yield branches and excluded areas ≈ 10−20 μm wide, corresponding to multicellular sprouts 1–2 cells wide headed by a single tip cell. In this scenario the branches are wider, but are more sparse, and the overall density of the cell-covered area is decreased (Supplement Fig. B.9). Further increase in T* yields ≈ 100 μm wide branches, each led by an area corresponding to 10–100 leader cells. In this limit the expansion becomes oscillatory: the lack of inhibitor production results in a quick expansion of a compact cluster. As the inhibitor production turns on, the extended spatial production of the inhibitor yields a VEGFR1 concentration high enough that it can choke the further expansion of the cells. In a wide range of parameters, however, the tip splitting mechanism is robust even if the tip cells do not produce diffusing inhibitors. Accordingly, branching patterns do develop in experiments where the population density of tip cells were altered [84].
4.5.2. VEGF internalization by the cells
Internalization of VEGF by endothelial cells [81, 82, 83] is expected to alter the spatial distribution of sVEGFR1 by freeing up molecules that could have bound in the absence of internalization. To gauge the effect of VEGF internalization on the patterning mechanism, we keep track of VT, the local total amount of VEGF
| (52) |
and expand Eqs (5) as
| (53) |
| (54) |
where γV denotes the internalization rate of VEGF, thus its internalization is assumed to follow first order kinetics, where cells are present (σ = 1). We performed simulations with the lattice model, using the quasi steady state approximation.
As expected, for large enough values of γV, the free VEGF concentration V drops close to zero around the cell-covered area (Fig. 10). This change translates into slightly lower overall cell densities, comparable with the effect of an increased inhibitor release rate Γ* (Supplemental Fig. B.6) – but does not effect the basic patterning mechanism.
Fig. 10:
Patterning in the presence of VEGF internalization. The area occupied by the cells (A) and the concentration fields of the free growth factor (VEGF, B) and of the inhibitor (sVEGFR1, C) are shown for a lattice model simulation (γV = 10−3). Cumulative radial density profiles (ρ(r,t), D) and maximal density values (E) are shown for four values of γV, the degradation rate of VEGF. F) Sprout expansion in simulations calculated by the same method used to evaluate experimental results. Each line indicates mean values obtained from n=4 distinct simulations and shaded areas represent the standard error of the mean.
5. Discussion
5.1. Vascular patterns are formed by multiple guidance systems
Vascular patterning in amniotes is an adaptive, self-organized process [5]. At the tissue scale a hypoxia sensing feedback mechanism controls vascular density [85], and hemodynamic forces of blood flow – that depend on the state of the entire vasculature – can guide the remodeling of vascular network topology [86, 87]. An important element of vascular patterning is the formation of new blood vessels through a process of multicellular sprouting, which is – in itself – a complex process likely involving multiple guidance mechanisms [5].
Besides the sVEGFR1 system considered here, endothelial cells could also be guided by ECM structures, which can serve as a spatial “memory” [88, 89, 90]: both endocardial [91] and endothelial [92] cells were reported to leave degraded ECM fragments or “channels” behind. Multicellular sprouts readily develop when a positive feedback between the direction of active cell movement (cell polarity) and ECM “memory” is assumed [93, 94, 95] – a mechanism very similar to ants use to organize pheromone trails [96]. ECM structures may also be generated by mechanical forces [97, 98, 99, 100], a mechanism likely determining patterning on highly malleable matrigel substrates [101].
A special type of cell-cell interaction, a temporary lateral inhibition mediated through delta and notch cell surface receptors is also operational within angiogenic sprouts [80] and thought to be responsible for restricting the invasive (tip) phenotype to a few cells of the sprout [79]. While lateral inhibition of tip cells through the delta-notch system strongly influences vascular morphology, however, branching continued to occur in experiments where delta-notch signaling was blocked [84, 102]. Endothelial cells can frequently switch phenotype: leading tip cells are frequently overtaken by follower cells which then assume a tip cell phenotype [103, 80, 102]. The interplay between the Delta-Notch and sVEGFR1 guidance systems remains an interesting problem for future studies.
Endothelial cell movements guided by autocrine chemotactic signaling were proposed as a potential mechanism for vascular pattern emergence [29, 30, 104]. The mechanism relies on the secretion of a diffusing chemotactic morphogen, likely to be VEGF. An autocrine chemoattractant is expected to result in cell aggregation [105], but an interplay between elastic compression and active motility can yield branching patterns [106, 31]. While such autocrine VEGF signaling may also contribute to the patterning of vascular sprouts [30], it is unlikely to be a required mechanism for sprouting activity: endothelial sprouts readily elongate even in the presence of large concentrations of exogenous VEGF in the culture medium [107, 108]. A mathematically similar patterning process can also result from a number of other considered mechanism: If a secreted proteolytic agent increases the availability or “activates” ECM-bound VEGF, then a local gradient of the bio-active VEGF may be produced in the microenvironment of an endothelial cell cluster. Similarly, the binding of paracrine growth factors to angioblast-produced ECM can drive patterning by creating spatially-restricted guidance cues required for directed cell migration [109]. The common feature of these mechanisms is that it operates –contra-intuitively– with attractive gradients pointing towards the endothelial cells.
Following experimental evidence for the possible role of secreted inhibitors in vascular patterning, here we investigate a markedly distinct mechanism, where endothelial cells are guided by self-generated VEGF gradients, pointing away from the vascular structure. Branching patterning under similar, diffusion-limited conditions is well studied. In particular, the Mullins-Sekerka instability [110], which renders a smooth interface unstable by triggering a spontaneous tip-splitting process, was shown to yield a characteristic dense branching morphology. As a tip extending into the diffusive external field senses increasingly steep gradients, it further enhances its growth creating the amplification mechanism underlying the instability.
Here we explore a diffusive patterning mechanism in which the gradients are produced by a reaction between an immobile activator (the VEGF) and a diffusive inhibitor (the sVEGFR1). As Eq. (9) can be reduced to a diffusion equation in the Rf ⪢ 1 limit, in this case 1 − Rf will be identical to the field variable of the Mullins-Sekerka diffusion limited growth model. However, the biologically relevant regime is different, as cells are not expected to secrete inhibitors in a great excess compared with the activator (VEGF). The three growth regimes (compact, tip splitting and arrested) are not present in the standard diffusion limited growth models, although were reported in bacterial patterning where additional equations complicate the simple Mullins-Sekerka analysis [1]. We found that the reaction-diffusion system can generate steeper gradients in the stationary expansion state than those develop in a Mullins-Sekerka system. Thus, the presented model is an interesting, biologically motivated generalization of the diffusive patterning problem.
5.2. The VEGF system
VEGF-A and its receptors VEGFR1 (Flt1) and VEGFR2 (Flk1) play a key role in the regulation of vasculogenesis and angiogenesis. VEGF-A isoforms are secreted by a variety of cell types except the majority of the endothelial cells [33, 34, 9], whereas VEGFR1 and VEGFR2 receptors are expressed primarily by those [9, 111]. VEGF-A has multiple isoforms generated by alternative mRNA splicing, having different binding affinities for heparan sulphate proteoglycans (HSPGs) and Neuropilins as well as for VEGF receptors. Except for one, all isoforms contain a HSPG binding domain, and therefore can be sequestered in the extracellular matrix (ECM). Mouse embryos lacking all HSPG-binding VEGF-A isoforms indicated that ECM-binding isoforms are essential for the establishment of steep extracellular VEGF-A gradients [112, 78].
ECM-bound VEGF can be released after a protease cleavage as a diffusible, active protein [113, 114, 48, 112, 3, 115]. Recent analysis of available kinetic data, however, do not support the view that a localized VEGF release is required for an effective signalization process – instead it appears to be a multicellular cooperative phenomenon [81]. As the binding sites of VEGF for ECM and sVEGFR1 are distinct, VEGF and sVEGFR1 could interact in the ECM-bound form [116, 117]. Moreover, ECM-bound VEGF (without cleavage) can effectively activate endothelial cells [118, 119]. Given these complexities, in the model we focus on the ECM-bound VEGF population and do not represent the freely diffusing VEGF proteins. Our study suggest, however, that effective VEGF concentrations in tissues are much lower than the 100 pM required in vitro to elicit detectable proliferative or migratory response. This could also reflect the finding, that endothelial cells are more sensitive to VEGF in the presence of appropriate ECM in the tissue environment [17, 60]. Hence, without ECM binding the sVEGFR1-VEGF control system operates in a regime (high V*) which is not sensitive enough to guide patterning.
A variety of VEGF-induced changes (proliferation, migratory activity and chemotaxis) are likely to contribute to the expansion of the vasculature. Vascular sprouts contain highly motile cells, and a directional bias towards the tip provides vascular building blocks in excess of local proliferation both in mouse allantois explants [103] and during the formation of the first vascular plexus in avians [120]. Endothelial cell streaming along the dorsal aorta also provides cells from the extraembryonic blood islands to the expanding vasculature around the heart [121]. Similar directed endothelial motion is also present in the sprouts forming within a 3D gel environment [102]. Long-range migration of endothelial cells along vascular segments can thus locally expand the vasculature. We condensed this complex process into a phenomenological formalism, directed growth.
In our experiments, we applied an antibody which targets both membrane-bound and diffusive forms of VEGFR1. Hence, while our experiments can test model predictions (Figs 2 vs 3), they leave the possibility open that the membrane-bound form of VEGFR1 could also guide endothelial sprouting behavior through some completely different mechanism. For example, tip cell selection involves the VEGF pathway and the excess of tip cells also yields to denser vascular sprouts [84]. The close correspondence of experimental and model simulation 535 results, however, support the plausibility of a vascular patterning mechanism guided by a diffusing inhibitor.
5.3. Model choices
The regulation of endothelial cell behavior is in the forefront of research interest due to its relevance in normal development and in various diseases. Recent quantitative models focused on the dynamics of extracellular factors [82], including sVEGFR1 [122]. In this study we focus on how well established molecular interactions can shape the developing vascular morphology. The morphology of the vasculature is of key importance, it determines the density of vascular segments in a given area, thus it determines how blood vessels can supply tissues with oxygen and other necessary factors, or how much tumor cells need to migrate to enter circulation. The aim of this work is to establish how the sVEGFR1/VEGF diffusing inhibitor/activator system can guide vascular patterning. Hence, we intentionally left out several other known details of endothelial cell biology, like the delta-notch mechanism underlying the cellular decision to engage in invasive behavior, or the complexity of growth factor processing within cells or in the environment. Instead, we constructed a model which contains the relevant molecular interactions between the morphogens, but is still simple enough to allow mathematical analysis. After establishing the patterning mechanism with the simplest modeling assumptions, we augmented the models to learn how spatial variation in inhibitor production or activator internalization modulate the self-organized patterns.
We used 2D lattice and a phase-field models to represent the interactions of cells and the diffusive inhibitor sVEGFR1. We argue that any mathematical model of a complex system contains several hidden assumptions. Therefore, employing multiple and complementary modeling approaches is crucial to increase our confidence in explicitly stated model components. Moreover, both models offer advantages: the lattice model is simple and transparent, while the phase-field method opens up the possibility of analytical calculations. The lattice model can be considered as a variant of the Eden model [123], often used to represent biological growth patterns.
The phase-field method has been successfully applied to various problems, such as dendritic crystal growth [66, 67, 124], morphological changes in biological membranes [125, 126], cell motion [127, 128] and describing the dynamics of multicellular systems [71, 129]. Recently the phase-field approach has been also adapted to model tumor angiogenesis [130, 131, 132]. In these models the tumor cells and the adjacent stroma tissue produces VEGF, thereby forming a concentration gradient guiding the growth of pre-existing capillaries. However, during vasculogenesis a steep VEGF concentration gradient is unlikely to develop spontaneously since VEGF is expressed throughout the embryo and a large amount is stored in the ECM. The model proposed here thus expands these previous studies to explain vasculogenesis, the early embryonic vascular patterning process.
Matching model variables to experimentally observable quantities is of key importance in every investigation relying on mathematical models. Here we compare quantities at two scales: both at the level of signaling molecules (like binding and diffusion properties) and at the scale of multicellular structures (like sprout density, branch width and growth speed). Fortunately there are empirical constraints for most of these parameters – albeit their values may vary within an order of magnitude. Our parameters (Table 1) includes two unusual choices: the value for VEGFR1 diffusivity (DR), and the value for VEGF threshold (V*). The choice of the low value of V* reflects our judgment based on the available literature, and it is not required for dense sprouting morphology: simulations performed with V* = 100 pM can also yield branching patterns (data not shown). Two or three orders of magnitude larger diffusivity values, however, were estimated for diffusion of proteins in aqueous solutions or in porous gels [82, 133]. In our model, as well as in other reports [82], simulations performed with such a high diffusivity creates shallow gradients in the order of 1 pM/mm, two orders of magnitude below the experimentally observed VEGF sensitivity threshold [74]. Moreover, D in the range of 10−5 − 10−4 mm2/s yields unrealistically wide branches or compact growth. Such estimates for protein diffusivity, however, do not take into account the binding of sVEGFR1 to the ECM environment. In the presence of reversible adsorption and desorption, theoretical estimates for the effective diffusion parameter scale with the ratio of free and bound molecules [134]. Thus, if the adsorption of the diffusing agent is efficient enough to keep 99% of the molecules immobilized, the effective diffusivity will drop by two orders of magnitude. Based on the presented data, we suggest that such a limited diffusivity of sVEGFR1 is crucial to guide blood vessel patterning.
5.4. Conclusion
The presented results demonstrate that endothelial cells are capable to effectively regulate vascular morphology at the multicellular scale – utilizing a secreted inhibitor and a reaction-diffusion mechanism. The mechanism yields a spontaneous dense branching morphology with a constant vessel density, an ideal distribution architecture for capillaries. In a tissue environment this control mechanism is likely to guide endothelial cells in combination with other factors, like ECM biochemical and mechanical patterning, hypoxia sensing, and various intercellular signaling interactions.
Supplementary Material
Highlights.
Pattern formation guided by an autocrine inhibitor through a reaction-diffusion process
Connected molecular parameters to statistical characteristics of the vasculature
Specific model predictions tested by experiments
Acknowledgments
Funding
This work was supported by the US National Institute of Health [grant number GM102801] and the Hungarian National Research, Development and Innovation Office [grant number OTKA 118119 ANN].
Appendix A. Quasi steady state approximation
The model equations obtained in Reaction-diffusion subsection are:
| (A.1) |
| (A.2) |
that can be reduced by applying quasi steady state approximation (QSSA). We exploit that receptor-ligand binding and complex dissociation evolve in a much faster time scale than changes in the total amounts of receptor and ligand. Hence complex formation equilibrates rapidly and can be assumed as a steady-state process:
| (A.3) |
and the association and dissociation rates, kon and koff respectively, can be replaced by the equilibrium constant:
| (A.4) |
Thus, the concentration of bound sVEGFR1 can be expressed as a function of the concentration of free sVEGFR1 as
| (A.5) |
and the time derivative can be written as
| (A.6) |
By introducing the total receptor concentration (R)
| (A.7) |
and substituting it into Eq. (A.5) we obtain a quadratic equation for Rb as a function of R with two positive real roots:
| (A.8) |
Since VEGF can be either active or inactivated by sVEGFR1 and its concentration is spatially uniform, the active VEGF can be written as
| (A.9) |
and substitution of Eq. (A.8) into Eq. (A.9) yields only one positive solution for V :
| (A.10) |
The subtraction of Eq. (A.1) from Eq. (A.2) yields the time derivative of the total receptor concentration:
| (A.11) |
replacing Eqs. (A.5–A.6) into this equation gives the QSSA dynamics of the freely diffusible receptor:
| (A.12) |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Vicsek T, Fluctuations and scaling in biology, Oxford University Press; New York, 2001. [Google Scholar]
- [2].Miura T, Shiota K, Depletion of FGF acts as a lateral inhibitory factor in lung branching morphogenesis in vitro, Mechanisms of Development 116 (1–2) (2002) 29–38. arXiv:12128203. [DOI] [PubMed] [Google Scholar]
- [3].Ferrara N, Gerber H-P, LeCouter J, The biology of vegf and its receptors., Nat Med 9 (6) (2003) 669–676. doi:10.1038/nm0603-669. URL http://dx.doi.org/10.1038/nm0603-669 [DOI] [PubMed] [Google Scholar]
- [4].Phng L-K, Gerhardt H, Angiogenesis: A team effort coordinated by notch, Developmental Cell 16 (2) (2009) 196–208. doi:10.1016/j.devcel.2009.01.015. URL http://dx.doi.org/10.1016/j.devcel.2009.01.015 [DOI] [PubMed] [Google Scholar]
- [5].Czirok A, Endothelial cell motility, coordination and pattern formation during vasculogenesis, Wiley Interdisciplinary Reviews: Systems Biology and Medicine 5 (5) (2013) 587–602. doi:10.1002/wsbm.1233. URL http://dx.doi.org/10.1002/wsbm.1233 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Breier G, Albrecht U, Sterrer S, Risau W, Expression of vascular endothelial growth factor during embryonic angiogenesis and endothelial cell differentiation., Development 114 (2) (1992) 521–532. [DOI] [PubMed] [Google Scholar]
- [7].Breier G, Clauss M, Risau W, Coordinate expression of vascular endothelial growth factor receptor-1 (flt-1) and its ligand suggests a paracrine regulation of murine vascular development., Dev Dyn 204 (3) (1995) 228–239. doi:10.1002/aja.1002040303. URL http://dx.doi.org/10.1002/aja.1002040303 [DOI] [PubMed] [Google Scholar]
- [8].Millauer B, Wizigmann-Voos S, Schnürch H, Martinez R, Møller NP, Risau W, Ullrich A, High affinity vegf binding and developmental expression suggest flk-1 as a major regulator of vasculogenesis and angiogenesis., Cell 72 (6) (1993) 835–846. [DOI] [PubMed] [Google Scholar]
- [9].Flamme I, Breier G, Risau W, Vascular endothelial growth factor (vegf) and vegf receptor 2 (flk-1) are expressed during vasculogenesis and vascular differentiation in the quail embryo., Dev Biol 169 (2) (1995) 699–712. doi:10.1006/dbio.1995.1180. URL http://dx.doi.org/10.1006/dbio.1995.1180 [DOI] [PubMed] [Google Scholar]
- [10].Flamme I, von Reutern M, Drexler HC, Syed-Ali S, Risau W, Overexpression of vascular endothelial growth factor in the avian embryo induces hypervascularization and increased vascular permeability without alterations of embryonic pattern formation., Dev Biol 171 (2) (1995) 399–414. doi:10.1006/dbio.1995.1291. URL http://dx.doi.org/10.1006/dbio.1995.1291 [DOI] [PubMed] [Google Scholar]
- [11].Yoshida A, Anand-Apte B, Zetter BR, Differential endothelial migration and proliferation to basic fibroblast growth factor and vascular endothelial growth factor., Growth Factors 13 (1–2) (1996) 57–64. [DOI] [PubMed] [Google Scholar]
- [12].Yancopoulos GD, Davis S, Gale NW, Rudge JS, Wiegand SJ, Holash J, Vascular-specific growth factors and blood vessel formation., Nature 407 (6801) (2000) 242–248. doi:10.1038/35025215. URL http://dx.doi.org/10.1038/35025215 [DOI] [PubMed] [Google Scholar]
- [13].Waltenberger J, Claesson-Welsh L, Siegbahn A, Shibuya M, Heldin CH, Different signal transduction properties of kdr and flt1, two receptors for vascular endothelial growth factor., J Biol Chem 269 (43) (1994) 26988–26995. [PubMed] [Google Scholar]
- [14].Olsson A-K, Dimberg A, Kreuger J, Claesson-Welsh L, Vegf receptor signalling — in control of vascular function, Nature Reviews Molecular Cell Biology 7 (5) (2006) 359–371. doi:10.1038/nrm1911. URL http://dx.doi.org/10.1038/nrm1911 [DOI] [PubMed] [Google Scholar]
- [15].Cao Y, Linden P, Shima D, Browne F, Folkman J, In vivo angiogenic activity and hypoxia induction of heterodimers of placenta growth factor/vascular endothelial growth factor., J Clin Invest 98 (11) (1996) 2507–2511. doi:10.1172/JCI119069. URL http://dx.doi.org/10.1172/JCI119069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Alt W, Biased random walk models for chemotaxis and related diffusion approximations., J Math Biol 9 (2) (1980) 147–177. [DOI] [PubMed] [Google Scholar]
- [17].Wijelath ES, Murray J, Rahman S, Patel Y, Ishida A, Strand K, Aziz S, Cardona C, Hammond WP, Savidge GF, Rafii S, Sobel M, Novel vascular endothelial growth factor binding domains of fibronectin enhance vascular endothelial growth factor biological activity., Circ Res 91 (1) (2002) 25–31. [DOI] [PubMed] [Google Scholar]
- [18].Stenzel D, Lundkvist A, Sauvaget D, Busse M, Graupera M, van der Flier A, Wijelath ES, Murray J, Sobel M, Costell M, Takahashi S, Fässler R, Yamaguchi Y, Gutmann DH, Hynes RO, Gerhardt H, Integrin-dependent and -independent functions of astrocytic fibronectin in retinal angiogenesis., Development 138 (20) (2011) 4451–4463. doi:10.1242/dev.071381. URL http://dx.doi.org/10.1242/dev.071381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Weinstein BM, What guides early embryonic blood vessel formation?, Developmental Dynamics 215 (1) (1999) 2–11. doi:10.1002/(sici)1097-0177(199905)215:1¡2::aid-dvdy2¿3.0.co;2-u. URL http://dx.doi.org/10.1002/(SICI)1097-0177(199905)215:1<2::AID-DVDY2>3.0.CO;2-U [DOI] [PubMed] [Google Scholar]
- [20].Czirok A, Rongish BJ, Little CD, Vascular network formation in expanding versus static tissues: Embryos and tumors, Genes & Cancer 2 (12) (2011) 1072–1080. doi:10.1177/1947601911426774. URL http://dx.doi.org/10.1177/1947601911426774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Montesano R, Orci L, Tumor-promoting phorbol esters induce angiogenesis in vitro, Cell 42 (2) (1985) 469–477. doi:10.1016/0092-8674(85)90104-7. URL http://dx.doi.org/10.1016/0092-8674(85)90104-7 [DOI] [PubMed] [Google Scholar]
- [22].Davis GE, Black SM, Bayless KJ, Capillary morphogenesis during human endothelial cell invasion of three-dimensional collagen matrices, In Vitro Cellular & Developmental Biology - Animal 36 (8) (2000) 513. doi:10.1290/1071-2690(2000)036¡0513:cmdhec¿2.0.co;2. URL http://dx.doi.org/10.1290/1071-2690(2000)036<0513:CMDHEC>2.0.CO;2 [DOI] [PubMed] [Google Scholar]
- [23].Sakaguchi K, Shimizu T, Horaguchi S, Sekine H, Yamato M, Umezu M, Okano T, In vitro engineering of vascularized tissue surrogates, Scientific Reports 3. doi:10.1038/srep01316. URL http://dx.doi.org/10.1038/srep01316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Kendall RL, Thomas KA, Inhibition of vascular endothelial cell growth factor activity by an endogenously encoded soluble receptor., Proceedings of the National Academy of Sciences 90 (22) (1993) 10705–10709. doi:10.1073/pnas.90.22.10705. URL http://dx.doi.org/10.1073/pnas.90.22.10705 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Hiratsuka S, Minowa O, Kuno J, Noda T, Shibuya M, Flt-1 lacking the tyrosine kinase domain is sufficient for normal development and angiogenesis in mice, Proceedings of the National Academy of Sciences 95 (16) (1998) 9349–9354. doi:10.1073/pnas.95.16.9349. URL http://dx.doi.org/10.1073/pnas.95.16.9349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Kappas NC, Zeng G, Chappell JC, Kearney JB, Hazarika S, Kallianos KG, Patterson C, Annex BH, Bautch VL, The vegf receptor flt-1 spatially modulates flk-1 signaling and blood vessel branching., J Cell Biol 181 (5) (2008) 847–858. doi:10.1083/jcb.200709114. URL http://dx.doi.org/10.1083/jcb.200709114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Bautch VL, Vegf-directed blood vessel patterning: From cells to organism, Cold Spring Harbor Perspectives in Medicine 2 (9) (2011) a006452–a006452. doi:10.1101/cshperspect.a006452. URL http://dx.doi.org/10.1101/cshperspect.a006452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Chappell JC, Taylor SM, Ferrara N, Bautch VL, Local guidance of emerging vessel sprouts requires soluble flt-1., Dev Cell 17 (3) (2009) 377–386. doi:10.1016/j.devcel.2009.07.011. URL http://dx.doi.org/10.1016/j.devcel.2009.07.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Gamba A, Ambrosi D, Coniglio A, de Candia A, Di Talia S, Giraudo E, Serini G, Preziosi L, Bussolino F, Percolation, morphogenesis, and burgers dynamics in blood vessels formation., Phys Rev Lett 90 (11) (2003) 118101. [DOI] [PubMed] [Google Scholar]
- [30].Serini G, Ambrosi D, Giraudo E, Gamba A, Preziosi L, Bussolino F, Modeling the early stages of vascular network assembly., EMBO J 22 (8) (2003) 1771–1779. doi:10.1093/emboj/cdg176. URL http://dx.doi.org/10.1093/emboj/cdg176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Merks RMH, Perryn ED, Shirinifard A, Glazier JA, Contact-inhibited chemotaxis in de novo and sprouting blood-vessel growth, PLoS Computational Biology 4 (9) (2008) e1000163. doi:10.1371/journal.pcbi.1000163. URL http://dx.doi.org/10.1371/journal.pcbi.1000163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Hornig C, Barleon B, Ahmad S, Vuorela P, Ahmed A, Weich HA, Release and complex formation of soluble vegfr-1 from endothelial cells and biological fluids., Lab Invest 80 (4) (2000) 443–454. [DOI] [PubMed] [Google Scholar]
- [33].Poole TJ, Finkelstein EB, Cox CM, The role of fgf and vegf in angioblast induction and migration during vascular development., Dev Dyn 220 (1) (2001) 1–17. doi:3.0.CO;2-2. URL http://dx.doi.org/3.0.CO;2-2 [DOI] [PubMed] [Google Scholar]
- [34].Zhang QX, Magovern CJ, Mack CA, Budenbender KT, Ko W, Rosengart TK, Vascular endothelial growth factor is the major angiogenic factor in omentum: mechanism of the omentum-mediated angiogenesis., J Surg Res 67 (2) (1997) 147–154. doi:10.1006/jsre.1996.4983. URL http://dx.doi.org/10.1006/jsre.1996.4983 [DOI] [PubMed] [Google Scholar]
- [35].Osborne JM, Fletcher AG, Pitt-Francis JM, Maini PK, Gavaghan DJ, Comparing individual-based approaches to modelling the self-organization of multicellular tissues, PLOS Computational Biology 13 (2) (2017.02.13) e1005387. doi:10.1371/journal.pcbi.1005387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Chidlow JH, Glawe JD, Alexander JS, Kevil CG, Vegf164 differentially regulates neutrophil and t cell adhesion through itgal- and itgam-dependent mechanisms, AJP: Gastrointestinal and Liver Physiology 299 (6) (2010) G1361–G1367. doi:10.1152/ajpgi.00202.2010. URL http://dx.doi.org/10.1152/ajpgi.00202.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Helm C-LE, Fleury ME, Zisch AH, Boschetti F, Swartz MA, Synergy between interstitial flow and vegf directs capillary morphogenesis in vitro through a gradient amplification mechanism, Proceedings of the National Academy of Sciences 102 (44) (2005) 15779–15784. doi:10.1073/pnas.0503681102. URL http://dx.doi.org/10.1073/pnas.0503681102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Helm C-LE, Zisch A, Swartz MA, Engineered blood and lymphatic capillaries in 3-D vegffibrin-collagen matrices with interstitial flow, Biotechnology and Bioengineering 96 (1) (2006) 167–176. doi:10.1002/bit.21185. URL http://dx.doi.org/10.1002/bit.21185 [DOI] [PubMed] [Google Scholar]
- [39].van der Walt S, Colbert SC, Varoquaux G, The NumPy array: A structure for efficient numerical computation, Computing in Science & Engineering 13 (2) (2011) 22–30. doi:10.1109/mcse.2011.37. URL https://doi.org/10.1109/mcse.2011.37 [Google Scholar]
- [40].Jones E, Oliphant T, Peterson P, et al. , SciPy: Open source scientific tools for Python, [Online] (2001. –). URL http://www.scipy.org/
- [41].Millman KJ, Aivazis M, Python for scientists and engineers, Computing in Science & Engineering 13 (2) (2011) 9–12. doi:10.1109/mcse.2011.36. URL https://doi.org/10.1109/mcse.2011.36 [Google Scholar]
- [42].Oliphant TE, Python for scientific computing, Computing in Science & Engineering 9 (3) (2007) 10–20. doi:10.1109/mcse.2007.58. URL https://doi.org/10.1109/mcse.2007.58 [Google Scholar]
- [43].van der Walt S, Schonberger JL, Nunez-Iglesias J, Boulogne F, Warner JD, Yager N, Gouillart E, Yu T, scikit-image: image processing in python, PeerJ 2 (2014) e453. doi:10.7717/peerj.453. URL https://doi.org/10.7717/peerj.453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Bradski G, The OpenCV Library, Dr. Dobb’s Journal of Software Tools. [Google Scholar]
- [45].Zivkovic Z, Improved adaptive Gaussian mixture model for background subtraction, Proceedings of the 17th International Conference on Pattern Recognition, 2004. ICPR 2004.doi:10.1109/icpr.2004.1333992. URL http://dx.doi.org/10.1109/ICPR.2004.1333992 [Google Scholar]
- [46].Zivkovic Z, van der Heijden F, Efficient adaptive density estimation per image pixel for the task of background subtraction, Pattern Recognition Letters 27 (7) (2006) 773–780. doi:10.1016/j.patrec.2005.11.005. URL http://dx.doi.org/10.1016/j.patrec.2005.11.005 [Google Scholar]
- [47].Houck KA, Leung DW, Rowland AM, Winer J, Ferrara N, Dual regulation of vascular endothelial growth factor bioavailability by genetic and proteolytic mechanisms., J Biol Chem 267 (36) (1992) 26031–26037. [PubMed] [Google Scholar]
- [48].Robinson CJ, Stringer SE, The splice variants of vascular endothelial growth factor (vegf) and their receptors., J Cell Sci 114 (Pt 5) (2001) 853–865. [DOI] [PubMed] [Google Scholar]
- [49].Tanaka K, Yamaguchi S, Sawano A, Shibuya M, Characterization of the extracellular domain in vascular endothelial growth factor receptor-1 (flt-1 Tyrosine kinase), Japanese Journal of Cancer Research 88 (9) (1997) 867–876. doi:10.1111/j.1349-7006.1997.tb00463.x. URL http://dx.doi.org/10.1111/j.1349-7006.1997.tb00463.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Inoue T, Kibata K, Suzuki M, Nakamura S, Motoda R, Orita K, Identification of a vascular endothelial growth factor (vegf) antagonist, sflt-1, from a human hematopoietic cell line nalm-16, FEBS Letters 469 (1) (2000) 14–18. doi:10.1016/s0014-5793(00)01246-1. URL http://dx.doi.org/10.1016/S0014-5793(00)01246-1 [DOI] [PubMed] [Google Scholar]
- [51].Takahashi H, Shibuya M, The vascular endothelial growth factor (vegf)/vegf receptor system and its role under physiological and pathological conditions, Clinical Science 109 (3) (2005) 227–241. doi:10.1042/cs20040370. URL http://dx.doi.org/10.1042/CS20040370 [DOI] [PubMed] [Google Scholar]
- [52].Ahmad S, Hewett PW, Al-Ani B, Sissaoui S, Fujisawa T, Cudmore MJ, Ahmed A, Autocrine activity of soluble flt-1 controls endothelial cell function and angiogenesis, Vascular Cell 3 (1) (2011) 15. doi:10.1186/2045-824x-3-15. URL http://dx.doi.org/10.1186/2045-824X-3-15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Eden E, Geva-Zatorsky N, Issaeva I, Cohen A, Dekel E, Danon T, Cohen L, Mayo A, Alon U, Proteome half-life dynamics in living human cells, Science 331 (6018) (2011) 764–768. doi:10.1126/science.1199784. URL http://dx.doi.org/10.1126/science.1199784 [DOI] [PubMed] [Google Scholar]
- [54].Park M, Lee S-T, The fourth immunoglobulin-like loop in the extracellular domain of flt-1, a vegf receptor, includes a major heparin-binding site, Biochemical and Biophysical Research Communications 264 (3) (1999) 730–734. doi:10.1006/bbrc.1999.1580. URL http://dx.doi.org/10.1006/bbrc.1999.1580 [DOI] [PubMed] [Google Scholar]
- [55].Orecchia A, Vascular endothelial growth factor receptor-1 is deposited in the extracellular matrix by endothelial cells and is a ligand for the 5 1 integrin, Journal of Cell Science 116 (17) (2003) 3479–3489. doi:10.1242/jcs.00673. URL http://dx.doi.org/10.1242/jcs.00673 [DOI] [PubMed] [Google Scholar]
- [56].Searle J, Mockel M, Gwosc S, Datwyler SA, Qadri F, Albert GI, Holert F, Isbruch A, Klug L, Muller DN, et al. , Heparin strongly induces soluble fms-like tyrosine kinase 1 release in vivo and in vitro–brief report, Arteriosclerosis, Thrombosis, and Vascular Biology 31 (12) (2011) 2972–2974. doi:10.1161/atvbaha.111.237784. URL http://dx.doi.org/10.1161/ATVBAHA.111.237784 [DOI] [PubMed] [Google Scholar]
- [57].Sela S, Natanson-Yaron S, Zcharia E, Vlodavsky I, Yagel S, Keshet E, Local retention versus systemic release of soluble vegf receptor-1 Are mediated by heparin-binding and regulated by heparanase, Circulation Research 108 (9) (2011) 1063–1070. doi:10.1161/circresaha.110.239665. URL http://dx.doi.org/10.1161/CIRCRESAHA.110.239665 [DOI] [PubMed] [Google Scholar]
- [58].Dowd CJ, Cooney CL, Nugent MA, Heparan sulfate mediates bfgf transport through basement membrane by diffusion with rapid reversible binding, Journal of Biological Chemistry 274 (8) (1999) 5236–5244. doi:10.1074/jbc.274.8.5236. URL http://dx.doi.org/10.1074/jbc.274.8.5236 [DOI] [PubMed] [Google Scholar]
- [59].Shvartsman SY, Wiley HS, Deen WM, Lauffenburger DA, Spatial range of autocrine signaling: Modeling and computational analysis, Biophysical Journal 81 (4) (2001) 1854–1867. doi:10.1016/s0006-3495(01)75837-7. URL http://dx.doi.org/10.1016/S0006-3495(01)75837-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Wijelath ES, Rahman S, Namekata M, Murray J, Nishimura T, Mostafavi-Pour Z, Patel Y, Suda Y, Humphries MJ, Sobel M, Heparin-ii domain of fibronectin is a vascular endothelial growth factor-binding domain: Enhancement of vegf biological activity by a singular growth factor/matrix protein synergism, Circulation Research 99 (8) (2006) 853–860. doi:10.1161/01.res.0000246849.17887.66. URL http://dx.doi.org/10.1161/01.RES.0000246849.17887.66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Gabhann FM, Popel AS, Systems biology of vascular endothelial growth factors, Microcirculation 15 (8) (2008) 715–738. doi:10.1080/10739680802095964. URL http://dx.doi.org/10.1080/10739680802095964 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Stokes C, Lauffenburger D, Williams S, Migration of individual microvessel endothelial cells: stochastic model and parameter measurement, Journal of Cell Science 99 (2) (1991) 419–430. arXiv:http://jcs.biologists.org/content/99/2/419.full.pdf. URL http://jcs.biologists.org/content/99/2/419 [DOI] [PubMed] [Google Scholar]
- [63].Kouvroukoglou S, Endothelial cell migration on surfaces modified with immobilized adhesive peptides, Biomaterials 21 (17) (2000) 1725–1733. doi:10.1016/s0142-9612(99)00205-7. URL http://dx.doi.org/10.1016/S0142-9612(99)00205-7 [DOI] [PubMed] [Google Scholar]
- [64].Szabo A, Unnep R, Mehes E, Twal WO, Argraves WS, Cao Y, Czirok A, Collective cell motion in endothelial monolayers, Physical Biology 7 (4) (2010) 046007. doi:10.1088/1478-3975/7/4/046007. URL http://dx.doi.org/10.1088/1478-3975/7/4/046007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Wheeler AA, Boettinger WJ, McFadden GB, Phase-field model for isothermal phase transitions in binary alloys, Phys. Rev. A 45 (10) (1992) 7424–7439. doi:10.1103/physreva.45.7424. URL http://dx.doi.org/10.1103/PhysRevA.45.7424 [DOI] [PubMed] [Google Scholar]
- [66].Wheeler A, Murray B, Schaefer R, Computation of dendrites using a phase field model, Physica D: Nonlinear Phenomena 66 (1–2) (1993) 243–262. doi:10.1016/0167-2789(93)90242-s. URL http://dx.doi.org/10.1016/0167-2789(93)90242-S [Google Scholar]
- [67].Kobayashi R, Modeling and numerical simulations of dendritic crystal growth, Physica D: Nonlinear Phenomena 63 (3–4) (1993) 410–423. doi:10.1016/0167-2789(93)90120-p. URL http://dx.doi.org/10.1016/0167-2789(93)90120-p [Google Scholar]
- [68].Wang S-L, Sekerka R, Wheeler A, Murray B, Coriell S, Braun R, McFadden G, Thermodynamically-consistent phase-field models for solidification, Physica D: Nonlinear Phenomena 69 (1–2) (1993) 189–200. doi:10.1016/0167-2789(93)90189-8. URL http://dx.doi.org/10.1016/0167-2789(93)90189-8 [Google Scholar]
- [69].Wheeler AA, McFadden GB, Boettinger WJ, Phase-field model for solidification of a eutectic alloy, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 452 (1946) (1996) 495–525. doi:10.1098/rspa.1996.0026. URL http://dx.doi.org/10.1098/rspa.1996.0026 [Google Scholar]
- [70].Boettinger WJ, Warren JA, Beckermann C, Karma A, Phase-field simulation of solidification, Annu. Rev. Mater. Res 32 (1) (2002) 163–194. doi:10.1146/annurev.matsci.32.101901.155803. URL http://dx.doi.org/10.1146/annurev.matsci.32.101901.155803 [Google Scholar]
- [71].Nonomura M, Study on multicellular systems using a phase field model, PLoS ONE 7 (4) (2012) e33501. doi:10.1371/journal.pone.0033501. URL http://dx.doi.org/10.1371/journal.pone.0033501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Gonzalez-Cinca R, Ramirez-Piscina L, Casademunt J, Hernandez-Machado A, Kramer L, Toth Katona T, Borzsonyi T, Buka A, Phase-field simulations and experiments of faceted growth in liquid crystals, Physica D: Nonlinear Phenomena 99 (2–3) (1996) 359–368. doi:10.1016/s0167-2789(96)00162-5. URL http://dx.doi.org/10.1016/s0167-2789(96)00162-5 [Google Scholar]
- [73].Kertesz J, Vicsek T, Diffusion-limited aggregation and regular patterns: fluctuations versus anisotropy, Journal of Physics A: Mathematical and General 19 (5) (1986) L257–L262. doi:10.1088/0305-4470/19/5/008. URL http://dx.doi.org/10.1088/0305-4470/19/5/008 [Google Scholar]
- [74].Shamloo A, Ma N, Poo M-M, Sohn LL, Heilshorn SC, Endothelial cell polarization and chemotaxis in a microfluidic device, Lab Chip 8 (8) (2008) 1292–1299. doi:10.1039/b719788h. URL http://dx.doi.org/10.1039/b719788h [DOI] [PubMed] [Google Scholar]
- [75].Wurdinger T, Tannous BA, Saydam O, Skog J, Grau S, Soutschek J, Weissleder R, Breakefield XO, Krichevsky AM, mir-296 regulates growth factor receptor overexpression in angiogenic endothelial cells, Cancer Cell 14 (5) (2008) 382–393. doi:10.1016/j.ccr.2008.10.005. URL http://dx.doi.org/10.1016/j.ccr.2008.10.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Akeson A, Herman A, Wiginton D, Greenberg J, Endothelial cell activation in a vegf-a gradient: Relevance to cell fate decisions, Microvascular Research 80 (1) (2010) 65–74. doi:10.1016/j.mvr.2010.02.001. URL http://dx.doi.org/10.1016/j.mvr.2010.02.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Barkefors I, Le Jan S, Jakobsson L, Hejll E, Carlson G, Johansson H, Jarvius J, Park JW, Li Jeon N, Kreuger J, Endothelial cell migration in stable gradients of vascular endothelial growth factor a and fibroblast growth factor 2: effects on chemotaxis and chemokinesis, Journal of Biological Chemistry 283 (20) (2008) 13905–13912. doi:10.1074/jbc.m704917200. URL http://dx.doi.org/10.1074/jbc.M704917200 [DOI] [PubMed] [Google Scholar]
- [78].Gerhardt H, Golding M, Fruttiger M, Ruhrberg C, Lundkvist A, Abramsson A, Jeltsch M, Mitchell C, Alitalo K, Shima D, Betsholtz C, Vegf guides angiogenic sprouting utilizing endothelial tip cell filopodia., J Cell Biol 161 (6) (2003) 1163–1177. doi:10.1083/jcb.200302047. URL http://dx.doi.org/10.1083/jcb.200302047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Bentley K, Mariggi G, Gerhardt H, Bates PA, Tipping the Balance: Robustness of Tip Cell Selection, Migration and Fusion in Angiogenesis, PLoS Computational Biology 5 (10) (2009) e1000549. doi:10.1371/journal.pcbi.1000549. URL http://dx.plos.org/10.1371/journal.pcbi.1000549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Jakobsson L, Franco CA, Bentley K, Collins RT, Ponsioen B, Aspalter IM, Rosewell I, Busse M, Thurston G, Medvinsky A, Schulte-Merker S, Gerhardt H, Endothelial cells dynamically compete for the tip cell position during angiogenic sprouting, Nature Cell Biology 12 (10) (2010) 943–953. doi:10.1038/ncb2103. URL http://www.nature.com/doifinder/10.1038/ncb2103 [DOI] [PubMed] [Google Scholar]
- [81].Vempati P, Mac Gabhann F, Popel AS, Quantifying the Proteolytic Release of Extracellular Matrix-Sequestered VEGF with a Computational Model, PLoS ONE 5 (7) (2010) e11860. doi:10.1371/journal.pone.0011860. URL http://dx.plos.org/10.1371/journal.pone.0011860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Vempati P, Popel AS, Mac Gabhann F, Formation of vegf isoform-specific spatial distributions governing angiogenesis: computational analysis, BMC Systems Biology 5 (1) (2011) 59. doi:10.1186/1752-0509-5-59. URL http://dx.doi.org/10.1186/1752-0509-5-59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [83].Kilpatrick LE, Friedman-Ohana R, Alcobia DC, Riching K, Peach CJ, Wheal AJ, Briddon SJ, Robers MB, Zimmerman K, Machleidt T, Wood KV, Woolard J, Hill SJ, Real-time analysis of the binding of fluorescent VEGF165a to VEGFR2 in living cells: Effect of receptor tyrosine kinase inhibitors and fate of internalized agonist-receptor complexes, Biochemical Pharmacology 136 (2017) 62–75. doi:10.1016/j.bcp.2017.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Hellstrom M, Phng L-K, Hofmann JJ, Wallgard E, Coultas L, Lindblom P, Alva J, Nilsson A-K, Karlsson L, Gaiano N, Yoon K, Rossant J, Iruela-Arispe ML, Kalen M, Gerhardt H, Betsholtz C, Dll4 signalling through Notch1 regulates formation of tip cells during angiogenesis, Nature 445 (7129) (2007) 776–780. doi:10.1038/nature05571. [DOI] [PubMed] [Google Scholar]
- [85].Maxwell PH, Ratcliffe PJ, Oxygen sensors and angiogenesis, Seminars in Cell & Developmental Biology 13 (1) (2002) 29–37. doi:10.1006/scdb.2001.0287. URL http://linkinghub.elsevier.com/retrieve/pii/S1084952101902873 [DOI] [PubMed] [Google Scholar]
- [86].Garcia-Cardena G, Slegtenhorst BR, Hemodynamic Control of Endothelial Cell Fates in Development, Annual Review of Cell and Developmental Biology 32 (1) (2016) 633–648. doi:10.1146/annurev-cellbio-100814-125610. URL http://www.annualreviews.org/doi/10.1146/annurev-cellbio-100814-125610 [DOI] [PubMed] [Google Scholar]
- [87].Secomb TW, Hemodynamics, Wiley Online Library, 2016, pp. 975–1003. doi:10.1002/cphy.c150038. [Google Scholar]
- [88].Friedl P, Wolf K, Tube travel: The role of proteases in individual and collective cancer cell invasion, Cancer Research 68 (18) (2008) 7247–7249. doi:10.1158/0008-5472.can-08-0784. URL http://dx.doi.org/10.1158/0008-5472.CAN-08-0784 [DOI] [PubMed] [Google Scholar]
- [89].Fisher KE, Sacharidou A, Stratman AN, Mayo AM, Fisher SB, Mahan RD, Davis MJ, Davis GE, Mt1-mmp- and cdc42-dependent signaling co-regulate cell invasion and tunnel formation in 3D collagen matrices, Journal of Cell Science 122 (24) (2009) 4558–4569. doi:10.1242/jcs.050724. URL http://dx.doi.org/10.1242/jcs.050724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Ilina O, Bakker G-J, Vasaturo A, Hofmann RM, Friedl P, Two-photon laser-generated microtracks in 3D collagen lattices: principles of mmp-dependent and -independent collective cancer cell invasion, Physical Biology 8 (1) (2011) 015010. doi:10.1088/1478-3975/8/1/015010. URL http://dx.doi.org/10.1088/1478-3975/8/1/015010 [DOI] [PubMed] [Google Scholar]
- [91].Rupp PA, Visconti RP, Czirok A, Cheresh DA, Little CD, Matrix metalloproteinase 2-integrin v 3 Binding is required for mesenchymal cell invasive activity but not epithelial locomotion: A computational time-lapse study, Molecular Biology of the Cell 19 (12) (2008) 5529–5540. doi:10.1091/mbc.e07-050480. URL http://dx.doi.org/10.1091/mbc.E07-05-0480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Bayless KJ, Microtubule depolymerization rapidly collapses capillary tube networks in vitro and angiogenic vessels in vivo through the small gtpase rho, Journal of Biological Chemistry 279 (12) (2004) 11686–11695. doi:10.1074/jbc.m308373200. URL http://dx.doi.org/10.1074/jbc.M308373200 [DOI] [PubMed] [Google Scholar]
- [93].Painter KJ, Modelling cell migration strategies in the extracellular matrix, Journal of Mathematical Biology 58 (4–5) (2008) 511–543. doi:10.1007/s00285-008-0217-8. URL http://dx.doi.org/10.1007/s00285-008-0217-8 [DOI] [PubMed] [Google Scholar]
- [94].Mente C, Prade I, Brusch L, Breier G, Deutsch A, Parameter estimation with a novel gradient-based optimization method for biological lattice-gas cellular automaton models, Journal of Mathematical Biology 63 (1) (2010) 173–200. doi:10.1007/s00285-010-0366-4. URL http://dx.doi.org/10.1007/s00285-010-0366-4 [DOI] [PubMed] [Google Scholar]
- [95].Szabo A, Varga K, Garay T, Hegedus B, Czirok A, Invasion from a cell aggregate—the roles of active cell motion and mechanical equilibrium, Physical Biology 9 (1) (2012) 016010. doi:10.1088/1478-3975/9/1/016010. URL http://dx.doi.org/10.1088/1478-3975/9/1/016010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Vittori K, Talbot G, Gautrais J, Fourcassie V, Araujo AF, Theraulaz G, Path efficiency of ant foraging trails in an artificial network, Journal of Theoretical Biology 239 (4) (2006) 507–515. doi:10.1016/j.jtbi.2005.08.017. URL http://dx.doi.org/10.1016/j.jtbi.2005.08.017 [DOI] [PubMed] [Google Scholar]
- [97].Vernon RB, Lara SL, Drake CJ, Iruela-Arispe ML, Angello JC, Little CD, Wight TN, Sage EH, Organized type i collagen influences endothelial patterns during “spontaneous angiogenesis in vitro”: Planar cultures as models of vascular development, In Vitro Cellular & Developmental Biology - Animal 31 (2) (1995) 120–131. doi:10.1007/bf02633972. URL http://dx.doi.org/10.1007/BF02633972 [DOI] [PubMed] [Google Scholar]
- [98].Manoussaki D, Lubkin SR, Vemon RB, Murray JD, A mechanical model for the formation of vascular networks in vitro, Acta Biotheoretica 44 (3–4) (1996) 271–282. doi:10.1007/bf00046533. URL http://dx.doi.org/10.1007/BF00046533 [DOI] [PubMed] [Google Scholar]
- [99].Namy P, Ohayon J, Tracqui P, Critical conditions for pattern formation and in vitro tubulogenesis driven by cellular traction fields, Journal of Theoretical Biology 227 (1) (2004) 103–120. doi:10.1016/j.jtbi.2003.10.015. URL http://dx.doi.org/10.1016/j.jtbi.2003.10.015 [DOI] [PubMed] [Google Scholar]
- [100].van Oers RFM, Rens EG, LaValley DJ, Reinhart-King CA, Merks RMH, Mechanical Cell-Matrix Feedback Explains Pairwise and Collective Endothelial Cell Behavior In Vitro, PLOS Computational Biology 10 (8) (2014.08.14) e1003774. doi:10.1371/journal.pcbi.1003774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Califano J, Reinhart-King C, The effects of substrate elasticity on endothelial cell network formation and traction force generation, 2009. Annual International Conference of the IEEE Engineering in Medicine and Biology Society doi:10.1109/iembs.2009.5333194. URL http://dx.doi.org/10.1109/IEMBS.2009.5333194 [DOI] [PubMed] [Google Scholar]
- [102].Arima S, Nishiyama K, Ko T, Arima Y, Hakozaki Y, Sugihara K, Koseki H, Uchijima Y, Kurihara Y, Kurihara H, Angiogenic morphogenesis driven by dynamic and heterogeneous collective endothelial cell movement, Development 138 (21) (2011) 4763–4776. doi:10.1242/dev.068023. URL http://dev.biologists.org/cgi/doi/10.1242/dev.068023 [DOI] [PubMed] [Google Scholar]
- [103].Perryn ED, Czirok A, Little CD, Vascular sprout formation entails tissue deformations and VE-cadherin-dependent cell-autonomous motility, Developmental Biology 313 (2) (2008) 545–555. doi:10.1016/j.ydbio.2007.10.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Ambrosi D, Bussolino F, Preziosi L, A review of vasculogenesis models, Journal of Theoretical Medicine 6 (1) (2005) 1–19. doi:10.1080/1027366042000327098. URL http://dx.doi.org/10.1080/1027366042000327098 [Google Scholar]
- [105].Keller EF, Segel LA, Initiation of slime mold aggregation viewed as an instability, Journal of Theoretical Biology 26 (3) (1970) 399–415. doi:10.1016/0022-5193(70)90092-5. URL http://dx.doi.org/10.1016/0022-5193(70)90092-5 [DOI] [PubMed] [Google Scholar]
- [106].Merks RM, Brodsky SV, Goligorksy MS, Newman SA, Glazier JA, Cell elongation is key to in silico replication of in vitro vasculogenesis and subsequent remodeling, Developmental Biology 289 (1) (2006) 44–54. doi:10.1016/j.ydbio.2005.10.003. URL http://dx.doi.org/10.1016/j.ydbio.2005.10.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107].Vernon RB, Sage E, A novel, quantitative model for study of endothelial cell migration and sprout formation within three-dimensional collagen matrices, Microvascular Research 57 (2) (1999) 118–133. doi:10.1006/mvre.1998.2122. URL http://dx.doi.org/10.1006/mvre.1998.2122 [DOI] [PubMed] [Google Scholar]
- [108].Koh W, Stratman AN, Sacharidou A, Davis GE, Chapter 5 in vitro three dimensional collagen matrix models of endothelial lumen formation during vasculogenesis and angiogenesis, Angiogenesis - In Vitro Systems (2008) 83–101 doi:10.1016/s0076-6879(08)02005-3. URL http://dx.doi.org/10.1016/S0076-6879(08)02005-3 [DOI] [PubMed] [Google Scholar]
- [109].Kohn-Luque A, de Back W, Starruß J, Mattiotti A, Deutsch A, Perez-Pomares JM, Herrero MA, Early embryonic vascular patterning by matrix-mediated paracrine signalling: A mathematical model study, PLoS ONE 6 (9) (2011) e24175. doi:10.1371/journal.pone.0024175. URL http://dx.doi.org/10.1371/journal.pone.0024175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110].Mullins WW, Sekerka RF, Morphological stability of a particle growing by diffusion or heat flow, Journal of Applied Physics 34 (2) (1963) 323–329. doi:10.1063/1.1702607. URL http://dx.doi.org/10.1063/1.1702607 [Google Scholar]
- [111].Neufeld G, Cohen T, Gengrinovitch S, Poltorak Z, Vascular endothelial growth factor (vegf) and its receptors., FASEB J 13 (1) (1999) 9–22. [PubMed] [Google Scholar]
- [112].Ruhrberg C, Gerhardt H, Golding M, Watson R, Ioannidou S, Fujisawa H, Betsholtz C, Shima DT, Spatially restricted patterning cues provided by heparin-binding vegf-a control blood vessel branching morphogenesis., Genes Dev 16 (20) (2002) 2684–2698. doi:10.1101/gad.242002. URL http://dx.doi.org/10.1101/gad.242002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Park JE, Keller GA, Ferrara N, The vascular endothelial growth factor (vegf) isoforms: differential deposition into the subepithelial extracellular matrix and bioactivity of extracellular matrix-bound vegf., Mol Biol Cell 4 (12) (1993) 1317–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114].Poltorak Z, Cohen T, Sivan R, Kandelis Y, Spira G, Vlodavsky I, Keshet E, Neufeld G, Vegf145, a secreted vascular endothelial growth factor isoform that binds to extracellular matrix., J Biol Chem 272 (11) (1997) 7151–7158. [DOI] [PubMed] [Google Scholar]
- [115].Woolard J, Bevan HS, Harper SJ, Bates DO, Molecular diversity of vegf-a as a regulator of its biological activity., Microcirculation 16 (7) (2009) 572–592. doi:10.1080/10739680902997333. URL http://dx.doi.org/10.1080/10739680902997333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].Keyt BA, Berleau LT, Nguyen HV, Chen H, Heinsohn H, Vandlen R, Ferrara N, The Carboxylterminal Domain(111165) of Vascular Endothelial Growth Factor Is Critical for Its Mitogenic Potency, Journal of Biological Chemistry 271 (13) (1996) 7788–7795. doi:10.1074/jbc.271.13.7788. URL http://www.jbc.org/lookup/doi/10.1074/jbc.271.13.7788 [DOI] [PubMed] [Google Scholar]
- [117].Sack KD, Teran M, Nugent MA, Extracellular matrix stiffness controls VEGF signaling and processing in endothelial cells: VEGF signaling is controlled by ECM stiffness, Journal of Cellular Physiology 231 (9) (2016) 2026–2039. doi:10.1002/jcp.25312. URL http://doi.wiley.com/10.1002/jcp.25312 [DOI] [PubMed] [Google Scholar]
- [118].Ashikari-Hada S, Habuchi H, Kariya Y, Kimata K, Heparin Regulates Vascular Endothelial Growth Factor 165 -dependent Mitogenic Activity, Tube Formation, and Its Receptor Phosphorylation of Human Endothelial Cells: Comparison of the effects of heparin and modified heparins, Journal of Biological Chemistry 280 (36) (2005) 31508–31515. doi:10.1074/jbc.M414581200. URL http://www.jbc.org/lookup/doi/10.1074/jbc.M414581200 [DOI] [PubMed] [Google Scholar]
- [119].Chen TT, Luque A, Lee S, Anderson SM, Segura T, Iruela-Arispe ML, Anchorage of VEGF to the extracellular matrix conveys differential signaling responses to endothelial cells, The Journal of Cell Biology 188 (4) (2010) 595–609. doi:10.1083/jcb.200906044. URL http://www.jcb.org/lookup/doi/10.1083/jcb.200906044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [120].Czirok A, Zamir EA, Szabo A, Little CD, Multicellular sprouting during vasculogenesis, Current Topics in Developmental Biology 81 (2008) 269–289. doi:10.1016/S0070-2153(07)81009-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Sato Y, Poynter G, Huss D, Filla MB, Czirok A, Rongish BJ, Little CD, Fraser SE, Lansford R, Dynamic Analysis of Vascular Morphogenesis Using Transgenic Quail Embryos, PLOS ONE 5 (9) (2010) e12674. doi:10.1371/journal.pone.0012674. URL http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0012674 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [122].Walpole J, Chappell JC, Cluceru JG, Mac Gabhann F, Bautch VL, Peirce SM, Agent-based model of angiogenesis simulates capillary sprout initiation in multicellular networks, Integr. Biol 7 (9) (2015) 987–997. doi:10.1039/c5ib00024f. URL http://dx.doi.org/10.1039/c5ib00024f [DOI] [PMC free article] [PubMed] [Google Scholar]
- [123].Eden M, A two-dimensional growth process, Dynamics of fractal surfaces 4 (1961) 223–239. [Google Scholar]
- [124].Karma A, Rappel W-J, Quantitative phase-field modeling of dendritic growth in two and three dimensions, Phys. Rev. E 57 (4) (1998) 4323–4349. doi:10.1103/physreve.57.4323. URL http://dx.doi.org/10.1103/PhysRevE.57.4323 [Google Scholar]
- [125].Campelo F, Hernandez-Machado A, Model for curvature-driven pearling instability in membranes, Physical Review Letters 99 (8). doi:10.1103/physrevlett.99.088101. URL http://dx.doi.org/10.1103/PhysRevLett.99.088101 [DOI] [PubMed] [Google Scholar]
- [126].Du Q, Liu C, Wang X, A phase field approach in the numerical study of the elastic bending energy for vesicle membranes, Journal of Computational Physics 198 (2) (2004) 450–468. doi:10.1016/j.jcp.2004.01.029. URL http://dx.doi.org/10.1016/j.jcp.2004.01.029 [Google Scholar]
- [127].Shao D, Rappel W-J, Levine H, Computational model for cell morphodynamics, Physical Review Letters 105 (10). doi:10.1103/physrevlett.105.108104. URL http://dx.doi.org/10.1103/PhysRevLett.105.108104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [128].Shao D, Levine H, Rappel W-J, Coupling actin flow, adhesion, and morphology in a computational cell motility model, Proceedings of the National Academy of Sciences 109 (18) (2012) 6851–6856. doi:10.1073/pnas.1203252109. URL http://dx.doi.org/10.1073/pnas.1203252109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129].Yoshimura K, Kobayashi R, Ohmura T, Kajimoto Y, Miura T, A new mathematical model for pattern formation by cranial sutures, Journal of Theoretical Biology 408 (2016) 66–74. doi:10.1016/j.jtbi.2016.08.003. URL http://dx.doi.org/10.1016/j.jtbi.2016.08.003 [DOI] [PubMed] [Google Scholar]
- [130].Travasso RD, Castro M, Oliveira JC, The phase-field model in tumor growth, Philosophical Magazine 91 (1) (2011) 183–206. doi:10.1080/14786435.2010.501771. URL http://dx.doi.org/10.1080/14786435.2010.501771 [Google Scholar]
- [131].Travasso RDM, Corvera Poire E, Castro M, Rodrguez-Manzaneque JC, Hernandez-Machado A, Tumor angiogenesis and vascular patterning: A mathematical model, PLoS ONE 6 (5) (2011) e19989. doi:10.1371/journal.pone.0019989. URL http://dx.doi.org/10.1371/journal.pone.0019989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [132].Vilanova G, Colominas I, Gomez H, Capillary networks in tumor angiogenesis: From discrete endothelial cells to phase-field averaged descriptions via isogeometric analysis, Int. J. Numer. Meth. Biomed. Engng 29 (10) (2013) 1015–1037. doi:10.1002/cnm.2552. http://dx.doi.org/10.1002/cnm.2552 [DOI] [PubMed] [Google Scholar]
- [133].Carlier A, Geris L, Bentley K, Carmeliet G, Carmeliet P, Van Oosterwyck H, MOSAIc: A multiscale model of osteogenesis and sprouting angiogenesis with lateral inhibition of endothelial cells, PLoS Computational Biology 8 (10) (2012) e1002724. doi:10.1371/journal.pcbi.1002724. URL http://dx.doi.org/10.1371/journal.pcbi.1002724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [134].Santamaria-Holek I, Grzywna ZJ, Miguel Rubi J, A non-equilibrium thermodynamics model for combined adsorption and diffusion processes in micro- and nanopores, Journal of Non-Equilibrium Thermodynamics 37 (3). doi:10.1515/jnetdy-2011-0029. URL http://dx.doi.org/10.1515/jnetdy-2011-0029 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.