A Simple Hydraulic Analog Model of Oxidative Phosphorylation

Abstract

Mitochondrial oxidative phosphorylation is the primary source of cellular energy transduction in mammals. This energy conversion involves dozens of enzymatic reactions, energetic intermediates, and the dynamic interactions among them. With the goal of providing greater insight into the complex thermodynamics and kinetics (“thermokinetics”) of mitochondrial energy transduction, a simple hydraulic analog model of oxidative phosphorylation is presented. In the hydraulic model water tanks represent the forward and back “pressures” exerted by thermodynamic driving forces: The matrix redox potential (ΔG_redox), the electrochemical potential for protons across the mitochondrial inner membrane (ΔG_H⁺), and the free energy of ATP (ΔG_ATP). Net water flow proceeds from tanks with higher water pressure to tanks with lower pressure through “enzyme pipes” whose diameters represent the conductances (effective activities) of the proteins that catalyze the energy transfer. These enzyme pipes include the reactions of dehydrogenase enzymes, the electron transport chain (ETC), and the combined action of ATP synthase plus the ATP:ADP exchanger that spans the inner membrane. Additionally, reactive oxygen species production is included in the model as a leak that is driven out of the ETC pipe by high pressure (high ΔG_redox), and a proton leak dependent upon the ΔG_H⁺ for both its driving force and the conductance of the leak pathway. Model water pressures and flows are shown to simulate thermodynamic forces and metabolic fluxes that have been experimentally observed in mammalian skeletal muscle in response to acute exercise, chronic endurance training, and reduced substrate availability, as well as account for the thermokinetic behavior of mitochondria from fast- and slow-twitch skeletal muscle and the metabolic capacitance of the creatine kinase reaction.

Mitochondrial Energy Transduction

Mitochondria combust fuels to CO₂ and H₂O and convert the energy released to ATP free energy (ΔG_ATP). As shown schematically in Figure 1A, the energy transduction takes place in three major steps: 1) Dehydrogenase (DH) enzymes collect electrons from fuels, which generates a matrix oxidation-reduction potential (ΔG_redox) down the electron transport chain (ETC). 2) The ETC converts ΔG_redox energy into an electrochemical potential for protons (ΔG_H⁺) across the inner mitochondrial membrane. This transduction is achieved by coupling electron flow down the voltage drop of the ETC to the translocation (“pumping”) of protons across the inner membrane (from the matrix toward the cytosol). The proton electrochemical gradient (ΔG_H⁺) so generated is the sum of electrical (ΔΨ) and chemical (ΔpH) potentials and is sometimes referred to as the “protonmotive force” (Δp). 3) Finally, F₁-ATP synthase (Complex V) uses proton flux from cytosol to matrix driven by ΔG_H⁺ to phosphorylate ADP in the mitochondrial matrix. Matrix ATP⁴⁻ is then translocated to the cytosol in exchange for cytosolic ADP³⁻ by the adenine nucleotide translocase (ANT), which is driven by the ΔΨ component of ΔG_H⁺. Along the way, two energy dissipation processes can occur: 1) Single electron (monovalent) reduction of an O₂ molecule to the superoxide radical (O₂^.−) is a free radical initiation reaction sometimes called the “electron leak” and 2) ΔG_H⁺ can drive H⁺ across the inner membrane back into the matrix via pathways other than Complex V. Under physiological conditions, the electron leak rate represents a very small, <0.1%, fraction of the electrons transported down the ETC. In contrast, the proton leak rate can, under certain conditions, dissipate a substantial fraction of the energy released from fuel oxidation (7).

Figure 1: Simple Models of Oxidative Phosphorylation.

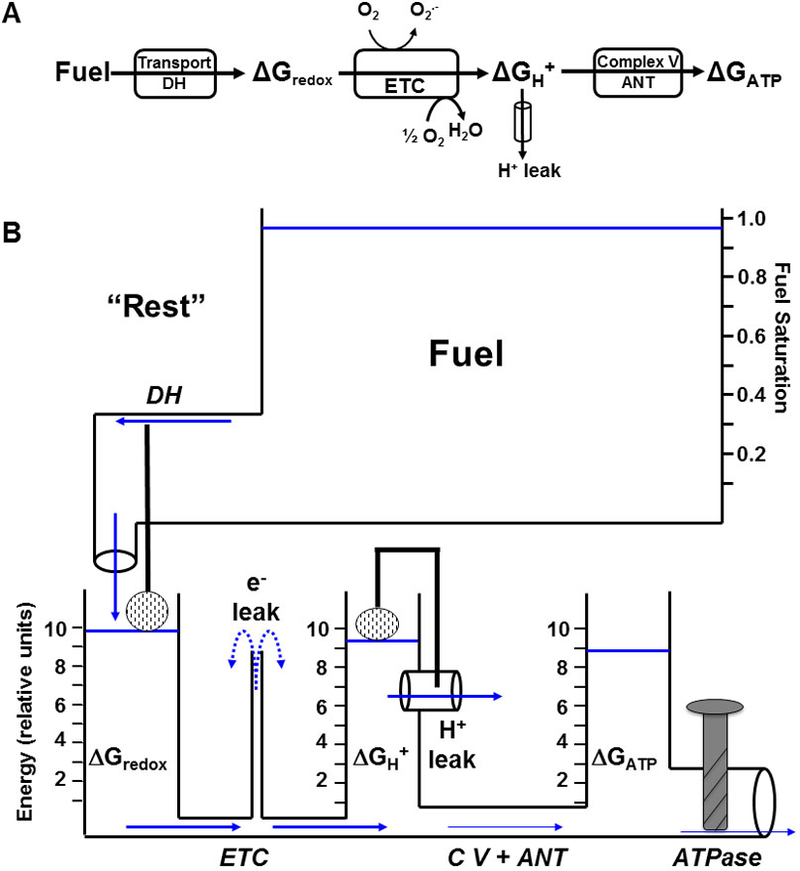
Modular (A) and hydraulic analog (B) models of oxidative phosphorylation showing the transduction of energy from oxidative fuels which are transported into the mitochondria and converted into matrix redox potential (ΔG_redox) by dehydrogenase enzymes (DH). ΔG_redox is then converted into a protonmotive force (Δp or ΔG_H+) by the electron transport chain (ETC). Δp is converted to ATP by Complex V (C V ) and transported out of the mitochondria by adenine nucleotide translocase (ANT) where it contributes to the free energy of ATP hydrolysis (ΔG_ATP) available to be used by cytosolic ATPases. Electron leak (O₂^.−) from the ETC and proton leak back across the inner mitochondrial membrane are also depicted. In the hydraulic model, the water level in each tank represents the availability of the respective free energy forms and the diameter of the pipes is proportional to the activity of the enzymes along that portion of the pathway. The height of the water in each tank exerts a pressure on both the upstream and downstream adjacent pipes. Water flow (or flux, J) between two tanks is thus proportional to the difference in water levels between each tank (ΔG₁ – ΔG₂) as well as the size of the pipe (conductance, L) between them.

Mitochondrial Energy Transduction is a Linear Force:Flow Relationship

Recently, Robert Balaban’s laboratory (16) showed in mitochondria isolated from pig skeletal muscle that each of the three major steps of oxidative phosphorylation in Figure 1 can be described with a linear force:flow relationship:

$$\text{Flow = }\left(\text{Net Driving Force}\right)\text{ x }\left(\text{Conductance}\right)$$ [1]

Ohm’s Law is perhaps the most familiar example of such a linear force:flow relationship, in which flow is current, net driving force is voltage, and conductance is the reciprocal of resistance. In mitochondrial oxidative phosphorylation flow is metabolic flux (which takes various forms in the pathway, see below), net driving force is the difference between two free energies (ΔΔG), and conductance is the reciprocal of enzyme/enzyme pathway resistance to metabolic flow.

Energy and Stoichiometry of Each Step

In order to calculate the net driving force (ΔΔG) of a step, for example (ΔG_redox −ΔG_H⁺), each energy must be adjusted by the appropriate stoichiometry and in some cases a conversion factor such as the Faraday to match the units. For example, down the entire ETC this stoichiometry is 10 protons translocated (“pumped”) for each pair of electrons that reduce ½O₂ to H₂O (49), a stoichiometry of (10H⁺):(2e⁻). Thus, each pair of electrons traveling down the ETC encounters the “backpressure” of 10 protons, which opposes net electron advancement. The net driving force through the step is the difference: (2e⁻x ΔG_redox) minus (10H⁺ x ΔG_H⁺). Similarly, the stoichiometry of ΔG_H⁺ to ΔG_ATP conversion must take into account the protons used for both the matrix synthesis of ATP and the inner membrane exchange of ATP-for-ADP and transport of inorganic phosphate. These stoichiometries are 2⅔ H⁺ per matrix ATP synthesized (8H⁺/3ATP) at Complex V (68), plus the ΔG_H⁺ of one additional H⁺ to power ADP³⁻:ATP⁴⁻ exchange at ANT (ΔΨ component of ΔG_H⁺) (8) and inorganic phosphate (Pi) transport into the matrix via the phosphate transporter (ΔpH component of ΔG_H⁺), for a total of 3⅔ H⁺ per cytosolic ATP. Again, the net driving force through the step is the difference: (3⅔ x ΔG_H⁺) minus (ΔG_ATP). In this review, we seek the clarity offered by the simplicity of Equation 1, and so we will not proceed to the quantitative relationships used to calculate oxidation-reduction potential difference down the ETC and its conversion to redox free energy (ΔG_redox), the electrochemical potential for protons across the inner membrane (ΔG_H⁺), and the chemical free energy of cytosolic ATP (ΔG_ATP). Instead, the reader is referred to the lucid presentation of these ideas by Nicholls and Ferguson (49), who over 30 years ago began making these difficult concepts accessible to the rest of us in their Bioenergetics series (49). In addition, Glancy et al. describe in quantitative terms how the apparent conductance of each step is determined from the experimental measurements of flow and these net driving forces (16).

Hydraulic Model

Linear force:flow relationships along at least some portion of the oxidative pathway were experimentally demonstrated by numerous visionary pioneers in the field of mitochondrial bioenergetics, such as Rottenberg (57), Klingenberg (52), Van Dam (66), Westerhoff (69), Stucki (62), Wanders (67), Davis (12), Lemasters (39), Brand (48), Nicholls (50), Balaban (31), Wilson (72) and others. All were inspired by Onsager’s Nobel-winning contributions (53, 54). We have developed a simple hydraulic analog model to make Mitchell’s chemiosmotic theory (46) more approachable for specialists and non-specialists alike. This hydraulic model is shown in Figure 1B. The three energetic intermediates (“pools”) mentioned above, ΔG_redox, ΔG_H⁺, and ΔG_ATP, are represented by water tanks. The water level (pressure) of each tank corresponds to the free energy and stoichiometry of that intermediate. Equal water levels correspond to thermodynamic equilibrium between two intermediates. Net water flow obviously proceeds from higher pressure to lower pressure. The energy tanks are connected by enzyme pipes. The diameter of each pipe represents the conductance (inverse of resistance) of that step; large diameter pipes represent high abundance (or high V_max) enzymes, while narrow pipes indicate high resistance to flow (low abundance or V_max). Flow between any two tanks is therefore given by Equation 2, Poiseuille’s Law, which, of course, takes the same form as Equation 1:

$$\text{Water flow = }\left(\text{pressure difference}\right)\text{ x }\left(\text{pipe conductance}\right)$$ [2]

Under laminar water flow conditions, pipe conductance can be calculated as: Π r⁴/(8 η L), where r is pipe radius, η is water viscosity, and L is pipe length. Because physical flow, energetic driving force, and conductance are arranged identically in both the analog model and the energy transductions of the target system they describe, this hydraulic model could be described as a “formal analogy” of oxidative phosphorylation. Water outflow through an “ATPase” pipe (cytosolic ATP breakdown) drives energy-requiring (endergonic) processes, such as muscle contraction, ion pumping, or biosynthesis (the water outflow could be shown turning a paddle wheel, for example). In Figure 1B, which depicts a “resting skeletal muscle cell,” the ATPase valve is barely open, with just enough water (ATP) flow to power the basic “housekeeping” functions of resting tissue. As a result, very little pressure drop is required from ΔG_redox → ΔG_H⁺ → ΔG_ATP. The height of the ΔG_redox tank is set by water flow delivered from a Fuel tank through a dehydrogenase (DH) pipe. This flow is driven by a “substrate pressure” (water height in the fuel tank), which is the extent of DH enzyme saturation: Fractional saturation = [S]/([S] + K_M). Fuel inflow to the ΔG_redox tank is resisted by the diameter of the DH pipe and also by a float valve representing kinetic feedback inhibition by products of the substrate oxidation (e.g., high NADH/NAD⁺ and Acetyl CoA/CoA ratios). It should be noted that, while the model shows only one DH pipe, in reality there are many “dehydrogenase input pipes” in mitochondria. Further, only those DH steps that are NAD-linked, for example pyruvate dehydrogenase and beta-hydroxyacyl CoA dehydrogenase, deliver electrons to NADH and Complex I of the ETC as shown in the model. In other words, this model can be expanded upon to include multiple fuel inflow pipes if mitochondrial fuel selection is the discussion of interest.

Leak Reactions

Superoxide production (e⁻ leak) is depicted as water leaving the top of a pipe that represents the ETC pathways by which single electrons leave an ETC carrier and monovalently reduce molecular O₂ to the superoxide radical, O₂^.−. As shown in this resting condition with high fuel availability, the “pressures” (water heights) of the ΔG_redox and ΔG_H⁺ tanks are robust and above the top of the e⁻ leak pipe (Fig. 1B). Thus, “high pressure ETC water” (highly reduced ETC electron carriers) is shown leaking from the top of the e⁻ leak pipe, simulating the production of superoxide radicals. Similarly, the proton leak pathway is shown as a leak pipe projecting from the ΔG_H⁺ tank, because proton backleak across the inner membrane is driven by ΔG_H⁺, according to: J_H⁺_leak = ΔG_H⁺ x C_M,H⁺ (where C_M,H⁺ is the apparent conductance of this leak pathway). There is the potential for much greater leak flow through this higher conductance proton leak pathway. Brand and coworkers have clearly shown that, at least in mitochondria isolated from skeletal muscle and liver, proton leak kinetics are “non-Ohmic,” meaning that the apparent conductance (C_M,H⁺) is not a constant value, but rather rises with the driving force, ΔG_H⁺ (4). Our own data from experiments on rat liver mitochondria (unpublished observations by Dr. Carrie Lyons) shown in Figure 2, illustrate this non-Ohmic behavior. Non-Ohmic kinetics are simulated in the model with a float valve that opens the proton leak pipe as the ΔG_H⁺ “water level” rises. Thus, both the driving force (water height above the leak pipe), as well as the pipe conductance, increase as ΔG_H⁺ rises. Note that a larger diameter proton leak pipe would tend to lower both ΔG_redox and ΔG_H⁺, thus reducing superoxide flow from the e⁻ pipe. This feature of the model simulates the protective antioxidant effect that proton leak might offer, as conceptualized by both Brand and Skulachev in their “uncoupling to survive” hypothesis (6, 60).

Figure 2: Mitochondrial Proton Leak Kinetics.

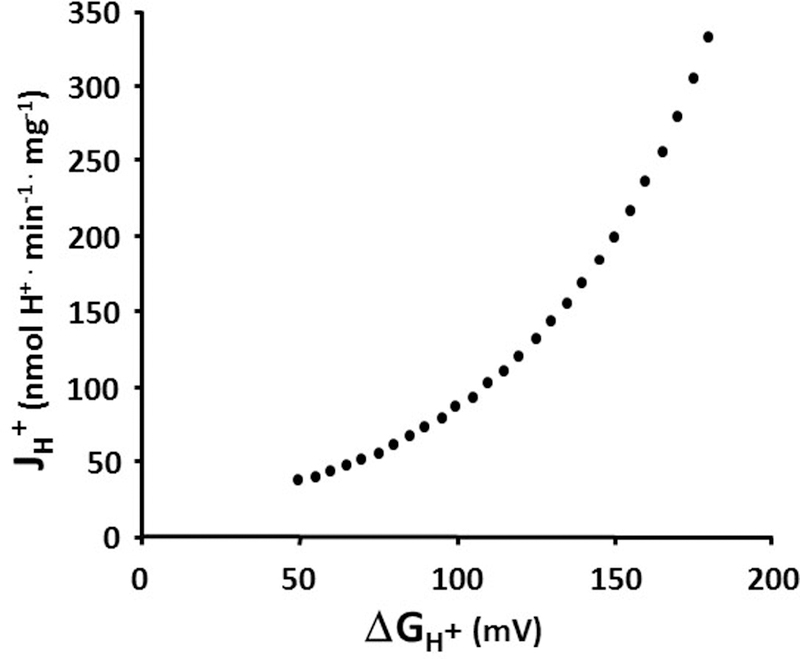
Non-phosphorylating proton flux back across the mitochondrial inner membrane in rat liver mitochondria increases exponentially with the proton motive force (ΔG_H+).

Both electron leak and proton leak contribute to the complexity of the mitochondrial energy transduction pathway. The representations of these two leak pathways within the hydraulic model provide a simple analogy to explain these intricacies. For example, while students often find it intuitive that an increase in proton leak dissipates ΔG_H⁺ and decreases ATP synthesis, they may struggle to understand why this is associated with an increase in O₂ consumption rate. Using the hydraulic model as a simulator, it is obvious that increasing the diameter of the proton leak pipe would naturally increase water flow through the ETC pipe (increase O₂ consumption rate), while water flow through the C V + ANT pipe (ATP production rate) could remain very low or zero.

Transition to Exercise

In transition to the contractile activity of mild exercise, a Ca²⁺ signal opens the ATPase valve sufficiently for water outflow through the ATPase to match the increased energy demand (Figure 3A). The moment the ATPase valve opens, a metabolic transient ensues in which water outflow through the ATPase exceeds water delivery coming from the CV + ANT pipe (70). The ΔG_ATP tank water level therefore begins to fall, creating a greater pressure drop from ΔG_H⁺ → ΔG_ATP. This greater pressure head elicits greater water flow through CV + ANT and, in turn, the ΔG_H⁺ water height falls and so on upstream, until all flows are again equal in every segment and equal to the outflow through the ATPase. The result is a new, steady state, higher flow rate with lower water levels in every tank (except, usually, the fuel reservoir, which has immense capacitance relative to the other tanks; see below for elaboration of this capacitance issue). In comparing Figure 3A to Figure 1B, note that in transition from “resting” to “mild exercise” the energy level of the ΔG_ATP tank went from about “9 energy units” down to about 7½, while ΔG_H⁺ fell from about 9½ to about 8½, etc.

Figure 3: Effects of Exercise and Training.

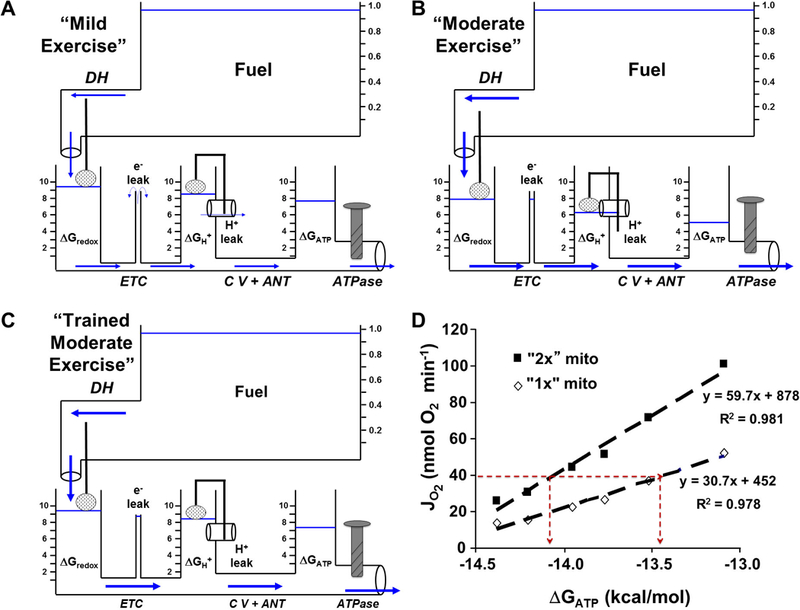
A) Mild exercise in the hydraulic model. A mild increase in cellular contractile activity slightly opens the ATPase valve and water flow through the ATPase pipe (ATP utilization) causes the ΔG_ATP tank water level to fall. In turn, water flow (fuel oxidation and ATP synthesis) from upstream tanks increases to match the demand (steady state ATP turnover). B) Simulating moderate exercise by a larger opening of the ATPase valve (more contractile activity) results in even greater water flow (ATP sythesis) and a further fall in the level of the water tanks (free energies). Note that with the lower levels of the water tanks, the leak reactions are reduced. C) Endurance training resulting in increased mitochondrial content in skeletal muscle is depicted as an increase in pipe diameters. Repeating the “moderate exercise” bout by opening the ATPase valve (same contractile activity) to the same level as in B now results in better maintenance of the water levels in the tanks (free energies). D) Experimental support for the hydraulic model predictions in C. Doubling mitochondrial content results in a greater free energy level (ΔG_ATP) at a given rate of oxygen consumption (J_O2) in isolated rat hindlimb skeletal muscle mitochondria.

The Leaks “Dry Up” in Transition to Exercise

As shown in Figure 3B, transition to a higher, moderate exercise intensity demands yet higher flow through the system, resulting in even lower steady state water tank heights. Under these conditions, the reduced pressures “upstream” withdraw the driving forces for the leaks. As a consequence, transition to higher ATP demand has a “drying up” effect on both the proton and electron (32, 61) leaks.

Increasing Pipe Diameters: Ca²⁺ and Greater Abundance (endurance training)

Table 1 summarizes the apparent resistance of each mitochondrial segment in pig mixed skeletal muscle mitochondria, as determined by Glancy et al. (16). In each case, resistances are expressed in the electrical units of Ohms, which were calculated as described above using the appropriate stoichiometries and conversion constants. Two patterns are obvious: 1) The ETC is the segment with the most resistance to energy transfer and 2) Ca²⁺ acutely reduces the resistance of every segment by a factor of about two. In the hydraulic analog model, therefore, the “ETC pipe” should have the smallest diameter and Ca²⁺ should acutely make all pipes grow wider. Thus, what was not depicted in the transition from Figure 1B to either Figure 3A or B were increased pipe diameters that would attend the Ca²⁺ activation of the ATPase. The concomitant Ca²⁺ widening (activation) of the mitochondrial “pipes” would reduce the magnitude of the energy drops required to elicit the higher flux during exercise. However, it is important to emphasize that in skeletal muscle this compensatory influence of Ca²⁺ merely ameliorates the fall in energy status that occurs in the transition from rest to exercise; rising cytosolic [Ca²⁺] does not eliminate the requirement for an energy decline when ATP demand rises. Stated yet another way, in skeletal muscle a fall in cytosolic ΔG_ATP is always observed in transition from a lower to a higher energy turnover rate (10). In cardiac muscle, in contrast, Ca²⁺ activation of the mitochondrial pathway is extreme, proportionally matching the Ca²⁺ activation of ATPases. Balaban has shown in cardiac muscle in vivo that this Ca²⁺-mediated “parallel activation” mechanism obviates any fall in energy levels when hearts transition from one ATP turnover to a higher one (2).

Table 1: Contribution of Each Pathway to the Total Mitochondrial Resistance to Energy Transfer.

The calculated resistances of 1) fuel transport and dehydrogenase activity (DH), 2) ETC activity (ETC), and 3) ATP synthase and ANT (CV + ANT) to the total resistance of the energy transduction pathway in the absence and presence of Ca²⁺.

Mitochondrial Resistance to Energy Transfer (Ohms)
Segment	No Calcium		+ Calcium (840 nM)
	Resistance	% Total	Resistance	% Total
Dehydrogenases	25.6	9.1	15.1	12.6
Electron Transport Chain	171.5	60.8	70.2	58.3
Complex V + ANT	84.8	30.1	35.0	29.1
Total	281.9	100.0	120.4	100.0

Endurance Training

John Holloszy’s landmark study of 1967 revealed that endurance training increases the mitochondrial content of skeletal muscle (22). Trained muscle is therefore modeled with larger pipes, as shown in Figure 3C. Compared to Figure 3B, the “bigger pipes” of trained muscle allow the same flow (same exercise intensity) to be achieved with smaller pressure gradients. The model simulates the improved defense of energetic homeostasis observed after a program of endurance training, as experimentally demonstrated by Dudley, Tullson, and Terjung in 1987 (13). Similar to many in vitro experiments performed by Phil Gollnick (personal communication), our data shown in Figure 3D demonstrate this concept. Viewed one way, doubling the mitochondrial content in the system doubles the oxidative flux at a given ATP free energy (thus doubling mitochondrial power output, see below). Another view is that a given flux (a given exercise intensity) is achieved at a more negative (more robust) ATP free energy in the “trained” system (see horizontal line corresponding to 40 nmol O₂/min). Decades ago, Holloszy described (24) this concept that training-induced increases in muscle mitochondrial content enable better defense of energy phosphate status in response to a given intensity of exercise (in the model, higher water levels at a given flow). The important consequences of this stronger homeostatic defense on fuel selection have been elucidated by many of Holloszy’s postdoctoral trainees [e.g., Bob Fitts (14), Frank Booth (23), Ron Terjung (64), and Ken Baldwin (3)]. Connett (9, 11) and Saltin and Gollnick (18) also offered insightful metabolic models that predicted the carbohydrate-sparing effect mediated by the elevated mitochondrial content of endurance-trained skeletal muscle.

Substrate Availability

In Figure 4, the same trained muscle exercising at the same intensity as in Figure 3C now encounters declining fuel availability (fuel tank water level has fallen from nearly 1.0 to 0.6). For simplicity, let’s consider this perturbation as an instantaneous step change. The decreased fuel pressure would initiate a transient in which water delivery through the “DH pipe” would suddenly fail to match the flows below. The imbalance would first cause a fall in ΔG_redox, which would have a series of consequences: 1) Downstream, the (ΔG_redox −ΔG_H⁺) pressure head, thus flow through the ETC pipe, would decrease lowering the ΔG_H⁺ level. This pattern would continue to propagate downstream into the (Complex V + ANT) pipe and ΔG_ATP tank. 2) Upstream, however, the falling float valve in the ΔG_redox tank (less NADH feedback inhibition) would restore flow through the DH pipe and, similarly, the falling water levels in the ΔG_H⁺ and ΔG_ATP tanks would also elicit “recoil” recoveries in the pipe flows upstream of them. Once steady state conditions were fully restored (flows equal in all pipes), one clear outcome of this fuel perturbation would be lower water levels (energetic driving forces) in every tank. But, an intriguing question is whether the system would recover to the original flow at these lower energy levels? This simple example reveals that the hydraulic model forces us to consider the connectivity property of metabolic control analysis (21, 28). If flow out of the ATPase pipe is insensitive to the ΔG_ATP tank water level, then flow should recover to the initial, pre-fuel depleted, rate. However, if it is sensitive i.e, if the ATPase has finite negative elasticity to the energy available from ATP, then fuel depletion would require additional stimulation of the ATPase (more Ca²⁺ signal to open the ATPase pipe further) to fully recover the initial flow rate. This is, in fact, observed during prolonged exercise. As Gollnick and Saltin demonstrated, the progressive depletion of muscle glycogen elicits greater and greater recruitment of higher threshold motor units (17). In the context of the illuminating studies by Jeneson et al. (26), this may reflect a redistribution of flux control away from the module of ATP utilization, the ATPase (and, indeed, away from the central nervous system), and toward the module of ATP production, mitochondria. Consistent with these ideas, carbohydrate depletion during prolonged moderate-to-heavy intensity exercise to exhaustion results in an unchanging flux (VO₂), progressively falling muscle [PCr] (ΔG_ATP), greater motor unit activation, and a rising perception of effort (65). In this fuel-depletion scenario, the model simulates the in vivo data of Sahlin’s laboratory (58) and our in vitro results. Messer et al. (42) showed that as sub-saturating concentrations of either malate or pyruvate were decreased i.e., as the ratio [S]/([S]+K_M) fell, a given flux required a lower (less negative or less robust) ΔG_ATP.

Figure 4: Effect of Reduced Fuel Availability.

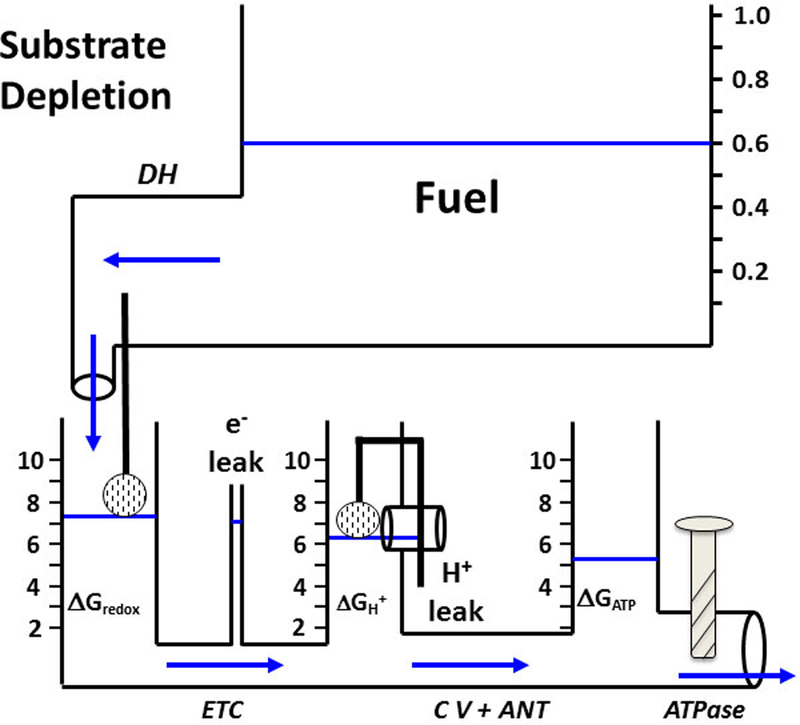
Substrate depletion simulated by reducing the water level in the fuel tank results in lower water levels (free energies) in the downstream tanks and drives less water flow (lower ATP production). Compare with Figure 3C.

ATP: Biological “Energy Currency”

Both the training scenario, which enhanced mitochondrial defense of ATP free energy, and substrate depletion, which degraded it, address the critical issue of ΔG_ATP homeostasis. The hydraulic model provides intuitive appreciation that mitochondria perform two equally important functions related to cellular energy metabolism: 1) ATP synthesis (J_p) and 2) defense of ΔG_ATP. The product of these two variables is the power output of mitochondria (mP_o): mP_o = J_p x ΔG_ATP, which drives ATP-utilizing processes. In other words, the analogy of ATP as biological “energy currency” should include both features of a currency, units of exchange (“bills” = ATP molecules) and denominations (“bill value” = free energy of ATP i.e., ΔG_ATP). Just as devalued currency has less purchasing power, mitochondria in untrained or fuel-depleted muscle generate ATP that delivers a diminished driving force to an endergonic process such as force production or ion pumping. This simple hydraulic model clearly demonstrates that, while falling ΔG_ATP stimulates metabolic flow from upstream driving forces, increasing the ATP synthesis rate, it also diminishes the “pressure” of each ATP delivered to sites of ATP utilization. Indeed, Roger Cooke has shown that actomyosin force production declines linearly as log[Pi] rises (hence ATP hydrolysis delivers less driving force) (55). Masuda, Dobson, and Veech showed similar linear dependence of ΔG_ATP with the Na⁺ gradient maintained across the sarcolemma of rodent ventricles (41), and Hasselbach demonstrated that the cytosolic-sarcoplasmic reticulum Ca²⁺ gradient is also proportional to ΔG_ATP (20). A skeletal muscle mitochondrial system “weakened” by a lack of training or fuel scarcity must allow greater devaluation of ATP currency to match a given demand. But, because the ATP stoichiometry of cellular ATPases is fixed, to the extent ΔG_ATP falls, force production by actomyosin (56) and ion gradients across sarcolemmal (41) and sarcoplasmic reticulum (29) membranes also may deteriorate.

Mitochondria in Type I and Type II Muscle Fibers

Compared to type II (white, fast, glycolytic) fibers, type I (red, slow, oxidative) muscle cells typically contain 2–3 times more mitochondrial protein (59) and as little as ½ the total creatine (PCr + Cr) (35). Curiously, at rest, feline type II biceps muscle fibers maintain a much more robust (more negative) ATP free energy than type I soleus, despite essentially identical mass-specific VO₂ (33). As seen in Figure 5A, mitochondria isolated in our lab by Matt Jackman behaved similarly: higher (more negative) “static head” ΔG_ATP was developed by rabbit gracilis (99% type IIb) compared to soleus (98% type I). Previously Jackman and Willis reported 2-fold higher NAD-linked isocitrate dehydrogenase (IDH) and glycerol-3-phosphate (G3P) dehydrogenase activities in these type IIb compared to type I mitochondria (25). IDH is generally considered a critical locus of flux control in the citric acid cycle and G3P oxidation is a well-known source of superoxide production (47). In the hydraulic model, type IIb mitochondria would therefore, in relative terms, have a larger DH pipe diameter, which is consistent with the ability to develop higher static head ΔG_redox, and thus, ΔG_ATP (Figure 5A). This, coupled with lower conductance downstream (see the diminished slope in Figure 5A), suggests greater tendency to fuel the electron leak, even as downstream pressures are “relaxed” by transition to higher flow. This prediction is experimentally supported by Figures 5B and C. Notice that white muscle mitochondria generate much higher superoxide (“e⁻ leak”) with the glycolytic substrates shown (and particularly with the substrates of the cytosolic-mitochondrial electron shuttles). The concept of cost-benefit tradeoff therefore emerges from the hydraulic model. Because the creatine kinase reaction is maintained near to equilibrium, higher static head ΔG_ATP, thus a higher cytosolic ATP/ADP ratio, means a high PCr/Cr ratio, which is an obvious benefit to a fiber tailored for rapid transition to high power output. But the cost may be that the high “upstream pressures” required to develop this higher “ATP pressure” predict the potential for higher free radical production, which is consistent with Brian Glancy’s data from our lab shown in Figures 5B and C.

Figure 5: Differences between Fast and Slow Twitch Muscle Mitochondria.

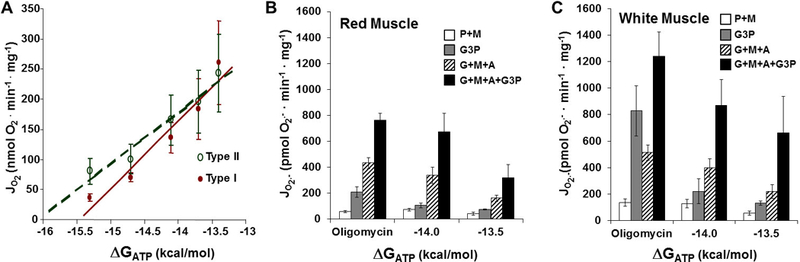
A) Mitochondria isolated from rabbit gracilis (Type II, glycolytic) muscle maintain a higher free energy level (ΔG_ATP) at a given oxygen consumption rate (J_O2) than soleus (Type I, oxidative) muscle mitochondria. Greater free energy availability (higher water levels) in the hydraulic model predicts increases in the leak reactions. Mitochondria isolated from rat white, glycolytic hindlimb muscle produce more superoxide (C) than mitochondria isolated from red, oxidative hindlimb muscle (B) under conditions simulating rest (oligomycin) and mild (−14.0) and moderate (−13.5) exercise. P+M: pyruvate (1 mM) and malate (1 mM), G3P: glycerol 3-phosphate (10 mM), G+M+A: glutamate (10 mM), malate (1 mM), and arsenite (10 mM).

PCr and Creatine Kinase: Metabolic Capacitance

Figure 6A expands the model to include the concept of metabolic capacitance (63). A high volume phosphocreatine (PCr) tank is added and linked to the ATP tank by two large diameter creatine kinase pipes, CK_m (CK located in the mitochondrial intermembrane space) and CK_c (cytosolic CK). The high volume of this tank simulates both high PCr concentration and the large equilibrium constant of the CK reaction. The large diameter of these CK pipes reflects the extremely high catalytic potential (V_max) of cellular creatine kinase, which has been shown to maintain near-thermodynamic equilibrium between cytosolic ΔG_ATP and ΔG_PCr across essentially the entire range of aerobic ATP turnover (34). As shown in Figure 6B, in transition to contractile activity the opening of the ATPase valve will, as before, cause the ΔG_ATP water level to fall. But the capacitance of the high volume PCr tank dramatically reduces the rate at which the ATP water level declines. Nevertheless, as always, an aerobic steady state can only be achieved when the flow at the ATPase (ATP demand) is matched by delivery from the fuel tank, and each step therefore must attain the same pressure difference according to Equation 2. Therefore, with or without the PCr tank, the pressure difference required for steady state is:

$$\text{pressure drop = flow/conductance}$$ [3]

The presence of the PCr tank and CK pipes changes neither the steady state flow nor the conductances of the other pipes, so the magnitude of the pressure drops from ΔG_redox → ΔG_H⁺ → ΔG_ATP required to achieve steady state remain unchanged. The addition of PCr simply extends the time required to achieve those lower steady state water levels. In Figures 6B and 6C, the hydraulic model depicts the delayed “kinetics of O₂ uptake” observed in the presence of CK and PCr (15, 44). Notice that, at all times, the water levels of the PCr and ATP tanks remain nearly equal; near equilibrium between the PCr and ATP pools is ensured by the high CK V_max (large diameter pipe). As clearly described by Ron Meyer, H. Lee Sweeney, and Martin Kushmerick, the “additional water” of the PCr tank simply offers metabolic capacitance to the system and therefore extends the time required to achieve steady state (19, 27, 30, 43, 45).

Figure 6: Capacitance of the Creatine Pool.

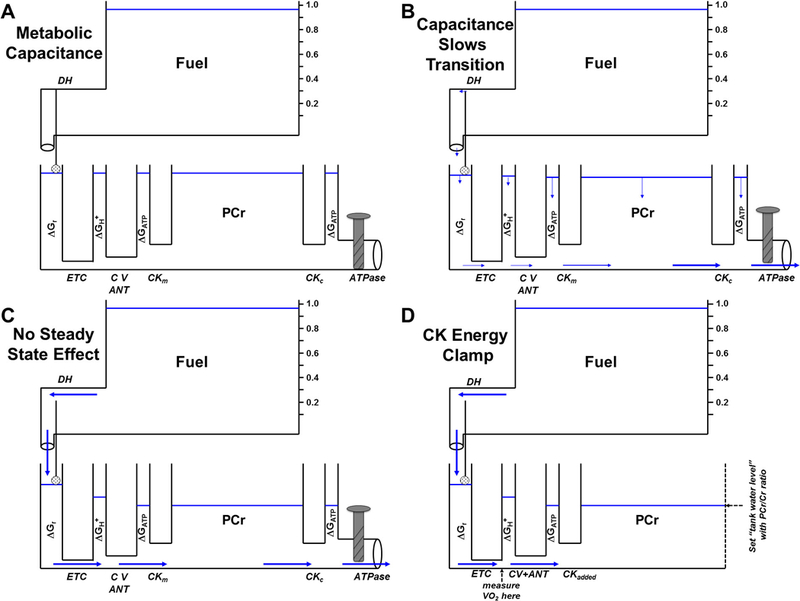
A) Addition of a high capacitance water tank with adjacent large diameter pipes to the hydraulic model representing the high concentrations of phosphocreatine (PCr) and creatine kinase (CK) and equilibrium with ΔG_ATP in skeletal muscle. B) Upon opening the ATPase valve, the transition to steady state is slowed due to the large amount of water in the PCr tank. C) The large PCr capacitance does not affect steady state height of the other water tanks. D) The Creatine Kinase Energy Clamp. In isolated mitochondria with no added ATPase, ΔG_ATP can be set and maintained at steady state by adding saturating CK, 5 mM ATP, and known ratios of PCr and creatine (Cr). In the presence of a constant fuel source, the resulting water flow (metabolic flux) is thus completely controlled by the diameters of the pipes (effective mitochondrial enzyme activities).

The “Creatine Kinase Energy Clamp”

With the generous guidance of Richard Connett, we adapted these ideas to develop a methodological tool with which to study mitochondrial metabolism at constant, experimentally-established ATP free energy levels, the “Creatine Kinase Energy Clamp” (Figure 6D). This procedure takes advantage of the immense capacitance that mM levels of PCr+Cr in a buffering medium impose upon microgram quantities of respiring mitochondria. In the CK clamp, 5 mM ATP, 5–30 mM TCr (total creatine = PCr+Cr), and saturating activity of CK are added to ensure complete equilibrium is maintained between ATP/ADP and PCr/Cr. Figure 6D shows that CK simply acts as the ATPase in the procedure, and the essentially infinite capacitance of the total creatine pool ensures that a constant and experimentally set ΔG_ATP “backpressure” opposes mitochondrial flux (measured as O₂ consumption rate). As developed in Messer et al. (42), this clamp has complete concentration control of the ATP turnover loop, leaving mitochondria, therefore, with complete flux control (5). This procedure was utilized in the experiments depicted in Table 1 and Figures 3D and 5 and has also been used to investigate fuel selection, insulin resistance, oxygen uptake kinetics, and Ca²⁺ activation of skeletal muscle mitochondria from rats, pigs, sparrows, and/or humans (15, 16, 36–38, 42).

Conclusions

Our aim in developing the hydraulic analog model was to provide a simple analogy with which to view the complex thermodynamics and kinetics that underlie the control of mitochondrial oxidative phosphorylation. An added benefit of using a hydraulic analog system is the laws governing water flow are structurally similar to the non-equilibrium thermodynamic relationships that can describe the major steps of oxidative phosphorylation. As a result, the model can closely simulate the thermodynamic forces and metabolic flows that are routinely observed in different muscle cell types in response to a variety of environmental perturbations. The hydraulic analog model is a simple and effective teaching tool, and might also provide a framework to plan and interpret studies of mitochondrial bioenergetics.