A Comparison of Mixture Modeling Approaches in Latent Class Models With External Variables Under Small Samples

Abstract

The purpose of the present study is to compare performances of mixture modeling approaches (i.e., one-step approach, three-step maximum-likelihood approach, three-step BCH approach, and LTB approach) based on diverse sample size conditions. To carry out this research, two simulation studies were conducted with two different models, a latent class model with three predictor variables and a latent class model with one distal outcome variable. For the simulation, data were generated under the conditions of different sample sizes (100, 200, 300, 500, 1,000), entropy (0.6, 0.7, 0.8, 0.9), and the variance of a distal outcome (homoscedasticity, heteroscedasticity). For evaluation criteria, parameter estimates bias, standard error bias, mean squared error, and coverage were used. Results demonstrate that the three-step approaches produced more stable and better estimations than the other approaches even with a small sample size of 100. This research differs from previous studies in the sense that various models were used to compare the approaches and smaller sample size conditions were used. Furthermore, the results supporting the superiority of the three-step approaches even in poorly manipulated conditions indicate the advantage of these approaches.

Introduction

Recently, researchers in the behavioral sciences have been concerned with grouping. To identify unobserved heterogeneity in the population, mixture models are very useful and popular statistical tools. Mixture models can classify individuals into subgroups using similar responses according to some variables or similar change patterns (B. Muthén, 2004). Therefore, when individuals in the population have unobserved heterogeneity, the population can be divided into meaningful subgroups, also called “latent classes,” which cannot be observed through the data itself but through statistical analysis.

The latent class model has been used in diverse research fields such as education (Bowers & Sprott, 2012; Gage, 2013), psychology (Galatzer-Levy, Nickerson, Lits, & Marmar, 2013), adolescence (Aldridge & Roesch, 2008), criminology (Feingold, Tiberio, & Capaldi, 2014; Lovegrove & Cornell, 2014), medical science (Steffen, Glanz, & Wilkens, 2007), and marketing (Sell, Mezei, & Walden, 2014). These studies applied mixture models by including latent classes and external variables to figure out not only the identification of the latent class but also the cause and effect of its classification. Thus, identifying latent classes and estimating the relationship between latent classes and external variables are two major parts of the mixture model.

When analyzing a mixture model with external variables, two methods are typically used, the “one-step approach” and the “three-step approach.” The one-step approach is a method that analyzes all variables simultaneously, and the three-step approach is a method that analyzes data in a step-by-step approach by identifying latent classes, assigning individuals to groups, and estimating the relationship between latent classes and external variables.

The one-step approach had been used for a long time until Vermunt (2010) pointed out its disadvantages. This approach is not considered effective for applied researchers since the latent classes have to be identified again whenever the combinations of external variables are changed. Moreover, indicators and external variables affect the latent class identification sometimes by giving different results (Bakk, Tekle, & Vermunt, 2013; Vermunt, 2010).

On the other hand, the three-step approach was developed to address the shortcomings of the one-step approach (Bolck, Croon, & Hagenaars, 2004; Vermunt, 2010). In the three-step approach, classification of individuals and estimation of relationships are not analyzed simultaneously but in consecutive order. Therefore, regardless of the different combination of external variables, the classification of individuals can be maintained. Nevertheless, the three-step approach was found to underestimate the relationship between latent classes and external variables (Bolck et al., 2004). To overcome this underestimation, bias-correction methods of the three-step approach have been suggested (Bakk et al., 2013; Gudicha & Vermunt, 2013; Vermunt, 2010). There are two bias-correction methods of the three-step approach, which are the maximum-likelihood (ML) approach (i.e., “the three-step ML”) and Bolck et al.’s (2004) modified approach (known as the “three-step BCH”) by Vermunt (2010).

In addition to the one-step and three-step approaches, Lanza, Tan, and Bray (2013) recently developed a new approach, called the “LTB approach.” The LTB approach can analyze a mixture model with only the distal outcome variables as an external variable while one-step and three-step approaches can analyze a mixture model with both predictor variables and distal outcome variables. The advantage of the LTB approach lies in estimating the distribution of the distal outcome variable empirically. Since it is not necessary to follow the specific distribution, the LTB approach is a flexible model-based approach.

Since bias-correction methods of the three-step approach and the LTB approach were developed, simulation studies (e.g., Asparouhov & Muthén, 2014; Bakk et al., 2013; Bolck et al., 2004; Gudicha & Vermunt, 2013; Lanza et al., 2013; Vermunt, 2010) were conducted to compare the performance of existing methods. In these simulation studies, researchers focused on the estimation of the association between latent classes and external variables and found that the three-step approaches were similar to or more biased than the one-step approach (Asparouhov & Muthén, 2014; Bakk et al., 2013; Gudicha & Vermunt, 2013; Vermunt, 2010). In addition, the LTB approach was found to be less biased than an uncorrected three-step approach (Lanza et al., 2013). More recent simulation studies compared the approaches in latent class modeling with distal outcomes under various conditions (e.g., heteroscedasticity of variances of distal outcomes, bimodal distal outcome distribution) and recommended the three-step ML or the three-step BCH approaches (Asparouhov & Muthén, 2015; Bakk & Vermunt, 2016).

However, it is necessary to expand on the previous simulation results because those studies were conducted under limited conditions. In fact, simulation studies (e.g., Asparouhov & Muthén, 2014, 2015; Bakk et al., 2013; Bakk, Oberski, & Vermunt, 2016; Bakk & Vermunt, 2016; Bolck et al., 2004; Gudicha & Vermunt, 2013; Lanza et al., 2013; Vermunt, 2010) were conducted in mixture models with a sample size of 500 or more. In reality, empirical studies with mixture models (e.g., Aldridge & Roesch, 2008; Castle, Sham, Wessely, & Murray, 1994; Feingold et al., 2014; Galatzer-Levy et al., 2013; Rosen et al., 2009) often include multiple external variables with sample sizes smaller than 500. Therefore, simulation studies need to be based on more realistic sample size conditions reflecting empirical studies.

Because of the gap in the current research, it is necessary to incorporate more realistic conditions for comparing the approaches in a simulation study. Hence, this study was performed under small sample size conditions by using a simulation study to compare the mixture modeling approaches.

As such, this study aims to compare the one-step approach, the three-step ML approach, the three-step BCH approach, and the LTB approach in their estimation of the relationship between latent classes and external variables. This study is equivalent to previous studies (e.g., Asparouhov & Muthén, 2014, 2015; Bakk et al., 2013; Bakk et al., 2016; Bakk & Vermunt, 2016; Bolck et al., 2004; Gudicha & Vermunt, 2013; Lanza et al., 2013; Vermunt, 2010) in conducting simulations based on estimating the association between latent classes and external variables, but the difference is that this study includes smaller sample size conditions than those in previous studies. Therefore, in this research, two simulation models with more realistic conditions of sample size and quality of classification were used. The two models are (1) latent class models with three predictor variables and (2) latent class models with a distal outcome variable. The sample size conditions were manipulated from 100 to 1,000, and for the quality of classification, which is referred to as entropy, values from 0.6 to 0.9 were used. This range of values reflects more realistic guidelines for a mixture model. Specific reasons for the conditions are presented in the “Manipulated Conditions” section.

The research questions of this study are the following:

• Research Question 1: When a latent class model is analyzed with three predictor variables under various sample sizes and entropy conditions, how different are the approaches in the accuracy and efficiency of parameter estimation?

• Research Question 2: When a latent class model is analyzed with a distal outcome variable under various conditions including sample size, entropy, and homoscedasticity/heteroscedasticity of variances, how different are the approaches in the accuracy and efficiency of parameter estimation?

In summary, two studies were conducted using the two simulation models: (1) Study 1, based on a simulation model, which is a latent class model with three predictor variables, comparing the estimation of the one-step approach to that of the three-step ML approach and (2) Study 2, based on a simulation model, which is a latent class model with a distal outcome variable, comparing the one-step approach, the three-step ML approach, the three-step BCH approach, and the LTB approach in estimating the relationship between latent classes and distal outcome variables.

Approaches of the Latent Class Model With External Variables

The One-Step Approach

The one-step approach is a method that simultaneously analyzes all variables in the final model as in general structural equation modeling (Vermunt, 2010). As the one-step approach can analyze a measurement model and structural model at the same time, this approach can classify latent classes and estimate the relationship with external variables simultaneously.

The advantage of the one-step approach is that all variables in the model can be analyzed at the same time. Several simulation studies (e.g., Bolck et al., 2004; Gudicha & Vermunt, 2013; Vermunt, 2010) found that the one-step approach is less biased than the three-step approach in estimating the association between latent classes and external variables. Nevertheless, there are some disadvantages as the one-step approach is not suitable for applied researchers as previously described, and latent class classifications are affected by external variables (Vermunt, 2010). Thus, if the combination of explanatory variables is varied or different distal outcome variables are included, classifications will sometimes be altered when a different model is analyzed. Then, the risk of misspecification or distortion of classifications is high (Bakk et al., 2013).

The Three-Step Approaches: ML and BCH

Unlike the one-step approach, the three-step approach divides latent class classification and association analysis of latent classes and external variables into three steps: The first step identifies latent classes using observed indicators, the second step assigns individuals into latent classes and corrects classification error probability, and last, the third step analyzes the relationship between latent classes and external variables (Vermunt, 2010). In this section, the recently developed bias-correction method and the consistency of the three-step approach following Vermunt’s terms are described (Bakk et al., 2013; Gudicha & Vermunt, 2013; Vermunt, 2010).

Specifically, in the first step, the probability of an individual belonging to a latent class is estimated without external variables. In the second step, each individual is assigned to a particular latent class classified in the first step and the classification error probability is calculated. Consideration of the classification error is critical in the three-step approach because class membership is not observed but estimated (Bakk et al., 2013; Goodman, 1974). There are two representative rules of assigning individuals to posterior classes by using the probability: modal assignment referred to as hard partitioning and proportional assignment referred to as soft partitioning (Bakk et al., 2013; Vermunt, 2010). Modal assignment entails each individual assigned to a latent class with the largest posterior membership probability. Meanwhile, proportional assignment involves weight equal to posterior membership probability given to each individual. Compared with proportional assignment, modal assignment is the most common rule (Gudicha & Vermunt, 2013), and the misspecification is smaller (Bakk et al., 2013). In latent class analysis software programs including Mplus and Latent GOLD, modal assignment is the default. For these reasons, the modal assignment rule was used in this study. Since classification cannot be perfect because of the unknown true latent class, the probability of classification error is measured in Step 2. In the third step, the relationship between latent classes and external variables are estimated using the predicted latent class and probability of classification error from the second step.

The advantage of the three-step approach is that class solution is not changed even when a combination of explanatory variables or distal outcome variables differ. Therefore, this approach is suitable for applied researchers (Vermunt, 2010). On the other hand, the disadvantage of the three-step approach is that the relationship between latent classes and external variables are biased downward (Bolck et al., 2004; Vermunt, 2010). This underestimation occurs within the classification error, that is the larger the classification error, the larger the downward bias in the estimates (Vermunt, 2010). To correct the bias, two bias-correction methods have been developed, which are the three-step ML and the three-step BCH. The three-step ML approach from Vermunt (2010) estimates the latent class model with external variables using ML estimation. The three-step BCH approach by Bolck et al. (2004) and further developed by Vermunt (2010) estimates the latent class model using weighted analysis. While the three-step ML approach deals with equal and unequal variances of distal outcomes across latent variables (e.g., DE3STEP and DU3STEP in Mplus, respectively), the three-step BCH assumes homoscedasticity of variances. For more detailed information, readers should refer to Vermunt (2010), Gudicha and Vermunt (2013), Bakk et al. (2013), and Bakk and Vermunt (2016). According to the previous simulation studies, while the three-step ML approach is recommended when the external variables are predictors or categorical outcomes (Bakk et al., 2013; Vermunt, 2010), the three-step BCH approach is preferred when the external variables are continuous or count outcome variables (Bakk & Vermunt, 2016). These two methods are now incorporated into Mplus (Muthén & Muthén, 1998-2017) and Latent GOLD (Vermunt & Magidson, 2016).

The LTB Approach

The LTB approach, proposed by Lanza et al. (2013), can be used only in a latent class model with distal outcome variables as external variables. Therefore, when using this approach, estimating the relationship between a latent class variable and distal outcome variable is focused. Although the latent class variable is unobservable, researchers can estimate the conditional distribution of the distal outcome variable for each latent class. To estimate the conditional distribution of the distal outcome variable given the latent class, Lanza et al. (2013) proposed a conditional independence assumption. This is similar to the local independence assumption of the latent class model (Collins & Lanza, 2010). Since the LTB approach estimates the distribution of the outcome variable empirically, it is not necessary to follow a specific form of distribution such as normal or Gaussian distribution. Therefore, Lanza’s approach can be called a flexible, semiparametric model-based approach.

In addition, Lanza et al. (2013) found that the LTB approach was less biased than the three-step approach. Their study, however, used an uncorrected three-step approach. Later, Asparouhov and Muthén’s (2014) simulation study illustrated that the LTB approach appeared to be slightly worse than the bias-correction method of the three-step approach in terms of coverage. Since the performance of the LTB approach was limited, Bakk et al. (2016) suggest improved LTB approaches, but these new approaches have to date not been developed.

Previous Simulation Studies

To compare performances of the approaches in estimating the association between latent classes and external variables, several recent simulation studies have been conducted. Previous simulation studies can be categorized according to their simulation models: latent class models including external variables as predictor variables (Bolck et al., 2004; Gudicha & Vermunt, 2013; Vermunt, 2010), as distal outcome variables (Asparouhov & Muthén, 2015; Bakk et al., 2013; Bakk et al., 2016; Bakk & Vermunt, 2016; Lanza et al., 2013), and as both predictor and outcome variables (Asparouhov & Muthén, 2014). A brief summary of previous simulation studies is presented in Table 1.

Table 1.

Summary of Previous Simulation Studies.

Research	Model	Approach	Simulation design		Sample size condition
Bolck, Croon, and Hagenaars (2004)	LCM with predictor	One-step	2 LC		1,000
		Three-step	10 DI
			1 PV
Vermunt (2010)	LCM with predictor	One-step	3 LC		500
		Three-step ML	6 DI		1,000
		Three-step BCH	3 PV		10,000
Gudicha and Vermunt (2013)	LCM with predictor	One-step	3 LC		500
		Three-step ML	6 CI		1,000
		Three-step BCH	3 PV		10,000
Bakk, Tekle, and Vermunt (2013)	LCM with outcome	One-step	3 LC		500
		Three-step ML	6 DI		1,000
		Three-step BCH	1 OV		10,000
Lanza, Tan, and Bray (2013)	LCM with outcome	Three-step LTB	5 LC		500
			8 DI		1,000
			1 OV
Asparouhov and Muthén (2014)	LCM with predictor	One-step	2 LC		500
		Three-step ML	5 DI		2,000
			1 PV
	LCM with outcome	One-step	2 LC		500
		Three-step ML	5 DI		2,000
		LTB	1 OV
Asparouhov and Muthén (2015)	LCM with outcome	One-step	2LC		500
		Three-step ML	5DI		2,000
		Three-step BCH	1OV
		LTB
Bakk and Vermunt (2016)	LCM with outcome	Three-step ML	2LC	4LC	500
		Three-step BCH	6DI	8DI	1,000
		LTB	1OV	1OV	2,000
Bakk, Oberski, and Vermunt (2016)	LCM with outcome	Three-step BCH	4LC		500
		LTB	8DI		1,000
		Improved LTB	1OV

Note. LCM = latent class model; LC = latent class; DI = dichotomous indicator; CI = continuous indicator; PV = predictor variable; OV = outcome variable; ML = maximum likelihood; LTB = Lanza, Tan, and Bray (2013) approach; BCH = Bolck, Croon, and Hagenaars (2004) approach.

Bolck et al. (2004) compared a one-step approach and a three-step approach for estimating the effect of a predictor variable to latent classes. In their study, the one-step approach was less biased in parameter estimation than the three-step approach. They also demonstrated that modal assignment had more accurate estimation than random assignment in correcting the downward bias of the three-step approach. Vermunt (2010) extended the study of Bolck et al. (2004) and suggested two bias-correction methods of the three-step approach based on an ML and BCH in conjunction with the three-step approach. He compared the one-step approach and the two three-step approaches with modal assignment and proportional assignment of the three-step approach. As a result, Vermunt (2010) reported that the two three-step approaches performed very well except for conditions with poor quality of classification and showed better performance than the one-step approach.

To build on the performance of the two three-step approaches, Gudicha and Vermunt (2013) used continuous indicators for latent class classification. In their results, the three-step BCH approach was more accurate but less efficient than the three-step ML and the one-step approach, but the three-step ML provided similar estimates to the one-step approach, except for the combination of a small sample size (n = 500) and poor quality of classification (.43). Bakk et al. (2013) generalized Vermunt’s (2010) correction methods of the three-step approach in a different direction than Gudicha and Vermunt (2013). In their study, outcome variables consisted of several types of variables such as nominal, ordinal, and continuous variables. They found that the three-step ML approach was the most efficient and recommended the one-step approach and the three-step ML approach in latent class models with nominal outcomes under low separation between classes because the three-step BCH approach failed with the occurrence of negative cell frequencies.

Lanza et al. (2013) conducted a simulation study to evaluate performances of a flexible model-based approach of a latent class model with outcome variables. Lanza’s flexible model-based approach produced less biased estimation than the three-step approach except when the outcome variable was a count variable.

Recently, Asparouhov and Muthén (2014) conducted a simulation study to compare the one-step and the three-step ML approaches with both predictor and distal outcome variables in latent class models. Moreover, they also considered the LTB approach for a latent class model with an outcome variable. They found that the performances of the one-step and the three-step ML approaches were similar when the simulation model was a latent class model with a predictor variable. In addition, the three-step ML approach had better coverage than the LTB approach while the LTB approach had slightly lower bias and mean squared error. In their study, there was no sample size effect in the range of 500 to 2,000. They suggested that much smaller or much larger sample sizes should be considered for future simulation studies. Asparouhov and Muthén (2015) then broadened the previous simulation study. They added the three-step BCH approach to estimate a distal outcome model. They found that the three-step ML and BCH approaches showed similarly good performance for continuous distal outcomes when the variances of the distal outcome variable were unequal across latent classes. Therefore, they recommended these two approaches.

To investigate the robustness of approaches in latent class modeling with continuous distal outcomes, Bakk and Vermunt (2016) conducted a simulation study with violations of assumptions such as bimodality and heteroscedasticity of distal outcome variables. Comparing the three-step ML, the three-step BCH, and the LTB approach, the results revealed that the three-step BCH approach is the most robust under all conditions. To overcome the inefficiency of the original LTB approach, Bakk et al. (2016) proposed various improved LTB approaches (e.g., using a linear or quadratic model, bootstrap or jackknife SEs, etc.), and these approaches were more efficient than the original LTB approach and the three-step BCH approach.

Most simulation studies focused on the estimation of the relationships between latent classes and external variables to identify effective latent class classification methods. Therefore, the criteria of evaluating the approaches were targeting the accuracy and efficiency of estimation. Previous simulation studies derived slightly different results and were conducted under manipulated conditions of sample sizes more than 500. However, considering that sample sizes smaller than 500 were used for mixture models in many empirical studies (e.g., Aldridge & Roesch, 2008; Castle et al., 1994; Feingold et al., 2014; Galatzer-Levy et al., 2013; Rosen et al., 2009), it is necessary to conduct simulation studies under realistic conditions with smaller sample sizes.

Simulation Study

Design

The present simulation studies were conducted to compare estimation of the one-step, the three-step ML, the three-step BCH, and the LTB approaches. Data sets were generated from two simulation models (i.e., a latent class model with three predictor variables and a latent class model with a distal outcome variable). Each simulation model was specified to have four latent classes with six dichotomous indicators. External variables were all continuous variables. In Figures 1 and 2, predictor variables and an outcome variable are represented by X1 to X3 and Y, respectively. Latent classes are represented by latent variable C, and indicators are represented by measured variables u1 to u6.

Figure 1.

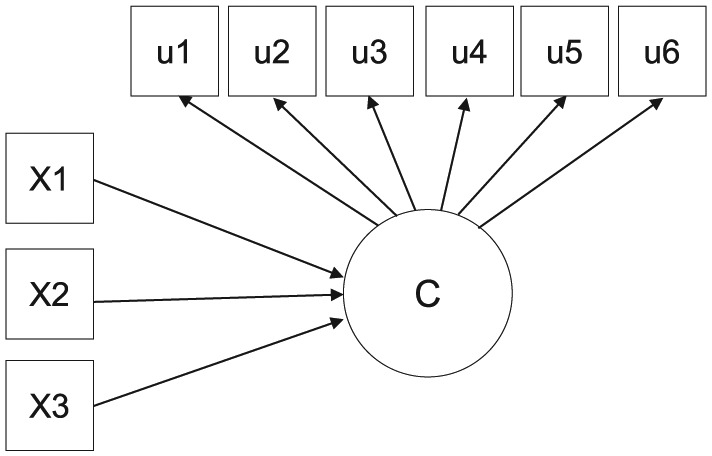
Research model of Study 1.Note. C = Latent class; X = predictor variable; u = indicator.

Figure 2.

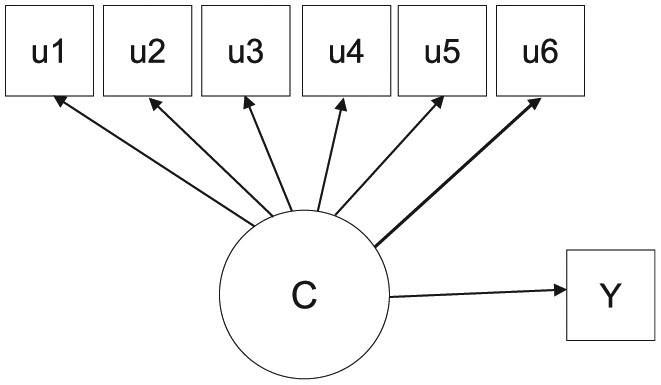
Research model of Study 2.Note. C = Latent class; Y = outcome variable; u = indicator.

Class 1 was specified so that all six indicators have high threshold values, but Class 4 was specified so that all have low threshold values. Class 2 was specified for the first three indicators to have high values and the last three indicators to have low values, but Class 3 was specified for the first three indicators to have low values and the last three indicators to have high values. The proportion of individuals in each latent class was specified to be 25%, respectively.

Manipulated Conditions

There are two major conditions in the current research, the sample size and the quality of classification (i.e., entropy). Both factors are hypothesized to be related to performances of the approaches in the latent class model with external variables (Bakk et al., 2013; Vermunt, 2010). For sample sizes, four levels were set as 100, 200, 300, 500, and 1,000. In previous simulation studies, the sample size conditions were 500 or larger (Asparouhov & Muthén, 2014, 2015; Bakk et al., 2013; Bakk et al., 2016; Bakk & Vermunt, 2016; Bolck et al., 2004; Gudicha & Vermunt, 2013; Lanza et al., 2013; Vermunt, 2010). However, in reality, many empirical studies used sample sizes smaller than 500 for mixture models. These studies include Aldridge and Roesch (2008) with a sample size of 354, Castle et al. (1994) with 447, Feingold et al. (2014) with 206, Galatzer-Levy et al. (2013) with 409, and Rosen et al. (2009) with 153. Therefore, including small sample sizes, 100, 200, 300, 500, and 1,000 was considered important in this study. The reason for focusing on smaller sample size is that a small sample size can be more sensitive to various conditions.

For the quality of classification, four levels were set as 0.6, 0.7, 0.8, and 0.9. According to Clark (2010), 0.8 is high level, 0.6 is medium level, and 0.4 is low level. Nagin (2005) also provided a rule of thumb that probability of correct class membership assignment be more than 0.7. Based on these guidelines, 0.6 was considered a minimum level of entropy in this study.

In addition, equal and unequal variance across latent classes were simulated for a distal outcome. Generally, there is an assumption of homoscedasticity of variance across latent classes, but this assumption often does not hold in reality. Moreover, each approach has a different degree of robustness and violations of this assumption. Therefore, we tried to explore the performance of the approaches by including this assumption in the simulation analysis. In the homoscedasticity condition of variances, the variances of each class were set to 1, and in the heteroscedasticity, the variances of each class were 1, 4, 9, and 25.

While the one-step approach and the three-step ML approach were used for a latent class model with predictor variables, the one-step, the three-step ML, the three-step BCH, and LTB approaches were used for a latent class model with a distal outcome. The reason for this arrangement is because the three-step BCH approach and the LTB approach are mainly used when the external variables are distal outcome variables.

For each analysis, 500 replications were used; 40 conditions (5 sample size × 4 entropy × 2 approaches) for Study 1 and 160 conditions (5 sample size × 4 entropy × 4 approaches × 2 variance) for Study 2 were manipulated. Thus, 100,000 data sets (200 conditions × 500 replications) were generated.

Data Generation and Analysis

Data generation and analysis was conducted using Mplus 7.4 (Muthén & Muthén, 1998-2017) estimating with robust standard error for mixture models. While the one-step and the three-step ML approaches were ML-based methods, the three-step BCH approach was a weighted method, and the LTB approach was a flexible model-based method. Our study did not use the improved LTB approach (Bakk et al., 2016) but the original LTB approach (Lanza et al., 2013) because new LTB approaches cannot be analyzed using Mplus yet. In the case of the two 3-step approaches, a modal assignment method was applied in Step 2. The modal assignment was accurate and efficient in comparison with random or proportional assignment methods to estimate parameters (Asparouhov & Muthén, 2014; Bolck et al., 2004). For the three-step ML approach, we used DE3STEP under the equal variances conditions and DU3STEP under the unequal variances conditions in Mplus.

Criteria of Evaluation

To evaluate the estimation, there are three criteria: bias, mean squared error, and coverage. The first criterion is bias, which provides information about the difference between the estimated value and true value of the parameter. That is, this criterion indicates the accuracy of the estimation of coefficients. In this simulation study, there are two types of bias that are about parameter and standard error. Biases of parameter and standard error are derived by Equations (1) and (2), respectively (Bandalos, 2006; Muthén & Muthén, 2002). In these equations, ${\hat{\mathrm{\theta }}}_{\mathrm{r}}$ means rth parameter estimators and r means the number of replications. In this study, R equals 500. Parameter bias means the average of the differences between the estimated value and true value across 500 replications. Standard error bias indicates the extent to which a method overstates or understates the estimate of its own sampling variability.

$$\mathrm{Bias}\left(\hat{\mathrm{\theta }}\right)=\sum _{r=1}^R\left(\frac{{\hat{\mathrm{\theta }}}_r-\mathrm{\theta }}{\mathrm{\theta }}\right)/R$$

$$\mathrm{Bias}\left(\widehat{\mathrm{SE}}\left(\hat{\mathrm{\theta }}\right)\right)=\sum _{r=1}^R\left(\frac{\widehat{\mathrm{SE}}{\left(\hat{\mathrm{\theta }}\right)}_r-\mathrm{SE}\left(\hat{\mathrm{\theta }}\right)}{\mathrm{SE}\left(\hat{\mathrm{\theta }}\right)}\right)/R$$

These criteria are considered satisfactory when the bias of parameter does not exceed the absolute value of 0.10 and the bias of standard error for the parameter does not exceed the absolute value of 0.05 (Bandalos, 2006; Muthén & Muthén, 2002).

The second criterion is mean squared error, which includes both the bias of parameter estimates and variance simultaneously. It provides information about how accurately and consistently it estimates parameters. Mean squared error is derived by Equation (3) (Muthén & Muthén, 2002). An estimate that has good mean squared error properties has small combined bias and variance. Therefore, the higher mean squared error value means the less the accuracy and efficiency of the estimated values.

$$\mathrm{MS}{\mathrm{E}}_{\hat{\mathrm{\theta }}}={\left(\mathrm{Bias}\left(\hat{\mathrm{\theta }}\right)\right)}^2+\mathrm{Var}\left(\hat{\mathrm{\theta }}\right)$$

The third criterion is coverage that gives information about the proportion of replications where a 95% confidence interval includes the true parameter value. The standard of coverage is between 0.91 and 0.98 (Bandalos, 2006; Muthén & Muthén, 2002).

Three-Way Analysis of Variance

After the simulation studies, the criteria of evaluation were treated as the dependent variables in a three-way analysis of variance (ANOVA) using sample size conditions, entropy conditions, and analysis approaches as the independent variables. Coverage was excluded because the criterion of coverage involves a range of 0.91 to 0.98, and this value is not increasing or decreasing according to the manipulated conditions. Therefore, three-way ANOVAs according to the approaches were conducted for parameter estimates bias, standard error bias, and mean squared error. For effect size, eta-square $({\mathrm{\eta }}^2)$ was measured. The eta-square measure is defined as the ratio of variance accounted for by the sum of squares for the effect and the total sum of squares.

Results

Study 1

Table 2 provides the simulation results of bias, mean squared error, and coverage in Study 1 comparing the one-step approach and three-step ML approach. Biases of parameter estimates and standard error were presented in absolute values. According to the results, the parameter estimates bias and standard error bias were very high under the conditions of small sample size and low entropy. Between the two approaches, the one-step approach was less accurate under the poor conditions than the three-step ML approach. Under the smallest sample size condition, the one-step approach was highly biased when the entropy was 0.6 and 0.7 while the three-step ML approach was highly biased only when the entropy was 0.6.

Table 2.

Biases, Mean Squared Error, and Coverage in Study 1 (One-Step Approach and Three-Step ML Approach).

Criterion	Method	Entropy	Sample size
			100	200	300	500	1,000
Parameter estimates bias	One-step	0.6	41.634	0.305	0.080	0.041	0.018
		0.7	1.639	0.114	0.052	0.021	0.009
		0.8	0.124	0.074	0.031	0.008	0.011
		0.9	0.058	0.039	0.011	0.011	0.014
	Three-step ML	0.6	0.791	0.242	0.244	0.150	0.085
		0.7	0.189	0.134	0.081	0.042	0.012
		0.8	0.022	0.062	0.031	0.006	0.008
		0.9	0.053	0.048	0.033	0.009	0.009
Standard error bias	One-step	0.6	0.990	0.454	0.126	0.054	0.036
		0.7	0.431	0.019	0.050	0.030	0.012
		0.8	0.039	0.057	0.019	0.030	0.018
		0.9	0.030	0.014	0.042	0.031	0.016
	Three-step ML	0.6	0.313	0.057	0.049	0.052	0.035
		0.7	0.044	0.029	0.028	0.050	0.030
		0.8	0.053	0.030	0.046	0.035	0.031
		0.9	0.060	0.042	0.048	0.036	0.021
Mean squared error	One-step	0.6	13050.584	1.373	0.099	0.042	0.016
		0.7	723.296	0.077	0.044	0.023	0.011
		0.8	0.103	0.043	0.028	0.016	0.007
		0.9	0.081	0.035	0.023	0.014	0.006
	Three-step ML	0.6	5.810	0.125	0.085	0.053	0.026
		0.7	0.184	0.085	0.058	0.036	0.017
		0.8	0.146	0.062	0.043	0.025	0.012
		0.9	0.123	0.054	0.036	0.021	0.010
Coverage	One-step	0.6	0.887	0.930	0.941	0.953	0.957
		0.7	0.915	0.956	0.947	0.954	0.944
		0.8	0.945	0.956	0.946	0.949	0.941
		0.9	0.940	0.953	0.947	0.947	0.939
	Three-step ML	0.6	0.931	0.925	0.920	0.937	0.947
		0.7	0.943	0.941	0.937	0.928	0.941
		0.8	0.947	0.947	0.938	0.943	0.942
		0.9	0.941	0.945	0.942	0.945	0.941

Note. ML = maximum likelihood.

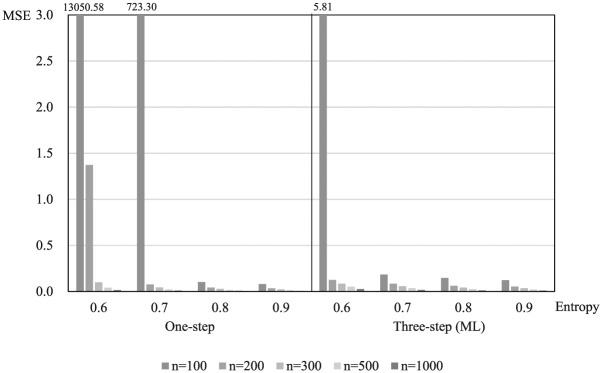
The mean squared error is useful to determine the performance of the approaches at one time because the mean squared error is defined as a combination of parameter estimates bias and standard error bias. The mean squared error was low in combination with large sample size and high entropy but high in combination with small sample size and low entropy. In this study, the mean squared error of the one-step approach was extremely high with a small sample size (i.e., 100) and low entropies (i.e., 0.6, 0.7). Meanwhile, the three-step ML approach was relatively stable even in bad conditions (see Figure 3). That is, in terms of biases and mean squared error, the three-step ML approach is better than the one-step approach.

Figure 3.

Mean squared error in Study 1.

Finally, in terms of coverage, the three-step ML approach demonstrated a better level of performance than the one-step approach under poor conditions. The two methods showed a range of 0.91 to 0.98 except for the condition with the smallest sample size and lowest entropy in the one-step approach.

Table 3 contains the results of a three-way ANOVA for the criterion of evaluation. According to the results for parameter estimates bias, the main effect and interaction effects including sample size (i.e., sample size, sample size × entropy, sample size × approach, sample size × entropy × approach) were statistically significant. The largest effect was the interaction between sample size and entropy (${\mathrm{\eta }}^2$ = .17) followed by the three-way interaction (${\mathrm{\eta }}^2$ = .16). For standard error bias, all main effects and interactions were statistically significant. The largest effect was the interaction of sample size and entropy (${\mathrm{\eta }}^2$ = .21), followed by the main effect of sample size (${\mathrm{\eta }}^2$ = .16), and last followed by the main effect of entropy (${\mathrm{\eta }}^2$ = .14). For mean squared error, all main effects except for the main effect of approach and all interactions were statistically significant. The largest effect was the interaction of sample size and entropy (${\mathrm{\eta }}^2$ = .20) followed by the three-way interaction (${\mathrm{\eta }}^2$ = .19). In parameter estimates bias, standard error bias, and mean squared error, the patterns were the same. The largest effect was the interaction of sample size and entropy, and the smallest effect was the main effect of approach.

Table 3.

ANOVA Results for Criteria According to Approaches in Study 1.

Criterion	Source	Sum of squares	df	Mean square	F	${\mathrm{\eta }}^2$
Parameter bias	Sample size (n)	581.02	4	145.26	2.72*	.06
	Entropy (e)	409.20	3	136.40	2.56	.04
	Approach (a)	132.59	1	132.59	2.48	.01
	n×e	1553.07	12	129.42	2.42*	.17
	n×a	541.61	4	135.40	2.54*	.06
	e×a	361.65	3	120.55	2.26	.04
	n×e×a	1469.58	12	122.47	2.29*	.16
Standard error bias	Sample size (n)	0.78	4	0.19	12.14***	.16
	Entropy (e)	0.67	3	0.22	14.05***	.14
	Approach (a)	0.15	1	0.15	9.33**	.03
	n×e	1.04	12	0.09	5.42***	.21
	n×a	0.30	4	0.07	4.70**	.06
	e×a	0.29	3	0.10	6.09***	.06
	n×e×a	0.43	12	0.04	2.22*	.09
Mean squared error	Sample size (n)	54251290.15	4	13562823.00	3.29*	.08
	Entropy (e)	35728661.73	3	11909554.00	2.89*	.05
	Approach (a)	14043182.34	1	14043182.00	3.41	.02
	n×e	128935600.90	12	10744633.00	2.61**	.20
	n×a	54155631.52	4	13538908.00	3.28*	.08
	e×a	35664207.33	3	11888069.00	2.88*	.05
	n×e×a	128709977.40	12	10725831.00	2.60**	.19

Note. ANOVA = analysis of variance. df = degrees of freedom.

^*p < .05. **p < .01. ***p < .001.

Study 2

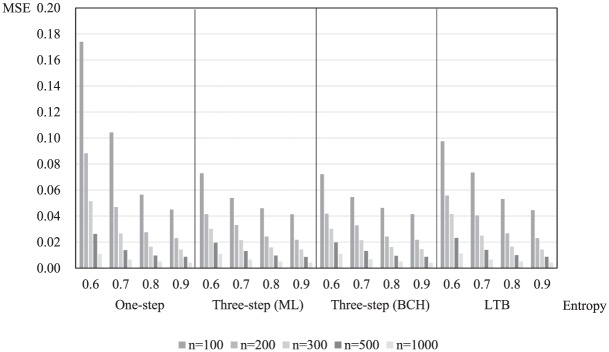
Tables 4 and 5 provide the simulation results of biases, mean squared error, and coverage in Study 2 comparing the one-step approach, the three-step ML approach, the three-step BCH approach, and the LTB approach under the condition of equal and unequal variances for the distal outcome variable across latent classes. Under the condition of equal variances, the parameter estimates bias of the one-step approach was generally smaller than those of the other approaches. However, standard error bias of the three-step ML and BCH approaches was generally smaller than those of the others. The mean squared error was low under conditions of large sample size and high entropy but high under conditions of small sample size and low entropy. The one-step approach showed the largest mean squared error, followed by the LTB approach, and then followed by the three-step ML and BCH approaches. That is, in terms of mean squared error, the three-step ML and BCH approaches were similar and better than the other approaches (see Figure 4). Last, in terms of coverage, both the three-step ML and BCH approaches seemed acceptable. On the other hand, when the entropy was 0.6 or 0.7, coverage of the LTB approach and the one-step approach seemed totally and partially unacceptable, respectively.

Table 4.

Biases, Mean Squared Error, and Coverage Under Equal Variances in Study 2 (One-Step Approach, Three-Step ML Approach, Three-Step BCH Approach, and LTB Approach).

Criterion	Method	Entropy	Sample size
			100	200	300	500	1,000
Parameter estimates bias	One-step	0.6	0.115	0.062	0.015	0.014	0.007
		0.7	0.075	0.039	0.018	0.011	0.007
		0.8	0.053	0.029	0.017	0.013	0.005
		0.9	0.048	0.027	0.017	0.012	0.005
	Three-step ML	0.6	0.216	0.192	0.150	0.108	0.041
		0.7	0.172	0.125	0.078	0.039	0.012
		0.8	0.101	0.052	0.031	0.015	0.005
		0.9	0.063	0.033	0.019	0.011	0.005
	Three-step BCH	0.6	0.212	0.194	0.147	0.101	0.043
		0.7	0.173	0.127	0.079	0.039	0.012
		0.8	0.100	0.052	0.030	0.014	0.005
		0.9	0.062	0.033	0.019	0.011	0.006
	LTB	0.6	0.169	0.093	0.061	0.029	0.007
		0.7	0.109	0.094	0.017	0.012	0.007
		0.8	0.062	0.033	0.018	0.014	0.005
		0.9	0.051	0.028	0.017	0.011	0.005
Standard error bias	One-step	0.6	0.289	0.133	0.076	0.178	0.064
		0.7	0.160	0.035	0.068	0.080	0.024
		0.8	0.028	0.039	0.044	0.034	0.028
		0.9	0.020	0.023	0.022	0.027	0.025
	Three-step ML	0.6	0.091	0.070	0.070	0.078	0.108
		0.7	0.023	0.054	0.021	0.044	0.029
		0.8	0.021	0.019	0.021	0.040	0.029
		0.9	0.011	0.017	0.018	0.031	0.022
	Three-step BCH	0.6	0.092	0.076	0.071	0.078	0.101
		0.7	0.028	0.054	0.024	0.042	0.026
		0.8	0.026	0.020	0.021	0.040	0.029
		0.9	0.013	0.017	0.018	0.031	0.022
	LTB	0.6	0.329	0.367	0.398	0.385	0.380
		0.7	0.248	0.279	0.259	0.227	0.209
		0.8	0.137	0.134	0.088	0.091	0.092
		0.9	0.062	0.061	0.039	0.048	0.037
Mean squared error	One-step	0.6	0.174	0.088	0.052	0.026	0.011
		0.7	0.104	0.047	0.027	0.014	0.007
		0.8	0.056	0.028	0.017	0.010	0.005
		0.9	0.045	0.023	0.014	0.009	0.004
	Three-step ML	0.6	0.073	0.041	0.030	0.020	0.011
		0.7	0.054	0.033	0.021	0.013	0.007
		0.8	0.046	0.024	0.016	0.010	0.005
		0.9	0.041	0.022	0.014	0.009	0.004
	Three-step BCH	0.6	0.072	0.042	0.030	0.020	0.011
		0.7	0.055	0.033	0.022	0.013	0.007
		0.8	0.046	0.024	0.016	0.010	0.005
		0.9	0.041	0.022	0.015	0.009	0.004
	LTB	0.6	0.098	0.056	0.042	0.023	0.011
		0.7	0.074	0.041	0.025	0.014	0.007
		0.8	0.053	0.027	0.017	0.010	0.005
		0.9	0.045	0.023	0.014	0.009	0.004
Coverage	One-step	0.6	0.837	0.899	0.925	0.946	0.954
		0.7	0.889	0.933	0.947	0.961	0.953
		0.8	0.930	0.950	0.955	0.951	0.950
		0.9	0.938	0.945	0.950	0.952	0.952
	Three-step ML	0.6	0.914	0.914	0.922	0.913	0.916
		0.7	0.935	0.933	0.941	0.944	0.940
		0.8	0.934	0.945	0.950	0.952	0.944
		0.9	0.940	0.943	0.945	0.954	0.950
	Three-step BCH	0.6	0.916	0.921	0.924	0.918	0.919
		0.7	0.936	0.933	0.944	0.946	0.941
		0.8	0.936	0.945	0.948	0.951	0.946
		0.9	0.939	0.942	0.946	0.953	0.950
	LTB	0.6	0.849	0.805	0.808	0.782	0.784
		0.7	0.869	0.856	0.863	0.880	0.881
		0.8	0.913	0.914	0.927	0.923	0.925
		0.9	0.931	0.932	0.940	0.941	0.945

Note. ML = maximum likelihood; LTB = Lanza, Tan, and Bray (2013) approach; BCH = Bolck, Croon, and Hagenaars (2004) approach.

Table 5.

Biases, Mean Squared Error, and Coverage Under Unequal Variances in Study 2 (One-Step Approach, Three-Step ML Approach, Three-Step BCH Approach, and LTB Approach).

Criterion	Method	Entropy	Sample size
			100	200	300	500	1,000
Parameter estimates bias	One-step	0.6	7.401	7.054	7.137	7.098	8.427
		0.7	3.439	2.366	2.357	1.696	1.573
		0.8	0.594	0.300	0.209	0.156	0.127
		0.9	0.175	0.099	0.055	0.049	0.051
	Three-step ML	0.6	0.146	0.159	0.101	0.042	0.035
		0.7	0.182	0.123	0.035	0.020	0.018
		0.8	0.176	0.075	0.039	0.016	0.020
		0.9	0.145	0.070	0.043	0.027	0.018
	Three-step BCH	0.6	0.166	0.206	0.156	0.089	0.050
		0.7	0.275	0.199	0.149	0.065	0.031
		0.8	0.210	0.091	0.060	0.047	0.028
		0.9	0.147	0.087	0.043	0.033	0.014
	LTB	0.6	0.166	0.268	0.410	1.538	2.957
		0.7	0.213	0.260	0.446	0.737	0.951
		0.8	0.197	0.106	0.137	0.140	0.122
		0.9	0.125	0.089	0.051	0.046	0.049
Standard error bias	One-step	0.6	0.551	0.535	0.545	0.530	0.552
		0.7	0.444	0.437	0.465	0.484	0.433
		0.8	0.158	0.140	0.083	0.059	0.016
		0.9	0.075	0.030	0.024	0.027	0.027
	Three-step ML	0.6	0.072	0.044	0.032	0.034	0.028
		0.7	0.016	0.024	0.029	0.043	0.012
		0.8	0.018	0.026	0.033	0.037	0.017
		0.9	0.017	0.016	0.020	0.025	0.023
	Three-step BCH	0.6	0.086	0.060	0.050	0.028	0.046
		0.7	0.031	0.042	0.026	0.038	0.019
		0.8	0.032	0.026	0.007	0.026	0.018
		0.9	0.019	0.021	0.014	0.026	0.022
	LTB	0.6	0.393	0.513	0.568	0.643	0.729
		0.7	0.482	0.598	0.674	0.743	0.816
		0.8	0.528	0.578	0.636	0.664	0.632
		0.9	0.629	0.644	0.701	0.729	0.712
Mean squared error	One-step	0.6	10.069	10.825	10.593	9.919	9.839
		0.7	6.422	5.534	4.523	3.409	1.875
		0.8	1.556	0.837	0.374	0.160	0.058
		0.9	0.654	0.272	0.158	0.096	0.044
	Three-step ML	0.6	0.642	0.331	0.234	0.136	0.066
		0.7	0.491	0.281	0.178	0.108	0.050
		0.8	0.424	0.219	0.149	0.091	0.044
		0.9	0.389	0.204	0.139	0.085	0.041
	Three-step BCH	0.6	0.649	0.365	0.262	0.162	0.092
		0.7	0.502	0.306	0.195	0.126	0.061
		0.8	0.443	0.227	0.157	0.098	0.048
		0.9	0.396	0.208	0.141	0.088	0.042
	LTB	0.6	2.021	2.559	2.890	3.307	3.780
		0.7	1.344	1.743	1.832	1.830	0.830
		0.8	0.818	0.504	0.262	0.146	0.058
		0.9	0.528	0.254	0.156	0.095	0.044
Coverage	One-step	0.6	0.689	0.682	0.664	0.635	0.574
		0.7	0.773	0.786	0.806	0.817	0.867
		0.8	0.914	0.930	0.952	0.954	0.952
		0.9	0.938	0.947	0.958	0.954	0.952
	Three-step ML	0.6	0.927	0.938	0.942	0.952	0.942
		0.7	0.941	0.946	0.945	0.941	0.950
		0.8	0.940	0.947	0.947	0.949	0.946
		0.9	0.941	0.945	0.950	0.952	0.951
	Three-step BCH	0.6	0.931	0.941	0.940	0.940	0.942
		0.7	0.942	0.940	0.955	0.946	0.951
		0.8	0.936	0.945	0.952	0.948	0.943
		0.9	0.943	0.942	0.946	0.952	0.949
	LTB	0.6	0.790	0.701	0.654	0.575	0.515
		0.7	0.838	0.758	0.737	0.721	0.755
		0.8	0.883	0.872	0.890	0.891	0.896
		0.9	0.923	0.920	0.924	0.920	0.931

Note. ML = maximum likelihood; LTB = Lanza, Tan, and Bray (2013) approach; BCH = Bolck, Croon, and Hagenaars (2004) approach.

Figure 4.

Mean squared error under equal variances condition in Study 2.

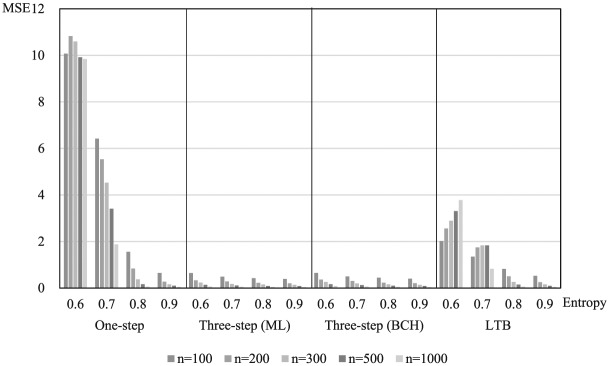
Under the condition of unequal variances, the level of difference was larger than under the condition of equal variances. The one-step approach showed the largest parameter estimates bias, and the LTB approach showed the largest standard error bias. The three-step ML and BCH approaches showed similar results and were more accurate than the other approaches. The one-step approach showed the largest mean squared error, followed by the LTB approach, and then followed by three-step ML and BCH approaches. Similar to the homogeneity condition of variance, the three-step ML and BCH approaches were better than the other approaches (see Figure 5). Last, in terms of coverage, the three-step ML and BCH approaches were acceptable under all conditions, the one-step approach was unacceptable when the entropy was 0.6 or 0.7, and the LTB approach was acceptable only when the entropy was 0.9.

Figure 5.

Mean squared error under unequal variances condition in Study 2.

Tables 6 and 7 contain the results of the three-way ANOVA for the three criteria for evaluation. Under the homogeneity condition of variance, according to the results of the parameter estimates bias, all main effects were statistically significant (0.16 for the sample size, 0.12 for the entropy, and 0.04 for the approach), but all interactions were not statistically significant. For standard error bias, all main effects and interactions were statistically significant. The largest effect size was the main effect of approach (${\mathrm{\eta }}^2$ = .45), followed by the main effect of entropy (${\mathrm{\eta }}^2$ = .28), and then the interaction of entropy and approach (${\mathrm{\eta }}^2$ = .17). For mean squared error, all effects were significant. The largest effect was the main effect of sample size (${\mathrm{\eta }}^2$ = .60) followed by that of entropy (${\mathrm{\eta }}^2$ = .15). For the interactions, the effect sizes were significant but small (${\mathrm{\eta }}^2$ = .05). In sum, when the latent class model included a distal outcome variable and the variances of the distal outcome variable were equal across latent classes, accuracy and efficiency of estimation were strongly affected by sample size, entropy, and approach.

Table 6.

ANOVA Results for Criteria According to Approaches Under Equal Variances in Study 2.

Criterion	Source	Sum of squares	df	Mean square	F	${\mathrm{\eta }}^2$
Parameter bias	Sample size (n)	0.40	4	0.10	13.29***	.16
	Entropy (e)	0.31	3	0.10	13.54***	.12
	Approach (a)	0.10	4	0.03	3.42**	.04
	n×e	0.07	12	0.01	0.80	.03
	n×a	0.02	16	0.00	0.18	.01
	e×a	0.07	12	0.01	0.77	.03
	n×e×a	0.02	48	0.00	0.05	.01
Standard error bias	Sample size (n)	0.01	4	0.00	5.17**	.00
	Entropy (e)	0.73	3	0.24	558.55***	.28
	Approach (a)	1.17	4	0.29	668.04***	.45
	n×e	0.02	12	0.00	2.99**	.01
	n×a	0.07	16	0.00	9.65***	.03
	e×a	0.44	12	0.04	84.92 ***	.17
	n×e×a	0.10	48	0.00	4.54***	.04
Mean squared error	Sample size (n)	0.12	4	0.03	4525.18***	.60
	Entropy (e)	0.03	3	0.01	1471.59***	.15
	Approach (a)	0.01	4	0.00	289.94***	.05
	n×e	0.01	12	0.00	140.01***	.05
	n×a	0.01	16	0.00	93.58***	.05
	e×a	0.01	12	0.00	95.62***	.05
	n×e×a	0.01	48	0.00	25.93***	.05

Note. ANOVA = analysis of variance; df = degrees of freedom.

^*p < .05. **p < .01. ***p < .001.

Table 7.

ANOVA Results for Criteria According to Approaches Under Unequal Variances in Study 2.

Criterion	Source	Sum of squares	df	Mean square	F	${\mathrm{\eta }}^2$
Parameter bias	Sample size (n)	1.96	4	0.49	0.86	.00
	Entropy (e)	144.06	3	48.02	84.02***	.15
	Approach (a)	261.63	4	65.41	114.44***	.28
	n×e	8.10	12	0.68	1.18	.01
	n×a	8.32	16	0.52	0.91	.01
	e×a	391.62	12	32.64	57.10***	.42
	n×e×a	13.02	48	0.27	0.47	.01
Standard error bias	Sample size (n)	0.04	4	0.01	1.17	.00
	Entropy (e)	3.19	3	1.06	127.23***	.16
	Approach (a)	10.94	4	2.73	327.50***	.55
	n×e	0.12	12	0.01	1.19	.01
	n×a	0.31	16	0.02	2.29**	.02
	e×a	3.46	12	0.29	34.55***	.17
	n×e×a	0.25	48	0.01	0.61	.01
Mean squared error	Sample size (n)	22.09	4	5.52	0.50	.00
	Entropy (e)	601.74	3	200.58	18.17***	.12
	Approach (a)	1030.78	4	257.69	23.34***	.20
	n×e	15.16	12	1.26	0.11	.00
	n×a	25.74	16	1.61	0.15	.00
	e×a	1238.78	12	103.23	9.35***	.24
	n×e×a	42.54	48	0.89	0.08	.01

Note. ANOVA = analysis of variance; df = degrees of freedom.

^*p < .05. **p < .01. ***p < .001.

Under the heterogeneity condition of variance, in terms of biases and mean squared error, the main effects and interactions including entropy and approach were statistically significant, but the main effects of sample size were not significant. For mean squared error, the largest effect was the interaction of entropy and approach (${\mathrm{\eta }}^2$ = .24), followed by the main effect of approach (${\mathrm{\eta }}^2$ = .20), and then followed by that of entropy (${\mathrm{\eta }}^2$ = .12). In conclusion, when the latent class model included a distal outcome variable and the variances of the distal outcome variable were unequal across latent classes, accuracy and efficiency of estimation were strongly affected by entropy and approach but not affected by sample size.

Conclusions and Discussion

The purpose of this study was to compare the performance of the one-step approach, the three-step ML approach, the three-step BCH approach, and the LTB approach in a mixture model with external variables. To carry out this objective, two simulation studies were conducted. The two simulation models are (1) a latent class model with three predictor variables and (2) a latent class model with a distal outcome variable. The sample size conditions were manipulated from 100 to 1,000, and for the quality of classification, which is referred to as entropy, values from 0.6 to 0.9 were used.

As a result, in Study 1, when the entropy value was 0.6 and the sample size was 100 or 200, estimation of the one-step approach showed a large discrepancy with the true value while the three-step ML approach resulted in relatively stable estimations. In Study 2, the three-step approaches appeared to be better than the other approaches in terms of all criteria. In the LTB approach, the coverage met the criteria only when the entropy level was very high. Thus, the three-step ML and BCH approaches showed relatively stable results even when the manipulated conditions were bad.

In summary, to estimate the relationship between latent classes and an external variable in a latent class model, the three-step approaches have the advantages of accuracy and efficiency of estimation even when the sample size is small and the entropy is low. This outcome is a major discovery, which can be helpful for applied researchers with small sample sizes because of practical limitations. In other words, researchers can use the three-step approaches in a latent class model with external variables even when the sample size is small such as 100 or 200. Until now, because previous simulation studies are based on sample sizes more than 500, there was no simulation evidence for smaller sample sizes. In this sense, this simulation result provides useful practical implications.

Furthermore, there are several implications of this study. First, this study manipulated more realistic simulation conditions than previous studies. For example, in sample size conditions, much smaller samples were tested than previous simulation studies, given that many empirical studies use samples of 100 to 300 because of limitations associated with collecting large samples. As several simulation studies provided guidelines on sample size and other complex conditions (MacCallum, Widaman, Preacher, & Hong, 2001; MacCallum, Widaman, Zhang, & Hong, 1999), this study also established guidelines for sample size according to the quality of classification in the context of a latent class model with external variables. Specifically, for good estimation in a latent class model with a distal outcome variable and unequal variances of the distal outcome variable across latent classes, the sample size should be more than 200 and the entropy value should be more than 0.8 to use the three-step approaches. Even in poorly manipulated conditions (i.e., n = 100, entropy = 0.6), according to the mean squared error results, the three-step approaches provide better estimates than the others.

Second, this study found that the three-step approach is best suited for small sample sizes and other poor conditions. Several simulation studies (e.g., Asparouhov & Muthén, 2014; Gudicha & Vermunt, 2013) found that the three-step approach and one-step approach are similar in parameter estimation, but they did not find the superiority of the three-step approach in terms of accuracy and efficiency of estimation under small sample size conditions. However, this study illustrates that the three-step ML and BCH approaches are more accurate and efficient in estimating parameters than the other approaches even if the sample size is 100.

Third, the aforementioned benefits of the three-step approach are recommended for applied researchers. The stability of latent class classification under a diverse combination of external variables and the corresponding research methods of applied researchers are major advantages of the three-step approaches (Vermunt, 2010). Moreover, the three-step approach overcomes the underestimation problem using the bias-correction method such as ML or BCH (Asparouhov & Muthén, 2014; Bakk et al., 2013; Gudicha & Vermunt, 2013; Lanza et al., 2013; Vermunt, 2010). Therefore, the three-step approaches are superior to the one-step approach in terms of latent class classification and parameter estimation. Moreover, applied researchers can easily use the three-step approaches in latent class models with external variables since the three-step approach can be used with Mplus (Muthén & Muthén, 1998-2017) and Latent Gold program (Vermunt & Magidson, 2016).

Fourth, this study compared not only the one-step approach and the three-step approaches but also the LTB approach, which estimates a model with an external variable as a distal outcome variable. In a previous simulation study by Asparouhov and Muthén (2014), the LTB approach performed worse than the three-step approach in terms of coverage. In the current study, the LTB approach performed the worst in terms of standard error bias and coverage as well. This approach met acceptable criteria only when entropy level was high. Since the LTB approach was found to perform at an unsatisfactory level when the entropy value was low, it can be used in limited situations when the quality of classification is almost perfect such as entropy values of 0.9 or higher.

Overall, these findings will be helpful to applied researchers, in diverse fields in behavioral sciences such as education, psychology, and sociology, to test latent class models with external variables using small sample sizes. This study tested cross-sectional latent class models with latent class membership with the same proportions. For future research, different proportions of latent class membership can be suggested, and growth mixture models with external variables can be simulated to compare the estimation of the approaches under various sample size conditions. Future studies will help generalize the usefulness of the three-step approach under various conditions.