Time and Other Considerations in Mediation Design

Abstract

This article serves as a practical guide to mediation design and analysis by evaluating the ability of mediation models to detect a significant mediation effect using limited data. The cross-sectional mediation model, which has been shown to be biased when the mediation is happening over time, is compared with longitudinal mediation models: sequential, dynamic, and cross-lagged panel. These longitudinal mediation models take time into account but bring many problems of their own, such as choosing measurement intervals and number of measurement occasions. Furthermore, researchers with limited resources often cannot collect enough data to fit an appropriate longitudinal mediation model. These issues were addressed using simulations comparing four mediation models each using the same amount of data but with differing numbers of people and time points. The data were generated using multilevel mediation models, with varying data characteristics that may be incorrectly specified in the analysis models. Models were evaluated using power and Type I error rates in detecting a significant indirect path. Multilevel longitudinal mediation analysis performed well in every condition, even in the misspecified conditions. Of the analyses that used limited data, sequential mediation had the best performance; therefore, it offers a viable second choice when resources are limited. Finally, each of these models were demonstrated in an empirical analysis.

Mediation is a popular and important topic, likely because it deals with the root of most research in psychology: understanding the process by which one variable influences another. Psychologists and other social scientists are often interested in whether a predictor, X, is related to an outcome, Y, and by what mechanism. Mediation is a way of answering this question. Mediation analysis determines how much of the effect that X has on Y goes through an intervening variable, M. If all the effect goes through M, the effect is being completely mediated. Otherwise, there is partial mediation. For example, a common mediation paradigm in psychology is the investigation of how some intervention leads to an outcome. Finding a mediator that explains the intervention’s influence can tell us more about how that intervention works.

Most mediation studies use cross-sectional data, utilizing either Baron and Kenny’s (1986) causal steps approach or by testing the indirect pathway in a structural equation model (SEM). The SEM approach has been shown to have higher power (MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002), and can also more easily accommodate suppression effects, multiple mediators, and moderated mediators. More recently, longitudinal mediation models, which use multiple time points to allow time to elapse between cause and effect, have been proposed as an alternative to these cross-sectional models that use only one time point. Three common longitudinal mediation models are cross-lagged panel mediation (CLPM), latent growth curve mediation, and latent change score mediation (see Preacher, 2015 or Selig & Preacher, 2009 for recent reviews). CLPM is the most popular of these, and as such is the focus of this study. In particular, we focus on a multilevel model extension of the CLPM, which allows mediation pathways to differ across individuals. The multilevel extension is especially useful when studying highly heterogeneous populations, when studying specific subpopulations or groups, or when the data have a nested structure.

Despite the tremendous advances in longitudinal mediation methodology in the literature, cross-sectional mediation remains popular in data analysis for several reasons. First, complex mediation models require more data, more time, and therefore more money and resources from the researcher. Especially for a researcher who is in the beginning stages of a project and is unsure whether the hypothesized mediation exists, longitudinal models require much more of a commitment than running a simple cross-sectional mediation study. Second, more complex models require more complex experimental designs. Researchers must not only choose the number of participants and time points required to fit a particular model, but they must also decide how often to collect data, what to collect at each time point, and how to deal with missingness and measurement invariance. Third, complex models are more difficult to understand, to implement, and to interpret their results. They are not often taught in a typical introductory statistics course, nor are they all easily implemented in popular software. Issues of nonconvergence, inadmissible parameter estimates, and other technical difficulties can also arise. Hence, even if longitudinal data are collected, it is often easier to fit a cross-sectional model.

The current study offers a novel perspective on mediation design to discover whether a simpler model can adequately perform using only a fraction of the data required for more complex analysis. To answer this question, we simulated data under a multilevel cross-sectional mediation model and a multilevel longitudinal mediation model under varying conditions, and evaluated how well the cross-sectional, sequential, dynamic, and cross-lagged panel models performed using subsets of the original data set. As a point of clarification, the purpose of this study is not to suggest using a fraction of a data set in practice. Rather, we use this simulation design as a tool to show what the results would have been had alternative mediation designs been considered. Specifically, we were interested in seeing how each of these designs and their corresponding models were impacted by the following potential issues: stability of variables over time, heterogeneity in the population, and inappropriate lag time between measurement occasions. Since we were primarily interested in which models best detect a mediation effect, model performance was evaluated using power and Type I error rates of testing the indirect path.

The rest of the article is organized as follows. First, six mediation models will be presented, followed by a brief review of their literature. Second, a simulation study will be described and the results presented. Third, an empirical data set will be analyzed to demonstrate the application of the models. Finally, we will discuss what conclusions can be drawn from this study as well as offer some discussion for further study.

Model Formulations for Studying Mediation

This study focuses on the following six mediation models: cross-sectional, sequential, dynamic, cross-lagged panel, multilevel cross-sectional, and multilevel longitudinal. This is by no means meant to be an exhaustive list of all possible mediation models, just the models considered here. All the models evaluated in this project were estimated within the SEM framework in MPlus. SEM is particularly useful for mediation analysis because it can test all paths simultaneously, and so the indirect path can be tested in one step. The dynamic mediation model was fit in MPlus using the Toeplitz method (Hamaker, Dolan, & Molenaar, 2002). All indirect paths were tested using Sobel standard errors. In general, the authors recommend using bootstrap standard errors for testing mediation. The same bootstrap procedure could not be used for all six of these models, however, as such Sobel standard errors were chosen because they can be used consistently across this study. Furthermore, the aim of this study is to compare relative power of the models not absolute power, and so consistency across models is more important in this context. Throughout this article, we make the same assumptions as Maxwell and Cole (2007): All variables are either collected without measurement error or are otherwise latent, and all cross-sectional correlations and path coefficients between adjacent time points are invariant across time. For simplicity’s sake, all of the variables have been centered, and so intercepts have been left out of all model formulations. It is also important to note that the current article does not attempt to discuss causality; it is assumed that the order of the causal pathway has already been established before performing any of these analyses.

Both cross-sectional mediation and multilevel cross-sectional mediation assume that the mediation is happening instantaneously, or within time of measurement. The four longitudinal models—sequential, dynamic, cross-lagged panel, and multilevel longitudinal—evaluate lagged mediation effects. Lag refers to the amount of time that transpires between adjacent measurement occasions, and so lagged effects are those that transpire across time from one measurement occasion to the next. For example, if the lag is specified as 1 day, the model assumes X on Day 1 affects values of M on Day 2, and M on Day 2 affects values of Y on Day 3. If lag times are not all the same, lag can be explicitly added to the model as a moderator (Selig, Preacher, & Little, 2012).

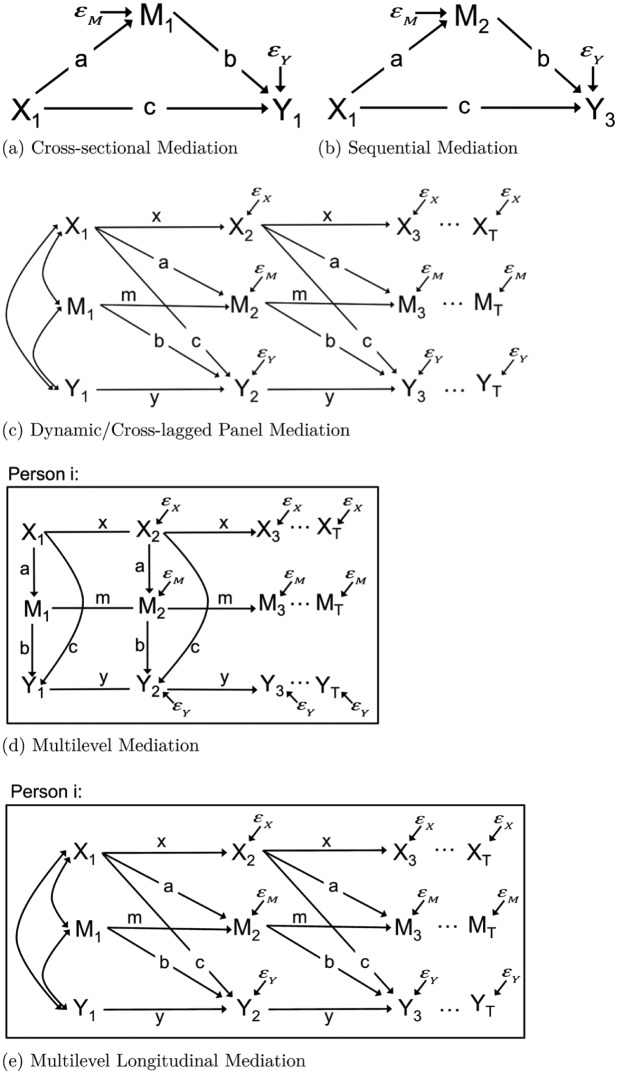
Path diagrams for all the models are pictured in Figure 1. For all models, a is the direct path between X and M, b is the direct path between M and Y, and c is the direct path between X and Y. The direct effect describes the effect that X has on Y that does not go through M. The indirect effect, or mediation effect, describes the effect that X has on Y through M. For all one-level models—cross-sectional, sequential, dynamic, and cross-lagged panel—the indirect effect is calculated by multiplying a and b path coefficients together,

Figure 1.

Path diagrams of mediation models.

$$\begin{array}{l}directeffect=c\\ indirecteffect=a\times b.\end{array}$$

The cross-sectional mediation (CSM) model (Figure 1a) is the simplest of the models presented here. Cross-sectional mediation uses only one measurement occasion, and so assumes that the cause and effect are happening within the time of data collection and are not affected by previous realizations of any of the variables involved. The sequential mediation (SM) model (Figure 1b), originally referred to as the MacArthur approach (Kraemer, Kiernan, Essex, Kupfer, 2008), requires that the data are collected in a particular sequence. Like the CSM model, data for X, M, and Y are each collected only once, but they are collected longitudinally. X is collected at the first time point, M at the second, and Y at the last time point. Therefore, this model allows effects to take place over time, but still does not account for previous realizations of the variables.

The remaining models account for previous realizations of the variables through autoregressive paths. The autoregressive paths of X, M, and Y are labeled $x$, $m$, and $y$, respectively. Autoregressive paths describe the strength of the relationship between previous values of a variable with current values, and can thus be used to calculate variable stability over time.

The dynamic mediation (DM) model (Figure 1c) is a time series model in which one person is measured over time. All variables are collected at every time point, usually for many time points. For the purposes of this project, the structure of the cross-lagged panel mediation (CLPM) and the DM model are the same except with regard to the number of people and the number of time points. The dynamic model uses only one participant and many time points, whereas the longitudinal model has many participants and fewer time points. The CLPM model assumes that paths are the same across people, whereas the dynamic model assumes that paths are the same across time.

The multilevel cross-sectional mediation (MCSM) model (Figure 1d) and the multilevel longitudinal mediation (MLM) model (Figure 1e) are random effects models, meaning that the path coefficients are allowed to vary across individuals. These models are particularly useful when the mediation is not expected to be the same for each participant. Each individual’s path coefficient—$a_i,b_i,c_i,x_i,m_i,$ and $y_i$—is a combination of the average path coefficient for the sample—$a$, $b$, $c$, $x$, $m$, and $y$—and error. Error terms can be separated into two levels, in which Level-1 error variances—variances of X, M, and Y—reflect within-person variability across time, and Level-2 error variances—variances of $a_i,b_i,c_i,x_i,m_i,$ and $y_i$—reflect between-person variability. Indirect paths are also calculated differently in multilevel mediation models in that Level-2 covariance between $a_i$ and $b_i$ are taken into account according to expectation rules (Kenny, Korchmaros, & Bolger, 2003),

$$\begin{array}{l}directeffect=c\\ indirecteffect=a\times b+cov(a_i\mathrm{,}{b}_i).\end{array}$$

In MCSM, mediation effects occur instantaneously as in CSM; in MLM, mediation effects occur over time as in the SM, DM, and CLPM models. Data were simulated under these models using their model-implied covariance matrices.

A Brief Review of the Current Models

Although cross-sectional mediation is historically the most popular mediation model, it has recently been losing favorability in the literature. This is because modeling effects that happen over time in a cross-sectional model almost always produces biased estimates of both the direct and indirect effects. The reason for this bias is twofold (Gollob & Reichardt, 1987). First, the cross-sectional model predicts outcomes at the same time point, not allowing the cause to yet have its effect. Second, autoregressive paths are excluded from the cross-sectional model, necessarily inflating estimates of cross-lagged paths. Maxwell and Cole (2007) evaluated these biases numerically in a complete mediation model and found that bias largely depends on the relative stabilities of X and M, stability being the correlation between a variable with itself at the previous measurement occasion, ${\rho }_{X_t{X}_{t-1}}$. If X and M are equally stable, there is no bias in estimating the direct path in a cross-sectional model. If X is more stable, the direct path will be positively biased and if M is more stable it will be negatively biased. Even if X and M are equally stable, the indirect path will be unbiased if, and only if, one of the following three conditions hold: (1) $a=0$, (2) $b=0$, or (3) $x^2=(1-\mathrm{mx})(1-\mathrm{xy})$. Under partial mediation the amount and direction of bias is more complex, and so the indirect path will almost always be biased (Maxwell, Cole, & Mitchell, 2011).

Although the sequential mediation model allows for the passage of time between causes and their effects, Mitchell and Maxwell (2013) have found that this model also suffers from bias when the underlying model is longitudinal. If autoregressive effects are not controlled, estimation of both the direct and indirect effects is biased. Under complete mediation, sequential mediation sometimes overestimates and sometimes underestimates the indirect effect, but if the stability of X is greater than the stability of M there is generally less bias. Under partial mediation, the sequential model typically overestimates the indirect effect. As autoregressive paths decrease, bias decreases, as well.

One limitation of Maxwell and Cole (2007), Maxwell et al. (2011), and Mitchell and Maxwell (2013), is that they only tested the performance of the cross-sectional or sequential model against the longitudinal model when the longitudinal model is the true model. In practice, a cross-sectional model may be the true model, and even when the underlying mediation is longitudinal it can be difficult to specify correctly in a model. Adding time into a model necessarily adds some challenges (Selig & Preacher, 2009). The first challenge is choosing measurement occasions. The researcher must decide how long X will need to affect M and Y, and how long for M to affect Y. This is often difficult to do. As Kenny (1975) has commented, “Normally the lag between measurements is chosen because of convenience, not theory, since theory rarely specifies the exact length of the causal lag” (p. 894). This is a problem because it is natural to think that the influence that a variable exerts on another variable will change over time, necessarily giving different results based on what measurement occasions are chosen. Gollob and Reichardt (1987) provide an example for this phenomenon using aspirin and headaches. Aspirin’s effect on headache alleviation will be different when measuring 2 minutes, 30 minutes, 3 hours, and 5 hours after ingestion. They argue that none of these lags are correct, but that there is a different effect for each lag.

Another challenge is to decide how many measurement occasions to collect. The minimum for fitting a longitudinal model is three waves of data, but it has been suggested that this is not enough (Reichardt, 2011). Having more time points allows more opportunities to measure path coefficients, and can therefore provide a more accurate estimation of them. It also allows the researcher to control more time points of formediating effects, resulting in less bias. Finally, the researcher has more flexibility in choosing a timeframe for the mediation effect in building their model if there are more time points to choose from.

Whether to collect additional time points or run additional participants is also a matter of considering the relative size of within- versus between-person variation. To the extent that there are individual differences in the mediation, a small sample size will likely provide biased estimates. Dynamic mediation is an extreme example of this, in which data are collected on only one individual. Depending on how representative this one person is, the resulting analysis may or may not be a good representation of the mediation in the population. On the other hand, if there is more variance within an individual over time than between individuals, including only one time point will likely provide biased estimates. CSM And SM are examples of this, in which only one time point for each variable is considered. Depending on how representative this one time point is, the resulting analysis may or may not be a good representation of the mediation in that individual. As such, all of these considerations—causal lag time, number of measurement occasions, variable stability, individual differences, and others—need to be explicitly considered when designing a mediation experiment, and so are evaluated in the following simulation study.

Simulation Study

The purpose of this simulation study is to evaluate the effects of variable stability, between-person variance, and misspecified lag time on detection of mediation effects in CSM, SM, DM, and CLPM models in order to see which perform best under various and sometimes misspecified conditions. Misspecified lag time is defined as the data being simulated under a longitudinal model and being evaluated with a cross-sectional model, or vice versa. All data for this study were generated under either the MCSM or MLM model, and different pieces of the resulting data were then analyzed by each of the analysis models. Power and Type I error rates in detecting the indirect effect were compared.

Design

Data were simulated in R using either the MCSM or MLM model (Figure 1d and 1e), depending on the assumed lag of the analysis model. CSM and MCSM assume cross-sectional mediation, while the other models assume longitudinal mediation. Consequently, both MCSM and MLM are required as population models in order to simulate data with the appropriate mediation lag for all of the analysis models. For each model, a total of 500 data sets were generated from 100 participants over 100 time points. The entire data set was used for MCSM and MLM analysis, whereas pieces of the data set were analyzed by the other models. Specifically, all 100 individuals in the first time point were analyzed with a CSM model. SM analysis used all 100 individuals of X at the first time point, M at the second, and Y at the third time point. All 100 time points for the first person in each data set were analyzed with a DM model. A cross-lagged panel mediation model was fit using the first 33 people and 3 time points (CLPM3), or the first 20 people and 5 time points (CLPM5). Realistically, lag time for a CLPM model would likely be longer than that for a DM model. For the purposes of this article, however, data for the CLPM models were collected consecutively to keep effect sizes similar across models. Again, the set up of this simulation is not meant to mirror a practical analysis in which the researcher uses only pieces of the original data set, but is merely a demonstration tool to show some consequences of different mediation study designs.

In summary, the CSM, SM, DM, CLPM3, and CLPM5 models were each fit to the same amount of data, 100 data points per variable, from the original data set. MCSM and MLM models were fit using all 10,000 original data points per variable, 100 times more data than the aforementioned five models. It is expected that MCSM and MLM will be more powerful than the other models in the simulation study; the main interest in this study is to compare power of the analysis models – CSM, SM, DM, CLPM3, and CLPM5. In fitting all of the longitudinal models, path coefficients were constrained to be constant over time. This approach maximizes power when there is little intraindividual change. The syntax used to analyze each of these models is available in supplentary material online.

A summary of conditions tested are presented in Table 1. A factorial design is used to test all combinations of the levels in the table. The path coefficients, $a$, $b$, and $c$ were set to either 0 or 0.36 at all combinations. The variances of X, M, and Y were set to 1 throughout this study by varying Level-1 error variance. To quantify the mediation effect, Pseudo R² and proportion of the effect that is mediated were calculated. Pseudo R² was calculated using

Table 1.

Simulation Conditions.

Simulation Parameters	Simulation Values
Simulating Models	MCSM, MLM
$a$, $b$, $c$	0, 0.36
$y$	0.36
X, M stabilitya	0.36, 0.50
Level-2 error variance	0, 0.0025, 0.01, 0.0225
Total variance of X, M, Yb	1

Note. MCSM, multilevel cross-sectional mediation; MLM, multilevel longitudinal mediation.

^aPath coefficients x and m were manipulated to keep X and M stabilities at their desired level. ^bLevel-1 error variance was manipulated to keep the total variance for each variable the same in every condition.

$$Pseudo{R}^2=\frac{{\sigma }_{ϵ0}^2-{\sigma }_{ϵ1}^2}{{\sigma }_{ϵ0}^2}\mathrm{,}$$

where ${\sigma }_{ϵ0}^2$ is the population Level-1 error variance for the intercept-only model, and ${\sigma }_{ϵ1}^2$ is the population Level-1 error variance for the model including only that parameter (Singer & Willett, 2003). Because variable variances were set to 1, when there are no predictors ${\sigma }_{ϵ0}^2$ necessarily equals 1, and so this simplifies to

$$Pseudo{R}^2=1-{\sigma }_{ϵ1}^2.$$

Using this formula, an $a$, $b$, or $c$ path coefficient of 0.36 explains about 13% of the variance in the outcome variable, which is generally thought of as a medium effect size using the interpretation of traditional R² (J. Cohen, 1988). The proportion of the effect that is mediated was calculated as

$$P_M=\frac{a\times b}{a\times b+c}.$$

When $a=b=c=0.36$, 26.5% of the effect of X on Y is being mediated by M (partial mediation). When either $a$ or $b=0$, 0% of the effect is being mediated (no mediation), and when $c=0$, 100% of the effect is being mediated (complete mediation).

To examine the influence of between-person variability, Level-2 error variance for all path coefficients was set to 0, 0.0025, 0.01, or 0.0225 to correspond to standard deviations in path coefficients of 0, 0.05, 0.10, and 0.15. Larger values represent more extreme between-person variability. Throughout this project, all Level-2 error covariances between path coefficients were set to 0, that is, ${\sigma }_{a_i{b}_i}=0$. This may not be the case in empirical data. For example, individuals with a more stable mediating variable may also be likely to have a more stable outcome variable, and so on, and so setting all covariances to 0 is problematic. However, there were a couple reasons for making this assumption in the current paper. First, variances had not yet been evaluated in this context before, and their effects should be established before beginning evaluation of covariances. Second, adding covariances to the model severely limits other conditions that can be tested while keeping the model stationary. For these reasons, nonzero covariances were left out of the current project, but offer a direction of future research.

To test the influence of X and M stability, X and M were either equally stable (${\rho }_{X_t{X}_{t-1}}={\rho }_{M_t{M}_{t-1}}=0.50$ or ${\rho }_{X_t{X}_{t-1}}={\rho }_{M_t{M}_{t-1}}=0.36$), X was more stable (${\rho }_{X_t{X}_{t-1}}=0.50;{\rho }_{M_t{M}_{t-1}}=0.36$), or M was more stable (${\rho }_{X_t{X}_{t-1}}=0.36;{\rho }_{M_t{M}_{t-1}}=0.50$). These correspond to different autoregressive path coefficients depending on other conditions. The stability of X is straightforward. In MCSM and MLM, the covariance between $X_t$ and $X_{t-1}$ is defined as

$${\sigma }_{X_t{X}_{t-1}}=x\cdot {\sigma }_X^2\mathrm{,}$$

where ${\sigma }_X^2$ is the variance of X. Because all variances were set to 1 in this simulation, the stability of X simplifies to

$${\rho }_{X_t{X}_{t-1}}=x.$$

The stability of M is a little more complicated. Given the same simplification of all variances being equal to 1, the stability of M is

$${\rho }_{M_t{M}_{t-1}}=m+\frac{a^{2}x}{1-\mathrm{xm}},$$

which depends not only on $m$ but also on $x$ and $a$. To maintain the stability of M to a specified level, $m$ paths were varied. For example, to keep the stability of M at 0.50 when $a=0.36$ and $x=0.50$, $m$ would be set to $0.418$. The stability of Y is even more complex but is not explicitly tested here; y paths are kept at 0.36 throughout all conditions.

Results

Type I error rates and power are reported to evaluate each of the model’s performance in mediation detection. Type I error rates outside of the range [0.025,0.075] are italicized, and those above are additionally bolded to signify an especially undesirable direction of departure from nominal Type I error. Powers are boldfaced if they are less than 0.80, usually the desired level of power in psychology and other social sciences.

Type I Error

To assess the effect that between-person variability has on mediation detection when there is no mediation, Level-2 error variance (BPvar) was varied and Type I error rates were assessed for each model. All Level-2 error variances were equal, and all covariances were set to 0. X and M are equally stable at 0.50. In order to detangle the effects of misspecified lag and between-person variance, the results shown refer to data simulated under MCSM for CSM results, and under MLM for the remaining models so that lag is always specified correctly. Effect sizes are the same in both MCSM and MLM. Hence, these results evaluate the effect of between-person variance when lag is specified correctly and X and M are equally stable. Type I errors under complete mediation appear in Table 2 and under partial mediation in Table 3.

Table 2.

Type I Error Rates of the Indirect Path Under Complete Mediation Vary by Between-Person Variance (BPvar).

Path			Model
a	b	BPvar	CSM	SM	DM	CLPM3	CLPM5	MCSMa	MLMb
0	0	0	0.000	0.000	0.002	0.000	0.000	0.000	0.000
		0.0025	0.000	0.000	0.000	0.002	0.002	0.028	0.008
		0.01	0.002	0.000	0.020	0.000	0.002	0.050	0.060
		0.0225	0.002	0.006	0.058	0.004	0.002	0.047	0.067
0	0.36	0	0.034	0.042	0.036	0.022	0.044	0.044	0.028
		0.0025	0.040	0.034	0.070	0.036	0.046	0.046	0.040
		0.01	0.026	0.030	0.126	0.022	0.052	0.056	0.058
		0.0225	0.069	0.089	0.240	0.048	0.058	0.052	0.054
0.36	0	0	0.030	0.044	0.032	0.024	0.042	0.070	0.032
		0.0025	0.048	0.038	0.074	0.012	0.066	0.054	0.060
		0.01	0.038	0.032	0.114	0.036	0.028	0.050	0.054
		0.0225	0.036	0.036	0.192	0.040	0.058	0.047	0.039

Note. X and M are equally stable at 0.50, the c path is 0, and the y path is 0.36 for all conditions. All path coefficients are fixed. Type I error rates outside of the range [0.025,0.075] are italicized, those over are boldfaced. CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

^aMCSM is the generating model for MCSM and CSM analysis. MCSM uses all 100 people and all 100 time points for analysis. ^bMLM is the generating model for MLM, SM, DM, and CLPM analysis. MLM uses all 100 people and all 100 time points for analysis.

Table 3.

Type I Error Rates of the Indirect Path Under Partial Mediation Vary by Between-Person Variance (BPvar).

Path			Model
a	b	BPvar	CSM	SM	DM	CLPM3	CLPM5	MCSMa	MLMb
0	0	0	0.000	0.000	0.000	0.000	0.000	0.000	0.000
		0.0025	0.000	0.000	0.004	0.000	0.000	0.032	0.028
		0.01	0.000	0.000	0.016	0.002	0.000	0.048	0.050
		0.0225	0.010	0.000	0.062	0.002	0.004	0.047	0.046
0	0.36	0	0.036	0.032	0.020	0.032	0.032	0.048	0.028
		0.0025	0.042	0.010	0.088	0.020	0.064	0.050	0.050
		0.01	0.042	0.044	0.166	0.048	0.070	0.072	0.054
		0.0225	0.089	0.075	0.267	0.053	0.075	0.052	0.064
0.36	0	0	0.026	0.054	0.040	0.038	0.058	0.066	0.030
		0.0025	0.042	0.034	0.058	0.042	0.050	0.042	0.064
		0.01	0.030	0.034	0.116	0.028	0.048	0.070	0.078
		0.0225	0.054	0.044	0.275	0.037	0.051	0.067	0.043

Note. X and M are equally stable at 0.50 and the c and y paths are 0.36 for all conditions. All path coefficients are fixed. Type I error rates outside of the range [0.025,0.075] are italicized, those over are boldfaced. CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

^aMCSM is the generating model for MCSM and CSM analysis. MCSM uses all 100 people and all 100 time points for analysis. ^bMLM is the generating model for MLM, SM, DM, and CLPM analysis. MLM uses all 100 people and all 100 time points for analysis.

Unsurprisingly, DM is most severely affected by increases in between-person variance. Type I error rate already begins to increase when Level-2 error variances are set to 0.0025, and reaches as high as 0.276 when error variance increases to 0.0225. Overall, these results suggest that DM is very sensitive to individual differences. Level-2 error variance must be less than 0.0025, a standard deviation of 0.05, for DM analysis to be appropriate. CSM and SM each have one instance of increased Type I error when error variance is 0.0225. However, these are only slight violations that happen at the most extreme level of between-person variance.

To assess the effect that X and M stability have on mediation detection when there is no mediation, stability of X and M were set to all combinations of 0.36 and 0.50 and Type I error rates were assessed for each model. All Level-2 error variances and covariances were set to 0. When lag is specified correctly, all Type I error rates are <0.05, and so these results are not shown. Results when lag is misspecified are shown in Table 4 for complete mediation and in Table 5 for partial mediation. Lag is misspecified when data are simulated under MLM and analyzed with CSM and MCSM, or simulated under MCSM and analyzed with SM, DM, CLPM, or MLM. Hence, these results evaluate the effect of X and M stability when lag is misspecified without between-person variability.

Table 4.

Type I Error Rates of the Indirect Path Under Complete Mediation Vary by Stability Under Misspecified Lag.

Path		Stability		Model
a	b	X	M	CSM	SM	DM	CLPM3	CLPM5	MCSMa	MLMb
0	0	0.36	0.36	0.000	0.000	0.000	0.000	0.000	0.000	0.000
		0.36	0.50	0.000	0.000	0.000	0.000	0.000	0.000	0.000
		0.50	0.36	0.000	0.000	0.000	0.000	0.004	0.000	0.000
		0.50	0.50	0.000	0.000	0.000	0.002	0.000	0.000	0.000
0	0.36	0.36	0.36	0.002	0.004	0.000	0.004	0.004	0.020	0.006
		0.36	0.50	0.002	0.002	0.000	0.000	0.002	0.022	0.004
		0.50	0.36	0.000	0.008	0.002	0.008	0.000	0.028	0.024
		0.50	0.50	0.018	0.004	0.002	0.006	0.016	0.044	0.020
0.36	0	0.36	0.36	0.004	0.014	0.002	0.000	0.006	0.020	0.010
		0.36	0.50	0.004	0.018	0.004	0.006	0.010	0.028	0.010
		0.50	0.36	0.000	0.012	0.002	0.004	0.004	0.024	0.004
		0.50	0.50	0.006	0.020	0.006	0.002	0.010	0.022	0.018

Note. The c path is 0 and the y path is 0.36 for all conditions. All path coefficients are fixed. Type I error rates outside of the range [0.025,0.075] are italicized, those over are boldfaced. CLPM, cross-lagged panel mediation; CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

^aMCSM is the generating model for SM, DM, CLPM, and MLM analysis. MCSM uses all 100 people and all 100 time points for analysis. ^bMLM is the generating model for CSM and MCSM analysis. MLM uses all 100 people and all 100 time points for analysis.

Table 5.

Type I Error Rates of the Indirect Path Under Partial Mediation Vary by Stability Under Misspecified Lag.

Path		Stability		Model
a	b	X	M	CSM	SM	DM	CLPM3	CLPM5	MCSMa	MLMb
0	0	0.36	0.36	0.002	0.000	0.000	0.000	0.002	0.002	0.000
		0.36	0.50	0.000	0.000	0.000	0.000	0.002	0.008	0.000
		0.50	0.36	0.000	0.000	0.000	0.000	0.000	0.000	0.000
		0.50	0.50	0.002	0.000	0.000	0.000	0.002	0.006	0.000
0	0.36	0.36	0.36	0.000	0.000	0.004	0.002	0.002	0.014	0.006
		0.36	0.50	0.000	0.004	0.004	0.008	0.002	0.022	0.016
		0.50	0.36	0.014	0.006	0.010	0.002	0.004	0.008	0.038
		0.50	0.50	0.000	0.002	0.004	0.002	0.014	0.040	0.014
0.36	0	0.36	0.36	0.012	0.016	0.002	0.000	0.008	1.000	0.024
		0.36	0.50	0.038	0.026	0.004	0.002	0.006	0.998	0.020
		0.50	0.36	0.028	0.042	0.004	0.004	0.004	1.000	0.014
		0.50	0.50	0.078	0.050	0.002	0.006	0.000	1.000	0.012

Note. The c and y paths are 0.36 for all conditions. All path coefficients are fixed. Type I error rates outside of the range [0.025,0.075] are italicized, those over are boldfaced. CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

^aMCSM is the generating model for SM, DM, CLPM, and MLM analysis. MCSM uses all 100 people and all 100 time points for analysis. ^bMLM is the generating model for CSM and MCSM analysis. MLM uses all 100 people and all 100 time points for analysis.

When a and c are nonzero, MCSM has extremely high Type I error rates. These results show that when the lag is unknown, MCSM should not be utilized. CSM has one slight violation in these conditions, as well, which appears to increase as stability of X and M increase.

Power

To assess the effect that between-person variability has on detecting a true mediation, Level-2 error variance was varied and power rates were assessed for each model. Again, these results address what is the effect of between-person variance when lag is specified correctly and X and M are equally stable at 0.50. All results are shown in Table 6. Across conditions, CSM and SM are the most powerful among the one-level models and seem to be unaffected by between-person variance. DM is most affected by increases in between-person variance. Under partial mediation, power decreases from 0.99 with no between-person variance to 0.79 at the most extreme variance. Nonetheless, DM is still more powerful than CLPM3 under most conditions.

Table 6.

Power in Detecting the Indirect Path Varies by Between-Person Variance (BPvar).

		Model
Direct Path	BPvar	CSM	SM	DM	CLPM3	CLPM5	MCSMa	MLMb
0	0	0.95	0.95	0.92	0.72	0.82	1.00	1.00
	0.0025	0.95	0.94	0.90	0.72	0.83	1.00	1.00
	0.01	0.96	0.96	0.79	0.76	0.81	1.00	1.00
	0.0225	0.95	0.97	0.74	0.69	0.81	1.00	1.00
0.36	0	0.99	0.99	0.99	0.85	0.92	1.00	1.00
	0.0025	1.00	0.99	0.95	0.85	0.90	1.00	1.00
	0.01	1.00	0.99	0.89	0.85	0.89	1.00	1.00
	0.0225	0.99	0.99	0.79	0.86	0.88	1.00	1.00

Note. X and M are equally stable at 0.50 and the a, b, and y paths are 0.36 for all conditions. All path coefficients are fixed. Powers less than 0.80 are boldfaced. CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

^aMCSM is the generating model for MCSM and CSM analysis. MCSM uses all 100 people and all 100 time points for analysis. ^bMLM is the generating model for MLM, SM, DM, and CLPM analysis. MLM uses all 100 people and all 100 time points for analysis.

To assess the effect that X and M stability have on detecting a true mediation, stability of X and M were set to all combinations of 0.36 and 0.50 and power rates were assessed for each model. All Level-2 error variances and covariances were set to 0. Results under correctly specified lag are shown in Table 7, and under misspecified lag in Table 8. Higher stability increases power insubstantially when lag is correctly specified, whereas the impact under misspecified lag is severe.

Table 7.

Power in Detecting the Indirect Path Varies by Stability.

	Stability		Model
Direct Path	X	M	CSM	SM	DM	CLPM3	CLPM5	MCSMa	MLMb
0	0.36	0.36	0.93	0.93	0.91	0.69	0.81	1.00	1.00
	0.36	0.50	0.92	0.95	0.95	0.74	0.86	1.00	1.00
	0.50	0.36	0.92	0.92	0.93	0.65	0.78	1.00	1.00
	0.50	0.50	0.95	0.95	0.92	0.72	0.82	1.00	1.00
0.36	0.36	0.36	0.98	0.97	0.96	0.81	0.86	1.00	1.00
	0.36	0.50	0.99	0.97	0.99	0.87	0.93	1.00	1.00
	0.50	0.36	1.00	0.97	0.96	0.80	0.90	1.00	1.00
	0.50	0.50	0.99	0.99	0.99	0.85	0.92	1.00	1.00

Note. Lag = 0 corresponds to data simulated under MCSM, Lag=1 corresponds to data simulated under MLM. The a, b, and y paths are 0.36 for all conditions. All path coefficients are fixed. Powers less than 0.80 are bolded. CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

^aMCSM uses all 100 people and all 100 time points for analysis. ^bMLM uses all 100 people and all 100 time points for analysis.

Table 8.

Power in Detecting the Indirect Path Varies by Stability Under Misspecified Lag.

	Stability		Model
Direct Path	X	M	CSM	SM	DM	CLPM3	CLPM5	MCSMa	MLMb
0	0.36	0.36	0.02	0.10	0.00	0.01	0.02	0.99	1.00
	0.36	0.50	0.05	0.10	0.01	0.02	0.01	1.00	0.98
	0.50	0.36	0.05	0.29	0.03	0.03	0.04	0.99	1.00
	0.50	0.50	0.12	0.27	0.05	0.03	0.04	1.00	0.99
0.36	0.36	0.36	0.15	0.19	0.02	0.02	0.01	0.99	0.99
	0.36	0.50	0.28	0.25	0.04	0.01	0.03	0.99	1.00
	0.50	0.36	0.20	0.49	0.06	0.02	0.02	0.97	1.00
	0.50	0.50	0.48	0.64	0.11	0.04	0.05	0.99	1.00

Note. Lag = 0 corresponds to data simulated under MCSM, Lag=1 corresponds to data simulated under MLM. The a, b, and y paths are 0.36 for all conditions. All path coefficients are fixed. Powers less than 0.80 are boldfaced. CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

^aMCSM uses all 100 people and all 100 time points for analysis. ^bMLM uses all 100 people and all 100 time points for analysis.

As expected, overall power is much lower under misspecified lag. The multilevel models are the only models to have similar power rates as they did under correctly specified lag. The model that performs next best is SM. SM power reaches as high as 64% when the stability of both X and M are at their highest, 0.50, and when the direct path is nonzero. Performance quickly drops with decreases in X and especially M stability, as well as when the direct path becomes 0. The next highest power reported is that by CSM, reaching as high as 48%, but quickly dropping under the same conditions. DM and CLPM models never have power higher than 11%, and most rates are much lower than that.

Conclusions

Type I error rates are well contained throughout this study with a couple of exceptions. DM was sensitive to increases in between-person variance, and MCSM performed poorly under misspecified lag. Overall, Type I error rates were much lower than the nominal 0.05 when both a = 0 and b = 0, but these results agree with those by MacKinnon et al. (2002) when the Sobel test is used.

Apart from the multilevel models, CSM and SM had the highest power, followed by DM, CLPM5 and CLPM3 had the lowest power. The power of DM was most affected by increases in between-person variance, and all models were mildly affected by increases in X and M stability. Most interesting are the power rates under misspecified lag. Apart from the multilevel models, CSM and especially SM performed the best in these conditions.

Empirical Example

The data for this example come from the Notre Dame Study of Health & Well-being; 786 mid-life and older adults reported on their positive emotion, negative emotion, and stress everyday for 56 days. Positive and negative emotion were measured using the daily version of the Positive and Negative Affect Schedule (PANAS; Watson, Clark, & Tellegen, 1988), and stress was measured using the Perceived Stress Scale (S. Cohen, Kamarch, & Mermelstein, 1983). It has been hypothesized that positive emotion may help undo the detrimental effect that stress has on negative emotion (Fredrickson, Mancuso, Branigan, & Tugade, 2000). Supporting this idea, Ong, Bergeman, Bisconti, and Wallace (2006) have shown that positive emotion significantly mediates the effect that stress has on negative emotion using a multilevel random coefficient model (MRCM; Raudenbush & Bryk, 2002). This hypothesis was further investigated here using CSM, SM, DM, CLPM3, CLPM5, MCSM, and MLM models.

The number of participants and time points used in each analysis is detailed in Table 9; unlike the simulation studies presented previously, CSM, SM, DM, and CLPM do not utilize the same amount of data in this example. Everybody that completed Day 1 of the study was included in CSM analysis. A randomly selected individual who completed everyday of the study was used in DM analysis. Anyone that completed surveys in the first 3 to 5 days was used in SM and CLPM analysis. Multiple imputation was employed to deal with missingness before beginning MCSM and MLM analysis on the full data set. Results from all of the models are presented in Table 10.

Table 9.

Data Used by Each of the Models.

Model	CSM	SM	DM	CLPM3	CLPM5	MCSM	MLM
No. of participants	660	663	1	690	693	786	786
No. of time points	1	3	56	3	5	56	56

Note. CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

Table 10.

Empirical Results.

Parameter		CSM	SM	DM	CLPM3	CLPM5	MCSM	MLM
Indirect	estimate	−0.042	0.008	0.005	−0.005	−0.003	0.081	−0.001
	se	0.015	0.016	0.008	0.002	0.001	0.005	0.001
	p-val	0.005	0.601	0.526	0.024	0.040	<0.001	0.181
Direct	estimate	0.725	0.367	−0.044	0.098	0.099	0.631	0.052
	se	0.029	0.037	0.041	0.029	0.021	0.010	0.008
	p-val	<0.001	<0.001	0.289	0.001	<0.001	<0.001	<0.001
$a$	estimate	−0.693	−0.584	−0.365	−0.125	−0.099	−0.375	−0.072
	se	0.046	0.050	0.194	0.031	0.023	0.018	0.014
	p-val	<0.001	<0.001	0.060	<0.001	<0.001	<0.001	<0.001
$b$	estimate	0.060	−0.014	−0.014	0.039	0.025	−0.200	0.013
	se	0.021	0.027	0.021	0.014	0.011	0.005	0.008
	p-val	0.004	0.600	0.504	0.006	0.019	<0.001	0.116
$x$	estimate			0.451	0.618	0.637	0.189	0.230
	se			0.083	0.20	0.014	0.100	0.016
	p-val			<0.001	<0.001	<0.001	0.058	<0.001
$m$	estimate			0.108	0.648	0.691	0.185	0.212
	se			0.099	0.022	0.016	0.021	0.010
	p-val			0.275	<0.001	<0.001	<0.001	<0.001
$y$	estimate			0.009	0.537	0.545	0.063	0.156
	se			0.097	0.027	0.020	0.021	0.030
	p-val			0.929	<0.001	<0.001	0.003	<0.001

Note. CSM = cross-sectional mediation; SM = sequential mediation; DM = dynamic mediation; CLPM = cross-lagged panel mediation; MCSM = multilevel cross-sectional mediation; MLM = multilevel longitudinal mediation.

When using a significance criterion of 0.05, all models except DM report a significant direct effect. All of these coefficients are positive, and so it can be reasonably supported that increases in stress lead to increases in negative emotion. Although CSM, CLPM3, CLPM5, and MCSM models report significant indirect effects, according to our simulation results MLM is the most reliable and it does not result in a significant mediation effect. Looking further into this discrepancy, it is shown that every model found a negative a path estimate. This finding falls in line with the expectation that increases in stress would lead to decreases in positive emotion. The relationship between positive emotion and negative emotion is less clear, as demonstrated by the mixed results among the models. There are at least two possibilities here. Either the b pathway coefficient is very small or zero, or there are subpopulations with opposite or otherwise conflicting results. In fact, Ong et al. (2006) explored the latter hypothesis in their article using psychological resilience (Block & Kremen, 1996) as a second-level predictor. They found that for individuals low in resilience, there is an inverse relationship between positive and negative emotion, and that this relationship interacts with stress. For highly resilient individuals, there was no relationship between positive and negative emotion. These results demonstrate the utility of multilevel models to answer more complex questions in mediation research.

All in all, the only other model to produce results consistent with that of MLM is SM. Both of these models report a significant negative a path, a significant positive c path, and a nonsignificant b pathway. These results demonstrate that the same conclusion drawn from performing MLM analysis without Level-2 predictors on data measuring 786 participants over 56 days, could have been found by performing SM analysis on 663 participants in the first 3 days. In other words, these results support that of the simulation study: When MLM analysis is not possible or the data are insufficient, SM is the best alternative.

Discussion

The goal of the current project was to determine whether a simpler mediation model that uses less data can perform as well as a more complex model in detecting a mediation effect. Models were evaluated and compared under conditions of alternative variable stabilities, between-person variation, and misspecified lag. Relative stabilities of X and M variables did not affect either Type I error rate or power by notable amounts, except in the case when lag was misspecified. Models performed much better under misspecified lags with higher stability variables, especially SM and CSM. Between-person variance most affected DM in terms of both Type I error rate and power. In all conditions, simulations showed that detecting a mediation effect under partial mediation was more powerful than under complete mediation.

The multilevel models had the highest power in all conditions, but they also used 100 times more data than the other models. MCSM had very high Type I error rates when lag was misspecified, but MLM never had a higher than nominal Type-1 error rate. Thus, if resources allow, the results of this paper highly recommend MLM as the superior model to evaluate mediation. Even in misspecified conditions, the MLM performed well. This is especially an advantage in mediation, when the researcher may not know whether the effect is cross-sectional or longitudinal or what the correct lag may be. As long as enough data points are collected, the MLM model can be trusted to provide an accurate result.

Of the remaining models, CSM and SM models were the next most powerful, with DM shortly thereafter. A CLPM with 5 time points and 20 people was always more powerful than a CLPM with 3 time points and 33 people, further supporting Reichardt’s (2011) argument that three waves are not enough. The CLPM models are the only two models to maintain Type-1 error in all conditions. SM and CSM were the only models to capture the mediation effect when the lag was misspecified. SM could still detect mediation up to 64% of the time and CSM up to about 48% of the time under misspecified lag. Although these results highly depend on the stability of X and M, their performances are still impressive considering that 0.089 is the highest Type I error rate from either of these models. Therefore, if resources do not allow for MLM analysis and the stabilities of X and M are expected to be high, SM is a viable alternative to MLM.

These results may be surprising to some readers who have read previous work comparing CSM and SM to longitudinal models such as Maxwell and Cole (2007), Maxwell et al. (2011), and Mitchell and Maxwell (2013), but these articles focused on bias. It very well may be that CSM and SM were so powerful in some of these conditions due to bias. Regardless, as long as Type I error is not inflated, bias would not pose a practical problem if the goal is to detect a mediation effect. That being said, this paper is in no way meant to discourage focus on effect sizes in the literature. We still believe effect size estimation is an important part of the research process. However, calculation of effect size for longitudinal models, especially longitudinal mediation models is a complex issue (Peugh, 2010; Preacher & Kelley, 2011; Roberts & Monaco, 2006). As such, many researchers rely on power more than effect size in evaluating complex models such as some of the models presented here. On the contrary, it is well-known that CSM and SM can be biased (i.e., Mitchell & Maxwell, 2013), thus their results should always be hesitantly interpreted.

Despite these limitations, this article serves as a fundamental first step in evaluating mediation models from the perspective of an empirical researcher interested in detecting a mediation effect. It is our goal that the methods used here set the stage for future projects from this perspective, and encourage future quantitative work in mediation that will be most useful to its users. This perspective has not been explored before, and so offers some new results. When ample time and resources are available, or the researcher desires to investigate more complex phenomena, these results highly recommend the use of a multilevel longitudinal mediation model. It has high power to find a mediation effect and still maintain Type I error rate even under misspecified lag. When multilevel longitudinal mediation analysis is not possible or desirable, the results of this article suggest utilization of cross-sectional and especially sequential mediation. Sequential mediation models perform especially well under misspecified conditions when the variable are highly stable. Accordingly, we recommend sequential mediation models as a low-cost option for researchers seeking to maximize power using minimal resources.