Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Nov 8;14(12):6690–6700. doi: 10.1021/acs.jctc.8b00909

Optimizing Nonbonded Interactions of the OPLS Force Field for Aqueous Solutions of Carbohydrates: How to Capture Both Thermodynamics and Dynamics

Seyed Hossein Jamali †, Thijs van Westen ‡,§, Othonas A Moultos †, Thijs J H Vlugt †,*
PMCID: PMC6293444  PMID: 30407814

Abstract

graphic file with name ct-2018-00909e_0007.jpg

Knowledge on thermodynamic and transport properties of aqueous solutions of carbohydrates is of great interest for process and product design in the food, pharmaceutical, and biotechnological industries. Molecular simulation is a powerful tool to calculate these properties, but current classical force fields cannot provide accurate estimates for all properties of interest. The poor performance of the force fields is mainly observed for concentrated solutions, where solute–solute interactions are overestimated. In this study, we propose a method to refine force fields, such that solute–solute interactions are more accurately described. The OPLS force field combined with the SPC/Fw water model is used as a basis. We scale the nonbonded interaction parameters of sucrose, a disaccharide. The scaling factors are chosen in such a way that experimental thermodynamic and transport properties of aqueous solutions of sucrose are accurately reproduced. Using a scaling factor of 0.8 for Lennard-Jones energy parameters (ϵ) and a scaling factor of 0.95 for partial atomic charges (q), we find excellent agreement between experiments and computed liquid densities, thermodynamic factors, shear viscosities, self-diffusion coefficients, and Fick (mutual) diffusion coefficients. The transferability of these optimum scaling factors to other carbohydrates is verified by computing thermodynamic and transport properties of aqueous solutions of d-glucose, a monosaccharide. The good agreement between computed properties and experiments suggests that the scaled interaction parameters are transferable to other carbohydrates, especially for concentrated solutions.

1. Introduction

Saccharides define a class of carbohydrates considered vital for a wide range of biological and industrial processes.1,2 Examples include the role of (poly-)sacharides or glyco-proteins in cryo- and lyopreservation of biomaterials and foods,3−8 the regulation of the osmotic pressure in living cells,9 the interplay between saccharides and proteins in the cell membrane,10,11 and use as a feedstock for the production of biofuels and renewable chemicals in biotechnology.1 Either in biology or in industrial applications, saccharides predominantly occur in aqueous solutions. To obtain a better understanding of the underlying mechanisms defining the biological function of a saccharide, or to obtain a better description of the thermophysical properties of saccharide solutions (as needed in technological applications), requires a molecular-level description of the interactions between sugars, water, and water–sugar. Classical molecular simulations provide a valuable tool for this; however, it is essential that the used force fields reproduce relevant volumetric, structural, and dynamic properties of the system of interest. For aqueous solutions of saccharides, this has proven a difficult task.

As several studies12−17 have shown, a common problem when applying carbohydrate force fields such as CHARMM,18−21 GLYCAM06,22 GROMOS,23,24 or OPLS-AA28 to saccharide solutions is the overestimation of the sugar–sugar interactions, leading to strong sugar aggregation at elevated sugar concentrations. As a result, both thermodynamic properties (densities, activity coefficients, thermodynamic factors, second virial coefficients, etc.) and transport properties (shear viscosities, diffusion coefficients, etc.) of concentrated solutions are generally not well reproduced.12−15,17 Recent work showed that rescaling the sugar–sugar nonbonded interactions to lower values improves the description.13,15,29 Basically, two strategies have been proposed. In the first approach (e.g., the work of Sauter and Grafmüller14 and Lay et al.15), only the dispersion interactions—more precisely, the energy parameters for some of the Lennard-Jones (LJ) interactions between sugars—are modified. In the second approach (e.g., Batista et al.13), only the partial atomic charges of the sugars are scaled. The first approach improves the description of thermodynamic properties, such as the osmotic pressure and second virial coefficient.14,15 However, transport properties appear to be less affected by solely modifying the dispersion interactions (see the Supporting Information of Lay et al.15 for results on the viscosity of glucose solutions). Results obtained using the second approach indicate that rescaling partial atomic charges leads to considerable improvements in the description of transport properties and suggest that thermodynamic properties (e.g., density) are also better described. The results of Batista et al.13 are not conclusive, however, as mixture properties known to be more sensitive to changes in the partial charges of the atoms (e.g., thermodynamic factors and osmotic coefficients) were not taken into account. Also, the only transport property studied was the viscosity, and diffusion coefficients were not considered.

In this work, we first present a more complete analysis on how the properties of aqueous carbohydrate solutions change when the LJ or electrostatic interactions are scaled. The force fields of Batista et al.13 (OPLS with scaled partial atomic charges) and Lay et al.15 (GLYCAM06 with scaled LJ interactions) are analyzed in more detail. We focus on the disaccharide sucrose (Figure 1) as a relevant test case, as this molecule has many applications, ranging from biology to food science.3,4,6,7 Our results show that only scaling partial charges is insufficient to reproduce both thermodynamic and transport properties of concentrated aqueous saccharide solutions. Scaling only the dispersion interactions leads to significantly better agreement, with qualitative improvements in transport properties, as well as thermodynamic properties. Although scaling the LJ interactions improves the force field, our analysis indicates that obtaining quantitative agreement between experiments and computed properties of saccharide solutions may require a global optimization procedure of the force field, with different scaling factors for LJ interactions of different atom pairs. Since the choice of atom pairs is rather arbitrary, and an optimization of many force field parameters is difficult, we here propose a different approach, in which all LJ energy parameters and all partial atomic charges of the sugars are scaled simultaneously.29 This procedure only requires optimization of two parameters: one scaling factor for LJ interactions and one scaling factor for partial atomic charges. For the optimization of sucrose nonbonded interaction parameters, the OPLS force field25,26 is used as a basis. The transferability of the refined OPLS force field is analyzed for d-glucose as a prototypical example of monosaccharides.

Figure 1.

Figure 1

Open in a new tab

Schematic and atomistic representations of sucrose. The atomistic representation was created by using iRASPA.79

This manuscript is organized as follows. In section 2, the details of simulations and equations used for computing transport and thermodynamic properties are provided. In section 3, a set of optimum scaling factors for nonbonded interaction parameters of the OPLS force field is obtained and the accuracy of the refined force field is investigated. Our conclusions are summarized in the last section.

2. Simulation Details

Force-field-based equilibrium MD simulations were carried out to compute thermodynamic properties (i.e., liquid densities and thermodynamic factors) and transport properties (i.e., shear viscosities, self-, and Fick diffusion coefficients) of water–sucrose mixtures at 298 K and 1 atm. The software package LAMMPS30 (version of February 16, 2016) was used to perform the MD simulations. The molecular configurations of aqueous sucrose solutions were made in Packmol.31 We considered five systems, with sucrose mass fractions (wsucrose) of 20%, 30%, 40%, 50%, and 60%. These systems contained 6, 9, 12, 16, and 20 sucrose molecules combined with 456, 399, 342, 304, and 253 water molecules, respectively. These systems yield homogeneous liquid solutions, as sucrose crystallizes in mixtures with a mass fraction above 67% at 298 K.32 The input files for these configurations are produced using VMD.33 The same procedure was followed to construct LAMMPS input files for four aqueous glucose solutions. To create mixtures with glucose mass fractions (wglucose) of 20%, 30%, 40%, and 50%, the systems contained 12, 18, 24, and 30 glucose molecules combined with 480, 420, 360, and 300 water molecules, respectively. At 298 K, α-d-glucose monohydrate forms in aqueous glucose solutions with mass fractions above 51%.34

Two groups of force fields are considered for sucrose: GLYCAM0622 and OPLS-AA.25,26 The three-site SPC/Fw water model is used.35 Nonbonded LJ interactions are truncated at a cutoff radius of 9 Å, and analytic tail corrections are included for the computation of energies and pressures.36 The standard mixing rules of the OPLS force field (see the Supporting Information) are applied for nonbonded LJ interactions between different atoms in different molecules, or atoms of the same molecule separated by at least three bonds.25,36 The Lorentz–Berthelot mixing rules are considered for the GLYCAM06 force field.36 The 1–4 nonbonded intramolecular interactions are scaled by a factor of 0.5 for the OPLS force field25 and a factor of 0 for the GLYCAM06 force field.22 Long-range electrostatic interactions are taken into account using the PPPM method with a relative precision of 10–6.36 The velocity-Verlet algorithm with a time step of 1 fs is used to integrate the equations of motion.36

Liquid densities are computed from an NPT ensemble, in which the temperature and pressure of the system are controlled by using the Nosé–Hoover thermostat and barostat.36 All transport properties and thermodynamic factors are computed in an NVT ensemble, where the temperature is kept fixed by using the Nosé–Hoover thermostat.36 The lengths of each simulation for computing transport and thermodynamic properties are 200 ns and (at least) 10 ns, respectively. To assert the statistical uncertainties, five independent simulations were performed for each condition.

The Einstein approach to calculating transport properties in equilibrium MD simulations is used.36−38 The shear viscosity is obtained from the off-diagonal components of the stress tensor (Pαβ), according to36,38,39

2. 1

where kB and t are the Boltzmann constant and time and V and T are the volume and temperature of the system. The angle brackets ⟨...⟩ denote an ensemble average. The self-diffusion coefficient of species i is calculated based on the mean-square displacement, as36,37

2. 2

in which Ni is the number of molecules of species i and rj,i is the position of jth molecule of species i. The finite-size effects of self-diffusion coefficients are taken into account by including the analytic correction proposed by Yeh and Hummer.40,41

There are two approaches to defining the mutual diffusion coefficient of a binary mixture:42−44 the well-known Fick diffusion coefficient (DFick) is mainly used in industrial applications, since Fick’s law relates the mass flux to gradients in concentrations, which can be measured experimentally. An equivalent formulation is based on the Maxwell–Stefan (MS) diffusion coefficient,45 which relates the mass flux to gradients in chemical potentials. For binary mixtures, Fick and MS diffusion coefficients are related by the thermodynamic factor, Γ, according to42,44,46−49

2. 3

with Γ defined as42,46,49−51

2. 4

where x1 and γ1 are the mole fraction and activity coefficient of species 1, respectively. For most binary mixtures (including those considered in this work), the deviations of the thermodynamic factor and solute activity coefficient from 1 are of opposite sign.50,52 For such cases, Γ > 1 determines the case that the interactions between different species are favored, whereas 0 < Γ < 1 determines the case that interactions between similar species dominate. The thermodynamic factor can thus be used as a measure for the degree of self-association of solutes. In some studies on water–carbohydrate solutions,15,16 the osmotic coefficient (Φ = 1 + ln(γsolvent)/ln(xsolvent)) is used instead. For the solutions studied, the osmotic coefficient contains the same information as the thermodynamic factor, with Φ > 1 determining the case that the interactions between different species are favored, while Φ < 1 determines the case that the interactions between similar species are strongest.

Fick diffusion coefficients can be obtained both from equilibrium or from nonequilibrium MD simulations.36,44,53−55 Here, we calculate Fick diffusivities based on eq 3, with MS diffusion coefficients and thermodynamic factors obtained from equilibrium MD simulations.44,56,57 Further details can be found in the review article of Liu et al.44

The MS diffusivity can be computed by calculating the Onsager coefficients (Λij):44,56

2. 5

The MS diffusivity of a binary system then follows from44,51

2. 6

The finite-size effects of Fick and MS diffusion coefficients are corrected using the analytic relation proposed by Jamali et al.58 The finite-size effects of MS diffusion coefficients can be as large as the magnitude of the computed MS diffusivities, depending on the nonideality of the mixture.58 As the modified force field is verified by comparing the mutual diffusivities with experiments, it is crucial to consider these finite-size effects and compute the mutual diffusion coefficients in the thermodynamic limit. To improve the sampling of the correlation functions in eqs 1, 2, and 5, an order-n algorithm is used.37,59

The thermodynamic factor is calculated from the so-called Kirkwood–Buff coefficients (Gij), which are obtained by integrating radial distribution functions over volume60,61 and applying appropriate finite-size corrections.62−65 For a binary mixture, the thermodynamic factor can be written as44

2. 7

where c1 is the number density of species 1. The finite-size effects of radial distribution functions are corrected for according to the work of van der Vegt and co-workers.62,63 Kirkwood–Buff coefficients (Gij) are computed in the thermodynamic limit using the method of Krüger et al.64,65

3. Results and Discussion

In this section, we first analyze several procedures for optimizing force fields of carbohydrate solutions. The quality of a procedure is measured by the accuracy with which thermodynamic factors and shear viscosities are estimated. Once the optimal procedure is established, we continue by developing and verifying a refined OPLS force field for aqueous solutions of sucrose. The transferability of the refined force field to aqueous solutions of other carbohydrates is examined by considering glucose. All computed properties presented in this section, and the force field parameters of both the original and refined OPLS force fields, are listed in the Supporting Information.

3.1. Analysis of Different Optimization Procedures

Batista et al.13 studied the effects of nonbonded electrostatic interactions in the GROMOS 56ACARBO and OPLS force fields for aqueous solutions of d-glucose. This study concluded that the properties of diluted solutions can be predicted accurately based on the 56ACARBO force field. At high glucose mass fractions (wglucose > 0.60), the overestimated self-association of glucose molecules was shown to result in overestimation of shear viscosities by up to 650%.13 To decrease the solute–solute interactions, all partial atomic charges of the glucose molecule were scaled by a factor 0.8. The estimation of shear viscosities of concentrated water–glucose mixtures was thereby improved significantly, with a maximum deviation from experiments of 27%.13 Besides an analysis on the density of the solution, these authors did not consider thermodynamic properties such as osmotic coefficients and thermodynamic factors to verify the performance of the optimized force field.

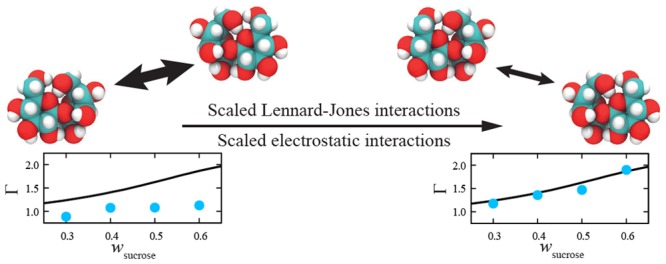
Inspired by the promising results of Batista et al.,13 we study a modified OPLS force field for which the partial atomic charges of sucrose are scaled by a factor 0.8. Similar to the work of Batista et al.,13 the LJ interactions parameters remain unchanged. In Figure 2, thermodynamic factors and shear viscosities computed based on the original OPLS force field and the OPLS force field with scaled partial atomic charges are compared to experimental data at 298 K and 1 atm. In agreement with the results of Batista et al.,13 the overestimation of shear viscosities is decreased by scaling the electrostatic interactions. This is especially the case for mixtures of high concentrations of sucrose, where sucrose–sucrose interactions mainly determine the properties of the mixture. Thermodynamic factors are less accurately reproduced. Our results show qualitatively incorrect changes as compared to the original OPLS force field, with larger deviations of thermodynamic factors from experiments. Estimated thermodynamic factors are closer to zero, meaning the self-association of sucrose has increased—not decreased. This suggests that merely scaling the partial atomic charges is insufficient to reproduce both thermodynamic and transport properties of carbohydrate solutions.

Figure 2.

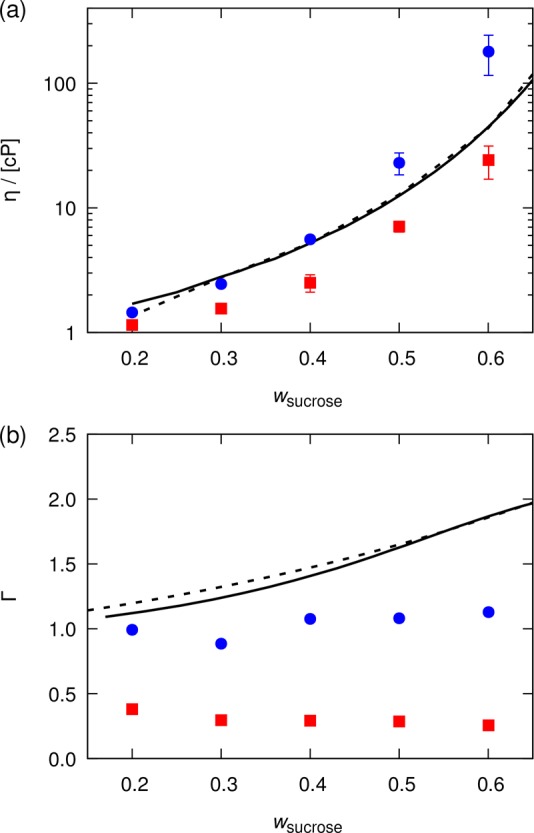
Figure 2

Open in a new tab

Computed (a) shear viscosities and (b) thermodynamic factors for water–sucrose mixtures as a function of the mass fraction of sucrose. The properties are computed based on the OPLS force field25 (blue circles) and the OPLS force field with scaled partial atomic charges13 (red squares). The SPC/Fw water model was used.35 Lines represent (a) experimental shear viscosities (solid,80 dashed81) and (b) thermodynamic factors (solid,82 dashed83). Error bars indicate 95% confidence intervals. No error bars are reported for the thermodynamic factors.

Another approach to optimizing a force field is to modify the LJ parameters of solute molecules. As a good rule of thumb, the size (σ) and energy (ϵ) parameters can be modified to improve the predictions of volumetric (e.g., liquid densities) and thermal (e.g., heat of vaporization) properties, respectively.2,23,27,66 In recent modifications of the MARTINI, CHARMM, and GLYCAM06 force fields for carbohydrate solutions,15,17 only the energy parameters were changed. An example is the work of Lay et al.,15 in which the CHARMM and GLYCAM06 force fields were modified by altering some of the LJ energy parameters (ϵij) defining the solute–solute interactions in aqueous solutions of glucose. On the basis of introducing modifications to carbon–carbon and carbon–oxygen interactions, accurate predictions of osmotic coefficients were obtained. However, shear viscosities were underestimated by about 60%.15

The modified GLYCAM06 force field of Lay et al. is analyzed in more detail in Figure 3. In this figure, computed thermodynamic factors and shear viscosities of water–sucrose mixtures are compared to results obtained based on the original GLYCAM06 force field. The modified energy parameters considerably improve the description of both properties, for a wide range of sucrose concentrations. Shear viscosities are especially well reproduced, showing a good agreement with experiments. We note that the improved results for viscosity as compared to those reported by Lay et al.15 may be due to using the SPC/Fw water model instead of TIP3P. The TIP3P water model is known to provide poor estimates for the shear viscosity of water.67−69 The SPC/Fw water model is one of the most accurate three-site models for estimating transport properties of water under ambient conditions.35,69,70 We chose a three-site model due to the smaller computational requirements compared to more complex models such as four-site (e.g., TIP4P/200571), five-site (e.g., TIP5P-E72), and polarizable (e.g., HBP73) water models. An extensive comparison of the performance of different water models can be found in the literature.66,68,69,74 Although thermodynamic factors are not as well described as shear viscosities, the observed increase in the thermodynamic factor is at least qualitatively correct. These results suggest that modifying the LJ energy parameters of solute molecules could be a sufficient procedure to develop a force field that accurately reproduces both thermodynamic and transport properties of carbohydrate solutions.

Figure 3.

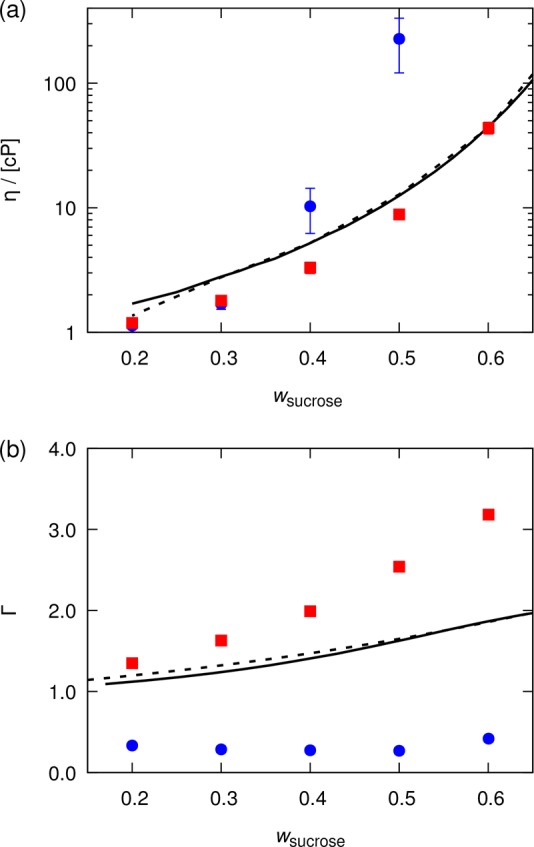
Figure 3

Open in a new tab

Computed (a) shear viscosities and (b) thermodynamic factors for water–sucrose mixtures as a function of the mass fraction of sucrose at 298 K and 1 atm. The properties are computed based on the GLYCAM06 force field22 (blue circles) and a modified GLYCAM force field as proposed by Lay et al.15 (red squares), in which some of the LJ sugar–sugar interactions are modified. The SPC/Fw water model was used.35 Lines represent (a) experimental shear viscosities (solid,80 dashed81) and (b) thermodynamic factors (solid,82 dashed83). Error bars indicate 95% confidence intervals. No error bars are reported for the thermodynamic factors.

While the approach of Lay et al. seems effective, this approach may require the modification of the LJ energy parameters of many different atom pairs, each with its own scaling factor. The choice of atoms whose ϵ is changed requires a profound understanding of the interactions between the atoms of the carbohydrate, which is not always known a priori. This, combined with the fact that the optimization of many force field parameters usually proceeds by trial and error (and is thus computationally expensive), leads us to suggest a different approach. On the basis of the results shown in Figures 2 and 3, we propose scaling the partial atomic charges and LJ energy parameters of all atoms of the carbohydrate. This can simultaneously improve the description of thermodynamic and transport properties, without requiring different scaling factors for different atom pairs. We propose to scale the nonbonded interaction parameters in such a way that experimental data for at least one thermodynamic property (e.g., thermodynamic factors) and one transport property (e.g., shear viscosities) can be reproduced by the force field. The advantage of this approach over the method of Lay et al.15 is a considerable reduction in the number of modification parameters to two: a single scaling factor for all LJ energy parameters of the carbohydrate and a single scaling factor for all partial atomic charges of the carbohydrate.

3.2. Refined OPLS Force Field

The optimization procedure proposed in the previous section is here applied to the OPLS force field, for aqueous solutions of sucrose. As in the previous section, thermodynamic factors and shear viscosities are considered as target properties. The following scaled LJ energy parameters (first number) and scaled partial atomic charges (second number) are considered: 1.0 and 1.0 (corresponding to the original OPLS force field), 1.0 and 0.8 (corresponding to the work of Batista et al.13), 0.8 and 1.0, and 0.8 and 0.8.

In Figure 4, computed thermodynamic factors and shear viscosities are compared to experimental data. In agreement with what is shown in Figure 2, scaling all partial atomic charges by a factor less than 1 decreases both the thermodynamic factors and shear viscosities. Scaling all LJ interactions by a factor less than 1 decreases the shear viscosities while increasing the thermodynamic factors. Adjusting LJ energy parameters can thus correct for a strong decrease in thermodynamic factors caused by scaling down partial atomic charges (as in Figure 2). Of these four combinations, the best combination is for the scaling factors of 0.8 and 1.0 for the LJ energy parameters and partial atomic charges, respectively. By interpolating between the computed thermodynamic factors and shear viscosities, corresponding to the four combinations of scaling factors, the optimum combination is a scaling factor of 0.8 for the LJ energy parameters and 0.95 for the partial atomic charges. Hereafter, the OPLS force field with this combination of scaling factors will be referred to as the refined OPLS force field. The interaction parameters of this force field (as well as the original OPLS force field) are listed in the Supporting Information.

Figure 4.

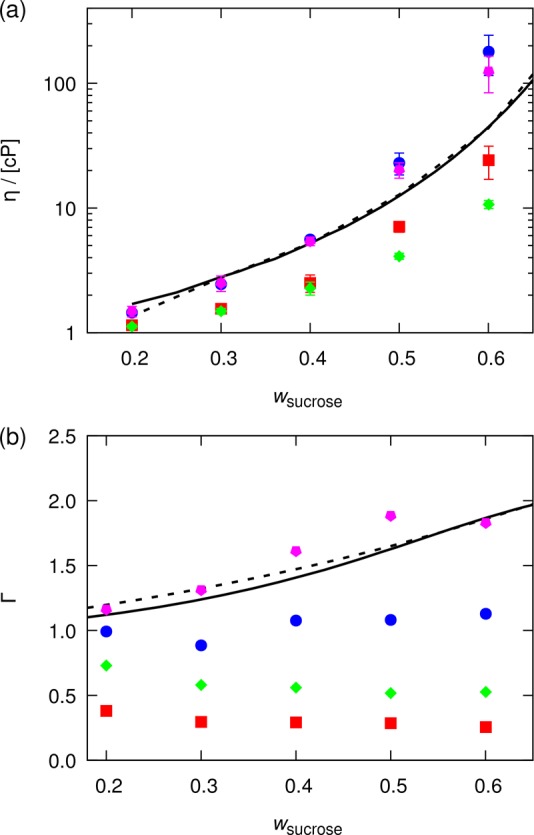
Figure 4

Open in a new tab

Computed (a) shear viscosities and (b) thermodynamic factors for water–sucrose mixtures as a function of the mass fraction of sucrose. All LJ energy (ϵ) parameters and partial atomic charges (q) of the OPLS force field25 are scaled by respectively 0.8 and 0.8 (green diamonds), 0.8 and 1.0 (magenta pentagons), 1.0 and 0.8 (red squares), and 1.0 and 1.0 (blue circles). The SPC/Fw water model was used.35 Lines represent (a) experimental shear viscosities (solid,80 dashed81) and (b) thermodynamic factors (solid,82 dashed83). Error bars indicate 95% confidence intervals. No error bars are reported for thermodynamic factors.

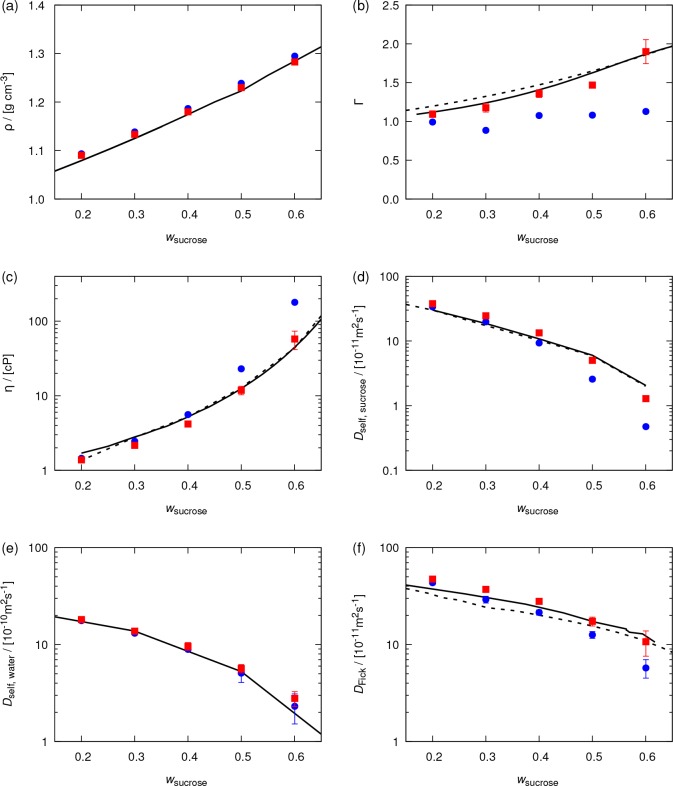
To verify that the refined OPLS force field outperforms the original OPLS force field, several thermodynamic and transport properties of the water–sucrose mixtures are computed at 298 K and 1 atm. In Figure 5, computed (a) liquid densities, (b) thermodynamic factors, (c) shear viscosities, (d) self-diffusivities of sucrose, (e) water, and (f) Fick diffusion coefficients are compared to experimental data for a wide range of concentrations. As compared to the original OPLS force field, thermodynamic properties (i.e., liquid densities and thermodynamic factors) computed using the refined OPLS force field show a considerably better agreement with experiments. In Figure 5a, excellent agreement between computed liquid densities and experimental data is observed. Since the size (σ) parameters of the LJ potentials are unaltered, the differences between liquid densities computed using the original and refined OPLS force fields are small. These differences reach a maximum value of 1%, at a sucrose mass fraction of 60%. Since the original OPLS force field overestimates solute–solute interactions at high concentrations of sucrose, the sucrose molecules tend to aggregate and form more packed liquid structures. This increases the density of the liquid, leading to overestimation of computed densities. Due to this overestimation of solute–solute interactions by the original OPLS force field, the thermodynamic factors are underestimated (see Figure 5b). The good agreement between computed thermodynamic factors and experimental data confirms an accurate description of the solute–solute and solute–water interactions by the refined OPLS force field.

Figure 5.

Figure 5

Open in a new tab

Computed (a) densities, (b) thermodynamic factors, (c) shear viscosities, (d) self-diffusivities of sucrose, (e) self-diffusivities of water, and (f) Fick (mutual) diffusion coefficients for water–sucrose mixtures as a function of the mass fraction of sucrose. Temperature and pressure are 298 K and 1 atm, respectively. The results of the original OPLS force field25 are shown by blue circles. The results of refined OPLS force field (scaled LJ energy parameters and partial atomic charges of all atoms of sucrose by factors of 0.8 and 0.95, respectively) are shown by red squares. Lines represent experimental data for (a) densities (solid,84 dashed85), (b) thermodynamic factors (solid,82 dashed83), (c) shear viscosities (solid,80 dashed81), (d) self-diffusivities of sucrose (solid,81 dashed86), (e) self-diffusivities of water (solid81), and (f) Fick diffusion coefficients (solid,87 dashed88). Error bars indicate 95% confidence intervals.

As shown in Figure 5c–f, transport properties computed using the refined OPLS force field are in excellent agreement with experimental data. At low sucrose concentrations, both the original and refined OPLS force fields yield similar values for the transport properties. Deviations become significant as the concentration of sucrose increases. In agreement with the work of Batista et al.,13 the shear viscosities (Figure 5c) computed based on the original OPLS force field are overestimated by up to 300% at a sucrose mass fraction of 0.6. For the refined OPLS force field, this deviation reaches a maximum of 30%. Figure 5d shows that the refined force field provides better estimates for the self-diffusion coefficients of sucrose at high sucrose mass fractions. This is due to less self-association, leading to higher mobility of sucrose molecules. In Figure 5e, no significant differences between self-diffusion coefficients of water computed using the original and refined OPLS force fields are observed. Both force fields were combined with the SPC/Fw water model, which mainly determines the self-diffusivity of water. As the concentration of sucrose increases, the sucrose–water interactions gradually become more important in determining the properties of the medium in which water molecules diffuse. This leads to the small differences observed between computed self-diffusivities at high sucrose mass fractions. In Figure 5f, Fick diffusion coefficients are compared with experiments. Similar to what is observed for the shear viscosity, Fick diffusivities computed using the refined OPLS force field are significantly closer to experimental values than those computed based on the original OPLS force field.

To verify whether the optimum scaling factors for LJ energy parameters (0.8) and partial atomic charges (0.95) are transferable to other carbohydrates, MD simulations were performed for aqueous solutions of the monosaccharide d-glucose at 298 K and 1 atm. Since mixtures of glucose with mass fractions above 51% produce α-d-glucose monohydrate, the following mass fractions of water–glucose mixtures are considered: 20%, 30%, 40%, and 50%. d-Glucose forms two anomers in an aqueous solution.75 Simulation input files are constructed for a ratio 1:2 of α-d-glucose to β-d-glucose.15,27,76,77 Lay et al.15 observed that the exact value of this ratio does not affect the outcome of MD simulations.

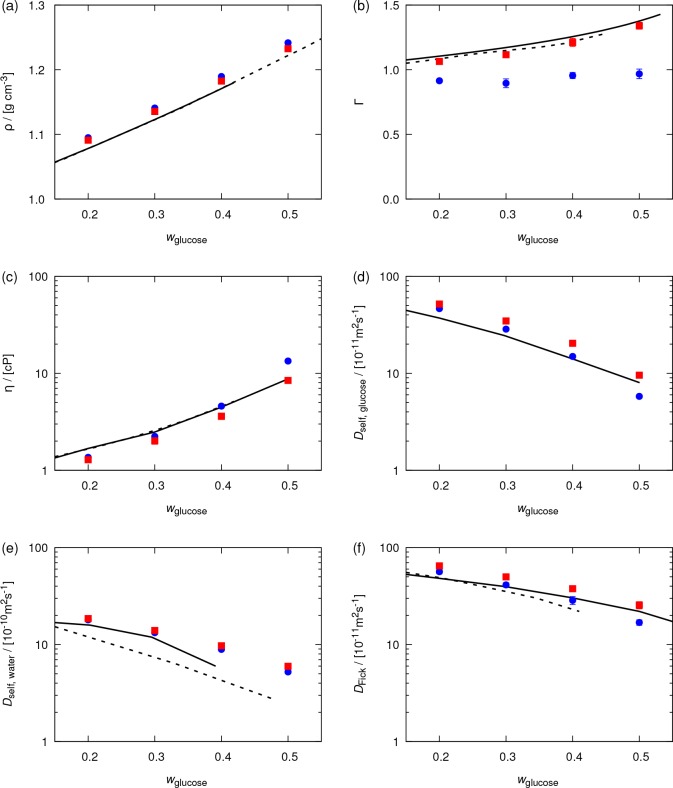
In Figure 6, computed thermodynamic and transport properties of water–glucose mixtures are compared with experiments. The order of the subfigures is the same as in Figure 5. The results shown in Figure 6a and b clearly show that, compared to the original OPLS force field, the refined OPLS force field leads to a significantly better description of thermodynamic properties. Computed thermodynamic factors are larger than 1 and close to experimental values; the unphysical self-association of glucose molecules at elevated concentrations is thus resolved by using the refined OPLS force field. Figure 6c–f shows the transport properties for glucose–water mixtures (i.e., the shear viscosity, self-diffusivity of glucose and water, and Fick diffusion coefficient). A good agreement between experimental data and computed transport properties is observed. At low mass fractions of glucose (wglucose ≤ 0.4), the original OPLS force field shows slightly better agreement with experimental data. However, it is important to note that, for these diluted solutions, the difference between the results obtained based on these two force fields is at most 40% (for self-diffusivity of glucose at a mass fraction of 40%). This is mainly due to the low concentration of glucose, which decreases the effect of the carbohydrate force field on mixture properties. As the mass fraction of glucose rises above 40%, the refined OPLS force field provides better estimates for transport properties. At these concentrations, the results computed based on the original OPLS force field deviate significantly from experiments.13

Figure 6.

Figure 6

Open in a new tab

Computed (a) densities, (b) thermodynamic factors, (c) shear viscosities, (d) self-diffusivities of glucose, (e) self-diffusivities of water, and (f) Fick (mutual) diffusion coefficients for water–glucose mixtures as a function of the mass fraction of glucose. Temperature and pressure are 298 K and 1 atm, respectively. The results of the original OPLS force field25 are shown by blue circles. The results of the refined OPLS force field (scaled LJ energy parameters and partial atomic charges of all atoms of glucose by factors of 0.8 and 0.95, respectively) are shown by red squares. Solid lines represent experimental data for (a) densities (solid,89 dashed90), (b) thermodynamic factors (solid,91 dashed92), (c) shear viscosities (solid,78 dahsed89), (d) self-diffusivities of glucose (solid90), (e) self-diffusivities of water (solid,90 dashed93), and (f) Fick diffusion coefficients (solid,94 dahsed95). Error bars indicate 95% confidence intervals.

By increasing the temperature of the water–glucose mixture, the solubility of glucose in water increases, and mixtures with higher mass fractions of glucose can be realized. For these concentrated solutions, the refined OPLS force field is expected to lead to significant improvements over the original OPLS force field. To verify this, we computed the shear viscosity of an aqueous solution with a glucose mass fraction of 60%, at 313.15 K and 1 atm. The shear viscosities computed based on the original and refined OPLS force fields are 32 ± 4 cP and 15.0 ± 1.5 cP, respectively. Compared to an experimental value of 13.08 cP for this mixture,78 the original OPLS force field leads to a considerable overestimation of the shear viscosity (of about 150%). The refined OPLS force field significantly improves the description at such a high glucose mass fraction.

4. Conclusions

For aqueous solutions of carbohydrates, most force fields predict self-aggregation of solute molecules due to the overestimation of solute–solute interactions. This overestimation results in large deviations of computed properties from experimental data, especially for concentrated solutions, which are relevant to food and biotechnological industries. To decrease the tendency of solute molecules to self-aggregate, we proposed scaling the Lennard-Jones energy parameters (ϵ) and partial atomic charges (q) of the OPLS force field. In this way, accurate estimates were obtained for thermodynamic and transport properties of aqueous solutions of sucrose with mass fractions in the range 20%–60%. For this optimization, the three-site SPC/Fw water model was used. No modification in the bonded and nonbonded interaction parameters of the water model was applied. The optimum scaling factors for the Lennard-Jones energy parameters and partial atomic charges were obtained by reproducing experimental thermodynamic factors and shear viscosities of aqueous sucrose solutions. These factors are 0.8 and 0.95, respectively. For both the original and refined OPLS force fields, MD simulations were performed to calculate thermodynamic properties (i.e., liquid densities and thermodynamic factors) and transport properties (i.e., shear viscosities, self-diffusivities of water and sucrose, and Fick diffusion coefficients). Excellent agreement is observed between the properties computed based on the refined OPLS force field and experiments, for a wide range of sucrose concentrations. The transferability of the optimum scaling factors was verified by performing MD simulations of aqueous solutions of d-glucose. The computed thermodynamic and transport properties agree well with available experimental data, especially at high concentrations of glucose. This suggests that the scaling factors are transferable to other carbohydrates. By using the refined OPLS force field, accurate estimates for thermodynamic and transport properties can be obtained. While the proposed method for optimizing the nonbonded interactions of a force field was verified for the OPLS force field, this method may also be used for other force fields combined with other water models.

Acknowledgments

This work was sponsored by NWO Exacte Wetenschappen (Physical Sciences) for the use of supercomputer facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organization for Scientific Research, NWO). T.J.H.V. acknowledges NWO–CW (Chemical Sciences) for a VICI grant. T.v.W. performed this work as part of the Industrial Partnership Programme “Hybrid Soft Materials” that is carried out under an agreement between Unilever Research and Development B.V. and NWO.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b00909.

  • The force field parameters of both the original and refined OPLS force fields, all computed thermodynamic and transport properties presented in this work (PDF)

  • sample LAMMPS script for simulating water–sucrose and water–glucose mixtures (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ct8b00909_si_001.pdf (729.7KB, pdf)
ct8b00909_si_002.zip (121.8KB, zip)

References

  1. Varki A.; Cummings R. D.; Esko J. D.; Stanley P.; Hart G. W.; Aebi M.; Darvill A. G.; Kinoshita T.; Packer N. H.; Prestegard J. H.; Schnaar R. L.; Seeberger P. H.. Essentials of Glycobiology, 3rd ed.; Cold Spring Harbor Laboratory Press: New York, 2017. [PubMed] [Google Scholar]
  2. Fadda E.; Woods R. J. Molecular Simulations of Carbohydrates and Protein-Carbohydrate Interactions: Motivation, Issues and Prospects. Drug Discovery Today 2010, 15, 596–609. 10.1016/j.drudis.2010.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Fennema O.; Powrie W. D. In Fundamentals of Low-Temperature Food Preservation; Chichester C. O., Mrak E. M., Stewart G. F., Eds.; Advances in Food Research; Academic Press, 1964; Vol. 13; pp 219–347. [DOI] [PubMed] [Google Scholar]
  4. Lee J.; Timasheff S. The Stabillization of Proteins by Sucrose. J. Biol. Chem. 1981, 256, 7193–7201. [PubMed] [Google Scholar]
  5. Karlsson J. O.; Toner M. Long-term Storage of Tissues by Cryopreservation: Critical Issues. Biomaterials 1996, 17, 243–256. 10.1016/0142-9612(96)85562-1. [DOI] [PubMed] [Google Scholar]
  6. Day J. G.; Stacey G. N.. Cryopreservation and Freeze-Drying Protocols, 2nd ed.; Humana Press: Totowa, 2007. [Google Scholar]
  7. Rahman M. S. Handbook of Food Preservation, 2nd ed.; CRC Press: Boca Raton, 2007. [Google Scholar]
  8. Roos Y. H.; Drusch S.. Phase Transitions in Foods, 2nd ed.; Academic Press: Oxford, 2015. [Google Scholar]
  9. Csonka L. N. Physiological and Genetic Responses of Bacteria to Osmotic Stress. Microbiol. Rev. 1989, 53, 121–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Vollmer W.; Blanot D.; De Pedro M. A. Peptidoglycan Structure and Architecture. FEMS Microbiol. Rev. 2008, 32, 149–167. 10.1111/j.1574-6976.2007.00094.x. [DOI] [PubMed] [Google Scholar]
  11. Vollmer W.; Bertsche U. Murein (Peptidoglycan) Structure, Architecture and Biosynthesis in Escherichia Coli. Biochim. Biophys. Acta, Biomembr. 2008, 1778, 1714–1734. 10.1016/j.bbamem.2007.06.007. [DOI] [PubMed] [Google Scholar]
  12. Sapir L.; Harries D. Linking Trehalose Self-Association with Binary Aqueous Solution Equation of State. J. Phys. Chem. B 2011, 115, 624–634. 10.1021/jp109780n. [DOI] [PubMed] [Google Scholar]
  13. Batista M. L. S.; Pérez-Sánchez G.; Gomes J. R. B.; Coutinho J. A. P.; Maginn E. J. Evaluation of the GROMOS 56A CARBO Force Field for the Calculation of Structural, Volumetric, and Dynamic Properties of Aqueous Glucose Systems. J. Phys. Chem. B 2015, 119, 15310–15319. 10.1021/acs.jpcb.5b08155. [DOI] [PubMed] [Google Scholar]
  14. Sauter J.; Grafmüller A. Predicting the Chemical Potential and Osmotic Pressure of Polysaccharide Solutions by Molecular Simulations. J. Chem. Theory Comput. 2016, 12, 4375–4384. 10.1021/acs.jctc.6b00295. [DOI] [PubMed] [Google Scholar]
  15. Lay W. K.; Miller M. S.; Elcock A. H. Optimizing Solute-Solute Interactions in the GLYCAM06 and CHARMM36 Carbohydrate Force Fields Using Osmotic Pressure Measurements. J. Chem. Theory Comput. 2016, 12, 1401–1407. 10.1021/acs.jctc.5b01136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lay W. K.; Miller M. S.; Elcock A. H. Reparameterization of Solute-Solute Interactions for Amino Acid-Sugar Systems Using Isopiestic Osmotic Pressure Molecular Dynamics Simulations. J. Chem. Theory Comput. 2017, 13, 1874–1882. 10.1021/acs.jctc.7b00194. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Schmalhorst P. S.; Deluweit F.; Scherrers R.; Heisenberg C.-P.; Sikora M. Overcoming the Limitations of the MARTINI Force Field in Simulations of Polysaccharides. J. Chem. Theory Comput. 2017, 13, 5039–5053. 10.1021/acs.jctc.7b00374. [DOI] [PubMed] [Google Scholar]
  18. MacKerell A. D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Kuchnir L.; Kuczera K.; Lau F. T. K.; Mattos C.; Michnick S.; Ngo T.; Nguyen D. T.; Prodhom B.; Reiher W. E.; Roux B.; Schlenkrich M.; Smith J. C.; Stote R.; Straub J.; Watanabe M.; Wiórkiewicz-Kuczera J.; Yin D.; Karplus M. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  19. Guvench O.; Hatcher E.; Venable R. M.; Pastor R. W.; MacKerell A. D. CHARMM Additive All-Atom Force Field for Glycosidic Linkages between Hexopyranoses. J. Chem. Theory Comput. 2009, 5, 2353–2370. 10.1021/ct900242e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Raman E. P.; Guvench O.; MacKerell A. D. CHARMM Additive All-Atom Force Field for Glycosidic Linkages in Carbohydrates Involving Furanoses. J. Phys. Chem. B 2010, 114, 12981–12994. 10.1021/jp105758h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Guvench O.; Mallajosyula S. S.; Raman E. P.; Hatcher E.; Vanommeslaeghe K.; Foster T. J.; Jamison F. W.; MacKerell A. D. CHARMM Additive All-Atom Force Field for Carbohydrate Derivatives and Its Utility in Polysaccharide and CarbohydrateProtein Modeling. J. Chem. Theory Comput. 2011, 7, 3162–3180. 10.1021/ct200328p. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kirschner K. N.; Yongye A. B.; Tschampel S. M.; González-Outeiriño J.; Daniels C. R.; Foley B. L.; Woods R. J. GLYCAM06: A Generalizable Biomolecular Force Field. Carbohydrates. J. Comput. Chem. 2008, 29, 622–655. 10.1002/jcc.20820. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Oostenbrink C.; Villa A.; Mark A. E.; Van Gunsteren W. F. A Biomolecular Force Field Based on the Free Enthalpy of Hydration and Solvation: The GROMOS Force-field Parameter Sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
  24. Lins R. D.; Hünenberger P. H. A New GROMOS Force Field for Hexopyranose-based Carbohydrates. J. Comput. Chem. 2005, 26, 1400–1412. 10.1002/jcc.20275. [DOI] [PubMed] [Google Scholar]
  25. Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
  26. Damm W.; Frontera A.; Tirado-Rives J.; Jorgensen W. L. OPLS All-Atom Force Field for Carbohydrates. J. Comput. Chem. 1997, 18, 1955–1970. . [DOI] [Google Scholar]
  27. Kony D.; Damm W.; Stoll S.; Van Gunsteren W. F. An improved OPLS-AA force field for carbohydrates. J. Comput. Chem. 2002, 23, 1416–1429. 10.1002/jcc.10139. [DOI] [PubMed] [Google Scholar]
  28. Lopez C. A.; Rzepiela A. J.; de Vries A. H.; Dijkhuizen L.; Hunenberger P. H.; Marrink S. J. Martini Coarse-Grained Force Field: Extension to Carbohydrates. J. Chem. Theory Comput. 2009, 5, 3195–3210. 10.1021/ct900313w. [DOI] [PubMed] [Google Scholar]
  29. Zhang Y.; Zhang Y.; McCready M. J.; Maginn E. J. Evaluation and Refinement of the General AMBER Force Field for Nineteen Pure Organic Electrolyte Solvents. J. Chem. Eng. Data 2018, 63, 3488. 10.1021/acs.jced.8b00382. [DOI] [Google Scholar]
  30. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  31. Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  32. Young F. E.; Jones F. T. Sucrose Hydrates. The Sucrose-Water Phase Diagram. J. Phys. Colloid Chem. 1949, 53, 1334–1350. 10.1021/j150474a004. [DOI] [Google Scholar]
  33. Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  34. Young F. E. D-Glucose-Water Phase Diagram. J. Phys. Chem. 1957, 61, 616–619. 10.1021/j150551a023. [DOI] [Google Scholar]
  35. Wu Y.; Tepper H. L.; Voth G. A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124, 024503 10.1063/1.2136877. [DOI] [PubMed] [Google Scholar]
  36. Allen M. P.; Tildesley D. J.. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Croydon, 2017. [Google Scholar]
  37. Frenkel D.; Smit B.. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: London, 2002. [Google Scholar]
  38. Zwanzig R. Time-Correlation Functions and Transport Coefficients in Statistical Mechanics. Annu. Rev. Phys. Chem. 1965, 16, 67–102. 10.1146/annurev.pc.16.100165.000435. [DOI] [Google Scholar]
  39. Hess B. Determining the Shear Viscosity of Model Liquids from Molecular Dynamics Simulations. J. Chem. Phys. 2002, 116, 209. 10.1063/1.1421362. [DOI] [Google Scholar]
  40. Yeh I.-C.; Hummer G. System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. J. Phys. Chem. B 2004, 108, 15873–15879. 10.1021/jp0477147. [DOI] [Google Scholar]
  41. Dünweg B.; Kremer K. Molecular Dynamics Simulation of a Polymer Chain in Solution. J. Chem. Phys. 1993, 99, 6983–6997. 10.1063/1.465445. [DOI] [Google Scholar]
  42. Taylor R.; Krishna R.. Multicomponent Mass Transfer; John Wiley & Sons: New York, 1993. [Google Scholar]
  43. Poling B. E.; Prausnitz J. M.; O’Connel J. P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: Singapore, 2001. [Google Scholar]
  44. Liu X.; Schnell S. K.; Simon J.-M.; Krüger P.; Bedeaux D.; Kjelstrup S.; Bardow A.; Vlugt T. J. H. Diffusion Coefficients from Molecular Dynamics Simulations in Binary and Ternary Mixtures. Int. J. Thermophys. 2013, 34, 1169–1196. 10.1007/s10765-013-1482-3. [DOI] [Google Scholar]
  45. Krishna R.; Wesselingh J. The Maxwell-Stefan Approach to Mass Transfer. Chem. Eng. Sci. 1997, 52, 861–911. 10.1016/S0009-2509(96)00458-7. [DOI] [Google Scholar]
  46. Kooijman H. A.; Taylor R. Estimation of diffusion coefficients in multicomponent liquid systems. Ind. Eng. Chem. Res. 1991, 30, 1217–1222. 10.1021/ie00054a023. [DOI] [Google Scholar]
  47. Guevara-Carrion G.; Janzen T.; Muñoz-Muñoz Y. M.; Vrabec J. Mutual Diffusion of Binary Liquid Mixtures Containing Methanol, Ethanol, Acetone, Benzene, Cyclohexane, Toluene, and Carbon Tetrachloride. J. Chem. Phys. 2016, 144, 124501. 10.1063/1.4943395. [DOI] [PubMed] [Google Scholar]
  48. Guevara-Carrion G.; Gaponenko Y.; Janzen T.; Vrabec J.; Shevtsova V. Diffusion in Multicomponent Liquids: From Microscopic to Macroscopic Scales. J. Phys. Chem. B 2016, 120, 12193–12210. 10.1021/acs.jpcb.6b09810. [DOI] [PubMed] [Google Scholar]
  49. Krishna R.; van Baten J. M. Describing Diffusion in Fluid Mixtures at Elevated Pressures by Combining the Maxwell-Stefan Formulation with an Equation of State. Chem. Eng. Sci. 2016, 153, 174–187. 10.1016/j.ces.2016.07.025. [DOI] [Google Scholar]
  50. Taylor R.; Kooijman H. A. Composition Derivatives of Activity Coefficient Models (For the Estimation of Thermodynamic Factors in Diffusion). Chem. Eng. Commun. 1991, 102, 87–106. 10.1080/00986449108910851. [DOI] [Google Scholar]
  51. Krishna R.; van Baten J. M. The Darken Relation for Multicomponent Diffusion in Liquid Mixtures of Linear Alkanes: An Investigation Using Molecular Dynamics (MD) Simulations. Ind. Eng. Chem. Res. 2005, 44, 6939–6947. 10.1021/ie050146c. [DOI] [Google Scholar]
  52. Smith J. M.; Van Ness H. C. Introduction to Chemical Engineering Thermodynamics, 7th ed.; McGraw-Hill: Singapore, 2004. [Google Scholar]
  53. Wheeler D. R.; Newman J. Molecular Dynamics Simulations of Multicomponent Diffusion. 1. Equilibrium Method. J. Phys. Chem. B 2004, 108, 18353–18361. 10.1021/jp047850b. [DOI] [Google Scholar]
  54. Wheeler D. R.; Newman J. Molecular Dynamics Simulations of Multicomponent Diffusion. 2. Nonequilibrium Method. J. Phys. Chem. B 2004, 108, 18362–18367. 10.1021/jp047849c. [DOI] [Google Scholar]
  55. Nichols J. W.; Wheeler D. R. Fourier Correlation Method for Simulating Mutual Diffusion Coefficients in Condensed Systems at Equilibrium. Ind. Eng. Chem. Res. 2015, 54, 12156–12164. 10.1021/acs.iecr.5b02849. [DOI] [Google Scholar]
  56. Liu X.; Bardow A.; Vlugt T. J. H. Multicomponent Maxwell-Stefan Diffusivities at Infinite Dilution. Ind. Eng. Chem. Res. 2011, 50, 4776–4782. 10.1021/ie102515w. [DOI] [Google Scholar]
  57. Liu X.; Schnell S. K.; Simon J.-M.; Bedeaux D.; Kjelstrup S.; Bardow A.; Vlugt T. J. H. Fick Diffusion Coefficients of Liquid Mixtures Directly Obtained From Equilibrium Molecular Dynamics. J. Phys. Chem. B 2011, 115, 12921–12929. 10.1021/jp208360s. [DOI] [PubMed] [Google Scholar]
  58. Jamali S. H.; Wolff L.; Becker T. M.; Bardow A.; Vlugt T. J. H.; Moultos O. A. Finite-Size Effects of Binary Mutual Diffusion Coefficients from Molecular Dynamics. J. Chem. Theory Comput. 2018, 14, 2667–2677. 10.1021/acs.jctc.8b00170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Dubbeldam D.; Ford D. C.; Ellis D. E.; Snurr R. Q. A New Perspective on the Ordern Algorithm for Computing Correlation Functions. Mol. Simul. 2009, 35, 1084–1097. 10.1080/08927020902818039. [DOI] [Google Scholar]
  60. Kirkwood J. G.; Buff F. P. The Statistical Mechanical Theory of Solutions. I. J. Chem. Phys. 1951, 19, 774. 10.1063/1.1748352. [DOI] [Google Scholar]
  61. Ben-Naim A.Molecular Theory of Solutions; Oxford University Press: Oxford, 2006. [Google Scholar]
  62. Milzetti J.; Nayar D.; van der Vegt N. F. A. Convergence of Kirkwood-Buff Integrals of Ideal and Nonideal Aqueous Solutions Using Molecular Dynamics Simulations. J. Phys. Chem. B 2018, 122, 5515–5526. 10.1021/acs.jpcb.7b11831. [DOI] [PubMed] [Google Scholar]
  63. Ganguly P.; van der Vegt N. F. A. Convergence of Sampling Kirkwood-Buff Integrals of Aqueous Solutions with Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 1347–1355. 10.1021/ct301017q. [DOI] [PubMed] [Google Scholar]
  64. Krüger P.; Schnell S. K.; Bedeaux D.; Kjelstrup S.; Vlugt T. J. H.; Simon J.-M. Kirkwood-Buff Integrals for Finite Volumes. J. Phys. Chem. Lett. 2013, 4, 235–238. 10.1021/jz301992u. [DOI] [PubMed] [Google Scholar]
  65. Krüger P.; Vlugt T. J. H. Size and Shape Dependence of Finite-volume Kirkwood-Buff Integrals. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2018, 97, 051301 10.1103/PhysRevE.97.051301. [DOI] [PubMed] [Google Scholar]
  66. Onufriev A. V.; Izadi S. Water Models for Biomolecular Simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1347 10.1002/wcms.1347. [DOI] [Google Scholar]
  67. Song Y.; Dai L. L. The Shear Viscosities of Common Water Models by Non-Equilibrium Molecular Dynamics Simulations. Mol. Simul. 2010, 36, 560–567. 10.1080/08927021003720553. [DOI] [Google Scholar]
  68. Vega C.; Abascal J. L. F. Simulating Water with Rigid Non-Polarizable Models: A General Perspective. Phys. Chem. Chem. Phys. 2011, 13, 19663. 10.1039/c1cp22168j. [DOI] [PubMed] [Google Scholar]
  69. Tsimpanogiannis I. N.; Moultos O. A.; Franco L. F. M.; Spera M. B. d. M.; Erdos M.; Economou I. G. Self-diffusion Coefficient of Bulk and Confined Water: A Critical Review of Classical Molecular Simulation Studies. Mol. Simul. 2018, 1–29. 10.1080/08927022.2018.1511903. [DOI] [Google Scholar]
  70. Medina J.; Prosmiti R.; Villarreal P.; Delgado-Barrio G.; Winter G.; González B.; Alemán J.; Collado C. Molecular Dynamics Simulations of Rigid and Flexible Water Models: Temperature Dependence of Viscosity. Chem. Phys. 2011, 388, 9–18. 10.1016/j.chemphys.2011.07.001. [DOI] [Google Scholar]
  71. Abascal J. L. F.; Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
  72. Rick S. W. A Reoptimization of the Five-site Water Potential (TIP5P) for Use with Ewald Sums. J. Chem. Phys. 2004, 120, 6085–6093. 10.1063/1.1652434. [DOI] [PubMed] [Google Scholar]
  73. Jiang H.; Moultos O. A.; Economou I. G.; Panagiotopoulos A. Z. Hydrogen-Bonding Polarizable Intermolecular Potential Model for Water. J. Phys. Chem. B 2016, 120, 12358–12370. 10.1021/acs.jpcb.6b08205. [DOI] [PubMed] [Google Scholar]
  74. Mao Y.; Zhang Y. Thermal Conductivity, Shear Viscosity and Specific Heat of Rigid Water Models. Chem. Phys. Lett. 2012, 542, 37–41. 10.1016/j.cplett.2012.05.044. [DOI] [Google Scholar]
  75. Lehninger A. L.; Nelson D. L.; Cox M. M. Lehninger Principles of Biochemistry, 6th ed.; W.H. Freeman and Company: New York, 2013. [Google Scholar]
  76. Nishida Y.; Ohrui H.; Meguro H. 1H-NMR Studies of (6r)- and (6s)-deuterated D-hexoses: Assignment of the Preferred Rotamers about C5-C6 bond of D-glucose and D-galactose Derivatives in Solutions. Tetrahedron Lett. 1984, 25, 1575–1578. 10.1016/S0040-4039(01)90014-0. [DOI] [Google Scholar]
  77. Nishida Y.; Hori H.; Ohrui H.; Meguro H. 1H NMR Analyses of Rotameric Distribution of C5-C6 bonds of D-Glucopyranoses in Solution. J. Carbohydr. Chem. 1988, 7, 239–250. 10.1080/07328308808058917. [DOI] [Google Scholar]
  78. Telis V.; Telis-Romero J.; Mazzotti H.; Gabas A. Viscosity of Aqueous Carbohydrate Solutions at Different Temperatures and Concentrations. Int. J. Food Prop. 2007, 10, 185–195. 10.1080/10942910600673636. [DOI] [Google Scholar]
  79. Dubbeldam D.; Calero S.; Vlugt T. J. H. iRASPA: GPU-accelerated Visualization Software for Materials Scientists. Mol. Simul. 2018, 44, 653–676. 10.1080/08927022.2018.1426855. [DOI] [Google Scholar]
  80. Asadi M.Beet-Sugar Handbook; John Wiley & Sons: Hoboken, NJ, 2007. [Google Scholar]
  81. Rampp M.; Buttersack C.; Lüdemann H.-D. c, T -Dependence of the Viscosity and the Self-diffusion Coefficients in Some Aqueous Carbohydrate Solutions. Carbohydr. Res. 2000, 328, 561–572. 10.1016/S0008-6215(00)00141-5. [DOI] [PubMed] [Google Scholar]
  82. Robinson R. A.; Stokes R. H. Activity Coefficients in Aqueous Solutions of Sucrose, Mannitol and Their Mixtures at 25. J. Phys. Chem. 1961, 65, 1954–1958. 10.1021/j100828a010. [DOI] [Google Scholar]
  83. Starzak M.; Mathlouthi M. Temperature Dependence of Water Activity in Aqueous Solutions of Sucrose. Food Chem. 2006, 96, 346–370. 10.1016/j.foodchem.2005.02.052. [DOI] [Google Scholar]
  84. Mathlouthi M., Reiser P.. Sucrose; Springer: Boston, MA, 1995. [Google Scholar]
  85. Fucaloro A. F.; Pu Y.; Cha K.; Williams A.; Conrad K. Partial Molar Volumes and Refractions of Aqueous Solutions of Fructose, Glucose, Mannose, and Sucrose at 15.00, 20.00, and 25.00 C. J. Solution Chem. 2007, 36, 61–80. 10.1007/s10953-006-9100-7. [DOI] [Google Scholar]
  86. Girlich D.; Lüdemann H. D.; Buttersack C.; Buchholz K. c, T-Dependence of the Self Diffusion in Concentrated Aqueous Sucrose Solutions. Z. Naturforsch., C: J. Biosci. 1994, 49, 258–264. 10.1515/znc-1994-3-415. [DOI] [Google Scholar]
  87. Henrion P. N. Diffusion in the Sucrose + Water System. Trans. Faraday Soc. 1964, 60, 72. 10.1039/tf9646000072. [DOI] [Google Scholar]
  88. Irani R. R.; Adamson A. W. Transport Processes in Binary Liquid Systems. J. Phys. Chem. 1958, 62, 1517–1521. 10.1021/j150570a012. [DOI] [Google Scholar]
  89. Comesaña J. F.; Otero J. J.; García E.; Correa A. Densities and Viscosities of Ternary Systems of Water + Glucose + Sodium Chloride at Several Temperatures. J. Chem. Eng. Data 2003, 48, 362–366. 10.1021/je020153x. [DOI] [Google Scholar]
  90. Castaldi M.; D’Errico G.; Paduano L.; Vitagliano V. Transport Properties of the Binary System Glucose-Water at 25 °C. A Velocity Correlation Study. J. Chem. Eng. Data 1998, 43, 653–657. 10.1021/je980054c. [DOI] [Google Scholar]
  91. Stokes R. H.; Robinson R. a. Interactions in Aqueous Nonelectrolyte Solutions. I. Solute-Solvent Equilibria. J. Phys. Chem. 1966, 70, 2126–2131. 10.1021/j100879a010. [DOI] [Google Scholar]
  92. Miyajima K.; Sawada M.; Nakagaki M. Studies on Aqueous Solutions of Saccharides. Activity Coefficients of Monosaccharides in Aqueous Solutions at 25 C. Bull. Chem. Soc. Jpn. 1983, 56, 1620–1623. 10.1246/bcsj.56.1620. [DOI] [Google Scholar]
  93. Talon C.; Smith L. J.; Brady J. W.; Lewis B. A.; Copley J. R. D.; Price D. L.; Saboungi M.-L. Dynamics of Water Molecules in Glucose Solutions. J. Phys. Chem. B 2004, 108, 5120–5126. 10.1021/jp035161e. [DOI] [Google Scholar]
  94. Gladden J. K.; Dole M. Diffusion in Supersaturated Solutions. II. Glucose Solutions. J. Am. Chem. Soc. 1953, 75, 3900–3904. 10.1021/ja01112a008. [DOI] [Google Scholar]
  95. van de Ven-Lucassen I. M. J. J.; Kerkhof P. J. A. M. Diffusion Coefficients of Ternary Mixtures of Water, Glucose, and Dilute Ethanol, Methanol, or Acetone by the Taylor Dispersion Method. J. Chem. Eng. Data 1999, 44, 93–97. 10.1021/je9801866. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct8b00909_si_001.pdf (729.7KB, pdf)
ct8b00909_si_002.zip (121.8KB, zip)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES