Huffaker revisited: spatial heterogeneity and the coupling of ineffective agents in biological control

Abstract

In a classic study, Huffaker demonstrated that abiotic forms of spatial heterogeneity could induce stability in predator-prey interactions. Recent theories suggest that space can also act to destabilize predator-prey systems and that stability can arise from coupling of unstable units. Here, using Huffaker’s classic experimental design refitted with modern empirical and statistical techniques, we reassess the effect of space on predator-prey interactions when the prey are pests of agriculture, and when predators must compete with pathogens for shared prey resources. Using an empirical system including aphids, ladybird beetles and entomopathogenic fungi, we show that while two different control agents were ineffective at controlling pests in insolation, coupling them together not only improved control of the pest, but also reduced the occurrence of large, spatially-clustered pest outbreaks. Our results suggest that as agriculture becomes increasingly isolated and consolidated across landscapes, endogenous forms of spatial heterogeneity, which arise from interactions between diverse assemblages of control agents, may break down. We suggest that improving connectivity across landscapes is important for maintaining effective biological control in agroecosystems.

Introduction

In 1958, C. B. Huffaker conducted what would become a classic study on the role of dispersal in the coexistence of predators and prey (Huffaker 1958). At the time, the Lotka-Volterra equations were well-known to predict regular, repeatable cycles between predators and prey, yet empirical studies failed to reproduce these theoretical results (Gause 1934; Gause et al. 1936). These early empirical studies were done in well-mixed environments to mimic the assumptions of the Lotka-Voltera model. Predators had easy access to prey, but rather than decreasing in numbers before prey were completely exhausted, in most cases predators overexploited prey, leading to extinction of the whole system. Citing Nicholson’s (Nicholson 1933, 1954) criticism of the early empirical studies being contained in microcosms that were “too small to even approximate a qualitative, to say nothing of a quantitative, conformity to theory,” Huffaker designed experiments using a series of spatial arrays or “universes” composed of carefully arranged oranges (prey resources), while manipulating the dispersal abilities of predatory and prey mite species. He discovered that reducing the dispersal of predators by slowing them with petroleum jelly and encouraging dispersal in prey by providing wooden dowels for long distance migration introduced sufficient spatial heterogeneity to keep prey from going extinct immediately, allowing predator-prey cycles to be observed (Huffaker 1958). This early study established the importance of spatial heterogeneity in maintaining predator/prey cycles, providing one mechanism to explain the discordance between experimental evidence that predator/prey pairs go extinct and the overwhelming evidence from nature that predators and their prey do indeed persist over many years.

In his conclusions, Huffaker cautioned that the use of spatially homogenous monocultures in agriculture could have unintended consequences for biological control, which are simply predator-prey systems where control agents are released to consume pest prey (Huffaker 1958; Huffaker et al. 1963). This is still a concern for agroecosystems today, particularly in small, biodiverse farms that currently persist within a matrix of large monocultures and urban land (Perfecto et al. 2009). Small-scale farms, which produce upwards to 80% of food for human consumption in only 53% of the current agricultural land, are often unable to afford, or prefer not to apply pesticides and herbicides, relying instead on a diverse set of natural enemies to control pest problems (Altieri 1999; Badgley et al. 2007; Montenegro 2009; Graeub et al. 2016). As homogenization and consolidation of agriculture continues to gain speed, questions arise as to how biological control in small, biodiverse farms will be affected (Altieri 1999; Agarwal et al. 2002; Perfecto et al. 2009; Lambin and Meyfroidt 2011).

In the past, many biological control programs that sought to eliminate pest species with a single, highly efficient control agent found it difficult to stabilize predator-prey dynamics (Nicholson and Bailey 1935; Murdoch 1975). Strong agents caused cycles of three repeating phases: 1) control agent overexploits pests 2) control agent declines due to lack of prey, and 3) pests resurge to outbreak levels under enemy-free conditions (Luck 1990; Arditi and Berryman 1991). Theory based on the Lotka-Volterra equations predicted that the magnitude of booms and busts would increase with every successive control agent-pest cycle until a stochastic event pushed the control agent to extinction (Luck 1990; Arditi and Berryman 1991). Using a diversity of control agents was one suggested solution (Murdoch 1975). Yet, in light of the then-popular competitive exclusion principle, incorporating more than one predator on a single prey (the pest) would be unlikely to work since only a single predator would survive, leading back to the same problem of prey overexploitation and extinction of the desired predator-prey control system (Denoth et al. 2002; Louda et al. 2003; Straub et al. 2008). Huffaker’s study moved in a different direction and sought to challenge the growing consensus that predator-prey systems are inherently unstable. Taking Nicholson’s critique of previous empirical work, he sought to create background conditions that more closely reflected some key elements of the environments faced by real predator-prey systems in nature, effectively removing the “mean-field” assumption of the well-mixed system and explicitly creating a spatially extended framework.

The prevalence of strong negative interactions in biological control, including intraguild predation where predators consume one another in addition to shared resources, dissuaded many from advocating multiple control agents to resolve pest problems (Rosenheim et al. 1995; McCann et al. 1998; Denoth et al. 2002; Straub et al. 2008). However, recent theoretical work found that strong negative interactions between a predator control agent and a pathogen control agent can result in a system that is stable even when the agents are completely unstable when isolated from one another (Ong and Vandermeer 2015). These strong negative interactions could be responsible for autonomous biological control—the observation that a diversity of natural enemies are able to keep levels of pests below economic thresholds, but above levels for natural enemies to persist without boom-bust dynamics (Lewis et al. 1997; Vandermeer et al. 2010; Ong and Vandermeer 2014).

Though Huffaker’s study and many theoretical studies that followed established spatial prey refuges as a stabilizing force for consumer-resource dynamics, contemporary theoretical work has shown that space can also induce unstable dynamics, including chaos (Huffaker 1958; Folt and Schulze 1993; Pascual 1993; Petrovskii and Malchow 2001). Though the specific size of a pest population may become unpredictable, chaotic systems can still be considered “stable” in pest control if the possible range of pest population sizes is constrained to an envelope below economic thresholds (Ong and Vandermeer 2015). These are important considerations for diverse biological systems where large, unpredictable fluctuations in population sizes are common phenomena (Berryman 1982; Dwyer et al. 2004). Thus, in this paper we distinguish between stable and effective biological control. Stable implies dynamic stability, where trajectories tend towards (but not necessarily reach) some non-zero equilibrium. Effective biological control implies that pest populations are both stable and that equilibrium values are lower than in control treatments where no natural enemies are present. Ineffective control implies that pest populations in natural enemy treatments are equal to or greater than control treatments. Ineffective control could be either unstable or stable, but this is less important for management applications.

Here, we borrow Huffaker’s classic framework to test how the coupling of competing pathogen and predator natural enemies improves or worsens control of pests when placed in a spatial context where dispersal is constrained or free. But rather than impose spatial heterogeneity on the lattice as Huffaker did, we examine how differences in dispersal capacities and intra, interspecific interactions naturally create spatial heterogeneity. Though we know much about how intra and interspecific interactions affect dispersal behavior (via alarm pheromones etc.), we know very little about how this then scales up to spatial patterns and questions of species persistence (Kring 1972; Schellhorn and Andow 1999; Perfecto and Vandermeer 2008).

Huffaker’s results imply that prey must be able to move freely in order to escape overexploitation by their predators. Thus, when only one species of natural enemy is present, we expect high rates of dispersal to encourage the formation of spatial refuges for pests. In these refuges, pests can build populations that are large enough to support long-term persistence of the natural enemy population, improving biological control. However, if natural enemies cannot find pests efficiently, outbreaks can occur. When two natural enemies are combined, the effects of space on biological control are unclear. On the one hand, competition between enemies may increase spatial heterogeneity through the delineation of territories or other behavioral divisions of space. If more spatial refuges for pests result from having multiple natural enemies, search efficiency of those natural enemies should also improve since there are more pest populations to encounter. Alternatively, the presence of multiple natural enemies could cause spatial clustering in pests, reducing the number of spatial refuges. In this case we might expect more outbreaks to occur since enemies are less likely to find prey.

Materials and methods

Experimental Setup

Spatial arrays of 3” pea plant cuttings (Pisum sativum var. Dwarf Grey) were set up under a 12hr-dark 12hr-light cycle. Each independent array (or “universe,” as Huffaker referred to them) consisted of a 4X5 network of clear plastic chambers (3 ¾” top diameter, 2 ½” bottom diameter, 4 ¾” height) that were sealed to prevent escape by arthropods, but not airtight. Each chamber included a test tube filled with dH₂O (distilled water) and a pea plant cutting inserted through a hole in the test tube top. The chambers were connected laterally using plastic corridors of two diameters: 0.219” (small) and 0.47” (large) cut to 2” in length. A single universe consisted of all small or all large corridors to represent a low or high dispersal treatment, respectively. Chambers were connected using a von Neumann neighborhood design with edge effects. Both low (L) and high dispersal (H) universes were subjected to four treatments: 1) aphids (Acyrthosiphon pisum) only, 2) aphids and ladybird beetles (Hippodamia convergens) (B), 3) aphids and the entomopathogenic fungus (Beauveria bassiana) (F), 4) aphids, beetles, and fungus (FB). All units started with an initial population of 50 aphids, 25 in the (1,1) position and 25 in the (4,5) position of the spatial array (diagonal corners). Eight beetles were added to the (4,1) position of the array for treatments including beetles. For fungal treatments, the initial aphid populations were sprayed with 2 pumps of a B. bassiana emulsion made by vortexing 4 mL dH₂O and 1.28 mL B. bassiana obtained as the commercially available product “Mycotrol-O” with a concentration of 2 × 10³ viable spores per quart. Universes were surveyed twice a week using direct counting methods. The number of healthy aphids was recorded for 28 time points or until extinction occurred. During census, pea cuttings were replaced as necessary so that fresh resources were always available in the array. However, once a pea plant was colonized by one or more aphids, no new pea cuttings would be provided in that chamber until all aphids went locally extinct or moved to neighboring chambers. In this way aphid populations were able to locally overexploit resources. After every local extinction event, chambers were thoroughly cleaned with 70% ethanol and fresh pea cuttings provided. In total we ran 66 universes with 10 replicates of the L treatment, 5 H, 10 BL, 7 BH, 10 FL, 6 FH, 10 FBL, and 8 FBH. Given the available laboratory space, we were able to run 16 universes at a time. Two replicates from each treatment were run simultaneously. Differences in times to extinction led to the different number of replicates per treatment.

Parameter Estimation

We modeled population dynamics using a coupled map lattice. The lattice was 4X5, the same as in the experimental setup. Given our biweekly sampling, aphids are capable of both short distance movements to adjacent cells, and long-distance movements across the array within a single time step. Thus, in order to align our data and model appropriately, we include both local and long-distance migration parameters in our model. At each time step the entire lattice first experienced local population dynamics, then local dispersal, and then long-distance dispersal. The local population dynamics were determined by the Ricker function (Ricker 1954) with parameters r and K. After local population dynamics a fraction, m₁, of individuals from each site dispersed locally to neighboring sites. These dispersing individuals were evenly distributed to the 2–4 sites in the focal site’s von Neumann neighborhood. After local dispersal a fraction, m₂, of individuals migrated to all the sites in the lattice. We define this as long distance dispersal. These individuals were evenly distributed among the 19 other sites. These population and dispersal dynamics are described by the following equations:

$$\begin{gathered} N_{ij}\left(t+\frac{1}{3}\right)=N_{ij}(t)e^{r\left(1-\frac{N_{ij}(t)}{K}\right)} \\ {N}_{ij}\left(t+\frac{2}{3}\right)=m_1\left(\overline{N_{ij}\left(t+\frac{1}{3}\right)}-N_{ij}\left(t+\frac{1}{3}\right)\right) \\ {N}_{ij}(t+1)=m_2\left(\overline{N\left(t+\frac{2}{3}\right)}-N_{ij}\left(t+\frac{2}{3}\right)\right) \end{gathered}$$ (1)

Here t is the time step and is equal to integer values 2, …, 28 to match the conditions of the experiment. The subscripts i and j indicate the location of the site and range from 1, …, 4 and 1, …, 5, respectively. The parameters, r and K, are the population growth rate and carrying capacity, respectively. The parameters, m₁ and m₂, are the fraction of individuals who disperse locally and globally. $\overline{N_{ij}}$ is the average number of individuals in the sites in N_ij’s von Neumann neighborhood. $\overline{N}$ is the average number of individuals in all sites except for N_ij.

We ran these rules for the same time frame and starting conditions as in the experiment (described earlier). Population values were assumed to be Poisson distributed or negative binomial distributed with mean given by the above model. For each treatment we pool all replicates and estimate the maximum likelihood parameter values, across all replicates, using simulated annealing (Bolker 2008). The Poisson model had a lower AIC than the negative binomial one, so was used. Model estimates converged for all parameters except for carrying capacities of aphids under low dispersal conditions. The large incidence of extinctions made carrying capacities irrelevant for these treatments because aphids had negative growth rates. Thus, populations never increased to the point where carrying capacities could be estimated. For each parameter (r, K, m₁, m₂), a likelihood profile was created. To do this, a given parameter is held constant at a series of values, and then for each value, the model is re-optimized with all other parameters in the model allowed to vary. The resulting likelihoods for each parameter value are the likelihood profile of the given parameter. Using the likelihood ratio test, likelihood cutoffs are calculated to create a 95% confidence interval in the parameter estimate (Bolker 2008).

Spatio-temporal projections

Once parameterized we used our coupled map lattice to project populations under each treatment for 200 time steps assuming both the original 4X5 experimental design with edge effects and a 30X30 spatial grid placed on a torus. We constructed confidence bands by simulating the model 1000 times for each treatment and taking the 95% quantiles of the total aphid population size at each time step. We added parameter uncertainty into our simulations by randomly drawing new parameters for each simulation based on the confidence intervals estimated for each parameter. For each simulation, spatial patterning was measured using Moran’s I, where I > 0 implies clustered, and I < 0 implies dispersed patterns. We constructed 95% confidence bands for Moran’s I using the same process as population size. Simulated and experimental results for aphid population size and spatial patterning were overlaid to visualize model fits to data. Differences in treatments were considered significant for some time frame if confidence bands did not overlap. All analyses were conducted in R (R Core Team, 2016).

Results

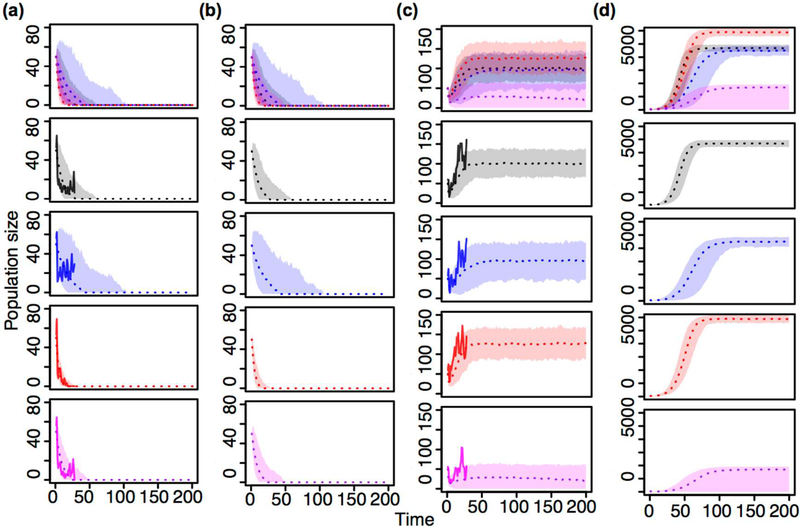
Long-term persistence of aphids was projected only for high-dispersal treatments (Fig. 1). This occurred when the simulated spatial array matched the experimental dimensions (4X5) and also when the array was extended to the larger, 30X30 torus (Fig. 1 c and d). In all other treatments, aphids were projected to go extinct.

Fig. 1. Projected aphid population time series.

Total aphid population sizes are projected in coupled mapped lattice models for 200 time units using parameters fit by maximum likelihood inference to the experimental data where aphids had (a, b) low dispersal and (c, d) high dispersal. Models assume either (a, c) the same 4X5 bounded dimensions of the experiment or (b, d) a 30X30 spatial grid placed on a torus. Rows in plots correspond to experimental treatments where aphids were alone (black, second row) or in the presence of the following natural enemies: entomopathogenic fungus only (blue, third row), ladybird beetle only (red, fourth row), and fungus and beetle combined (purple, fifth row). In top row, all plots are overlaid to show differences between treatments. Solid lines in (a, c) are the mean population of aphids averaged across repetitions (n varies, see Methods) in the experiment. Each time unit corresponds to a biweekly census in the experiment. 95% confidence bands are plotted around mean model predictions (dotted lines) for n=1000 simulations.

Overall, aphid growth rates were higher when the dimension of dispersal corridors was larger. Under these high-dispersal conditions, the presence of natural enemies consistently reduced aphid growth rates from controls. The fungus-only treatment had the lowest growth rate, followed by fungus-beetle, and finally the beetle-only treatment (Table S1). Under low dispersal conditions, fungus actually increased aphid growth rates relative to controls. The beetle only treatment had the lowest growth rate followed by the fungus-beetle treatment (Table S1).

Aphid populations in low dispersal treatments were all projected to decline, making aphid carrying capacity estimates impossible to predict. However, under high dispersal conditions, aphid carrying capacities significantly increased when beetles were present alone. Fungus alone had no effect on carrying capacity, but the combined fungus-beetle treatment caused a 3-fold reduction in carrying capacity (Table S1).

Under low dispersal conditions, both natural enemies had the same effects on aphid migration rates. When each of these natural enemies was introduced alone, local aphid migration rates decreased and long-distance migration rates increased (Table S1). The effect of the fungus on aphid migration rates remained consistent under high dispersal conditions. However, beetles reversed effects, increasing local and reducing long-distance aphid migration rates when dispersal corridors were larger (Table S1). Combining fungi and beetles had no effect on local or long-distance migration rates when dispersal was low. However, when dispersal was high, combining the natural enemies caused local migration rates to decrease and long-distance migration rates to increase (Table S1).

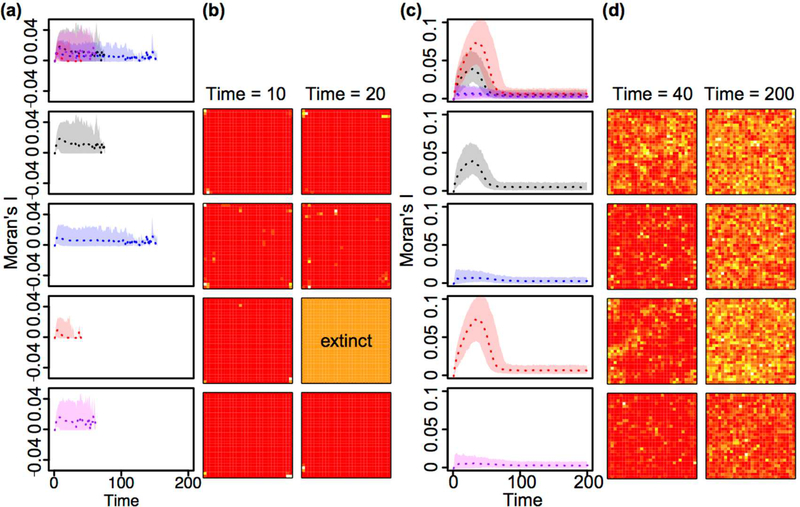
Spatial patterns of aphids in the experiment and in the model assuming the same spatial configuration as the experiment were not significantly different from random and did not differ between treatments (Fig. S1). However, when the model was projected to the larger 30X30 torus, spatial patterns emerged. For low-dispersal 30X30 torus simulations, pest populations were projected to go extinct but remained significantly clustered until extinction (Fig. 2a and b). Under high-dispersal 30X30 torus conditions, local clustering of aphids was significantly reduced when fungi were present alone or in combination with beetles. In contrast, beetle-only treatments caused spatial clustering of aphids to increase (Fig. 2c and d).

Fig. 2. Projected spatial clustering of aphids on a 30X30 torus.

Plotted are the means (dotted line), and 95% quantile confidence bands of Moran’s I for n=1000 simulations of the coupled lattice model assuming a 30X30 spatial grid on a torus using parameters estimated from treatments where aphids had low (a) or high dispersal (c) and no natural enemies (black, second row), or while in the presence of the following natural enemies: entomopathogenic fungus only (blue, third row), ladybird beetle only (red, fourth row), and fungus and beetle combined (purple, fifth row). In top row, all plots are overlaid to show differences between treatments. Example spatial plots for low (b) or high dispersal (d) show different levels of clustering for treatments (corresponding with rows in a and c) at time 10 and 20 for low dispersal treatments and at time 40 when clustering peaks for beetle only treatment and equilibrium, time 200 for high dispersal treatments. White colors correspond to larger, and red to lower population sizes of aphids. A completely orange lattice indicates population extinction. Moran’s I > 0 indicates clustered, < 0 indicates dispersed and 0 = random spatial patterns.

Discussion

As predicted, long-term persistence of the system only occurred under high-dispersal conditions where aphids and natural enemies could move more easily through the array (Fig. 1) (Huffaker 1958). Without sufficient dispersal, pests and by extension any iteration of the pest-natural enemy system cannot persist (Fig. 1). These results largely confirm Huffaker’s conclusion that space can stabilize predator-prey interactions by providing refuge to prey from predators. We note however, that all instances of pest persistence are not equally beneficial from the perspective of biological control.

Though our experimental setup did not individually control the movements of each component of the system as Huffaker did, intra and interspecific interactions amongst the pest and two natural enemies were sufficient to create an endogenous form of spatial heterogeneity (Perfecto and Vandermeer 2008; Vandermeer et al. 2008; Liere et al. 2012). Based on body size alone, rates of diffusion are greatest for the pathogen, followed by the pest and finally the predator. In addition, each natural enemy had a characteristic effect on the vital rates and dispersal behavior of the pest, which was further mediated by the overall connectivity in the matrix (Table S1). Thus, each combination of enemies and connectivity gives rise to different spatial patterns and consequences for biological control.

Fungus had consistent effects on migration rates for aphids regardless of the diameter of corridors between cells. In both cases, fungus caused aphids to reduce local migration rates and increase long-distance migration rates (Table S1), reflecting an adaptive response to avoid pathogen outbreaks that occur more easily with host clustering (Shah and Pell 2003). We see this play out in the spatial dynamics, where local clustering of aphids is significantly reduced when fungus is present (Fig. 2c and d). We note that aphid growth rates actually increased relative to controls in low dispersal treatments with fungus (Table S1). Infection by the entomopathogenic fungus can cause a stress-response in aphids that encourages molting (quick progression to adulthood), and greater fecundity rates prior to death (Kim and Roberts 2012; Ortiz-Urquiza and Keyhani 2013). However, in high dispersal treatments where aphids survive long-term, the presence of fungus reduced growth rates in aphids, as expected. The effect of beetles on migration rates of aphids was dependent on whether the arrays allowed low or high dispersal. In low dispersal treatments, beetles mirrored fungus effects by causing local aphid migration rates to reduce and long-distance migration rates to increase (Table S1). Since aphids are already clustered in low dispersal treatments (Moran’s I > 0), beetles very easily discover and decimate local clusters of aphids, which are hindered from migrating due to the small diameter of the corridors between cells (Fig. 2a and b). This is evidenced by short aphid survival times and low aphid growth rates in the beetle only low-dispersal treatments (Fig. 1 and Table S1). Beetle movement is highly constrained in the low dispersal treatments. Thus, aphids that are able to migrate longer distances survive, causing the increase in long-distance migration rates (Fig. 2b). These results are similar to the Janzen-Connell hypothesis where survival of seedlings is greatest for those that are transported furthest from parent trees where natural enemies are less common (Janzen 1970; Connell 1971). However, in high dispersal treatments, beetles caused the reverse effect with local aphid migration rates increasing and long-distance migration rates decreasing (Table S1). Aphids are known to exhibit dropping behavior as a quick evasive tool when exposed to predators (Losey and Denno 1998). When aphids can easily move through the spatial array, beetle predation events disrupt clusters of aphid populations causing short-distance migration to neighboring cells. Yet, migration requires a pause in feeding, imparting a high metabolic and reproductive cost for aphids (Rankin and Burchsted 1992). Thus, long-distance migration events are unfavorable unless the risk of predation or infection is high. Beetles can also move more easily in high dispersal arrays, but the search behavior of ladybird beetles is considerably random (Dixon 1959). Long predator search times appear to allow new, local clusters of aphids to build before rediscovery by the predator. This is evidenced by the increased aphid clustering that occurs with high dispersal-beetle only treatments (Fig. 2). When predator search times are sufficiently long, aphids are not consistently exposed to predation, reducing the need for long-distance dispersal events.

Under low dispersal conditions, we could not estimate carrying capacities of aphids because of the large incidence of extinctions (Table S1, Materials and methods). We did find that single natural enemy treatments increased local migration and reduced long-distance migration, but the combination of natural enemies eliminated effects on migration so that there were no differences from controls. Since aphids were a limiting resource in low dispersal treatments, competition between natural enemies in the combined natural enemy treatment may have reduced the effects of natural enemies on pest movement. Indeed, strong competition between natural enemies is well-documented in biological control systems (Rosenheim et al. 1995; Denoth et al. 2002; Louda et al. 2003; Straub et al. 2008).

Under high dispersal conditions, the combination of both natural enemies best controlled aphids by reducing aphid clustering and equilibrium pest densities through a marked reduction in their carrying capacity (Fig. 1). This is a particularly surprising result since neither natural enemy alone reduced the carrying capacity of the pest (Table S1). In fact, the beetle significantly increased the carrying capacity of aphids (Fig. 1). Since no new food resources were made available to aphids after they occupied a cell, aphid carrying capacity should increase only if aphids move to new cells and discover new food resources (Materials and methods). Increases in local migration rates of aphids under the presence of beetles can explain the positive effect on aphid carrying capacity. This counterintuitive result aligns well with the paradox of biological control, where highly efficient control agents overexploit pest resources and cause outbreaks (Luck 1990; Arditi and Berryman 1991). In this theory, pest populations surge after control agents decline from starvation. Our experiment may accelerate this process since predators become physically separated from their prey when they overexploit local clusters. Though the fungus alone reduced spatial clustering of aphids, carrying capacity was not reduced (Figs. 1–2, Table S1). Increases in long-distance migration were canceled out by a reduction in aphid growth rates under fungus exposure to have no effect on carrying capacity (Fig. 1 and Table S1). Thus, equilibrium densities of aphids under the presence of fungus alone are no different than high dispersal controls (Fig. 1). However, when both natural enemies are combined, aphid populations are doubly threatened, reducing carrying capacities and increasing long-distance migration to a much larger extent than either enemy alone. This synergistic effect may result from combining intense predation by the beetle predator and the reduction in spatial clustering that occurs with the pathogen (Fig. 2). Much like in the original theoretical work that inspired our experiment (Ong and Vandermeer 2015), we find that a combination of two ineffective control agents can effectively rescue control, not only reducing equilibrium pest densities, but also reducing local spatial clusters and limiting the carrying capacity of pests.

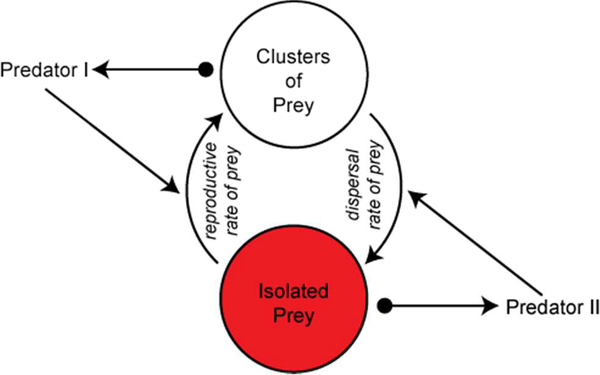
It is tempting to generalize these results. Allowing that all species on earth are faced with the combination of predators and pathogens acting simultaneously (Ong and Vandermeer 2014, 2015), we can envision the effects of spatial extent in a very simple dynamic. If the pathogen induces long-distance migration (as it here does), and if the predator is more effective at finding spatial clusters of prey (as it here is), then the pathogen, if its virulence is appropriately constrained, effectively causes the prey to “move” to “refuges.” The refuges are the areas of recently migrated individuals that have not yet locally reproduced enough to form a cluster that is sufficiently attractive to the predator. The stability condition (or persistence condition) is thus a critical combination of dispersal rates of all three elements, plus the nonlinear trait-mediated effects of the pathogen and predator on the dispersal of the prey. Generalizing to a system of two predators and a prey, the key nonlinearities (trait-mediated effects) of one predator increasing the migration rate of the prey, the other increasing the local cluster formation, creates the conditions for stabilizing the whole system (with appropriate parameter values). We summarize this speculative generalization in Figure 3.

Fig. 3.

Hypothesized generalization of coexistence of two competitors (the two predators) in a spatially extended system, where one of the predators has a trait-mediated effect in inducing the prey to disperse faster and the other has a trait-mediated effect in inducing the prey to form spatial clusters. In the absence of predator II, the prey will tend to occur as isolates, inducing extinction of predator I. In the absence of predator I, the prey will tend to occur in the clusters, inducing extinction of predator II. Arrowheads indicate positive effect, balls represent negative effect.

In our experiment we find that the combination of two natural enemies does indeed increase spatial heterogeneity and this heterogeneity does improve biological control from single enemy treatments. The “clustered” versus “isolated” prey form two types of spatial refugia, allowing enemies to avoid competition by concentrating on their “niche,” or preferred form of prey refugia. Complementarity arising from partitions in space or time are common in the literature on biological control (Denoth et al. 2002; Ramirez and Snyder 2009; Gable et al. 2012). For example, natural enemies are known to partition time by concentrating on early or late season populations, and space by concentrating on populations existing at various heights in the vegetation strata. Yet the “clustered” versus “isolated” populations in our experiments imply that spatio-temporal separations allowing for complementarity can exist in constant flux. Once a cluster has been discovered and decimated by one predator, surviving prey become isolated populations that are a niche to a different type of predator. However, connectivity is essential to maintain this kind of dynamic spatio-temporal heterogeneity. Autonomous biological control and coexistence between competing natural enemies can naturally arise as competitors partition prey by space and time. Yet, somewhat paradoxically, improving the connectivity of landscapes is necessary for these complementarity-inducing partitions to arise. Thus, if we are to improve natural pest control in agriculture, we may need to increase the rate at which pests (and their associated natural enemies) can move through the farm.