Applications of community detection techniques to brain graphs: Algorithmic considerations and implications for neural function

Abstract

The human brain can be represented as a graph in which neural units such as cells or small volumes of tissue are heterogeneously connected to one another through structural or functional links. Brain graphs are parsimonious representations of neural systems that have begun to offer fundamental insights into healthy human cognition, as well as its alteration in disease. A critical open question in network neuroscience lies in how neural units cluster into densely interconnected groups that can provide the coordinated activity that is characteristic of perception, action, and adaptive behaviors. Tools that have proven particularly useful for addressing this question are community detection approaches, which can identify communities or modules: groups of neural units that are densely interconnected with other units in their own group but sparsely interconnected with units in other groups. In this paper, we describe a common community detection algorithm known as modularity maximization, and we detail its applications to brain graphs constructed from neuroimaging data. We pay particular attention to important algorithmic considerations, especially in recent extensions of these techniques to graphs that evolve in time. After recounting a few fundamental insights that these techniques have provided into brain function, we highlight potential avenues of methodological advancements for future studies seeking to better characterize the patterns of coordinated activity in the brain that accompany human behavior. This tutorial provides a naive reader with an introduction to theoretical considerations pertinent to the generation of brain graphs, an understanding of modularity maximization for community detection, a resource of statistical measures that can be used to characterize community structure, and an appreciation of the usefulness of these approaches in uncovering behaviorally-relevant network dynamics in neuroimaging data.

Modularity has been hailed as fundamental property of the human brain dating back to Greek philosophy, and it has continued to inform theories from phrenology [86] and cognitive science [79, 36, 172], to brain mapping and functional localization [168]. The relevance of modularity for brain structure and function stems from its fundamental advantages for evolution and development. Research across the biological sciences suggests that modular organization allows for rapid adaptation [115, 100] and provides robustness to either sudden or gradual perturbations in genes or environment [123, 115, 116]. Unlike homogeneously connected networks, modular networks can effectively buffer the impact of perturbations by keeping their effects relatively local [152] while simultaneously enabling efficient information processing [75, 11], supporting functional specialization [88] and efficient learning [74]. These benefits of modularity are particularly relevant for the human brain, which evolved under evolutionary pressures for adaptability [132], energy efficiency, and cost minimization [60, 49, 173, 55, 34], and which also develops under biological pressures to balance segregation and integration of function [49].

Exactly how modularity is instantiated in the brain is a question that has fascinated neuroscientists for more than a century. The answer to this question is complicated by the fact that the brain is a complex system composed of neural units that communicate with one another in dynamic spatiotemporal patterns [5]. How these patterns of communication are organized, reflecting thought, cognition, and behavior remains a mystery [44]. A particularly appropriate mathematical language to describe these patterns – and to determine the role that modularity might play within them – is network science [155]. In its simplest form, network science summarizes a system by isolating its component parts (nodes) and their pairwise interactions (edges) in a graph [40]. Over the last decade, the application of network science to neuroscience (also known as network neuroscience [16]) has offered intuitions for the fundamental principles of organization and function in the brain [48].

A quintessential concept in network neuroscience is the notion of network modularity, wherein neural units are structurally or functionally connected to one another in clusters or modules [139]. Intuitively, modularity is an architectural design feature that allows system processes to implement local integration of information, while maintaining systems-level adaptability. Graphs that display modular structure [82] can give rise to more complex dynamics than graphs that display random structure [196]. Modular networks of coupled oscillators also promote synchronizability [7] as well as the formation of chimera states, characterized by the coexistence of synchronized and desynchronized elements [216]. Modularity often exists across multiple hierarchical levels [138], enabling rapid responses to fluctuating external input [122, 25, 142], and supporting complex dynamics alongside functional efficiency [187, 113]. The functional properties that modularity confers to a system provide strong motivation for studying modular organization in brain graphs across both health and disease (Fig. 1).

Fig. 1. Brain graphs and communities within them.

One can construct a brain graph in several ways, and subsequently study its modular architecture using community detection techniques developed for graphs. Here, we illustrate an example pipeline in which we use non-invasive neuroimaging in humans to obtain regional timeseries of continuous neural activity (Left). Next, we define a weighted undirected graph and represent that graph in an adjacency matrix, each element of which provides an estimate of the statistical similarity between the time series of region i and the time series of region j (Middle). Finally, we apply community detection techniques to the brain graph to identify modules. Here, a module is composed of nodes (regions) that are more densely interconnected with one another than expected in some appropriate random network null model. If we have temporally extended data, we can also consider defining a temporal graph, and using dynamic community detection techniques to study the temporal evolution of modules and their relation to cognition (Right). In this review, we discuss considerations, methods, statistics, and interpretations relevant to this process.

In this tutorial, we survey the literature pertinent to an understanding of modular structure in brain graphs, and its relevance for human cognition. We begin by discussing common methods for building brain graphs from diverse data sources representing distinct types of neurophysiological signals. We then turn to a description of community detection approaches commonly applied to such graphs, and we place a particular emphasis on the method of modularity maximization. Next, we offer a resource of statistical measures that can be used to characterize community structure in brain graphs, including measures of their topology and embedding into physical space. We complement the discussion of methods and statistics for single graphs with a description of extensions of community detection approaches for time-evolving graphs. Next, we provide a resource of statistical measures that can be used to characterize dynamic community structure in brain graphs. We then review applications of these techniques to questions in neuroscience to give the reader an appreciation of the usefulness of these approaches in uncovering behaviorally-relevant network dynamics in neuroimaging data. Finally, we discuss methodological innovations that are needed to advance our understanding of how patterns of coordinated activity in the human brain account for behavior.

Building brain graphs

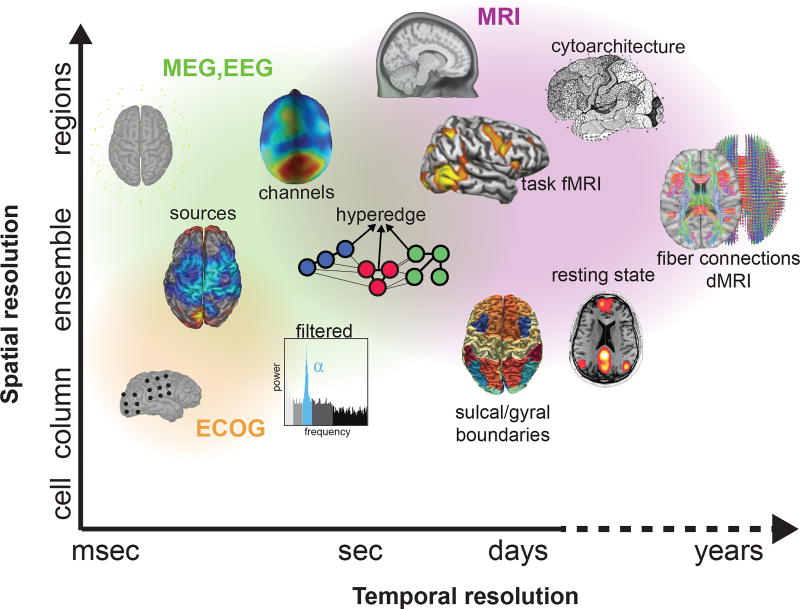
In its general form, a brain graph is composed of (i) a set of nodes characterizing anatomical, functional, or computational units, and (ii) a set of edges representing pairwise relations between two nodes (Fig. 2). Brain graphs can be built from many types of neuroimaging data, including magnetic resonance imaging (MRI), electrocorticography (ECoG), electroencephalography (EEG), and magnetoencephalography (MEG). Across all modalities, one seeks a definition of nodes that distills the brain into its most fundamental pieces relevant to the hypothesis being tested, and a definition of edges that constitutes the fundamental relation relevant to the function under study [51]. The choice of nodes and edges guides the appropriate interpretations that can be drawn from the graph [171, 51, 215].

Fig. 2. Defining brain graphs: common datatypes.

Various neuroimaging techniques can be used to measure brain network dynamics. Due to their prominence in the literature, we focus on direct measurements from implanted electrodes on the cortical surface (ECoG; orange), sensors on or above the scalp (EEG or MEG; green), and indirect measurements from BOLD and diffusion (MRI; purple). Each technique is associated with a specific spatial and temporal scale that can offer different insights into brain structure and function.

a) Defining nodes: In MRI studies, nodes can be defined using anatomical landmarks [1], cytoarchitecture [45, 212], sulcal and gyral landmarks [105, 68, 69, 207], or boundaries of functional activation [167, 222], either in controlled [219] or uncontrolled [223, 127] tasks. Indeed, functional atlases [61, 151] can incorporate activation information across many tasks [71] or parse which regions tend to be activated independently [171]. Nodes at a large-scale can also be defined based on connectivity at a small scale. For example, in connectivity-based parcellation [214, 26], one begins with voxel-level estimates of structural connectivity from diffusion MRI [210], and then applies a clustering technique to extract modules of densely interconnected voxels; each module is then treated as a node in the brain graph [73].

In ECoG, MEG, and EEG studies, graphs are constructed to study synchronized activity of neuronal ensembles [163, 89, 46]. Frequently, nodes are chosen to reflect electrodes in EEG or ECoG (e.g., [119, 50, 118]) and sensors in MEG (e.g., [22, 15, 197]). However, electrode and sensor time series reflect a combination of signals from cortical and subcortical sources, and are susceptible to artifacts from muscles contractions, head movements, and environmental noise [211]. To address these limitations, one can apply source reconstruction [for review, 99, 177], and then use those sources as nodes [191, 147]. One can also use multiple functional neuroimaging measurements such as simultaneous fMRI and EEG recordings [47] to define nodes [148]. Importantly, each method of node determination has implications for network estimates of brain dynamics, as described more thoroughly in several recent reviews [106, 198, 192].

Defining edges

Edges can reflect structural connections across spatial scales [30], such as bundles of axonal fibers between regions (e.g., [218, 146, 112]) or synapses between neurons. In humans, structural connections are measured using diffusion MRI [for review, see 10, 210], and fiber trajectories are estimated using tractography methods [143, 27]. The resultant brain graph can be used to identify specific connections that enable efficient and rapid communication between regions [18], or collections of connections with diverse higher order structures [94, 190, 189].

Edges can also reflect coordinated activity between regions thought to underlie cognition [83, 84, 92], where coordination is quantified by correlation, coherence, phase lag index, or a measure of synchronization between time series [23, 107], or by effective connectivity methods that estimate casual relations [85]. Such functional time series can be derived from MRI [111, 108, 109, 96] or from EEG in cognitively relevant frequency bands [52, 43]. An important caveat for estimates of functional connectivity between two regions is that they can be driven by a third source [37, 98].

When studying relations among edges in time-varying graphs – where a graph is constructed from each of many time windows–, one can use a hypergraph to formalize the idea that groups of edges, rather than single edges alone, represent a fundamental unit of interest [20, 65, 102]. This approach is partially motivated by evidence suggesting that edges can develop differentially in a coordinated fashion over the lifespan [66], leading to architectural features that cannot simply be defined by graphs composed of dyads [20]. Such developmental coordination of functional connections might be driven by intrinsic computations [20], and subsequently have mutually trophic effects on underlying structural connectivity [17]. Co-varying functional connections in early life could support the emergence of cognitive systems observed in adulthood [102]. Hypergraphs can formalize these relationships, and thereby offer a unique perspective on brain graph architecture.

Evaluating community structure in brain graphs

After choosing nodes and edges, we let G = (V, A) be a complex network of N nodes, where V = {1, ⋯, N} is the node set, and A ∈ ℝ^N×N is the adjacency matrix whose elements A_ij give the weight of the edge between node i and node j. In a binary graph, elements are either values of 0 or 1, which indicate whether an edge exists, while in a weighted graph, elements have non-binary values that reflect the strength of their pairwise connection. If the edge weight between a node pair is symmetric, the graph is called undirected, and A_ij = A_ji for all (i, j); the graph is called directed otherwise. In an undirected binary graph, the degree of a node, k_i, is given by the number of its non-zero edges: k_i = Σ_j∈N A_ij. To evaluate community structure in the brain graph, we note that a community structure is a partition 𝒞 = {C₁, ⋯, C_K}, where C_i ⊂ V consists of the nodes in the ith community and K is the number of communities in G. Here we only consider non-overlapping community structure, which means that C_i∩C_j = ∅ if i ≠ j. We note that in the case of a temporal graph with L layers, and where the adjacency matrix of layer l has elements A_ijl, one can similarly define a community structure as a set of L partitions.

The overarching goal of community detection is to provide an understanding of how nodes are joined together into tightly knit groups, or modules, and whether such groups are organized into natural hierarchies in the graph. Community structure exists in a variety of real world systems including several social, biological, and political systems [82], and community detection methods can be used to uncover that structure algorithmically. Recent applications of these methods to real-world systems have uncovered segregated committees in the US House of Representatives [169], segregated protein classes in protein-protein interaction networks [56], and segregated functional groups of areas in brain graphs [19]. Uncovering community structure can provide important intuition about the system’s function, and the large-scale functional units that drive the system’s most salient processes [93].

Mathematics of modularity maximization

Many methods exist for community detection [81]. Some draw on notions in physics such as the Potts model [174], while others draw on notions in mathematics such as random walks [225] and spectral properties of the adjacency matrix [153, 158, 154, 224]. Still others more closely track other concepts and techniques in computer science and engineering [e.g., 57]. In this section, we will primarily discuss a single method – modularity maximization – due to its frequent use in the network neuroscience community. However, readers interested in understanding various other algorithms and approaches may enjoy several other recent reviews [82, 170]. Importantly, the summary metrics that we define and discuss for both static and time-varying graphs are applicable to any study of community structure, independent of the specific method used to identify that structure.

Modularity maximization refers to the maximization of a modularity quality function, whose output is a hard partition of a graph’s nodes into communities. The most common modularity quality function studied in network neuroscience to date is

$$Q=\sum _{\mathit{\text{ij}}}[(A_{\mathit{\text{ij}}}-\gamma P_{\mathit{\text{ij}}})]\delta (C_i,C_j),$$ (1)

where A_ij is the ij^th element of the adjacency matrix, i is a node assigned to community C_i and node j is assigned to community C_j. The Kronecker delta δ(C_i, C_j) is 1 if i, j are in the same community and zero otherwise, γ is called a structural resolution parameter [14]. The element P_ij is the expected weight of the edge connecting nodes i, j under a specific random network null model. A common null model is the Newman-Girvan null model which is given by k_ik_j/2m where k_i is the degree of node i and m is the number of non-zero elements in the upper triangle of the undirected adjacency matrix [157]. This null model encodes the intuition that two nodes of high degree are more likely to share an edge than two nodes of low degree. For a discussion of alternative null models, see [14].

The structural resolution parameter, γ, is often set to unity for simplicity. However, due to a well-known resolution limit [174], this choice will tend to produce a fixed number of communities, even if a stronger community structure could be identified at smaller or larger topological scales. To deal with this limitation, it is common to vary γ over a wide range of values. The benefit of such a parameter sweep is that it can also uncover hierarchical organization in the graph: robust community structure across several topological scales [169]. Some graphs contain a single scale (or several discrete scales) at which community structure is present. For these graphs, it has been suggested that a useful method by which to identify that scale(s) is to search for γ values at which all partitions estimated (from multiple runs of the modularity maximization algorithm) are statistically similar [14].

Maximization of the modularity quality function defined above is NP-hard. Because an exact solution is unknown, various heuristics have been devised to maximize (or nearly maximize) Q without resorting to an exhaustive search of all possible partitions, which for most real-world graphs proves to be computationally intractable [170]. Heuristics vary in terms of their relative speed, fidelity, and appropriateness for large versus small graphs. One common heuristic is a Louvain locally-greedy algorithm [38], which contains two phases: one where modularity is optimized by allowing only local changes of communities, and one where the identified communities are aggregated to build a new network of communities. These two phases are repeated iteratively until modularity no longer increases. A second common heuristic is based on simulated annealing, which appears particularly natural when one realizes that finding the modularity of a network is analogous to finding the ground-state energy of a spin system [175, 104]. In this approach, nodes are combined into communities, and such communities are maintained with some probability dependent on whether they increase or decrease the modularity quality index; the probability of accepting a decrease in modularity slowly decreases as the solution space is explored. A third and complementary approach is based on extremal optimization, and optimizes the global variable (modularity quality index) by improving extremal local variables (contribution of a single node to the modularity quality index) [72]. For example, a simple heuristic randomly partitions the network into two communities, and the node with the lowest fitness (extremal) is moved from its partition to the opposite partition. This procedure is repeated until an optimal division of the network into two components is completed; then each component is iteratively bipartitioned in the same way. Generally speaking, greedy algorithms tend to be relatively swift [59], while simulated annealing [103], extremal optimization [72], and others [160] can be slower yet provide quite stable partitions. With most heuristics, one should perform the optimization many times in order to create an ensemble of partitions, and both understand and report the variability in those solutions.

The modularity landscape is rough, containing many near degeneracies [97]. This means that there are many structurally diverse alternative partitions of nodes into communities with modularity values very close to the optimum. Near degeneracy is particularly prevalent in large binary graphs, and less prevalent in small weighted graphs. Degeneracy becomes especially problematic when the partitions identified by multiple optimizations of the modularity quality function are dissimilar. In these cases, we might wish to identify a single representative partition from the set of partitions observed. One common approach to identify a consensus community structure is similarity maximization [70], where the partition of interest is that which has the greatest similarity to all other observed partitions. A second common approach is an association-recluster method [128, 14, 30], which uses a clustering algorithm to find a consensus partition by exploiting the fact that across an ensemble of partitions, a single node may be affiliated with the same other nodes. Partition degeneracy can also be addressed by expressing the best partition as an average across multiple near-optimal partitions, and by treating the community allegiance of nodes as fuzzy variables [28] or via probabilistic clustering [110].

Summarizing community structure in brain graphs

Topological summary statistics

Several summary statistics that can be derived from community detection methods are reported in neuroimaging studies. Many of these can be defined based on the network’s topology, independent of any embedding of that network into a physical space (Fig. 3). Here we offer a summary of these statistics, and point the reader to a few (certainly not all) recent references that have used them in the neuroimaging literature to address questions of import to neuroscientists.

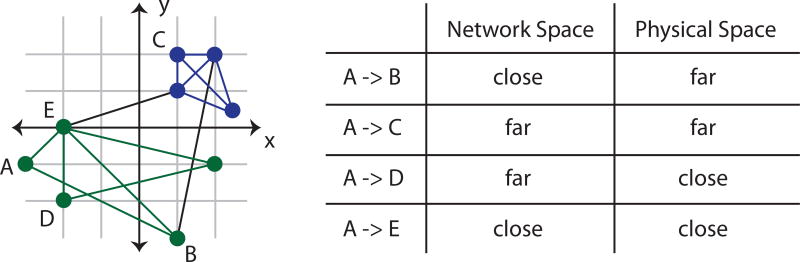
Fig. 3. Distinction between network space and physical space.

Spatial network statistics are important for understanding how a network is embedded into physical space. Here we illustrate the distinction between network space and physical space, motivating the importance of using stastistics in both spaces to understand a system’s organization. (Left) An example graph that has been embedded into a physical (2-dimensional Euclidean) space. (Right) A list of connections between nodes and their respective network and physical distances, demonstrating that long physical distances need not be long network distances, and visa versa.

b) Number of communities:: The number of communities provides an indication of the scale of community structure in a network. Note that N_Ck = |C_k| is the number of nodes in module C_k. A large number of communities suggests a small scale of structure in the network, while a small number of communities suggests a large scale of structure in the network.

c) Size of communities:: The average size of communities, and the distribution of community sizes are also useful diagnostics of community structure. The number of nodes N divided by the number of communities K gives the mean size of communities in the graph.

d) Modularity quality index:: For community structure identified with modularity-based approaches, the modularity quality index Q serves as a useful measure of the quality of the partition of nodes into communities (see Eq. (1)). To some degree, higher values indicate more optimal partitions than lower values, after accounting for caveats of the roughness of the modularity landscape [97], the size of the graph, and the edge weight distribution, among potentially other confounds. For a recent review of the use of this metric in neuroimaging studies, see [195].

e) Within- and between-module connectivity:: It is also of interest to calculate the strength of edges inside of modules, and the strength of edges between modules. We refer to these notions as within- and between-module connectivity, respectively and define

$$I_{k_1,k_2}=\frac{{\sum }_{i\in C_{k_1},j\in C_{k_2}}{A}_{\mathit{\text{ij}}}}{N_{C_{k_1}}{N}_{C_{k_2}}},$$ (2)

to be the strength between module C_k1 and module C_k2. When the two modules are identical (k₁ = k₂), this measure amounts to the average strength of that module, and we interpret it as the recruitment of the module. When the two modules are different (k₁ ≠ k₂), we might also wish to compute the relative interaction strength

$${\mathit{\text{RI}}}_{k_1,k_2}=\frac{I_{k_1,k_2}}{\sqrt{I_{k_1,k_1}{I}_{k_2,k_2}}},$$ (3)

to account for statistical differences in module size. Within- and between-module connectivity has been shown to vary appreciably with learning [21], differ across motor versus working memory function [62], mark neuromodulatory effects [185], track neurodevelopment [101, 24], and change in psychiatric disease [180].

f) Intra-module strength z-score:: One might also wish to quantify how well connected a node is to other nodes in its community, a notion that is formalized in the intra-module strength z-score [103]:

$$z_i=\frac{S_{C_i}-{\overline{S_C}}_i}{{\sigma }_{{\overline{S_C}}_i}},$$ (4)

where S_Ci denotes the strength (i.e., total edge weight) of node i’s edges to other nodes in its own community C_i, the quantity ${\overline{S_C}}_i$ is the mean of S_Ci over all of the nodes in C_i, and ${\sigma }_{{\overline{S_C}}_i}$ is the standard deviation of S_Ci in C_i. This statistic was recently applied to brain graphs to study the learning of categories [193].

g) Participation coefficient:: One might also wish to measure how the connections emanating from a node are spread among nodes in the different communities, a notion that is formalized in the participation coefficient [103]:

$$P_i=1-\sum _{k=1}^K{(\frac{S_{{\mathit{\text{iC}}}_k}}{S_i})}^2,$$ (5)

where S_iCk is the strength of edges of node i to nodes in community C_k. This statistic has been used to better understand how learning is impacted by patterns of intermodular connectivity [193], how brain function is altered in antipsychotic-naive first-episode schizophrenia patients [131], and how structural modular segregation mediates the relationship between age and executive function in youth [24].

Spatial summary statistics

It is often interesting to quantify how a network is embedded into physical space (Fig. 3), and specifically the spatial properties of communities. Currently, relatively few measures exist and future work should focus on this important area. Below we present five measures previously proposed to quantify the spatial aspects of community structure. Many of these statistics have not yet been used in the neuroimaging literature, and there is therefore an open opportunity to use them to better understand the spatial embedding of modular structure in the brain.

h) Community average pairwise spatial distance:: The community average pairwise spatial distance, l_Ck is the average Euclidean distance between all pairs of nodes within a community [76]:

$$l_{C_k}=\frac{2}{N_{C_k}(N_{C_k}-1)}\sum _{i,j\in C_k}\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ,$$ (6)

where r_i is the position vector of node i. The average pairwise spatial distance of the entire network is given by the same equation calculated over all nodes within the network.

i) Community spatial diameter:: The community spatial diameter, d_Ck is defined as the maximum Euclidean distance between all pairs of nodes within a community [76]:

$$d_{C_k}=\mathit{\text{max }}(\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ).$$ (7)

The spatial diameter of the entire network is given by the same equation, but calculated over all nodes within the network.

j) Community spatial extent:: The spatial extent of a community is an inverse estimate of the density of a community and quantifies the area or volume of the community, normalized by the number of nodes within the community [76]. Specifically, we can define

$$s_{C_k}=\frac{1}{N_{C_k}}{V}_h{({\mathbf{r}}_i)}_{i\in C_k},$$ (8)

where V_h is the volume (3 dimensions) or area (2 dimensions) of the region bounded by the points of the convex hull of nodes within the community. The convex hull is the minimal convex set containing all of the points within the community and is informally described as the polygon created by connecting all points that define the perimeter of the community. It should be noted that in this definition of the spatial extent, the normalization assumes the average size of a region is approximately constant. If this is not the case, the equation could be modified to take into account the boundaries or sizes of individual regions to better estimate the inverse measure of density. This statistic has been used to assess the spatial embedding of synchronized functional clusters estimated from two-photon calcium imaging data acquired in a chronically epileptic dentate gyrus of a mouse model of temporal lobe epilepsy [76].

k) Community radius:: We can define the community radius ρ_Ck as the length of the vector of standard deviations of all nodes in the community [134]:

$${\rho }_{C_k}={(\frac{1}{N_{C_k}}\sum _{i\in C_k}{\Vert {\mathbf{r}}_i\Vert }^2-\frac{1}{N_{C_k}^2}{\Vert \sum _{i\in C_k}{\mathbf{r}}_i\Vert }^2)}^{\frac{1}{2}}.$$ (9)

The average community radius of the entire network is a dimensionless quantity that expresses the average relationship between individual community radii and the network as a whole

$$\rho =\frac{1}{N}\sum _k{N}_{C_k}\frac{{\rho }_{C_k}}{R},$$ (10)

where N_Ck serves to weight every community by the number of nodes it contains, and R is a normalization constant equal to the radius of the entire network: $R=\sqrt{(\frac{1}{N}{\sum }_{i=1}^N{\Vert {\mathbf{r}}_i\Vert }^2-\frac{1}{N^2}{\Vert {\sum }_{i=1}^N{\mathbf{r}}_i\Vert }^2)}$. In the context of human brain graphs, this statistic has previously been used to assess the changes in the spatial extent of modules as they are identified across different levels of the topological hierarchy [134].

l) Community laterality:: Laterality is a property that can be applied to any network in which each node can be assigned to one of two categories, J1 and J2, and describes the extent to which a community localizes to one category or the other.

For an individual community C_k, the laterality Λ_Ck is defined as [70]:

$${\mathrm{\Lambda }}_{C_k}=\frac{|N_{J1}-N_{J2}|}{N_{C_k}},$$ (11)

where N_J1 and N_J2 are the number of nodes located in each category, respectively. The value of Λ_Ck ranges between zero (i.e., the number of nodes in the community are evenly distributed between the two categories) and unity (i.e., all nodes in the community are located in a single category).

The laterality of a given partition, 𝒞, of a network is defined as:

$${\mathrm{\Lambda }}_{𝒞}=\frac{1}{N}(\sum _k{N}_{C_k}{\mathrm{\Lambda }}_{C_k}-\langle \sum _k{N}_{C_k}{\mathrm{\Lambda }}_{C_k}\rangle ),$$ (12)

where 〈Σ_kN_CkΛ_Ck〉 denotes the expectation value of the laterality under the null model specified by randomly reassigning nodes to the two categories while keeping the total number of nodes in each category fixed. One of the most important functional specializations of the brain is laterality, and prior work has used this statistic to demonstrate subtle interhemispheric discrepancies in functional brain graphs during linguistic processing due to task demands [70].

Strength and significance of communities

When reporting values for either topological or spatial diagnostics, it is important to consider potential sources of error or variation that would inform the confidence in the measured values. For example, there may be error in the estimated weights of individual edges in the network, either from errors in the images themselves, or errors in the statistical estimates of structural or functional connectivity from those images. There may also be variance associated with multiple estimates of a network, either from different subjects, or from the same subject at different instances in time or in different brain states. In each case, it is useful to discuss the potential errors or sources of variance contributing to the estimated diagnostics of community structure, and to quantify them where possible.

In addition to accurately describing the potential sources of error in one’s data, it can also be useful to explicitly measure the significance of a given community structure. In this section, we describe two notions that can be used to quantify the strength and significance of communities. (Note that in this section, we use a few variable names that have been defined differently in earlier sections, largely to remain consistent with the traditional use of these variable names in their relevant subfields.)

m) Normalized persistence probability:: The persistence probability is a measure of the strength of a community in a graph with salient community structure [165]. Given an adjacency matrix A, we construct an N-state Markov chain with transition matrix P by performing a row-normalization on A. Specifically, the transition probability from i to j is given by

$$p_{\mathit{\text{ij}}}=\frac{A_{\mathit{\text{ij}}}}{{\sum }_j{A}_{\mathit{\text{ij}}}}.$$ (13)

Under some mild conditions, there exists a unique equilibrium distribution π ∈ ℝ^N that satisfies π = πP. Roughly speaking, this implies that if an individual takes a random walk on V with transition probabilities given by P, then — after some sufficiently long period of time — the probability that the individual is on the ith node is π_i regardless of where the individual started.

Now, given P and any distribution π on V, we can construct a K-state Markov chain with transition probability

$$Q={[\text{diag}(\pi \mathrm{H})]}^{-1}{\mathrm{H}}^{\mathrm{T}}\text{ diag}(\pi )\text{PH},$$ (14)

where H is an N×K binary matrix coding the partition 𝒞; that is, h_ni indicates whether the nth node is in the kth community. We call the K-state Markov chain a lumped Markov chain. We can check that Π = πH is an equilibrium distribution of the lumped Markov chain, which satisfies Π = ΠQ, and therefore the lumped Markov chain can be treated as an approximation of the transition of communities in the original Markov chain. We note that then, the expected escape time of C_k is τ_k = (1 − q_kk)⁻¹, which implies that if now the individual is in C_k, then on average it will take τ_k jumps for the individual to jump to another community. The persistence probability of the kth comunity is therefore defined as q_kk; the larger this value, the longer the expected escape time, and the more significant the community.

In practical applications, the persistence probability is influenced by the size of the community. Larger communities always have larger persistence probabilities. Importantly, this fact can bias empirical results for graphs whose community size distribution is relatively broad. To address this limitation, we can normalize the persistence probability as follows

$${\stackrel{\sim }{q}}_k=\frac{N}{N_{C_k}}{q}_{\mathit{\text{kk}}}.$$ (15)

The kth community is significant if q̃_k ≫ 1. Intuitively, this normalization assumes that the graph is fully connected and that the weights of edges are all equal; then, the persistence probability of the k-th cluster is $\frac{N_{C_k}}{N}$. Whenever a community has a persistence probability that is larger than some threshold α, we will refer to it as an α-community. If all communities are α-communities, we call the entire partition an α-partition.

n) Statistical comparison to a permutation-based null model:: Given a community structure 𝒞, we can in fact compute the contribution of each community to the modularity quality index as follows:

$$Q(C_k|𝒞)=\sum _{i,j\in C_k}(A_{\mathit{\text{ij}}}-\gamma P_{\mathit{\text{ij}}}),$$ (16)

where as before γ is the structural resolution parameter, A is the adjacency matrix, and P is a null model adjacency matrix. Intuitively, Q(C_k|𝒞) measures how strong the kth community is, and it is interesting to ask whether it is stronger than expected under some appropriate null model.

To address this question, we can algorithmically generate a community structure 𝒞^r, which has exactly the same number of communities and the same number of nodes in each corresponding community as in 𝒞, by simply permuting the order of nodes in V. We use this permutation-based approach to construct an ensemble of partitions, and for each partition we can calculate Q(C_k|𝒞^r). Now, we define

$$\mathrm{S}(C_k|𝒞)=\frac{Q(C_k|𝒞)-Q_{\mathit{\text{max}}}(k)}{Q_{\mathit{\text{max}}}(k)-Q_{\mathit{\text{min}}}(k)},$$ (17)

where $Q_{\mathit{\text{min}}}(k)={\text{min}}_{i}Q(C_k^{r(i)}|{𝒞}^{r(i)})$ and $Q_{\mathit{\text{max}}}(k)={\text{max}}_{i}Q(C_k^{r(i)}|{𝒞}^{r(i)})$. The quantity S(C_k|𝒞) is a normalized measure that provides information about how strong the community is in comparison to what is expected under a permutation-based null model. This method was recently used to identify hyperedges in a set of functional brain graphs ordered over the developmental time period spanning 8 years of age to 22 years of age [102].

Modularity maximization for temporal graphs

The methods described above can be applied to a single graph, or separately to all graphs in a graph ensemble. However, in the study of neural function and its relation to cognition, or its change with age and disease, we often have an ordered set of graphs, where the order is based on time (Fig. 4). In this case, it is useful to consider methods for modularity maximization in temporal graphs — a set of graphs ordered according to time from earliest time to latest time [188]. A recent generalization of modularity maximization for graphs with L layers is given by the multilayer modularity quality function [144]:

$$Q_{\mathit{\text{multilayer}}}=\frac{1}{2\mu }\sum _{\mathit{\text{ijlr}}}\{(A_{\mathit{\text{ijl}}}-{\gamma }_l{P}_{\mathit{\text{ijl}}}){\delta }_{\mathit{\text{lr}}}+{\delta }_{\mathit{\text{ij}}}{\omega }_{\mathit{\text{jlr}}}\}\delta (C_{\mathit{\text{il}}},C_{\mathit{\text{jr}}}),$$ (18)

where the adjacency matrix of layer l has elements A_ijl, and the null model matrix of layer l has elements P_ijl, γ_l is the structural resolution parameter of layer l, ω_jlr is the temporal resolution parameter and gives the strength of the inter-layer link between node j in layer l and node j in layer r, δ is the Kronecker delta, and μ is the total edge weight. Small values of the temporal resolution parameter result in greater independence of partitions across neighboring layers, and large values of the temporal resolution parameter result in greater dependence of partitions across neighboring layers. Note that ω can vary from 0 to infinity.

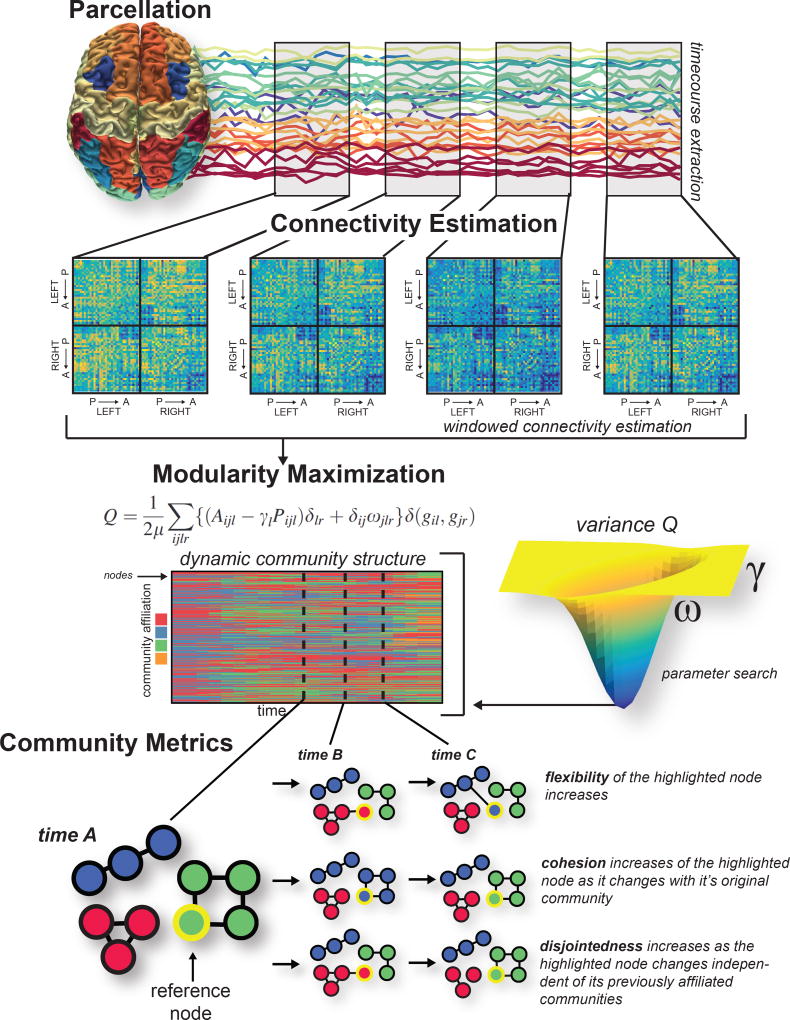
Fig. 4. Building temporal brain graphs and characterizing their dynamic community structure.

Here we illustrate methodological steps to build a temporal brain graph and to estimate its dynamic community structure. First, we define nodes, shown here as a whole-brain parcellation. Next, in each time window, we define edges, shown here as statistical similarities in regional time series. We build a multilayer graph from the ordered set of graphs across all time windows, and we link graphs in neighboring layers by identity links (edges between node i in layer t and itself in layer t − 1 and t + 1). After constructing the multilayer brain graph, we can apply a community detection technique such as the maximization of a multilayer modularity quality function. This process produces a time-dependent partition of nodes into communities or modules. Because multilayer modularity maximization contains tunable parameters, we might also wish to search the 2-dimensional parameter space to find a parameter pair that results in a stable partition (for example, here reflected by a low variance of Q_multilayer across multiple iterations of the maximization algorithm). Finally, the dynamic community structure can be quantitatively characterized with graph statistics (e.g., flexibility, cohesion, and disjointedness).

Determining appropriate choices for the values of the structural (γ) and temporal (ω) resolution parameters is an important enterprise. In some cases, one might have information about the system under study that would dictate the number of communities expected, or their relative size, or their relative variation over time. However, if such information is not available for the system under study, then one must turn to data-driven methods to obtain values for γ and ω that most accurately reflect the spatial and temporal scales of community structure within the data. Several heuristics have been suggested in the literature, including (i) comparison to statistical null models (which we will describe in a later section) [14], (ii) identifying a point in the γ-ω plane where the set of partitions obtained from multiple maximizations of the multilayer modularity quality function are statistically similar [53], or (iii) identifying the point in the γ-ω plane where the dynamic community structure displays certain features [202].

Topological summary statistics for dynamic community structure

Several summary statistics exist which are frequently reported to characterize dynamic community structure in empirical studies. A few particularly simple statistics include (i) the mean and temporal variance of the number of communities, (ii) the mean and temporal variance of the size of communities, and (iii) the multilayer modularity quality index Q_multilayer. In addition to these simple statistics — which have their correlaries in the single-layer case — we can also define several statistics that explicitly capitalize on the temporal nature of the data.

o) Flexibility:: The flexibility of a single node i, ξ_i, is defined as the number of times a node changes in community allegiance across network layers, normalized by the number of possible changes [19]. Mathematically,

$${\xi }_i=\frac{g_i}{L-1},$$ (19)

where g_i is the number of times that the particle changes its community. The flexibility of the entire multilayer graph is then given by the mean flexibility of all nodes

$$\mathrm{\Xi }=\frac{1}{N}\sum _i{\xi }_i.$$ (20)

Intra-individual differences in this metric have been linked to mood [35] and attention [186], while inter-individual differences in this metric have been linked to learning [19], cognitive flexibility and working memory performance [41], and reinforcement learning [91]. The metric has also been shown to be an intermediate phenotype for schizophrenia risk [42], and is altered by an NMDA-receptor antagonist [42].

p) Node disjointedness:: Node disjointedness describes how often a node changes communities independently. Specifically, we are interested in when a node moves from community s to community k, and no other nodes move from community s to community k. If node i makes $g_i^{\mathit{\text{ind}}}$ such changes out of L − 1 possible changes, we define the node disjointedness as follows [203]:

$${\mathrm{\Delta }}_i=\frac{g_i^{\mathit{\text{ind}}}}{L-1}.$$ (21)

q) Cohesion strength:: The node cohesion can be defined as the number of times a node changes communities mutually with another node. Specifically, node cohesion is a pairwise measure that is expressed as a cohesion matrix, M, where edge weight M_ij denotes the number of times a pair of nodes moves to the same community together, $g_{\mathit{\text{ij}}}^{\mathit{\text{mut}}}$ divided by L − 1 possible changes. The cohesion strength of node i is then defined as follows [203]:

$${\mathrm{\Omega }}_i=\sum _{j\ne i}{M}_{\mathit{\text{ij}}}.$$ (22)

This metric has been shown to be more sensitive to individual differences in motor skill learning than either node disjointedness or node flexibility [203].

r) Promiscuity:: The promiscuity ψ_i of node i is defined as the fraction of all communities in which the node participates at least once, across all network layers [162], and importantly can determine whether a node’s flexibility may be high simply because it is switching between two communities or is truly flexible across all communities. The network promiscuity Ψ can be defined as the average promiscuity over all nodes

$$\mathrm{\Psi }=\frac{1}{N}\sum _i{\psi }_i.$$ (23)

s) Stationarity:: To define stationarity, we first write the autocorrelation J(C_l, C_l+m) between a given community at layer l, C_l, and the same community at layer l + m, C_l+m, as

$$J(C_l,C_{l+m})=\frac{|C_l\cap C_{l+m}|}{|C_l\cup C_{l+m}|},$$ (24)

where |C_l ∩ C_l+m| is the number of nodes present in community C in layer l and in layer l + m, and |C_l ∪ C_l+m| is the number of nodes present in community C_k at layer l or layer l + m [161]. Then if l_i is the layer in which community C first appears, and l_f is the layer in which it disappears, the stationarity of community C_k is

$${\zeta }_{C_k}=\frac{{\sum }_{l=l_i}^{l=l_f-1}J(C_l,C_{l+1})}{l_f-l_i}.$$ (25)

The stationarity of the entire multilayer network is then given by

$$\zeta =\frac{1}{N_{C_k}}\sum _k{\zeta }_{C_k}.$$ (26)

While initially defined in the context of social networks [161], the stationarity has also proven useful as a marker of temporal variation in functional brain graphs in healthy adult humans in the process of motor skill acquisition [19].

Statistical Validation and Prediction

After estimating community structure from a single brain graph, or from a multilayer brain graph, one is next faced with the questions of (i) whether and how that community structure is statistically significant, (ii) how to compare community structure in one graph ensemble to community structure in a second graph ensemble, and (iii) how to infer underlying mechanisms driving the observed community structure. Answering these questions requires tools from statistics that are directly informed by network architecture, and tools from generative modeling that can provide insights into possible mechanisms.

The statistical significance of a community structure can only be determined in relation to a defined null model. One of the most common approaches to defining null models for brain graphs is via permutation: for example, the placement or weight of the edges in the true graph can be permuted uniformly at random (Fig. 5). In prior work, this null model has been referred to both as a connectional null model [19] or a random edges null model [188]. If the graph is a temporal multilayer brain graph, one could also consider permuting the inter-layer links uniformly at random (sometimes referred to as a nodal null model). One could also consider permuting the order of the layers uniformly at random (sometimes referred to as a temporal null model) [19]. For a discussion of related null models specifically for dynamic graphs, see [188, 120].

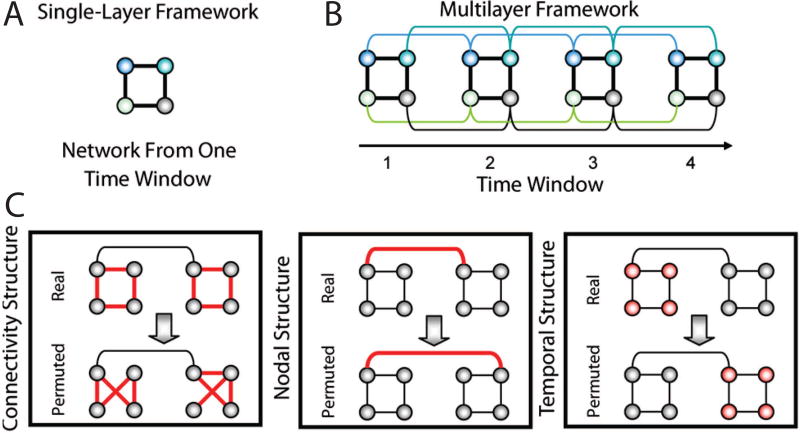
Fig. 5. Permutation-based null models for statistical testing of community structure.

(A) Schematic of a toy network with four nodes and four edes in a single time window. (B) Multilayer network framework in which the networks from four time windows are linked by connecting nodes in a time window to themselves in the adjacent time windows (colored curves). (C) Statistical framework composed of a connectional null model (Left), a nodal null model (Middle), and a temporal null model (Right) in which intranetwork links, internetwork links, and time windows, respectively, in the real network are randomized in the permuted network. (We show all of the randomized links in red.) Figure reproduced with permission from [19].

When graphs are built from functional data, one can also consider null models that are constructed from surrogate time series [14, 120]. Perhaps the simplest surrogate data technique begins by permuting the elements of each time series uniformly at random and then continues by recomputing the measure of functional connectivity between pairs of time series [205]. This approach is sometimes referred to as a random shuffle null model. While a fundamental benchmark, this null model is quite lenient, and it is commonly complemented by more stringent tests [14]. For example, the Fourier Transform surrogate preserves the linear correlation of the series by permuting the phase of the time series in Fourier space before taking the inverse transform to return the series to temporal space. A related technique – the Amplitude Adjusted Fourier Transform – works similarly except that it also preserves the amplitude distribution of the original time series [204]. For helpful additional discussion of surrogate data time series, see [181, 182].

After confirming that the community structure observed in the empirical graph is unlike that observed in either graph-based or time-series-based null models, one might next wish to compare two sets of empirical graphs. Specifically, one might wish to state that the community structure in one graph ensemble (e.g., healthy brains) is significantly different from the community structure in another graph ensemble (e.g., brains from individuals with disorders of mental health). One simple approach would be to use traditional parametric statistics to determine group differences in a summary measure such as the many defined in the earlier sections of this review. Broadly speaking, this approach assumes the data are normally distributed with a mean that is parameterized by a linear model. Common techniques include t-tests, F-tests, and analyses of variance. However, the assumption that network statistics are normally distributed is often violated in real-world data. In such cases, it is more appropriate to use non-parametric permutation testing, which accounts for the true variation in the empirically observed data. This method is computationally costly since it requires an estimation of the null distribution via unlabeled simulation of the available data. For a recent review of this method as it applies to neuroimaging data, see [159].

Finally, moving beyond statistical validation, one might also wish to understand the mechanisms by which community structure arises in one’s data of interest, and predict how alterations in those mechanisms could lead to altered community structure. These sorts of topics are particularly important in understanding normative development and aging, and in understanding changes in graph architecture with disease or injury. To begin to build an intuition for possible mechanisms of community structure, it is natural to turn to generative network modeling techniques [31], in which wiring rules are posited and the resultant graph is compared to the empirically observed graphs; if the observed graph displays similar architecture to the modeled graph, then the wiring rule is said to constitute a potential mechanism. Such generative models can be either static or growing models [126], and can be defined either in a deterministic or probabilistic manner [194]. A particularly useful model for mesoscale structure — including but not limited to community structure — is the stochastic blockmodel, which has recently been used in the context of both structural [32] and functional [164] brain graphs (Fig. 6). Importantly, stochastic blockmodels have also recently been extended to multilayer graphs [200], suggesting their potential utility in understanding mechanisms of brain dynamics as well.

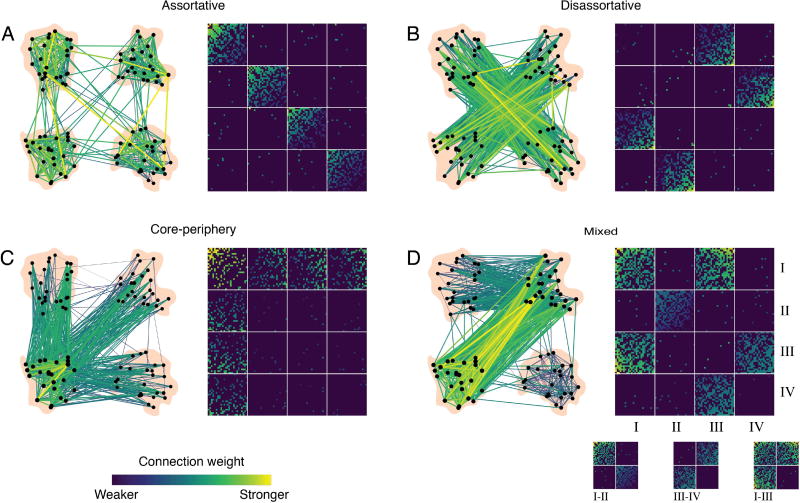
Fig. 6. Stochastic blockmodels can detect other types of meso-scale structure unseen by modularity maximization.

Networks can exhibit different types of meso-scale structure. (A) Assortative communities are sub-networks whose internal density of connections exceeds their external density. (B) Disassortative (multi-partite) communities are sub-networks where connections are made preferentially between communities so that communities’ external density exceed their internal density. (C) Core-periphery organization consists of a central core that is connected to the rest of the network and then peripheral nodes that connect to the core but not to one another. (D) These meso-scale structures can be present simultaneously in the same network. For example, communities I–II interact assortatively, III–IV interact disassortatively, while I–III interact as a core and periphery. Reproduced with permission from [32].

Collectively, these statistical approaches provide a rich set of tools to examine the robustness and reliability of brain graphs constructed from neuroimaging techniques sensitive to neural structure and activity across different spatial scales. Furthermore, recent advancements in generative network modeling provide new avenues to examine the mechanisms supporting network modularity that will complement work using community detection to characterize the static and dynamic evolution of these networks.

From modularity in neural systems to behavior

Mounting evidence supports the notion that modularity in brain graphs is important for healthy task-based and resting-state dynamics. Functional network communities correspond to groups of regions that are activated by the performance of specific cognitive and behavioral tasks requiring for example perception, action, and emotion [63]. Interestingly, evidence suggests that the human brain transitions among functional states that maximize either segregation or integration of communities, and the integrated states are associated with faster and more accurate performance on a cognitive task [185, 184]. Several studies have identified relationships between individual differences in modularity and memory performance [209, 58, 3, 185, 78, 199]. Changes in global modularity predict effective memory retrieval [213], account for reaction time on correct responses [209], and relate to individual variability on other measures of behavioral performance [199]. Converging evidence from electroencephalography studies in which community detection approaches are applied [206, 166] further suggest that increased integration is required for successful working memory function [39, 124, 226].

The relationship between network modularity and performance is also expressed in the resting brain. Global network modularity at rest has been shown to predict inter- and intra-individual differences in memory capacity [201]. When network modularity in resting state dynamics decreases following sleep deprivation, it accounts for behavioral performance impairments [29]. Aging brains typically become less modular at the global scale [137, 90, 54], including specific modularity decreases in the executive control network and attention subsystems associated with typical cognitive decline [33]. Similarly, increased modularity is associated with improved learning and neuroplasticity. Patients with brain injury [8] as well as older adults [87] with more modular brain networks at baseline have been shown to exhibit greater improvements following cognitive training.

Importantly, community detection approaches have also revealed the importance of time-evolving changes in modular networks that underlie human behavior. When participants successfully learn a simple motor skill across several days, the community organization and its dynamics change as the skill becomes more automatic [19, 21]. Motor skill learning is also accompanied by a growing autonomy of the sensorimotor system, and by a disengagement of frontal-cingulate circuitry which predicts individual differences in learning rate [21]. Even at much shorter time-scales and over the course of a single session, dynamic community structure can capture changes in task demands and changes in cognitive state [6, 95, 41, 35, 62].

Finally, the importance of modular network organization for healthy brain function is underscored by its alteration in clinical samples [80]. Connectopathy has been documented in patients with several mental health disorders including but not limited to schizophrenia, depression, anxiety, dementia, and autism [140, 136, 220]. Schizophrenia has been characterized by diminished small-world organization [141, 133, 176], altered modular organization [221, 130, 140, 121, 17, 4], and dysmodularity: an overall increase in both structural and functional connectivity that greatly reduces the anatomical specialization of network activity [64]. Other disorders of mental health, such as depression, have also been documented to exhibit altered network modularity [135, 217, 179], and emerging evidence suggests that changes in inter-module connectivity could underlie common reward deficits across both mood and psychotic disorders [183].

Methodological considerations and future directions

There are several methodological considerations that are important to mention in the context of applying modularity maximization techniques to neuroimaging data condensed into brain graphs. Perhaps one of the most fundamental consideration relates to the notion that one might be able to identify an “optimal” structural or temporal resolution parameter with which to uncover the graph’s most salient community structure. Such a notion presupposes that the graph displays strongest community structure at only a single topological or temporal scale. Yet, in many real-world systems — including brain graphs — modules exist across a range of topological scales from small to large, each contributing in a different manner to the system’s overall function. Moreover, such nested modules might display dynamics over different temporal scales, enabling segregation and integration of computational processes from transient control to long-distance synchrony. Thus, while choosing an optimal resolution parameter may not only be difficult, it may also be unfounded, depending on the architecture of the single-layer graph or multilayer graph under study.

Several approaches have been proposed to address the multi-scale organization of brain graphs (Fig. 8; for a recent review, see [30]). One intuitive solution is to sweep across the topological and temporal scales of the system by incrementally changing the resolution parameters [77]. The advantage of this approach is that it allows us to track the stability of partitions across topological scales and identify robust modules. Nevertheless the communities in this approach are identified independently at each scale and thus a secondary algorithm is necessary for the reconstruction of a continuous topological community structure. An explicit multi-scale community detection algorithm can be used to address this limitation, by allowing simultaneous identification of the community organization across several scales [144]. A recent application of this approach to neuroimaging data has uncovered notable topological heterogeneity in the community structure of both structural and functional brain graphs, and in the extent of coupling across these modalities [9] (Fig. 9).

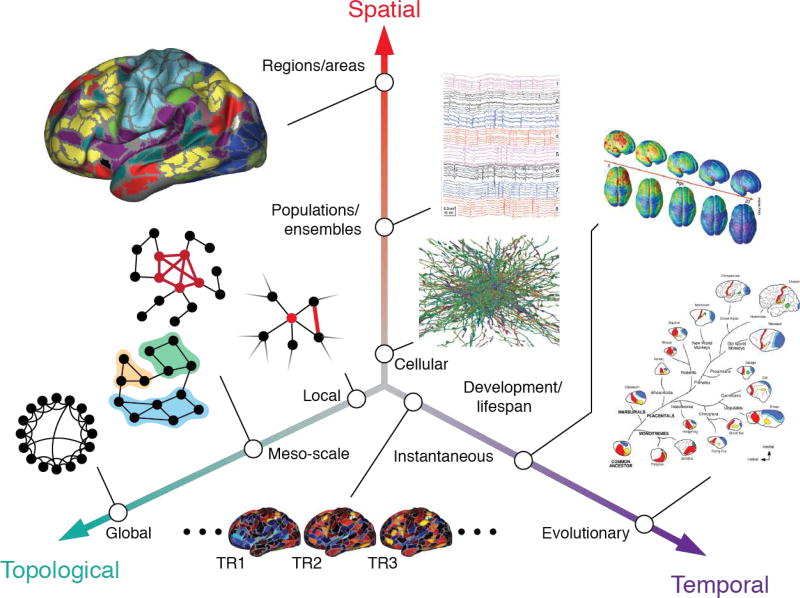
Fig. 8. The multiscale brain.

Brain networks are organized across multiple spatiotemporal scales and also can be analyzed at topological (networks) scales ranging from individual nodes to the network as a whole. Figure reproduced with permission from [30].

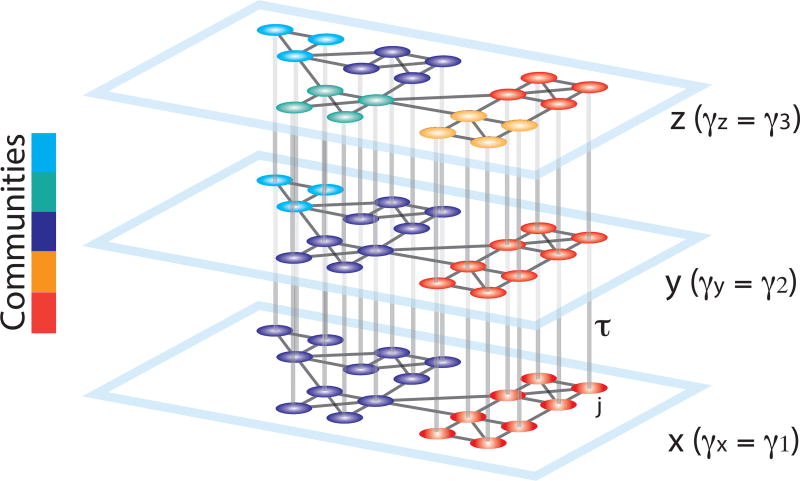
Fig. 9. Schematic representing the construction of a multilayer network for use in multi-scale modularity maximization.

Duplicates of a graph are connected in a multilayer fashion to construct a 3D graph. The smallest resolution parameter γ is assigned to the first layer (x), and it is linearly increased for the neighboring layers (y, z). The topological scale coupling parameter, τ, tunes the strength of dependence of the communities across layers. Since the community assignments are dependent on the adjacent layers, nodes that display high clustering over neighboring topological scales are identified as a single community spanning several scales. In this schematic, the large communities identified at initial layers progressively break into smaller sub-communities, revealing the hierarchical community organization of the graph. Reproduced with permission from [9].

In addition to understanding community structure across different scales in a single data modality, it is becoming increasingly important to identify and characterize community structure across different data modalities. The multilayer network formalism, which we described in this review in the particular context of temporal graphs, can also be used to link graphs from different imaging modalities together [208, 145]. Intuitively, community structure — and the topological or temporal scales at which it is most salient — can differ significantly across imaging modalities. In functional brain graphs estimated over long time scales, the community structure is of neural origin, and thus communities at coarser scales imply higher temporal independence and functional segregation between the communities. By contrast, in structural brain graphs, the community structure can be more reflective of the brain’s spatial organization, constituted by small focal clusters, mesoscale distributed circuits, and gross-scale hemispheres. Since the topological organization of a brain graph can differ across scales in different imaging modalities, it is useful to apply methods that can explicitly compare and contrast community structure across a range of topological and temporal resolutions [9].

Advantages and Disadvantages of the Graph Approach

A key advantage of community detection techniques is their relative simplicity. Nevertheless, this same simplicity can challenge mechanistic understanding of the organizational principles that shape emerging real-time dynamics of the system. This challenge is particularly apparent in the interpretation of the value of the modularity quality index: researchers often interpret higher (lower) modularity values as an increase (decrease) in overall segregation (integration) of brain networks. Yet, it is critical to realize that one can change the structure of a network in a host of ways that all lead to comparable changes in the value of the modularity quality index, but also lead to strikingly different large-scale functional dynamics. Moreover, modularity values themselves are dependent on the resolution parameter at which they are calculated, and direct comparison between modularly values in two graphs using the same resolution parameter hinges on the assumption that both graphs display “optimal” community structure at the same topological scale. Modularity values are also difficult to compare in two graphs that exhibit community structure at different topological scales, as the resolution parameters used for the calculation of the modularity are different. Thus, in general, the interpretability of the modularity value is quite limited.

More generally, it is important to bear in mind that community detection techniques such as modularity maximization assess one specific type of organization in a graph. It may therefore be useful to combine this approach with other techniques to examine complementary types of organization present in the same graph or present in the time series irrespective of the graph [for several recent reviews, see 117, 114, 120]. Within the network science discipline, community detection can be used to examine a specific type of meso-scale organization [for others, see 32], while other graph measures can be used to examine organization at other scales [150]. Examples of these other measures include centralities [13], clustering coefficient [178], path-length [12], and global and local efficiency [129] to name a few. Future work could also use generalizations of these network measures to multilayer data (see [125] for a recent review, and see [188] for a toolbox for use in applying those notions to neuroimaging data). Furthermore, these tools may also provide novel avenues for studying the coupling between the time-varying and multi-scale community structure in functional brain graphs and the underlying hierarchical scaffold in structural brain graphs [9].

Finally, it is important to note that the most common approach used to construct a brain graph treats brain regions as nodes and inter-regional connections as edges. Although this simple graph model has proven useful in advancing our understanding of the organization of brain networks in health and disease, it suffers from an implicit assumption of node homogeneity. That is, each node is distinguished not by any feature of its own, but by its relation to other nodes. Future work could aim to explore and advance community detection methods for annotated graphs [156] in the context of brain networks to account for the heterogeneous function and anatomy of different brain regions [149] (Fig. 10). Moreover, exploring alternative ways to construct brain networks such as hypergraphs [20, 102], and alternative methods to identify community structure such as link-communities [2, 67], could offer important and complimentary information regarding the organizational principles of brain network architecture.

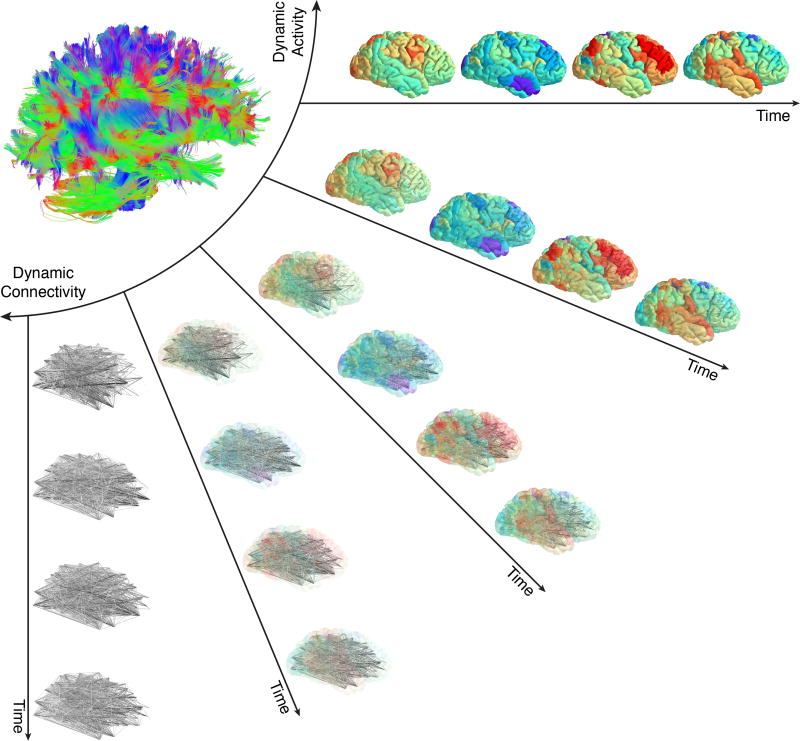
Fig. 10. Mesoscale network methods can address activity, connectivity, or the two together.

In the human brain, the structural connectome supports a diverse repertoire of functional brain dynamics, ranging from the patterns of activity across individual brain regions to the dynamic patterns of connectivity between brain regions. Current methods to study the brain as a networked system usually address connectivity alone (either static or dynamic) or activity alone. Methods developed to address the relations between connectivity and activity are few in number, and further efforts connecting them will be an important area for future growth in the field. In particular, the development of methods in which activity and connectivity can be weighted differently – such as is possible in annotated graphs – could provide much-needed insight into their complimentary roles in neural processing. Figure reproduced with permission from [120].

Conclusion

Here, we have reviewed recent efforts to model brain structure and function using graphs. We focused on describing methods to identify, characterize, and interpret community structure in such graphs, with the goal of better understanding cognitive processes and resulting behavior in health and disease. We began by describing how brain graphs are commonly built, and then we discussed two community detection algorithms based on modularity maximization: one constructed for use on single graphs, and one constructed for use on multilayer graphs. We also offered a collation of summary statistics that can be used to characterize topological features of community structure, spatial features of community structure, and features of dynamic community structure. We closed with a discussion of methodological considerations and future directions, as well as a few comments on the advantages and disadvantages of the graph approach. Our hope is that this review will serve as a useful introduction to the study of community structure in brain graphs, and will spur the development of new tools to more accurately parse and interpret modularity in human brain structure and function.

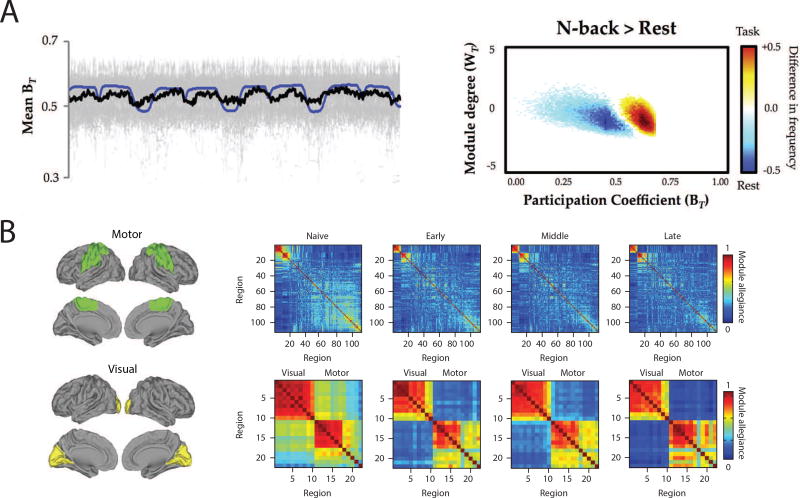
Fig. 7. From modularity to behavior.

Dynamic changes in the modular organization of functional brain networks capture the short- and long-term network reconfigurations triggered by the requirements of an on-going task or following weeks of training. (A) Dynamic task-related fluctuations of community structure during task performance. (Left) Time series plot demonstrated the close relationship between mean B_T (participation coefficient) across 100 subjects (thick black line; individual subject data plotted in gray and task-block repressors plotted in blue). (Right) distinct changes in community structure during N-back task (a common working memory task) compared to the resting state. Note that during N-back performance, the frequency of time points where the network is more integrated significantly increases (red/yellow) compared to the rest blocks (marked by a significant increase in the network segregation) [185]. (B) Learning-induced autonomy of sensorimotor systems captured by a reduction in the probability that motor and visual regions are allied to one another in a single community. The module allegiance matrices are calculated over different phases of learning (naive, early, middle, and late). The bottom row magnifies the visual and motor modules’ allegiance matrices (highlighted with green and yellow brain overlay on the left). Note that the strength of the allegiance between the visual and motor modules decreases as the motor sequences become more automatic, which signifies the increased autonomy of these systems over the course of learning [21]. Figure reproduced with permission from [185] and [21]