Bayesian Functional Joint Models for Multivariate Longitudinal and Time-to-Event Data

Abstract

A multivariate functional joint model framework is proposed which enables the repeatedly measured functional outcomes, scalar outcomes, and survival process to be modeled simultaneously while accounting for association among the multiple (functional and scalar) longitudinal and survival processes. This data structure is increasingly common across medical studies of neurodegenerative diseases and is exemplified by the motivating Alzheimer’s Disease Neuroimaging Initiative (ADNI) study, in which serial brain imaging, clinical and neuropsychological assessments are collected to measure the progression of Alzheimer’s disease (AD). The proposed functional joint model consists of a longitudinal function-on-scalar submodel, a regular longitudinal submodel, and a survival submodel which allows time-dependent functional and scalar covariates. A Bayesian approach is adopted for parameter estimation and a dynamic prediction framework is introduced for predicting the subjects’ future health outcomes and risk of AD conversion. The proposed model is evaluated by a simulation study and is applied to the motivating ADNI study.

1. Introduction

The growing public health threat posed by Alzheimer’s disease (AD) has raised the urgency to discover and assess markers for the early detection of the disease. In this regard, a great deal of e ort has been dedicated to building models for predicting AD based on a single marker, or a combination of multiple markers, which captures the heterogeneity among subjects and detects the disease progression of subjects at risk [1]. Since mild cognitive impairment (MCI) is often considered as a transitional stage to AD, MCI patients are usually enrolled as the target population for early prognosis and evaluating interventions [2]. Existing research has identified a number of biomarkers in predicting an individual’s likelihood of converting to AD, as well as differences in biomarker values among MCI and AD individuals [3, 4]. It is widely acknowledged that magnetic resonance imaging (MRI) based measures of atrophy in key brain regions, such as the hippocampus, are predictive of progression from MCI to AD[5, 6]. Although most of the current studies measure regional atrophy using a single volume-based value, some researchers [7, 8] demonstrated that the surface-based morphology analysis offers more advantages because this method studies patterns of subregion atrophy and produces detailed pointwise correlation between atrophy and cognitive decline. Li and Luo [9] proposed a functional joint model (FJM) that incorporates surface-based hippocampus measure as a functional predictor in the joint model of longitudinal and survival framework. They developed a dynamic prediction method and demonstrated that using such a functional predictor, in addition to other scalar markers, improves predictive performance of the progression of MCI to AD [10]. However, the proposed FJM only accommodates baseline imaging marker as a time-invariant function predictor. Since the imaging markers (e.g., hippocampus) from MRI, along with other neurocognitive markers, are often collected repeatedly in the studies of AD, it is of scientific interest to investigate the combined predictive performance of these repeatedly measured functional and scalar outcomes.

Several methods for the analysis of repeatedly measured functional outcome exist in the literature. One category of the methods is based on functional principal component analysis (FPCA), as well as its extension for multilevel FPCA by Di et al. [11], longitudinal FPCA by Greven et al. [12] and by Park et al. [13]. These methods modeled subject-specific deviations from a population mean by using low dimensional basis functions estimated from the empirical covariance matrix. However, they were inflexible to estimate the effect of covariates (e.g., age) on the functional outcome. Brumback and Rick [14] and Guo [15] proposed a function-on-scalar mixed effect model in which population level effects and individual level deviations were modeled by using penalized splines. Wavelet-based Bayesian functional mixed models were presented in Morris and Carroll [16], which used a discrete wavelet transform of the observed functional data and modeled coefficients in the wavelet domain. Goldsmith and Kitage [17] developed a Bayesian framework for penalized spline function-on-scalar regression, allowing the joint modeling of population level fixed effects, individual level random effects, and residual functions. However, these works focused on the statistical inference on longitudinal functional data without considering the survival process and not for prediction purpose.

Joint model is an appropriate framework to modeling longitudinal data and time-to-event data since it has potential to reduce parameter estimate bias, account for dropout in longitudinal studies, and enable the inclusion of longitudinal covariates (both scalar and functional) measured with error in time-to-event models [18, 19]. Multivariate joint models have been well studied by considering multivariate continuous, binary, ordinal, or a mixture of different outcome types. Hickey et al. [20] gave an excellent review of multivariate joint modeling research. However, no previous study investigates how to incorporate the longitudinal functional (high-dimensional) outcome in a multivariate joint model framework. To this end, we propose a novel joint model that incorporates the growing volume of repeatedly measured functional outcomes in the longitudinal-survival setting. Specifically, we develop a multivariate functional joint model (MFJM) that could simultaneously analyze a longitudinal functional outcome, a longitudinal scalar outcome, and a survival outcome. The principle of the MFJM is to define three type of submodels: (1) a functional mixed effect submodel for the longitudinal functional outcome, (2) a regular mixed effects submodel, or multiple regular mixed effects submodels, to describe the evolution of the longitudinal scalar outcome(s), and (3) a Cox submodel for the survival outcome which is linked with (1) and (2) using a common latent structure. The MFJM is flexible to account for the correlation between repeated measures and correlation among multiple outcomes. We estimate the coefficient functions in the functional regression using penalized spline approach and parameters are jointly estimated in a Bayesian framework.

Compared with the existing literature, we make two major contributions to both multivariate joint modeling and functional data analysis: 1) We propose a multivariate joint model considering both longitudinal functional and scalar outcomes. To the best of our knowledge, this paper is the first to model the repeatedly measured functional outcomes, scalar outcomes, survival process simultaneously while accounting for the associations among the processes. 2) We propose a dynamic prediction framework that provides accurate personalized predictions of disease risk and progression. We investigate the potential capability of the longitudinal functional outcome in improving the prediction of AD progression. Previous studies involving functional data mainly focused on model inference rather than prediction of risk and longitudinal outcome trajectories. These important predictive tools can provide valuable information to monitor each patient’s disease progression and to make early decisions about targeted prevention and treatment selection.

The rest of the article is organized as follows. In Section 2, we describe the motivating Alzheimer’s Disease Neuroimaging Initiative (ADNI) study and the data structure. In Section 3, we discuss the multivariate functional joint model, Bayesian inference procedure, and dynamic prediction framework. In Section 4, we apply the proposed method to the motivating ADNI study. In Section 5, we conduct a simulation study to assess the performance of the method. Concluding remarks and discussion are presented in Section 6.

2. A Motivating Clinical Study

The methodology development is motivated by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study. The primary goal of the study is to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), cerebrospinal fluid (CSF) markers, and neuropsychological assessments can be combined to measure the progression of AD. The phase one of the ADNI study (ADNI-1) recruited more than 800 adults, of which about 200 cognitively normal individuals, 400 mild cognitive impairment (MCI) patients, and 200 early AD patients. Participants were reassessed at 6, 12, 18, 24 and 36 months, and additional follow-ups were conducted annually as part of ADNI-2. At each visit, various neuropsychological assessments, brain image, and clinical measures were collected. Detailed information about the ADNI study procedures, including participant inclusion and exclusion criteria and complete study protocol can be found at http://www.adni-info.org.

MCI is commonly considered as a transitional stage between normal cognition and Alzheimer’s disease and used as the target population for evaluating prognosis and early treatment. To this end, our analysis focuses on 355 MCI patients in the ADNI-1 study without missing data in covariates of interests, and we consider time from baseline to AD diagnosis among MCI patients to be the survival event of interest. In the ADNI-1 study, the 355 MCI patients were followed up for a mean of 3.2 years (SD 2.6; range 0.4-9.3) before AD diagnosis or censoring. Among them, 180 patients were diagnosed with AD (survival event) and 175 had stable MCI over a mean follow-up period of 2.3 years and 4.2 years, respectively.

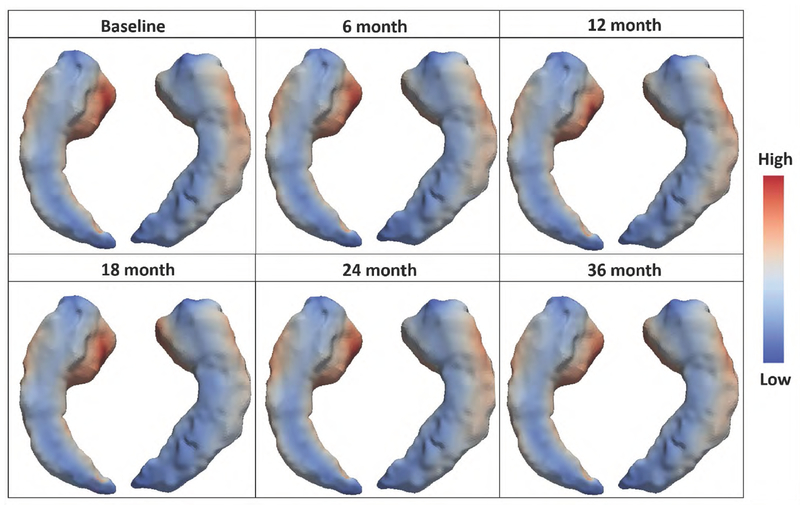
Longitudinal AD Assessment Scale-Cognitive (ADAS-Cog) score and Hippocampal volume (HV) were reported to be the strongest predictor of AD progression in the cognitive and imaging domains, respectively [21]. However, when the high-dimensional MRI data are aggregated to single volume data such as HV, enormous information is lost [8], as the more recent surface-based morphology analysis (based on the longitudinal changes of cortical thickness in thousand of vertices) provides crucial disease progression information for early detection of AD [22]. In this study, we adopt the surface-based analysis of imaging data which retains more information about Hippocampus morphology. In the surface-based analysis, the hippocampus is modeled as a surface model which is a mesh of triangles. Each triangle is known as a face and the place where the corners of the triangles meet is called a vertex. The coordinate of each vertex is determined during image processing and allows one to compute many morphometric measures, e.g., hippocampal radial distance (HRD). Figure 1 illustrates the longitudinal profile of the surface-based hippocampus images (mapped on a three-dimensional hippocampus template) of one MCI patient at different visits. The colors represent the hippocampal radial distance (HRD) which measures the distance from the medial core to each point on the surface (referred to as vertex) and reflects the hippocampal cortical thickness. As AD progresses and the hippocampus atrophies, the radial distance of some subfields shrinks. It has been shown that the baseline vertex-based HRD is predictive of time of MCI-to-AD as a functional predictor [10]. In this paper, we propose a Bayesian personalized prediction model based on a multivariate functional joint model (MFJM) of longitudinal ADAS-Cog 11 score as a scalar predictor, longitudinal vertex-based HRD as a functional predictor, and the time to AD diagnosis.

Figure 1.

The longitudinal profile of surface-based hippocampal images of one MCI patient: hippocampal radial distances are denoted by colors.

The image processing procedure is detailed in the Web Supplement. We first extract the hippocampal surfaces (left and right) from original MRI scans (Step 1 in Web Figure 1) using FIRST [23], an integrated surface analysis tool developed as part of the FSL library [24]. The surfaces are then conformally mapped to a two-dimensional (2D) rectangle plane, in the form of matrix, to form two feature images (Step 2). We then register each feature image (patient and visit) to a common template and calculate the hippocampal radial distance (HRD) of each vertex to the predefined medical core, which represents the hippocampal cortical thickness (Step 3). These steps account for the spatial information and image smoothing. Then the HRD values on the 2D image matrices are aggregated over the y-axis of the image into a one-dimensional (1D) image vector such that the corresponding HRDs of the vertices are represented as a 1D functional data (denoted by y_i(s, t_ij) for subject i visit j) defined on domain $\mathcal{S}$ (Step 4). Each point in the image vector domain (i.e., $\mathcal{S}$) corresponds to a coordinate on x-axis of the 2D hippocampal image matrix. It was revealed that left hippocampus atrophy was associated with delayed verbal memory [25], where the delayed verbal memory was one of the important predictors for determine whether a subject was a MCI converter or not [26]. Thus, our analysis focus on the surface morphology and HRD of the left hippocampus.

3. Methods

3.1. Multivariate functional joint model (MFJM) framework

In the context of clinical trials and observational studies, for each subject i (i = 1, ⋯ , I) at visit j ( j = 1, ⋯ ,J_i) and on a 1D domain s ∈ [0, S_max] = S, we observe data {$y_{\mathit{ij}}^{\ast }$, y_ij(s), x_ij}, where $y_{\mathit{ij}}^{\ast }=y_i^{\ast }(t_{\mathit{ij}})$ is a scalar response observed at time t_ij from the study onset, y_ij(s) = y_i(s, t_ij) is a functional response curve observed at time t_ij on domain S, and x_ij = [x_ij1, ⋯ , x_ijP] is a P-dimensional scalar covariates vector. The domain of the functional response S is not the same as the time domain t, over which the survival event is followed. We propose a longitudinal submodel to describe the evolution of the scalar outcome over time. The model is represented as

$$y_i^{\ast }(t_{ij})=m_i^{\ast }(t_{ij})+{\in }_{ij}^{\ast },m_i^{\ast }(t_{ij})={\beta }_0+t_{ij}{\beta }_t+\sum _p^P{x}_{ijp}{\beta }_p+{\mathit{V}}_R(t_{ij})\zeta +b_i^{\ast },$$ (1)

where $m_i^{\ast }(t_{\mathit{ij}})$ is the unobserved true value of the scalar longitudinal outcome at time t_ij, β₀ is the intercept, β_t is the change of scalar outcome overtime, β_p’s are the regression coefficients. To allow additional flexibility and smoothness in modeling the effects of some covariates, we adopt a smooth time function ${\mathit{V}}_R(t)\zeta ={\sum }_{r=1}^R{\zeta }_r(t-k_r{)}_{+}$ using the truncated power series spline basis expansion V_R(t) = {(t − κ₁)₊, ⋯ , (t − κ_R)₊}, where ζ = [ζ₁, ⋯ , ζ_R]^T are the spline coefficients, κ = {κ₁, ⋯ , κ_R} are the knots, and (t − κ_r)₊ = t − κ_r if t > κ_r and 0 otherwise. We consider a sufficient large number of knots that can ensure the desired flexibility and we select the knot location to have sufficient subjects between adjacent knots. The choice of knots is important to obtain a well fitted model and penalizing the spline coefficients to constrain their influence could help to avoid overfitting [27]. The random intercepts $b_i^{\ast }$ are independent and identically distributed (iid), and the measurement errors ${ϵ}_{\mathit{ij}}^{\ast }~N(0,{\sigma }_{{ϵ}^{\ast }}^2)$ are independent from $b_i^{\ast }$. The inclusion of covariate-specific random effects as a random slope is a direct extension of model (1).

We assume the functional response y_i(s, t_ij) is linear in time, which is a direct extension of the linear assumption in the scalar model. The longitudinal functional submodel is defined as

$$y_i(s,t_{ij})=m_i(s,t_{ij})+{\in }_{ij}(s),m_i(s,t_{ij})=B_0(s)+t_{ij}{B}_t(s)+\sum _p^P{x}_{ijp}{B}_p(s)+b_i(s),$$ (2)

in which m_i(s, t_ij) is the unobserved true value of the longitudinal functional outcome at time t_ij over domain S, B₀(s) is the overall mean function, B_t(s) and B_p(s)’s are fixed effect coefficient functions corresponding to time t and the scalar covariates x_ij. The random intercept function b_i(s) for subject i represents the subject-specific effect, and ϵ_ij(s) is a white noise error process with covariance $\mathit{Cov}\{{ϵ}_{\mathit{ij}}(s),{ϵ}_{\mathit{ij}}(s^{\prime })\}={\sigma }_{ϵ}^2$ if s = s^′ and 0 otherwise. We assume that the random function b_i(s) are iid, the error process ϵ_ij(s) are iid and are independent from b_i(s). For identifiability we require that b_i(s) comprises solely the random deviation that is specific to the subject; any repeated visit-specific deviation is viewed as part of ϵ_ij(s). As in traditional mixed models, the inclusion of “random slope functions” would allow subject-specific impacts of changing covariate levels and should be considered in future applications.

The event history is recorded for each subject i with observed event time $T_i=\mathit{min}(T_i^{\ast },C_i)$ and the event indicator ${\delta }_i=I(T_i^{\ast }\le C_i)$, where $T_i^{\ast }$ and C_i are the true event time and censoring time, respectively. The survival submodel is

$$h_i(t)=h_0(t)\exp \{{\mathit{w}}_i^{⊺}\gamma +{\alpha }^{\ast }{m}_i^{\ast }(t)+{\int }_S\alpha (s)m_i(s,t)ds\},$$ (3)

where h₀(t) is the baseline hazard function, and w_i is a vector of time-independent covariates with regression coefficient vector γ. The association parameter α* quantifies the strength of correlation between the unobserved true longitudinal function $m_i^{\ast }(t)$ and the event hazard at the same time point t, and the association function α(s) quantifies the correlation between the unobserved true longitudinal function m_i(s, t) and the event hazard at the time point. In this paper, we assume a constant functional parameter α(s) ≡ α for identifiability and discuss the case that α(s) varies over the domain of S. We implicitly assume that the risk for an event at time t depends on the unobserved true value of the longitudinal outcomes at the same time point in Model (3). However, other functional forms for the association structure such as time-dependent slopes or cumulative effects of $m_i^{\ast }(t)$ and m_i(s, t) can also be included in the survival submodel. Models (1), (2), and (3) consist of the multivariate functional joint model (MFJM) framework.

To modeling the longitudinal functional data, we adopt the functional mixed effect model and expand the random intercept function b_i(s) using a functional principal component analysis (FPCA) approach. FPCA is a dimensionality reduction tool for functional data which leads to low dimensional projection basis (eigenfunction) and makes analyzing data easier. Specifically, we first express the random intercept function b_i(s) in model (2) using the Karhunen-Loève decomposition. The spectral decomposition of the covariance function of b_i(s)’s is given by ${\Sigma }^{(b)}(s,s^{\prime })={\sum }_{k=1}^{\infty }{\lambda }_k{\varphi }_k(s){\varphi }_k(s^{\prime })$, where λ₁ ≥ λ₂ ≥ ⋯ ≥ 0 are non-increasing eigenvalues and ϕ_k(s)’s are the corresponding eigenfunctions. The Karhunen-Loève expansion of b_i(s) is $b_i(s)={\sum }_{k=1}^{\infty }{\xi }_{\mathit{ik}}{\varphi }_k(s)$, where the functional principal component (FPC) scores ξ_ik are uncorrelated random variables with mean zero and variance λ_k. In practice, we adopt a truncated approximation for b_i(s) given by $b_i(s)\approx {\sum }_{k=1}^{K_{\varphi }}{\xi }_{\mathit{ik}}{\varphi }_k(s)$. Thus y_i(s, t_ij) is written as

$$y_i(s,t_{ij})\approx B_0(s)+t_{ij}{B}_t(s)+\sum _p^P{x}_{ijp}{B}_p(s)+\sum _{k=1}^{K_{\varphi }}{\xi }_{ik}{\varphi }_k(s)+{\in }_{ij}(s).$$

The number of eigenfunctions for random intercept function K_ϕ is pre-specified fixed constants. A sufficiently large value should be chosen for K_ϕ to capture the variation in the random functions, and sensitivity to the choices should be assessed. However, selecting the number of eigenfunctions larger than necessary leads to increased computing burden [17]. For computing efficiency, we assume the correlation between $y_i^{\ast }(t_{\mathit{ij}})$ and y_i(s, t_ij) is manifested by the correlation between $b_i^{\ast }$ and the first elements in ${\xi }_i=[{\xi }_{i1},\cdots ,{\xi }_{{\mathit{iK}}_{\varphi }}]$, and ${\mathit{b}}_i=[b_i^{\ast },{\xi }_i]~\mathit{MVN}(0,\Sigma )$, where

$$\Sigma =\left[\begin{array}{cccc}\hfill {\sigma }_{b^{\ast }}^2,\hfill & \hfill \rho {\sigma }_{b^{\ast }}\sqrt{{\lambda }_1},\hfill & \hfill \cdots ,\hfill & \hfill 0\hfill \\ \hfill \rho {\sigma }_{b^{\ast }}\sqrt{{\lambda }_1},\hfill & \hfill {\lambda }_1,\hfill & \hfill \cdots ,\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0,\hfill & \hfill 0,\hfill & \hfill \cdots \hfill & \hfill {\lambda }_{K_{\varphi }}\hfill \end{array}\right].$$

We may also estimate the correlation between the scalar random effects and all FPC components via an covariance matrix whose off-diagonal elements are nonzero. Such a covariance matrix may provide a full representation of the correlation between the mixed outcomes. However, as the computational burden increases dramatically as the covariance matrix gets more complex, we have to consider the trade-off among modeling flexibility, estimation accuracy, and computation.

In practice, functional outcomes are not truly functions but are observed on a finite grid of length M that cover the domain S, i.e., {s₁, ⋯ , s_M}. Let B(s) be the M × (P + 2) matrix with columns containing B₀(s), B_t(s), and B_p(s)’s evaluated on the finite grid and let ϕ(s) be a M × K_ϕ matrix with columns containing eigenfunctions ϕ_k(s). We express the coefficient function and the eigenfunction in each column of B(s) and ϕ(s) in terms of a known cubic B-spline with equally spaced knots, which leads to a M × K_ψ matrix $\psi (s)=[{\psi }_1^{⊺}(s),\cdots ,{\psi }_{K_{\psi }}^{⊺}(s)]$ with basis functions as columns. For example, the coefficient function $B_0(s)={\sum }_{l=1}^{K_{\psi }}{B}_{0l}{\psi }_l(s)=[{\mathit{B}}_0{\psi }^{⊺}(s){]}^{⊺}$ and the eigenfunction ${\varphi }_k(s)={\sum }_{l=1}^{K_{\psi }}{B_{{\varphi }_k}}_l{\psi }_l(s)=[{\mathit{B}}_{{\varphi }_k}{\psi }^{⊺}(s){]}^{⊺}$, where B₀ and B_ϕk are row vectors of spline coefficients B_0l and $B_{{\varphi }_{k}l}$, respectively. Other spline bases could be used, but the parameters of the B-spline have good mixing properties in the context of Bayesian posterior simulation [28] and B-spline is widely used in functional data analysis literature for its flexibility [29]. Let B_t and B_k’s have the same meaning as B₀, then $\mathit{B}=[{\mathit{B}}_0^{⊺},{\mathit{B}}_t^{⊺},{\mathit{B}}_1^{⊺},\cdots ,{\mathit{B}}_P^{⊺}{]}^{⊺}$ and ${\mathit{B}}_{\varphi }=[{\mathit{B}}_{{\varphi }_1}^{⊺},\cdots ,{\mathit{B}}_{{\varphi }_{K_{\varphi }}}^{⊺}{]}^{⊺}$ denote (P + 2) × K_ψ and K_ϕ × K_ψ matrices respectively, whose rows are spline coefficients for B(s) and ϕ(s). Therefore, the coefficient functions are written as $\mathit{B}(s)=[\mathit{B}{\psi }^{⊺}(s){]}^{⊺}$, the eigenfunctions are $\varphi (s)=[{\mathit{B}}_{\varphi }{\psi }^{⊺}(s){]}^{⊺}$, and the random intercept function is $b_i(s)={\xi }_i(\varphi (s){)}^{⊺}={\xi }_i{\mathit{B}}_{\varphi }{\psi }^{⊺}(s)$, with ξ_i being the row vector of FPC scores for the random intercept function. For the choice of number of basis functions K_ψ for B-spline, we refer to Ruppert [30] and choose them large (e.g., 10) to capture the complexity in coefficient functions. We adopt penalization technique to prevent overfitting and induce smoothness in the resulting coefficient functions. Thus the functional longitudinal submodel is rewritten as

$$\begin{array}{cc}\hfill y_i(s,t_{ij})\approx & m_i(s,t_{ij})+{\in }_{ij}(s),\mathrm{where}\hfill \\ \hfill m_i(s,t_{ij})\approx & {\mathit{B}}_0{\psi }^{⊺}(s)+t_{ij}{\mathit{B}}_t{\psi }^{⊺}(s)+\sum _p^P{x}_{ijp}{\mathit{B}}_p{\psi }^{⊺}(s)+{\xi }_i{\mathit{B}}_{\varphi }{\psi }^{⊺}(s).\hfill \end{array}$$ (4)

We assume a constant associate function α(s) ≡ α, and thus the survival submodel is

$$h_i(t)=h_0(t)\exp \{{\mathit{w}}_i^{⊺}\gamma +{\alpha }^{\ast }{m}_i^{\ast }(t)+\alpha {\int }_S{m}_i(s,t)ds\}.$$ (5)

The integral in the survival submodel is computed by numeric integration.

Let $\theta =[{\beta }^{⊺},{\zeta }^{⊺},{\mathit{B}}^{⊺},({\xi }_i:i=1,\cdots ,I),({\lambda }_k:k=1,\cdots ,{\mathit{K}}_{\varphi }),\rho ,{\mathit{B}}_{\varphi }^{⊺},\gamma ,{\alpha }^{\ast },\alpha ,{\sigma }_{b\ast }^2,{\sigma }_{ϵ\ast }^2,{\sigma }_{ϵ}^2,{\theta }_{h_0^{\ast }}^{⊺}{]}^{⊺}$ be the unknown parameter vector to be estimated, where β = [β₀, β_t, β₁, ⋯ , β_p]^T , and vector ${\theta }_{h_0^{\ast }}$ denotes the parameters in the baseline hazard function $h_0^{\ast }(\cdot )$. The observed data $y_i^{\ast }(t_{ij})$, y_i(s, t_ij), x_ij, t_ij, w_i for i = 1, ⋯ , I and j = 1, ⋯ , J_i are known; as well as the cubic B-spline basis functions ψ(s), which can be generated using the bs function in the R package spline.

The conditional likelihood from the longitudinal scalar data $y_i^{\ast }=[y_{i1}^{\ast },\cdots ,y_{{\mathit{iJ}}_i}^{\ast }{]}^{⊺}$ is

$$p(y_i^{\ast }\mid \theta ,{\mathit{b}}_i)=(2\pi {\sigma }_{{ϵ}^{\ast }}^2{)}^{-J_i∕2}\exp \left\{-\frac{1}{2{\sigma }_{{ϵ}^{\ast }}^2}\sum _{j=1}^{J_i}{\left[y_{ij}-({\beta }_0+t_{ij}{\beta }_t+\sum _p^P{x}_{ijp}{\beta }_p+\sum _{r=1}^R{\zeta }_r(t-k_r)+b_i^{\ast })\right]}^2\right\}.$$

The conditional likelihood for the functional longitudinal data ${\mathit{y}}_i(s)=[y_{i1}^{⊺}(s),\cdots ,y_{{\mathit{iJ}}_i}^{⊺}(s){]}^{⊺}$ is

$$p(y_i(s)\mid \theta ,{\mathit{b}}_i)=\mid 2\pi {\sigma }_{ϵ}^2{\mathit{I}}_{s\times s}{\mid }^{-J_i∕2}\exp \left\{-\frac{1}{2}\mathrm{tr}([{\mathit{y}}_i(s)-{\mathit{m}}_i(s){]}^{⊺}[{\mathit{y}}_i(s)-{\mathit{m}}_i(s)]({\sigma }_{ϵ}^2{\mathit{I}}_{s\times s}{)}^{-1})\right\},$$

where ${\mathit{m}}_i(s)=[m_i^{⊺}(s,t_{i1}),\cdots ,m_i^{⊺}(s,t_{{\mathit{iJ}}_i}){]}^{⊺}$, |·| is the determinant of a matrix and tr is the trace of a matrix. The density function of the random effects b_i is $p({\mathit{b}}_i\mid \theta )=(2\pi {)}^{-(K_{\varphi }+1)∕2}\mid \Sigma {\mid }^{-1∕2}\exp (-\frac{1}{2}{\mathit{b}}_i^{⊺}{\Sigma }^{-1}{\mathit{b}}_i)$, where (K_ϕ + 1) is the dimension of the covariance matrix Σ. The conditional likelihood from the survival data is

$$p(T_i,{\delta }_i,\mid \theta ,{\mathit{b}}_i)=h_i(T_i\mid \theta ,{\mathit{b}}_i{)}^{{\delta }_i}{S}_i(T_i\mid \theta ,{\mathit{b}}_i)=h_i(T_i\mid \theta ,{\mathit{b}}_i{)}^{{\delta }_i}\exp [-{\int }_0^{T_i}{h}_i(t\mid \theta ,{\mathit{b}}_i)dt],$$

where $h_i(T_i\mid \theta ,{\mathit{b}}_i)=h_0^{\ast }(T_i)\exp \{{\mathit{w}}_i^{⊺}\gamma +{\alpha }^{\ast }{m}_i^{\ast }(T_i)+\alpha {\int }_S{m}_i(s,T_i)\mathit{ds}\}$, and function $h_0^{\ast }(\cdot )$ can be approximated by a piecewise-constant function or a B-spline function.

Under the local independence assumption (i.e., conditional on the random effects vector b_i, all components in ${\mathit{y}}_i^{\ast }$, y_i(s), and T_i are independent), the joint likelihood function is

$$L(\theta )=\prod _{i=1}^{I}p({\mathit{y}}_i^{\ast },{\mathit{y}}_i(s),T_i,{\delta }_i\mid \theta )=\prod _{i=1}^I\int p(y_i^{\ast }\mid \theta ,{\mathit{b}}_i)p({\mathit{y}}_i(s)\mid \theta ,{\mathit{b}}_i)p(T_i,{\delta }_i,\mid \theta ,{\mathit{b}}_i)p({\mathit{b}}_i\mid \theta )d{\mathit{b}}_i.$$ (6)

3.2. Bayesian inference

For model estimation, we propose a Bayesian modeling approach based on Markov Chain Monte Carlo (MCMC) posterior simulations, which provides a flexible way for statistical inference. The Bayesian approach has a number of advantages and has been previously exploited in the univariate joint modeling framework [31] and functional regression [32]. Liu and Li [33] compared the performance of Bayesian approaches to classical frequentist (maximum likelihood) approaches under multivariate joint model framework, demonstrating superiority of the Bayesian methods with respect to bias, root-mean square error, and coverage.

We use vague priors on all elements in parameter vector θ. Specifically, the prior distributions of parameters β, γ, α*, α are N(0, 100), and Inverse-Gamma(0.01, 0.01) for variance paramete ${\sigma }_{{ϵ}^{\ast }}^2$ and ${\sigma }_{{ϵ}^{\cdot }}^2$ We impose smoothness on coefficient function estimates through the prior specification on spline coefficients B and B_ϕ, and assume the following priors for the columns of the matrices:

$$\begin{array}{cc}\hfill {\mathit{B}}_k& ~N(0,{\sigma }_k^2{Q}^{-1}),\text{for}1\le k\le (P+2),\hfill \\ \hfill {\mathit{B}}_{{\varphi }_k}& ~N(0,{\sigma }_{{\varphi }_k}^2{Q}^{-1}),\text{for}1\le k\le K_{\varphi },\hfill \end{array}$$

where Q is a pre-specified K_ψ × K_ψ penalty matrix enforces smoothness through the connection between Bayesian priors and quadratic penalization [27]. As suggested in Goldsmith et al. [17], we use Q = μQ₀ + (1 − μ)Q₂ where Q₀ and Q₂ are zeroth- and second-order derivative penalty matrices, with the upper left parts as

$$Q_0=\Psi (s)\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right]{\Psi }^{⊺}(s)\text{and}{Q}_2=\Psi (s)\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill -2\hfill & \hfill 5\hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill 1\hfill & \hfill -4\hfill & \hfill 6\hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -4\hfill & \hfill 6\hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right]{\Psi }^{⊺(s)},$$

where ψ(s) is the cubic B-spline evaluation matrix defined previously. Selecting 0 < μ ≤ 1 balance the universal shrinkage encoded in Q₀ and the smoothness constraint of Q₂, while ensuring Q is positive definite and priors are proper. In the simulation and real data analysis we set μ = 0.1 and sensitivity analyses have indicated robustness to the choice of μ in the analysis. We use random walk prior of Lang & Brezger [34] on the spline coefficients ζ_r, for r = 1, ⋯ , R, for smoothing and penalization. Specifically, we use a first order random prior distribution for ${\zeta }_{r+1}~N({\zeta }_r,{\sigma }_{\zeta }^2)$, for r = 1, ⋯ , R−1, where ζ₁ is treated as a fixed unknown parameter. The variance component ${\sigma }_k^2$, ${\sigma }_{{\varphi }_k}^2$, and ${\sigma }_{\zeta }^2$ are assigned Inverse-Gamma(0.01, 0.01) as prior distribution. The parameters ${\sigma }_{b^{\ast }}^2$ and λ_k in the covariance matrix Σ are assigned Inverse-Gamma(0.01, 0.01) prior distribution, and correlation coefficient ρ is assigned Uniform(−1, 1).

The model fitting is performed in Stan by specifying the full likelihood function and the prior distributions of all unknown parameters. Stan adopts a No-U-Turn sampler (NUTS), which is an extension to Hamiltonian Monte Carlo (HMC) that avoids random walk behavior by using the gradient of the log-posterior and eliminates the need to set a number of steps that required in HMC [35]. NUTS uses a recursive algorithm to build a set of likely candidate points that spans a wide swath of the target distribution, stopping automatically when it starts to double back and retrace its steps [36]. Empirically, NUTS offers faster convergence and parameter space exploration compared with other MCMC algorithms such as Gibbs sampler. We use the history plots and view the absence of apparent trend in the plot as evidence of convergence. In addition, we use the Gelman-Rubin diagnostic to ensure the scale reduction $\widehat{R}$ of all parameters are smaller than 1.1 [37]. After fitting the model to the training dataset (the dataset used to build the model) using Bayesian approaches, we obtain D (e.g., D=5,000 after burn-in) samples for the parameter vector denoted by {θ^(d), d = 1, ⋯ , D}. All estimations can then be obtained by calculating simple summaries (e.g., mean, variance, quantiles) of the posterior distributions of D samples {θ^(d), d = 1, ⋯ , D}. Based on the estimated coefficient vector $\widehat{\mathit{B}}$ (posterior mean), the estimated coefficient function is calculated by $\widehat{\mathit{B}}(s)=[\widehat{\mathit{B}}{\psi }^{⊺}(s){]}^{⊺}$. The Bayesian approach allows for the easy construction of posterior credible intervals for the coefficient function B(s) as [$\widehat{q}$_B,0.025(s),$\widehat{q}$_B,0.975(s)], where $\widehat{q}$_B,u(s) is the u-quartile of the MCMC samples B(s)^(d) = [B^(d)ψ^T(s)]^T, d = 1, ⋯ , D. To facilitate easy reading and implementation of the proposed multivariate functional joint model, we provide a sample Stan code in the Web Supplement.

3.3. Dynamic prediction framework

We next illustrate the dynamic prediction framework based on the proposed model. Given a new subject N’s outcome histories ${\mathit{y}}_N^{\{t\}}=\{y_N^{\ast }(t_{\mathit{Nj}}),y_N(s,t_{\mathit{Nj}});0\le t_{\mathit{Nj}}\le t\}$ and covariates ${\mathit{X}}_N^{\{t\}}=\{{\mathit{x}}_N(t_{\mathit{Nj}}),{\mathit{w}}_N;0\le t_{\mathit{Nj}}\le t\}$ up to time t, and δ_N = 0 (no event), we want to predict the personalized scalar outcome $y_N^{\ast }(t^{\prime })$ and functional outcome y_N(s, t′) at a future time point t′ > t (e.g., t′ = t + Δt), as well as the conditional probability of event-free or survival at time t′, denoted by ${\pi }_N(t^{\prime }\mid t)=P(T_N^{\ast }\ge t^{\prime }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}})$. The key step for prediction is to obtain the subject N’s subject-specific random intercept $b_N^{\ast }$ and random function b_N(s). This could be achieved by sampling $b_N^{\ast }$ and FPC scores vector ξ_N jointly from their posterior distribution $p({\mathit{b}}_N\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},\theta )$, where ${\mathit{b}}_N=[b_N^{\ast },{\xi }_N]$, and reconstructing random function b_N(s) = ξ_NB_ϕψ(s)^T. Conditional on the dth posterior sample θ^(d), d = 1, ⋯ , D, we draw the dth sample of the b_N from the posterior distribution

$$\begin{array}{cc}\hfill p({\mathit{b}}_N\mid T_N^{\ast }>t,y_N^{\{t\}},{\theta }^{(d)})=& \frac{p(y_N^{\{t\}},T_N^{\ast }>t,{\mathit{b}}_N\mid {\theta }^{(d)})}{p(y_N^{\{t\}},T_N^{\ast }>t\mid {\theta }^{(d)})}\propto p(y_N^{\{t\}},T_N^{\ast }>t,{\mathit{b}}_N\mid {\theta }^{(d)})\hfill \\ \hfill =& p(y_N^{\{t\}}\mid {\theta }^{(d)},{\mathit{b}}_N)p(T_N^{\ast }>t\mid {\theta }^{(d)},{\mathit{b}}_N)p({\mathit{b}}_N\mid {\theta }^{(d)}).\hfill \end{array}$$

where $p({\mathit{y}}_N^{\{t\}}\mid {\theta }^{(d)},{\mathit{b}}_N)$ is the joint conditional probability of longitudinal scalar and functional outcomes, $p(T_N^{\ast }>t\mid {\theta }^{(d)},{\mathit{b}}_N)$ is the survival probability, and p(b_N|θ^(d)) is the probability of random effect. For each of θ^(d), d = 1, ⋯ , D, we use adaptive rejection Metropolis sampling (ARMS) [38] to draw one sample of random effect vector b_N. This process is repeated for the D saved values of θ so that D samples of random effect vector b_N are obtained. The predictions can be calculated by plugging in the samples of the parameter vector and random effect vector $\{{\theta }^{(d)},{\mathit{b}}_N^{(d)},d=1,\cdots ,D\}$ into the proposed models. For example, based on model (1), the expected values of the longitudinal scalar outcome for subject N at time t′ is calculated with respect to the posterior distribution of the parameters $\{\theta \mid {\mathcal{D}}_I\}$ as

$$\begin{array}{cc}\hfill & E\{y_N^{\ast }(t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}},{\mathcal{D}}_1\}\hfill \\ \hfill =& \int E\{y_N^{\ast }(t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta \}p(\theta \mid {\mathcal{D}}_1)d\theta ,\hfill \end{array}$$ (7)

where ${\mathcal{D}}_I$ denotes the sample on which the model is fitted. The first part of the integrand is given as

$$\begin{array}{cc}\hfill & E\{y_N^{\ast }(t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}},\theta \}\hfill \\ \hfill =& \int E\{y_N^{\ast }(t^{\prime })\mid T_N^{\ast }>t,y_N^{\{t\}},{\mathit{X}}_N^{\{t\}},b_N^{\ast },\theta \}p(b_N^{\ast }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta )d{b}_N^{\ast }\hfill \\ \hfill =& \int \{{\beta }_0+t^{\prime }{\beta }_t\underset{p}{\overset{P}{\Sigma }}{x}_{N_p}{\beta }_p+V_R(t^{\prime })\zeta +b_N^{\ast }\}p(b_N^{\ast }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta )d{b}_N^{\ast }\hfill \\ \hfill =& {\beta }_0+t^{\prime }{\beta }_t+\underset{p}{\overset{P}{\Sigma }}{x_N}_p{\beta }_p+V_R(t^{\prime })\zeta +\int b_N^{\ast }p(b_N^{\ast }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta )d{b}_N^{\ast }.\hfill \end{array}$$ (8)

The integration with respect to θ in Equation (7) and the integration with respect to $b_N^{\ast }$ in Equation (8) can be approximated using a Monte Carlo simulation scheme [39], where the dth Monte Carlo sample is

$$E^{(d)}\{y_N^{\ast }(t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},{\mathcal{D}}_1\}={\beta }_0^{(d)}+t^{\prime }{\beta }_t^{(d)}+\underset{p}{\overset{P}{\Sigma }}x{N}_p{\beta }_p^{(d)}+V_R(t^{\prime }){\zeta }^{(d)}+(b_N^{\ast }{)}^{(d)},d=1,\cdots ,D.$$

Similarly, based on model (4), the expected values of the longitudinal functional outcome for subject N at time t′ is

$$\begin{array}{cc}\hfill & E\{y_N(s,t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},{\mathcal{D}}_I\}\hfill \\ \hfill =& \int E\{y_N(s,t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta \}p(\theta ,\mid {\mathcal{D}}_I)d\theta ,\hfill \end{array}$$

where the first part of the integrand is given as

$$\begin{array}{cc}\hfill & E\{y_N(s,t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta \}\hfill \\ \hfill =& \int E\{y_N(s,t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},{\xi }_N,\theta \}p({\xi }_N\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta )d{\xi }_N\hfill \\ \hfill =& {\mathit{B}}_0{\psi }^{⊺}(s)+t^{\prime }{\mathit{B}}_t{\psi }^{⊺}(s)+\underset{p}{\overset{P}{\Sigma }}{x}_{N_p}{\mathit{B}}_p{\psi }^{⊺}(s)+\int {\xi }_N{\mathit{B}}_{\varphi }{\psi }^{⊺}(s)p({\xi }_N\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta )d{\xi }_N.\hfill \end{array}$$

In addition, based on model (5), the conditional probability of event-free at time t′ is

$$\begin{array}{cc}\hfill {\pi }_N(t^{\prime }\mid t)=& \int P(T_N^{\ast }\ge t^{\prime }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta )p(\theta ,\mid {\mathcal{D}}_I)d\theta ,\text{and}\hfill \\ \hfill P(T_N^{\ast }\ge t^{\prime }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}}{X}_N^{\{t\}},\theta )=& \int P(T_N^{\ast }\ge t^{\prime }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},{\mathit{b}}_N)p({\mathit{b}}_N\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},\theta )d{\mathit{b}}_N\hfill \\ \hfill =& \int \frac{P(T_N^{\ast }\ge t^{\prime }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},{\mathit{b}}_N)}{P(T_N^{\ast }\ge t\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},X_N^{\{t\}},{\mathit{b}}_N)}p({\mathit{b}}_N\mid T_N^{\ast }>t,{\mathit{y}}_N^{(t)},X_N^{\{t\}},\theta )d\mathit{b}N.\hfill \end{array}$$

The Monte Carlo samples of $E\{y_N(s,t^{\prime })\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}},{\mathcal{D}}_I\}$ and π_N(t′|t) can be obtained by simply replacing {θ, b_N} in the model with $\{{\theta }^{(d)},{\mathit{b}}_N^{(d)}:d=1,\cdots ,D\}$. All prediction results can then be obtained by calculating simple summaries (e.g., mean, variance, quantiles) of the D samples.

Suppose that subject N has not experienced the event of interest by time t′, then the outcome histories are updated to ${\mathit{y}}_N^{\{t^{\prime }\}}$. We can dynamically update the posterior distribution to $p({\mathit{b}}_N\mid T_N^{\ast }>t^{\prime },{\mathit{y}}_N^{\{t^{\prime }\}},\theta )$, draw new samples, and obtain the updated predictions. We assess the performance of the proposed predictive measures in discriminate between patients who had the event from patients who did not. Such discrimination performance is measured by the integrated area under the time-dependent receiver operating characteristic curve that accommodates censoring time [40].

4. Application to the ADNI Study

We apply the proposed Bayesian MFJM to the motivating ADNI-1 study. Besides the longitudinal ADAS-Cog 11 and imaging marker, we include the following variables as scalar covariates: baseline age (bAge, mean: 74.4, SD: 7.3, range 55.1-89.3), gender (gender, 36.1% female), years of education (Edu, mean: 15.6, SD: 3.0, range 4-20), and presence of at least one apolipoprotein E-ε 4 allele (APOE-ε4, 56%), given their potential effects on AD progression [41, 42, 43]. To investigate the different forms of imaging information, we include the baseline hippocampal volume (bHV), baseline hippocampal surface based on hippocampal radial distance (bHRD), and longitudinal hippocampal radial distance (lHRD).

We proposed three joint models with the same longitudinal submodel of the scalar outcome, ADAS-Cog 11, which is defined by

$$\begin{array}{cc}\hfill ADAS-Co{g}_i(t_{ij})=& m_i(t_{ij})+{\epsilon }_{ij}\hfill \\ \hfill m_i^{\ast }(t_{ij})=& {\beta }_0+{\beta }_{1}APOE-\epsilon 4_i+{\beta }_{2}bAg{e}_i+{\beta }_t{t}_{ij}+\underset{r=1}{\overset{3}{\Sigma }}{\zeta }_r(t_{ij}-k_r{)}_{+}+b_{i1}^{\ast }.\hfill \end{array}$$

The three joint models are varied in the survival part that incorporate different levels of imaging information in prediction of AD progression. In the first joint model (refer to as model JM), we incorporate the baseline hippocampal volume (bHV) as a scalar predictor, along with other covariates and underline process $m_i^{\ast }(t)$ of the ADAS-Cog 11, in the survival part. This gives the survival submodel in JM as

$$h_i(t)=h_0(t)\exp \{{\gamma }_1{\mathit{gender}}_i+{\gamma }_{2}bAg{e}_i+{\gamma }_{3}Ed{u}_i+{\gamma }_{4}APOE-\epsilon 4+{\gamma }_{5}bH{V}_i+{\alpha }^{\ast }{m}_i^{\ast }(t)\}.$$

The second model is a function joint model (refer to as model FJM) which includes baseline hippocampal radial distance bHRD(s), instead of hippocampal volume, as a time-independent functional predictor in the survival submodel. The model was proposed and applied to ADNI study in the previous work [10], in which the survival submodel is defined as

$$\begin{array}{cc}\hfill h_i(t)=& h_0(t)\exp \{{\gamma }_1{\mathit{gender}}_i+{\gamma }_{2}bAg{e}_i+{\gamma }_{3}Ed{u}_i+{\gamma }_{4}APOE-\epsilon 4\hfill \\ \hfill & +{\int }_{s}bHR{D}_i(s)B_{bHRD}(s)ds+{\alpha }^{\ast }{m}_i^{\ast }(t)\}.\hfill \end{array}$$

The third model is a multivariate functional joint model (refer to as model MFJM) that accounts for the longitudinal hippocampal radial distance lHRD(s, t) in the survival submodel, where lHRD(s, t) is modeled as

$$\begin{array}{cc}\hfill {\mathit{lHRD}}_i(s,t_{\mathit{ij}})=& m_i(s,t_{\mathit{ij}})+{\epsilon }_{\mathit{ij}}(s)\hfill \\ \hfill m_i(s,t_{\mathit{ij}})=& B_0(s)+B_1(s)\mathit{APOE}-\epsilon 4_i+B_2(s)b{\text{Age}}_i+B_t(s)t_{\mathit{ij}}+b_{i1}(s),\hfill \end{array}$$

and the survival submodel is

$$\begin{array}{cc}\hfill h_i(t)=& h_0(t)\exp \{{\gamma }_1{\mathit{gender}}_i+{\gamma }_{2}Ed{u}_i++{\gamma }_{3}bAg{e}_i+{\gamma }_{4}APOE-\epsilon 4_i\hfill \\ \hfill & +{\alpha }^{\ast }{m}_i^{\ast }(t)+\alpha {\int }_s{m}_i(s,t)ds\}.\hfill \end{array}$$

In the MFJM, we expand the random functions $b_{i1}(s)={\sum }_{k=1}^{k_{\varphi }=4}{\xi }_{\mathit{ik}}{\varphi }_k(s)$, and consider the correlation between $b_{i1}^{\ast }$ and ξ_i1. We express coefficient functions B_p(s) and eigenfunctions ϕ_k(s) in term of a known cubic B-spline basis functions ψ(s) with 10 knots. We allow a flexible and smooth disease progression along time by using truncated power series splines with 3 knots at the location k = (1, 2, 3) in years, which ensures sufficient patients within each interval. Baseline hazard function h₀(t) is approximated by a piecewise constant function. Specifically, the observed survival time is divided into H = 7 intervals by every 1/Hth quantiles. We have also explored other selections of K_ϕ and H and obtained very similar results.

The three candidate models are compared via assessing their predictive performance, manifested by the time-dependent AUCs, at different time points over the follow-up period. To avoid overestimation of the prediction, we conduct a 10-fold cross validation. Parameters of the joint model are estimated from the training dataset and applied to the validation dataset. The conditional event-free probability corresponding to the time frame (t, t + Δt] are predicted for each patient in the validation datasets as describe in Section 3.3. Because the ADNI patients were reassessed approximately every half year, we select t at 1, 1.5, and 2 years, and Δt as 0.5 and 1 years for analysis. Then the time-dependent AUCs are calculated based on the predicted probabilities of all patients.

Table 1 displays the time-dependent AUCs from the three candidate models. Model FJM and MFJM have notably larger AUCs than model JM for most combinations of t and Δt. This suggests that including functional predictor HRD in the survival submodel improves the capability of the joint model in predicting risk of AD diagnosis. However, the predictive capability of longitudinal HRD does not shown much advantage than the baseline HRD information, except the early phase of the follow-up. This may explained by the fact that different markers may be more or less discriminative at different stages of disease, and MRI abnormalities usually occurring earlier before any symptom of cognitive impairment appears [44, 45]. We have also assessed the MFJM accounting for the correlations between $b_{i1}^{\ast }$ and the first two FPC components [ξ_i1, ξ_i2]. The model has no notable improvement in term of prediction.

Table 1:

Areas under the ROC curve (AUC) by three candidate models in the ADNI study.

Δ t	t	JM 1	FJM	MFJM
0.5	1	0.715	0.754	0.821
	1.5	0.691	0.738	0.734
	2	0.781	0.809	0.812
1	1	0.696	0.747	0.792
	1.5	0.735	0.776	0.777
	2	0.749	0.769	0.766

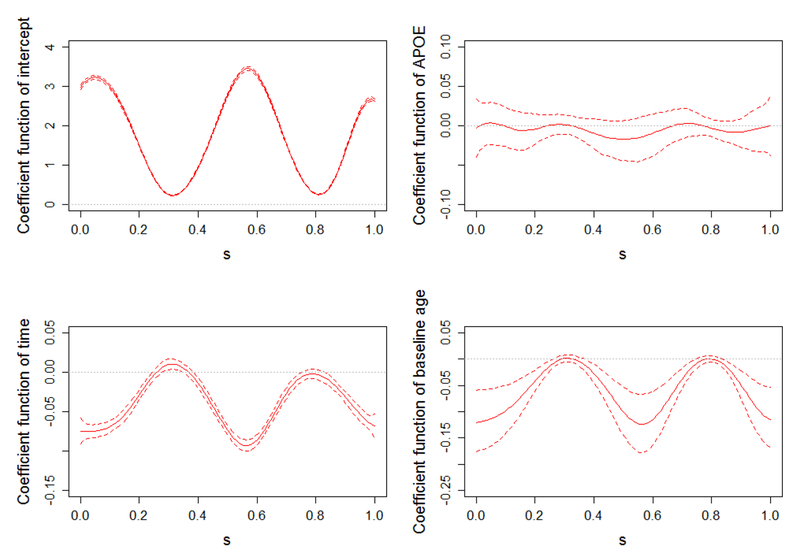
We select MFJM as the final model because it has a competitive good discrimination capability in both early and late phases. Parameter estimates from model MFJM using whole dataset are presented in Table 2. In the longitudinal submodel of scalar outcome, people with APOE-ε4 allele(s), on average, have higher (worse) ADAS-Cog 11 score (2.207 unit) than people without this genetic variation. Also, the ADAS-Cog 11 score increases (deteriorates) as time progresses, i.e., an average increase of 1.121 unit (95% CI: [0.648-01.584]) per year for MCI patients. In the survival submodel, the presence of APOE-ε4 allele(s) increases the hazard of AD diagnosis by 51% (exp(0.409) − 1, 95% CI: [8%-109%]), which is consistent with the literature [46]. Furthermore, larger ADAS-Cog 11 score increases the risk of AD diagnosis, i.e., one unit increase in ADAS-Cog 11 score increases the hazard of AD diagnosis by 19% (exp(0.173) − 1, 95% CI: [14%-24%]). The association parameter α is negative, indicating that the decrease of HRD (i.e., hippocampal atrophy) is associated with the increasing risk of AD diagnosis. The estimated coefficient functions in the longitudinal model for functional outcome HRD is presented in Figure 2. APOE-ε4 allele(s) is not associated with the thickness of hippocampus because the estimated coefficient function ${\widehat{B}}_1(s)$ (upper right panel) fluctuates around zero across the domain S. The estimated coefficient function ${\widehat{B}}_t(s)$ (lower left panel) quantifies the change of HRD over time, and notable atrophy can be viewed on both ends and middle part of hippocampus. The baseline age of the patients have a similar effect on hippocampus. As shown in the estimated coefficient function ${\widehat{B}}_2(s)$ (lower right panel), the older patients, on average, have thinner hippocampus on both ends and middle parts.

Table 2:

ADNI data analysis results from model MFJM.

	Parameters	Mean	SE	2.5%	97.5%
For scalar longitudinal outcome
ADAS-Cog 11	APOE-ε4	2.207	0.397	1.464	3.006
	bAge	0.172	0.258	−0.346	0.668
	Time (Years)	1.121	0.240	0.648	1.584
For survival process
MCI to AD	Female	0.094	0.172	−0.241	0.442
	bAge	−0.113	0.086	−0.278	0.059
	Edu (years)	0.029	0.026	−0.022	0.080
	APOE-ε4	0.409	0.164	0.081	0.736
	α*	0.173	0.021	0.135	0.215
	α	−1.105	0.437	−1.969	−0.259

Figure 2.

Estimated coefficient functions (solid lines) in the functional longitudinal submodel with 95% pointwise uncertainty band (dashed lines) and reference lines (dotted lines) at zero.

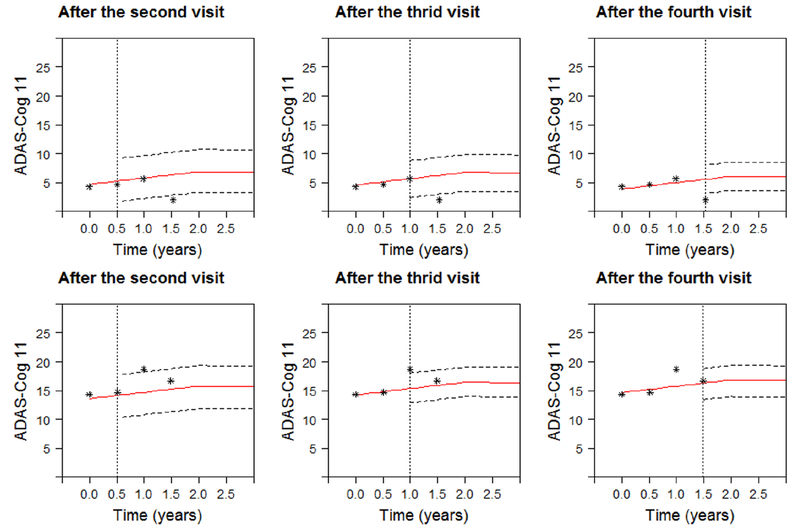
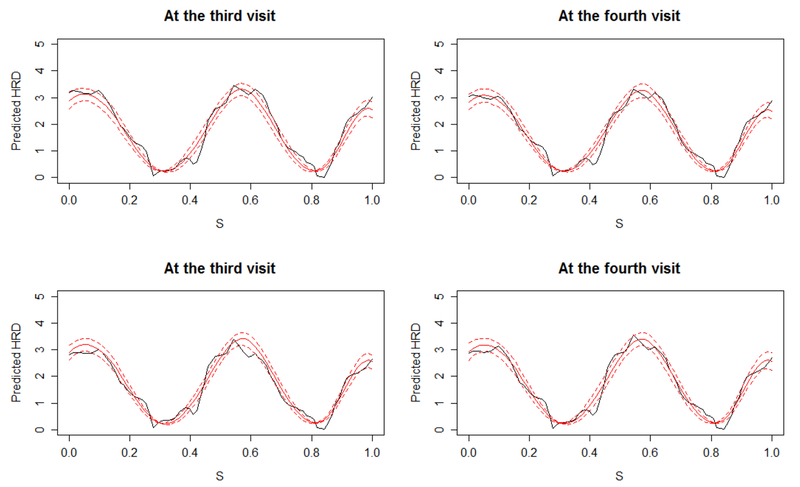
To illustrate the personalized dynamic predictions, we select two target patients as validation data, and predict their future health outcomes and event-free probabilities based on MFJM estimated using the remaining data as training set. Patient A had a baseline age of 73, no APOE-ε4, as compared with a more severe Patient B, 78 years old at baseline, and with APOE-ε4. Figure 3 demonstrates how the predicted ADAS-Cog 11 scores are updated over time for the two patients. From the left to the right on Figure 3, by using more follow-up data, predictions are closer to the true observed values and the 95% uncertainty band is narrower. Figure 4 shows the predicted HRD at third and fourth visits based on the previous observations. The predicted expected HRD (red line) is close to the true observation (black line), however we do not observe significant difference between HRD at the third and the fourth visits and we suggest to use the predicted HRD with caution. Figure 5 displays the predicted probability of being free of AD diagnosis. For Patient A, the event-free probability curve does not show large change because Patient A’s predicted ADAS-Cog 11 scores are relatively low. In comparison, Patient B has higher predicted ADAS-Cog 11 scores and worse cognitive function, and thus has considerably drop in the event-free probability. This suggests that Patient B has a higher risk of AD diagnosis and should be monitored frequently.

Figure 3.

Predicted ADAS-Cog 11 for Patient A (upper panels) and Patient B (lower panels). Solid line is predicted longitudinal trajectories. Dashed lines construct a 95% pointwise uncertainty band. The dotted vertical lines represent the time of prediction t.

Figure 4.

Predicted HRD (red) with 95% pointwise uncertainty band (dashed lines) for Patient A (upper panels) and Patient B (lower panels) at third and forth visit. The solid black curve represents the true observation at the time point.

Figure 5.

Predicted event-free probability with 95% pointwise uncertainty band (dashed lines) for Patient A (upper panels) and Patient B (lower panels). The dotted vertical lines represent the time of prediction t.

5. Simulation Study

In this section, we conduct a simulation study to evaluate the proposed models. We generate 100 datasets with sample size I = 150 subjects and each subject has J_i=4 measurements at time 0, 5, 10, and 15. The simulated data structure is similar to the motivating ADNI study. We generate longitudinal functional response y_i(s, t_ij) on an equally spaced grid of length 25 and longitudinal scalar response $y_i^{\ast }(t_{\mathit{ij}})$ according to the longitudinal submodels

$$\begin{array}{cc}\hfill y_i^{\ast }(t_{ij})=& m_i^{\ast }(t_{ij})+{ϵ}_{ij}^{\ast },\hfill \\ \hfill y_i(s,t_{ij})=& m_i(s,t_{ij})+{ϵ}_{ij}(s),\text{where}\hfill \\ \hfill m_i^{\ast }(t_{ij})=& {\beta }_0+t_{ij}{\beta }_t+x_{i1}{\beta }_1+b_i^{\ast },\text{and}\hfill \\ \hfill m_i(s,t_{ij})=& B_0(s)+t_{ij}{B}_t(s)+x_{i1}{B}_1(s)+\underset{k=1}{\overset{K_{\varphi }=2}{\Sigma }}{\xi }_{ik}{\varphi }_k(s),s\in [0,1]=S.\hfill \end{array}$$

We set β₀ = 4, β_t = 1, and β₁ = 0.5. The intercept function is B₀(s) = −1.5 − sin(2πs) − cos(2πs). The time effect is $B_t(s)=\frac{1}{10}\Phi (\frac{s-0.5}{{0.2}^2})$, where Φ(.) is the standard Normal density function. The fixed effect is B₁(s) = sin(2πs)−cos(4πs), and we generate scalar predictors using x_i1 ~ N(0, 2). Similar to previous simulation study [17], the orthogonal eigenfunctions for random intercept functions are chosen to be ϕ₁(s) ∝ 1.5 − sin(2πs) − cos(2πs) and ϕ₂(s) ∝ sin(4πs) and scaled such that ${\int }_S{[{\varphi }_1(s)]}^2\mathit{ds}=1$ and ${\int }_S{[{\varphi }_2(s)]}^2\mathit{ds}=1$. The subject-specific random effect and FPC scores [$b_i^{\ast }$, ξ_i1, ξ_i2] are generated from multivariate normal distribution with zero-mean and covariance matrix Σ with ${\sigma }_{b^{\ast }}^2={0.6}^2$, λ₁ = 1, λ₂ = 0.5 and ρ = 0.5, respectively. The measurement error for scalar response ϵ_ij is simulated from N(0, 0.2). The white noise component ϵ_ij(s) is simulated from N(0, 0.1) across s.

We choose a constant baseline hazard function h₀(t) = 0.01 and the survival submodel is

$$h_i(t)=h_0(t)\exp \{w_i{\gamma }_1+{\alpha }^{\ast }{m}_i^{\ast }(t)+\alpha {\int }_S{m}_i(s,t)ds\},$$

where w_i is simulated from N(0, 1), γ₁ = 0.76, α* = 0.5, and α = 0.3. We generated random survival times based on the closed-form of T* derived from survival function:

$$\begin{array}{cc}\hfill S_i(t)=& \exp \{\frac{\lambda \exp (w_i{\gamma }_1+{\alpha }^{\ast }({\beta }_0+{\beta }_1{x}_{i1}+b_i^{\ast })+\alpha {\int }_S[B_0(s)+x_{i1}{B}_1(s)+{\Sigma }_{k=1}^2{\xi }_{ik}{\varphi }_k(s)]ds)}{{\alpha }^{\ast }{\beta }_t+\alpha {\int }_S{B}_t(s)ds}\times \hfill \\ \hfill & [\exp (t\times ({\alpha }^{\ast }{\beta }_t+\alpha {\int }_S{B}_t(s)ds))-1]\},\hfill \end{array}$$

and thus,

$$\begin{array}{cc}\hfill T_i^{\ast }=& \log \{\frac{-\log (S_i(t))\times ({\alpha }^{\ast }{\beta }_t+\alpha {\int }_S{B}_t(s)ds)}{h_0(t)\exp (w_i{\gamma }_1+{\alpha }^{\ast }({\beta }_0+{\beta }_1{x}_{i1}+b_i^{\ast })+\alpha {\int }_S[B_0(s)+x_{i1}{B}_1(s){\Sigma }_{k=1}^2{\xi }_{ik}{\varphi }_k(s)]ds)+1}\}∕\hfill \\ \hfill & ({\alpha }^{\ast }{\beta }_t+\alpha {\int }_S{B}_t(s)ds),\hfill \end{array}$$

where S_i(t) is simulated from a uniform distribution between 0 and 1. Censoring time is independently simulated from another uniform distribution to achieve a censoring rate about 30%. Due to censoring, each subject has an average of 3 repeated measurements.

For estimation, the coefficient functions B₀(s), B_t(s) , B₁(s), and FPC eigenfunctions ϕ_k(s), k = 1, ⋯ , K_ϕ are expanded by cubic B-spline basis with Kψ = 10. We set the number of estimated principal components ${\widehat{\mathit{K}}}_{\varphi }\in \{2,3\}$. Note that when ${\widehat{\mathit{K}}}_{\varphi }=3$ the number of estimated FPC components is larger than the number of true FPC components, which is held at K_ϕ = 2. Model parameters are estimated for the C = 100 data sets using the methodology described in Section 3.2. Estimation and inference is based on posterior means and quartiles of 5000 iteration from the sampler after discarding the first 1000 as burn-in. We perform diagnostics for one simulated dataset indicate that these levels are sufficient for convergence and exploration of the full posterior distribution. On average, the computing process takes 1.1 hours for each simulated dataset on a personal computer (RAM 8G, CPU 3.30GHz). The ability to estimate the true coefficient is assessed by the average mean squared error (AMSE), e.g., $\mathit{AMSE}({\widehat{\beta }}_1)=\frac{1}{100}{\sum }_{c=1}^{100}{({\widehat{\beta }}_1-{\beta }_1)}^2$. Table 3 presents the AMSE, in addition to bias (the average of the posterior means minus the true values), standard error (SE, the square root of the average of the variance), standard deviation (SD, the standard deviation of the posterior mean), and coverage probabilities (CP) of 95% credible intervals when ${\widehat{\mathit{K}}}_{\varphi }=2$. Table 3 suggests that the proposed model performs reasonable well with relatively small bias and AMSE values.

Table 3:

Parameter estimation in the simulation study based on 100 datasets when ${\widehat{\mathit{K}}}_{\varphi }=2$.

	Bias	AMSE	SE	SD	CP
β0 = 4	<0.001	0.003	0.053	0.055	0.930
βt = 1	−0.003	<0.001	0.019	0.019	0.960
β1 = 0.5	<0.001	<0.001	0.004	0.003	0.980
γ1 = 0.76	−0.017	0.017	0.116	0.122	0.920
α* = 0.5	0.031	0.005	0.059	0.062	0.910
α = 0.3	−0.023	0.053	0.232	0.231	0.930

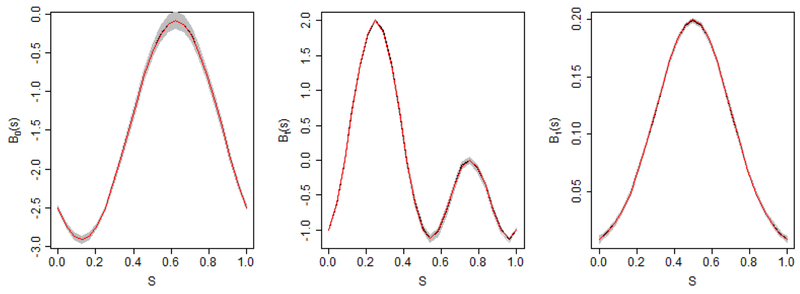
Figure 6 displays the coefficient functions estimated under ${\widehat{\mathit{K}}}_{\varphi }=2$. The true coefficient functions (black solid lines), their mean estimated curves (red solid lines), along with 100 estimated curves based on each individual dataset (grey solid lines). The figures suggest that the estimated coefficient functions from the model are reasonably close to the true coefficient functions. The simulation results for scenario ${\widehat{\mathit{K}}}_{\varphi }=3$ are presented in Web Table 1 and Web Figure 2. It suggests that increasing ${\widehat{\mathit{K}}}_{\varphi }$ has limited effects on parameter estimation in either longitudinal sub-models and survival sub-models. The bias and AMSE values have slight increase but are still relatively small. The estimated coefficient functions are reasonably close to the true coefficient functions.

Figure 6.

The estimates of the coefficient functions in the simulation study based on 100 runs and ${\widehat{\mathit{K}}}_{\varphi }=2$. The red solid lines are mean estimated curves and the grey solid lines are 100 estimated curves based on each individual dataset.

For each testing dataset, we predict subject-specific conditional survival probability at different time points t and Δt using the MCMC samples from the fitted model and available measurements up to time t. Table 4 presents the time-dependent AUCs by averaging the separate analyses of 100 datasets. The true AUCs are computed using the prerespecified parameter values and random effects when generate the data. The predict AUCs are relative closed to the true AUCs, suggesting a good prediction performance of the MFJM in terms of validation.

Table 4:

Areas under the ROC curve (AUC) for the simulation study.

Δ t	t	True	${\mathit{AUC}}_t^{\Delta t}$
5	0	0.831	0.830
	5	0.811	0.810
	10	0.829	0.827
10	0	0.847	0.846
	5	0.875	0.875
	10	0.824	0.823

6. Discussion

The proposed multivariate functional joint model (MFJM) is an important complement to both functional data analysis and joint modeling for longitudinal and survival data. Our model allows the longitudinal functional outcome, longitudinal scalar outcome, and survival outcome to be modeled simultaneously and can be applied to many areas of research when MRI data and clinical variables are collected longitudinally. We use the functional mixed effect model and functional principal component (FPC) analysis techniques to approximate the longitudinal functional data, and expand the coefficient functions and eigenfunctions in the model using a penalized spline approach. We then develop the process of making personalized dynamic prediction of future outcomes and risks of event of interest using both repeated functional and scalar outcomes.

The model inference is conducted using a Bayesian approach. One advantage of Bayesian approach is the availability of Markov chain Monte Carlo (MCMC) sampling algorithms, which allow estimation from posterior probability density functions that are not analytically tractable, and which require complex multi-dimensional integration over the random effects. The surge in MCMC sampling can be partly explained by the wide use of the Bayesian computing languages, such as Stan, which eliminate the need of complex analytical derivation of the posterior distributions. Moreover, Bayesian method is well-suited for dynamic prediction using joint models. With the MCMC samples from the posterior distributions of the parameters for the original data, we can devise a simple simulation scheme to obtain a Monte Carlo estimate of risk prediction and longitudinal trajectories [39, 47]. In addition, uncertainty about posterior parameter estimates is readily calculated from the MCMC output without the need for further complex derivation and calculations. This facilitates the calculation of the uncertainty intervals of functional coefficients and functional predictions.

Simulation indicates that the proposed Bayesian MFJM yields accurate inference and prediction. The application of our developed methodology to the motivating data yields novel insight into the effect of regional atrophy on the AD progression. More importantly, the proposed dynamic prediction approach can utilize the functional and scalar predictors to make correct predictions for new subjects. The inclusion of longitudinal functional predictor hippocampal radial distance (HRD) into the survival submodel improves the predictive performance in the early phase of disease among MCI patients. When new measurements are available, the predictions can be updated with improved accuracy and efficiency. The practical impact of such dynamic prediction tools can be dramatic for the neurodegenerative diseases (e.g., Alzheimer’s disease) because the longitudinal functional data are increasingly collected in the studies of these diseases. They provide unique insight and valuable guidance for clinical decision making on patient prognosis, targeted treatment, and for targeted recruitment for clinical trials.

There are some limitations we will address in the future. First, our method requires to select the number of the FPC components prior to analysis. Although we suggest a large number of FPC components, determining whether a selection is sufficient to describe the major variation in the functional data require additional analyses with even larger values, which can incur considerable computational expense. Second, we jointly model all parameters of interest in a Bayesian context, the computation time of the proposed Bayesian procedure could be a serious concern particularly as sample sizes, dimension of functional data, and the number of estimated principal components grow. Future work focusing on variation Bayes or other approximation may address the computational concern. Another option is to use a two-step method which models longitudinal functional outcome using functional principal components approaches and then plugs in the estimates of FPC scores into the survival model. These approaches are more computationally attractive and scalable than joint modeling approach but may be accompanied by poorer inferential performance [32, 48]. It is worthwhile to investigate when using these methods is a reasonable alternative to the joint analysis. For example, the two-setp method may provide tools for choosing the dimension of the FPC components via rapid comparisons of different selections. Third, we assume a constant associate function α(s) ≡ α to quantify the association between the functional outcome and the hazard. If the primary interest is prediction, we can allow α(s) varies over the domain of S and expand it by the cubic B-spline basis functions and estimate the spline coefficients. Another direct extension of the model is the inclusion of covariate-specific random effects, such as random time-slope function, in the functional mixed effect model (2). In this paper, we introduce the correlation between the scalar and functional outcomes using the correlation between the scalar random effects and the first FPC component derived from the random function. Accounting for the correlations between the random effects and the first few FPC components may represent the correlation between the scalar and functional outcomes more accurate, but may also lead to increased computing burden. It is worthwhile to further explore other correlation structures, e.g., adopting an idea of latent trial model [49, 50], especially when additional covariate-specific random effects are in the model. Moreover, the inverse-gamma prior distribution, which we used for variance parameters in the model inference, can be sensitive to the choice of the hyperparameters (shape and scale) in case where variance estimates are close to zero [51]. We tested the model inference on one training dataset from our application study using uniform and half-Cauchy prior distribution instead, and achieved reasonably similar results. We suggest further tests are needed in other applications and datasets on a case-by-case basis. We would like to investigate the effect of these extensions and address the limitations to improve predict performance in our future research.