Abstract
Chronic livestock diseases cause large financial loss and affect animal health and welfare. Controlling these diseases mostly requires precise information on both individual animal and population dynamics to inform the farmer’s decisions, but even successful control programmes do by no means assure elimination. Mathematical models provide opportunities to test different control and elimination options rather than implementing them in real herds, but these models require robust parameter estimation and validation. Fitting these models to data is a difficult task due to heterogeneities in livestock processes. In this paper, we develop an infectious disease modeling framework for a livestock disease (paratuberculosis) that is caused by Mycobacterium avium subsp. paratuberculosis (MAP). Infection with MAP leads to reduced milk production, pregnancy rates, and slaughter value and increased culling rates in cattle and causes significant economic losses to the dairy industry. These economic effects are particularly important motivations in the control and elimination of MAP. In this framework, an individual-based model (IBM) of a dairy herd was built and MAP infection dynamics was integrated. Once the model produced realistic dynamics of MAP infection, we implemented an evaluation method by fitting it to data from three dairy herds from the Northeast region of the US. The model fitting exercises used least-squares and parameter space searching methods to obtain the best-fitted values of selected parameters. The best set of parameters were used to model the effect of interventions. The results show that the presented model can complement real herd statistics where the intervention strategies suggest a reduction in MAP prevalence without elimination. Overall, this research not only provides a complete model for MAP infection dynamics in a dairy herd but also offers a method for estimating parameters by fitting IBM models.
Introduction
Chronic livestock diseases like paratuberculosis (PTB) and bovine tuberculosis (bTB) are commonly reported worldwide [1,2]. Bovine TB is caused by the pathogen Mycobacterium bovis (M. bovis) while PTB is caused by Mycobacterium avium subsp. paratuberculosis (MAP). In the UK, bTB has been spreading over the last two decades, putatively due to the presence of a wildlife reservoir in badgers [3]. In the United States (US), 68% of dairy herds have apparently at least one cow that is infected with MAP [4]. Both diseases pose a potential threat not only to animal health and production, but also to public health. Historically, bTB has been a contributor to human TB cases worldwide and PTB infections in humans have been associated with an increased risk of Crohn’s disease in humans [5]. Recently, it has been reported that these diseases may pose additional collateral risks for public health due to dispensed antibiotics as a treatment in some cases contributing to the spread of antibiotic resistance [6].
In the US cattle industry, the cost of PTB was estimated at $250 million every year [7]. The MAP Infection usually occurs in the first year of a ruminant’s life [8] and transmission can occur vertically [9] and/or horizontally via ingestion of fecal material contaminated by MAP [10]. As PTB is a slowly progressive disease, the progression of individual animals through different MAP infection states is a complex continuous process alternating excreting and non-excreting stages with a late onset of clinical signs [11,12]. It has a large economic impact for producers due to decreased milk production [13–15], premature culling [16,17], reduced slaughter value [18], low fertility [19,20], and an increased animal replacement rate [21]. However, MAP is difficult to diagnose due to the long incubation period [22,23], lack of early clinical signs [24–26], and imperfect testing [27].
In the last two decades, different mathematical models have been developed on a within-herd scale to understand MAP transmission dynamics [28,29] and effectiveness of recommended control strategies [30–33]. These models were used to assess the impact of contact structure on the MAP transmission [28], efficacy of test-and-cull policy [29,30,34,35], impact of low diagnostic test sensitivity in decision making [8,36], stopping some transmission pathways using hygiene improvement [37], improved calf management [38], impact of super-shedders in transmission [25,39], and economic efficacy of recommended programs [34]. Most of these studies suggest that culling a test positive animal is an effective solution to reduce the prevalence within a herd. However, none of the previous models considered the pervasiveness of MAP in the farm environment and the value of individual animal information along with real dairy herd data. Moreover, controlling MAP requires management of testing and culling strategies to reduce the prevalence, but these are unregulated and reliant on farmers’ decisions [40]. The decision to cull an animal is not straightforward and poses a multiscale problem where an individual animal, farm dynamics, infectious status, disease symptoms, and management profit are related [41]. Substantial costs are also related to the implementation of control measures and prevention [21,25,42]. Previous MAP models have explored many potential interventions programs, most considered population-level decision making rather than individual-level animal information. Recently, individual-based models (IBMs) have been proposed to show the value of the information about the infection, daily life events and management policy for each individual animal within the farm [37,41,43–46].
Mathematical models of infectious diseases are tools to enhance the understanding both of infection biology and efficacy of intervention policies in human and veterinary medicine [47]. However, translating modeling results into practice requires appropriate real-world assumptions to be built into the model. We hypothesize that in case of MAP, use of model results will be more realistic when the model has been built on up-to-date infection biology and epidemiology, parametrized from adequate real herd data, and fitted back to that real-world scenario to test the recommended intervention strategies. In this paper, our aim is to build an IBM framework of MAP infection that is fitted to and validated by in-depth longitudinal data from three northeastern dairy farms. The objective of this study was four-fold: first, we extended an existing IBM of a dairy herd to resemble the population level parameters (i.e. milk yield, herd size) with three real herds to create three in silico herds; second, we fitted the milk-yield measurement of individual animal to those herds; third, we fitted the model-predicted apparent MAP prevalence to the observed data to obtain herd-specific infection parameters; and fourth, we integrated a risk-based control strategies on those three in silico herds to evaluate the efficacy of risk-based controls. Finally, we discuss the value of observational data to feed information to simulation models, thereby making simulations more reflective and predictive of real-world circumstances.
Materials and method
The Individual-based model
We used a multiscale agent-based simulation of a dairy herd (MABSDairy), an improved version of dairy herd published in Al-Mamun et al. [37,44]. The MABSDairy is a multiscale stochastic IBM that simulates individual cows in a standard US cattle herd with a daily time step. In brief, each cow resides in one of three different management operations: adult/milking (aged >720 days), calf (aged 1–60 days) and heifer rearing housing (aged 61–719 days). Adult cows must calve to produce milk and the lactation cycle refers to the period between one calving and the next. The lactation cycle includes the processes of a voluntary waiting period (interval during the postpartum period), insemination, and the dry off period (a non-lactating period prior to an impending parturition to optimize milk production in the subsequent lactation). For fitting purpose, we modified the milk production Wood lactation curve by adding a herd-specific term and a herd-specific random component [48]. The function is defined as
where Yt is the yield on day t after calving, d is days in milk (DIM), a is a scaling factor for initial yield, b is a rate factor for the increase in yield to peak, c is a rate factor for the decline after the peak, fi farm specific factor and fr is a random number. We used base milk yield parameters from Dematawewa et al. for parities 1 and ≥2 in the basic model [49].
MAP infection dynamics
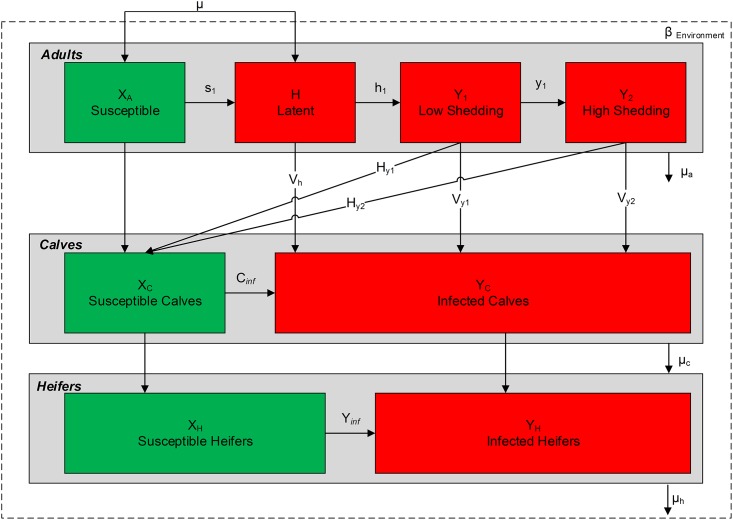
The infection compartments in the milking herd were divided into four categories: susceptible (XA), latent (H), low shedding (Y1), and high shedding (Y2). In calf rearing housing, there were two infection categories: susceptible (XC) and infected (YC). In heifer rearing housing, there were also two infection categories: susceptible (XH) and infected (YH). We included six different transmission routes: adult-to-adult, adult-to-calf (vertical transmission), adult-to-calf (horizontal transmission), environmental contamination, calf-to-calf, and heifer-to-heifer. The detailed infection structure is shown in Fig 1.
Fig 1. A flow diagram of animal movements among infection categories for the adult, calves, and heifers within the herd.
Each horizontal gray box classifies the animals according to their initial age group. The green and red boxes define the susceptible and infected states, respectively, for each animal in the three age categories. The probabilities of exit at each time point from susceptible to latent, latent to low shedding and low shedding to high shedding animals are s1, h1, and y1, respectively. Vertical transmission probabilities from latent, low shedding and high shedding animals are Vh, Vy1, and Vy2, respectively. Horizontal transmission probabilities to calves from low shedding and high shedding animals are Hy1 and Hy2, respectively. The probability an animal gets infected by the environment is βenvironment. Calf-to-calf and heifer-to-heifer transmission probabilities are Cinf and Yinf, respectively. Stochastic death/sale probabilities for adult, calves, and heifers are μa, μc, and μh, respectively. μ is the replacement animals coming from heifer compartment upon completion of two years.
In the milking herd group, adult animals could be infected by low and high shedding adults. The probability of fecal-oral transmission for adult animals can be given by:
Susceptible adult animals in the milking herd compartment were susceptible to MAP infection by contact with low shedding (Y1) and high shedding (Y2) animals with transmission rates of and , respectively. βA is the adult-to-adult transmission coefficient, βenvironment is the MAP contamination risk from the environment and N is the total number of animals in the milking herd, N = XA+H+Y1+Y2. The horizontal infection probability to calves can be determined by
βa is the horizontal transmission coefficient for an adult to newborn calves and Nc is the total number of calves at every day, Nc = Xc + Yc. A calf can also become infected vertically (i.e., in utero infection) by an adult and it is modelled using the certain proportions [30].
A calf stays in calf rearing housing for the first 60 days after birth. The probability of direct transmission was calculated as
βc is the horizontal calf-to-calf transmission coefficient, Nc is the total number of calves at each day, Xc is susceptible calves, Yc is infected calves. During the first day after birth, a calf may also be infected horizontally by infected adults present in the maternity pen or vertically by an infected dam.
Susceptible calves became susceptible heifers and infected calves became infected heifers. Infected heifers could infect susceptible heifers by the heifer-to-heifer transmission path
βh is the horizontal heifer-to-heifer transmission coefficient, and the total number of heifers is . After one year, the infected heifers became latent heifers and eventually entered the milking herd as latent adults. For simplifying the model, we assumed that heifer remains in the heifer rereading housing are transiently shedding while they ended up in the adult herd as latent animals.
Observed herd data
The longitudinal dataset was obtained from a longitudinal study of three commercial dairy farms in the northeastern US: farm A in New York State, farm B in Pennsylvania, and farm C in Vermont [24,50]. All three farms participated in the Regional Dairy Quality Management Alliance (RDQMA) project, which was a multistate research program conducted under a cooperative research agreement between the USDA Agricultural Research Service, and four universities: Cornell University, Pennsylvania State University, University of Pennsylvania, and University of Vermont. The project consisted of longitudinal data collection for endemic infectious diseases of public and animal health concern in dairy herds. For a more complete description, including information on farms, samplings, and microbial analyses, see Pradhan et al. [50]. Briefly, the milking herds consisted of 330, 100, and 140 cows on farms A, B, and C, respectively. Sampling commenced in February, March, and November 2004 on farms A, B, and C, respectively, and continued for approximately 7 years, until 2010. The project design included a biannual collection of individual fecal samples and a quarterly collection of individual serum samples from all milking and non-lactating cows. Additionally, culled cows were tracked as much as possible from the farm to the slaughterhouse, where four gastrointestinal tissues and a fecal sample were collected with the cooperation of USDA Food Safety and Inspection Service personnel. The harvested tissues included two lymph nodes located at the ileocecal junction and two pieces of ileum, one taken from 20 cm proximal to the ileocecal valve and the other taken from very near the ileocecal valve. In addition to the sampling of animals, the farm environment was sampled in approximately 20 locations on a biannual basis. All fecal and environmental samples were tested by 4-tube culture for the presence of viable MAP organisms, reported as colony-forming units per tube. All serum samples were tested using the ParaCheck ELISA (Prionics USA Inc., La Vista, NE) for antibody reactions to MAP antigens. On each of the farms, demographic data, production data and herd management information were collected. Precise demographic data included birth date, birth location, calving dates, fertility data, animal location data (pen status at any point in time), dry-off dates, culling information and cull dates. These demographic data were collected for each animal present on the farms. All infection data, strain typing data, herd management, demographic, and production data were maintained in a relational database.
Model parameters
The parameterization of the base dairy herd model is described in Al-Mamun et al. [37,51]. Initial infection parameter values were updated according to Mitchell et al. 2015 [47]. Table 1 provides the base parameters for the initial MAP transmission before fitting the model to the RDQMA herds.
Table 1. Base parameter values of Mycobacterium avium subsp. paratuberculosis (MAP) infection within a dairy herd.
| Symbols | Description | Initial value | References |
|---|---|---|---|
| Vh | The proportion of calves from latent animals infected at birth | 0.15 | [30] |
| Vy1 | The proportion of calves from low-shedding animals infected at birth | 0.15 | [30] |
| Vy2 | The proportion of calves from high-shedding animals infected at birth | 0.17 | [30] |
| βA | Adult-to-adult transmission coefficient | 0.05 | [37] |
| βa | Adult-to-calf transmission coefficient | 0.383 | [37] |
| βc | Calf-to-calf transmission coefficient | 0.0025 | [37] |
| βh | Heifer-to-heifer transmission coefficient | 0.001 | Calibrated in the model |
| Transmission rate between low shedders (Y1) and susceptible (XA) | 2/year | Calibrated in the model | |
| Transmission rate between high shedders (Y2) and susceptible (XA) | 20/year | Calibrated in the model |
Model fitting method
The goal of the model-fitting exercise was to estimate key parameters in order to produce results consistent with the epidemiology observed on the three farms. Our fitting exercise was two-fold: first, we fitted our base dairy herd models with farm-specific parameters (total population and milk yield), then we fitted the model predicted apparent prevalence results based on antemortem ELISA and fecal testing and postmortem tissue and fecal testing results for the farm. To assess the goodness-of-fit we sampled from the defined parameter ranges in multiple rounds and ran the three in silico dairy herds. The model fitting was done using a nonlinear fitting method named Nelder-Mead Simplex Method [52], which is used for unconstrained optimization. While fitting the milk yield and apparent prevalence, the best-fit parameters were extracted.
To determine the specific range for each parameter, we used multidimensional parameter space searching method. The point estimate of each parameter was taken as a mean value and, using Latin Hypercube Sampling, 100,000 parameter combinations were generated spanning the specified range ±75% of the mean values. The searching was done in two stages. In the first stage, we set a broad range to identify the particular regions of the parameter range and chose the best 10,000 (10%) parameter sets. In the next stage, we ran the simulation with 10% parameter sets to compare with the best fit curve by minimizing the sum of square error. The parameter ranges presented in the results section were calculated from the top 1% simulations.
Intervention strategies
Once the three in silico herds were stable using fitted values, we tested different proposed intervention strategies. We chose risk-based testing and culling strategies suggested by Al-Mamun et al. [37]. In brief, all cows that tested negative throughout testing were marked as low risk or green cows. The cows that tested positive were divided into two groups: yellow and red. Red animals had at least 2 positive tests out of the last 4 tests and yellow cows had one positive test. We proposed two controls: control I, culling red animals straightway (aggressive culling); and control II, culling only red animal with a delay of 305 DIM (delayed culling). The simulations results were then compared against the observed pre-fitted data from the three herds using three intervention strategies: no control, control I, control II.
Simulation background
First, the base dairy herd model was initiated with a certain proportion of adult animals for farms A (330), B (100) and C (140). Second, after a 2 years burn-in period the model was run for 7 more years to resemble the observations of the real herds. During the 2 years burn-in period, each farm was assumed to be self-sufficient in producing their own replacement, so that no animal purchase from outside was needed. The model was initiated with a pre-determined distribution of animals with different parities. At each time step, the algorithm first determined the group of animals. If it found adult animals, it checked reproductive status (voluntary waiting period (VWP), waiting to be inseminated, and pregnant) and milk yield status. Any cow on the 280 days of pregnancy was assumed to calve. For a newborn calf, the stillbirth probability was checked; if the calf was not stillborn, it was flagged as a calf. Only female calves were kept in the herd, and male calves were removed immediately after birth. Once an adult animal calved, it transitioned to VWP status and continued in the milking herd loop until it was removed due to culling or death. Mortality was allowed in the calf rearing loop; otherwise, calves were transferred into the heifer loop at the 61st day of age. In the heifer loop, heifers were inseminated at the 400 days of age in order to become pregnant, so that they would calve at the 680 days of age. When heifers were ready to calve for the first time, they transitioned to the milking herd in the model. The model was fitted for the 7 years data for each farm. Third, for testing intervention strategies, each model was fitted to the first 4 years of data- that is called pre-intervention fit, and then the intervention was tested in 2 phases. In the first phase, 3 years and then extended more 2 years to see how the suggested strategies result in long-term. The base model was developed as custom codes in MATLAB and other data analysis were done using R.
Results
The purpose of the fitting exercise was to obtain a better fit to the estimates of three herds prior fitting to the apparent prevalence. The model predicted total number of animals (adult, calves, and heifers) closely resembles the data from the three real farms (shown in Table 2).
Table 2. The comparison of observed and predicted values from three in silico farms in terms of a total number of animals, and average daily milk yield (in kg) for 305 days, presented as mean (95% confidence interval).
| Total number of animals | Milk yield: parity 1 | Milk yield: parity ≥ 2 | |
|---|---|---|---|
| Herd A | |||
| Observed | 720 (708–754) | 36.07 (29.61–40.73) | 39.48 (27.11–49.86) |
| Predicted | 714 (693–737) | 36.15 (30.44–40.73) | 39.49 (27.56–50.18) |
| Herd B | |||
| Observed | 194 (102–230) | 33.38 (24.34–40.35) | 34.52 (17.42–47.40) |
| Predicted | 200 (182–219) | 32.97 (26.51–38.31) | 34.97 (21.86–48.29) |
| Herd C | |||
| Observed | 262 (116–339) | 27.49 (19.03–34.68) | 27.49 (19.03–34.68) |
| Predicted | 221 (184–257) | 27.16 (20.23–32.98) | 27.90 (17.12–38.06) |
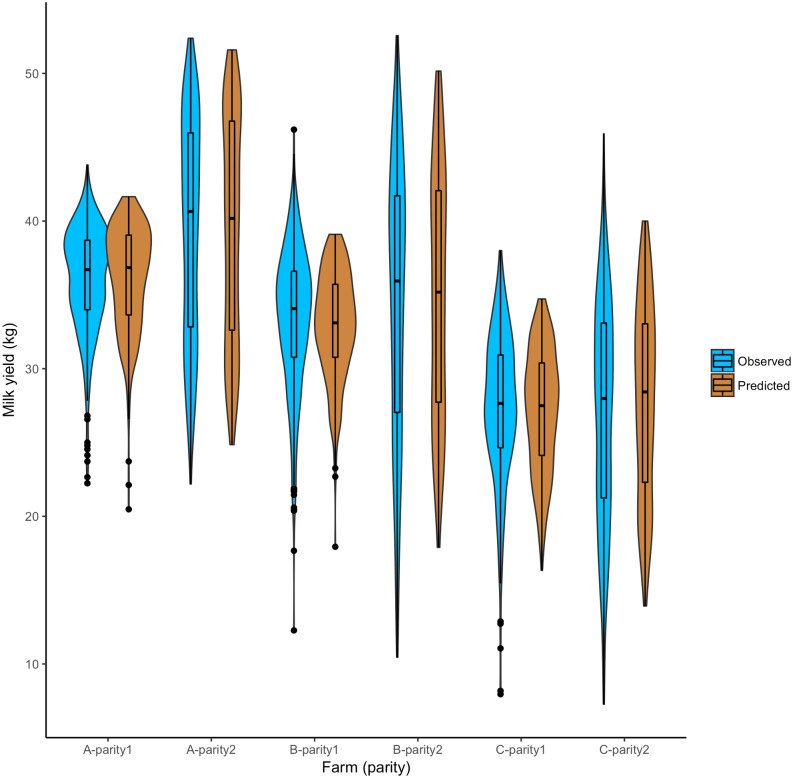
Fig 2 shows the concordance between predicted and observed milk yield data from three herds. It is evident that the models predicted milk yield estimations matched with the observed milk yield from three northeastern herds. The best fit model predictions to the observed milk yield curve for parity 1 and parity ≥2 are shown in supplementary S1 Fig. The best fitting lines also describe that the model was able to capture inherent randomness from the data into the model. The estimation of the critical parameters a, b, c, and fi of the modified lactation curve are presented in Table 3.
Fig 2. The comparison of observed and model predicted milk yield distribution for 1% simulation using best-fit parameters for the milk yield.
In the box plot, the bottom and top end of the bars are minimum and maximum values respectively, the top of the box is the 75th percentile, the bottom of the box is the 25th percentile, and the horizontal line within the box is median; outliers are presented as a solid black circle and the density of the milk yield is presented by the width of the violin.
Table 3. The estimated parameters from the fitting exercise for the modified milk yield function for three farms A, B, and C.
| a | b | c | Herd specific parameter (fi) | |
|---|---|---|---|---|
| Farm A-Parity 1 | 17.87 | 0.21 | 0.0020 | 3.59 |
| Farm A-Parity≥2 | 25.23 | 0.20 | 0.0033 | 5.19 |
| Farm B-Parity 1 | 16.09 | 0.19 | 0.0020 | 6.60 |
| Farm B-Parity≥2 | 23.38 | 0.20 | 0.0039 | 8.33 |
| Farm C-Parity 1 | 15.25 | 0.19 | 0.0027 | 6.55 |
| Farm C-Parity≥2 | 16.50 | 0.22 | 0.0040 | 9.00 |
Model fitting exercise for disease parameters
Table 4 represents the observed apparent prevalence and apparent incidence and the tracking of the animals in the next biannual testing for three farms for seven years, 2004–2010. The observed prevalence shows zero infected animals in the last half of 2010, for the sake of persistence scenario we replace that with the previous quarter value. During our simulation, we normalized the prevalence with the previous half of the year so that it remains consistent for our simulation. We simulated the three in silico farms to fit with the observed apparent prevalence data from herd A, B, and C.
Table 4. The calculation of apparent prevalence and apparent incidence and the tracking of the animals in the next testing in bi-annually phase for three farms (2004–2010).
| Year | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test phase | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Herd A | ||||||||||||||
| Total positive cows a | 14 | 25 | 34 | 28 | 34 | 32 | 21 | 23 | 24 | 17 | 14 | 9 | 7 | 0 |
| Animals tested | 315 | 330 | 364 | 349 | 354 | 364 | 338 | 332 | 337 | 347 | 341 | 347 | 296 | 239 |
| Apparent prevalence | 4.4 | 7.6 | 9.3 | 8.0 | 9.6 | 8.8 | 6.2 | 6.9 | 7.1 | 4.9 | 4.1 | 2.6 | 2.4 | 0.0 |
| New casesb | 14 | 16 | 18 | 12 | 13 | 13 | 7 | 10 | 11 | 6 | 5 | 2 | 0 | 0 |
| Cow-years at riskc | 239 | 293 | 284 | 272 | 276 | 280 | 198 | |||||||
| Apparent incidenced | 0.13 | 0.10 | 0.09 | 0.06 | 0.06 | 0.02 | 0 | |||||||
| Herd B | ||||||||||||||
| Total positive cows | 9 | 8 | 6 | 3 | 6 | 5 | 4 | 3 | 3 | 2 | 5 | 5 | 1 | 0 |
| Animals tested | 106 | 122 | 128 | 128 | 113 | 113 | 115 | 114 | 111 | 109 | 113 | 109 | 82 | 1 |
| Apparent prevalence | 8.5 | 6.6 | 4.7 | 2.3 | 5.3 | 4.4 | 3.5 | 2.6 | 2.7 | 1.8 | 4.4 | 4.6 | 1.2 | 0.0 |
| New cases | 9 | 1 | 2 | 0 | 5 | 4 | 1 | 0 | 1 | 1 | 4 | 1 | 0 | 0 |
| Cow-years at risk | 72 | 99 | 95 | 94 | 93 | 83 | 37 | |||||||
| Apparent incidence | 0.14 | 0.02 | 0.10 | 0.01 | 0.02 | 0.06 | 0 | |||||||
| Herd C | ||||||||||||||
| Total positive cows | 0 | 17 | 26 | 23 | 19 | 22 | 18 | 20 | 18 | 15 | 13 | 8 | 7 | 0 |
| Animals tested | 0 | 121 | 145 | 149 | 178 | 161 | 145 | 155 | 157 | 145 | 142 | 117 | 102 | 0 |
| Apparent prevalence | NA | 14.0 | 17.9 | 15.4 | 10.7 | 13.7 | 12.4 | 12.9 | 11.5 | 10.3 | 9.2 | 6.8 | 6.9 | NA |
| New cases | 0 | 17 | 9 | 7 | 5 | 9 | 5 | 4 | 4 | 5 | 2 | 2 | 1 | 0 |
| Cow-years at risk | 13 | 114 | 123 | 110 | 117 | 108 | 33 | |||||||
| Apparent incidence | 1.27 | 0.14 | 0.11 | 0.08 | 0.08 | 0.04 | 0.03 | |||||||
aTest positive cows by considering enzyme-linked immunosorbent assay (ELISA) testing, fecal testing and tissue testing.
bNumber of cows tested positive for the first time
cObservation time (in years) from entry in the study (at the first testing) until each cow tested positive or left the study (by culling, i.e. the infection status of the cow is right censored)
dNew cases per year / cow-years at risk
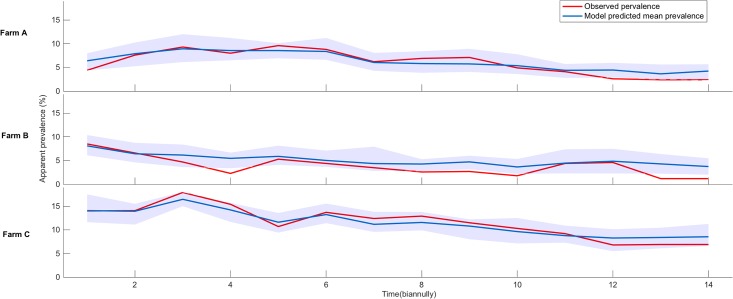
Fig 3 shows the model predicted prevalence with a 95% confidence interval while fitting against the observed prevalence. It should be noted that our model confidence interval slightly overpredicts the prevalence of herd B, but for other two herds, it forecasts the best fitting. Through this model fitting exercise, our aim was to estimate the critical infection parameters for each herd, so that we can suggest herd specific intervention strategies.
Fig 3. The fitting results of three in silico herds A (top), B (middle), and C (bottom) compared to the observed apparent prevalence for 7 years by biannual sampling.
The shaded region shows the 95% confidence interval of the best 1% simulation runs.
Estimated parameters
Table 5 provides the best fit estimates of herd-specific infection parameters for three northeastern dairy herds. Among the three herds, the model suggested that dam-to daughter transmission routes were the major transmission routes with the coefficient (βa) values of 0.4046, 0.1781 and 0.825 for farm A, B, and C, respectively. Environmental contamination (βenvironment) was the second major transmission routes while adult-to-adult transmission route was ranked third. Interestingly, we found that the importance of adult-to-calf transmission was highest in herd C, in which the initial number of latent animals were highest in numbers among the three herds. Based on the best 1% parameter sets, herd C again had the highest number of latent animals present (shown in supplementary S1 Table).
Table 5. The values of fitted parameters for three farms A, B, and C.
| Parameters | Herd A | Herd B | Herd C |
|---|---|---|---|
| Adult to adult transmission coefficient (βA) | 0.0069 | 0.0023 | 0.0005 |
| Adult to calf transmission coefficient (βa) | 0.40 | 0.18 | 0.86 |
| Environmental transmission coefficient (βenvironment) | 0.087 | 0.071 | 0.016 |
| Calf to calf transmission coefficient (βc) | 5.3×10−06 | 3.61×10−06 | 5.2×10−06 |
| Heifer to heifer transmission coefficient (βh) | 4.36×10−06 | 1.18×10−06 | 1.98×10−06 |
| Initial Latent animals (Hi) | 18 | 12 | 81 |
| Initial low shedding animals () | 15 | 2 | 12 |
| Initial high shedding animals | 22 | 8 | 9 |
It is also noticeable that herd A has the highest adult-to-adult transmission probability among the three farms. Also, the initial starting distribution of the infected animals was very important for the fitting. It is seen that herd C start with the highest proportion of latent (73%) and low shedding (31%) animals among the three farms. The best-fitted parameters set is shown in the supplementary table (shown in supplementary S1 Table).
Intervention strategies
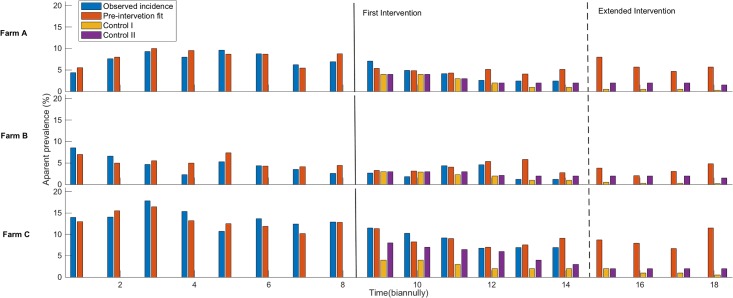
Once the three in silico herds were obtained from the fitting exercises, our next aim was to test the risk-based test and culling policy for each farm. Fig 4 presents the summary of the pre-intervention, post-intervention, and extended intervention results to the three fitted dairy herds. The results clearly show that the suggested intervention policy reduces the overall apparent prevalence for three herds, but it is noticeable that for high endemic herds the risk-based culling was comparatively less effective than the low endemic herds. To investigate further, we extended our intervention 2 years beyond the observations, but we did not see any elimination of MAP infection for the risk-based culling policy with control II. Culling red animals immediately (control I) was the best policy for all herds to decrease prevalence. Furthermore, we also calculated the number of years taken by the model to reduce the prevalence by 25% and 5% while two control programs were implemented after the pre-intervention period for three farms (shown in S2 Fig).
Fig 4. The apparent prevalence during the pre- and post-intervention period during the simulation of three in silico herds with two control strategies.
Control I: culling red animals immediately and control II: culling only red animal with a delay of 305 days in milk. The two control measures are simulated in separating runs of the three in silico herds.
Discussion and conclusion
Paratuberculosis is endemic in the bovine population in the US, which makes elimination unlikely at this time. When elimination is not possible, we have to rely on implementing the best herd-specific control strategies. Previous mathematical modeling studies show variable results for investigating infection dynamics [28,30,32], test-and-culling strategies [30,53], vaccination [29,54,55], and intermittent MAP shedding [35,47]. None of these combine the individual animal’s information with herd management policy while fitting the model to real herd data. To enhance this effort, IBM techniques can play an important role in modeling decisions for individual animal in an endemic herd. However, implementing the IBM results in real herds require realistic estimation of the herd and infection-specific parameters to test different intervention strategies. This paper presents an IBM framework of MAP where the model predicted infection dynamics are fit to and validated by the observed datasets conducted in three Northeastern US dairy herds. The fitting results show that the IBM is capable of reproducing the observed milk yield of each herd and estimating key herd-related parameters. Next, the model estimates critical transmission parameters for three herds and provides the best fit to the observed apparent prevalence data. Finally, we applied risk-based test and culling intervention strategies to the best fitted in silico herd models, showing that suggested interventions may be more beneficial for low prevalence herds than for moderate prevalence herds.
Precise information about the animal’s daily life events, such as age, milk yield, parity status, infection status, clinical signs, and adult, calf and heifer rearing management policies may assist to design real-world control strategies. Many MAP infected animals remain subclinically affected at the time of the initial infection, so precise information on the infection status of animals, combined with their economic status, is valuable for implementing effective and economically viable control strategies. The base herd fitting results suggest that the IBM recreates the observed animal distribution of the real herds (shown in Table 1). It also captures the observed milk yield curves and provides the estimates of herd-specific milk yield parameters. This feature is very important to evaluate the economic efficacy of the implemented interventions [56]. Lower milk yield is an important factor in the decision to cull an animal, but when culling an animal due to PTB test results is recommended, the effect on milk yield is not necessarily understood [57]. This leads to a lack of interest, on behalf of the herd manager, to cull based on test results alone. We observed this in the RDQMA herds, where only 0.01% of culling decisions were listed as being due to PTB, and all of those were in high-shedding animals. Furthermore, previous studies show that low- and high-path animals produce more milk before their first positive test than always-negative animals, especially high-path animals [14,35,58]. Mean milk production decreases after a first positive test, although non-progressing animals recover some productivity over time [57,58]. To account the overall impact of milk yield on culling, we used threshold values of milk yield for parity 1 and 2 for each farm and calculated median milk yield values for each parity from observed data.
The in silico dairy herd models reconfirm the apparent prevalence trends of the RDQMA herds (shown in Fig 3). In reality, calculation of the real-time prevalence is a complex process because such fine-grained testing detail is rarely available immediately. Moreover, different testing methods and variable test sensitivities make the task more difficult. Here, we used antemortem ELISA, fecal testing and postmortem tissue and fecal testing results to determine the test positive animals. For antemortem fecal culture tests, the sensitivity is determined to be 23–29% for infected cattle and 70–74% for infectious cattle [24]. At the slaughterhouse, the histology of biopsies yields sensitivity of 90 ± 5% and specificity of 100% and tissue culture yields sensitivity of 60% and specificity of 100% [59]. In comparison, ELISA tests used by the RDQMA study provide 20% sensitivity for infected cattle and 96% specificity; these numbers are aligned with the previous reports by Nielsen and Toft [60]. For simplicity, we chose a range of 25–35% sensitivity for infected animals and 96% specificity. It is one of the limitations of our model that we chose combined sensitivity and specificity estimates, whereas real herds may choose among three different testing strategies (fecal culture, ELISA, and PCR). With fecal culture, the results may take up to 3 months. Because of the time delay, many farmers rely on imperfect ELISA testing. Testing practices and recommendations vary in different geographical regions, with some finding that strategies like adaptive test scheme, age-specific sensitivities, and frequent testing can improve control. Recently, a simulation model built for the standard Danish dairy herd suggested an adaptive test scheme [8]. The age-specific test sensitivities were calculated from the test-records of 18,972 Danish dairy cows with MAP specific IgG antibodies on their final test-record [61]. However, care should be taken because using frequent testing may result in culling of many false positive animals [47].
To control PTB, it is important to determine which transmission routes are playing a major role in MAP transmission and persistence in the farm. Traditionally, the dam-to-daughter route is considered the primary route for transmitting MAP, but it can vary due to herd management policies (8). It is difficult to estimate this parameter directly from the epidemiological data due to imperfect testing and the wide variety of management policies. The role of environmental contamination is also difficult to measure from the epidemiological data, as MAP is pervasive within a dairy herd. However, our model suggests that dam-to-daughter transmission is indeed the primary transmission route, while environmental transmission is secondary route, in all three RDQMA herds (shown in Table 5). In our longitudinal data, we have the results of culturing environmental samples collected quarterly from several locations from farms. The culture results suggest that manure storage areas and shared alleyways were most likely to be positive for three herds [59], but no relationship was found between non-pen environmental sample status and the distance between shedding animals and the sample’s location, and neighboring pens did not significantly affect the results of the pen-level analysis. In our model, we included βenvironment by using a probability distribution for the sake of simplicity. A recent mathematical study presented a theoretical method to quantify the level of environmental contamination through fecal-culture [62]. To quantify the precise role of different environments, further investigation of infection sources may be needed, potentially by examining the pathogens’ genomic sequencing data. Our model is adaptive in nature and can include a rigorous assessment of environmental contamination once data become available.
To date, the best-suggested control strategies against MAP are test and cull strategies. However, targeted test and cull requires combined information of individual animal, herd management, and hygiene policy. In a previous effort, we suggested risk-based culling strategies with four different options: aggressive culling, culling open red cows after 305 DIM, culling dam and offspring, and culling dam but not the offspring and we tested these intervention strategies along with different hygiene conditions on endemic herds [37]. In this study, we further investigated two risk-based control strategies: aggressive culling and culling open red cows after 305 DIM on three pre-fitted herds. We found that Control I resulted in the probability of PTB elimination being 0.24 after three years and 0.47 after five years in a low endemic herd (farm B). We also found that culling of open red cows after 305 DIM resulted in the probability of PTB elimination being 0.11 in three years and 0.24 after five years. Previous modeling studies also predict PTB elimination in low endemic herds [31,32,36,46,47]. In high endemic herds (such as farm A), however, we found the probability of PTB elimination to be only 0.06 after 5 years using Control I, and we did not find any elimination for farms C and A when using Control II over five years.
For moderate and higher endemic herds, farmers will likely want to focus on reducing prevalence, rather than elimination, and it is important to simulate how long it takes to reduce the prevalence to below a certain level. S2 Fig shows that a low endemic herd is likely to reach 5% of initial prevalence within two years for Control II, while a high endemic herd needs extended time to reach to that point, more than ten years in some cases. These suggest that culling high shedding animals may not provide elimination in high endemic herds, although it can lower the prevalence. Kirkby et al. showed that serial testing, along with hygiene, play a critical role in the PTB elimination process in Danish dairy herds, but these may not be economically justifiable [8,32,36]. These models were parameterized specifically for Danish conditions, so caution should be taken in transferring conclusions to other countries. Control activities are not uniformly coordinated nationally and internationally due to the variation in different farm management policies and government programs. It is important to note that our current model does not include any economic justification of the suggested control strategies, but the same base model has previously been used to show the economic justification of culling in case of the MAP in a separate study [56].
In conclusion, an important aspect of the model building is to validate the model with real-life data. In this study, we present an IBM framework of infectious disease in livestock operations and validate it using a longitudinal dataset from three northeastern dairy herds. The assessment of model predictions has lead us to the conclusion that the evaluation of modeling results is still a combination of intuitive model results, validation of the model with quality data, assumptions integrated into the modeling process, and estimation of key critical parameters. Moreover, this study opens multiple paths for further investigations. The extended model can include the impact of MAP infection on milk yield while including the economics of milk production for these three farms. Another extension of the model may include the clinical and molecular data of the infected animals, but adding molecular data requires further quantification of who infects whom (62,63). The current model is adaptive in nature, allowing us to add strain-specific data for each individual animal. This framework can be adapted for other infectious diseases to quantify the importance of key transmission routes and individual-level data to population-level phenomena, and to make decision based on implemented intervention policies. In summary, the quality of the conclusions drawn from model studies is closely linked to the quality of the data used for estimation of the parameters and model validation. Models validated with real-world data are more likely to produce useful and valid results.
Supporting information
(DOCX)
The milk yield was calculated using equation shown in the method section.
(TIF)
(TIF)
Data Availability
The minimal data set underlying the study are available within the paper. The data are taken from the existing published papers by Kudahl et al. (2011), Smith et al. (2015;2016;2017) as cited in the paper. The detail data are shown in the manuscript especially in Table 4.
Funding Statement
This work was supported by National Institute of Food and Agriculture of the United States Department of Agriculture through NIFA Award No. 2014- 67015-2240. The funder provided support in the form of salaries for authors [MA Al-Mamun], but did not have any additional role in the study design, data collection, and analysis, decision to publish, or preparation of the manuscript. The specific roles of these authors are articulated in the ‘author contributions’ section.
References
- 1.BROUGHAN JM, JUDGE J, ELY E, DELAHAY RJ, WILSON G, CLIFTON-HADLEY RS, et al. A review of risk factors for bovine tuberculosis infection in cattle in the UK and Ireland. Epidemiol Infect. Cambridge University Press; 2016;144: 2899–2926. 10.1017/S095026881600131X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rathnaiah G, Zinniel DK, Bannantine JP, Stabel JR, Gröhn YT, Collins MT, et al. Pathogenesis, Molecular Genetics, and Genomics of Mycobacterium avium subsp. paratuberculosis, the Etiologic Agent of Johne’s Disease. Front Vet Sci. 2017;4: 187 10.3389/fvets.2017.00187 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brooks-Pollock E, Roberts GO, Keeling MJ. A dynamic model of bovine tuberculosis spread and control in Great Britain. Nature. Nature Publishing Group; 2014;511: 228–231. 10.1038/nature13529 [DOI] [PubMed] [Google Scholar]
- 4.NAHMS. National Animal Health Monitoring System (2007) Dairy 2007-Johne’s Disease on U.S. Dairies, 1991–2007,National Animal Health Monitoring Systems. Fort Collins, CO; 2007.
- 5.Behr M, Collin D. Paratuberculosis:Organism, Disease, Control. CABI; 2010. [Google Scholar]
- 6.Woolhouse M, Ward M, van Bunnik B, Farrar J. Antimicrobial resistance in humans, livestock and the wider environment. Philos Trans R Soc Lond B Biol Sci. The Royal Society; 2015;370: 20140083. 10.1098/rstb.2014.0083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ott SL, Wells SJ, Wagner BA. Herd-level economic losses associated with Johne’s disease on US dairy operations. Prev Vet Med. 1999;40: 179–92. Available: http://www.ncbi.nlm.nih.gov/pubmed/10423773 [DOI] [PubMed] [Google Scholar]
- 8.Kirkeby C, Græsbøll K, Nielsen SS, Christiansen LE, Toft N, Halasa T, et al. Adaptive Test Schemes for Control of Paratuberculosis in Dairy Cows. Sreevatsan S, editor. PLoS One. Public Library of Science; 2016;11: e0167219 10.1371/journal.pone.0167219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Whittington RJ, Windsor PA. In utero infection of cattle with Mycobacterium avium subsp. paratuberculosis: A critical review and meta-analysis. Vet J. W.B. Saunders; 2009;179: 60–69. 10.1016/J.TVJL.2007.08.023 [DOI] [PubMed] [Google Scholar]
- 10.van Roermund HJW, Bakker D, Willemsen PTJ, de Jong MCM. Horizontal transmission of Mycobacterium avium subsp. paratuberculosis in cattle in an experimental setting: Calves can transmit the infection to other calves. Vet Microbiol. 2007;122: 270–279. 10.1016/j.vetmic.2007.01.016 [DOI] [PubMed] [Google Scholar]
- 11.Mitchell RM, Schukken Y, Koets A, Weber M, Bakker D, Stabel J, et al. Differences in intermittent and continuous fecal shedding patterns between natural and experimental Mycobacterium avium subspecies paratuberculosis infections in cattle. Vet Res. Veterinary Research; 2015;46: 66 10.1186/s13567-015-0188-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nielsen SS. Use of diagnostics for risk-based control of paratuberculosis in dairy herds. Pr. 2009;31: 150–154. 10.1136/inpract.31.4.150 [Google Scholar]
- 13.Aly SS, Anderson RJ, Adaska JM, Jiang J, Gardner IA. Association between Mycobacterium avium subspecies paratuberculosis infection and milk production in two California dairies. J Dairy Sci. 2010;93: 1030–1040. 10.3168/jds.2009-2611 [DOI] [PubMed] [Google Scholar]
- 14.Nielsen SS, Krogh MA, Enevoldsen C. Time to the occurrence of a decline in milk production in cows with various paratuberculosis antibody profiles. J Dairy Sci. Elsevier; 2009;92: 149–55. 10.3168/jds.2008-1488 [DOI] [PubMed] [Google Scholar]
- 15.Sorge US, Kelton DF, Lissemore KD, Sears W, Fetrow J. Evaluation of the Dairy Comp 305 Module “Cow Value” in Two Ontario Dairy Herds. J Dairy Sci. 2007;90: 5784–5797. 10.3168/jds.2006-0813 [DOI] [PubMed] [Google Scholar]
- 16.Lombard JE, Garry FB, McCluskey BJ, Wagner BA. Risk of removal and effects on milk production associated with paratuberculosis status in dairy cows. J Am Vet Med Assoc. 2005;227: 1975–1981. 10.2460/javma.2005.227.1975 [DOI] [PubMed] [Google Scholar]
- 17.Tiwari A, VanLeeuwen JA, Dohoo IR, Stryhn H, Keefe GP, Haddad JP. Effects of seropositivity for bovine leukemia virus, bovine viral diarrhoea virus, Mycobacterium avium subspecies paratuberculosis, and Neospora caninum on culling in dairy cattle in four Canadian provinces. Vet Microbiol. Elsevier; 2005;109: 147–158. 10.1016/J.VETMIC.2005.05.011 [DOI] [PubMed] [Google Scholar]
- 18.Kudahl AB, Nielsen SS. Effect of paratuberculosis on slaughter weight and slaughter value of dairy cows. J Dairy Sci. 2009;92: 4340–4346. 10.3168/jds.2009-2039 [DOI] [PubMed] [Google Scholar]
- 19.Marcé C, Beaudeau F, Bareille N, Seegers H, Fourichon C. Higher non-return rate associated with Mycobacterium avium subspecies paratuberculosis infection at early stage in Holstein dairy cows. Theriogenology. 2009;71: 807–816. 10.1016/j.theriogenology.2008.10.017 [DOI] [PubMed] [Google Scholar]
- 20.Smith RL, Strawderman RL, Schukken YH, Wells SJ, Pradhan aK, Espejo L a, et al. Effect of Johne’s disease status on reproduction and culling in dairy cattle. J Dairy Sci. Elsevier; 2010;93: 3513–3524. 10.3168/jds.2009-2742 [DOI] [PubMed] [Google Scholar]
- 21.Garcia A. B., Shalloo L. Invited review: The economic impact and control of paratuberculosis in cattle. J Dairy Sci. Elsevier; 2015;98: 5019–39. 10.3168/jds.2014-9241 [DOI] [PubMed] [Google Scholar]
- 22.Li L, Katani R, Schilling M, Kapur V. Molecular Epidemiology of Mycobacterium avium subspp. Paratuberculosis on Dairy Farms. Annu Rev Anim Biosci. 2015; 155–178. 10.1146/annurev-animal-021815-111304 [DOI] [PubMed] [Google Scholar]
- 23.Slater N, Mitchell RM, Whitlock RH, Fyock T, Pradhan AK, Knupfer E, et al. Impact of the shedding level on transmission of persistent infections in Mycobacterium avium subspecies paratuberculosis (MAP). Vet Res. BioMed Central; 2016;47: 1–12. 10.1186/s13567-016-0323-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pradhan AK, Mitchell RM, Kramer AJ, Zurakowski MJ, Fyock TL, Whitlock RH, et al. Molecular epidemiology of Mycobacterium avium subsp. paratuberculosis in a longitudinal study of three dairy herds. J Clin Microbiol. 2011;49: 893–901. 10.1128/JCM.01107-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Magombedze G, Ngonghala CN, Lanzas C. Evalution of the “Iceberg Phenomenon” in Johne’s Disease through Mathematical Modelling. Rao C V., editor. PLoS One. Public Library of Science; 2013;8: e76636 10.1371/journal.pone.0076636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Elliott GN, Hough RL, Avery LM, Maltin C a, Campbell CD. Environmental risk factors in the incidence of Johne’s disease. Crit Rev Microbiol. 2014;7828: 1–20. 10.3109/1040841X.2013.867830 [DOI] [PubMed] [Google Scholar]
- 27.Kirkeby C, Græsbøll K, Halasa T, Toft N, Nielsen SS. Mean effective sensitivity for Mycobacterium avium subsp. paratuberculosis infection in cattle herds. BMC Vet Res. BMC Veterinary Research; 2015;11: 190 10.1186/s12917-015-0512-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mitchell RM, Whitlock RH, Stehman SM, Benedictus A, Chapagain PP, Grohn YT, et al. Simulation modeling to evaluate the persistence of Mycobacterium avium subsp. paratuberculosis (MAP) on commercial dairy farms in the United States. Prev Vet Med. 2008;83: 360–380. 10.1016/j.prevetmed.2007.09.006 [DOI] [PubMed] [Google Scholar]
- 29.Lu Z, Schukken YH, Smith RL, Grohn YT. Stochastic simulations of a multi-group compartmental model for Johne’s disease on US dairy herds with test-based culling intervention. J Theor Biol. Elsevier; 2010;264: 1190–1201. 10.1016/j.jtbi.2010.03.034 [DOI] [PubMed] [Google Scholar]
- 30.Lu Z, Mitchell RM, Smith RL, Van Kessel JS, Chapagain PP, Schukken YH, et al. The importance of culling in Johne’s disease control. J Theor Biol. 2008;254: 135–146. 10.1016/j.jtbi.2008.05.008 [DOI] [PubMed] [Google Scholar]
- 31.Kudahl AB, Nielsen SS, Østergaard S. Economy, efficacy, and feasibility of a risk-based control program against paratuberculosis. J Dairy Sci. 2008;91: 4599–609. 10.3168/jds.2008-1257 [DOI] [PubMed] [Google Scholar]
- 32.Kudahl AB, Østergaard S, Sørensen JT, Nielsen SS. A stochastic model simulating paratuberculosis in a dairy herd. Prev Vet Med. 2007;78: 97–117. 10.1016/j.prevetmed.2006.05.015 [DOI] [PubMed] [Google Scholar]
- 33.Kudahl aB, Nielsen SS, Ostergaard S. Strategies for time of culling in control of paratuberculosis in dairy herds. J Dairy Sci. Elsevier; 2011;94: 3824–3834. 10.3168/jds.2010-3933 [DOI] [PubMed] [Google Scholar]
- 34.Smith RL, Al-Mamun MA, Gröhn YT. Economic consequences of paratuberculosis control in dairy cattle: A stochastic modeling study. Prev Vet Med. Elsevier B.V.; 2017;138: 17–27. 10.1016/j.prevetmed.2017.01.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Smith RL, Schukken YH, Gröhn YT. A new compartmental model of Mycobacterium avium subsp. paratuberculosis infection dynamics in cattle. Prev Vet Med. Elsevier B.V.; 2015;122: 298–305. 10.1016/j.prevetmed.2015.10.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kirkeby C, Græsbøll K, Nielsen SS, Christiansen LE, Toft N, Rattenborg E, et al. Simulating the Epidemiological and Economic Impact of Paratuberculosis Control Actions in Dairy Cattle. Front Vet Sci. Frontiers; 2016;3: 90 10.3389/fvets.2016.00090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Al-Mamun MA, Smith RL, Schukken YH, Gröhn YT. Use of an Individual-based Model to Control Transmission Pathways of Mycobacterium avium Subsp. paratuberculosis Infection in Cattle Herds. Sci Rep. Nature Publishing Group; 2017;7: 11845 10.1038/s41598-017-12078-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Marcé C, Ezanno P, Weber MF, Seegers H, Pfeiffer DU, Fourichon C. Invited review: modeling within-herd transmission of Mycobacterium avium subspecies paratuberculosis in dairy cattle: a review. J Dairy Sci. Elsevier; 2010;93: 4455–70. 10.3168/jds.2010-3139 [DOI] [PubMed] [Google Scholar]
- 39.Liu L, Oza S, Hogan D, Perin J, Rudan I, Lawn JE, et al. Global, regional, and national causes of child mortality in 2000–13, with projections to inform post-2015 priorities: an updated systematic analysis. Lancet. 2015;385: 430–440. 10.1016/S0140-6736(14)61698-6 [DOI] [PubMed] [Google Scholar]
- 40.Carslake D, Grant W, Green LE, Cave J, Greaves J, Keeling M, et al. Endemic cattle diseases: comparative epidemiology and governance. Philos Trans R Soc Lond B Biol Sci. The Royal Society; 2011;366: 1975–86. 10.1098/rstb.2010.0396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kirkeby C, Græsbøll K, Nielsen SS, Toft N, Halasa T. Epidemiological and economic consequences of purchasing livestock infected with Mycobacterium avium subsp. paratuberculosis. BMC Vet Res. BMC Veterinary Research; 2017;13: 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chi J, VanLeeuwen JA, Weersink A, Keefe GP. Direct production losses and treatment costs from bovine viral diarrhoea virus, bovine leukosis virus, Mycobacterium avium subspecies paratuberculosis, and Neospora caninum. Prev Vet Med. Elsevier; 2002;55: 137–153. 10.1016/S0167-5877(02)00094-6 [DOI] [PubMed] [Google Scholar]
- 43.Al-Mamun MA, Smith RL, Schukken YH, Gröhn YT. Modeling of Mycobacterium avium subsp. paratuberculosis dynamics in a dairy herd: An individual based approach. J Theor Biol. 2016; 10.1016/j.jtbi.2016.08.014 [DOI] [PubMed] [Google Scholar]
- 44.Al-Mamun MA, Grohn YT. MABSDairy: A Multiscale Agent Based Simulation of a Dairy Herd. Proc 50th Annu Simul Symp. 2017; 8:1–8:12. http://dl.acm.org/citation.cfm?id=3106388.3106396
- 45.Robins J, Bogen S, Francis A, Westhoek A, Kanarek A, Lenhart S, et al. Agent-based model for Johne’s disease dynamics in a dairy herd. Vet Res. Veterinary Research; 2015;46: 68 10.1186/s13567-015-0195-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kirkeby C, Græsbøll K, Halasa T. Evaluating the impact of transmission mode, calibration level and farmer compliance in simulation models of paratuberculosis in dairy herds. Sci Rep. Nature Publishing Group; 2018;8: 9100 10.1038/s41598-018-27518-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mitchell RM, Whitlock RH, Gröhn YT, Schukken YH. Back to the real world: Connecting models with data. Prev Vet Med. 2015;118: 215–225. 10.1016/j.prevetmed.2014.12.009 [DOI] [PubMed] [Google Scholar]
- 48.WOOD PDP. Algebraic Model of the Lactation Curve in Cattle. Nature. Nature Publishing Group; 1967;216: 164–165. 10.1038/216164a0 [Google Scholar]
- 49.Dematawewa CMB, Pearson RE, VanRaden PM. Modeling Extended Lactations of Holsteins. J Dairy Sci. Elsevier; 2007;90: 3924–3936. 10.3168/JDS.2006-790 [DOI] [PubMed] [Google Scholar]
- 50.Pradhan aK, Van Kessel JS, Karns JS, Wolfgang DR, Hovingh E, Nelen K a, et al. Dynamics of endemic infectious diseases of animal and human importance on three dairy herds in the northeastern United States. J Dairy Sci. Elsevier; 2009;92: 1811–1825. 10.3168/jds.2008-1486 [DOI] [PubMed] [Google Scholar]
- 51.Al-Mamun MA, Grohn YT. MABSDairy: A Multiscale Agent Based Simulation of a Dairy Herd. Proceedings of the 50th Annual Simulation Symposium. San Diego, CA, USA: Society for Computer Simulation International; 2017. p. 8:1–8:12. http://dl.acm.org/citation.cfm?id=3106388.3106396
- 52.Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence Properties of the Nelder--Mead Simplex Method in Low Dimensions. SIAM J Optim. Society for Industrial and Applied Mathematics; 1998;9: 112–147. 10.1137/S1052623496303470 [Google Scholar]
- 53.Smith RL, Schukken YH, Lu Z, Mitchell RM, Grohn YT. Development of a model to simulate infection dynamics of Mycobacterium bovis in cattle herds in the United States. J Am Vet Med Assoc. 2013;243: 411–423. 10.2460/javma.243.3.411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lu Z, Schukken YH, Smith RL, Mitchell RM, Gröhn YT. Impact of imperfect Mycobacterium avium subsp. paratuberculosis vaccines in dairy herds: A mathematical modeling approach. Prev Vet Med. Elsevier B.V.; 2013;108: 148–158. 10.1016/j.prevetmed.2012.08.001 [DOI] [PubMed] [Google Scholar]
- 55.Lu Z, Schukken YH, Smith RL, Gröhn YT. Using vaccination to prevent the invasion of Mycobacterium avium subsp. paratuberculosis in dairy herds: A stochastic simulation study. Prev Vet Med. Elsevier B.V.; 2013;110: 335–345. 10.1016/j.prevetmed.2013.01.006 [DOI] [PubMed] [Google Scholar]
- 56.Verteramo Chiu LJ, Tauer LW, Al-Mamun MA, Kaniyamattam K, Smith RL, Grohn YT. An agent-based model evaluation of economic control strategies for paratuberculosis in a dairy herd. J Dairy Sci. Elsevier; 2018; 10.3168/JDS.2017-13175 [DOI] [PubMed] [Google Scholar]
- 57.Smith R L, Grohn Y T, Pradhan A K, Whitlock R H, Van Kessel J S, Smith J M, Wolfgang D R, Schukken YH. A longitudinal study on the impact of Johne’s disease status on milk production in individual cows. J Dairy Sci. Elsevier; 2009;92: 2653–61. 10.3168/jds.2008-1832 [DOI] [PubMed] [Google Scholar]
- 58.Smith RL, Gröhn YT, Pradhan AK, Whitlock RH, Van Kessel JS, Smith JM, et al. The effects of progressing and nonprogressing Mycobacterium avium ssp. paratuberculosis infection on milk production in dairy cows. J Dairy Sci. 2016;99: 1383–1390. 10.3168/jds.2015-9822 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Smith RL, Schukken YH, Pradhan AK, Smith JM, Whitlock RH, Van Kessel JS, et al. Environmental contamination with Mycobacterium avium subsp. paratuberculosis in endemically infected dairy herds. Prev Vet Med. Elsevier B.V.; 2011;102: 1–9. 10.1016/j.prevetmed.2011.06.009 [DOI] [PubMed] [Google Scholar]
- 60.Nielsen SS, Toft N. Ante mortem diagnosis of paratuberculosis: A review of accuracies of ELISA, interferon-γ assay and faecal culture techniques. Vet Microbiol. Elsevier; 2008;129: 217–235. 10.1016/J.VETMIC.2007.12.011 [DOI] [PubMed] [Google Scholar]
- 61.Nielsen SS, Toft N, Okura H. Dynamics of Specific Anti-Mycobacterium avium Subsp. paratuberculosis Antibody Response through Age. PLoS One. 2013;8 10.1371/journal.pone.0063009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Davidson RS, McKendrick IJ, Wood JC, Marion G, Greig A, Stevenson K, et al. Accounting for uncertainty in model-based prevalence estimation: paratuberculosis control in dairy herds. BMC Vet Res. 2012;8: 159 10.1186/1746-6148-8-159 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
The milk yield was calculated using equation shown in the method section.
(TIF)
(TIF)
Data Availability Statement
The minimal data set underlying the study are available within the paper. The data are taken from the existing published papers by Kudahl et al. (2011), Smith et al. (2015;2016;2017) as cited in the paper. The detail data are shown in the manuscript especially in Table 4.