Abstract
The primary visual cortex of carnivores and primates is dominated by the OFF visual pathway and responds more strongly to dark than light stimuli. Here, we demonstrate that this cortical OFF dominance is modulated by the size and spatial frequency of the stimulus in awake primates and we uncover a main neuronal mechanism underlying this modulation. We show that large grating patterns with low spatial frequencies drive five times more OFF-dominated than ON-dominated neurons, but this pronounced cortical OFF dominance is strongly reduced when the grating size decreases and the spatial frequency increases, as when the stimulus moves away from the observer. We demonstrate that the reduction in cortical OFF dominance is not caused by a selective reduction of visual responses in OFF-dominated neurons but by a change in the ON/OFF response balance of neurons with diverse receptive field properties that can be ON or OFF dominated, simple, or complex. We conclude that cortical OFF dominance is continuously adjusted by a neuronal mechanism that modulates ON/OFF response balance in multiple cortical neurons when the spatial properties of the visual stimulus change with viewing distance and/or optical blur.
Keywords: area V1, receptive field, thalamocortical, thalamus, visual cortex
Introduction
Animals that use vision to navigate in their environments, from flies to primates, have two main visual channels that respond to local luminance increments (ON) and decrements (OFF) in the visual scene (Hubel and Wiesel 1968; Joesch et al. 2010). ON and OFF thalamic afferents segregate in different horizontal domains of the visual cortex in carnivores (McConnell and LeVay 1984; Zahs and Stryker 1988; Jin et al. 2008; Kremkow et al. 2016), and this segregation is likely to be also present in primates (Kremkow et al. 2016). Within each cortical domain, individual neurons receive convergent input from both ON and OFF thalamic afferents, but OFF thalamic inputs dominate in OFF cortical domains and ON thalamic inputs in ON cortical domains (Jin et al. 2011; Wang et al. 2015).
ON and OFF thalamic inputs are not equal partners in cortical space and do not have equal synaptic impact. In cat visual cortex, OFF thalamic inputs cover larger cortical regions and make stronger connections than ON thalamic inputs (Jin et al. 2008, 2011), making the cortex OFF dominated. The predominance of OFF-dominated neurons in primary visual cortex was first reported in cats (Jin et al. 2008) and has now been demonstrated in primates, tree shrews, and mice (Yeh et al. 2009; Veit et al. 2014; Tan et al. 2015; Jimenez et al. 2018, but see Polack and Contreras 2012), yielding support to previous studies in human visual cortex that found stronger visual-evoked potentials for dark than light stimuli (Zemon et al. 1988, 1995). The cortical OFF dominance is likely to emerge at cortical layers where ON and OFF visual pathways converge, which takes place in the middle cortical layers of cats (Wang et al. 2015) and the superficial layers of primates (Yeh et al. 2009).
Cortical OFF dominance could explain why we see dark targets better than light targets under low light (Blackwell 1946; Short 1966), why darks are more salient than lights in noisy backgrounds (Komban et al. 2011, 2014) and why dark pixels are weighted more than light pixels when estimating luminance variance in textured images (Chubb et al. 1994, 2004; Chubb and Nam 2000). However, cortical OFF dominance is not a fixed property of the cortex but changes with the stimulus conditions (Onat et al. 2011; Kremkow, Jin, et al. 2014; Liu and Yao 2014). In anesthetized cats, cortical OFF dominance is strongest at low spatial frequencies and becomes progressively weaker as spatial frequency increases (Onat et al. 2011; Kremkow, Jin, et al. 2014), a relation that is also found in natural images where dark regions dominate at low spatial frequencies (Cooper and Norcia 2015). Here, we demonstrate that cortical OFF dominance is strongly modulated by coordinated changes in spatial frequency and size that simulate changes in viewing distance (e.g., the retinal image of an object decreases in spatial frequency and increases in size as the object approaches the observer). In addition, we show that this modulation of ON/OFF response balance involves multiple classes of cortical neurons with different receptive field (RF) properties that can be ON or OFF dominated, simple, or complex. Taken together, our results indicate that multiple V1 neurons adjust their ON/OFF response balance continuously based on the spatial properties of the visual stimulus.
Materials and Methods
Surgery and Preparation
Two adult male rhesus monkeys were implanted with a head post, a scleral eye coil, a recording chamber, and a chronic multielectrode array with up to seven independently movable electrodes (Swadlow et al. 2005; Chen et al. 2008). The electrodes were made of platinum tungsten filaments with a 40 μm diameter that were pulled and sharpened to a fine tip of approximately 1 μm. Animals were trained to grasp a bar and fixate their eyes on a small cross of 0.12°. After fixating for 0.5 s, gratings were presented and a trial was aborted if the fixation deviated more than 1° or if the animal released the bar before the end of stimulus presentation. All procedures were performed in accordance with the guidelines of the US Department of Agriculture and approved by the Institutional Animal Care and Use Committee at the State University of New York, College of Optometry.
Visual Stimuli
Visual stimuli were presented on a cathode ray tube monitor located at 57 cm from the animal (Sony GDM F520, refresh rate: 160 Hz). We used a fast sequence of static grating stimuli to map the RFs of V1 single neurons (Ringach et al. 1997) and sinusoidal drifting gratings to measure their stimulus tuning for orientation, spatial frequency, contrast, size, phase, and color. The fast grating sequence was made of 576 distinct gratings with 88 different orientations, 41 different spatial frequencies, and 4 different phases, presented at 80 Hz (monitor refresh rate: 160 Hz). The combinations of orientation, spatial frequency, and phase were uniformly sampled from a subspace of Hartley functions previously shown to be effective at mapping cortical RFs (Ringach et al. 1997). By using this Hartley subspace, we avoid presenting all possible combinations of orientation, spatial frequency, and phase (88 × 41 × 4 = 14,432 combinations vs. 576) and make the process of RF mapping more efficient. Within this Hartley subspace, each grating combination of orientation and spatial frequency is presented at four different phases and the 576 gratings (all the same size) are randomly presented multiple times for a period of several minutes (~10 000 gratings in ~2 min per cortical cell).
The RF of each neuron was mapped with four grating sequences that had identical grating combinations of orientation, spatial frequency, and phase. However, the grating size was different for each sequence. We call these grating sequences size-8, size-4, size-2, and size-1 because all gratings within each sequence were made of 8 × 8 (size-8 sequence), 4 × 4 (size-4 sequence), 2 × 2 (size-2 sequence), or 1 × 1 monitor pixels (size-1 sequence), which corresponds approximately to 0.4°, 0.2°, 0.1°, and 0.05° per grating pixel, respectively. Therefore, the gratings from each sequence had all the same size, and the gratings from different sequences had the same combinations of orientation, spatial frequency, and phase but differed in size. We chose these specific values of grating sizes to span the entire size range that could be generated with a fast monitor refresh rate (160 Hz), from the smallest (48 × 48 monitor pixels) to largest gratings (384 × 384 monitor pixels).
The spatial frequency of all gratings within each sequence was scaled with grating size. Therefore, the spatial frequency range covered by all gratings within each sequence was 0.047–0.53 cycles per degree (cpd) for the size-8 sequence (grating size: 19.2°), 0.09–1.07 for the size-4 sequence (grating size: 9.6°), 0.19–2.14 for the size-2 sequence (grating size: 4.8°), and 0.38–4.28 cpd for the size-1 sequence (grating size: 2.4°). Due to the scaling of spatial frequency with size, a grating of size-8 was equivalent to a grating of size-4, size-2, and size-1 seen with a viewing distance two, four, and eight times longer. Since all sequences had the same grating combinations of orientation, spatial frequency, and phase, the distributions of spatial frequency were identical for the four grating sequences after shifting the spatial frequency axis by a scale factor (e.g., average ± standard deviation [range] of spatial frequencies for size-8 sequence: 0.31 ± 0.11 cpd [0.047–0.53 cpd]). By using gratings scaled in both size and spatial frequency, we were able to study changes in ON/OFF response balance that would be expected from changes in the viewing distance of the grating. For example, the retinal projection of a letter in this page increases in size and decreases in spatial frequency when the viewing distance decreases. Similarly, the retinal projection of a grating in our stimuli increases in size and decreases in spatial frequency when the sequence changes from size-1 to size-8. Notice that our stimulus design has 41 different spatial frequencies per grating size, 4 different sizes and multiple repetitions of each stimulus combination. Therefore, this stimulus design allows us to study the separate contribution of spatial frequency and size to ON/OFF response balance.
Stimulus Tuning
The stimulus tuning for orientation/direction, spatial frequency, size, and contrast was measured with drifting gratings. The drifting gratings could have 16 equally spaced circular directions (orientation/direction tuning), 8 different spatial frequencies from 0.01 to 6 cpd (spatial frequency tuning), 8 different sizes from 0.6° to 8° (size tuning), 8 different contrasts from 2% to 95% (contrast response function), and each grating drifted 2 s per trial. The phase tuning was measured with static gratings optimized for orientation, spatial frequency, and size (2 s per trial at 2 Hz). In some cells, responses to equiluminant red–green (RG) and blue–yellow (BY) gratings were also measured. First, the dot product of the emission spectra of the red, green, and blue monitor phosphors and the Smith–Pokorny 2-degree cone fundamentals were measured with a Photo Research PR 650 SpectraScan spectroradiometer to determine the excitations for the long (L), medium (M), and short (S) wavelength-sensitive cones. Then, equiluminant stimuli were prepared in the same color space used by Derrington et al. (1984) with the methods described by Zaidi and Halevy (1993) and Jansen et al. (2015). This color space is described by two chromatic axes, popularly known as the RG or BY axes, and a luminance or light–dark (LD) axis. The chromatic axes are cone opponent, with the RG axis defined by the change in the difference between the L and M cone activations, and the BY axis defined by the change in S cone activation. Color responses were measured at eight equally spaced intervals in the isoluminant plane (RG and BY axes) using eight sinusoid gratings composed of colors specified by vectors passing through the origin. For some cells, additional responses were measured for the plane defined by the BY and LD axes and for the plane defined by the RG and LD axes (for these stimuli, the LD content was limited to a maximum of 15% contrast). The optimal orientation and size of the chromatic gratings were determined from the peak responses to achromatic stimuli. The optimal spatial frequency was determined from the peak responses to RG and BY gratings and an intermediate spatial frequency was used when the two chromatic axes differed in their peak spatial frequency responses. For some cells, color responses were also measured for 16 colors equally spaced around the color circle in the isoluminant plane. For these cells, the grating was modulated between the color and the origin, appearing as alternating bars of color and gray.
The cells were first studied with the fast sequence of large gratings (size-8 sequence) to quickly measure the spatial position of RF and accurately align the following stimuli with the RF center. Then, the RF was measured again with a sequence of size-4 gratings (for a few cells with very small RFs, we started mapping the RFs with the size-4 instead of the size-8 sequence). If the RF obtained with the size-4 gratings passed our criteria of signal to noise, it was measured again with a sequence of size-2 gratings. If the RF with size-2 gratings passed our criteria of signal to noise, it was measured again with size-1 gratings. After finishing the RF mapping, sinusoidal gratings were presented within a circular Gaussian aperture to measure tuning to different stimulus properties in the following order: orientation, spatial frequency, size, contrast, phase, and color. Orientation tuning was measured with a drifting grating with spatial frequency and size adjusted to generate strong visual responses. Spatial frequency tuning was measured with a grating drifting at the preferred orientation. Size tuning was measured with a drifting grating optimized for orientation and spatial frequency. Contrast sensitivity, phase tuning, and color tuning were measured with gratings optimized for orientation, spatial frequency, and size. In some cells, we repeated the measurements of orientation tuning with the preferred spatial frequency and size, after the entire stimulus tuning of the cell was properly characterized.
In the measurements of stimulus tuning, grating responses were baseline-subtracted, and signal-to-noise ratios were calculated as the maximum response between 0.25 and 2 s following the stimulus onset and divided by the standard deviation of the baseline (250 ms preceding stimulus onset). In measurements of phase tuning, the maximum response was defined as the average of the two maximum responses following the stimulus onset (since the gratings were turned on and off twice in each trial). Tuning curves were fit only when the maximum signal-to-noise ratio was equal or greater than an arbitrary value set to 25. Two tests were used to assess the veracity of chromatic responses and classify cells as color responsive: a contrast test and a phase test (Jansen et al. 2014). The contrast test compared isoluminant responses to the response of a luminance grating with 15% contrast and a cell was classified as color responsive if the response to any of the 8-16 isoluminant stimuli was significantly greater than the response to the 15% luminance grating. This contrast level was chosen because it exceeded the maximum L and M cone contrast (13.3%) available in our equiluminant stimuli. In addition, it exceeded the largest luminance artifact expected from differences in S cone response due to variations in macular pigment density (Cottaris 2003). The second chromatic test was a phase test. Gratings were presented in either the BY-LD or RG-LD plane, in which luminance and chromatic gratings are combined. A cell that shows chromatic tuning should respond similarly regardless of the phase of a superimposed luminance grating. Consequently, a cell was classified as color tuned if the responses in BY-LD or RG-LD planes did not vary significantly with the relative phase of the luminance grating.
For all response properties, spikes were binned at 10-ms intervals to make peristimulus time histograms (PSTHs). Then, the PSTHs were used to obtain the mean (F0), first (F1), and second (F2) harmonic responses with Fourier analysis. Orientation tuning curves were fit to the F0, F1, and F2 values and the fit with the highest amplitude was used for subsequent analysis if the goodness of fit R2 was larger than or equal to 0.60. The phase of the F1 response was also used for analysis of shifts in response phase with spatial frequency (see the following).
Orientation and phase tuning were fit with a double von Mises function (Swindale et al. 2003; Lashgari et al. 2012) as follows:
| (1) |
where R is the response, θ is the direction of the drifting grating, and are the peak amplitudes of the response to the preferred and nonpreferred directions of movement, and are the angles of the preferred and nonpreferred direction of movement (in radians), and and are inversely related to the peak widths. The larger the value of k1, the narrower the tuning to the preferred direction of movement. The larger the value of k2, the narrower the tuning to the nonpreferred direction.
The circular variance (CV) was calculated for orientation tuning (Ringach et al. 2002) as follows:
| (2) |
| (3) |
where is the amplitude of the Fourier harmonic, and is the orientation in radians, and i is the unit imaginary number.
The phase of the response to a drifting grating was measured with a fast Fourier transform of the PSTH and was defined as the phase of the fundamental frequency. To calculate shifts in the response phase with spatial frequency, we sorted the response phases in ascending order of spatial frequency. For example, if we used gratings with eight increasingly higher spatial frequencies, S1–S8, we obtained eight phases: P1 for S1, P2 for S2, and so on. Then, we subtracted the response phase of the grating with lowest spatial frequency (P1) from the response phases of gratings with higher spatial frequencies. Therefore, the response phase of the grating with lowest spatial frequency (P1) was always zero and the response phases of gratings with increasingly higher spatial frequencies were P2–P1, P3–P1, and so on. The response phase is a circular variable that ranges between zero and one, with zero and one being the same phase and the largest possible phase difference being 0.5. Therefore, all phase shifts were constraint within a limit of 0.5. The same procedure was used to calculate phase shifts with grating contrast and size.
Mapping Cortical RFs with Grating Sequences
The RFs were mapped by spike-trigger-averaging the grating stimuli from each grating sequence (576 gratings with 88 different orientations, 41 different spatial frequencies, and 4 different phases, presented at 80 Hz for ~2 min of visual stimulation). Grating stimuli were averaged into 10 time bins (corresponding to 10 stimulus frames preceding the spike in time). The averaged time bin with the maximum absolute value was chosen as the averaged RF or the stimulus spike-triggered average. Contrast polarity was measured as the difference between the maximum ON and OFF responses within the RF divided by the sum. If contrast polarity was positive, the cell was classified as ON dominated and, if negative, it was classified as OFF dominated. This criterion to classify cortical cells in ON dominated and OFF dominated is based on a bimodal distribution of contrast polarity in primary visual cortex. In cat visual cortex, the index of contrast polarity shows a pronounced and highly significant bimodal distribution centered at zero (Wang et al. 2015). In macaques, the distribution also shows a hint of bimodality (see Fig. 4) although the sample of neurons is not large enough to reach significance. Our results do not change if we classify cortical neurons as ON dominated and OFF dominated only when the dominant ON (or OFF) RF subregion is significantly stronger than the RF subregion with opposite contrast polarity using a Wilcoxon test. The signal-to-noise ratio of the receptive field (RFsnr) was calculated as the maximum response within the RF divided by the baseline (baseline: maximum response within a 12.5-ms window preceding the spike). Only RFs with a signal-to-noise ratio ≥1.6 and a minimum total spike count of 100 were selected for further analysis. All single neurons had <2% of interspike intervals lasting <1 ms.
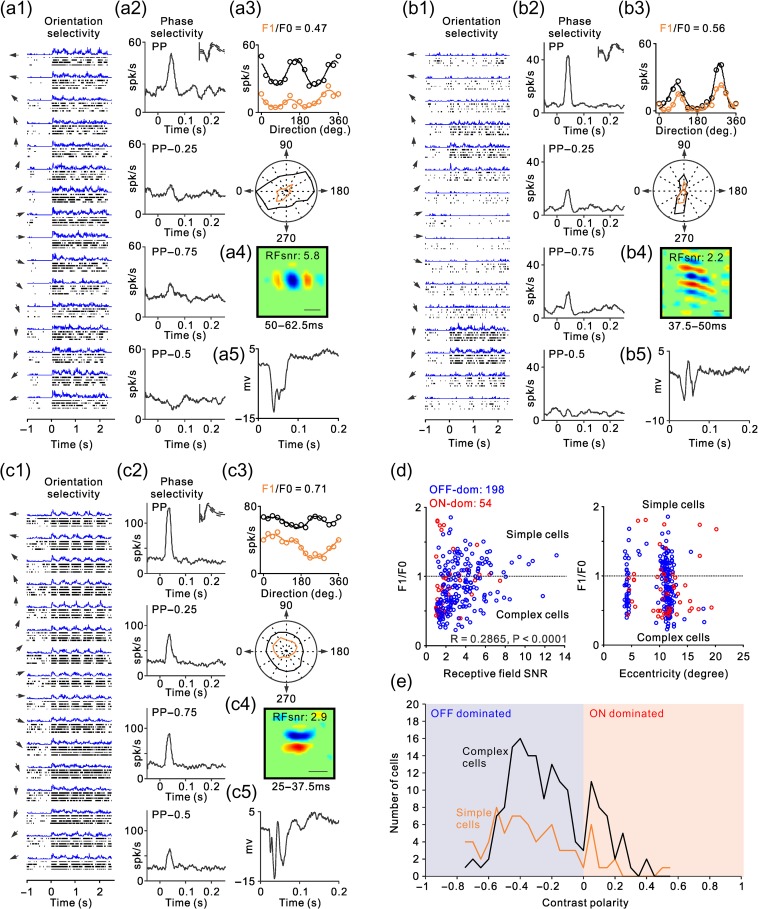
Figure 4.
Examples of ON–OFF RF organization in complex cells. (a–c) Same as Figure 3b–c but for examples of complex RFs. (d) Scatter plot illustrating the relation of linearity of spatial summation (F1/F0) with the signal to noise of the RF (left) and visual eccentricity (right). The F1/F0 ratio should be higher than one when the ON and OFF subregions are spatially segregated and should approach zero when the ON and OFF subregions are spatially overlapped. The signal-to-noise ratio (SNR) should approach one when ON and OFF subregions are identical in position, size, and strength because the ON–OFF subtraction approaches zero plus the noise (the signal equals the noise and the SNR equals one). The SNR should be higher than one if the relative strength of ON and OFF subregions varies at each spatial location and the complex RF has ON and OFF subregions. The two clusters for visual eccentricity correspond to neurons recorded in the operculum and the superior bank of the calcarine sulcus. (e) Distribution of RF contrast polarity for complex cells (black) and simple cells (orange). OFF-dominated RFs are shown on the left (blue) and ON-dominated RFs on the right (red).
A 2D Gabor function was fit to the RF (Jones and Palmer 1987; Ringach 2002) using the following equations:
| (4) |
| (5) |
| (6) |
where x′ and y′ are translated coordinates of the Gaussian envelope with rotation θ, A is the amplitude, 2σx′ and 2σy′ are the width and length of the Gaussian envelope, λ is the spatial wavelength of the sinusoid, and Φ is the spatial phase of the grating.
A 2D FFT (2dFFT) was obtained from the Gabor function. The maximum absolute value of the 2dFFT was obtained at 16 equally spaced intervals circling the origin. These 16 values were then used to calculate the 2dFFT CV (eq. 2), which we refer to as the Gabor CV.
Temporal Impulse Responses and Phase Selectivity
Temporal impulse responses were calculated as follows. First, we made PSTHs from −50 to 400 ms around the stimulus onset for each of the 576 gratings used to map the RFs. Then, we selected the PSTHs of the 10 gratings that generated the strongest responses and subtracted the PSTH for each grating from the PSTH of the grating with opposite phase (Williams and Shapley 2007). Finally, we selected the subtracted PSTHs with the largest amplitude, being amplitude defined as the maximum minus the minimum value of the subtracted PSTH within 25–70 ms. Once the 10 preferred gratings were selected, we averaged their PSTHs (without orthogonal subtraction) to obtain the temporal impulse response at the preferred phase (PP). The temporal impulse responses at the three other phases were calculated by averaging the responses to the same 10 preferred gratings but with phases 0.25 (PP − 0.25 and PP − 0.75) or 0.5 cycles (PP − 0.5) apart from the preferred phase. The non preferred phase was defined as PP − 0.5. The peak response was defined as the average response to the preferred phase between 25 and 70 ms after stimulus onset. The valley response was defined as the average response to the non preferred phase between 25 and 70 ms after the stimulus onset. The phase selectivity was then calculated as one minus the ratio between the valley response and the peak response. The signal-to-noise ratio of the temporal impulse response (IRsnr) was calculated as the peak response to the gratings of preferred phase divided by the baseline. The baseline was defined as the average response between −40 and 0 ms around stimulus onset.
Cortical cells were classified as simple or complex based on the linearity of spatial summation of their responses to sinusoidal drifting gratings. Simple cells sum their inputs roughly linearly and, therefore, they respond to a sinusoidal grating with a sinusoidal modulation of their firing rate (resembling a half-rectified linear replica of the stimulus). In contrast, complex cells process their inputs nonlinearly and respond to a sinusoidal grating with an increase in mean firing with no or poor sinusoidal modulation. Therefore, when the ratio of the fundamental sinusoidal frequency of the response (F1) over the mean rate (F0) was greater than one, the cell was classified as simple, otherwise the cell was classified as complex (Movshon et al. 1978a, 1978b; Skottun et al. 1991).
Measuring Changes in Contrast Polarity with Spatial Frequency
To investigate how ON/OFF response balance changes with spatial frequency, we measured the contrast polarity of the cortical RF by spike-trigger-averaging subsets of the 576 gratings within each sequence (covering different spatial frequency ranges). For example, to calculate the RF for a spatial frequency range >0.2 cpd in the grating sequence of size-8, we spike-trigger-averaged only gratings with spatial frequency >0.2 cpd in the sequence of size-8. As a control, we also calculated cortical RFs for a subset of gratings randomly selected regardless of spatial frequency. The measurements of contrast polarity illustrated in Figure 9a–d were obtained by measuring RFs with grating subsets that had different low-spatial frequency cutoffs. For example, a low-spatial frequency cutoff of 0.2 cpd indicates that we selected all gratings within the sequence with spatial frequency >0.2 cpd. The measurements of weighted contrast polarity from Figure 9e were obtained by using a sliding window. For each grating sequence, the sliding window had a width of approximately 1/4 the spatial frequency range (0.12 cpd for size-8, 0.24 cpd for size-4, 0.49 cpd for size-2, and 0.98 cpd for size-1) and a slide step of approximately 1/3 the width of the sliding window. For example, for grating sequence of size-8, we obtained RFs calculated with spatial frequency ranges 0.047–0.167, 0.087–0.207, 0.127–0.247, and so on. The contrast polarity obtained with this sliding window was then multiplied by the number of ON-dominated and OFF-dominated cells measured for each grating size. A sigmoidal function was fit to this weighted contrast polarity data using the following function:
| (7) |
where CPw is the weighted contrast polarity, CPmax is the maximum contrast polarity, SF is the lowest value of the spatial frequency range, SF50 is the half-maximal spatial frequency, both raised to the n power, and B is the baseline.
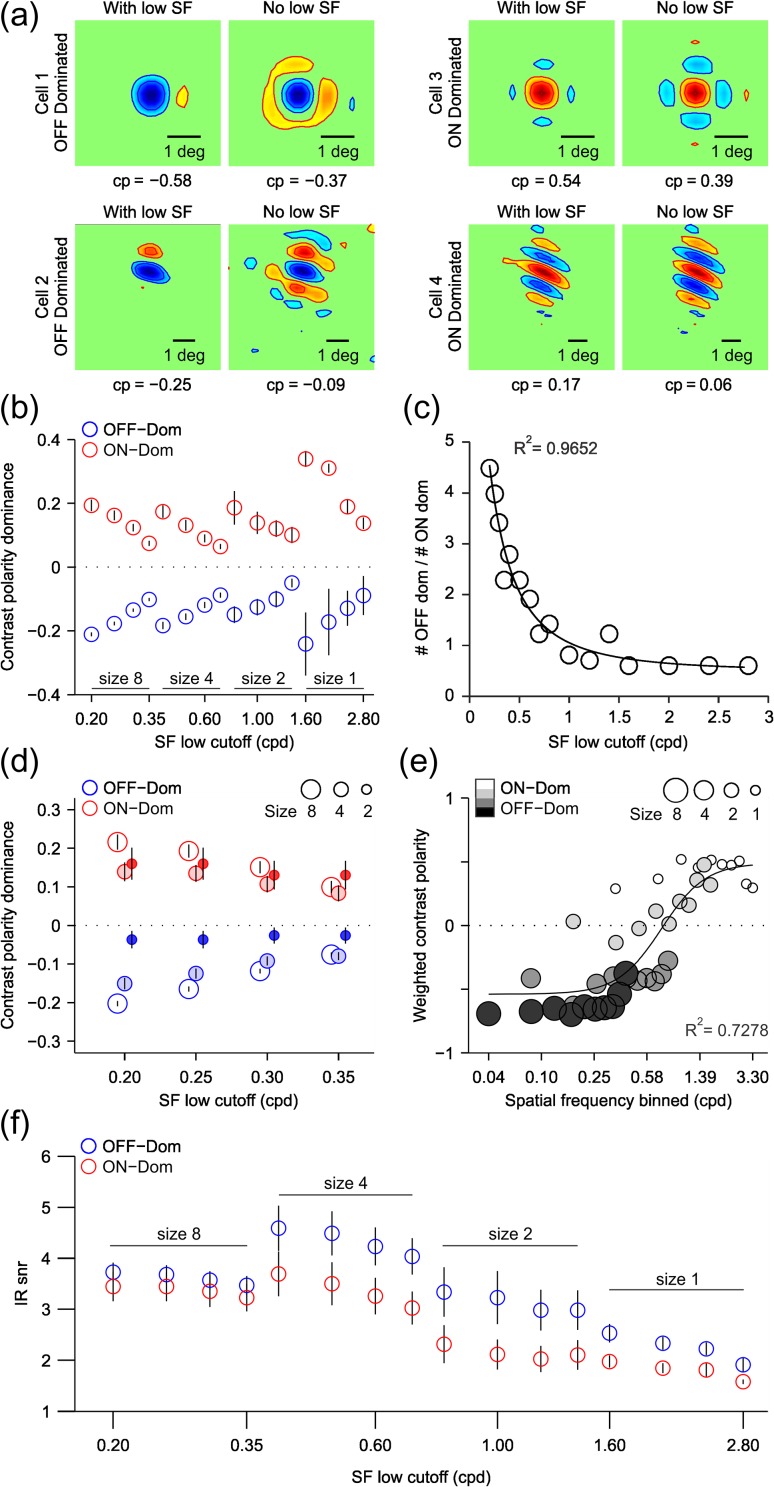
Figure 9.
ON/OFF response balance equalizes for each single neuron as spatial frequency increases and grating size decreases. (a) RFs from four example cells calculated by grating spike-trigger-averaging using the full spatial frequency range of the grating sequence (left, with low SF) or with spatial frequencies lower than 0.2 cpd removed (right, no low SF). The left panels are OFF-dominated cells and right panels are ON-dominated cells. Contrast polarity (CP) is shown below each RF. Notice that the contrast polarity decreases for all four cells when the low spatial frequencies are removed. (b) contrast polarity as a function of spatial frequency for OFF-dominated (blue) and ON-dominated (red) RFs measured with four different grating sizes (8, 4, 2, 1) and different spatial frequency ranges. The x-axis shows the value of the lowest spatial frequency within the range. Error bars show standard errors. (c) Ratio of OFF-dominated to ON-dominated RFs as a function of spatial frequency across all four grating sizes. The circles show the data values and the solid line is a Gaussian fit to the data (r2 = 0.97). (d) contrast polarity for three grating sizes (circles of different size) for four matched spatial frequency ranges. (e) Weighted contrast polarity (y-axis) measured across grating sizes with a moving spatial frequency window. X-axis gives the lower value of each spatial frequency window (see Materials and Methods for more details). The solid line is the fit of a sigmoidal function to the data (r2=0.73). (f) Signal-to-noise ratio of the temporal impulse response (IRsnr) plotted as a function of spatial frequency for OFF-dominated (blue circles) and ON-dominated (red circles) neurons across all grating sizes. Error bars are standard errors. The x-axis shows the value of the lowest spatial frequency within the range (same for b, c, and f).
Statistical Analyses
Throughout the paper, statistical significance was evaluated with two-sided Wilcoxon tests when comparing central values of a distribution, linear regression when estimating the strength of the relation between two variables and Chi-square tests when comparing observed with expected frequencies of different RF types.
Computational Model of Changes in Cortical OFF Dominance
The relation between changes in cortical OFF dominance and stimulus spatial frequency was modeled as follows. First, we used a cosine function to simulate the luminance distribution of the stimulus (S) along the x-axis of visual space (x), as shown in equation (8). The stimulus was a sinusoidal grating that could have one of 200 different spatial frequencies (sf) that ranged from 0.01 to 3 cpd. Visual space (x) was expressed in radians using 10 000 different values that ranged from –pi to pi.
| (8) |
We then simulated the response of separate ON and OFF retinothalamocortical pathways (Ton and Toff) by passing the stimulus through a luminance/response function with higher saturation for the light (Sl) than the dark half-cycles (Sd) of the grating (Kremkow, Jin, et al. 2014), as shown in equations (9) and (10). The differences in the luminance/response saturation were determined by the luminance that generated the half-maximum response (Sl50: 0.1 and Sd50: 0.5) and the exponents (n: 1.4 and m: 2).
| (9) |
| (10) |
We then normalized the responses by dividing Ton (x, sf) and Toff (x, sf) by their respective maximums, and convolved them with a cortical RF (CRF) of 1.2° diameter with a central ON subregion and two OFF flanks (ON/OFF strength: 1/0.3). This normalization equalizes the maximum response of thalamocortical neurons with different spatial frequency preferences (i.e., the average thalamic neuron with a preference for gratings of 1 cpd has the same maximum response as the average thalamic neuron with a preference for 0.5 cpd). We then passed the result of the convolution through a spiking nonlinearity (s) to generate ON (Con) and OFF cortical responses (Coff), as shown in equations (11) and (12).
| (11) |
| (12) |
Finally, we calculated the ratio between OFF and ON cortical response strength measured as the central value of the convolution for each spatial frequency, as shown in equation (13) and illustrated in Figure 13e.
| (13) |
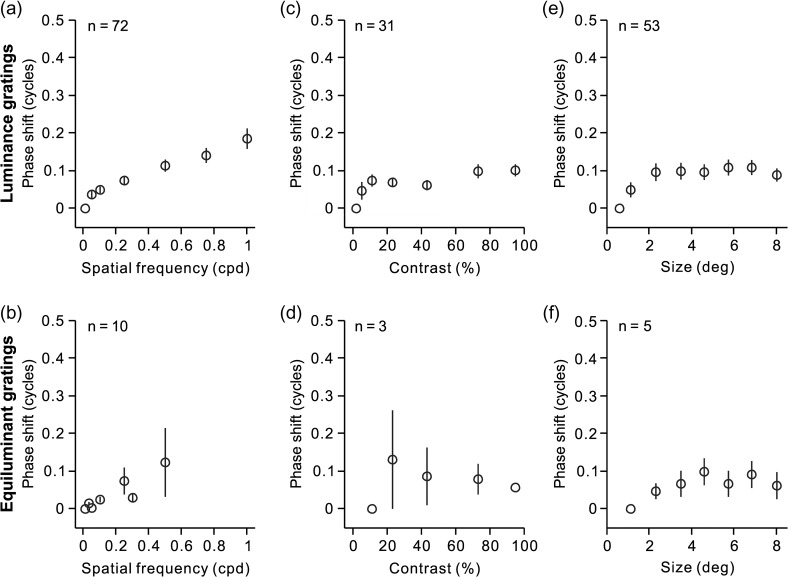
Figure 13.
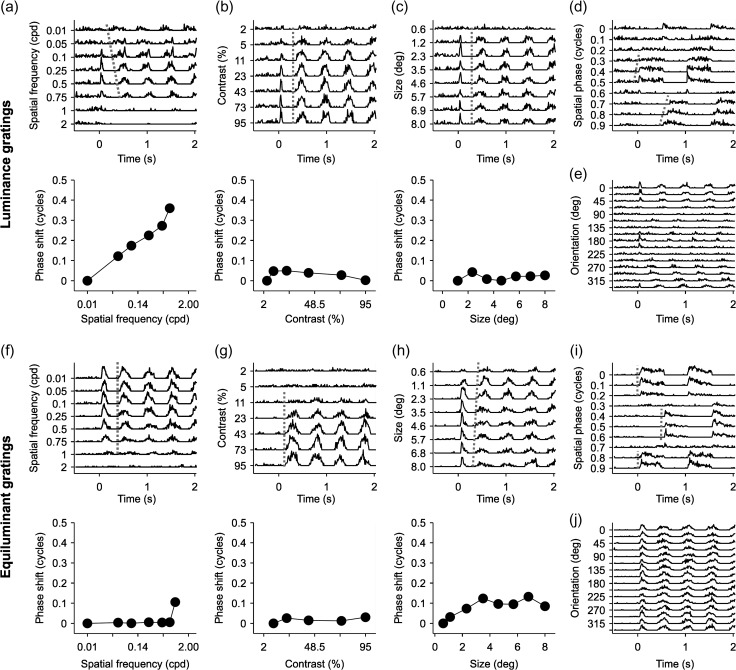
Changes in spatial frequency have a limited effect on the temporal phase of visual responses to drifting gratings. (a, c, e) Average phase shifts for spatial frequency, contrast, and phase measured with drifting luminance gratings (units are fractions of a cycle). (b)(d, f) Average phase shifts for spatial frequency, contrast, and phase measured with drifting equiluminant gratings. Notice that not all cortical simple cells could be measured with all stimulus conditions. Measurements of spatial frequency were obtained in 72 cells, luminance contrast in 31 cells and grating size in 53 cells. Measurements with equiluminant gratings were restricted to a small population of simple cells that were color responsive (10 for spatial frequency, 3 for color contrast, and 5 for grating size). Error bars show standard errors of the mean.
Results
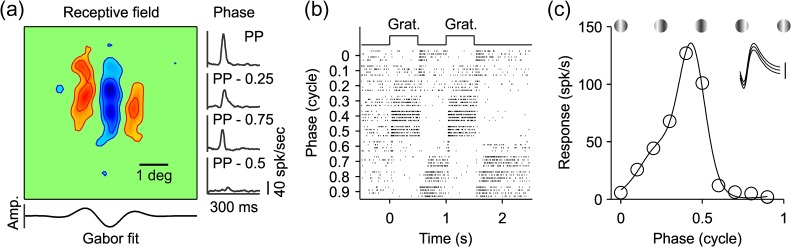
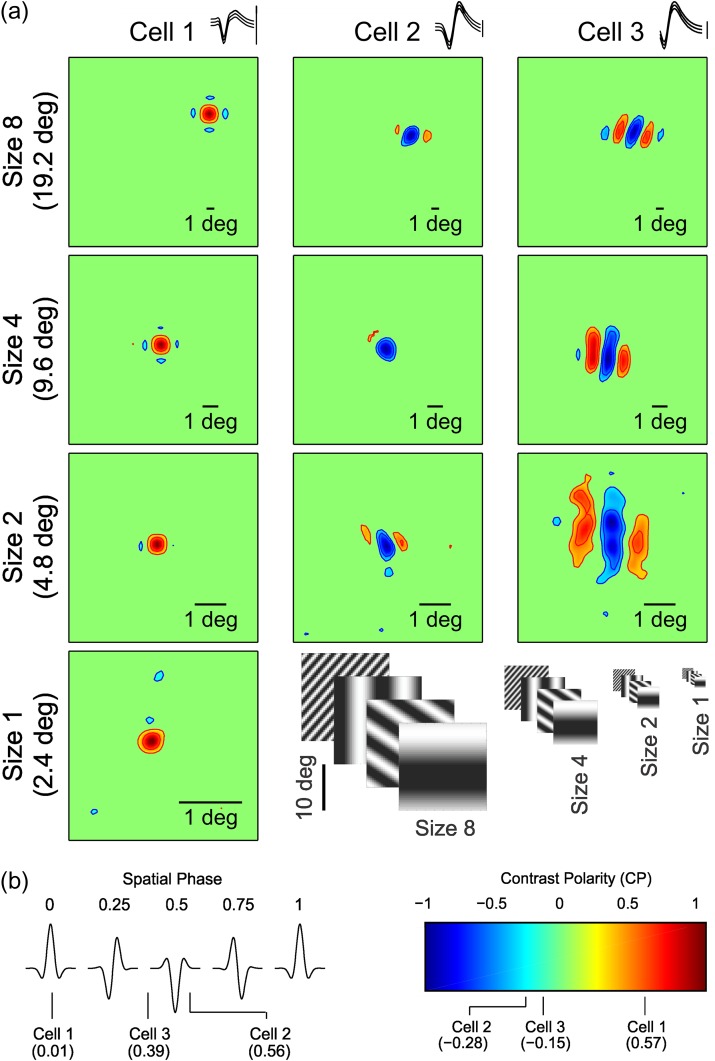
We recorded from well-isolated neurons in macaque visual cortex and used two different methods to measure their preferred spatial phase and dominant contrast polarity (OFF or ON). In the first method, we presented a fast sequence of 576 gratings and calculated the RF by grating spike-trigger-averaging (Ringach et al. 1997). We then measured the preferred spatial phase from a Gabor fit of the RF (Fig. 1a, left), and the phase tuning from the temporal impulse responses obtained with gratings of different phases (Fig. 1a, right, see Materials and Methods for more details). In the second method, we measured directly the phase tuning from the neuronal responses to flashed stationary gratings with different phases optimized for orientation, spatial frequency, and size (Fig. 1b–c).
Figure 1.
RF and phase tuning from an example cell. (a) RF mapped by spike-trigger-averaging gratings of size-2. Red areas indicate ON responses, blue areas indicate OFF responses. Intensity of color indicates response strength. This cell has an OFF-dominated RF (contrast polarity: −0.15). Scale bar is 1° of visual angle. Gabor fit to RF is shown below illustrating the preferred phase (PP), (0.39) measured at a horizontal slice through maximum of the RF (Amp: response amplitude). The right side shows average response to the 10 preferred gratings with PP and average responses with the same grating subset (same orientations and spatial frequencies) but with phases that are 0.25 (PP − 0.25, PP − 0.75) or 0.5 (PP − 0.5) cycles apart from PP. (b) Spike rasters showing the phase tuning of the cell. Each raster line shows responses to a grating optimized for orientation, spatial frequency and size that was turned on for 0.5 s (Grat.) and off for 0.5 s, over a period of 2 s. Y-axis shows grating phase (fraction of a full cycle). X-axis is time course in seconds. (c) Phase tuning measured in spikes/second from the grating responses illustrated in (b) (open circles indicate each phase tested). Solid line is the tuning curve derived from the fit of the von Mises function. The preferred phase is defined as the peak of the tuning curve (0.43 in this example). Inset shows spike waveform for this cell: center line is the average waveform, bounded on top and bottom by the standard deviation. Vertical scale bar (100 μV). Example gratings are shown above. Note that white bars are centered in the grating for phase 0 and 1, and a dark bar is centered at phase 0.5.
Stimulus spike-trigger-averaging has been used extensively in the past to map the RF of simple cells (Jones and Palmer 1987; DeAngelis et al. 1993; Reid and Alonso 1995; Alonso and Martinez 1998; Ringach 2002; Rust et al. 2005; Touryan et al. 2005; Fournier et al. 2014). However, it is thought to be a poor method to map the RFs of complex cells (Rust et al. 2005; Touryan et al. 2005; Schwartz et al. 2006). Surprisingly, our grating sequences allowed us to map the RFs of nearly all cortical cells that we recorded, simple cells, and complex cells. We used a sequence of large gratings (size-8: 22.4°/side) to map the cortical RFs very fast at different retinal eccentricities (average: 88 ± 40 seconds of stimulus presentation, 7099 ± 3113 gratings, n = 269 cells). The large gratings allowed us to accurately estimate the RF position (Fig. 2a), spatial phase and contrast polarity (Fig. 2b). After the RF position was measured with the sequence of large gratings (Fig. 2a, size-8), we mapped the RF again with a sequence of smaller gratings centered at the RF position measured with the large gratings (Fig. 2a, size-4, -2, and -1). Since the sequence of large gratings was dominated by low spatial frequencies (range: 0.047–0.53 cpd), the grating spike-trigger-averaging overestimated the RF size. Making the gratings smaller and the spatial frequency higher helped improve the estimates of RF size (Fig. 2a) but eventually made the RFs too noisy to be measured (Fig. 2a, size-1 for cells 2 and 3). Therefore, we used sequences with smaller gratings only when the measurements with the larger grating had good signal-to-noise ratios (snr ≥ 1.6 within 2 min of stimulation for a sequence of ~10 000 gratings).
Figure 2.
RFs mapped with different grating sizes. (a) RFs for three example cells (columns) mapped with grating sequences of different sizes (rows). The gratings used in the size-8 sequence are eight times larger than the gratings used in size-1 sequence (size-1: 2.8°/side). Scale bars depict 1° of visual angle (notice that the scale bars are different for each figure panel). RFs are normalized to the stronger of the OFF or ON responses within the RF (cell 3 is the same cell shown in Fig. 1). Spike waveforms are shown at the top (middle line: average, flanking lines: standard deviation). Vertical scale bar (100 μV). (b) Left panel: Gabor functions illustrating the spatial phase of idealized RFs (the preferred spatial phase is shown at the top). The spatial phase for each cell shown in (a) appears at the bottom (derived from the Gabor fits to grating size-2). Right panel: color bar indicates contrast polarity. The contrast polarity for each cell, measured with grating size-2, appears below.
Both Simple and Complex RFs can be ON or OFF Dominated
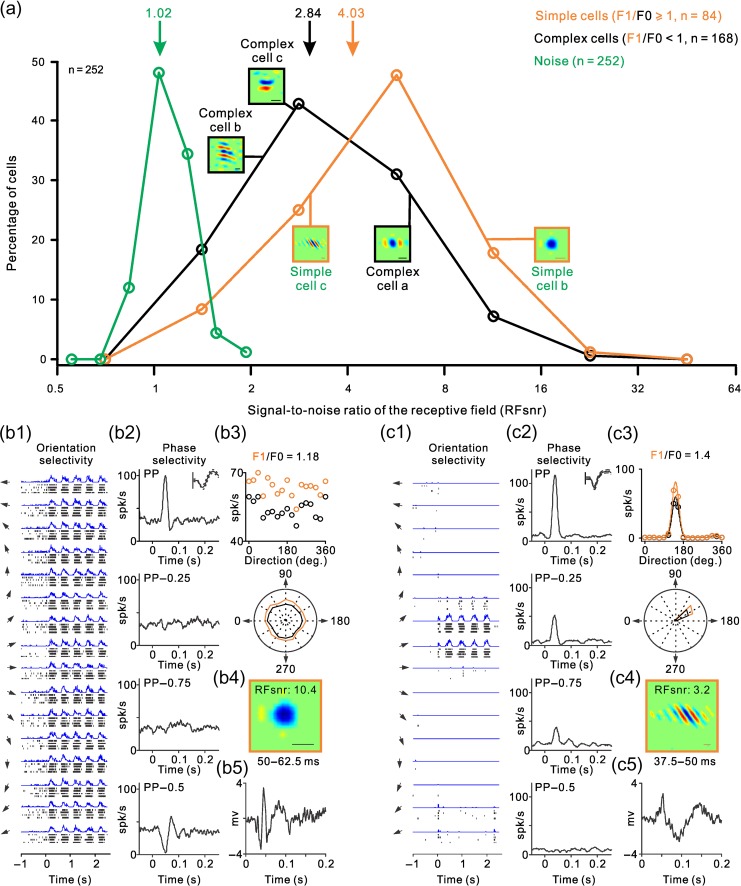
Neurons in primary visual cortex are frequently classified into simple and complex cells based on the spatial overlap of their ON and OFF RF subregions (Hubel and Wiesel 1962; Movshon et al. 1978a, 1978b). In complex cells, ON and OFF RF subregions are spatially overlapped, therefore, the ON–OFF spatial subtraction performed by methods of stimulus spike-trigger-averaging is assumed to approach zero (Rust et al. 2005; Touryan et al. 2005; Schwartz et al. 2006). This assumption is supported by multiple studies that were able to map simple RFs but not complex RFs by spike-trigger-averaging stimuli such as sparse noise, sparse bars, white noise, and gratings (Jones and Palmer 1987; DeAngelis et al. 1993; Alonso and Martinez 1998; Ringach 2002; Rust et al. 2005; Touryan et al. 2005; Fournier et al. 2014). Contrary to this assumption, we hypothesize that both simple and complex RFs should be ON or OFF dominated because the visual cortex is organized in ON and OFF domains that bias the contrast polarity of all RFs toward ON or OFF (Smith et al. 2015; Wang et al. 2015; Kremkow et al. 2016; Lee et al. 2016). To test this hypothesis, we calculated the signal-to-noise ratio of simple and complex RFs measured with grating spike-trigger-averaging. If the ON and OFF responses of complex RFs were perfectly balanced in strength and spatial distribution, the ON–OFF subtraction in the grating spike-trigger-average should approach the noise level (i.e., the signal-to-noise ratio of the RF should equal one). However, if the ON–OFF subtraction is greater than the noise because ON or OFF responses dominate in different spatial regions of the RF (i.e., ON and OFF response strengths are unequal in a given spatial region), the signal-to-noise ratio should be greater than one (e.g., 2 if the ON–OFF difference is two times larger than the noise). Simple and complex cells were classified based on their response modulation to sinusoidal drifting gratings (optimized for orientation and spatial frequency). If the sinusoidal modulation of the response at the fundamental frequency of the grating (F1) was larger than the response mean rate (F0), F1/F0 > 1, the cell was classified as simple. Otherwise (F1/F0 < 1), the cell was classified as complex (Skottun et al. 1991).
As expected from the differences in ON–OFF spatial segregation, the signal-to-noise ratio of the RFs was significantly higher in simple cells than complex cells (4.03 vs. 2.84, P < 0.0001, two-sided Wilcoxon test). However, the distributions overlapped extensively (Fig. 3a). Figure 3 illustrates two representative examples of simple cells at the two sides of this distribution. The cell illustrated in Figure 3b responded to all stimulus orientations (Fig. 3b1,b3) with exquisite phase selectivity (Fig. 3b2), had an OFF-dominated RF with high signal to noise (Fig. 3b4, RFsnr: 10.4) and was located in the middle cortical layers (Fig. 3b5). Four different measures indicate that the RF of this simple cell was strongly OFF dominated. First, the RF (Fig. 3b4) had a strong OFF-dominant subregion that generated responses 10.4 larger than the noise (RFsnr: 10.4). Second, a drifting grating strongly increased the cell firing rate when the RF center was aligned with dark half-cycle of the grating (Fig. 3b1, peaks in the PSTH) and strongly suppressed the response when it was aligned with the light half-cycle (Fig. 3b1, valleys in the PSTH). Third, stationary gratings briefly flashed within the RF drove a strong response when the RF center was aligned with the dark half-cycle of the grating (Fig. 3b2, preferred phase: PP) and strongly suppressed the response when aligned with the light half-cycle (Fig. 3b2, non preferred phase, PP − 0.5). Fourth, the ratio between the response at the fundamental frequency of the grating (F1) and the mean rate (F0) was larger than one (Fig. 3b3), as would be expected if OFF and ON responses were spatially segregated (Movshon et al. 1978a, 1978b; Skottun et al. 1991).
Figure 3.
ON–OFF RF organization of simple and complex RFs with examples of simple RFs. (a) Distribution of signal-to-noise ratios in the RFs of simple cells (orange), complex cells (black), and baseline noise (green). Notice the extensive overlap in the distribution of simple and complex RFs. Arrows at the top show distribution means and small square panels illustrate example RFs. (b) Response properties of an example simple cell. b1 shows the rasters and PSTHs of responses to gratings drifting at different directions (arrows illustrate the direction of motion, stimulus onset is marked as 0 in the x-axis). b2 shows the phase selectivity measured as the average response to the 10 preferred gratings, at the preferred phase and phases apart by 0.25 (PP − 0.25 and PP − 0.75) and 0.5 cycles (PP − 0.5). The spike waveform is shown at the top right corner of the panel (continuous line: average, dashed lines: standard deviation). Vertical scale bar (100 μV). b3 shows the response amplitude to gratings drifting at different directions measured as mean rate (F0, in black) and as the sinusoidal modulation of the PSTH at the fundamental frequency of the stimulus (F1, in orange). The response amplitudes to different grating directions are illustrated as a scatter plot (top) and polar plot (bottom). The F1/F0 ratio is shown at the top. b4 shows the RF measured with grating spike-triggered average at the temporal window shown at the bottom (50–62.5 ms). RFsnr is the signal-to-noise ratio of the RF. Line scale at the bottom right corner is 1°. b5 illustrates the local field potential measured with flashed gratings averaged across different orientations. (c) Same as b but for another example simple cell.
The simple cell illustrated in Figure 3c was in deeper cortical layers than the cell from Figure 3b (Fig. 3c5), had higher orientation and direction selectivity (Fig. 3c1,c3), poorer phase selectivity (Fig. 3c2) and lower signal to noise in the RF (RFsnr: 3.2). As in the cell from Figure 3b, a drifting grating generated a response that resembled a rectified linear replica of the sinusoidal grating (Fig. 3c1) with an even higher F1/F0 ratio than the cell from Figure 3b (Fig. 3c3, F1/F0: 1.4). However, the signal to noise of the RF was three times lower (Fig. 3c4, RFsnr: 3.2) even if the spontaneous activity was almost zero (Fig. 3c1). Also, unlike the simple cell illustrated in Figure 3b, stationary gratings generated strong responses at different spatial phases (Fig. 3c2, PP, PP − 0.25 and PP − 0.75) and did not suppress the cell firing rate at the non preferred phase (Fig. 3c2, PP − 0.5). These two cell examples demonstrate that phase selectivity can be very diverse in simple cells; it can be very high in some cells (Fig. 3b2) and poor in others (Fig. 3c2).
Similar to the simple cell from Figure 3b, the complex cell illustrated in Figure 4a responded to all stimulus orientations (Fig. 4a1,a3), showed some phase selectivity (Fig. 4a2), was OFF dominated, and the signal to noise of the RF was high (RFsnr: 5.8). Importantly, even complex cells with lower phase selectivity (Fig. 4b,c) had RFs with clear ON and OFF subregions that resembled simple RFs (Fig. 4b4,c4). These complex cells had extensive ON–OFF spatial overlap in their RFs as it is indicated by the weak sinusoidal modulation of their visual responses to drifting gratings (Fig. 4a1,b1,c1) and their low F1/F0 ratios (Fig. 4a3,b3,c3). At the same time, these complex cells had RF subregions that resembled the ON and OFF subregions of simple RFs (Fig. 4a4,b4,c4), and their phase selectivity could be as high as in some simple cells (Fig. 4a2,b2). These results indicate that whereas the ON–OFF spatial overlap is larger in complex than simple RFs (lower F1/F0 ratio), the relative strength of ON and OFF responses within each RF subregion can vary almost as much in both cell types. Therefore, these cell examples demonstrate that both simple and complex RFs can have very diverse ON–OFF spatial organization (i.e., ON and OFF subregions) and phase selectivity (see also Crowder et al. 2007).
If the F1/F0 ratio was a reliable indicator of RF ON–OFF spatial organization, it should be strongly correlated with the RF signal to noise. Both the F1/F0 and signal to noise should be highest in RFs with the largest ON–OFF spatial segregation and lowest in RF with the largest ON–OFF spatial overlap. Moreover, as ON and OFF responses become spatially overlapped within the RF, the F1/F0 should decrease and the ON–OFF subtraction in the grating spike-trigger-average should approach the noise level making the RF signal to noise close to one. Consistent with this prediction, the signal-to-noise ratio of the RFs was significantly correlated with the F1/F0 ratio. However, the correlation was very weak (Fig. 4d, r = 0.2865, P < 0.0001, n = 252). This weak correlation indicates that the spatial differences in the relative strength of ON and OFF responses throughout the RF are poorly associated with the amount of ON–OFF spatial overlap. Most cortical RFs, simple or complex, can be mapped with fast sequences of large gratings at different eccentricities with similar signal-to-noise ratios (Fig. 4d). Moreover, both simple and complex RFs can be ON or OFF dominated (Fig. 4e). Therefore, the grating spike-triggered-average is an excellent method to quantify ON and OFF dominance in simple and complex RFs but cannot reliably distinguish between the two RF types.
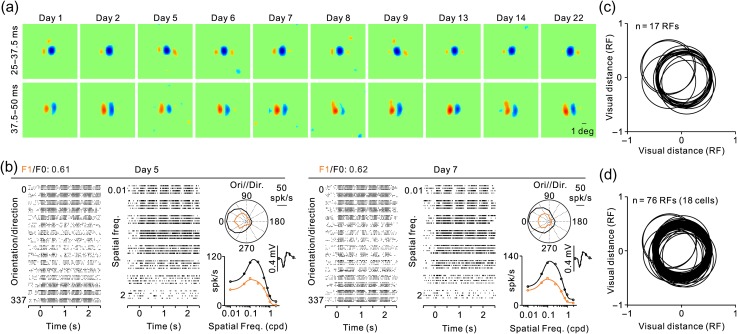
The measurements of complex RFs with sequences of large gratings were very reliable and could be accurately replicated within the same day or across days. In a complex cell recorded for nearly a month, the RFs measured in multiple days were remarkably similar (Fig. 5a) and always showed a dominant OFF subregion at short stimulus latencies (25–37.5 ms) followed by two parallel ON and OFF subregions with longer latencies (37.5–50 ms). Measurements of orientation/direction selectivity and spatial frequency tuning in 2 different days were also similar and had a consistent F1/F0 ratio of approximately 0.6 (Fig. 5b). This repeatability of RF structure and position across multiple days (Fig. 5c) indicates that the small fixation eye movements in our animals (Chen et al. 2008) cause negligible distortions in our RF estimates. It also demonstrates that the ON–OFF subregions of complex RFs are robust and do not vary with small fluctuations in firing rate that occur across days or trial blocks of visual stimulation.
Figure 5.
RF of a complex cell measured multiple times over 1 month. (a) RF measurements with grating spike-triggered-averaging shown for two different time windows, 25–37.5 ms (top row) and 37.5–50 ms (bottom row). Notice that the RF has a strong OFF subregion at short response latencies and two parallel ON and OFF subregions at longer latencies that match the preferred orientation of the cell. (b) Rasters showing the orientation and spatial frequency selectivity of the cell measured in 2 different days (left and right panels). Within each day, the figure illustrates rasters for different directions of motion (left) and different spatial frequencies (middle), a polar plot of the orientation/direction tuning (top right), and the spatial frequency tuning (bottom right). Measurements are shown in black for mean firing rate (F0) and orange for sinusoidal responses at the frequency of the drifting grating (F1). The spike waveform is shown on the top right corner of the spatial frequency tuning. (c) Central position of the strongest RF subregion from the cell illustrated in a and b measured in different days. Each circle has a diameter equal to the dominant RF subregion and its center is the RF center measured on a different day. Units of distance are given in RF subregion diameters. (d) Same as c but for multiple cells with RFs mapped in multiple days. For each cell, the RF position measured in the first day was aligned at 0.
Changes in Cortical OFF Dominance with Stimulus Conditions
Multiple studies have demonstrated that neuronal responses in primary visual cortex are dominated by the OFF visual pathway (Zemon et al. 1988, 1995; Jin et al. 2008, 2011; Yeh et al. 2009; Xing et al. 2010; Komban et al. 2014; Veit et al. 2014; Tan et al. 2015; Wang et al. 2015; Kremkow et al. 2016; Lee et al. 2016; Rekauzke et al. 2016; Taylor et al. 2018). Moreover, more recent studies demonstrated that this cortical OFF dominance changes with the spatial frequency of the stimulus when measured with voltage-sensitive dye imaging and multiunit recordings in anesthetized cats (Onat et al. 2011; Kremkow, Jin, et al. 2014).
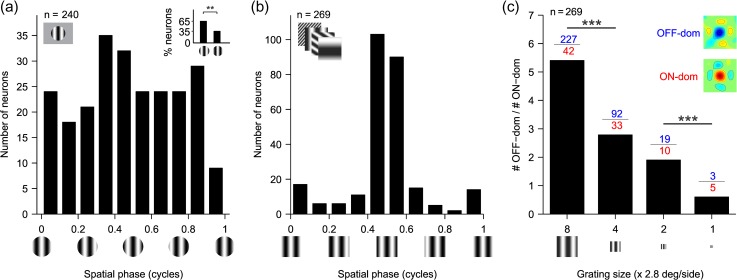
Consistent with these studies, our cortical cell population in the awake primate was slightly biased toward OFF-centric phases when measured with optimized gratings (Fig. 6a, inset, 0.5 ± 0.125: 65%; 0 ± 0.125: 35%,P = 0.0012, Chi-square test), and the OFF bias became very pronounced when using sequences of large gratings with low spatial frequencies (Fig. 6b). The ratio of OFF- to ON-dominated neurons was greater than 5 when we used sequences of large gratings with low spatial frequency and it was reduced to less than one when we used sequences of small gratings with high spatial frequency (Fig. 6c, R2=0.991, P < 0.001). The strong dependency of cortical OFF dominance on grating size and spatial frequency included both simple cells (average OFF/ON ratio for size-8 and -4: 6.8 and 3.8, n = 62 and 38, P = 0.045, Chi-square test) and complex cells (average OFF/ON ratio for size-8 and -4: 5.4 and 2.2, n = 167 and 73, P < 0.001, Chi-square test).
Figure 6.
The number of OFF-dominated RFs decreases as the grating size decreases and the spatial frequency increases, as if the viewing distance to the grating had increased. (a) Histogram of preferred spatial phase measured with optimized gratings. Inset: histogram of percentage of OFF- (left bar) and ON- (right bar) dominated RFs (65% vs. 35%, n = 110, P = 0.0012, Chi-square test). In this inset, OFF-dominated RFs have a preferred phase of 0.5 ± 0.125 and ON-dominated RFs have a preferred phase of 0 ± 0.125. Grating phase is illustrated below the x axis. (b) Histogram of preferred phases calculated from Gabor fits of RFs measured with gratings of size-8. Grating phase is illustrated below the x axis. (c) Ratio of number of OFF-dominated RFs (blue) to the number of ON-dominated RFs (red) measured with size-8, size-4, size-2, and size-1 grating sequences. The four sequences have identical gratings but scaled for size and spatial frequency to simulate an increase in viewing distance (decrease in size and increase in spatial frequency) by two times (size-4), four times (size-2), or eight times (size-1) relative to the gratings of size-8. The inset shows example RFs for OFF- and ON-dominated cells. ***P < 0.001 with Chi-square tests.
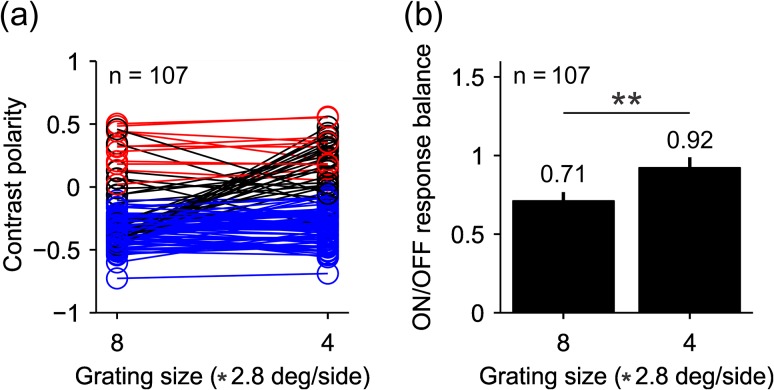
To further investigate how spatial frequency affects the ON/OFF response balance, we selected a population of 107 neurons whose RFs were mapped with the two largest grating sizes (size-8 and -4). In this sample, approximately a quarter of the neurons switched polarity from OFF to ON dominance when the grating size was reduced (25/107, Fig. 7a black lines, 12 simple cells and 13 complex cells). The larger grating size significantly increased the ratio of OFF-to-ON-dominated neurons (91/16 vs. 76/31, P < 0.001, Chi-square test) and the response OFF dominance (Fig. 7b, ON/OFF response balance: 0.71 vs. 0.92, P = 0.0012, Wilcoxon test). Taken together with previous measurements in cats (Onat et al. 2011; Kremkow, Jin, et al. 2014), these results demonstrate that spatial frequency modulates cortical OFF dominance in the awake brain of primates and the anesthetized brain of carnivores. Importantly, the results show that the visual cortex equalizes ON/OFF response balance when gratings become smaller and higher in spatial frequency, as when increasing the viewing distance of the grating.
Figure 7.
Some cells switch contrast polarity when the size of the grating is reduced. (a) contrast polarity for a subset of cells that could be mapped with the two largest gratings sizes, 8 and 4 (2.8 * 8 or 4 °/side). Cells that do not switch contrast polarity are represented by red circles and lines when they are ON dominated (n = 11) and blue circles and lines when they are OFF dominated (n = 71). Black circles and lines represent cells that switched polarity (n = 25). Notice that the number of RFs measured with both grating sizes (n = 107) is smaller than the number of RFs measured just with grating size-4 (n = 125) because some RFs were mapped with size-4 but not size-8. (b) The average ratio of ON–OFF responses across the 107 cells was closer to one for gratings with size-4 than size-8 (P = 0.0012, Wilcoxon test).
Neuronal Mechanisms Underlying Changes in Cortical OFF Dominance
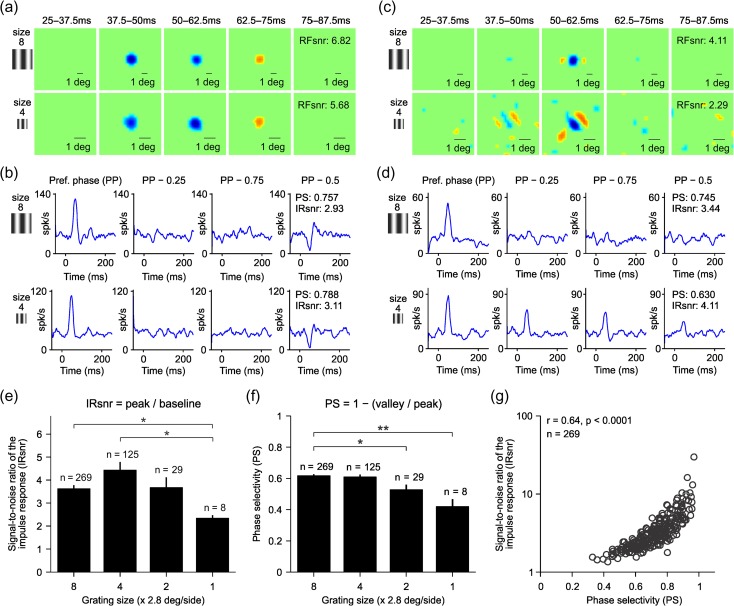
What could be the neuronal mechanisms underlying the changes in the ON/OFF dominance of single neurons? One possibility is that the ON/OFF dominance changes because neuronal responses become weaker. For example, if the spatial frequency becomes too high to evoke a response, random spontaneous activity should make the ON/OFF dominance ratio approach a value of one. This extreme scenario is not possible because all RFs selected for analysis had high signal to noise and clear ON–OFF subregions (see Fig. 3a and Materials and Methods). However, to investigate a possible relation between response strength and ON/OFF response balance, we measured changes in signal to noise and phase selectivity as a function of spatial frequency. To measure the signal to noise and phase selectivity, we selected the 10 gratings of the sequence that generated the largest response. Then, we calculated the average impulse response for these 10 preferred gratings (Williams and Shapley 2007) and for the same grating set (same orientation and spatial frequency) but for phases that were 0.25 (PP − 0.25 and PP − 0.75) and 0.5 cycles different from the preferred one (Fig. 8a,b). We calculated the signal-to-noise ratio from the temporal impulse response to the preferred grating phases and the phase selectivity from the ratio between the temporal impulse responses to non preferred and preferred phases (see Materials and Methods). In some cells (Fig. 8a,b), reducing the grating size reduced slightly the signal to noise of the RF (Fig. 8a, RFsnr: 6.82 vs. 5.68) but did not reduce the signal to noise of the temporal impulse response (Fig. 8b, IRsnr: 2.93 vs. 3.11) or the phase selectivity (Fig. 8b, PS: 0.76 vs. 0.79). In other cells, making the grating size smaller made the RF considerably noisier (Fig. 8c, RFsnr: 4.11 vs. 2.29) and lowered the phase selectivity (Fig. 8d, PS: 0.75 vs. 0.63) but did not reduce the signal to noise of the temporal impulse response (Fig. 8d, IRsnr: 3.44 vs. 4.11).
Figure 8.
Spatial frequency-dependent changes in OFF dominance are not due to changes in the signal to noise of the visual response. (a) Example of an OFF-dominated RF from a simple cell shown at different time lags between stimulus and response, measured with two different grating sizes (top: size-8, bottom: size-4). The interval of each time lag is shown above each RF panel. (b) Temporal impulse response calculated from the average response to the 10 preferred gratings (PP) and with the same grating set (same orientations and spatial frequencies) but with spatial phases apart from the preferred by a quarter cycle (PP – 0.25 and PP – 0.75) and half-cycle (PP – 0.5). The spatial frequencies and orientations of the 10 selected gratings are the same across all four panels (only spatial phase changes). RFsnr: signal-to-noise ratio of the RF. IRsnr: signal-to-noise ratio of the impulse response. (c–d) Same as a–b but for an OFF-dominated complex cell. (e) Average signal-to-noise ratio of the impulse response measured with different grating sizes. (f) Average phase selectivity measured with different grating sizes. (g) Strong correlation between phase selectivity and the signal-to-noise ratio of the impulse response. *P < 0.05; **P < 0.01, Wilcoxon test.
On average, the signal to noise of the temporal impulse response (Fig. 8e) and phase selectivity (Fig. 8f) were lowest for the smallest gratings but independent of ON/OFF response balance. For example, reducing the grating size from eight to four reduced by half the ratio of OFF/ON dominated neurons (Fig. 6c) but increased the average signal to noise (Fig. 8e) and did not affect the average phase selectivity (Fig. 8f). Across all cells, the signal to noise of the response was positively correlated with phase selectivity (Fig. 8g, r = 0.64, P < 0.001, n = 269) but not with the signal to noise of the RF (r = −0.08, P = 0.17, n = 269). Therefore, we conclude that changes in cortical OFF dominance cannot be explained by a reduction in response strength.
The changes in cortical OFF dominance that we report could originate from an increase in spatial frequency, a reduction in grating size or a combination of both. To investigate the contribution from each stimulus parameter, we measured spatial frequency changes in ON/OFF response balance for a fixed grating size. Figure 9a illustrates the effect of removing spatial frequencies lower than 0.2 cpd from the grating spike-trigger-average for four example cells. Two cells were OFF dominated (cells 1 and 2) and two cells were ON dominated (cells 3 and 4). Two cells were strongly dominated by one contrast polarity (cell 1: OFF dominated, cell 3: ON dominated) and two cells were more ON/OFF balanced (cells 2 and 4). In all example cells, the removal of low spatial frequencies made ON and OFF responses more similar in strength (i.e., contrast polarity closer to zero) regardless of their ON or OFF dominance (Fig. 9a). The shift toward greater ON/OFF balance could be demonstrated in both OFF-dominated (Fig. 9a, shift from −0.58 to −0.37 for cell 1 and −0.25 to −0.09 for cell 2) and ON-dominated neurons (Fig. 9a, shift from 0.54 to 0.39 for cell 3 and 0.17 to 0.06 for cell 4), and it could be replicated for all grating sizes (Fig. 9b). Importantly, the equalization of ON/OFF response balance associated with the removal of low spatial frequencies involved most of the neurons that we studied. For example, removing spatial frequencies lower than 0.2 cpd increased ON/OFF response balance in 79% of the cells studied with the size-8 grating sequence (n = 269).
The ratio of OFF- to ON-dominated neurons was strongly correlated with the lowest spatial frequency (low-spatial frequency cutoff) of the grating sequence and could be accurately described with a Gaussian function (Fig. 9c, R2 = 0.9652, half-width: 0.69 cpd). On average, the removal of low spatial frequencies increased the ON/OFF balance by 28% in OFF-dominated neurons (−0.32 vs. −0.23, P < 0.0001, Wilcoxon test) and by 23% in ON-dominated neurons (0.31 vs. 0.24, P < 0.0001, Wilcoxon test). This increase in ON/OFF balance was four times larger than what would be expected from the reduction in the number of gratings included in the average (OFF-dominated: 28% vs. 6%, ON-dominated: 23% vs. 7%, P < 0.0001, Wilcoxon tests). These results strongly indicate that increasing the spatial frequency of the stimulus makes cortical neurons more ON/OFF balanced in their visual responses regardless of their dominant contrast polarity, ON or OFF.
ON and OFF responses also became more similar in strength when the grating size was reduced even if the spatial frequency was kept constant (Fig. 9d). However, unlike for spatial frequency, changes in grating size affected differently ON- and OFF-dominated neurons. Reducing grating size by four times (from size-8 to size-2) increased ON/OFF balance by 5.49 times in OFF-dominated neurons (−0.203 to −0.037 for 0.2 cpd low-spatial frequency cutoff, P < 0.00001, Wilcoxon test) but only by 1.35 times in ON-dominated neurons (0.216–0.160 for 0.2 cpd low-spatial frequency cutoff, P = 0.198, Wilcoxon test). This difference was even more pronounced if the average contrast polarity was weighted by the number of ON-dominated and OFF-dominated neurons measured with different spatial frequency ranges and grating sizes (Fig. 9e). Again, making the gratings smaller and the spatial frequency higher reduced the strong OFF dominance driven by the large and low-spatial frequency gratings. This relation between the weighted contrast polarity and spatial frequency was well described by a sigmoidal function (R2 = 0.73, zero-crossing: 0.77 cpd) that crossed zero around the average peak spatial frequency of our cell population (0.97 ± 1.11 cpd). It is important to emphasize that while cortical responses were more OFF dominated at low spatial frequencies, the spatial resolution was higher for OFF-dominated than ON-dominated neurons (average spatial frequency peak: 1.05 ± 1.14 cpd vs. 0.69 ± 0.96 cpd, n = 185 vs. 54, P = 0.046, Wilcoxon test; average eccentricity: 10.3° ± 3.3° ranging from 3.8° to 20.4°). Also, consistent with our previous analyses (Fig. 8e), the reduction in signal to noise with spatial frequency and/or grating size did not explain the changes in contrast polarity. For example, a change in grating size from eight to four caused a pronounced reduction in the ratio of OFF-/ON-dominated neurons (Fig. 6c) but an increase in the average signal to noise of the response (Fig. 9f). These results indicate that the ON/OFF dominance of the RF changes with both the spatial frequency and size of the stimulus. Increasing the spatial frequency makes ON and OFF responses equal in strength in both ON- and OFF-dominated neurons while reducing the grating size equalizes ON/OFF balance more in OFF-dominated than ON-dominated neurons.
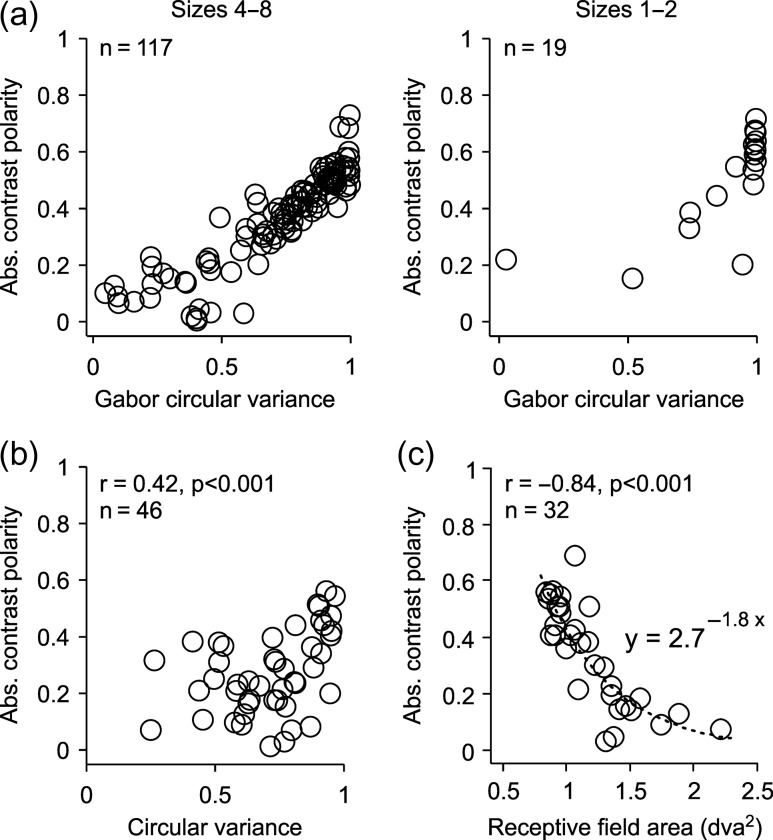
As the grating size was reduced and the spatial frequency increased, the pool of cortical RFs that were ON or OFF dominated was also reduced, a finding that is consistent with our previous results in anesthetized cats (Kremkow, Jin, et al. 2014). The RFs mapped with the large low-spatial frequency gratings had diverse ON/OFF dominances ranging from 0 (perfect ON/OFF response balance) to 0.8 (strong ON or OFF dominance). In contrast, the RFs mapped with small high-spatial frequency gratings were restricted to those with the strongest ON or OFF dominance (Fig. 10a), poorest orientation selectivity (Fig. 10a,b), and smallest RFs within our cell sample (Fig. 10c). Therefore, at the limits of spatial resolution within our cell population, ON- and OFF-dominated neurons driven by small high-spatial frequency gratings were restricted to those that could reliably distinguish black from white (strong ON or OFF dominance) but could not discriminate different orientations (poor orientation selectivity).
Figure 10.
Reducing stimulus size restricts the pool of ON- and OFF-dominated cortical RFs to those with greater ON or OFF dominance, less orientation selectivity, and smallest RFs. (a) Absolute contrast polarity plotted as a function of Gabor circular variance for the two largest (left, eight and four) and two smallest grating sizes (right, two and one). The Gabor circular variance is the circular variance calculated from a Gabor fit to the RF. Only the most accurate Gabor fits were selected (r2 ≥ 0.75, same for (a) and (c)). (b) Absolute contrast polarity plotted as a function of circular variance measured with drifting gratings. Circular variance was extracted from a von Mises fit to the orientation tuning and only the most accurate fits were selected (r2 ≥ 0.6). (c) Absolute contrast polarity plotted as a function of RF area extracted from a Gabor fit.
Changes in ON/OFF Response Balance Affect the Structure of Complex RFs
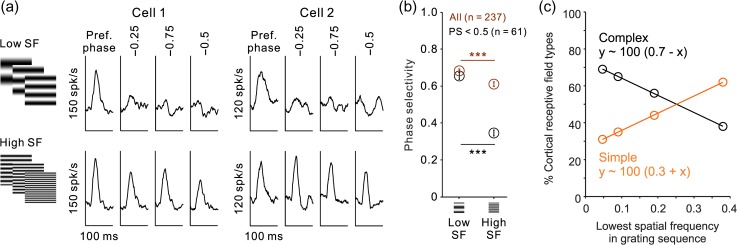
The results above indicate that high spatial frequencies equalize the ON/OFF response balance of most cortical neurons. Therefore, because ON and OFF responses are spatially overlapped in complex RFs, an increase in ON–OFF response balance should make complex RFs to lose their ON–OFF subregion organization and phase selectivity. To test this hypothesis, we measured the phase selectivity of cortical RFs using grating spatial frequencies that were either lower (Fig. 11a, low sf) or higher (Fig. 11a, high sf) than the preferred spatial frequency of the cell. We first calculated the temporal impulse responses for the 10 gratings that generated the strongest response, selected from a subset of gratings with either lower or higher spatial frequency than the preferred spatial frequency. Then, we calculated the temporal impulse response for the same grating subset but with phases separated by 0.25 (PP − 0.25 and PP − 0.75) or 0.5 phase cycles (PP − 0.5) from the preferred phase (Pref. phase). As we predicted, many complex cells that were phase selective when stimulated with low-spatial frequency gratings (Fig. 11a, top) lost their phase selectivity when stimulated with high-spatial frequency gratings (Fig. 11a, bottom). Moreover, increasing the grating spatial frequency reduced the average phase selectivity by 12% in the entire cell population (Fig. 11b, from 0.68 to 0.61, P < 0.0001, Wilcoxon test) and by 89% in complex cells showing low phase selectivity to gratings of high spatial frequency (Fig. 11b, from 0.66 to 0.35 for PS < 0.5, P < 0.0001, Wilcoxon test). Also as we predicted, decreasing the phase selectivity, equalized the ON/OFF response balance and decreased the percentage of complex RFs that could be mapped with grating spike-trigger-average due to a loss of ON–OFF subregion organization (Fig. 11c). Remarkably, the percentage of complex RFs that could be mapped with grating spike-trigger-averaging decreased linearly as a function of the lowest spatial frequency in the grating sequence, which was 0.05 for gratings of size-8, 0.1 for gratings of size-4, 0.2 for gratings of size-2, and 0.4 for gratings of size-1 (Fig. 11c). These results are consistent with previous studies that demonstrated a change in the linearity of receptive field spatial summation with spatial frequency (Movshon et al. 1978a, 1978b; Skottun et al. 1991), luminance contrast (Crowder et al. 2007), and the amount of intracortical inhibition (Pernberg et al. 1998). Taken together with these studies, our results suggest that both simple and complex RFs can signal the contrast polarity of low-spatial frequency gratings.
Figure 11.
Increasing the grating spatial frequency reduces the phase selectivity of cortical responses and the percentage of complex RFs that can be mapped by grating spike-trigger-averaging. (a) Temporal impulse responses from two example neurons (cells 1 and 2) measured with gratings presented at the preferred phase (Pref. phase) and at phases separated from the preferred one by 0.25 (−0.25 and −0.75) or 0.5 phase cycles (−0.5). The temporal impulse responses were calculated as the average response to the 10 preferred gratings from the size-8 sequence, selected from a grating set that had either lower (top) or higher (bottom) spatial frequency than the preferred spatial frequency of the cell. Notice that the phase selectivity is lower for high spatial frequencies (bottom, responses similar across all phases) than for low spatial frequencies (top, responses stronger to the preferred phase than other phases). (b) Phase selectivity for all cells (all, dark red) and for those with low phase selectivity at high spatial frequencies (PS < 0.5, black). (c) Percentage of RFs, complex (black) and simple (orange), mapped with the four grating sequences, size-8, size-4, size-2, and size-1, plotted as a function of the lowest spatial frequency within the sequence (0.05, 0.1, 0.2, and 0.4, respectively). Notice that the percentage of complex RFs mapped with grating sequences decreases linearly with the increase in the lowest spatial frequency of the sequence.
Changes in OFF Dominance Do Not Affect the Temporal Phase of the Visual Cortical Response
The RFs from ON and OFF thalamic inputs to a cortical simple cell are partially overlapped in visual space (Reid and Alonso 1995; Alonso et al. 2001; Sedigh-Sarvestani et al. 2017). Therefore, changes in the relative strength of ON and OFF responses could potentially change the central position of the RF and the temporal phase of the response. To quantify these potential distortions in response timing, we measured the temporal phase of visual responses to drifting gratings presented at different spatial frequencies (while adjusting the temporal frequency to keep the temporal phase equal). In this analysis, a change from complete ON dominance to complete OFF dominance should be associated with a temporal shift of 0.5 cycles if the ON and OFF subregions are 50% overlapped. Figure 12a–e illustrates the simple cell that showed the most pronounced temporal shift in our sample (0.4 cycles). In this cell, changes in spatial frequency caused temporal shifts that were four times larger (Fig. 12a) than the shifts caused by changes in grating contrast (Fig. 12b) or size (Fig. 12c) but similar to the shifts caused by changes in spatial phase (Fig. 12d). However, because this cell was direction selective (Fig. 12e), the temporal shift associated with changes in spatial frequency could be due to the cell direction selectivity (Adelson and Bergen 1985; Reid et al. 1987; McLean and Palmer 1989; DeAngelis et al. 1993; Lien and Scanziani 2018) and not the ON–OFF dominance. Consistent with this interpretation, large temporal shifts were rare in the rest of the simple cells that we studied including those that responded strongly to equiluminant drifting gratings (Fig. 12f–j). On average, changes in spatial frequency were associated with relatively small temporal shifts in the visual response (Fig. 13a–b) that were just slightly larger than the average temporal shifts caused by changes in grating contrast (Fig. 13c–d) and grating size (Fig. 13e–f). Therefore, we conclude that changes in spatial frequency cause negligible changes in the temporal phase of visual cortical responses.
Figure 12.
Example cells illustrating changes in the temporal phase of visual responses to drifting gratings with different spatial frequencies. (a–e) Visual responses measured with black/white gratings in an example cell. PSTHs for (a) spatial frequency, (b) contrast, and (c) size tuning appear above, and measurements of phase shifts appear below. The parameters for each response property appear on the y-axis for each PSTH series. Phase shifts are shown as a fraction of a cycle. Phase shifts were calculated from the F1 harmonic for all responses where F1 > F0. (d) PSTHs showing the tuning for spatial phase for the same cell, which was measured with static gratings that were turned on and off at 1 Hz. The gratings were presented at 10 different spatial phases (0–0.9), starting at a time zero. (e) PSTHs showing the orientation tuning for the same cell, which was measured with gratings drifting at 2 Hz. (f–j) Same as (a–e) for a second cell using RG equiluminant gratings.
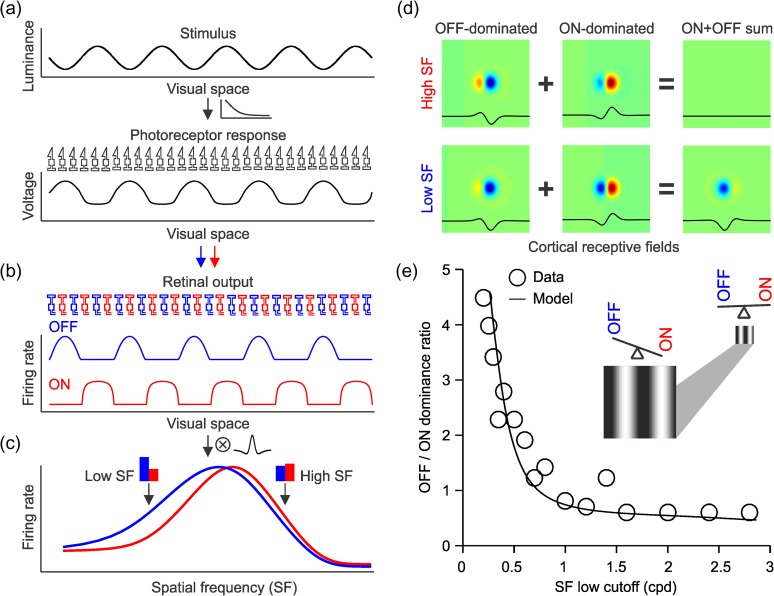
ON Luminance/Response Saturation Explains Changes in Cortical OFF Dominance
A simple model that uses an early saturating nonlinearity at the photoreceptor can accurately simulate the changes in ON/OFF dominance with spatial frequency that we describe (Fig. 14a). The saturating retinal nonlinearity enlarges the spatial retinal representation of the light half of the grating more than the dark half (Fig. 14a–b). In turn, the enlarged light stimuli make the spatial convolution of the retinogeniculate output and the cortical RF more OFF dominated at low spatial frequencies (Fig. 14c). This simple model makes cortical neurons more OFF-dominated when stimulated with gratings of low spatial frequency (Fig. 14d) and accurately replicates the changes in cortical ON/OFF dominance that we describe (Fig. 14e, see Materials and Methods for a more detailed description of the model). Because dominant subregions are generally wider than flank subregions (and respond to wider grating bars), flank/dominant responses should become more balanced at the highest spatial frequencies, as shown in our results. However, differences in luminance/response saturation between ON and OFF pathways (Fig. 14b) are enough to replicate our results (Fig. 14e) even if differences in spatial resolution between dominant and flank subregions (and differences in grating size) are not considered. It should be noted that our model does not explain changes in ON/OFF response balance that are dependent only on grating size. Size suppression may independently increase ON/OFF response balance and sharpen orientation selectivity (Chen et al. 2005; Xing et al. 2005).
Figure 14.
ON luminance/response saturation explains changes in cortical OFF dominance with spatial frequency. (a) The grating stimulus was simulated with a cosine function (top) and we assumed a photoreceptor nonlinearity that distorted the representation of the grating at the level of the response of the photoreceptor array (bottom). (b) The responses of separate ON and OFF pathways were simulated by rectifying the photoreceptor response and passing the output of the rectification through a higher luminance response saturation for ON than OFF responses as in the study of Kremkow, Jin, et al. (2014). (c) When the responses from these ON and OFF pathways are convolved with a cortical RF, OFF responses dominate at low spatial frequencies (low SF) as in the study of Kremkow, Jin, et al. (2014). (d) When a complex RF is made by adding OFF dominated and ON-dominated simple cells with opposite phases, the ON–OFF sum is zero (top). At low spatial frequencies, however, OFF responses become stronger and the complex cell becomes OFF dominated (bottom). (e) This simple model accurately replicates the relation between spatial frequency low cutoff and the ratio of OFF-to-ON-dominated neurons that we demonstrated experimentally. The circles illustrated the data and the line the model. The cartoon illustrates how ON–OFF balance changes when viewing distance increases, which makes the grating smaller and the spatial frequency higher.
Discussion
As a visual target moves farther away from view, the size of its image projected on the retina decreases and its spatial frequency increases. As shown here, these stimulus changes are associated with a pronounced modulation of ON/OFF response balance in visual cortex. Large grating sizes with low spatial frequencies drove five times more neurons with OFF-dominated than ON-dominated RFs; however, the ratio of OFF-/ON-dominated RFs approached a value of one when the stimulus size was reduced and the spatial frequency increased. We show that this pronounced modulation in ON/OFF dominance resulted from changes in the relative strength of ON and OFF responses within each neuron and not from a response reduction restricted to OFF-dominated neurons. We also show that, as the stimuli became smaller, the ON and OFF dominance became restricted to cells with the smallest RFs, strongest ON/OFF dominance, and poorest orientation selectivity, a set of properties that are ideal to signal the light/dark polarity of small stimuli regardless of their orientation. In summary, our results indicate that changes in the spatial frequency of a stimulus due to changes in viewing distance and/or optical blur (Held et al. 2012) modulate the balance of ON and OFF cortical responses encoding the stimulus.
Dark/Light Asymmetries are Modulated by the Stimulus Spatial Frequency and Size
Gratings with low spatial frequencies have been previously shown to drive stronger OFF than ON cortical responses in anesthetized cats (Onat et al. 2011; Kremkow, Jin, et al. 2014) and a similar relationship was demonstrated in natural images with dark pixels being more common at low spatial frequencies (Cooper and Norcia 2015). Our results provide further support for this relationship by showing that low spatial frequencies drive five times more neurons with OFF-dominated than ON-dominated RFs in area V1 of awake primates.
The finding that cortical OFF dominance is most pronounced at low spatial frequencies may appear paradoxical given that the ON pathway has lower spatial resolution than the OFF pathway in both retina (Wassle et al. 1981; Chichilnisky and Kalmar 2002) and visual cortex [cat: (Kremkow, Jin, et al. 2014); primate: this paper]. This paradox can be explained by an early saturating nonlinearity in the luminance/response function of the retina that strengthens ON responses to high spatial frequencies and small stimuli but also makes ON RFs larger [(Kremkow, Jin, et al. 2014), see also (Westheimer 2008)]. The luminance/response saturation strengthens ON cortical responses to small stimuli because it increases the size of the activated retinal population, effectively enlarging the stimuli in the retinal representation (e.g., widening the light half-cycle of a grating or enlarging small light spots in dark background). We call this stimulus enlargement neuronal blur because it resembles the effect of optical blur but is mediated by neurons instead of optics and affects differently lights and darks (Kremkow, Alonso, et al. 2014; Kremkow, Jin, et al. 2014; Pons et al. 2017; Mazade et al. 2018). The neuronal blur also enlarges the ON RFs. Therefore, it should make visual acuity lower for the ON than the OFF visual pathways and cortical retinotopic mapping more precise for dark than light stimuli, a prediction that has been experimentally demonstrated in cats, tree shrews, and mice (Kremkow et al. 2016; Lee et al. 2016; Jimenez et al. 2018). At the same time, the greater contrast/response gain associated with the ON luminance/response saturation should help to detect small light reflections with low contrast, which are common in natural scenes (Cooper and Norcia 2015). The ON luminance/response saturation can also help to normalize the cortical responses to the brightest specular highlights that frequently create overexposed areas in photography and can be also important to estimate image mean luminance. Consistent with this prediction, the psychometric curve for luminance judgments in humans shows a saturation at maximum luminance that resembles the ON luminance/response function (Nam and Chubb 2000).
Our results demonstrate that, as spatial frequency increases and the stimulus size is reduced, ON and OFF responses become more similar in strength. Importantly, this ON/OFF equalization is not achieved by reducing the responses from OFF-dominated neurons, which would compromise visual acuity (i.e., the OFF pathway has the best spatial resolution). Instead, the ON/OFF equalization is obtained by reducing the ON/OFF dominance in both OFF-dominated and ON-dominated neurons, a change that should help to detect edges more effectively by flanking them with equally strong ON and OFF subregions (Canny 1986). We also show that, at the spatial resolution limit, the smallest stimuli can recruit only the ON- and OFF-dominated RFs that are smallest, show the strongest ON/OFF dominance and poorest orientation tuning, a set of properties that may be needed for measurements of surface appearance in natural scenes (Motoyoshi et al. 2007).
Dark/Light Asymmetries in Visual Perception
It would be surprising if the pronounced cortical OFF dominance of carnivores and primates (Jin et al. 2008; Yeh et al. 2009; Xing et al. 2010; Onat et al. 2011; Samonds et al. 2012; Kremkow, Jin, et al. 2014; Liu and Yao 2014; Veit et al. 2014; Wang et al. 2015; Rekauzke et al. 2016) did not have a perceptual correlate. Although asymmetries in the perception of darks and lights have been quantified over the past decades, the first report of these asymmetries can be traced back to the work of Leonardo Da Vinci (MacCurdy 1938) and Galileo Galilei (Galilei 1632). Early psychophysical studies reported higher contrast sensitivity for detecting darks than lights in humans (Blackwell 1946; Short 1966; Bowen et al. 1989; Tyler et al. 1992; Kontsevich and Tyler 1999). However, physiological experiments demonstrated higher contrast sensitivity for ON than OFF pathways (Chichilnisky and Kalmar 2002; Zaghloul et al. 2003; Kremkow, Jin, et al. 2014). This paradox between psychophysics and physiology may be explained by differences in mean luminance, stimulus duration, and background across experiments, which affect both human contrast sensitivity (Komban et al. 2011; Luo-Li et al. 2016) and the strength of neuronal responses (Komban et al. 2014; Kremkow, Jin, et al. 2014). Importantly, even at high contrast, humans still detect faster and more accurately dark than light targets (Komban et al. 2011), read dark text on white backgrounds faster than light text on dark backgrounds (Bauer and Cavonius 1980; Buchner and Baumgartner 2007). Moreover, humans rely more on luminance values that are darker than the mean when judging luminance variance in textures (Chubb and Nam 2000), sometimes using mostly the darkest elements with nearly −1 Weber contrast (Chubb et al. 1994, 2004). Therefore, in a wide variety of tasks and stimulus conditions, humans see darks more accurately and faster than lights.
Functional Significance of Changes in ON/OFF Response Balance
Cortical OFF dominance may originate as a need to compensate for the presence of more darks than lights in natural scenes (Geisler 2008; Ratliff et al. 2010; Cooper and Norcia 2015). It could also originate as a consequence of the neuronal blur within the ON pathway (Kremkow, Jin, et al. 2014; Pons et al. 2017) that could explain why the spatiotemporal resolution is higher in the OFF than the ON pathway (Komban et al. 2014; Kremkow, Jin, et al. 2014), and why cortical retinotopy is more precise for OFF than ON responses (Kremkow et al. 2016; Lee et al. 2016). In addition, our results indicate that cortical OFF dominance could help signal changes in optical blur and the viewing distance of a stimulus. As a stimulus moves closer to the observer, its projection on the retina increases in size and decreases in spatial frequency making cortical responses more OFF dominated. Similarly, as the observer focuses objects at far distance, the retinal projection of surrounding stimuli becomes blurred and lower in spatial frequency making cortical responses more OFF dominated. High spatial frequencies decrease with optical blur and low illumination (the pupil also becomes larger). Therefore, the visual cortex may be able to reach its highest ON/OFF response balance when the observer brings small distant targets into focus in brightly illuminated scenes.
Notes
Conflict of Interest: None declared.
Funding
Supported by the National Institute of Health (EY027361).
References
- Adelson EH, Bergen JR. 1985. Spatiotemporal energy models for the perception of motion. J Opt Soc Am A. 2:284–299. [DOI] [PubMed] [Google Scholar]
- Alonso JM, Martinez LM. 1998. Functional connectivity between simple cells and complex cells in cat striate cortex. Nat Neurosci. 1:395–403. [DOI] [PubMed] [Google Scholar]
- Alonso JM, Usrey WM, Reid RC. 2001. Rules of connectivity between geniculate cells and simple cells in cat primary visual cortex. J Neurosci. 21:4002–4015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer D, Cavonius C. 1980. Improving the legibility of visual display units through contrast reversal In: Grandjean E, Vigliani E, editors. Ergonomic Aspects of Visual Display Terminals. London: Taylor & Francis; p. 137–142. [Google Scholar]
- Blackwell HR. 1946. Contrast thresholds of the human eye. J Opt Soc Am. 36:624–643. [DOI] [PubMed] [Google Scholar]
- Bowen RW, Pokorny J, Smith VC. 1989. Sawtooth contrast sensitivity: decrements have the edge. Vision Res. 29:1501–1509. [DOI] [PubMed] [Google Scholar]
- Buchner A, Baumgartner N. 2007. Text - background polarity affects performance irrespective of ambient illumination and colour contrast. Ergonomics. 50:1036–1063. [DOI] [PubMed] [Google Scholar]
- Canny J. 1986. A computational approach to edge detection. IEEE Trans Pattern Anal Mach Intell. 8:679–698. [PubMed] [Google Scholar]
- Chen G, Dan Y, Li CY. 2005. Stimulation of non-classical receptive field enhances orientation selectivity in the cat. J Physiol. 564:233–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Martinez-Conde S, Macknik SL, Bereshpolova Y, Swadlow HA, Alonso JM. 2008. Task difficulty modulates the activity of specific neuronal populations in primary visual cortex. Nat Neurosci. 11:974–982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chichilnisky EJ, Kalmar RS. 2002. Functional asymmetries in ON and OFF ganglion cells of primate retina. J Neurosci. 22:2737–2747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chubb C, Econopouly J, Landy MS. 1994. Histogram contrast analysis and the visual segregation of IID textures. J Opt Soc Am A Opt Image Sci Vis. 11:2350–2374. [DOI] [PubMed] [Google Scholar]
- Chubb C, Landy MS, Econopouly J. 2004. A visual mechanism tuned to black. Vision Res. 44:3223–3232. [DOI] [PubMed] [Google Scholar]
- Chubb C, Nam JH. 2000. Variance of high contrast textures is sensed using negative half-wave rectification. Vision Res. 40:1677–1694. [DOI] [PubMed] [Google Scholar]
- Cooper EA, Norcia AM. 2015. Predicting cortical dark/bright asymmetries from natural image statistics and early visual transforms. PLoS Comput Biol. 11:e1004268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cottaris NP. 2003. Artifacts in spatiochromatic stimuli due to variations in preretinal absorption and axial chromatic aberration: implications for color physiology. J Opt Soc Am A Opt Image Sci Vis. 20:1694–1713. [DOI] [PubMed] [Google Scholar]
- Crowder NA, van Kleef J, Dreher B, Ibbotson MR. 2007. Complex cells increase their phase sensitivity at low contrasts and following adaptation. J Neurophysiol. 98:1155–1166. [DOI] [PubMed] [Google Scholar]
- DeAngelis GC, Ohzawa I, Freeman RD. 1993. Spatiotemporal organization of simple-cell receptive fields in the cat’s striate cortex. I. General characteristics and postnatal development. J Neurophysiol. 69:1091–1117. [DOI] [PubMed] [Google Scholar]
- Derrington AM, Krauskopf J, Lennie P. 1984. Chromatic mechanisms in lateral geniculate nucleus of macaque. J Physiol. 357:241–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier J, Monier C, Levy M, Marre O, Sari K, Kisvarday ZF, Fregnac Y. 2014. Hidden complexity of synaptic receptive fields in cat V1. J Neurosci. 34:5515–5528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galilei G. 1632. Dialogo sopra i due massimi sistemi del mondo In: Tolemaico e Copernicano. Florence, Italy: Battista Landini. [Google Scholar]
- Geisler WS. 2008. Visual perception and the statistical properties of natural scenes. Annu Rev Psychol. 59:167–192. [DOI] [PubMed] [Google Scholar]
- Held RT, Cooper EA, Banks MS. 2012. Blur and disparity are complementary cues to depth. Curr Biol. 22:426–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. 1962. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 160:106–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. 1968. Receptive fields and functional architecture of monkey striate cortex. J Physiol. 195:215–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen M, Li X, Lashgari R, Kremkow J, Bereshpolova Y, Swadlow HA, Zaidi Q, Alonso JM. 2014. Chromatic and achromatic spatial resolution of local field potentials in awake cortex. Cereb Cortex. 25:3877–3893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jimenez LO, Tring E, Trachtenberg JT, Ringach DL. 2018. Local tuning biases in mouse primary visual cortex. J Neurophysiol. 120:274–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J, Wang Y, Swadlow HA, Alonso JM. 2011. Population receptive fields of ON and OFF thalamic inputs to an orientation column in visual cortex. Nat Neurosci. 14:232–238. [DOI] [PubMed] [Google Scholar]
- Jin JZ, Weng C, Yeh CI, Gordon JA, Ruthazer ES, Stryker MP, Swadlow HA, Alonso JM. 2008. On and off domains of geniculate afferents in cat primary visual cortex. Nat Neurosci. 11:88–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joesch M, Schnell B, Raghu SV, Reiff DF, Borst A. 2010. ON and OFF pathways in Drosophila motion vision. Nature. 468:300–304. [DOI] [PubMed] [Google Scholar]
- Jones JP, Palmer LA. 1987. An evaluation of the two-dimensional Gabor filter model of simple receptive fields in cat striate cortex. J Neurophysiol. 58:1233–1258. [DOI] [PubMed] [Google Scholar]
- Komban SJ, Alonso JM, Zaidi Q. 2011. Darks are processed faster than lights. J Neurosci. 31:8654–8658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komban SJ, Kremkow J, Jin J, Wang Y, Lashgari R, Li X, Zaidi Q, Alonso JM. 2014. Neuronal and perceptual differences in the temporal processing of darks and lights. Neuron. 82:224–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kontsevich LL, Tyler CW. 1999. Nonlinearities of near-threshold contrast transduction. Vision Res. 39:1869–1880. [DOI] [PubMed] [Google Scholar]
- Kremkow J, Alonso JM, Zaidi Q. 2014. Mystery Behind Galileo’s Visual Illusion Discovered. In. https://www.youtube.com/watch?v=sbBpMYx48A4.
- Kremkow J, Jin J, Komban SJ, Wang Y, Lashgari R, Li X, Jansen M, Zaidi Q, Alonso JM. 2014. Neuronal nonlinearity explains greater visual spatial resolution for darks than lights. Proc Natl Acad Sci U S A. 111:3170–3175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kremkow J, Jin J, Wang Y, Alonso JM. 2016. Principles underlying sensory map topography in primary visual cortex. Nature. 533:52–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lashgari R, Li X, Chen Y, Kremkow J, Bereshpolova Y, Swadlow HA, Alonso JM. 2012. Response properties of local field potentials and neighboring single neurons in awake primary visual cortex. J Neurosci. 32:11396–11413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee KS, Huang X, Fitzpatrick D. 2016. Topology of ON and OFF inputs in visual cortex enables an invariant columnar architecture. Nature. 533:90–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lien AD, Scanziani M. 2018. Cortical direction selectivity emerges at convergence of thalamic synapses. Nature. 558:80–86. [DOI] [PubMed] [Google Scholar]
- Liu K, Yao H. 2014. Contrast-dependent OFF-dominance in cat primary visual cortex facilitates discrimination of stimuli with natural contrast statistics. Eur J Neurosci. 39:2060–2070. [DOI] [PubMed] [Google Scholar]
- Luo-Li G, Alais D, Freeman AW. 2016. Orientation discrimination requires coactivation of on- and off-dominated visual channels. J Vis. 16:18. [DOI] [PubMed] [Google Scholar]
- MacCurdy E. 1938. The notebooks of Leonardo da Vinci. (London): Jonathan Cape.
- Mazade R, Niell CM, Alonso JM. 2018. Seeing with a biased visual cortical map. J Neurophysiol. 120:272–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McConnell SK, LeVay S. 1984. Segregation of on- and off-center afferents in mink visual cortex. Proc Natl Acad Sci USA. 81:1590–1593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean J, Palmer LA. 1989. Contribution of linear spatiotemporal receptive field structure to velocity selectivity of simple cells in area 17 of cat. Vision Res. 29:675–679. [DOI] [PubMed] [Google Scholar]
- Motoyoshi I, Nishida S, Sharan L, Adelson EH. 2007. Image statistics and the perception of surface qualities. Nature. 447:206–209. [DOI] [PubMed] [Google Scholar]
- Movshon JA, Thompson ID, Tolhurst DJ. 1978. a. Receptive field organization of complex cells in the cat’s striate cortex. J Physiol. 283:79–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon J, Thompson I, Tolhurst D. 1978. b. Spatial summation in the receptive fields of simple cells in the cat’s striate cortex. J Physiol. 283:53–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nam JH, Chubb C. 2000. Texture luminance judgments are approximately veridical. Vision Res. 40:1695–1709. [DOI] [PubMed] [Google Scholar]
- Onat S, Nortmann N, Rekauzke S, Konig P, Jancke D. 2011. Independent encoding of grating motion across stationary feature maps in primary visual cortex visualized with voltage-sensitive dye imaging. Neuroimage. 55:1763–1770. [DOI] [PubMed] [Google Scholar]
- Pernberg J, Jirmann KU, Eysel UT. 1998. Structure and dynamics of receptive fields in the visual cortex of the cat (area 18) and the influence of GABAergic inhibition. Eur J Neurosci. 10:3596–3606. [DOI] [PubMed] [Google Scholar]
- Polack PO, Contreras D. 2012. Long-range parallel processing and local recurrent activity in the visual cortex of the mouse. J Neurosci. 32:11120–11131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pons C, Mazade R, Jin J, Dul MW, Zaidi Q, Alonso JM. 2017. Neuronal mechanisms underlying differences in spatial resolution between darks and lights in human vision. J Vis. 17:5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratliff CP, Borghuis BG, Kao YH, Sterling P, Balasubramanian V. 2010. Retina is structured to process an excess of darkness in natural scenes. Proc Natl Acad Sci U S A. 107:17368–17373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reid RC, Alonso JM. 1995. Specificity of monosynaptic connections from thalamus to visual cortex. Nature. 378:281–284. [DOI] [PubMed] [Google Scholar]
- Reid RC, Soodak RE, Shapley RM. 1987. Linear mechanisms of directional selectivity in simple cells of cat striate cortex. Proc Natl Acad Sci U S A. 84:8740–8744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rekauzke S, Nortmann N, Staadt R, Hock HS, Schoner G, Jancke D. 2016. Temporal asymmetry in dark-bright processing initiates propagating activity across primary visual cortex. J Neurosci. 36:1902–1913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringach DL. 2002. Spatial structure and symmetry of simple-cell receptive fields in macaque primary visual cortex. J Neurophysiol. 88:455–463. [DOI] [PubMed] [Google Scholar]
- Ringach DL, Sapiro G, Shapley R. 1997. A subspace reverse-correlation technique for the study of visual neurons. Vision Res. 37:2455–2464. [DOI] [PubMed] [Google Scholar]
- Ringach DL, Shapley RM, Hawken MJ. 2002. Orientation selectivity in macaque V1: diversity and laminar dependence. J Neurosci. 22:5639–5651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rust NC, Schwartz O, Movshon JA, Simoncelli EP. 2005. Spatiotemporal elements of macaque v1 receptive fields. Neuron. 46:945–956. [DOI] [PubMed] [Google Scholar]
- Samonds JM, Potetz BR, Lee TS. 2012. Relative luminance and binocular disparity preferences are correlated in macaque primary visual cortex, matching natural scene statistics. Proc Natl Acad Sci U S A. 109:6313–6318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz O, Pillow JW, Rust NC, Simoncelli EP. 2006. Spike-triggered neural characterization. J Vis. 6:484–507. [DOI] [PubMed] [Google Scholar]
- Sedigh-Sarvestani M, Vigeland L, Fernandez-Lamo I, Taylor MM, Palmer LA, Contreras D. 2017. Intracellular, in vivo, dynamics of thalamocortical synapses in visual cortex. J Neurosci. 37:5250–5262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Short AD. 1966. Decremental and incremental visual thresholds. J Physiol. 185:646–654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skottun BC, De Valois RL, Grosof DH, Movshon JA, Albrecht DG, Bonds AB. 1991. Classifying simple and complex cells on the basis of response modulation. Vision Res. 31:1079–1086. [DOI] [PubMed] [Google Scholar]
- Smith GB, Whitney DE, Fitzpatrick D. 2015. Modular representation of luminance polarity in the superficial layers of primary visual cortex. Neuron. 88:805–818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swadlow HA, Bereshpolova Y, Bezdudnaya T, Cano M, Stoelzel CR. 2005. A multi-channel, implantable microdrive system for use with sharp, ultra-fine “Reitboeck” microelectrodes. J Neurophysiol. 93:2959–2965. [DOI] [PubMed] [Google Scholar]
- Swindale NV, Grinvald A, Shmuel A. 2003. The spatial pattern of response magnitude and selectivity for orientation and direction in cat visual cortex. Cereb Cortex. 13:225–238. [DOI] [PubMed] [Google Scholar]
- Tan Z, Sun W, Chen TW, Kim D, Ji N. 2015. Neuronal representation of ultraviolet visual stimuli in mouse primary visual cortex. Sci Rep. 5:12597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor MM, Sedigh-Sarvestani M, Vigeland L, Palmer LA, Contreras D. 2018. Inhibition in simple cell receptive fields is broad and OFF-subregion biased. J Neurosci. 38:595–612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Touryan J, Felsen G, Dan Y. 2005. Spatial structure of complex cell receptive fields measured with natural images. Neuron. 45:781–791. [DOI] [PubMed] [Google Scholar]
- Tyler CW, Chan H, Liu L. 1992. Different spatial tunings for ON and OFF pathway stimulation. Ophthalmic Physiol Opt. 12:233–240. [DOI] [PubMed] [Google Scholar]
- Veit J, Bhattacharyya A, Kretz R, Rainer G. 2014. On the relation between receptive field structure and stimulus selectivity in the tree shrew primary visual cortex. Cereb Cortex. 24:2761–2771. [DOI] [PubMed] [Google Scholar]
- Wang Y, Jin J, Kremkow J, Lashgari R, Komban SJ, Alonso JM. 2015. Columnar organization of spatial phase in visual cortex. Nat Neurosci. 18:97–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wassle H, Boycott BB, Illing RB. 1981. Morphology and mosaic of on- and off-beta cells in the cat retina and some functional considerations. Proc R Soc Lond B Biol Sci. 212:177–195. [DOI] [PubMed] [Google Scholar]
- Westheimer G. 2008. Illusions in the spatial sense of the eye: geometrical-optical illusions and the neural representation of space. Vision Res. 48:2128–2142. [DOI] [PubMed] [Google Scholar]
- Williams PE, Shapley RM. 2007. A dynamic nonlinearity and spatial phase specificity in macaque V1 neurons. J Neurosci. 27:5706–5718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xing D, Shapley RM, Hawken MJ, Ringach DL. 2005. Effect of stimulus size on the dynamics of orientation selectivity in Macaque V1. J Neurophysiol. 94:799–812. [DOI] [PubMed] [Google Scholar]
- Xing D, Yeh CI, Shapley RM. 2010. Generation of black-dominant responses in V1 cortex. J Neurosci. 30:13504–13512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh CI, Xing D, Shapley RM. 2009. “Black” responses dominate macaque primary visual cortex v1. J Neurosci. 29:11753–11760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaghloul KA, Boahen K, Demb JB. 2003. Different circuits for ON and OFF retinal ganglion cells cause different contrast sensitivities. J Neurosci. 23:2645–2654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahs KR, Stryker MP. 1988. Segregation of ON and OFF afferents to ferret visual cortex. J Neurophysiol. 59:1410–1429. [DOI] [PubMed] [Google Scholar]
- Zaidi Q, Halevy D. 1993. Visual mechanisms that signal the direction of color changes. Vision Res. 33:1037–1051. [DOI] [PubMed] [Google Scholar]
- Zemon V, Eisner W, Gordon J, Grose-Fifer J, Tenedios F, Shoup H. 1995. Contrast-dependent responses in the human visual system: childhood through adulthood. Int J Neurosci. 80:181–201. [DOI] [PubMed] [Google Scholar]
- Zemon V, Gordon J, Welch J. 1988. Asymmetries in ON and OFF visual pathways of humans revealed using contrast-evoked cortical potentials. Vis Neurosci. 1:145–150. [DOI] [PubMed] [Google Scholar]