Effect of in vivo post-translational modifications of the HMGB1 protein upon binding to platinated DNA: a molecular simulation study

Abstract

Cisplatin is one of the most widely used anticancer drugs. Its efficiency is unfortunately severely hampered by resistance. The High Mobility Group Box (HMGB) proteins may sensitize tumor cells to cisplatin by specifically binding to platinated DNA (PtDNA) lesions. In vivo, the HMGB/PtDNA binding is regulated by multisite post-translational modifications (PTMs). The impact of PTMs on the HMGB/PtDNA complex at atomistic level is here investigated by enhanced sampling molecular simulations. The PTMs turn out to affect the structure of the complex, the mobility of several regions (including the platinated site), and the nature of the protein/PtDNA non-covalent interactions. Overall, the multisite PTMs increase significantly the apparent synchrony of all the contacts between the protein and PtDNA. Consequently, the hydrophobic anchoring of the side chain of F37 between the two cross-linked guanines at the platinated site—a key element of the complexes formation - is more stable than in the complex without PTM. These differences can account for the experimentally measured greater affinity for PtDNA of the protein isoforms with PTMs. The collective behavior of multisite PTMs, as revealed here by the synchrony of contacts, may have a general significance for the modulation of intermolecular recognitions occurring in vivo.

INTRODUCTION

Cisplatin, or cis-diamminedichloridoplatinum(II), is a major anticancer drug in the treatment of several solid tumors (1–5). Cisplatin induces cell death by binding to DNA and inhibiting replication and transcription (1). Unfortunately, drug efficiency is severely limited by resistance mechanisms (6,7), either intrinsic or developed by tumor cells after an initial sensitivity (8). The d(GpG) and d(ApG) intrastrand cross-links (9) account for about 90% of the cisplatin–DNA lesions formed in vivo (9–11). The distorted DNA is recognized and forms adducts with chromosomal non-histone nucleoproteins containing the High Mobility Group Box (HMGB), e.g. HMGB1 and HMGB4 (12,13). This is a pharmaceutically relevant event, since it can inhibit the cisplatin–DNA damage repair (12) and favor tumor-cell death (14,15). A correlation between higher binding affinity of HMGB proteins toward cisplatin–DNA lesions and lower DNA-repair efficiency has been observed in various instances (12,15–18).

The structural determinants of the major complex between HMGB1 box-A and platinated DNA ([Pt(NH₃)₂]²⁺-d(CCUCTCTG*G*ACCTTCC)-d(GGAGAGACCTGGAAGG), PtDNA) have been revealed by a fundamental X-ray study of Lippard and co-workers (19). Beside this major intrastrand adduct, the drug can form also interstrand adduct with DNA (20). Here, the protein binds to the PtDNA from the minor groove using non-covalent interactions (21) contemplating also a key insertion of the phenyl ring of F37 into a hydrophobic notch created by the two cross-linked guanines at the damaged site (19). The relevance of this complex in vivo is challenging since several post-translational modifications (PTMs), including lysine acetylation and serine phosphorylation at multiple sites (22), can modulate the binding affinity of HMGB1 isoforms for PtDNA (22–28). PTMs have been defined as covalent modifications of amino-acid residues in proteins (29) that allow the hydrophobicity and other physico-chemical properties of the protein to be tuned for specific biological functions (30,31). For instance, a single-site lysine acetylation is known to affect the interaction with DNA of H3 histone (32), while multisite acetylation of the H4 histone tail introduces both specific and cumulative effects on the protein conformation (33).

Acetylation of lysine and phosphorylation of serine both reduce positive charges on HMGB1 protein, hence one may expect a decreased electrostatic attraction for the negatively charged DNA (34,35). This is for instance the case of a widely studied complex, the nuclear factor-κB (NF-κB)/DNA complex (36,37), where multisite lysine acetylation markedly decreases the binding affinity for DNA (38). However, this instinctive assumption conflicts with the binding affinities measured experimentally for the HMGB1/PtDNA complexes (22–28) where the mixture of four in vivo HMGB1 isoforms (22) turned out to bind PtDNA with greater affinity than the protein without PTMs. A plausible explanation for these observations was that the conformational changes induced by the PTMs, rather than the charge, affect the binding of HMGB1 to PtDNA (22,23). Unlike the case of widely-investigated interactions between proteins and small molecules, in the HMGB1/PtDNA complex the rugged intermolecular interface involves many interfacial contacts building up a complex interaction network. How multisite PTMs can affect this kind of interaction network has not yet been explored.

Molecular dynamics (MD) simulations can give insight into the atomistic level of the molecular recognition interfaces and has already been successfully applied to some bio-systems including cytotoxic metallodrugs and their targets (39,40). Combining MD simulations and experimental evidences, the target preferences of several promising transition metal anticancer agents (41–45), such as platinum- and ruthenium-based compounds, have been elucidated.

In this work, we address the issue of multisite PTMs by enhanced sampling atomistic molecular simulations of the four known PTM isoforms (22) starting from the X-ray structure of the isoform without PTMs (19). We investigated both the structural properties of the complexes and the collective behaviors originating from multisite PTMs. The collective behaviors were investigated in terms of ‘synchrony’ in the formation of the non-covalent interactions between protein and PtDNA. In other words, given a pair of intermolecular direct contacts A and B, we investigated whether A is formed simultaneously to B, and how will this synchrony of contact be modulated by different in vivo PTMs patterns.

Anticipating our results, the PTMs turned out to affect the nature of the intermolecular contacts and to change the conformational fluctuations not only of specific regions, but also of the overall complex. In all cases, the PTMs render the interactions between protein and PtDNA more synchronic.

MATERIALS AND METHODS

Calculation details

The resolved X-ray structure of HMGB1 in complex with platinated DNA ([Pt(NH₃)₂]²⁺–d(CCUCT CTG*G*ACCTTCC)–d(GGAGAGACCTGGAAGG)) covers the box-region A from residue 8 to 78 (PDBID 1CKT (19)). To cover as much as possible the experimentally observed in vivo PTMs (22), we included in our simulations the N’-tail and the box-linker (Supplementary Figure S1 in supporting information (SI), from homology modeling based on a full-length structure of HMGB1 (PDBID: 2YRQ)), called noPTM hereafter. The in vivo PTM patterns reported in previous work (22) (A, B, C and D, Table 1) are added to noPTM using an in-house code. Next, 100-ns long MD simulation based on the AMBER ff99SB-ILDN (46–48) and Parmbsc1 (49) force fields was carried out for the following five systems: cisplatin–DNA (PtDNA) bound to the HGMB1 box A (HGMB1A hereafter) without PTM (noPTM) or to HGMB1A isoforms A, B, C and D. Then, replica exchange with solute scaling sampling simulations (50) were carried out on these complexes (i.e. PtDNA•A, PtDNA•B, PtDNA•C and PtDNA•D, as well as PtDNA•noPTM). Five more systems were built as follows. The proteins present in the replicas of the five complexes (before enhanced sampling) were inserted in a box of the same size as that used in the complexes simulations. Each protein box was filled with 0.15 M NaCl in water, as used in the complexes simulations (see Supplementary Table S8). The same enhanced sampling condition as for the complexes was then applied to each one of these systems. Technical details of the homology modeling, MD system setups, enhanced sampling simulations, and simulation parameters are reported in SI.

Table 1.

PTM sites in the four in vivo HMGB1 isoforms (A–D in Figure 1)

	Acetylated lysine	Phosphorylated serine	Number of PTM sites
A	K11, K29, K42, K75, K81, K89	–	6
B	K2, K11, K29, K42, K54, K58, K81, K85, K89	–	9
C	K11, K54, K81, K89	S14, S34, S52	7
D	K11, K29, K42, K81, K87	S34	6

Conformational analyses

The bending of PtDNA and the opening of paired bases as well as other helical parameters were calculated using Curves+ (51). The hydrogen bonds and the non-bonded contacts were calculated based on the contacts list generated from HBPLUS (52) and NUCPLOT (53). Direct or water-mediated hydrogen bonds were identified with the following criteria: Hydrogen (H)–acceptor (A) distance <2.7 Å, donor (D)–A distance <3.35 Å, D–H–A angle >90^o. PtDNA–protein hydrophobic interactions were assumed for distances between atom pairs of 3.9 Å or smaller. Herein, only hydrophobic side chains or polar/charged side chains not involved in direct or water mediated H-bonds and/or salt bridges were considered. The electrostatic contacts (salt-bridges) are the non-bonded contacts between positively charged protein residues and phosphate groups of PtDNA. The stacking contacts are the non-bonded contacts between aromatic residues and nucleobases. All the rest of non-bonded contacts are considered as van der Waals contacts. Before further processing, noisy intermolecular contacts have been filtered out to guarantee 95% confidence interval by bootstrap resampling (Supplementary Figure S2).

Conformational entropy analyses

The change of conformational entropy upon the binding of the proteins to PtDNA was estimated by quasi-harmonic approximation (54,55). The representative structures of each solute (protein-PtDNA complexes, free states of the proteins and PtDNA) were described as a disjoint multidimensional harmonic well (56), by which the conformational entropy is connected to the change in internal structural dynamics (55). The entropy from fast intra-well motion of the solute was estimated by the quasi-harmonic approximation (54,55).

Synchrony of contacts

For synchrony analysis, we need to define several quantities. The effective number of contacts (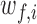) is the number of direct contacts (i.e. not water mediated contacts) between residue i and PtDNA at the simulation snapshot f, divided by the number of all such contacts:

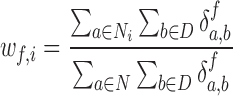(1)

N, N_i and D are the number of atoms of the protein, that of the residue i, and that of PtDNA, respectively. 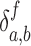= 1 if atom a and atom b are in contact, 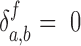otherwise. 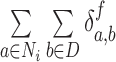is the number of contacts of residue i at snapshot f. 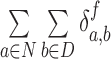is the number of contacts of all residues at snapshot f.

The pairwise synchrony (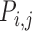) between two residues i and j is defined as the normalized sum of 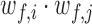over all considered simulations snapshots M:

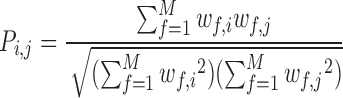(2)

P_i,j ranges between 0 and 1. If P_i,j= 1, PtDNA–protein contacts of two residues i andj are formed simultaneously for all M snapshots (fully synchronic residues pairs). P_i,j = 0 if this is never the case. Partially synchronic pairs are defined if 0.5 < P_i,j < 1. Here, the residues forming partially and/or fully synchronic pairs are represented as linked nodes (with edges) in a network (the synchronic network). The latter can be conveniently characterized by the synchrony index I:

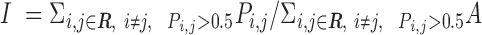(3)

Here, A = 1. R includes all R nodes of the synchronic network. I is the sum of the pairwise synchronies of all (partially and fully) synchrony nodes in a synchronic network divided by the number of edges between linked nodes. The latter corresponds to a fully synchronic network with the same topology as the calculated one. This ensures that the synchrony index can be used to compare the overall synchronies across different systems: the difference of the topology of different networks is canceled out.

Next, we notice that the synchronic network can be re-grouped into one or more synchronic subgroups; in each subgroup, all nodes are synchronous to one node (the synchronic center) and they may well be also synchronous to each other. There is a very large number of possible subdivisions in subgroups. Here, we identify the subdivision that minimizes the so-called Bethe free energy (57), following an established procedure (58). To this aim, we maximize a quantity – the net synchrony S(L)– that is anticorrelated to the Bethe free energy (57). L = (L1,…, L_R) is a set of labels which allows us to distinguish the synchronic subgroups: (58) 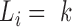when node k is the synchronic center of node i. For instance, L₂ = 4 means that the node 4 is the synchronic center of node 2. Thus, necessarily 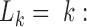the node k must be the synchronic center of itself.

S(L) reads: (58)

(4)

Here, the penalty term equals 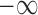if the required conditions above (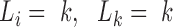) are not satisfied at the same time. S(L) is maximized by using the affinity propagation algorithm (58) (see SI for details).

To visualize the subgroups and the synchronic networks, we found convenient to project them onto a 2D space. In this way, nodes involved in (a)synchronic contacts are located relatively (far) close to each other (59–61). This is done by performing a standard multidimensional scaling procedure: principal coordinates analysis (59–61). The synchrony code is available upon request from the authors.

RESULTS AND DISCUSSION

The present investigation comprises the four PTM-bearing HMGB1 box-A isoforms (22) (A-D hereafter, see Table 1) detected in vivo in complex with the platinated DNA (PtDNA hereafter). These feature 4–9 acetylated lysine and 0–3 phosphorylated serine residues (Table 1) (22). Comparison is made with the isoform without PTM in complex with the platinated DNA (PtDNA•noPTM). The PtDNA•A-D and PtDNA•noPTM complexes underwent 100-ns long Hamiltonian replica exchange enhanced sampling simulations (50) with 16 replicas. To improve sampling efficiency, care was taken to reduce memory effects and to increase swapping efficiencies across replicas (Supplementary Figure S3). The conformations generated in the first 50 ns were discarded based on a convergence analysis reported in SI (see Simulations in Materials and Method section and Supplementary Figure S4).

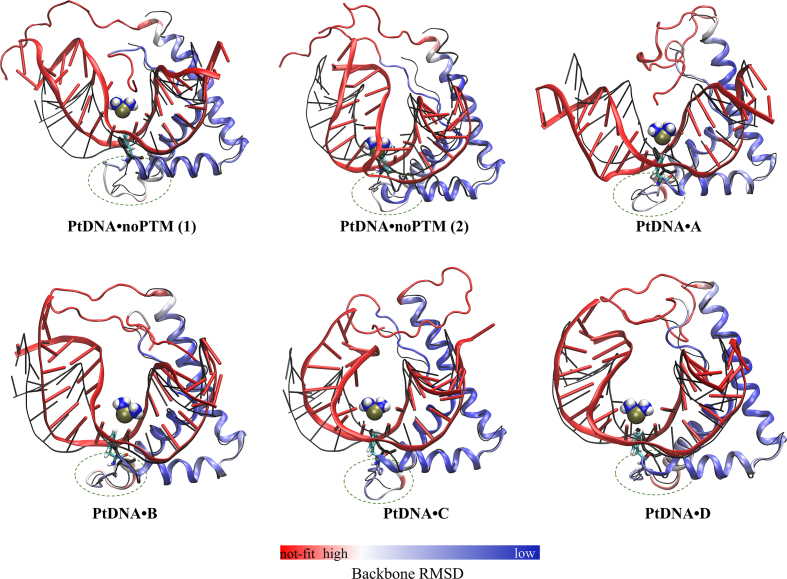
More than ten structural representatives of each system were identified by a cluster analysis (see Supplementary Figures S5 and S6). The first ten representatives cover most (90–99%) of the conformational space of each system (Supplementary Figure S6). Figure 1 presents the highly-populated structures of each system and their backbone deviation (i.e. standard deviation of each residue) relative to the X-ray structure.

Figure 1.

Most populated structures of the five complexes investigated here emerging from our enhanced sampling simulations. PtDNA•noPTM(1) and PtDNA•noPTM(2) are both significantly populated structures of the isoform without PTMs. The X-ray structure of the isoform without PTMs (9) is depicted in a ‘black thin line’ representation. The major groove is directed to north and the minor groove to south. The loops connecting the proteins’ α-helixes 1 and 2 are inscribed in dotted-line circles. The protein is colored from blue to red (see bar at the bottom of the Figure) according to the backbone RMSD relative to the X-ray structure. The PtDNA is colored in red. F37 (sticks) and [Pt(NH₃)₂]²⁺ (van der Waals spheres) are colored according to the atomic codes: N, blue; H, white; Pt, gold; C, cyan.

Structural properties and conformational fluctuations

The protein

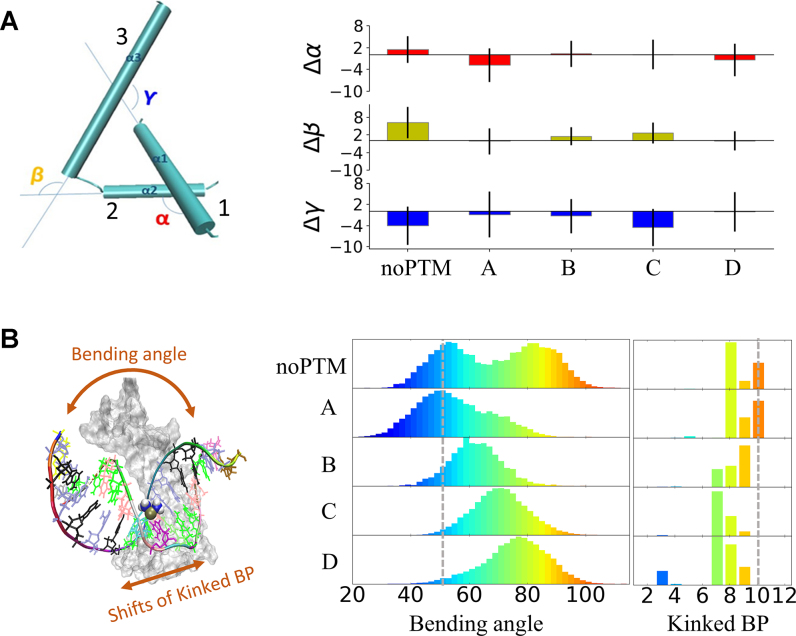
The helical secondary structure of the protein is well conserved during the simulations (Supplementary Table S1). The root-mean-square deviation (RMSD) of the protein backbone relative to that of the X-ray structure is ∼1.6 Å (Supplementary Table S2). The major contribution comes from residues nearby the terminal regions and the loop connecting the α-helixes 1 and 2 (inscribed in dotted-line circles in Figure 1). Changes within the three α-helixes domains (box-region), corresponding to changes in the proteins’ ‘L-shape’, are characterized in terms of interhelical spatial angles α, β, and γ (Figure 2A). Similarity with the X-ray structure is observed for the ‘L-shapes’ of A, B, and D (Figure 2A); whereas, with respect to the X-ray structure, β is increased and γ is decreased for noPTM and C, indicating a slightly larger bending toward the PtDNA.

Figure 2.

(A) Conformation of the helices in the box-region. Left: definition of the inter-helical spatial angles (α, β and γ). Right: histogram showing deviations of α, β and γ relative to the X-ray structure (α = 115°, β = 114° and γ = 117°); error bars indicate the standard deviations. (B) Distributions of bending angle and shifts of kinked base-pair (Kinked BP). Left: graphical representation of bending angle and shifts of Kinked BP. Right: distribution of bending angle and Kinked BP shifts of the platinated DNA. Distributions from lower to higher values are colored spanning from blue to red. Bending angle and Kinked BP of the X-ray structure are marked as grey dot lines.

Compared to the box-region, the two protein terminals experience much greater (>2-fold) root-mean-square fluctuations (RMSFs) (Supplementary Table S3). This is not unexpected for such unstructured loops (28). More interesting is the fact that the terminals’ RMSFs decrease on passing from noPTM (∼0.8 Å) to the four PTM isoforms (∼0.3–0.5 Å, Supplementary Table S3). Consistent with a larger flexibility of noPTM relative to A–D, noPTM features two main structures in solution, whereas the other isoforms feature only one structure (Figure 1). We conclude that major differences between noPTM and A–D are due to the conformational fluctuations of the proteins’ terminals.

The PtDNA

The platinated DNA preserves its double helix structure across the five adducts (Supplementary Figure S5). However, it undergoes more significant overall rearrangements than the protein molecule, with the RMSD of the PtDNA backbone ranging from 3.3 to 6.1 Å (Supplementary Table S2). The conformation of the PtDNA was characterized in terms of: (i) bending angle, calculated as sum of the individual bending angles of the inter-base axis (51,62) (this corresponds to the overall bending of PtDNA) and (ii) kinked base pair (Kinked BP), that is the base pair step where the maximum bending of the inter-base axis occurs (63,64) (it corresponds to the point of kinking of PtDNA) (Figure 2B).

The PtDNA’s bending angle ranges from ∼30° to ∼100°, with bi- and uni-modal distributions in PtDNA•noPTM and in PtDNA•A-D, respectively (Figure 2B). Similar distributions of the so-called helix axes subtending angle (65), which may be employed to characterize the overall bending of the PtDNA (65), are observed for PtDNA•noPTM and PtDNA•A-D (Supplementary Figure S7). The Kinked BP is located at base pair step 10 in the X-ray structure (marked as dot line in Figure 2b) while it extends across base pair steps from 7 to 10 in our simulations (see Figure 2B, notice that base pairs 8 and 9 are those platinated (19)). We note that this softened bending of DNA around the platinated site has recently been confirmed also experimentally (66).

The average values of the bond angles involving the platinum atom and the two N7 donor atoms in PtDNA•noPTM are similar to those of the X-ray structure and their standard deviations are less than 5% of such average values (Supplementary Figure S8). Hence, the bi-modal distribution of the bending angle for PtDNA•noPTM is not accompanied by structural changes at the cross link. Similar conclusions can be drawn for PtDNA•A-D (Supplementary Figure S8). In contrast, the base pairing conformations, e.g. shear, stretch, stagger, etc. (67), around the cross-linked base pair, experience larger fluctuations in PtDNA•noPTM than in PtDNA•A-D (Supplementary Figure S9). Also, the translations and rotations of the cross-linked base pairs (defined in literature (67)) in PtDNA•noPTM are larger than those in PtDNA•A-D (Supplementary Figure S9). All these differences are associated with greater helical rise and twist of PtDNA•noPTM relative to PtDNA•A-D (67,68). The bending in the X-ray structure was ∼47° (marked as dot line in Figure 2B) and corresponds to the bending angle of one of the two maxima (the lowest) of PtDNA•noPTM. We therefore suggest that PtDNA•noPTM samples two major conformations in aqueous solution, one similar to that identified in the solid state (19) and the other, more bent due to the helical twists, present only in water solution.

The base pairs around the cisplatin lesion in PtDNA•A–D undergo less conformational fluctuations than in PtDNA•noPTM, under the same sampling conditions (Supplementary Figure S9). In addition, the RMSF of the whole PtDNA is smaller in all the PTM complexes than in noPTM (Supplementary Table S3). These results demonstrate that the structural stability of both the protein and PtDNA are improved after PTMs.

PtDNA-protein contacts

Nature of the intermolecular contacts

π-stacking (STC) and Van der Waals (VWC) contacts constitute altogether >¾ of the PtDNA-protein contacts across all adducts (Supplementary Table S4) with STC involving mainly F37 and Y15 (Supplementary Figure S10). Direct and water-mediated hydrogen bonds (HBC), along with salt bridges, contribute by 15–19%, 5–7% and ∼1%, respectively (Supplementary Tables S4 and S5 and Supplementary Figures S10 and S11).

Overall, the nature of the contacts (and hence the percentage of VWC, STC, and HBC) changes significantly on passing from noPTM to A–D (Supplementary Figure S10). Most of the PTMs are involved in direct HBC and/or VWC with PtDNA (highlighted by color bands in Supplementary Figure S10). In contrast, PTMs on K29, S52, K54, K58 and K75 are water-exposed. A description of the energetics associated with these interactions (Supplementary Figure S12), as calculated with the non-bonded terms of the force field, is presented in the SI.

Mobility of the protein and in particular of the ‘hydrophobic anchor’ F37

Lippard and co-workers, in their seminal work on the platinated DNA/HMGB1 complex structure (19), as well as Furuita et al. (69), have identified the key structural determinant for platinated DNA/HGMB1 binding. This is the stacking configuration of the F37 side-chain inside the platinated guanines’ cavity (see Figure 3). Important contributions to the stacking interaction between F37 and the cross-linked G bases include: (A) the stacking between the aromatic rings and (B) the interaction between the hydrogen atom of the phenyl in para position and the centroid of an aromatic ring of the guanine (13). These authors concluded that tighter is the stacking, stronger the binding (19). Indeed, the strength of the binding of the HMGB1 box-A to a platinated DNA is highly sensitive to the local structure of this notch (69).

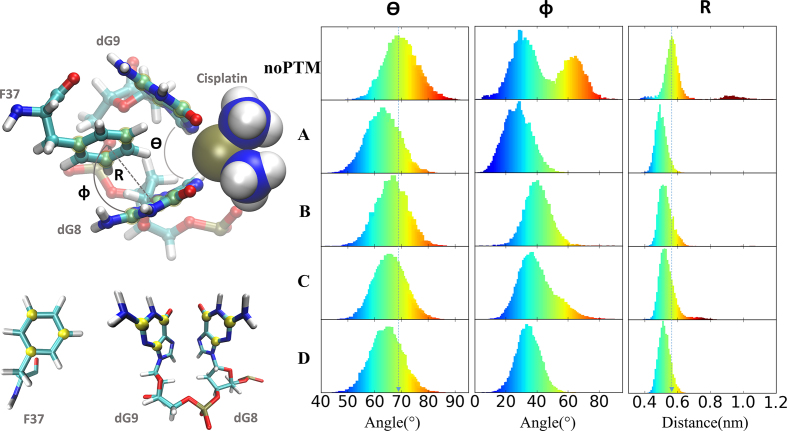
Figure 3.

Left, top: Geometrical parameters θ, Φ, and R describing the F37 stacking configuration in the notch formed by the platinated nucleobases dG8*-dG9*. Left, bottom: The planes of the rings, used to define the three parameters, are defined by the carbon atoms shown in yellow. Right: distributions of the values of the geometrical parameters in the simulations presented here.

Several structural properties (Figure 3), such as the opening of the cross-linked guanines (dG8*-dG9*) (θ), the stacking angle between F37 and dG8* rings (Φ) and the distance between F37 side-chain and dG8* (R), may be used to characterize this stacking configuration (69). Φ turns out to spread by over 80^o in noPTM, while it is 60^o or less in A–D. R distribution is broader in noPTM than in A–D (Figure 3). This is due, at least in part, to the larger rearrangements experienced by the F37 ring in noPTM (Supplementary Figure S13). θ is wider in noPTM (∼68^o) than in A–D (∼63^o, see Figure 3). The analysis of all these geometrical parameters indicates that F37 stacking is tighter in A–D than in noPTM. Hence, A–D binding can well be stronger than that of noPTM, consistent with the experimental result that isoforms A-D globally bind with higher affinity (dissociation constant, K_d = 50 nM (22)) than noPTM (K_d = 120 nM (70)).

Our discussion of the energetics complements our previous work on noPTM where the calculations reproduced quantitatively the experimental binding free energy for noPTM (71). To further substantiate the qualitative considerations of isoforms A–D made above, one could calculate the binding free energies for A–D, taken singularly. However, such calculation is expected, from one hand, to be highly expensive and requiring special allocations of resources, as in our previous study (71), and, from the other hand, be inconclusive at this stage because we do not know the contribution of each species to the measured value of 50 nM for isoforms A–D taken globally (22).

Synchrony of contacts

Our calculations have shown that the nature of the contacts changes significantly on passing from noPTM to A–D. Moreover, PTMs also cause decreased mobility of several regions of the protein (including the hydrophobic anchor F37, which highly contributes to this specific binding) and of the PtDNA helical parameters around the platinum lesion, including a smaller opening of the notch with consequent decrease of the dG8*–F37 distance. To understand the cooperativity of the changes of individual contact domains between the protein and the PtDNA upon the overall effect of multisite PTMs, we introduced a novel concept, the synchrony of all the intermolecular contacts. The latter quantifies the interactions between platinated DNA and protein that occur simultaneously.

The starting point of our discussion is the so-called ‘synchronic network’, which describes the relationship among protein residues whose contacts with PtDNA occur simultaneously during the simulation (for the formal definition of subsequent concepts and quantities, see the Method section). The synchronic network is made of several ‘synchronic subgroups’, since not all residues are synchronous to a single node of the network. The degree of synchrony of the whole network (the ‘synchrony index’) ranges from 0, in the case of a fully asynchronic network, to 1, in the case of a fully synchronic network. Hence, larger the value of the synchrony index, greater the probability of forming synchronic contacts.

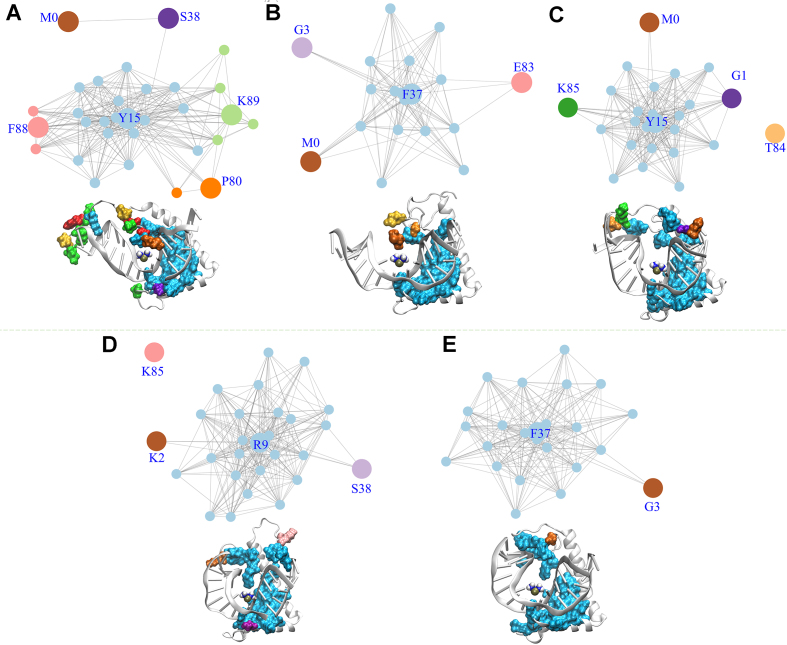
The PtDNA•noPTM network consists of four multi-residue subgroups (Y15, K89, F88, and P80) and two single-residue subgroups (M0 and S38) (Figure 4A). The subgroups consist of residues in the box-region, the N’-tail and the box-linker. This is also shown in a cartoon view of the complex 3D structure (Figure 4A) in which the amino acids are colored as the subgroup to which they belong. The intermolecular contacts associated to different subgroups are asynchronous to each other (Supplementary Figures S14 and S15). The subgroup of the box-region (including F37) accounts for ∼66% of the overall contacts (Supplementary Table S6).

Figure 4.

Synchronic networks for noPTM (A), A (B), B (C), C (D) and D (E) complexes. The residues belonging to the different synchronic subgroups of each network are displayed also in 3D structure.

Unlike the noPTM case, the PtDNA•A–D networks consist mostly of only one multi-residue subgroup (Figure 4B–E), accounting for as much as 85–93% of the contacts (Supplementary Table S6). These involve both the box-region and the termini of the protein (Figure 4B–E). In the PtDNA•A-D networks, three to five residues bearing PTMs (a site bearing PTM is indicated as S_PTM) out of six to nine S_PTM are in this subgroup, indicating that several PTM-bearing residues contribute directly to the single synchronic subgroup.

We conclude that, unlike the noPTM case, almost all residues in the A–D complexes form synchronic contacts (comprising the stacking contacts of F37) with platinated DNA.

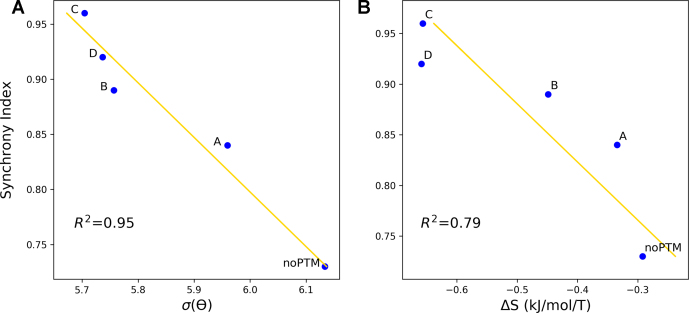
The degree of synchrony of the whole contacts network is measured by the network ‘synchrony index’: larger is the index, larger is the synchrony of all residues contact with PtDNA on average (see Materials and Methods). Consistently, the calculated network synchrony index is 0.73, 0.84, 0.89, 0.96 and 0.92 for PtDNA•noPTM and PtDNA•A–D, respectively. Figure 5A shows that the index turns out to correlate well with the fluctuations of a key descriptor of the local structure of the cross-linked guanines (θ, defined above). The larger are the fluctuations of θ, the larger the structural fluctuations of the notch, and hence the weaker the DNA/protein binding (19,69). This correlation provides a quantitative link between synchrony property and the key binding structure which determines the thermodynamic stability of the complex.

Figure 5.

Correlations between the synchrony indexes and: (A) the fluctuations of θ, expressed here as standard deviation of the distribution of values during the simulations, σ(θ); (B) the conformational entropy of binding (ΔS), calculated using the quasi-harmonic approximation (55). The calculated values are shown as blue dots, the linear fit as a gold line. The R² values are also reported.

The synchrony index turns out to correlate also fairly well with the change of conformational entropy upon binding (Figure 5B). This has been calculated using the quasi-harmonic approximation (55), see Materials and Methods. Our findings therefore suggest that higher is the synchrony of the interactions, higher is the entropic cost. This entropic cost may be overcome by other contributions, such as the entropic gain of the solvent and of the counterions and/or the enthalpic gain associated with the platinated DNA/protein binding (72–74). Indeed, we have found that higher is the synchrony index, larger is the decrease of entropy associated with the binding process but tighter is the binding at the notch.

We next investigated the conformational properties of the protein isoforms noPTM and A–D in water solution in the free state. We find that as many as 73%, 99%, 73% and 98% of the residues of noPTM exhibit larger RMSF values than A, B, C and D, respectively (Supplementary Figure S16). This points to larger fluctuations of the proteins in the free state in water solution in the absence of PTM. Hence, we may expect that higher is the conformational rigidity of the protein in the free state, higher is the synchrony of contacts in the formation of the complex. We conclude that the increase in synchrony associated with the presence of PTMs may originate, at least in part, from an increase of conformational rigidity of the proteins in the free state in water solution upon formation of the PTMs.

Overall, PtDNA•A–D feature significant differences with respect to PtDNA•noPTM. Moreover, isoforms PtDNA•A–D were the major components isolated in in vivo conditions (22), thus it is likely that PtDNA•noPTM does not play a dominant role in the specific case of platinum drugs. However, the multiple conformations of noPTM witness the ability of the protein to undergo structural changes, consequent to PTMs, allowing it to perform specific tasks on request.

CONCLUDING REMARKS

Although the PtDNA/HMGB1 complex is not the sole arbiter of cisplatin cytotoxicity (75–78), its well thermodynamic and structural characterization has provided a benchmark for the application of theoretical approaches to a better understanding of intermolecular recognition processes. Here, we have investigated the impact of multisite PTMs of HMGB1 isoforms occurring in vivo upon the formation of platinated DNA/HMGB1 complexes at atomistic level. The PTM patterns analyzed in the present case (Table 1) are those sorted out from a cellular milieu using a Pt-cross-linked DNA as a probe (22). Acetylation of lysines and phosphorylation of serines both reduce the positive charges on the HMGB1 protein, hence one may expect diminished electrostatic attraction for negatively charged DNA; (34,35) however, PTMs were experimentally found to increase the binding affinity of the PtDNA•protein complex (22). Our simulation suggests that the reduction of positive charges, consequent to lysine acetylation and serine phosphorylation, affects the nature of nonbonded contacts on passing from PtDNA•noPTM to PtDNA•A–D. The hydrophobic contacts constitute altogether > ¾ of the intermolecular contacts in all cases (Supplementary Table S3), while direct and water-mediated hydrogen bonds vary from 15 to 19% and from 5% to 7%, respectively. The change of these contacts can indeed affect the energetics of PtDNA•protein interactions (Supplementary Figure S12).

Interestingly, our calculations also showed that the occurrence of PTMs turns out to decrease the apparent flexibility of the hydrophobic anchor F37 sandwiched by the two cross-linked guanines. The stability of this hydrophobic binding is known to be a key element of the binding affinity between the protein and platinated DNA (19,69). Our simulation results are in line with the experimental findings that overall, A–D bind to PtDNA with higher affinity than noPTM (22): indeed, the F37 stacking is stronger in A–D than in noPTM (Figure 3).

Besides the F37, other two separate domains of the protein, the protein terminal loops, are also much less flexible in PtDNA•A–D than in PtDNA•noPTM. This is due, at least in part, to the inherent higher structural rigidity on passing from noPTM to A–D in water solution.

To identify a link between the structural rigidity of the protein terminal loops and the better fitting between the F37 and the two cross-linked guanines in A–D, we defined a mathematical quantity which monitors the synchrony in the formation of all the intermolecular contacts between protein and PtDNA. The degree of synchrony of the protein–PtDNA interactions, which is characterized in this work by synchronic networks and synchrony indexes, were significantly increased for all the four PTM isoforms. High synchrony of the protein–PtDNA contacts requires better collectivity or cooperativity of these individual contact domains, which means that the overall protein–PtDNA interfaces are more stable after PTMs. Moreover, we observed a fair anti-correlation between the fluctuation of the descriptor of the key binding site F37 and the synchrony index. The latter characterizes the synchrony of the protein–PtDNA interface globally. Therefore, the stabilized binding of F37 on the interface is due to better synchrony of all the contacts regulated by the PTMs. The synchrony analysis represents a different, independent, and valuable point of view to investigate standard thermodynamic variables such as the configurational entropy or the binding free energy. In addition, it is a convenient way to show interface contacts’ cooperativity (Figure 4) and conformational flexibility (Figure 5). Both aspects do not emerge from other types of analysis. Thus, it is possible to conclude that the synchrony analysis represents a new tool to investigate intermolecular recognition processes.

In summary, our study on the PTMs of HMGB1-PtDNA complexes reveals that a collective behavior of multisite PTMs can contribute to stabilize the key contact between the F37 and the cross-linked site of PtDNA. This in turn may contribute to the experimentally observed increasing of binding affinity of the complexes on passing from noPTM to A–D.

SUPPORTING INFORMATION

Clustering analysis, secondary structures, RMSD, RMSF of the proteins; RMSF, RMSD, helix axes subtending angle, bond angles around the platinate atom, helical parameters of the PtDNA; intermolecular contacts, water-mediated hydrogen bond contacts between the protein and PtDNA; homology modeling, MD parameters, simulation, other technical details of analyses employed in this work, and the energetics of the intermolecular contacts.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Horizon 2020 research and innovation program of the European Commission under the Marie Sklodowska-Curie Grant Agreement [642069 to W.L., P.C., G.R.]; National Natural Science Foundation of China [21505134 to W.L.]; F.A. and G.N. thank the University of Bari and the Consorzio Interuniversitario di Ricerca in Chimica dei Metalli nei Sistemi Biologici (CIRCMSB) for support. Funding for open access charge: Horizon 2020 research and innovation program of the European Commission under the Marie Sklodowska-Curie Grant Agreement [642069].

Conflict of interest statement. None declared.