Computational methods for analyzing and modeling genome structure and organization

Abstract

Recent advances in chromosome conformation capture technologies have led to the discovery of previously unappreciated structural features of chromatin. Computational analysis has been critical in detecting these features and thereby helping to uncover the building blocks of genome architecture. Algorithms are being developed to integrate these architectural features to construct better three-dimensional models of the genome. These computational methods have revealed the importance of 3D genome organization to essential biological processes. In this article, we review the state of the art in analytic and modeling techniques with a focus on their application to answering various biological questions related to chromatin structure. We summarize the limitations of these computational techniques and suggest future directions, including the importance of incorporating multiple sources of experimental data in building a more comprehensive model of the genome.

Graphical Abstract

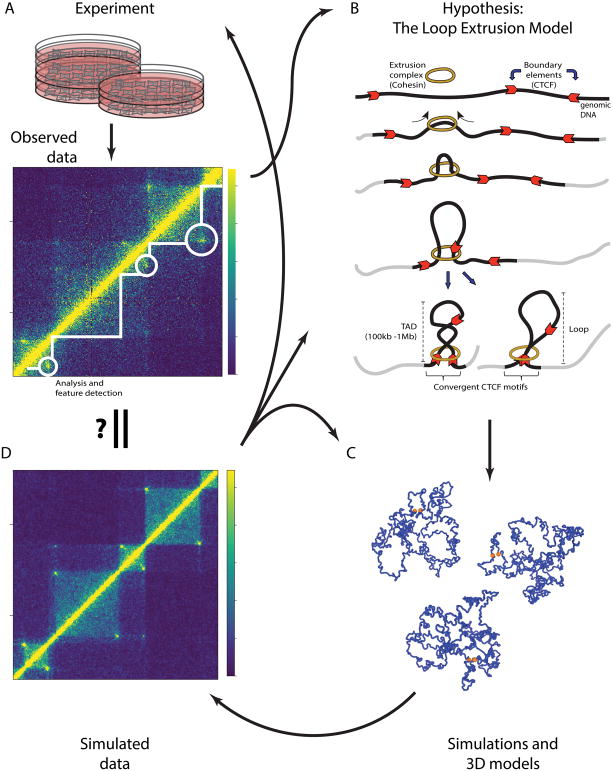
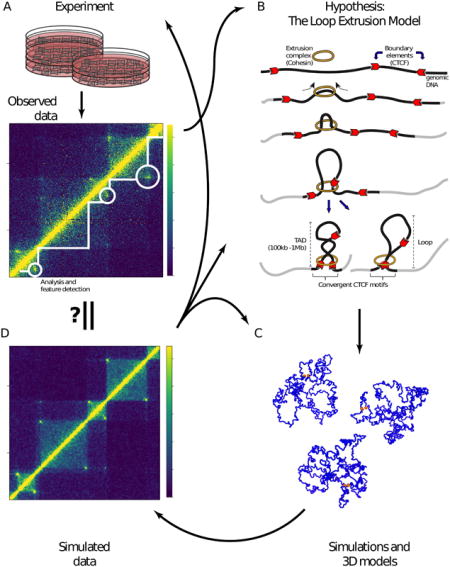
The iterative process of experimentation, hypothesis generation and confirmation of 3D genomic features, exemplified by the development of the loop extrusion model

INTRODUCTION

Growing evidence points to the significance of three-dimensional organization of chromatin for the biological functions of the genome (Bickmore & van Steensel, 2013; Pombo & Dillon, 2015; Sexton & Cavalli, 2015; Bonev & Cavalli, 2016). It has long been appreciated that each chromosome is localized to its own sub-volume, or “territory,” within the nucleus (M. Cremer et al., 2001; T. Cremer & Cremer, 2010). Chromosome territory formation represents the highest level of genome organization and is important for biological functions such as X-chromosome silencing (Chen et al., 2016; Deng et al., 2015), response to DNA damage repair (Mehta, Kulshreshtha, Chakraborty, Kolthur-Seetharam, & Rao, 2014) and various cell differentiation processes (Martou & De Boni, 2000; Borden & Manuelidis, 1988; Solovei et al., 2009). DNA-DNA interactions predominantly occur within each territory, and intrachromosomal interactions between distal regulatory elements such as enhancers and target gene promoters are critical for biological functions (de Laat & Duboule, 2013; de Wit & de Laat, 2012; Dixon et al., 2012; Gorkin, Leung, & Ren, 2014; Levine, Cattoglio, & Tjian, 2014; Nora et al., 2012).

The development of chromosome conformation capture (3C) and its high-throughput relatives, such as 4C-seq, ChIA-PET, Hi-C, HiChIP and PLAC-seq, has enabled researchers to uncover a hierarchy of sub-territory features involved in chromosome folding, including compartments (Lieberman-Aiden et al., 2009), topologically associating domains (Dixon et al., 2012; Nora et al., 2012; Phillips-Cremins et al., 2013; Dowen et al., 2014) and chromatin loops (Rao et al., 2014). The advent of these high-throughput technologies has resulted in the generation of a large amount of data, requiring computational approaches for its processing and analysis, many aspects of which have been thoroughly reviewed before (Ay & Noble, 2015; Forcato et al., 2017; Han & Wei, 2017; Davies, Oudelaar, Higgs, & Hughes, 2017; Schmitt, Hu, & Ren, 2016).

Additionally, it is important to synthesize information from various types of experiments to generate a more complete picture of genome organization and function. Toward this end, studies of in silico construction of 3D models of chromosome structure aim to reveal the mechanisms responsible for genome organization (Mirny, 2011; Ay & Noble, 2015; M. V. Imakaev, Fudenberg, & Mirny, 2015).

In this review, we will more fully describe the hierarchy of 3D genomic features introduced above, with a focus on the computational methods that are used for their detection. We will then review algorithms for the generation of 3D models of chromosomes, emphasizing their application for gaining a better understanding genome organization and function.

PART I: FEATURES OF 3D NUCLEAR ORGANIZATION AND METHODS FOR THEIR DETECTION

We will first describe the basic principles of processing and representing data from chromosome conformation experiments (3C) with a focus on the Hi-C method and variants of ChIA-pet, as these assays facilitated the generation of rich datasets that are best suited to the application of computational methods. We will review computational methods that helped to elucidate the organization of chromosome conformation at different scales using 3C data. We start by describing established practices on how to process Hi-C data and represent genome-wide interactions as a contact matrix. Next, we describe computational methods for automated detection of the compartmentalization of the genome into states representing different levels of chromatin activity. We then present methods for identifying finer units of chromatin organization such as the topologically associating domains, a spatially dense contiguous mass of chromatin that can range from tens of kilobases to megabases in scale. Finally, we describe approaches for detecting point contacts, or “loops”, that form between tightly interacting pairs of loci, which typically required higher resolution data to be resolved. At each feature level, we discuss the implications of their existence with respect to relevant biological processes. We conclude by providing a brief overview of methods for visual inspection of 3C data.

Inter- and intrachromosomal DNA-DNA contacts

In principal, the Hi-C protocol allows one to determine the interaction frequency between all pairs of DNA loci across the genome within a population of cells. (Lieberman-Aiden et al., 2009). The interacting DNA fragments are captured as a library of DNA-DNA hybrid sequences whose ends are sequenced and aligned to a reference assembly. Hi-C data is typically analyzed by binning counts of DNA-DNA contacts from uniquely aligned reads within equally-sized bins across the genome. In the resulting “contact matrix” the value C_ij in row i and column j is the number of observed interactions between DNA loci falling within the i^th and j^th bins (Lieberman-Aiden et al., 2009). The contact matrix therefore reflects pairwise interaction frequencies between all pairs of DNA loci along the genome within the nuclei of a population of cells. The bin size is typically referred to as the “resolution” of the experiment because it sets the minimum scale at which interactions can potentially be resolved. Raw binned counts need to be normalized to account for regional sources of bias, such as GC content and restriction fragment length, as well as differences in sequencing depth. A detailed discussion of the data processing pipeline for converting raw Hi-C sequenced reads into contact matrices of binned interaction counts and the attendant computational challenge of data normalization have been reviewed previously (Ay & Noble, 2015; Schmitt, Hu, & Ren, 2016). Briefly, one of two approaches is typically used to normalize binned data. Explicit factor normalization empirically assesses specific types of biases along the genome, including GC content and fragment length, and scales the binned counts accordingly (Yaffe & Tanay, 2011; Hu et al., 2012). In contrast, the iterative correction (and eigenvalue decomposition, or ICE) method assumes that the total counts in every row and column of a contact matrix should be the same, an expectation that is met by solving a convex optimization problem. This optimization produces a “bias vector” that characterizes the aggregated biases at each genomic bin position and used to normalize the count matrix. The original approach involves alternating between the rows and columns in an iterative manner until convergence (M. Imakaev et al., 2012), though other a more efficient and stable optimization algorithm has been described (Knight & Ruiz, 2013).

For visualization purposes, the contact matrix of raw or normalized interaction counts can be plotted as a heat map, or “contact map,” (Fig. 1) (Lieberman-Aiden et al., 2009). Due to the extremely wide dynamic range in the count data, the color scale of the heat map is typically either clipped or the data itself transformed (log, inverse hyperbolic sine, quantile, Pearson or Spearman correlation) to better show structure. Even with sparse data and low resolution binning, Hi-C should capture chromosome territories (Bolzer et al., 2005; M. Cremer et al., 2001; T. Cremer & Cremer, 2010), which manifest themselves as a dominant diagonal in a genome-wide contact map, representing a strong enrichment for intrachromosomal (cis) interactions relative to interchromosomal (trans) interactions (Fig. 1A). By contrast, interchromosomal contacts are relatively rare with non-specific ligations (the noise) making up a higher proportion of putative contacts than is the case for intrachromosomal contacts. Real interchromosomal interactions (the signal) are thus more difficult to discern. However, the coarsest possible level of contact aggregation, where all the contacts made by each chromosome are considered, has revealed that smaller chromosomes tend to show greater co-localization in the mammalian nucleus than their larger counterparts, likely towards the interior of the nucleus (Lieberman-Aiden et al., 2009).

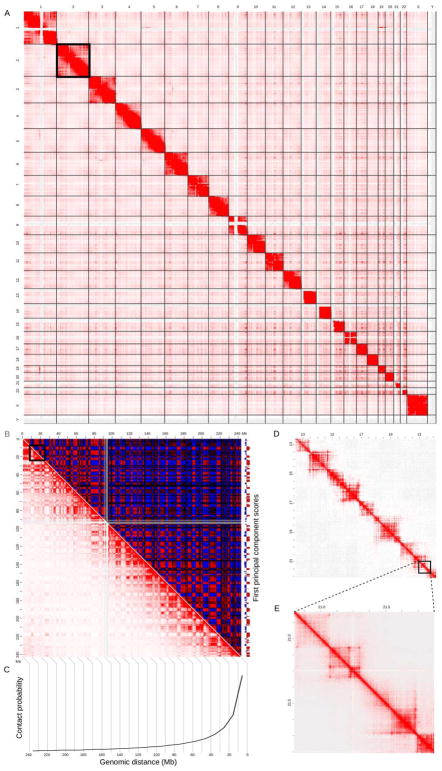
Figure 1. An exemplar Hi-C contact map highlighting various features identifiable at different resolutions.

A) A genome-wide contact matrix derived from a Hi-C experiment can be visualized using a heat map such as the one shown here derived from a Hi-C experiment on IMR90 cells (Rao et al., 2014). Note the prominent diagonal representing an enrichment of intrachromosomal contacts. Also discernible are enhanced levels of interchromosomal interaction among the smaller chromosomes. B) As in A, but only for chromosome 2 (boxed in A) with the upper triangle showing the Pearson correlation of the observed/expected matrix. This transformed matrix is subjected to eigenvalue decomposition to obtain the first principal component that captures the compartmentalization of the chromosome, as illustrated in the track on the right of the matrix. C) A schematic representation of the contact decay curve obtained by considering the average number of contacts within each diagonal row of bins moving away from the main diagonal. The curve captures the exponential decay in contacts with respect to genomic distance. Note that this decay curve is shown in a reverse orientation to that typically presented, in order to give the reader a better intuition of how it is derived. D) As in A, but for a subregion of chromosome 2 (boxed in B) and a resolution (50kb) that allows for the topologically associating domains (TADs) to be discerned. E) As in D, but for a smaller subregion (boxed in D) and a resolution (5kb) that allows for contact peaks to be discerned. All heat maps were produced using JuiceBox (Durand et al., 2016).

Contact maps for individual chromosomes are characterized by an enrichment for interaction counts along the diagonal, representing the very strong bias for capturing short-range interactions along the linear genome common to all 3C-based techniques (Fig. 1B lower triangle). Indeed, a hallmark of intrachromosomal interactions is that the number of captured contacts decays exponentially with respect to genomic distance. This “genomic distance effect” is a property of 3C methods in general, including 4C-seq, a high-throughput method for the detection of all interactions made by a single DNA locus (or “viewpoint”) with all other loci across the genome (van de Werken et al., 2012). The output of one 4C-seq experiment is a vector of binned intrachromosomal counts that corresponds to a single row or column in a Hi-C contact matrix with counts decaying exponentially as one moves away from the viewpoint, something made evident by simply plotting the vector. In a similar fashion, one can plot the average contacts versus genomic distance using Hi-C data, resulting in so-called “contact decay profiles” (Fig. 1C). Such plots provided key insights into the folding properties of the genome. (Lieberman-Aiden et al., 2009). Different decay rates have been associated with specific stages of the cell-cycle and differentiation (Zhu et al., 2017). Most strikingly, Naumova et al. showed that the nucleus assumes a very particular conformation during mitosis, accompanied by a distinct rate of decay with respect to contact distance. This observation facilitated the derivation of polymer models that recapitulate the experimentally-derived curves (Naumova et al., 2013).

Contact matrices derived from Hi-C data are foundational to identifying features of 3D genomic interactions, and contact decay curves represent a useful first approach to interrogating the nuclear structure of cells as they can be easily generated using even low-resolution data. Accurate contact decay curves are also essential for determining the baseline probability of contacts at a given distance in order to assess the significance of greater-than-expected local contacts (hotspots or peaks) in a contact map using methods to be discussed below.

Nuclear compartment structure

Going beyond the fundamental relationship between the frequency of DNA-DNA interactions and linear genomic distance, Lieberman-Aiden et al. used Hi-C data to partition the genome into two types of compartments, labeled “A” and “B.” The defining characteristic of a compartment is that pairs of loci within one type of compartment tend to interact with one another more frequently than they interact with loci from the other type of compartment (Lieberman-Aiden et al., 2009). These compartmental patterns were identified in Hi-C data from human cell nuclei by a three-step process. First, the contact matrix is adjusted to account for the genomic distance effect by dividing the observed counts in the contact matrix by the values expected given the bins’ distance from the diagonal. Second, the resulting observed/expected matrix is converted to a correlation matrix, in which the entry in row i and column j is the correlation between rows i and j of the observed/expected matrix (Fig. 1B upper triangle). Third, the transformed matrix is subjected to principal component analysis, or eigenvalue decomposition, in order to segment the genome based on the patterns of interaction that represent the majority of the variation in the Hi-C data (Fig. 1B component score track at right). In general, regions in which the first principal component is positive correspond to one compartment, while regions with negative values correspond to the second compartment (Lieberman-Aiden et al., 2009). Since the sign of component scores is arbitrary, regions are assigned to the A or B compartment type according to the linear genomic feature characteristics that are typically associated with these domains. For instance, Lieberman-Aiden and colleagues recognized that the A compartment tends to be enriched for gene density, chromatin accessibility, and associated histone modifications, such as histone 3 lysine 27 and 36 trimethylation (Lieberman-Aiden et al., 2009). Subsequently, A and B compartments were shown to be associated with early and late replication timing, respectively (Ryba et al., 2010; Yaffe & Tanay, 2011; M. Imakaev et al., 2012). In general, the A compartment contains relatively accessible, active euchromatin, whereas the B compartment tends to contain inaccessible, inactive heterochromatic regions (Solovei, Thanisch, & Feodorova, 2016; van de Werken et al., 2017).

Subsequent studies resolved the two major compartments seen in mammalian genomes into further subcompartments. Yaffe and Tanay, for instance, found a third, gene-poor cluster by applying k-means clustering to the interchromosomal contact matrix (Yaffe & Tanay, 2011). Later on, by applying an unsupervised Gaussian hidden Markov model clustering algorithm to far higher resolution Hi-C data, Rao and colleagues found that the A compartment could be partitioned into two subcompartments and the B compartment into three, each having their own distinctive chromatin characteristics (Rao et al., 2014). Indeed, A- and B-type subcompartments may well be self-organized by the inherently self-interacting propensities of their respective epigenetic modifications in a manner akin to liquid phase separation (Strom et al., 2017; Larson et al., 2017; Hult et al., 2017). Recent work has shown that the subcompartment types can be very well predicted by their chromatin state (Di Pierro, Cheng, Lieberman Aiden, Wolynes, & Onuchic, 2017).

Compartmental analysis is now performed routinely. The analysis can be performed using relatively low coverage and large bin sizes, yielding easily interpretable results even when restricted to the two main A and B compartment types.

Topologically Associating Domains

Nuclear compartment structure is a feature that was immediately observed from Hi-C data due to the fact that it can observed at relatively low resolution. Deeper sequencing and higher resolution contact matrices were required in order to observe additional, finer grained features. Deeply sequenced Hi-C libraries derived from Drosophila led to the discovery of “physical domains” of elevated self-interaction (Sexton et al., 2012), which are only evident at higher resolutions. Interrogation of the 3D conformation around the Xist locus in the mouse using the 5C technique revealed similar self-interacting regions, called topologically associating domains (TADs), in mammals (Fig. 1D and 2A) (Nora et al., 2012). These distinctive triangular features along the diagonal of a Hi-C contact matrix represent broad domains of enriched interactions. TADs can be detected genome-wide in both mouse and human cells using Hi-C data at 40 kb resolution and were found to be relatively well conserved across cell types and even across the two species. Furthermore, TAD boundaries were found to be enriched in housekeeping genes, and binding of PNA polymerase II (PolII) and CCCTC-binding factor (CTCF) (Dixon et al., 2012; Dixon, Gorkin, & Ren, 2016).

Figure 2. The iterative process of experimentation, hypothesis generation and confirmation of 3D genomic features, exemplified by the development of the loop extrusion model.

A) A Hi-C experiment results in the production of a contact matrix, which is visualized using a heat map. Computational analysis facilitates the detection of 3D genomic features such as topologically associating domains (TADs; white lines) and loops (white circles). Observations of such 3D features, aided by integration of linear genomic features (not shown), result in the development of a hypothesis as to their origin. B) A schematic representation of the loop extrusion model (described in the text), a hypothesis explaining the formation of TADs and loops. C) A polymer model of the chromosome is built based on a hypothesis such as the loop extrusion model. Simulations of the polymer model then produce an ensemble of 3D structures (only three are shown here) of the chromosome. The boundary element are highlighted as orange spheres while the rest of the chromosome is in blue. D) The ensemble of structures from loop extrusion model simulations are used to compute a contact map (Sanborn et al., 2015). This contact map is then compared to observed data (see A) leading to refinement of the hypothesis (see B) and/or details regarding its implementation, such as optimizing parameters (see C). Additionally, functional experiments can also be conducted to validate the hypothesis, potentially necessitating the generation and testing of new ones.

Many methods have been developed to identify TADs. Initially, the boundaries of TADs in Drosophila were identified as restriction fragments in a Hi-C library that exhibited a peak in the local rate of contact decay (or “distance-scaling factor”) (Sexton et al., 2012). Subsequently, Dixon et al. identified TADs genome-wide using Hi-C data by means of the “directionality index” metric, which quantifies the extent to which read-pairs make intrachromosomal contacts either upstream or downstream of each genomic locus. TAD boundaries exhibit distinctive patterns in the directionality index score along the genome, and these patterns are identified by a hidden Markov model (Dixon et al., 2012). Another approach is to use “the insulation score,” defined as the sum of contact counts falling within a diamond-shaped area that touches the diagonal of the contact matrix. A series of scores is computed by running the diamond across all bins falling along the diagonal. Borders between TADs are then identified as those bins that exhibit a local minimum in the insulation score, which conversely represents a local maximum of insulation between adjoining domains (Crane et al., 2015). Many additional methods have been developed to identify TADs, which have been thoroughly contrasted and compared in two recent studies (Dali & Blanchette, 2017; Forcato et al., 2017).

TADs have been hypothesized to arise from an entirely different process from that responsible for the nuclear compartment structure during interphase. This process was described in the so-called “loop-extrusion model” (Fig. 2B) (Sanborn et al., 2015; Fudenberg et al., 2016), with similar models having previously been hypothesized to play a role during mitosis (“DNA methylation and late replication probably aid cell memory, and type I DNA reeling could aid chromosome folding and enhancer function”, 1990; Alipour & Marko, 2012). This model posits that loop-extruding factors bind to locations along the DNA and proceed to spool out two strands in opposing directions until they are halted at boundary elements, leading to the formation of loops. The loop extrusion factors and boundary elements correspond to macromolecular complexes. A TAD manifests itself due to the preferential interactions among the loci that lie between a pair of boundary elements. Simulation studies suggest that TAD formation is most likely driven by the continuous loading and unloading of the extrusion factors from the chromatin (Fudenberg et al., 2016). In accordance with CTCF’s observed enrichment at TAD boundaries, CTCF has been proposed to be the most important contact domain boundary element, whose DNA binding motifs most often show a convergent orientation at each end of a loop (Rao et al., 2014; de Wit et al., 2015; Vietri Rudan et al., 2015). The cohesin protein complex is believed to be a necessary component in the extrusion mechanism, quite possibly with the support of additional factors. However, the actual mechanism behind loop extrusion is not known, and no component with a motor function has been characterized to date. However, recent studies have shown that a protein complex closely related to cohesin, namely condensin, can perform extrusion, at east in yeast (Terakawa et al., 2017; Ganji et al., 2018). Furthermore, experimental support for the loop extrusion model by cohesin during interphase in mammalian systems has shown that TADs are eradicated, or at least diminished, by the removal of cohesin from chromatin and that energy is required for extrusion to occur (Schwarzer et al., 2017; Rao et al., 2017; Haarhuis et al., 2017; Vian et al., 2018). On the other hand, compartmental patterns were shown to decrease when cohesin levels on DNA increased, but remain intact in Hi-C data, and in fact become more fully resolved, when the proposed extruding factor is removed. These results indicate that TAD structures in mammals arise from a mechanism that is independent of the overall A/B compartment structure. In addition to giving rise to contact domains, the loop extrusion model has been used to explain the formation of loops, which reveal themselves as hotspots, or peaks of interaction, in a contact map and will be discussed in more detail in the next section (Sanborn et al., 2015).

Contact enrichment and loops

Historically, the 3C method was developed as an assay to confirm or rule out the existence of hypothetical point contacts between two distinct loci identified by two specific PCR primers (Dekker, Rippe, Dekker, & Kleckner, 2002). All subsequent 3C-based techniques, including 4C(-seq), 5C, and Hi-C and related methods, have applied this same basic approach to achieve higher throughput and more unbiased, genome-wide assessments of DNA-DNA interactions. The problem of identifying significant intrachromosomal interactions from genomic data first arose with the advent of 4C-seq, as it was one of the first high-throughput 3C methods (van de Werken et al., 2012). Loci which make specific contacts with the 4C viewpoint are evident as peaks in a plot of the 4C-seq interaction count vector (described previously). Peaks are identified as bins that show statistical significance relative to an empirical or theoretical background model (van de Werken et al., 2012).

A conceptually similar approach was taken to identify Hi-C contacts that exhibit statistically significant deviation relative to a background model. These methods attempt to control for confounding factors such as noise, sparsity and other properties of Hi-C data. One of the earliest such methods was Fit-Hi-C (Ay & Noble, 2015), which incorporates the genomic distance effect and ICE biases to model the background distribution. The HiC-DC method improves on Fit-Hi-C by also modeling the sparsity and accounting for the fact that genomic count data typically exhibits higher variance than expected (overdispersion) (Carty et al., 2017). Accordingly, HiC-DC yields more conservative estimates of statistical significance.

In contrast to contacts that are deemed significant relative to a global background model, a “loop” is a localized peak of enrichment for DNA-DNA contacts (Fig. 1E and 2A) (Rao et al., 2014). Loops often represents functionally important interactions, such as those between promoters and enhancers or between CTCF binding loci. The latter have been implicated in the formation of domains and overall 3D organization of the genome; hence, identification of loops may be necessary to fully appreciate principles of 3D organization and its role in transcriptional regulation. Since loops represent a specific type of significant contact, the Fit-Hi-C and HiC-DC methods typically include loops among their outputs. In contrast, HiCCUPS was specifically designed to identify loops (Rao et al., 2014). The method compares each entry in a contact matrix to various assemblages of surrounding entries to estimate the background, using very high resolution contact matrices (5kb) as input. HiCCUPs identifies the “peak”, or most enriched bin, in a neighborhood, which represents contacts which correspond to loops. Using extremely deeply sequenced Hi-C data consisting of billions of reads, Rao and colleagues were able to detect thousands of loop contacts in human cells using the HiCCUPs method, many of which connected two CTCF-bound sites (Fig. 2B) (Rao et al., 2014). Intriguingly, the vast majority of the CTCF-anchored looping contact points harbored CTCF motifs that showed a convergent orientation. This result helped to inspire the loop extrusion model, showcasing how a computationally-derived result can provide valuable biological insight and aid hypothesis generation (Fig. 2B).

Recently, a novel category of genomic loci was described as “frequently interacting regions” (FIREs) (Schmitt, Hu, Jung, et al., 2016). These are regions that are putatively enriched for enhancer-promoter interactions. FIREs are apparent in a Hi-C contact matrix as stretches of enrichment along one row or column of the contact matrix, starting a couple of hundred kilobases away from the diagonal. FIREs were characterized computationally based on Hi-C data from a variety of human and mouse tissues. Contact counts were normalized using explicit factor normalization and then aggregated within a bidirectional 15–200kb region from the diagonal of the contact matrix and assigned a significance score. Significant bins were shown to be enriched at sites of tissue-specific chromatin interactions and co-binding by CTCF and cohesin.

3C-based assays have been developed that focus on subsets of loci rather than the entire genome, facilitating identification of long-range DNA-DNA interactions. By performing an additional immunoprecipitation step, the ChIA-PET assay identifies sets of 3C interactions that are enriched for binding of specific protein complexes, such as CTCF loops, which may or may not be as the tether that brings two loci together (Handoko et al., 2011). This and recently developed related assays, such as HiChIP and PLAC-seq (Mumbach et al., 2016; Fang et al., 2016), require less sequencing depth than Hi-C to achieve similar resolution. ChiaSig (Paulsen, Rodland, Holden, Holden, & Hovig, 2014) and Mango (Phanstiel, Boyle, Heidari, & Snyder, 2015) are methods for identifying significant interactions from ChIA-PET assays. These methods model the genomic distance effect and immunoprecipitation effects on different loci. The two tools perform similarly, with Mango having the best concordance with Hi-C data (Phanstiel et al., 2015). The capture-C assay (Hughes et al., 2014) and targeted DNase-Hi-C (Ma et al., 2015) are also designed to measure interactions involving a specified set of loci (such as promoters). In this case, specificity is achieved by selecting and sequencing only a subset 3C interactions that are captured by oligonucleotide probes corresponding to loci of interest. As with the selection of contacts associated with specific proteins by immunoprecipitation, oligonucleotide selection approaches attempt to address the problem of sparsity that typifies genome-wide Hi-C data. In this case, this is achieved by interrogating a much smaller subset of potential pairwise interactions, those made by well-defined regions of the genome. The CHICAGO method was developed for the analysis of capture Hi-C data. This method uses a background model that incorporates the genomic distance effect and locus specific noise model to robustly identify capture-C interactions (Cairns et al., 2016). Finally, we note that the CHiCAGO, Fit-Hi-C and HiC-DC methods all assume a uniform genomic distance effect between all equidistant pairs of loci. In practice, the genomic distance effect can vary depending whether a pair of loci are in the same compartment or within the same TAD.

3D Genomic Feature Visualization

Computational methods automate the detection of features that can typically be identified by visualizing contact maps. Indeed, in most cases the features described in this part of the review were first observed by eye (Fig. 1 and 2A,D). We used JuiceBox (Durand et al., 2016), for instance to produce the heat maps in Fig. 1. It is common practice to include other 1D genomic features in such visualizations to aid hypothesis generation regarding the 3D organization of chromatin, such as the principal component scores in Fig. 1B. Visualization tools (reviewed in (Yardımcı & Noble, 2017)) are thus essential for the study and validation of detected features.

IN-SILICO MODELING OF GENOME STRUCTURE

In Part I, we focused on computational approaches used to identify different structural features in the 3D genome. We will now discuss various methods to construct 3D models of the genome, where the aforementioned features manifest themselves as different aspects of the 3D model. 3D modeling approaches are potentially powerful because they can provide insights into the principles of 3D genome organization, allow one to visualize multiple genomic features simultaneously in their 3D context, and provide a simulated environment for testing various models based on experimental data. Much of the methodology behind various 3D modeling approaches has been reviewed before (Ay & Noble, 2015; M. V. Imakaev et al., 2015; Rosa & Zimmer, 2014; Dekker, Marti-Renom, & Mirny, 2013; Mirny, 2011). Here we provide an overview of these methods and discuss their strength in various contexts and give some examples of using them to understand genome architecture.

3D modeling of genome folding

Early attempts to model the 3D structure of genomes (reviewed in (Mirny, 2011; Rosa & Zimmer, 2014)) treated each chromosome as a polymer and applied polymer physics to simulate the chromosomes’ behavior in the nuclei. Most of these models rely on a small set of parameters that characterize the global structural properties of the polymer. The definition and setting of parameters in turn depend on certain hypotheses regarding how the modeled chromosomes fold. With these parameters set, one can use statistical physics to simulate the motion of the polymers and then validate the results against experimental data. These models do not require fitting or training against experimental data, and they are often used to test mechanistic theories of genome organization. In general, the focus of these models is on the global and large-scale properties of the genome, such as formation of chromosome territories, rather than the interrogation of specific interactions between certain loci. Next we will provide examples of some studies using such methods.

Folding of the budding yeast genome

The budding yeast genome organization has been well studied by microscopy (Jin, Fuchs, & Loidl, 2000; Bystricky, Laroche, van Houwe, Blaszczyk, & Gasser, 2005; Schober et al., 2008; Berger et al., 2008; Therizols, Duong, Dujon, Zimmer, & Fabre, 2010) and chromosome conformation capture (Dekker et al., 2002; Rodley, Bertels, Jones, & O’Sullivan, 2009; Duan et al., 2010; Kim et al., 2017). These experimental studies suggest that the budding yeast chromosomes are folded into the so-called Rabl configuration: the chromosome arms emanate from the spindle pole body where the centromeres cluster. Several groups have performed numerical simulations of the budding yeast chromosomes (Tjong, Gong, Chen, & Alber, 2012; Tokuda, Terada, & Sasai, 2012; Wong et al., 2012), where the chromosomes are modeled as block polymers with each block representing either the centromeres, telomeres or ribosomal DNA. The block parameters are set according to the Rabl configuration. For example, the centromeres are confined within a certain region of the nucleus representing the spindle pole body. Aside from the Rabl restraints, the polymers are subjected to stochastic thermal motions mimicking the effects of solvents (water) and other chemicals omitted from the simulations on the polymers. The snapshots from these simulations, each corresponding to one particular conformation of the genome, are collected, and the ensemble of snapshots can then be used to compute statistical averages of various structural features of the genome. These features are then compared to the corresponding experimental ones for validation. The simulated structures of the genome in these studies agree qualitatively with the experimentally observed ones. The simulated structures also manifest the heterogeneity of the genome structure ensemble, in which individual nuclei in the experimental samples can exhibit very different chromosome conformations.

Folding of the mitotic chromosome

Chromosomes condense into a highly compact conformation during the cell cycle’s metaphase. As mentioned in Part I, a study based on chromosome conformation capture revealed distinct features of the mitotic chromosome: the loss of chromosome compartments and intrachromosomal contact domains such as TADs (Naumova et al., 2013). An exciting aspect of this study was the application of polymer models to explain the features of chromosome compaction during mitosis. By comparing the modeled and observed intrachromosomal contact probability decay as a function of genomic distance, the authors concluded that a consecutive array of loops organized along a central axis of the chromosome better explain the experimental data than three other models tested (Naumova et al., 2013). This model suggested a two-stage folding of mitotic chromosomes: formation of the array of linearly organized loops followed by the axial compression the fiber of loop bases. In a more recent study of mitotic chromosome folding, Hi-C data were obtained at different stages of mitosis and in the corresponding condensins-depleted conditions, and separate polymer models were built for each experimental condition (Gibcus et al., 2018). Based on the assumption that the chromosome is confined in a cylinder and arranged as a helical loop array, the authors were able to fit a contact decay profile of the polymer model of a 40 Mb chromosome segment to the observed profile from the Hi-C data. These models illustrate a pathway for mitotic chromosome folding and the potential functions of condensins in this process. It is worth mentioning that the loop-extrusion model, which will be discussed further in the next section, has also been used to explain the compaction of chromosomes during mitosis and the segregation of sister chromatids (Goloborodko, Imakaev, Marko, & Mirny, 2016).

Folding of topologically associating domains

As described in Part I, TADs, or contact domains, are one of the major features of intrachromosomal interactions observed in chromosome conformation capture data. Several polymer models have been proposed recently to study the nature of TADs and the mechanism of TAD formation.

The “strings and binders switch” (SBS) model simulates the effect of macromolecules (the binders) binding on chromosome (the string) folding (Barbieri et al., 2012). The important feature of the SBS model is that the chromosome polymer has a series of binding sites, each of which has a certain binding affinity to some binders present in the simulation. The binders “glue” the different binding sites on the polymer together in a concentration dependent manner. In the SBS model, the formation of TADs is a consequence of folding of different regions of the chromosome induced by the distinct cluster of binders on it.

Similar in spirit to the SBS model, the loop-extrusion model involves external factors, called loop-extrusion factors, binding on the DNA polymer and inducing loop formation. The details of this model are discussed in Part I (see also Fig. 2). The loop extrusion model accounts for TAD formation as a balance between loop extrusion and boundary maintenance, which are represented as competing interactions in the polymer model. Recent simulations based on the loop-extrusion model suggest the loop-extrusion factors’ density on chromosome and their processivity can potentially be regulated to change the global organization of chromosome (Gassler et al., 2017).

However, neither the SBS model nor the loop extrusion model explicitly describes what happens to the regions of DNA that are looped out, where the modeled contact frequency in these regions is generally different from the experimental data. Another model hypothesizes that these regions are DNA with negative supercoiling induced by transcription and that transcription is the force that maintains the loop extrusion factors’ processivity in the loop extrusion model (Racko, Benedetti, Dorier, & Stasiak, 2017). In this new model, the polymer chain has ancillary beads branching out from the backbone and acting as handles of torsional restraints or torques exerted on the polymer. In an early version of this model, the authors showed that the supercoiled DNA exhibits contact frequencies that better resemble experimental data (Benedetti, Dorier, Burnier, & Stasiak, 2014) than a simple loop without supercoiling restraints.

Visualization of 3D genome structure

Consensus-based modeling approaches refer to the class of methods that infer a single 3D genome structure from one Hi-C data set (Ay & Noble, 2015; M. V. Imakaev et al., 2015). These consensus methods assume that it is possible to find a single structure that accurately represents the 3D structures of DNA in the cellular population being analyzed. When applied to bulk Hi-C data, this assumption is generally not true because the underlying genome structures in the experimental sample that give rise to the observed data is highly variable. For example, different cells in the sample can be in different cell-cycle stages, some of which have compact chromosome conformations that resembles the metaphase genome while others have less condensed conformation that is typical to interphase genome. Nonetheless, consensus models are easy to understand and to visualize. They allow visualization of different genomic features in the 3D context. Several software tools have been developed to render the inferred model in 3D (Serra et al., 2017; Nowotny et al., 2016; Asbury, Mitman, Tang, & Zheng, 2010). In the context of modelling single-cell haploid Hi-C data, the consensus assumption is more justifiable and has been used to provide 3D visualization of the Hi-C data (Nagano et al., 2017; Stevens et al., 2017).

Ensemble polymer models for joint analysis of genome structure and function

The broad spectrum of genomic and high-resolution microscopy data present a challenge for computational modeling. How can one model the genome in a way that is consistent with all the available data? Because most genomic assays to date are performed on a population of cells, one of the major obstacles in developing such a unified approach is how to model the heterogeneity in the experimental samples. To date, no experimental evidence indicates that chromosomal DNA can have a small set of stable 3D conformations. In fact, chromosomes are thought to be subjected to conformational changes resulting from various dynamic biological processes, such as transcription and replication. In 3C-based experiments, we do not know which subset of conformations were actually sampled from all the possible conformations. Furthermore, estimation of thermodynamic averages might also be necessary in order to validate the model using repeated measurements of single-cell data. The computational challenge here is that the deconvolution of highly complex ensemble data cannot in general be guaranteed to have a unique solution.

Nonetheless, attempts have been made to directly model the ensemble of chromatin structures, including the polymer models mentioned in the previous sections. The primary shortcoming of these models is that their performance heavily relies on the choice of modeling parameters, which are held fixed during the simulations and are not optimized to reproduce experimental data. Other approaches aim to overcome this problem by using machine learning algorithms to learn the parameters from experimental data (Baáù et al., 2011; Rousseau, Fraser, Ferraiuolo, Dostie, & Blanchette, 2011; Kalhor, Tjong, Jayathilaka, Alber, & Chen, 2012; Tjong et al., 2012; Hu et al., 2013; Giorgetti et al., 2014; Wang, Xu, & Zeng, 2015; Zhang & Wolynes, 2015; Di Pierro, Zhang, Aiden, Wolynes, & Onuchic, 2016; Tjong et al., 2016; Li et al., 2017; Di Pierro et al., 2017). For example, the Alber group inferred an ensemble of chromosome structures consistent with not only the Hi-C experiments but also the lamina-DamID data (Li et al., 2017). This modeling approach interprets different types of data as different distance restraints that are lumped together in an objective function to be optimized. The ensemble of structures are generated by multiple rounds of initialization and optimization of the objective function. However, as discussed above, the uniqueness of the solution cannot be guaranteed because the problem is formulated as a non-convex optimization problem in a very high-dimensional space and finding the global minimum of this optimization problem is intractable. Another limitation is that the variability of the generated structures requires careful tuning of the initialization and optimization procedure. Also, the weight of each generated structure in the ensemble is difficult to estimate, which in turn makes it difficult to consistently estimate ensemble averages from these structures (Carstens, Nilges, & Habeck, 2016). Another inference approach taken by the Wolynes group follows the maximum-entropy principle to generate an ensemble of structures from a consistently-estimated probability distribution. This probability distribution can be used to derive various quantitative comparisons between different models (Di Pierro et al., 2016), which are built, for example, from data obtained from different experimental conditions. However, the challenge in building this first-principle-based model is its computational complexity, which currently limits the approach to modeling individual chromosomes, ignoring interchromosomal interactions. The recent development of single-cell chromosome conformation capture (Nagano et al., 2013, 2017) inherently avoids the problem of convolving multiple structure in one data set, and pioneering work toward reconstruction of the chromosome structure from these single-cell data have been carried out (Stevens et al., 2017; Nagano et al., 2017).

CONCLUSIONS AND FUTURE DIRECTIONS

Imaging data and high-throughput genomic data, such as Hi-C, have dramatically advanced our understanding of the 3D organization of the genome and its role in transcriptional regulation and packaging of chromatin during development and in pathological states. Insights garnered from computational analyses have led to novel hypotheses regarding mechanisms responsible for maintaining 3D organization of chromatin and its impact on regulatory functions. These hypotheses can be validated by simulation and additional experiments, leading to an iterative process of hypothesis generation and confirmation, as exemplified by the development of the loop extrusion model (Fig. 2).

There is ongoing work to computationally assess and improve the quality of high-throughput 3C-based data. Recently, two new methods for measuring the reproducibility of Hi-C data have been proposed (Yang et al., 2017; Yan, Yardimci, Yan, Noble, & Gerstein, 2017), with more methods for reproducibility and quality determination in development. Recent approaches to improve data quality at high resolutions involve imputing the high-resolution matrix. Wang and colleagues published a method to improve high resolution matrix by learning local interaction structures from Hi-C and Capture-C datasets jointly (Bo et al., 2016). RIPPLE is another method that uses linear epigenomic features to predict long range interactions between functional sites across the genome, imputing a specific subset of entries within the high resolution matrix (Roy et al., 2015). We anticipate future studies will leverage additional genomic data sets and cutting-edge machine learning approaches to build on such work.

From a biological standpoint, one area that will require additional effort is in identifying all of the components involved in 3D genome structure and characterizing the interactions among them. An example of this is the need to identify the additional factors responsible for extruding DNA in the loop-extrusion model. Furthermore, although 3C-based assays provide snapshots of the DNA structure, it will be important to study the dynamic nature of features related to nuclear architecture and function over time. The 4DN Consortium has been established with the goal of addressing both these issues (Dekker et al., 2017). The 4DN Consortium is also leading efforts to develop new assays for assessing genome structure and function. For example, population-based 3C data represent the ensemble average of the chromosome structures from a large number of cells, each of which potentially represents a different developmental or cell cycle stage. The deconvolution of 3D structural features relevant to different subpopulations of cells is therefore a difficult task. Methodological and experimental innovations are in development to solve this problem; for example, a recent study used chemicals to arrest cells in different cell cycle stages and performed Hi-C in the arrested cells to obtain more homogeneous chromosome contact signals (Gassler et al., 2017). More importantly, recently developed single cell Hi-C assays (Nagano et al., 2017; Ramani et al., 2017) allow for the analysis of individual conformations of chromatin in a single cell. However, the extreme sparsity of such data will require the development of additional computational methods. Also, traditional 3C assays only measure pairwise contacts, when the reality may well be more complicated in that multi-way contacts are likely to occur. New biochemical assays have been described that address this issue (Olivares-Chauvet et al., 2016), which again will require appropriate computational methods. Genome architecture mapping (GAM) is a promising orthogonal method to both imaging and 3C-based approaches that can detect high order genomic organizational features of chromatin with the added benefit that it can detect multi-way contacts (Beagrie et al., 2017).

Microscopy experiments represent an additional rich source of information that is orthogonal to that obtained from the biochemical and genomic techniques that were featured in this review. These experiments provide inherently single-cell measurement of 3D structure of the genome, thereby circumventing the heterogeneity problem in population-based 3C assays; however, many microscopy approaches are laborious and low throughput. Recently proposed high-throughput super resolution microscopy experimental methods promise to allow the imaging of multiple loci at the same time in single cells (Wang et al., 2016). This is an exciting development for the field, because results from such studies will allow for a more direct means to validate features inferred from sequencing data and to better assess their dynamics over time and across populations. Indeed, with this in mind, the 4DN Consortium is placing a strong emphasis on the joint analysis of various data types, because results from these new microscopy-based techniques will complement biochemical and genomic approaches to help build a more complete picture of a functioning genome. The integration of these two very disparate data types poses an additional challenge for computational biologists, but the outcome of this exercise can potentially yield a unified modeling framework for genome architecture.