Abstract
In this work, we explore the applicability and limitations of the current Third Order Density Functional Tight Binding (DFTB3) formalism for treating transition metal ions using nickel as an example. To be consistent with recent parameterization of DFTB3 for copper, the parametrization for nickel is conducted in a spin-polarized formulation and with orbital-resolved Hubbard parameters and their charge derivatives. The performance of the current parameter set is evaluated based on structural and energetic properties of a set of nickel-containing compounds that involve biologically relevant ligands. Qualitatively similar to findings in previous studies of copper complexes, the DFTB3 results are more reliable for nickel complexes with neutral ligands than for charged ligands; nevertheless, encouraging agreement is noted in comparison to the reference method, B3LYP/aug-cc-pVTZ, especially for structural properties, including cases that exhibit Jahn-Teller distortions; the structures also compare favorably to available X-ray data in the Cambridge Crystallographic Database for a number of nickel-containing compounds. As to limitations, we find it is necessary to use different d shell Hubbard charge derivatives for Ni(I) and Ni(II), due to the distinct electronic configurations for the nickel ion in the respective complexes, and substantial errors are observed for ligand binding energies, especially for charged ligands, d orbital splitting energies and splitting between singlet and triplet spin states for Ni(II) compounds. These observations highlight that future improvement in intra-d correlation and ligand polarization is required to enable the application of the DFTB3 model to complex transition metal ions.
Keywords: DFTB3, DFT, Hubbard parameters, nickel, spin states, Jahn-Teller distortion
TOC Graphics
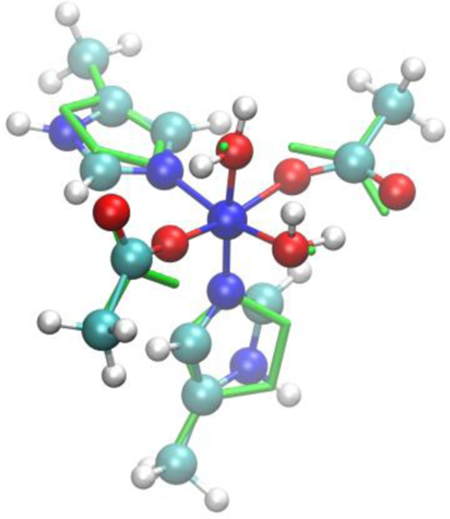
The Density Functional Tight Binding (DFTB) model parameterized for Nickel leads to reliable structural properties for Nickel-containing compounds, including Jahn-Teller distortions, but less accurate ligand binding energies. More sophisticated treatment of the d-d interactions is required to improve energetics, including the order of different spin states.
1. Introduction
Transition metal ions play various important structural and catalytic roles in biomolecules.1–2 To aid exprimental analysis regarding how transition metal ions contribute to biomolecular function, effective computational methodologies are needed. For structural properties, molecular mechanical (MM) force fields have been developed for treating metal ions at different levels of sophistication;3 these include simple van der Waals sphere models4–6, non-bonded dummy models,7 bonded force field models8–9, valence-bond models10–11 and ligand-field force field models12–15. To describe chemical reactions that involve transition metal ions, a quantum mechanical (QM) description is required, which include Density Functional Theory (DFT) and ab initio wavefunction approaches.16–17 The last several decades have seen tremendous progress in both classes of QM methods, and it has become possible to analyze the electronic structure of complex metal co-factors such as iron-sulfur clusters with modern electronic structure methods18. Nevertheless, these methods remain computationally expensive, thus even hybrid QM/MM calculations19–20 using a modest DFT or ab initio region are usually limited to minimum energy path type of calculation or free energy simulations with a minimal amount of sampling21. In some applications, the biological system of interest is highly flexible and therefore a meaningful study would require an extensive degree of sampling;22 examples include metalloenzymes that feature a high degree of catalytic promiscuity, metal ion transporters/transcription factors, proteins involved in the assembly of catalytic metal cofactors and peptides/proteins whose (mis)folding and aggregation behaviors are influenced by transition metal binding. For these problems, it is important to develop a QM method that allows adequate sampling while treating the transition metal ions with a reasonable level of accuracy. In this context, the traditional semi-empirical quantum chemical methods (MNDO23–25, AM126, PMx27–31, OMx32), although being 2–3 orders of magnitude faster than DFT and ab initio QM methods, face difficulties, since they are usually not accurate or transferable enough to deal with the complexity of transition metal ions. This is due in part to the fact that the basis of these semi-empirical methods is Hartree-Fock, in which electron correlation is neglected entirely.
Density Functional Tight Binding (DFTB) emerged33–35 in recent years as an alternative semi-empirical approach. It is rigorously rooted in DFT36, and almost all DFTB parameters are computed with DFT for atoms and small (diatomic) molecules; since it is derived from DFT, effects of electron correlation is included explicitly albeit in an approximate fashion. DFTB utilizes minimum valence basis sets and further reduces computational effort by approximations to the matrix elements, leading to 2–3 orders of magnitude faster computations than full DFT37. With careful parameterization, both the second-order (DFTB236) and third-order (DFTB338) formulations have proven applicable to many chemical, materials and biological problems, especially when sampling is important.34–35, 39–45
Specifically for metals, the first set of developed DFTB2 parameters was for zinc, which is a closed-shell d10 system46. Zheng et al.47 developed DFTB2 parameters for several first-row transition metal elements (i.e. Sc, Ti, Fe, Co and Ni); the model was shown to be adequate in predicting geometrical properties of organometallic compounds and small metal clusters48, although accuracy in energetics was lacking, especially concerning the order of different spin states. For the third-order model, DFTB3, parameters were developed for closed shell metal ions49 (Na, K and Ca), as well as for Mg and Zn50, in a framework consistent with the 3OB parameterization for the main group elements (C, H, N and O51, P and S52 and the halogens49) for chemical and biological applications. Recently, Gaus et al.53 developed parameters for Cu, which has a d10 or d9 electronic configuration, depending on the oxidation state. Their work considered spin polarization and spd l-dependent interactions; including the l-dependence in the Hubbard parameters was observed to be crucial to have a balanced treatment of Cu(I) and Cu(II) species.53 Structures and ligand binding energies were found to be generally in good agreement with reference B3LYP calculations with large basis sets (aug-cc-pVTZ), and in some cases the DFTB3 model was observed to outperform the parent DFT model (PBE) with medium sized basis sets, due to the use of higher-level methods for the parameterization. Overall, the performance for charge ligands was less satisfactory than for neutral ligands, an expected result considering the minimal basis set used in DFTB3; improving the treatment of electronic polarization will likely reduce the errors for charged and polarizable ligands, as found for intermolecular interactions42, 54–55. Finally, we note that Grimme et al.56 developed a tight-binding model for the entire periodic table, including transition metal ions; the model was fitted based on 32 transition metal complexes (which included only three Ni-containing compounds) and focused entirely on structural properties and vibrational frequencies without reported energetics.
In this work, we further explore the applicability of the DFTB3 model to transition metal ions by conducting parameterization for nickel, which is involved in enzymes vital in global carbon, nitrogen and oxygen cycles in fungi, algae, eubacteria and higher plants57–61. Seven of eight known nickel enzymes encompass the production or use of important gases (CO, CO2, CH4, NH3 and O2), e.g., Nickel Superoxide Dismutase62, Acireductone Dioxygenase63–64, Urease63, 65, CO Dehydrogenase66–67 and NiFe Hydrogenases68–69, highlighting the need of properly understanding nickel bonding and reactivity in biological environments.
We focus in this work on Ni(I) and Ni(II), which feature d9 and d8 electronic configurations, respectively. It must be stressed here that this study can only be carried out because these electronic configurations do not require to take into account the strong correlation between the electrons inside the compact d-shell. In particular, the d9 configuration contains a single hole that is equivalent to that of a non-correlated d1 configuration70 while in the d8 configuration the two possible ground states with S=0 and S=1 are usually well separated and many properties can be correctly predicted even when neglecting the intra-d correlation. A reliable treatment of these open-shell configurations would in principle require an explicit treatment of intra-d electron correlation, for example in the framework of LDA+U71 that would be impossible to avoid when dealing with d3 to d7 electron configurations. Prior to including such contributions to the DFTB model, however, it is worthwhile establishing what properties can be adequately described in the current DFTB3 framework, in which the intra-d interactions are treated in an averaged fashion, and what properties clearly require an improved treatment of the d electrons and other effects (e.g., ligand polarization and metal-ligand charge transfer). In particular, transition metal ions show a very strong correlation between their electronic structure, including the magnetic state, and the geometry leading to strong electron-vibration coupling phenomena that can play an important role in reactivity.72 Of particular importance is the Jahn-Teller effect where the geometry of the system is distorted towards lower symmetry because of the existence of two or more degenerate electron states whose electron distributions are different; similar distortions may also appear in the absence of degeneracy due to the so-called pseudo Jahn-Teller effect if the vibronic interactions are strong enough. In the case of Nickel we summarize some of these effects in Figures 1 and 2 corresponding with Ni(I) and Ni(II), respectively, and where we show the expected electron configuration, total spin and possible Jahn-Teller distortions for several coordination numbers. Capturing all these effects is a tough test for any approximate computational method and the chief goal of this work is to clearly define the limitations of the current DFTB3 model for the treatment of open-shell transition metal ions and to highlight opportunities for future developments in the DFTB Hamiltonian.
Figure 1.
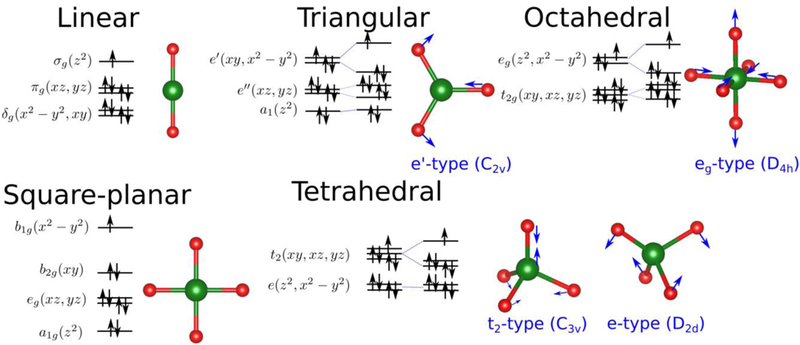
Expected electronic configuration and Jahn-Teller distortions for Ni(I) ions displaying a d9 configuration under different coordinations.
Figure 2.
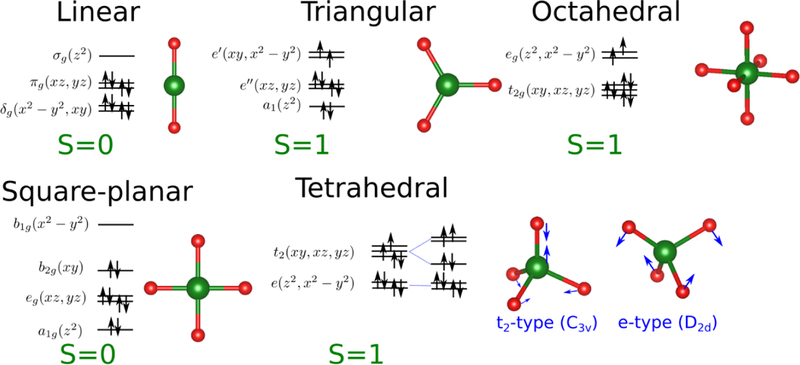
Expected electronic configuration, total spin and Jahn-Teller distortions for Ni(II) ions displaying a d8 configuration under different coordinations.
In the following, we first briefly summarize the DFTB3 formalism and then describe the parameterization protocol for nickel, particularly with respect to its 4s2 3d8 atomic configuration and the treatment of Ni(II). This is followed by an extensive evaluation of the resulting DFTB3/3OB model for structures and energetic properties of various complexes that contain nickel and biologically relevant ligands. We conclude by a summary of the results, along with perspectives on necessary improvements of DFTB3 for transition metal ions.
2. A brief review of DFTB3
DFTB represents a class of approximate DFT methods, which are described fully in the literature.33, 36, 42, 53, 73–77 The fundamental principle of DFTB is tightly bound electrons with perturbatively treated interactions.
Briefly, DFTB considers the electronic energy of the system as an expansion in terms of the deviation of electron density from a reference density, ρ0, which is taken as a superposition of precalculated atomic densities,
| (1) |
in which only valence electrons are described explicitly. Three-center integrals are neglected and the two-center Hamiltonian and overlap matrix elements are precalculated for a mesh38, 78 of interatomic distances using Slater-Koster sin/cos-rules79. This reduces the calculation runtime since no further integration is necessary.
With this treatment of electron density and expanding the electronic energy in a Taylor series of Δρ, the DFTB total energy can be written as
| (2) |
in which Exc,Vxc is the exchange-correlation energy and exchange-correlation potential, respectively.
DFTB3 includes up to third order terms74–75 in the Taylor expansion, and the DFTB3 total energy reads:
| (3) |
in which the first three terms represent the first-, second- and third-order electronic contributions, and Erep is the repulsive potential that includes the nuclear-nuclear repulsion and double-counting zero-th order terms. The LCAO coefficients (Cμi,Cvi) are solved self-consistently by applying variational principle to the energy expression, leading to the Kohn-Sham equations that define the corresponding Kohn-Sham orbitals, ψi(r).
The second-order kernel, γab, reduces to 1/rab for large interatomic distances and describes the Coulomb interaction of Δqa and Δqb partial charges; in the opposite limit, it describes the on-site self-repulsion and can be expressed as the Hubbard parameter (Ua),
| (4) |
where Ua is the second derivative of total energy for a neutral atom with respect to the occupation number of the highest occupied orbital. Ua correlates with the size of an atom in an inverse relationship,36 except for the hydrogen atom, for which a modification (referred to as the γh function) was made and observed to improve hydrogen bonding interactions.37, 77–78
In DFTB3, the Hubbard parameters are charge dependent (described with Γab in Eq. 3)78, 80 and therefore γab is charge dependent through the Hubbard parameters;38, 53 including the charge dependence improves the description of charged and polarizable species within the framework of a minimal basis. Additionally, orbital angular momentum (l) dependence of the Hubbard parameter and its charge derivative can be introduced as in the previous extension of DFTB2 that employs different Hubbard parameters for each element and for each orbital angular momentum48. This enhancement of flexibility in the Hamiltonian is especially significant for transition metals, which have notably different 3d and 4s orbitals81; including the l-dependence in the Hubbard parameters modifies the effective interaction of electrons in these orbitals through γab. Finally, spin-polarization effects have been treated in a collinear fashion as in references48, 53, 82–83:
| (5) |
It is important to note that applying this expression is reasonable when there are up to two spin states associated with the d-shell as is the case of Ni(II) (see Figure 2). However, it would be unrealistic to expect the formulation to deal with systems with many intermediate states (as occurring in configurations with 3–7 electrons in the d-shell), since the spin-dependent term does not depend on the magnetic quantum number ml. Moreover, the charge derivative of the Hubbard parameter has been considered within shell la. We adopt the protocol developed by Gaus et al53., in which the Hubbard derivatives are computed using the total atomic charges instead of populations associated with each shell. As described below, we find it is necessary to use different Hubbard derivative parameters for Ni(I) and Ni(II) for more reliable properties within the current DFTB3 formulation. This is ultimately related to the fact that electrons in the d-shell are strongly correlated and cannot be treated on the same footing as those corresponding with the valence shell of main elements.
3. Parametrization procedure
The DFTB3 parametrization protocol involves two steps: the parametrization of electronic parameters and of repulsive potentials. The parametrization is performed in a manner consistent with the 3-ob parameter set49–52, which is available on the www.dftb.org website under the name 3ob-3–1. The global parameter ζ=4.00 is employed for the scaled γXH along with the specified Hubbard derivatives for each atom in the 3ob set. The choice of reference method for the parametrization of repulsive potentials for transition metal elements has previously been carefully discussed;50, 53 to comply with previous studies, the B3LYP/aug-cc-pVTZ level of theory is again employed, although we are aware of the limitations of the B3LYP functional for Ni complexes17 (for example, for a quantiative description of Jahn-Teller distortions84). Atomic one-center electronic calculations are performed with the PBE85 functional as developed by Perdew and Zunger86, which has become standard for this parametrization step of DFTB models50–51, 53. The atom-centered wave functions ϕμ are formulated as Slater-type orbitals and as such employ wavefunction and density (rdens) compression radii. Since collinear spin-polarization calculations are employed, atomic spin-polarization constants derived with the PBE functional are utilized53, 87 (see Table S1).
3.1. Electronic Parameters
The ground state electronic configuration for nickel is 4s2 3d8 and it is used to determine the two-center integrals of the charge independent Hamiltonian and overlap integrals. The other possible choice is the 4s1 3d9 configuration; for a proper description of Ni(II) compounds, however, the atomic 4s2 3d8 configuration is more appropriate. As a consequence of this choice, slightly better geometries for Ni(II) species in comparison to Ni(I) is observed (vide infra and in the Supplementary Information). For calculating ϵc, ϵp, ϵd, Espin, Hubbard parameters as well as the Hamiltonian and overlap matrix elements, two in-house programs slateratom and sktwocnt are employed. Although the 4p orbitals of Ni are unoccupied, they are included in the basis set as polarization functions. The addition of polarization functions is consistent with previous parametrization of several elements within the DFTB3/3OB framework50, 53 and, as previously, it is noted that addition of polarization functions helps improve the bonding of Ni to other elements.
Several values obtained via atomic one-center PBE calculations are adjusted (ϵp, ϵd, Us, Up, Ud, ) in order to accommodate the complexity of the nickel electronic configuration, while the others are kept as computed (see Table 1). It is noted that the sign of ϵp greatly influences convergence of tetra-coordinated nickel complexes and the positive value of 0.046000 a.u. is ultimately chosen. With the ϵp value shifted, setting the value of Up to 0.251943 a.u. instead of the computed value of 0.158730 a.u. improves the results. It is also found advantageous to change Us from the computed value of 0.251943 a.u. to 0.158730 a.u. to ensure the smooth curvature of the repulsive potentials. The Hubbard parameter and its charge derivative for the 3d orbitals are adjusted so that the oxidation potential of Ni+⟶ Ni2+ calculated at the B3LYP/aug-cc-pVTZ level of theory is reproduced. This choice improves bond dissociation energies (BDEs) and other properties. Furthermore, with the Hubbard parameter value and its charge derivative adjusted, a slight change of ϵd from the computed value of −0.338730 a.u. to −0.398730 a.u. is needed to ensure the smooth curvature of the repulsive potentials.
Table 1.
Overview of the Nickel electronic parameters (in atomic units if not dimensionless), with ζ=4.00.a
| Parameter | Value |
|---|---|
| lmax | 2 |
| α0 | 0.50 |
| α1 | 1.37 |
| α2 | 3.74 |
| α3 | 10.24 |
| α4 | 28.00 |
| 2.50 | |
| 5.20 | |
| rdens | 16.00 |
| ϵs | −0.202977 |
| ϵp* | 0.046000 |
| ϵd* | −0.398730 |
| Espin | −0.036536 |
| 0.158730 | |
| 0.251943 | |
| 0.370410 | |
| −0.060288 | |
| Ni(I) * | −0.139760 |
| Ni(II) * | −0.210000 |
Values with asterisk * are adjusted, the rest are calculated using the PBE functional.
While the adjusted Hubbard parameters lead to satisfactory results for Ni(I) compounds, we find the same parameters do not described Ni(II) compounds with the same level of accuracy; this is the first clear indication that the average treatment of intra-d interactions in the current DFTB3 model is inadequate for the two unpaired electrons in the d8 configuration of Ni(II). To improve the performance with minimal variation in the model, we modify the Hubbard charge derivative for Ni(II), while the Hubbard parameters and their charge derivatives for s and p shells remain the same for both Ni(I) and Ni(II); the charge derivative is shifted to a lower value of −0.210000 for Ni(II) from −0.139760 for Ni(I). Previously, it was reported that the Hubbard derivatives do not significantly alter most properties and can be fitted in the last step of parametrization50; for open-shell systems that feature multiple unpaired d electrons, this statement may not be accurate and a proper choice of the Hubbard derivatives proved paramount to the current nickel parametrization (see below).
The values of and are chosen so that the geometrical properties are well reproduced, specifically angles of tetra- and hexa-coordinated complexes. It is observed that rdens greatly influences nickel-ligand bond lengths, and good agreement with the reference (B3LYP/aug-cc-pVTZ) is achieved when rdens is increased beyond a critical value. Thus rdens is set to a fairly large value, as in the previous parametrization of Ni by Zheng et al.47, and in the Mg parametrization50 where the value was set to 14.0 bohr.
3.2. Repulsive Parameters
The repulsive energy is written as the sum of pair-wise repulsive potentials :
| (6) |
For two atoms a and b, the repulsive potential is calculated by subtracting the DFTB electronic energy Eel from the total energy of reference systems calculated with B3LYP/aug-cc-pVTZ at different interatomic distances,37
| (7) |
The repulsive potentials are fitted against reference geometries and energies employing the erepfit program (an in-house developed program). The parameters defining the repulsive potentials are given in Table S2.
The Ni-Ni repulsive potential is fitted against a Ni(I)-Ni(I) geometry with r(Ni-Ni) set to 2.22 Å, which is the average r(Ni-Ni) from Ni(I)-Ni(I) and Ni(I)-Ni(II) geometries, both obtained with the B3LYP/aug-cc-pVTZ level of theory. All reference geometries and potential energy differences are based on Ni(I) compounds, except for [Ni(H2O)6]2+ and [Ni(NH3)6]2+ which are introduced in order to adjust the treatment of highly coordinated nickel complexes. The division points are chosen in a way that best reproduces energetic properties, as even a small change of division points could lead to substantial differences in sequential BDEs. Graph of the nickel-oxygen repulsive potential as a function of distance, as well as its first and second derivative is given in Figure 3, while all other Ni-X repulsive potentials are included in the Supplementary information (Figure S1).
Figure 3.

Illustration of Repulsive potential for Ni-O, as well as its first and second derivative as a function of distance.
4. Results and discussion
The parameterized DFTB3/3OB model for nickel is evaluated using structures from the Cambridge Structural Database (CSD). Additionally, the model is tested on a range of Ni(I) and Ni(II) complexes for a series of structural and energetic properties; comparison is made to both B3LYP/aug-cc-pVTZ and DFT (B3LYP or PBE)/6–31+G(d) levels of theory. Two different test sets are used and discussed below: the standard test set – comprising mostly of simple ligands, some of which are used for the parameterization; the diverse test set, which comprises of more complex ligands of biological relevance. Since nitrogen hybridization remains a problem for the current monopole-based DFTB3/3OB model, for all calculations involving nitrogen atoms, the “NHmod” repulsive potential is used; this impacts mostly on ligand proton affinities51. Since all tested molecules are small the dispersion correction has not been included in either DFTB or DFT calculations. For Ni(I) compounds, there is no ambiguity in the spin state; for Ni(II) compounds, the triplet state is mainly studied in both DFTB3/3OB and DFT calculations, except for the square-planar structures, for which singlet is expected to be more stable. The splitting between singlet and triplet spin states is briefly discussed below; detailed energetics are summarized in the excel spreadsheet in the Supplementary Information. For comparison, the xTB model of Grimme and co-workers56 has also been tested for selected systems.
4.1. Benchmark calculations
4.1.1. Comparison to CSD structures
Several structures from the CSD database (Figure 4) are used to compare DFTB3 and B3LYP/6–31+G(d) optimized geometries. These compounds are chosen based on the previous work of Hocking et al.,12 who examined the applicability of DFT methods to coordination compounds. Root mean square deviations (RMSD) are calculated with the VMD program88 and include all atoms (Table 2); errors in bond lengths of the first coordination sphere are also summarized in Table 2, with the original data listed in Table S3.
Figure 4.
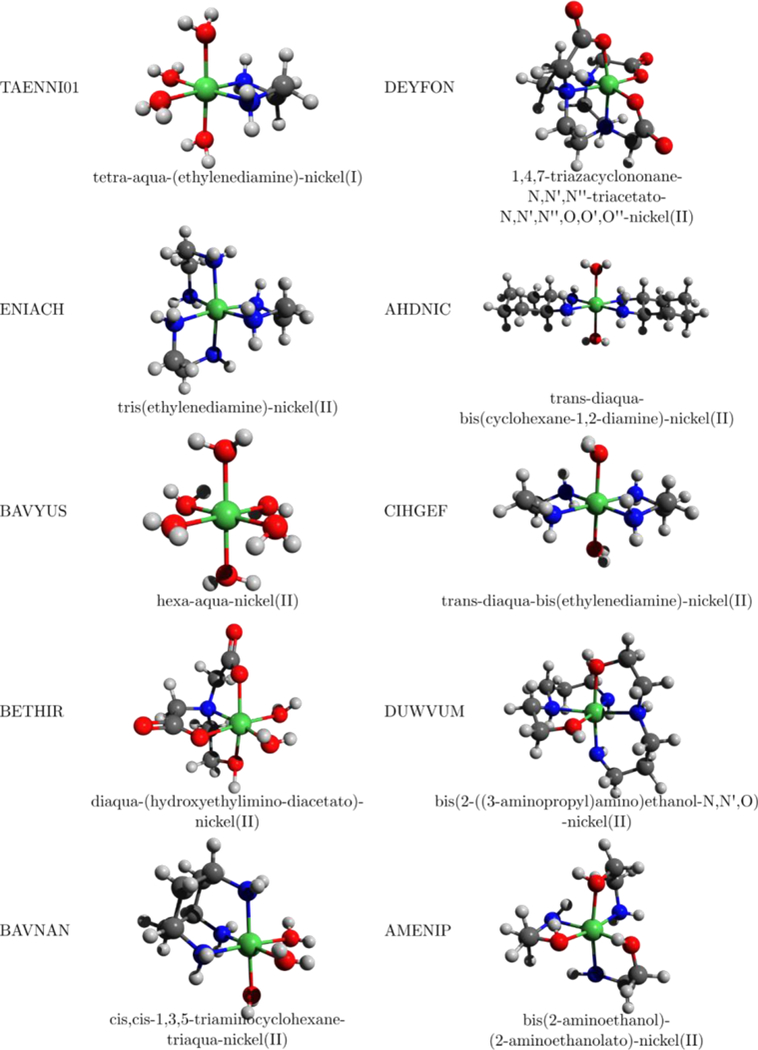
Graphical representation of X ray structures found in within CSD. Color scheme: nickel-green, nitrogen-blue, oxygen-red, carbon-black.
Table 2.
Root Mean Square Deviations of geometry (in Å) and errors in Ni-ligand distances (in Å) at DFTB3 and B3LYP levels for 10 Ni-containing compounds in comparison to experimental X-ray geometries in the Cambridge Structural Database (see Figure 4).
| CSD entry | DFTB3/3OB | B3LYP/6–31+G(d) | xTB56 |
|---|---|---|---|
| TAENNI0189 | 0.36 | 0.47 | 0.36 |
| ENIACH90 | 0.33 | 0.59 | 0.22 |
| BAVYUS91 | 0.57 | 0.61 | 0.44 |
| BETHIR92 | 0.47 | 0.39 | 0.53 |
| BAVNAN93 | 0.29 | 0.35 | 0.24 |
| DEYFON94 | 0.23 | 0.20 | 0.27 |
| AHDNIC95 | 0.26 | 0.28 | 0.23 |
| CIHGEF96 | 0.24 | 0.28 | 0.22 |
| DUWVUM97 | 0.38 | 0.24 | 0.40 |
| AMENIP98 | 0.47 | 0.80 | 0.50 |
| Error in Ni-O/N distances (Å) | |||
| MAD (Ni-O)a | 0.06 | 0.11 | 0.10 |
| MAX (Ni-O)a | 0.25 | 1.00 | 0.24 |
| MAD (Ni-N)a | 0.08 | 0.14 | 0.10 |
| MAX (Ni-N)a | 0.27 | 0.81 | 0.24 |
For here and rest of the text, MAD: Mean Absolute Deviation; MAX: Maximum Absolute Deviation. Only ligands directly coordinated to the nickel ion are considered.
It is evident from Tables 2 and S3 that DFTB3 geometries are generally in good agreement with the X-ray structures. In fact, for most compounds considered here, DFTB3 outperforms B3LYP/6–31+G(d), albeit the difference is small; the MAD for Ni-O/Ni-N distances is 0.06/0.08 Å for DFTB3 and 0.11/0.14 Å for B3LYP. In the case of AMENIP and ENIACH, rather large structural distortions are observed in the B3LYP calculations, while no such large deviation is observed in the DFTB3 calculations. As shown in Table 2, the xTB model56 gives very similar results as DFTB3/3OB, with only slightly larger MAD values for Ni-O and Ni-N distances.
4.1.2. Geometries of the Standard and Diverse Test sets
The bond lengths and angles of all structures in the Standard and Diverse test sets are summarized in Tables S4 and S5, respectively; the errors for bond lengths and angles are summarized in Table 3, which also compares the performance of DFTB3/3OB and PBE/6–31+G(d) calculations. Since DFTB3 is parameterized using PBE, including the PBE comparison below helps identify whether certain errors observed for DFTB3 are due to the use of that exchange-correlation functional or to other approximations specific to DFTB3.
Table 3.
Summary of errors in Ni-ligand distance and ligand-Ni-ligand angle at DFTB3 and PBE/6–31+G(d) levels in comparison to the reference data (B3LYP/aug-cc-pVTZ).a
| Dataset | Error | Ni-ligand distance (Å) | Ligand-Ni-ligand angle (degree) | ||||
|---|---|---|---|---|---|---|---|
| N | PBE 6–31+G(d) | DFTB3/3OB | N | PBE 6–31+G(d) | DFTB3/3OB | ||
| Standard | MAD | 103 (140) | 0.06 (0.04) | 0.06 (0.06) | 96 (176) | 5.1 (3.3) | 5.5 (6.4) |
| MAX | 0.20 (0.14) | 0.40 (0.23) | 37.9 (71.1) | 38.6 (42.3) | |||
| Diverse | MAD | 51 (51) | 0.06 (0.03) | 0.04 (0.05) | 44 (44) | 3.9 (3.7) | 7.4 (14.0) |
| MAX | 0.11 (0.05) | 0.04 (0.20) | 27.8 (27.9) | 40.7 (75.1) | |||
“N” is the number of bond distances and bond angles included for the error analysis; the numbers without parentheses are for Ni(I), and those with parentheses are for Ni(II). The reference structures are optimized at the B3LYP/aug-cc-pVTZ level.
Once rdens is properly adjusted, DFTB3 generally gives a decent description of the geometries in comparison to the reference (B3LYP/aug-cc-pVTZ) structures. For both the standard and diverse tests sets, the MAD value for Ni-ligand distance is about 0.04–0.06 Å, regardless of Ni(I) and Ni(II), which is comparable to the quality of PBE/6–31+G(d); for ligand-Ni-ligand bond angles, the MAD is in the range of 5–7 degrees for DFTB3, slightly larger than the value of 4–5 degrees at the PBE /6-31+G(d) level. As shown in Figure 5, DFTB3/3OB successfully captures the difference in structure between Ni(I) and Ni(II) compounds, including the expected Jahn-Teller distortions. For example, as indicated in Figures 1–2, with three ligands, Ni(I) is expected to deviate from the symmetric triangular structure, while no such distortion is expected for Ni(II); as shown in Figure 5a, this is well captured at both DFTB3/3OB and B3LYP/aug-cc-pVTZ levels for water ligand. Similarly, with four ligands, tetrahedral structures are expected to undergo distortion for both Ni(I) and Ni(II); this is observed consistently for both DFTB3/3OB and B3LYP/aug-cc-pVTZ for ammonia and hydrogen sulfide ligands (see Figure 5b-c), although the magnitude of distortion is slightly underestimated for [Ni(H2S)4]2+ at the DFTB3/3OB level. The xTB56 results are generally similar to DFTB3/3OB, with the Ni-N distances in better agreement with B3LYP references; the xTB model also qualitatively captures Jahn-Teller distortions, although the magnitude is overestimated in the case of [Ni(NH3)4]2+ (Figure 5b).
Figure 5.
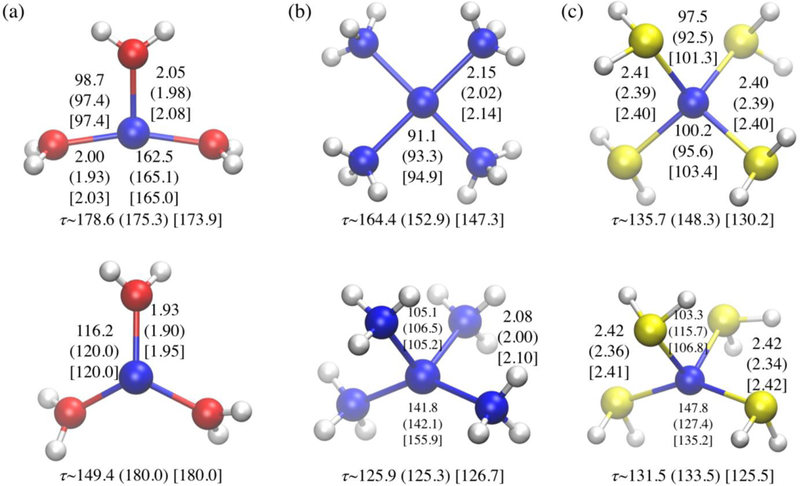
Examples for structures in the standard test set (with water, ammonia and hydrogen sulfide as the ligands); for each panel, the top structure is for Ni(I), and the bottom for Ni(II). Numbers (distances in Å and angles in degrees) without parentheses are the reference value at the B3LYP/aug-cc-pVTZ level; those with parentheses are DFTB3/3OB values; those with brackets are xTB56 values. The τ is the L-L-Ni-L dihedral angle that characterizes how close is the structure to be planar (τ=180 °) or tetradedral (τ=120 °).
We do observe, however, cases that exhibit substantially larger differences between DFTB3 and B3LYP, as reflected by the maximum deviations in ligand-Ni-ligand angles summarized in Table 3. Some of the examples are illustrated in Figures 6 and 7, for the standard and diverse test sets, respectively. For example, the Ni···H interaction appears to be overestimated in the current parameterization (see additional discussion in Supplementary Information). As a result, for a number of structures, especially those feature small anionic ligands such as OH−, the orientation of the ligand is distorted due to artificially strong Ni··H interactions (Figure 6a); the largest impact on the structure is observed for [Ni(H2S)5]2+, for which B3LYP predicts a square pyramidal structure while DFTB3/3OB predicts a trigonal bipyramidal structure with two equatorial H2S molecules significantly distorted due to artificially strong Ni···H interactions (Figure 6c). As another example, [Ni(CO)3]2+ deviates from a symmetrical triangular structure at the B3LYP level, while no distortion is observed at the DFTB3 level (Figure 6b); as shown in Table S4, PBE/6–31+G(d) also predicts a non-symmetric structure, thus the error in DFTB3, in this case, is not due to the exchange-correlation functional used in the model.
Figure 6.
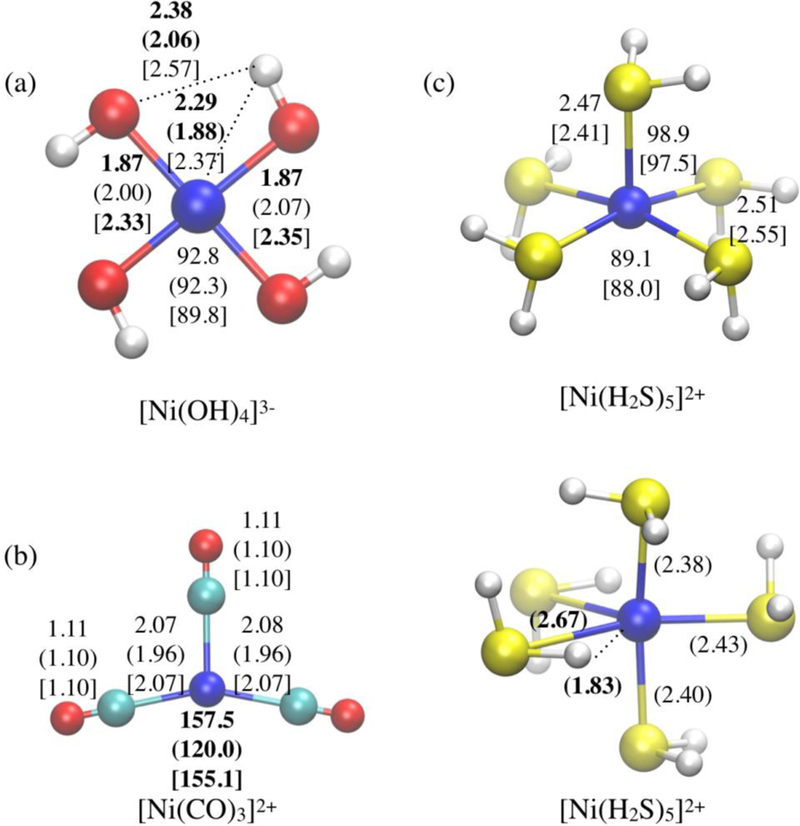
Examples for structures in the standard test set that exhibit significant deviation between DFTB3/3OB and the reference (B3LYP/aug-cc-pVTZ) geometries. Geometrical parameters (distances in Å and angles in degrees) with significant deviations are highlighted in bold; numbers without and with parentheses are the B3LYP/aug-cc-pVTZ and DFTB3/3OB values, respectively; those with brackets are xTB56 values.
Figure 7.
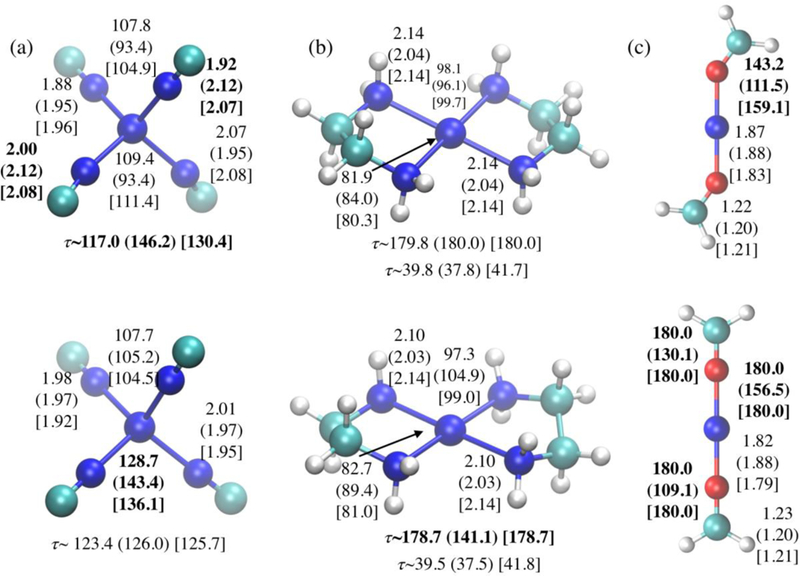
Examples for structures in the diverse test set that exhibit significant deviation between DFTB3/3OB and the reference (B3LYP/aug-cc-pVTZ) geometries. The ligands are CN−, ethylenediamine (en)2, and formaldehyde; for each panel, the top row is for Ni(I) and the bottom for Ni(II). Geometrical parameters (distances in Å and angles in degrees) with significant deviations are highlighted in bold; numbers without and with parentheses are the B3LYP/aug-cc-pVTZ and DFTB3/3OB values, respectively; those with brackets are xTB56 values.
It should be noted, however, that B3LYP is not optimal in all cases either. For example, [Ni(CO)3]2+ is expected to remain symmetrical (Figure 2), as found in DFTB3 calculations, yet B3LYP gives a distorted structure (Figure 6b). By contrast, [Ni(CO)3]+ is expected to deviate from the symmetrical triangular structure due to Jahn-Teller distortion (Figure 1), B3LYP/aug-cc-pVTZ predicts a highly symmetrical structure; the distortion, however, is captured at both DFTB3/3OB and PBE/6–31+G(d,p) levels (Table S4). Therefore, the functional dependence of DFT results for transition metal ions17 should always be kept in mind.
In the diverse set, the largest differences between DFTB3/3OB and B3LYP are observed for the structures illustrated in Figure 7. For [Ni(NC)4,]3- the deviation from tetrahedron is modest at the B3LYP level, while the structure is almost planar with DFTB3/3OB; for [Ni(NC)4]2- the deviation from tetrahedron is also exaggerated at the DFTB3 level (Figure 7a). For the complex with ethylenediamine, while DFTB3/3OB and B3LYP are consistent for the Ni(I) compound, the two ethylenediamines are out-of-plane at the DFTB3/3OB level for the Ni(II) compound (Figure 7b). For the compound with two formaldehydes, DFTB3/3OB predicts a more bent coordination for both Ni(I) and Ni(II) cases (Figure 7c). In all these examples, the errors for PBE/6–31+G(d) are substantially smaller (see Table S5), thus the exchange-correlation functional used for DFTB3/3OB is not to blame here.
As discussed below, these larger structural deviations lead to larger errors in single point ligand binding energy calculations at the B3LYP//DFTB3 level, as compared to our observations for copper compounds.53 As also shown in Figures 6–7, xTB also tends to have notable errors for most of these cases, and the magnitude of error can be either larger or smaller than that for DFTB3/3OB. Therefore, these problematic cases likely reflect the intrinsic limitations of the tight binding Hamiltonian employed in both models.
4.1.3. Sequential Bond Dissociation Energies
The sequential bond dissociation energies (sBDE) computed with DFTB3/3OB and various DFT methods for complexes in the standard and diverse test sets are presented in Tables S6 to S8; as a further evaluation of the DFTB3 structures, single point B3LYP/aug-cc-pVTZ calculations are also conducted and summarized in the tables. The errors are summarized in Table 4.
Table 4.
Summary of errors in the sequential bond dissociation energies (sBDEs) and ligand proton affinities (PAs) of different benchmark datasets for Ni-containing compounds.a
| Dataset | Error | PBE/6–31+G(d) | DFTB3/3OB | B3LYP//DFTB3 |
|---|---|---|---|---|
| Standard set sBDE | ||||
| Ni(I): neutral ligands | MAD | 8.8 | 6.3 | 4.2 |
| MAX | 16.2 | 14.1 | 13.6 | |
| Ni(I): chared ligands | MAD | 11.8 | 22.4 | 3.7 |
| MAX | 25.3 | 39.9 | 18.5 | |
| Ni(II): neutral ligands | MAD | 8.4 | 6.5 | 8.7/6.2b |
| MAX | 16.6 | 18.5 | 45.5/22.2b | |
| Ni(II): charged ligands | MAD | 14.4 | 26.8 | 4.6 |
| MAX | 27.4 | 52.5 | 16.4 | |
| Diverse set sBDE | ||||
| Ni(I) compounds | MAD | 11.8 | 10.0 | 2.8 |
| MAX | 22.3 | 32.3 | 11.3 | |
| Ni(II) compounds | MAD | 13.9 | 13.1 | 4.4 |
| MAX | 30.7 | 26.3 | 28.7 | |
| Standard set PA | ||||
| Ni(I) compounds | MAD | 12.7 | 5.4 | 3.5 |
| MAX | 17.9 | 21.4 | 8.9 | |
| Ni(II) compounds | MAD | 13.4 | 8.2 | 7.0 |
| MAX | 23.8 | 17.4 | 19.9 |
The reference is B3LYP/aug-cc-PVTZ. All calculations are done for 0K without including zero point energy correction.
The values after the slash exclude the extreme case of [Ni(H2S)5]2+, for which DFTB3/3OB predicts a very differet structure (see Figure 6c).
For Ni(I) complexes in the standard test set (Table S6) with neutral ligands, the MAD for the sBDE is 6.3 kcal/mol, which is slightly lower than the value of 8.8 kcal/mol for PBE/6–31+G(d); the errors are substantially larger for charged ligands, with a MAD value of 22.4 kcal/mol for DFTB3/3OB and 11.8 kcal/mol for PBE/6–31+G(d). As discussed in the previous study53 of copper compounds, the larger errors for the charged ligands reflect the minimal basis nature of DFTB3; indeed, the error (MAD) decreases drastically to 3.7 kcal/mol for single point B3LYP/aug-cc-pVTZ calculations at DFTB3/3OB structures for the charged ligands. Nevertheless, it is worth noting that the errors for the single point calculations remain substantially larger for the Ni(I) compounds (MAD in the range of 4 kcal/mol for neutral and charged ligands) than for the copper compounds, for which the single point MAD is about 1 kcal/mol, even for Cu(II) compounds.53 This difference reflects the significant errors in several nickel structures as discussed in the last subsection. For example, large errors are observed for water and hydroxide ligands, even with single point energy calculations; this is because the overestimated Ni···H interaction distorts the orientation of these ligands (e.g., see Figure 6a). The large error associated with [Ni(CO)4]+ is due in part to the fact that, as discussed above, B3LYP and DFTB3 predict different structures for [Ni(CO)3]+.
For Ni(II) compounds (Table S7), the MAD is slightly larger than Ni(I), although this is only after adjusting the charge derivative of d shell Hubbard parameter Ud to a lower value, highlighting the challenging nature of nickel relative to copper for the current DFTB3 model. Indeed, even with the adjusted Hubbard charge derivative, the MAD for Ni(II) with charged ligands (26.8 kcal/mol) is substantially higher than that for Cu(II) with charged ligands (with a MAD of 14.0 kcal/mol53). Again, single point B3LYP/aug-cc-pVTZ calculations at DFTB3/3OB structures generally reduces the errors, especially for charged ligands, the MAD remains significant due to the structural distortions discussed above, especially for hydroxide ligands and [Ni(H2S)5]2+ shown in Figure 7. For [Ni(NH3)6]2+, the single point error is rather large (−22.2 kcal/mol), not because the relevant structures are distorted but because the Ni···N distances are consistently underestimated by about 0.1 Å (see Figure 5b for example).
For the diverse test set (see Table S8), the basic trends follow those for the standard test set; the errors at the DFTB3/3OB and PBE/6–31+G(d) levels are comparable, and the errors are slightly larger for Ni(II) than for Ni(I). Single point energy calculations at DFTB3 structures reduce the errors significantly, leading to MADs in the range of 3–4 kcal/mol. Nevertheless, large errors are observed in several cases for which DFTB3 and B3LYP structures are substantially different (see Figure 7).
4.1.4. Ligand Proton Affinities
The ligand proton affinities for various compounds in the standard test set are calculated using DFTB3/3OB and compared to DFT calculations (Table S9). Within the DFTB3 formalism the proton affinities (EPA) are calculated as follows
| (8) |
in which EH+ is the energy of proton, and EAH and EA− are the energies of the protonated and deprotonated species, respectively. Note that due to the density expansion nature of DFTB, the energy of a proton is not zero.99
The DFTB3 results are in fair agreement with the B3LYP reference values, and the MAD values are considerably smaller than PBE/6–31+G(d); it is well-established that proton affinity is sensitive to the inclusion of polarization functions on the hydrogen atoms. A closer inspection of the results in Tables S9 reveals that the large MAD value for Ni (I) complexes is due mainly to phosphorus containing complexes, and for Ni(II) the same holds for nitrogen compounds. Overall, the performance is comparable to the previous results for copper ligands (the RMSDs for Cu(I) and Cu(II) are 6.0 and 5.7 kcal/mol, respectively).53 Again, one difference is that the errors do not reduce with single point energy calculations for nickel compounds, while the errors reduce to a MAD around 1 kcal/mol for copper compounds.53 This is largely because of the overestimated Ni···H interaction noted above, which are particularly severe for structures with deprotonated ligands (e.g., OH− vs. H2O as ligand). Thus systematically improving Ni···H interaction is essential for reducing errors in proton affinities (see discussions in Supplementary Information).
4.1.5. Electronic Structure
It is well established in coordination chemistry that depending on the ligand environment, d orbitals split in specific ways upon descent in symmetry. For octahedral (Oh) Ni(II) complexes, the electronic configuration is (t2g)6(eg)2. This splitting is well reproduced by our orbital angular momentum resolved DFTB3 model, although the ligand field splitting is overestimated (Figure 8), and this is noted for all structures under investigation to different extent.
Figure 8.
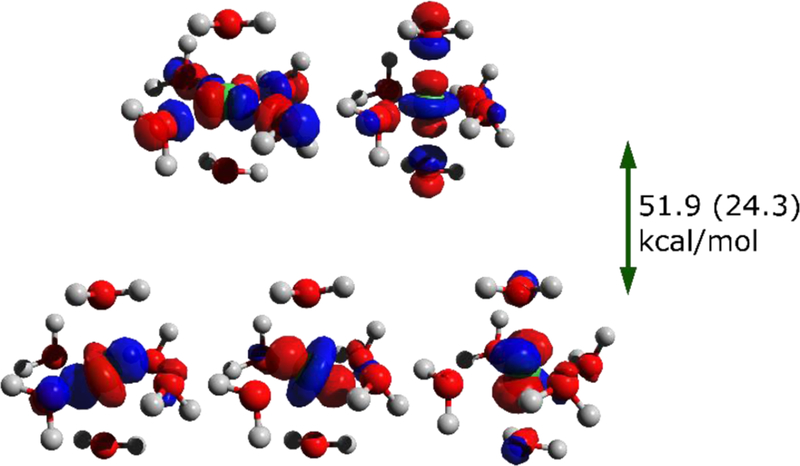
An illustration of d orbital splitting in Ni ion with [Ni(H2O)6]2+ as an example. Contours of d orbitals (isovalue 0.06 a.u.) and the splitting between the t2g and e sets computed with DFTB3/3OB are shown; the experimental value100 is enclosed in parentheses.
More importantly, for complexes with coordination number 4, two distinct geometries can be observed: square planar and tetrahedral. In the former case, electronic configuration reads as: (eg)4(a1g)2(b2g)2(b1g)0, giving1A1g as the ground state in the D4h symmetry. Tetrahedral nickel(II) complexes have an electronic configuration of (e)4(t2)4, giving3T1 state as the ground state, which is subject to the Jahn-Teller distortion; this is the T ⊗ e Jahn-Teller effect, which although weak, can be noticed by angular distortion leading to the D2d geometry. Other examples are summarized in Figures 1–2. Encouragingly, the DFTB3 calculations properly capture Jahn-Teller distortions in all tetrahedral complexes as reflected by the L-Ni-L angles (e.g., see Figure 5), although the magnitude of distortion can be different from B3LYP results (e.g., see Figure 7). For the case of three ligands, DFTB3 follows the expectation for most cases, even when B3LYP does not, as discussed above for [Ni(CO)3]+ and [Ni(CO)3]2+.
The fact that Jahn-Teller distortion is captured in DFTB3 (also noted in previous studies of copper11) is consistent with the observation that qualitative splitting of d orbitals is described by the model, suggesting that metal-ligand matrix elements computed for the parameterization are reliable. We note, however, that with the current spin-polarization model (Eq. 5), it is difficult to reliably describe the order of spin states, even for Ni(II), which has a d8 configuration. This is because the spin-polarization term employed here does not depend on the magnetic quantum number and involves only the spin population of the entire d shell ( in Eq. 5). Indeed, with the computed spin coupling values, the singlet-triplet splittings are very different from the B3LYP and PBE values (see the excel spreadsheet in Supplementary Information). Simple adjustments in the spin coupling parameters (e.g., by matching singlet-triplet splitting in Ni2+ at the B3LYP/aug-cc-pVTZ level) leads to considerable improvements but not a transferable model. Since we focus entirely on the triplet states (except for square planar structure) for Ni(II) compounds in this study, we have not pursued an extensive effort in refining the spin coupling parameters. Instead, we leave the improvement of spin states as important future work, which necessarily involves an explicit treatment of metal d orbitals with ml dependent d-d interactions.
4.1.6. Active site models for nickel enzymes
Finally, we test the DFTB3/3OB model using several active site models for nickel enzymes, selected based on a recent review that discussed the structure and mechanism of nickel-dependent enzymes.61 Due to the size of the models, the reference is taken to be B3LYP with a modest basis set, which includes Lanl2dz effective core potential and the associated basis set for Ni,101 and 6–31+G(d,p) for the other elements. As shown in Figure 9, the DFTB3/3OB structures are largely consistent with the B3LYP structures, with a RMSD value ranging from 0.11 to about 0.5 Å. The deviations are due mainly to the overestimated Ni···H interactions, which distort the orientation of small molecule ligands such as H2O (e.g., in Figure 9c-d). It is encouraging that the current DFTB3 model appears to work well, at least for structures, for even a Ni(III) case (Figure 9b for Ni-containing superoxide dismutase) and a bi-metallic case (Figure 9d for urease), although more stringent tests would involve molecular dynamics simulations in a QM/MM framework, as was done for copper proteins;11 this is left for future work.
Figure 9.
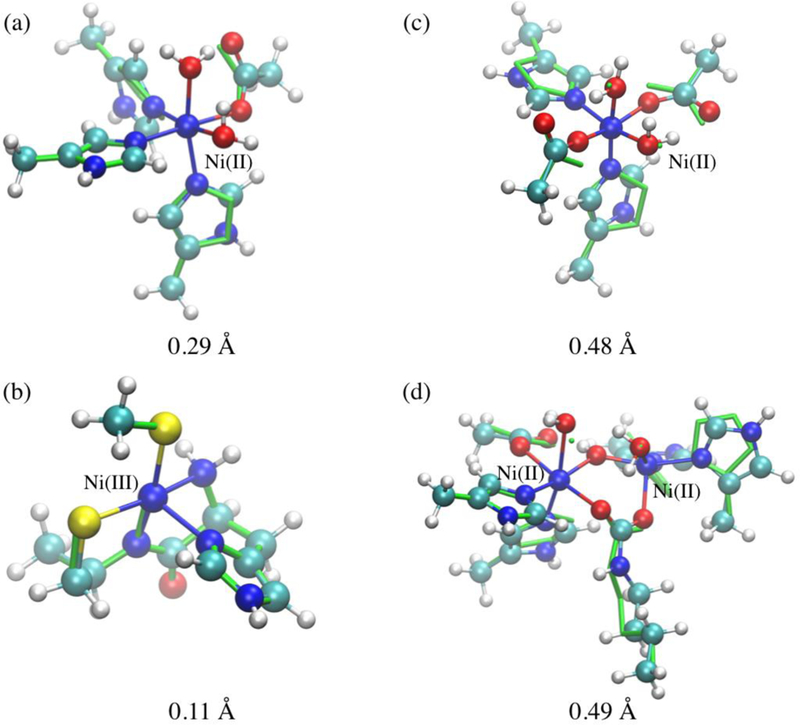
Superposition of optimized active site models for several nickel enzymes at the B3LYP and DFTB3/3OB levels. The B3LYP optimized structures are shown as CPK with atoms colored based on element type, and DFTB3 structures are shown in the line form in green. The RMSD value between the optimized structures (not including hydrogen atoms) is shown for each model. The formal oxidation state for Ni is Ni(II) for all cases, except for panel (b), which represents a model for Ni-containing superoxide dismutase (PDB code 1Q0D).
5. Concluding Remarks
DFTB3 has shown promise in treating simple metal ions such as Mg2+ and Zn2+ with more favorable computational efficiency than DFT,50, 53 making it attractive for the study of condensed phase systems. Since DFTB innately bears the principles of DFT, it is potentially better suited for the treatment of transition metals than other semi-empirical techniques, such as the traditional NDDO methods. Indeed, l-resolved DFTB3 was found to provide encouraging results for copper,11, 53 which has d10/d9 configuration depending on the oxidation state. Here we explore the applicability and limitation of the current DFTB3 model for treating more complex transition metal ions by conducting parametrization for nickel (I) and nickel (II).
Overall, the results for nickel are largely in line with previous findings for copper.53 Geometries are in general in favorable agreement with available X-ray structures and B3LYP/aug-cc-pVTZ calculations, although we are aware that this level of theory may not be the best choice for structures of transition metals; it was chosen as the reference here so that the DFTB3 nickel model is consistent with the 3OB parameterization for other elements reported so far. It is encouraging that Jahn-Teller distortion expected for three- and four-ligand cases is captured in most Ni(I) and Ni(II) compounds, although the magnitude of distortion is not always perfectly reproduced; this is consistent with the finding that d orbital splitting is qualitatively reproduced, although the result is often not quantitative. For the selected cases studied here, the xTB model of Grimme et al.56 also gives reliable structures, although the degree of Jahn-Teller distortion is also not always quantitatively reproduced. Considering that only three Ni-containing compounds were included in the parameterization, the performance of xTB model is satisfying, further suggesting that the DFTB framework is adequate to describe many key structural features.
It is observed that ligand binding energies and geometries are better reproduced for more covalent type complexes, such as those with carbon or sulfur in the first coordination sphere. DFTB3 treatment of charged ligands, especially for ligand binding energies, has considerable errors with MAD in the range of 20 kcal/mol; this is consistent with previous findings for copper and reflects the current limitations imposed by the use of a minimal basis set for treating transition metals and their interaction with highly polarizable ligands53.
There are several distinct differences in the nickel parameterization compared to previous work on copper. First, we find that it is necessary to use different charge derivatives for the Hubbard parameter for the d shell of Ni(I) and Ni(II) cases, while a single charge derivative of the d-shell Hubbard parameter was found adequate for both oxidation states of copper.53 Moreover, although single point B3LYP calculations at DFTB3 structures often reduce the error in ligand binding energies, especially for charged ligands, the error remains substantial (MAD of 3–4 and up to ~7 kcal/mol in contrast to the MAD of 1–2 kcal/mol observed for copper53) for many cases, reflecting that notable deficiencies exist in the structure. Some of the structural errors are due to overestimated Ni···H interactions most visible for small ligands such as water and hydroxide, while other types of structural distortions are also observed; in some cases, similar deviations are also observed with PBE/6–31+G(d) calculations, although many structural errors are unique to DFTB3, suggesting that the use of PBE as the exchange-correlation functional is not the main origin. Finally, with the computed spin coupling parameters based on atomic calculations, the current DFTB3 model has large errors in the singlet/triplet splitting of Ni(II) compounds, similar to previous parameterization of DFTB2 for transition metals.47 These challenges clearly highlight the higher level of complexity in the electronic structure of nickel as compared to copper, which has either a full d shell or a single hole (d9). An explicit treatment of the interactions among the electrons in different d orbitals, thus going beyond the averaged interaction over each l-shell in the current DFTB3 model, is required to overcome these fundamental limitations and make the DFTB approach applicable to treat first row transition metal ions with open d-shells. Nevertheless, the observation that many key properties of nickel compounds, such as Jahn-Teller distortions, have been captured already with the current DFTB3 model indicates that further efforts are clearly worthwhile.
Finally, we note that, similar to previous developments of 3OB parameters for DFTB3, we have limited ourselves to molecular species. An important topic of study is to understand the transferability of the DFTB3 model to solid state systems, in terms of both physical and chemical properties. While DFTB3/3OB has been applied to examine lattice energies of organic molecules,102–103 electronic properties such as band structures have not been studied systematically.
Supplementary Material
Acknowledgments
This project was supported by the Serbian-German collaboration project (DAAD) number 451-03-01038/2015-09/7 (to MG and ME), the Serbian Ministry of Science under project 172035 (to MG), NIH grant R01-GM106443 (QC) and the Spanish Ministry of Economy and Competitiveness through Grant FIS2015–64886-C5–2-P (P.G.-F.). P.G.-F. recognizes support from Ramón y Cajal Grant RyC-2013–12515.
Footnotes
Supplementary Information
Spin coupling parameters, detailed structural information for the test molecules and additional energetics data (sequential bond dissociation energies, ligand proton affinities; singlet-triple splitting for Ni(II) compounds, in Excel spread sheet format) are available. Also included is a brief discussion of an alternative parameterization that aims to improve Ni···H interactions.
References
- 1.Lippard SJ; Berg JM, In Principles of Bioinorganic Chemistry;, University Science Books: Mill Valley, CA, 1994. [Google Scholar]
- 2.Nelson DL; Cox MM, In Lehninger Principles of Biochemistry, 5th ed.; W.H. Freeman and Company: New York, 2008. [Google Scholar]
- 3.Li PF; Merz KM, Metal Ion Modeling Using Classical Mechanics. Chem. Rev 2017, 117, 1564–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Stote RH; Karplus M, Zinc-binding in proteins and solution - A simple but accurate non-bonded representation. Proteins 1995, 23, 12–31. [DOI] [PubMed] [Google Scholar]
- 5.Li PF; Roberts BP; Chakravorty DK; Jr., K. MM, Rational Design of Particle Mesh Ewald Compatible Lennard-Jones Parameters for +2 Metal Cations in Explicit Solvent J. Chem. Theory Comput 2013, 9, 2733–2748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li PF; Merz KM, Taking into Account the Ion-Induced Dipole Interaction in the Nonbonded Model of Ions J. Chem. Theory Comput 2014, 10, 289–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Duarte F; Bauer P; Barrozo A; Amrein BA; Purg M; Aqvist J; Kamerlin SCL, Force Field Independent Metal Parameters Using a Nonbonded Dummy Model J. Phys. Chem. B 2014, 118, 4351–4362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Peters MB; Yang Y; Wang B; Fusti-Molnar L; Weaver MN; Jr., K. MM, Structural Survey of Zinc-Containing Proteins and Development of the Zinc AMBER Force Field (ZAFF) J. Chem. Theory Comput 2010, 6, 2935–2947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hu LH; Ryde U, Comparison of Methods to Obtain Force-Field Parameters for Metal Sites J. Chem. Theory Comput 2011, 7, 2452–2463. [DOI] [PubMed] [Google Scholar]
- 10.Landis CR; Cleveland T; Firman TK, Valence bond concepts applied to the molecular mechanics description of molecular shapes. 3. Applications to transition metal alkyls and hydrides. J. Am. Chem. Soc 1998, 120, 2641–2649. [DOI] [PubMed] [Google Scholar]
- 11.Jin H; Goyal P; Das AK; Gaus M; Meuwly M; Cui Q, Copper oxidation/reduction in water and protein: studies with dftb3/mm and valbond molecular dynamics simulations. J. Phys. Chem. B 2016, 120, 1894–1910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hocking RK; Deeth RJ; Hambley TW, DFT study of the systematic variations in metal-ligand bond lengths of coordination complexes: the crucial role of the condensed phase Inorg. Chem 2007, 46, 8238. [DOI] [PubMed] [Google Scholar]
- 13.Piquemal JP; Williams-Hubbard B; Fey N; Deeth RJ; Gresh N; Giessner-Prettre C, Inclusion of the ligand field contribution in a polarizable molecular mechanics: SIBFA-LF. J. Comput. Chem 2003, 24, 1963–1970. [DOI] [PubMed] [Google Scholar]
- 14.Deeth RJ; Anastasi A; Diedrich C; Randell K, Molecular modelling for transition metal com- plexes: Dealing with d-electron effects. Coord. Chem. Rev 2009, 253, 795–816. [Google Scholar]
- 15.Xiang JY; Ponder JW, An angular overlap model for Cu(II) ion in the amoeba polarizable force field. J. Chem. Theory Comput 2014, 10, 298–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cramer CJ, In Essentials of Computational Chemistry: Theories and Models, 2nd ed.; John Wiley & Sons, Ltd.: England, 2004. [Google Scholar]
- 17.Cramer CJ; Truhlar DG, Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys 2009, 11, 10757–10816. [DOI] [PubMed] [Google Scholar]
- 18.Sharma S; Sivalingam K; Neese F; Chan GKL, Low-energy spectrum of iron-sulfur clusters directly from many-particle quantum mechanics. Nat. Chem 2014, 6, 927–933. [DOI] [PubMed] [Google Scholar]
- 19.Senn HM; Thiel W, QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed 2009, 48, 1198–1229. [DOI] [PubMed] [Google Scholar]
- 20.Brunk E; Rothlisberger U, Mixed quantum mechanical/molecular mechanical molecular dynamics simulations of biological systems in ground and electronically excited states. Chem. Rev 2015, 115, 6217–6263. [DOI] [PubMed] [Google Scholar]
- 21.Shaik S; Cohen S; Wang Y; Chen H; Kumar D; Thiel W, P450 Enzymes: Their Structure, Reactivity, and Selectivity-Modeled by QM/MM Calculations. Chem. Rev 2010, 110, 949. [DOI] [PubMed] [Google Scholar]
- 22.Cui Q, Quantum mechanical methods in biochemistry and biophysics. J. Chem. Phys 2016, 145, 140901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dewar MJS, The PMO Theory of Organic Chemistry. Plenum: New York, 1975. [Google Scholar]
- 24.Dewar MJS; Thiel W, Ground states of molecules. 38. MNDO method - approximations and parameters. J. Am. Chem. Soc 1977, 99, 4899–4907. [Google Scholar]
- 25.Thiel W; Voityuk AA, Extension of MNDO to d orbitals: Parameters and results for the second-row elements and for the zinc group. J. Phys. Chem 1996, 100, 616–626. [Google Scholar]
- 26.Dewar MJS; Zoebisch EG; Healy EF; Stewart JJP, The development and use of quantum-mechanical molecular-models. 76. AM1 - A new general-purpose quantum mechanical molecular model. J. Am. Chem. Soc 1985, 107, 3902–3909. [Google Scholar]
- 27.Stewart JJP, Optimization of parameters for semiempirical methods. 1. Method. J. Comput. Chem 1989, 10, 209–220. [Google Scholar]
- 28.Stewart JJP, Optimization of parameters for semiempirical methods. 2. Applications. J. Comput. Chem 1989, 10, 221–264. [Google Scholar]
- 29.Stewart JJP, Optimization of parameters for semiempirical methods. 3. Extension of PM3 to Be, Mg, Zn, Ga, As, Se, Cd, In, Sn, Sb, Te, Hg, Tl, Pb and Bi. J. Comput. Chem 1991, 12, 320–341. [Google Scholar]
- 30.Stewart JJP, Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model 2007, 13, 1173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Stewart JJP, Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model 2013, 19, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dral PO; Wu X; Sporkel L; Koslowski A; Thiel W, Semiempirical Quantum-Chemical Orthogonalization-Corrected Methods: Benchmarks for Ground-State Properties. J. Chem. Theory Comput 2016, 12, 1097–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Elstner M; Seifert G, Density functional tight binding. Phil. Trans. R. Soc. A 2014, 372 (2011), 20120483. [DOI] [PubMed] [Google Scholar]
- 34.Gaus M; Cui Q; Elstner M, Density Functional Tight Binding (DFTB): Application to organic and biological molecules. WIREs Comput. Mol. Sci 2014, 4, 49–61. [Google Scholar]
- 35.Cui Q; Elstner M, Density functional tight binding: values of semi-empirical methods in an ab initio era. Phys. Chem. Chem. Phys 2014, 16, 14368–14377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Elstner M; Porezag D; Jungnickel G; Elsner J; Haugk M; Frauenheim T; Suhai S; Seifert G, Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar]
- 37.Gaus M Extension and Parametrization of an Approximate Density Functional Method for Organic and Biomolecules. Karlsruher Institut fur Technologie (KIT), Karlsruhe, Germany, 2011. [Google Scholar]
- 38.Gaus M; Cui Q; Elstner M, DFTB-3rd: Extension of the self-consistent-charge density-functional tight-binding method SCC-DFTB. J. Chem. Theory Comput 2011, 7, 931–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Elstner M; Jalkanen KJ; Knapp-Mohammady M; Frauenheim T; Suhai S, DFT studies on helix formation in N-acetyl-(L-alanyl)(n)-N ‘-methylamide for n=1–20 Chem. Phys 2000, 256, 15–27. [Google Scholar]
- 40.Elstner M; Jalkanen KJ; Knapp-Mohammady M; Frauenheim T; Suhai S, Energetics and structure of glycine and alanine based model peptides: Approximate SCC-DFTB, AM1 and PM3 methods in comparison with DFT, HF and MP2 calculations. Chem. Phys 2001, 263, 203–219. [Google Scholar]
- 41.Otte N; Scholten M; Thiel W, Looking at Self-Consistent-Charge Density Functional Tight Binding from a semiempirical perspective. J. Phys. Chem. A 2007, 111, 5751–5755. [DOI] [PubMed] [Google Scholar]
- 42.Christensen AS; Kubar T; Cui Q; Elstner M, Semiempirical Quantum Mechanical Methods for Noncovalent Interactions for Chemical and Biochemical Applications. J. Chem. Theory Comput 2016, 116 (9), 5301–5337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Riccardi D; Schaefer P; Yang Y; Yu H; Ghosh N; Prat-Resina X; Konig P; Li G; Xu D; Guo H; Elstner M; Cui Q, Development of effective quantum mechanical/molecular me- chanical (QM/MM) methods for complex biological processes. J. Phys. Chem. B 2006, 110, 6458–6469. [DOI] [PubMed] [Google Scholar]
- 44.Frauenheim T; Seifert G; Elstner M; Hajnal G; Jungnickel G; Porezag D; Suhai S; Scholz R, A self-consistent charge density-functional based tight-binding method for predictive materials simulations in physics, chemistry and biology Phys. Stat. Sol. (b) 2000, 217, 41. [Google Scholar]
- 45.Frauenheim T; Seifert G; Elstner M; Niehaus T; Kohler C; Amkreutz M; Sternberg M; Hajnal Z; Carlo AD; Suhai S, Atomistic simulations of complex materials: ground-state and excited-state properties J. Phys. Condens. Matt 2002, 14, 3015–3047. [Google Scholar]
- 46.Elstner M; Cui Q; Munih P; Kaxiras E; Frauenheim T; Karplus M, Modeling zinc in biomolecules with the self consistent charge-density functional tight binding (SCC-DFTB) method: Applications to structural and energetic analysis. J. Comput. Chem 2003, 24, 565. [DOI] [PubMed] [Google Scholar]
- 47.Zheng G; Witek HA; Bobadova-Parvanova P; Irle S; Musaev DG; Prabhakar R; Morokuma K; Lundberg M; Elstner M; Kohler C; Frauenheim T, Parameter calibration of transition-metal elements for the spin-polarized self-consistent-charge density-functional tight-binding (DFTB) method: Sc, Ti, Fe, Co, and Ni. J. Chem. Theo. Comp 2007, 3, 1349. [DOI] [PubMed] [Google Scholar]
- 48.Kohler C; Seifert G; Frauenheim T, Density functional based calculations for Fe-n (n <= 32). Chem. Phys 2005, 309, 23–31. [Google Scholar]
- 49.Kubillus M; Kubar T; Gaus M; Rezac J; Elstner M, Parameterization of the DFTB3 Method for Br, Ca, Cl, F, I, K, and Na in Organic and Biological Systems. J. Chem. Theory Comput 2015, 11, 332–342. [DOI] [PubMed] [Google Scholar]
- 50.Lu X; Gaus M; Elstner M; Cui Q, Parameterization of DFTB3/3OB for Magnesium and Zinc for chemical and biological applications. J. Phys. Chem. B 2015, 119, 1062–1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gaus M; Goez A; Elstner M, Parametrization and Benchmark of DFTB3 for Organic Molecules. J. Chem. Theory Comput 2013, 9, 338–354. [DOI] [PubMed] [Google Scholar]
- 52.Gaus M; Lu X; Elstner M; Cui Q, Parameterization of DFTB3/3OB for Sulfur and Phosphorus for chemical and biological applications. J. Chem. Theory Comput 2014, 10, 1518–1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gaus M; Jin H; Demapan D; Christensen AS; Goyal P; Elstner M; Cui Q, DFTB3 parametrization for copper: the importance of orbital angular momentum dependence of hubbard parameters. J Chem Theory Comput 2015, 11, 4205–4219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Christensen AS; Elstner M; Cui Q, Improving intermolecular interactions in dftb3 using extended polarization from chemical-potential equalization. J. Chem. Phys 2015, 143, 084123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Christensen AS; Kromann JC; Jensen JH; Cui Q, Intermolecular interactions in the condensed phase: Evaluation of semi-empirical quantum mechanical methods. J. Chem. Phys 2017, 147, 161704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Grimme S; Bannwarth C; Shushkov P, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1−86). J. Chem. Theory Comput 2017, 13 (5), 1989–2009. [DOI] [PubMed] [Google Scholar]
- 57.Ragsdale SW, Nickel and the carbon cycle J. Inorg. Biochem 2007, 101, 1657–1666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Fontecilla-Camps JC, Struct. Bonding 1998, 91, 1. [Google Scholar]
- 59.Gerendas J; Polacco JC; Freyermuth SK; Sattelmacher B, Significance of nickel for plant growth and metabolism J. Plant Nutr. Soil Sci 1999, 162, 241–256. [Google Scholar]
- 60.Li Y; Zamble DB, Nickel Homeostasis and Nickel Regulation: An Overview. Chem. Rev 2009, 109, 4617. [DOI] [PubMed] [Google Scholar]
- 61.Ragsdale SW, Nickel-based Enzyme Systems. J. Biol. Chem 2009, 284, 18571–18575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zelko IN; Mariani TJ; Folz RJ, Superoxide dismutase multigene family: A comparison of the CuZn-SOD (SOD1), Mn-SOD (SOD2), and EC-SOD (SOD3) gene structures, evolution, and expression Free Radic. Biol. Med 2002, 33, 337–349. [DOI] [PubMed] [Google Scholar]
- 63.Pochapsky TC; Ju T; Dang M; Beaulieu R; Pagani GM; Ouyang B, In Nickel and Its Surprising Impact in Nature Sigel A; Sigel H; Sigel RKO, Eds. John Wiley&Sons Ltd: West Sussex, United Kingdom, 2007; p 473. [Google Scholar]
- 64.Ju T; Goldsmith RB; Chai SC; Maroney MJ; Pochapsky SS; Pochapsky T, One protein, two enzymes revisited: A structural entropy switch interconverts the two isoforms of acireductone dioxygenase J. Mol. Biol 2006, 363, 523–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hausinger RP; Karplus PA, In Handbook of Metalloproteins, Wieghardt K; Huber R; Poulos TL; Messerschmidt A, Eds. John Wiley & Sons Ltd.: West Sussex, United Kingdom, 2001; p 867. [Google Scholar]
- 66.Lindahl PA; Graham DE, In Nickel and Its Surprising Impact in Nature Sigel A; Sigel H; Sigel RKO, Eds. John Wiley & Sons Ltd.: West Sussex, United Kingdom, 2007; p 357. [Google Scholar]
- 67.Ragsdale SW; Pierce E, Acetogenesis and the Wood-Ljungdahl pathway of CO2 fixation Biochim. Biophys. Acta 2008, 1784, 1873–1898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lubitz W; Gastel MV; Gartner W, In Nickel and Its Surprising Impact in Nature, Sigel A; Sigel H; Sigel RKO, Eds. John Wiley & Sons Ltd.: West Sussex, United Kingdom, 2007; p 279. [Google Scholar]
- 69.Vignais PM; Billoud B, Occurrence, classification, and biological function of hydrogenases: An overview Chem. Rev 2007, 107, 4206–4272. [DOI] [PubMed] [Google Scholar]
- 70.Griffith JS, The Theory of Transition Metal Ions. Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- 71.Anisimov VI; Aryasetiawan F; Lichtenstein AI, First-principles calculations of the electronic structure and spectra of stongly correlated systems: The LDA+U method. J. Phys. Condens. Matt 1997, 9, 767–808. [Google Scholar]
- 72.Bersuker IB, Electronic Structure and Properties of Transition Metal Compounds: Introduction to the Theory. Wiley: New York, 2010. [Google Scholar]
- 73.Cui Q; Elstner M, Density functional tight binding: values of semi-empirical methods in an ab initio era. Phys. Chem. Chem. Phys 2014, 16 (28), 14368–14377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Seifert G, Tight-binding density functional theory: An approximate Kohn-Sham DFT Scheme J. Phys. Chem. A 2007, 111, 5609–5613. [DOI] [PubMed] [Google Scholar]
- 75.Porezag D; Frauenheim T; Köhler T; Seifert G; Kaschner R, Construction of tightbinding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947. [DOI] [PubMed] [Google Scholar]
- 76.Seifert G; Porezag D; Frauenheim T, Calculations of molecules, clusters, and solids with a simplified LCAO-DFT-LDA scheme. Int. J. Quant. Chem 1996, 58 (2), 185–192. [Google Scholar]
- 77.Yang Y; Yu H; York D; Cui Q; Elstner M, Extension of the Self-Consistent-Charge Tight-Binding-Density-Functional (SCC-DFTB) method: third order expansion of the DFT total energy and introduction of a modified effective Coulomb interaction. J. Phys. Chem. A 2007, 111, 10861. [DOI] [PubMed] [Google Scholar]
- 78.Elstner M, SCC-DFTB: what is the proper degree of self-consistency? J. Phys. Chem. A 2007, 111, 5614–5621. [DOI] [PubMed] [Google Scholar]
- 79.Slater JC; Koster GF, Phys. Rev. B 1954, 94, 1498. [Google Scholar]
- 80.Elstner M, The SCC-DFTB method and its application to biological systems. Theor. Chem. Acc 2006, 116, 316. [Google Scholar]
- 81.Frenking G; Frohlich N, The nature of the bonding in transition-metal compounds Chem. Rev 2000, 100, 717–774. [DOI] [PubMed] [Google Scholar]
- 82.Kohler C; Frauenheim T; Hourahine B; Seifert G; Sternberg M, Treatment of collinear and noncollinear electron spin within an approximate density functional based method. J. Phys. Chem. A 2007, 111, 5622. [DOI] [PubMed] [Google Scholar]
- 83.Kohler C; Seifert G; Gerstmann U; Elstner M; Overhof H; Frauenheim T, Approximate density- functional calculations of spin densities in large molecular systems and complex solids. Phys. Chem. Chem. Phys 2001, 3, 5109–5114. [Google Scholar]
- 84.Atanasov M; Rauzy C; Baettig P; Daul C, Calculation of Spin-Orbit Coupling Within the LFDFT: Applications to [NiX4]2- (X=F-, Cl-, Br-, I-). Int. J. Quant. Chem 2004, 102, 119–131. [Google Scholar]
- 85.Perdew JP; Burke K; Ernzerhof M, Generalized gradient approximation made simple. Physical Review Letters 1996, 77, 3865. [DOI] [PubMed] [Google Scholar]
- 86.Perdew JP; Zunger A, Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar]
- 87.DFTB+, In User Manual, Version 17.1, https://www.dftbplus.org/fileadmin/DFTBPLUS/public/dftbplus/latest/manual.pdf.
- 88.Humphrey W; Dalke A; Schulten K, VMD - Visual Molecular Dynamics. J. Molec. Graphics. 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
- 89.Healy PC; Patrick JM; White AH, Crystal structure of Tetra-aqua(ehtylenediamine) nickel(II) sulfate dihydrate and of “tetra-aqua(2,2’-bipyridyl) nickel(II) sulfate dihydrate. Aust. J. Chem 1984, 37, 921–928. [Google Scholar]
- 90.Cramer RE; van Doorne W; Huneke JT, Crystal and molecular structure of tris(ethylenediamine)nickel(II) acetate dihydrate, [Ni(NH2CH2CH2NH2)3](O2C2H3)2–2H2O. Inorg. Chem 1976, 15, 529–535. [Google Scholar]
- 91.Knuuttila P, The crystal and molecular-structures of hexaquocobalt(II) diisonicotinate N-oxide and its isostructural nickel(II) homolog. Inorg. Chim. Acta 1981, 52, 141–147. [Google Scholar]
- 92.Polyakova IN; Polynova TN; Porai-Koshits MA, Koord. Khim. (Russ.) (Coord.Chem.) 1981, 7, 1894. [Google Scholar]
- 93.Huffman JC; Wentworth RAD; Tsai CC; Huffman CJ; Streib WE, Cis, cis-1,3,5-triaminocyclohexanetriaquanickel(II) nitrate, Ni(C6N3H15)(H2O)3(NO3)2. Cryst. Struct. Commun 1981, 10, 1493–1495. [Google Scholar]
- 94.van der Merwe MJ; Boeyens JCA; Hancock RD, Crystallographic and thermodynamic study of metal-ion size selectivity in the ligand 1,4,7-triazacyclononane-N,N’N”-triacetate. Inorg. Chem 1985, 24, 1208–1213. [Google Scholar]
- 95.Capilla AV; Aranda RA; Gomez-Beltran F, Cryst. Struct. Commun 1980, 9, 147. [Google Scholar]
- 96.Garcia-Granda S; Gomez-Beltran F, Acta Crystallogr., Sect.C: Cryst. Struct. Commun 1984, 40, 1145. [Google Scholar]
- 97.Nieminen K, Inorg. Chim. Acta 1986, 119, 61. [Google Scholar]
- 98.Bertrand JA; Eller PG; Fujita E; Lively MO; VanDerveer DG, Inorg. Chem 1979, 18, 2419. [Google Scholar]
- 99.Zhou H; Tajkhorshid E; Frauenheim T; Suhai S; Elstner M, Performance of the AM1, PM3, and SCC-DFTB methods in the study of conjugated Schiff base molecules Chem. Phys 2002, 277, 91–103. [Google Scholar]
- 100.Lever ABP, Inorganic Electronic Spectroscopy. Elsevier Publishing Company: Amstedam, The Netherlands, 1968. [Google Scholar]
- 101.Hay PJ; Wadt WR, Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys 1985, 82, 299–310. [Google Scholar]
- 102.Brandenburg JG; Grimme S, Accurate Modeling of Organic Molecular Crystals by Dispersion-Corrected Density Functional Tight Binding (DFTB). J. Phys. Chem. Lett 2014, 5, 1785–1789. [DOI] [PubMed] [Google Scholar]
- 103.LeBlanc LM; Otero-de-la-Roza A; Johnson ER, Composite and Low-Cost Approaches for Molecular Crystal Structure Prediction J. Chem. Theo. Comp 2018, 14, 2265–2276. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


