Measurability of the epidemic reproduction number in data-driven contact networks

Significance

The analysis of real epidemiological data has raised issues of the adequacy of the classic homogeneous modeling framework and quantities, such as the basic reproduction number in real-world situations. Based on high-quality sociodemographic data, here we generate a multiplex network describing the contact pattern of the Italian and Dutch populations. By using a microsimulation approach, we show that, for epidemics spreading on realistic contact networks, it is not possible to define a steady exponential growth phase and a basic reproduction number. We show the operational use of the instantaneous reproduction rate as a good descriptor of the transmission dynamics.

Abstract

The basic reproduction number is one of the conceptual cornerstones of mathematical epidemiology. Its classical definition as the number of secondary cases generated by a typical infected individual in a fully susceptible population finds a clear analytical expression in homogeneous and stratified mixing models. Along with the generation time (the interval between primary and secondary cases), the reproduction number allows for the characterization of the dynamics of an epidemic. A clear-cut theoretical picture, however, is hardly found in real data. Here, we infer from highly detailed sociodemographic data two multiplex contact networks representative of a subset of the Italian and Dutch populations. We then simulate an infection transmission process on these networks accounting for the natural history of influenza and calibrated on empirical epidemiological data. We explicitly measure the reproduction number and generation time, recording all individual-level transmission events. We find that the classical concept of the basic reproduction number is untenable in realistic populations, and it does not provide any conceptual understanding of the epidemic evolution. This departure from the classical theoretical picture is not due to behavioral changes and other exogenous epidemiological determinants. Rather, it can be simply explained by the (clustered) contact structure of the population. Finally, we provide evidence that methodologies aimed at estimating the instantaneous reproduction number can operationally be used to characterize the correct epidemic dynamics from incidence data.

Mathematical and computational models of infectious diseases are increasingly recognized as relevant quantitative support to epidemic preparedness and response (1–3). Independent of the type of modeling approach, our understanding of epidemic models is generally tied to two fundamental concepts. One is the basic reproduction number $R_0$, which is the average number of secondary cases generated by a typical infectious individual over the entire course of the infectious period in a fully susceptible population (4). The other is the generation time $Tg$, the time interval between the infection time of the infector and her/his infectees (5, 6). These quantities are the cornerstones of our understanding of basic epidemic models, as they encompass the condition for the occurrence of an epidemic outbreak ($R_0>1$) and the epidemic doubling time. Both the reproduction number and generation time are determined by the biological characteristics of the pathogen (e.g., probability of transmission given a contact), the pathogen–host system (e.g., timeline of pathogen replication inside the host), and the contact patterns of the population in which the infection spreads (4, 7). The concept of the reproduction number has been extended to stratified models (8) and to heterogeneous contact networks (9) to account for more complex interaction patterns. Furthermore, the definition of $R_0$ has been generalized by the effective reproduction number $R\left(t\right)$ (i.e., the average number of secondary cases generated by an infectious individual at time $t$), thus relaxing the hypothesis of a fully susceptible population (10).

$R_0$ and $Tg$ are mathematically well defined in the early stages of the epidemic in homogeneous models and are widely used in predictive approaches (10, 11). However, several studies have cautioned on the importance of the local contact structures (e.g., households, extended families, communities) in estimating the value of $R_0$ (12–17). Theoretical work has explored the definition of the reproduction number in models entailing community and household structure (18–24), although an operational way to compute $R_0$ is still lacking. For more complex models closely resembling the actual structure of the human populations (e.g., accounting for households, schools, workplaces) (25–34), the estimation of $R_0$ mainly relied on the direct count of secondary cases generated by the index case of the outbreak ($R_0^{\text{index}}$) and/or the analysis of the growth rate of the simulated epidemics. However, both methods have limitations and show marked differences in the estimated values (31, 32). Indeed, $R_0^{\text{index}}$ is computed from the analysis of the index case of an outbreak, which is not necessarily representative of a “typical” infectious individual. In addition to this, growing evidence shows that the classic exponential early growth of the epidemic is an oversimplification often not backed by real-world data (35, 36). For this reason, statistical methods were developed for the analysis of $R\left(t\right)$, assuming that the variations of this quantity are mostly due to the impact of the performed intervention strategies and behavioral changes in the population (10, 16, 17, 37). Unfortunately, for these methods, disentangling the role of connectivity patterns from interventions and behavioral changes in the definition of the reproduction number is challenging due to the lack of microscale data on human contact patterns for large fractions of the population. In summary, a clear operational way to compute $R$ is still lacking, and no predictive modeling studies have thus far focused on the harder task of analyzing the dynamics of the reproduction number over time.

Here, we study the very definition and measurability of $R_0$, $R\left(t\right)$, and $Tg$ with data-driven microsimulation models of the infection transmission process based on a highly detailed synthetic population of agents, where we can have complete access to microlevel data (e.g., keeping track of all interactions of the simulated agents and the entire transmission chain) (25–30). Namely, we consider an infection transmission model where the pathogen spreads on two high-resolution synthetic multiplex contact networks inferred from real-world sociodemographic data. We simulated the progression of a simple influenza transmission model accounting for the natural history of the disease and calibrated to match empirical epidemiological data on the inferred multiplex networks. We measure basic quantities, such as $R_0$, $R\left(t\right)$, and $Tg$, and show that the heterogeneity and clustering of human contact patterns (e.g., contacts between household members, classmates, work colleagues) determine a nontrivial variability of $R\left(t\right)$ and $Tg\left(t\right)$. This evidence, contrasted with the results from null models, highlights the challenges in measuring $R_0$ and $Tg$ in real-world systems. This raises questions about the adequacy of their definitions given the complex temporal dynamics of $R\left(t\right)$ and $Tg\left(t\right)$, both of which highly deviate from the classical theory. Our study suggests that epidemic inflection points, often ascribed to behavioral changes or control strategies, could also be explained by the natural contact structure of the population. Finally, we show that Bayesian analyses of the instantaneous reproduction number over time represent valuable tools for understanding complex epidemic dynamics, provided that reliable estimates of $Tg$ are available.

Results

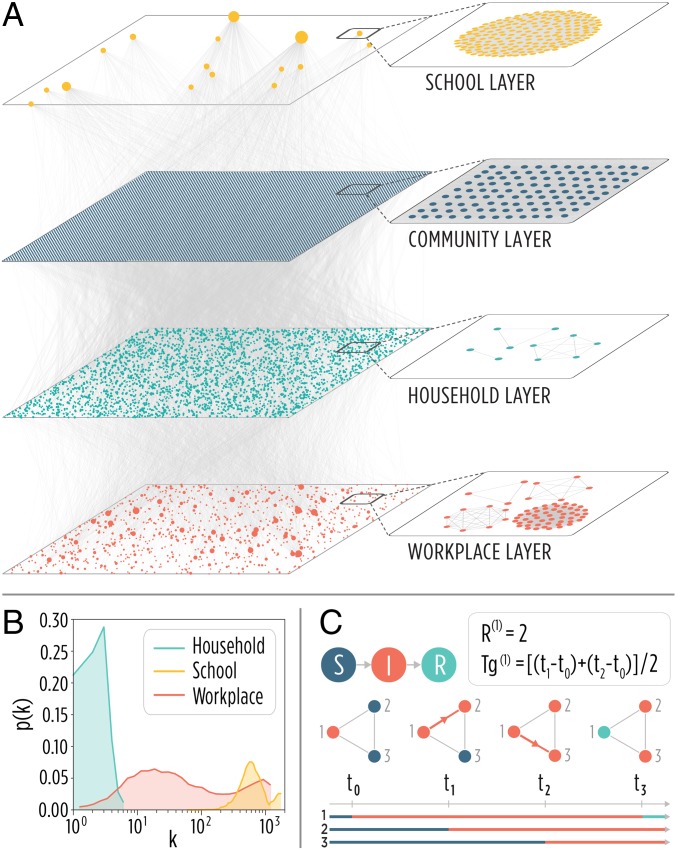
We use detailed sociodemographic data to generate two multiplex networks describing the contact patterns of about $\mathrm{500,000}$ agents, each representative of a subset of the Italian and Dutch populations (Materials and Methods discusses the methodology). The effective contacts through which the infection can spread are determined by the copresence of two individuals in the same settings. This effectively defines a weighted multiplex network (38–40) made by four layers representing the network of contacts between household members, schoolmates, work colleagues, and casual encounters in the general community (Fig. 1A) (15, 26, 34, 41, 42). Each node in the household layer represents one individual of the real population and is linked only to the other nodes representing members of her/his own household. A second layer represents contacts in school (i.e., every node represents one student or teacher and has contact only with other individuals attending/working in the same school). A third layer accounts for contacts in workplaces, and a fourth layer encodes contacts in the community, where we assume a complete network [i.e., each individual has a certain (low) probability of infecting any other individual of the population]. The four layers are characterized by remarkably different degree distributions (Fig. 1B). This representation of links between individuals readily highlights the typical strong clustering of human populations, where individuals tend to meet the same set of contacts (e.g., household members, schoolmates, colleagues) on a regular basis (43–45).

Fig. 1.

Model structure. (A) Visualization of the multiplex network representing a subsample of 10,000 individuals of the synthetic population. Note that the community layer is a complete graph, although not all edges are visible for the sake of readability of the illustration. (B) Degree distributions in the school, household, and workplace layers. (C) Schematic representation of the infection transmission model along with examples of the computation of individual reproduction number and generation time for the simulated transmission chains. I, infectious; R, removed; S, susceptible.

The influenza-like transmission dynamics are defined through a susceptible, infectious, removed (SIR) scheme (Fig. 1C). Essentially, susceptible individuals can acquire the infection through contacts with infectious individuals, and as soon as they are infected, they proceed to the infectious stage. Infectious individuals then move to the removed compartment according to a removal rate [such that an infectious individual spends an exponential amount of time (the removal time or infectious period) in the infectious stage before recovering]. We keep the transmission scheme as simple as possible (e.g., avoiding the introduction of other classes, such as a latent compartment, the distinction between symptomatic and asymptomatic individuals, hospitalized individuals, and so on) to avoid confounding effects. Of course, more refined models are needed to answer complex questions, such as the impact of control strategies.

We simulate the transmission dynamics as a stochastic process for each specific individual, each with her/his own characteristics (e.g., age, individual infectiousness, membership to a specific household or school, and so on), and accounting for the clustering of contacts typical of human populations. For instance, an agent can transmit the infection in a given school only if she/he studies or works there. In each layer, the infection transmission between nodes is calibrated in such a way that the fractions of cases in the four layers are in agreement with literature values (namely, 30% of all influenza infections are linked to transmission occurring in the household setting, 18% of all influenza infections are linked to transmission occurring in schools, 19% of all influenza infections are linked to transmission occurring in workplaces, and 33% of all influenza infections are linked to transmission occurring in the community) (26, 27, 33). Moreover, we set these layer-specific transmission rates such that the reproduction number of the index case ($R_0^{\text{index}}$) is 1.3 [in agreement with typical values reported for influenza in the literature (46)]. Finally, without loss of generality, we fix the removal time to 3 d (15, 47, 48).

In SI Appendix, we report all of the details of the transmission model (SI Appendix, section 1.1). In the text, we also report the corresponding analysis of $R\left(t\right)$ and $Tg\left(t\right)$ for a stochastic implementation of a homogeneous mixing SIR model at the individual level, where all individuals are identical and are in contact with the same fixed probability. Along with the homogeneous SIR model, we also studied a set of alternative null models with an increasing level of complexity from the homogeneous model to the data-driven model (details are in SI Appendix, sections 1.2–1.5). Null models include annealed (edges are constantly rewired) and quenched (edges are fixed over time) configuration models. Results reported in the text refer to the synthetic population for Italy.

Effective Reproduction Number and Generation Time.

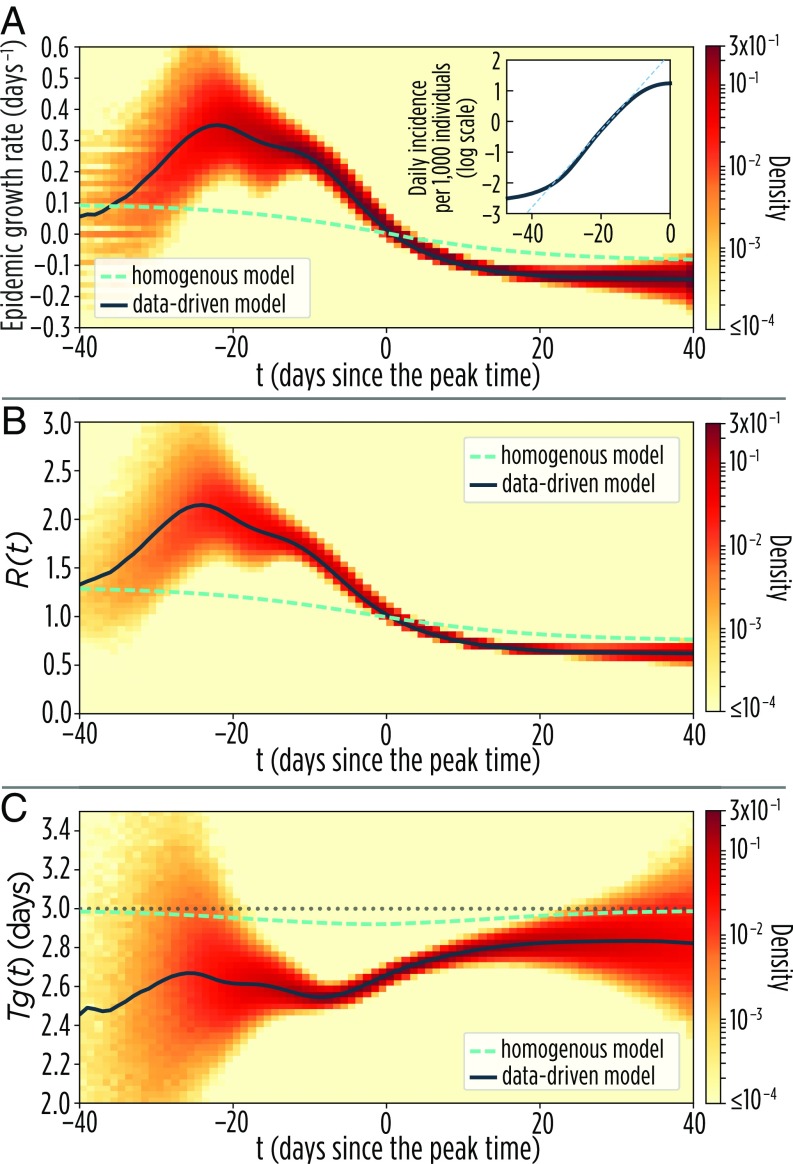
The first quantities generally investigated in epidemic models are the incidence (of new infections) as a function of time and the associated growth rate of the epidemic. In homogeneous models, the number of new cases increases exponentially at a nearly constant rate $r$ (5, 49, 50) during the early phase of the epidemic. This is not the case in the data-driven model, where we find a nonmonotonous behavior: an increasing trend over the initial phase of the epidemic occurs followed by a marked decrease about 20 d before the epidemic peak (Fig. 2A). Such a result is in sharp contrast with the classic theory, where the epidemic growth rate is expected to slowly and monotonically decrease over time in the early epidemic phase (Fig. 2A). This suggests that, in contrast to simple SIR models where the basic reproduction number can readily be defined through the relation $R_0=1+rTg$ (5), it is difficult to find a proper definition of the basic reproduction number in populations characterized by realistic connectivity patterns.

Fig. 2.

Fundamental epidemiological indicators. (A) Mean daily exponential epidemic growth rate, $r$, over time of the data-driven and homogeneous models. The colored area shows the density distribution of $r\left(t\right)$ values obtained in the single realizations of the data-driven model. Results are based on 50,000 realizations of each model. Results are aligned at the epidemic peak, which corresponds to time $t=0$. Inset shows the logarithm of the mean daily incidence of new influenza infections over time, which does not follow a linear trend. (B) Mean $R\left(t\right)$ of data-driven and homogeneous models. The colored area shows the density distribution of $R\left(t\right)$ values obtained in the single realizations of the data-driven model. (C) The three lines represent the mean $Tg\left(t\right)$ of data-driven and homogeneous models. The colored area shows the density distribution of $Tg\left(t\right)$ values obtained in the single realizations of the data-driven model. The horizontal dotted gray line represent the constant value of the duration of the infectious period.

The daily effective reproduction number and generation time can be computed from the microsimulations by keeping track of the exact number of secondary infections generated by each individual infected at time $t$ in the simulations (Fig. 1C). We find that $R\left(t\right)$ increases over time in the early phase of the epidemic, starting from $R_0^{\text{index}}=1.3$ to a peak of about 2.1 (Fig. 2B). In contrast, in the homogeneous model, which lacks the typical structures of human populations, $R\left(t\right)$ is nearly constant in the early epidemic phase and then rapidly declines before the epidemic peak (Fig. 2A) as predicted by classical mathematical epidemiology theory (4). The pattern found in the data-driven model can also be partly explained by the variation of the average degree induced by the infection of individuals with a higher number of adequate contacts [an effect already observed in heavy-tailed networks (51)], thus leading to an average growth of the reproduction number. The temporal dynamics of $R\left(t\right)$ does not show a constant phase, implying that $R_0$ loses its meaning as a fundamental indicator in favor of $R\left(t\right)$. Although we report the results averaged over 50,000 realizations of the model, this result is supported by our analysis of the outcome of each single simulation, highlighting that the early time increase of $R\left(t\right)$ is a common pattern in the performed simulations (SI Appendix, section 2.1). In Fig. 2C, we show an analogous analysis of the estimated generation time in the data-driven model. We find that the generation time is considerably shorter than the duration of the infectious period (i.e., 3 d in our simulations). The estimated average $Tg$ over the whole epidemic is 2.67 d ($\approx 11\%$ shorter than the theoretical value), with a more marked shortening right before the epidemic peak (Fig. 2C). This differs from what is predicted by the classic theory and the analysis of the homogeneous model (Fig. 2C), where the length of the infectious period corresponds to the generation time (6).

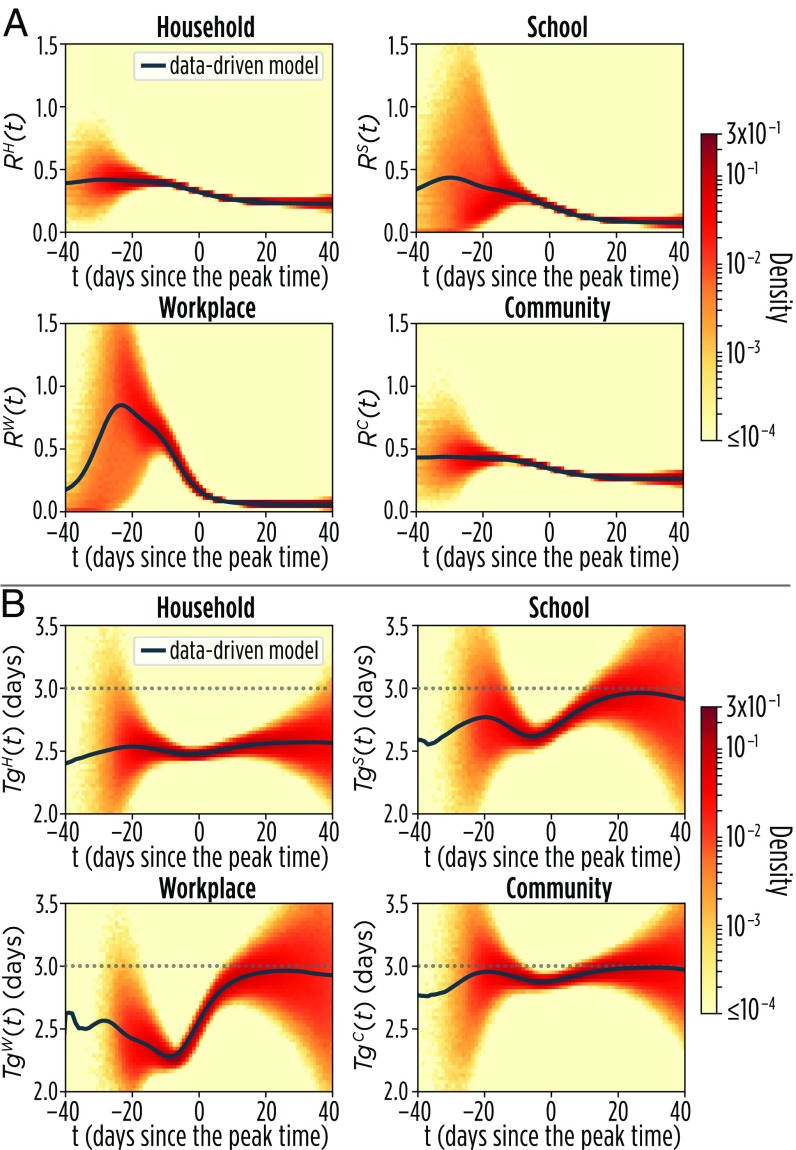
A closer look at the transmission process in the different layers of the multiplex network helps in understanding the origin of the deviations of $R\left(t\right)$ and $Tg\left(t\right)$ from the classical theory (Fig. 3). Specifically, we found that the average degree of infectious nodes as well as $R\left(t\right)$ tend to peak in the workplace layer (SI Appendix, section 2.2), and at least to some extent, the same happens in the school layer. However, $R\left(t\right)$ generally decreases in the household and community layers (Fig. 3A). Indeed, $R\left(t\right)$ in the household layer tends to be more uniform across the different nodes and thus, follows a general decreasing trend simply led by the depletion of susceptible contacts. We also found that, in the household layer, $Tg$ is remarkably shorter than in all other layers (Fig. 3B)—with an average fluctuating around 2.6 d, close to the value reported by analyzing real data for household transmission (26). To provide a simple illustration of the saturation effect in households, let us consider a household of three, with one index case and two susceptible members. If, at time $t$, the index case infects exactly one of the two susceptibles, then at time $t+1$, the index case has to compete with the other infectious individual to transmit the infection; the resulting generation time is shorter, simply because she/he cannot infect any other household member, although she/he may still be infectious. A similar argument was used in ref. 52 to explain why observed generation times are shorter than the infectious period. This evidence calls for considering within household competition effects when providing empirical estimates of the generation time (or serial interval) from household studies. Saturation effects are also responsible for shortening $Tg$ in the other transmission settings, with the exception of the general community (Fig. 3B). All of the observed patterns of $R\left(t\right)$ and $Tg\left(t\right)$ are robust with respect to changes in the sociodemographic structure of the population (i.e., we simulated the infection spreading in both the Italian and Dutch synthetic populations), influenza transmission intensity (measured in terms of $R^{\text{index}}$), and the distribution of the removal time (we tested exponential and gamma distributions). These analyses are reported in SI Appendix, sections 2.4–2.6.

Fig. 3.

Layer-specific patterns. (A) Mean $R\left(t\right)$ for the data-driven model in the four layers. The colored area shows the density distribution of $R\left(t\right)$ values obtained in the single realizations. (B) Mean $Tg\left(t\right)$ for the data-driven model in the four layers. The colored area shows the density distribution of $Tg\left(t\right)$ values obtained in the single realizations.

The 2009 H1N1 Influenza Pandemic in Italy.

To test the robustness of the results in a more realistic epidemic transmission model, we used the data-driven modeling framework to model the 2009 influenza pandemic in Italy. One of the characteristic signatures of the 2009 H1N1 pandemic was the presence of a differential susceptibility by age (34, 53, 54); this is included in the model by using values estimated for Italy as reported in the literature (55). We also consider prepandemic immunity by age in the population according to serological data (55). Vaccination is not considered, as vaccination started only during the tail of the pandemic and had a very limited uptake in Italy (vaccination coverage $<1\%$) (56). As in the previous section, the model has four unknown parameters: the four layer-specific transmission rates. They are calibrated through a Bayesian Markov chain Monte Carlo (MCMC) approach on seroprevalence data by age collected in Italy before and after the 2009 H1N1 influenza pandemic (55). Model details are provided in SI Appendix, section 1.1.

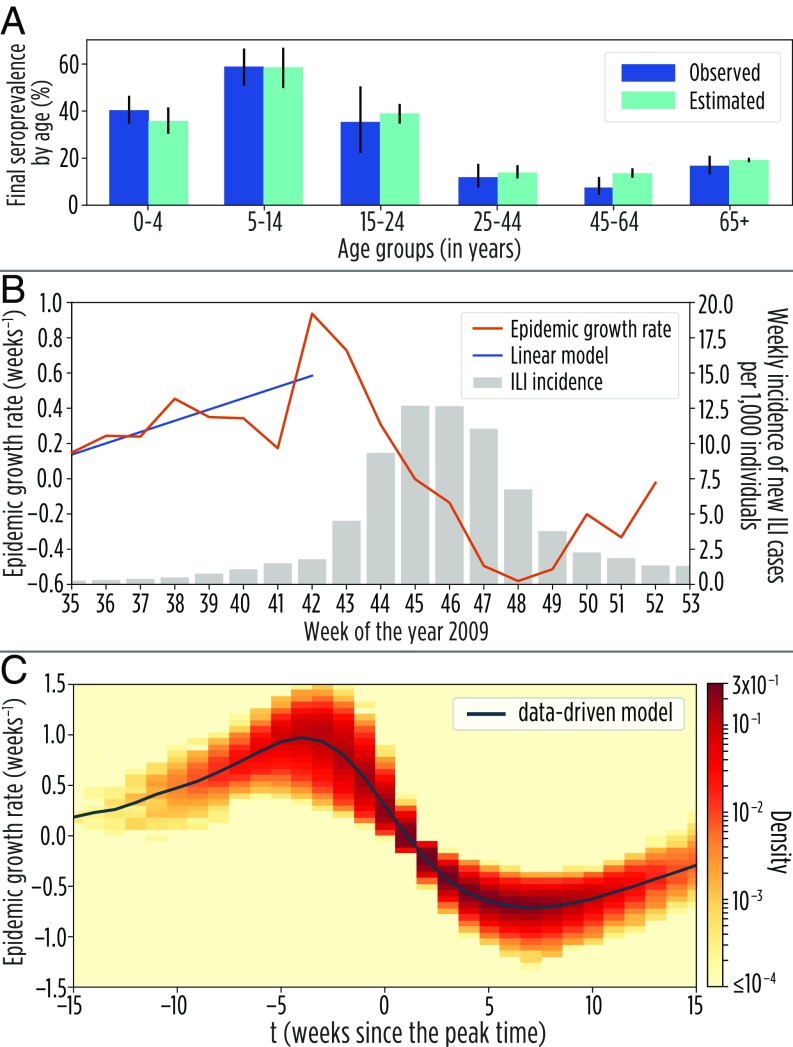
The calibrated model is able to well capture the seropositive rates by age at the end of the pandemic (Fig. 4A). The estimated growth rate from the influenza-like illness (ILI) cases reported in Italy over the course of the 2009 H1N1 influenza pandemic clearly shows an increasing trend during the early phase of the epidemic followed by a sharp drop about 3 weeks before the epidemic peak (Fig. 4B). The trend observed in the data is consistent with that obtained in model simulations (Fig. 4C). Fitting a linear regression model to the estimated growth rate over time in the ILI data results in an estimated coefficient of 0.064 (SE of 0.033), while the mean value obtained with a linear regression model of case incidence from all stochastic realizations is 0.064 ($95\%$ CI, −0.207–0.305). An increase in the initial growth rate of the epidemic has also been observed for other diseases and countries (57–59). Although alternative explanations may exist (60), our results provide a plausible explanation for these patterns based on the intrinsic structure of human contact networks. In terms of the dynamics of $R\left(t\right)$ and $Tg\left(t\right)$, the model calibrated on the 2009 influenza pandemic confirms the noticeable deviations of the data-driven model from the homogeneous modeling framework (SI Appendix, section 2.3).

Fig. 4.

The 2009 H1N1 influenza pandemic in Italy. (A) Seroprevalence rates by age as observed in a serosurvey conducted at the end of the 2009 H1N1 influenza pandemic in Italy (55) and as estimated by the calibrated model. (B) Epidemic growth rate over time $r\left(t\right)$ as estimated from the weekly incidence of new ILI cases in Italy over the course of the 2009 H1N1 influenza pandemic and the best-fitting linear model from week 35 to week 41 in 2009 (scale on the left axis). Weekly incidence of new ILI cases in Italy over the course of the 2009 H1N1 pandemic (scale on the right axis). Data are available at the ISS Influnet website (old.iss.it/flue/). Note that, over the period from week 35 to week 51 in 2009, schools were regularly open in Italy. (C) Temporal pattern of the mean weekly exponential epidemic growth rate ($r$) resulting from the analysis of the data-driven model calibrated on the 2009 H1N1 influenza seroprevalence data. The colored area shows the density distribution of $r\left(t\right)$ values obtained in the single realizations of the data-driven model.

Discussion

Our simulation results clearly highlight how the heterogeneity and clustering of human interactions (e.g., contacts between household members, classmates, work colleagues) alter the standard results of fundamental epidemiological indicators, such as the reproduction number and generation time over the course of an epidemic. Our results seem to be consistent in different countries (SI Appendix, section 2.4), suggesting that the observed patterns are due to the structure and clustering of human contact patterns rather than country-specific features. Furthermore, the analysis of alternative null models, such as degree-preserving and layer-preserving configuration models (SI Appendix, section 2.7), shows markedly different behaviors than those exhibited by the data-driven model, suggesting that the multiplex structure and the strong clustering effect typical of human populations, not captured by null models, are at the root of the observed behavior.

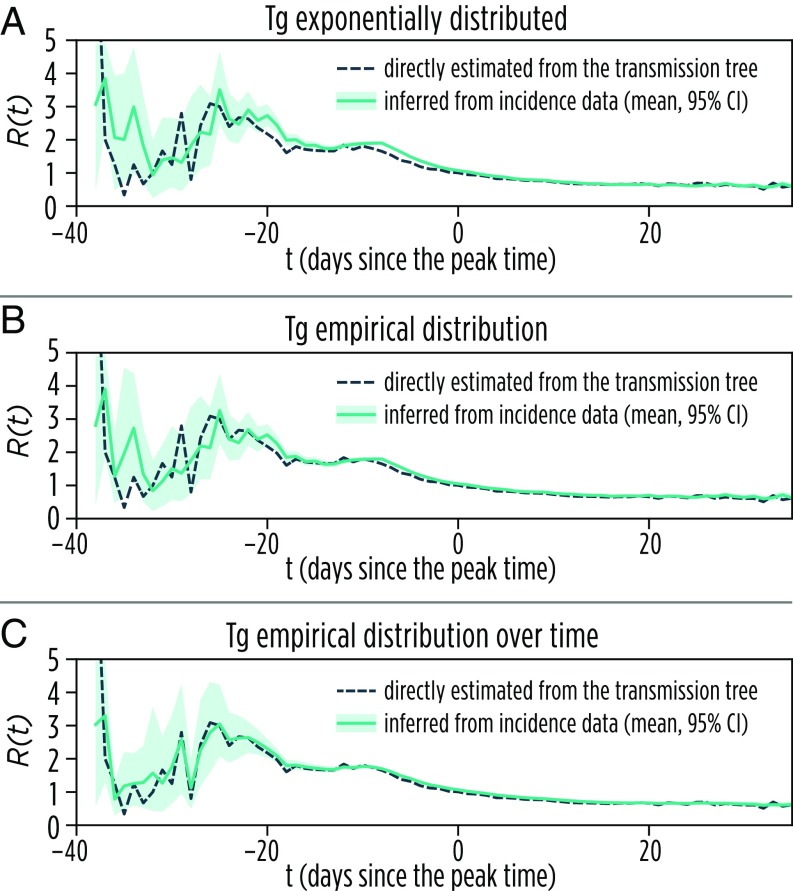
Our numerical study questions the measurability of $R_0$ in realistic populations and its adequacy even as an approximate descriptor of the epidemic dynamics. However, it is still possible to characterize the dynamics of an epidemic in terms of its effective reproduction number over time by estimating $R\left(t\right)$ from the daily number of new cases by using Bayesian approaches (11, 17) (Materials and Methods). In Fig. 5, we show the comparison between $R\left(t\right)$ as inferred from the time series of cases and $R\left(t\right)$ resulting from the microsimulation data of the transmission chain for one stochastic model realization (other realizations are shown in SI Appendix, section 2.8). The overall good agreement between the estimated and actual values shows that it is possible to operationalize the estimation of $R\left(t\right)$ to provide projections of the epidemic dynamics. The goodness of the obtained estimates depends on the knowledge of the distribution of the generation time (Fig. 5) and on the availability of a reliable time series of cases not markedly affected by noise and underreporting (10).

Fig. 5.

Estimation of $R\left(t\right)$. (A) Daily $R\left(t\right)$ as inferred from the daily incidence of new infections for one stochastic model realization. $Tg$ is assumed to be exponentially distributed with an average of 3 d. (B) The same as A but the distribution of $Tg$ has been derived from the analysis of the transmission tree of the selected model simulation. (C) The same as A but using the distribution of $Tg$ over time as derived from the analysis of the transmission tree of the selected model simulation. The goodness of the estimate of $R\left(t\right)$ increases with a more precise knowledge of the generation time value and distribution.

Conclusion

The analysis presented here takes advantage of “in silico” numerical experiments to open a window of understanding in the analysis of realistic epidemic scenarios. Although a lot of theoretical work has been done to define the reproduction number in nonhomogeneous models (19–24), a unified theory is still lacking. While we are not providing a theoretical framework for the computation/definition of the reproduction number and the generation time on realistic contact networks, we provide evidence that estimates of $R\left(t\right)$ can be used to characterize the epidemic without resorting to untenable assumptions that may eventually mislead our understanding of the epidemic transmission potential and temporal dynamics.

Materials and Methods

Data-Driven Contact Network.

The model considers a weighted multiplex network (38) $\overrightarrow{G}=\left(G_H,G_S,G_W,G_C\right)$, where $H,S,W,$ and $C$ represent household, school, workplace, and community layers, respectively. Let us define $V$ as the set of all nodes, which is common to all layers, and $E_{\alpha }$ as the set of edges in layer $\alpha$. We can thus characterize each layer $G_{\alpha }=\left(V,E_{\alpha }\right)$ by the layer-specific adjacency matrix $A^{\alpha }$, where elements $a_{ij}^{\alpha }=w_{\alpha }>0$ if there is a link between nodes $i$ and $j$ in layer $\alpha$ and $a_{ij}^{\alpha }=0$ otherwise.

Homogeneous Mixing Network.

This model assumes a single fully connected network. Following the notation introduced above, we have $a_{ij}=w$ for each $i$ and $j$, where $w=1/\left(N-1\right)$ and $N$ is the total number of individuals in the population.

The Epidemic Transmission Model.

On each of the introduced networks, we simulate the influenza transmission process as an SIR model. The SIR model assumes that individuals can be in one of the following three states: susceptible, infectious, and removed. Two types of transitions between states are possible: (i) from susceptible to infectious and (ii) from infectious to removed. The transition from susceptible to infectious requires a contact between an infectious individual and a susceptible individual. Specifically, given that, at time step $t$, node $j$ is infectious and its neighbor node $i$ is susceptible, the probability that $j$ infects $i$ (i.e., $i$ changes its status from susceptible to infectious) is given by $\beta =pw$, where $p$ is the transmission probability per contact and $w$ is the contact weight. However, the transition from infectious to removed does not involve contact between individuals. Given that, at time step $t$, node $i$ is in the infectious state, it has a probability $\gamma$ to recover at time step $t+1$.

Estimation of R(t) from Transmission Events Time Series.

Following the same approach used in refs. 11 and 17, we assume that the daily number of new cases $C\left(t\right)$ at time $t$ can be approximated by a Poisson according to the following equation:

$$C\left(t\right)\approx Pois\left(R\left(t\right)\sum _{s=1}^t\varphi \left(s\right)C\left(t-s\right)\right),$$

where $\varphi$ is the generation time distribution and $R\left(t\right)$ is the effective reproduction number at time $t$. The likelihood $L$ of the observed time series of cases from day 1 to $T$ is thus given by

$$L=\prod _{t=1}^{T}P\left(C\left(t\right),R\left(t\right)\sum _{s=1}^t\varphi \left(s\right)C\left(t-s\right)\right),$$

where here, $P\left(k,\lambda \right)$ is the probability mass function of a Poisson distribution (i.e., the probability of observing $k$ events if these events occur with a known rate $\lambda$). The posterior distribution of $R\left(t\right)$ is then explored using MCMC sampling.