Scientific prize network predicts who pushes the boundaries of science

Abstract

Scientific prizes confer credibility to persons, ideas, and disciplines, provide financial incentives, and promote community-building celebrations. We examine the growth dynamics and interlocking relationships found in the worldwide scientific prize network. We focus on understanding how the knowledge linkages among prizes and scientists’ propensities for prizewinning relate to knowledge pathways between disciplines and stratification within disciplines. Our data cover more than 3,000 different scientific prizes in diverse disciplines and the career histories of 10,455 prizewinners worldwide for over 100 years. We find several key links between prizes and scientific advances. First, despite an explosive proliferation of prizes over time and across the globe, prizes are more concentrated within a relatively small group of scientific elites, and ties among elites are highly clustered, suggesting that a relatively constrained number of ideas and scholars push the boundaries of science. For example, 64.1% of prizewinners have won two prizes and 13.7% have won five or more prizes. Second, certain prizes strongly interlock disciplines and subdisciplines, creating key pathways by which knowledge spreads and is recognized across science. Third, genealogical and coauthorship networks predict who wins multiple prizes, which helps to explain the interconnectedness among celebrated scientists and their pathbreaking ideas.

Scientific prizes arguably play many roles in advancing scientific discoveries, yet they have been the subject of few quantitative analyses. Prizes are among the highest forms of recognition scientists accord one another (1). By promoting high-risk, high-return science (2–4) or new lines of research (5, 6), prizes identify top scientific achievements (7–10). The Nobel Prize, for example, is awarded for work that provides “the greatest benefit to mankind” (11). Besides identifying notable ideas, prizes perform cultural functions meant to improve research. They identify successful role models who inspire achievements once thought to be impossible (8, 11, 12) and act as signals of scientific credibility (13). Many scientists can name their prizewinning “heroes” and with ritualistic fanfare follow each year’s announcement of prizewinners (14, 15). At the University of Chicago, faculty follow a cultural practice of standing and applauding Nobel prizewinners when they enter a room. Prizes may also forecast the direction of future scientific investments. Prizewinning papers are cited in patents faster than similarly cited, nonprizewinning papers (7, 16) and often include prizewinners with direct or indirect capital (e.g., Howard Hughes Medical Research Award) that stimulates research (4, 6).

While debate about the positive role of prizes remains unsettled (17–20), scientific prizes continue to proliferate. Thousands of prizes now exist across diverse sciences, topics, and regions of the world, and for different levels of scientific discovery (8). Besides the Nobel prize, for example, there is the highly prestigious Albert Einstein Medal in theoretical physics, the Lasker Award in biomedical science, the Davy Medal in chemistry, the Fields Medal in mathematics, and the Copley Medal, which is discipline nonspecific. While prizes aim to expand attention to scientific ideas, they also connect science. In some cases, a single scientist can be a winner of multiple prizes within and across disciplines. Rainer Weiss, winner of the 2017 Nobel Prize in Physics, was already an Einstein, Shaw, and Harvey prizewinner. The Clark Medal, also known as the “Baby Nobel,” has 12 of 23 (52%) medalists who went onto become Nobelists (21, 22). The increasing proliferation of prizes and connections among prizes suggest that the prize network embodies information about scientists poised to grow in acclaim as well as scientific knowledge likely to propagate within and between fields (23).

Harriet Zuckerman’s landmark work (11) provides a foundation for analysis of the prize network and prizewinners. She studied the similarities and differences in Nobelists’ demographic, family, religion, coauthorship, and research topics. Other foundational research has studied the stratification of awards (24, 25) and the Matthew effect and social network relations among prizewinners (26, 27).

With the unprecedented expansion of science and the availability of large-scale datasets on prizes, prizewinners, citations, and collaborations worldwide, analyses of the global scientific prize network’s properties and their potential association with scientific advances and stratification are now possible. Here, we address two main questions. First, we derive the statistical properties of the global scientific prize network in terms of growth dynamics over time and the ensuing transition probabilities between prizes that can interlock subfields within a discipline and fields between disciplines. Second, we examine how genealogical ties and coauthor ties are associated with prizewinning and the concentration of prizes among scientists. We demonstrate that, despite a proliferation of diverse prizes over time and across the globe, prizes are more concentrated within a relatively small scientific elite.

For our analysis, we collected comprehensive data on 3,062 scientific prizes worldwide, which includes more than 10,455 winners spanning more than 100 y in over 50 countries. For each winner, we recorded his or her publication and citation data, institutional affiliations, years of scientific activity, genealogical relationships, and coauthorship ties. With these data, we examined fundamental questions about the global scientific prize network (see Materials and Methods for details).

Our analysis proceeds as follows. First, we derived the statistical properties of the global scientific prize network, focusing on growth dynamics and the transition probabilities that reveal how prizes interlock knowledge within and between disciplines. Second, we model how a prizewinner’s genealogical and coauthorship networks are associated with prizewinning and the concentration of prizes among a few prizewinners.

Results

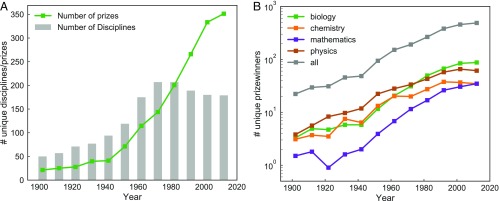
Fig. 1A shows the sharp annual increase in the number of prizes relative to the growth of scientific subdisciplines. We observe that the number of prizes grew at a faster rate than the number of new disciplines [per the Web of Science (WoS)]. The WoS lists the number of disciplines and subdisciplines. For example, psychology is disaggregated into its subdisciplines: applied psychology, biological psychology, clinical psychology, developmental psychology, educational psychology, experimental psychology, mathematical psychology, multidisciplinary psychology, psychoanalysis psychology, and social psychology. We compare the rate of growth of prizes to the most disaggregated level of disciplinary categories in the WoS. Up to 1980, there were fewer prizes than there were scientific fields; after 1980, the pattern reversed; prizes now outnumber subdisciplines by an almost 2:1 margin. The number of scientific prizes has roughly doubled every 25 y; currently, more than 350 prizes are conferred each year compared with about 20 prizes conferred annually roughly 100 y ago.

Fig. 1.

A century of scientific prizes. A and B represent the relative proliferation of scientific prizes (A) and prizewinners (B) from 1900 to 2015. A shows the proliferation of prizes and the proliferation of separate scientific (sub)disciplines. Before 1980, there is a similar proliferation rate for disciplines and prizes, although there were nearly twice as many scientific disciplines as prizes; after 1980, prizes continue to proliferate at the pre-1980 rate and by 2015 outnumber the number of scientific fields at a 2:1 ratio.

The proliferation of prizes across disciplines suggests that opportunities have grown to recognize a greater diversity of ideas and scholars. However, the pattern of results appears to show that the proliferation of prizes has instead led to greater social stratification among prizewinners. The data indicate that the absolute number of prizewinners has grown more slowly over time than the number of prizes (Fig. 1B) even though prizes that used to be awarded each year to a single scientist, such as the Nobel, are now awarded each year to teams of scientists. Along with these trends, prizewinning has become more concentrated within a small set of prizewinners. While the pie of prizes expanded, relatively fewer scholars received ever bigger slices of the prize pie.

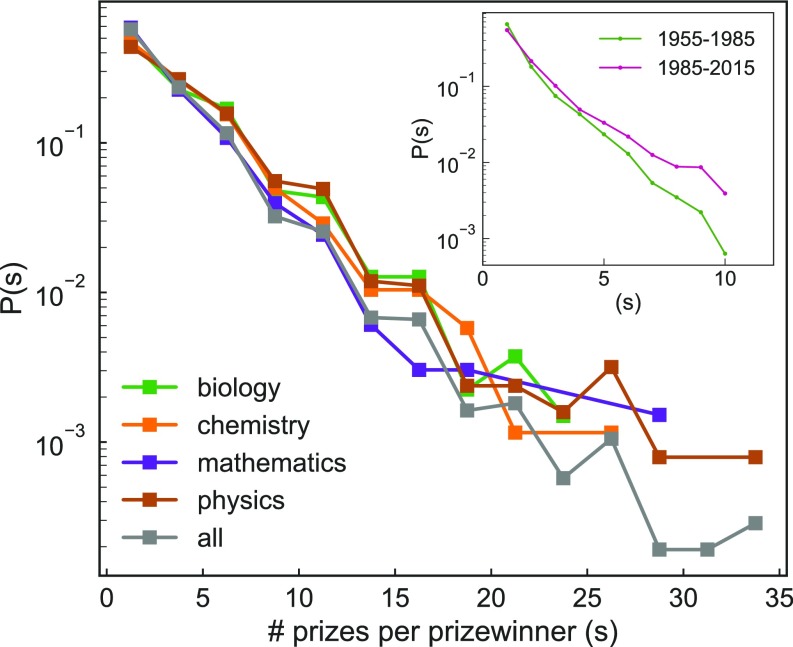
The emergence of a subset of scientists who win numerous prizes creates this concentration. This uneven distribution of prizes per scientist is evident along several measures shown in Fig. 2. Fig. 2 plots the number of prizes per prizewinner for four dominant disciplines and all prizewinners in our sample. The prize-per-scientist distribution is noteworthy in that it is roughly equivalent across disciplines with each discipline following an exponential distribution (P < 10⁻⁴) (28). The distribution indicates that fully 64.1% of winners won at least 2 different prizes over their careers, 13.7% of the winners won 5 or more prizes, and some scientists have won more than 20 prizes.

Fig. 2.

The exponential distribution of scientific prizewinning. Plot and Inset show the number of prizes per prizewinner and the change in the distribution of prizes per winner before and after 1985, the midpoint of our data. The distribution on prizes per prizewinner fits an exponential distribution and indicates that many different prizes are won by a relatively small number of scholars. For example, over 60% of prizewinners are two-time winners of different prizes and about 15% are five-time winners of different prizes. The Inset shows that this heavy concentration of diverse prizes among a relatively small scientific elite has intensified. Despite there being nearly twice as many prizes after 1985 than before 1985, fewer scientists win a larger share of available prizes.

Fig. 2, Inset, shows that the contemporary concentration of prizes in the hands of a few prizewinners is a reverse of the distribution that existed before 1985. Before 1985, the prizes are more evenly distributed among prizewinners than in the post-1985 periods. After 1985, there has been a significant increase in concentration at nearly every level of multiple prizewinner (P < 10⁻²¹). These data suggest that the explosive expansion of the prize network has expanded the pie for recognizing acclaimed work and the number of influential scientists in an absolute sense; however, at the same time, science has become more stratified within a relatively small and concentrated scientific elite (1). The scientific elite has also become transdisciplinary; scientists who win multiple prizes do so not just within one discipline but across different disciplines.

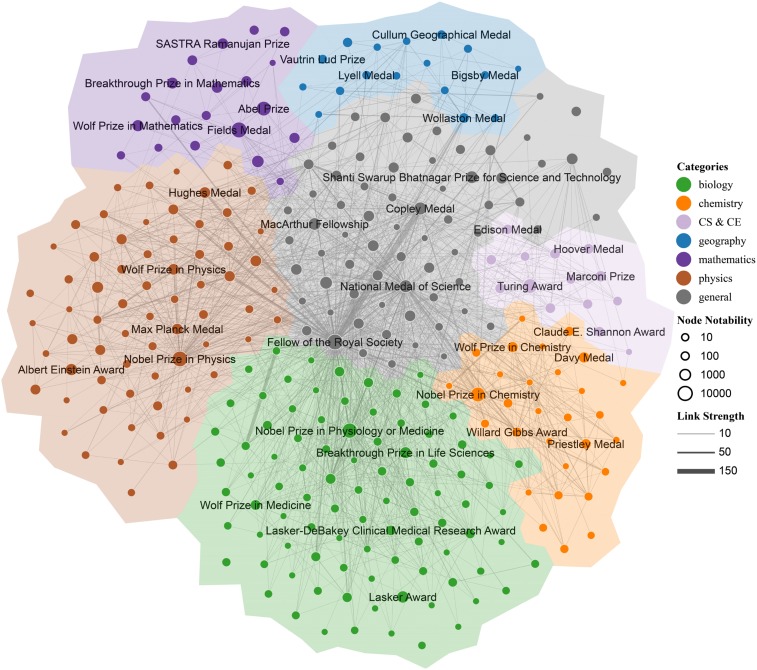
The prize network’s topology reveals a pecking order among prizes and interlocking knowledge pathways between and among prizes (29). To create the prize network, we defined a network where the nodes are prizes (e.g., Nobel or Fields Medals) and node size represents a prize’s notability based on its average Wikipedia page views per month (30). Links between nodes i and j occur when prizes i and j are won by the same scientist. Links are weighted by the count of prizewinners who have won both prizes i and j.

Fig. 3 shows that the number of scientific prizes varies by discipline and is clustered by discipline (a modularity value of 0.492) (31). Notably, disciplines have a similar hierarchy of prizes. We ranked prize’s notability by their Wikipedia page views, which ranges from 10 to 10,000. Most disciplines have one to three most notable prizes (10,000 views), a middle layer of notable prizes (1,000 views), and a ring of specialized prizes (10 or 100 views). This pattern of recognition indicates that, despite differences in talent, number of areas of specialty, funding, age of field, and number of journals, fields have similar prize pecking orders.

Fig. 3.

The scientific prize network. In the network, nodes denote prizes, and node size reflects the prize’s relative notability within its discipline. Links are formed between a pair of prizes when the same scientist wins both prizes. The link weight is proportional to the number of scientists who won both prizes. Most prizes cluster within a discipline, but certain prizes create knowledge interlocks between disciplines.

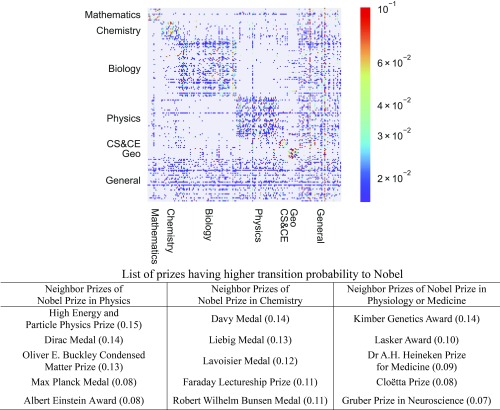
Fig. 3 shows that interlocks exist among certain prizes when prizes i and j are won by the same scientist. The interlocks between prizes provide a picture of the backbone of the network linking prizes and disciplines (32–34). A critical measure of the relationship between prizes is encapsulated in the transition probability among prizes, where the probability represents the likelihood of winning a prize conditional on having won another prize. The stronger the transition probability, the more likely it is that a scientist’s ideas will spread through science via the special attention and acclaim the prizes give to the ideas.

To quantify the interlock transition probabilities, we formulated a probability adjacency matrix of the prize network. In the matrix, the values (i, j) denote the probability that prize i is a precursor to prize j and vice versa. In our data, the scale of interlocking is broad, with i and j prize pairings have a range of frequencies from 1 to 150 dual winners (per Fig. 2). The blocks within the matrix indicate the intensity levels of the transition probabilities between any two prizes.

Fig. 4 shows the transition matrix and indicates three important results. First, prize interlocks are densest within disciplines. This finding quantitatively reinforces the modularity shown in Fig. 3 and suggests that the strongest relationships among prizes occur between the subdisciplines of the same discipline. Nevertheless, disciplines vary in the interlocking of their prizes. Chemistry and physics are the most interlocked, while math and geography are least interlocked. Second, while some prizes appear to be stepping-stones to prizes of high notability, in most cases, high transition probabilities between prizes are symmetric rather than directional. Third, certain interlocks occur between disciplines. This suggests that certain prizewinners and their ideas connect disciplines via the prize network (35, 36). Consistent with this inference, Howard Hughes Medicine Institute (HHMI) Award winners has been found to be more highly cited across disciplines and to combine more novel lines of inquiry than a control group of similarly accomplished, non-HHMI, NIH-funded researchers (4).

Fig. 4.

Scientific prize transition matrix. When two different prizes are won by the same scholar(s), they form an interlock between prizes. The interlock designates a pathway of knowledge flows within and between subdisciplines. Interlocks also represent the propensity for winning a prize conditional on winning another prize. These propensities are represented by the values in the transition matrix of the prize network. Chemistry and physics have relatively high transition probabilities among prizes relative to math and biology. General prizes play the unique role of integrating diverse sciences. The table below the transition matrix shows the prizes with the highest transition propensities to the Nobel prizes (the transition probabilities are shown in brackets).

The concentration of interlocks raises questions about the factors associated with becoming a multiprizewinner. Social and genealogical networks could play a role in prizewinning through teamwork (37, 38), information search (39, 40), and access to novel, interdisciplinary ideas (41–44). To investigate this hypothesis, we linked 2,034 winners to their scientific genealogy trees and extracted their coauthorship network from publication lists. Two winners connect when they have an advisor–student relationship (PhD or postdoctoral researcher) or coauthor at least one paper (Materials and Methods).

Fig. 5 shows the backbone of the prizewinner network and reveals three important findings. First, a giant component of 1,504 (74%) winners is connected through their genealogy ties and connections to coauthors who are themselves prizewinners. Second, prizewinners are not randomly distributed throughout science. Notably, genealogical ties are relatively evenly dispersed while coauthorship ties are densely packed in the center of the prizewinner’s network. These patterns of career collaborations—primary collaborative ties with an advisor and subsequent collaborative ties with coauthors—suggests that advisors are important to winning at least one prize, but future prizewinning is associated with expanding one’s network to prizewinning coauthors. Third, the interconnections among prizewinners are not localized: they span the globe, institutions, and time periods. Thus, not only are prizes highly concentrated within a small scientific elite but also the scientific elite is itself a highly interconnected cluster of interdependent influentials.

Fig. 5.

Social network of prizewinners. Nodes (not shown) represent prizewinners, and links represent the presence of genealogical or collaborative relationships between winners. Network shown here contains 830 winners, in which only strong coauthorship ties (links with more than three coauthored papers) are shown. Genealogical relationships, which are a scholar’s primary, formative relationships, are more evenly distributed throughout the network than are coauthorship ties, which are noticeably concentrated in the dense center of the network and continue to grow in number throughout most scholars’ careers.

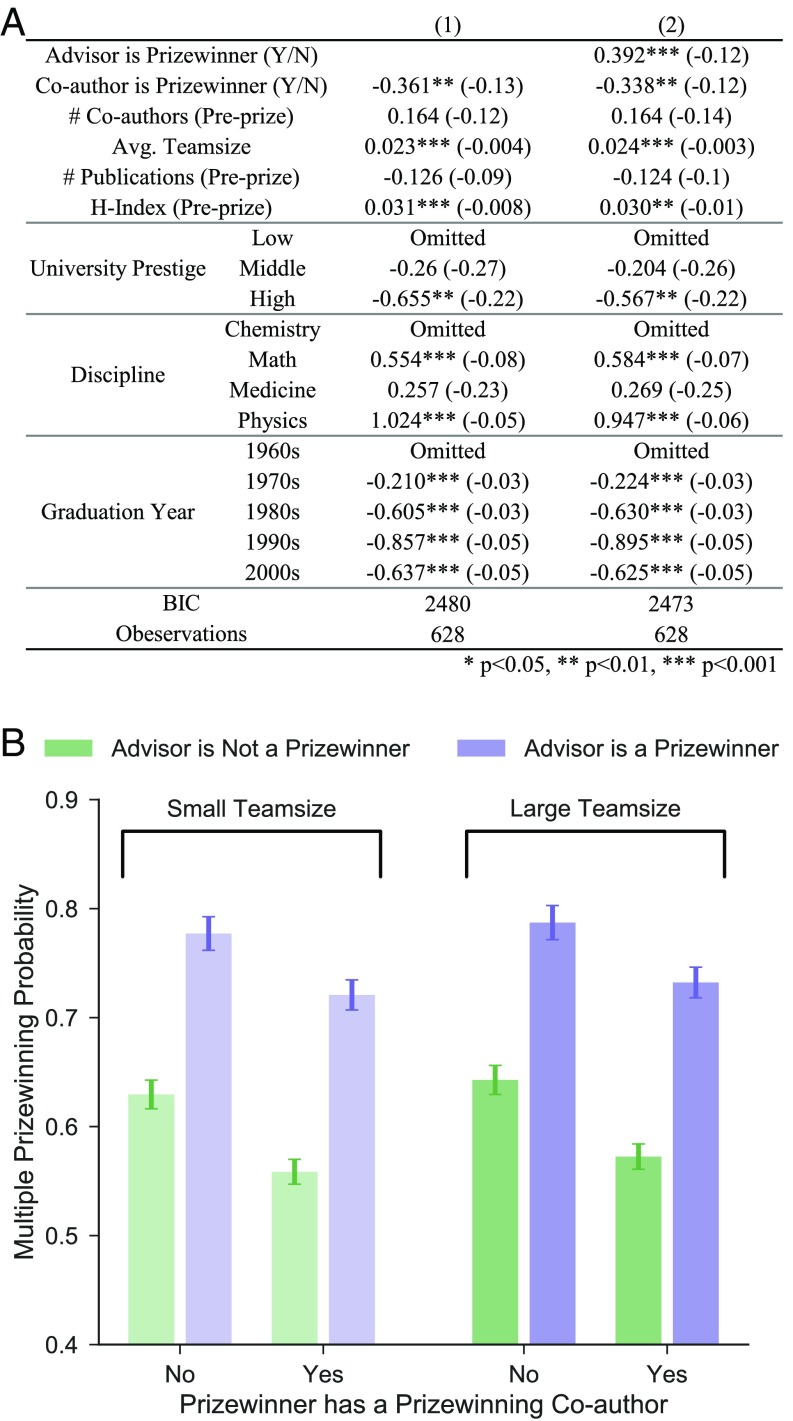
To investigate the possible conditions explaining a scientist’s propensity for winning multiple prizes, we regressed the number of prizes a scientist wins (conditional on a scientist having won at least one prize) on variables measuring the scientist’s genealogical and coauthorship ties using an ordered logistic model. Our control variables include measures of individual talent, team work, graduation year, university rank, and discipline (37, 45–47) (Materials and Methods).

Fig. 6A shows the regression results for the predictors of multiple prizewinning, conditional on having won at least one prize. Before presenting the main findings, we note several general patterns in the data displayed in model 1, the control variable regression. (i) Controlling for time and discipline, we observe that university prestige is positively related to multiprizewinning. While this result is not surprising, it does reinforce earlier work (47–49) indicating that the highest ranked universities are more supportive of, and likely to be a source of, acclaimed research. (ii) The number of publications is not related to multiprizewinning, but the average citation impact of publications (H index) is positively and significantly related to multiprizewinning. This pattern suggests that quality, not quantity, is a factor in multiprizewinning. (iii) Team authorship is positively correlated with multiprizewinning. Previous work has shown that the number of authors on a team is related to novel problem solving (42). Number of coauthors on a paper could also be related to the marketing of a scholar’s work (41). Although we cannot fully disentangle team size, research quality, and the marketing of a scholar’s work (50) with our data, the fact that multiprizewinning is unrelated to the total number of coauthors of a scientist—a more direct measure of the number of persons who are aware of and have an interest in marketing a scholar’s research—suggests that team collaboration is at least partly related to research quality. (iv) The other side of learning from coauthors has to do with how credit for joint work is assigned to members of the team. The Matthew effect suggests that scientists who are awarded a prize are more likely to win future prizes due to social processes where success breeds success (51). In these data, we have the unusual situation where a prizewinner also has a coauthor who is a prizewinner, making predictions from the Matthew effect indefinite for the case where coauthors are of equivalent eminence. On the one hand, being a prizewinner should enhance a scholar’s chances of winning additional prizes, while on the other hand having a prizewinning coauthor could have the Matthew effect work against the scholar’s propensity to win multiple prizes. While the intricacies of these dynamics cannot be fully explored in our data (52), we do find a strong negative relationship between having a prizewinning coauthor and being a multiprizewinner.

Fig. 6.

Ordered logistic regression estimates of the propensity to win multiple prizes, 1960–2015. (A) The table reports estimates of a scientist’s propensity for winning multiple prizes conditional on having won one prize. The independent variables include a scientist’s genealogical and coauthorship networks, individual human capital variables, and controls for discipline, university prestige, and graduation date (SEs are shown in brackets). (B) The predicted probabilities to win multiple prizes if a scientist has a prizewinning coauthor or prizewinning genealogy by small or large average team size as measured by number of authors on a paper.

Model 2 shows the relationship between genealogy and multiprizewinning, taking into account control variables. The overall fit of the model increases significantly when genealogical information is added to the regression as indicated by the seven-point drop in the Bayesian information criterion statistic (53). A scientist with a prizewinning genealogical network has a significantly higher propensity for becoming a multiprizewinner than a scientist without one. Fig. 6B shows a scientist’s propensity of being a multiprizewinner when genealogical, collaborator, and average team size relationships are taken into effect. We observe that genealogy is always significantly associated with a greater propensity for multiprizewinning in small and large teams and when a scientist has or does not have a prizewinning coauthor. In large teams for example, the probability of being a multiprizewinner is 79% when a scientist has a prizewinning genealogy but lacks a prizewinning collaborator. When a scientist has a prizewinning genealogy and a prizewinning collaborator, the propensity of being a multiple prizewinner drops significantly but insubstantially from 79 to 73%. These results suggest that the increasing concentration of prizewinners is related to genealogical and coauthor relationships, as well as social perceptions of a scientist’s contributions to joint research.

Discussion

We used large-scale data on scientific prizes and prizewinners to quantify the proliferation of prizes, identify the connections prizes and prizewinners make within and across disciplines, and explain the increasing concentration of scientific fame within a proportionately smaller and more tightly interconnected elite.

Several areas of future work follow from our analyses. First, while we analyzed the explosive growth in scientific prizes, we did not explain why it has occurred (54). Presumably, prizes grow to represent a broader range of ideas and specializations. Although we showed that while more scientists win prizes each year, it is also true that, increasingly, a smaller and smaller set of winners win multiple prizes. The increasing concentration would seem to work at cross-purposes with the inclusiveness and equality ethos of science. Thus, future research might delve more deeply into the nature of prizes and stratification of science.

Second, an arguably less optimistic finding is that while prizes have increased in number, the set of scientific influentials is increasingly made up of a smaller and more intertwined set of scientists. These scientists are linked through genealogical and coauthorship networks. If these networks operate like other social networks, they may provide continuous learning opportunities, better divisions of specialized labor, and support for risk-taking—but may also be vulnerable to in-group thinking that can keep good ideas out or create in-group biases (35, 55). Further work on how these networks form, possibly through the Matthew effect or preferential attachment (51, 56), could help explain whether and when in-group biases or learning processes are dominant (57).

Third, a final area of future research could focus on how prize interlocks—prizes that are often won by the same scientists—influence knowledge transfer. In the paper, we drew on research that indicated that such interlocks in a network perform the function of knowledge pathways between different regions of the network. It would seem plausible that interlocks in this network function similarly by transferring knowledge between disciplines. For example, Daniel Kahneman, a psychologist and winner of the Nobel Prize in Economics, noted that the Nobel legitimated his ideas about nonrational decision-making, which in turn increased the flow of psychological ideas in economics (58). Similarly, our results indicate that the transition propensities between prizes sometimes show that “stepping-stone” prizes precede the winning of a highly notable prize. These stepping-stones provide information for predicting who may win the next big prize. In other cases, the most notable prizes are won without having won a stepping-stone prize initially. A future line of research would be to understand the reasons by which some scientists follow a predicable path to fame while other do not. If one could develop appropriate measures to track systematically knowledge transfers through interlocks between persons, subdisciplines, team science awards, or hub disciplines per Boyack et al. (59), they could conceivably predict scientific trends, novel combinations of ideas, and, possibly, the next big idea in science.

Materials and Methods

Data Sources.

We merged three large datasets: (i) prizewinners, (ii) scientific genealogy, and (iii) publications. We parsed and curated the prizewinner data from the open web sources, including Wikipedia, and the official websites for prizes, such as https://www.nobelprize.org/. These contain information on each winner’s name, prize name, prize year(s), gender, birth place, and career institutional affiliation(s). The scientific genealogy data were acquired from the Academic Family Tree (AFT) (https://neurotree.org/neurotree/) and the Mathematics Genealogy Project (https://www.genealogy.math.ndsu.nodak.edu/). In these datasets, advisors and their students are listed. From the WoS dataset, we extracted publication and collaboration for every scholar in the AFT datasets. The WoS contains more than 60 million papers published from 1900 to 2015. The AFT uses a sophisticated algorithm to disambiguate a scholar’s identity and publications, which enables a validated link from the AFT publication lists to the WoS.

Prize Notability Scores.

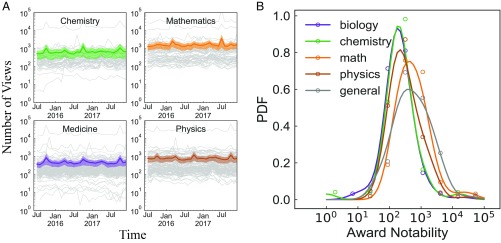
To measure differences in how much public notability a prize receives, we used the Wikipedia Pageviews application programming interface to compute the monthly page views of each prize from July 1, 2015, to December 31, 2017. Fig. 7 shows the monthly page views for each prize in biology, chemistry, mathematics, physics, and general prizes given to multiple disciplines.

Fig. 7.

Statistics of Wikipedia page views. In A, each gray line is the monthly page views of a prize, and the colored line with SE is the average over prizes in the field. In B, distributions of the average monthly views for each prize are shown; dots represent the fraction of prizes in each binned set of prizes by their page views, and lines are the probability distributions estimated from the Gauss kernel density function.

Prize Network.

The prize network was constructed using 307 leading prizes and 6,061 weighted links between prizes (we consider prizes with at least 10 recorded winners). In the prize network, prizes are nodes, and links between two prizes i and j are formed when at least one scientist has won both prizes. Fig. 3 shows only the critical links identified by the principal link extracting algorithm (60, 61) for P value equal to 0.3.

Genealogical and Collaboration Networks.

The network of scientific winners is constructed using scientists’ genealogical and coauthorship information. The genealogy structure for scientists is an acyclic tree, and each link in the network represents ties between advisors and their PhD students or postdoctoral researchers. The coauthorship links are formed if two scientists coauthored at least one paper. We combined the two networks into one, which contains 2,034 winners, ∼1960–2017. In total, 1,504 (74%) of the winners are connected in a giant component.

Model Specification for a Scientist’s Propensity for Winning Multiple Prizes.

We used an ordered logistic regression model to predict the probability that a scientist is a multiple prizewinner. The dependent variable is the number of prizes the scientist won. The independent variables we used are the following: (i) a dummy indicating if the scientist has a prizewinning genealogy or not; (ii) a dummy indicating if the scientist has a prizewinning coauthor or not; (iii) the total number of unique coauthors; (iv) the average number of coauthors of each paper published; (v) the number of publications; (vi) the H index; (vii) the university rank (dummy on high/middle/low based on the total citations the university receives); (viii) research fields (dummy on chemistry/math/medicine/physics); and (ix) graduation year (dummy on each decade). We have removed the coauthored papers with advisors and prizewinning coauthors from the computations of variables related to publications and citations. The ordered logit regression equation is as follows:

$$\begin{array}{l}\text{ln}\left(\frac{p}{1-p}\right)\sim \text{Advisor}\_\text{is}\_\text{Prizewinner}+\text{Coauthor}\_\text{is}\_\text{Prizewinner}+\#\text{Coauthors}\\ +\mathrm{Avg}\_\text{Teamsize}+\#\text{Publications}+H\_\text{Index}+\text{University}\_\text{Rank}\left(\text{dummy}\right)\\ +\text{Discipline}\left(\text{dummy}\right)+\text{Graduation}\_\text{Year}\left(\text{dummy}\right).\end{array}$$