Intrinsically ultrastrong plasmon–exciton interactions in crystallized films of carbon nanotubes

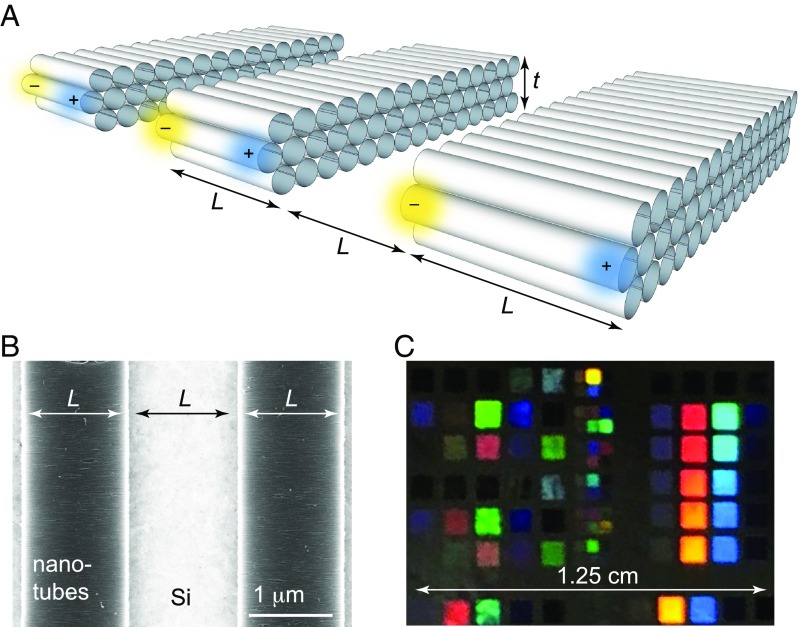
Significance

Carbon nanotubes, each a cylindrical nanocrystal of carbon atoms, can be crystallized into monolithic, two-dimensionally ordered films through a simple vacuum filtration technique. A particularly fascinating property of these crystallized nanotube films is that they function as a unique type of antenna whose excitations comprise intrinsically ultrastrongly coupled plasmons and excitons. This type of intrinsic coupling contrasts to the many existing demonstrations of strongly coupled hybrid systems, in which emitters are coupled to external photonic or plasmonic cavities. Technologically, crystallized nanotube films could provide a materials-driven pathway from fundamental concepts in quantum electrodynamics to advanced telecommunications hardware. Their applicability could also extend to battery anodes, high-ampacity conductors, and microelectromechanical systems.

Abstract

In cavity quantum electrodynamics, optical emitters that are strongly coupled to cavities give rise to polaritons with characteristics of both the emitters and the cavity excitations. We show that carbon nanotubes can be crystallized into chip-scale, two-dimensionally ordered films and that this material enables intrinsically ultrastrong emitter–cavity interactions: Rather than interacting with external cavities, nanotube excitons couple to the near-infrared plasmon resonances of the nanotubes themselves. Our polycrystalline nanotube films have a hexagonal crystal structure, ∼25-nm domains, and a 1.74-nm lattice constant. With this extremely high nanotube density and nearly ideal plasmon–exciton spatial overlap, plasmon–exciton coupling strengths reach 0.5 eV, which is 75% of the bare exciton energy and a near record for room-temperature ultrastrong coupling. Crystallized nanotube films represent a milestone in nanomaterials assembly and provide a compelling foundation for high-ampacity conductors, low-power optical switches, and tunable optical antennas.

When optical emitters are strongly coupled to a cavity, they hybridize with it via rapid energy exchanges known as vacuum Rabi oscillations (1). If the Rabi oscillation frequency (Ω/2) is so fast that it approaches the resonance frequencies of the emitters (ω₀) and the cavity, the system has then reached ultrastrong coupling (2). Instead of the cavity and emitters exchanging energy one quantum at a time, a single cavity excitation can then borrow energy from the vacuum field and excite two or more emitters. Ultrastrong coupling could lead to single-photon nonlinearities that provide a pathway from fundamental concepts in quantum electrodynamics to advanced telecommunications hardware (3, 4).

There are many emitter–microcavity systems that have achieved strong or ultrastrong coupling. The emitters can range from atoms (4), to quantum dots (5), fluorescent molecules (6–9), carbon nanotubes (10–13), and superconducting qubits (14). The cavities can be either photonic microcavities, which can have very high quality factors (Q), or surface plasmon resonators, whose mode volume (V) can be in the deep subwavelength regime.

To achieve strong or ultrastrong coupling, emitters are typically placed near or in optical cavities, or optical cavities are fabricated around emitters. In either case, the emitter–cavity system is a hybrid system, in which the emitter and cavity are separate objects. In such hybrid systems, the spatial overlap between the emitters and the cavity is often the key factor that limits the light–matter coupling strength. In this work, we generate crystallized films of carbon nanotubes and show that this material exhibits intrinsically ultrastrong interactions. Instead of coupling to external cavities, nanotube excitons (15) couple internally to nanotube plasmon resonances. The nanotubes thus play a dual role as both plasmonic cavities and emitters.

The plasmon resonances considered here comprise longitudinal charge oscillations along the nanotubes coupled to electromagnetic fields (16–23). They are notable for their electrostatic tunability and ability to effectively confine light to a small V. As a result of these small volumes, the strong exciton strength of carbon nanotubes, the extremely high density of nanotubes in the crystallized films, and the nearly ideal plasmon–exciton spatial overlap deriving from the intrinsic nature of the cavity–matter interactions, the normalized plasmon–exciton interaction strengths reach Ω/ω₀ = 75%. These plasmon–exciton polaritons (“plexcitons”) are thus far into the ultrastrong regime, which is typically defined by Ω/ω₀ ≳ 30% (2), and one of the most strongly coupled systems that has been achieved in any material.

Crystallized nanotube films could play an exciting role in active, nonlinear optical devices. For instance, they could lead to nanolasers in which the gain medium is intrinsically built into the lasing cavity. Moreover, χ⁽³⁾ optical nonlinearities, already strong in dispersed carbon nanotubes, should be dramatically enhanced by ultrastrong plasmon–exciton coupling (24). Many of the technological goals of ultrastrong coupling, including low-power optical modulators and resonant photodetectors, could be more simply achieved with a single material rather than a binary system.

From a fundamental electromagnetics standpoint, the highly anisotropic optical properties of crystallized nanotube films could make them a resource for hyperbolic metamaterials or plasmonic hypercrystals (25) that support low-loss hyperplasmons. The intrinsic nature of our system’s ultrastrong coupling also suggests a natural scalability to the single cavity–single emitter quantum regime. Outside of nanophotonics, the crystallized nanotube films that we fabricate could have diverse applications like high-ampacity conductors (26) and battery anodes. Their successful assembly is a milestone in the larger endeavor of assembling nanostructures into macroscopic functional materials.

Assembly of Crystallized Films of Carbon Nanotubes

Our crystallized nanotube films are fabricated by adapting and modifying a carbon nanotube vacuum filtration technique (27, 28). A powder of arc-discharge single-wall carbon nanotubes, of 1.41 nm average diameter, is dispersed in water with the surfactant sodium dodecylbenzenesulfonate (Methods). Atomic force microscopy confirms that the nanotubes are unbundled in solution (SI Appendix). A very weak vacuum then slowly pulls the suspension through a track-etched polycarbonate membrane, causing the nanotubes to self-organize and align in the plane of the membrane. The membrane is then dried, and the 1-in.-diameter nanotube films are transferred to silicon or sapphire substrates.

Surprisingly, the nanotubes in these solution-assembled films cannot only be aligned into monolithic, wafer-scalable films, as has been previously shown (27), but can be crystallized into polycrystalline films with large, ∼25-nm domains. Cross-sectional transmission electron microscopy (TEM) of a 200-nm-thick film shows a 2D hexagonal crystal of nanotubes, with at least 50% of the nanotubes crystallized (Fig. 1 A–C and SI Appendix). Selected area TEM diffraction confirms the hexagonal lattice structure (Fig. 1D).

Fig. 1.

Crystallized carbon nanotube films. (A–C) Cross-sectional TEM images of the crystallized nanotube films at three magnifications. (D) Grazing incidence XRD spectra of a crystallized nanotube film (blue curve) and a control film of randomly oriented nanotubes (black curve). The peak at $2\theta$ = 5.8° corresponds to an internanotube lattice spacing of 1.74 nm. The X-ray beam size is 2 cm². (Inset) Selected-area electron diffraction image of the region in C confirming the hexagonal lattice structure. (E) Scanning electron micrograph of the top surface of a crystallized nanotube film. The nanotube alignment axis is vertical.

Grazing incidence X-ray diffraction (XRD) spectroscopy provides further verification of the film’s crystallinity (Fig. 1D and SI Appendix). The prominent XRD peak at 2$\theta$ = 5.8°, which is 15 times stronger than the XRD peak in a control film of randomly oriented nanotubes, corresponds to an internanotube lattice constant of 1.74 nm and a 2D nanotube density of 3.8 × 10⁵ μm⁻². For context, crystallization of nanotubes has also been seen in naturally but randomly produced nanotube ropes generated during nanotube growth (29). However, large-area crystalline films have not previously been observed, nor have crystallized nanotube films been observed to self-assemble in solution.

Intrinsically Ultrastrong Plasmon–Exciton Interactions in Crystallized Nanotube Films

To investigate their plasmon–exciton interactions (30), we etch the crystallized nanotube films into nanoribbon plasmon resonators (Fig. 2) and study them with μ-Fourier transform infrared (μ-FTIR) spectroscopy at room temperature. In this geometry, the electric field and charge oscillation of the plasmon modes are polarized along the nanotube alignment direction, with the etched ends of the nanotubes providing confinement. Approximately 10⁸ nanotubes are in each μ-FTIR measurement area (SI Appendix).

Fig. 2.

(A) Plasmonic resonators comprising crystallized nanotube films etched into nanotube nanoribbons. The etched nanotube length is L, and interribbon spacing is L. For the depicted transverse-magnetic plasmon resonance, the electric field and charge oscillation are both parallel to the nanotube alignment axis. (B) A scanning electron micrograph of a crystallized nanotube film that has been etched into plasmon resonators. The nanotube alignment axis is horizontal. (C) A photograph of a crystallized film after it is etched. The color of diffracted light varies with the pitch (2L; A and B) of the grating. Each 1-mm or 0.5-mm square in this photograph consists of a one-dimensional array of etched nanotube nanoribbons, with L ranging from 80 nm to 2 μm and the pitch of each array being 2L.

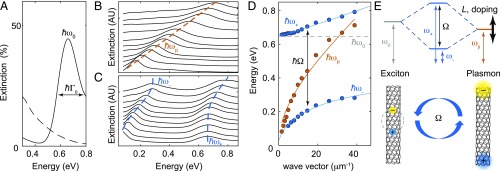
The lowest-energy semiconducting-nanotube exciton, the S₁₁ exciton, has a center energy of ħω₀ = 0.66 eV and an inhomogeneous linewidth of ħΓ₀ = 0.2 eV (Fig. 3A and SI Appendix). We chemically control the nanotubes’ doping level by exposing them to HNO₃ vapor, a strong oxidizer, which induces a high density of positive charge carriers. These carriers deplete the nanotube valence band and bleach the transition strength of S₁₁ (31–33). By increasing the free charge density, this surface charge-transfer process also significantly blue-shifts the plasmon resonance energies. We can then reverse this process with vacuum annealing, which eliminates the adsorbates on the nanotubes. After annealing, the on-axis resistivity of our crystallized films increases by a factor of 30 (from ρ = 2.6 × 10⁻⁴ ohm⋅cm to ρ₀ = 7.8 × 10⁻³ ohm⋅cm; SI Appendix), and S₁₁ is restrengthened. This resistivity ratio is limited by the presence of metallic nanotubes (∼1/3 of the nanotubes) in our films and would be much higher in films of purely semiconducting nanotubes.

Fig. 3.

Intrinsically ultrastrong plasmon–exciton interactions. (A) The extinction spectra of a crystallized nanotube film in its annealed, resistive state (solid line), showing a strong S₁₁-exciton peak, and a highly chemically doped film (dashed line), where S₁₁ is bleached. The film thickness is t = 49 nm. (B) The extinction spectra of plasmon resonators etched into this film, with a fixed, high doping level and varying lithographically defined nanotube lengths (L values). For clarity, each curve is vertically offset and normalized by its maximum. (See SI Appendix, Fig. S5, for unnormalized curves.) From top to bottom, L = (80, 100, 130, 175, 225, 260, 325, 400, 500, 650, and 800) nm. The dashed line is a guide for the eye. (C) In their annealed, resistive state, the nanotube resonators have extinction spectra with two peaks each, corresponding to excitons and plasmons that hybridize to form polaritons. (D) Orange indicates peak energy of the highly doped plasmon resonators from B vs. wave vector (q), defined as q = π/L. The solid line is a fit to ${\omega }_p\propto \sqrt{q}$. Blue indicates peak energies of the plasmon–exciton polaritons from C, showing an anticrossing with a Rabi splitting of Ω = 0.485 eV. The solid line is a fit to Eq. 2. (E) Energy-level diagram and depiction of the nanotube excitons hybridizing with the nanotube plasmons to form ultrastrongly coupled plasmon–exciton polaritons.

In their highly doped state, the nanotube resonators have a strong single extinction peak corresponding to the fundamental transverse magnetic localized surface plasmon resonance (Fig. 3B) (20, 22), whose extinction is 99% polarized along the nanotube alignment axis (SI Appendix). As with graphene nanoribbon resonators (34), the resonance frequency (ω_p) is approximately proportional to $\sqrt{qt}$ (22), where the wave vector q = π/L, L is the nanoribbon width (i.e., the etched length of the nanotubes), and t is the out-of-plane thickness of the material (SI Appendix). Because the S₁₁ exciton is suppressed in this highly doped state, ω_p crosses unperturbed through ω₀ as L is reduced.

In more moderate doping states, the plasmon resonance and the S₁₁ exciton coexist (Fig. 3C and SI Appendix). Because the S₁₁ excitons are bleached by high free charge densities, and the plasmon resonances require free charges, this coexistence might seem counterintuitive. However, the persistence of the S₁₁ exciton in even ambient conditions, where atmospheric adsorbates induce a moderately high doping level, has been observed by many prior studies (15, 32, 33).

In their annealed, resistive state, the nanotube resonators have peaks corresponding to both ω₀ and ω_p. The width of the plasmon resonances, ħΓ_p, ranges from 0.1 to 0.2 eV and is limited by the etch profile of the nanoribbons. In this annealed state, as L is reduced, a large anticrossing between ω_p and ω₀ becomes evident (Fig. 3C). This anticrossing is the key signature of strong coupling. Near the anticrossing, the bare ω_p and ω₀ resonances hybridize to form ω_± polaritons (Fig. 3 D and E). The Rabi splitting, ħΩ, which we compute as the experimentally measured minimum of $\hslash \left({\omega }_{+}-{\omega }_{-}\right)$, reaches 0.485 eV for t = 49 nm resonators. In slightly thinner resonators (t = 37 nm; Fig. 4C), ħΩ = 0.50 eV, and Ω/ω₀ = 75%.

Fig. 4.

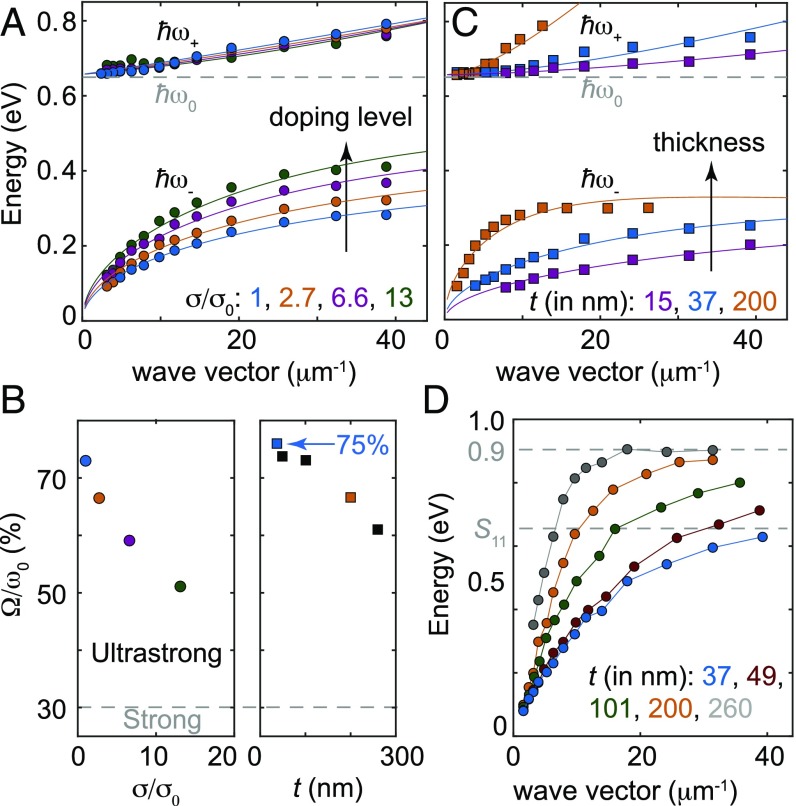
Tunability of plasmon–exciton interactions. (A) Polariton energies vs. wave vector for resonators at four different doping levels. The film conductivity for each curve is specified in the legend as a multiple of σ₀ = 1/ρ₀. The film thickness is t = 49 nm. (B, Left) Ω vs. film conductivity (σ), with t fixed to 49 nm. (Right) Ω vs. t, with σ fixed to σ₀ (i.e., immediately after the film has been vacuum annealed). The colored points are color-coded to match the curves in A and C. (C) Polariton energies of resonators as a function of q and t, with the doping level at its minimum (σ = σ₀). (D) Plasmon resonator energies when the nanotubes are maximally doped (i.e., immediately after HNO₃ exposure). When q and the doping level are both high, ω_p saturates at 0.9 eV.

The normalized coupling strength between the nanotube plasmon–exciton polaritons is thus significantly beyond the ultrastrong-coupling threshold. In fact, it is among the strongest of any room-temperature system known to date. For context, Ω/ω₀ = 62% has been observed for organic dye molecules that are coupled to silver microcavities (8), and Ω/ω₀ = 90% has been observed in III–V planar microcavities (35). For carbon nanotubes coupled to external cavities, Ω/ω₀ = 12% has been attained, and Ω/ω₀ ∼ 70% has been predicted to be achievable (12). More recently, Ω/ω₀ = 13.3% has been achieved for carbon nanotubes embedded in planar microcavities (13). At cryogenic temperatures, the record cavity–matter coupling strength is Ω/ω₀ = 130%, achieved using superconducting qubits coupled to superconducting resonators (14).

Tuning the Plasmon–Exciton Interaction Strength

A distinctive feature of carbon nanotube plasmons is their exceptional tunability. Length, thickness, and doping level are all tuning factors, allowing ω_p to span frequencies from the terahertz up to the near infrared. Because doping level determines the exciton transition strength, it modifies not only ω_p but also Ω (Fig. 4 A and B). In turn, this tuning of Ω allows access to a broad range of polariton energies. This access could translate into electrically tunable optoelectronic devices like photodetectors (36, 37), lasers, and quasi-coherent incandescent light sources (38).

Due to coupled antenna effects, increasing the thickness of the nanotube film leads to higher-energy plasmon resonances (22). The plasmon–exciton anticrossing can therefore be reached at smaller wave vectors (i.e., higher L values) (Fig. 4C). Because the plasmonic mode volumes of thicker films are larger than those of thinner ones, their Rabi splittings are also modestly lower, although still extremely strong: a 260-nm-thick film exhibits Ω/ω₀ = 60%.

Nonetheless, these thick films should be particularly suitable for optoelectronics due to their large dipole strength. For very thin films (e.g., the t = 15 nm film in Fig. 4C), ω_p is much less than ω₀ at even the shortest nanotube length that we could etch (L = 80 nm). In this case, due to the weak plasmon–exciton coupling, the higher energy resonance is nearly purely excitonic and barely shifts with L (SI Appendix). This behavior is consistent with the fact that the exciton energies of isolated nanotubes do not observably shift with L (39).

The plasmon–exciton coupling can be described by a two-coupled-oscillator Hamiltonian:

$$H={\omega }_p\left(a^{†}a\right)+{\omega }_0\left(b^{†}b\right)+\text{Ω}\left(a^{†}+a\right)\left(b^{†}+b\right)+{\text{Ω}}^2/{\omega }_0{\left(a^{†}+a\right)}^2,$$ [1]

where a^† (a) and b^† (b) are the exciton and plasmon creation (annihilation) operators, respectively (40, 41). The first two terms represent exciton and plasmon self-energies, and the second two terms represent plasmon–exciton interactions. Eq. 1 includes counterrotating interaction terms, which are neglected in the frequently used Jaynes–Cummings Hamiltonian, an approximation to Eq. 1, but must be considered in ultrastrong coupling. Neglecting the contribution from line widths to the polariton energies (Methods), the full Hopfield solution (9, 40, 41) to Eq. 1 is

$${\omega }^4-{\omega }^2\left({{\omega }_p}^2+{{\omega }_0}^2+g^2\right)+{{\omega }_p}^2{{\omega }_0}^2=0,$$ [2]

where g is the plasmon–exciton interaction strength, and we have neglected imaginary terms associated with the finite line widths (9). To fit our data, we use Eq. 2, fix ω₀ to its experimentally observed value of 0.66 eV, and parametrize ω_p as $\hspace{0.17em}{X}_0/\sqrt{L}$ and g as $X_1/\sqrt{L}$, where $X_0$ and $X_1$ are fitting factors (Methods). Although this model is certainly only phenomenological, it exhibits excellent agreement with all of our experimental data (Figs. 3D and 4 A and C).

Highly conductive nanotube films can also exhibit strong light–matter interactions. At high energies, the ${\omega }_p\propto 1/\sqrt{L}$ relationship breaks down, and $\hslash {\omega }_p$ saturates at 0.9 eV (Fig. 4D). Although S₁₁ is nearly completely suppressed at high doping levels, many higher-energy nanotube excitons are not (SI Appendix). Consequently, even at high nanotube doping levels, the plasmons strongly interact with these higher-energy excitons and have flat, saturating dispersion relationships. In the future, smaller-diameter nanotubes, which have higher-energy optical transitions (10), could allow the 0.9-eV threshold to be crossed. However, our currently achieved tuning range already allows carbon nanotube plasmonics to be applied to C-band near-infrared telecommunications.

Conclusions

Intrinsically ultrastrong coupling represents a compelling concept in active nanophotonics. It could drive the next generation of tunable infrared devices, including nanoscale light sources, multispectral detectors, and wavefront-shaping chips based on tunable metamaterials (24) and metasurfaces. As ultrastrongly coupled systems, nanotube antennas could serve as physical representations of the Dicke Hamiltonian and a testbed for its quantum-phase transition to superradiance (42). In turn, superradiating antennas could function as bright single-photon sources for quantum communications. Crystals of nanotubes could thus serve as a bridge between fundamental concepts in quantum optics and practical technologies.

Methods

Fabrication of Crystallized Carbon Nanotube Films.

A vacuum filtration method is used to prepare the crystalline carbon nanotube films from nanotube solutions. This method is a modified version of the method used in refs. 22 and 27. The setup consists of a fritted glass filter and a 15-mL funnel (Millipore XX1002500) purchased from Fisher Scientific Company. The vacuum filtration method consists of four steps: (i) dispersing nanotubes in a surfactant solution, (ii) modifying the surface of a filter membrane, (iii) vacuum-filtering the nanotube suspension through the modified membrane, and (iv) transferring the nanotube film onto a target substrate.

An arc-discharge powder of single wall carbon nanotubes, with average diameter of 1.41 nm, 2:1 semiconducting:metallic fraction, and an average length of 500 nm (P2-SWCNT; Carbon Solutions, Inc.), is dispersed into an aqueous solution of 0.4% (wt/vol) sodium dodecylbenesulfonate (SDBS; Sigma-Aldrich). The initial nanotube concentration is 0.4 mg/mL. Bath sonication is applied to the suspension for 15 min, followed by tip sonication for 45 min. During tip sonication, the suspension is immersed in cold water to prevent heating. The suspension is then centrifuged for 1 h at 38,000 rpm (178,000 × g) to remove any remaining nanotube bundles and amorphous carbon. The supernatant is then diluted by a factor of 5 with deionized water, making the SDBS concentration ∼0.08%. The suspension is then further diluted by a factor of 3 with 0.08% SDBS solution.

The filtration membranes for the vacuum filtration process (Whatman Nuclepore track-etched polycarbonate hydrophilic membranes, 0.05-µm pore size) are first treated with a 2-torr air plasma for 30 s. This treatment provides a negative charge surface on the membrane, which proved to be an important step for achieving a high degree of nanotube alignment and high packing density. Oxygen plasma was also used, but whereas oxygen plasma would etch the membrane, air plasma was gentler and yielded better results.

The nanotube suspension is then filtered through the plasma-treated membranes. For the first 3 mL solution, a weak vacuum pressure (2.8 torr) is used to pull the suspension through the membrane at a very slow rate, ∼0.4 mL/h. This slow filtration speed gives the nanotubes enough time to align and to cover the whole membrane uniformly. After 3 mL has been pulled through the membrane, the vacuum pressure is increased to 8.4 torr, which results in a filtration rate of 0.8 mL/h. Finally, before the meniscus contacts the membrane, a high vacuum pressure of 370 torr is applied to dry the liquid. The film thickness is observed to be proportional to the volume of the precursor used (14 nm per 1 mL of suspension). SI Appendix, Fig. S2, shows a photo of a membrane with a nanotube film.

The substrates used in this work are high-resistivity silicon and sapphire wafers. For the silicon substrates, the native oxide is first removed by buffered hydrofluoric acid to reduce the coupling of nanotube plasmons to optical phonons in the oxide (20). A drop of water is placed on the substrate, and the membrane is then placed on the substrate with the nanotube surface face down. The membrane is then covered by a glass slide, and gentle pressure is applied to make the nanotube film adhere. The membrane is then dried with gentle N₂ gas and then dissolved in chloroform. To remove the surfactant and polymer residue, the nanotube film on the substrate is then annealed at 500 °C in a vacuum oven at 10⁻⁷ torr for 2 h.

Fabrication of Nanoribbons and Charge-Transfer Doping.

Conventional electron beam lithography is used to pattern the CNT films. A bilayer resist consisting of a poly(methyl methacrylate) (PMMA) layer and a hydrogen silsesquioxane (HSQ) layer was spin-coated on the nanotube film. After e-beam exposure, the HSQ is developed as a hard mask. The PMMA layer and nanotubes are then etched with oxygen reactive ion etching. The residual PMMA and HSQ are then stripped with chloroform. The strip length to spacing ratio is fixed at 1:1, as shown in Fig. 2A.

To induce strong p-type surface charge transfer doping, the sample is exposed to HNO₃ vapor for 10 min. For a moderate doping level, the sample is first strongly doped and then annealed on a hot plate at 120 °C. Doping conditions 1–3 in Fig. 4A are realized with respective heating times of 2, 7, and 30 min.

Characterization of Crystallized Nanotube Films.

The crystalline properties of nanotube films are characterized with a Siemens D5000 XRD spectrometer. The conductivities are measured by Keithley 2400 equipped with an inline four-probe system. The extinction spectra are all measured in a Bruker Nicolet 8700 μ-FTIR system, except for the high-frequency plasmon resonances in thick films (ħω_p > 0.85 eV; Fig. 4D), which are measured in PerkinElmer Lambda 950 UV-VIS-NIR spectrometer.

Fitting the Data to the Hopfield Model.

To perform the fits to Eq. 2, we fix ω₀ to its experimentally observed value of 0.66 eV/ħ. We then parameterize ω_p as $X_0/\sqrt{L}$ and g as $X_0/\sqrt{L}$, where X₀ and X₁ are fitting parameters. The ω_p parameterization derives from the dispersion of a quasi-2D nanoribbon (3, 34).

The parameterization for g follows from the following reasoning. For strongly coupled ensembles of emitters, the maximum cavity-emitter coupling strength is $g\propto \sqrt{Nf/\epsilon V}$, where N is the number of emitters, f is their oscillator strength, ε is the dielectric constant, and V is the mode volume (40). In our system, N is the number of nanotubes in a resonator and independent of L. We also approximate f and ε as constants with respect to L, and we approximate the plasmon–exciton overlap as a constant.

To paramaterize V, we model our plasmon resonators as quasi-2D resonators and apply the same treatment that is typically given to graphene nanoribbon plasmon resonators (3, 34). As fundamental modes, the plasmon modes we are considering extend a distance of λ_sp, the plasmon wavelength, in the nanotube alignment direction. Their extent in the out-of-plane direction is also ∼λ_sp (3, 34). In the in-plane but perpendicular to nanotube alignment direction, the nanoribbons are quasi-infinite, making the extent of the plasmon mode constant in this dimension with respect to L. Thus, as for graphene nanoribbons, V ∼ λ_sp². Using the 2D dispersion relationship, λ_sp ∼ $\sqrt{L}$, and $g\propto \sqrt{Nf/\epsilon V}$, we then arrive at $g\propto \hspace{0.17em}1/\sqrt{L}$.

The full Hopfield solution to Eq. 1 includes not only the terms in Eq. 2 but also imaginary terms representing the line width of the oscillators. These terms can reduce the plasmon–exciton coupling strength. However, because the plasmon and exciton linewidth are both significantly smaller than ω₀, ω_p, and g, we neglect them in Eq. 2.

With X₀ and X₁ as fitting parameters and ω₀ a fixed, experimentally derived parameter, we then fit Eq. 2 to the experimental data. To perform these fits, we used MATLAB (Mathworks, Inc.) and its nonlinear least squares fitting algorithm.