Quantifying the role of mineral bridges on the fracture resistance of nacre-like composites

Significance

Nacre, commonly called mother of pearl, is a biological composite that displays an exceptional combination of strength and noncatastrophic fracture behavior. The quantitative understanding of the structure–property correlations observed in nacre could provide powerful guidelines for the design of lightweight composite materials. By fabricating nacre-like brick-and-mortar composites from aligned alumina microplatelets interconnected by titania mineral bridges, we have been able to isolate and quantify the influence of mineral bridge density on the composite’s fracture properties. Because the model synthetic material is structured from ceramic constituents at the same length scale as biological nacre, it sheds light on the fundamental role of mineral bridges in natural brick-and-mortar structures, while also demonstrating outstanding mechanical properties.

Abstract

The nacreous layer of mollusk shells holds design concepts that can effectively enhance the fracture resistance of lightweight brittle materials. Mineral bridges are known to increase the fracture resistance of nacre-inspired materials, but their role is difficult to quantify due to the lack of experimental systems where only this parameter is controllably varied. In this study, we fabricate tunable nacre-like composites that are used as a model to experimentally quantify the influence of the density of mineral bridges alone on the fracture properties of nacre-like architectures. The composites exhibit a brick-and-mortar architecture comprising highly aligned alumina platelets that are interconnected by titania mineral bridges and infiltrated by an epoxy organic phase. By combining experimental mechanical data with image analysis of such composite microstructures, an analytical model is put forward based on a simple balance of forces acting on an individual bridged platelet. Based on this model, we predict the flexural strength of the nacre-like composite to scale linearly with the density of mineral bridges, as long as the mineral interconnectivity is low enough to keep fracture in a platelet pullout mode. Increasing the mineral interconnectivity beyond this limit leads to platelet fracture and catastrophic failure of the composite. This structure-property correlation provides powerful quantitative guidelines for the design of lightweight brittle materials with enhanced fracture resistance. We illustrate this potential by fabricating nacre-like bulk composites with unparalleled flexural strength combined with noncatastrophic failure.

Stiffness, strength, and fracture toughness are an antagonistic combination of materials properties that are difficult to achieve in man-made composite materials. In contrast, biological composites, like nacre, access this combination of properties by employing hierarchical structures and complex chemical and physical interactions across multiple length scales (1–4). In bioinspired composites research, work has been conducted toward identifying the underlying design principles of these biological materials for translation to future engineering composites (5–7). However, the structural complexity of these multiscale biological composites makes it oftentimes difficult to identify and quantify the individual structure–property relationships. Biological materials vary depending on species, region of sampling, and season, and variation of even a single parameter can alter the balance of physical interactions across the hierarchical structure, resulting in compounded effects on the mechanical behavior.

A biological material whose structure and properties have been extensively studied is the nacreous layer of the mother of pearl (7–10). Interest in this biological material stems from its ability to combine high strength, stiffness, and toughness using intrinsically weak mineral building blocks (9, 10). Nacre consists of mineral platelets arranged in brick-and-mortar structure at very high mineral content. The platelets are separated by a thin biopolymer layer (11), interconnected to one another through stiff and strong mineral bridges (12, 13). Notably, the strongest nacre-inspired composites all have mineral bridge interconnectivity (14–16). The interaction of mineral content, aspect ratio, and interconnectivity between the platelets all play a role in the stiffness, strength, and toughness of the biological composite (17).

Because of their clear impact on the strength of nacre-like composites, the effect of mineral bridges on the mechanical response of brick-and-mortar architectures has been the subject of investigation (14, 15, 18, 19). Mathematical models and experimental studies offer interesting predictions to guide the design of mineral bridges in nacre-like composites. For example, a statistical model has been proposed to evaluate the mineral bridge contribution to Young’s modulus and toughness (20). Based on empirical observations of nacre from Haliotis iris, the authors found that mineral bridges, rather than the organic matrix, are responsible for the capacity of nacre to sustain high external loads (20). Later work showed that the number of mineral bridges per platelet in biological nacre appears to be optimized with respect to the platelet thickness, enhancing the strength of nacre while maintaining toughness (21, 22). This relationship emerges from a balance between the force needed to break a platelet and the force needed to shear a mineral bridge. The argument that mineral bridges influence the strength of nacre gained further support from dimensional analysis and finite-element simulations of mineral bridge size effects in an idealized model of nacre (23). In this work, mineral bridges in the range of 10–40-nm diameter were found to be optimal for transfer of shear stresses across platelet–platelet interfaces. Very recently, multimaterial 3D printing technologies were shown to be a promising route for building nacre-like model materials with tunable architecture (18).

Despite the insights obtained so far, only a few quantitative descriptions for how mineral bridges contribute to the mechanics of the nacre structure have been reported. Proposed analytical models have yet to be validated experimentally in nacre-like materials with tunable mineral bridges at the length scales and properties comparable to the biological system. Working at the same length is critical when studying brittle materials that are scale sensitive (7). This requirement is not fulfilled by current 3D printing technologies, which produce brick-and-mortar designs with platelets about 10–100× larger than the biological material. Further, biological nacre has a very high ratio between the stiffness of the platelets, E_p, and the stiffness of the matrix, E_m:E_p/E_m is on the order of 10⁹. In comparison, typical 3D-printed multimaterial polymers have an E_p/E_m ratio on the order of 10⁴. Thus, these polymer models likely overemphasize the role of the matrix contributing toward the strength of the composite, especially when extrapolating to composites with high mineral content (18, 22). In this context, building simplified nacre-inspired composites with structural features and constituent mechanical properties comparable to those found in the biological material should allow for a more systematic study of the structure–property relationships underlying the effect of mineral bridges on the mechanics of nacre.

Nacre-like composites featuring a brick-and-mortar structure and mineral interconnectivity at length scales and modulus ratio comparable to those of the biological counterpart were recently developed using a vacuum-assisted magnetic alignment process (VAMA) (15). Analysis of the mechanical properties of brick-and-mortar architectures produced via this approach led to important qualitative insights into the role of interconnectivity on the strength of nacre-like composites. However, the simultaneous variation of the platelet content and the fraction of mineral bridges did not allow for a quantitative description of the isolated effect of mineral bridges on the composite properties. Quantifying the effect of such bioinspired structural features on the properties of the resulting materials is crucial for the design of future high-performance composites.

Here, we quantify the effect of mineral bridges alone on the mechanical response of nacre-like composites featuring length scales and stiffness ratio comparable to those found in the biological material. To this end, nacre-like composites with fixed mineral density (volume fraction) and tunable density of mineral bridges were prepared. This was accomplished by mapping the design space of the sintering process to identify the sets of temperatures and pressures that lead to composites with fixed mineral volume fraction but variable mineral bridge densities. By choosing a broad range of mineral bridge connectivity, we study the effect of this important structural feature on the mechanical response of brick-and-mortar architectures (9, 12). Composites with tunable mineral bridge densities are investigated by image analysis and flexural bending tests to obtain structure–property relationships for these model nacre-like materials. Using the experimental data, we develop a shear-lag model that quantitatively describes the relationship between mineral connectivity and composite strength, elastic modulus, and toughness. Moreover, we observe that residual stresses introduced during scaffold fabrication strongly affect the ultimate strength that is achievable with these composites. Despite these residual stresses, we present nacre-like composites with optimum mineral bridging and small platelet sizes that exhibit the highest strength reported for brick-and-mortar structures while also maintaining noncatastrophic failure.

Materials and Methods

Composite Fabrication.

Nacre-like composites were fabricated using a previously reported VAMA process (SI Appendix). Samples with magnetically aligned platelets were converted into inorganic scaffolds by a prefiring process followed by sintering under pressure. Curing of scaffolds infiltrated with monomers led to nacre-like specimens with well-defined brick-and-mortar structures.

Characterization.

Composites specimens were characterized in terms of mineral fraction and mechanical properties using standard methodologies (SI Appendix). Mineral connections between platelets were quantified by image analysis of scanning electron micrographs to determine the fraction of mineral bridges, γ.

Results and Discussion

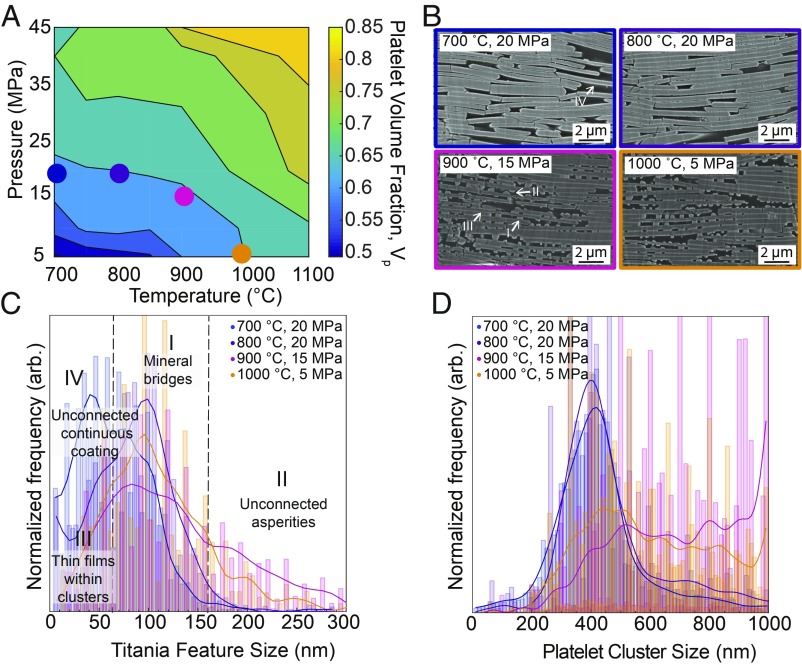
Pressure sintering of mineral scaffolds obtained through the VAMA process strongly affects the mineral volume fraction and the microstructure of the resulting nacre-like architecture. Because they promote particle rearrangement and atomic diffusion, increasing temperatures and applied pressures enhance the mineral fraction of the scaffold. The higher diffusion of atoms at higher temperatures also results in stronger dewetting of the titania from the alumina platelet surface. Due to the relatively low temperature, the dewetting of titania occurs without alloying with alumina (24). Therefore, the strength of the titania–alumina interface is expected to be independent of the sintering temperature. Dewetting affects the density of titania mineral bridges between the alumina platelets. By mapping the sintering design space, we can select temperatures and pressures that lead to nacre-like scaffolds of constant mineral volume fraction but different mineral bridge densities (Fig. 1A). Based on the sintering map, a series of scaffolds sintered between 700 and 1,000 °C and exhibiting a platelet volume (V_p) of 60 ± 2% were selected for further study. At this volume fraction the platelets are sufficiently close to enable the formation of interconnecting mineral bridges and thin films within clusters, while keeping a concentration of polymer phase that is high enough to promote energy dissipation via plastic deformation after rupture of the bridges (SI Appendix).

Fig. 1.

The size distribution of titania features in scaffolds with mineral volume fraction fixed at 60 ± 2%. (A) The scaffold mineral density depends on both temperature and pressure. (B) Interfacial titania features increase in size as the sintering temperature increases. The titania feature size is quantified by image analysis and thresholded to determine (C) the fraction of mineral bridges or (D) the size of platelet clusters within the scaffold. Titania features in the form of (B, I) mineral bridges, (B, II) unconnected asperities, (B, III) thin films within platelet clusters, and (B, IV) unconnected continuous coating are indicated by arrows in B for the case of samples sintered at 900 °C as an example.

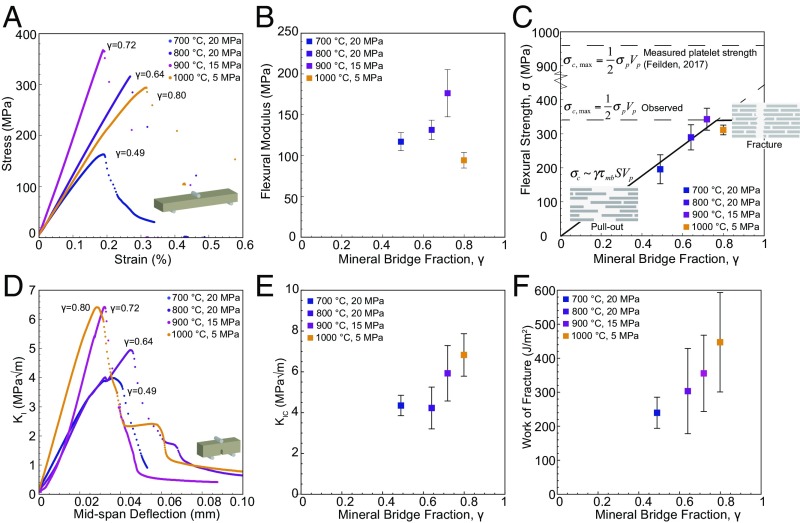
Image analysis enabled quantification of the density of mineral bridges and interplatelet connections present in each nacre-like scaffold (Fig. 1C and SI Appendix). To this end, we measured the fraction of titania features forming contacts between platelets for all of the investigated samples and defined this as the mineral bridging fraction γ (Materials and Methods). Using this approach, we obtained γ values of 0.49, 0.64, 0.72, and 0.80 for the samples sintered at 700, 800, 900, and 1,000 °C, respectively. Having identified a series of composites with constant V_p and variable γ, it is now possible to experimentally evaluate the isolated effect of mineral bridges on the composite flexural strength, elastic modulus, and fracture toughness (Fig. 2)

Fig. 2.

Mechanical behavior of nacre-like composites with varying mineral bridge fraction. Stress–strain curves from flexural tests (A) show that the elastic modulus (B) and strength (C) increase with mineral bridging fraction up to 900 °C. Thereafter, the strength and modulus decrease for the 1,000 °C sintered sample. Cartoons shown in C illustrate the transition in failure mode as the mineral bridge fraction is increased. (D) Stress intensity factor K_I as a function of midspan deflection measured for single edge notched beams under bending. The noncatastrophic nature of the fracture process is evidenced by the several data points detected after the peak stress. (E) The fracture toughness, K_IC, and (F) work of fracture both increase with mineral bridge fraction γ, despite the loss of stiffness and strength at sintering temperatures above 900 °C.

The obtained flexural stress–strain curves (Fig. 2A) show that an increase in the mineral bridge fraction from 0.49 to 0.72 simultaneously enhances the elastic modulus (E) and the strength (σ) of the composites. Since the volume fraction of these composites is comparable, these results clearly indicate that mineral bridges are key to the observed increase in the E and σ values of the nacre-like materials. Indeed, the strength and elastic modulus was found to scale directly with the mineral bridge fraction for γ values up to 0.75 (Fig. 2 B and C). The fact that the elastic modulus decreases for a mineral bridge fraction above 0.75 suggests that there are additional structural changes occurring within the scaffold at the higher sintering temperature required to reach the highest γ values. As already indicated by the image analysis data (Fig. 1 C and D), platelets rearrange into clusters at sintering temperatures equal to or above 900 °C, leading to a heterogeneous microstructure that cannot be described using solely the mineral bridging fraction γ. Thus, the interpretation of the mechanical data obtained for samples sintered at these higher temperatures must consider the presence of clusters and the heterogeneous nature of the resulting microstructures. Image analysis of fracture surfaces suggests that the fracture mechanism changes from intracluster to intercluster as the temperature increases from 900 to 1,000 °C (SI Appendix).

Regardless of the fracture mode, all of the investigated nacre-like composites were still able to carry load beyond the peak stress. This is quite remarkable if compared with the typical catastrophic failure of materials exhibiting similar levels of elastic modulus and strength. Thus, our data demonstrate that the discrete mineral bridges responsible for the simultaneous increase in stiffness and strength do not sacrifice the toughening mechanisms of the nacre-like architecture. Instead, the rupture of the mineral bridge at high stresses results in a brick-and-mortar structure that encodes some of the toughening mechanisms expected for this architecture, namely platelet pullout, plastic deformation of the organic phase, crack deflection, and possibly friction between broken bridges. Such toughening mechanisms enhance the energy required to fracture the composites, which is quantified here as the critical stress intensity factor K_IC and the work of fracture (Fig. 2 E and F). Like the stiffness and strength, K_IC and the work of fracture follow a linear dependence on the mineral bridge fraction, despite the stress localization effects that would be expected from imperfect packing (25). The maximum work of fracture obtained (400 J/m²) is one order of magnitude higher than those reported for alumina ceramics with similar grain sizes (26). Such impressive improvement in toughness is achieved with a reduction of only about 50% in elastic modulus compared with alumina. In comparison with laminate structures featuring 1,000× coarser structural features (27), our multilayered ceramics exhibit up to 80% higher initiation fracture toughness (K_IC) but 10-fold lower work of fracture (WOF) (27). The lower WOF of our finer microstructure is explained by the absence of stable delamination followed by large-scale bridging, which is typically observed in coarser laminate structures. The high intrinsic toughening (high K_IC) achieved with the nacre-like architecture and the enhanced extrinsic toughening of laminates and coarse structures alike (high K_IR and WOF) (28–30) may open opportunities for the design of hierarchical composites, whose fracture resistance emerges from complementary mechanisms operating at multiple lengths scales.

To be able to better quantify the effect of mineral bridges on the mechanical response of the nacre-like composites, we interpret our flexural strength data using an adapted shear-lag model, similarly to the approach suggested first by Jackson et al. (8) and later by Lin and Meyers (21) and Meyers et al. (22). In a shear-lag model, the strength of a discontinuously reinforced composite is estimated by considering the amount of stress transferred through shear forces across the interface between the continuous softer phase and the stiffer elements. This leads to two possible fracture scenarios. If the stress transferred is lower than the reinforcement strength, fracture requires pullout of the reinforcing element from the soft matrix. By contrast, when the transferred stress exceeds the strength of the reinforcement, the composite fails by fracture of the stiff phase. If fracture of the stiff phase takes place, the maximum possible increase in composite strength has been reached, which comes at the expense of the toughness mechanisms associated with platelet pullout. This explains why most biological materials optimize their interfaces to be strong but weak enough to promote pullout of the reinforcement and thus the onset of energy-dissipating toughening mechanisms (11).

For our nacre-like samples that showed intracluster failure (γ < 0.75), SEM analysis reveals that the density of broken platelets found on the fracture surfaces increases as the sintering temperature increased from 700 to 900 °C. Combined with the observation that the strength of our composites reaches a maximum at the sintering temperature of 900 °C, the microstructural evidence of increasing incidence of platelet fracture suggests that the failure mode transitions from platelet pullout to platelet fracture around this temperature. This transition is in agreement to previous findings by Grossman et al. (15).

On the basis of these experimental observations, we modeled the failure strength of samples sintered between 700 and 900 °C using a shear-lag analysis assuming platelet pullout as the main failure mode. Shear-lag analysis predicts the composite strength to vary under pullout mode as follows (SI Appendix, Eqs. S2–S4):

$${\sigma }_c\hspace{0.17em}=\hspace{0.17em}\frac{\tau S{V}_p}{2}+(1-V_p){\sigma }_m,$$ [1]

where τ is shear strength of the matrix or of the platelet–matrix interface, S is the aspect ratio of the platelet, $V_p$ is the volume fraction of platelets, and ${\sigma }_m$ is the matrix strength.

Adapting the model to describe the mineral bridge contributions to the composite strength requires some simplifying assumptions. First, the contribution of the polymer tensile strength to the composite strength, $\left(1-V_p\right){\sigma }_m$, is assumed to be negligible. This is a reasonable assumption if one considers that the elastic modulus of the platelets (E_p ∼ 300 GPa) is two orders of magnitude higher than that of the polymer matrix (E_m ∼ 3 GPa). In this case, stresses will be predominantly transferred through the stiffer mineral phase as long as the mineral bridges are intact. The ability to transfer stresses between platelets through a very stiff phase while keeping a softer polymer phase for toughening after the bridges fail is a clear advantage of using stiff mineral bridges between “bricks” compared with simply utilizing a “mortar” phase with high stiffness and strength. Second, we assume that stress transfer efficiency scales with the mineral bridge fraction between platelets. In its general form, shear-lag theory considers stresses to be distributed over the entire platelet area. Here, it is reasonable to assume that stresses are transferred predominantly through the fraction of platelet area covered by the stiff mineral bridges. Thus, using the mineral bridging fraction γ as a scaling term captures the fact that stresses can only be transferred over this reduced bridge contact area. As a result of these simplifying assumptions, the adapted form for the shear-lag description of the mineral-bridge contribution to composite strength under pull-out is

$${\sigma }_c\approx \frac{\gamma {\tau }_{mb}S{V}_p}{2},$$ [2]

where τ_mb is the interfacial strength between the mineral bridge and the alumina platelet.

It is important to note that the assumption that the strength is controlled primarily by the mineral phase does not hold for nacre-like composites with weaker mineral interconnectivity, as explored by Niebel et al. (31). In such cases, the contribution of the polymer phase must also be taken into account. Since this work explores only one polymer phase, and the strengths of the scaffolds reported are 3–4× higher than the strength of that polymer phase, we do not consider this effect here.

Having established a quantitative correlation between the composite strength and the mineral bridge fraction, we can now compare our theoretical predictions with the experimental data from our model system. We find that the flexural strength of our brick-and-mortar composites with mineral bridges is well explained by the modified shear-lag description. The linear dependence of the strength data on the mineral bridging fraction γ (Fig. 2B) found in our experiments is in good agreement with the theoretically derived scaling relation (Eq. 2). This agreement confirms that mineral bridge fraction is the single relevant variable in this dataset. More broadly, the proposed scaling relation provides an explicit quantitative correlation between a microscopic structural parameter and a macroscopic fracture property. We note that the mineral bridging fraction of our strongest composites (γ ∼ 0.70) is significantly higher than that observed in biological nacre, which typically ranges from 0.05 to 0.2 (32). This difference might arise from the distinct shear strengths of the mineral bridges in the biological (${\tau }_{mb}^{bio}$) and synthetic (${\tau }_{mb}^{syn}$) composites. Because the interface between alumina platelets and titania bridges is expected to be much weaker than that in biological nacre (${\tau }_{mb}^{syn}<{\tau }_{mb}^{bio}$), high shear stresses ($\tau =\gamma {\tau }_{mb}$) can only be applied on the synthetic platelet surface if the fraction of artificial mineral bridges is significantly higher than that observed in the natural composite (${\gamma }^{syn}>{\gamma }^{bio}$).

The scaling argument proposed above should be valid when the fracture process occurs predominantly through a platelet pullout mechanism. The fact that the composite strength remains unchanged between 900 and 1000 °C suggests that the failure mode of these composites is no longer dominated by pullout but instead by platelet fracture. The strength of composites failing under such mechanism can also be predicted using a shear-lag model. As shown in detail in SI Appendix, the composite strength in this case is given by

$${\sigma }_{c,max}\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}{\sigma }_{p,eff}{V}_p,$$ [3]

where σ_c,max is the maximum strength that the composite can reach.

Since σ_c,max and V_p are experimentally known, this simple equation can be used to indirectly estimate the effective strength of our alumina platelets (σ_p,eff). Taking the maximum observed composite strength (σ_c,max) of ∼350 MPa, we estimate from this equation that the platelet strength should be on the order of 1 GPa. This value seems rather low, as literature values for uncoated platelets from the same manufacturer and of similar thickness are reported to be between 3 and 5 GPa (33). To understand the discrepancy between the previously measured platelet strength and the one deduced from our model, other factors that could potentially contribute to this reduced effective platelet strength must be revisited.

A reasonable explanation for the lower effective strength of our platelets can be conceived in light of another important experimental finding revealed by the microstructural analysis of sintered scaffolds. We observed by SEM imaging of composite cross-sections that sintering under pressure leads to extensive bending of the alumina platelets (SI Appendix, Fig. S3A). Since the platelets are flat in the green scaffold, these deformations must result from the application of external pressure during sintering. The low atomic diffusion in titania below 900 °C makes platelet bending the only possible mechanism of densification in scaffolds subjected to high pressures. Interestingly, we found that scaffolds with bent platelets expand ∼15% when heated up a second time to 1,000 °C without any pressure. Microstructural analysis of such heat-treated scaffolds reveals that the measured macroscopic expansion arises from the partial relaxation of the platelets back to a flat configuration (SI Appendix, Fig. S3B). If the mineral bridges are small enough, heating the scaffold without external pressure allows the titania to become mobile again and thus the elastic deformations to recover. This experiment clearly indicates that high residual stresses are stored in the bent platelets after the sintering process. Since the sintering temperatures are several hundred degrees lower than the usual sintering temperature for alumina, it is unlikely that any residual stresses from hot pressing are alleviated through creep mechanisms in the platelets. The residual stresses associated with this bending effect are eventually sustained at room temperature by the mineral bridges formed during the sintering process.

The bending stresses introduced during sintering can reduce the effective strength of the platelets by allowing fracture to initiate at lower stresses on the tensile face of the platelet. This in turn should reduce the maximum composite strength. One can estimate the effect of the residual bending stress, λ, on the composite strength by substituting an effective platelet strength, ${\sigma }_{p,eff}={\sigma }_p-\lambda$ into Eq. 3:

$${\sigma }_{c,max}=\frac{1}{2}\left({\sigma }_p-\lambda \right)V_p.$$ [4]

Because σ_c,max, V_p, and σ_p have been experimentally determined, we use this equation to predict the level of residual stresses stored in the platelets due to pressure-induced bending. Following this rationale, we estimate the residual stress induced by bending to lie within the range 2–4 GPa. Calculations based on image analysis and beam theory show indeed that the residual stresses on the platelets can be as high as 4–6 GPa (SI Appendix and Fig. S3F). The reasonable agreement between the experimentally determined values and the stress level expected from these calculations suggests that residual stresses are likely the reason for the lower maximum scaffold strength compared with the theoretical expectation.

With the gained understanding, we can use the theoretical model to design and fabricate optimized nacre-like composites with improved composite strength. The theoretical analysis indicates that the mineral volume fraction (V_p) and the residual stresses (λ) have opposite effects on the flexural strength of our nacre-like composite. These two variables are strongly affected by the processing conditions, namely the pressure and sintering temperature (Fig. 1A). Higher sintering temperatures and pressures should in principle increase the composite strength by enhancing V_p. However, this effect is counterbalanced by the introduction of residual bending stresses that reduce the composite strength. Therefore, unless the processing route is further optimized to minimize the residual stresses at higher mineral fractions, other strategies are required to circumvent these contradicting effects. One possible way to improve the flexural strength of the composite without optimizing the balance between V_p and λ is to increase the strength of the reinforcing elements (σ_p) by using smaller platelets. Although smaller platelets are also subjected to residual stresses after hot pressing, Griffith’s criterion predicts higher fracture strength for smaller reinforcement sizes on the platelet length scale. This could increase the load-bearing capacity of the nacre-like architecture by extending the maximum strength limit imposed by the platelet fracture mode (Eq. 3).

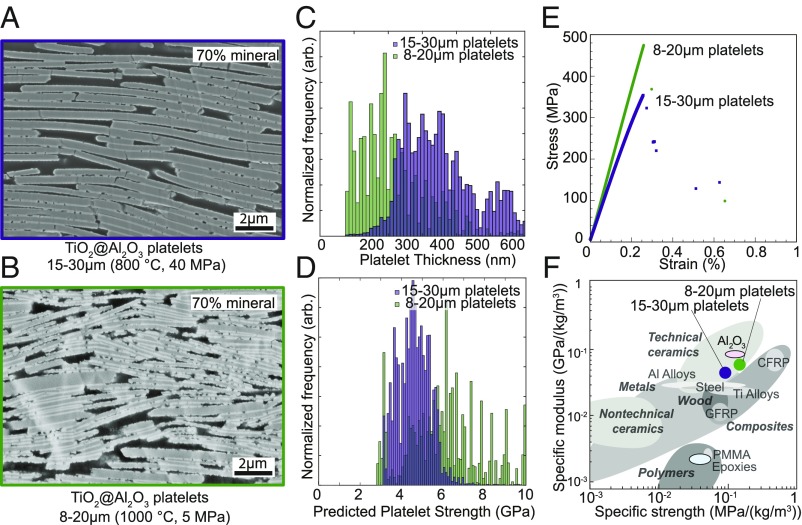
To test the hypothesis of enhancing K_IC utilizing thinner platelets, a series of composites was produced using platelets with smaller thickness, which intrinsically should be stronger. To keep the aspect ratio constant, we selected platelets that were also shorter in length. Because the smaller platelets resulted in a denser packing of 0.7, the processing of the original model system with large platelets was modified to reach this higher mineral content and allow for the evaluation of the effect of the platelet size alone on the mechanics of our composites (Fig. 3 A and B). Image analysis (SI Appendix, Fig. S4) shows that bent platelets are still present in the composites with smaller platelets, thus confirming the continuing presence of residual stresses. However, Griffith’s criterion predicts that the platelet strength scales with the inverse of the square root of the platelet thickness. Comparing the thickness distributions between the two size grades of titania-coated alumina platelets used in our experiments, we find that the larger grade of platelets have a mean thickness of 325 nm, while the smaller platelets have a mean thickness of only 163 nm (Fig. 3C). From the ratio between these mean size values, Griffith’s criterion predicts a 41% increase in platelet strength by decreasing the platelet thickness from 325 to 163 nm. Assuming reasonable values for the elastic modulus and surface energy of the platelets (SI Appendix, Table S1), one can also estimate the actual distribution of platelet strengths for the two investigated grades (Fig. 3D). Since the composite strength scales linearly with the platelet strength (Eq. 3), the increase in platelet strength should directly reflect in a higher flexural strength for the nacre-like composites.

Fig. 3.

Effect of platelet size on the mechanical properties of nacre-like composites. (A and B) Microstructures of composites containing (A) 15–30-μm and (B) 8–20-μm platelets at a volume fraction of 0.70. Thinner and smaller platelets improve packing in the scaffold and allow higher mineral densities to be achieved under lower external pressures. (C) Size distribution and (D) estimated failure strength of the two sets of investigated platelets. (E) Stress–strain curves for nacre-like composites contain small and large platelets. (F) Comparison of the specific mechanical properties of the investigated composites with literature data. The specific strength of composites prepared with smaller platelets is over 20% higher than previously reported for brick-and-mortar polymer matrix composites.

Indeed, fracture bending tests show a 25% increase in the maximum ultimate strength of the composite by replacing large platelets with smaller ones. Such replacement increases the composite strength from 370 ± 28 MPa to 473 ± 20 MPa. Representative stress–strain curves obtained for these samples show that the composite retains a noncatastrophic failure despite the very high flexural strength achieved (Fig. 3E). The reasonable agreement between the model and the experimentally measured strength data suggests that the reduced platelet size is the main reason for the improvement in strength of the composites. This composite has the highest yet reported combination of specific stiffness and strength for bulk nacre-like architectures (Fig. 3F). Our nacre-like composite is 2× higher in specific strength and 6× higher in specific stiffness compared with glass fiber reinforced polymers. Despite its lower specific strength, the specific stiffness level achieved is comparable to that of carbon fiber reinforced composites with the added value of providing 2D reinforcement using stiff elements at much smaller length scales.

Conclusions

Mechanical measurements on model nacre-like composites show that mineral bridges increase the flexural strength of brick-and-mortar architectures by enhancing stress transfer throughout the stiff inorganic phase. Stress transfer becomes more efficient by increasing the density of mineral bridges between the stiff inorganic platelets of the brick-and-mortar structure. The enhanced stress transfer achieved through increased bridging at the microscale translates directly into higher composite strengths at the macroscale. The flexural strength of such nacre-like composites was found to increase linearly with the density of mineral bridges between platelets until the stress level carried by the inorganic phase reaches the strength of individual platelets. In addition to the mechanical strength, the fracture toughness of the composites also shows a linear dependence on the density of mineral bridges. This shows that mineral bridges can enhance the flexural strength of nacre-like composites while still promoting the onset of toughening mechanisms typical of brick-and-mortar architectures. As a result, antagonistic properties such as flexural strength, elastic modulus, and fracture toughness can be simultaneously obtained. The linear dependence of the flexural strength on the bridging density can be explained using a simple shear-lag model applied to individual platelets. For the manufacturing process used in this study, we observe the flexural strength of the composite to be limited by residual stresses introduced into the material during pressing at high temperatures. Our shear-lag model properly captures this effect by considering that the residual stresses reduce the effective strength of the platelets. To compensate for this undesired effect, we show that composites with higher flexural strength can be made using thinner, stronger platelets. Thinner platelets increase the strength of the composite as expected from Griffith’s criterion. These nacre-like composites exhibit the highest yet reported combination of specific stiffness and strength. Besides the remarkable fracture resistance achieved, our work on nacre-like composites demonstrates the potential of bioinspired synthetic architectures in providing a tunable model system to investigate the underlying design principles of more complex hierarchical biological materials.