Changing demographics of scientific careers: The rise of the temporary workforce

Abstract

Contemporary science has been characterized by an exponential growth in publications and a rise of team science. At the same time, there has been an increase in the number of awarded PhD degrees, which has not been accompanied by a similar expansion in the number of academic positions. In such a competitive environment, an important measure of academic success is the ability to maintain a long active career in science. In this paper, we study workforce trends in three scientific disciplines over half a century. We find dramatic shortening of careers of scientists across all three disciplines. The time over which half of the cohort has left the field has shortened from 35 y in the 1960s to only 5 y in the 2010s. In addition, we find a rapid rise (from 25 to 60% since the 1960s) of a group of scientists who spend their entire career only as supporting authors without having led a publication. Altogether, the fraction of entering researchers who achieve full careers has diminished, while the class of temporary scientists has escalated. We provide an interpretation of our empirical results in terms of a survival model from which we infer potential factors of success in scientific career survivability. Cohort attrition can be successfully modeled by a relatively simple hazard probability function. Although we find statistically significant trends between survivability and an author’s early productivity, neither productivity nor the citation impact of early work or the level of initial collaboration can serve as a reliable predictor of ultimate survivability.

Contemporary science has been characterized by an exponential growth in practitioners and publications (1) and a rise of team science, both in terms of the increasing prevalence of team-authored work and the growth of team sizes (2–4). The gradual shift from individual to team science is driven by a variety of factors, including increasing capital intensivity of science (5) and the increased need for technicians and staff scientists (6). At the same time, there has been a substantial growth in the number of awarded PhD degrees in recent decades (7), which has not been accompanied by a similar increase in the number of academic positions (8), leading to concerns about the lack of opportunities for new PhDs in science (9, 10) and even warnings regarding possible scientific workforce bubbles (11, 12). In an environment with substantial growth in PhDs granted and only modest growth in the number of faculty positions, the idea of each professor regularly reproducing himself or herself in each cohort of graduate students becomes untenable. These and similar data have led to calls for rethinking academic careers, and to discussions of the need for policy interventions to address this growing problem (5, 9, 13).

How does the shifting landscape of science over the past half-century affect the roles of new researchers and their overall careers? There is an abundance of studies that focus on the criteria that may affect researchers’ success in terms of the impact of their work, especially in terms of citations to publications. However, another, and perhaps more fundamental, aspect of success is the ability to perform research over the full extent of someone’s career, rather than leaving the field prematurely. A smaller fraction of literature focuses on understanding the factors leading to successful academic careers in this broader sense and, more recently, the factors contributing to abandoning scientific careers (14–16). Prior work has identified productivity (14, 16–20), impact (20, 21), number of collaborators (14, 17), gender (22), prestige of PhD granting and hiring institutions (23, 24), prestige of the advisors (24, 25), gender of the advisors (16), and level of specialization (26) as important factors correlated with career success. Some of these studies have found that these factors are correlated. For example, there is a correlation between the citation success of early papers and later increase in productivity (27). There is also a reported correlation between gender and productivity (19, 28, 29), gender and citations, and gender and collaboration. Finally, there is a correlation between institutional prestige and productivity (30, 31), as well as institutional prestige and impact (32). Directionality of these correlations is difficult to establish and is not the focus of this paper.

On the other hand, there are relatively few studies that focus on modeling scientific careers (30, 33–38) in the context of survivability. An early study of this type (35) used a sample of 500 authors during the period 1964–1970 and has established a division of all authors into transient and continuants and found that the levels of productivity are correlated with career length. Two recent studies (36, 37) used survival analysis and hazard models to examine gender differences in retention of science and social science assistant professors. These studies established that the chances of survival of assistant professors in science and engineering are less than 50%; that the “median time to departure is 10.9 y” (36); and that, in social sciences, “half of all entering faculty have departed by year 9” (37).

Despite various efforts, there is a clear gap in our knowledge of careers of the scientific workforce in general (and not only tenure-track scientists). Furthermore, large-scale investigation of the trends in careers of the scientific workforce across entire disciplines and over long periods of time (many decades) is still in its infancy.

In this study, we analyze the changing careers of the scientific workforce of entire disciplines without making assumptions regarding the positions individuals comprising the workforce have in the scientific community (i.e., not limited to those who have tenure track jobs, as was the case in many of the earlier studies). We specifically focus on the role that different authors play in knowledge production. Furthermore, we investigate whether one can identify early factors (during a researcher’s apprenticeship phase) that would indicate a scientist’s ability to maintain a research-active career over many years. Our big-data approach is facilitated by an extensive longitudinal dataset containing millions of bibliographic items covering the entire period of contemporary science.

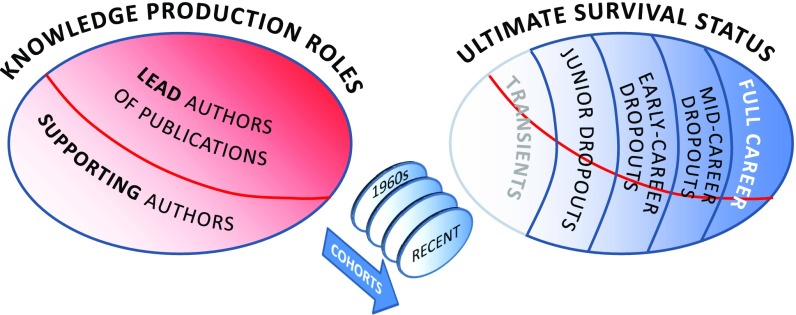
To capture the above-stated changes in the demographics of the scientific workforce, we created a survival model of authors based both on the primary role they play in the production of knowledge and their ultimate survival status in science. Each author is placed in one of two categories based on his or her primary authorship role: lead authors and supporting authors. Lead authors are all authors who have led a publication at any time in their career, whereas supporting authors are the ones who have never had that role in their career. Furthermore, we place each author (whether lead or supporting) into one of the five categories in terms of his or her ultimate survival status: transients (authors with a single publication), junior dropouts (multipaper authors leaving after 0–10 y after the first publication), early-career dropouts (multipaper authors leaving after 11–15 y after the first publication), midcareer dropouts (multipaper authors leaving after 16–20 y after the first publication), and full-career scientists (multipaper authors who have careers longer than 20 y). This classification is presented schematically in Fig. 1. The balance between supporting and lead authors in each of the survival categories is different, as indicated by the tilted curve in Fig. 1. Most transient scientists belong to the supporting author group, whereas as we move toward the full-career status, the proportion shifts in favor of lead authors. To study the changing landscape of scientific careers in terms of knowledge production roles and survivability, we focus our analysis on cohorts: a group of authors who first appear on the scientific stage at the same time (in the same year). Our study is facilitated by the availability of extensive longitudinal data allowing us to follow up half a century of cohorts and to assess their eventual careers.

Fig. 1.

Model of scientific careers. For each cohort of authors entering the field, we determine the knowledge production role as a “lead author” (researcher who leads the production of a scientific publication at any time in his or her career) or a “supporting author” (those who will never lead the production of a scientific publication). Furthermore, each new author will fall into one of five categories of ultimate career status: transients (authors who only had one publication), dropouts (authors who leave the field prematurely at different levels of their careers), and full-career scientists (authors who ultimately survive in the field). In each survival category, there will be some authors classified as lead and some as supporting (the repeated red curve). We follow 50 cohorts starting from the 1960s.

In this study, we focus on researcher cohorts in three scientific disciplines covering different areas of science: astronomy (physical sciences), ecology (life sciences), and robotics (engineering and computer science). We focus on researchers who have published in principal journals belonging to these fields (listed in SI Appendix). These are the journals that are well established, usually publish a large fraction of original research in a particular field, and are considered to be good representatives of those fields. We used a number of studies to identify the core journals. For astronomy, we used the list of core journals provided in ref. 39; for ecology, we used the lists provided in refs. 40, 41. We define authors and derive their metrics from principal journals alone. Some of these authors may publish some fraction of their work in other journals (either other journals in the same or a related area or, in some cases, in multidisciplinary journals). This incompleteness will reduce the metrics and, in some cases, may affect the determination of career length or authorship role. Quantifying the incompleteness and its effects is difficult, given the lack of topical classification at the article level. However, since the analyses in the paper are relative (i.e., one time period vs. another, authors with one set of characteristics vs. another), the incompleteness will not affect some time periods or authors more than the others; thus, the relative trends should be unaffected. Our choice is conservative because the alternative, including all works that match some name, would greatly exacerbate the name disambiguation problem and potentially confound the results.

All of the analyses are derived from the bibliographic data extracted from the full Clarivate Analytics Web of Science database. We used the entire temporal span of the database (from 1900 to 2015) to establish the starting and ending years of activity of each author, and thus to identify the cohorts. For astronomy and ecology, we follow cohorts from 1961, and for robotics, we follow cohorts since 1985 (none of the core robotics journals published before 1983). The number of authors belonging to these cohorts and included in the analysis is 71,164 in astronomy, 20,704 in ecology, and 17,646 in robotics.

To identify unique authors, we perform, for each field-specific dataset separately, disambiguation of author names using the hybrid initials method. The scheme represents an improvement over standard initials methods because it either ignores or takes into account the middle initial depending on the name frequency (42), minimizing the splitting of unique authors due to inconsistent use of the middle initial while maximizing the author separation. Percentages of authors whose identity has been compromised due to either splitting or merging have been estimated by simulation and are between 3% and 5% (42), which is below a level that would significantly affect our results. Ambiguity is relatively low because we focus on principal journals alone.

The roles that authors play in knowledge production (lead and supporting) are established from author lists in the following way. Authors on single-authored papers are given a lead author status. To establish the roles in multiauthored papers, we have first verified that the author lists are ordered by author contributions (with the first author almost always matching the corresponding author) in all three disciplines under study, except in rare cases when they are ordered alphabetically. We find no evidence for a deliberate alphabetical listing in papers with fewer than approximately four authors, and in such cases, we adopt the first author as a lead author. For longer lists of authors, we check if the author list is alphabetical (based on up to seven first-listed authors), and if it is not, we again take the first listed author as a lead author. If the list is alphabetical, we determine the lead author only if the corresponding author is not the first author. The fraction of articles for which the lead author could not be determined is relatively small (1.6%, 0.2%, and 0.3% for astronomy, ecology, and robotics, respectively).

For each unique author, we establish the cohort year as the year when he or she first appeared as an author in any role (lead author or supporting author). Since our data extend to periods before the starting time for the analysis, the cohort year, as well as the year of the departure from the field, can be established reliably. An author is considered currently active if he or she has published (in any role) in the last 3 y covered by database. Of the active authors, some have achieved full-career status (defined as at least 20 y of active publishing), whereas for others, their ultimate survival status is currently unknown and they are excluded from those analyses where such information is required.

Results

Growth of Supporting Author Scientists.

Previous results on the growth of team science and the changing structure of such teams allow us to propose that one component of the changing career demographics of scientist is a differentiation into heterogeneous career paths, with some scientists becoming lead authors and others specializing as nonlead supporting team members. Here, we establish the extent to which each of these groups has contributed to the creation of knowledge over the past half-century.

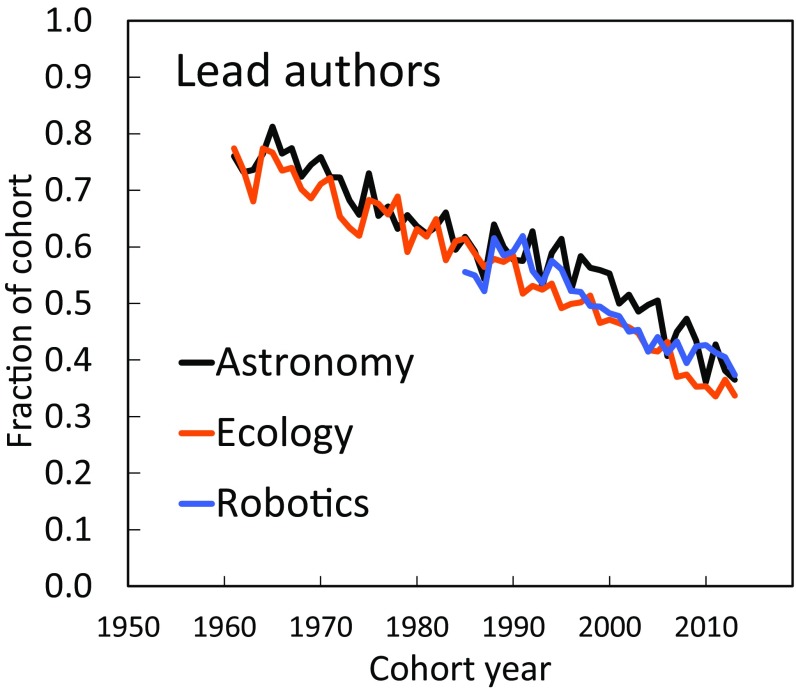
Fig. 2 shows the fraction of authors from each cohort that, at any point in their career, will contribute to the field as lead authors. The fraction of lead authors has been experiencing a dramatic downward trend in all three disciplines since the 1960s, leading to a complementary increase in the share of supporting authors. Furthermore, the proportion of lead authors has been similar in all three fields, indicating that the shift of roles may follow a universal pattern. While in the early cohorts, from the 1960s and 1970s, the vast majority (∼75%) of entering authors had a lead author role, this percentage has dropped to less than 40% in most recent cohorts. The strong shift is unrelated to the presence of transient authors. If those were excluded from the cohort, the drop in the share of lead authors remains similar: from ∼85% in the 1960s to ∼50% in the current decade. Is the increasing fraction of supporting authors an inevitable outcome of increasing team sizes? To test this possibility, we performed modeling in which we went through all of the papers in each dataset and tried to replace the coauthors (all authors except the lead author) who are classified as supporting authors with the authors who have the status of being lead authors and were active at the time of paper publication. In this modeling, the number of authors per paper remains the same, as well as the individual (lead author) productivity (because we only replace coauthors), yet we were able to populate mock author lists solely with lead authors. This demonstrates that having large team sizes does not automatically require the recruitment of supporting scientists. It also signifies that large teams are not entirely the product of collaboration among eventual full-role scientists (which may be more prevalent in small teams) but rather involve the recruitment of a special workforce of supporting scientists.

Fig. 2.

Fraction of each cohort that contributes to or will contribute to the knowledge production as lead authors. The status of lead author means that the author has led a publication at any time in his or her career. An increasing fraction of entering authors never acquire the lead role but participate in knowledge production solely as supporting scientists.

Survival Function and the Decreased Half-Life of Cohorts.

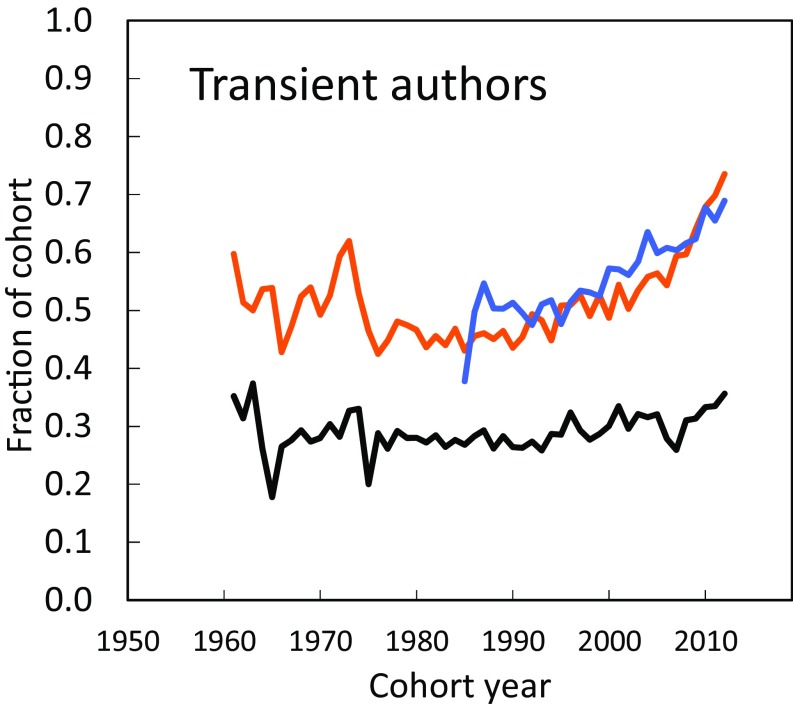
The minimal level of contribution to scientific knowledge is the production of a single paper. The existence of such authors was first pointed to by Price and Gürsey in 1976 (35), who named this type of author “transients” and established that they accounted for 25% of the population of scientists in the late 1960s. In Fig. 3, we find that the fraction of transients has remained relatively constant in most cohorts, although this category of authors has started to increase in recent cohorts across all three fields (since about the 1990s), especially in robotics and ecology. Notably, we also find that, unlike the fraction of lead authors, which is universal, the number of transients is field-dependent, with levels in astronomy similar to the ones Price and Gürsey (35) found and much higher rates (50–70%) in ecology and robotics. Interestingly, one-quarter of recent transients in all three fields were lead authors. This fraction was as high as one-half in the 1960s. This suggests that the threshold for lead authorship is often crossed even in the population that never genuinely embarks on a research path in that discipline.

Fig. 3.

Fraction of each cohort that has published only one paper (transient authors). The share of transients has increased in the past two decades, especially in ecology and robotics. The trend in the fraction of authors who are lead authors (Fig. 1) remains similar when transients are excluded from cohorts.

Comparing our astronomy results to similar findings from astronomy by Yoachim (43), we can see that even making different methodological choices about the population at risk, the journal lists, and the disambiguation methods, the results are robust. This gives us additional confidence in the findings.

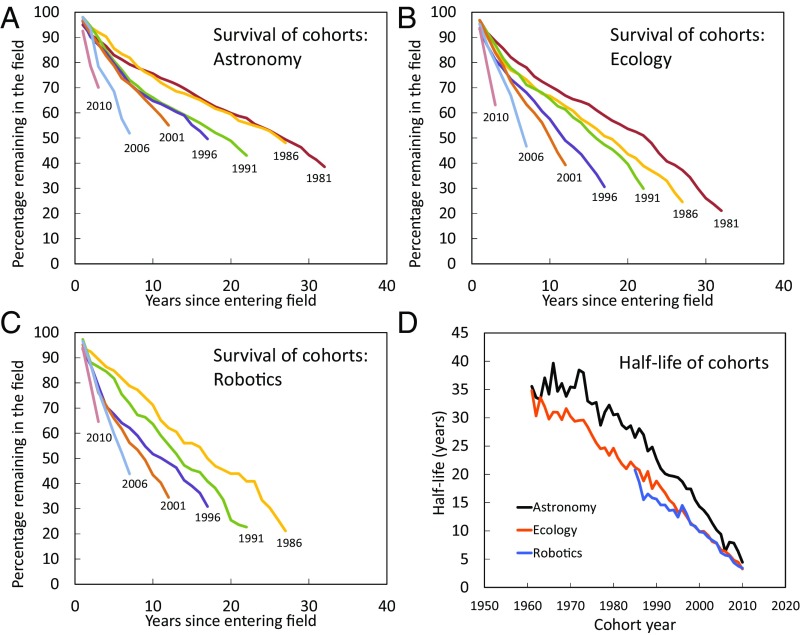
For authors who persist after the initial publication, we employ survival analysis to study their scientific career longevity. In Fig. 4, we show the survival curves of select cohorts spanning the period of the most recent four decades. Survival curves are calculated as the fraction of a cohort remaining after x years. While the survival curves of contemporaneous cohorts in different fields have different slopes, we see that the curves undergo a similar evolution in each field: from relatively long survival times in the 1980s to very rapid attrition of the scientific workforce in most recent times. We observe that until the 1980s (1990s for astronomy), more than half of each cohort had “full” (20+ y) careers. However, in recent decades, this is no longer the case. The results correspond to a continuous decline in the expected career length.

Fig. 4.

Survival functions of select cohorts in three fields (A–C) and the half-life (time needed for half of the cohort to abandon the field) of all cohorts from all three fields (D). The decline in survivability over the past half-century has been remarkable.

To expand the survival analysis to every cohort and to cover the full period from 1961, we calculate, for each cohort, its “half-life,” the time it takes to lose 50% of the cohort. Half-lives are determined from a linear fit to the survival function, regardless of whether the cohort has yet reached 50%. Half-lives for the three fields as a function of cohort year are shown in Fig. 4D. In astronomy, the half-life has dropped from about 37 y in 1960s to just 5 y in 2007. In ecology and robotics, the half-lives are even shorter and have also been decreasing at similar rates. When we analyze lead authors and supporting authors separately, we find that in ecology and robotics, their half-lives are similar, whereas in astronomy, the half-lives of supporting authors are shorter than those of the lead authors by about 5 y. Most recently (2010 cohort) half-lives are 9 and 4 y, respectively.

Career Progression Model.

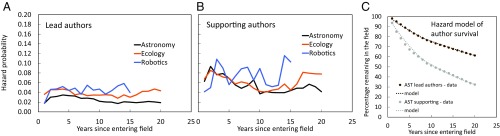
To pave the way for a more fundamental understanding of the processes that lead to the attrition of the workforce, we describe the career trajectory of an individual researcher using a simplified version of the model shown in Fig. 1. In the simplified version, we focus only on nontransient authors. Further, we neglect the difference among types of dropouts. During a career, a researcher can be in one of the following four states: B, the beginning of a career (defined with the first paper); S, achievement of the supporting author role; L, achievement of the lead author role; and X, cessation of the career. An author can initially be in the S state and transition into the L state. The S → L transition is considered irreversible (i.e., L → S is not allowed in the model). Authors continue in their states until reaching state X. We train the model using the data at our disposal. We find that the S → L transformation takes place in the first 5 y of a career: Authors who become leads achieve this status quickly. For the survival model, we are interested in the likelihood of observing the transition S → X or L → X (i.e., the hazard probability). We show the hazard probability in Fig. 5 separately for lead and supporting authors. For lead authors, the hazard probability is relatively constant, at around 0.03. For supporting authors, the exit probability is higher and shows a two-mode behavior: a decrease in the first 8 y and reaching a more stable value subsequently. We model the hazard function as a piece-wise linear + constant function:

$$h=a\left(t-t_{\text{break}}\right)+b\hspace{0.17em}\text{for}\hspace{0.17em}t\le t_{\text{break}},\hspace{0.17em}\text{and}\hspace{0.17em}h=b=\text{const}.\hspace{0.17em}\text{for}\hspace{0.17em}t>t_{\text{break}},$$

where a and b are constants and t_break = 8 is the time where the hazard function changes behavior. For astronomy, the model is tested against the data (Fig. 5C). The survival curves are now based on all cohorts, so they represent time-averaged survival for lead and supporting authors. The model reproduces the salient features of the empirical curve. Remarkably, the analysis shows that the hazard is relatively constant throughout the career (i.e., that there are no punctuated bottlenecks at which a large fraction of a cohort would leave the field).

Fig. 5.

Hazard model. Hazard probabilities for lead authors (A) and supporting authors (B). (C) Comparison of the linear + constant hazard model (dotted lines) with the empirical survival functions in the field of astronomy (AST).

Early Indicators of Scientific Survivability.

Given the increasing uncertainty of achieving a full career in science, one wonders whether there are any characteristics of scientists early in their careers that could indicate their survival status (38). We define “early” as the first 5 y of a researcher’s presence in the field (what we might call his or her “apprenticeship” years). Given our focus on the roles that scientists play in the production of knowledge, we focus on the variables that are directly related to this process: productivity, impact, and collaboration. These variables have been identified in prior work as correlated with career trajectories. We do not focus on some other variables that have been identified as important for career longevity and success, such as gender and the prestige of an institution a scientist is affiliated with, which are more pertinent in the context of studies that focus on career aspects that involve institutional and job roles (hiring, tenure, and promotion). While our models do not explicitly control for gender, two recent studies analyzing career longevity of academic faculty found no differences in faculty attrition by gender (except in the field of mathematics) since 1990 (36, 37).

In this analysis, we look at the total productivity in the first 5 y of a career (in any authorship role) and examine two types of impact: average impact of early work (the number of citations per paper received in the first 5 y) and the peak impact (the maximum number of citations received in a 5-y window to a single, early-career publication). Finally, for collaboration, we focus on the number of direct collaborators in the first 5 y of the career. Direct collaborators are defined as coauthors on a paper led by the author in question, as well as all of the unique lead authors of papers on which the author in question is a coauthor. If neither author is a lead author on some publication, such authors do not constitute direct collaboration.

To aggregate the data from cohorts that span a long time period, one needs to take into account that all three variables have significantly increased over time. For example, a researcher from the 1960 cohort who had 10 citations per paper may have been the most impactful in that cohort (∼100 percentile), whereas the same number of citations for a cohort from 2000 may place the researcher in middle of the cohort (∼50 percentile). Therefore, we establish normalized measures by determining the percentiles for each variable and for each author in a given cohort.

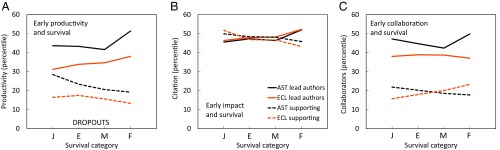
Fig. 6 shows mean productivity, citation, and collaboration levels for authors of different survival categories: junior dropouts (J; leaving 6–10 y after the first publication); early-career dropouts (E; 11–15 y); midcareer dropouts (M; 16–20 y); and, finally, the scientists who achieved full careers (F; >20 y). The values for robotics, which contains fewer cohorts and a smaller sample size, is noisier, and we omit it for clarity. The trends are shown separately for lead and supporting authors. The trends are fairly consistent between astronomy and ecology (with the exception of collaboration). Furthermore, we find that the trends involving average number of citations per paper and maximum number of citations are very similar, and we show only the ones involving average number of citations. Fig. 6 reveals that lead and supporting authors follow different trends. Overall, lead authors, regardless of survival category, have significantly higher production and collaboration levels than supporting authors, whereas their impact levels are similar. Supporting authors, while working on fewer papers and with fewer direct collaborators, nevertheless contribute to projects of similar impact. For lead authors, there is a slight positive trend between the early level of all three metrics and eventual survival (except for ecology and collaboration, where there is no significant trend). In particular, based on the means comparisons, lead researchers who go on to full careers (F) tend to have, on average, higher levels of productivity, citation, and (for astronomy) collaboration.

Fig. 6.

Early predictors of survivability in astronomy (AST) and ecology (ECL). Normalized productivity (A), impact (B), and collaboration (C) metrics based on the number of publications from the first 5 y of an author’s career are shown for lead (full lines) and supporting (dashed lines) authors in two disciplines for authors of different survival status: junior dropouts (J; leaving after 6–10 y after the first publication), early-career dropouts (E; 11–15 y), midcareer dropouts (M; 16–20 y), and, finally, the scientists who achieved full careers (F; >20 y).

The four-state career model, which provides an estimate of the career termination hazard rate by career state, not only supports the empirical survival functions well but shows that the hazard rate is relatively constant throughout a career, thus also supporting the model developed by Petersen et al. (34).

The above plots focused on individual variables. To quantify the effect of the variables on survival taking into account internal correlations, we use the Cox proportional hazard survival model. For this analysis, we use career lengths in annual increments (rather than grouping into only four categories) and the Efron method to correct for ties. Although many of the cases include careers of greater than 20 y, we recode career length as maximizing at 20 y (hence, all careers greater than 20 y, corresponding to full-career survival status, are treated as right-truncated). In addition, because we are testing the effects of the first 5 y of performance on subsequent exit, all our cases in this analysis have career lengths of at least 6 y. We are then testing, among the set of researchers who accumulate 5 y of background experience, how career lengths differ by publications, citations, and number of collaborators during their first 5 y (net of the effects of the other variables). We use the untransformed publications and citations data, as we will be focusing on comparisons within cohorts.

Given the very different survival curves for the lead and supporting authors (Fig. 5), we estimate the effects separately for each group. Tables 1 and 2 give the models. Column 1 in Tables 1 and 2 shows the effects of background characteristics (publications, citations, and number of collaborators) on hazards of exit (with values greater than 1 increasing the rate of exit and values less than 1 decreasing the rate of exit). Table 1 shows the results for lead authors, and Table 2 shows the results for supporting authors. Column 2 repeats this analysis using the maximum number of citations among the researchers for the first 5 y of publications. We see that when we control for the net effects of the other indicators across the 50 y (1960–2010) for lead authors, publications significantly reduce the hazard of exit, while there is little effect of citations (either measure) or number of collaborators. For supporting researchers, publications also have a negative effect on exit, although the effect is weaker than for lead authors. Citations (either measure) also have an effect, although the effect is positive (increasing exit). The number of collaborators has no effect.

Table 1.

Cox proportional hazard regressions, for lead authors, by cohort

Lead authors	(1)	(2)	(3)	(4)	(5)	(6)	(7)
	All	All	1960s	1970s	1980s	1990s	2000s
No. of publications	0.891*** (0.004)	0.891*** (0.004)	0.945* (0.021)	0.950*** (0.013)	0.925*** (0.012)	0.886*** (0.008)	0.857*** (0.009)
Average citations per paper	0.999 (0.001)		0.987** (0.004)	0.990*** (0.003)	0.994* (0.002)	0.998 (0.001)	1.000 (0.001)
Maximum citations on a paper		1.000 (0.000)
No. of collaborators	1.001 (0.003)	1.001 (0.003)	1.042 (0.032)	0.975 (0.016)	0.963** (0.012)	0.996 (0.005)	0.997 (0.005)
Cases	34,037	34,037	1,862	4,764	6,195	9,511	11,705
Exits	9,034	9,034	617	1,227	1,843	3,531	1,816
LR χ2	1,111.49	1,110.52	22.14	82.20	160.91	557.17	508.79
P > χ2	0.00	0.00	0.00	0.00	0.00	0.00	0.00

Publication productivity, citations, and collaborators pertain to the first 5 y of an author’s career. Standard errors shown in parentheses. LR, likelihood ratio. ***P < 0.001; **P < 0.01; *P < 0.05.

Table 2.

Cox proportional hazard regressions, for supporting authors, by cohort

Supporting authors	(1)	(2)	(3)	(4)	(5)	(6)	(7)
	All	All	1960s	1970s	1980s	1990s	2000s
No. of publications	0.966*** (0.008)	0.966*** (0.008)	0.972 (0.099)	1.056 (0.066)	1.042 (0.046)	1.017 (0.015)	0.938*** (0.012)
Average citations per paper	1.001** (0.000)		1.003 (0.007)	0.990* (0.005)	1.005* (0.002)	1.001* (0.000)	1.000 (0.000)
Maximum citation on a paper		1.000* (0.000)
No. of collaborators	1.006 (0.015)	1.003 (0.016)	1.223 (0.244)	1.038 (0.093)	0.964 (0.061)	0.942* (0.023)	0.994 (0.024)
Cases	10,677	10,677	195	761	1,540	3,136	5,045
Exits	4,290	4,290	91	308	767	1,865	1,259
LR χ2	59.16	55.76	1.83	7.70	5.77	10.95	103.24
P > χ2	0.00	0.00	0.61	0.05	0.12	0.01	0.00

Publication productivity, citations, and collaborators pertain to the first 5 y of an author’s career. Standard errors shown in parentheses. LR, likelihood ratio. ***P < 0.001; **P < 0.01; *P < 0.05.

A test of the proportional hazard assumption that the effects of the predictors are constant over time rejects the null hypothesis for publications (and is close to significant for citations). Furthermore, the data above suggest that the career conditions are changing over time and that publications, citations, and collaborations rates have also been changing over time. Hence, we estimate the effects across cohorts separately (Tables 1 and 2, columns 3–7). For lead authors, we see that publications have consistently been a significant predictor of career longevity. We also see that citations reduced the hazard of exit in the early cohorts; however, more recently, the model is dominated by publications, with citations having little independent effect. In contrast, for supporting authors, publications have very weak effects until the most recent cohort. Table 3 shows that these effects are largely consistent across fields, although we find that the effect of publications is significant for supporting researchers in astronomy.

Table 3.

Cox proportional hazard regressions, for lead and supporting authors, by field

Lead and supporting authors	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
	All (lead authors)	AST (lead authors)	ECL (lead authors)	ROB (lead authors)	All (supporting authors)	AST (supporting authors)	ECL (supporting authors)	ROB (supporting authors)
No. of publications	0.891*** (0.004)	0.921*** (0.005)	0.867*** (0.012)	0.924*** (0.024)	0.966*** (0.008)	0.969*** (0.082)	1.012 (0.052)	1.105 (0.099)
Average citations per publication	0.999 (0.001)	1.001 (0.001)	0.999 (0.001)	0.996 (0.003)	1.001** (0.000)	1.001** (0.000)	1.009*** (0.001)	0.992 (0.005)
No. of collaborators	1.001 (0.003)	1.001 (0.003)	1.018 (0.009)	0.979 (0.018)	1.006 (0.015)	1.019 (0.016)	0.937 (0.066)	0.822 (0.102)
Cases	34,037	22,178	9,499	2,360	10,677	6,791	2,988	898
Exits	9,034	4,613	3,488	933	4,290	2,476	1,409	405
LR χ2	1,111.49	417.21	129.20	27.42	59.16	39.73	26.73	6.33
P > χ2	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.09

Publication productivity, citations, and collaborators pertain to the first 5 y of an author’s career. Standard errors shown in parentheses. AST, astronomy; ECL, ecology; LR, likelihood ratio; ROB, robotics. ***P < 0.001; **P < 0.01; *P < 0.05.

In Tables 1 and 2, we report the hazard ratios from a multivariate Cox proportional hazard model. We are estimating the relative hazard to exiting, truncating at 20 y (so we are estimating the relative hazard of leaving academic publishing before 20 y). The table is reporting the change in the hazard ratio for exiting from a one-unit change in each variable, controlling for the effects of all of the other variables. These hazard ratios can be interpreted by estimating how far they are from 1.0. For example, for lead authors across all years, publications have a coefficient of 0.891 (Tables 1 and 2, column 1). This means that one publication reduces the hazard of exit by about 11% (1.000–0.891 = 0.109). In terms of the probability of achieving a full career, it grows gradually from 50% for authors with one early publication to 85% for authors with 20 publications. In contrast, one citation reduces the hazard very little (0.1%). Therefore, for lead investigators, each publication has substantially more impact on survival than does each citation (about 100-fold greater). In contrast, for supporting authors, one publication reduces the hazard of exit by about 3% (1.000–0.966), while citations again have very little effect. However, looking across the cohorts, we see this effect for supporting authors is largely limited to the most recent cohort (Tables 1 and 2, column 7). We can also see that for the full span of cohorts (Tables 1 and 2, column 1), the effect of publications for lead authors is much greater than that for supporting authors (11% vs. 3%), and that when we compare across cohorts (Tables 1 and 2, columns 3–7), the effect of publications for reducing exit is stronger (the hazard ratio is lower) for lead authors than for supporting authors.

Discussion

Recent work on the organization of science has focused on the internal structures of research teams and has argued that one likely outcome of this shift in the nature of scientific work has been the growth of supporting scientists, whose careers depend on being members of such teams (6, 13). Less obviously, there has also been a concomitant increase in high-stakes evaluation and competition for funding, increasing the emphasis on productivity (44–47). One solution to this new emphasis on productivity is increasing the division of labor (48, 49). The growth of scientific team sizes is being accompanied by a transition in the organization of scientific work from craft to bureaucratic industrial principles, with increased division of labor and standardization of tasks (13, 50, 51). The result is a growth of scientists whose function is to support the projects that others are leading. Our results confirm this scenario, showing that an increasing fraction of entering authors never transition from a supporting author to lead author role. We also show that such a trend is not an inevitable outcome of the increasing sizes of teams, per se, but arises due to the different roles that some authors now have in large teams compared with the roles that members of smaller teams have (team members vs. collaborators). In some fields, such as ecology and robotics, lead and supporting authors have similar half-lives, while in others, such as astronomy, the half-lives of supporting authors is significantly shorter.

Of course, there are well-known productivity advantages from organizing teams with a division of labor, and with having some team members specializing in supporting roles (48). Hence, it is perhaps not surprising that science is shifting to larger teams, with more specialization, and that, increasingly, some scientists are specializing in supporting roles. Note that we are not assuming status or skill distinctions in our classification of lead and supporting authors (50). We are arguing that such supporting scientists are critical to the production of contemporary science (6). However, it is also the case that institutions, such as universities and funding agencies, build around these traditional status distinctions, for example, between postdoctoral scientists and tenure track professors (6). However, our survival analyses suggest that the criteria predicting longevity for supporting scientists are quite distinct from those for lead researchers and it may not be appropriate to impose similar criteria on both groups when making decisions about who to hire or whose contract to renew. We argue there is a need to reform career structures in universities to account for the changing nature of the population composition and reproduction cycles in team science, with social insect colonies rather than parent-child reproduction as a more appropriate model.

While we cannot address this with our current data, we point to a tension between the research production and teaching functions that academic laboratories provide (5, 12, 44, 50, 52). These two trends are bringing fundamental changes to scientific careers, with decreasing opportunities for lead researcher positions and increasing production of, and demand for, a scientific workforce to fill positions as permanent supporting scientists. Together, these trends suggest downward pressure on career longevity (as more people exit the academic science labor force) and the growth of dependent supporting scientist positions to support the relatively shrinking share of lead researchers. However, one concern is that such supporting scientist positions do not fit well with the employment system in most universities, which are structured around a graduate apprenticeship, a short period of postdoctoral training, and then movement into a tenure track (and eventually tenured) professor position (5). Instead, these support workers may be relegated to a series of short-term postdoctoral contracts or other forms of contingent academic work. While the traditional model implies an up-or-out academic pipeline (with significant shares of the research workforce dropping out of research-active academic positions at each stage), the growth of permanent supporting scientists may suggest an alternative career path that, while perhaps with shorter survival than the traditional lead researcher path, may be a growing share of the academic labor force. Furthermore, such careers may be premised on a different set of criteria than is typically predictive of the career survival of lead researchers.

Our findings show that the shift in the mode of knowledge production from solo authors and small core teams (2) has coincided with a differentiation in the scientific workforce in terms of their roles. The increased need for both the specialization and possession of specialized technical knowledge to manipulate increasingly complex instrumentation and data has created an essential group of supporting contributors to knowledge. Unfortunately, the existing job roles and educational structures may not be responding to these changes. Our results suggest that, while essential, these supporting researchers are suffering from greater career instability and worse long-term career prospects in some fields.