Abstract
Long-range Lennard-Jones (LJ) interactions have a significant impact on the structural and thermodynamic properties of nonpolar systems. While several methods have been introduced for the treatment of long-range LJ interactions in molecular dynamics (MD) simulations, increased accuracy and extended applicability is required for anisotropic systems such as lipid bilayers. The recently refined Lennard-Jones particle-mesh Ewald (LJ-PME) method extends the particle-mesh Ewald (PME) method to long-range LJ interactions, and is suitable for use with anisotropic systems. Implementation of LJ-PME with the CHARMM36 (C36) additive and CHARMM Drude polarizable force fields improves agreement with experiment for density, isothermal compressibility, surface tension, viscosity, translational diffusion, and 13C T1 relaxation times of pure alkanes. Trends in the temperature dependence of the density and isothermal compressibility of hexadecane are also improved. While the C36 additive force field with LJ-PME remains a useful model for liquid alkanes, the Drude polarizable force field with LJ-PME is more accurate for nearly all quantities considered. LJ-PME is also preferable to the isotopic long-range correction for hexadecane because the molecular order extends to nearly 20 Å, well beyond the usual 10–12 Å cutoffs used in most simulations.
Keywords: Lennard-Jones, particle-mesh Ewald, CHARMM, Drude, polarizable force field, hexadecane, temperature dependence
Graphical Abstract
1. INTRODUCTION
The CHARMM36 (C36)1 additive force field (FF) for lipids has been widely used for molecular dynamics (MD) simulations of pure and complex lipid bilayers since its publication in 2010. It has been extended from the original set of six lipids (five phosphatidylcholines and one phosphatidylethanolamine) to sphingolipids,2 polyunsaturated lipids,3 glycolipids,4 and lipopolysaccharides.5 While the initial validation of the FF was primarily based on bilayer surface areas and densities (from X-ray and neutron diffraction data), and chain order and dynamics (from deuterium and 13C NMR data), subsequent comparisons with experiment for head group order parameters,6, 7 bending constants, and spontaneous curvatures8, 9 have been very positive. The FF has also been tested with lipid mixtures containing cholesterol with glycerophospholipids and/or sphingolipids, and agrees with X-ray form factors and NMR order parameters.10–13 This has allowed for accurate interpretations of liquid ordered/disordered phases of lipid mixtures14 and lipid composition effects on hydrogen bonding and lipid clustering.12, 13 Although simulations with the C36 lipid FF have been successful, the FF does have inherent flaws. It was appreciated at the time of publication that the surface tensions for bilayers and monolayers are inconsistent with experiment, and that the dipole potential is too large.1 More recently, after taking periodic boundary conditions into account,15 it has been demonstrated that diffusion constants are overestimated by a factor of 3 for at least two lipids.16
The C36 lipid FF (and other additive lipid FFs17, 18) has two attested shortcomings: it was parameterized without accounting for long-range Lennard-Jones (LJ) interactions for most parameters,19 and it is not polarizable. Polarizability is known to affect dipole potentials20 and dielectric constants .21 For example, of decane in CHARMM27r22 (C27r; the precursor to C36) is 1.02, approximately half the experimental value of 1.97.21 This underestimate of increases the interaction of charges on opposite sides of the bilayer. It is not unreasonable to speculate that the balance of forces leading to good agreement with experimental bilayer surface areas for C36 is partly due to cancellation of errors. The natural solution here is to use a polarizable FF.
The CHARMM Drude FF accounts for atomic polarizability by implementing the classical Drude oscillator model.23 The value of for decane is 2.06, in near-perfect agreement with experiment. Because free energy of solvation scales with , improvement of this quantity should give better energetics of transfer between polar and nonpolar media. However, like C36, most of the Drude lipid FF was originally parameterized without inclusion of long-range LJ interactions.1, 20 The lack of long-range LJ interactions is clearly related to the difficulties of reproducing monolayer surface tensions, given the importance of these terms for alkane/air interfaces.24
This paper sets the groundwork for a reparametrization of the C36 and Drude lipid FFs with explicit inclusion of long-range LJ interactions. Following the strategy used for the development of C36, alkanes, the principal component of saturated lipid chains, are considered first.22 The main focus is on including the long-range LJ terms in a computationally efficient manner that is applicable anisotropic systems. This has proven to be difficult because most methods for including long-range LJ terms are only applicable to isotropic systems.25, 26 Fortunately, recent work has refined the particle-mesh Ewald (PME) method for Lennard-Jones interactions.27 Lennard-Jones PME (LJ-PME) can be used with bilayers, monolayers, and other anisotropic systems in both constant pressure and constant volume ensembles. The implementation of LJ-PME utilized here involves the calculation of LJ interaction coefficients using geometric combining rules. It can be used in tandem with electrostatic PME, lowering the direct-space cutoff necessary for accurate calculations and computational efficiency. This paper introduces the implementation of LJ-PME in CHARMM, and explores its effects on equilibrium and transport properties of alkanes in the condensed phase.
By way of outline, Section 2 provides simulation specifications and describes the implementation of LJ-PME in CHARMM. Section 3 presents simulation results. Section 4 discusses the effects of LJ-PME, evaluates trends in the temperature dependence of thermodynamic properties, and summarizes the study.
2. METHODS
2.1. Common Simulation Specifications and Torsional Parameters.
To investigate the effects of LJ-PME, simulations were run using four distinct force fields: C36 without a correction for long-range LJ interactions, C36 with LJ-PME (denoted C36/LJ-PME), Drude without a correction, and Drude with LJ-PME (Drude/LJ-PME).
All simulations were performed in CHARMM.28 Initial coordinates of systems containing 256 molecules of pure normal forms of hexadecane (C16H34), pentadecane (C15H32), and heptane (C7H16) were built using packmol.29 Resulting mean cubic box sizes of between 50 and 51 Å for hexadecane (the longest chain tested) were sufficiently larger than the average radius of gyration (5.07 ± 0.02 Å) and root-mean-square end-to-end distance (14.7 ± 0.1 Å) to avoid finite-size effects. The Nosé-Hoover thermostat30 was used to maintain system temperature, and a modified Andersen-Hoover barostat to maintain constant pressure.31, 32 For the C36 simulations, a thermostat coupling constant of 2000 kcal/mole-ps2 was used for all simulations, and a piston mass of 1200 amu for NPT simulations. Drude simulations specified the relaxation time of the thermostat to be 0.1 ps, applied to real atoms, and the relaxation time of the barostat to be 0.1 ps in NPT simulations. All simulations were performed using periodic boundary conditions and SHAKE algorithm to constrain covalent bonds involving hydrogens.33
Long-range electrostatic interactions were evaluated using PME34 with when LJ-PME was not used and with use of LJ-PME. Sec. 2.6 provides the details on the real-space cutoff scheme for the LJ portion of the FF. The standard errors (se) were estimated as the standard deviation (σB) in block averages divided by the square root of the number of blocks ():
| (1) |
Quantities calculated from simulations were: density , isothermal compressibility , viscosity , surface tension , translational diffusion constant , Nuclear Magnetic Resonance (NMR) C13 spin-lattice relaxation time (T1), coefficient of thermal expansion , and radial distribution function . Simulations were performed using each FF for each set of simulation specifications in Table 1 using a 1-fs timestep. A separate set of simulations were used to examine the dependence of and on (Sec. 3.2). In these simulations, 64 molecules of C16H34 were simulated at 298.15 K for 10 ns using a 2-fs timestep in the NPT ensemble to calculate and in the NVT ensemble to calculate .
Table 1.
Simulations. Species, temperatures (T), number and length of runs (), ensembles used, and quantities evaluated. For each set of specifications, simulations of 256 molecules were performed using C36 and Drude, with and without LJ-PME.
| Species | T (K) | (ns) | Ensemble | Use |
|---|---|---|---|---|
| C16H34 | 303.15, 310.15, 323.15, 393.15 | 1 × 30 | NPT | , ,, |
| C16H34 | 303.15, 310.15, 323.15; 323.15 |
3 × 100 (C36) 2 × 100 (Drude) |
NVT |
; |
| C16H34 | 303.15, 310.15, 323.15 | 1 × 50 | NVT | |
| C15H32 | 312.15 | 2 × 30 | NPT | |
| C7H16 | 312.15 | 2 × 30 | NPT |
For simulations used to calculate , , and , initial coordinates were obtained from the equilibrated NPT simulations used to determine . A coordinate set representing the average of each simulation was used to start a simulation in the NVT ensemble. Systems for the surface tension simulations consisted of an alkane slab surrounded by vacuum layers, as described previously,24 with the x and y dimensions matching the equilibrated boxsize from the NPT simulations used to calculate and the z dimension (normal to the surface) elongated. For example, for hexadecane at 303.15 K in the Drude FF, the dimensions of the box were 50.1197 Å × 50.1197 Å × 100 Å.
This paper uses standard alkane parameters in C361 and Drude.21 There have been several adjustments to the alkane torsional parameters since publication of C27r.1 Table 2 lists the parameters used here to avoid confusion. The form of the CHARMM torsion potential, where is the dihedral angle, is
| (2) |
Table 2.
Torsional Parameters for Alkanes
| Term | Drude | C36 Lipid FF1 | ||||
|---|---|---|---|---|---|---|
| N | Δ | N | δ | |||
| CH3-CH2-CH2-CH3 | 0.150 | 1 | 0 | 0.060 | 2 | 0 |
| 0.170 | 2 | 0 | 0.035 | 5 | 0 | |
| 0.114 | 3 | 0 | ||||
| 0.094 | 4 | 0 | ||||
| 0.070 | 5 | 0 | ||||
| CH3-CH2-CH2-CH2 | 0.093 | 1 | 0 | 0.162 | 2 | 0 |
| 0.143 | 2 | 0 | 0.047 | 3 | 180 | |
| 0.055 | 4 | 0 | 0.105 | 4 | 0 | |
| 0.102 | 5 | 0 | 0.177 | 5 | 0 | |
| CH2-CH2-CH2-CH2 | 0.073 | 1 | 0 | 0.101 | 2 | 0 |
| 0.043 | 2 | 0 | 0.142 | 3 | 180 | |
| 0.119 | 3 | 180 | 0.074 | 4 | 0 | |
| 0.098 | 4 | 0 | 0.097 | 5 | 0 | |
| 0.046 | 5 | 0 | ||||
2.2. Density and Isothermal Compressibility.
Density was determined by averaging the volume of the simulation box after equilibration. Isothermal compressibility was evaluated from
| (3) |
where is Boltzmann’s constant, is the average volume, is the fluctuation in volume, and T is the temperature.25
2.3. Viscosity, Translational Diffusion Constant, and Surface Tension.
Shear viscosity was evaluated using the Green-Kubo formula:25
| (4) |
where are the off-diagonal elements of the pressure tensor, and V is the volume of the simulation box. The pressure tensor was assumed to be symmetric (). CHARMM28 was used to compute the correlation function of the three unique off-diagonal elements, average them, and sum the integral.
The surface tensions of the alkane-vacuum interfaces were evaluated from:
| (5) |
where Lz is the size of the simulation box normal to the interface,35 Pzz is the normal component of the internal pressure tensor, and Pxx and Pyy are the tangential components. A prefactor of 0.5 accounts for the fact that the systems contained two interfaces.
Translational diffusion constants were obtained from the Einstein relation , where r is the displacement of a molecule at time t. The Yeh and Hummer36 correction was used to account for periodic boundary conditions:
| (6) |
where is the diffusion constant measured from simulation, L is the box length, ξ = 2.837297, η is the viscosity of the fluid, and is the infinite system result.
2.4. NMR Spin-Lattice Relaxation Times.
T1 were calculated using the standard formula for dipolar relaxation from the reorientational correlation function of the CH vectors in the motional narrowing limit:37
| (7) |
where N is the number of protons bonded to the carbon, is the CH vector, and the constant preceding the integral contains an effective CH bond length of 1.117 Å.38
2.5. Analysis of Temperature Dependence.
The volumetric coefficient of thermal expansion describes the dependence of volume, and therefore also of density, on temperature at constant pressure:
| (8) |
The same trajectories used to determine were used to calculate at 313.15 K and to compare with the experimental value of molar volume () at that temperature. A linear dependence of on temperature was assumed.
To find the functional form of the temperature dependence of , chi-squared statistical values were calculated for regressions of the form , with values of 1/3, 1/2, 1, 2, 3, 4, and 5 for c. The statistic is given by:
| (9) |
where N is the number of data points in the sample, is the value of the ith sample, and is the value predicted by the distribution. Values of were minimized to determine c.
2.6. Implementation of LJ-PME in CHARMM.
The contributions of long-range dispersion to the energy and pressure that are neglected by cutoff methods were historically accounted for by various correction terms. A popular correction, the isotropic long-range correction (LRC),25 is derived by assuming that the radial distribution function is unity beyond . The isotropic LRC is usually satisfactory for bulk fluids of small molecules, but fails when anisotropy is significant, as is the case for lipid bilayers and other interfacial systems. The pressure-based LRC,26 where LJ interactions outside are approximated with the application of an additional pressure which is periodically calculated from the difference of the instantaneous pressures at the selected and a very long , is applicable to larger molecules, but not to interfaces. CHARMM also supports the IPS (Isotropic Periodic Sum) method39 to approximate long-range LJ interactions. This method defines a local region for each particle, and sums the remaining region (including images) as an integral of virtual images of the local region statistically distributed in an isotropic and periodic manner. The version denoted 3D-IPS is not applicable to interfacial systems. 2D-IPS and the more computationally efficient 3D-IPS/DFFT40 do accurately model interfaces.24, 41 The IPS methods have not been widely implemented because of assumptions of homogeneity.
The preceding methods are all available in CHARMM. Others42–44 have proposed a slab-based correction to specifically address inhomogeneity at interfaces. This method approximates long-range LJ forces with an additive force contribution in the direction perpendicular to the interface. The added force is a function of the density of an isotropic slice within the simulation box. Janeck43 shows accurate treatment of surface tensions for Lennard-Jones fluids with an adaptation of this slab-based method. It is possible to explicitly include long-range effects in slab-like systems using the two-dimensional Ewald formulation of Hautman and Klein.45 Although formally correct, this 2D Ewald method requires a factor of 20 more computational effort to evaluate than regular 3D Ewald methods. It has been shown46 that conventional 3D Ewald methods, including the LJ-PME approach, deliver equivalent properties to the 2D method when modified to include empty space between layers, without incurring the extra computational overhead.
As is well known, long-range electrostatic forces can be evaluated explicitly and with high computational efficiency, thereby eliminating the need to truncate interactions using a cutoff. The use of cutoffs leads to substantial artifacts for electrostatics,47 and the PME48 method is widely used for this reason. The PME approach for dispersion has its origins in the 1957 work of Nijboer and de Wette,49 who generalized the Coulomb operator partitioning to faster decaying interactions. Williams used this generalized partitioning in 1971 to develop an Ewald-like treatment of dispersion interactions,50 which was later expanded by Karasawa and Goddard to include energy derivatives.51 Though in 1995 Pedersen and coworkers demonstrated a modification of Ewald dispersion to use the highly efficient PME methodology,34 the use of a cutoff on the Lennard-Jones attractive (r−6) term has persisted. Recently, a number of workers52–55 have increased the computational efficiency of the PME method for r−6 potentials, and the method is being incorporated into popular simulation programs.27 The repulsive potential term decays much more quickly and is therefore neglected at long range by simply truncating the interaction past . Hence, the name of the method, “LJ-PME,” should not be understood to correct the entire LJ potential.
For the kernel, the Ewald partitioning of the summation over unit cells can be expressed as:
| (10) |
where we assume geometric mean combination rules:
| (11) |
and introduce the shorthand notation in addition to the screening function , which depends on the attenuation parameter (we avoid the often-used for this quantity to disambiguate it from the isothermal compressibility). The decomposition of the lattice sum yields two terms. The first is short-ranged and rapidly convergent in a standard pairwise summation, while the second long-range, nonsingular term converges rapidly in reciprocal space and can be treated using Fast Fourier Transforms (FFTs). The attenuation parameter determines the relative computational efforts in real and reciprocal space. For suitably chosen and FFT grids, the answer is independent of , which is chosen to minimize computational cost with the pairwise adjusted accordingly.
The multiplicatively separable form assumed above is important for the PME treatment of the long-range term, which proceeds by first discretizing the density due to all particles on a grid, transforming the density to a potential via FFTs, and then probing the potential grid at each atomic center to yield the energy and forces. However, the CHARMM FFs use the Lorentz-Berthelot (LB) combination rule, which defines off-diagonal hard sphere radii in a form incongruous with the multiplicatively separable form described above:
| (12) |
One potential remedy for this situation is to express the interaction coefficient using a binomial expansion:
| (13) |
This expansion transforms in Eq. 10 to a sum of seven terms, possessing the requisite separable form of which only four are unique by symmetry. The need for multiple FFTs is avoided using the strategy developed by Wennberg et al.27 Briefly, their approach proceeds by a subtle change to the partitioning introduced above:
| (14) |
Again, the first term on the righthand side is treated in real space and the second term in Fourier space. The net effect is that a multiplicatively separable form is used to determine the long-range correction in Fourier space. This approach is also compatible with pair-specific LJ parameters (NBFIX terms) that are often used in FFs, with in Eq. 14 replaced by the corresponding NBFIX parameters.
In real space, the exact functional form of the potential is used up to , and another term is present to partially account for spurious short-range multiplicatively separable terms introduced in reciprocal space. This scheme is no longer rigorously insensitive to the choice of , but the difference between the two sets of combination rules is small enough at long range that this is a very good approximation. A discontinuity in the potential energy is averted at by applying a shift to account for the difference between the treatments at short and long range:
| (15) |
In Eq. 15, the first term cancels the repulsive part of the LJ potential at , while the second term ensures a smooth transition from the real-space treatment to the multiplicatively separable regime. Although this correction guarantees a smooth potential, there may still be discontinuities in the forces. Differentiation of equation (15) yields
| (16) |
where Eq. 16 quantifies the force discontinuity due to the truncation of the repulsive term and the handoff between the two combination rules; the logarithm of the absolute value of this quantity is displayed in Fig. 1, for selected pairs of atom types, as a function of and As expected, the lowest discontinuity error occurs where is large, i.e., there are long-range terms present to account for the truncation of the attractive LJ term, and also where is large. Assuming a typical force on each atom to be ~10 kcal/mol/Å, the white contour lines in Fig. 1 represent an error in the contribution to the forces of about 1 part per million, which will be incurred every time a pairwise interaction crosses . To further quantify the consequences of the force discontinuities, NVE simulations were carried out on n-hexadecane and neat water, demonstrating that the energy drift is within 0.2 kcal/mol/ns, even with as low as 7 Å; the supporting information contains full details of these tests. Because the microcanonical ensemble is maintained so well, a correction for the force discontinuity is not included in the current CHARMM implementation; there is an option to use potential switching56 for ensuring continuous energies and gradients in free energy calculations.
Figure 1.
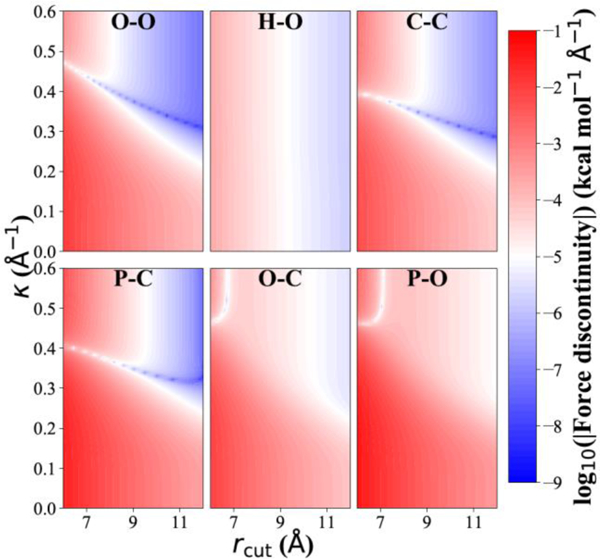
The logarithm of the magnitude of the force discontinuities present when only potential shifting is used to smooth the potential, as a function of and . Parameters for various atom types are taken from the C36 lipid FF.
Finally, the instantaneous virial stress tensor is required to generate constant pressure ensembles. The real-space contribution is exactly analogous to the standard outer-product form, involving forces and positions, that is used to evaluate the LJ virial. The reciprocal-space tensor is obtained by summation over reciprocal space lattice vectors , with norm ,
| (17) |
and including the term, in contrast to the Coulombic case.
3. RESULTS
3.1. Alkanes in C36 and Drude.
Results for , , , , and of hexadecane at biologically relevant temperatures are listed in Table 3. The final column of each table lists the deviation from experiment, averaged over the temperatures. Table 3 also includes results for , , and for systems simulated using the isotropic LRC with the Drude FF.
Table 3.
Hexadecane Simulation Averages and Standard Errors for Density (), Isothermal Compressibility (), Sheer Viscosity (), Surface Tension (), and Translational Diffusion at Various Biological Temperatures
| Temperature (K) | Average deviation from Exp. | ||||
|---|---|---|---|---|---|
| 303.15 | 310.15 | 323.15 | |||
| C36 | 0.7483 ± 0.0001 | 0.7416 ± 0.0001 | 0.7289 ± 0.0001 | −2.7 % | |
| C36, LJ-PME | 0.7654 ± 0.0003 | 0.7593 ± 0.0001 | 0.7481 ± 0.0001 | −0.40 % | |
| Drude | 0.7544 ± 0.0002 | 0.7483 ± 0.0003 | 0.7375 ± 0.0001 | −1.8 % | |
| Drude, LJ-PME | 0.7620 ± 0.0002 | 0.7564 ± 0.0001 | 0.7460 ± 0.0002 | −0.70 % | |
| Drude, LRC | 0.7649 ± 0.0002 | 0.7591 ± 0.0001 | 0.7490 ± 0.0002 | −0.40 % | |
| Exp.57 | 0.7665 | 0.7617* | 0.7528 | ||
| C36 | 12.48 ± 0.12 | 13.16 ± 0.11 | 14.40 ± 0.09 | 41 % | |
| C36, LJ-PME | 10.04 ± 0.16 | 10.48 ± 0.22 | 11.35 ± 0.20 | 13 % | |
| Drude | 9.99 ± 0.35 | 9.99 ± 0.31 | 11.94 ± 0.46 | 12 % | |
| Drude, LJ-PME | 8.78 ± 0.14 | 9.49 ± 0.15 | 10.22 ± 0.16 | 0.60 % | |
| Drude, LRC | 8.51 ± 0.17 | 9.11 ± 0.23 | 9.68 ± 0.25 | −3.7 % | |
| Exp.57 | 8.896 | 9.307* | 10.059 | ||
| C36 | 2.16 ± 0.06 | 1.89 ± 0.14 | 1.47 ± 0.03 | −22 % | |
| C36, LJ-PME | 2.55 ± 0.13 | 2.05 ± 0.12 | 1.81 ± 0.07 | −8.4 % | |
| Drude | 2.37 ± 0.08 | 2.22 ± 0.11 | 1.80 ± 0.13 | −8.4 % | |
| Drude, LJ-PME | 2.70 ± 0.20 | 2.52 ± 0.10 | 1.95 ± 0.20 | 2.6 % | |
| Drude, LRC | 3.07 ± 0.32 | 2.34 ± 0.30 | 2.08 ± 0.26 | 6.8 % | |
| Exp.57 | 2.766 | 2.388* | 1.866 | ||
| C36 | 18.03 ± 0.49 | 16.86 ± 0.68 | 16.74 ± 0.67 | −34.6 % | |
| C36, LJ-PME | 24.79 ± 0.80 | 22.77 ± 0.72 | 19.73 ± 0.60 | −18.6 % | |
| Drude | 21.97 ± 0.41 | 21.89 ± 0.33 | 20.58 ± 0.26 | −17.2 % | |
| Drude, LJ-PME | 27.74 ± 0.56 | 26.26 ± 0.57 | 25.06 ± 0.42 | 1.60 % | |
| Exp.57 | 26.7 | 26.1* | 25.0 | ||
| D [10−6 cm2/s] | C36 | 5.48 ± 0.03 | 6.41 ± 0.04 | 8.47 ± 0.08 | 34 % |
| C36, LJ-PME | 4.16 ± 0.04 | 4.95 ± 0.05 | 6.53 ± 0.08 | 3.0 % | |
| Drude | 4.81 ± 0.03 | 5.77 ± 0.07 | 7.45 ± 0.06 | 1.8 % | |
| Drude, LJ-PME | 4.30 ± 0.01 | 5.02 ± 0.05 | 6.63 ± 0.10 | 5.0 % | |
| Exp.58 | 6.32 | ||||
The effects of long-range Lennard-Jones interactions are statistically significant for all cases. LJ-PME increases by 2% for C36 and 1% for Drude. As consistent with an increase in density, decrease (20% for C36, 10% for Drude), increase (17% for C36, 12% Drude), and D decrease (23% for C36, 11% for Drude).
Results using the isotopic LRC for and are 0.3% higher and 4% lower that for LJ-PME, respectively. These are close, but not statistically equivalent. (Statistical errors in are large, so it is not possible to assign statistical significance to the differences.) Recall that the isotropic LRC assumes that for r >. As is evident from the for hexadecane plotted in Fig. 2, only becomes constant at approximately 18 Å, well beyond the standard = 12 Å.
Figure 2.
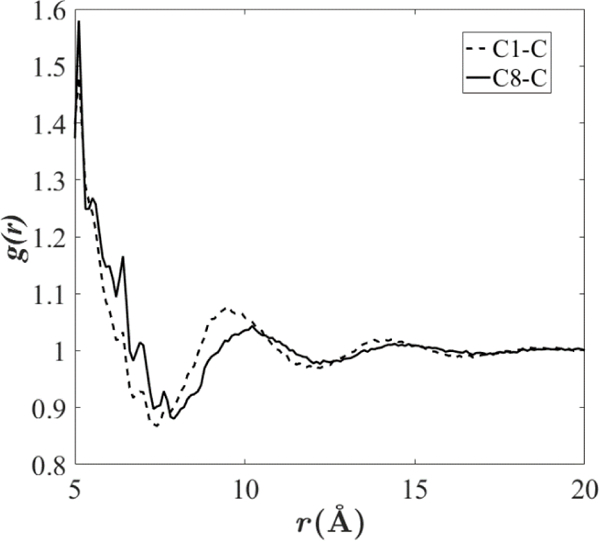
Radial distribution functions for hexadecane at 323.15 K using the Drude FF without long-range LJ interactions. “C1-C” is between C1 and all other carbons; “C8-C” is between C8 and all other carbons. The first two peaks arising from nearest and next-nearest neighbors are not shown
C36 without long-range LJ shows the largest differences from experiment for all quantities reported in Table 3. This is expected because the alkanes in C36 were originally parameterized with a pressure-based correction.22 Both polarizability and the use of LJ-PME improve agreement with experiment in all cases, and in nearly all cases, Drude/LJ-PME achieves results closest to experiment. The agreement with experimental surface tensions is also best for Drude/LJ-PME (an average error of 1.6%).
Fig. 3 plots T1 for heptane and pentadecane at 312.15 K. Agreement with experiment for carbons near the center of pentadecane is excellent for all but C36. The terminal carbon (C1) is not as well described as the others in the Drude FF, indicating that a slight adjustment of the C1 torsional parameters should be considered. Differences with experiment are uniformly larger for heptane (approximately 25% lower for Drude/LJ-PME, and 40–65% higher for the others). The reduction in T1, when long-range LJ terms are included, is consistent with the increase in . This is because rotational diffusion of the long molecular axis, commonly referred to as tumbling, makes a significant contribution to the reorientational correlation functions of alkanes,59 and the rotational correlation time τ (the integral of the correlation function) is proportional to viscosity. Hence, from Eq. 7, an increase in τ reduces T1. The effect of tumbling on hexadecane T1 is somewhat smaller than for heptane, because the contribution of isomerization is larger. Heptane T1 times are more influenced by rotational diffusion about the long axis (spinning) than those of hexadecane. Spinning of symmetric molecules is relatively insensitive to viscosity but is highly sensitive molecular shape and packing.60 The large difference between Drude and Drude/LJ-PME results suggests a modulation of the relaxation associated with spinning.
Figure 3.
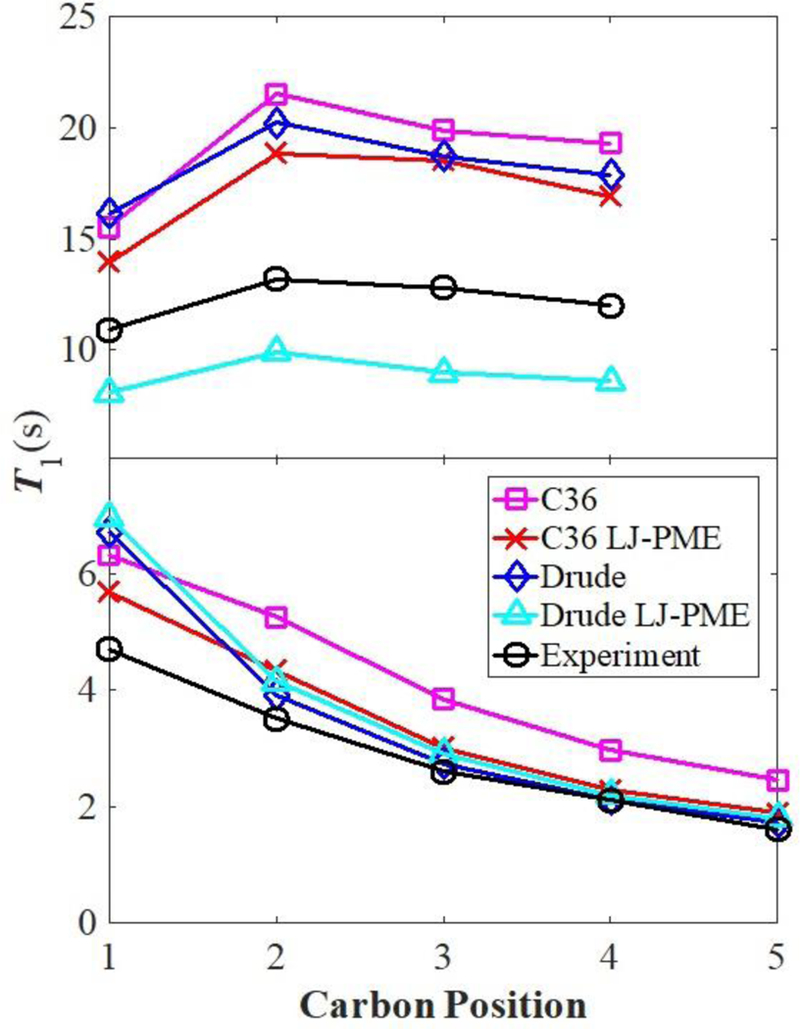
Comparison of NMR spin-lattice relaxation times from simulation and experiment for heptane (top) and pentadecane (bottom).
3.2. Dependence on for Non-Bonded Interactions.
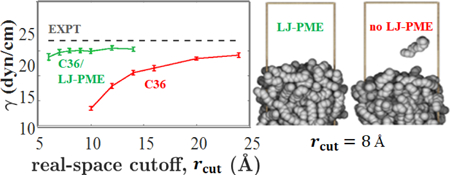
To investigate the dependence of and on , simulations of bulk hexadecane and the hexadecane/vacuum interface were carried out at 298.15 K using C36 and C36/LJ-PME for a range of values for . As Fig. 4 indicates, LJ-PME is relatively insensitive to , and a value as low as 9 Å may be used for systems of pure alkanes. Without LJ-PME, does not converge until approximately 24 Å, and is still increasing at this value of . The snapshots in Fig. 5 illustrate the effect of cutoff for C36. The system simulated with LJ-PME has a smooth interface consistent with a surface tension of 25 dyn/cm (left). The surface is borderline unstable for = 8 Å, and a molecule can be seen evaporating (right).
Figure 4.
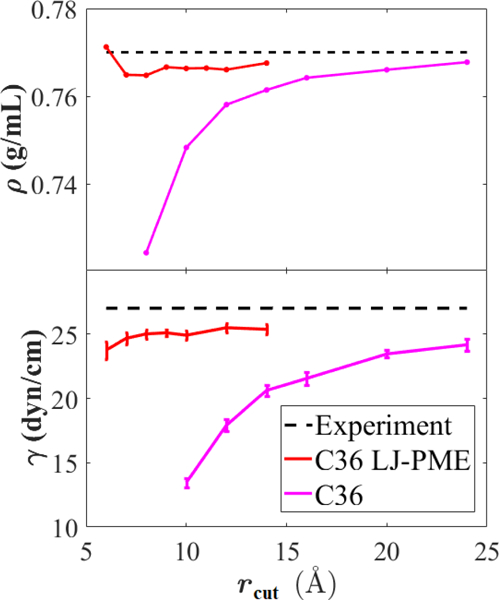
Density (top) and surface tension (bottom) of hexadecane vs. for C36 and C36 LJ-PME compared with experiment. Standard errors are comparable to symbol for density.
Figure 5.
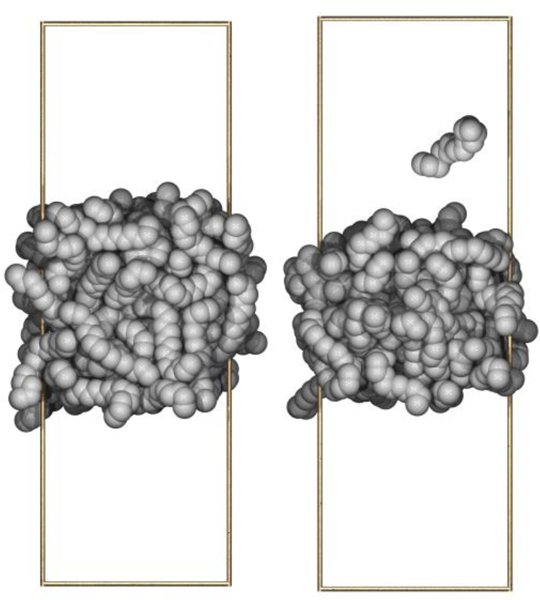
Hexadecane fluid/vacuum interface for = 8 Å for C36 with long-range Lennard-Jones interactions (left) and without (right). The boundaries of the unit cell are depicted with brass rods.
3.3. Temperature Dependence of Density and Isothermal Compressibility.
At 313.15 K, the volumetric coefficient of thermal expansion for hexadecane is 9.07 10−4 K-1.61 This value is compared with simulation by fitting at three or four temperatures using a linear regression (Fig. 6). While the trends are qualitatively correct, from simulation overestimate experiment by 20–40% (Table 4). This indicates that the error in , and therefore density, will increase if simulations are run at higher temperatures. Slopes of the lines of best fit for Drude and Drude/LJ-PME are nearer to the slope of the experimental line of best fit; however, over the range of temperatures shown, for C36/LJ-PME most closely match the experimental data.
Figure 6.
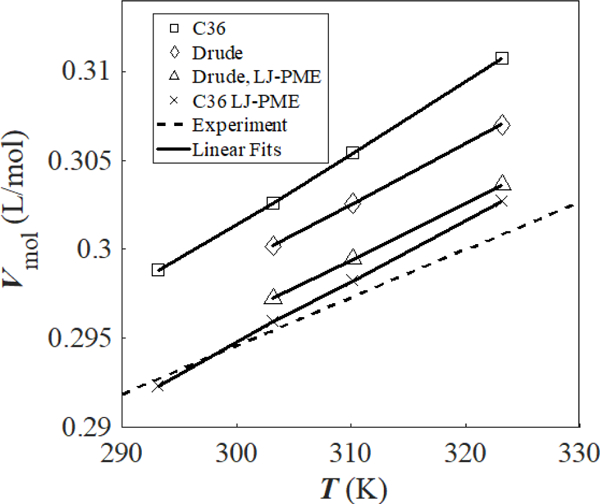
Temperature dependence of of hexadecane. Solid lines show the fit used to calculate values for in Table 4.
Table 4.
Thermal expansion coefficients calculated for each FF over the range of biological temperatures tested, found using a linear fit
| Force Field | (K−1) |
|---|---|
| C36 | 1.30 |
| C36 LJ-PME | 1.16 |
| Drude | 1.11 |
| Drude LJ-PME | 1.07 |
| Exp. | 0.907 |
Table 5 lists and at 393.15 K for an evaluation of the FFs at an elevated temperature. Deviations from experiment are generally 2–3 times larger than at biological temperatures (Table 3). The best agreement is obtained for Drude/LJ-PME.
Table 5.
Hexadecane Simulation Averages and Standard Errors for and at 393.15 K
| Temperature (K) | Avg. Error from Exp. | ||
|---|---|---|---|
| 393.15 | |||
| C36 | 0.6570 ± 0.0002 | −6.6 % | |
| C36, LJ-PME | 0.6775 ± 0.0002 | −3.7 % | |
| Drude | 0.6897 ± 0.0002 | −2.0 % | |
| Drude, LJ-PME | 0.6896 ± 0.0002 | −2.0 % | |
| Exp. | 0.7036 | ||
| C36 | 32.98 ± 0.80 | 103 % | |
| C36, LJ-PME | 20.44 ± 0.14 | 26 % | |
| Drude | 21.20 ± 0.23 | 30 % | |
| Drude, LJ-PME | 17.26 ± 0.23 | 6.0 % | |
| Exp. | 16.24 | ||
Experimental for hexadecane at temperatures from 298.15–433.15 K, calculated from measurements of the velocity of sound, can be fit with a polynomial regression.61 As evident from Fig. 7, provides a good fit to the data (Table 6 lists b for each fit), and Drude/LJ-PME again is the best model.
Figure 7.
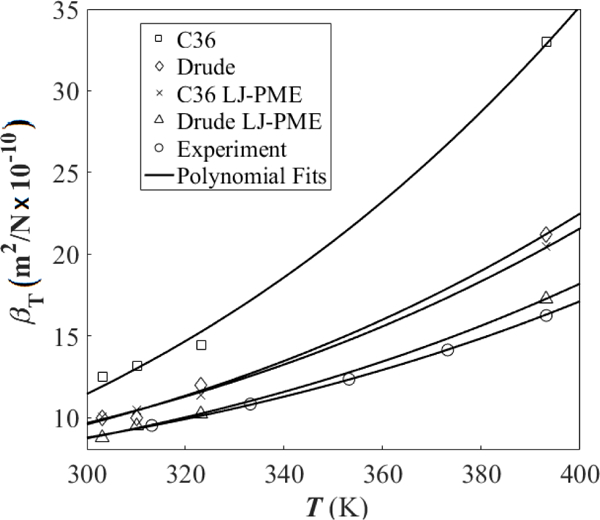
Temperature dependence of for hexadecane. Curves show fits to the simulation and experimental data with a regression of the form . The exponent of was chosen using analysis of the experimental data.
Table 6.
Parameter b describing temperature dependence of for hexadecane.
| Force Field | b () |
|---|---|
| C36 | 13.6 |
| C36 LJ-PME | 6.81 |
| Drude | 7.38 |
| Drude LJ-PME | 5.41 |
| Exp. | 4.77 |
4. DISCUSSION AND CONCLUSIONS
Long-range LJ dispersion interactions have a significant impact on numerous properties of alkanes. While they are especially important at the alkane-vacuum interface, they increase and thereby decrease and increase . This effect is less pronounced in systems of polar molecules (where long-range electrostatic interactions tend to dominate and are accounted for by PME). For example, increasing from 8 Å to 25 Å has a substantially smaller effect on the calculated surface tension of pure water than of pure hexadecane.24 Specifically, water surface tension at 323.15 K for the C27r FF is 41.5 ± 0.5 dyn/cm for Å and 51.3 ± 0.4 dyn/cm for Å; an increase of nearly 25 %. For hexadecane, and 22.7 ± 0.4 dyn/cm at 8 and 25 Å respectively; an increase of nearly 400 %. Nevertheless, increasing to include more long-range LJ interactions brings closer experiment in both cases.
The simplest way to include long-range LJ interactions is to use the isotropic correction.25 This correction assumes the system is isotropic in pressure, which precludes its use for anisotropic systems. A key assumption in the isotopic LRC is that the is 1 at distances larger than . The present study shows that fluids of larger molecules like hexadecane have significant structure beyond the usual 10–12 Å cutoffs (Fig. 2), indicating that the isotopic LRC is less generally applicable than previously assumed. The pressure-based LRC26 is also not applicable to anisotropic systems, while assumptions of homogeneity limit the appeal of the IPS methods.24, 39
The LJ-PME formalism solves a long-standing problem in the simulation field: the rigorous and computationally efficient treatment of long-range LJ interactions. Its recent reformulation permits the use of arbitrary LJ combination rules, making it ideally suited to macromolecular FFs. While the modified LJ-PME method suffers from small discontinuities in the forces at , microcanonical simulations of n-hexadecane and water boxes reveal that these force discontinuities have a negligible impact on simulations, even for as low as 7 Å. Our implementation defaults to potential shifting, with an option to use switching to remove force discontinuities. Properties evaluated for alkane systems are consistent for values of as low as 9 Å (Fig. 4), and adjustments for different styles of combining rules are straightforward (see Sec. 2.6).
The present study focuses on alkanes, a natural starting point for parametrization of lipid force fields. In Drude and C27r, which was later slightly modified to become C36, alkanes were originally parameterized using a pressure-based correction to account for long-range LJ interactions.21, 22 This correction was needed, among other reasons, to bring the densities of alkanes into satisfactory agreement with experiment. The C36 lipid FF did not include long-range LJ interactions (explicitly or with a correction) for reasons of consistency with other CHARMM FFs.
The results here (Table 3) indicate that use of the new LJ-PME approach to evaluate density and surface tension has an effect similar to earlier methods for estimating the long-range LJ interactions. That is, the densities of both the C36 and the Drude systems increased slightly at all temperatures tested, while the surface tensions increased more significantly, bringing all measurements of these quantities closer to experimental target values. In some cases, the isotropic LRC yielded results nearer to experiment than LJ-PME. For example, Drude densities with the isotropic LRC are nearer to experiment than with LJ-PME. This result is expected because the Drude FF was originally parameterized using a spatially isotropic, pressure-based correction.21 However, a distinction must be drawn between similarity with experimental results and accurate treatment of the long-range forces in simulation. Fig. 2 shows that use of the isotropic LRC for C16H34 is not valid with the standard value of because ≠ 1. Fig. 4 shows that increasing causes to converge to the value obtained using LJ-PME, indicating that LJ-PME treats the long-range dispersion forces accurately.
In a recent study, Fischer et al.62 evaluated the effect of LJ-PME on properties of 146 organic liquids as parametrized in three different force fields. While a quantitative comparison with this work is difficult (alkanes were not included, different programs where used, and LJ cutoff is lower), most of the trends are similar. In particular, surface tensions increased when LJ-PME was implemented. The increase was not uniform because the contributions of long-range electrostatics differed among the molecules. Many, but not all, of the surface tensions generated with LJ-PME overestimated experiment. This implies that the attractive term in the LJ interaction () is too large for these molecules, even though two of the three FFs were developed with an analytic correction for long-range LJ interactions. The effect of LJ-PME on bulk properties was typically smaller. These results are similar to those obtained here for alkanes, although the surface tension of hexadecane underestimates experiment by approximately 20% even with LJ-PME (Table 3). The present study shows that the effect of long-range LJ forces on surface tension is treated accurately with LJ-PME (see convergence in Fig. 4), indicating the fault lies in parameterization. Therefore, to ensure proper tuning of the coefficient, future parameterization efforts should include surface tension as a target and accurately sum LJ forces.
Like surface tension, isothermal compressibility () is significantly affected by long-range Lennard-Jones interactions. The Drude FF consistently over-estimates , indicting the systems are not sufficiently compact because the long-range attractive LJ interactions are absent. In contrast, use of the isotropic LRC results in consistent under-estimation. With LJ-PME, there is less error in the compressibility measurements and no clear trend of over- or under-estimation in the range of temperatures applicable to biological phenomena.
LJ-PME brings the dynamical properties viscosity and self-diffusion closer to experiment, as consistent with an increase in density. Without LJ-PME, both C36 and Drude underestimate viscosity and overestimate diffusion.
NMR spin lattice relaxation times (T1) for carbons of pentadecane are reasonably described for C36/LJ-PME and the Drude models (Fig. 3, bottom), and improvements are likely to be found by modifying the torsion angles. The relatively worse results found for heptane (Fig. 3, top) highlight the difficulties of accurately capturing the nuances of molecule shape on rotational diffusion. It would be of interest to simulate rotational relaxation of highly symmetric molecules such as benzene to refine force field to this level of detail. However, because the primary application of the CHARMM FFs is to biopolymers and membranes, pentadecane is the more important target.
While many MD simulations are run at temperatures near standard or body temperature, simulations at elevated temperatures also yield valuable information for biomolecular systems. Simulations of pure bilayers with higher-than-biological melting temperatures can be compared with experimental data to check for force field accuracy.63, 64 Furthermore, simulations of large systems, such as membrane-bound proteins, are routinely run at high temperatures to populate the energy landscape using the replica exchange method.65
Modeling atomic polarizability provides MD methods with additional degrees of freedom, which should increase the transferability of parameters, allowing polarizable FFs to achieve better temperature dependence trends. Fig. 6 and Table 4 show that Drude/LJ-PME obtains the closest agreement with the experimental thermal expansion coefficient of hexadecane. The slope of the linear regression for vs. is also nearest to the experimental slope for Drude/LJ-PME; however, the y intercept of the line of best fit is too high, causing to be slightly higher than experimental values across the temperatures tested. Although C36/LJ-PME has smaller errors from experiment in over the temperatures represented in the figure, the effective thermal expansion coefficient is not as close to the experimental value. Thus, Drude/LJ-PME obtains densities closer to experiment 393.15 K (Table 5).
Because the dependence on temperature of is quartic, errors in temperature dependence are exacerbated at elevated temperatures (Fig. 7). The b parameter of C36 without LJ-PME is almost three times larger than experiment (Table 6), causing a greater than 100% overestimation of at 400 K. With LJ-PME, this is dramatically improved, but C36/LJ-PME still overestimates at 400 K by about 25 %. In contrast, Drude/LJ-PME over-estimates b by only 13%. At 393.15 K, Drude/LJ-PME overestimates by only 6 % and under-estimates density by only 2 % (Table 5). This improvement in temperature dependence could simply be attributed to the specific parameterization. A more general explanation is that polarizable models, with their additional degrees of freedom and enhanced electrostatic response capabilities, enable modeling of the larger range of configurations available as temperature increases. Polarization effects are incorporated in the additive, fixed-charge force fields in a mean-field way through parametrization, which is typically performed at the room temperature and might lead to larger errors at elevated temperatures.
Consistent with the second explanation, polarizable force fields have previously been shown to perform better at elevated temperatures in systems of pure water,66 water/salt solutions,67 and polypeptides.68 Jiang et al.67 found that, for various concentrations of aqueous NaCl, the Drude polarizable FF developed by Kiss and Baranyai, AH/BK3,69, 70 yields and nearer to experimental values at 373.15 and 473.15 K than the additive SPC/E+SD models.71, 72 The induced-dipole AMOEBA force field shows close agreement with experimental temperature dependence for of pure water up to 363 K, whereas the additive, five-site TIP5P model underestimates density above 320 K.66 Polarizability also improves the temperature dependence of spontaneous folding: A study on cooperative helix formation in the (AAQAA)3 peptide indicates that, in events driven by hydrogen bonding, the temperature dependence of secondary structure is more accurately represented by Drude than by C36.68
In summary, LJ-PME is a rigorous method for including long-range LJ interactions in simulations. It allows the use of a shorter real-space cutoff for LJ and electrostatic interactions, thereby increasing computational efficiency. The use of LJ-PME improves agreement with experiment for density, isothermal compressibility, viscosity, diffusion constant, and surface tension at all temperatures simulated for both the C36 additive and Drude polarizable FFs. Additionally, LJ-PME improves agreement with experimental trends in temperature dependence for calculations of and , though results at biological temperatures (303 to 323 K) are better than at 393.15 K. It is now practical and advisable to include long-range LJ interactions in subsequent FF development. While the C36 additive force field with LJ-PME remains a useful model for liquid alkanes, overall, the Drude force field with LJ-PME shows the closest agreement with the experiments considered here.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Alexander MacKerell and Andreas Krämer for helpful discussions. This research was supported by the Intramural Research Program of the NIH, National Heart, Lung and Blood Institute, NSF Grant MCB-1149187, and used the high-performance computational capabilities at the National Institutes of Health, Bethesda, MD (NHLBI LoBoS and Biowulf clusters).
Footnotes
SUPPORTING INFORMATION
The supporting information contains two sections. The first section evaluates the energy conservation of the LJ-PME method via simulations of pure water and pure hexadecane. The second section provides simulation results for systems of pure octane. This information is available free of charge via the internet at http://pubs.acs.org.
REFERENCES
- 1.Klauda JB, Venable RM, Freites JA, O’Connor JW, Tobias DJ, Mondragon-Ramirez C, Vorobyov I, MacKerell AD, and Pastor RW Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J. Phys. Chem. B. 2010, 114(23), 7830–7843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Venable RM, Sodt AJ, Rogaski B, Rui H, Hatcher E, MacKerell AD, Pastor RW, and Klauda JB CHARMM all-atom additive force field for sphingomyelin: Elucidation of hydrogen bonding and of positive curvature. Biophys. J. 2014, 107(1), 134–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Klauda JB, Monje V, Kim T, and Im W Improving the CHARMM force field for polyunsaturated fatty acid chains. J. Phys. Chem. B. 2012, 116(31), 9424–9431. [DOI] [PubMed] [Google Scholar]
- 4.Patel DS, Park S, Wu EL, Yeom MS, Widmalm G, Klauda JB, and Im W Influence of ganglioside GM1 concentration on lipid clustering and membrane properties and curvature. Biophys. J. 2016, 111(9), 1987–1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wu EL, Fleming PJ, Yeom MS, Widmalm G, Klauda JB, Fleming KG, and Im WE coli outer membrane and interactions with OmpLA. Biophys. J. 2014, 106(11), 2493–2502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ollila OHS and Pabst G Atomistic resolution structure and dynamics of lipid bilayers in simulations and experiments. Biochim. Biophys. Acta-Biomembr. 2016, 1858(10), 2512–2528. [DOI] [PubMed] [Google Scholar]
- 7.Botan A, Favela-Rosales F, Fuchs PFJ, Javanainen M, Kanduc M, Kulig W, Lamber A, Loison C, Lyubartsev A, Miettinen MS, Monticelli L, Maatta J, Ollila OHS, Retegan M, Rog T, Santuz H, and Tynkkynen J Toward atomistic resolution structure of phosphatidylcholine headgroup and glycerol backbone at different ambient conditions. J. Phys. Chem. B. 2015, 119(49), 15075–15088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sodt AJ and Pastor RW Bending free energy from simulation: Correspondence of planar and inverse hexagonal lipid phases. Biophys. J. 2013, 104(10), 2202–2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Venable RM, Brown FLH, and Pastor RW Mechanical properties of lipid bilayers from molecular dynamics simulation. Chem. Phys. Lipids. 2015, 192, 60–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lim JB, Rogaski B, and Klauda JB Update of the cholesterol force field parameters in CHARMM. J. Phys. Chem. B. 2012, 116(1), 203–210. [DOI] [PubMed] [Google Scholar]
- 11.Boughter CT, Monje-Galvan V, Im W, and Klauda JB Influence of cholesterol on phospholipid bilayer structure and dynamics. J. Phys. Chem. B. 2016, 120(45), 11761–11772. [DOI] [PubMed] [Google Scholar]
- 12.Wang E and Klauda JB Examination of mixtures containing sphingomyelin and cholesterol by molecular dynamics simulations. J. Phys. Chem. B. 2017, 121(18), 4833–4844. [DOI] [PubMed] [Google Scholar]
- 13.Bera I and Klauda JB Molecular simulations of mixed lipid bilayers with sphingomyelin, glycerophospholipids, and cholesterol. J. Phys. Chem. B. 2017, 121(20), 5197–5208. [DOI] [PubMed] [Google Scholar]
- 14.Sodt AJ, Sandar ML, Gawrisch K, Pastor RW, and Lyman E The molecular structure of the liquid-ordered phase of lipid bilayers. J. Am. Chem. Soc. 2014, 136(2), 725–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Camley BA, Lerner MG, Pastor RW, and Brown FLH Strong influence of periodic boundary conditions on lateral diffusion in lipid bilayer membranes. J. Chem. Phys. 2015, 143(24), 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Venable RM, Ingolfsson HI, Lerner MG, Perrin BS, Camley BA, Marrink SJ, Brown FLH, and Pastor RW Lipid and peptide diffusion in bilayers: The Saffman-Delbruck model and periodic boundary conditions. J. Phys. Chem. B. 2017, 121(15), 3443–3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Oostenbrink C, Villa A, Mark AE, and Van Gunsteren WF A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25(13), 1656–1676. [DOI] [PubMed] [Google Scholar]
- 18.Madej BD, Dickson CJ, Skjevik AA, Betz RM, Walker RC, and Teigen K Lipid14: The Amber lipid force field. Abstr. Pap. Am. Chem. Soc. 2014, 248, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pastor RW and MacKerell AD Development of the CHARMM force field for lipids. J. Phys. Chem. Lett. 2011, 2(13), 1526–1532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chowdhary J, Harder E, Lopes PEM, Huang L, MacKerell AD, and Roux B A polarizable force field of dipalmitoylphosphatidylcholine based on the classical Drude model for molecular dynamics simulations of lipids. J. Phys. Chem. B. 2013, 117(31), 9142–9160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vorobyov IV, Anisimov VM, and MacKerell AD Jr. Polarizable empirical force field for alkanes based on the classical drude oscillator model. J. Phys. Chem. B. 2005, 109(40), 18988–18999. [DOI] [PubMed] [Google Scholar]
- 22.Klauda JB, Brooks BR, MacKerell AD, Venable RM, and Pastor RW An ab initio study on the torsional surface of alkanes and its effect on molecular simulations of alkanes and a DPPC bilayer. J. Phys. Chem. B. 2005, 109(11), 5300–5311. [DOI] [PubMed] [Google Scholar]
- 23.Lamoureux G and Roux B Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm. J. Chem. Phys. 2003, 119(6), 3025–3039. [Google Scholar]
- 24.Klauda JB, Wu XW, Pastor RW, and Brooks BR Long-range Lennard-Jones and electrostatic interactions in interfaces: Application of the isotropic periodic sum method. J. Phys. Chem. B. 2007, 111(17), 4393–4400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Allen MP and Tildesley DJ Computer simulations of liquids. Clarendon Press: Oxford, England: 1987. [Google Scholar]
- 26.Lague P, Pastor RW, and Brooks BR Pressure-based long-range correction for Lennard-Jones interactions in molecular dynamics simulations: Application to alkanes and interfaces. J. Phys. Chem. B. 2004, 108(1), 363–368. [Google Scholar]
- 27.Wennberg CL, Murtola T, Pall S, Abraham MJ, Hess B, and Lindahl E Direct-space corrections enable fast and accurate Lorentz-Berthelot combination rule Lennard-Jones lattice summation. J. Chem. Theory Comput.. 2015, 11(12), 5737–5746. [DOI] [PubMed] [Google Scholar]
- 28.Brooks BR, Brooks CL, Mackerell AD, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, and Karplus M CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30(10), 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Martinez L, Andrade R, Birgin EG, and Martinez JM PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30(13), 2157–2164. [DOI] [PubMed] [Google Scholar]
- 30.Hoover WG Canonical dynamics: Equilibrium phase-space distributions. Physical Review A. 1985, 31(3), 1695. [DOI] [PubMed] [Google Scholar]
- 31.Nose S and Klein ML Constant pressure molecular dynammics for molecular systems. J. Chem. Phys. 1983, 78(5), 6928. [Google Scholar]
- 32.Anderson HC Quantum chemistry by random walk: Higher accuracy. J. Chem. Phys. 1980, 72(8), 2384. [Google Scholar]
- 33.Ryckaert JP, Ciccotti G, and Berendsen HJC Numerical integration of the cartesian equations of motion of a system with constrations: Molecular dynamics of n-alkanes. J. Compu. Phys. 1977, 23(3), 327. [Google Scholar]
- 34.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, and Pedersen LG A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103(19), 8577–8593. [Google Scholar]
- 35.Zhang YH, Feller SE, Brooks BR, and Pastor RW Computer-simulation of liquid/liquid interfaces .1. Theory and application to octane/water. J. Chem. Phys. 1995, 103(23), 10252–10266. [Google Scholar]
- 36.Yeh IC and Hummer G System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions. J. Phys. Chem. B. 2004, 108(40), 15873–15879. [Google Scholar]
- 37.Lipari G and Szabo A Effect of librational motion on flourescence depolarization and nuclear magnetic-resonance relaxation in macromolecules and membranes. Biophys. J. 1980, 30(3), 489–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ottiger M and Bax A Determination of relative N-H-N N-C ‘, C-alpha-C ‘, andC(alpha)-H-alpha effective bond lengths in a protein by NMR in a dilute liquid crystalline phase. J. Am. Chem. Soc. 1998, 120(47), 12334–12341. [Google Scholar]
- 39.Wu XW and Brooks BR Isotropic Periodic Sum: A method for the calculation of long-range interactions. J. Chem. Phys. 2005, 122(4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wu XW and Brooks BR Using the Isotropic Periodic Sum method to calculate long-range interactions of heterogeneous systems. J. Chem. Phys. 2008, 129(15). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Venable RM, Chen LE, and Pastor RW Comparison of the extended Isotropic Periodic Sum and particle mesh Ewald methods for simulations of lipid bilayers and monolayers. J. Phys. Chem. B. 2009, 113(17), 5855–5862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mecke M, Winkelmann J, and Fischer J Molecular dynamics simulation of the liquid-vapor interface: The Lennard-Jones fluid. J. Chem. Phys. 1997, 107(21), 9264–9270. [Google Scholar]
- 43.Janecek J Long range corrections in inhomogeneous simulations. J. Phys. Chem. B. 2006, 110, 6264–6269. [DOI] [PubMed] [Google Scholar]
- 44.MacDowell LG and Blas FJ Surface tension of fully flexible Lennard-Jones chains: Role of long-range corrections. The Journal of Chemical Physics. 2009, 131, 074705. [DOI] [PubMed] [Google Scholar]
- 45.Hautman J and Klein ML An Ewald summation method for planar surfaces and interfaces. Molecular Physics. 1992, 75(2), 379–395. [Google Scholar]
- 46.Goujon F, Bonal C, and Malfreyt P Calculation of the long-range interactions for interfacial properties. Molecular Simulation. 2009, 35(7), 538–546. [Google Scholar]
- 47.Feller SE, Pastor RW, Rojnuckarin A, Bogusz S, and Brooks BR Effect of electrostatic force truncation on interfacial and transport properties of water. J. Phys. Chem.. 1996, 100(42), 17011–17020. [Google Scholar]
- 48.Darden T, York D, and Pedersen L Particle mesh-Ewald - An N.log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98(12), 10089–10092. [Google Scholar]
- 49.Nijboer BRA and Dewette FW On the calculation of lattice sums. Physica. 1957, 23(4), 309–321. [Google Scholar]
- 50.Williams DE Accelerated convergence of crystal-lattice potential sums. Acta Crystallographica Section a-Crystal Physics Diffraction Theoretical and General Crystallography. 1971, A 27(SEP1), 452. [Google Scholar]
- 51.Karasawa N and Goddard WA Acceleration of convergence for lattice sums. J. Phys. Chem.. 1989, 93(21), 7320–7327. [Google Scholar]
- 52.Veld PJI, Ismail AE, and Grest GS COMP 6-Application of Ewald summations to long-range dispersion forces. Abstr. Pap. Am. Chem. Soc. 2007, 234. [DOI] [PubMed] [Google Scholar]
- 53.Isele-Holder RE, Mitchell W, and Ismail AE Development and application of a particle-particle particle-mesh Ewald method for dispersion interactions. J. Chem. Phys. 2012, 137(17). [DOI] [PubMed] [Google Scholar]
- 54.Isele-Holder RE, Mitchell W, Hammond JR, Kohlmeyer A, and Ismail AE Reconsidering dispersion potentials: Reduced cutoffs in mesh-based Ewald solvers can be faster than truncation. J. Chem. Theory Comput.. 2013, 9(12), 5412–5420. [DOI] [PubMed] [Google Scholar]
- 55.Wennberg CL, Murtola T, Hess B, and Lindahl E Lennard-Jones lattice summation in bilayer simulations has critical effects on surface tension and lipid properties. J. Chem. Theory Comput.. 2013, 9(8), 3527–3537. [DOI] [PubMed] [Google Scholar]
- 56.Steinbach PJ and Brooks BR New spherical-cutoff methods for long-range forces in macromolecular simulation. J. Comput. Chem. 1994, 15(7), 667–683. [Google Scholar]
- 57.Small DM Handbook of lipid research 4: The physical chemistry of lipids. Plenum Press: New York: 1986. [Google Scholar]
- 58.Dymond JH and Harris KR The temperature and density dependence of the self-diffusion coefficeint of normal-hexadecane. Molecular Physics. 1992, 75(2), 461–466. [Google Scholar]
- 59.Zhang YH, Venable RM, and Pastor RW Molecular dynamics simulations of neat alkanes: The viscosity dependence of rotational relaxation. J. Chem. Phys. 1996, 100, 2652–2660. [Google Scholar]
- 60.Berne BJ and Pecora R Dynamic Light Scattering with Applications to Chemistry, Biology, and Physics Vol. New York City, New York: John Wiley & Sons, Inc; 1976. [Google Scholar]
- 61.Khasanshin T, Samuilov V, and Shchemelev A Determination of the thermodynamic properties of liquid n-hexadecane from the measurements of the velocity of sound. Journal of Engineering Physics and Thermmophysics. 2009, 82(1), 149–156. [Google Scholar]
- 62.Fischer NM, van Maaren PJ, Ditz JC, Yildirim A, and van der Spoel D Properties of organic liquids when simulated with long-range Lennard-Jones interactions. J. Chem. Theory Comput.. 2015, 11, 2938. [DOI] [PubMed] [Google Scholar]
- 63.Zhuang X, Makover JR, Im W, and Klauda JB A systematic molecular dynamics simulation study of temperature dependent bilayer structural properties. Biochim. Biophys. Acta-Biomembr. 2014, 1838(10), 2520–2529. [DOI] [PubMed] [Google Scholar]
- 64.Zhuang X, Davila-Contreras EM, Beaven AH, Im W, and Klauda JB An extensive simulation study of lipid bilayer properties with different head groups, acyl chain lengths, and chain saturations. Biochim. Biophys. Acta-Biomembr. 2016, 1858(12), 3093–3104. [DOI] [PubMed] [Google Scholar]
- 65.Swendsen RH and Wang JS Replica Monte-Carlo simulation of spin-glasses. Physical Review Letters. 1986, 57(21), 2607–2609. [DOI] [PubMed] [Google Scholar]
- 66.Ren P and Ponder JW Temperature and pressure dependence of the AMOEBA water model. J. Phys. Chem. B. 2004, 108(13427–13437). [Google Scholar]
- 67.Jiang H, Mester Z, Moultos AA, and Economou IG Thermodynamic and transport properties of H2O + NaCl from polarizable force fields. J. Chem. Theory Comput.. 2015, 11, 3802–3810. [DOI] [PubMed] [Google Scholar]
- 68.Huang J and MacKerell AD Jr. Induction of peptide bond dipoles drives cooperative helix formation in the (AAQAA)3 peptide. Biophys. J. 2014, 107(4), 991–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kiss PT and Baranyai A A systematic development of a polarizable potential of water. J. Chem. Phys. 2013, 138, 204507–204517. [DOI] [PubMed] [Google Scholar]
- 70.Kiss PT and Baranyai A A new polarizable force field for alkali and halide ions. J. Chem. Phys. 2014, 141, 114501–114515. [DOI] [PubMed] [Google Scholar]
- 71.Berendsen HJC, Grigera JR, and Straatsma TP The missing term in effective pair potentials. J. Phys. Chem.. 1987, 91, 6269–6271. [Google Scholar]
- 72.Smith DE and Dang LX Computer-simulations of NaCl association in polarizable water. J. Chem. Phys. 1994, 100(5), 3757–3766. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


