Abstract
Linear ethers such as polyethylene glycol (PEG) have extensive industrial and medical applications. Additionally, phospholipids containing an ether linkage between the glycerol backbone and hydrophobic tails are prevalent in human red blood cells and nerve tissue. This study uses ab initio results to revise the CHARMM additive (C36) partial-charge and dihedral parameters for linear ethers and develop parameters for the ether-linked phospholipid 1,2-di-O-hexadecyl-sn-glycero-3-phosphocholine (DHPC). The new force field, called C36e, more accurately represents the dihedral potential energy landscape and improves the densities and free energies of hydration of linear ethers. C36e allows more water to penetrate into a DHPC bilayer, increasing the surface area per lipid compared to simulations carried out with the original C36 ether parameters, and improving the overall structural properties obtained from X-ray and neutron scattering. Comparison with an ester-linked DPPC bilayer (1,2-dipalmitoyl-sn-phosphatidylcholine) reveals that the ether linkage increases water organization in the headgroup region. This effect is a likely explanation for the experimentally lower water permeability of bilayers composed of ether-linked lipids.
TOC Graphic
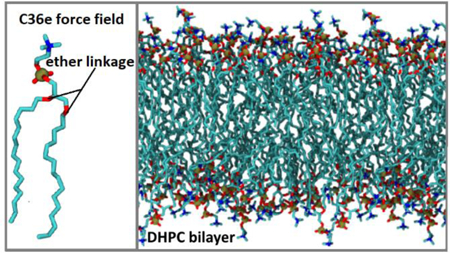
1. Introduction
Compounds containing ether groups are widely used in industry and medicine. Ether groups consist of both a polar oxygen atom capable of participating in hydrogen bonds and a nonpolar aliphatic region. Beyond the local hydrogen-bonding capacity, they are nonpolar and can serve as solvents in organic synthesis. Polyethylene glycol (PEG) is a polyether which, for example, is used in protein purification,1 can be taken as an osmotic laxative,2 and aids in the absorption of cosmetic products into the skin.3 Phospholipids that contain an ether linkage between the glycerol backbone and tail (hereafter referred to as ether lipids) are prevalent in mammalian nerve tissue and blood. Up to 52% of phospholipids in nerve myelin4 and 15% in human red blood cells5 are ether-linked. Additionally, ether lipids are predominant in membranes of archaea and are thought to contribute to the resilience of extremophiles over a wide range of temperatures, salinities, pressures, and pHs.6 Recent experimental findings verify that the ether linkage alters bilayer structure, water permeability7 and water organization in the bilayer.8
Molecular dynamics (MD) simulations of ethers and ether lipids have a range of applications. Recently, MD simulations of aqueous PEG have been used to characterize the role of PEG chain length in protein purification,9 and a study of PEG-grafted membrane interactions with alginate gel foulant investigated the antifouling property of PEG which can inhibit water purification in the process of membrane separation.10 MD simulations comparing ether- and ester-linked lipids11, 12 have probed the chemical effects of the ether linkage. However, the surface areas per lipid for ether-linked bilayers in the biologically-relevant constant number, pressure, and temperature (NPT) ensemble have been systematically underestimated. In one such study, Pan et al.12 modified the CHARMM36 (C36)13, 14 force field (FF) to model a bilayer of ether-linked 1,2-di-O-hexadecyl-sn-glycero-3-phosphocholine (DHPC). The partial-charge and dihedral parameters for the ether linkage were adapted from the C36 lipid force field and an earlier study by Shinoda et al.15 The partial charge on the ether oxygen was −0.40e, similar to the C36 charge on the ether oxygen in PEG (−0.34e). The resulting surface area per lipid () of DHPC was too low by over 8 Å2/lipid in the NPT ensemble, and the authors resorted to fixing the volume of the simulation box to avoid condensing.12 These results indicate a deficiency in the C36 parameters for linear ethers such as PEG.
C36 partial-charge assignments for the ether oxygen and adjacent carbons in linear ethers were chosen empirically with the goal of reproducing neat liquid properties and hydration energies.14 Lennard-Jones parameters were directly transferred from parameterization of cyclic ethers. It was later shown that dihedral parameters for the linear ether dimethoxyethane (C4H10O2; hereafter DMOE) underestimated the gauche character of the central O-C-C-O dihedral, resulting in reduced populations of TGT and TGG’ conformations (C-O-C-C, O-C-C-O, and C-C-O-C dihedrals, respectively) in mixtures with water.16 In the referenced study, Lee et al. presented revised dihedral parameters but did not reinvestigate the partial-charge assignments for linear ethers. The revised parameters yielded good agreement with experimental persistence lengths of a 27-mer PEG and various lengths of polyethylene oxide in water, but the official C36 release of the FF did not include the revisions.
The present study demonstrates that C36 parameters do not yield accurate densities for small chains of PEG, and the free energy of hydration () of diethoxyethane (C6H14O2; hereafter DEOE), a model for the glycerol-ether linkage in ether lipids, also deviates from experiment. Furthermore, in agreement with the findings of Pan et al.,12 applying C36 parameters for PEG to the glycerol-ether linkage of a DHPC bilayer results in bilayer condensation and that is too low. Comparison of simulated and experimental scattering density profiles (SDP) indicates that water is not penetrating deeply enough into the bilayer, an issue that is likely related to the electronegativity of the ether oxygen and surrounding carbons.
Motivated by the preceding inaccuracies, ab initio results were applied to the development of a new FF for linear ethers and ether lipids, called C36e. Specifically, electrostatic potential (ESP) mapping is used to assign partial charges to linear ethers, and dihedral parameters are fit to reproduce potential energy scans. Resulting densities and for linear ethers are compared with experiment. The parameters for linear ethers are then applied to a DHPC bilayer and improve agreement with experimental SDP, , and form factors. Results for DHPC bilayers are compared with 1,2-dipalmitoyl-sn-phosphatidylcholine (DPPC), identical to DHPC except having ester linkages between the glycerol backbone and saturated tails. This comparison is used to examine the structural and chemical effects of the ether vs. ester linkage on membrane area compressibility modulus (), dipole potential drop (), and water organization in the headgroup region.
This approach is consistent with previous development of the C36 lipid FF by Klauda et al.13 In that study, QM-based charges of DPPC model compounds in the gas phase were compared with AM1-based charges of hydrated lipid bilayers and were found to be very similar, typically differing by 0.05e or less. Torsional parameters for C36 were assigned from direct fits to vacuum QM-based conformational energies of model compounds. Also consistent with C36 development, the present study aims to reproduce the experimental surface area lipid and density profiles from neutron and X-ray scattering experiments.
Section 2 of this paper describes the methodology of quantum mechanical (QM) calculations and MD simulations. Section 3 presents and discusses new C36e parameters and resulting properties of linear ethers and bilayers. Section 4 draws conclusions pertaining to the revised FF and the effects of the ether linkage on water organization in an ether lipid bilayer.
2. Methodology
This section describes the methodology used in ab inito calculations (2.1), fitting the C36e FF to the QM results (2.2), and MD simulations (2.3 and 2.4).
2.1. Quantum Mechanical Calculations.
The NWChem program17 was used for all ab inito calculations. For the purpose of developing new partial-charge parameters, the ESP best-fit partial charges were found for several linear ether molecules using the optimized geometry of the all-trans state: 1,2-diethoxyethane (DEOE), 1,2-dimethoxyethane (DMOE), diethylene glycol (PEG2), triethylene glycol (PEG3), 1,2-dibutoxyethane (DBOE), and 2,5-dioxanonane. Charges were computed from the MP2 densities using the CHELPG method.18 In this method, atomic charges are fit to reproduce the molecular ESP at several points around the molecule.
To develop new dihedral parameters, potential energy scans were computed about the O-C-C-O and C-O-C-C dihedrals of DEOE and DMOE (Fig. 1) from [−180:10:180] degrees with other geometries relaxed.
Figure 1. Fitted dihedrals.
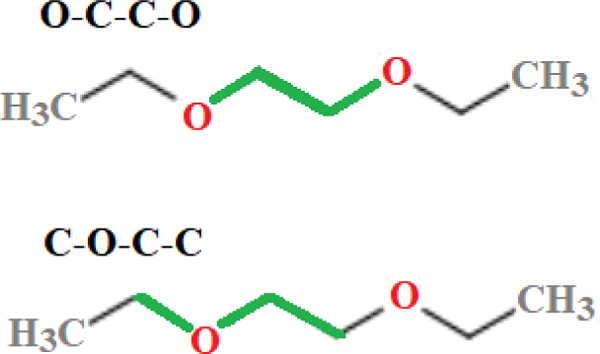
O-C-C-O and C-O-C-C dihedrals (highlighted in green) of diethoxyethane (DEOE).
All optimization and ESP fitting was completed at the MP2/cc-pVDZ level using the DRIVER module with a starting structure near the corresponding geometry, and also for DMOE in the all-trans state using the aug-cc-pVDZ basis set to observe the effect of basis size on partial charges.
Conformational energies at the CCSD(T)/aug-cc-pVTZ level were estimated for the optimized configurations using Hybrid Methods for Interaction Energies (HM-IE) developed by Klauda et al.19 The HM-IE assume that the effects of electron correlation and basis set size are additive. Energies at the CCSD(T) level of theory with a large basis set (LBS = aug-cc-pVTZ in this case) are estimated by calculating CCSD(T) energies with a smaller basis set (SBS = aug-cc-pVDZ) and a correction is added for the difference between the MP2 energies with a LBS and a SBS as follows:
| (1) |
Since the MP2 energies are needed to compute the CCSD(T) energies, two sets of calculations were necessary to find .
2.2. C36 Potential Energy Scan and Dihedral Fitting Procedure.
Potential energies were computed for various conformations of DMOE and DEOE using the CHARMM program20 and the C36 FF. In C36, the form of the dihedral potential for a single dihedral is:
| (2) |
where is the dihedral angle and , n, and are fitting parameters. The multiplicity n can take values from 1 to 6.
The initial configuration was set to all trans and then the specified torsion was rotated for successive energy evaluations (other torsions remained trans). At each conformation, the desired torsion was held constant while coordinates were relaxed, and the relative energy was found by subtracting the minimum.
The O-C-C-O and C-O-C-C dihedrals (Fig. 1) for DEOE were fit separately. Two potential energy scans were performed, rotating the intended dihedral between [−180:10:180] degrees with the torsional parameters and set to zero. A script by Guvench and MacKerell21 was used to find the final dihedral parameters. The script uses Monte Carlo simulated annealing to minimize mean-squared error between the C36 potential energy and the QM relative conformational energies.
Finally, to compare the final parameters, scans were completed with C36 and C36e about each fitted dihedral between[−180:10:180] degrees with all other geometries relaxed.
2.3. Molecular Dynamics Simulations of Linear Ethers.
MD simulations of linear ethers, listed in Table 1, were used to find the densities () of linear ethers and the free energies of hydration () of DEOE and DMOE.
Table 1.
MD Simulations of Linear Ethers. Temperature (T), run time (turn), and number of replicates (nrun), of each simulation. PME denotes that long-range interactions are summed for electrostatic, but not Lennard-Jones, interactions; LJ-PME indicates that electrostatic and Lennard-Jones interaction are included.
|
(K) |
Cutoff Method |
trun (ns) |
nrun | Use | |
|---|---|---|---|---|---|
| DEOE | 288.15 | PME | 30 | 1 | ρ |
| LJ-PME | 30 | 1 | ρ | ||
| 298.15 | PME | 2* | 3 | ||
| DMOE | 288.15 | PME | 30 | 1 | ρ |
| LJ-PME | 30 | 1 | ρ | ||
| 298.15 | PME | 2* | 3 | ||
| PEG2 | 293.15 | PME | 30 | 1 | ρ |
| LJ-PME | 30 | 1 | ρ | ||
| PEG3 | 293.15 | PME | 30 | 1 | ρ |
| LJ-PME | 30 | 1 | ρ | ||
Time per run for each value of attenuation parameter.22
of DEOE and DMOE were obtained using free energy perturbation (FEP) according to the protocol developed by Deng and Roux.22 Details can be found in Supplemental Information, section S1. A single molecule was simulated in a vacuum for the initial stage of the thermodynamic cycle, and in the aqueous phase for the final stage. The water boxes used in the aqueous phase were pre-equilibrated and contained between 460 and 470 waters.
Two different cutoff schemes were employed to treat long-range Lennard-Jones (LJ) interactions to determine densities. Both schemes use a cutoff of 12 Å for evaluating non-bonded interactions directly in real space; outside of , electrostatic interactions are evaluated in reciprocal space with the particle-mesh Ewald method (PME). In the first scheme, a force-switching function was used to modulate LJ interactions near the interface between real and reciprocal space, and outside of the interactions are neglected. In the second scheme, a potential-switching function modulates LJ interactions near the interface, and outside of the long-range LJ interactions are computed with the newly-implemented LJ-PME.23, 24
All simulations were run using CHARMM20 with a 1-fs timestep and an initial cubic box length of between 29 – 30 Å. The NPT ensemble was used with the Nosé−Hoover thermostat to maintain system temperature and a modified Andersen-Hoover barostat to maintain constant pressure.25–27 Standard error in was estimated from uncorrelated blocks of data (five 6-ns blocks for each 30-ns simulation), and in from replicates.
2.4. Molecular Dynamics Simulations of Bilayers.
Table 2 lists simulations of pure DHPC and pure DPPC bilayers presented in this study. Structural and mechanical properties calculated include form factors (), SDP, , and . Properties focusing on the interaction of water with the ether and ester linkages are: pair-correlation functions, , of the ether oxygen (in DHPC) and ester and carbonyl oxygens (in DPPC) with water; and z-profiles of the electrostatic potential (), water potential of mean force (), and density-weighted orientation of water dipole, .
Table 2.
MD bilayer simulations. Temperature (T), run time (trun), number of replicates (nrun), and quantities evaluated.
| T (FF) | Use | ||
|---|---|---|---|
| DHPC | 333 K (C36 and C36e) |
, , SDP , , |
|
| 321 K (C36e) |
, , SDP | ||
| 333 K (C36e); 0.15 M NaCl |
, SDP | ||
| DPPC | 333 K (C36) |
, , , |
|
Bilayer simulations contained a total of 80 lipids (40 per leaflet) and 30 waters per lipid. Initial coordinates were produced by the CHARMM-GUI28 Membrane Builder29–31 for DPPC. Necessary atom-type substitutions and deletions were made to produce the ether linkage of DHPC. “C36” denotes partial-charge assignments based on C36 charges for PEG and unchanged dihedral parameters (see Sec. S2 and Table S1). “C36e” denotes the new partial-charge and dihedral parameters found in Sec. 3.1. Simulations were run in NAMD using a 2-fs timestep and Langevin damping coefficient of 1/ps. Data were analyzed after equilibration, from 30 – 100 ns. Standard errors between replicates were calculated for and scattering parameters, and from uncorrelated blocks for . “NBFIX” parameters for carboxylate, ester, and phosphate oxygens32 were used in simulations with NaCl.
The scattering densities of functional groups from simulation were obtained with the software package SIMtoEXP.33 For ready comparison with the experimental SDP,12 three Gaussians were used to describe the volume probabilities of the lipid headgroup: one each for the glycerol and ether linkage (G1), the phosphate and CH2CH2N moiety (G2), and the trimethyl groups of the terminal choline (G3). For calculating the bilayer hydrocarbon thickness (2DC), the total hydrocarbon region was represented by an error function. Matlab R2016a34 was used to fit the Gaussian and error functions and obtain the difference between electron density maxima (DHH). X-ray and neutron form factors were calculated using SIMtoEXP33 with a Fourier transform of the total densities.
Area compressibility moduli of DHPC and DPPC bilayers were calculated using fluctuations in area:35
| (3) |
Here, is the mean square fluctuation in area per lipid, nL is the number of lipids per leaflet, and kB is Boltzmann’s constant.
The electrostatic potential profile along the bilayer normal was calculated by integration of the Poisson equation:
| (4) |
where is the total time-averaged charge density and is the permittivity of free space. is greater at the center of the membrane than in bulk water. The total dipole potential drop across the membrane, , is here defined as the difference in the electrostatic potential of bulk water, , from that inside the membrane:36
| (5) |
CHARMM20 was used to find the water density and dipole orientation with respect to position along the bilayer normal, The software package Visual Molecular Dynamics (VMD)37 was used to find the pair-correlation functions, , for ether oxygens of DHPC and carbonyl and ester oxygens of DPPC with water hydrogens, and to capture images of the bilayers. Peak positions and integrals of were computed with Matlab R2016a.34
3. Results and Discussion
Section 3.1 presents parameters for linear ethers and simulation results. Section 3.2 presents parameters for the ether-linked lipid DHPC, simulation results for DHPC bilayers. Section 3.3 has a comparison of DHPC with ester-linked DPPC bilayers.
3.1. Parameterization of linear ethers of low molecular weight.
Fig. 2 shows the partial charges on heavy atoms (and terminal hydrogens in PEG3) obtained from the MP2 densities and averaged for symmetry. Charges on other hydrogen atoms can be found in supplementary material Table S2. DEOE and DBOE were chosen as models for the glycerol-ether linkage in DHPC because of their saturated hydrocarbon chains. The charges on ether oxygens and surrounding carbons are significantly greater in magnitude than the C36 partial-charge assignments for a PEG monomer. The C36 PEG oxygen has a partial charge of −0.34e in units of positive elementary charge (e), and −0.01e for neighboring carbons; QM results indicate PEG oxygens have a charge of approximately −0.60 e (depending on chain length), and around 0.4e for neighboring carbons. The longer hydrocarbon tails of DBOE exert a stabilizing effect on the charges of the four neighboring carbons; they range from (0.38e, 0.44e), whereas in the shorter-chained DEOE, the charges on the two central carbons are lesser in magnitude (0.31e) and carbons in positions 2 and 7 carry a greater charge (0.53e). To model the glycerol-ether linkage of phospholipids, the final partial-charge parameters for C36e (Fig. 3) were chosen to mimic charges of the longer-chained DBOE. Supplemental Information Table S2 contains all ab initio partial charges, including those on hydrogens and 2,5-dioxanonane. Changes were made to the general FF file and the lipids file. Compatible FF files and a stream file with all updated parameters is available for download at: https://terpconnect.umd.edu/~jbklauda/research/download.html.
Figure 2.
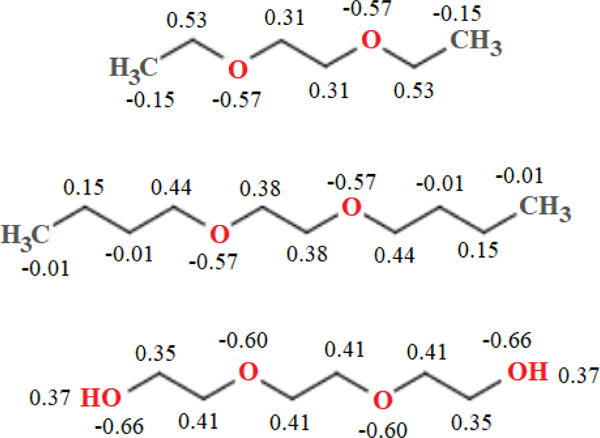
Partial charges for model linear ethers, MP2/cc-pVDZ and CHELPG method (averaged for symmetry). From top: 1,2-diethoxyethane, 1,2-dibutoxyethane, and triethylene glycol. Charges are in multiples of elementary charge, , and are shown for heavy atoms and terminal hydrogens of triethylene glycol.
Figure 3.
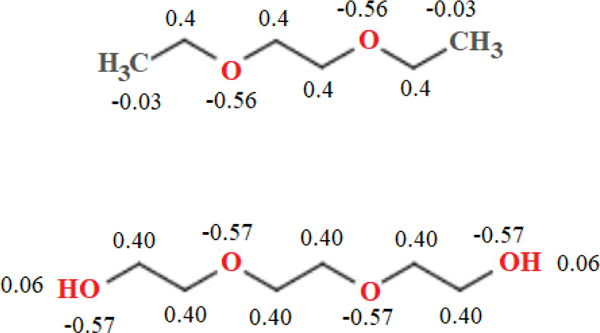
C36e partial-charge assignments for model linear ethers. 1,2-diethoxyethane (top); triethylene glycol (bottom). Charges are in multiples of elementary charge, , and are shown for heavy atoms and terminal hydrogens of triethylene glycol.
Figure 4 plots the torsional potential about two dihedrals of DEOE: C-O-C-C and the central O-C-C-O (Fig. 1). Of note is the difference between the trans and gauche wells of the two dihedrals. The gauche well of O-C-C-O is only 0.265 kcal/mol higher than the trans; the C-O-C-C gauche well is 1.47 kcal/mol higher. The curvatures also differ. The gauche well of O-C-C-O is well-defined at 70°; the C-O-C-C well reaches a local minimum at 90° and has a large radius of curvature through 50°. All QM and simulation results for potential energy scans about both dihedrals of DEOE can be found in supplementary information Table S3.
Figure 4.
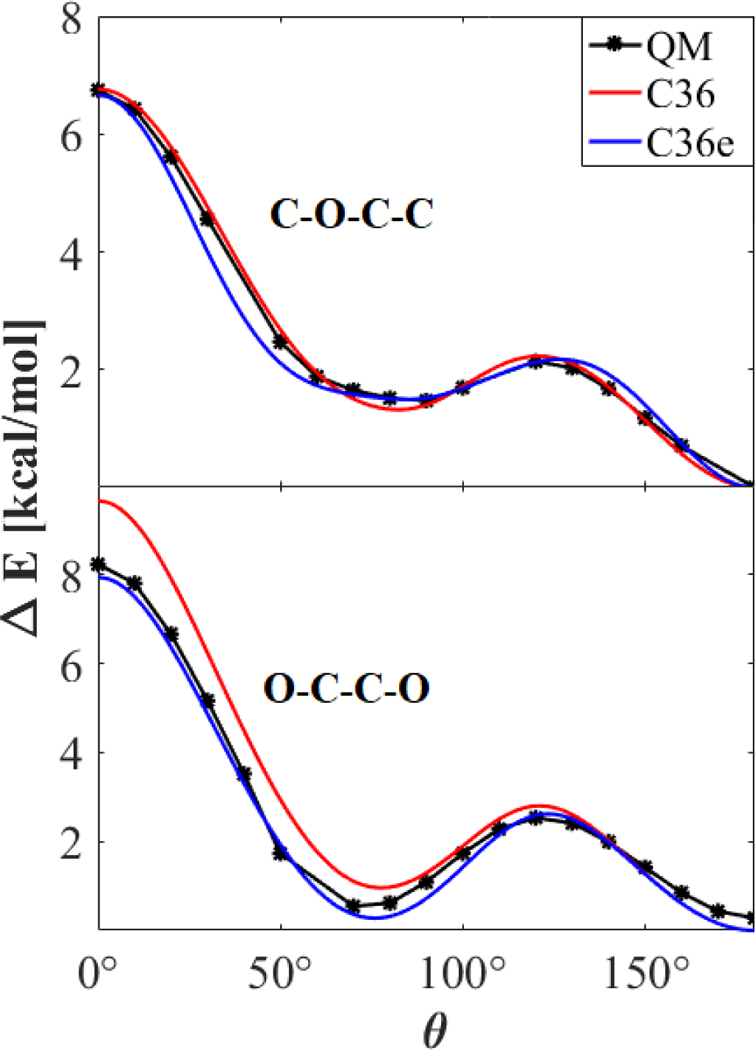
Potential energy scan about dihedrals of DEOE. C-C-O-C (top); O-C-C-O (bottom); MP2/cc-pVDZ//Eint[MP2:CC]. Other torsions remained trans.
While C36 is well-parameterized for C-O-C-C, it exhibits an elevated gauche well and cis barrier for O-C-C-O (at 70° and 0°, respectively). The elevated gauche well causes an underestimation of the gauche character of DEOE and DMOE. This is corroborated by Lee et al.,16 who reported the TGT, TGG`, TTT, TTG, and TGG populations of DMOE at mole fractions of 1.0, 0.6, and 0.3. In C36, all XTX populations are over-estimated, whereas all XGX populations are underestimated, with the exception of slight over-estimation of TGT at 0.3 and TGG at 1.0 mole fraction. At all mole fractions, the TGG` populations were significantly under-estimated. In a DHPC bilayer, where an O-C-C-O chain connects the aliphatic lipid tails to the headgroup, this affects the tilt of the lipids.
Reparameterization for C36e shows better agreement with the QM data for the O-C-C-O dihedral. While C-O-C-C is not improved overall, the gauche well shows improvement. Final torsional parameters are listed in Table 3.
Table 3.
Adjusted C36e torsional parameters.
| Dihedral | kφ | n | δ |
|---|---|---|---|
| C-O-C-C | 0.31 | 2 | 0.0 |
| 0.42 | 3 | 0.0 | |
| 0.16 | 4 | 0.0 | |
| 0.26 | 5 | 0.0 | |
| O-C-C-O | 0.40 | 1 | 180.0 |
| 1.20 | 2 | 0.0 | |
C36e improves agreement with experiment for the densities of PEG (Table 4). The newly-implemented LJ-PME increases and has a greater effect on nonpolar species. Whereas PME enables swift estimation of long-range electrostatic interactions, CHARMM’s use of Lorentz-Berthelot combination rules inhibited use of this method with long-range LJ interactions until recently.24 Newly-implemented LJ-PME is accurate with anisotropic systems such as interfaces and allows use of a lower real-space cutoff for nonbonded interactions. Long-range LJ interactions significantly impact the , isothermal compressibility, and liquid-vacuum surface tensions of nonpolar fluids. Recent investigation into liquid hexadecane indicates that use of LJ-PME with C36 improves agreement with experiment for liquid alkanes.23 Table 4 shows that it also improves agreement with experimental of ethers, most notably DMOE and DEOE, which have nonpolar, hydrocarbon end groups.
Table 4.
Densities linear ethers (g/mL). Diethylene glycol (PEG2), triethylene glycol (PEG3), 1,2-diethyoxyethane (DEOE), and 1,2-dimethoxyethane (DMOE). Per cent difference from experiment is indicated to the right of the average and standard error for each entry.
| Exp. (T) |
C36 | C36e | C36e, LJ-PME | ||||
|---|---|---|---|---|---|---|---|
| PEG2 | 1.119738 (288.15 K) |
1.01868 ± 0.0005 |
−9.02% | 1.08376 ± 0.0004 |
−3.21% | 1.09023 ± 0.0006 |
−2.63% |
| PEG3 | 1.127439 (288.15 K) |
1.05511 ± 0.0004 |
−6.41% | 1.09005 ± 0.0003 |
−3.33% | 1.10134 ± 0.0005 |
−2.31% |
| DEOE | 0.848438 (293.15 K) |
0.8375 ± 0.0001 |
−1.28% | 0.8192 ± 0.0001 |
−3.44% | 0.8388 ± 0.001 |
−1.13% |
| DMOE | 0.862839 (293.15 K) |
0.8473 ± 0.0011 |
−1.80% | 0.8331 ± 0.0007 |
−3.44% | 0.8483 ± 0.0005 |
−1.68% |
C36e also demonstrates the correct trend of increasingly favorable hydration () for the shorter DMOE chain than for the longer DEOE (Table 5). The original parameterization of DMOE included experimental as a target;14 thus, C36 agrees well with of DMOE. However, of the longer chain DEOE is far too negative with C36. Experimentally, the longer chain solvates less favorably than the shorter chain, but C36 exhibits the opposite trend. C36e shows the correct trend and much-improved for DEOE, which is of greater interest as a model compound for the linkage of saturated ether lipids.
Table 5.
(kcal/mol) of linear ethers 1,2-diethoxyethane and 1,2-dimethoxyethane at 298.15 K. Per cent difference from experiment is indicated to the right of the average and standard error for each entry.
3.2. Ether-linked bilayer parameterization and comparison with experiment.
C36e introduces parameters for the saturated ether lipid DHPC. A critical comparison with experiment is the area per lipid, and this is considered first. Fig. 5 shows the equilibration of during each of three replicates of a DHPC bilayer at 333 K. The time series of for all other bilayer simulations are shown in supplementary information Fig. S2. As is evident from Table 6, for C36e is substantially closer to experiment (+3% error) than C36 (−14%). Compared with C36, C36e exhibits a 13% increase in and a 12% decrease in bilayer thickness. Each functional group comprising the lipid headgroup shifts about 1 Å closer to the bilayer center, and the bilayer hydrocarbon thickness decreases by 3 Å. Table 6 compares the resulting structural parameters of C36e with those of C36 and the experimental SDP.12
Figure 5.
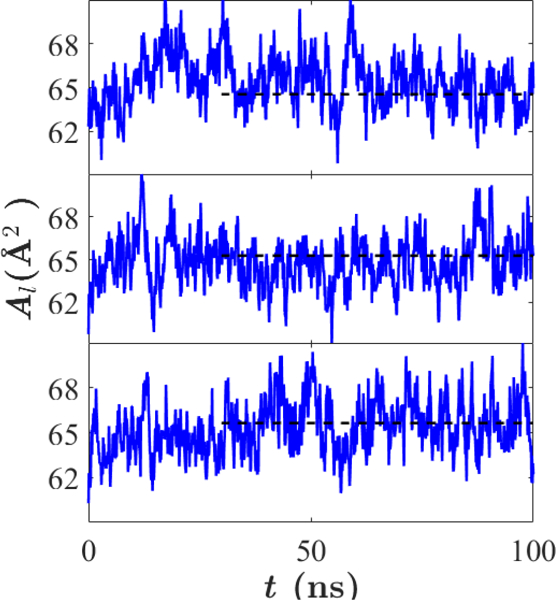
as a function of time for three replicates of DHPC bilayers using C36e. Mean , represented by a dashed line, was calculated after equilibration from 30 – 100 ns. Temperature = 333 K.
Table 6.
Structural parameters of a DHPC bilayer; SDPs from experimental model and simulation.a “C36e, salt” simulations included 0.15 M NaCl.
| Temp. = 333 K |
Temp. = 321 K |
|||||
|---|---|---|---|---|---|---|
| Exp.12 | C36 | C36e | C36e, salt | Exp.7 | C36e | |
| (Å2) | 67.2 | 57.7 ± 0.3 | 65.4 ± 0.2 | 64.8 ± 0.1 | 65.1 | 63.2 ± 0.3 |
| DB (Å) | 36.8 | 43.0 | 37.7 ± 0.3 | 37.65 ± 0.10 | − | 38.7 ± 0.1 |
| 2DC (Å) | 27.1 | 31.8 ± 0.1 | 28.4 ± 0.1 | 30.25 ± 0.06 | 27.6 | 28.9 ± 0.1 |
| DHH (Å) | 38 | 41.7 ± 0.1 | 38.7 ± 0.3 | 38.55 ± 0.12 | 38.2 | 39.0 ± 0.1 |
| DH1 (Å) | 5.4 | 4.93 ± 0.04 | 5.15 ± 0.06 | 4.19 ± 0.03 | 5.3 | 5.0 ± 0.1 |
| zG1 (Å) | 14.2 | 16.92 ± 0.03 | 15.60 ± 0.06 | 16.26 ± 0.03 | − | 15.88 ± 0.03 |
| (Å) | 2.4 | 2.41 ± 0.01 | 2.71 ± 0.04 | 2.670 ± 0.01 | − | 2.77 ± 0.02 |
| zG2 (Å) | 19.2 | 20.94 ± 0.02 | 19.61 ± 0.06 | 19.74 ± 0.03 | − | 19.95 ± 0.03 |
| (Å) | 2.6 | 2.39 ± 0.01 | 2.65 ± 0.04 | 2.677 ± 0.02 | − | 2.71 ±0.02 |
| zG3 (Å) | 20.1 | 22.15 ± 0.03 | 20.8 ± 0.07 | 21.08 ± 0.02 | − | 21.22 ± 0.03 |
| (Å) | 2.8 | 3.13 | 3.20 ± 0.04 | 3.192 ± 0.01 | − | 3.25 ± 0.02 |
is the area per lipid. DB, 2DC, DHH, and DH1 are the overall bilayer thickness, the bilayer hydrocarbon thickness, the distance between electron density maxima, and the distance between the hydrocarbon surface and the maximum electron density in the same leaflet, respectively. Gaussian parameters (mean and standard deviation ) are listed for the glycerol-ether linkage (G1), the phosphate and CH2CH2N moiety (G2), and the trimethyl groups of the terminal choline (G3).
Table 6 also lists scattering parameters for DHPC with 0.15 M NaCl (4 NaCl molecules total). While most parameters are not significantly affected by salt, the bilayer hydrocarbon thickness (2DC) increases by almost 2 Å (1 Å per leaflet). The peak position of the ether functional group () also shifts outward along z by 0.66 Å, while other functional groups are not similarly affected. This indicates compaction of the G1 (ether) functional group into the headgroup in the presence of salt, as the hydrocarbon region of the bilayer expands slightly.
C36e exhibits experimental trends in the temperature dependence of and bilayer hydrocarbon thickness (2DC). Table 6 shows that experimental for DHPC increases by 2.1 Å2 when the temperature increases from 321 to 333 K; this is in near quantitative agreement with the 2.2 Å2 obtained with C36e. C36e also matches the 0.5 Å decrease in 2DC observed experimentally.
C36e shows closer agreement with experimental X-ray and neutron scattering factors than does C36 (Fig. 7 and 8, respectively). The minima of the first three lobes of the X-ray form factors nearly match the experimental curve, indicating accurate . The shape of the first lobe comports with experiment, and the relative heights of the second two lobes are within error margins. As would be expected from the underestimation of , the parameter set based on C36 ethers produces form factors with inaccurate minima; i.e., are shifted to the left. This leftward shift is also found in the neutron form factors (Fig. 8), especially at high percentages of D2O. C36e shows excellent agreement with neutron form factors.
Figure 7.
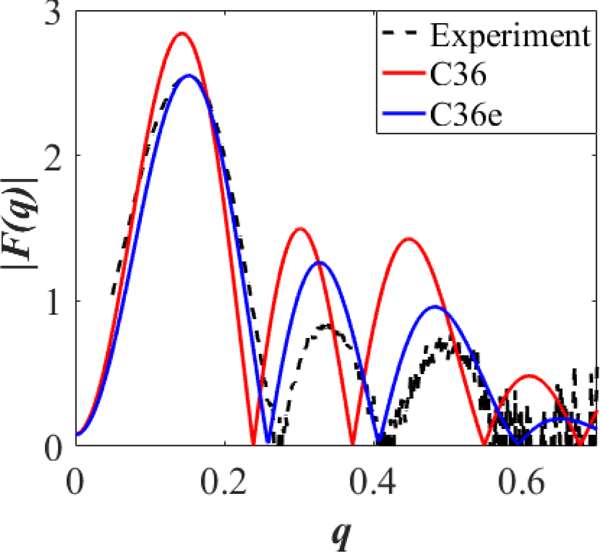
X-ray form factors for a DHPC bilayer at 333 K. Form factors from simulation and experimental form factors () as a function of the total scattering vector . For readability, error bars are not shown for experimental ; they are approximately 0.5* for values of and 0.3* for .
Figure 8.
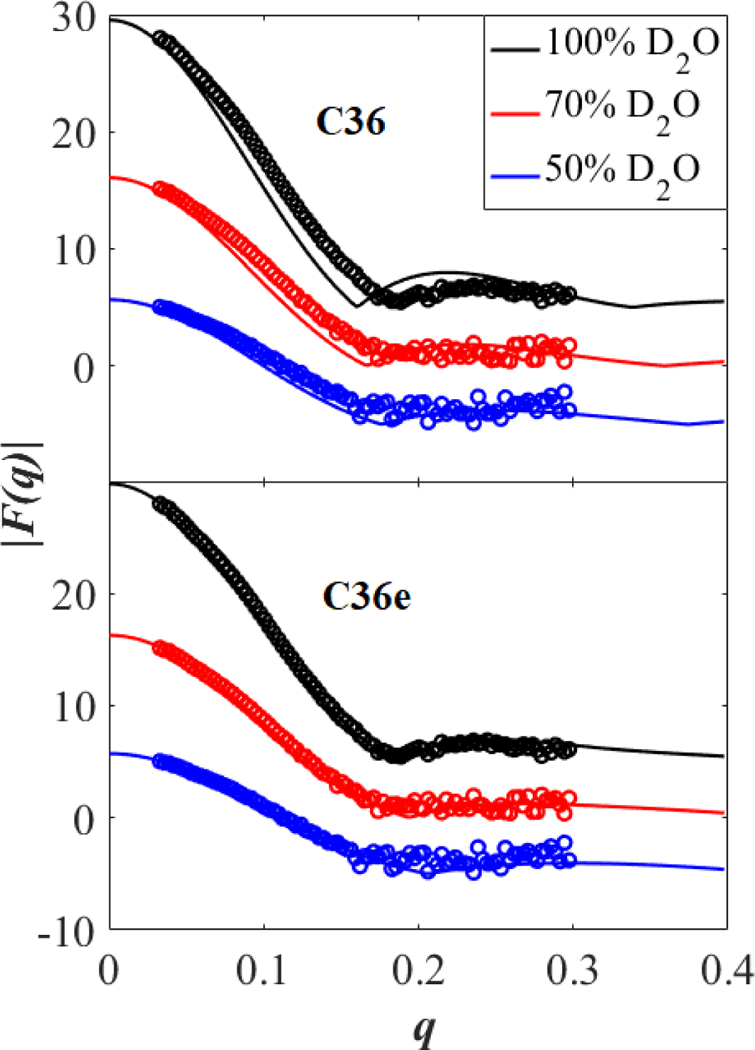
Neutron form factors for a DHPC bilayer at 333 K. from simulation (solid lines) and experiment (open circles) in 100, 70, and 50 % D2O as a function of the total scattering vector . Form factors at 100 and 50 % D2O are shifted vertically for clarity.
While positions of minima are reliable, error in heights are quite large for high values of wave vector . In Fig. 7, errors in height of are approximately 0.5* for values of and 0.3* for .
The electron density profiles of water and the G1 ether linkage group (Fig. 9, top) indicate that water associates more with the G1 group in C36e: The water density profile intersects the peak of the G1 functional group. This is expected, because the increase in magnitude of the partial charge on the ether oxygen makes it more electronegative. The C36e water volume probability curve (Fig. 9, bottom) nearly covers that of the G1 functional group, indicating water penetration to the z position of the ether linkage.
Figure 9.
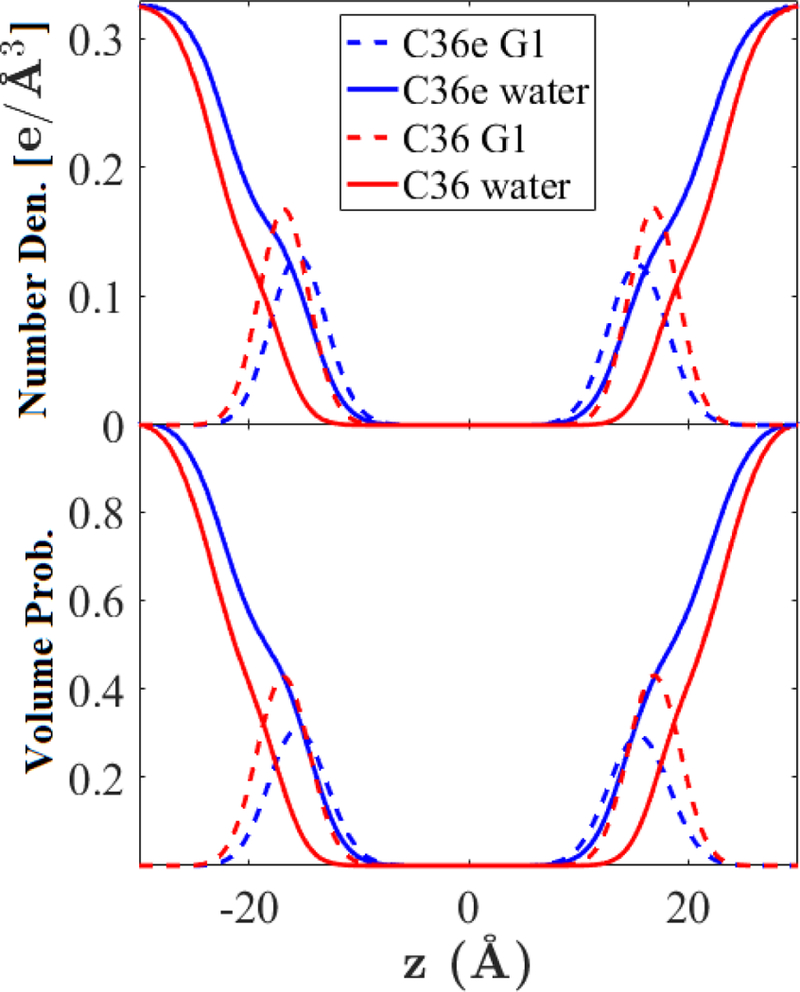
Electron number densities (top) and volume probabilities (bottom) of the glycerol-ether linkage (G1) and water in a DHPC bilayer at 333 K.
C36e exhibits more instances of hydrogen bonding between the ether oxygen and water than does C36. Hydrogen bond lengths (oxygen to hydrogen) vary from 1.5 – 2.5 Å. Fig. 10 shows the pair-correlation function for the ether oxygen-water hydrogen pair. The first peak positions () and number of waters in the first hydration shell () are ; for C36e and ; for C36. Thus, in C36e, each ether oxygen binds with a single water on average, whereas this association is less than half as likely with C36 ether parameters.
Figure 10.
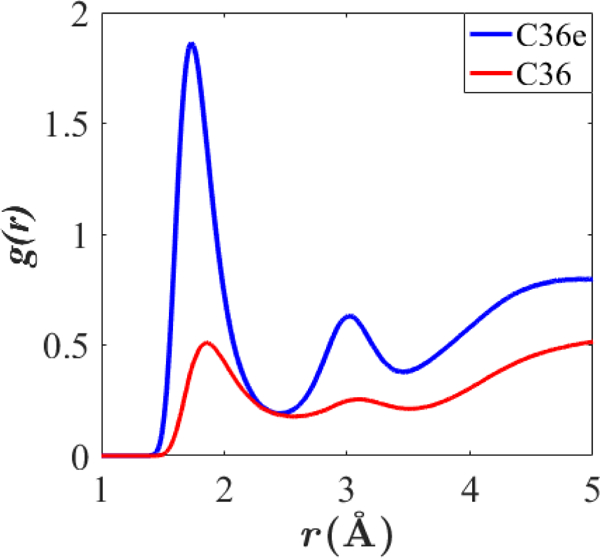
Pair-correlation function for the ether oxygen-water hydrogen pair in C36e and C36. DHPC bilayers, 333 K.
The volume probabilities of each functional group (defined in section 2.4) are compared in Fig. 11. Note the total saturation of the headgroup region with water in C36e vs. the truncation in C36 at the glycerol-ether linkage. This causes to increase with C36e. The resulting decrease in bilayer thickness is evident from the contraction along .
Figure 11.
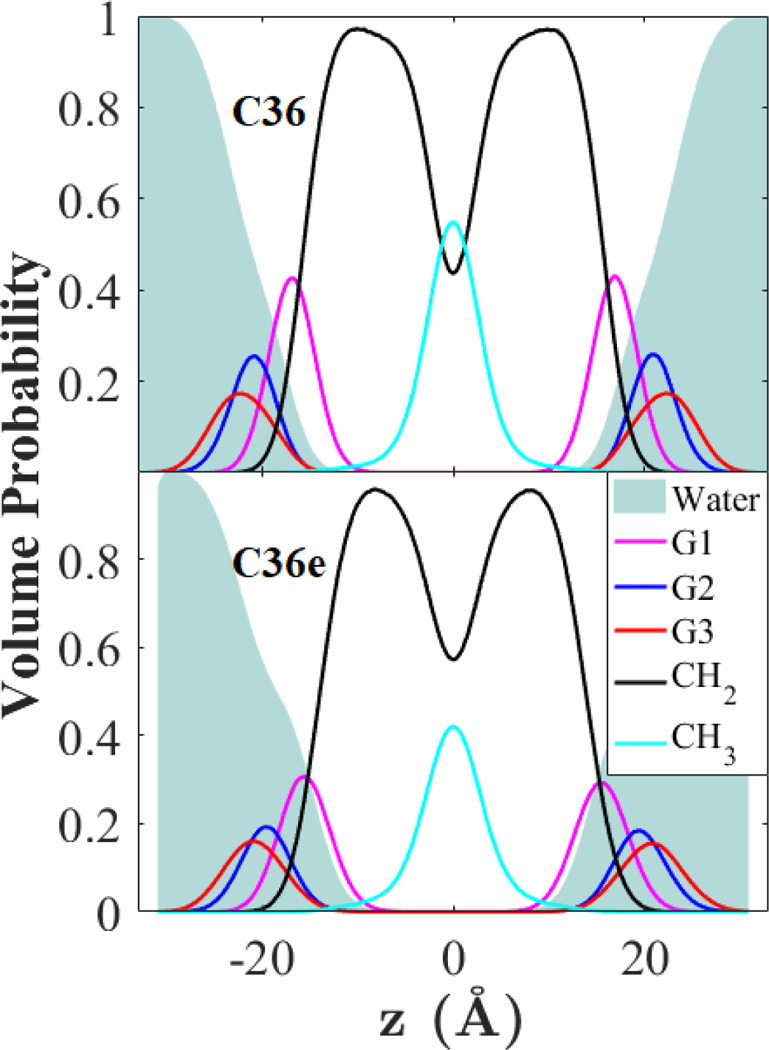
SDP of a DHPC bilayer at 333 K. Volume probabilities of selected functional groups.
3.3. Water Organization in Ether- and Ester-Linked Lipids.
The effect of the ether linkage in DHPC, as compared with the more common ester linkage, is of interest as a well-localized chemical perturbation that affects physical properties. Like DHPC, DPPC has two 16-carbon saturated chains attached to the glycerol backbone; the only chemical difference between these two lipids is linkage between the glycerol backbone and hydrocarbon tails. Thus, the ether linkage in DHPC is responsible for its slightly larger ,7, 12 lower water permeability,7 and lower dipole potential.8
A recent all-atom MD study by Kruczek et al.11 compared the organization of water in DHPC and DPPC bilayers. The authors proposed that increased water organization in the headgroup region of DHPC contributes to its relatively lower water permeability. They found that waters near the DHPC headgroups were less mobile (lower lateral diffusion coefficient) and more ordered (higher autocorrelation times) than in a DPPC bilayer. Additionally, they found to be higher for the DHPC bilayer, indicating it is more rigid. However, the parameterization scheme used in their study resulted in an underestimate of for DHPC (sim. 60.0 Å2 at 323 K; exp. 65.1 Å2 at 321 K). Furthermore, in contrast to experiment, for the simulated DHPC bilayer was lower than that of a DPPC bilayer at the same temperature. The condensation of the DHPC bilayer is consistent with both greater water organization and higher .
The present study examines water organization as a function of z, the position along the bilayer normal, using C36e parameters, which yield a higher for DHPC than for DPPC. Fig. 12 plots the density-weighted water dipole orientation, , and water potential of mean force (). Indeed, waters in the headgroup region of DHPC display greater water dipole organization, particularly around the terminal choline () and ether linkage (vertical black dashes). This is indicated by the greater magnitude of . The are nearly identical except for compaction along z observed with DHPC due to its greater . The increased organization around the ether linkage is counter-intuitive because the ether oxygen is less electronegative than the carbonyl oxygen of DPPC, as determined from the partial-charge assignments ( ether oxygen in DHPC, carbonyl oxygen in DPPC). However, perhaps due to steric hindrance arising from close proximity with the ester oxygen, the carbonyl oxygen in DPPC does not associate as strongly with water as the ether oxygen in DHPC. Fig. 13 plots the pair-correlation functions of various lipid oxygens with water hydrogens. The peak position () of the correlation function for the DHPC ether oxygen with water is the smallest, indicating the shortest bond association length; the integral of this peak is also the greatest, indicating the greatest number of associations per ether oxygen ( ; ). The carbonyl oxygen of DPPC has a comparable but slightly lesser interaction with the water ( ; ), and the ester oxygen of DPPC does not appear to associate strongly with water, despite its significant partial charge ().
Figure 12.
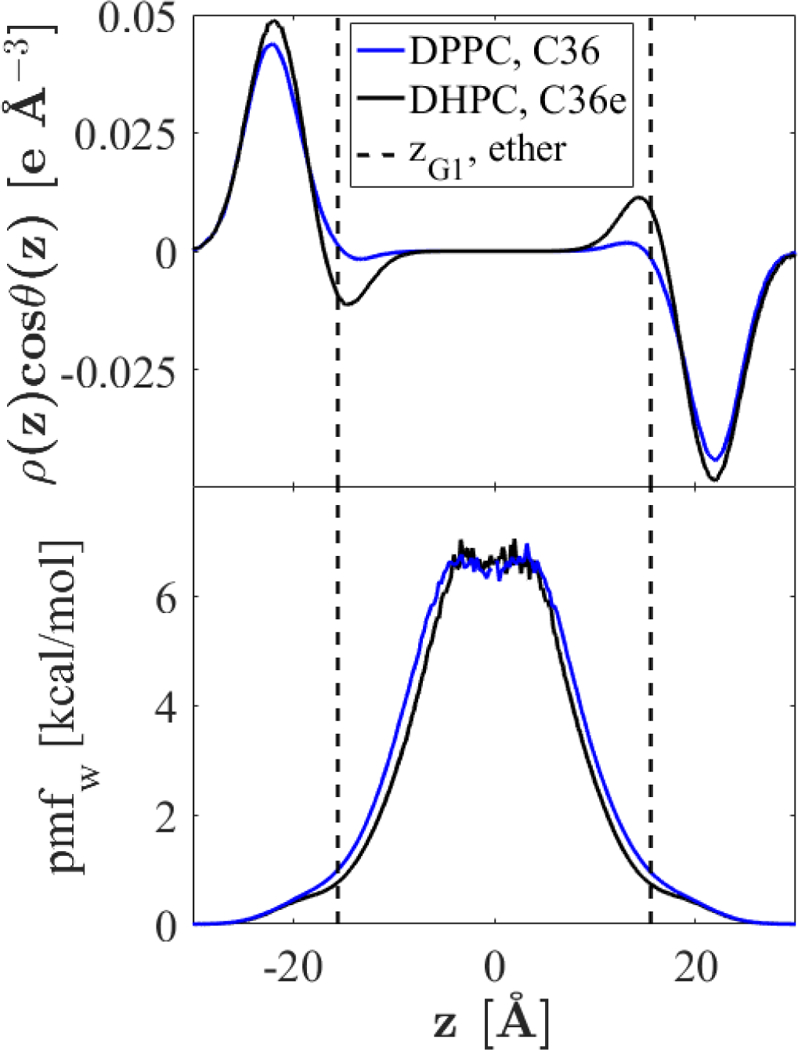
Water dipole orientation and potential of mean force at 333 K. Orientation of the water dipole with respect to the bilayer normal, scaled by the local water density (top). Water potential of mean force (bottom); region from [−10, 10] is not smooth due to infrequent permeation.
Figure 13.
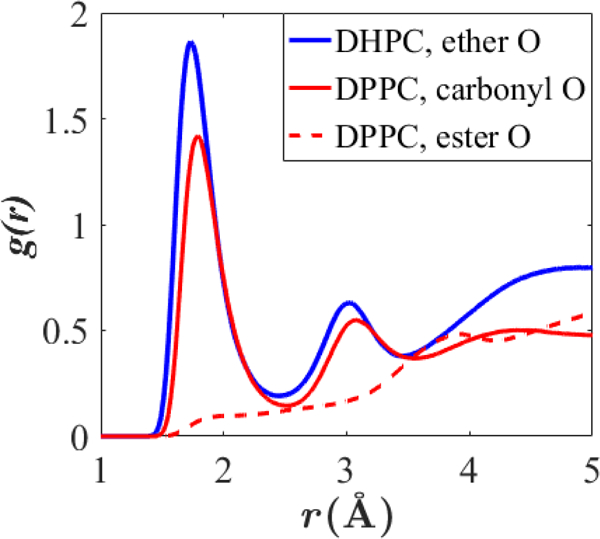
Pair-correlation function for various lipid oxygens with water hydrogen for DHPC and DPPC bilayers at 333 K.
The previously-mentioned MD study by Kruczek et al.11 found the artificially condensed DHPC bilayer to have a significantly larger than DPPC (418 dyn/cm for DHPC and 359 dyn/cm for DPPC), but the value found for DPPC at 321 K is considerably larger than the experimental value at a nearly equivalent temperature (231 dyn/cm at 323 K).41 Parameterization of DPPC in C36 yields and in good agreement with experiment at 323 K; matches the experimental value of 63.0 and estimates of are 210 and 230 dyn/cm for systems of 648 and 72 lipids, respectively.42 C36 DPPC therefore provides a more reliable comparison to DHPC with C36e. Results, listed in Table 7, indicate that of DHPC is not significantly different from that of DPPC (the 95% confidence intervals are approximately twice that of the standard error). Thus, the claim by Kruczek et al.11 that increased stiffness of DHPC bilayers relative to DPPC contributes to decreased permeability is not supported here. The increase in observed in that study likely resulted from the relatively low .
Table 7.
Compressibility moduli and area per lipid of DHPC (C36e) and DPPC (C36).
The comparable values for listed in Table 7 imply that the ether linkage does not contribute to the increased membrane stiffness of observed in archaea.43 In addition to the ether linkage, archaeal membranes contain methylated tails composed of repeating 5-carbon isopranoid or isoprenoid chains. Acyl chains with this structure have been shown to increase bilayer stiffness in simulations with C36 using ester-linked lipids.44
The electrostatic potential drop, , as a function of the z position along the bilayer normal, is plotted in Fig. 14 for DHPC and DPPC at 333 K. determines the electric field strength inside the membrane and has been shown to affect the conformation of ion-translocating proteins.46 However, precise experimental values of for bilayers remain controversial because direct measurement is not currently possible.46 Experimental estimates vary significantly depending on methods. Two studies using different methods agree that DHPC bilayers should have a lower than DPPC bilayers by about half.8, 47
Figure 14.
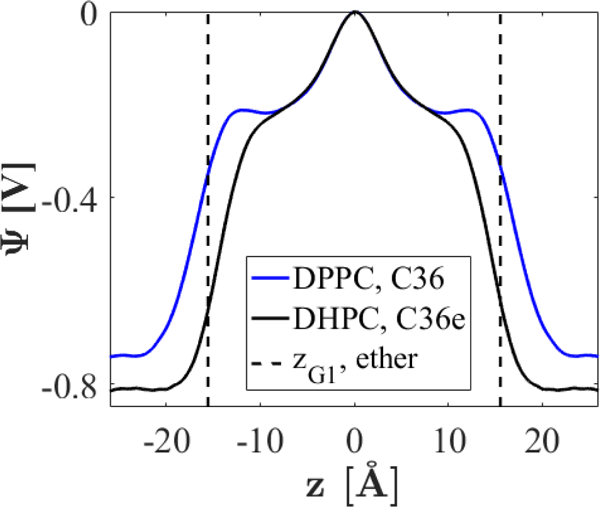
Electrostatic potential drops for DHPC and DPPC bilayers at 333 K.
As was noted previously,13 C36 systematically over-estimates across lipid bilayers according to consensus of experimental values. Experimental estimates of for DPPC range from 220 – 280 mV,46 while results with C36 are closer to 800 mV from the interleaflet region to water. C36e yields a slightly greater for DHPC, contrary to experimental estimates. A previous FF adaptation for ether-DPhPC bilayers, developed by Shinoda et al. for use with CHARMM27,15 successfully yields lower for ether-DPhPC than for ester-DPhPC, but there are some issues with this FF. First, as with C36, the magnitude of for both lipids is significantly higher than experimental predictions, with of about 500 mV for ether-DPhPC and 1000 mV for ester-DPhPC, over four times higher than the experimental prediction.48 Secondly, the ether-DPhPC bilayer has lower (74.1 Å2) than the ester-DPhPC bilayer (77.7 Å2). This is likely incorrect, as DPhPC is identical to DPPC except for methylated tails, and the ether linkage is expected to increase .7, 12 Pan et al.12 adapted these parameters for a DHPC bilayer and found that, indeed, the for DHPC was 9 Å2 too low, precluding use of the biologically-relevant NPT ensemble. Charge parameters for the ether linkage used in these studies were lower in magnitude for ether oxygens and bonded carbons than C36e assignments. Results for the C36 PEG-based charge set in Table 5, also with decreased polarity in the ether linkage, yield DHPC that is again 10 Å2 too low. It is reasonable to assume from the poor results obtained with these alternate charge sets and from QM ESP results for linear ethers (Fig. 2) that, while such reduced polarity may achieve a lower dipole potential for DHPC bilayers, it does not accurately represent the ether linkage. The inability of C36 to produce accurate more likely results from underestimation of the dielectric constants of nonpolar liquids (models of lipid tails) in additive force fields.
The present study prioritizes agreement with bilayer structural parameters. While it is probable that use of a polarizable FF, such as the CHARMM Drude FF,49–51 would yield more experimentally-consistent values for , adjustments to the Drude FF for lipids would be necessary to compare DPPC and DHPC.
4. Conclusions
Changing the partial-charge assignments and associated dihedral parameters for linear ethers improves agreement with the QM dihedral potential energy landscape for 1,2-diethoxyethane (DEOE), while at the same time bringing free energy of hydration in closer agreement with the experimental value. Applying these new C36e parameters to small chains of polyethylene glycol considerably improves agreement with experimental densities.
Application of C36e parameters to the glycerol-ether linkage of a DHPC bilayer required a reduction in magnitude of partial charge on carbons in the glycerol chain to allow for deeper water penetration. This is consistent with charge assignments for glycerol in the similar, but ester-linked lipid, DPPC. The resulting structure of a DHPC bilayer shows close agreement with experimental scattering factors and improved agreement of scattering density parameters, including surface area per lipid. C36e accurately reproduces the experimental temperature dependence of neutron/X-ray form factors.
Examination of water-lipid associations reveals that water penetrates to the level of the ether linkage (Fig. 9). Organization of the water dipole in the vicinity of the ether linkage is higher in a DHPC bilayer than in a DPPC bilayer around its ester linkage (Fig. 12, top). Additionally, water associates more strongly with the ether oxygen in DHPC than with either the carbonyl oxygen or the ester oxygen in DPPC (Fig. 13). The strong association between the ether oxygen and water, and the tendency of the ether oxygen to orient the water dipole, both increase the organization of water around the ether linkage. This increase in water organization occurs despite the greater surface are per lipid and comparable area compressibility as compared with the ester-linked DPPC bilayer (Table 7), and is a likely explanation for the lower water permeability of the ether-linked DHPC.
The surface area per lipid decreases only slightly in the presence of 0.15 M NaCl (Table 6). The overall bilayer thickness is not significantly affected, but the bilayer hydrocarbon thickness increases by 1.8 Å, and the position of the glycerol and ether linkage functional group shifts outward from the bilayer center. This indicates compaction of the headgroup region in the presence of sodium ions.
Systematic under-estimation of area per lipid in previous MD studies of ether-linked bilayers has undermined comparison of the ester and ether linkages. C36e yields close agreement with experimental scattering factors for a DHPC bilayer in the NPT ensemble, making this comparison possible. The ether linkage is responsible for the experimentally lower water permeability of DHPC relative to DPPC7 and is thought to contribute to the resilience of archaeal membranes over a range of pH.43 C36e enables modeling of the effects of the ether linkage on membrane water permeability and stability over a range of salinities, pressures, and temperatures.
Supplementary Material
Figure 6.
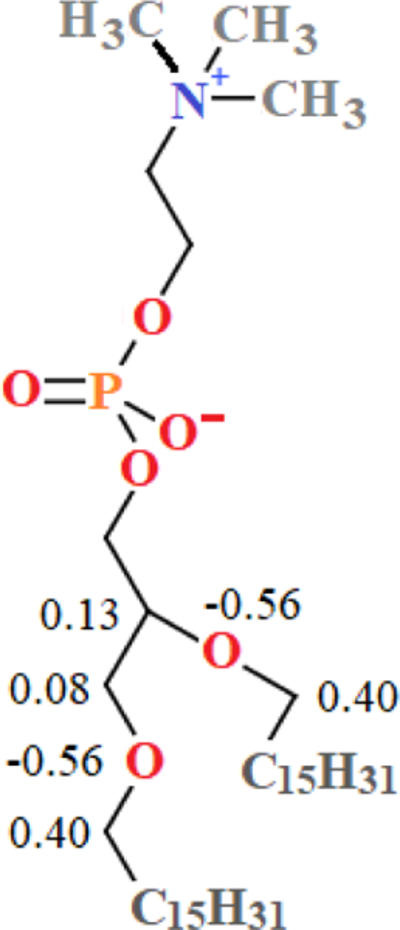
C36e partial-charge assignments for glycerol-ether linkage and associated atoms of DHPC. Partial charges are shown multiples of elementary charge, . Charges not shown for heavy atoms are identical to partial-charge assignments for the corresponding atoms of DPPC.
ACKNOWLEDGEMENTS
We thank Richard Venable for helpful technical advice. This research was supported by the Intramural Research Program of the NIH, National Heart, Lung and Blood Institute, NSF Grant MCB-1149187, and the use of the high-performance computational capabilities at the National Institutes of Health, Bethesda, MD (NHLBI LoBoS and Biowulf clusters), the Maryland Advanced Research Computing Center (MARCC), and the University of Maryland (Deepthought2, http://hpcc.umd.edu).
Footnotes
References
- 1.Ingham KC Protein precipitation with polyethylene glycol Methods in Enzymology. 1984, 104, 351–356. [DOI] [PubMed] [Google Scholar]
- 2.Raymond P Mallory-Weiss tear associated with polyethylnene glycol electrolyte lavange solution. . Gastrointest Endosc. 1991, 37(3), 410–411. [DOI] [PubMed] [Google Scholar]
- 3.Jang HJ, Shin CY, and Kim KB Safety evaluation of polyethylene glycol (PEG) compounds for cosmetic use. Toxicology Research. 2015, 31(2), 105–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Obrien JS and Sampson EL Lipid composition of normal human brain - Gray matter white matter and myelin. J. Lipid Res. 1965, 6(4), 537–&. [PubMed] [Google Scholar]
- 5.Williams JH, Kuchmak M, and Witter RF Fatty acids in phospholipids isolated from human red cells. Lipids. 1966, 1(6), 391–&. [DOI] [PubMed] [Google Scholar]
- 6.van de Vossenberg J, Driessen AJM, and Konings WN The essence of being extremophilic: the role of the unique archaeal membrane lipids. Extremophiles. 1998, 2(3), 163–170. [DOI] [PubMed] [Google Scholar]
- 7.Guler DS, Ghosh DD, Pan J, Mathai JC, Zeidel ML, Nagle JF, and Tristram-Nagle S Effects of ether vs. ester linkage on lipid bilayer structure and water permeability. Chemistry and Physics of Lipids. 2009, 160(1), 33–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gawrisch K, Ruston D, Zimmerberg J, Parsegian VA, Rand RP, and Fuller N Membrane dipole potentials, hydration forces, and the ordering of water at membrane surfaces. Biophysical Journal. 1992, 61, 1213–1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Oelmeier SA, Dismer F, and Hubbuch J Molecular dynamics simulations on aqueous two-phase systems - Single PEG-molecules in solution. Bmc Biophysics. 2012, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Xiang Y, Xu RG, and Leng YS Molecular dynamics simulations of a poly(ethylene glycol)-grafted polyamide membrane and its interaction with a calcium alginate gel. Langmuir. 2016, 32(18), 4424–4433. [DOI] [PubMed] [Google Scholar]
- 11.Kruczek J, Saunders M, Khosla M, Tu Y, and Pandit SA Molecular dynamics simulations of ether- and ester-linked phospholipids. BBA - Biomembranes. 2017, 1859, 2297–2307. [DOI] [PubMed] [Google Scholar]
- 12.Pan J, Cheng X, Heberle FA, Mostofian B, Kucerka N, Drazba P, and Katsaras J Interactions between ether phospholipids and cholesterol as determined by scattering and molecular dynamics simulations. The Journal of Physical Chemistry B. 2012, 116, 14829–14838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Klauda JB, Venable RM, Freites A, O’Connor JW, Tobias DJ, Mondragon-Ramirez C, Vorobyov I, MacKerell AD Jr., and Pastor RW Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. Journal of Physical Chemistry B. 2010, 114, 7830–7846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vorobyov I, Anisimov VM, Greene S, Venable RM, Moser A, Pastor RW, and MacKerell AD Jr. Additive and classical Drude polarizable force fields for linear and cyclic ethers. Journal of Chemical Theory and Computation. 2007, 3, 1120–1133. [DOI] [PubMed] [Google Scholar]
- 15.Shinoda K, Shinoda W, Baba T, and Mikami M Comparative molecular dynamics study of ether- and ester-linked phospholipid bilayers. Journal of Chemical Physics. 2004, 121(19), 9648–9654. [DOI] [PubMed] [Google Scholar]
- 16.Lee H, Venable RM, MacKerell AD Jr., and Pastor RW Molecular dynamics studies of polyethylene oxide and polyethylene glycol: Hydrodynamic radius and shape anisotropy. Biophysical Journal. 2008, 95(4), 1590–1599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Valiev M, Bylaska EJ, Govind N, Kowalski K, Straatsma TP, Van Dam HJJ, Wang D, Niepolcha J, Arpa E, Windus TL, and de Jong WA NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. . Computational Physics Communications. 2010, 181, 1477–1493. [Google Scholar]
- 18.Brenerman CM and Wilberg KB Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. Journal of Computational Chemistry. 1990, 11(3), 361–370. [Google Scholar]
- 19.Klauda JB, Garrison SL, Jiang J, Arora G, and Sandler SI HM-IE: Quantum chemical hybrid methods for calculating interaction energies. Journal of Physical Chemistry A. 2004, 108, 107–112. [Google Scholar]
- 20.Brooks BR, Brooks CL, MacKerell AD Jr., Nilsson R, Petrella J, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kucerka N, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, and Karplus M CHARMM: The biolmolecular simulation program. Journal of Computational Chemistry. 2009, 30, 1545–1615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Guvench O and MacKerell AD Jr. Automated conformational energy fitting for force-field development. Journal of Molecular Modeling. 2008, 14(8), 667–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Deng Y and Roux B Hydration of amino acid side chains: Nonpolar and electrostatic contributions calculated from staged molecular dynamics free energy simulations with explicit water molecules. Journal of Physical Chemistry B. 2004, 108, 16567–16576. [Google Scholar]
- 23.Leonard AN, Simmonett AC, Pickard FC IV, Huang J, Venable RM, Klauda JB, Brooks BR, and Pastor RW Comparison of additive and polarizable models with explicit treatment of long-range Lennard-Jones interactions using alkane simulations. Journal of Chemical Theory and Computation. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wennberg CL, Murtola T, Pall S, Abraham MJ, Hess B, and Lindahl E Direct-space corrections enable fast and accurate Lorentz-Berthelot combination rule Lennard-Jones lattice summation. Journal of Chemical Theory and Computation. 2015, 11(12), 5737–5746. [DOI] [PubMed] [Google Scholar]
- 25.Nose S and Klein ML Constant pressure molecular-dynamics for molecular-systems. Mol. Phys. 1983, 50(5), 1055–1076. [Google Scholar]
- 26.Anderson HC Molecular dynamics simulations at constant pressure and/or temperature. Journal of Chemical Physics. 1980, 72(4), 2384. [Google Scholar]
- 27.Hoover WG Canonical Dynamics - Equilibrium Phase-Space Distributions. Phys. Rev. A. 1985, 31(3), 1695–1697. [DOI] [PubMed] [Google Scholar]
- 28.Jo S, Kim T, Iyer VG, and Im W CHARMM-GUI: A web-based graphical user interface for CHARMM. Journal of Computational Chemistry. 2008, 29(11), 1859–1865. [DOI] [PubMed] [Google Scholar]
- 29.Jo S, Lim JB, Klauda JB, and Im W CHARMM-GUI membrane builder for mixed bilayers and its application to yeast membranes. Biophysical Journal. 2009, 97(1), 50–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wu EL, Cheng X, Jo S, Rui H, Song KC, Lee J, Davila-Contreras EM, Beaven AH, Monje-Galvan V, Venable RM, Klauda JB, and Im W CHARMM-GUI Membrane Builder Toward Realistic Biological Membrane Simulations. J. Comput. Chem. 2014, 35(27), 1997–2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lee J, Cheng X, Swails JM, Yeom MS, Eastman PK, Lemkul JA, Wei S, Buckner J, Jeong JC, Qi Y, Jo S, Pande VS, Case DA, Brooks CL, MacKerell AD, Klauda JB, and Im W CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. Journal of Chemical Theory and Computation. 2016, 12(1), 405–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Venable RM, Luo Y, Gawrisch K, Roux B, and Pastor RW Simulations of anionic lipid membranes: Development of interaction-specific ion parameters and validation using NMR data. Journal of Physical Chemistry B. 2013, 117(35), 10183–10192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kucerka N, Katsaras J, and Nagle JF Comparing membrane simulations to scattering experiments: Introducing the SIMtoEXP software. Journal of Membrane Biology. 2010, 235(1), 43–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.MATLAB and Statistics Toolbox Release 2016a. 2016, The MathWorks, Inc.: Natick, Massachusetts, United States. [Google Scholar]
- 35.Feller SE and Pastor RW Constant surface tension simulations of lipid bilayers: The sensitivity of surface areas and compressiblities. Journal of Chemical Physics. 1999, 111, 1281–1287. [Google Scholar]
- 36.Feller SE, Pastor RW, Rojnuckarin A, Bogusz S, and Brooks BR Effect of electrostatic force truncation on interfacial and transport properties of water. Journal of Physical Chemistry. 1996, 100(42), 17011–17020. [Google Scholar]
- 37.Humphrey W, Dalke A, and Schulten K VMD - Visual Molecular Dynamics. Journal of Molecular Graphics. 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
- 38.Lide DR and Milne GWA, eds. Handbook of Data on Organic Compounds, 3 ed Vol. I 1994, CRC Press, Inc.: Boca Raton, FL. [Google Scholar]
- 39.O’Neil MJ, ed. The Merck Index - An Encyclopedia of Chemicals, Drugs, and Biologicals, 13 ed. 2001, Merck and Co., Inc.: Whitehouse Station, NJ, 1723. [Google Scholar]
- 40.Cabani S, Gianni P, Mollica V, and Lepori L Thermodynamic study of aqueous dilute solutions of organic compounds; part 5.: Open-chain saturated bifunctional compounds. Transactions of the Faraday Society. 1978, 67, 1933–1942. [Google Scholar]
- 41.Nagle JF and Tristram-Nagle S Structure of lipid bilayers. Biocimica et Biophysica Acta-Reviews on Biomembranes. 2000, 1469, 159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Venable RM, Brown FLH, and Pastor RW Mechanical properties of lipid bilayers from molecular dynamics simulation. Chemistry and Physics of Lipids. 2015, 192, 60–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sprott GD, Archaeal membrane lipids and applications, in Encyclopedia of Life Sciences. 2011, John Wiley & Sons, Ltd: Ottawa, ON, Canada. [Google Scholar]
- 44.Lim JB and Klauda JB Lipid chain branching at the iso- and anteiso-positions in complex chlamydia membranes: A molecular dynamics study. Biochimica Et Biophysica Acta-Biomembranes. 2011, 1808(1), 323–331. [DOI] [PubMed] [Google Scholar]
- 45.Rawicz W, Olbrich KC, McIntosh T, Needham D, and Evans E Effect of chain length and saturation on elasticity of lipid bilayers. Biophysical Journal. 2000, 79(1), 328–3239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Clarke RJ The dipole potential of phospholipid membranes and methods for its detection. Advances in Colloid and Interface Science. 2001, 89, 263–281. [DOI] [PubMed] [Google Scholar]
- 47.Wang L, Bose PS, and Sigworth FJ Using cryo-EM to measure the dipole potential of a lipid membrane. PNAS. 2006, 103(49), 18528–18533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Peterson U, Mannock DA, Lewis R, Phol P, McElhaney RN, and Pohl EE Origin of membrane dipole potential: Contribution of the phospholipid fatty acid chains. Chemistry and Physics of Lipids. 2002, 117, 19–27. [DOI] [PubMed] [Google Scholar]
- 49.Vorobyov IV, Anisimov VM, and MacKerell AD Polarizable empirical force field for alkanes based on the classical drude oscillator model. Journal of Physical Chemistry B. 2005, 109(40), 18988–18999. [DOI] [PubMed] [Google Scholar]
- 50.Chowdhary J, Harder E, Lopes PEM, Huang L, MacKerell AD, and Roux B A polarizable force field of dipalmitoylphosphatidylcholine based on the classical Drude model for molecular dynamics simulations of lipids. Journal of Physical Chemistry B. 2013, 117(31), 9142–9160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li H, Chowdhary J, Huang L, He XB, MacKerell AD, and Roux B Drude polarizable force field for molecular dynamics simulations of saturated and unsaturated zwitterionic lipids. Journal of Chemical Theory and Computation. 2017, 13(9), 4535–4552. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


