Automated in vivo patch-clamp evaluation of extracellular multielectrode array spike recording capability

Abstract

Much innovation is currently aimed at improving the number, density, and geometry of electrodes on extracellular multielectrode arrays for in vivo recording of neural activity in the mammalian brain. To choose a multielectrode array configuration for a given neuroscience purpose, or to reveal design principles of future multielectrode arrays, it would be useful to have a systematic way of evaluating the spike recording capability of such arrays. We describe an automated system that performs robotic patch-clamp recording of a neuron being simultaneously recorded via an extracellular multielectrode array. By recording a patch-clamp data set from a neuron while acquiring extracellular recordings from the same neuron, we can evaluate how well the extracellular multielectrode array captures the spiking information from that neuron. To demonstrate the utility of our system, we show that it can provide data from the mammalian cortex to evaluate how the spike sorting performance of a close-packed extracellular multielectrode array is affected by bursting, which alters the shape and amplitude of spikes in a train. We also introduce an algorithmic framework to help evaluate how the number of electrodes in a multielectrode array affects spike sorting, examining how adding more electrodes yields data that can be spike sorted more easily. Our automated methodology may thus help with the evaluation of new electrode designs and configurations, providing empirical guidance on the kinds of electrodes that will be optimal for different brain regions, cell types, and species, for improving the accuracy of spike sorting.

NEW & NOTEWORTHY We present an automated strategy for evaluating the spike recording performance of an extracellular multielectrode array, by enabling simultaneous recording of a neuron with both such an array and with patch clamp. We use our robot and accompanying algorithms to evaluate the performance of multielectrode arrays on supporting spike sorting.

INTRODUCTION

Much current effort focuses on scaling up the number of neurons being simultaneously recorded with extracellular multielectrode arrays in the living mammalian brain, with new technologies potentially capable of recording thousands, and someday perhaps even millions, of individual neurons (Berényi et al. 2014; Mora Lopez et al. 2017; Neto et al. 2016; Rios et al. 2016; Scholvin et al. 2016; Shobe et al. 2015). An open question is what parameters (electrode number, density, geometry) of these multielectrode arrays are most important for supporting accurate interpretation of the resulting data sets. For example, one widespread hope is that increasing the density or number of electrodes on such an array may facilitate spike sorting, the process of assigning extracellular spikes to the neurons that generated them (for a review, see Einevoll et al. 2012). Spike sorting can be facilitated when multiple electrodes sense the spikes of a given neuron, i.e., if there is “spatial oversampling” (Scholvin et al. 2016) of the relevant signals, which enables data processing via a number of approaches including clustering and triangulation (for a review, see Buzsáki 2004), blind source separation (Hill et al. 2010; Jäckel et al. 2012; Leibig et al. 2016; Takahashi and Sakurai 2005), and template matching (Franke et al. 2010, 2015; Pachitariu et al. 2016; Roberts and Hartline 1975; Vollgraf and Obermayer 2006). Spatial oversampling is a feature of many neural recording strategies, including stereotrodes (McNaughton et al. 1983) and tetrodes (Harris et al. 2000; Henze et al. 2000; O’Keefe and Recce 1993; Wilson and McNaughton 1993) as well as silicon-based arrays of tens or hundreds of electrodes (Anastassiou et al. 2015; Berényi et al. 2014; Blanche et al. 2005; Mora Lopez et al. 2017; Neto et al. 2016; Rios et al. 2016; Scholvin et al. 2016; Shobe et al. 2015). However, although increasing spatial oversampling by using very dense arrays could in principle boost the performance of spike sorting, it would also increase manufacturing cost, operating complexity, and data storage and analysis costs. Furthermore, there might be fundamental properties of recorded spikes that could confound spike sorting regardless of electrode sophistication.

To help make it easy to evaluate the spike recording performance of a given electrode array, and to enable systematic analysis of design principles of multielectrode arrays, we developed an automated strategy for collecting a “ground truth” recording of a single neuron, via automatic patch-clamp recording in vivo (Kodandaramaiah et al. 2016), at the same time that the neuron is recorded by a given extracellular array–in our case, an array of close-packed extracellular electrodes that we fabricated, with pads just a few micrometers apart, for dense spatial oversampling (Scholvin et al. 2016). We used such an array to densely survey signals in a volume of brain tissue, allowing detailed analysis of the information added by such closely packed electrodes in the service of spike sorting. Thus the patch-clamp recording would yield spikes of only a single neuron, whereas that neuron’s spikes and those of other nearby neurons would be mixed together to result in the signals picked up on the extracellular electrodes. Our automated system brings the patch pipette and the extracellular electrode array into close registration to each other, important for obtaining simultaneous recordings on each of a single neuron, while avoiding collisions. A key insight was that by broadcasting a voltage from the patch pipette and recording it on the electrode array, we could halt pipette movement before a collision with the electrode array, important for achieving simultaneous dual recordings without electrode damage.

We demonstrated the utility of our robot by performing 51 recordings in the primary visual cortex of 19 anesthetized (0.5–1.2% isoflurane) mice, 2 of which were allowed to wake up during the recording session. Twenty-nine recordings had mean extracellular spike amplitudes of the patched neuron >15 μV, which was also at least one median absolute deviation (MAD) above the average of the extracellular trace of each particular recording (in the spike sorting literature, MAD is also called standard deviation of the noise; Quiroga et al. 2004). We selected the 12 recordings with the greatest such amplitudes (>50 μV) for further analysis in this study, although we note that the other recordings could be useful for studying things not examined in this study, such as how spike waveform is modulated by neural morphology. These 12 recordings included whole cell (n = 10) as well as cell-attached (n = 2) recordings.

As a test case, we examined the capability of our chosen electrode array to accurately report spikes during a burst, by comparing extracellular spikes to the patch data. Bursting may modulate spike amplitude and shape (Connors et al. 1982; Fee et al. 1996) and confound spike sorting (Harris et al. 2000; Lewicki 1998). We examined neurons putatively in cortical layers 2/3 and 5 and used the patch recording to measure the changes in extracellular amplitude and spike half-width during bursting, assessing the detectability of such spikes on the extracellular electrode array by plotting a partial receiver-operating characteristic (PROC) curve and its associated partial area under the curve (PAUC; Krzanowski and Hand 2009), for a simple but intuitive thresholding strategy. As expected, extracellular electrodes struggled to report burst spikes that decreased in amplitude: we found a significant PAUC improvement when burst spikes were removed from the analysis, which was most notable in recordings of putative layer 5 neurons.

We next aimed to evaluate the potential that increasing numbers of electrodes might have for improving spike sorting performance. We wanted to develop an assessment of potential spike sorting performance that was fully automated and scalable to arbitrary numbers of electrodes and electrode densities, so we devised a method for calculating an intracellular voltage estimator from a specified subset of the available extracellular voltage traces. By using this intracellular voltage estimator to perform spike detection and calculating the PAUC, we could estimate the potential spike sorting performance of a given electrode array. In the case of our given multielectrode array, we found that increasing the number of electrodes helped, as expected.

The design of our intracellular voltage estimator bears some discussion. Our first step was to derive a transformation (mathematically speaking, a convolution) between the intracellular and extracellular spike waveforms, minimizing the mean squared error to derive the transformation. This approach is reminiscent of the approach of Freygang and Frank (1959), who designed an “equivalence circuit” that transformed a recorded intracellular voltage into a signal resembling a simultaneously recorded extracellular voltage. The relationship they derived was dependent on the capacitance of the neuron’s membrane and the resistances of tissue and electrodes. Rather than modeling our system in terms of circuit elements, we derived a minimal mean squared error transformation between intra- and extracellular voltages in a phenomenological sense, because we were only interested in understanding the quality of our extracellular electrodes’ reporting capability. (Our model assumes linear time invariance of the system.) Once we derived this relationship for each electrode, in the form of a filter kernel, we convolved the extracellular voltage traces with the filter kernel and asked how well the intracellular voltage could be modeled using extracellular voltages from varying numbers of electrodes. We linearly regressed the thus convolved extracellular voltages against the actual intracellular voltage, yielding an intracellular voltage estimator. We then used the same thresholding framework that we had previously used to evaluate bursting on a single electrode (above) on this intracellular voltage estimator. We found that potential spike sorting performance varied with electrode density and recording volume, with the best performance being achieved at the fullest density of our electrode arrays. These results may motivate the design of electrode arrays with even higher density electrode packing, and the automated strategy we developed for data collection and analysis may provide a platform for the evaluation of new electrode array designs.

MATERIALS AND METHODS

Electrode array design and preparation.

Electrode arrays were designed and constructed at the MIT Microsystems Technology Laboratories. Recording sites were ~9 × 9 μm in size and spaced 2 μm apart in two or four columns. Before experiments, recording sites were electroplated with the conductive polymer poly(3,4-ethylenedioxythiophene) (PEDOT), to increase signal-to-noise ratio (SNR) to a target impedance of 400–600 kΩ, using 0.5–1 nA of constant current for 10–12 s. Shorts (defined as having an impedance <300 kΩ) and open circuits (defined as having an impedance that did not drop with electroplating and was typically >2 MΩ) were identified, and probes with at least ~90% working electrodes (as defined as not shorted and not open) were selected for use. Only the signals recorded from working electrodes were used for analysis. For a subset of recordings, the back of the electrode array was painted with a fine paint brush with 1% DiI (1,1′-dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate; Invitrogen) dissolved in 100% ethanol and left to dry, to mark the array’s track for histological analysis. For reuse, probes were rinsed with deionized water and cleaned with protease (0.25% trypsin-EDTA; Life Technologies) followed by isopropanol.

Surgical procedures.

All animal procedures were approved by the MIT Committee on Animal Care. We performed surgery on male C57Bl/6 mice of 8–12 wk of age (Taconic) for head plate installation under isoflurane anesthesia (1.5–2.5%) with buprenorphine (0.1 mg/kg) and meloxicam (2 mg/kg) administered as analgesics. An anesthetized mouse was placed in a stereotaxic frame (Kopf), and the scalp was shaved, ophthalmic ointment (Puralube vet ointment; Dechra) was applied to the eyes, and iodine solution (Betadine) and 70% ethanol were used to sterilize the surgical area. An incision was made to the scalp, and two self-tapping stainless steel screws with attached stainless steel wires were implanted in the skull over the cerebellum and frontal cortex, to act as electrical references and to provide extra stability for a head plate. The head plate was secured with dental cement (C&B Metabond), and the exposed skull was covered with a layer of silicon elastomer (Kwik-Cast; WPI).

Recordings commenced after 1–5 wk. For the subset of awake recordings, mice were habituated to head restraint over 3 days for 15, 30, and then 45 min with periodic condensed milk reward. On the day of or before recording, craniotomies were performed under isoflurane anesthesia as before. Circular (200–300 μm in diameter) craniotomies were performed stereotaxically either with a hand drill or with our robotic system for making automated craniotomies (Pak et al. 2015). Coordinates for the electrode array were [−2.8 mm anterior/posterior, 3.0 mm medial/lateral] for motor-controlled (Thorlabs) probe insertion perpendicular to the brain surface (~23° from vertical) of the primary visual cortex (V1) to a final tip depth of 543 μm for the 64-channel recording included in this study, spanning layer 2/3, or 960–1,000 μm for the 128- and 256-channel recordings, spanning layers 2–5 (see Fig. 1A). Craniotomies for pipette insertion were located 500 or 1,000 μm medial to the electrode array craniotomy, for targeting layer 2/3 or 5, respectively, with a pipette angled at 35–40° from vertical (Fig. 1A). Craniotomies were periodically doused with saline or lactated Ringer’s solution, to prevent dehydration, and were covered with silicone elastomer (Kwik-Cast; WPI) postexperiment.

Fig. 1.

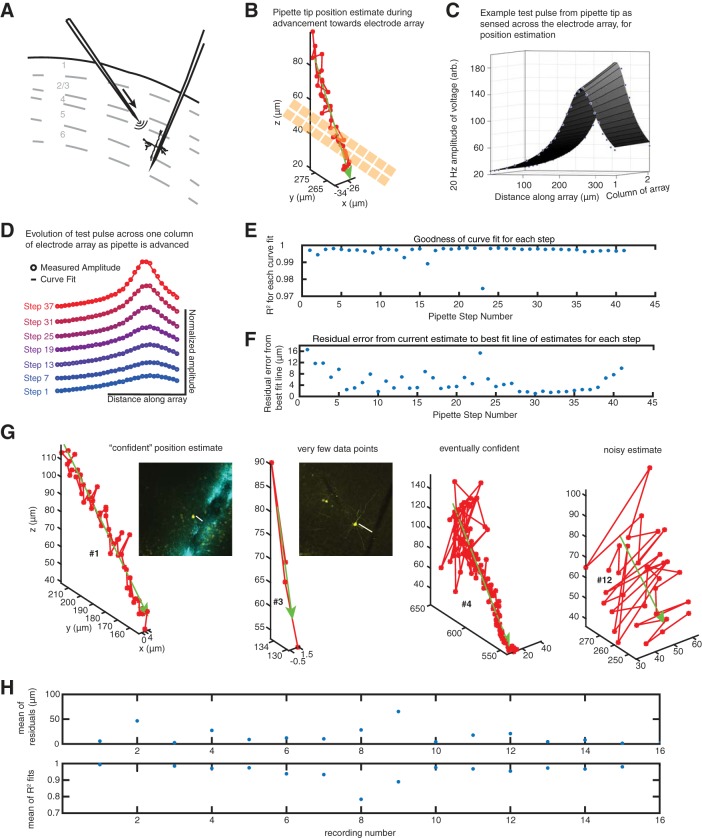
A strategy for dual automated patch clamp and extracellular electrode array recordings in vivo. A: schematic of mouse cortical layers (gray dashed lines) with an electrode array inserted perpendicularly to the brain surface (from top right). A patch pipette targets a neuron (from top left) in either layer 2/3 or layer 5, with the goal of having the electrode array and patch pipette colocalized (i.e., recording activity of the same neuron). Curves emanating from pipette represent current emitted from the pipette for sensing on the electrode array. B: pipette tip-to-electrode array distance prediction from computational model. As the pipette is lowered toward the array (gold squares) in discrete 2-um steps, distance is estimated (red circles, with a green best-fit line across data points), shown for an exemplar recording (data in C–F also correspond to this recording). C: 20-Hz amplitude of a voltage pulse from the pipette as sensed across the electrode array (blue dots represent electrodes), and 1/r curve fit (surface plot). Electrode spacing on the array was 11 μm between adjacent electrode centers. D: amplitude (circles) and curve fit (solid lines), illustrated for a single column of the electrode array, as the pipette approaches the array in discrete 2-μm steps. E: goodness of fit for our 1/r model during each step as the pipette approaches the electrode array. F: at each step, a distance between the pipette tip and the electrode with the largest 20-Hz amplitude signal is approximated. Residual error to a best-fit line that estimates the 3-dimensional (3D) trajectory of the pipette tip in space is calculated post hoc (blue dots). G: position estimates, as in ­B, for 4 of the 16 recordings in which the model was used, illustrating varying “confidence” in the model. Number labels (#) correspond to recording number in H. Histology for the 2 recordings in which both the patched neuron was recovered (left) and the track from the electrode array was apparent (2nd from left) are shown, with biocytin-filled neuron in yellow (and DiI from the array in cyan for left experiment). Distances indicated between the neuron and the electrode array are 40 and 75 μm, respectively. H: mean, over all pipette steps, of residuals (top) and mean of R² fits (bottom) for each of the 16 recordings in which the model was used.

Recording session preparation.

In preparation for a particular recording session, a mouse was initially anesthetized with 2–5% isoflurane in an induction chamber and affixed by its head plate to a metal holder, with its body snugly inside a three-dimensionally (3D) printed tube. A fluidic heating pad was placed in contact with the tube to maintain core body temperature. A cone was placed over the nose for continuous delivery of isoflurane anesthesia. A thin layer of eye lube (Puralube by Dechra, or Lacri-Lube by Refresh) was placed over the eyes to maintain moisture. For anesthetized recording sessions, isoflurane was tuned to 0.5–1.2%. For an awake session, a mouse anesthetized as above was woken up by the cessation of isoflurane delivery. Electrical ground was shared between the patch and electrode array recording apparatuses through a silver chloride pellet placed above the skull in saline or lactated Ringer’s solution. The electrical reference for the electrode array recording was connected to either the cerebellum or cortex skull screw wire. The electrode array was then inserted at a rate of roughly 5 μm/s to its target depth.

Recording session.

Once the electrode array was inserted, one or several successive attempts at automated patch-clamp recording commenced after 10 min or so. Patch-clamp recordings were performed using the robotic autopatcher system (Kodandaramaiah et al. 2012). Standard intracellular solution was prepared as described in Kodandaramaiah et al. (2016), with 0.4% biocytin (wt/vol; Sigma), 135 mM potassium gluconate, 0.1 mM CaCl₂, 0.6 mM MgCl₂, 1 mM EGTA, 10 mM HEPES, 4 mM Mg-ATP, 0.4 mM Na-GTP, and 8 mM NaCl, with dropwise addition of 5 M KOH to adjust the pH to 7.2 and addition of potassium gluconate in increments of 25 mg until the final osmolarity reached 290–295 mosmol/kg H₂O. Pipettes of 1.2-mm outer diameter (no. G120F-4; Warner Instruments) were pulled to resistance of 4.5–8 MΩ with either a Flaming-Brown puller (Sutter P-97) or a gravity puller (Narishige PC-10).

The autopatching sessions began with insertion of a pipette into the brain under positive pressure, to avoid clogging, to a stereotaxically estimated depth of 150–200 μm from the target region. The target region was defined as the part of the electrode array that was in the desired cell layer.

For avoiding collisions between the pipette tip and electrode array, we Fourier transformed the 100-mV square-wave (20 Hz) pulses applied to the pipette tip and sensed on each electrode of the extracellular multielectrode array. We then fit the amplitude of the 20-Hz bin vs. electrode position within the array with a five-parameter model of 1/r voltage falloff, using MATLAB’s curve-fitting toolbox. This model took advantage of the known spacing of the electrodes. Three parameters were for 3-D position, with one parameter as an overall proportionality constant and one for added noise (the noise factor significantly improved fits, because signal strength did not decay toward zero).

During autopatcher operation, if a seal was formed but a membrane break-in was not achieved through pulses of suction or a brief voltage pulse, the neuron was recorded from in cell-attached mode (n = 2 of the 12 recordings chosen for further analysis in Figs. 2–5) in the current-clamp configuration (with no current injected). If a break-in was achieved and a whole cell recording begun, the patching system was switched to current-clamp mode, where 1-s-long hyperpolarizing and depolarizing current steps were injected to measure cell electrical properties and spiking threshold for a subset of the recordings chosen for further analysis in Figs. 2–5 (n = 6 recordings). Regardless of whether the recording was cell-attached or whole cell, a visual stimulus, as described below, was then played to elicit activity.

Fig. 2.

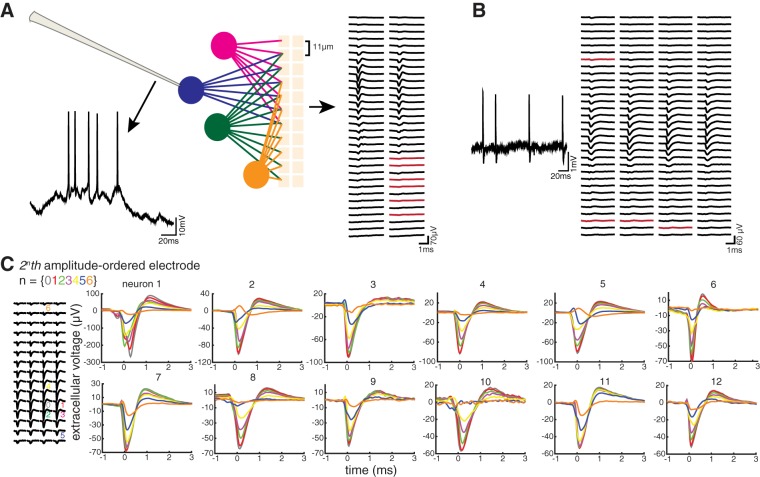
Colocalized recordings: basic properties. A: voltage trace from a representative patched neuron recorded in the whole cell configuration (left), with a schematic of the patched neuron (blue) and other neurons (magenta, green, yellow) being sensed by an array of close-packed electrodes (gold; in our case, ~9 × 9–μm electrodes spaced ~2 μm apart; lines emanating from neurons representing signal propagation). Right: for each electrode in a 2-column, 64-electrode array, snapshots of bandpass-filtered (2nd-order infinite impulse response IIR Butterworth, 100–6,000 Hz) voltage are triggered off the timing of the peak of the derivative of the spikes of the patched neuron and then averaged. These patch-triggered mean extracellular spikes are displayed in the spatial configuration corresponding to the location of the electrodes in the array. In this analysis, a spike that occurs within 20 ms of another spike is considered to be within a burst (Staba et al. 2002), and later spikes in a burst (from the 2nd one onward) are not included in this average because their waveforms may differ significantly from that of nonburst spikes or the first spike in a burst (Henze et al. 2000). Electrodes that are shorted (i.e., impedance <300 kΩ) or open (i.e., impedance >2 MΩ) are shown in red. B: a representative trace from a patched neuron recorded in the cell-attached configuration (left) and patch-triggered mean extracellular spikes on 128 electrodes of a 4-column, 256-electrode array (right). Shorts and opens are shown in red. C: patch-triggered mean extracellular spikes from the 2ⁿ-th electrode among the list of amplitude-ordered electrodes (n = 0–6) from each of the 12 neurons, color-coded as indicated. Amplitude ordering means ranking good (i.e., nonshorted/open) electrodes by their patch-triggered mean extracellular spike amplitudes, from largest to smallest. Neurons are ordered by these aforementioned mean spike amplitudes so that neuron 1 has the greatest amplitude and neuron 12 has the smallest.

Fig. 5.

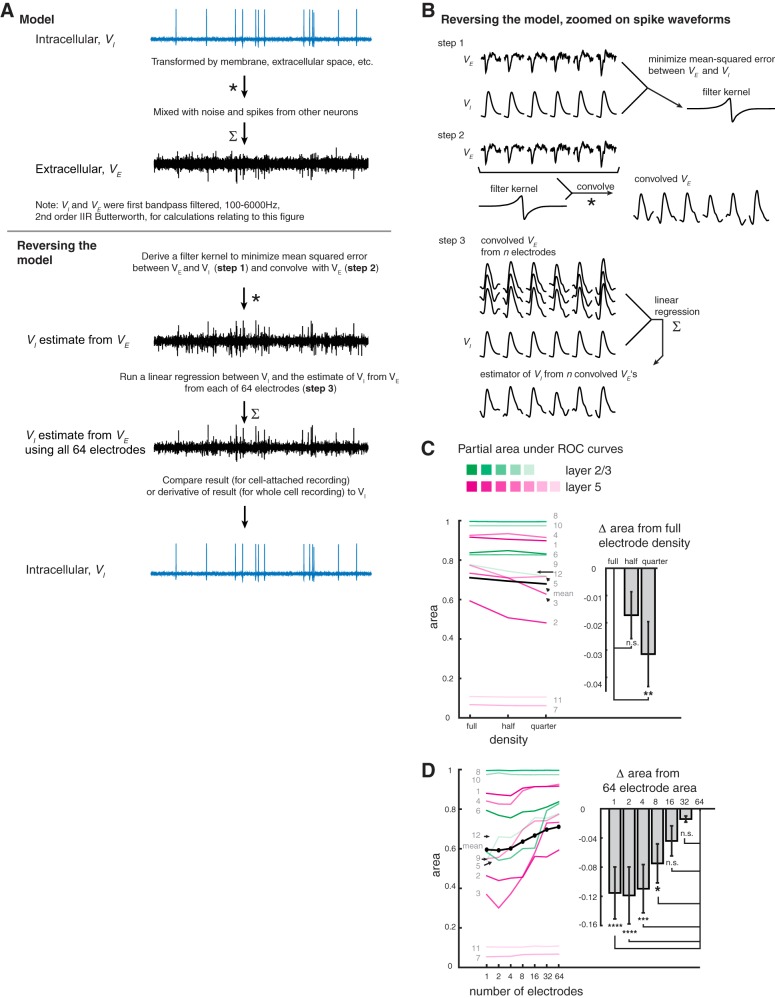
An algorithm for assessing potential spike sorting performance as a function of electrode density and quantity. A, top: a model in which the intracellular voltage (V_I) is transformed by membrane capacitance and resistance, conductance delays, etc., and mixed with noise and spikes from other neurons to produce an extracellular voltage (V_E) as sensed on an electrode. Bottom: reversal of the model in A, in which the V_E is transformed to better resemble the V_I and is unmixed from noise and spikes of other neurons to better approximate V_I. Unmixing is performed by linearly regressing the transformed V_E against the V_I. B: details of the inverted model, zoomed on individual spike waveforms. Top: step 1, a transformation that minimizes the mean squared error between the V_E from a single electrode (we will consider each individual electrode in turn) and calculates V_I, yielding a filter kernel (shown are 6 spikes from an actual recording for ease of visualization.) Middle: step 2, the V_E from the same electrode used in step 1 is convolved with its corresponding convolution filter kernel to create the “convolved V_E.” Bottom: step 3, electrodes are ordered by amplitude, as described for Fig. 2C, and the electrodes to be included in the analysis [i.e., 64, 32, or 16 electrodes (full, half, and quarter density, respectively) for C or the first N electrodes for D) are chosen. Steps 1 (top) and 2 (middle) are applied to the voltage of each of these chosen electrodes, and a multiple linear regression is performed between these convolved V_Es and the bandpass-filtered patch voltage. The resulting regression coefficients are multiplied by their respective convolved V_Es and summed, yielding a single estimator of patch voltage from V_Es (step 3, bottom). C: partial areas under the curve (PAUC) for partial receiver operating characteristic s (PROCs) from each neuron, as in Fig. 4A, but thresholding on the derivative of the estimator of patch voltage. Inset: comparison of scenarios when the estimator of patch voltage was generated from the top 64 amplitude-ordered electrodes in a recording as a full set (full density), when every 2nd electrode was skipped (i.e., the 1st, 3rd, 5th, etc., electrodes were included for a total of 32 electrodes; half density), or when 4 electrodes at a time were skipped (i.e., the 1st, 5th, 9th, etc., electrodes were included for a total of 16 electrodes; quarter density). These results and the results in D were generated when all spikes of the patched neuron were included (i.e., not excluding burst spikes). A significant effect of electrode density was observed (repeated-measures one-way ANOVA, F = 5.656, P = 0.0104, n = 12 neurons from 7 mice). The mean PAUC of the full-density group was significantly greater from that of the quarter-density group (mean of full-density area minus mean of quarter-density area, or “mean difference” was 0.03148; Dunnett’s multiple comparisons test, with corrected **P = 0.0054), but not that of the half-density group [mean difference = 0.01722, P = 0.1401, n.s. (not significant, P > 0.05)]. D, left: PAUC values derived from the derivative of the estimator of patch voltage generated from the top N amplitude-ordered electrodes in a recording (individual neurons colored as in C, mean in black). Inset: PAUC differences from the 64-electrode group (light gray, with error bars representing SE of the difference). A significant effect of number of electrodes was observed (repeated-measures one-way ANOVA, F = 8.364, P < 0.0001, n = 12 neurons from 7 mice). The mean PAUC for 64 electrodes was compared with that for N = 32, 16, 8, 4, 2, and 1 electrode(s). The mean differences from subtracting the 2 values, and the P values, are as follows: 0.01407 and 0.9817 (N = 32 electrodes; n.s.), 0.04402 and 0.28332 (N = 16; n.s.), 0.07483 and 0.0149 (N = 8; *P 0.01–0.05), 0.1095 and 0.0002 (N = 4; ***P = 0.0001–0.001), 0.1187 and 0.0001 (N = 2; ****P ≤ 0.0001), and 0.1153 and 0.0001 (N = 1; ****P ≤ 0.001; Dunnett’s multiple comparisons test).

Because our focus was on demonstrating the utility of our system, and not on characterizing natural neural responses to stimuli, when one neuron (neuron 12 in Fig. 2C) in the whole cell configuration did not initially exhibit spiking in response to visual stimuli, 50-pA steady-state current was injected, resulting in spiking. One neuron (neuron 6 in Fig. 2C) in the whole cell configuration was initially injected with 100-pA steady-state current for an entire ~7.6-min visual stimulus presentation by mistake. The neuron was subsequently recorded from during another visual stimulus presentation, and this latter recording is the one included in the data presented.

Recording selection and explanation.

For the analyses shown in Figs. 2–5, we focused on the 12 recordings that exhibited the highest mean nonburst extracellular spike amplitude (>50 μV) on the electrode with the greatest such spike magnitude (which we informally refer to as the “closest electrode,” although of course we do not know for sure which electrode is physically closest to the neuron being patched), which happened to correspond to the 12 recordings with the greatest SNR on the “closest electrode” (>5). In this paper, we define SNR as the mean nonburst spike magnitude divided by MAD. MAD is the statistical measure we use for the noise of an extracellular trace; we use the version of MAD that is an unbiased estimator for the standard deviation for normal data, which is defined as the median of the absolute value of the trace divided by 0.6745 (after the trace is median subtracted). MAD is a robust statistic because it is not greatly influenced by outliers (e.g., spikes). (In previous extracellular literature, MAD is sometimes referred to as the standard deviation of the noise, e.g., Quiroga et al. 2004). In contrast, the standard deviation of an extracellular trace is dependent on both noise level and spiking characteristics. Specifically, the standard deviation of an extracellular trace will increase with spike magnitude and spike rate. For those who are more familiar with the use of standard deviation to measure the dispersion of an extracellular trace, we note that, in practice, standard deviation ranged from one to two times the MAD of a trace (mean 1.2×).

Mean extracellular waveforms were calculated as follows: snapshots of bandpass-filtered [2nd-order infinite impulse response (IIR) Butterworth, 100–6,000 Hz] voltage were triggered off of the timing of each patch-reported spike time (patch-reported spike times were defined as the time of the peak of the derivative of the patch-measured spike). These snapshots were averaged for each electrode, yielding one mean spike waveform for each electrode (see e.g., Fig 2A, right, and Fig. 2B, right). The amplitude of the spike was then determined by finding the maximum voltage deflection from zero; in practice, this was usually the absolute value of the spike’s trough.

Three patch recordings were obtained in the same mouse and target cell layer in which a previous recording had taken place (the electrode array remained in the same place between recordings, and a new pipette insertion was made). These later recordings were deemed unlikely to be from the same neurons that were patched earlier in the session, and in addition, the first patching attempt would likely have led to the death of the neuron patched. Consistent with this, the earlier and later recordings differed substantially in either mean extracellular spike amplitude on the “closest electrode” or firing rate, or both. Specifically, neuron 2 (numbers as in Fig. 2C and Tables 1 and 2) and neuron 5 had respective mean (SD) extracellular spike amplitudes and firing rates of −100 (31) μV and 5.2 Hz vs. −82 (27) and 19 Hz. Neurons 7 and 11 had respective mean extracellular spike amplitudes and firing rates of −81 (48) μV and 10.2 Hz vs. −66 (35) μV and 6.5 Hz. Neurons 8 and 10 had respective mean extracellular spike amplitudes and firing rates of −65 (10) μV and 1.8 Hz vs. −57 (9) μV and 0.17 Hz.

Table 1.

Properties of 12 neurons recorded with extracellular spikes of >50-μV magnitude

						Spike Count
Neuron	Mouse	Layer	Type	Awake	No. of Working Electrodes	All	Burst	Firing Rate, Hz	Burst Count	Burst Rate, Hz	Spikes per Burst	Burst Duration, ms	Burst ISI, ms
1	A	5	Whole	Yes	236	3,877	989	8.50	327	0.72	4.0 (1.7)	28 (18)	9 (4)
2	B	5	Cell attached	No	122	2,372	969	5.20	489	1.07	3.0 (1.0)	14 (8)	7 (3)
3	C	5	Whole	No	236	323	15	0.71	15	0.03	2.0 (0.0)	15 (3)	14 (3)
4	D	5	Whole	Yes	214	2,926	1,328	6.42	566	1.24	3.3 (1.6)	24 (17)	10 (4)
5	B	5	Whole	No	122	8,748	4,004	19.18	2,296	5.04	2.7 (1.0)	15 (11)	9 (4)
6	E	2/3	Whole	No	58	1,136	291	2.49	168	0.37	2.7 (1.4)	20 (15)	12 (5)
7	F	5	Whole	No	225	4,640	1,625	10.18	693	1.52	3.3 (1.5)	17 (10)	7 (4)
8	B	2/3	Whole	No	122	823	93	1.80	65	0.14	2.4 (0.8)	18 (12)	12 (4)
9	G	2/3	Cell attached	No	238	205	6	0.45	6	0.01	2.0 (0.0)	15 (3)	15 (3)
10	B	2/3	Whole	No	122	78	16	0.17	15	0.03	2.1 (0.3)	7 (2)	6 (2)
11	F	5	Whole	No	225	2,976	1,199	6.53	522	1.14	3.3 (0.3)	15 (8)	6 (4)
12	D	2/3	Whole	No	214	1,592	216	3.49	187	0.41	2.2 (0.4)	13 (8)	11 (5)

Some recordings are from the same mouse, as denoted. Layer was inferred from stereotaxic coordinates. Working electrodes refers to the no. of electrodes on the multielectrode array that were not open or shorted. Spike count is based on the patch recording and is reported for both burst and nonburst spikes. Firing rates varied from 0.2 to 19.2 Hz. The no. of bursts (burst count) is given as well as the burst rate (no. of bursts per unit time) for the recording. The no. of spikes per burst, mean burst duration, and mean burst interspike interval (ISI) are given as means (SD).

Table 2.

Properties of the 12 neurons of Table 1 as recorded on the “closest” extracellular electrode

							<2·MAD	Thresholding Range Between 2 and 6·MAD
		Spike Amplitude, μV		SNR			Spikes	Spikes		Portion of spikes			Half-Width Ratio
Neuron	MAD, μV	Nonburst	Burst	Nonburst	Other Deflections in Spike Range	Intra-to-Extra Peak Offset, ms	All	Nonburst	Burst	Nonburst	Burst	Mean burst spike number	Burst/nonburst
1	14	−267 (134)	−135 (124)	19.24	36	0.30	37	28	269	0.01	0.27	4.7 (1.4)	1.7
2	7	−100 (24)	−79 (32)	13.85	2,720	0.16	1	15	56	0.01	0.06	3.4 (1.0)	1.2
3	8	−91 (18)	−63 (16)	11.71	766	0.07	0	1	1	0.00	0.07	2.0 (0.0)	1.2
4	9	−77 (12)	−54 (18)	5.61	370	0.00	6	38	605	0.02	0.46	3.6 (1.8)	1.4
5	9	−82 (20)	−62 (27)	9.09	8,441	0.04	58	110	926	0.02	0.23	3.4 (1.0)	1.2
6	9	−69 (15)	−65 (19)	7.64	262	0.00	3	100	51	0.12	0.18	2.7 (1.0)	1.0
7	13	−68 (32)	−47 (37)	5.23	37,073	0.03	141	1928	1141	0.64	0.70	3.2 (1.3)	1.3
8	6	−64 (10)	−56 (9)	11.05	11	0.12	0	1	0	0.00	0.00		1.0
9	6	−60 (17)	−63 (9)	9.80	1,725	0.03	2	10	1	0.05	0.17		1.2
10	6	−57 (8)	−41 (8)	9.66	4	0.16	0	0	1	0.00	0.06		1.0
11	8	−53 (26)	−38 (31)	6.26	20,807	0.03	86	682	657	0.38	0.55	3.2 (1.1)	1.3
12	8	−52 (17)	−52 (17)	6.55	3,928	0.10	2	443	65	0.32	0.30	2.1 (0.4)	1.2

MAD, median absolute deviation (see equation in materials and methods). Spike amplitude is denoted for both burst and nonburst spikes. Signal-to-noise ratio (SNR) is defined as the mean nonburst spike amplitude divided by MAD. Other deflections in spike range is a measurement of the noise and activity recorded from other neurons on the electrode that may confound spike detection and classification (for details of this calculation, see results). Intra-to-extra peak offset is the difference between the timing of the neuron’s spike as recorded by the extracellular electrode minus the timing of the same as recorded by the patch pipette, with details as follows: the timing of the maximum of the derivative of the mean patch-recorded spike waveform is defined as 0, and the reported offset is the time elapsed after 0 representing the maximum deflection of the mean extracellular spike waveform. We use a minimum spike detection threshold of 2·MAD and so report the number of spikes below it (as detected on the extracellular trace). To look at the number of spikes with amplitudes near or in the noise, we defined a noise range of between 2 and 6 times MAD, based on spike detection thresholds found in the spike sorting literature. (For most neurons, most extracellular spikes were greater in amplitude than 6·MAD.) Spikes in this range may be lost in the spike detection step of spike sorting. We report the number and portion of spikes, nonburst and burst, in this range, relative to the total number of nonburst and burst spikes, respectively. For some recordings burst spikes in particular are found in this range. Mean burst spike number (e.g., 2, 3, 4, …) is reported for the burst spikes in the 2–6·MAD range for each recording. Half-width ratio is the half-width of the mean burst spike divided by the half-width of the mean nonburst spike. When half-width ratio is 1, the mean burst and nonburst spikes have the same width; when half-width ratio is >1, the burst spike is longer than the nonburst spike. Mean values are reported as means (SD).

Visual stimulus.

A small (4 × 6-in.) LCD screen was placed at a roughly 45° angle with respect to the mouse’s anteroposterior axis, in the mouse’s right visual field. Roughly 7.6 min of a visual stimulus were played, consisting of sinusoidal drifting gratings (generated with Psychtoolbox) and/or a natural scene of reeds blowing in the wind (from the Chicago Motion Database, courtesy of Stephanie Palmer’s laboratory, University of Chicago) to elicit neural activity. The drifting grating presentation consisted of 10 s of gray screen, followed by the presentation of a sinusoidal drifting grating of a particular orientation (12 different orientations separated by 30° each, 1 cycle per second, 1/720 cycles per pixel) for 2 s, followed by 1s of gray screen, with each orientation (and subsequent gray screen) repeated 12 times in a pseudorandom fashion. A photodiode was placed in the lower left of the LCD screen and was digitized along with the patch signal, for synchronization. A typical recording session consisted of one or more 7.6-min presentations in succession. For neurons in which the drifting gratings and natural scene were presented in succession, the recording that exhibited the greatest mean extracellular spike amplitude (as explained above) was analyzed, with the exception of one recording that had the greatest spike amplitude but appeared to exhibit drift in its extracellular signal (that is, the extracellular spike amplitude decreased over time throughout the recording, although this was not quantified in detail). The absolute value of the difference of the mean spike amplitude between multiple recordings of the same neuron was, on average, 7.4% (4.1%) (n = 7 neurons from 5 mice).

Data acquisition and processing.

For a subset of recordings (n = 5), separate systems were used to acquire signals from the patch-clamp pipette (pClamp software with Multiclamp 700B amplifier, Molecular Devices CV-7B headstage amplifier, and DigiData 1440A for digitization) and electrode array (Intan RHD2000 evaluation system), each using a sampling rate of 25 kHz. To account for potential clock drift, a 25-Hz square-wave synchronization pulse was recorded by both systems, for post hoc temporal alignment. The rest of the extracellular array recordings (n = 7) were acquired with a direct-to-drive data acquisition system (Willow system, LeafLabs; Kinney et al. 2015) at 30 kHz simultaneously with the patch-clamp signal acquired on the Multiclamp as before and routed for synchronized digitization with the electrode array signals. For our spike sorting style analyses, both the patch-clamp and electrode (“extracellular”) data were initially bandpass filtered from 100 to 6,000 Hz (2nd-order IIR Butterworth), to isolate the spikes in the signal.

Spike detection on the patch recordings was performed as follows. For whole cell recordings, spikes were detected by threshold crossing, usually set halfway between the spike peak and resting potential. Spike thresholds were increased as necessary if the membrane did not fall below the original threshold during bursts. Cell-attached recordings were noisier than whole cell recordings. For cell-attached recordings, we used the peak of the derivative of the voltage (rather than the voltage itself), which allowed for easier discrimination of spikes over noise. We applied a matched filter to enhance the waveforms corresponding to the derivatives of the cell-attached voltage and to suppress spurious spikes resulting from signal jumps across two time bins (a phenomenon occasionally observed in cell-attached but not whole cell recordings, presumably an artifact of motion). The timing of the patch-reported spikes (“patch spike times” for short) of both whole cell or cell-attached recordings was calculated by taking the time of the maximum of the derivative of each spike. This was chosen because the derivative of an intracellular voltage has been previously demonstrated to relate to the rising phase of the extracellularly measured spike voltage (Anastassiou et al. 2015; Freygang and Frank 1959; Henze et al. 2000). In practice, there was typically less variability in the timing of the intracellular derivative maximum relative to the extracellular spike trough than with the timing of the raw intracellular waveform maximum relative to the extracellular spike trough.

Once we had spike times, bursts were identified for each neuron. A spike was considered within a burst if it occurred within 20 ms after an earlier spike, a criterion used, for example, in Staba et al. (2002). Each spike in a burst was numbered.

For the descriptive analyses of the extracellular correlates of intracellular spikes (see Fig. 3B, bottom; Fig. 4E, bottom; Fig. 4H, bottom; Table 2), extracellular spike amplitude was calculated as the minimum extracellular voltage (bandpass filtered from 100 to 6,000 Hz with a 2nd-order IIR Butterworth) within ±1 ms of each patch spike time. The extracellular recording of neuron 4 had large artifacts, presumably due to motion, so values reported in Tables 1 and 2 were post mean subtraction (as described below; table values for other neurons were before mean subtraction).

Fig. 3.

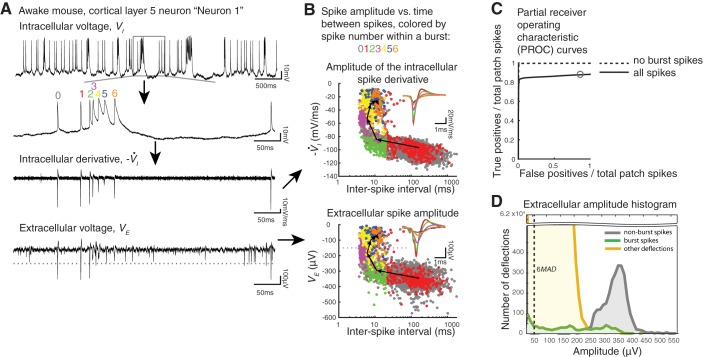
Evaluation of detection and classification of burst spikes via simple thresholding. A: voltage traces from a neuron in layer 5 of the primary visual cortex of an awake, head-fixed mouse (neuron 1 from Fig. 2C). This exemplar neuron had the largest mean extracellular spikes among all our recordings (n = 12 recordings from 7 mice). Top: 5 s of whole cell patch recording (current clamp) of spikes recorded during delivery of visual stimuli (see materials and methods). V_I, intracellular voltage. 2nd from top: zoom-in to 500 ms of the top recording containing a burst, with spike number within a burst labeled with numbers and colors. A nonburst spike is labeled with a gray 0. The set of all spikes, for a given neuron, with a specific label (e.g., green 2) is referred to as a “burst spike group.” 2nd from bottom: the negative of the derivative (−V̇_I) of the trace immediately above. Bottom: the extracellular voltage (V_E) trace (bandpass filtered, 2nd-order infinite impulse response Butterworth, 100–6,000 Hz) from 1 electrode of a colocalized, 256-electrode recording. This electrode exhibited the greatest mean extracellular spike amplitude and is referred to informally as the “closest electrode.” For use in computing partial receiver operating characteristic (PROC) curves later, we plot an example threshold as a gray dotted line (at −150 μV). B: spike amplitude vs. bursting state for the neuron in A. Bottom: spike amplitudes measured on the “closest electrode” (as in bottom trace in A) at the times of patch-clamp-measured spikes, labeled with colors/numbers as in A, plotted vs. time since the previous spike (on a log scale, with spikes of later burst spike groups plotted on top of those of earlier ones). Gray dotted line corresponds to the threshold plotted in A, bottom, and is used to define a particular point on the PROC curve in C. Each black arrow points from the mean (voltage, time) coordinate of a particular burst spike group to the mean of the next burst spike group. Inset: mean extracellular spikes for each burst spike group, color coded as in A, and overlaid (with later burst spike groups on top of earlier ones). Top: as at bottom, but for peaks of the negative of the derivative of the intracellularly measured spikes (as shown in A, 2nd from bottom). C: PROC curve (e.g., true positive rate vs. false positives divided by patch spikes, plotted as a threshold, such as indicated by gray lines in A and B, is systematically varied) for the “closest electrode” recording of the neuron in A. True positives (TPs) correspond to extracellular spikes with amplitude above the threshold and that occur within 1 ms of the times of patch-reported spike times, expressed as a fraction of the total number of patch spikes; false positives (FPs) correspond to the number of detected extracellular spikes that do not occur within 1 ms of a patch spike time, expressed as a ratio to the total number of patch spike times. Gray circle corresponds to the TP and FP values associated with the −150-μV threshold shown in A and B. We generated such curves when all spikes were considered (black line) as well as when bursting spikes (e.g., spikes that were preceded by another spike within 20 ms, in the patch-clamp recording) were eliminated (black dashed line). D: histogram of extracellular voltage deflections greater than the chosen noise floor of 2 times the median absolute deviation (MAD) across the entire recording, with nonburst (gray) and burst spikes (green) of the patched neuron as well as other deflections (yellow).

Fig. 4.

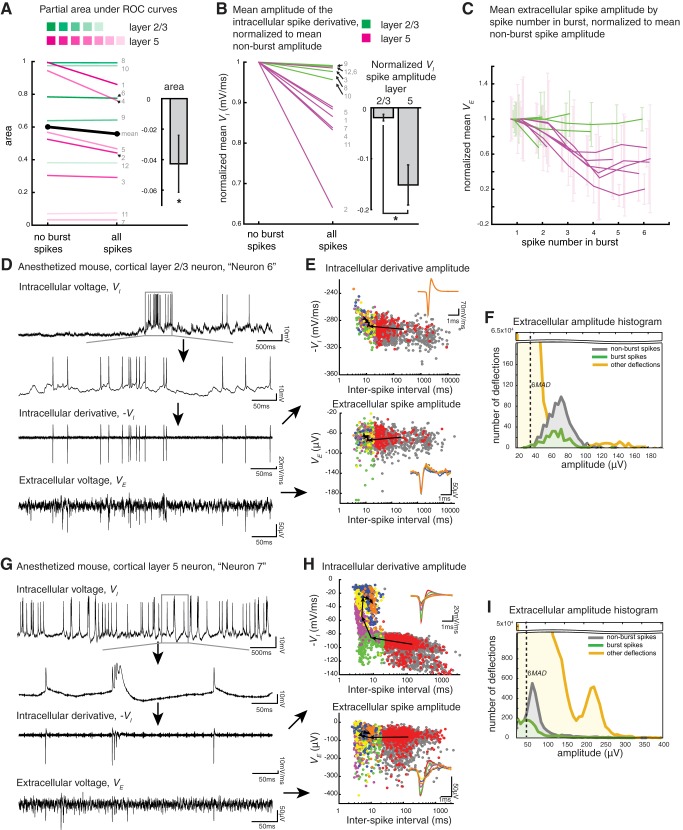
Characterization of bursting in cortical cell layers 2/3 and 5. A: partial areas under the partial receiver operating characteristic (PROC) curves (PAUC) for each of the 12 neurons, in the no-burst spikes vs. all spikes conditions, for layer 2/3 (green) and layer 5 neurons (magenta), as well as the mean across all 12 neurons from 7 mice (black). Neuron number, as in Fig. 2C, is shown in gray, and line darkness is determined by the amplitude ranking introduced in Fig. 2C (neurons are rank ordered within a cell layer, and the darkest shade represents the patched neuron with a highest mean spike amplitude on the closest electrode, with decreasing darkness as indicated for smaller spike amplitudes). Inset: PAUC difference (Δ area) between the all-spikes vs. nonburst conditions (mean across neurons; error bar is SE). *P = 0.0432, paired t-test (n = 12 neurons from 7 mice). B: mean amplitude of the intracellular spike derivative, normalized to mean nonburst amplitude for each neuron, in the no-burst spikes vs. all spikes conditions, for layer 2/3 (green) and layer 5 neurons (magenta), with neuron numbers as in A. Inset: normalized intracellular derivative of spike amplitude difference (Δ) between the all-spikes vs. nonburst conditions, for layer 2/3 vs. layer 5 neurons (mean across neurons in each cell layer; error bars are SE). *P = 0.0195, 2-sample t-test between layer 2/3 neurons (n = 5 neurons from 4 mice) and layer 5 neurons (n = 7 neurons from 5 mice). C: change in extracellular spike amplitude by spike number in burst. For each recording, mean extracellular amplitude (V_E) is normalized to the mean amplitude of the first spike in the burst and plotted for burst spike numbers 1–6. Values are only plotted if there were at least 5 spikes at that burst number. Errors bars are SD, shifted slightly along the x-axis for better visibility. As in B, layer 2/3 neurons are shown in green and layer 5 neurons in magenta. D–F: as in Fig. 3, A, B, and D, but for a representative (in terms of extracellular spike amplitude) neuron in cortical layer 2/3 of an anesthetized (0.5–1.2% isoflurane) mouse (neuron 6 from Fig. 2C). V_I, intracellular voltage; −V̇_I, negative derivative of intracellular voltage; 6MAD, 6 times median absolute deviation. G–I: as in C–E, but for a representative cortical layer 5 neuron (neuron 7).

Detection and classification analyses.

For analyses of the how well spikes can be detected and classified in the extracellular traces, we first bandpass filtered the extracellular traces from 100 to 6,000Hz (2nd-order Butterworth IIR) and performed a mean subtraction to remove potential artifacts that were shared across electrodes. Specifically, we calculated the mean time series trace across all recording sites (mean of each voltage at a particular time point, calculated for all time points), trace_mean, and then multiplied it by a weight of magnitude, m_i, and subtracted it from the trace of each individual recording site, trace_j. The magnitude m_i was calculated as (trace_mean·trace_i)/(trace_mean·trace_mean), similar to Ludwig et al. (2009). These traces were multiplied by −1 so that spike deflections would be in the positive direction.

Thresholds are often used in various forms of spike sorting, with the choice of threshold representing a trade-off between letting in false positive spikes and losing false negative spikes. For this study, we wanted to present a general methodology for evaluating spike sorting quality of a given electrode array that emphasized intuition, so we varied thresholds systematically rather than picking a single threshold. We then used receiver-operator characteristic (ROC) analyses, standard statistical analyses for binary classifiers. We performed these analyses on both the preprocessed extracellular traces and the intracellular voltage estimators we developed (and that are described subsequently below).

ROC analyses look at the trade-off between false negatives and false positives across a range of thresholds. For an analysis with N = 100 thresholds, we collected the set of deflections above the threshold, θ_i, with i∈[1,⋯,100], calculating the values of θ_i as described below. For each deflection, we then recorded the value and time of the deflection peak. For the intracellular voltage estimator (see below), deflections were collected from the estimator (for cell-attached recordings) or the derivative of the estimator (for whole cell recordings), to make such traces more similar to the bandpass-filtered extracellular voltages or to the intracellular traces as we processed them for spike time extraction. We set our minimum threshold to two times the median absolute deviation, θ_i = 2·MAD, to capture low-amplitude spikes. [We find that, at worst, this threshold finds 97% of the patched neuron’s spikes (neuron 7, 141/4,640 spikes missed, Table 1; <2·MAD, Table 2), and more commonly, 0 or <10 spikes are missed by this threshold (<2·MAD, Table 2).] Our maximum threshold, θ_N, was set to the maximum of the extracellular trace or the estimator (for cell-attached recordings) or the derivative of the estimator (for whole cell recordings). The rest of the thresholds were spaced evenly between θ_i and θ_N. These sets of deflections may include spikes from the patched neuron, spikes from other neurons, and noise deflections.

For a given threshold level, deflections derived as above were defined as true positives (TP) or false positives (FP) by comparing their timing to ground truth patch spike times as follows: we iterated over the patch spike times, and whenever there was a deflection within ±1 ms of a given patch spike time, TP was increased by 1. After this process was complete, the remaining deflections that had not been classified as TP were defined as FP (i.e., FP = signal spike times − TP). Histograms showing the numbers of TP and FP for extracellular traces by amplitude (threshold) can be found in Fig. 3D and Fig. 4, F and I, where TP numbers are split into burst and nonburst spikes and FP are labeled “other deflections.” (Note that for these plots, mean subtraction was not performed.)

Next, TP rate (also known as sensitivity) was calculated by dividing TP by the total number of patch spike times. When TP rate is 1, there are no false negatives, i.e., no missed ground truth spikes. ROC analyses most commonly plot the TP rate vs. the FP rate, where the FP rate is FP/total negatives. However, by setting our minimum threshold very low, there were tens of thousands of FPs at lower thresholds (note the y-axis break in Fig. 3D and Fig. 4, F and I). We were interested in threshold-style spike sorting performance at thresholds before the FP overwhelmed the TP and thus focused our analysis on a partial ROC (PROC), limiting the analysis to when FP is less than or equal to the total number of patch spike times. We normalized FP by the total number of patch spike times to aid in comparison across recordings. When FP/total spikes = 0, there are no FP, and when FP/total spikes = 1, there were as many deflections in the signal that did not match the ground truth spikes as there were ground truth spikes. (FP/total spikes is related to the FP rate by a constant: FP/total spikes = total negatives/total spikes × FP rate.) As we iterated across threshold levels, the trade-off between TP rate and FP/total spikes was summarized by the PROC curve, with TP rate and FP/total spikes plotted on the vertical and horizontal axes, respectively (see e.g., Fig. 3C, solid line).

To analyze the effect of bursting on spike sorting, PROC curves were generated in the following fashion: FP values were calculated as described above, but we calculated TP values after removing the times of burst spikes from patch spike times (“nonburst patch spike times”) and calculating TP rate by dividing by the number of nonburst patch spike times (see e.g., Fig. 3C, dashed line). For this analysis and for the generation of all PROC curves in this paper, the “nonburst spikes” group includes the first spike in any burst, as well as spikes not within bursts.

The PROC curve is summarized by the partial area under the PROC curve (PAUC; Krzanowski and Hand 2009), where FP/total patch spikes ∈[0,1] (see e.g., Fig. 4A) and captures in a single number the possible performance of a given electrode array, for a given neuron, in terms of spike detection across thresholds. If many TPs can be detected before a substantial number of FPs are detected, the PROC will rise steeply and the PAUC will be large. A PAUC value of 1 indicates that a threshold exists such that there is perfect classification, i.e., no FP or false negatives.

Intracellular voltage estimator.

Given that our automated system acquires ground truth patch data, we wanted to utilize these data in an automated method to evaluate the potential performance of spike sorting for different electrode array configurations. We used the known patch voltage as our transformation target because it contains large, detectable deflections at the patched spike times. Because the frequency content and timing of patch vs. extracellular spike waveforms are different from each other (and in fact vary from extracellular electrode to electrode; see Fig. 2, A–C, as well as Gold et al. 2006), we first needed to find filter kernels with which to convolve the extracellular traces, which would transform the frequencies and timing of the extracellular spike traces into those of the patch trace. Once we had convolved the extracellular traces with these kernels, we regressed these convolved extracellular voltage traces against the intracellular trace to create intracellular voltage estimators.

In outline, we modeled our estimate of the intracellular voltage as an extracellular voltage convolved with a filter kernel plus noise (see appendix for detail). Because of the convolution theorem, we could transform our equation to Fourier space, which simplifies it into the familiar equation of a line. We could then perform simple linear regression to derive the slope separately for each frequency, and inverse Fourier transform the equation to reveal our minimal mean squared error kernel (see example in Fig. 5B, step 1).

The process was as follows: first (“0”), data were preprocessed. Both the extracellular voltage traces and patch-clamp voltage trace were filtered (bandpass, 2nd-order IIR Butterworth, 100–6,000 Hz) to remove nonspike information. The extracellular voltage traces were mean-subtracted with respect to the other working electrodes (as described previously in Detection and classification analyses) and then zeroed out everywhere but ±4 ms from the patch spike times. 1) The zeroed and filtered extracellular traces and filtered patch trace were then Fourier transformed in bins of 512 time points, which overlapped twofold and were apodized with a Blackman window. This bin value, which corresponds to 17 ms for a recording sampled at 30 kHz, or 20 ms for a recording sampled at 25 kHz, was chosen to conservatively encompass spike waveforms and capture rich frequency information. For each extracellular trace, a separate simple linear regression was then performed for each frequency between these signals (extracellular and intracellular), and the resulting regression coefficients were inverse Fourier transformed to obtain the convolution filter kernel (example in Fig. 5B, step 1). 2) The kernels were applied to their respective filtered extracellular voltage traces (not the selectively zeroed time series; Fig. 5, A and B, step 2). 3) The resulting convolved traces from some specified n extracellular traces were regressed on the intracellular voltage trace (Fig. 5, A and B, step 3), creating new estimators. Spike detection and classification was performed on these intracellular voltage estimators as described in Detection and classification analyses.

Histology.

Of the 16 recordings made utilizing the pipette location model, 3 were performed in mice where only a single whole cell recording was made; the brains of these mice were selected for histological analysis. Of these three brains, two appeared to have a single neuron labeled (Fig. 1G), albeit with some background staining, whereas the signal from a single neuron was not clear in the third brain. Brain slices of 40 μm were prepared using the protocol of Kodandaramaiah et al. (2012), with incubation performed using streptavidin conjugated to Alexa-488 for visualization of the biocytin-filled neuron. Slices were imaged with a confocal microscope (Zeiss) with a ×20 lens. Data presented in Fig. 1G are from maximum intensity projections of a single brain slice, performed in ImageJ.

Statistics.

Statistics were computed using GraphPad Prism 7. For repeated-measures ANOVAs and Dunnett post hoc tests, sphericity was assumed (repeated-measures ANOVA in Prism 7). If statistics were rerun without sphericity assumed (repeated-measures ANOVA with Geisser-Greenhouse correction in Prism 7), a Geisser-Greenhouse correction was used, which generally raised the P value of both the ANOVA and post hoc test results. In this case, the main effect in the ANOVAs of Fig. 5, C and D, remained statistically significant (P = 0.0069 and P = 0.0214, respectively), but the results were altered as follows. The statistically significant difference between the full density and quarter density groups in Fig. 5C remained, however now with P = 0.0410. The statistically significant difference between the 64-electrode and 1, 2, and 4 electrodes remained (P = 0.0345, 0.0479, and 0.0306, respectively), but the 64- vs. 8-electrode comparison was no longer significant (P = 0.0719).

Data and analysis sharing.

All raw data from this paper, as well as code to generate figures, is publicly available on the website http://scalablephysiology.org .

RESULTS

A strategy for dual automated patch clamp and extracellular electrode array recordings in vivo.

We developed a way to automatically colocalize a patch pipette for whole cell recording and an extracellular multielectrode array in vivo (Fig. 1A). Without such a strategy, our initial attempts at dually recording from the same neuron with both a patch pipette and an electrode array were unsuccessful: either the patched neuron was not detectable on the array, or the pipette resistance would precipitously drop (e.g., from 7 to <3 MΩ) while being lowered. We took the latter as evidence that the pipette may have collided with the array. On trials in which that happened, we observed a large, 20-Hz square-wave signal on one or more electrodes of the array (>200 μV, peak to peak, after filtering; bandpass, 2nd-order IIR Butterworth, 100–6,000 Hz) that increased with each pipette step (up to perhaps 1,000 μV) just preceding the collision, time-locked to the 10-mV, 20-Hz square wave being applied to the patch pipette. We hypothesized that by monitoring the patch pipette signal on the electrode array, we could slow down or halt the movement of the pipette in an optimal way, obtaining neurons that were dually recorded, while avoiding patch pipette collision with the electrode array.

In initial testing, our patch pipette emitted 20-Hz square-wave pulses of ±10 mV, as the autopatcher “hunted” for a neuron by advancing in discrete, 2-μm steps, as in the original autopatcher protocol (Fig. 1A; Kodandaramaiah et al. 2012). Because the signal from the pipette was not noticeable on the extracellular signal until a collision was imminent, we increased the pipette square-wave amplitude to ±100 mV, which allowed us to sense the signal on the electrode array upon initial pipette insertion, with a pipette tip-to-electrode array distance that was stereotaxically estimated to be 150–200 μm. Once a neuron was detected, the square-wave pulses used to measure resistance were lowered back to ±10mV, the normal range of autopatcher operation.

For some of our 51 recordings (n = 35), we estimated when the pipette tip and electrode array were sufficiently close, by a combination of readings from actuators, which may not have been in perfect alignment, and by intuition gleaned from several pipette insertions in which these voltage pulses were sensed as a large (>200 μV) and increasing (with each pipette step) signal on at least one electrode of the array preceding a collision. Of the 35 recordings obtained in this way, 21 had extracellular spike amplitude >15 μV, and 9 had amplitude >50 μV. With this system we observed 13 pipette-to-array collisions in addition to the 35 successes, for a collision-free yield of 35/(13 + 35) = 73%.

For the remaining recordings (n = 16), we used a model for predicting collisions, which we developed and then periodically queried during the neuron hunt to stop pipette movement appropriately (Fig. 1B, exemplar recording). To isolate the pipette signal on the electrode array, we first Fourier transformed the voltage on each electrode and extracted the amplitude of the 20-Hz time bin. We found that the resulting electrode array signals could be fit with a 1/r falloff model (Fig. 1C) when sensed across the electrodes of the array, consistent with the pipette tip playing the role of a point source in a resistive medium. The known spacing between the electrodes on the array was used in the model to provide a calibration of absolute scale, and thus allowed us to infer the absolute distance between the pipette tip and the electrode array (although this was not validated precisely, so we call this distance the inferred distance in this paper). As the pipette advanced toward the electrode array in 2-μm steps, the falloff curve evolved (Fig. 1D), and the R² value for the goodness of fit with a 1/r curve was monitored (Fig. 1E). For 4 of 16 recordings, one or two negative R² values were observed, indicating a bad measurement or curve fit, and these data points were excluded from analysis. These constituted 2/51, 1/24, 1/119, and 1/33 measurements for their respective recordings, for a total of 5 bad data points out of 451 data points when pooled across all 16 recordings (1.1%). We attempted to patch a neuron if the autopatcher detected one with an inferred distance from the array between ~15 and ~50 μm.

Beyond observing high R² values, which gives confidence in the model, we did not do any further calculations in real time to assess the accuracy of the fit. We did, however, perform a post hoc evaluation of how well the model estimates at each step conformed to a best-fit line of the trajectory of the pipette in 3-D space as it was advanced into the brain (Fig. 1F for exemplar, Fig. 1H, top, for population data). Although residual error was often in the 5- to 10-μm range for our recordings (Fig. 1H, top), such as in this example, some fits were noisier, with occasional jumps in predicted distance of 25 μm or higher between 2-μm steps of the pipette (Fig. 1G). Histological validation of this system was attempted for three recordings, with two recordings each yielding one neuron labeled and a clearly visible track from the extracellular probe (Fig. 1G left and second from left). The final model estimate corresponded well to the histologically determined distance between filled neuron and probe track (40 vs. ~40 μm) in the former recording and less well in the second recording (55 vs. ~75 μm). We note that there were only four data points in the latter recording, and sometimes distance estimates appeared to improve as the pipette advanced toward the array (Fig. 1G, second from right), although this was not always the case (Fig. 1G, right).

Our methodology may be synergistic with the stereotaxic positioning apparatus recently reported (Neto et al. 2016). Of the 16 recordings obtained using this system, 8 and 3 neurons had extracellular spike amplitude >15 and 50 μV, respectively. We detected a single probe collision after implementation of this system out of 27 trials, but it occurred before we started to periodically query the model; this was presumably due to a gross actuator misalignment.

Colocalized recordings: basic properties.

We chose the 12 neurons with the largest extracellular amplitude to explore their value in examining the recording power of a given array, a close-packed electrode array of our design, with electrodes spaced by just a few micrometers apart (Scholvin et al. 2016). Such a close-packed array allowed us to analyze the resulting dense signals and examine how such spatial oversampling strategies might contribute to spike sorting capability. These neurons were recorded in putative (i.e., estimated based on pipette stereotaxic depth) cortical layer 2/3 (n = 5) or layer 5 (n = 7) of primary visual cortex in anesthetized (0.5–1.2% isoflurane), head-fixed mice. For two of these recordings, isoflurane was turned off after a whole cell patch-clamp recording was obtained, and awake recordings took place 15–20 min later, well after the animal’s first postrecovery whisking motions (see Table 1.) All recordings were ~7.6 min long, and data presented in this paper are from the first 456 s of the recording, for comparison across recordings, including those that were slightly longer than 456 s. The neuron recorded by the patch pipette was localized (Fig. 2A, middle) to the region interrogated by our array of close-packed electrodes [~9 × 9-μm electrodes spaced ~2 μm apart, with 64 (n = 1), 128 (n = 4), or 256 electrode (n = 7) counts, arranged in 2 or 4 columns]. Ten of our patch recordings were made in the whole cell configuration and two were made in cell-attached mode (Table 1, type). When the patched neuron spiked (Fig. 2A, left), these spikes were also sensed by the extracellular electrode array, and the patch-reported spike times were then used to identify the associated extracellular spike waveforms. The mean waveform sensed by each electrode is shown in Fig. 2A, right, averaged over all the extracellular spikes identified by their association with patch-reported spike times. Because waveforms of spikes within a burst may differ significantly from those of nonburst spikes (or the first spike of a burst), later burst spikes (2ⁿ-th spikes within a burst) were not used when the mean waveforms were computed. We defined a burst spike as a spike that occurred within 20 ms of the previous spike, a criterion used, for example, in Staba et al. (2002). The plot of mean waveforms across the extracellular electrode array helped visualize the spatial extent of where a patched neuron’s waveforms ended up (Fig. 2A, right, generated from 845 spikes; Fig. 2B for a neuron recorded in the cell-attached configuration, generated from 199 spikes).

To visualize how spike waveforms varied across electrodes in a compact way, we ordered all of the working electrodes (see materials and methods) for each recording by their mean spike amplitude, from largest to smallest. We then plotted the mean waveforms (excluding spikes within a burst) for the 2ⁿ-th ordered electrode for each patched neuron, where n = {0, 1, 2, 3, 4, 5, 6} (Fig. 2C), so that the falloff of amplitude across electrodes, thus rank ordered, could be rapidly visualized. Using these close-packed arrays, we found that the spatial extent of the signals picked up from a single neuron typically spanned hundreds of micrometers (Fig. 2A, right, and Fig. 2B). Future colocalized experiments might find that such spatial signatures of neurons are predictive of their locations or cellular properties. Neurons with such a wide spatial extent of extracellular voltage may bias analyses of spike-triggered local field potential (LFP) when their spikes bleed into the LFP frequency spectrum and contaminate the spike-triggered LFP (Ray 2015). Ray (2015) reviewed the challenges of spike-triggered LFP based on models. Our colocalized recording technique could enable investigators to empirically examine such phenomena and derive, in the future, best practices for spike-triggered LFP analysis.

Evaluation of spike detection on the “closest electrode” via simple thresholding.

Using this set of 12 recordings, we explored what such colocalized neuron spiking data could reveal about the spike sorting capability of a given multielectrode array. To set the stage, we first defined a few initial terms and analyses. For a given dual recording, we identified the electrode pad with the greatest amplitude spikes that correspond to the patch-reported spikes, which we informally refer to as the “closest electrode.” This is the electrode with the highest amplitude copy of the patched neuron’s spiking activity, and thus is a good place to start when looking for intuitive measures of spike quality. To measure the noise dispersion of an extracellular trace, we use the median absolute deviation (MAD), which unlike standard deviation is not greatly influenced by outliers (e.g., spikes), making it a robust statistic (see materials and methods for further detail). In previous extracellular literature, MAD is sometimes referred to as the standard deviation of the noise (e.g., in Quiroga et al. 2004). In Table 2, we report MAD for the “closest electrode” for each recording (range: 6–14 μV).

Next, we examined the spike amplitude on the “closest electrode” for each recording. In Table 2, we report these amplitudes, split into nonburst and burst spikes. Nonburst spikes include all spikes not in a burst, as well as the first spikes of bursts. We examined nonburst and burst spikes separately because burst spikes sometimes have lower spike amplitudes than nonburst spikes (discussed in more detail in Evaluation of detection and classification of burst spikes via simple thresholding). The 12 recordings we chose for detailed analysis had mean nonburst spike amplitudes >50 μV; the neuron with the highest such amplitude had a nonburst spike amplitude of −267 (124) μV. We calculate the SNR as the mean nonburst spike amplitude divided by MAD, which ranged from 5 to 19 across these recordings. This measure is not a full picture of how detectable patched spikes are on the “closest electrode,” because many of the spike amplitudes have large variance (see spike amplitude and SD values in Table 2 and amplitude distributions in Fig. 3B and Fig. 4, E and H).

Having established some basic analyses, we next sought to begin to characterize the spike sorting capability of a given multielectrode array. An initial step in spike sorting is spike detection, in which potential spikes from extracellular traces are gathered so that they can be categorized as spikes from individual neurons or noise. Most spike sorting algorithms use thresholding for spike detection, which simply and intuitively records all the deflections crossing a particular threshold from an extracellular trace. A multiple of a noise dispersion measure of the trace, usually standard deviation or MAD, is commonly used to set this threshold. A lower threshold is likely to capture more spikes but also may let in many noise deflections that must be correctly identified and categorized as not spikes in the spike sorting process. We were interested in using our data to describe the impact the initial threshold may have on spike sorting, specifically by looking at the spikes from a single neuron that may be lost in this detection step. A review of the literature found that thresholds were commonly set in the range of two to six times the study’s noise dispersion measure (Leibig et al. 2016; Marre et al. 2012; Quiroga et al. 2004; Rossant et al. 2016; Swindale and Spacek 2014). On the basis of these numbers, to quantify potential spikes lost, we look at the spikes in a thresholding range we defined as 2–6·MAD. (The lower bound is set by our minimum analysis threshold of 2·MAD, see materials and methods for more details and spike counts <2·MAD in Table 2.) In the thresholding range data in Table 2, we count the number and portion of spikes in this range between 2 and 6 times MAD, split into burst and nonburst spikes. We find that most of our recorded neurons (8/12) have 5% or less of their nonburst spikes in this range. However, three neurons have >30% of their nonburst spikes in this range, and one neuron has >60% of its nonburst spikes in this range; these three neurons also have three of our four lowest SNRs (Table 2). For some patched neurons, we see a larger portion of the neuron’s burst spikes in the 2–6·MAD range than nonburst spikes; these neurons have lower amplitude burst spikes than nonburst spikes (see portion of spikes for neurons 1, 4, and 5 in Table 2). Because we are looking at the extracellular traces from the “closest electrode,” which has the highest amplitude, spikes in this 2–6·MAD range are unlikely to appear above this range on other extracellular electrodes. Differences in noise on different electrodes will lead to some differences in which spikes cross a given threshold, even if the spike amplitude on another electrode is lower.

These data highlight that spikes will be omitted from spike classification steps of spike sorting, having been lost at the spike detection step, even with the recording advantages of multielectrode arrays where each recording site is another opportunity to record a neuron’s spikes at a high magnitude or SNR. The set of spikes assigned to each neuron at the end of spike sorting may be incomplete, due not to poor categorization but to the spikes not having been available to be categorized. As we show in our demonstration data set, for some neurons this could be more than half the spikes, which would give a very inaccurate picture of the spiking on that neuron and might lead to major biases in analyses after spike sorting. This potential loss of spikes in the spike detection step of spike sorting may be partially ameliorated by spike sorting methods that perform spike detection, categorize (or “sort”) those spikes into sets of spikes from individual neurons, and then perform a second detection step on the extracellular traces based on the distributions of spike waveforms found in the sets of sorted spikes (e.g., convolving with a spike waveform template). Colocalized recordings with ground truth spike times are necessary to characterize this issue and design spike sorting methods to handle it accurately.

We are also interested in the number of spikes from neurons other than the patched neuron that are reported on the “closest electrode.” A particular neuron’s spiking activity may appear with high SNR on an extracellular electrode, with all spikes above the detection threshold, but if one or many other neurons also have high SNR spikes on that electrode, the categorization of spikes from said particular neuron, at least with a simple threshold, may be difficult. To represent how many spikes from other neurons (and noise deflections) are in the same amplitude range as the patched neuron’s spikes, we count all the deflections greater than the mean amplitude minus one standard deviation of the patched neuron’s nonburst spikes (Table 2, other deflections in spike range). We see that some recordings have as few as four other deflections in spike range, whereas others have tens of thousands of other deflections in spike range. Thus application of simple thresholds to data jointly acquired from the same neuron, via simultaneous patch and extracellular array recording, can be used to gain some intuition into the frequency of confounds to spike sorting when using an extracellular multielectrode array.

Evaluation of detection and classification of burst spikes via simple thresholding.

As another example of an analysis we could do with our system to evaluate a performance characteristic of a given extracellular array, we examined the impact of burst spikes on a simple thresholding model of spike sorting. Nine of 12 of our patched neurons burst at least 50 times during the 456-s recording session analyzed (Table 1, burst count). Bursting is known to modulate spike amplitude and shape in extracellular recordings (Henze et al. 2000), but such changes are difficult to characterize without ground truth spike times because an electrode typically senses the spikes of several neurons in its immediate vicinity. When later spikes in a burst have lower amplitude or a changed shape, they may be classified as spikes from other neurons (as described in Chung et al. 2017) or be lost below the detection threshold. In Table 2, we give the spike amplitudes for burst spikes vs. nonburst spikes. Eight of our recordings had a >10-μV difference in mean spike amplitude in burst vs. nonburst spikes. As a metric for the change in spike waveform shape during bursting, we analyzed spike half-width (i.e., the width of the spike at half-maximal spike amplitude) for the mean nonburst spike vs. the mean burst spike, calculating the ratio for each recording (Table 2, half-width ratio); values >1 indicate that a burst spike is longer in duration than a nonburst spike. Such changes in spike shape during a burst can result in misclassified or missed spikes.

To more systematically explore how spike amplitude varied with time since the preceding spike, as well as the number of preceding spikes, within a burst, we performed a number of analyses of how these parameters relate to each other. We explain these analyses in the context of an exemplar neuron (Fig. 3; neuron 1 in Fig. 2C and Tables 1 and 2), a cortical layer 5 neuron recorded in an awake mouse (that had earlier been anesthetized with isoflurane but had since recovered). This neuron exhibited the largest extracellular spikes of all those we analyzed (Table 2, spike amplitude), and thus we use it for this initial illustration, before analysis of all the neurons. This neuron exhibited both single, isolated spikes as well as bursts of two or more spikes (Fig. 3A, top 2 traces). Later spikes within a burst (e.g., spikes 4 and 5 in Fig. 3A) often began from a voltage level elevated above baseline, and higher than the voltage preceding earlier spikes in the burst (e.g., spikes 1 and 2 in Fig. 3A). This bursting pattern, where some burst spikes were initiated at a higher voltage level, is similar to bursting of deep cortical neurons observed by other groups (Chagnac-Amitai and Connors 1989; Connors et al. 1982; Contreras 2004; Helmchen et al. 1999) and was also apparent in other layer 5 neurons in our recordings (e.g., Fig. 4G, top 2 traces).

How does the modulation of the intracellular spike waveform during a burst translate to changes in observed extracellular voltage? To explore this, we first looked at the negative of the derivative of the intracellular voltage (Fig. 3A, second trace from bottom) and compared its dynamics during bursting with those observed in the simultaneously obtained extracellular recording. We did this comparison because the derivative of the intracellular potential (V̇_I) has been experimentally observed to closely match the initial rising phase in the waveform of an extracellular spike (Anastassiou et al. 2015; Freygang and Frank, 1959; Henze et al. 2000). We denote the intracellular potential as V_I and the extracellular potential measured at the “closest electrode” as V_E. Many spikes in V̇_I (Fig. 3A, second trace from bottom) can be seen in V_E (Fig. 3A, bottom), but later events in the burst appear smaller or may be indistinguishable from noise. To characterize this modulation more systematically, we examined both V̇_I and V_E (Fig. 3B, top and bottom, respectively) for each spike, plotting them against the time interval since the previous spike (denoted as interspike interval). Plots for V̇_I and V_E both show a decrease in magnitude from early to late spikes in a burst, with a shape resembling an “L” with a corner around x = 20 ms. We note that this corner was not dependent on our chosen criteria of 20 ms for a spike being within a burst: although the coloring of the plot points depends on this cutoff, the shape of the curve does not.

For the neuron explored in Fig. 3, the first spike in a burst (red, n = 327) had a mean amplitude of 97 mV/ms (16) for V̇_I and −345 (60) μV for V_E. Later burst spikes had substantially lower amplitude, e.g., the fourth spike in a burst (yellow, n = 189) had mean amplitudes of 31 mV/ms and −100 (61) μV, respectively. This decrease in V̇_I and V_E magnitude represents a slowing of the initial rising phase of a spike during the progression of a burst. We can see shape change as a result of this slowing of the initial rising phase for burst spikes in Fig. 3B, inset, where we plot the intracellular and extracellular mean waveforms for burst spikes 1–6. Neuron 1 has the highest value of our measure of spike shape change; its half-width ratio is 1.7 (Table 2, neuron 1, half-width ratio). The decrease in V_E magnitude and spike shape, of course, has the potential to introduce errors, i.e., false negatives, or missed spikes, due to the reduction of magnitude, which could confound thresholding methods as well as methods of spike sorting that depend on stereotypy of spike shape over time.

We next sought to quantify how the burst-related changes in spike shape might affect spike detection. To get a general picture of the effect of bursting, independent of a given choice of threshold, in a simple and intuitive way, we decided to systematically vary the threshold and perform a ROC analysis, a standard statistical technique that allowed us to summarize the performance of spike detection across a range of thresholds. Instead of picking a single voltage threshold, which may be arbitrary, we systematically varied the threshold applied to the signal of the “closest electrode” and categorized all deflections above that threshold as TP or FP spikes by comparison with the patch ground truth. An example threshold of −150 μV is shown in Fig. 3A, bottom.

We defined a TP as a deflection in the extracellular signal that matched the timing of a patch-reported spike within 1 ms, with the timing of the patch-reported spike being the time of the maximum of the derivative of that spike; a maximum of 1 TP was assigned per intracellular spike. A FP was a deflection in the extracellular signal that did not match the timing of an intracellular spike. This deflection might be noise, or a spike from another neuron. We then created PROC plots. On the y-axis, we plotted TP rates (TP/total number of patch spikes) as thresholds varied. For the x-axis, we limited our analysis to when FP ≤ total number of patch spikes, to increase the dynamic range around the area of interest for a spike sorter. Specifically, it would likely make no difference to an electrophysiologist if FPs exceeded true spikes by 10 times vs. 100 times; in either case the recording may simply be deemed unworthy of further analysis, whereas knowing whether the FP rate was 10 vs. 30% may be useful. So that this partial ROC was comparable between recordings, we plotted FP on the x-axis divided by total number of patch spikes (see materials and methods for further description and rationale). We plotted this PROC for all the spikes (Fig. 3C, all spikes; the symbol corresponds to the −150-μV threshold level in Fig. 3A, bottom, and Fig. 3B, bottom). We then used the same method to create a second PROC curve but this time excluded spikes within a burst (as determined on the patch trace) in our calculation of the TP rate (Fig. 3C, no burst spikes). We note that the TP rate does not reach one in this PROC for all spikes (Fig. 3C), indicating that there is not a threshold such that all patch spikes are detected before FP becomes greater than the total number of patch spikes. When burst spikes are removed from the PROC (Fig. 3C), the TP rate does approach 1. This indicates that many of the burst spikes are mixed in with other deflections composed of spikes from other neurons and noise, and a simple threshold is unable to tell them apart. Given that bursting changes spike shape, spike sorting methods that depend on spike shape might also struggle; however, an explicit representation of burst spike number and timing might reveal patterns that could be used to facilitate classification, because clearly there is structure in how spike shape changes during a burst (e.g., Fig. 3B).

To examine how the activity of the patched neuron compared with the other electrical activity picked up on the extracellular electrode for this exemplar neuron, we plotted an amplitude histogram of extracellularly recorded nonburst and burst spikes that corresponded to the patch-reported spikes, as well as all other voltage deflections exceeding the 2·MAD noise floor across the entire recording (Fig. 3D). These latter voltage deflections may originate from other neurons or noise. Whereas nonburst spikes formed a clear peak, burst spikes were more mixed in with the other deflections. We note that for this neuron, 1% of the nonburst spikes (28) and 27% of the burst spikes (269) fall into our thresholding range, between 2 and 6 times MAD (Table 2, thresholding range) and thus have a potential to be lost to spike sorting before the spike classification process.

Characterization of bursting in cortical cell layers 2/3 and 5 using simple thresholding.

One opportunity offered by our automated dual recording system is the ability to examine how a given electrode array functions in different brain regions or cell layers. Our close-packed electrode arrays spanned multiple cortical cell layers, so we had an opportunity to assess whether spiking properties differed across cell layers in a way that would differentially confound attempts at spike detection and classification. Different brain regions contain different neurons with variable firing rate, spike shapes, and neural densities. Spike sorting algorithms may perform better or worse when based on these variables, but little data exists characterizing these differences. Biases introduced by varying spike sorting performance may impact downstream analyses of spike trains between different brain regions or between different neuron types in the same region. In this paper, we use our technique to explore one example of differences in spike sorting performance between two brain areas that may bias downstream analyses.

To systematically explore the population of 12 recordings, we used PAUC as a performance measure (Krzanowski and Hand 2009). The value of PAUC ranges from 0 to 1, where a value of 1 indicates that there are no false positive or false negative deflections for any given threshold (see materials and methods). For each recording, we calculated PAUC for all spikes and nonburst spikes (Fig. 4A, left) for layer 2/3 and layer 5 neurons, as well as a group mean. When values for all neurons were pooled, the PAUC value when all spikes were considered was significantly less than the PAUC value when only nonburst spikes were considered, indicating decreased spike detection performance (Fig. 4A, inset; mean area of the all spikes group minus the nonburst spikes group is −0.0416 with an SE of 0.0186, n = 12 neurons from 7 mice).

Although there was a significant effect of bursting on the PAUC when all neurons were pooled, we noted that this effect was more commonly observed in layer 5 neurons than in layer 2/3 neurons (Fig. 4A). Whereas for some layer 2/3 neurons this can be explained by a low number of burst spikes (e.g., neuron 9), we also found that layer 2/3 neurons exhibited generally lower spike amplitude modulation with bursting. We can see this difference in the derivative of the amplitude of the intracellular spike (Fig. 4B, left; n = 5 neurons from 4 mice for layer 2/3 and n = 7 neurons from 5 mice for layer 5). Layer 5 neurons had a significantly greater burst-related decrease in spike slope than layer 2/3 neurons (Fig. 4B, inset; derivative of the amplitude of the intracellular spike for the all spikes group minus the nonburst spikes group is −0.0193 for layer 2/3 neurons and −0.1515 for layer 5 neurons, with SE of 0.0065 and 0.0394, respectively). For the two cell-attached recordings, we analyzed the raw spike height rather than its derivative. In Fig. 4C we plotted the normalized mean extracellular amplitude vs. burst spike number for each recording and found a general trend where for many layer 5 neurons, the spike amplitude decreases throughout a burst more than for layer 2/3 neurons. Thus spikes later in bursts have a greater potential to be lost in the spike detection process, which we also see when we look at which burst spike numbers are in the 2–6·MAD range (see mean burst spike number in Table 2). Finally, the mean half-width ratio is also larger for layer 5 at 1.34 (0.16) than layer 2/3 at 1.08 (0.12) [means (SD)], suggesting that the shape of layer 5 burst spike waveforms, e.g., Fig. 4, G–J, changes more than layer 2/3 (e.g., Fig. 4, D–F; half-width ratios for each recording in Table 2). Layer specific spike amplitude and shape modulation may result in more burst spikes lost during spike sorting of layer 5 neurons than for spike sorting of layer 2/3 neurons. This potential difference in spike accuracy may bias measures in which spike times from layers 2/3 and layer 5 are compared, e.g., spike-spike or spike-field correlation measures.

A large drop in PAUC when burst spikes were included was not always observed in the layer 5 neurons that exhibited large spike modulation during bursting; this is particularly evident in the neuron with the lowest PAUC (neuron 7 in Fig. 4, A, B, G, H, and I). This low PAUC value is indicative of an extracellular trace in which there were many other deflections in the spike range (Table 2, other deflections in spike range, and Fig. 4I), confounding the spike detection and classification of the trace. The PAUC value did not change when including burst spikes because it was already at a floor.

An algorithm for assessing potential spike sorting performance as a function of electrode density and quantity.

So far we have only analyzed extracellular traces on single electrode pads, to probe the limits of spike sorting, but of course one might take advantage of many pads on an extracellular electrode array in the quest to sort spikes. How might potential spiking sorting performance change with electrode density and number? We devised an automated algorithm (Fig. 5A) based on a simple model in which a neuron’s intracellular voltage is transformed by the resistances and capacitances of the membrane, extracellular space, etc., and mixed with noise and spikes from other neurons to create the extracellularly measured voltage (Fig. 5A, top, model). We then created an estimator of the intracellular spikes from the extracellular voltage, which in outline worked by first deriving a transformation from the extracellular to intracellular voltage (Fig. 5A, bottom, reversing the model, steps 1 and 2). We then regressed a specified set of transformed extracellular traces against the actual intracellular trace to create an intracellular voltage estimator (Fig. 5A, bottom, reversing the model, step 3). In detail, the algorithm involved the following steps. In step 1 (Fig. 5B), we calculated a convolution filter kernel that would minimize the mean squared error between the extracellular and intracellular signal (see materials and methods for details of step 1 and appendix for equations and derivation thereof). In step 2, the extracellular voltage from a single electrode was convolved with the convolution filter kernel, to create the “convolved extracellular voltage.” In step 3, multiple linear regression was performed between a specified set of convolved extracellular voltage traces, corresponding to a set of electrode pads of interest, and the actual patch-clamp voltage trace. The resulting regression coefficients were multiplied with their respective convolved extracellular voltages and summed, yielding a single estimator of patch voltage from extracellular voltages from a given set of electrodes. The estimators by design resembled the shape of the patch voltage traces, so for the 10 whole cell recordings we analyzed, we took the derivative of the estimator to make it resemble the shape of an extracellular recording for the following spike sorting analyses (we did not use the derivative for cell-attached recordings). In this way, we aimed to make a simple estimator of the power of a given set of electrodes to support spike sorting, by seeing how accurately they could recapitulate the information contained in the patch trace.

We calculated the PAUC as before, with a sliding threshold, for the intracellular voltage estimators processed in this manner. The PAUC in this case represents potential spike sorting performance using the specified set of electrodes. Calculating the PAUC for different subsets of the electrode array allows us to compare the potential spike sorting performance for different possible electrode array layouts.

We chose the set of extracellular voltage traces to be convolved as follows: working electrodes were ranked by their mean extracellular spike amplitude, from largest to smallest, as in Fig. 2C. With this ordering in place, groups of electrodes were then chosen, depending on the analysis. The top 64 amplitude-ordered electrodes (“full density”), every 2nd electrode (i.e., the 1st, 3rd, 5th, etc., electrodes, for a total of 32 electrodes; “half density”), or every 4th electrode (i.e., the 1st, 5th, 9th, etc., electrodes, for a total of 16 electrodes; “quarter density”) was used for Fig. 5C. The top N amplitude-ordered electrodes were used for Fig. 5D, where N ranged from 1 to 64. We chose this ordering scheme for the purposes of the current study, rather than ordering by actual spatial location, because we wanted to compare between recordings taken with different electrode arrays, with electrode count varying from 64 to 256 electrodes, spaced in a 2- or 4-column array, in each case focusing on the 64 electrodes that sensed the patched neuron most strongly. (An end user focused on a specific array may well want to use actual spatial distance as the sorting parameter.)

Increased electrode density improved potential spike sorting performance.

We explored whether there was a spike sorting benefit to having electrodes packed at the high density of the electrode arrays used in this study. This has practical implications, because given a fixed number of electrodes in a planar array, there is a necessary trade-off between recording more densely and recording from a greater amount of tissue. We created an estimator of the patched neuron’s voltage generated from the full, half, or quarter density of the ordered electrodes (Fig. 5C). We observed a significant effect of electrode density (repeated-measures one-way ANOVA, F = 5.656, P = 0.0104, n = 12 neurons from 7 mice). The mean PAUC of the full-density group was significantly greater than that of the quarter-density group (Fig. 5C, inset; mean of full-density area minus mean of quarter-density area, or “mean difference,” was 0.03148), but not the half-density group (mean difference = 0.01722). With the caveat that our electrode ordering was not based on raw spatial ordering, as described above, practically speaking, this suggests that an array with two or more columns with electrodes spaced 11 μm apart (center to center, or “pitch”) may be more amenable to spike sorting than a similar array with 22-μm spacing.

Increased electrode number, at fixed electrode density, improved spike discriminability.

Finally, we analyzed our data at full electrode density while varying the number of electrodes included in the analysis, using the amplitude ranking as described above so that we could compare across multiple kinds of electrode array. We included the top {1, 2, 4, 8, 16, 32, 64} amplitude-ordered electrodes in the construction of the estimator of patch voltage from extracellular voltages (Fig. 5D). We observed a significant effect of number of electrodes (repeated-measures one-way ANOVA, F = 7.003, P < 0.0001, n = 12 neurons from 7 mice). The mean PAUC for 64 electrodes was significantly greater than that for 8, 4, 2, and 1 electrodes, but not 32 or 16 electrodes. The mean of the 64 electrodes group minus mean of the N electrode group (mean difference), where N = 1, 2, 4, 8, 16, or 32, was as follows: 0.1153, 0.1187, 0.1095, 0.07483, 0.04402, or 0.01407. With the caveat that our electrode ordering was not based on raw spatial ordering, as described above, practically speaking, these data suggest that increasing the number of close-packed electrodes may improve spike sorting. To ground these results in different terms, if a spike sorter were willing to accept 2 FPs for every 100 patch spikes, he or she would collect 100 TPs for neuron 8, regardless of electrode configuration. However, for neuron 4, he or she would collect 46 TPs with an estimator based off of 1 electrode vs. 74 TPs with an estimator based off of all 64 electrodes while accepting 2 FPs for every 100 patch spikes. There was no obvious trend between extracellular amplitude of the patched neuron’s spike and PAUC, or between amplitude and increase in PAUC with more electrodes. This is likely due to spike sortability depending on an interaction between many factors, including spike amplitude on the electrode(s), co-occurring activity of other surrounding neurons, bursting, and how bursting manifests itself in different cell layers.

DISCUSSION

Our paper describes new automated techniques as well as demonstrations of the utility of these techniques. On the technique side, we have developed a novel approach to validating the performance of a given electrode architecture, in a given brain region. By combining automatic patch clamping (Kodandaramaiah et al. 2012) with extracellular recording with arrays of electrodes, in our case, close-packed electrodes capable of spatially oversampling neural activity (Scholvin et al. 2016), in a fashion that allows these two kinds of electrodes to be brought into extremely close proximity (i.e., enough to enable dual recording) with minimal damage, we were able to obtain dual recordings with a minimum of human intervention. This technique may enable others to assess the potential spike sorting performance of electrode designs in a diversity of brain regions and species.

We also pursued computational technique development, including a method for reconstructing intracellular voltage from extracellular voltages, using a minimal mean squared error strategy and used it to evaluate potential spike sorting performance when electrodes are systematically added or removed post hoc from a densely recorded data set. In this way we were able to examine the extent to which arrays of close-packed electrodes exhibiting spatial oversampling help with data analysis of spike data recorded from the mouse cortex. Our results suggest that further increasing the density and number of electrodes beyond the current state of the art might provide additional benefits for spike sorting. Electrodes positioned in 3D rather than 2D configurations may help, too, but that was not explored here. These results, and the computational framework we developed, should also be applicable to the field of in vitro recording with high-density arrays, where arrays of tens of thousands of sensors have been put to scientific use, with electrode density that approaches that of the close-packed electrodes in this study (Ballini et al. 2014; Jäckel et al. 2017; Tsai et al. 2015, 2017).

Bursting, however, remains a challenge for spike sorting, regardless of electrode count, because spike shapes change in sometimes complicated ways during bursting, in ways that may not be fully understood because the changes are cell type-specific.

Bursting as a confound to spike sorting.

It is well known that bursting may pose a problem for spike sorting (Harris et al. 2000; Lewicki 1998). Using our technologies, we have demonstrated a series of analyses of the impact of bursting on spike detection and classification made possible by our colocalized recordings. In almost all of our layer 5 recordings (e.g., Fig. 3B), we observed a pattern in which extracellular spike voltage declined, sometimes to below commonly used thresholds, during a burst of spiking. This decline was visible both in the extracellular recordings and in the time derivative of the intracellular voltage. Whether some or all of these low-amplitude burst spikes, often with spike shapes different from that of nonburst spikes, can be detected and correctly categorized is an important question for spike sorting. One possibility is that the dynamics of bursting could be computationally modeled, perhaps biophysically, and incorporated into spike sorting algorithms to detect and categorize spikes likely to belong to a burst. Colocalized recording technologies will provide the data sets necessary to test such spike sorting algorithms, enabling evaluation of their performance on extracellular data from a variety of cell types and brain regions, and under different stimulus conditions.

The relatively higher waveform modulation in layer 5 vs. layer 2/3 neurons during bursting may be accounted for by the elevated, subthreshold depolarization envelope observed in intracellular recordings of bursts. The latter has been associated with sensory-evoked dendritic calcium transients observed in intrinsically bursting neurons in layer 5, but not in layer 2/3 neurons (Helmchen et al. 1999). Further studies could examine whether such processes play a role here; in the current study, we treated this phenomenologically, as an observation that could be detected with our automated system.

Close-packed electrode arrays for improved spike sorting.

We found that close-packed electrodes which spatially oversample a given neuron from many sites in space improved potential spike sorting performance. There is precedent for spike sorting performance improving with increased number of electrodes, e.g., when spike sorting is done on four electrodes rather than one, using an estimator of optimal spike sorting performance based on clustering (Harris et al. 2000). Our approach, combined autopatching and dense electrode recording, extends these results to high channel counts and could help with systematic assessment of different electrode types in the future.

In sum, our hope is to offer a strategy that is automated and simply deployed for understanding the meaning of a given extracellular recording in the brain. We have shown several examples of how it can help clarify the interpretation of electrical signals recorded on a given electrode, but such a technique may be generally of importance for analyzing a diversity of electrode types.

GRANTS

S. B. Kodandaramaiah was supported by an MIT McGovern Institute Neurotechnology (MINT) grant, the Minnesota Discovery, Research and Innovation Economy (MnDRIVE) fund, and NIH Grant R21NS103098-01. C. Chronopoulos, C. Lamantia, and J. P. Kinney acknowledge support from NIH Grant 1R43MH101943. M. Tegmark acknowledges NSF6937191 and the Rothberg Family Foundation. E. S. Boyden acknowledges support from NIH Grants 1R01EY023173, 1R24MH106075, 1R43MH101943, 1R01NS102727, 2R01DA029639, and Director’s Pioneer Award 1DP1NS087724, as well as the MIT Media Laboratory Synthetic Intelligence Project, the IET A. F. Harvey Engineering Research Prize, the Howard Hughes Medical Institute Simons Faculty Scholars Program, gifts from Charles Hieken and John Doerr, and the New York Stem Cell Foundation Robertson Award.

DISCLOSURES

C. Chronopoulos, C. Lamantia, and J. P. Kinney work for LeafLabs, LLC, which manufactures the Willow data acquisition system used in the experiments detailed in this paper.

AUTHOR CONTRIBUTIONS

B.D.A., C.M.-K., J.G.B., J.K., J.S., C.C., C.L., S.B.K., and E.S.B. conceived and designed research; B.D.A. performed experiments; B.D.A., C.M.-K., J.G.B., L.S., M.T., and E.S.B. analyzed data; B.D.A., C.M.-K., J.G.B., J.K., J.S., L.S., M.T., and E.S.B. interpreted results of experiments; B.D.A. and C.M.-K. prepared figures; B.D.A., C.M.-K., and E.S.B. drafted manuscript; B.D.A., C.M.-K., J.K., L.S., M.T., and E.S.B. edited and revised manuscript; B.D.A., C.M.-K., and E.S.B. approved final version of manuscript.

APPENDIX

We are interested in estimating the patch-clamp voltage time series y(t) from a series of extracellular voltage recordings x_i(t) from different electrodes i = 1, 2, …. We assume that the relation between the functions x_i(t), y(t), and noise is time independent and linear, which implies that

$$y\left(t\right)=(w_i\star x_i)\left(t\right)+n_i\left(t\right),$$

where the star denotes convolution, for some convolution kernel w_i(τ) that we want to estimate and some random noise term n_i(t) that includes both voltage contributions from other neurons and any noise from the detector system electrical properties. Fourier transforming this equation and using the convolution theorem simplifies it to

$$\widehat{y}\left(\omega \right)={\widehat{w}}_i\left(\omega \right){}^{}\widehat{x}{}_i\left(\omega \right)*+{\widehat{n}}_i\left(\omega \right),$$

where ω ≡ 2πf denotes angular frequency, hats denote Fourier transforms, and ${}^{}\widehat{x}{}_i\left(\omega \right)*$ is the complex conjugate of ${\widehat{x}}_i\left(\omega \right)$. We use the normalization convention where the Fourier transform is unitary, i.e., where $\widehat{x}\left(\omega \right)\equiv {\left(2\pi \right)}^{-\frac{1}{2}}\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{e}^{-i\omega t}x\left(t\right)dt$. This formulation allows us to estimate our kernel w for each frequency separately. In practice, we split our time series into chunks of 512 samples each, overlapping twofold (i.e., the first chunk contains samples 1–512, the next chunk is 257–768, the next is 513–1,024, and so on), and evaluate ${}^{}\widehat{x}{}_i\left(\omega \right)*$ and $\widehat{y}\left(\omega \right)$ separately for each chunk. If we focus on a particular frequency and plot all the points $\left\{{}^{}\widehat{x}{}_i\left(\omega \right)*,\widehat{y}\left(\omega \right)\right\}$ in a two-dimensional scatter plot, the desired coefficient ${\widehat{w}}_i\left(\omega \right)$ is simply the slope of the relation, with the residual scatter around the best-fit line corresponding to the noise contribution ${\widehat{n}}_i\left(\omega \right)$. We estimate this slope ${\widehat{w}}_i\left(\omega \right)$ using simple linear regression, which provides the optimal estimator in the sense of minimizing the mean squared error. Via Parseval’s theorem, the optimal (mean squared error minimizing) estimator of our desired real-space convolution kernel w_i(τ) is simply the inverse Fourier transform of these regression coefficients, ${\widehat{w}}_i\left(\omega \right)$.

In summary, each electrode time series x_i(t) gives us a prediction $\left(w_i\star x_i\right)\left(t\right)$ of the patch-clamp time series. We linearly combine them into a single estimate y_est(t) of the patch-clamp time series y(t):

$$y_{est}\left(t\right)\equiv {\displaystyle \sum }_i{\alpha }_i\left(w_i\star x_i\right)\left(t\right),$$

where α_i are determined via simple linear regression to minimize the mean squared prediction error.