Abstract
It has become increasingly clear that learning in visuomotor rotation tasks, which induce an angular mismatch between movements of the hand and visual feedback, largely results from the combined effort of two distinct processes: implicit motor adaptation and explicit reaiming. However, it remains unclear how these two processes work together to produce trial-by-trial learning. Previous work has found that implicit motor adaptation operates automatically, regardless of task relevance, and saturates for large errors. In contrast, little is known about the automaticity of explicit reaiming and its sensitivity to error magnitude. Here we sought to characterize the automaticity and sensitivity function of these two processes to determine how they work together to facilitate performance in a visuomotor rotation task. We found that implicit adaptation scales relative to the visual error but only for small perturbations—replicating prior work. In contrast, explicit reaiming scales linearly for all tested perturbation sizes. Furthermore, the consistency of the perturbation appears to diminish both implicit adaptation and explicit reaiming, but to different degrees. Whereas implicit adaptation always displayed a response to the error, explicit reaiming was only engaged when errors displayed a minimal degree of consistency. This comports with the idea that implicit adaptation is obligatory and less flexible, whereas explicit reaiming is volitional and flexible.
NEW & NOTEWORTHY This paper provides the first psychometric sensitivity function for explicit reaiming. Additionally, we show that the sensitivities of both implicit adaptation and explicit reaiming are influenced by consistency of errors. The pattern of results across two experiments further supports the idea that implicit adaptation is largely inflexible, whereas explicit reaiming is flexible and can be suppressed when unnecessary.
Keywords: explicit reaiming, implicit adaptation, motor adaptation, motor control, motor learning
INTRODUCTION
Compensating for movement errors is critical to the motor learning process (Cheng and Sabes 2006; Jordan and Rumelhart 1992; Miall and Wolpert 1996; Pouget and Snyder 2000; Thoroughman and Shadmehr 2000). Thus characterizing the sensitivity of the behavioral response to these errors should reveal fundamental principles and constraints of the motor system (Fine and Thoroughman 2006, 2007; Marko et al. 2012; Scheidt et al. 2001; Semrau et al. 2012; Wei and Körding 2009). For over 20 years, the motor control field has sought to characterize this sensitivity function, using system identification techniques borrowed from engineering (Cheng and Sabes 2006; Thoroughman and Shadmehr 2000). These techniques generally consist of imposing a transient and often varying perturbation on the system to observe the behavioral response (Fine and Thoroughman 2006, 2007; Scheidt et al. 2001; Wei and Körding 2009).
Despite employing this theory-driven and elegant approach, the observed sensitivity functions have been highly variable and appear to depend on a number of experimental factors. In a seminal study, Scheidt and colleagues (Scheidt et al. 2001) found that the motor system adapted to transient and random force perturbations on a trial-by-trial basis in a force field adaptation task. This adaptive response appears to be sensitive to the direction of the perturbation but insensitive to both the timing and magnitude (i.e., strength) of the perturbation (Fine and Thoroughman 2006). However, if the perturbations are drawn from a nonzero mean distribution (Fine and Thoroughman 2007), occur frequently (Fine and Thoroughman 2007), or are applied in a consistent fashion (Gonzalez Castro et al. 2014), then the adaptive response becomes more sensitive. Additionally, experience with an error in a more stable environment has been shown to increase response sensitivity to reoccurrences of that error (Herzfeld et al. 2014).
Similar results have been found in studies of visuomotor rotations: Implicit adaptation appears to be highly sensitive to the direction of the rotation but less sensitive to its magnitude (Butcher and Taylor 2018). In fact, the time course of implicit adaptation begins to saturate in response to rotations greater than ~6° (Kim et al. 2018; Marko et al. 2012; Morehead et al. 2017; Wei and Körding 2009), despite prolonged periods of training with both nonzero mean and consistent rotational perturbations (Morehead and Smith 2017). This was made clear by employing a task-irrelevant error-clamp task, in which cursor feedback of the supposed hand’s position is consistently offset from the target path by a fixed angular value regardless of the hand’s true location (Morehead et al. 2017). Despite the task irrelevance of this feedback, robust adaptation is observed even when movement angles are uncorrelated with the angle of the rotational perturbation.
At first glance, the lack of sensitivity of this adaptive response is puzzling given the variety of motor behaviors and skills we can employ. However, when subjects have control of the angular position of the cursor, thus making it task relevant, sensitivity is restored (Morehead et al. 2017). This suggests that additional learning processes, such as explicit reaiming, may play a role in making the appropriate behavioral response given the demands of the task (Abeele and Bock 2001; Bock et al. 2003; Bond and Taylor 2015; Brudner et al. 2016; Hegele and Heuer 2010; Heuer and Hegele 2008; McDougle et al. 2015; Taylor et al. 2014; Werner and Bock 2010). Indeed, the varying sensitivity functions measured in the aforementioned studies vacillated around conditions when the subjects could potentially affect the outcome in the task. For example, Wei and Körding (2009) used a task in which visual error changed randomly on every trial. In this situation, aiming anywhere except straight toward the target would actually be counterproductive. In contrast, the adaptive response becomes more proportional when force perturbations have a nonzero mean (Fine and Thoroughman 2007). Similarly, when force perturbations were made to be more consistent by increasing the number of trials in a row for which a particular perturbation is present, the learning rate increased (Gonzalez Castro et al. 2014).
Although we note that there are other substantial differences between these aforementioned studies, such as rotational vs. force perturbations, we hypothesize that controllability over performance is a critical factor, which engages explicit reaiming to restore performance. Because we cannot directly, or at least reliably, manipulate the subjective experience of control, we operationalize controllability as environmental consistency. We reason that a more consistent environment gives greater opportunity for the deployment of effective strategy for controlling errors, whereas it is not possible to control error in an environment that has constantly changing movement-feedback contingencies. Specifically, we propose that explicit reaiming may only play a role when the perturbations are consistent and the visual errors are quite large (and/or implicit adaptation is saturated). Furthermore, given the number of studies showing that implicit adaptation appears to be highly stereotyped (Bond and Taylor 2015; Morehead et al. 2017; Wei et al. 2010), we hypothesize that implicit adaptation will not respond to environmental consistency. Here, in two experiments, we set out to test these ideas by examining the sensitivity functions of both explicit reaiming and implicit adaptation to a range of perturbations that varied in their degree of consistency.
MATERIALS AND METHODS
Participants.
Eighty human subjects [57 women, 23 men; mean age 20.4 yr (SD 3.24)] were recruited for experiment 1, and 26 subjects [18 women, 8 men; mean age 19.69 yr (SD 1.35)] were recruited for experiment 2. The sample size for experiment 1 was guided by the typical convention of 10–20 subjects per condition (4 conditions) for visuomotor adaptation tasks. The sample size for experiment 2 was determined by an a priori power analysis using the slope of explicit reaiming sensitivity function from experiment 1 between the Consistent-2 (mean slope = −0.374) and Consistent-7 (mean slope = −0.152) conditions. Robust power (80%) was obtained with the calculated effect size of 0.88 for a two-tailed t-test between two independent means. This analysis determined that we needed 13 subjects per condition. All subjects were drawn from the research participation pool maintained by the Department of Psychology at Princeton University and received either course credit or monetary compensation for participating. Subjects were right handed, as verified by the Edinburgh handedness Inventory (Oldfield 1971), and self-reported having normal or corrected-to-normal vison. The experimental protocol was approved by the Princeton University Institutional Review Board, and all subjects provided written informed consent.
Apparatus.
Subjects preformed horizontal movements in a center-out reaching task. These movements were recorded with a digitizing pen and a Wacom tablet, with the tablet sampling movement trajectories at 60 Hz. All stimuli were displayed by a 17-in. Planar touch-sensitive monitor with a refresh rate of 60 Hz and computed by a Dell OptiPlex 7040 machine running Windows 7. The touch-sensitive monitor allowed subjects to report their intended movement by simply tapping on the screen (Fig. 1; Bond and Taylor 2017). Visual feedback of the hand was obstructed by the monitor, which was mounted 25 cm above the tablet. A small circular cursor (0.15-cm radius) provided feedback information to subjects. The game was controlled by custom software coded in MATLAB, using Psychtoolbox extensions (Brainard 1997; Kleiner et al. 2007).
Fig. 1.

Experimental setup for both experiments. The subject holds a digitizing pen in his right hand, which is covered by the touch screen. The left hand is used to tap the touch screen on the blue ring to report the aiming location before each trial. After the subject taps on the screen, the blue aiming ring disappears and the orange target turns green.
Procedure.
Subjects began each trial with their right hand at the center of the visual workspace. After subjects held this position for 300 ms, a circular orange target (0.25-cm radius) appeared 7 cm from the starting position. An “aiming” ring consisting of a blue circle that was centered on the starting location and had a radius of 7 cm appeared along with the target (Fig. 1). Subjects were instructed to report their intended aiming location by tapping the aiming ring on the surface of the touch screen with their left hand. Once a touch was recorded, the target turned from orange to green, the aiming ring disappeared, and subjects were able to reach with their right hand. If a subject attempted to reach his/her right hand before tapping the touchscreen with the left hand, the message “Remember to report aim” was displayed and the trial was restarted.
Subjects were instructed to make a fast, straight “shooting” movement through the target with their right hand. They were informed that it was not necessary to stop on the target but that they should be careful to move far enough to pass completely through the target. Subjects were provided with continuous, online feedback of the cursor (0.15-cm radius) throughout the movement. Once the subject’s hand passed 7 cm, end-point feedback was displayed for 1 s. If the final position of the cursor overlapped with the target (<1° of angular deviation), subjects heard a pleasant “ding” sound; otherwise, they heard an unpleasant “buzz.” If the time from leaving the start position to reaching out 7 cm exceeded 800 ms, the feedback “too slow” was given. (This occurred on ~1% of trials, and these trials were excluded from further analysis. The average movement time was well below 250 ms for all conditions) After feedback presentation, subjects were guided back to the start position by a white ring that was centered on the starting location and whose radius represented the distance between subjects’ hand position and the starting location. Veridical feedback of the cursor was restored once the hand was within 1 cm of the starting position.
We pseudorandomized the target locations across the workspace and across subjects so that any potential visual or biomechanical biases would average out (Ghilardi et al. 1995; Jiang et al. 2018). On each trial, the target could appear in one of eight locations, spaced 45° apart to cover the full circular space defined by the aiming ring. The exact angular configuration of the target locations differed across subjects. There were five sets of target configurations, where the target set could be rotationally shifted 0°, 9°, 18°, 24°, or 36°. Each subject was exposed to only one configuration of target locations.
To assay the sensitivity function of implicit adaptation and explicit reaiming, an angular rotation of ±0°, 2°, 4°, 8°, and 16° was imposed on the cursor in experiment 1. These rotation sizes were chosen to correspond to the set of lateral displacements used in Wei and Körding (2009). Furthermore, the rotations were counterbalanced such that the mean rotation size over the experiment was 0°. For experiment 2, a 32° rotation was exchanged for the 2° rotation, such that the rotational perturbations imposed during the task were ±0°, 4°, 8°, 16°, and 32°.
A secondary goal of this experiment was to determine whether the sensitivity function changed based on the consistency of the rotation (i.e., how frequently the rotations changed during training), which has been reported by prior studies (Fine and Thoroughman 2007; Gonzalez Castro et al. 2014). To this end, in experiment 1 subjects were equally divided into four groups: Consistent-1, Consistent-2, Consistent-3, and Consistent-7. In the Consistent-1 condition, the rotation changed on every trial, effectively making this an inconsistent condition, although the target location remained the same for seven trials. In the Consistent-2, Consistent-3, and Consistent-7 conditions, each “miniblock” consisted of two, three, or seven trials, respectively, where the rotation changed after each miniblock. For these conditions, the target location also changed at the onset of each miniblock. Although changing the target location after every miniblock causes those conditions with greater error consistency to also have greater target consistency, we felt that it was important to ensure that the change in perturbation size occurred in the same way both within a condition (between miniblocks) and between groups. The exception is the Consistent-1 condition, where we did not sync the target and perturbation changes because a pilot experiment showed that there is no learning when both the target and perturbation change on every trial, likely because of the generalization function of implicit adaptation. In all cases, visual perturbations were pseudorandomly generated such that no rotation size was immediately repeated and each rotation size occurred at each target location at least once. Experiment 2 consisted of only the Consistent-2 and Consistent-7 conditions, which had miniblock lengths of two and seven trials, respectively.
The experiments proceeded by first providing veridical feedback for eight familiarization trials and then pseudorandomly generated visual rotations of the cursor for 504 trials in the Consistent-1 and Consistent-7 conditions and 432 trials in the Consistent-2 and Consistent-3 conditions. The discrepancy in trial length is the result of complete counterbalancing. The entire experiment took ∼1 h.
It should be noted that subjects were informed that the mapping between their hand and the cursor might change during the experiment and that they should tap on the aiming ring where they intended to aim in order to hit the target. Subjects were not told the nature of the visual perturbation or when the visual disturbance would be in effect during the experiment.
Data and statistical analyses.
All data and statistical analyses were performed in MATLAB. The digitizing tablet recorded the trajectory of the right hand, and the touchscreen monitor recorded the terminal position of the location tapped with the left hand. These data were transformed to define heading hand angles and aiming angles during training as follows: The hand angle trajectories and aiming locations were transformed from Cartesian to polar coordinates and rotated to a common axis with the convention that the target was positioned at 0° (directly to the right). As our primary interest concerns only the feedforward portion of the reach, we focused on the initial heading of the hand angle by examining the average angle of the hand between 1 and 3 cm into movement. Aiming angle was defined as the angle between the target and the tapped location on the touchscreen. Implicit adaptation was calculated by subtracting the subjects’ aiming angle from their hand angle (Bond and Taylor 2017; Taylor et al. 2014). For all measures, positive angles indicate a counterclockwise deviation from the target. As we have only two measured values, with implicit adaptation being computed as the subtraction of aiming angle from hand angle, we performed statistical analyses only on aiming angles and implicit adaptation angles, our primary variables of interest, and we report hand angles only for completeness.
In the following statistical analyses, unless otherwise specified the average of the second trial of every miniblock was used. This allowed us to control for the confounding additive effects inherent in having different-length miniblocks for each condition. For predictive purposes, the rotation size is considered to be the rotation size of the miniblock. Thus subjects experienced the rotation on the first trial of the miniblock, and we evaluated their response on the next (second) trial. For the Consistent-1 condition, the rotation size is considered to be the rotation experienced on the previous trial (n − 1, where n is the trial being evaluated). Although counterbalancing the perturbations resulted in a different number of trials between groups (432 trials in Consistent-2 and 3, 504 trials in Consistent-1 and -7), the total number of trials should not affect trial-by-trial adaptation since the study is designed to prevent the accumulation of learning. Additionally, equating the number of trials analyzed across the conditions did not significantly change the result.
To quantify the sensitivity function for each consistency condition, we fit separate linear functions to each subject’s aiming angles and implicit adaptation angles with respect to the rotation size. A significant slope indicates that the subject changed his/her behavior in response to the error. Differences in slopes between consistency conditions were evaluated by submitting the slopes to a one-way ANOVA; post hoc t-tests were conducted when appropriate and corrected by the Bonferroni method. We also sought to determine whether the overall slope of the sensitivity function was similar across rotation sizes. Previous studies have reported that the sensitivity of the response scales with the rotation size before reaching a saturation point at higher rotation magnitudes (Morehead et al. 2017; Wei and Körding 2009). To assess this possibility, we adopted the method of Wei and Körding (2009) and fit a second linear function to the range from −4° to 4°, which corresponds to lateral displacement between −2 cm and 2 cm in their study. The slopes of this second function and the overall function were compared with a pairwise t-test. In experiment 2, an additional analysis was conducted on the range from −8° to 8°. This range was chosen post hoc to preserve the ratio of 1:4 between the smaller test range and the full range experienced in the experiment.
The intercept (or offset) of these functions is of less interest, but significant intercepts could be viewed as an accumulation of learning throughout training or the development of a more general bias during training (Ghilardi et al. 1995).
RESULTS
Experiment 1.
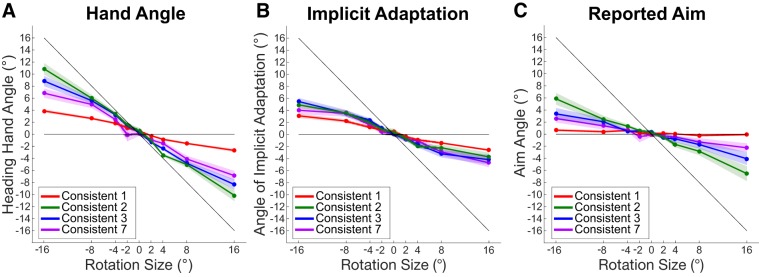
In this experiment, we sought to assess the sensitivity of implicit adaptation and explicit reaiming as a function of the magnitude and consistency of rotational perturbations, which ranged from 0 to 16° within a subject and changed every one, two, three, or seven trials across subjects. Subjects attempted to counteract these perturbations for all consistency conditions, as can be seen by the change in the angle of the hand in response to the imposed error (Fig. 2A). For the majority of conditions, these changes in hand angle are the result of the combined output of implicit adaptation (Fig. 2B) and explicit reaiming (Fig. 2C) processes. To quantify the sensitivity of these processes, we fit a linear function to each process for each subject over the imposed rotations. For all consistency conditions, we found that the slope of the sensitivity function was significant for both implicit adaptation (P < 0.01) and explicit reaiming (P < 0.001; see Table 1). The intercept of these linear fits was not different from zero, except in the case of Consistent-1, which had a small yet significant positive shift for both implicit adaptation [mean = 0.209°; t(19) = 2.573, P = 0.02] and explicit reaiming [mean = 0.29°, t(19) = 3.218, P = 0.005], suggesting that learning largely did not accumulate throughout the experiment.
Fig. 2.
Average response of second trial in each miniblock in degrees to imposed visual perturbations of −16° to 16° for each consistency condition: Consistent-1, Consistent-2, Consistent-3, and Consistent-7. The analyses include 20 subjects per condition. Black diagonal line represents unity between input and output; a participant who learned fully would fall on this line. Shaded regions represent SE. A: angle of the hand heading direction. B: angle of calculated implicit adaptation (hand angle – explicit reaiming). C: angle of explicit reaiming, which was reported by touching screen with left hand.
Table 1.
Statistics for slope of linear fit between imposed rotation and response: implicit adaptation or explicit reaiming
| Implicit Adaptation |
Explicit Reaming |
|||||
|---|---|---|---|---|---|---|
| Mean | Confidence interval | Mean r value | Mean | Confidence interval | Mean r value | |
| Slope of linear fit −16:16° | ||||||
| Consistent-1 | −0.192 | −0.214 to −0.170 | 0.894 | −0.028 | −0.045 to −0.012 | 0.488 |
| Consistent-2 | −0.298 | −0.365 to −0.231 | 0.824 | −0.374 | −0.508 to −0.240 | 0.794 |
| Consistent-3 | −0.335 | −0.423 to −0.248 | 0.869 | −0.230 | −0.352 to −0.108 | 0.702 |
| Consistent-7 | −0.300 | −0.363 to −0.237 | 0.789 | −0.152 | −0.232 to −0.071 | 0.651 |
| Slope of linear fit −4:4° | ||||||
| Consistent-1 | −0.263 | −0.317 to −0.209 | 0.755 | −0.060 | −0.108 to −0.012 | 0.553 |
| Consistent-2 | −0.465 | −0.606 to −0.325 | 0.708 | −0.354 | −0.521 to −0.188 | 0.632 |
| Consistent-3 | −0.491 | −0.646 to −0.336 | 0.756 | −0.181 | −0.334 to −0.028 | 0.529 |
| Consistent-7 | −0.329 | −0.444 to −0.213 | 0.535 | −0.111 | −0.247 to 0.024 | 0.485 |
Values are mean, confidence interval, and mean r value for the slope of the linear fit between imposed rotation and response. The linear equation was fit to the data of each subject for the whole range (−16:16°) and only the small rotations (−4:4°).
Although significant slopes were found for all the implicit adaptation sensitivity functions, they do not appear to be perfectly linear, as can be seen in Fig. 2B. The sensitivity appears to saturate for large rotations, which has been observed in previous studies (Morehead and Smith 2017; Wei and Körding 2009). To determine whether implicit adaptation sensitivity is better described as a piecewise function, we followed the method of Wei and Körding (2009) to compare the slope for small rotations (−4° to 4°) vs. the overall function. We find that these slopes are different for the Consistent-1 [t(19) = 2.971, P = 0.008], Consistent-2 [t(19) = 3.227, P = 0.004], and Consistent-3 [t(19) = 2.941, P = 0.008] conditions. It should be noted that the Consistent-1 condition is nearly identical to the study by Wei and Körding (2009), replicating their findings. However, the slopes were not different for the Consistent-7 condition. Given the visual similarity in the functions between consistency conditions, we suspect that this is likely attributable to noise, an issue we addressed in experiment 2. We performed the same comparisons between slopes within each consistency condition for explicit reaiming and found no significant differences (all P values > 0.05), although it appears that there may be differences in the slopes between consistency conditions.
To determine whether there were significant differences in the slope of the sensitivity function between consistency conditions, we submitted the slopes for both implicit adaptation and explicit reaiming to separate one-way ANOVAs. For implicit adaptation, although we find a significant difference between conditions [F(3) = 3.55, P = 0.02], this effect is driven by the difference between the Consistent-1 condition and all other conditions: Consistent-2 [t(38) = 2.958, P = 0.005], Consistent-3 [t(38) = 3.099, P = 0.003], Consistent-7 [t(38) = 3.166, P = 0.003]. This suggests an overall reduction in the sensitivity of implicit adaptation when there is no consistency in error (Fig. 2B). Explicit reaiming also differs with consistency [F(3) = 8.15, P < 0.001]. Interestingly, by comparing the Consistent-1 and Consistent-2 conditions, a post hoc t-test revealed that increasing the consistency by a single trial radically increases the sensitivity [t(38) = 5.02, P < 0.001; Fig. 2C]. However, as the consistency is further increased the sensitivity function tends to decrease, comparing Consistent-2 with Consistent-3 [t(38) = 1.561, P = 0.13], Consistent-2 with Consistent-7 [t(38) = 2.789, P = 0.008], and Consistent-3 with Consistent-7 [t(38) = 1.05, P = 0.30; Fig. 2C]. Although all of these comparisons show a decrease in sensitivity with corresponding increase in consistency, only the test between Consistent-2 and Consistent-7 is statistically significant.
We compared the slope of implicit adaptation and explicit reaiming within each condition to determine whether one was more sensitive to the imposed perturbation. Implicit adaptation was significantly more sensitive to perturbation size than explicit reaiming in the Consistent-1 condition [t(19) = 11.620, P < 0.001] and in the Consistent-7 condition [t(19) = 2.433, P = 0.02]. Greater sensitivity of implicit adaptation over explicit reaiming in the Consistent-1 condition suggests that explicit reaiming can be “turned off” when it is not useful, whereas implicit adaptation proceeds regardless. There was no difference in the slopes of implicit adaptation and explicit reaiming in the Consistent-2 [t(19) = 0.810, P = 0.43] and Consistent-3 [t(19) = 1.078, P = 0.30] conditions. The relative magnitudes of explicit reaiming and implicit adaptation are generally equivalent when learning is useful to task performance.
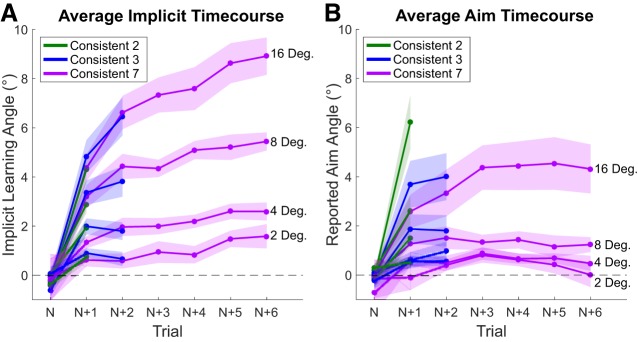
It is worth noting that our analysis of sensitivity focused only on the changes in behavior following the first experience with a new rotation in a miniblock. For the Consistent-2, -3, and -7 conditions, the same rotational perturbation continued for additional trials. Thus, somewhat trivially, subjects could continue to implicitly adapt and explicitly reaim. This is apparent in Fig. 3, although the response appears to decelerate with continued training in the miniblock, which is likely attributable to progressively decreasing visual errors. Consequently, these trials become increasingly contaminated by prior performance and thus provide an impure measure of the error sensitivity function. Therefore, we limited our error sensitivity function estimations to only the second trial of the miniblock.
Fig. 3.
Time course of implicit adaptation (A) and explicit reaiming (B) throughout each miniblock. Each miniblock is the average of the trials in a row for which each rotation size was consistent (2 trials for Consistent-2, 3 trials for Consistent-3, 7 trials for Consistent-7). Shaded regions represent SE with 20 subjects in each condition.
Although not considered in our statistical analyses, Fig. 3A does highlight the degree of sensitivity that implicit adaptation shows for rotation magnitude. This can be seen in the separation of the time course for each rotation magnitude. There is even clear differentiation between rotations as close as 2° and 4° (Kim et al. 2018). Reaiming, however, does not show as clean a separation (Fig. 3B).
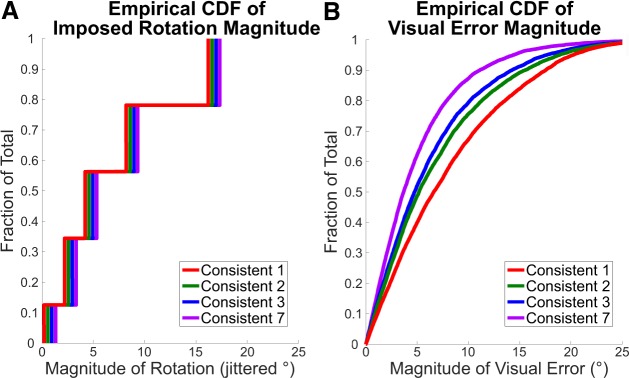
Next, we were interested in determining whether the change in explicit reaiming sensitivity as a function of consistency was due to a fundamental feature of the learning process or was a result of a statistical property of the training environment. One possible explanation is that explicit reaiming is actually sensitive to the changes in visual error between trials. For example, in the Consistent-7 condition, visual error was progressively smaller within a miniblock but quite large between miniblocks. In contrast, in the Consistent-1 condition, every trial was effectively between miniblocks, and thus larger visual errors were experienced more frequently. Indeed, the cumulative distribution of visual errors [cumulative distribution function (CDF)] varied significantly by condition for both means [F(3) = 87.98, P < 0.001] and standard deviations [F(3) = 8.11, P < 0.001; Fig. 4B]. Most notably, the mean of the CDF for Consistent-2 is larger than the means of the Consistent-3 [t(38) = 3.032, P = 0.004] and Consistent-7 [t(38) = 10.2, P < 0.001] groups. The standard deviation of the CDF for the Consistent-2 condition was also larger than that of Consistent-3 [t(38) = 2.251, P = 0.03] and Consistent-7 [t(38) = 3.348, P = 0.002]. These cumulative distributions suggest that decreasing the consistency of the perturbation increased the average change in visual error. This may account for the increase in the magnitude of the aiming response, with the caveat that this relationship breaks down when the visual error is completely unpredictable. It should be noted that we cannot produce a causal claim with this experimental setup, as changes in visual error are by definition influenced by aiming behavior.
Fig. 4.
Empirical cumulative distribution function (CDF) for imposed rotation magnitude (A) and visual error magnitude (B). The imposed rotations are jittered for clarity.
In sum, we found that error sensitivity of implicit adaptation was largely invariant across consistency conditions. These findings are consistent with previous studies employing procedures to isolate implicit adaptation, although using prolonged block designs (Bond and Taylor 2015; Morehead et al. 2017). Furthermore, we found that sensitivity functions for three of the four consistency conditions tended to saturate for implicit adaptation, which is largely consistent with results from previous studies (Kim et al. 2018; Morehead et al. 2017; Wei and Körding 2009). However, the sensitivity function for implicit adaptation at the most consistent condition did not significantly saturate. In contrast, the sensitivity of explicit reaiming changed as a function of consistency but showed linearity as a function of rotation size. To clarify these issues, we conducted a follow-up study (experiment 2) to both replicate our central findings and extend them by including larger rotation sizes. Here we limited the study to two consistency conditions: Consistent-2 and Consistent-7.
Experiment 2.
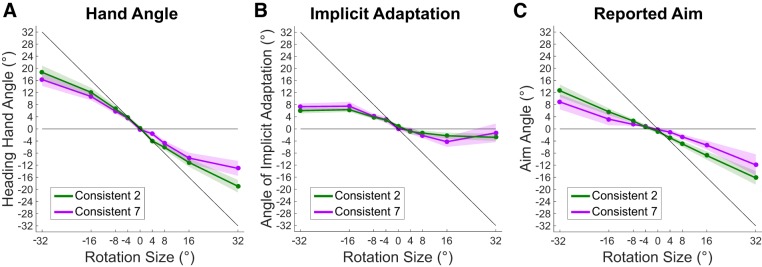
Similar to experiment 1, implicit adaptation and explicit reaiming were sensitive to the rotational perturbations for both consistency conditions. The average slope of implicit adaptation was significant for the Consistent-2 [t(12) = 7.389, P < 0.001] and Consistent-7 [t(12) = 3.827, P = 0.002] conditions (Fig. 5 and Table 2). Likewise, the slopes were significant for explicit reaiming in the Consistent-2 [t(12) = 6.907, P < 0.001] and Consistent-7 [t(12) = 3.685, P = 0.003] conditions. This replicates the sensitivity of implicit adaptation and explicit reaiming to rotation size from experiment 1.
Fig. 5.
Responses to imposed visual perturbations of −32° to 32°. A: angle of the hand heading direction. B: angle of calculated implicit adaptation (hand angle – explicit reaiming). C: angle of explicit reaiming. Shaded regions represent SE with 13 subjects per condition.
Table 2.
Statistics for slope of linear fit between imposed rotation and response: implicit adaptation or explicit reaiming
| Implicit Adaptation |
Explicit Reaiming |
|||||
|---|---|---|---|---|---|---|
| Mean | Confidence interval | Mean r value | Mean | Confidence interval | Mean r value | |
| Slope of linear fit from −32:32° | ||||||
| Consistent-2 | −0.176 | −0.223 to −0.129 | 0.782 | −0.451 | −0.579 to −0.323 | 0.910 |
| Consistent-7 | −0.196 | −0.296 to −0.096 | 0.750 | −0.310 | −0.475 to −0.145 | 0.692 |
| Slope of linear fit from −16:16° | ||||||
| Consistent-2 | −0.291 | −0.364 to −0.218 | 0.828 | −0.455 | −0.600 to −0.310 | 0.947 |
| Consistent-7 | −0.378 | −0.483 to −0.273 | 0.782 | −0.265 | −0.437 to −0.092 | 0.742 |
| Slope of linear fit from −8:8° | ||||||
| Consistent-2 | −0.358 | −0.481 to −0.236 | 0.758 | −0.467 | −0.644 to −0.290 | 0.865 |
| Consistent-7 | −0.410 | −0.519 to −0.301 | 0.732 | −0.251 | −0.381 to −0.121 | 0.670 |
| Slope of linear fit from −4:4° | ||||||
| Consistent-2 | −0.477 | −0.676 to −0.278 | 0.889 | −0.453 | −0.723 to −0.183 | 0.791 |
| Consistent-7 | −0.454 | −0.785 to −0.122 | 0.808 | −0.234 | −0.422 to −0.046 | 0.732 |
Values are mean, confidence interval, and mean r value for the slope of the linear fit between imposed rotation and response. The linear equation was fit to the data of each subject for the whole range (−32:32°), the range from experiment 1 (−16:16°), the range of small rotations that captures the 1-to-4 ratio of small to large rotations (−8:8°), and the range of small rotations used in experiment 1 (−4:4°).
Unlike in experiment 1, the intercepts of the linear fits to implicit adaptation were significantly larger than zero for both Consistent-2 and Consistent-7 conditions, although quite small (mean = 1.436° and 1.552°, respectively). The intercept of the linear fits to explicit reaiming were significantly below zero for the Consistent-2 condition [mean = −1.342°, t(12) = 2.881, P = 0.01] but not the Consistent-7 condition. These small deviations in the intercept may be the result of a previously held bias or, less likely, learning that accumulated during training.
The nonlinearity of implicit adaptation previously seen in experiment 1 conditions Consistent-1, -2, and -3, replicated in the Consistent-2 condition of experiment 2. Nonlinearity was found when comparing the average slope between rotations of ±4° and the full range [±32°; t(12) = 3.124, P = 0.008], as well as when comparing between ±8° and the full range [t(12) = 3.886, P = 0.002]. As in experiment 1, the Consistent-7 condition did not show this effect for the comparison of the partial range ±4° to the full range [t(12) = 1.815, P = 0.09]. However, the range from ±8° did have an average slope significantly different from the full range [t(12) = 3.878, P = 0.002]. The same tests performed on explicit reaiming produced no significant results, consistent with the findings from experiment 1: Implicit adaptation shows a strong tendency to saturate at relatively larger perturbation sizes, whereas explicit reaiming continues to contribute proportionately to learning throughout the whole range.
To compare sensitivity as a function of consistency, we submitted the slopes of implicit adaptation and explicit reaiming to separate two-sample t-tests. As in experiment 1, we found that the sensitivity of implicit adaptation did not change as a function of consistency [t(24) = 0.350, P = 0.73]. Unlike experiment 1, however, explicit reaiming behavior was not significantly different between Consistent-2 and Consistent-7 [t(24) = 1.327, P = 0.20]. This result held when we restricted the comparisons of the two conditions to the range of rotational perturbations tested in experiment 1 [−16:16°, t(24) = 1.661, P = 0.110]. This suggests that the subtle scaling of sensitivity of implicit adaptation and explicit reaiming as a function of consistency, which we observed in experiment 1, is not a robust effect.
A within-condition comparison between implicit adaptation and reaiming showed that explicit reaiming was more sensitive to these large perturbations than implicit adaptation in the Consistent-2 condition [t(12) = 3.844, P = 0.002]. However, this did not hold for the Consistent-7 condition [t(12) = 0.932, P = 0.37]. As in experiment 1, we do not see a reliable pattern indicating that implicit adaptation is more or less sensitive than explicit reaiming when adaptive learning is relevant to task performance.
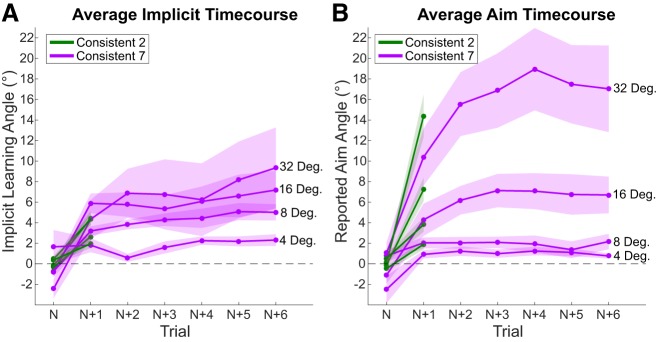
Finally, implicit adaptation shows less separation of responses to the larger perturbation sizes used in this experiment (Fig. 6A). This is in stark contrast to what was seen for the smaller perturbations in experiment 1 (Fig. 3A). Explicit reaiming, on the other hand, is sensitive to the range of perturbations in this experiment and shows clear differentiation throughout the time courses for large perturbation sizes (>8°; Fig. 6B).
Fig. 6.
Average time course of implicit adaptation (A) and explicit reaiming (B) throughout each miniblock. Shaded regions represent SE with 13 subjects per condition.
DISCUSSION
To determine the sensitivity function of implicit adaptation and explicit reaiming, we probed the motor system with small visual perturbations. In addition, we investigated the impact of error consistency on the aforementioned sensitivity of implicit and explicit processes by manipulating the number of trials in a row for which the perturbation was consistent. In two experiments, we perturbed visual feedback during center-out reaching movements. Both explicit reaiming and implicit adaptation are sensitive to and respond differentially depending on the size of the visual errors. By varying the consistency of the perturbation, we found that the sensitivity of implicit adaptation to small visual errors is impeded when the environment is completely unpredictable but stereotyped over all other levels of consistency. Likewise, the sensitivity of explicit reaiming was practically null when the environment was inconsistent but stabilized with increased consistency in the perturbations. These results suggest that both implicit adaptation and explicit reaiming are sensitive to very small perturbations, although implicit adaptation saturates for larger perturbations, and only minimal consistency of the perturbations is needed to stabilize these sensitivity functions.
Implicit adaptation was most sensitive to changes in error at very small error magnitudes and saturated between 8° and 16°, in keeping with previous results (Kim et al. 2018; Marko et al. 2012; Morehead et al. 2017; Wei and Körding 2009). This nonlinearity of implicit adaptation largely replicated across both experiments in most consistency conditions, with the only exception being the Consistent-7 condition. We suspect that the failure of this condition to replicate is likely the result of sampling error, as the general shape of its sensitivity curve is similar to those of the other conditions. Unlike implicit adaptation, explicit reaiming showed no nonlinearity, and we infer that it is similarly sensitive to the full range of visual perturbations that we tested. These findings are consistent with previous studies suggesting that implicit adaptation is more stereotyped than explicit reaiming and does not scale its response to a broad range of large perturbations (Bond and Taylor 2015, 2017).
We hypothesized that previous accounts of environmental consistency influencing motor learning could be fully attributable to explicit processes. However, we found that implicit adaptation was also affected by consistency. Changing error magnitude on every trial produces less implicit adaptation than when there is some consistency to allow for predictive responses. This suggests that there is a minimum amount of error consistency necessary to achieve the full possible amount of implicit adaptation. Once this minimum consistency requirement is met, however, additional consistency does not produce greater adaptation. This finding modifies previous work suggesting that implicit adaptation is extremely stereotyped and insensitive to environmental features or task demands (Morehead et al. 2017).
Consistency was important to the magnitude of the reaiming response. Moving from no error consistency to two trials in a row with the same error magnitude produced a sharp increase in explicit reaiming. Surprisingly, further increases in error consistency decreased this response, as found in experiment 1 (a similar trend was seen in experiment 2).
As we analyzed only the second trial of each miniblock to control for accumulation of learning, we believe that this reduction in the sensitivity of explicit reaiming with increasing error consistency is the result of the statistical properties of our task: While the mean of the errors and the mean change in error from one trial to the next were zero for all conditions, the relative size of the change in error was larger for conditions with lower environmental consistency (see Fig. 4). This resulted in more circumstances in which the error magnitude was very high in conditions with low error consistency compared with those with high error consistency. Herzfeld et al. (2014) previously found that under certain conditions sensitivity to an error increases with repeated exposures. Thus the increased exposure to large perturbations in the less consistent conditions could have influenced sensitivity. However, Herzfeld and colleagues did not separate implicit and explicit learning. Additionally, both results could be explained if explicit reaiming is more engaged when there is a sudden change to the error signal in a sufficiently consistent environment, as we argued above when discussing the CDF results in experiment 1; this would account for the modest increase in explicit reaiming that we see in low-consistency conditions.
Although not tested in these experiments, the sensitivity function of explicit reaiming may be related to possible reward in the environment. Recent work has shown that explicit reaiming is sensitive to bivalent feedback (Holland et al. 2018). One reason that explicit reaiming is seemingly not sensitive to very small perturbations could be that the system categorizes these errors as “close enough” and treats them as correct (i.e., within the subject’s natural motor noise), allowing implicit adaptation to “clean up” the residual error. Under this framework, explicit reaiming would be expected to begin making adjustments when movement is perceived to be sufficiently off-target. This phenomenon would likely be different across individuals and contexts.
The trade-off between implicit adaptation, which is most sensitive at small error sizes, and explicit reaiming, which is sensitive to a wide range of errors, suggests that the two may be working in tandem to produce the appropriate response for any particular visual error. Specifically, we speculate that implicit adaptation allows for small updates to the internal model, necessary to avoid accumulation of small errors and to avoid drift in the system. The explicit system is simultaneously available for fast learning of large perturbations. Whereas slow, gradual adaptation is sufficient for most learned tasks, sometimes a leap in learning is necessary to accommodate a radical environmental change.
Whether implicit adaptation and explicit reaiming are independent of one another, or if they necessarily function in tandem, is currently an open question. Implicit adaptation continues even when an explicit strategy has already fully compensated for any visual perturbation and when the adaptation conflicts with task goals, suggesting that the two processes are independent (Mazzoni and Krakauer 2006; Taylor and Ivry 2011). However, there is also evidence that implicit adaptation is affected by performance or reward (Kim et al. 2018; Leow et al. in press; Reichenthal et al. 2016). We did not observe a reliable change in the sensitivity of implicit adaptation as a function of the degree of consistency or explicit reaiming: The sensitivity function of implicit adaptation was identical between the Consistent-2 and -7 groups, despite these groups having different degrees of consistency and explicit reaiming. Nonetheless, this remains an important question for future research.
Given mounting evidence, in this study and others, that implicit adaptation saturates at quite small perturbation sizes and well before reaching target learning when the perturbation is large, we suggest that the main function of implicit adaptation is calibrating to small errors. How then can we accomplish the full remapping necessary for skill learning? This remapping has been experimentally shown to be possible: Long-term adaptation studies conducted with subjects practicing throwing movements while wearing prism goggles showed that after weeks of practice subjects are able to make movements immediately after donning the disrupting prism goggles similarly precise as when they are not wearing them (Martin et al. 1996). Similarly, researchers have anecdotally found that they could interact normally with their environment after weeks acclimating to wearing inversion goggles (Stratton, 1896, 1897; review in Sachse et al. 2017). In a visuomotor experiment, Semrau et al. (2012) found that adaptation is influenced by environmental factors introduced days earlier. Although these experiments do not account for explicit reaiming and implicit adaptation separately, our experience with everyday visual perturbations argues that the mapping is eventually implicit. For example, a new pair of glasses essentially imposes a scaling on the world, but we do not feel as though we are using an explicit strategy to compensate for this.
One possibility is that implicit adaptation does eventually constitute the fully remapped motor behavior but this process proceeds on a far longer timescale than usually studied in visuomotor adaptation experiments. However, this is contradicted by recent work examining the time series of implicit adaptation under error-clamp conditions. Adaptation in this paradigm does not show the continuous, if slow, rise expected if implicit adaptation was eventually fully responsible for learning (Morehead et al. 2017). An extended, multiday experiment that can examine explicit and implicit processes separately may provide insight into this open question.
GRANTS
This work was supported by National Institute of Neurological Disorders and Stroke Grant R01 NS-084948 to J. A. Taylor.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
S.A.H. and J.A.T. conceived and designed research; S.A.H. performed experiments; S.A.H. analyzed data; S.A.H. and J.A.T. interpreted results of experiments; S.A.H. prepared figures; S.A.H. and J.A.T. drafted manuscript; S.A.H. and J.A.T. edited and revised manuscript; S.A.H. and J.A.T. approved final version of manuscript.
REFERENCES
- Abeele S, Bock O. Sensorimotor adaptation to rotated visual input: different mechanisms for small versus large rotations. Exp Brain Res 140: 407–410, 2001. doi: 10.1007/s002210100846. [DOI] [PubMed] [Google Scholar]
- Bock O, Abeele S, Eversheim U. Human adaptation to rotated vision: interplay of a continuous and a discrete process. Exp Brain Res 152: 528–532, 2003. doi: 10.1007/s00221-003-1643-x. [DOI] [PubMed] [Google Scholar]
- Bond KM, Taylor JA. Flexible explicit but rigid implicit learning in a visuomotor adaptation task. J Neurophysiol 113: 3836–3849, 2015. doi: 10.1152/jn.00009.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bond KM, Taylor JA. Structural learning in a visuomotor adaptation task is explicitly accessible. eNeuro 4: ENEURO.0122-17.2017, 2017. doi: 10.1523/ENEURO.0122-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spat Vis 10: 433–436, 1997. doi: 10.1163/156856897X00357. 9176952 [DOI] [Google Scholar]
- Brudner SN, Kethidi N, Graeupner D, Ivry RB, Taylor JA. Delayed feedback during sensorimotor learning selectively disrupts adaptation but not strategy use. J Neurophysiol 115: 1499–1511, 2016. doi: 10.1152/jn.00066.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butcher PA, Taylor JA. Decomposition of a sensory prediction error signal for visuomotor adaptation. J Exp Psychol Hum Percept Perform 44: 176–194, 2018. doi: 10.1037/xhp0000440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng S, Sabes PN. Modeling sensorimotor learning with linear dynamical systems. Neural Comput 18: 760–793, 2006. doi: 10.1162/neco.2006.18.4.760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fine MS, Thoroughman KA. Motor adaptation to single force pulses: sensitive to direction but insensitive to within-movement pulse placement and magnitude. J Neurophysiol 96: 710–720, 2006. doi: 10.1152/jn.00215.2006. [DOI] [PubMed] [Google Scholar]
- Fine MS, Thoroughman KA. Trial-by-trial transformation of error into sensorimotor adaptation changes with environmental dynamics. J Neurophysiol 98: 1392–1404, 2007. doi: 10.1152/jn.00196.2007. [DOI] [PubMed] [Google Scholar]
- Ghilardi MF, Gordon J, Ghez C. Learning a visuomotor transformation in a local area of work space produces directional biases in other areas. J Neurophysiol 73: 2535–2539, 1995. doi: 10.1152/jn.1995.73.6.2535. [DOI] [PubMed] [Google Scholar]
- Gonzalez Castro LN, Hadjiosif AM, Hemphill MA, Smith MA. Environmental consistency determines the rate of motor adaptation. Curr Biol 24: 1050–1061, 2014. doi: 10.1016/j.cub.2014.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hegele M, Heuer H. Implicit and explicit components of dual adaptation to visuomotor rotations. Conscious Cogn 19: 906–917, 2010. doi: 10.1016/j.concog.2010.05.005. [DOI] [PubMed] [Google Scholar]
- Herzfeld DJ, Vaswani PA, Marko MK, Shadmehr R. A memory of errors in sensorimotor learning. Science 345: 1349–1353, 2014. doi: 10.1126/science.1253138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heuer H, Hegele M. Constraints on visuo-motor adaptation depend on the type of visual feedback during practice. Exp Brain Res 185: 101–110, 2008. doi: 10.1007/s00221-007-1135-5. [DOI] [PubMed] [Google Scholar]
- Holland P, Codol O, Galea JM. Contribution of explicit processes to reinforcement-based motor learning. J Neurophysiol 119: 2241–2255, 2018. doi: 10.1152/jn.00901.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang W, Yuan X, Yin C, Wei K. Visuomotor learning is dependent on direction-specific error saliency. J Neurophysiol 120: 162–170, 2018. doi: 10.1152/jn.00787.2017. [DOI] [PubMed] [Google Scholar]
- Jordan MI, Rumelhart DE. Forward models: supervised learning with a distal teacher. Cogn Sci 16: 307–354, 1992. doi: 10.1207/s15516709cog1603_1. [DOI] [Google Scholar]
- Kim HE, Morehead JR, Parvin DE, Moazzezi R, Ivry RB. Invariant errors reveal limitations in motor correction rather than constraints on error sensitivity. Commun Biol 1: 19, 2018. doi: 10.1038/s42003-018-0021-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleiner M, Brainard D, Pelli D, Ingling A, Murray R, Broussard C. What’s new in Psychtoolbox-3. Perception 36: 1–16, 2007. [Google Scholar]
- Leow LA, Marinovic W, de Rugy A, Carroll TJ. Task errors contribute to implicit aftereffects in sensorimotor adaptation. Eur J Neurosci. In press. doi: 10.1111/ejn.14213. [DOI] [PubMed] [Google Scholar]
- Marko MK, Haith AM, Harran MD, Shadmehr R. Sensitivity to prediction error in reach adaptation. J Neurophysiol 108: 1752–1763, 2012. doi: 10.1152/jn.00177.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin TA, Keating JG, Goodkin HP, Bastian AJ, Thach WT. Throwing while looking through prisms. II. Specificity and storage of multiple gaze-throw calibrations. Brain 119: 1199–1211, 1996. doi: 10.1093/brain/119.4.1199. [DOI] [PubMed] [Google Scholar]
- Mazzoni P, Krakauer JW. An implicit plan overrides an explicit strategy during visuomotor adaptation. J Neurosci 26: 3642–3645, 2006. doi: 10.1523/JNEUROSCI.5317-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDougle SD, Bond KM, Taylor JA. Explicit and implicit processes constitute the fast and slow processes of sensorimotor learning. J Neurosci 35: 9568–9579, 2015. doi: 10.1523/JNEUROSCI.5061-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miall RC, Wolpert DM. Forward models for physiological motor control. Neural Netw 9: 1265–1279, 1996. doi: 10.1016/S0893-6080(96)00035-4. [DOI] [PubMed] [Google Scholar]
- Morehead JR, Smith M. The magnitude of implicit sensorimotor adaptation is limited by continuous forgetting (Abstract). Advances in Motor Learning and Motor Control. Washington, DC, November 10, 2017. [Google Scholar]
- Morehead JR, Taylor JA, Parvin DE, Ivry RB. Characteristics of implicit sensorimotor adaptation revealed by task-irrelevant clamped feedback. J Cogn Neurosci 29: 1061–1074, 2017. doi: 10.1162/jocn_a_01108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9: 97–113, 1971. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- Pouget A, Snyder LH. Computational approaches to sensorimotor transformations. Nat Neurosci 3, Suppl: 1192–1198, 2000. doi: 10.1038/81469. [DOI] [PubMed] [Google Scholar]
- Reichenthal M, Avraham G, Karniel A, Shmuelof L. Target size matters: target errors contribute to the generalization of implicit visuomotor learning. J Neurophysiol 116: 411–424, 2016. doi: 10.1152/jn.00830.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachse P, Beermann U, Martini M, Maran T, Domeier M, Furtner MR. “The world is upside down”—The Innsbruck goggle experiments of Theodor Erismann (1883–1961) and Ivo Kohler (1915–1985). Cortex 92: 222–232, 2017. doi: 10.1016/j.cortex.2017.04.014. [DOI] [PubMed] [Google Scholar]
- Scheidt RA, Dingwell JB, Mussa-Ivaldi FA. Learning to move amid uncertainty. J Neurophysiol 86: 971–985, 2001. doi: 10.1152/jn.2001.86.2.971. [DOI] [PubMed] [Google Scholar]
- Semrau JA, Daitch AL, Thoroughman KA. Environmental experience within and across testing days determines the strength of human visuomotor adaptation. Exp Brain Res 216: 409–418, 2012. doi: 10.1007/s00221-011-2945-z. [DOI] [PubMed] [Google Scholar]
- Stratton GM. Some preliminary experiments on vision without inversion of the retinal image. Psychol Rev 3: 611–617, 1896. doi: 10.1037/h0072918. [DOI] [Google Scholar]
- Stratton GM. Vision without inversion of the retinal image. Psychol Rev 4: 341–360, 1897. doi: 10.1037/h0075482. [DOI] [Google Scholar]
- Taylor JA, Ivry RB. Flexible cognitive strategies during motor learning. PLoS Comput Biol 7: e1001096, 2011. doi: 10.1371/journal.pcbi.1001096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor JA, Krakauer JW, Ivry RB. Explicit and implicit contributions to learning in a sensorimotor adaptation task. J Neurosci 34: 3023–3032, 2014. doi: 10.1523/JNEUROSCI.3619-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoroughman KA, Shadmehr R. Learning of action through adaptive combination of motor primitives. Nature 407: 742–747, 2000. doi: 10.1038/35037588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei K, Körding K. Relevance of error: what drives motor adaptation? J Neurophysiol 101: 655–664, 2009. doi: 10.1152/jn.90545.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei K, Wert D, Körding K. The nervous system uses nonspecific motor learning in response to random perturbations of varying nature. J Neurophysiol 104: 3053–3063, 2010. doi: 10.1152/jn.01025.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner S, Bock O. Mechanisms for visuomotor adaptation to left-right reversed vision. Hum Mov Sci 29: 172–178, 2010. doi: 10.1016/j.humov.2010.02.004. [DOI] [PubMed] [Google Scholar]