Abstract
The changes in firing probability produced by a synaptic input are usually visualized using the poststimulus time histogram (PSTH). It would be useful if postsynaptic firing patterns could be predicted from patterns of afferent synaptic activation, but attempts to predict the PSTH from synaptic potential waveforms using reasoning based on voltage trajectory and spike threshold have not been successful, especially for inhibitory inputs. We measured PSTHs for substantia nigra pars reticulata (SNr) neurons inhibited by optogenetic stimulation of striato-nigral inputs or by matching artificial inhibitory conductances applied by dynamic clamp. The PSTH was predicted by a model based on each SNr cell’s phase-resetting curve (PRC). Optogenetic activation of striato-nigral input or artificial synaptic inhibition produced a PSTH consisting of an initial depression of firing followed by oscillatory increases and decreases repeating at the SNr cell’s baseline firing rate. The phase resetting model produced PSTHs closely resembling the cell data, including the primary pause in firing and the oscillation. Key features of the PSTH, including the onset rate and duration of the initial inhibitory phase, and the subsequent increase in firing probability could be explained from the characteristic shape of the SNr cell’s PRC. The rate of damping of the late oscillation was explained by the influence of asynchronous phase perturbations producing firing rate jitter and wander. Our results demonstrate the utility of phase-resetting models as a general method for predicting firing in spontaneously active neurons and their value in interpretation of the striato-nigral PSTH.
NEW & NOTEWORTHY The coupling of patterned presynaptic input to sequences of postsynaptic firing is a Gordian knot, complicated by the multidimensionality of neuronal state and the diversity of potential initial states. Even so, it is fundamental for even the simplest understanding of network dynamics. We show that a simple phase-resetting model constructed from experimental measurements can explain and predict the sequence of spike rate changes following synaptic inhibition of an oscillating basal ganglia output neuron.
Keywords: basal ganglia, direct pathway, oscillations, substantia nigra, synaptic response
INTRODUCTION
Neurons in substantia nigra pars reticulata (SNr) receive synaptic input from the direct and indirect pathways of the basal ganglia and send their axons to basal ganglia target structures in the brain stem and thalamus. In conjunction with similar cells in the internal pallidal segment, they form the final common path for the output of the basal ganglia (e.g., Gerfen and Wilson 1996). Like other basal ganglia output neurons, SNr cells are autonomous oscillators (Atherton and Bevan 2005; Ding et al. 2011) that fire tonically at high rates in vivo (DeLong 1971; Hikosaka and Wurtz 1983; Wilson et al. 1977). Synaptic inputs to these neurons produce their effects on the output of the basal ganglia by perturbing the otherwise rhythmic firing activity of SNr cells, producing transient changes in spike probability. The most common measure of these output perturbations is the poststimulus time histogram (PSTH), which estimates the expected value of firing rate of the neuron as a function of time from the stimulus. PSTHs have been used for decades to characterize the effects of synaptic stimulation on spiking activity of neurons everywhere, including the substantia nigra (e.g., Collingridge and Davies 1981; Freeze et al. 2013; Hikosaka et al. 1993). Although the construction of the PSTH is straightforward, its interpretation has always been controversial, especially for neurons that have a substantial background firing rate, like the basal ganglia output neurons.
The earliest efforts to understand the PSTH interpreted the primary response (initial peak or trough) as a transformation of the postsynaptic potential (PSP) and/or its time derivative (Kirkwood and Sears 1978; Knox and Poppele 1977; Moore et al. 1970). The secondary response, a set of later, sometimes oscillatory changes in spike probability, was interpreted separately as a manifestation of the spiking autocorrelation. In this view, the PSP was thought to sum with the background fluctuations of the cell membrane, moving it toward or away from a fixed spike threshold. Spike probability was considered increased or decreased in proportion to the distance from threshold, with a contribution from the derivative of the PSP because spikes are more likely triggered on the depolarizing slope of the PSP. These ideas were tested by comparing the PSTH with the shape of the PSP evoked far from threshold to avoid contamination by spikes (e.g., Fetz and Gustafsson 1983; Gustafsson and McCrea 1984; Poliakov et al. 1996). Although qualitatively similar to the observed PSTH, these simple transformations of the PSP never yielded an accurate quantitative prediction of spike rate changes after a stimulus, especially in the case of strong inhibition (Fetz and Gustafsson 1983). General nonlinear system identification methods produced more accurate predictions but did not have a direct biophysical interpretation (Herrmann and Gerstner 2002; Mease et al. 2014; Poliakov et al. 1997).
More recent approaches to understanding the function of oscillating neurons have focused on the phase-resetting curve (PRC), which characterizes the changes in spike timing caused by input arriving at each phase of the repetitive firing oscillation (e.g., Gutkin et al. 2005; Stiefel and Ermentrout 2016). Phase models based on the PRC are analogous to descriptions based on the membrane potential trajectory but replace membrane voltage with phase as the single variable representing the state of the neuron. Phase encapsulates all the individual state variables (including the membrane potential) that vary together as the cell traverses its interspike trajectory. The PRC incorporates the influence of all the intrinsic ionic conductances, including voltage-sensitive ones, which can alter the response to synaptic conductance throughout the interspike interval (ISI). Although phase models were originally applied to rhythmically firing neurons, they have been shown to predict spike times of neurons that are firing repetitively, but whose rhythmicity is lost because their oscillation is densely perturbed by noise (Ermentrout et al. 2011; Wilson et al. 2014) or by structured inputs (Wilson 2017). The phase model should, when its assumptions are met, quantitatively predict the PSTH in repetitively firing neurons (Gutkin et al. 2005; Stiefel and Ermentrout 2016), but there have been few experimental tests of the model.
Here we apply a phase model of an SNr neuron to predict the synaptic effect of direct-pathway inhibition on spiking of basal ganglia output neurons. We characterized direct-pathway synaptic currents in SNr cells and measured the PSTH in response to direct pathway synaptic activation by optogenetic stimulation in mice. We measured the PRCs of individual neurons and used them to construct phase models of individual cells to test their predictive utility. Our results indicate that phase models can quantitatively predict the major features of both the primary and secondary components of the PSTH.
MATERIALS AND METHODS
All experimental procedures followed National Institutes of Health guidelines, and all animal experiments were approved by the Institutional Animal Care and Use Committee of The University of Texas at San Antonio.
Brain slice preparation.
To make brain slices containing SNr, 60- to 90-day-old C57BL/6 mice of either sex were deeply anesthetized with isoflurane. Following decapitation, brains were rapidly removed and sectioned at 300 μM with a vibrating microtome in the coronal or parasagittal plane. Slices were collected in normal artificial cerebrospinal fluid containing the following (in mM): 126 NaCl, 2.5 KCl, 1.25 NaH2PO4, 2 CaCl2, 2 MgSO4, 10 d-glucose, and 26 NaHCO3, bubbled continuously with a 95–5% O2-CO2 mixture. Slices were stored at 28°C for at least 2 h before recording.
Recording.
A brain slice was submerged in the recording chamber and superfused continuously with oxygenated artificial cerebrospinal fluid heated to 33–35°C. All recordings were made in the presence of the AMPA receptor antagonist NBQX (5 μM) and the NMDA receptor antagonist CPP (5 μM). Picrotoxin (100 μM) was used to block GABAergic spontaneous inhibitory postsynaptic potentials (IPSPs) in dynamic clamp recordings, when natural IPSPs were not evoked. Recording pipettes were fabricated from borosilicate glass (G150F-4; Warner Instruments, Hamden, CT) using a Flaming-Brown pipette puller (model P-97; Sutter Instruments, Novato, CA) to obtain electrode resistances of 4–6 MΩ. Cells were visualized with an Olympus BX50WI microscope equipped with a ×40 water-immersion objective and Dodt gradient contrast optics.
Cells were recorded using the perforated-patch technique with gramicidin or in whole cell configuration. For perforated patch, 0.5–0.7 μg/ml of gramicidin was added to filtered pipette solution containing the following (in mM): 135 K-methylsulfate, 10 HEPES, 5 EGTA, and 2 MgCl2. Electrodes were tip-filled with gramicidin-free solution and back filled with solution containing gramicidin. After a seal was established, 10–30 min were allowed for sufficient access for current-clamp recordings (20–70 MΩ). Recordings were started when the access resistance decreased enough to reveal action potentials overshooting 0 mV. Whole cell patch recordings were performed using a pipette solution containing the following (in mM): 140.5 CsCl, 7.5 NaCl, 10 HEPES, 0.2 EGTA, 2 Mg-ATP, and 0.21 Na-GTP. The chloride reversal potential based on the contents of this solution was 3 mV.
All recordings were made with a MultiClamp 700B amplifier (Molecular Devices, Palo Alto, CA), with the output filtered at 10 kHz. Data were acquired using a HEKA Instruments (New York, NY) ITC-18 A/D converter sampling each channel at 20 kHz and custom software written using Igor Pro (WaveMetrics, Portland OR). A second computer running RTXI (the Real-Time eXperiment Interface; http://rtxi.org/) and using a National Instruments (Austin, TX) PCIe-6251 A/D board was used to apply simulated inhibitory postsynaptic conductances (IPSGs) and some of the injected current waveforms. Current and conductance waveforms were prepared offline and played to the cell using the Igor Pro and RTXI systems, and the current commands from the two systems were combined using a summing amplifier.
Direct pathway inhibitory postsynaptic currents.
To measure the kinetics and reversal potential of inhibitory postsynaptic currents (IPSCs) produced by direct pathway striatal projection neuron (dSPN) inputs to SNr neurons, channelrhodopsin was expressed in dSPNs (Fig. 1). Adeno-associated virus (AAV9.CAGGS.Flex.ChR2.tdTomato-WPRE.SV40; University of Pennsylvania Vector Core) was injected into the dorsal striatum of TAC1-IRES2-Cre-D mice [B6;129S-Tac1tm1.1(cre)Hze; Jackson Laboratory] 40–60 days of age. The injection sites were (relative to bregma) 0.6 mm anterior, 2.25 mm lateral, and 3.0 mm ventral. Animals were euthanized and brain slices prepared 14 days after virus injection. Viral protein expression in axons projecting into SNr was confirmed by observation of tdTomato in slices using green (565 nm) illumination. The channelrhodopsin current was activated using blue (475 nm) light (~5 mW total power) directed at substantia nigra through the ×40 objective. Stimulus pulses were applied at 2 Hz, and IPSC amplitude was controlled by adjusting the duration of each pulse (range: 0.5–2.0 ms). After the IPSC amplitudes attained a steady state, IPSCs were recorded in whole cell configuration for 60 s (Fig. 2).
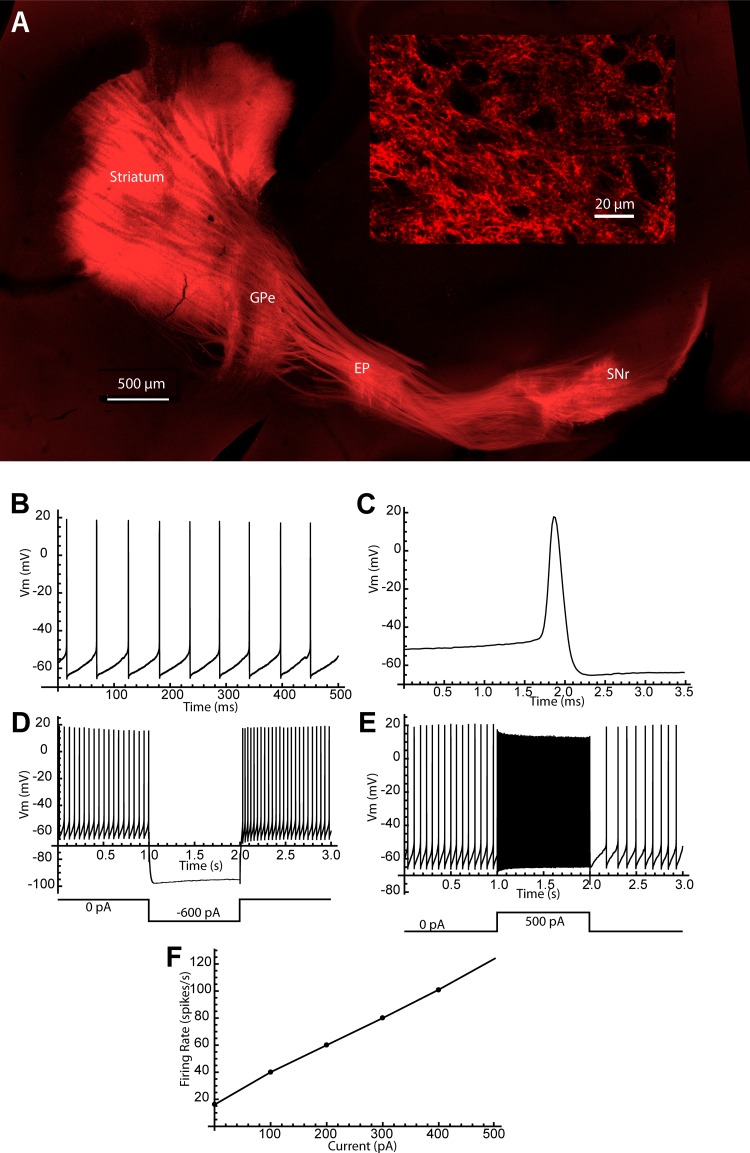
Fig. 1.
Direct pathway channelrhodopsin transfection and substantia nigra pars reticulata (SNr) cell identification. A: fluorescent labeling of the direct pathway by viral injection in the striatum in the TAC1 Cre mouse. Direct pathway axons project in the external globus pallidus (GPe) and entopeduncular nucleus (EP) as well as the substantia nigra, where they arborize mostly in the SNr. Axonal labeling in the SNr (inset) forms a network of small boutons throughout the neuropil. B: spontaneous firing of a representative SNr cell. C: SNr cell action potentials were very brief. D: the SNr response to hyperpolarizing current pulses was accompanied by only a small sag, even at very negative voltages. E: SNr neurons could fire at high rates in response to depolarizing current pulses. F: a frequency-intensity curve for the cell in B–E.
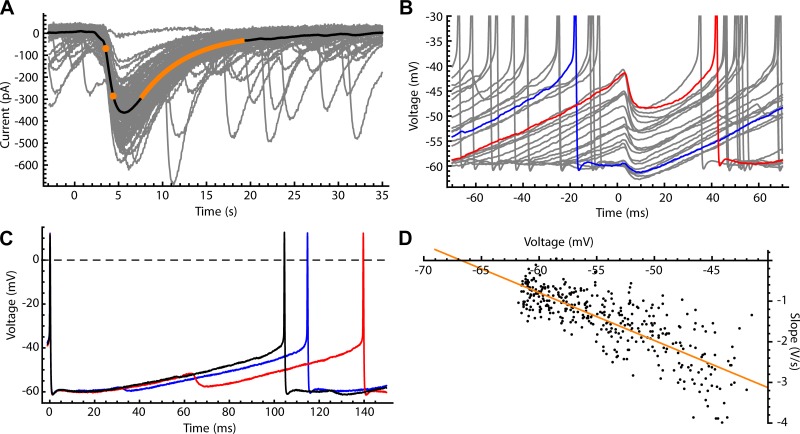
Fig. 2.
Synaptic inhibition of substantia nigra pars reticulata (SNr) neurons by direct pathway axons. A: photo-evoked direct pathway inhibitory postsynaptic currents (IPSCs) recorded from SNr neurons in whole cell configuration using CsCl intracellular solution (gray traces). Mean photo-evoked IPSC is shown in black, illustrating the measurement of rise time (20–80%, orange dots) and decay time constant (from the illustrated single-exponential fit, orange line). B: sample of photo-evoked inhibitory postsynaptic potentials (IPSPs) recorded in perforated-patch configuration (gray). IPSP amplitude is sensitive to membrane voltage at the time of onset; IPSPs earlier in the interspike interval (ISI) (e.g., blue) occur at more negative membrane potentials and are smaller than IPSPs later in the ISI (red). C: ISI voltage trajectories with no IPSP (black), an early IPSP (blue), and a late IPSP (red). Both early and late IPSPs lengthen the ISI, but late IPSPs have a larger effect. D: chloride reversal potential measured in the perforated-patch configuration. The IPSP onset slope was plotted vs. the membrane potential. A linear fit (orange) was obtained by least-squares linear regression, and the x-intercept of the fit line (where IPSP slope = 0) was taken as reversal potential (Erev).
Measurement of the GABAA reversal potential.
Reversal potential (Erev) was measured using perforated patch in current clamp. Direct pathway IPSPs were photo evoked at 2 Hz during autonomous firing. The maximum onset slope of each IPSP was measured and plotted vs. the membrane potential at that point. A linear fit was obtained by least-squares linear regression, and the x-intercept of the fit line (where IPSP slope = 0) was taken as Erev.
Poststimulus time histograms.
Twenty to forty 12-s episodes of direct pathway synaptic stimulation or simulated IPSGs produced by dynamic clamp were delivered to each neuron. The stimulus times were separated by a minimum interval of 200 ms plus a random (Poisson) delay with a mean of 300 ms, giving a mean interstimulus interval of 500 ms. Thus each cell received ~480–960 stimuli. For direct pathway stimulation, the light pulse was adjusted to lengthen the first poststimulus ISI by a median value of ~20%. For dynamic clamp, the simulated IPSG waveform had a rise time constant of 1.3 ms, a decay time constant of 5 ms, and a peak of 2 nS. Spike times were taken at a detection threshold of −20 mV. To construct the PSTH, spikes were counted in 2-ms bins with respect to each stimulus onset, and the counts were normalized by the number of stimuli times the bin width.
Phase-resetting curves.
PRCs were estimated based on the spike responses to 20–40 10 s episodes of noise stimulation. The noise stimuli were contiguous sequences of square current pulses, each 0.5 ms in duration, with amplitudes drawn from a Gaussian distribution (mean = 0, SD = 40 pA). Spike times were accumulated for all episodes, and the PRC of each neuron was computed using a previously described multiple regression method (Wilson et al. 2014). This method estimates the instantaneous PRC (iPRC), which is the slope of the relationship between charge delivered to the membrane by both depolarizing and hyperpolarizing current pulses and the proportional change in ISI, calculated at each phase in the ISI. The PRC was plotted so that a phase advance was positive. The average ISI during the noise stimuli was used as the norm for measuring changes in interval. The pulses were drawn from a distribution with zero mean, and the average firing rate did not change significantly in the presence of the current pulses. The standard errors of the estimates of slope were also calculated, to calculate confidence intervals for the estimates (e.g., Fig. 3A). Unlike responses to synaptic input or artificial conductance inputs, this PRC is independent of driving force and so predicts responses to both hyperpolarizing and depolarizing current pulses. To smooth the PRC without losing the sharp features present at late phases in these cells, we utilized a smoothing algorithm based on a composite of local fourth-order polynomial fits. Each component of the fit replaced a single data point and was determined by minimizing the sum of squared errors weighted by a Gaussian function centered around that point. To prevent oversmoothing of the right side of the PRC, the width of the error weighting function was decreased with phase to optimize the fit at late phases.
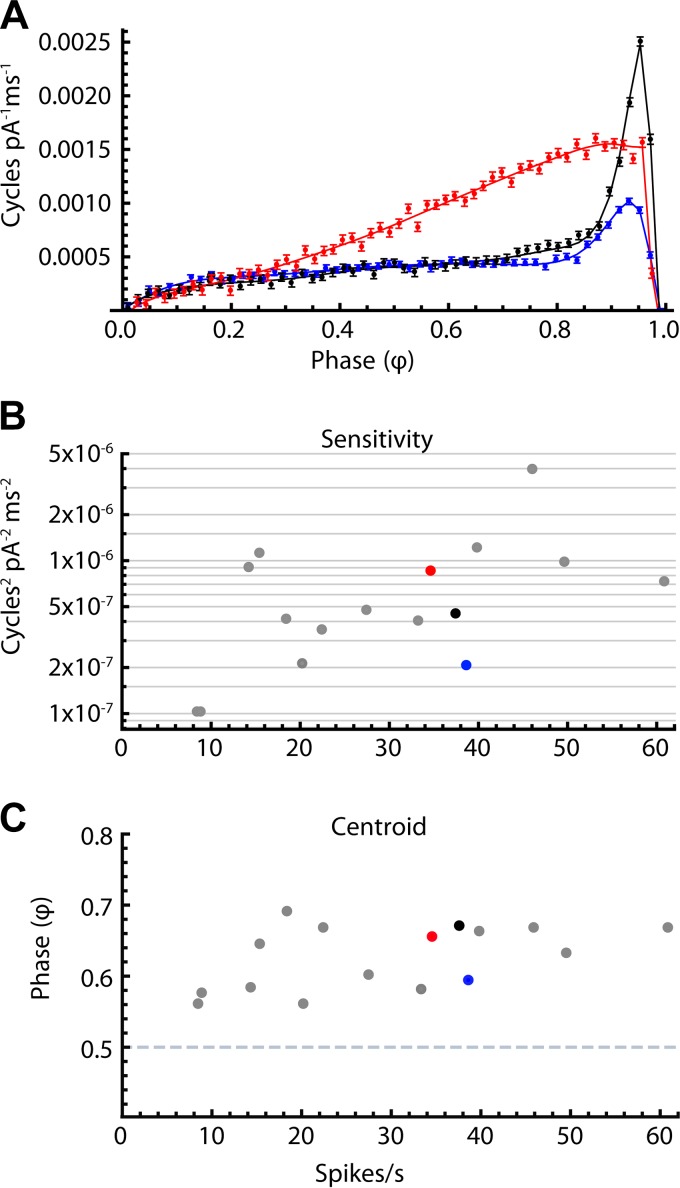
Fig. 3.
Phase-resetting curve (PRC) variation among substantia nigra pars reticulata (SNr) neurons. A: 3 example PRCs from neurons with similar firing rates: blue, 38.6 Hz, black, 37.5 Hz, and red, 34.6 Hz. For all neurons, sensitivity to stimulus current was low at early phases, and generally peaked at a late phase before falling rapidly at phases approaching 1. Both the mean amplitude and the shape of the PRC varied among cells. B: overall sensitivity vs. mean firing rate for all cells. Colored dots correspond to the PRCs in A. Sensitivity was quantified as the mean squared PRC value across all phase bins. There was no significant correlation between mean firing rate and sensitivity (r2 = 0.16, n = 16). C: centroid vs. mean firing rate for all cells. The mean centroid phase was 0.63 (SD = 0.04). There was no significant correlation between mean firing rate and centroid (r2 = 0.23, n = 16).
Phase models of SNr neurons.
Simulations were performed in Mathematica (Wolfram) or in some cases using a specialized program written in C. Programs used for these simulations are available from the authors on request. The phase model utilizes the experimentally estimated PRC of each neuron to predict the spiking of that cell in response to an external current stimulus Iext(t). The PRC measured for each neuron was interpolated as a function Z(φ), where φ is the phase of the cell's spiking oscillation. The model is specified by a phase equation representing the evolution of φ, which advances at an unperturbed rate ω in the absence of input. Phase is cyclic. Thus, when φ reaches 1, φ is reset to 0 and a spike time is collected.
| (1) |
To investigate the effects of noise sources that shape the PSTH, additions were made to account for the cell's intrinsic noise and for slow changes in firing rate. To account for intrinsic noise, I(t) was taken as the sum of Iext(t) and an intrinsic noise current Iint(t), which was simulated by a Gaussian random variable sampled at each time step in the numerical integration (Δt = 0.05 ms). The standard deviation of Iint(t), or σint, was calculated based on a theoretical expression to approximate the experimental coefficient of variation of ISIs (CVISI) in the absence of stimulation (Ermentrout et al. 2011; Wilson et al. 2014):
| (2) |
To account for slow changes in firing rate, each cell's autonomous rate was sampled for a 2-s period without stimulation every 24 or 36 s and ω was updated to the most recent experimental value throughout each simulated experiment.
Phase model for conductance input.
Because the standard phase model has no representation of membrane potential or driving force, a modification was necessary to calculate synaptic current from synaptic conductance. As an approximation to account for major changes in IPSC driving force across the ISI, we assumed that the interspike membrane potential can be represented as a function of φ or ν(φ). To construct ν(φ), the interspike membrane potential trajectories were collected from the stimulus-free periods interspersed in each experiment. Each trajectory was sampled by interpolation of the voltage data at 1,001 equally spaced time points, taking the 2 spike times as the end points. The mean of the resampled trajectories was then expressed as a function of φ (values from 0 to 1). Based on ν(φ), we obtain the phase equation for conductance input G(t).
| (3) |
A similar approach was utilized in previous studies where a “shunted PRC” was used to model the effects of synaptic conductances (Dodla and Wilson 2017; Netoff et al. 2012). Incorporating the internal noise described above, we obtain the phase equation for our complete model.
| (4) |
This method differs from that used by Preyer and Butera (2005) and by Achuthan et al. (2011) in that the PRC is measured using current and not conductance. It isolates the nonlinearity due to driving force and predicts spiking for current waveforms of any shape and polarity.
Damping of the PSTH oscillation by firing rate jitter and wander.
A damped sine wave function was utilized to test the hypothesis that the rate of PSTH oscillation damping could be explained by the measured firing rate jitter (j) and wander (w), where jitter represents the noise fluctuations within the ISIs and wander represents firing rate changes over periods much longer than the ISIs. The value of j was taken as the average CV of unperturbed ISIs in 2-s epochs, and w was measured by the CV of mean firing rates sampled across epochs for the duration of an experiment. It was hypothesized that the late portion of the PSTH could be represented by a sine wave with a frequency f and an amplitude decreasing over time because of phase dispersion by jitter and wander, each described as a Gaussian random variable. For jitter, the standard deviation of phase (σJ) increases with the square root of time (Ly and Ermentrout 2011):
| (5) |
For wander, the standard deviation of phase (σW) increases linearly with time:
| (6) |
Assuming jitter and wander are independent, the phase variances they cause are additive, giving the following equation for the standard deviation of phase (σ):
| (7) |
Moving from the time domain to the frequency domain, a Gaussian filter producing temporal dispersion with standard deviation σ becomes a Gaussian function of frequency with a peak at f = 0 and a standard deviation σF = 1 / 2πσ. For a given frequency, the value of the Gaussian function represents the time-varying amplitude of a damped sine wave, D(t), shaped by the specified j and w:
| (8) |
| (9) |
| (10) |
PSTH data, excluding the initial response, were fitted with Eq. 10, where the only free parameters were the initial amplitude A0 and the sine wave phase φ0.
RESULTS
IPSCs produced by direct pathway stimulation.
To activate direct pathway synaptic inputs to SNr neurons, we expressed channelrhodopsin 2 (ChR2) in striatal dSPNs. An adeno-associated virus (AAV) encoding tdTomato-tagged ChR2 under the control of a Cre-dependent promoter (see materials and methods) was injected into the striatum of TAC1-Cre mice. The tac1 promoter regulates production of the substance P precursor protein and is selectively activated in dSPNs, which are known to express substance P (Christensson-Nylander et al. 1986; Yung et al. 1996). After 2 wk, tdTomato fluorescence was observed in direct pathway axons originating from dSPNs and terminating in SNr (Fig. 1).
As expected (e.g., Chang et al. 1981; Kawaguchi et al. 1990), axons from direct pathway neurons made dual collateral arborizations in transit through the globus pallidus, and arborized in the entopeduncular nucleus and substantia nigra, primarily in pars reticulata. Within substantia nigra, the axonal arborizations patterns were topographical, following the pattern described by Deniau et al. (1996). Within the arborizations, labeled axons formed a network of small punctate boutons surrounding fine elements of the neuropil (Fig. 1A, inset). SNr neurons maintained continuous firing (9.6–27.8 spikes/s, mean = 13.6 ± 5.7 spikes/s, n = 11) in the absence of synaptic activation, and fired at high frequency when depolarized with injected current steps (Fig. 1) and could be slowed to arbitrarily low rates with hyperpolarization, as expected for the GABAergic projection neurons of the SNr (e.g., Zhou and Lee 2011). We occasionally encountered neurons whose firing resembled that of dopaminergic neurons in the substantia nigra pars compacta. These cells were not included in the sample.
To record direct pathway IPSCs in SNr neurons, coronal brain slices were prepared, and direct pathway axons were stimulated with brief pulses of blue light. Photo-evoked IPSCs were recorded in whole cell voltage clamp at −80 mV. Mean IPSCs ranged from 30 to 552 pA (0.35–6.4 nS) and had 20–80% rise times of 0.9 ± 0.3 ms and a decay time constant of 6.2 ± 3.4 ms (n = 10 cells) (example in Fig. 2A). These values were consistent with measurements reported previously by Connelly et al. (2010) using electrical stimulation of the direct pathway.
To measure the Erev for direct-pathway synaptic input, recordings were obtained in perforated-patch current-clamp mode while the SNr neurons maintained their autonomous firing activity. Instead of changing the membrane potential by injecting current, the natural variation in membrane potential during the interspike trajectory was used to collect synaptic potentials evoked at a range of potential levels. As expected for GABAergic IPSPs, the amplitudes of synaptic potentials produced by direct pathway stimulation depended on the cell's membrane potential at the IPSP onset (Fig. 2B). The IPSPs were largest when the stimulus fell late in the ISI, when the cell was most depolarized (Fig. 2C). For estimation of Erev, we measured the maximum slope (dV/dt) of each IPSP, as dV/dt is expected to be proportional to the underlying synaptic current, and plotted the IPSP slopes vs. the membrane potentials at the corresponding time points (Fig. 2D). The data for each cell were fitted with a straight line, and the x-intercept of the line was taken as Erev. The measured values of Erev were −74 ± 8 mV (n = 8 cells). This agrees with measurements of the reversal potential for GABAA synapses in SNr neurons reported previously by Gulácsi et al. (2003).
Phase resetting in SNr neurons.
Synaptic inhibition delivered during the ISI systematically delayed the next spike. Moreover, synaptic inhibition late in the ISI, when the driving force and synaptic current were large, produced longer delays than synaptic inhibition at earlier times (Fig. 2C). In addition to this effect of input timing on synaptic current, the spike-delaying effect of a synaptic input depended on the cell's intrinsic phase-dependent sensitivity to current input, as measured by the infinitesimal phase resetting curve (PRC). The PRC quantifies the increase or decrease in ISI duration produced by an input, as a function of the phase at which the input arrives. PRCs may be measured by applying isolated single synaptic or current inputs during repetitive firing, like the stimuli used here to measure the PSTH. Alternatively, more efficient methods for PRC estimation use broadband noise stimuli (Izhikevich 2007; Netoff et al. 2012; Wilson et al. 2014). For this purpose, we subjected each neuron to small-amplitude noise stimulation (40 pA SD, 0.5-ms pulse length), which caused a small increase in ISI variability. The PRCs were then calculated by a previously described multiple linear regression method (Wilson et al. 2014) that calculates the contribution of every noise pulse falling during the ISI. Our measurements represent an estimate of the infinitesimal PRC, meaning PRC scaled to the amplitude of the input, and so are in units of phase change per unit charge. The error bars associated with the PRC values at each point are standard errors of the estimates.
The size and shape of the PRC varied among SNr neurons. Three PRCs from neurons with similar firing rates are overlaid in Fig. 3A to illustrate the observed diversity of PRC shapes. The data points and error bars represent the raw PRC value and the estimated error of that value for each phase bin. The solid lines are smoothed interpolations of each cell’s PRC. The PRCs of SNr cells were all of type 1, meaning that the time of spiking was always advanced by depolarizing currents and always delayed by hyperpolarizing ones. Sensitivity to stimulus current was relatively low at early phases, and peaked at a late phase before falling rapidly at phases approaching one. Both the peak sensitivity and the trajectory of sensitivity across middle phases varied among cells. A common feature of SNr cell PRCs is their distinctive peak at late phases. Some cells showed low sensitivity until a small peak at late phase (Fig. 3A, blue). Others exhibited a sharp peak at late phase (Fig. 3A, black), while still others ramped smoothly upward from early to late phases with no sharp peak before falling off near the end (Fig. 3A, red). For each PRC, the overall sensitivity was quantified by calculating the mean square of the PRC values for all phase bins. Sensitivity varied substantially across SNr neurons, independent of firing rate. Figure 3B shows the sensitivity (plotted on a log scale) vs. mean firing rate for all the cells. No significant correlation was observed between the unperturbed mean firing rate of each neuron and the sensitivity (r2 = 0.16). The shape of the PRC also varied somewhat among cells. To quantify the overall skew of the PRC, we measured the centroid, or center of mass. If the PRC were symmetrical, with equal overall sensitivity at early and late phases, the centroid phase would be 0.5. In our PRC data (Fig. 3C) the mean centroid phase was 0.63 with an SD of 0.04 (n = 16 cells), indicating that despite the variations among PRC shapes, there was a consistent strong negative skew, and this also was independent of firing rate (r2 = 0.23).
The direct pathway PSTH.
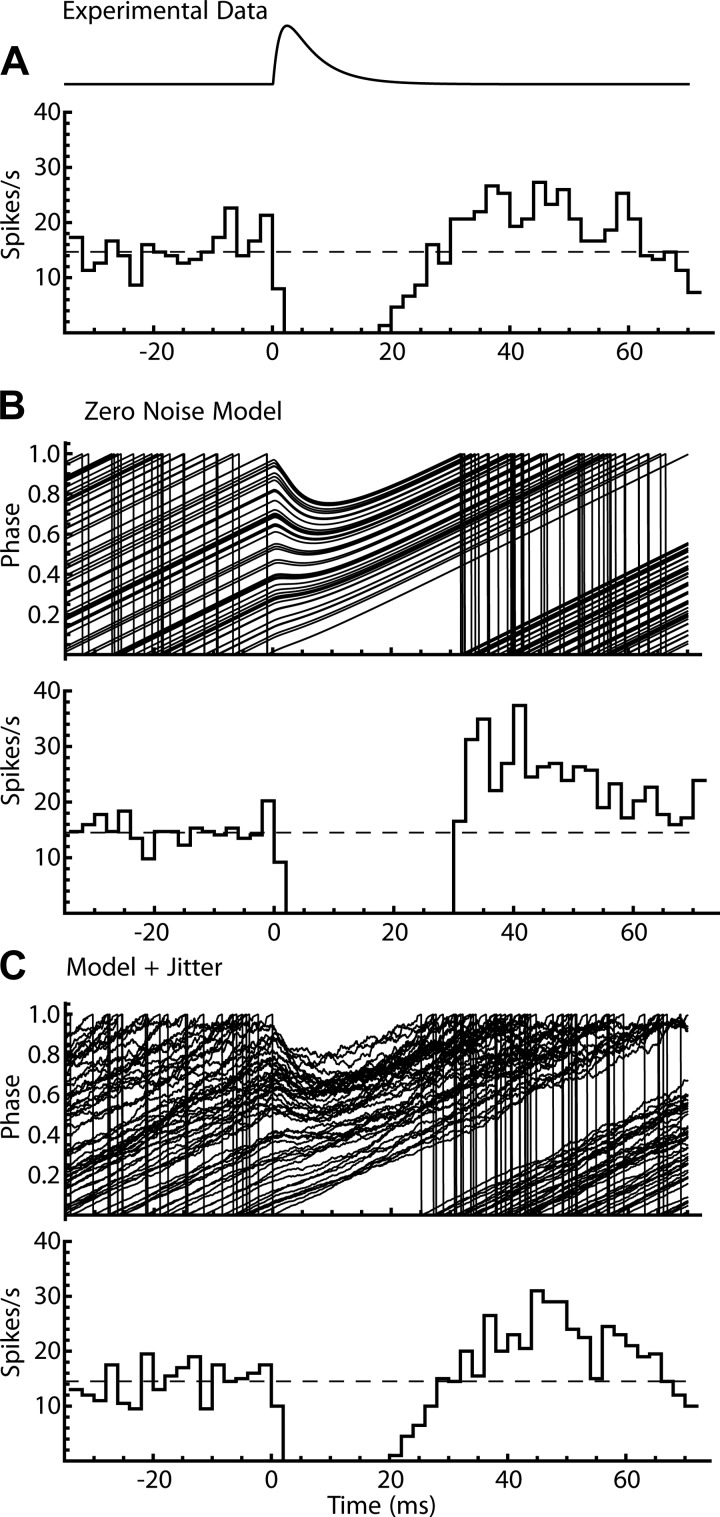
SNr neuron PSTHs for direct pathway synaptic input were obtained by photo stimulation of ChR2-expressing dSPN axons (see materials and methods). To compensate for the differences in sensitivity among neurons, the stimulus intensity delivered to each neuron was adjusted to yield a median 20% increase in the first ISI following the stimulus onset. Because the SNr cells fire autonomously, PSTH values for times before the stimulus are equal to the mean autonomous firing rate. The main features of the PSTH were a rapid dip in firing rate typically lasting 5–30 ms, followed by a rise above the baseline rate, and a subsequent oscillation that persisted several cycles before damping back to the baseline firing rate (Fig. 4A). The period of the oscillation in each neuron’s PSTH was similar to the mean ISI of that neuron in the absence of stimulation (Moore et al. 1970).
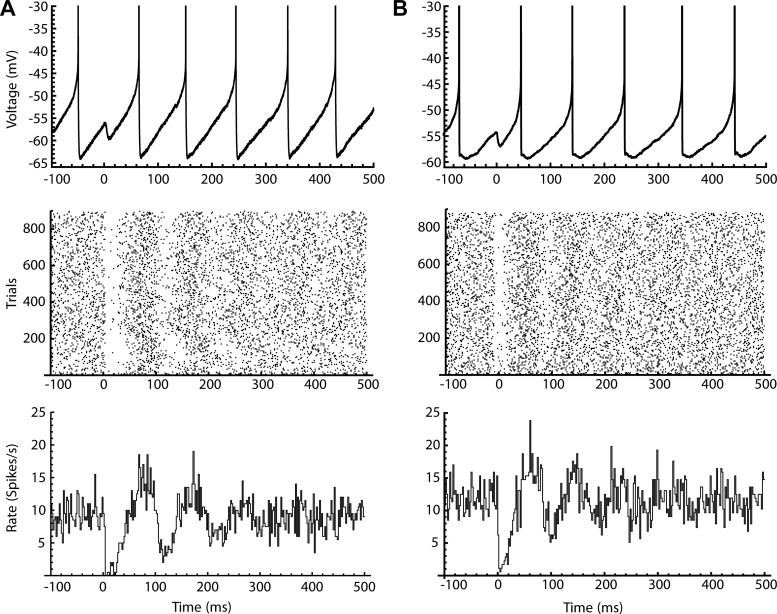
Fig. 4.
Poststimulus time histogram (PSTH) shapes produced by direct pathway synaptic input and conductance clamped artificial synaptic input. A: photo stimulation of direct-pathway synaptic input. Top: a photo-stimulated inhibitory postsynaptic potential (IPSP) in a voltage trace during repetitive firing. Middle: spike raster of over 800 trials aligned at photo-stimulation. Bottom: PSTH of spiking aligned to the photo-stimulation. B: same as A, but using dynamic clamp to apply the inhibitory postsynaptic conductance (IPSG) to a single isolated neuron in the presence of glutamate and GABA receptor antagonists.
SNr neurons are synaptically coupled, and the response observed might reflect local network interactions (Brown et al. 2014; Higgs and Wilson 2016). To determine whether the complex PSTH waveforms obtained with direct pathway stimulation were dependent on network interactions within the slice, we mimicked direct pathway input to individual, isolated SNr neurons using dynamic clamp, and blocked most excitatory and inhibitory synaptic transmission with NBQX, CPP, and picrotoxin. A simulated IPSG waveform (τrise = 1.3 ms, τdecay = 5 ms) was constructed to approximate the kinetics of direct pathway IPSCs. The simulated IPSGs were applied to real SNr neurons using the software-based RTXI system (see materials and methods). The command to the current-clamp amplifier was calculated in real time (sampling interval = 0.05 ms) based on Vm, the programmed Erev (−74 mV), and the programmed IPSG waveform, producing an inhibitory current with a natural dependence on Vm.
Injection of simulated IPSGs produced PSTHs showing all the features seen using photo stimulation of direct pathway synapses, including the rapid initial dip, the rise and the following damped oscillation (Fig. 4B). Although local coupling among SNr cells undoubtedly has some influence on the response to direct pathway inhibition, that effect was not responsible for any qualitative feature of the PSTH. Direct pathway PSTH shapes arise primarily from the intrinsic firing properties of the SNr neurons.
Predicting the primary response.
To investigate whether phase resetting of SNr neurons could explain and predict the PSTH, we used a modified phase model based on the experimentally estimated PRC of each neuron. Because the PRC was measured using injected current (not conductance), it does not account for phase-dependent changes in driving force. Predicting the responses to synaptic input requires an additional step to incorporate the phase dependence of the synaptic current due to the membrane potential trajectory during the ISI (see materials and methods).
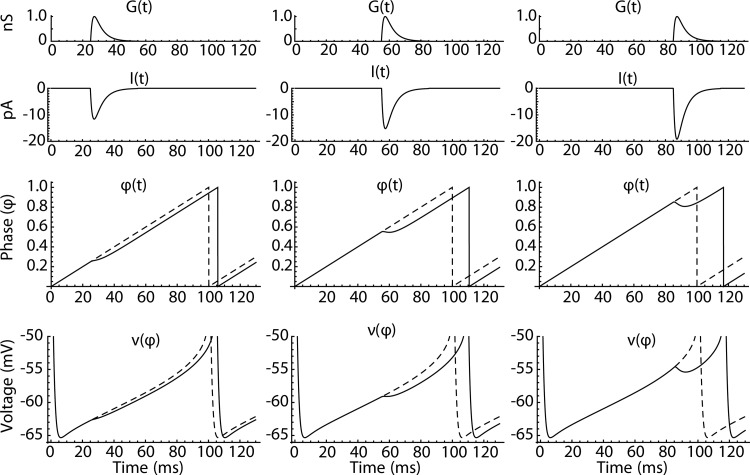
The phase model (Eq. 3) is illustrated in Fig. 5. A synaptic conductance waveform, G(t), arrives at a specific time during the cell's ISI. Figure 5, left, middle, and right, illustrates cases in which the input arrives during the early, middle, and late portions of the ISI. The synaptic conductance G(t) is the same for all stimulus times, but the synaptic current, I(t), varies because of the phase-dependent changes in driving force produced by ν(φ) (Fig. 5, bottom). Thus I(t) is greatest when the input arrives late in the ISI, when the synaptic driving force is large. The synaptic current acts through the PRC to produce a transient slowing or reversal of the otherwise constant phase advance. For the inhibitory response to direct pathway stimulation, this leads to a delay in the next spike time, which again is largest for late input.
Fig. 5.
Operation of the phase model. Left, middle, and right: simulations of a noiseless phase model (see Eq. 3) where the synaptic conductance waveform G(t) (top traces) arrives early, midway, and late in the interspike interval. The synaptic conductance produces a synaptic current I(t) (top middle traces), which alters the phase trajectory (bottom middle traces). The bottom traces show the trajectory of the voltage function of phase, ν(φ), which determines the driving force for I(t).
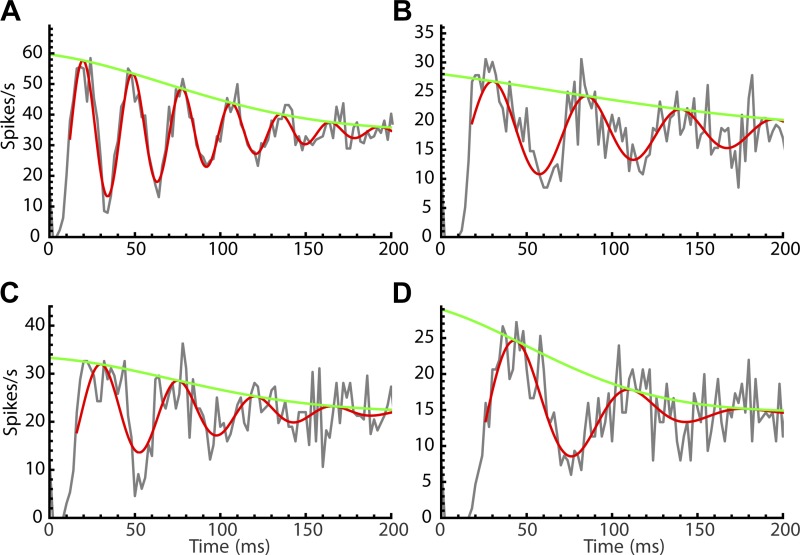
To generate PSTH data for each neuron in the sample, a phase model was constructed using the PRC measured for that neuron and run with the same set of IPSG trains used experimentally to generate the PSTH for that cell. The model PSTH was calculated and compared with the experimental data. Simulations performed using the noiseless phase equation (Eq. 3) yielded primary responses (the initial depression of firing probability and its recovery) that were similar in duration but differed in shape from the experimental data (compare Fig. 6, A and B). At the end of the pause, the recovery of spike rate was steeper, and the rebound overshoot was higher and sharper than in the experimental PSTH.
Fig. 6.
Poststimulus time histogram (PSTH) produced by the phase model of a substantia nigra pars reticulata neuron. A: applied inhibitory postsynaptic conductance waveform and experimental PSTH, shown for a duration equal to the mean unperturbed interspike interval (ISI). B: phase trajectories of the noiseless phase model, and the corresponding PSTH. The model produced a pause in firing similar to that seen in the cell data, but the spike rate increased more steeply after the pause, and the overshoot was higher and sharper compared with the experimental data. C: phase trajectories of the same model but incorporating fast noise producing ISI jitter and the corresponding PSTH. Addition of fast noise smoothed the recovery and overshoot of spike rate at the end of the pause.
Unlike the phase model in Eq. 3 and Fig. 5, real SNr neurons are subject to phase-perturbing currents that do not arise from the inhibitory input producing the PSTH. These include background spontaneous synaptic currents (Higgs and Wilson 2016) and stochastic opening of ion channels that produce noise throughout the ISI (White et al. 2000). These produce fast currents that can be treated as currents acting via the PRC to perturb phase. Noise sources are assumed to be independent on each ISI and so produce the ISI jitter seen in the absence of direct pathway stimulation. To determine whether noise sources present in the real cells could account for the time course of the primary response, internal noise was added to the models. Fast noise, producing jitter, was modeled as white noise current added to the external current input. Its amplitude was calculated to match the spontaneous variance of ISIs in the model to that observed during short epochs without stimulation (see materials and methods). Adding jitter to the phase model yielded PSTHs with smoother ramps and rebounds at the end of the primary response (Fig. 6C).
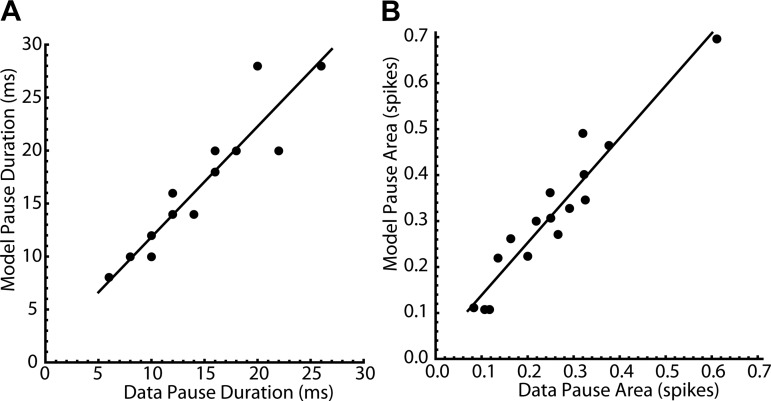
To evaluate the accuracy of the model predictions, the duration of the primary response, or pause duration, was measured as the time from the stimulus until the PSTH recovered to the baseline firing rate. The model pause durations (mean = 15.8 ± 6.2 ms) matched those from the experimental data on the same cell (mean = 13.8 ± 5.6 ms) (r2 = 0.876, Fig. 7A). The integral of the primary response, or pause area, was measured by subtracting the baseline rate and then integrating the rate change across the duration of the pause. The model pause areas (mean = −0.312 ± 0.155 spikes) also reliably predicted the corresponding cell data (mean = −0.252 ± 0.130 spikes) (r2 = 0.916, Fig. 7B).
Fig. 7.
Predictions of pause duration and area by the noisy phase models. A: model pause duration vs. experimental pause duration for each cell. Pause duration was measured as the time from the stimulus until the poststimulus time histogram recovered to the baseline firing rate. Model pause durations (mean = 15.8 ± 6.2 ms) were highly correlated with the corresponding experimental data (mean = 13.8 ± 5.6 ms) (r2 = 0.876). B: model pause area vs. experimental pause area for each cell. Pause area was measured by subtracting the baseline rate, and then integrating the rate change across the duration of the pause. Model pause areas (mean = −0.312 ± 0.155 spikes) were highly correlated with the corresponding experimental data (mean = −0.252 ± 0.130 spikes) (r2 = 0.916).
The PSTH oscillation and its damping.
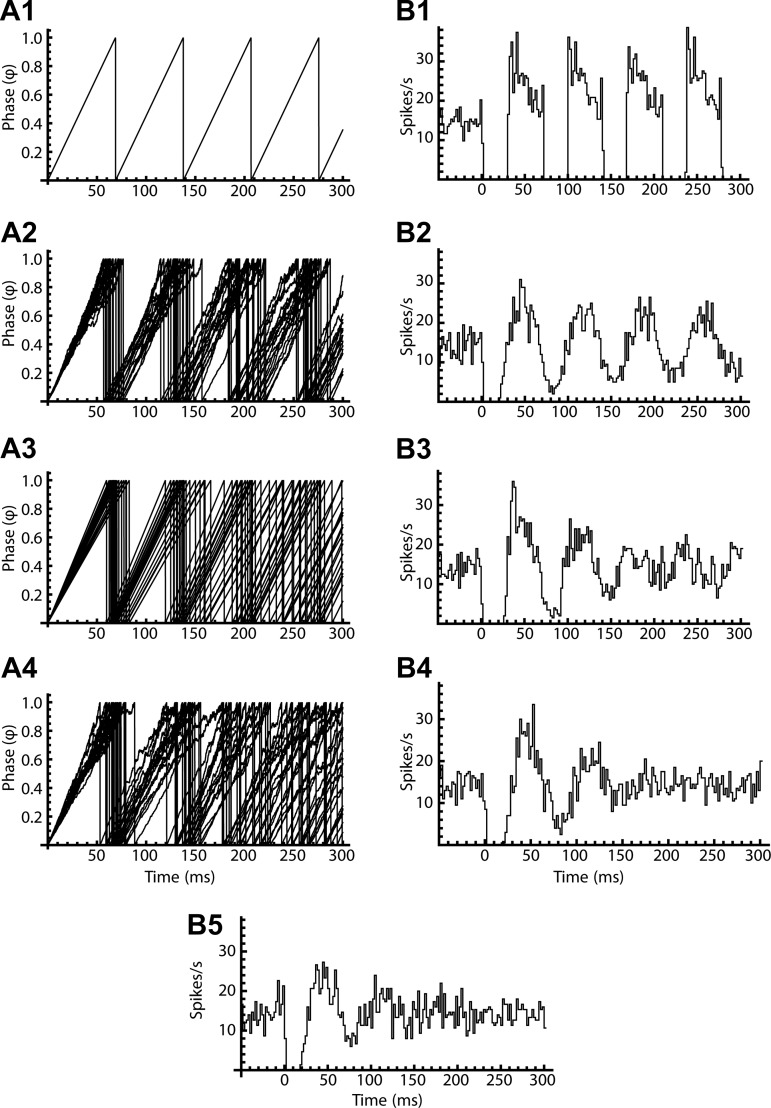
If the neuron fired perfectly regular ISIs after the initial perturbation caused by the stimulus, synchronized phase trajectories would remain synchronized, and the PSTH oscillation would continue forever without damping (Fig. 8, A1 and B1). Although adding jitter to the models produced some damping of the oscillation over time, this was insufficient to predict the damping of the oscillation seen in real neurons (Fig. 8, A2 and B2). The amount of jitter used in these simulations was adjusted to reproduce the interval histogram seen in unperturbed firing (see materials and methods). Although adding greater amounts of jitter would accelerate the damping of the oscillations, this would also produce an unrealistic increase in ISI variation. However, SNr neurons also exhibit slow continuous shifts in firing rate, on a time scale longer than individual ISIs. These produce wander in the mean interval, independent of its rapid variations, as previously described for neurons in the globus pallidus (Deister et al. 2013). Rate wander was incorporated into the model by changing the oscillation rate (ω) to match the variation in mean firing rate observed from trial to trial during the experiments. Adding wander to the model produced greater phase trajectory desynchronization and provided more accurate prediction of PSTH oscillation damping (Fig. 8, A3 and B3). Models incorporating both jitter and wander (Fig. 8, A4 and B4) predicted both the primary response and the damping of the secondary oscillation observed in the cell data (Fig. 8B5).
Fig. 8.
Desynchronization of phase and damping of poststimulus time histogram (PSTH) oscillations by 2 kinds of noise. A1–A4: phase trajectories for models initialized at a phase of 0 (i.e., synchronized). B1–B4: model PSTHs for corresponding simulations initialized at uniformly distributed phases (0–1). In a noiseless model (A1 and B1), phase trajectories remain synchronized forever, and there is no damping of the PSTH. In a model with jitter (A2 and B2), the trajectories desynchronize gradually, but the effect is insufficient to explain the experimental PSTH damping seen in the late portion of the illustrated data (B5). A model with slow noise or wander (A3 and B3) predicts desynchronization and PSTH damping more adequately but does not explain the shape of the first overshoot response (see Fig. 7). A model with both jitter and wander (A4 and B4) predicts both the shape of the primary response and the damping of the secondary oscillation.
The differing effects of jitter and wander can be explained by the way they accumulate over time. For jitter, the standard deviation of phase increases with the square root of time, but for wander it is linear with time (see materials and methods). Based on this, we predicted the damping of the PSTH oscillation based on the measured CV of unperturbed ISIs (jitter) and the CV of unperturbed firing rates sampled during the experiment (wander) (materials and methods, Eq. 9 and 10). In Fig. 9, we show the fitted equation (Eq. 10) and its amplitude envelope (Eq. 9) superimposed on PSTH data from cells with different levels of jitter and wander. Note that the levels of jitter and wander were not free parameters in the fits but were specified based on the unperturbed firing of the cells. The quality of these fits suggests that temporal dispersion by wander and jitter largely explained the damping of the PSTH oscillations.
Fig. 9.
A quantitative explanation of poststimulus time histogram (PSTH) oscillation damping by jitter and wander. A–D: experimental PSTH data fitted with Eq. 9 (the amplitude envelope) and Eq. 10 (the damped sine wave). The jitter [j = interspike interval coefficient of variation (CV)] and wander (w = firing rate CV) were measured from periods of unperturbed firing interspersed in each experiment. A: cell 1: j = 0.065, w = 0.051. B: cell 2: j = 0.071, w = 0.083. C: cell 3: j = 0.104, w = 0.057. D: cell 4: j = 0.130, w = 0.136.
Changes in phase probability density explain the PSTH.
The PSTH is an average over trials with different initial conditions and different outcomes. The differences between trials arise primarily from differences in the immediate firing history of the cell — the cell’s phase at the time of the stimulus. The PSTH is an outcome of a stimulus-induced change in the probability distribution of phases for a large collection of trials. By design, the PSTH randomizes initial phase on trials, so the initial phase probability distribution is uniform. The synaptic stimulus distorts the probability distribution of phases and thereby changes the firing rate at times after the stimulus. The influence of the stimulus on the probability distribution depends on the shape of the PRC. Because the SNr cell’s PRC is so heavily skewed, on trials in which the synaptic input arrives early after a previous spike, the input barely influences the timing of the next spike. For a small proportion of trials, those for which the cell was well advanced in phase at the time of stimulation, the stimulus has a powerful delaying effect because of the combination of the peaked PRC and the late increase in synaptic driving force (see Fig. 2).
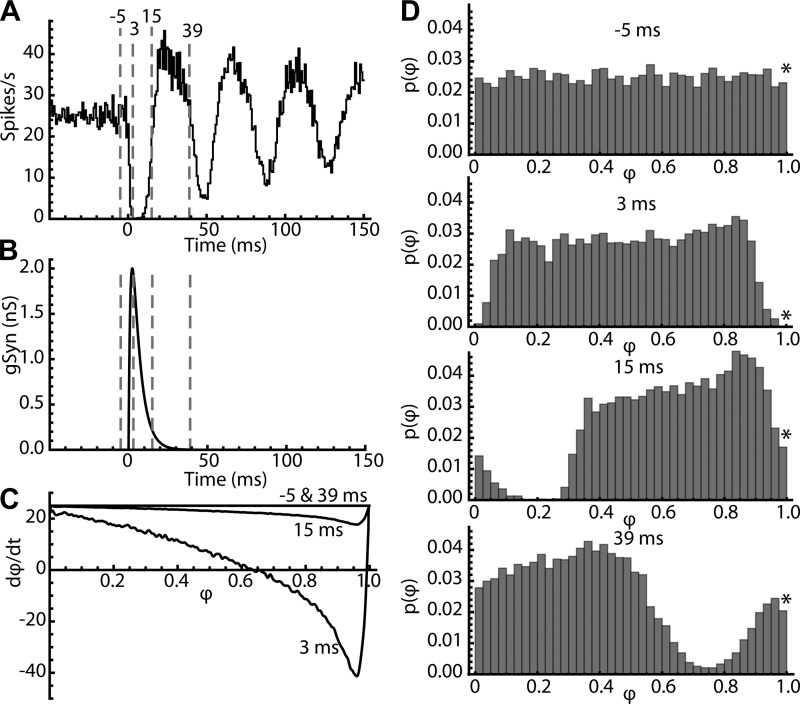
The effect of the stimulus is therefore best illustrated by its effect on the probability distribution of phases, calculated for all trajectories starting at all possible phases. This is illustrated in Fig. 10. For this figure, 10,000 trials were run on a phase model (including jitter) with the same PRC used in Fig. 8. The resulting PSTH is shown in Fig. 10A, and the stimulus conductance change is shown in Fig. 10B. The synaptic current generated by this stimulus varied on each trial because of phase-evolution of synaptic driving force during the ISI. The effect of the stimulus on the rate of change of phase (dφ/dt) is shown in Fig. 10C for four time points relative to the synaptic stimulus: 5 ms before its onset (−5 ms), near its peak (3 ms), late in its decay (15 ms) and after it was effectively over (39 ms). In the phase model (Eq. 3) synaptic current directly alters the rate of change of phase (dφ/dt). The curves in Fig. 10C show the effect of the stimulus on dφ/dt as a function of the phase of a trajectory for each of the four time points. In the absence of stimulus current (−5 and 39 ms), phase advances at the cell’s firing rate, 25 cycles/s. While the synaptic current is present, the phase advance slows, stops, or even reverses for some trajectories, depending on their phase at the time of the stimulus. This distorts the probability distribution of phases from its initial uniform shape.
Fig. 10.
Perturbation of the phase probability distribution explains the poststimulus time histogram (PSTH). A: PSTH for 2-nS inhibitory synaptic conductance in a phase model with the average substantia nigra pars reticulata neuron phase-resetting curve. Four specific times in the histogram are marked with dotted lines. B: the time course of the inhibitory conductance. C: the net rate of change of phase for the neuron at all phases consists of 2 components, a constant one (in this case 25 cycles/s) that is the unperturbed firing rate, and a time- and phase-varying one caused by the synaptic current acting through the PRC. Before and after the stimulus current phase advance consists of the constant component alone. At various times during the stimulus current, the phase advance is slowed or even reversed on trials according to their phases at the time of stimulus arrival. D: the probability distribution of phase at the four marked times. Before the stimulus, phase is uniformly distributed. *Value of the PSTH is proportional to the phase probability density at phases approaching 1. At the peak of the stimulus, trials at late phases are delayed, producing a compaction at phases around 0.85 and a rarefaction in the distribution at later phases. After the stimulus is complete, the entire distribution, distorted by the effects of the stimulus, moves to the right at the unperturbed rate, producing alternating increases and decreases in firing rate. The phase bin width of 0.025 corresponds to 1 ms at the unperturbed oscillation rate of the model neuron.
The effects of this stimulus on the probability distribution of phase are shown in Fig. 10D. Before the stimulus onset, phases are distributed uniformly as required for the PSTH. The firing rate is the expected value of the rate of movement across the boundary at phase = 1. The proportion of trials represented by the last bin in the histogram is approximately proportional to the average firing rate of the cell at that moment and the corresponding value of the PSTH. By the peak of the current at 3 ms, trajectories that were scheduled to fire have been shifted to the left by the negative rate of change of phase over the rising portion of the synaptic conductance, producing an accumulation of trajectories at phases between 0.7 and 0.9 (Fig. 10D, 3 ms). Cells that had fired in the moment before the stimulus were relatively unaffected by the stimulus and have advanced in phase. However, the early phases have not been replaced because of the reduced phase probability at the boundary. This produces a rarefaction of trajectories at very early phases. As the stimulus subsides (e.g., at 15 ms), there is no further distortion of the phase distribution, but the distorted distribution has shifted to the right and continues shift at a rate determined by the cell’s baseline firing rate, producing the subsequent oscillating changes in the PSTH.
The distortion of the phase distribution and the resulting oscillations in the PSTH are gradually reduced by diffusive effects of asynchronous current noise and over time they decay away. All features of the PSTH, both those previously called primary and those called secondary, are predicted by the evolution of the phase distribution. The primary features of the PSTH arise from the initial distortion of the phase distribution occurring during the synaptic conductance. The secondary features are caused by the propagation of that distortion through time and its decay because of the influence of other stimuli, including other synaptic inputs as well as the cell’s intrinsic current noise.
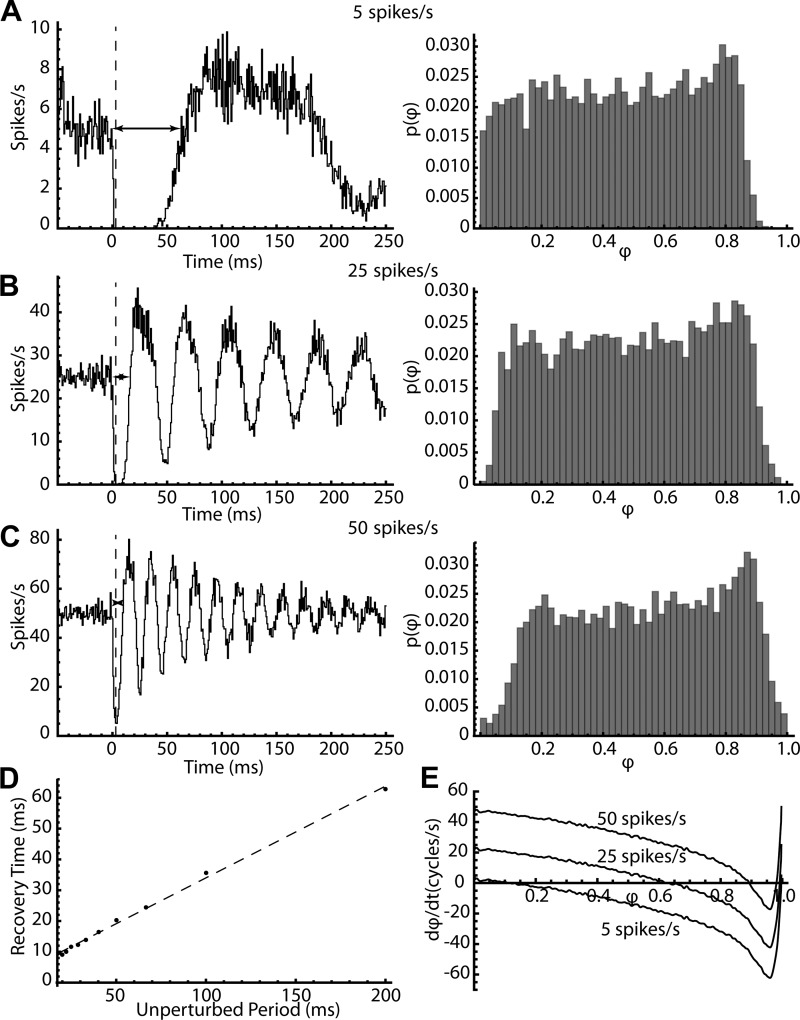
The phase model can also explain the previously unexplained features of the primary component of the PSTH (the initial trough). Previous studies unsuccessfully sought to predict the depth and duration of the PSTH trough based on the synaptic membrane potential change or its derivative (which approximates the synaptic current). The phase model predicts that the depth and duration of the PSTH trough depends on the amplitude and duration of the synaptic current (not voltage), but also the unperturbed firing rate of the cell. The effect of firing rate is illustrated in Fig. 11. The stimulus was the same as in Fig. 10, but the firing rate was adjusted to 5, 25, or 50 spikes/s. When the phase model was firing slowly, the synaptic stimulus produced a profound initial pause in firing that lasted over 50 ms. The same stimulus produced a much briefer initial trough at 25 spikes/s and a much shallower and shorter one when the cell was firing at 50 spikes/s. The reasons for the differences in trough amplitude and duration are apparent from the phase distributions at the peak of the stimulus (Fig. 11, A–C, right). At the peak of the stimulus, the delay of trajectories at late phases is much greater at lower firing rates. At this time point, the model with the lowest firing rate shows the greatest delay of trajectories at late phases. In contrast, the models with the highest baseline rates shift the entire distribution to the right faster, so when the stimulus is over, the distribution moves quickly to the right and spiking resumes earlier. The effect of firing rate on the duration of the initial trough is illustrated in Fig. 11D using the time from the stimulus to recovery from the trough (horizontal lines in Fig. 11, A–C). The recovery time is proportional to the period of unperturbed firing.
Fig. 11.
The effect of firing rate on the poststimulus time histogram (PSTH) and phase probability distribution. A–C: PSTHs (left) and phase probability distribution at the peak of the synaptic conductance (right) for model cells firing at 5 spikes/s (A), 25 spikes/s (B), or 50 spikes/s (C). The dotted line in each PSTH indicates the peak of the synaptic conductance. Horizontal lines with arrowheads show the width of the initial trough. D: the trough-width (recovery time) for model neurons at rates varying from 5 to 50 spikes/s. The dotted line is a linear fit to the points, with slope 0.30 and intercept (minimum trough width) of 4.2. E: the rate of change of phase vs. phase for 3 firing rates, plotted for the time corresponding to the peak of the synaptic conductance.
DISCUSSION
The coupling of synaptic conductance to postsynaptic spiking forms the foundation of synaptic integration. The absence of a tractable model that can accurately predict firing in response to a known synaptic conductance is a serious gap in our understanding of neuronal function (Fetz and Gustaffson 1983; Poliakov et al. 1994; Powers et al. 2005). This gap has long separated the body of knowledge collected with extracellular recording from that of intracellular recording, and it continues to impede our ability to combine information gained using the two methods.
The voltage and threshold model.
Classic studies attempted to explain how synaptic inputs shape the pattern of neuron firing. Moore et al. (1970) subdivided the PSTH of a postsynaptic neuron into two components: a primary response reflecting the sign and amplitude of synaptic coupling, and a secondary response dependent on periodicities in the firing of the presynaptic and postsynaptic cells. The mathematical model of Knox and Poppelle (1977) argued that the derivative of the synaptic potential (synaptic current) determines the primary component of the PSTH. Subsequent groups tested this prediction experimentally in repetitively firing neurons (Fetz and Gustaffson 1983; Gustaffson and McCrea 1984; Poliakov et al. 1994, 1996). These studies postulated that the PSP voltage waveform, measured from the resting potential, would sum linearly with the unperturbed interspike voltage trajectory of the neuron, and that spiking would occur whenever the voltage crossed a fixed threshold. The best experimental predictions were obtained using a weighted combination of the PSP waveform and the synaptic current (e.g., Fetz and Gustaffson 1983; Kirkwood and Sears 1978). However, the weighting of the voltage and current contributions was ad hoc, and even so the predictions were not always good, especially in the case of large IPSPs (Fetz and Gustaffson 1983; Gustaffson and McCrea 1984). Accurate prediction of PSTHs has been achieved using nonlinear systems identification methods (e.g., Mease et al. 2014; Powers et al. 2005), but these do not provide a biophysically satisfying intuition for the underlying process.
In retrospect, it is not surprising that an explanation based on PSP shape, voltage trajectory, and a spike threshold did not provide robustly accurate predictions of the PSTH. The PSP waveform measured from a resting state does not capture the dynamics of synaptic integration in spiking neurons. In repetitively firing neurons, the PSP does not decay but is instead incorporated into the ionic current interaction that governs the interspike voltage trajectory (Farries et al. 2012; also see Fig. 2). The voltage trajectory in the presence of the synaptic input is not the sum of the isolated PSP and the unperturbed trajectory. Moreover, the onset of the action potential is not determined solely by membrane potential but is equally dependent on all the other state variables governing excitability, including the activation and inactivation states of voltage-dependent sodium and potassium currents, all of which are changing continuously during the ISI. The concept of a spike threshold does not apply well to a multidimensional biophysical oscillator operating on a continuous limit cycle.
The phase model.
For oscillating neurons, the phase model offers an alternative description of the process that couples synaptic current to spiking. The phase resetting approach was designed as a general framework for oscillators (Kuramoto 1984; Winfree 1980) and has been elaborated for use with oscillating neurons in a rich series of theoretical and experimental studies (see reviews by Krogh-Madsen et al. 2012; Stiefel and Ermentrout 2016). It acknowledges the multidimensionality of interactions between subthreshold voltage dependent ion channels contributing to spike timing. Every ion channel introduces additional dimensions to the system of differential equations that describes a neuron’s oscillation, and the trajectory of a neuron between spikes is a path through the resulting multidimensional space. The phase model incorporates the multidimensionality of the neuron throughout the ISI, but gains simplicity by representing only a single trajectory in that space, the closed cycle of a cell’s oscillation during repetitive firing. Inasmuch as the input to the neuron does not remove it substantially from that trajectory, all perturbations can be approximated as changes in the location of the neuron on that cycle. Like the voltage and threshold model, the phase model is one dimensional. However, the effects of both spike and subthreshold ion channels are included in the form of phase-dependent changes in sensitivity to perturbations described by the PRC.
The phase model is only an approximation, and it cannot be expected to be applicable for all neurons or under all patterns of synaptic input (e.g., Krogh-Madsen et al. 2012). Our results indicate that the phase model is more robust than sometimes supposed. In should be noted that the method used here does not depend on one of the two approximations usually applied to phase models — the assumption that time and phase stay tightly coupled so that the PRC can be expressed as a function of time rather than phase. This assumption restricts use of the model to stimuli that do not produce large changes in phase (for review see Schwemmer and Lewis 2012). The analysis used here maintained the PRC as a function of phase, not time. The other phase-resetting assumption is that the dynamics controlling the cell's trajectory during unperturbed firing also dominate responses to large or persistent inputs. The applicability of this approximation must be tested experimentally by measuring the PRC and responses to inputs in the same neuron. In other basal ganglia neurons oscillating spontaneously or with depolarizing input, the model accurately predicted ISIs and even spike sequences (Wilson et al. 2014; Wilson 2017), even when the cells were densely perturbed and no longer firing rhythmically. In the results presented here, the phase-resetting model of the SNr neuron reproduced all the features, both primary and secondary, of the PSTH evoked by direct pathway striato-nigral inhibition. The phase model also offers an intuition about the generation of the PSTH that explains its features and its dependence on stimulus parameters. It provides a single explanation for both primary and secondary components of the PSTH. Both arise from the distortion of the probability distribution of phase that occurs while the synaptic current is present and is complete when the current subsides. All the features of the PSTH are created by that distortion and its gradual decay to a steady-state distribution. The rate of damping of the PSTH is explained by the erosion of the probability distribution under the influence of cellular noise and subsequent asynchronous synaptic inputs.
The shape of the PSTH.
The depth and duration of the initial trough in the PSTH are determined by the amplitude and duration of the inhibitory conductance, and by the postsynaptic cell’s firing rate. These factors determine how the stimulus alters the rate of phase change for trajectories that are approaching the firing point, as shown in Fig. 10. Inhibition powerfully delays the phase evolution in those advanced trajectories, producing a trough in the probability distribution late in phase, and an earlier peak produced by accumulation of delayed trajectories. That change is complete when the synaptic current is over. Afterwards, the entire distribution, including the peak and trough, drifts to the right at a constant rate corresponding to the cell’s unperturbed firing rate. The PSTH is proportional to the instantaneous probability of cells achieving a phase of one under the influence of this rightward drift. At all but the highest firing rates, the initial trough in firing probability substantially outlasts the synaptic current, and so the duration of the trough in the PSTH is largely determined by the cell’s unperturbed firing rate.
The trough is followed by an increase in firing rate that is associated with the arrival of the peak in the phase probability distribution. The increase in firing probability that follows the trough is not a rebound in the usual sense. That is, it is not caused by an increase in the availability of inward currents or inactivation of outward currents. It is simply the arrival of the delayed trajectories to the firing point. Likewise, subsequent oscillations in the PSTH are the repeating manifestations of the distorted, traveling phase probability distribution. The decay of the oscillatory response is caused by interference by other phase-altering events, like membrane noise or asynchronous synaptic input. These exert their effects by producing many small phase shifts, both advancing and delaying phase. Like other inputs, these asynchronous perturbations have their largest effect when they occur when the cell’s phase is near the peak in the PRC. They erode the distribution of phases, eventually returning it to its baseline state. Subsequent organized synaptic inputs occurring after the first conductance change is over but before the phase probability returns to a uniform distribution will interact with the perturbed distribution like interference waves. This mechanism allows for synaptic integration over a time window even longer than the ISI.
Synaptic integration in the striatal direct pathway.
PRC shapes vary widely among cell types, and even among neurons of the same type (e.g., Burton et al. 2012; Wilson et al. 2014). These differences reflect different styles of synaptic integration, dictated by the constellation of ion channels activated during each cell's ISIs (Ermentrout et al. 2012; Farries and Wilson 2012). The late peak and sudden plunge of the PRC seen in SNr neurons provides a very rapid onset to their response to direct pathway (and other) inhibition. This occurs because the inhibitory current has its largest phase-delaying effect on those trajectories for which the cell is close to firing, and because of the variation in chloride driving force throughout the ISI. Inhibition is most effective late in the ISI, when the PRC peaks and the driving force for inhibition is at its maximum, increasing the current generated by GABAergic conductances. If the PRC peaked earlier in the ISI, or if the change in driving force were not so large, inhibition would not be effective at slowing the phase advancement on the critical trajectories in which the cell is almost ready to fire, and those trajectories would leak through to fire shortly after the stimulus onset, producing a more gradual depression of firing probability.
Because the direct pathway axons make inhibitory synaptic connections on oscillating neurons of the SNr, a brief synaptic activation of the direct pathway is translated into an oscillatory change in spike frequency in SNr cells. This oscillation long outlasts the synaptic current or any time constant of the membrane; it is determined by the cell’s unperturbed firing rate and its regularity. Each synaptic input alters the phase of the SNr cell, and in so doing, promotes a sequence of excitability changes that will affect the response to subsequent inputs. For an individual synapse these changes are very small, but they can accumulate across synapses activated in temporal sequence. The effects of inputs that recur at about the firing rate of the SNr neurons will reinforce each other, regularizing the cell’s firing and entraining it to their timing. Inputs that arrive with no such pattern will interfere negatively, each undoing the organizing influence of the others and making firing irregular. For each postsynaptic cell, these effects will be different, as they are dependent on its firing rate. The phase model provides a tool to understand these interactions and to predict how physiological or pathological signals propagate through the basal ganglia and its output.
GRANTS
This work was supported by National Institute of Neurological Disorders and Stroke Grant NS-097185 and a grant from the Perry and Ruby Stevens Charitable Foundation.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
D.V.S., M.H.H., and C.J.W. conceived and designed research; D.V.S., M.H.H., and S.L. performed experiments; D.V.S., M.H.H., S.L., and C.J.W. analyzed data; D.V.S., M.H.H., and C.J.W. interpreted results of experiments; D.V.S., S.L., and C.J.W. prepared figures; D.V.S. drafted manuscript; D.V.S., M.H.H., S.L., and C.J.W. edited and revised manuscript; D.V.S., M.H.H., S.L., and C.J.W. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Salma Quraishi and Juan Morales for helpful comments on the manuscript.
REFERENCES
- Achuthan S, Butera RJ, Canavier CC. Synaptic and intrinsic determinants of the phase resetting curve for weak coupling. J Comput Neurosci 30: 373–390, 2011. doi: 10.1007/s10827-010-0264-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atherton JF, Bevan MD. Ionic mechanisms underlying autonomous action potential generation in the somata and dendrites of GABAergic substantia nigra pars reticulata neurons in vitro. J Neurosci 25: 8272–8281, 2005. doi: 10.1523/JNEUROSCI.1475-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown J, Pan WX, Dudman JT. The inhibitory microcircuit of the substantia nigra provides feedback gain control of the basal ganglia output. eLife 3: e02397, 2014. doi: 10.7554/eLife.02397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burton SD, Ermentrout GB, Urban NN. Intrinsic heterogeneity in oscillatory dynamics limits correlation-induced neural synchronization. J Neurophysiol 108: 2115–2133, 2012. doi: 10.1152/jn.00362.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang HT, Wilson CJ, Kitai ST. Single neostriatal efferent axons in the globus pallidus: a light and electron microscopic study. Science 213: 915–918, 1981. doi: 10.1126/science.7256286. [DOI] [PubMed] [Google Scholar]
- Christensson-Nylander I, Herrera-Marschitz M, Staines W, Hökfelt T, Terenius L, Ungerstedt U, Cuello C, Oertel WH, Goldstein M. Striato-nigral dynorphin and substance P pathways in the rat. I. Biochemical and immunohistochemical studies. Exp Brain Res 64: 169–192, 1986. doi: 10.1007/BF00238213. [DOI] [PubMed] [Google Scholar]
- Collingridge GL, Davies J. The influence of striatal stimulation and putative neurotransmitters on identified neurones in the rat substantia nigra. Brain Res 212: 345–359, 1981. doi: 10.1016/0006-8993(81)90467-4. [DOI] [PubMed] [Google Scholar]
- Connelly WM, Schulz JM, Lees G, Reynolds JN. Differential short-term plasticity at convergent inhibitory synapses to the substantia nigra pars reticulata. J Neurosci 30: 14854–14861, 2010. doi: 10.1523/JNEUROSCI.3895-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deister CA, Dodla R, Barraza D, Kita H, Wilson CJ. Firing rate and pattern heterogeneity in the globus pallidus arise from a single neuronal population. J Neurophysiol 109: 497–506, 2013. doi: 10.1152/jn.00677.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLong MR. Activity of pallidal neurons during movement. J Neurophysiol 34: 414–427, 1971. doi: 10.1152/jn.1971.34.3.414. [DOI] [PubMed] [Google Scholar]
- Deniau JM, Menetrey A, Charpier S. The lamellar organization of the rat substantia nigra pars reticulata: segregated patterns of striatal afferents and relationship to the topography of corticostriatal projections. Neuroscience 73: 761–781, 1996. [DOI] [PubMed] [Google Scholar]
- Ding S, Wei W, Zhou FM. Molecular and functional differences in voltage-activated sodium currents between GABA projection neurons and dopamine neurons in the substantia nigra. J Neurophysiol 106: 3019–3034, 2011. doi: 10.1152/jn.00305.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodla R, Wilson CJ. Effect of phase response curve shape and synaptic driving force on synchronization of coupled neuronal oscillators. Neural Comput 29: 1769–1814, 2017. doi: 10.1162/NECO_a_00978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout GB, Beverlin B II, Troyer T, Netoff TI. The variance of phase-resetting curves. J Comput Neurosci 31: 185–197, 2011. doi: 10.1007/s10827-010-0305-9. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Beverlin BII, Netoff T. Phase response curves to measure ion channel effects on neurons. In: Phase Response Curves in Neuroscience, edited by Schultheiss NW, Prinz AA, Butera RJ. New York: Springer, 2012, p. 207–236. doi: 10.1007/978-1-4614-0739-3_9. [DOI] [Google Scholar]
- Farries MA, Wilson CJ. Biophysical basis of the phase response curve of subthalamic neurons with generalization to other cell types. J Neurophysiol 108: 1838–1855, 2012. doi: 10.1152/jn.00054.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetz EE, Gustafsson B. Relation between shapes of post-synaptic potentials and changes in firing probability of cat motoneurones. J Physiol 341: 387–410, 1983. doi: 10.1113/jphysiol.1983.sp014812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeze BS, Kravitz AV, Hammack N, Berke JD, Kreitzer AC. Control of basal ganglia output by direct and indirect pathway projection neurons. J Neurosci 33: 18531–18539, 2013. doi: 10.1523/JNEUROSCI.1278-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerfen CR, Wilson CJ. The basal ganglia. In: Handbook of Chemical Neuroanatomy, Integrated Systems of the CNS, Part III, edited by Björklund A, Hökfelt T, Swanson L. Amsterdam, The Netherlands: Elsevier Science, 1966, p. 369–466. [Google Scholar]
- Gulácsi A, Lee CR, Sík A, Viitanen T, Kaila K, Tepper JM, Freund TF. Cell type-specific differences in chloride-regulatory mechanisms and GABA(A) receptor-mediated inhibition in rat substantia nigra. J Neurosci 23: 8237–8246, 2003. doi: 10.1523/JNEUROSCI.23-23-08237.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gustafsson B, McCrea D. Influence of stretch-evoked synaptic potentials on firing probability of cat spinal motoneurones. J Physiol 347: 431–451, 1984. doi: 10.1113/jphysiol.1984.sp015074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutkin BS, Ermentrout GB, Reyes AD. Phase-response curves give the responses of neurons to transient inputs. J Neurophysiol 94: 1623–1635, 2005. doi: 10.1152/jn.00359.2004. [DOI] [PubMed] [Google Scholar]
- Herrmann A, Gerstner W. Noise and the PSTH response to current transients: II. Integrate-and-fire model with slow recovery and application to motoneuron data. J Comput Neurosci 12: 83–95, 2002. doi: 10.1023/A:1015739523224. [DOI] [PubMed] [Google Scholar]
- Higgs MH, Wilson CJ. Unitary synaptic connections among substantia nigra pars reticulata neurons. J Neurophysiol 115: 2814–2829, 2016. doi: 10.1152/jn.00094.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higgs MH, Wilson CJ. Measurement of phase resetting curves using optogenetic barrage stimuli. J Neurosci Methods 289: 23–30, 2017. doi: 10.1016/j.jneumeth.2017.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hikosaka O, Sakamoto M, Miyashita N. Effects of caudate nucleus stimulation on substantia nigra cell activity in monkey. Exp Brain Res 95: 457–472, 1993. doi: 10.1007/BF00227139. [DOI] [PubMed] [Google Scholar]
- Hikosaka O, Wurtz RH. Visual and oculomotor functions of monkey substantia nigra pars reticulata. I. Relation of visual and auditory responses to saccades. J Neurophysiol 49: 1230–1253, 1983. doi: 10.1152/jn.1983.49.5.1230. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Dynamical Systems in Neuroscience: the Geometry of Excitability and Bursting. Cambridge, MA: MIT, 2007. [Google Scholar]
- Kawaguchi Y, Wilson CJ, Emson PC. Projection subtypes of rat neostriatal matrix cells revealed by intracellular injection of biocytin. J Neurosci 10: 3421–3438, 1990. doi: 10.1523/JNEUROSCI.10-10-03421.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkwood PA, Sears TA. The synaptic connexions to intercostal motoneurones as revealed by the average common excitation potential. J Physiol 275: 103–134, 1978. doi: 10.1113/jphysiol.1978.sp012180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knox CK, Poppele RE. Correlation analysis of stimulus-evoked changes in excitability of spontaneously firing neurons. J Neurophysiol 40: 616–625, 1977. doi: 10.1152/jn.1977.40.3.616. [DOI] [PubMed] [Google Scholar]
- Krogh-Madsen T, Butera R, Ermentrout GB, Glass L. Phase resetting neural oscillators: topological theory versus the real world. In: Phase Response Curves in Neuroscience, edited by Schultheiss NW, Prinz AA, Butera RJ. New York: Springer, 2012, p. 33–51. doi: 10.1007/978-1-4614-0739-3_2. [DOI] [Google Scholar]
- Kuramoto Y. Chemical Oscillations, Waves, and Turbulence. New York: Springer, 1984. doi: 10.1007/978-3-642-69689-3. [DOI] [Google Scholar]
- Ly C, Ermentrout GB. Analytic approximations of statistical quantities and response of noisy oscillators. Physica D 240: 719–731, 2011. doi: 10.1016/j.physd.2010.12.004. [DOI] [Google Scholar]
- Mease RA, Lee S, Moritz AT, Powers RK, Binder MD, Fairhall AL. Context-dependent coding in single neurons. J Comput Neurosci 37: 459–480, 2014. doi: 10.1007/s10827-014-0513-9. [DOI] [PubMed] [Google Scholar]
- Moore GP, Segundo JP, Perkel DH, Levitan H. Statistical signs of synaptic interaction in neurons. Biophys J 10: 876–900, 1970. doi: 10.1016/S0006-3495(70)86341-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Netoff T, Schwemmer MA, Lewis TJ. Experimentally estimating phase response curves of neurons: theoretical and practical issues. In: Phase Response Curves in Neuroscience, edited by Schultheiss NW, Prinz AA, Butera RJ. New York: Springer, 2012, p. 95–129. doi: 10.1007/978-1-4614-0739-3_5. [DOI] [Google Scholar]
- Poliakov AV, Miles TS, Nordstrom MA. A new approach to the estimation of post-synaptic potentials in human motoneurones. J Neurosci Methods 53: 143–149, 1994. doi: 10.1016/0165-0270(94)90171-6. [DOI] [PubMed] [Google Scholar]
- Poliakov AV, Powers RK, Binder MD. Functional identification of the input-output transforms of motoneurones in the rat and cat. J Physiol 504: 401–424, 1997. doi: 10.1111/j.1469-7793.1997.401be.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poliakov AV, Powers RK, Sawczuk A, Binder MD. Effects of background noise on the response of rat and cat motoneurones to excitatory current transients. J Physiol 495: 143–157, 1996. doi: 10.1113/jphysiol.1996.sp021580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers RK, Dai Y, Bell BM, Percival DB, Binder MD. Contributions of the input signal and prior activation history to the discharge behaviour of rat motoneurones. J Physiol 562: 707–724, 2005. doi: 10.1113/jphysiol.2004.069039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preyer AJ, Butera RJ. Neuronal oscillators in aplysia californica that demonstrate weak coupling in vitro. Phys Rev Lett 95: 138103, 2005. doi: 10.1103/PhysRevLett.95.138103. [DOI] [PubMed] [Google Scholar]
- Schwemmer MA, Lewis TJ. The theory of weakly coupled oscillators. In: Phase Response Curves in Neuroscience, edited by Schultheiss NW, Prinz AA, Butera RJ. New York: Springer, 2012, p. 3–31. doi: 10.1007/978-1-4614-0739-3_1. [DOI] [Google Scholar]
- Stiefel KM, Ermentrout GB. Neurons as oscillators. J Neurophysiol 116: 2950–2960, 2016. doi: 10.1152/jn.00525.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White JA, Rubinstein JT, Kay AR. Channel noise in neurons. Trends Neurosci 23: 131–137, 2000. doi: 10.1016/S0166-2236(99)01521-0. [DOI] [PubMed] [Google Scholar]
- Wilson CJ. Predicting the response of striatal spiny neurons to sinusoidal input. J Neurophysiol 118: 855–873, 2017. doi: 10.1152/jn.00143.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ, Barraza D, Troyer T, Farries MA. Predicting the responses of repetitively firing neurons to current noise. PLOS Comput Biol 10: e1003612, 2014. doi: 10.1371/journal.pcbi.1003612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ, Young SJ, Groves PM. Statistical properties of neuronal spike trains in the substantia nigra: cell types and their interactions. Brain Res 136: 243–260, 1977. doi: 10.1016/0006-8993(77)90801-0. [DOI] [PubMed] [Google Scholar]
- Winfree AT. The Geometry of Biological Time. New York: Springer, 1980. doi: 10.1007/978-3-662-22492-2. [DOI] [Google Scholar]
- Yung KK, Smith AD, Levey AI, Bolam JP. Synaptic connections between spiny neurons of the direct and indirect pathways in the neostriatum of the rat: evidence from dopamine receptor and neuropeptide immunostaining. Eur J Neurosci 8: 861–869, 1996. doi: 10.1111/j.1460-9568.1996.tb01573.x. [DOI] [PubMed] [Google Scholar]
- Zhou F-M, Lee CR. Intrinsic and integrative properties of substantia nigra pars reticulata neurons. Neuroscience 198: 69–94, 2011. doi: 10.1016/j.neuroscience.2011.07.061. [DOI] [PMC free article] [PubMed] [Google Scholar]