Visuomotor feedback gains are modulated by gaze position

Abstract

During goal-directed reaching, people typically direct their gaze to the target before the start of the hand movement and maintain fixation until the hand arrives. This gaze strategy improves reach accuracy in two ways. It enables the use of central vision at the end of movement, and it allows the use of extraretinal information in guiding the hand to the target. Here we tested whether fixating the reach target further facilitates reach accuracy by optimizing the use of peripheral vision in detecting, and rapidly responding to, reach errors during the ongoing movement. We examined automatic visuomotor corrections in response to displacements of the cursor representing the hand position as a function of gaze fixation location during unimanual goal-directed reaching. Eight fixation targets were positioned either in line with, or at different angles relative to, the straight-ahead movement direction (manipulation of fixation angle), and at different distances from the location of the visual perturbation (manipulation of fixation distance). We found that corrections were fastest and strongest when gaze was directed at the reach target compared with when gaze was directed to a different location in the workspace. We found that the gain of the visuomotor response was strongly affected by fixation angle, and to a smaller extent by fixation distance, with lower gains as the angle or distance increased. We submit that fixating the reach target improves reach accuracy by facilitating rapid visuomotor responses to reach errors viewed in peripheral vision.

NEW & NOTEWORTHY It is well known that directing gaze to the reach target allows the use of foveal visual feedback and extraretinal information to improve the accuracy of reaching movements. Here we demonstrate that target fixation also optimizes rapid visuomotor corrections to reach errors viewed in peripheral vision, with the angle of gaze relative to the hand movement being a critical determinant in the gain of the visuomotor response.

INTRODUCTION

Gaze behavior during action planning and control has been studied in a variety of natural and controlled settings, ranging from making sandwiches (Hayhoe 2000) or tea (Land et al. 1999) to relatively constrained object manipulation (Bowman et al. 2009; Flanagan and Johansson 2003; Johansson et al. 2001) and pointing (Neggers and Bekkering 2000, 2001; Prablanc et al. 1979) tasks. Despite the diversity of these tasks, gaze behavior exhibits one remarkable commonality across various settings, which is that gaze typically shifts to the target of an action before, or at the beginning of, the hand movement toward the target, and remains on target until around the time the hand arrives. A substantial body of research has thus sought to uncover the reason, or reasons, people exhibit this tendency.

One advantage of fixating gaze on the target is that it allows the use of foveal and parafoveal vision to guide the hand as it approaches the target, visual feedback that is critical in tasks requiring high precision (Carlton 1981; Land et al. 1999; Paillard 1982; Woodworth 1899). A second advantage of fixating the target is that it permits the use of extraretinal information [i.e., an efference copy of the eye movement command and/or proprioceptive information from the eye muscles (Bridgeman and Stark 1991)] to guide the hand, which is particularly important when the hand is not visible (Neggers and Bekkering 2001; Prablanc et al. 1979, 1986). Conversely, when gaze is not fixated on the target, humans make large errors in their reaching movements when no visual feedback is provided (e.g., Bock 1986; Henriques et al. 1998, 2002). The aim of the current study is to test whether fixating gaze at the target confers a third advantage, namely, optimizing the use of peripheral vision in detecting and responding to viewed errors in the hand trajectory well before the hand reaches the vicinity of the target.

When reaching toward a fixated target, peripheral vision (>10° eccentricity) of the initial trajectory of the hand can be used to correct for reach errors (Abahnini et al. 1997; Bard et al. 1985; Blouin et al. 1993; Paillard 1982; 1996). It is well established that an error in the viewed trajectory of the hand (caused by displacing the cursor) elicits a robust involuntary motor response with a latency of ~150 ms (e.g., Brenner and Smeets 2003; Sarlegna et al. 2003; Saunders and Knill 2003). The gain of these responses has been shown to be dependent on the features of the task, such as the size and shape of the target (Franklin and Wolpert 2008; Knill et al. 2011). By perturbing the viewed hand path at different points during the reach, it has been demonstrated that peripheral visual feedback is used continuously throughout reaching to rapidly correct for errors in hand position (Dimitriou et al. 2013; Saunders and Knill 2003, 2005).

In a recent study, we examined such rapid visuomotor corrections using a bimanual reaching task in which participants were required to simultaneously move handles, held in their left and right hands, to visual targets located on the left and right of midline, respectively, while fixating one of the targets (de Brouwer et al. 2017). Halfway through the movement, the cursors representing the positions of the handles passed beneath an occluder (Saunders and Knill 2004), at which point one or both cursors could be shifted laterally. To assess the speed and strength (i.e., gain) of the corrective response, we measured the lateral force participants applied in “channel” trials in which lateral handle motion was restricted (Dimitriou et al. 2013; Scheidt et al. 2000). We found that corrections were both quicker and stronger at the hand reaching toward the foveated target compared with the hand reaching toward the nonfoveated target (see also Diedrichsen et al. 2004).

One possible explanation of this result is that the ability to detect and respond to reach errors viewed in peripheral vision is optimal when the hand (or cursor representing the hand) is aimed toward the foveated location, a possibility suggested by Paillard (1996) but not evaluated. At the neural level, cells in parietal area 7a (also called area PG) appear to respond best to peripheral visual stimulus motion toward the gaze location, regardless of stimulus position in the receptive field (Motter and Mountcastle 1981; Steinmetz et al. 1987), indicating a selective coding of visual motion directions relative to the line of gaze. However, in our previous experiment (de Brouwer et al. 2017), which focused on the comparison of unimanual and bimanual reaches, it is also true that the location of the perturbation was closer to the fovea when the perturbation was applied to the hand moving toward the foveated target. Thus, another possible explanation for our result is that the visuomotor system might just be better at detecting errors when they are closer to the foveated location, given that static and dynamic visual acuity decrease as a function of retinal eccentricity (Frisén and Glansholm 1975; Lewis et al. 2011; Weymouth 1958).

To critically test these accounts, we examined how visuomotor corrections, in response to lateral shifts in cursor position halfway of the reach movement, depend on the location of gaze fixation relative to the location of the error (i.e., cursor shift). Specifically, we varied both the magnitude and angle, relative to movement direction, of the vector between the fixation point and the location of the error. To assess how these two factors influence the sensitivity of the rapid corrective responses, we also varied target size by including narrow vs. wide targets. We show that the gain of the corrective response during reaches to narrow and wide targets is modulated by both the magnitude (fixation distance) and angle (fixation angle) of this vector, with a stronger influence of the latter. Specifically, the response gain decreased as the fixation distance and the fixation angle increased. Our results suggest that the human visuomotor system is specialized to detect errors when the hand movement is directed toward the foveated location.

MATERIALS AND METHODS

Twenty-one individuals participated in the first session of the experiment. Fifteen of these participants (20–30 yr, 4 men) completed the second and third session of the experiment and were compensated $50 for their participation. The other six participants were compensated $15 for their participation and were excluded from further testing because the experimenter could not achieve sufficiently accurate eye tracking calibration (maximum error <3° of visual angle). All participants were self-reported right-handed and had normal or corrected-to-normal vision. The study was part of a research program that was approved by a Queen’s University Research Ethics Board, and participants provided written informed consent before participating in the first session.

Experimental Setup

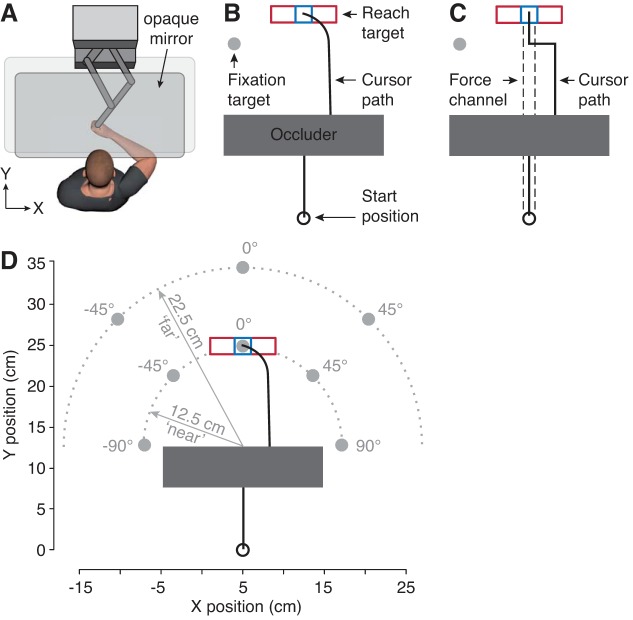
Participants performed unimanual reaching movements with their right arm in the horizontal plane. Participants were seated in a chair with their forehead resting against a pad and their right hand holding onto the handle of a robotic manipulandum (KINARM End-Point Robot; BKIN Technologies; Fig. 1A). Kinematics and forces at the handle were measured with a temporal resolution of 1,129 Hz. Eye movements were recorded using a built-in video-based eye tracker (Eyelink 1000; SR Research) with a temporal resolution of 500 Hz. Stimuli were projected on a horizontal opaque mirror positioned midway between a monitor and the handle such that the stimuli appeared in the plane of the handle. The mirror prevented the participant from viewing their arm.

Fig. 1.

Experimental setup and task. A: participants performed reaching movements in the horizontal plane while holding onto a robotic manipulandum. B: example nonchannel perturbation trial. Participants reached from a start position to a narrow (blue) or wide (red) reach target while fixating their gaze at a fixation target (gray circle). On a subset of trials, the hand cursor was visually perturbed by displacing it 3 cm to the left or right after it passed under a visual occluder. C: example force channel trial. In one-half of the trials, the participants’ movements were constrained along a straight line from the start to target position, allowing us to measure the forces applied to the virtual walls of the channel (broken lines). In cursor perturbation trials, the cursor automatically moved back to this line 250 ms after the perturbation. D: fixation targets were placed at different distances (12.5 cm, “near”; 22.5 cm, “far”) from the perturbation location and at different angles (0°, ±45°, ±90°) with respect to the movement direction.

Stimuli

The hand position was represented on the screen as a cursor (1-cm-diameter circle) aligned with the handle. Movements were made from a starting position (2-cm-diameter circle) to a reach target located 25 cm in front of the start position and 5 cm to the right of the midline of the screen (Fig. 1B). We used a narrow (2 × 2 cm) and wide (8 × 2 cm) rectangular reach target as a basic test for the sensitivity of corrective responses to task demands (de Brouwer et al. 2017; Knill et al. 2011). A 20 × 5 cm occluder was located between the start position and reach target such that the far edge of the occluder was at the halfway point of the required reaching movement (i.e., 12.5 cm from the start position). To test how corrective responses depend on the location of gaze relative to the location of the error, we instructed participants to look at a fixation target (2-cm-diameter circle), presented at one of eight different locations, during the reach. The fixation targets were presented at two different distances (“fixation distance”) from the center of the far edge of the occluder (i.e., the point where the unperturbed cursor reappeared after passing beneath the occluder) and five different angles (“fixation angle”) with respect to the vector between the center of the far edge of the occluder and the reach target (i.e., the straight-ahead movement direction; Fig. 1D). Five near-fixation targets were positioned at a fixation distance of 12.5 cm from the occluder (i.e., the distance of the reach target), with fixation angles of −90°, −45°, 0° (i.e., at the reach target), 45°, and 90° with respect to straight ahead. Three far fixation targets were positioned at a fixation distance of 22.5 cm from the occluder, with fixation angles of −45°, 0°, and 45°. The 0° near, ±45° near, ±90° near, 0° far, and ±45° far fixation locations were 0, 9.6, 17.7, 10, and 16.3 cm from the center of the reach target, respectively. Note that the fixation distance and fixation angle are defined in the horizontal plane of the task, the plane in which the stimuli were presented.

Note, however, that the distance between the fixation positions and the perturbation location can also be defined in terms of visual angle, which is nonlinearly related to the distance in Cartesian coordinates. We defined the visual angular distance θ_i for each fixation target as the scalar angle between the vector p from the eye to the perturbation point and the vector f_i from the eye to each of the fixation targets according to

$${\text{θ}}_i={\text{cos}}^{-1}\left(\frac{p\cdot {{\displaystyle f}}_i}{\Vert p\Vert \cdot \Vert {{\displaystyle f}}_i\Vert }\right)$$

For this analysis, we approximated the coordinates of the cyclopean eye as being horizontally in line with the start position and target, 5 cm in front of the start position, and 20 cm above the start position. Because the stimuli were projected in the plane of the handle via a mirror, the height (z component) of each vector was 40 cm.

Procedure

Task.

The procedure was similar to the procedure reported in our previous work (de Brouwer et al. 2017). To initiate a trial, the participant was required to move the hand cursor to the start position and hold this position (i.e., keep the center of the cursor within the 2-cm-diameter circle) for 250 ms. At this point, the reach target, the fixation target, and the occluder appeared on the screen. The fixation target was briefly flashed at a frequency of 5 Hz for 1 s, indicating to the participant to direct their gaze to this target and maintain fixation until the end of the reaching movement. After a delay of 750 ms from the last flash of the fixation target, five successive beeps (400 Hz; 80 ms) were presented, each 600 ms apart, cueing participants to first prepare (first 3 beeps) and then execute (between beeps 4 and 5) the reach movement. Specifically, participants were instructed to initiate their movement on the fourth beep and arrive at the target on the fifth beep. On all trials, the cursor passed beneath the visual occluder. On cursor perturbation trials, the cursor was displaced 3 cm to the left or right of the handle position underneath the occluder such that, when it reappeared at the far edge of the occluder, participants would correct its position to hit the target. The trial ended when the center of the cursor was in the area of the target. Following trial completion, a text message, displayed centrally on the screen, provided feedback on movement time (either “good”, “too fast,” or “too slow”). An error in the feedback calculation caused movement times to be slightly longer than the targeted movement time of 600 ms.

Channel trials.

We used channel trials to assess the gain of corrective responses. Note that such trials provide a highly sensitive and reliable method for measuring corrective responses in a manner that is not contaminated by limb dynamics (Franklin and Wolpert 2008; Scheidt et al. 2000). In these trials, the movement of the handle moved by the participant was restricted along a straight-line path from the start position to the target position by a mechanical channel generated by the manipulandum (stiffness 6,000 N/m, damping 1.5 N·m⁻¹·s⁻¹; Fig. 1C). This allowed us to measure the corrective forces exerted in the channel wall in response to the visual perturbation. In channel trials with a cursor perturbation, the cursor was automatically shifted back to a position on a straight line connecting the start position and the target position 250 ms after the perturbation, consistent with previous work (Dimitriou et al. 2013; Franklin and Wolpert 2008; Gallivan et al. 2016). Because this shift occurred around the time of the correction, participants generally believed that they were responsible for bringing the cursor back in-line to the target. To guard against an adaptive decrease in the magnitude of the corrective response across trials (Franklin and Wolpert 2008), only one-half of the trials of each experiment consisted of channel trials, which were randomly interspersed with nonchannel trials.

Nonchannel trials.

In nonchannel trials, only the first 7.5 cm of the movement were constrained by a mechanical channel (stiffness 6,000 N/m, damping 1.5 N·m⁻¹·s⁻¹), after which the channel was ramped down over 50 ms. Thus, the initial movement from the start position to the near edge of the occluder was constrained to a straight line. This was done to ensure that the cursor exited the occluder close to the line between the start position and the center of the target or, in perturbation trials, 3 cm to the left or right of this line.

The experiment consisted of 48 trial types: 2 target widths × 3 perturbation sizes (−3, 0, and 3 cm) × 8 fixation targets. All participants performed 40 repetitions of each perturbation trial type (20 of which were channel trials) and 20 repetitions of each nonperturbation type (10 of which were channel trials), resulting in a total of 1,600 trials that were equally divided across 10 experimental blocks. Participants performed three sessions on separate days, consisting of a practice block of 48 trials and two experimental blocks of 160 trials in the first session and a practice block of 20 trials and four blocks of 160 trials in the second and third sessions. The order of trials was randomized within each block.

Data Analysis

Kinematic and force data were resampled to 1,000 Hz and temporally aligned to the perturbation of the cursor, that is, the moment the cursor reappeared at the far edge of the occluder. Trials were excluded from the analysis if the movement time, defined as the time between the moment that the cursor had fully moved out of the start position and the moment that the center of the cursor was inside the rectangular target area, was longer than 1,200 ms (3.2% of trials).

Channel trials.

To obtain a measure of the strength of corrections in response to a cursor shift, lateral forces measured in channel trials were first averaged across an interval from 180 to 230 ms following perturbation onset (Franklin and Wolpert 2008). Trials were excluded from the analyses if the average force in this window was outside a range of the mean force ±3 SDs for each participant and trial type (0.3% of channel trials). For each participant and trial type, we subtracted the mean of the forces following a leftward cursor perturbation from the mean of the forces following a rightward cursor perturbation. [Note that a 2 (target width: narrow, wide) × 2 (cursor jump direction: leftward, rightward) × 3 (fixation position: ±90 near, ±45 near, ±45 far) × 2 (fixation side: left of target, right of target; 0° fixations excluded) ANOVA on the absolute values of the corrective forces revealed a main effect of cursor jump direction (P = 0.028) and an interaction between cursor jump direction and target size (P = 0.049). Specifically, responses were stronger following rightward cursor jumps compared with leftward cursor jumps, and this effect was slightly greater for narrow targets. These effects are likely because of biomechanical factors. Importantly, we did not observe an interaction between cursor jump direction and either fixation position (P = 0.155), our key independent variable, or fixation side (P = 0.089).] The resulting corrective force differences were averaged across fixation targets at the same relative location to the left and right of the reach target (i.e., across the ±45° near fixation targets, the ±90° near fixation targets, and the ±45° far fixation targets). As can be seen in Fig. 3, very similar responses were obtained for fixation targets in the left and right workspace. [Consistent with this observation, the ANOVA mentioned above did not reveal a main effect of fixation side (P = 0.132), an interaction with target width (P = 0.193), or fixation position (P = 0.085).]

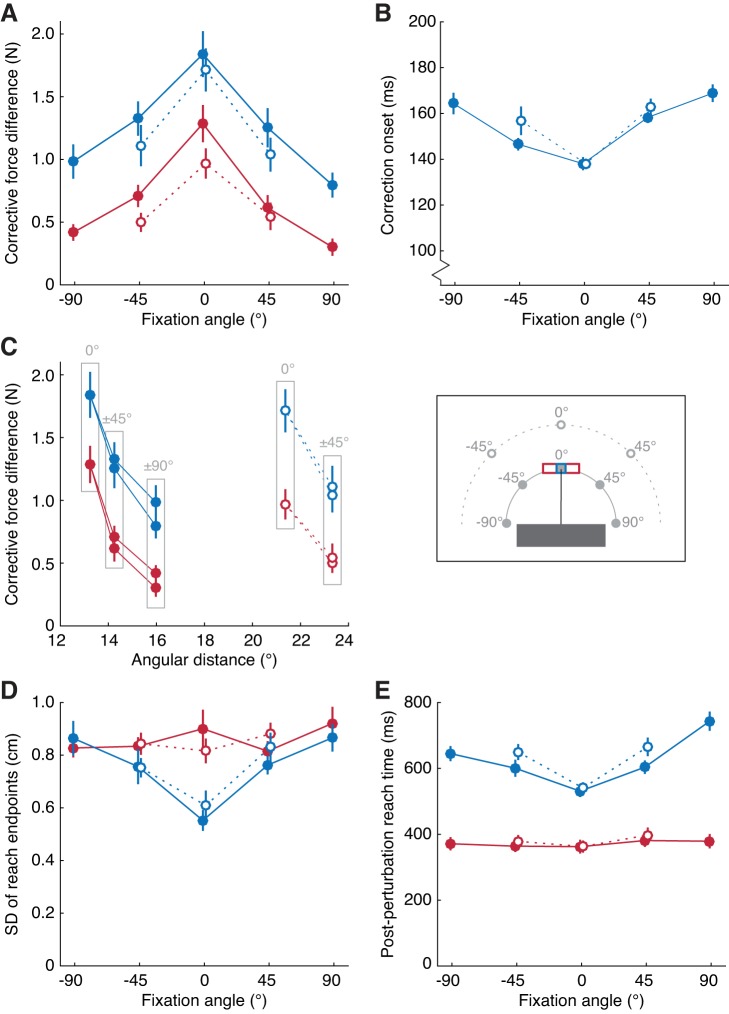
Fig. 3.

Group-averaged results. Blue dots and lines correspond to reaches to narrow targets; red dots and lines correspond to reaches to wide targets. Continuous lines and filled dots correspond to “near” fixation targets (12.5 cm from the point where the cursor, on average, exits the occluder); dotted lines and open dots correspond to “far” fixation targets (22.5 cm from the perturbation point). A: mean force differences averaged across the 180- to 230-ms interval following cursor perturbation, as a function of the angle of fixation relative to the movement direction in the horizontal plane (see inset). B: mean onset of the corrective force response (see Data Analysis) as a function of fixation angle. C: mean force differences as in A, as a function of the distance between the perturbation point and the fixation target in visual angle (see Data Analysis). Labels indicate the angle of fixation relative to the movement direction in Cartesian coordinates. D: mean variability in the horizontal coordinate of the reach end point in nonchannel trials, as a function of fixation angle. E: mean duration between the perturbation and the cursor reaching the target in nonchannel trials, as a function of fixation angle.

To compute the onset times of the force corrections, we compared the individual force traces for leftward and rightward perturbations of a single trial type. We first applied unpaired uncorrected t-tests at each time point following the perturbation to find the minimum P value. Next, we defined the onset of the correction as the first sample for which P < 0.05, searching back in time from the minimum P value (de Brouwer et al. 2017; Reichenbach et al. 2013). These values were separately verified by using an extrapolation method applied to the averaged difference between force profiles for leftward and rightward perturbations per trial type, averaged across subjects. To determine the onset times, we fitted a line through the points at which the average force difference reached 25 and 50% of the first peak difference in force response and determined at which time point this line crossed zero (Oostwoud Wijdenes et al. 2014). This method yielded slightly earlier correction onsets but a very similar pattern of results. Onset times were only computed for trial types with narrow targets because the computation of onset times for wide targets yielded unreliable results because of the lower force responses.

Nonchannel trials.

We also examined the effect of fixation position on the kinematics of the hand movement in nonchannel trials in which a cursor perturbation occurred. To this end, we analyzed two different measures: postperturbation reach time and horizontal end point variability (i.e., variability in the direction of the perturbation). We computed the postperturbation reach time as the time it takes from the moment of the perturbation to bring the cursor to the target. Thus, this variable provides a temporal measure of reach performance. We computed the horizontal end point variability by defining movement offset as the first of five consecutive samples where the resultant hand velocity is below 5 cm/s and taking the x position of the hand at this time point. Thus, this variable provides a spatial measure of reach performance. The postperturbation reach time and horizontal end point variability were computed for each trial type and then averaged across leftward and rightward cursor jumps and across fixation targets at the same relative location to the left and right of the reach target.

Gaze data.

Blinks and missing samples from the eye tracker were interpolated where possible. For each trial, we computed the average gaze position during the first 20 ms following the perturbation. We verified that, at this time point, gaze was generally “anchored” at this position until the end of the reach. The recorded gaze position at the time of perturbation often showed errors in the y-direction due to the fact that the fixation targets were located in the horizontal plane, requiring a combination of version and vergence eye movements that are difficult to disentangle using monocular eye tracking. We therefore discarded trials based on relative gaze position at the time of perturbation, that is, if the distance between the gaze position in a trial and the average gaze position for a specific fixation target in a block of trials was greater than 4.8 cm (i.e., one-half the minimum distance between two adjacent fixation dots; 6.5% of trials). In the large majority of correct trials (96.5%; remaining trials not excluded), gaze remained on the fixation target after the time of perturbation (at least) until the hand arrived at the target, which occurred on average 373 ± 21 ms (mean ± SE) after the perturbation in channel trials and 499 ± 18 ms in nonchannel trials.

RESULTS

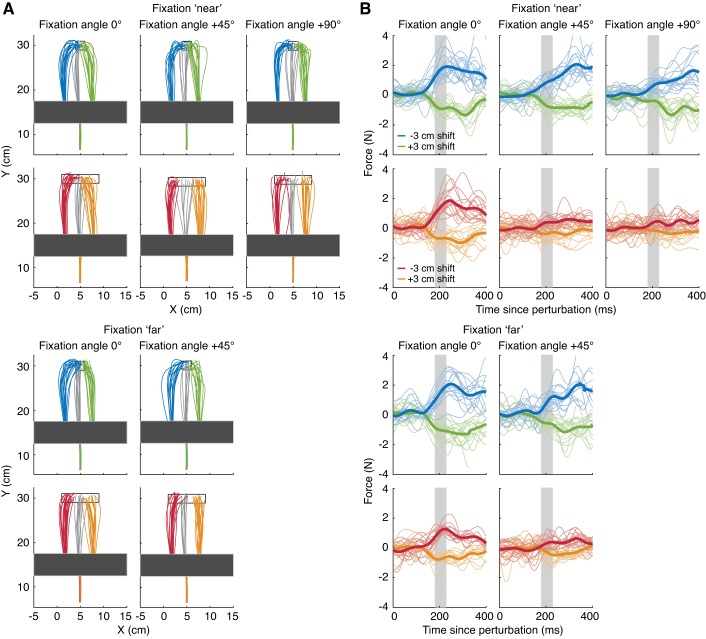
We measured corrections in response to a lateral displacement of the hand cursor during reaches to narrow and wide targets. Participants’ gaze was directed to one of eight fixation locations in the horizontal plane of movement during the reach, whereas the target was always presented at the same location. Figure 2A shows cursor paths from nonchannel trials for a representative participant. Separate panels are shown for each fixation target and target width, and paths are color coded according to the perturbation condition. Figure 2B shows, for corresponding channel trials, the forces exerted in the channel wall for leftward and rightward perturbation trials. As shown by both the cursor paths and force responses in Fig. 2B, participants made less vigorous corrections when reaching to the wide target.

Fig. 2.

Raw data of an example participant. A: cursor paths in response to a leftward (blue and red), no (gray), or rightward (green and orange) perturbation of the hand cursor during reaches to narrow (1st and 3rd row) and wide (2nd and 4th row) targets in trials without a force channel. B: forces measured in channel trials in response to a leftward (blue and red) or rightward (green and orange) perturbation of the hand cursor during reaches to narrow (1st and 3rd row) and wide (2nd and 4th row) targets. Thin traces indicate the forces on individual trials, thick traces indicate the average force. The gray shaded area indicates the 180- to 230-ms interval across which the force differences were averaged to obtain a single measure of the strength of the response.

Channel Trials

To obtain a single measure of the strength of the corrective response for each condition, we subtracted the mean force in the 180- to 230-ms interval (Fig. 2B) following a leftward cursor displacement from the mean force in the same interval following a rightward cursor displacement. For illustrative purposes, we show the results at all fixation locations, but for statistical analyses, we averaged the data across corresponding fixation locations to the left and right of the target. Figure 3A shows the corrective force differences during reaches to narrow and wide targets, for each fixation location. For both narrow and wide targets, corrective forces were affected by fixation angle and fixation distance. These effects were confirmed by a 2 (target width) × 2 (fixation angle; excluding ±90°) × 2 (fixation distance) repeated-measures ANOVA. Consistent with previous research (Gallivan et al. 2016; Knill et al. 2011; Nashed et al. 2012), corrective responses were greater for narrow than for wide targets [F(1,13) = 51.5, P < 0.001]. Furthermore, corrective responses were greater for fixation at 0° than for fixation at ±45° [F(1,13) = 62.0, P < 0.001] and greater for fixation at near locations than for fixation at far locations [F(1,13) = 37.8, P < 0.001]. There was no significant target width × fixation angle interaction [F(1,13) = 1.0, P = 0.328], target width × fixation distance interaction [F(1,13) = 1.3, P = 0.280], or fixation angle × fixation distance interaction [F(1,13) = 0.6, P = 0.442], but we did find a significant angle × distance × target width interaction [F(1,13) = 4.9, P = 0.046]. To examine this three-way interaction and the corrective forces at all fixation angles, we performed separate ANOVAs for the near and far distances. For the near fixations, now including the ±90° fixation angle, we found a significant effect of angle [Greenhouse-Geisser corrected F(1.2,15.4) = 72.6, P < 0.001] and target width [F(1,13) = 47.5, P < 0.001] but no significant interaction [Greenhouse-Geisser corrected F(1.4,18.2) = 0.5, P = 0.527]. Pairwise comparisons showed that corrective forces at 0°, ±45°, and ±90° were all significantly different from each other (all P < 0.001), with the largest responses for fixation at 0° and the smallest responses for fixation at ±90°. For the far fixations, we again found a significant effect of angle [F(1,13) = 64.9, P < 0.001] and target width [F(1,13) = 66.2, P < 0.001]. In addition, a significant interaction between target width and angle [F(1,13) = 12.5, P = 0.004] showed that the effect of angle was greater for narrow targets than for wide targets.

As described above, we opted to use a fixed interval (180–230 ms) over which to average forces rather than adapt the interval to the timing of correction onsets to calculate the strength of corrections. However, for completeness, we also evaluated corrective force differences using the latter approach. Specifically, we adjusted the intervals to the correction onsets, averaging the forces over an interval from 25 to 75 ms after correction onset: from 163 to 213 ms for the conditions with fixation in line with the movement and from 180 to 230 ms for the conditions with a fixation angle of 45° with respect to the movement direction. The statistical results were not affected by this alternate method, except for the interaction between target width and fixation angle that was marginally significant when using this alternate method [F(1,13) = 4.9, P = 0.046].

Figure 3B shows the correction onset times of the force responses during reaches to narrow targets, as determined using t-tests (see Data Analysis). Correction onset times ranged from 138 ± 3 and 138 ± 2 ms (mean ± SE), respectively, for the near and far fixation locations in line with the movement (0°), to 167 ± 4 ms for the fixation location at 90°. A 2 (fixation angle; excluding ±90°) × 2 (fixation distance) repeated-measures ANOVA revealed that corrections were faster when fixation was in line with the movement compared with when fixation was at 45° [F(1,13) = 55.9, P < 0.001]. Consistent with this effect, a separate paired t-test showed that corrections were faster for fixation at the ±45° near location than for fixation at the ±90° near location [t(13) = 4.6, P < 0.001]. The ANOVA further showed that fixation distance had a marginally significant effect on correction onsets [F(1,13) = 4.6, P = 0.051]. A marginally significant interaction between fixation angle and fixation distance [F(1,13) = 3.6, P = 0.079] reflected the result that fixation distance did not affect correction onsets when fixation was in line with the movement.

In our experiment, we varied the distance and angle of the fixation position relative to the location of the perturbation that occurred halfway of the reach movement. An alternative explanation for our effects could be that the magnitude and timing of corrective responses are dependent on the distance between the reach target and the fixation location. However, the results clearly show a greater decrease in corrective responses from the “ideal response” (i.e., when fixating the reach target) for a 45° increase in fixation angle than for a 10-cm increase in fixation distance. Because the “far” fixation target at 0° and the “near” fixation targets at ±45° were placed at equal distance from the target, we can rule out this explanation. A second alternative explanation could be that corrections are dependent on the visual angle between the fixation positions and the perturbation location. In our experiment, we defined the distance between the perturbation location and the fixation positions in the natural coordinates of the task (i.e., hand or Cartesian coordinates). However, this distance can also be defined in terms of visual angle, which is nonlinearly related to Cartesian distance. Figure 3C shows the gain of the corrective response as a function of angular distance for all eight fixation targets, where angular distance is defined as the scalar angle between the line of gaze when fixating the perturbation and the line of gaze when fixating the fixation target (see Data Analysis). Importantly, if the gain of the response depends solely on gaze angle, then the gains should be well fit by a single regression line. As can be seen in Fig. 3, this is clearly not the case. Whereas the results show a clear decrease in corrective force with an increase in fixation angle, the effects of angular distance and Cartesian fixation distance are negligible.

To summarize, corrections in response to a lateral shift in cursor position were both slower and weaker when the magnitude of the fixation angle was larger. Furthermore, corrective forces were weaker when the fixation distance was greater, whereas correction onsets were not significantly affected by fixation distance. Overall, the reduction in corrective forces with increasing fixation angles was more pronounced than the reduction in corrective forces with increasing fixation distance. The effect of fixation angle became even more pronounced when plotting the results as a function of angular gaze distance. Averaged across participants, corrective forces for the fixation targets at 45° and 90° were on average 59% and 38%, respectively, of the responses seen for when the fixation targets were in line with the movement direction (0°). The corrective forces for far fixation locations were ~81% of the corrective forces seen for the near fixation locations.

Nonchannel Trials

Figure 3D shows the variability of the reach end points along the x-axis. For fixation targets in line with the target, variability was smaller for narrow targets than for wide targets. However, this target width effect was much smaller or absent for fixation targets at ±45° and ±90°. A 2 (target width) × 2 (fixation angle; excluding ±90°) × 2 (fixation distance) repeated-measures ANOVA revealed main effects of target width [F(1,13) = 30.3, P < 0.001] and fixation angle [F(1,13) = 9.1, P = 0.010] but not fixation distance [F(1,13) = 0.5, P = 0.475] on variability in reach end points. We further found significant interactions between width and angle [F(1,13) = 27.9, P < 0.001] and between distance and angle [F(1,13) = 5.7, P = 0.033] but not between width × distance [F(1,13) = 3.8, P = 0.072] or width × angle × distance [F(1,13) = 3.0, P = 0.109]. Consistent with the width × angle interaction, separate paired t-tests showed an effect of angle between the ±45° and the ±90° fixation angle for narrow [t(13) = 5.1, P < 0.001] but not for wide [t(13) = 1.3, P = 0.218] targets.

Figure 3E shows the postperturbation reach time, time between the cursor perturbation and the cursor being at the target. Postperturbation reach times were longer for narrow than for wide targets [F(1,13) = 267.5, P < 0.001], for greater fixation angles [F(1,13) = 134.6, P < 0.001; excluding ±90°], and for greater fixation distance [F(1,13) = 19.5, P = 0.001]. Postperturbation reach times were more affected by fixation angle and distance during reaches to narrow targets than during reaches to wide targets [width × angle F(1,13) = 41.1, P < 0.001; width × distance F(1,13) = 7.9, P = 0.015]. Furthermore, the effect of distance was greater for the ±45° fixation angle than for the 0° fixation angle [distance × angle F(1,13) = 11.9, P = 0.004], at which the postperturbation reach time was unaffected by fixation distance. There was no significant three-way interaction [F(1,13) = 3.1, P = 0.101]. Consistent with the width × angle interaction, separate paired t-tests showed an effect of angle between the ±45° and the ±90° fixation angle for narrow [t(13) = 5.7, P < 0.001] but not for wide [t(13) = 0.4, P = 0.681] targets.

Overall, the kinematics of reaches to wide targets were less affected by fixation location than the kinematics of reaches to narrow targets. The pattern of results for narrow targets is consistent with the pattern of results for force channel trials: variability was lowest and postperturbation reach times were shortest when fixating the reach target, and performance deteriorated with increasing fixation angle or distance. Similar to the results for correction onsets, postperturbation reach times were only affected by fixation distance when fixation was not in line with the movement.

DISCUSSION

Here we examined the effect of gaze position on the magnitude, speed, and accuracy of corrections to a lateral shift in the position of the hand cursor during reaching. For all gaze positions, we found that cursor perturbations elicited a rapid correction of the movement trajectory, which, in channel trials, were detected as a rapid change of force exerted in the channel wall. Notably, we found that corrections were both faster and stronger, and the end points of perturbed reaches were less variable, when gaze was directed at the reach target compared with when gaze was directed to a different location in the workspace. Corrections were influenced both by the distance between the perturbation location and the fixation target (fixation distance) and by the angle between the movement direction and the vector between perturbation location and the fixation target (fixation angle) in task coordinates. However, the influence of fixation angle relative to the movement direction was considerably stronger than the influence of fixation distance. Our analysis on the visual angle distance between the fixation positions and the perturbation location confirmed our conclusion that the direction of gaze relative to hand movement, in task coordinates, is a critical determinant in the strength of the gain of the rapid visuomotor response. These results suggest that the human visuomotor system exhibits enhanced detection for visual errors in the reach movement when the hand is moving toward the foveated location.

When reaching toward a target, people typically fixate the target well before the hand arrives and then maintain this fixation until around the time the reach is completed (Johansson et al. 2001; Land et al. 1999; Neggers and Bekkering 2000; Prablanc et al. 1979). Fixating the target is thought to facilitate reaching in at least two ways. First, it allows the use of foveal and parafoveal vision toward the end of the reach, when fine adjustments may be necessary (e.g., Land et al. 1999). Second, fixating the target allows the use of nonvisual gaze-related signals to be used in guiding the hand to the target (Neggers and Bekkering 2001; Prablanc et al. 1986). The current results suggest that fixating the target further improves reaching performance by upregulating visuomotor corrections that occur in response to reach errors viewed in peripheral vision. Our finding that the visuomotor gain was highest when fixating the reach target, compared with all other tested locations, confirms the results of a previous paper in which we examined simultaneous bimanual reaching, where each hand moved straight ahead to its own target (de Brouwer et al. 2017). There, we found that the gain of the visuomotor response was greater when gaze was directed toward the target of the perturbed vs. unperturbed hand. The main objective of the present study was to determine the factors that confer this advantage.

We found that, independent of the fixation angle (i.e., the angle between movement direction and the line between the perturbation location and the fixation target), the gain of the visuomotor reflex was influenced by fixation distance (i.e., the distance between the fixation target and the perturbation location). Specifically, the gain was weaker (~19%) for fixation locations further from the perturbation location (far locations) than for fixation locations closer to the perturbation location (near locations). This effect is small, especially considering the large increase in visual angle at greater fixation distances in our task. It is well known that visual acuity decreases as a function of retinal eccentricity (Frisén and Glansholm 1975; Weymouth 1958;), and several aspects of motion perception deteriorate with increasing eccentricity, such as resolution thresholds of moving stimuli (Brown 1972; Lewis et al. 2011), absolute motion thresholds (Tynan and Sekuler 1982), differential motion and velocity thresholds (McKee and Nakayama 1984), and detection and discrimination of motion direction (Levi et al. 1984). Our results suggest that there is also an effect of eccentricity on the detection of the displacement of a moving stimulus. However, this result might not directly relate to the conscious perception of displacement detection, since it has been shown that rapid corrections to shifts in target (Goodale et al. 1986) or cursor (Saunders and Knill 2003) position do not require awareness. The decrease in the gain of the visuomotor response with increasing distance between the error and the point of gaze could be explained in the framework of Bayesian estimation and optimal feedback control (Todorov 2004). When the perturbation occurs further in peripheral vision, this might increase the uncertainty of visual cues and thereby reduce the gain of the feedback response (Acerbi et al. 2017; Izawa and Shadmehr 2008).

By varying the distance and angle of the fixation location from the perturbation location, we also varied the distance between the fixation location and the reach target. Importantly, our results show that this distance was not a major factor in determining the gain of the automatic visuomotor response. Specifically, we found that the corrective response was almost as strong in the 0° far condition, where gaze was located 10 cm beyond the target, as it was in the 0° near condition, where gaze was located at the target. In addition, the corrective response was considerably stronger in the 0° far condition than in the ±45° near condition, where the gaze was slightly closer to the reach target.

We also found that, independent of the fixation distance, the visuomotor gain decreased with the magnitude of the fixation angle relative to the movement direction. We showed that this effect was not because of an increase in angular gaze distance in polar coordinates. In fact, the effect of fixation angle became even more pronounced when we considered the corrective forces as a function of angular gaze distance. Specifically, we found that corrective forces decreased in magnitude (by ~41% for fixation at ±45° and by ~62% for fixation at ±90° for an identical distance) and had later onsets with increasing absolute fixation angle relative to the movement direction in Cartesian (task) coordinates. The results of the force channel trials were confirmed by the results of the nonchannel trials, that is, reach end points were more variable and postperturbation reach times were longer with increasing fixation angle, especially for narrow reach targets that require higher movement accuracy. Interestingly, the correction onsets and postperturbation reach times were very similar for the near and far fixation locations in line with the movement direction, showing no effect of fixation distance. Together, these results support the idea that the human visuomotor system is specialized for detecting errors in reaching movements directed toward the foveated location (Paillard 1996). This notion is broadly consistent with the observation that a large proportion of visual stimulus-responsive neurons in the parietal cortex of macaque monkeys respond strongly to peripheral motion toward the gaze location, at a wide range of velocities (Motter et al. 1987) and regardless of stimulus position in the receptive field (Motter and Mountcastle 1981). In addition, the response of these neurons is modulated by the angle of gaze during a fixation task (Andersen and Mountcastle 1983). As such, these neurons, which are considered part of the visuomotor network in parietal cortex (Passarelli et al. 2011), could provide reliable signals of the direction of motion in the visual surround relative to the central line of gaze and therefore appear to be well suited for the visual guidance of arm movements (Steinmetz et al. 1987).

As noted above, fixating the reach target is thought to facilitate accurate reaching by enabling the use of nonretinal gaze-related signals that can be used to guide the hand. These signals may include efference copy of the eye movement command and proprioceptive signals from the eye muscles (Bridgeman and Stark 1991; Desmurget et al. 1998; Lewis et al. 1998). When fixating at a location other than the reach target, it is not obvious how such signals may be exploited. However, it is possible that, when fixating a location other than the reach target but that is in line with the movement direction, the brain can use nonretinal gaze-related signals to determine the required direction of the reach.

In the current paper, we used a force channel to obtain a sensitive and accurate measure of the rapid visuomotor response (de Brouwer et al. 2017; Dimitriou et al. 2013; Gallivan et al. 2016). However, a limitation of this approach is that only lateral forces, which correct for lateral displacements of the hand cursor, can be measured. Although it is known that rapid visuomotor responses are also observed when the position or velocity of the hand cursor is perturbed in line with direction of the reaching movement (Knill et al. 2011; Saunders and Knill 2005), it remains to be determined whether our findings extend to such perturbations. A second limitation of the current work stems from the limited number of fixation locations we could reasonably examine, given the number of trials required to obtain robust measures of the gain of the visuomotor response. In choosing fixation locations, our primary objective was to vary the fixation angle while keeping fixation distance equal to that of the reach target. This resulted in five fixation locations. We then added three additional fixation locations at a greater fixation distance to vary the fixation distance independent of fixation angle. In future work, it might be interesting to examine fixation distances shorter than that of the reach target, including fixating the actual perturbation location, and the start position of the reach. Importantly, however, with the current fixation targets, we can draw clear conclusions about fixation angle.

In summary, we have shown that visuomotor feedback gains during unimanual goal-directed reaching are strongly influenced by gaze position. In particular, we have demonstrated that both fixation distance and fixation angle influence the gain of the rapid visuomotor response, with the latter effect being stronger. Overall, our findings suggest that the human visuomotor system is highly sensitive to errors in movement direction when the hand is moving toward the foveated location.

GRANTS

This research was funded by the Natural Sciences and Engineering Research Council of Canada and the Canadian Institutes of Health Research.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.J.d.B., J.P.G., and J.R.F. conceived and designed research; A.J.d.B. analyzed data; A.J.d.B., J.P.G., and J.R.F. interpreted results of experiments; A.J.d.B. prepared figures; A.J.d.B. drafted manuscript; A.J.d.B., J.P.G., and J.R.F. edited and revised manuscript; A.J.d.B., J.P.G., and J.R.F. approved final version of manuscript.