Bayesian geostatistical modelling of PM₁₀ and PM_2.5 surface level concentrations in Europe using high-resolution satellite-derived products

Abstract

Air quality monitoring across Europe is mainly based on in situ ground stations, which are too sparse to accurately assess the exposure effects of air pollution for the entire continent. The demand for precise predictive models that estimate gridded geophysical parameters of ambient air at high spatial resolution has rapidly grown. Here, we investigate the potential of satellite-derived products to improve particulate matter (PM) estimates. Bayesian geostatistical models addressing confounding between the spatial distribution of pollutants and remotely sensed predictors were developed to estimate yearly averages of both, fine (PM_2.5) and coarse (PM₁₀) surface PM concentrations, at 1 km² spatial resolution over 46 European countries. Model outcomes were compared to geostatistical, geographically weighted and land-use regression formulations. Rigorous model selection identified the Earth observation data which contribute most to pollutants' estimation. Geostatistical models outperformed the predictive ability of the frequently employed land-use regression. The resulting estimates of PM₁₀ and PM_2.5, which represent the main air quality indicators for the urban Sustainable Development Goal, indicate that in 2016, 66.2% of the European population was breathing air above the WHO air quality guidelines thresholds. Our estimates are readily available to policy makers and scientists assessing the effects of long-term exposure to pollution on human and ecosystem health.

Graphical abstract

Highlights

• •Assessment of PM₁₀ and PM_2.5 concentrations across Europe at 1 km² resolution
• •Estimates of population exposure to pollution levels exceeding WHO and EU thresholds
• •Bayesian geostatistical models outperform the commonly employed LUR and GWR.

1. Introduction

The contribution of particulate matter (PM) concentration to air pollution and the effects of high levels of these pollutants to human health and wellbeing have been documented extensively in the literature. Exposure to high concentrations of PM has been associated with increased rates of morbidity and mortality, caused primarily by cardiovascular, respiratory and, to a lesser extent, cerebrovascular diseases (Anderson et al., 2012).

Although a relatively dense air quality monitoring network exists in Europe, maintained by the European Environment Agency's (EEA) member states, large areas within the continent remain unmonitored. A number of approaches have been used to provide gridded pollutants' concentration estimates. On European and global scale, these include empirical models based on chemistry transport model outputs (van Donkelaar et al., 2006), land-use regression (LUR) (Beelen et al., 2009, Vienneau et al., 2013), kriging (Beelen et al., 2009) and geographically weighted regression (GWR) (van Donkelaar et al., 2016).

Unlike the aforementioned implementations, Bayesian inference allows the uncertainty in predictions to be assessed and taken into account in further analyses. The assessment of exposure burden by utilizing high-resolution population estimates becomes straightforward, in a way that is not possible in traditional approaches, since full posterior predictive distributions can be derived. However, predictions of pollutant levels at high-spatial resolution over the entire Europe are computationally complex (Shaddick et al., 2013). The computational burden can be reduced through approximate Bayesian inference using integrated nested Laplace approximation (INLA) (Rue et al., 2009, Lindgren et al., 2011). The potentials of this approach have been demonstrated on PM₁₀ data covering a small study area in northern Italy (Cameletti et al., 2013).

Most of the data-driven air-quality assessments incorporate geographical covariates derived from satellite-based observations. Remotely sensed products provide spatial coverage over the entire domain of interest allowing regular monitoring of the pollutants' spatial distributions. The main satellite-derived product used for the estimation of surface PM concentration is the aerosol optical depth (AOD), which represents the integrated radiation scattering and absorption by aerosols in an atmospheric column from the surface to the top of the atmosphere. AOD is used as a proxy for PM since it depends on the mass concentration and size distribution of the particles. A number of methods have been developed for near-surface PM estimation using columnar AOD (Chu et al., 2016). Large geographical scale predictions are usually based on Moderate Resolution Imaging Spectroradiometer (MODIS) Dark Target AOD (Levy et al., 2013) available at ∼10 km² spatial resolution. The recently developed multi-angle algorithms for AOD retrievals using spaceborne observations such as the Medium Resolution Imaging Spectrometer (MERIS)/Advanced Along-Track Scanning Radiometer (AATSR) (North et al., 2009) and the Multi-Angle Implementation of Atmospheric Correction (MAIAC) (Lyapustin et al., 2011) algorithms provide AOD distributions at 1 km² spatial resolution rendering the product suitable for high resolution PM modelling (Chudnovsky et al., 2014, Hu et al., 2014, Beloconi et al., 2016). However, there are many challenges in predicting PM conditioning on observed AOD. Due to the vertical structure of AOD, the strength of the PM-AOD relationship varies greatly in both space and time (Lee et al., 2011, Hu et al., 2014). Thus, it was shown that MODIS Dark Target AOD provides little additional information in a model that already accounts for local emissions, meteorology, land-use and regional variability at monthly and annual averaged temporal resolution level (Paciorek and Liu, 2009).

The primary objective of this work was to assess the benefits of combining satellite-derived products in a rigorous geostatistical modelling framework to estimate pollutants' spatial variability over 46 European countries. Particularly, the contribution of the MAIAC aerosol information adjusted with a set of georeferenced predictors, including the novel Copernicus land products (Copernicus, 2018) and meteorological data was evaluated for estimating high-resolution (1 km²) pollutant maps of PM₁₀ and PM_2.5 using hierarchical Bayesian spatial models. We compared different model formulations and assessed the effect of confounding between spatially varying predictors and the spatial process, which incorporates geographical correlation in the pollutants' concentration. Furthermore, the Bayesian formulation allowed us to quantify the prediction uncertainty, to determine at high spatial resolution areas that exceed the European Union (EU) and World Health Organization (WHO) air quality guidelines' (AQG) thresholds as well as to estimate the number of people living in such areas. Model fit was done using the INLA algorithm. The models provide improved gridded air-quality estimates for policy makers and scientists assessing the effects of pollution on human and ecosystem health.

2. Materials and methods

2.1. Study area and data

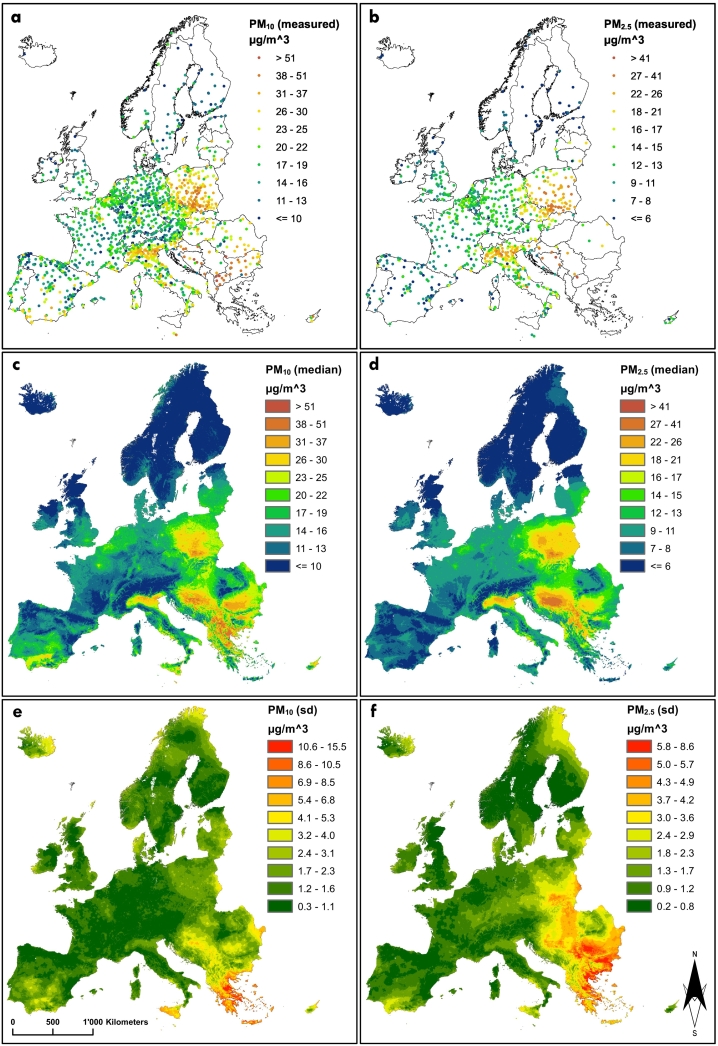
The PM₁₀ and PM_2.5 data were obtained from the Air Quality e-Reporting database (Air Quality e-Reporting, 2018) maintained through the Eionet (European environment information and observation network). The monitoring network covers up to 38 European countries, including the 28 EU member states and 33 member countries of the EEA. The repository consists of a multi-annual hourly time series data for a list of air pollutants. In this work the analysis is based on the yearly averaged data (reported in μg/m³) of 2016 (currently the most recent year with available raw data) at stations with ≥75% data capture. Fig. 1 (a–b) illustrates the locations of the monitoring sites used in this work, together with the yearly averaged measured concentrations of PM₁₀ and PM_2.5. All data used in our analyses were converted to the Lambert Azimuthal Equal Area (ETRS89-LAEA5210) projection recommended by the EEA (European Environment Agency, 2006) for storing raster data, statistical analysis and map display purposes.

Fig. 1.

Particulate matter. a, b: Annual average concentrations of PM₁₀ and PM_2.5 in 2016 at 2289 and 1091 monitoring sites across Europe, respectively. c, d: Predicted annual average of PM₁₀ and PM_2.5 concentrations (i.e. median of the posterior predictive distribution) at 1 km² spatial resolution in Europe in 2016. e, f: Prediction uncertainty (i.e. standard deviation (sd) of the posterior predictive distribution) of PM₁₀ and PM_2.5.

The satellite-derived product of columnar aerosol optical depth was considered as proxy of surface PM concentration. The recently-developed MAIAC algorithm for aerosol retrievals is based on time-series analysis and image processing of MODIS satellite data. MAIAC uses empirically tuned, regionally prescribed, aerosol properties following the AERONET (AErosol RObotic NETwork) climatology and provides AOD values over land at 1 km² spatial resolution globally. A total number of 19 tiles from each of the MODIS Terra and Aqua satellites, covering the study area (ftp://dataportal.nccs.nasa.gov/DataRelease/Europe_Sept-2017/), were downloaded and preprocessed. Each image was reprojected to our study area using the MODIS Reprojection Tool (MRT, 2016) accessed through the R environment (R Core Team, 2015). The raster package (Hijmans, 2015) was used to mosaic the resulting products. To reduce the number of the missing pixels, first daily, and then yearly averages from two satellites (i.e. Terra and Aqua) were computed.

Several studies have evaluated the effects of land-use/cover, urban mapping, local climate and meteorology information on the estimation of both PM₁₀ and PM_2.5 (e.g. Liu et al., 2005, Liu et al., 2009, Benas et al., 2013, Vienneau et al., 2013, Chudnovsky et al., 2014, Stafoggia et al., 2016, He and Huang, 2018. These parameters influence the relationship between AOD and PM and can be used as predictors in assessing the geographical variation of pollutants' concentration. In order to be able to estimate PM over the whole Europe, we analysed satellite-derived products only with continental or global coverage. Table 1 summarizes the covariates used in this work. On its own, this data portfolio represents a powerful resource for numerous environmental applications in Europe.

Table 1.

Data sources and spatio-temporal resolution of the predictors used in our models.

Product	Temporal resolution	Spatial resolution	Source
Aerosol optical depth (AOD)	Terra (∼10:30 GMT) and Aqua (∼13:30 GMT)	1 km	MODIS MAIAC
Corine land cover v.18_5 (LC)	Year 2012	100 m	Copernicus
Tree cover density (TCD)	Year 2015	20 m	Copernicus
Imperviousness (IMP)	Year 2015	20 m	Copernicus
European settlement map (ESM)	Year 2012	100 m	Copernicus
Digital elevation model (DEM)	Year 2000	30 m	EEA
Night time lights (NTL)	Year 2012	1 km	NOAA
Land surface temperature day & night (LST)	Terra (∼10:30 GMT) and Aqua (∼13:30 GMT)	1 km	MODIS Aqua and Terra
Normalized difference vegetation index (NDVI)	Terra (∼10:30 GMT) and Aqua (∼13:30 GMT)	1 km	MODIS Aqua and Terra
Road density (RD)	February 2016	1 km	OpenStreet maps
Specific humidity (SHUM)	Every 6 h	∼22 km	NCEP/CFSv2
Precipitation (PREC)	Every 6 h	∼22 km	NCEP/CFSv2
Wind speed (WS)	Every 6 h	∼22 km	NCEP/CFSv2
Distance to sea (DISS)	Year 2015	Vector	EEA
Distance to roads (DISR)	February 2016	Vector	OpenStreet maps

The land-use/cover data were extracted from the pan-European component of the Copernicus Land Monitoring Service (Copernicus, 2018). For the temporal alignment with the observations from stations the latest CORINE Land Cover (CLC) dataset (year 2012) was used. To better understand the urban surface characteristics that surround the monitoring stations, a squared buffer zone of 1 km² spatial resolution around each station was created and the dominant CLC category within each buffer zone was computed and assigned to the respective site. The 45 land classes available in CLC were aggregated to form the following 4 main categories: (i) continuous urban fabric - road and rail networks and associated land - port areas (LC1); (ii) discontinuous urban fabric - industrial or commercial units - mine, dump and construction sites - artificial, non-agricultural vegetated areas (LC2); (iii) agricultural areas - wetlands - water bodies (LC3); and (iv) forest and semi-natural areas (LC4). Thus, it was expected that the pollution levels gradually decrease for stations situated in LC2–LC4 categories compared to the LC1, considered as the baseline.

Additionally, the high resolution layers of tree cover density (TCD) and imperviousness (IMP), as well as the European settlement map (ESM) were accessed from the same source (Copernicus, 2018). The PM₁₀ and PM_2.5 levels were expected to be higher in build-up areas and lower in zones with higher tree density and therefore less emission sources. The digital elevation model (DEM) product (DEM, 2012), obtained from the EEA website, was used to assess the change in pollutants' concentration with increasing altitude. In general, locations at higher altitudes are less populated; the pollution dispersion processes are also easier to occur (Hu et al., 2014).

The land surface temperature (LST, 2016) and the normalized difference vegetation index (NDVI, 2016) generated from the MODIS Aqua and Terra platforms, the night time lights (NTL, 2012) product from the National Oceanic and Atmospheric Administration (NOAA), as well as the climatic data (humidity, precipitation and wind speed) from the National Centers for Environmental Prediction (NCEP) Climate Forecast System (CFSv2) (Saha et al., 2011) were pre-processed using the Google Earth Engine (GEE) API (Google Earth Engine Team, 2015). GEE makes it possible to rapidly process vast amount of satellite imagery on global scale with the power of Google's cloud computing. The climatic data were included in the models since the weather conditions can greatly affect the aerosol dilution and dispersion processes. In particular, surface temperature can enhance the photochemical reactions in the atmosphere, and hence, the production of PM (Gupta and Christopher, 2009). The relative humidity influences the hygroscopic growth of particles and consequently the estimated AOD relative to the ground level PM, as the latter is measured at controlled relative humidity (Liu et al., 2005, Paciorek et al., 2008). The NDVI was found to be a significant predictor of PM concentration in several previous works (e.g. Chudnovsky et al., 2014, Stafoggia et al., 2016. The wind speed can increase the vertical mixing and therefore dilute PM concentrations (Liu et al., 2007, Chudnovsky et al., 2013).

Road density (RD) was computed using the OpenStreet Maps project's collection of road shapefiles covering the continent. Particularly, the major roads comprising the motorway, trunk, primary and secondary road categories, as well as the links between them were taken into consideration. The same dataset was used to compute the distance to roads (DISR) covariate applying simple geographic information system (GIS) techniques. Distance to sea (DISS) was calculated using the Europe coastline shapefile (ECS, 2015) downloaded from the EEA website. The contribution of these predictors (or their proxies) to the estimation of PM₁₀ and PM_2.5 spatial distributions was previously evaluated in literature (Vienneau et al., 2013, Chudnovsky et al., 2014, Hu et al., 2014, Yanosky et al., 2014, Stafoggia et al., 2016).

High-resolution gridded population data were obtained from the Gridded Population of the World, Version 4 (GPWv4) database. Particularly, the population density (adjusted to match 2015 revision UN WPP country totals) dataset (SEDAC, 2016), available at 30 arc-second (∼1 km²) spatial resolution for the years 2000, 2005, 2010, 2015 and 2020 was employed to estimate the population in 2016 at 1 km² pixel level by applying cubic splines interpolation. The resulting estimates were aggregated at country level using the European administrative country boundaries shapefile from Eurostat's GISCO service (EuroStat, 2016).

2.2. Methods

The pollutants' concentration data are likely to be spatially correlated. In the geostatistical framework location specific random effects are introduced and modelled by a Gaussian process which captures the spatial correlation via the covariance matrix as a function of distance between locations. In linear geostatistical models covariates that are spatially smooth (in our case most of the satellite-derived products) are often collinear with the spatially smooth random effects. This is known as spatial confounding (Hodges and Reich, 2010) and it can have a significant effect on the estimation and interpretation of regression parameters. Within the Bayesian formulation, we developed restricted geostatistical regression (RGR) models (Hanks et al., 2015) which address spatial confounding by imposing a linear orthogonality constraint and compared them to classical geostatistical regression (GR) and the frequently applied non-spatial LUR models. For each of these formulations, we fitted all possible combinations of the covariates, i.e. 32 768 (=2¹⁵) distinct models for each pollutant and ordered them according to Bayesian model comparison criteria.

Let Y _s represent the log-observed annual average of PM₁₀ or PM_2.5 concentration at site s (s = 1,…S). The following stationary, isotropic GR model is considered for each pollutant:

$${\mathit{Y}}_{\mathit{s}}={\beta }_0+X_s\mathit{\beta }+{\omega }_s+{ϵ}_s$$ (1)

where β₀ is the intercept term, β the k × 1 vector of regression coefficients associated with X_s, w_s the spatial random effect and ϵ_s the random error which is assumed to be independent and identically distributed (i.i.d.) $\mathcal{N}(0,{\sigma }_{ϵ}^2)$. All the continuous covariates were standardized by subtracting the mean and dividing by the standard deviation calculated using the yearly averaged measurements from all the monitoring stations. For the estimation of model parameters the data were extracted at the locations of the stations, while for the prediction at unknown locations, each covariate was aggregated within a fixed 1 km² grid using bilinear or nearest neighbour interpolation methods (for continuous and categorical data, respectively). We assumed that the spatial random effect w_s = (w₁,…,w_S)^T arise from a multivariate normal distribution:

$$\mathit{\omega }\sim \mathcal{N}\left({\mathbf{0}}_S,{\sigma }_{\omega }^2{\mathbf{\Sigma }}_{\mathit{\omega }}\right)$$ (2)

with 0_S a S × 1 zeros vector, ${\sigma }_{\omega }^2$ the spatial process variance and Σ_ω is the S × S dense correlation matrix with elements ${({\mathbf{\Sigma }}_{\mathit{\omega }})}_{ij}=\mathcal{C}(\parallel {\mathit{s}}_i-{\mathit{s}}_j\parallel )$, where $\mathcal{C}(\cdot )$ is the Matern function given by

$$\mathcal{C}(d_{ij})=\frac{1}{\mathrm{\Gamma }(\nu )2^{\nu -1}}{\left(\kappa d_{ij}\right)}^{\nu }{K}_{\nu }\left(\kappa d_{ij}\right)$$ (3)

with d_ij the distance between stations i and j, κ is a scaling parameter, ν a smoothing parameter (fixed to 1 in our application) and K_ν is the modified Bessel function of second kind and order ν. This specification implies that the range r (the distance at which the spatial variance becomes less than 10%) is given by $r=\frac{\sqrt{8\nu }}{\kappa }$.

We addressed spatial confounding by running RGR models for each pollutant. These models separate the linear effects β from the spatial effects ω_s through the following linear orthogonality constraint:

$${\int }_{\mathcal{S}}{\mathit{X}}_{\mathit{s}}{\mathit{\omega }}_{\mathit{s}}d\mathit{s}=0$$ (4)

Restricting the random field to be orthogonal to the spatial covariates changes the interpretation of the spatial field to be a Bayesian version of the restricted maximum likelihood (Ingebrigtsen et al., 2015) where the spatial effects are estimated conditional on the covariate effects.

The Bayesian model formulation is completed by specifying prior distributions for the parameters and the hyperparameters. Particularly, the log-gamma priors were chosen for the ${\sigma }_{ϵ}^{-2}$, ${\sigma }_{\omega }^{-2}$ and r parametrized on the log-scale, i.e. $\log ({\sigma }_{ϵ}^{-2})$, $\log ({\sigma }_{\omega }^{-2})\sim \log Ga(1,5\cdot 10^{-5})$ and log(r) ∼ log Ga(1,10²). Normal priors $\mathcal{N}(0,10^3)$ were assigned for the regression coefficients and a vague normal one for the intercept.

Bayesian inference estimates the marginal posterior distributions $p({\varphi }_j|\mathit{Y})=\int p({\varphi }_j|\mathit{\theta },\mathit{Y})p(\theta |\mathit{Y})d\mathit{\theta }$ of the elements ϕ = (β,w)^T where θ is the vector of hyperparameters and Y are the data. Geostatistical models often rely on Markov chain Monte Carlo (MCMC) simulation techniques to estimate the p(ϕ_j|Y). However, for large number of locations, the computations involving the spatial covariance matrix are not feasible. One solution to overcome this drawback is using the stochastic partial differential equations (SPDE) approach and integrated nested Laplace approximation (INLA) algorithm for the fast approximation of the marginal posterior distributions (Rue et al., 2009, Lindgren et al., 2011). This method is only briefly described here; the extensive theoretical explanations are provided elsewhere (Blangiardo and Cameletti, 2015).

In the SPDE/INLA approach the spatial process is represented as a Gaussian Markov random field (GMRF) with mean zero and a symmetric positive definite precision matrix Q (defined as the inverse of Σ_ω). First, a GMRF representation of the Matern field is constructed on a set of non-intersecting triangles partitioning the domain of the study area (Lindgren et al., 2011). Subsequently, the INLA algorithm is used to estimate the posterior distribution of the latent Gaussian process and hyperparameters using Laplace approximation (Rue et al., 2009).

Furthermore, we fitted the LUR and the GWR models. LUR is a non-spatial multiple linear regression model and is formulated as the one in Eq. (1) without the structured spatial effect w_s. In GWR the spatially-varying relationships are explored between the dependent and independent variables with equation taking the following form:

$${\mathit{Y}}_{\mathit{s}}={\beta }_{s0}+\sum _{j=1}^k{\beta }_{sj}{X}_{sj}+{ϵ}_s$$ (5)

where Y_s again denotes the log-observed annual average of PM₁₀ or PM_2.5 concentration at site s (s = 1,…S), β_s0 is the intercept parameter at s, X_sj is the value of the jth covariate at s, k is the number of independent variables, β_sj is the local regression coefficient for the jth covariate at s and ϵ_s is the random error at s. As data are geographically weighted, nearer observations have more influence in estimating the local set of regression coefficients than observations farther away; the model measures the inherent relationships around each regression point s, where each set of regression coefficients is estimated by a weighted least squares approach (Gollini et al., 2015). The matrix expression for this estimation is

$${\widehat{\mathit{\beta }}}_{\mathit{s}}={\left(X^{T}WX\right)}^{-1}{X}^{T}W{\mathit{Y}}_{\mathit{s}}$$ (6)

where X is the matrix of the independent variables with a column of 1s for the intercept, ${\widehat{\mathit{\beta }}}_{\mathit{s}}={({\beta }_{s0},\dots ,{\beta }_{sk})}^T$ is the vector of k + 1 local regression coefficients and W is the diagonal matrix denoting the geographical weighting of each observed data at location s. This weighting is determined by a kernel function. In this work the gaussian, exponential, boxcar, bisquare and tricube kernels were tested and the optimal kernel bandwith was selected using the leave-one-out cross-validation (CV) score which accounts for model prediction accuracy. The GWR models were fitted using the GWmodel package (Lu et al., 2014) available in the R software.

The GR, RGR and LUR models with the best predictive performance were selected based on the lowest logarithmic score (logscore) – measure of the predictive ability of an individual model (Ntzoufras, 2011):

$$L_{CV}=-\sum _{s=1}^S\log CP{O}_s$$ (7)

where the leave-one-out conditional predictive ordinate (CPO) is based on the cross-validatory predictive densities π(Y_s , Y_−s) and is given by CPO_s = π(Y_s , Y_−s) for each excluded location s. For the GWR, the optimal models were obtained using the model.selection.gwr function (Gollini et al., 2015), which uses a pseudo stepwise procedure to select the independent variable subset based on the corrected Akaike information criterion (AIC_c) (Hurvich et al., 1998) values.

Subsequently, we validated all the models using the 5-fold-cross-validation method; each dataset was randomly divided 5 times in 80% (training set) and 20% (validation set) splits of the total number of PM sites and the following performance metrics were examined for each fold: mean absolute error (MAE), mean absolute prediction error (MAPE), root mean squared error (RMSE) and the coefficient of determination (R²).

For each pollutant, prediction was obtained at the cell centroids of a 1 km² resolution grid covering the study area (approximately 5.8 million pixels) after fitting the models to the full datasets (for a better spatial coverage and therefore for obtaining more accurate parameter estimates and predictions). The results were based on 1000 samples drawn from the posterior predictive distributions. The sample-based medians and the standard deviations (measure of the uncertainty of the predictions) of these distributions were used for mapping. Fit of the best model and prediction took less than half an hour for each pollutant on an Intel Xeon E5-2697 CPU machine (2 × 2.60 GHz, 128 GB RAM).

To determine the most polluted European areas, the first-level Nomenclature of Territorial Units for Statistics (NUTS) (EuroStat, 2016) classification of the EU was used to define the regions' borders. To identify the most polluted capitals, buffer zones with radius varying from 1 to 30 km away from the center of each city (SimpleMaps, 2016) were considered. The high-resolution PM₁₀ and PM_2.5 estimates (pixel-level posterior medians) were first clipped by each region and then averaged over the resulting sectors (i.e. over the NUTS areas and buffer zones). For every capital spline curves were employed to profile the relationship between pollutants' concentration and distance from the city center within a 30 km buffer.

3. Results

3.1. Model selection and comparison

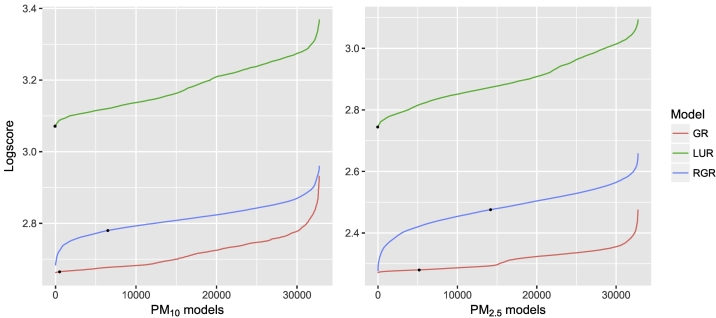
Fig. 2 shows the variation in the predictive performances of the GR, RGR and LUR models. The geostatistical models highly outperformed the LUR in terms of predictive ability (based on the lowest logscore values). The models without the orthogonality constraint (GR) were slightly better compared to their RGR counterparts. The figure also highlights the importance of carrying out the variable selection process. In fact, for PM₁₀ concentration, the models which include all the covariates had the 19th best predictive performance for LUR, the 596th best for GR, and the 6586th best for RGR formulations. Similar results were observed for the PM_2.5 dataset. The five best selected combinations of covariates for each of these three set of models are shown in Table 2. For the GWR models, the pseudo stepwise model selection procedure resulted in all the predictors being important for both PM₁₀ and PM_2.5 concentration. The set of covariates giving the best predictions differ between the GR/RGR and the GWR/LUR models. Particularly, the MAIAC AOD covariate is included in each of the five best LUR models for both PM₁₀ and PM_2.5 concentrations and also in the best GWR model. However, Bayesian geostatistical models indicated that AOD does not improve the predictions of annual averages of PM concentrations. Furthermore, the number of covariates resulting in best fit of the geostatistical models was much lower than the ones in GWR/LUR. The GR models provided the highest cross-validated R² values of 0.72 for PM₁₀ and 0.78 for PM_2.5 concentration (Table 3, Table 4). The out-of-sample MAE, MAPE and RMSE metrics of the predictive performance were also the lowest for the spatial models without the orthogonality constraint. The estimated range parameters (r) as well as the variances of the spatial process (${\sigma }_{\omega }^2$) were lower in RGR compared to the geostatistical models without the orthogonality constraint. This was expected, since, the spatial effects in RGR account for the variation after the linear effect in mean of each covariate is assessed. Thus, potential confounding between the spatial random effect and the spatially-smooth covariates is avoided.

Fig. 2.

Model selection. Predictive performance of the GR, RGR and LUR models (ordered according to the logscore values) arising from all possible combinations of covariates (i.e. 32768 models) for each pollutant. The black dots indicate the models which include all the covariates.

Table 2.

First five covariate combinations with the highest predictive ability (i.e. lowest logscore) for restricted geostatistical regression (RGR), geostatistical regression (GR) and land-use regression (LUR) models.

Pollutant	Model	Covariates	Logscore
PM10	RGR	TCD + IMP + DEM + LST + SHUM + WS + DISS	2.68271
		TCD + IMP + DEM + NTL + LST + SHUM + WS	2.68307
		TCD + IMP + DEM + LST + SHUM + DISS	2.68355
		IMP + DEM + LST + SHUM + WS + DISS	2.68412
		IMP + DEM + NTL + LST + SHUM + WS	2.68423
	GR	TCD + IMP + DEM + NTL + NDV I + SHUM + PREC + LC	2.66186
		IMP + DEM + NTL + NDV I + SHUM + PREC + LC	2.66190
		TCD + IMP + DEM + NTL + NDV I + RD + SHUM + PREC	2.66207
		IMP + DEM + NTL + NDV I + RD + SHUM + PREC + LC	2.66208
		TCD + IMP + DEM + NTL + NDV I + SHUM + PREC + WS + LC	2.66215
	LUR	AOD+IMP +ESM +DEM +NTL+LST +NDV I +SHUM +PREC+WS+DISS+DISR+LC	3.07056
		AOD+IMP +ESM +DEM +NTL+LST +NDV I +SHUM +PREC +DISS +DISR+LC	3.07066
		AOD+IMP +ESM +DEM +NTL+LST +NDV I +SHUM +WS +DISS +DISR+LC	3.07067
		AOD+IMP +ESM +DEM +NTL+LST +NDV I+RD+SHUM +PREC+WS+DISS+DISR+LC	3.07071
		AOD+ESM +DEM +NTL+LST +NDV I +SHUM +PREC +WS +DISS +DISR+LC	3.07077
PM2.5	RGR	IMP + DEM + LST + SHUM + WS + DISS	2.27595
		IMP + DEM + LST + WS + DISS	2.27803
		IMP + DEM + LST + SHUM + DISS	2.28041
		IMP + DEM + LST + DISS	2.28149
		IMP + DEM + NTL + LST + SHUM + WS + DISS	2.28541
	GR	IMP + ESM + DEM + NTL + WS + DISS	2.27044
		IMP + ESM + DEM + NTL + LST + WS + DISS	2.27049
		IMP + DEM + NTL + LST + WS + DISS	2.27070
		IMP + DEM + NTL + WS + DISS	2.27071
		IMP + ESM + DEM + NTL + NDV I + WS + DISS	2.27090
	LUR	AOD+ESM +DEM +NTL+LST +NDV I +RD+SHUM +PREC +DISS +DISR+LC	2.74321
		AOD+IMP +ESM +DEM +NTL+LST +NDV I +RD+SHUM +PREC +DISS+DISR+LC	2.74326
		AOD+IMP +DEM +NTL+LST +NDV I +RD+SHUM +PREC +DISS +DISR+LC	2.74340
		AOD+TCD+IMP +ESM +DEM +NTL+LST +NDV I+RD+SHUM +PREC+DISS+DISR+LC	2.74376
		AOD+TCD+IMP +DEM +NTL+LST +NDV I +RD+SHUM +PREC +DISS+DISR+LC	2.74388

Table 3.

Posterior medians, 95% Bayesian credible intervals and cross-validation performance metrics of the restricted spatial regression, geostatistical regression, geographically weighted regression and non-spatial land-use regression models with the best predictive ability of PM₁₀ concentrations.

	PM10
	Restricted geostatistical regression	Geostatistical regression	Land-use regression	Geographically weighted regression
Covariate	Median (2.5%, 97.5%)	Median (2.5%, 97.5%)	Median (2.5%, 97.5%)	Median (2.5%, 97.5%)
Intercept	2.98 (2.97, 2.99)	2.84 (2.59, 3.07)	3.02 (2.98, 3.05)	3.00 (2.96, 3.05)
AOD	–	–	0.13 (0.12, 0.14)	0.09 (0.05, 0.11)
TCD	−0.01 (−0.01, −0.00)	−0.01 (−0.01, −0.00)	–	−0.00 (−0.01, −0.00)
DEM	−0.13 (−0.14, −0.13)	−0.14 (−0.16, −0.13)	−0.08 (−0.09, −0.06)	−0.11 (−0.16, −0.08)
IMP	0.03 (0.03, 0.04)	0.03 (0.02, 0.04)	0.01 (0.00, 0.03)	0.02 (0.00, 0.03)
ESM	–	–	0.02 (0.00, 0.03)	0.00 (0.00, 0.02)
NTL	–	0.04 (0.03, 0.05)	0.05 (0.03, 0.07)	0.05 (0.04, 0.07)
LST	0.14 (0.13, 0.15)	−	0.11 (0.09, 0.13)	0.05 (0.00, 0.12)
NDVI	–	−0.02 (−0.04, −0.01)	0.06 (0.05, 0.07)	0.01 (−0.02, 0.04)
SHUM	−0.05 (−0.06, −0.04)	−0.05 (−0.08, −0.02)	−0.06 (−0.08, −0.04)	−0.05 (−0.10, −0.00)
PREC	–	−0.05 (−0.08, −0.02)	−0.01 (−0.02, −0.00)	−0.01 (−0.04, 0.02)
DISS	0.09 (0.08, 0.10)	–	0.05 (0.03, 0.06)	0.02 (−0.02, 0.07)
RD	–	–	–	0.00 (−0.01, 0.01)
DISR	–	–	0.06 (0.05, 0.07)	0.03 (0.00, 0.05)
LC
LC2	–	−0.02 (−0.04, 0.01)	−0.02 (−0.06, 0.02)	−0.04 (−0.07, −0.00)
LC3	–	−0.03 (−0.07, −0.00)	−0.08 (−0.13, −0.02)	−0.05 (−0.11, −0.01)
LC4	–	−0.12 (−0.17, −0.08)	−0.18 (−0.25, −0.11)	−0.14 (−0.21, −0.07)
a${\sigma }_{ϵ}^2$	0.02 (0.02, 0.03)	0.02 (0.02, 0.03)	0.07 (0.07, 0.07)	0.03
b${\sigma }_w^2$	0.10 (0.07, 0.14)	0.21 (0.13, 0.35)	–	–
cr (km)	376.3 (305.6, 478.9)	748.0 (563.3, 1031.3)	–	–
dMAE	0.14	0.14	0.20	0.16
eMAPE	0.05	0.05	0.07	0.05
fRMSE	0.19	0.19	0.27	0.21
gR2	0.71	0.72	0.43	0.66

^a${\sigma }_{ϵ}^2$ - variance of the random error.

^b${\sigma }_w^2$ - variance of the spatial process.

^cr - range (the distance at which the spatial variance becomes less than 10%).

^dMAE - mean absolute error.

^eMAPE - mean absolute prediction error.

^fRMSE - root mean squared error.

^gR² - coefficient of determination.

Table 4.

Posterior medians, 95% Bayesian credible intervals and cross-validation performance metrics of the restricted spatial regression, geostatistical regression, geographically weighted regression and non-spatial land-use regression models with the best predictive ability of PM_2.5 concentrations.

	PM2.5
	Restricted geostatistical regression	Geostatistical regression	Land-use regression	Geographically weighted regression
Covariate	Median (2.5%, 97.5%)	Median (2.5%, 97.5%)	Median (2.5%, 97.5%)	Median (2.5%, 97.5%)
Intercept	2.51 (2.51, 2.52)	2.29 (2.06, 2.50)	2.58 (2.52, 2.63)	2.64 (2.59, 2.71)
AOD	–	–	0.14 (0.12, 0.16)	0.13 (0.08, 0.16)
TCD	–	–	–	−0.00 (−0.01, 0.01)
DEM	−0.15 (−0.16, −0.14)	−0.13 (−0.15, −0.11)	−0.10 (−0.13, −0.07)	−0.10 (−0.13, −0.05)
IMP	0.04 (0.03, 0.05)	0.03 (0.02, 0.05)	–	0.01 (0.00, 0.02)
ESM	–	0.01 (0.00, 0.03)	0.03 (0.00, 0.05)	0.01 (0.00, 0.02)
NTL	–	0.05 (0.03, 0.07)	0.07 (0.04, 0.10)	0.07 (0.04, 0.09)
LST	0.11 (0.10, 0.13)	–	0.11 (0.08, 0.15)	0.07 (−0.01, 0.17)
NDVI	–	–	0.12 (0.09, 0.14)	0.06 (0.04, 0.08)
SHUM	0.02 (0.01, 0.04)	–	−0.04 (−0.08, −0.01)	−0.08 (−0.11, −0.03)
PREC	–	–	0.05(0.03, 0.07)	0.03 (0.01, 0.05)
WS	−0.05 (−0.06, −0.04)	−0.05 (−0.08, −0.02)	–	−0.01 (−0.03, 0.01)
DISS	0.21 (0.20, 0.23)	0.15 (0.06, 0.24)	0.16 (0.13, 0.18)	0.06 (0.02, 0.12)
RD	–	–	−0.02 (−0.04, 0.00)	−0.01 (−0.02, 0.00)
DISR	–	–	0.06 (0.04, 0.08)	0.03 (0.01, 0.04)
LC
LC2	–	–	−0.03 (−0.09, 0.02)	−0.05 (−0.09, −0.01)
LC3	–	–	−0.08 (−0.17, 0.02)	−0.05 (−0.10, −0.01)
LC4	–	–	−0.28 (−0.41, −0.16)	−0.17 (−0.25, −0.10)
a${\sigma }_{ϵ}^2$	0.02 (0.02, 0.03)	0.03 (0.02, 0.03)	0.09 (0.08, 0.10)	0.03
b${\sigma }_w^2$	0.18 (0.12, 0.29)	0.18 (0.12, 0.28)	–	–
cr (km)	588.6 (445.5, 807.5)	698.1 (522.2, 964.4)	–	–
dMAE	0.15	0.14	0.23	0.17
eMAPE	0.06	0.06	0.10	0.07
fRMSE	0.21	0.20	0.30	0.24
gR2	0.77	0.78	0.50	0.69

^a${\sigma }_{ϵ}^2$ - variance of the random error.

^b${\sigma }_w^2$ - variance of the spatial process.

^cr - range (the distance at which the spatial variance becomes less than 10%).

^dMAE - mean absolute error.

^eMAPE - mean absolute prediction error.

^fRMSE - root mean squared error.

^gR² - coefficient of determination.

The above results indicate that for both pollutants, the GR model had the best predictive ability. Therefore, we present estimates and inference based on GR models with the covariate combination giving the lowest logscore (i.e. the 1st GR model in Table 2). All the parameter estimates (i.e. the regression coefficients) presented in Table 3, Table 4 were obtained using the Laplace approximation implemented within the INLA framework. We found a significant positive association of PM₁₀ concentration with imperviousness layer and night time light intensity and a negative association of PM₁₀ with tree cover density, elevation, normalized difference vegetation index (NDVI), surface humidity and precipitation; highest levels of PM₁₀ concentration were estimated in urban and industrial areas (i.e. over land cover categories LC1 and LC2), followed by agricultural (LC3) and forest (LC4) areas (Table 3). The PM_2.5 concentration was positively associated with imperviousness surfaces, human settlements, night time lights intensity and distance to sea and negatively correlated with elevation and wind speed (Table 4).

3.2. High-resolution model-based pollutant maps

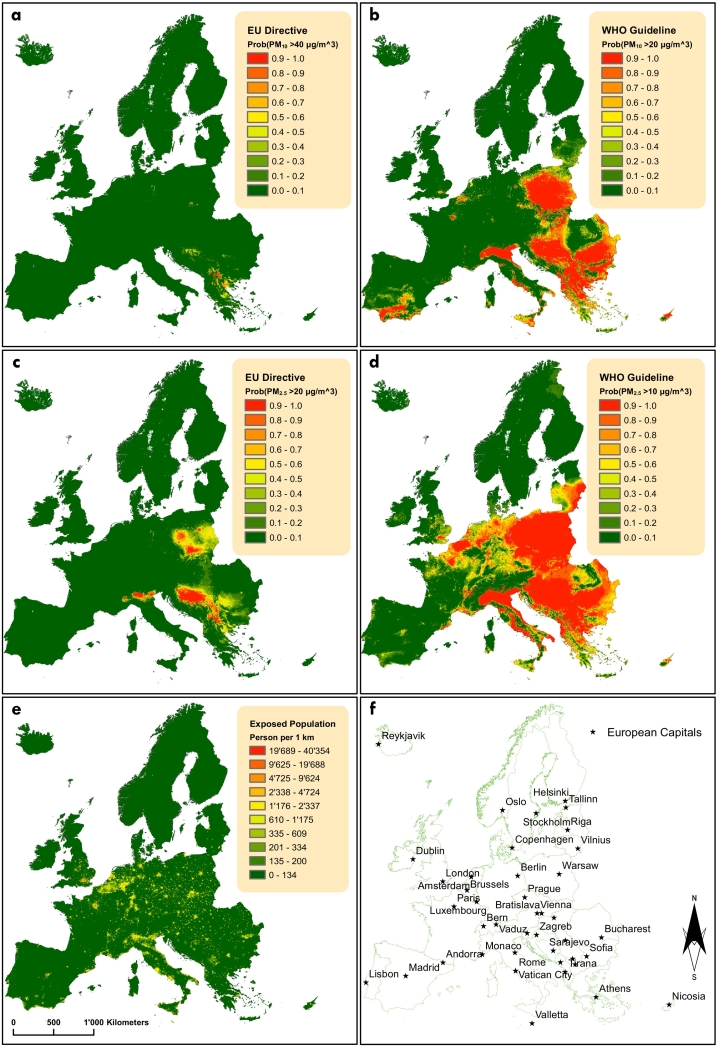
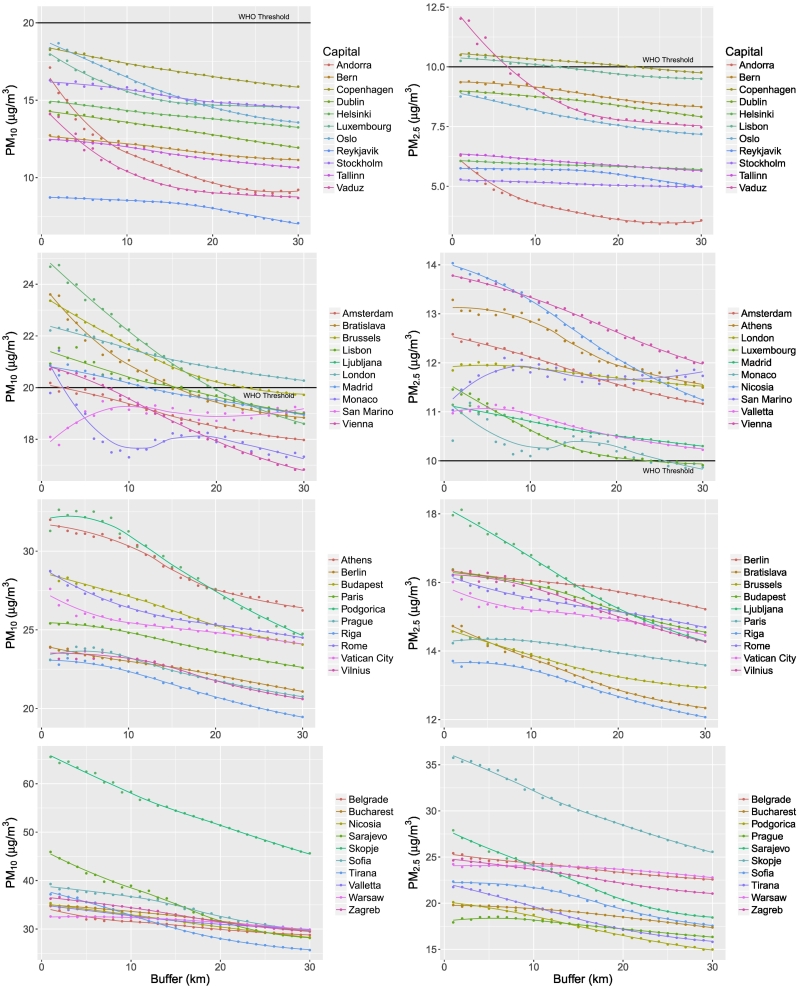
Fig. 1 (c–f) depicts the predictions and their uncertainty (i.e. the median and the standard deviation of the posterior predictive distribution based on 1000 samples) for both pollutants at 1 km² spatial resolution based on the best GR model. The highest levels of PM₁₀ concentration were estimated in Macedonia (FYROM), Poland, Bulgaria and Malta (Table 5). The most heavily polluted regions in terms of PM_2.5 concentration included Poland, FYROM, Croatia, Berlin region and northern Italy (the Po Valley). As expected, higher uncertainty was estimated in areas away from monitoring stations. Thus, for most of central Europe, the uncertainty is low and increases in northern and south-eastern parts of the continent. The most polluted capitals (Fig. 3f) in terms of PM are Skopje, Sofia and Sarajevo (Fig. 4). The same figure shows that for most of the European capitals, the PM concentration decrease with increasing distance away from their centre. Furthermore, for some capitals, such as Tirana and Skopje, there is a steep decrease in PM with distance, while for others, like Bucharest and Warsaw, the reduction is moderate and even increasing in case of San Marino.

Table 5.

Pollution levels (in μg/m³) at the first-level nomenclature of territorial units for statistics (NUTS) classification of the European Union.

Region	PM10	PM2.5	Region	PM10	PM2.5
(AT1) East Austria	14.20	10.22	(DEF) Schleswig-Holstein	14.69	9.85
(AT2) South Austria	11.01	7.75	(DEG) Thuringia	12.73	9.62
(AT3) West Austria	8.88	6.75	(DK0) Denmark	14.29	7.80
(BE1) Brussels Capital Region	20.93	13.56	(EE0) Estonia	10.86	5.58
(BE2) Flemish Region	19.30	12.29	(EL3) Attica	21.82	9.82
(BE3) Walloon Region	14.47	9.46	(EL4) Aegean Islands, Crete	15.83	7.20
(BG3) North and East Bulgaria	25.27	13.58	(EL5) North Greece	27.63	13.06
(BG4) South-West and South-Central Bulgaria	22.84	12.87	(EL6) Central Greece	21.18	9.73
(CH0) Switzerland	8.45	6.54	(ES1) North-West Spain	10.98	6.77
(CY0) Cyprus	22.33	9.62	(ES2) North-East Spain	11.43	5.96
(CZ0) Czech Republic	17.17	13.39	(ES3) Community of Madrid	15.31	8.40
(DE1) Baden-Württemberg	13.57	8.96	(ES4) Central Spain	14.09	6.35
(DE2) Bavaria	12.89	9.50	(ES5) East Spain	12.73	6.80
(DE3) Berlin	20.88	15.19	(ES6) South Spain	19.57	6.47
(DE4) Brandenburg	16.27	12.39	(FI1) Mainland Finland	7.58	5.19
(DE5) Free Hanseatic City of Bremen	17.71	12.03	(FI2) Âland	9.48	3.72
(DE6) Hamburg	17.03	12.87	(FR1) Région parisienne	17.76	10.96
(DE7) Hessen	13.78	9.67	(FR2) Bassin parisien	13.51	9.05
(DE8) Mecklenburg-Vorpommern	14.94	10.52	(FR3) North France	17.02	11.40
(DE9) Lower Saxony	14.92	10.35	(FR4) East France	12.57	9.19
(DEA) North Rhine-Westphalia	15.69	10.43	(FR5) West France	13.33	8.36
(DEB) Rhineland-Palatinate	12.65	8.75	(FR6) South-West France	11.25	7.12
(DEC) Saarland	12.95	9.39	(FR7) Central-East France	10.94	7.63
(DED) Saxony	15.43	11.91	(FR8) Mediterranean France	12.03	7.56
(DEE) Saxony-Anhalt	14.85	11.00	(HR0) Croatia	22.37	16.90
(HU1) Central Hungary	21.27	13.17	(PL4) North-West Poland	22.33	16.38
(HU2) Transdanubia	20.48	14.10	(PL5) South-West Poland	25.33	18.38
(HU3) Great Plain and North	20.95	14.18	(PL6) North Poland	20.49	13.57
(IE0) Ireland	11.05	7.37	(PT1) Mainland Portugal	14.37	6.92
(IS0) Iceland	7.13	4.36	(RO1) North-West and Central Romania	15.23	9.45
(ITC) North-West Italy	17.69	13.36	(RO2) North-East and South-East Romania	19.42	11.30
(ITF) South Italy	16.03	10.12	(RO3) South Romania - Muntenia, Bucuresti	23.78	13.36
(ITG) Sardinia, Sicily	17.99	7.80	(RO4) South-West Oltenia, West Romania	17.90	14.26
(ITH) North-East Italy	17.29	12.51	(SE1) East Sweden	10.13	4.57
(ITI) Central Italy	16.11	10.48	(SE2) South Sweden	10.46	6.24
(LI0) Liechtenstein	9.36	8.05	(SE3) North Sweden	7.04	3.42
(LT0) Lithuania	17.73	10.87	(SI0) Slovenia	16.00	11.94
(LU0) Luxembourg	13.35	9.08	(SK0) Slovakia	19.00	14.19
(LV0) Latvia	15.75	10.36	(UKC) North-East UK	9.39	5.96
(ME0) Montenegro	17.51	10.82	(UKD) North-West UK	11.65	6.93
(MK0) Macedonia (FYROM)	32.00	17.06	(UKE) Yorkshire and the Humber	12.67	8.16
(MT0) Malta	29.14	10.10	(UKF) East Midlands	15.02	8.97
(NL1) North Netherlands	16.80	9.72	(UKG) West Midlands	13.82	8.55
(NL2) East Netherlands	17.01	9.93	(UKH) East of England	15.56	9.55
(NL3) West Netherlands	17.67	10.58	(UKI) Greater London	19.73	11.29
(NL4) South Netherlands	17.54	10.42	(UKJ) South-East UK	15.97	9.22
(NO0) Norway	8.71	3.98	(UKK) South-West UK	12.83	7.81
(PL1) Central Poland	25.48	18.88	(UKL) Wales	11.42	7.11
(PL2) South Poland	29.27	21.91	(UKM) Scotland	7.52	4.33
(PL3) East Poland	22.08	17.67	(UKN) Northern Ireland	10.08	6.88

Fig. 3.

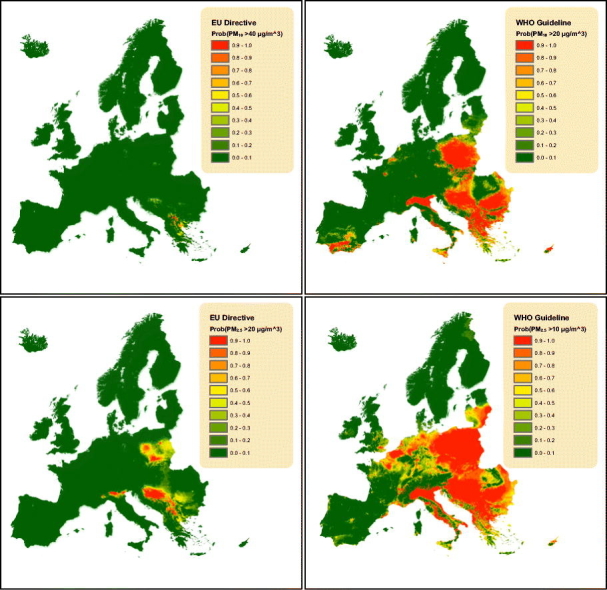
Exceedance probability maps in 2016 based on international air quality guidelines thresholds. a, b: Probability that PM₁₀ concentration exceeds the EU Directive and WHO thresholds, respectively. c, d: Probability that PM_2.5 concentration exceeds the EU Directive and WHO thresholds, respectively. e: Population exposed to PM₁₀ and PM_2.5 concentrations above the WHO thresholds. f: Location of the European capitals.

Fig. 4.

Air quality in 41 European capitals in 2016. The air pollution profiles of PM₁₀ and PM_2.5 within 30 km buffer zone from the centre of each capital. The black horizontal line corresponds to the WHO thresholds.

3.3. Population living in areas that exceed the international air quality thresholds

The Bayesian framework allowed us to make probabilistic statements about areas exceeding the international air quality thresholds. We evaluated the compliance with the AQGs based on long-term, rather than on the short-term or episodic exposure to pollutants. Particularly, two different limit values were taken into consideration: the European Air Quality Directive with annual thresholds of 40 μg/m³ for PM₁₀ and 20 μg/m³ for PM_2.5 concentrations and the WHO air quality guideline with values of 20 μg/m³ and 10 μg/m³, respectively (EU, 2008, WHO, 2006). Fig. 3 (a–d) depicts the probabilities of PM₁₀ and PM_2.5 concentrations exceeding the thresholds in 2016. They were calculated by the proportion of samples drawn from the posterior predictive distributions of PM that have pollution levels above the thresholds. While most parts of the continent meet the requirements of the EU Directive, the stricter WHO threshold standards, which are considered as an achievable objective to minimize the health impact, are still to be reached, especially for the PM_2.5 concentrations. The European capitals that have not reached the WHO limits and the distances from the city centres at which the pollution levels meet the standards are illustrated in Fig. 4. The exceedance maps (Fig. 3b, d) were used to estimate the total number of population exposed to elevated levels of the above-mentioned pollutants. In particular, we overlayed the gridded population data at 1 km² spatial resolution with the threshold maps and calculated the total population in pixels that have exceedance probability higher than 50% (Fig. 3e). Results show that in 2016, 35.6% and 63.9% of the population within the study area were exposed to PM₁₀ and PM_2.5 levels above the WHO thresholds, respectively, while more than 66.2% were living in areas exceeding both thresholds (Table 6). Our high-resolution results indicate a decrease in PM_2.5 exposure in Europe in 2016 when compared to findings put forth in a recent WHO report (WHO et al., 2016) based on global estimates at ~10 km² spatial resolution. Indeed, in 2014 just 1% of the population in low- and middle-income (World Bank, 2016) European countries and only 18% of the population in high-income countries breathed clean (below the AQGs limit values) air.

Table 6.

Estimated number of people exposed to PM₁₀ and PM_2.5 levels above the WHO thresholds in 2016 (median and 95% credible intervals of the posterior distributions).

Country	Populationa	Exposed to PM10	Exposed to PM2.5	Exposed to both
(AD) Andorra	67 462	0 (0, 8187)	0 (0,0)	0 (0, 8187)
(AL) Albania	2 925 168	2 760 328 (2 372 165, 2 872 254)	2 773 118 (2 317 413, 2 899 536)	2 839 928 (2 711 134, 2 902 285)
(AT) Austria	8 731 711	552 133 (205 305, 1 418 388)	5 622 958 (3 499 525, 6 841 414)	5 552 144 (3 456 660, 6 741 482)
(BA) Bosnia and Herzegovina	3 817 952	3 211 730 (2 930 650, 3 469 739)	3 621 987 (3 360 840, 3 769 263)	3 623 988 (3 396 449, 3 769 263)
(BE) Belgium	11 469 758	4 795 731 (2 712 409, 6 737 162)	10 216 848 (8 895 370, 10 780 086)	10 216 848 (8 961 789, 10 780 371)
(BG) Bulgaria	7 153 089	5 833 643 (5 149 469, 6 397 074)	6 074 697 (2 290 590, 7 115 259)	6 536 242 (5 686 108, 7 120 149)
(CH) Switzerland	9 202 540	74 374 (22 227, 217 827)	3 709 464 (771 040, 7 446 925)	3 186 486 (749 640, 6 040 566)
(CY) Cyprus	1 190 214	1 065 339 (808 584, 1 169 544)	946 342 (435 091, 1 148 452)	1 107 591 (939 295, 1 171 135)
(CZ) Czech Republic	10 618 625	4 894 115 (3 449 455, 6 256 099)	10 319 289 (8 640 556, 10 581 769)	10 319 289 (8 676 605, 10 581 769)
(DE) Germany	81 848 649	6 454 538 (3 459 511, 10 084 160)	57 079 581 (39 626 291, 71 089 190)	57 129 401 (40 103 236, 71 081 848)
(DK) Denmark	5 766 524	79 320 (93, 1 223 356)	1 425 992 (21 645, 3 976 153)	1 483 493 (26 436, 3 630 736)
(EE) Estonia	1 349 753	10 (10, 70 510)	2042 (2042, 60 279)	3244 (2003, 69 737)
(EL) Greece	11 050 816	9 113 513 (3 765 692, 10 822 578)	8 645 062 (2 474 767, 10 803 008)	10 075 255 (5 535 995, 10 958 087)
(ES) Spain	44 529 778	14 091 655 (11 108 136, 17 585 244)	12 751 382 (7 688 226, 18 846 075)	20 024 311 (16 152 157, 23 524 607)
(FI) Finland	5 979 902	505 (505, 562)	14 749 (14 532, 135 929)	14 804 (14 532, 135 931)
(FO) Faroe Islands	48 175	48 175 (48 175, 48 175)	48 175 (48 175, 48 175)	48 175 (48 175, 48 175)
(FR) France	65 346 726	15 339 351 (12 454 680, 18 158 156)	38 463 737 (34 478 334, 43 008 767)	38 727 999 (34 805 552, 43 279 674)
(GG) Guernsey	53 479	0 (0, 22 306)	1877 (1877, 53 099)	1877 (1877, 53 104)
(GI) Gibraltar	31 233	31 233 (31 233, 31 233)	26 873 (26 873, 31 233)	31 233 (31 233, 31 233)
(HR) Croatia	4 221 881	3 001 732 (2 675 240, 3 343 463)	3 816 375 (3 254 063, 4 065 225)	3 823 186 (3 371 975, 4 065 225)
(HU) Hungary	10 027 750	6 871 493 (4 957 358, 8 293 607)	9 856 885 (4 483 879, 10 027 742)	9 876 097 (7 840 786, 10 027 742)
(IE) Ireland	4 814 831	14 560 (97, 352 894)	351 192 (12 511, 2 486 106)	418 148 (26 281, 2 492 510)
(IM) Isle of Man	93 479	93 479 (93 479, 93 479)	93 479 (93 479, 93 479)	93 479 (93 479, 93 479)
(IS) Iceland	330 470	6332 (6332, 13 532)	6645 (6645, 20 139)	6750 (6645, 22 464)
(IT) Italy	60 499 999	39 357 298 (33 111 421, 43 803 501)	50 068 301 (44 846 328, 54 193 507)	51 888 148 (48 081 086, 54 671 205)
(JE) Jersey	92 559	0 (0, 28 991)	922 (922, 92 559)	922 (922, 92 559)
(LI) Lichtenstein	37 363	0 (0, 0)	19 213 (0, 23 289)	19 213 (0, 23 289)
(LT) Lithuania	2 923 123	1 037 226 (400 488, 1 821 479)	2 089 688 (1 197 846, 2 875 473)	2 257 227 (1 482 890, 2 858 680)
(LU) Luxembourg	570 985	0 (0, 9736)	324 255 (16 766, 507 908)	324 255 (18 868, 507 908)
(LV) Latvia	2 125 289	770 177 (78 541, 1 338 556)	1 663 388 (717 373, 2 012 122)	1 531 437 (895 565, 1 748 986)
(MC) Monaco	13 681	13 681 (13 681, 13 681)	13 681 (13 681, 13 681)	13 681 (13 681, 13 681)
(ME) Montenegro	664 404	248 443 (132 918, 400 326)	408 590 (214 787, 594 498)	413 032 (258 897, 594 498)
(MK) Macedonia (FYROM)	2 123 204	1 931 983 (1 784 536, 2 059 485)	1 918 138 (1 586 410, 2 076 636)	1 997 365 (1 887 069, 2 091 835)
(MT) Malta	420 872	420 872 (403 898, 420 872)	359 704 (330, 420 872)	420 872 (408 539, 420 872)
(NL) Netherlands	17 718 000	1 861 514 (496 752, 4 887 712)	12 815 012 (6 248 996, 17 079 090)	12 990 321 (6 671 072, 17 085 633)
(NO) Norway	5 372 166	21 485 (2160, 147 472)	22 513 (19 430, 278 578)	57 357 (19 649, 328 364)
(PL) Poland	39 149 578	33 941 244 (31 587 503, 35 909 074)	38 845 342 (37 714 562, 39 119 913)	36 887 515 (36 525 696, 37 006 924)
(PT) Portugal	9 700 000	1 934 276 (404 008, 4 105 513)	2 022 657 (17 612, 5 682 987)	3 336 004 (864 776, 6 371 533)
(RO) Romania	19 740 811	12 536 787 (9 991 581, 14 301 109)	16 197 842 (10 628 372, 18 899 966)	17 070 172 (14 151 233, 18 953 342)
(RS) Serbia	8 995 232	8 590 739 (7 856 825, 8 839 038)	8 899 419 (8 698 848, 8 971 016)	8 914 417 (8 797 323, 8 972 319)
(SE) Sweden	10 521 396	27 883 (10 427, 154 071)	167 516 (30 336, 1 211 812)	206 439 (30 934, 1 211 871)
(SI) Slovenia	2 112 593	1 046 006 (695 290, 1 368 354)	1 945 928 (1 761 175, 2 049 285)	1 945 928 (1 761 195, 2 049 285)
(SK) Slovakia	5 486 419	3 266 930 (2 071 944, 4 163 482)	5 412 775 (3 801 816, 5 486 387)	5 414 138 (4 300 177, 5 486 387)
(SM) San Marino	30 187	17 017 (6643, 26 368)	30 187 (22 784, 30 187)	30 187 (23 308, 30 187)
(UK) United Kingdom	65 644 463	8 585 732 (950 331, 16 103 147)	29 162 597 (14 031 534, 43 841 121)	29 798 616 (16 620 607, 43 952 210)
(VA) Vatican	1970	1970 (1970, 1970)	1970 (1970, 1970)	1970 (1970, 1970)
Whole study area	544 614 259	193 944 552 (146 251 722, 238 593 466)	348 258 387 (254 015 642, 420 790 160)	360 659 184 (285 453 499, 423 103 297)
		35.6% (26.9%, 43.8%)	63.9% (46.6%, 77.3%)	66.2% (52.4%, 77.7%)

^aEstimate obtained via cubic spline interpolation of 2000, 2005, 2010, 2015 and 2020 population data at 1 km² pixel level.

4. Discussion

Over the past decade, the demand for rigorous predictive models incorporating satellite-derived products to estimate continent-wide geophysical parameters of ambient air at high spatial resolution, has rapidly grown. Our work is the first to estimate surface PM₁₀ and PM_2.5 concentrations at 1 km² geographical resolution over 46 European countries, incorporating remotely sensed data and validated models using rigorous methodology. We compared different model formulations and determined the predictive performance of satellite-derived products in estimating the burden of air pollution.

The geostatistical models outperformed the non-spatial LURs which assume statistical independence, overestimating the significance of the predictors. Our results showed that modelling the spatial correlation present in air pollution data not only corrects for the bias in the covariate effects but also improves considerably the pollutants' concentration estimates as indicated by the improved predictive performances. Small differences in the logscore values of the competing (in terms of variable selection) models (differences in 4th or 5th decimal digit in Table 2) correspond to small differences in the optimal models' predictive performances. However, as this measure represents the likelihood of observing the data given the model estimates, the smallest logscore indicates the best model. The range of the logscore values among models comprising all possible combination of the covariates shows that there is variation in their predictive performances and that the models which include all the covariates do not have the best predictive ability. Therefore, the variable selection process should be part of the modelling procedure to identify the most parsimonious model.

The predictive ability of the RGR models was slightly lower compared to GR; however, the use of these models allowed us to identify the most important satellite-derived products that are associated with PM by addressing potential confounding due to similar spatial structures in the pollutants and their predictors. Thus, there is a different set of covariates in the optimal models for GR and RGR formulations. Particularly for the PM₁₀ concentration, the effects of land surface temperature and of distance to the sea covariates are positive and statistically important in the RGR models (regression coefficients of 0.14 and 0.09, respectively) but not important in the GR models. Notably, these predictors have the largest spatial structure among all the tested covariates. Similarly, for the PM_2.5 models, land surface temperature and surface humidity, that have the largest spatial correlation, are important predictors in RGR but not in GR models. These results indicate the presence of spatial confounding and suggest that when confounding is addressed by orthogonalizing the spatial random effect, the covariates with an important association with PM concentration and large spatial correlation, can be better identified in RGR than in GR models. This is very important when the main aim of the study is to determine the most important factors related to the outcome. Here our main aim was to obtain the most accurate predictions of PM₁₀ and PM_2.5. The GR models outperformed the RGR in terms of predictive ability (based on the lowest logscore values) and therefore, they were chosen for subsequent analyses. It is also worth mentioning that the Bayesian credible intervals obtained from the RGR models are much narrower compared to those from GR. Similar conclusion were drawn in the Hughes and Haran (2013) work on simulated data. Last but not least, the RGR models offer an increased computational efficiency.

The optimal set of covariates with the highest predictive performance also differs between LUR/GWR and geostatistical models. Specifically, the MAIAC AOD covariate was included in each of the best five LUR models and in the optimal GWR model with a significant positive estimated coefficient. This is in line with the results of other studies which showed the importance of the high-resolution MAIAC AOD in improving predictions of both fine and coarse particle concentrations (Chudnovsky et al., 2014, Hu et al., 2014, Kloog et al., 2015, Stafoggia et al., 2016). However, when the spatially structured random term was added, the inclusion of the AOD covariate did not improve the model-based predictions. Similar results were observed in works which incorporated alternative AOD sources such as the MODIS Dark Target and the visible infrared imaging radiometer suite (VIIRS) AOD (available at 6 km² spatial resolution) products in the geostatistical framework (Paciorek and Liu, 2009, Schliep et al., 2015). In general, there is a much larger number of significant covariates included in optimal LUR and GWR models compared to GR and RGR formulations for both PM₁₀ and PM_2.5 concentrations. The dense in situ network available in Europe allows for an accurate estimation of the spatial correlation structure, especially over shorter distances. Incorporation into the model of this supplementary information in the data, i.e. the large spatial correlation, via the Gaussian process, improved model fit and prediction more than the set of geo-referenced predictors alone. In continents such as Africa, the number of stations is sparse and reliable estimation of the spatial correlation is not possible due to the large distances between the stations. Therefore we expect that the geostatistical models would require more predictors than those developed for Europe.

Rigorous variable selection indicated that the novel pan-European Copernicus land products, including the tree cover density, impervious surfaces, European settlement map and land-use/cover datasets were significant predictors for PM estimation. The elevation, night time lights intensity, NDVI, humidity, precipitation, distance to the sea and wind speed also increased the predictive ability of the optimal (based on logscore) models. The positive/negative associations of these covariates estimated using the GR models generally agree with those reported in the literature. The important positive association of PM₁₀ with impervious surface areas and the important negative effects of NDVI and elevation on PM₁₀ were also found in Stafoggia et al. (2016). The negative association of PM₁₀ with humidity and precipitation is also consistent with previous studies (Benas et al., 2013, Yanosky et al., 2014). For PM_2.5, negative associations with the wind speed and elevation were estimated in Hu et al., 2014, Yanosky et al., 2014. However, in contrast to other studies (Vienneau et al., 2013, Chudnovsky et al., 2014), we did not find an important effect of road density and distance to the roads on PM concentration in GR models.

The advantage of the geostatistical models is their ability to provide information about air pollution in areas where there is no monitoring (i.e. no stations). Furthermore, unlike previous implementations of LUR or GWR, the Bayesian framework allows the quantification of the prediction uncertainty, which can be taken into account in further analyses. In fact, samples of the posterior predictive distributions summarized by their quantiles provide estimates of the pollutant concentration and their uncertainty at pixel level. These samples can be used to obtain other quantities of interest such as exceedance probabilities. The results from these analyses clearly show areas of elevated levels of PM₁₀ and PM_2.5 within Europe, notably in either less economically developed regions, like Bulgaria and FYROM, where solid fuels are used for home heating and energy production/distribution systems are often aged, inefficient, unreliable and polluting; or in the industrial regions, like Po Valley in northern Italy, where the polluted air is effectively trapped by the Alps on the north, and Poland, where coal-burning predominates in electricity production and adds to the problems caused by high levels of car use and industrial plants. Estimates of people exposed to excess levels of PM₁₀ and PM_2.5 per country (Table 6) provide important information to policy makers, i.e. national governments and environmental agencies.

The developed methodology can be applied to estimate pollutants' concentration and evaluate international AQGs for any specific year or spatial domain. The operational application of the models for a different year or area of investigation requires re-estimation of the regression parameters and spatial process for each pollutant. Furthermore, since most of the spatio-temporal covariates are available at daily level and the raw PM₁₀ and PM_2.5 data are measured every hour, it is possible to fit spatial models at higher temporal resolution (e.g. to daily or monthly averaged data) and evaluate the effects of the short-term or episodic exposures to air pollution. In particular, many recent works indicate large variability in the daily PM-AOD association (Lee et al., 2011, Hu et al., 2014) and therefore yearly aggregation of the data, considered here, may not capture the true physical association between two products, explaining the lack of the statistical importance of the AOD in the developed GR/RGR models. Stafoggia et al. (2016) have shown that MAIAC AOD has better predictive ability when daily calibrations of the AOD-PM relations are considered. However, the spatio-temporal Bayesian geostatistical models applied to predict daily PM data for such a large area of investigation at high spatial resolution cannot be fitted in a reasonable computational time.

The importance of the AOD within a temporal geostatistical model on daily pollution data remains to be investigated. It should be also noted that the number of days with missing AOD varies in space with higher proportion of missing values in the northern part of the continent and at high altitudes due to the presence of clouds and higher surface reflectance. The results have shown, that even with missing values, annual averaged AOD was a significant predictor in both LUR and GWR models and not statistically important in geostatistical (GR/RGR) models. In order to evaluate the impact of missing AOD data on the predictive ability of the geostatistical models, we further aggregated the daily PM₁₀ and PM_2.5 data only at locations and days when AOD is available. The results (not shown) indicated that despite of a positive and significant effect of AOD, the predictive ability of the geostatistical models was lower when it was included, leading to the conclusion that the missing values have not influenced the results. Several empirical gap-filling methods have been developed to fill missing AOD data (Kloog et al., 2011). These analyses are crucial in models which take into account temporal component (e.g. for daily predictions); however, for yearly averaged predictions, filling AOD gaps using additional statistical approaches will inevitably introduce measurement errors and complicate result interpretation. Another drawback is the temporal misalignment between the observations at stations and some of the evaluated covariates (i.e. Corine land cover, night time lights) as well as the varying spatial resolution of the covariates. We analysed publicly available data (with continental or global coverage) at the original scale assuming homogeneity of their values within the coarser spatial resolution. Approaches have been proposed to address fusion of data with different spatial supports (Berrocal et al., 2012, Nguyen et al., 2012), however this is an active field of research.

We have shown the benefits of combining high-resolution satellite-derived products in a rigorous geostatistical modelling framework to estimate the spatial distribution of PM₁₀ and PM_2.5 concentrations across Europe. Investigation over such large areas are usually computationally complex, especially when the spatial correlation structure is taken into account. Furthermore, the need of predictors at continental level and their accurate pre-processing is crucial. However, rather than working with data for a particular country, modelling at continental scale, where large number of monitoring stations are available, allowed us to better estimate the spatial correlation structure as well as the relationship between the pollutants' concentration and the covariates and therefore obtain more accurate predictions. The recent developments in remote sensing and ‘approximate’ Bayesian inference allowed us to fit such models in a reasonable computational time, to evaluate the importance of each covariate and to estimate gridded pollutants' concentration at high spatial resolution with high predictive ability.

5. Conclusions

Our model-based high-resolution air-pollution exposure estimates are readily available and can contribute to human and ecosystem health research in Europe. Most of the previous Europe-wide estimations were based on LUR and GWR models which have lower predictive ability compared to the geostatistical models, as demonstrated in the present work. The Bayesian formulation allowed us to quantify the uncertainty in the predictions and to make probabilistic statements at high geographical resolution about the areas that exceed the AQGs thresholds. To our knowledge this research is the first to compute and compare continental exceedance maps of PM₁₀ and PM_2.5 using the EU Directive and WHO guidelines. Quantification of the prediction uncertainty can also be incorporated in future studies related to health risks assessments. Furthermore, by taking into account the spatial distribution of the population within the study area, we estimated the total number of people living in regions that exceed the international thresholds. This information can support governmental decisions in areas where the implementation of the air-quality policies has to be given priority.

Handling Editor: Xavier Querol