The State of the Solar Wind, Magnetosphere, and Ionosphere During the Maunder Minimum

Abstract

Both direct observations and reconstructions from various datasets, suggest that conditions were radically different during the Maunder Minimum (MM) than during the space era. Using an MHD model, we develop a set of feasible solutions to infer the properties of the solar wind during this interval. Additionally, we use these results to drive a global magnetospheric model. Finally, using the 2008/2009 solar minimum as an upper limit for MM conditions, we use results from the International Reference Ionosphere (ILI) model to speculate on the state of the ionosphere. The results describe interplanetary, magnetospheric, and ionospheric conditions that were substantially different than today. For example: (1) the solar wind density and magnetic field strength were an order of magnitude lower; (2) the Earth’s magnetopause and shock standoff distances were a factor of two larger; and (3) the maximum electron density in the ionosphere was substantially lower.

1. Introduction

In this study, we build upon previous analysis (Riley et al. 2015) to speculate on the properties of the solar wind at 1 AU during the “Maunder Minimum” (MM) as well as presenting some inferences for the likely configuration of the magnetosphere. Finally, we make some remarks about ionospheric conditions.

2. Methods

Riley et al. (2015) described a wide range of “observations” during the Maunder minimum, ranging from descriptions of eclipses during the period between 1650 and 1715 (Eddy 1976) to Be-10 (Berggren et al. 2009) and C-14 measurements (Reimer et al. 2004). These were then used to define a set of candidate photospheric magnetic field configurations (see Figure 2 in Riley et al. (2015)).

Using these candidate boundary conditions, we developed a set of MHD solutions (by integrating the time-dependent resistive MHD equations forward in time) and compared them with the limited observations. We concluded that the most likely state of the corona, at least during the deepest portion of the MM, was produced by a photospheric field composed of entirely ephemeral regions, likely of lower strength than observed today. In this study, we extrapolate these coronal solutions out to 1 AU, as well as applying a 1-D code to provide independent support for these 3-D results. To test the possible effects of the MM on the Earth’s magnetosphere, we ran the BATS-R-US model (De Zeeuw et al. 2004) as implemented at NASA’s Community Coordinated Modeling Center (CCMC). Additionally, to explore the effects in the ionosphere, we ran the International Reference Ionosphere (IRI) model (Bilitza and Reinisch 2008).

3. Results

Using the solar MHD model solutions, we inferred that the basic plasma/magnetic field properties of the MM heliosphere at Earth would be as summarized in Table 1, which also compares these values with typical space era solar minimum conditions. Based on this, we infer that the average speed of the solar wind was probably a factor of 1.7 times slower (240 km s⁻¹), the radial magnetic field was an order of magnitude lower (0.1 nT), and the density was approximately 24 times smaller (0.21 cm⁻³).

Table 1.

Inferred properties of the MM Sun: speed (v_r), radial magnetic field (B_r), and number density (n_p) are compared with typical values at 1 AU.

Quantity	MM at 20 R_s	MM at 1 AU	Typical 1 AU values
vr (km/s)	240	240	400
Br(nT)	10−4 G	0.09 nT	1
np (cm−3)	25	0.21	5

Riley et al. (2010) investigated conditions in the solar wind during the 2008/2009 minimum using a 1-D model that included the superradial expansion of the coronal magnetic field as well as correlation analysis between various observed parameters. In particular, we found: (1) from Ulysses high-latitude/high-speed measurements: $B_r^{SW}\propto n_p^{SW}$; 2) from Wilcox/Ulysses measurements, the photospheric magnetic field within large polar coronal holes, $B_{ch}\propto B_r^{SW}$; and (3) from hydrodynamic simulations: $n_p^{SW}\propto H$. Additionally, it had been established that coronal heating, H ∝ B (Pevtsov et al. 2003). Taken together, these suggest $n_p^{SW}\propto B_{ch}$, supporting the 3-D MHD results that a substantial drop in the photospheric magnetic field should result in a substantial drop in the number density of the solar wind at 1 AU.

Before we interpret the magnetospheric MHD simulations driven by these values, it is worth considering analytic approximations. We can compute the magnetopause stand-off distance using the following approximation (Spreiter et al. (1966)):

$$r\approx \sqrt[6]{\frac{2B_0^2}{{\mu }_0\rho v^2}}$$ (3.1)

where B₀ is the Earth’s dipole field strength and ρ and v refer to the density and speed of the solar wind. Using the values from Table 1, we estimate the MM stand-off distance in relation to today’s value to be:

$$r_{MM}\approx 2\times r_{2018}$$ (3.2)

We can also estimate the dawn-dusk electric field applied by the solar wind across the magnetosphere as:

$$E_y=-v_{SW}\times B_z$$ (3.3)

which, for the MM conditions we infer, implies: $E_y^{MM}\approx 0.006\times E_y^{2018}$, or a mere 1% of today’s value.

To estimate the bow-shock stand-off distance, we must first estimate the solar wind Magnetosonic Mach Number:

$$M_{ms}=\frac{v_{SW}}{\sqrt{v_A^2+C_s^2}}$$ (3.4)

which implies $M_{ms}^{MM}\approx M_{2018}$. The shock stand-off distance (Spreiter et al. (1966)) is thus: $\frac{\mathrm{\Delta }}{r}~1.1\frac{n_1}{n_2}~0.28$ where we have used: $\frac{n_2}{n_1}=\frac{(\gamma +1)M_1}{(\gamma -1)M_1^2+2}$. This is relative to the magnetopause stand-off, and, thus, proportionately, the bow-shock sits ahead of the magnetosphere by the same fraction as today’s configuration. Thus, with a typical value of r_shock ~ 14.5R_E today, the MM shock stand-off distance would be ~ 29R_E.

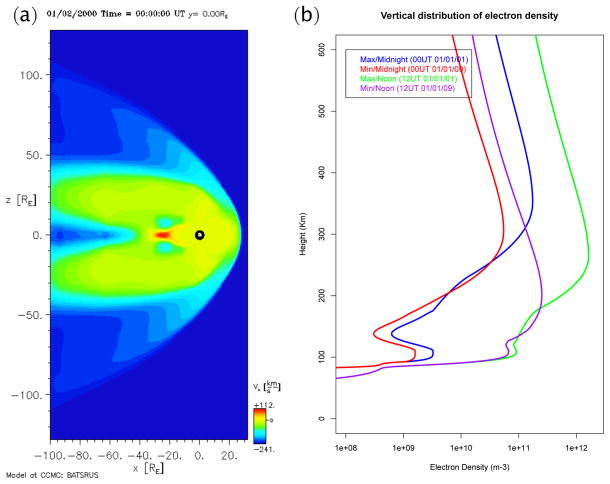
To test these analytic results, we ran a global MHD simulation of the Earth’s magnetosphere, setting the upstream solar values as in Table 1, and allowing the simulation to reach equilibrium (Figure 1(a)). The magnetopause standoff distance is 29R_E, consistent with the analytic calculations.

Figure 1.

(a) BATS-R-US magnetospheric solution showing V_x within the near-Earth environment. The Earth’s location is marked by the black circle. (b) IRI ionospheric solution showing electron density as a function of height for solar minimum, maximum, noon, and midnight conditions.

Finally, we ran the IRI to infer how the ionosphere may have appeared during the MM. Solutions for the 2008/2009 solar minimum (as an upper limit for MM conditions) as well as the 2001 solar maximum (at noon/midnight) are shown in Figure 1(b). These results suggest: (1) the maximum ionospheric density decreased significantly during MM; and (2) The F2 peak was located significantly lower. As pointed out by Smithtro and Sojka (2005) over-the-horizon radio-wave propagation would have been restricted to notably lower frequencies, and the paths of radio waves would have been significantly modified.

4. Discussion

The work summarized briefly here is only a starting point and suggests several potentially fruitful avenues to pursue in the future, to better understand the Maunder Minimum and the Earth’s response to it. For example, in the magnetosphere, our idealized simulations using the BATS-R-US code at the CCMC could be improved upon in several important ways. First, we assumed that the Earth’s intrinsic magnetic field did not change appreciably. However, it is well known that 300–400 years ago, the dipole moment was approximately 10% larger than today (e.g. Vogt et al. 2007). This would modestly increase the disparity between the magnetospheric pressure and that of the reduced solar wind, and, in particular, increase the stand-off distances inferred from this study. This, and other effects, however, would be relatively minor, and not change the inferences or conclusions reached here. Additionally, for simplicity, we ran the magnetospheric-only model. However, BATS-R-US has been coupled to several inner magnetospheric models, including the Rice Convection Model (RCM) and Comprehensive Ring Current Model (CRCM), as well as the Radiation Belt Environment (RBE) model. We chose not to include these because it was not clear that these models would be accurate under the new MM conditions imposed by the solar wind and global magnetospheric model. With the promising results presented here, however, the next logical step would be to add one of these components and explore the results.