Skeletal muscle-on-a-chip: an in vitro model to evaluate tissue formation and injury

Abstract

Engineered skeletal muscle tissues can be used for in vitro studies that require physiologically relevant models of native tissues. Herein, we describe the development of a three-dimensional (3D) skeletal muscle tissue that recapitulates the architectural and structural complexities of muscle within a microfluidic device. Using a 3D photo-patterning approach, we spatially confined a cell-laden gelatin network around two bio-inert hydrogel pillars, which induce uniaxial alignment of the cells and serve as anchoring sites for the encapsulated cells and muscle tissues as they form and mature. We have characterized the tissue morphology and strain profile during differentiation of the cells and skeletal muscle tissue formation by using a combination of fluorescence microscopy and computational tools. The time-dependent strain profile suggests the existence of individual cells within the gelatin matrix, which differentiated to form a multinucleated skeletal muscle tissue bundle as a function of culture time. We have also developed a method to calculate the passive tension generated by the engineered muscle tissue bundles suspended between two pillars. Finally, as a proof-of-concept we have examined the applicability of the skeletal muscle-on-chip system as a screening platform and in vitro muscle injury model. We studied the dose-dependent effect of cardiotoxin on the engineered muscle tissue architecture and its subsequent effect on the passive tension. This simple yet effective tool can be appealing for studies that necessitate the analysis of skeletal muscle structure and function, including preclinical drug discovery and development.

Introduction

The development of technological platforms that generate three-dimensional (3D) organoids recapitulating the structural and biological features of native tissues has led to promising in vitro systems for studying tissue morphogenesis and function. A number of studies have demonstrated the potential application of these tools in preclinical drug discovery.^1–7 Further, such technologies may expedite the development of patient-specific disease models and advance personalized treatment regimens.

Current research in this area has focused on the development of a number of organ- and tissue-on-chip platforms ranging from traditional monolayer cultures to multicellular three dimensional organoids.⁸ Organs-on-chips, which contain engineered microtissues that capture the physiological complexity of the native tissues within a continuous perfusion device, can be developed in a reproducible and cost-effective manner. These microphysiological systems also have the potential to supplement preclinical animal studies during drug discovery and development in order to improve the translatability of the drugs to the clinic.^9,10 In fact, functional organs-on-chips simulating the lungs, gut, heart, and blood–brain barrier already have been developed.^11–19

Engineered skeletal muscle tissue models are currently being developed. Skeletal muscle is the largest organ (by mass) of the human body, comprising approximately 40% of the mass of healthy individuals.²⁰ Skeletal muscle fibers contain sarcomeres that contract in unison to generate the forces that provides motion and activity to daily life. Major areas of health concern are skeletal muscle wasting, which can be attributed to a variety of factors including genetic conditions, autoimmune diseases, lack of use during aging or disability, space travel, and injury from sports, trauma, or tumor excision.^21–23 These conditions, if left untreated, can lead to significantly impaired strength and mobility. Ex vivo skeletal muscle models that emulate the structural organization, functional capabilities, and regenerative potential of native muscle could provide new tools for screening both drug and cell or tissue-based therapies.

Pioneering efforts by Vandenbergh and colleagues established the first in vitro functional 3D muscle tissues in a dish, in which the authors have shown the formation of cylindrical muscle bundles from primary rodent myoblasts.²⁴ Further studies have assessed the biological and contractile properties of engineered muscle constructs during formation and in response to various mechanical, electrical, and optical stimuli.^25–33 Previous efforts to calculate the mechanical stresses generated by muscle cells have employed various tools and methods including force transducers, movements of bright spots on myotubes, displacements of muscular thin films (MTFs), or traction force microscopy.^34–36 Although engineered skeletal muscle models have been extensively developed and studied, there exist fewer advancements in skeletal muscle-on-chip platforms.^37,38 Tissue-on-chip microfluidic platforms utilize continuous perfusion, thereby circumventing mass transport limitations associated with stagnant cell cultures. Continuous perfusion also allows temporal variations in drug concentrations to mimic physiological conditions in the human body. Furthermore, such micro-fluidic systems minimize the usage of reagents and compounds.

Herein, we describe the development of a skeletal muscle-on-a-chip platform and its application in studying skeletal muscle tissue morphogenesis, maturation, and cardiotoxin-induced changes in engineered muscle tissue architecture and passive tension. Specifically, we have used a 3D photo-patterning technology to create anchoring hydrogel structures and cell-laden hydrogel constructs. This approach has allowed us to spatially-organize the cells within a hydrogel network around the anchoring pillars to form uniaxially-aligned, densely-packed 3D cylindrical muscle tissues that reflect the structure of native skeletal muscle. Furthermore, we have quantified the strain patterns generated by the encapsulated cells as they differentiate to form a multinucleated tissue bundle in real time. We have also developed a method to quantify the passive tension of the muscle tissue bundle using finite element modeling. Finally, we have performed a proof-of-concept study to demonstrate toxin-induced changes in tissue architecture and passive tension, illustrating the potential utility of this platform as a screening platform.

Materials and methods

Cell culture

The C2C12 mouse murine myoblast cell line was obtained from ATCC. The cells were cultured in growth medium (GM), composed of Dulbecco’s Modified Eagle’s high glucose medium (Hyclone) supplemented with 10% fetal bovine serum (FBS, Gibco) and 1% penicillin/streptomycin (Gibco). The cells were grown to 70% confluency and passaged prior to usage in the experiments.

Synthesis of gelatin methacrylate (GelMA)

Gelatin methacrylate (GelMA) was synthesized as described previously.^39,40 Briefly, 10 g of bovine skin gelatin (Sigma Aldrich, St. Louis, MO, USA) was dissolved in 100 mL of PBS, and heated to 60 °C while stirring for an hour until the gelatin fully dissolved. The temperature was lowered to 50 °C, after which 8 mL of methacrylic anhydride (MA; Sigma Aldrich, Cat. No. 276685) was added dropwise to the gelatin solution, which was then stirred vigorously for 1 hour. The solution was diluted with 200 mL of warm PBS, dialyzed against MilliQ ultrapure water using 12–14 kDa cutoff dialysis tubing (Spectrum Laboratories, Rancho Dominguez, CA, USA) for seven days at 40 °C, changing water three times per day, to remove unreacted methacrylic anhydride and contaminants from the solution. The dialyzed GelMA solution was then flash frozen in liquid nitrogen and lyophilized in a freeze dryer for 4 days, and stored at −20 °C.

Synthesis of lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP)

The photoinitiator, LAP, was synthesized as described elsewhere.⁴¹ In brief, 2,4,6-trimethylbenzoyl chloride was added drop-by-drop to an equal molar solution of dimethyl phenylphosphonite under argon while stirring at room temperature. After 18 hours, the temperature was set to 50 °C, after which excess lithium bromide with 2-butanone was added to the reaction mixture. This resulted in the formation of a white precipitate within 10 minutes, after which the temperature was reduced to room temperature for 4 hours. The solution was filtered to isolate the precipitate, then washed three times using 2-butanone to ensure complete removal of excess lithium bromide. The product was dried using a vacuum to remove excess 2-butanone, yielding LAP in crystal form.

Fabrication of silicon mold

Micropatterned silicon wafers were fabricated as described previously.¹⁹ Briefly, the microfluidic channels and chamber design was photolithographically defined using NR9–1500PY negative photoresist (Futurrex, Frankling, NJ, USA) on a 4 inch diameter silicon wafer. The Si wafer was etched using a deep reactive ion etching (DRIE) process, in which SF6 gas was flowed at 100 sccm for 11 seconds of reaction time, followed by a passivation cycle when C4F8 gas was flowed at 80 sccm for 7 seconds. An etching depth of 75 μm was achieved using an etch rate of 0.7 μm per cycle. Next, the NR9–1500PY photoresist was removed by immersing in acetone for 4 hours before rinsing with methanol, isopropanol, and deionized water. The Si mold was blown dry with compressed nitrogen gas and silanized by vapor deposition of trichlorosilane (TCI Inc, Portland, OR, USA) to allow PDMS casting and removal.

Formation of PAm hydrogels on glass

To tether the PAm hydrogels within the microfluidic device, glass coverslips were chemically-methacrylated as described previously,^42,43 Briefly, round glass coverslips (12 mm round, #1 thickness, Fisher) and rectangular glass coverslips (24 mm × 50 mm, #1 thickness, Fisher) were rinsed with 100% ethanol for 15 minutes. After aspiration of the ethanol, the glass was treated with a methacrylate solution composed of 97.7% (v/v) of ethanol, 0.3% (v/v) glacial acetic acid, and 2% (v/v) 3-(trimethoxysilyl)propyl methacrylate (Sigma Aldrich) for 5 minutes, then washed with pure ethanol twice with gentle shaking. The ethanol was aspirated off, and the glass cover-slips were dried at 60 °C for 2 hours prior to use.

A polyacrylamide (PAm) precursor solution composed of 5% (wt/v) acrylamide (UltraPure Acrylamide, ThermoFisher Scientific), 0.225% (wt/v) N,N′-methylenebis(acrylamide) (Sigma Aldrich), and 0.12% (wt/v) ammonium persulfate (APS, Sigma Aldrich) in phosphate buffered saline (PBS) was first made. Fluorescent far red particles of 0.2 μm (ThermoFisher Scientific) were added to the precursor solution at a 1 : 100 dilution. Prior to polymerization, 0.6 μL of a 10% (wt/v) N,N,N′,N′-tetramethylethylenediamine (TEMED, Sigma Aldrich) in PBS was added to the precursor solution. After quickly mixing, 6 μL of the solution was dropped onto the center of a methacrylated 24 × 50 mm coverslip and subsequently covered with a non-methacrylated 12 mm round coverslip to make a PAm hydrogel of that shape and size. This process was repeated with a non-methacrylated square coverslip and a methacrylated 12 mm round coverslip. After a polymerization time of 30 minutes, the samples were immersed in DI water prior to gently removing the non-methacrylated glass by cleaving it off with a razorblade. The result was a set of PAm hydrogels tethered to the 24 mm × 50 mm glass rectangles and another set tethered to 12 mm circular glass, which would form the bottom and top surfaces of the microfluidic device, respectively (Fig. S1A†).

Fabrication of microfluidics device

To keep the PAm hydrogels hydrated, 6 μL of DI water was dropped onto the circular region of the microfabricated silicon wafer before covering it with the PAm-tethered 12 mm round coverslip, facedown. Polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) was prepared by vigorously mixing together base and curing agent in a 10 : 1 ratio by mass, then degassed in a vacuum chamber to remove bubbles. The PDMS was gently casted onto the silicon wafer containing the PAm hydrogel, then baked at 37 °C overnight to cure the PDMS (Fig. S1B†). The PDMS mold, with the PAm hydrogel attached, was then removed from the wafer, and 0.5 mm diameter holes were punched at the two ends to provide an inlet and outlet paths for perfusion. Finally, the PDMS was irreversibly bonded to the PAm-tethered rectangular coverglass after UV-ozone treatment and subsequent baking at 37 °C overnight, resulting in PAm hydrogels on the top and bottom of the central chamber of the microfluidic device (Fig. S1C†). PBS was perfused into the device to equilibrate the hydrogels prior to use.

Pillar formation

To form the PAm pillars, we employed a 3D photopatterning method described previously.⁴² First, a precursor solution composed of 5% Am and 0.225% BisAm in PBS was prepared. The photoinitiator, LAP, was added at a concentration of 2 mM, and the solution was perfused into the device. A transparency photomask with circular patterns of varying sizes (100 μm, 200 μm, 300 μm) and inter-pillar distances (500 μm, 1000 μm, and 1500 μm) was obtained, and the pattern of choice was mounted onto the stage of a fluorescence microscope, centered over an open spot in the lens turret. The device was positioned on top of the pattern of the photomask, exposed to collimated UV light of approximately 365 ± 40 nm excitation wavelength for 1 minute. The regions of the hydrogel precursor solution exposed to the UV light polymerized, resulting in circular pillars (Fig. 1A–C). Unreacted solution was removed by repeatedly washing with PBS. Thus, the complete device was constructed with top and bottom PAm hydrogel layers and PAm hydrogel pillars sandwiched between as anchors for the muscle tissues. The device was sterilized under UV light for 30 minutes prior to cell encapsulation.

Fig. 1.

3D photopatterning of support pillars and encapsulation of cells. (Left: Side view of full device; right: top view of central chamber) (A and B) To create support pillars, the bonded microfluidic chip was infused with acrylamide (Am) solution containing photoinitiator and was photopolymerized using a collimated UV light and a transparency photomask containing 100 μm diameter circle patterns. (C and D) After washing with PBS, a precursor solution composed of cells, GelMA, and photoinitiator was polymerized around the pillars using the same method as before, except with a capsule-shaped pattern. (E) PBS solution was used to wash the samples, and the device was perfused with maintenance media by using a syringe pump.

Encapsulation of cells in GelMA around PAm pillars

A 7% (wt/v) GelMA solution in PBS was prepared by dissolving the GelMA powder in PBS at 60 °C for 30 minutes. This solution was syringe filtered with 0.22 μm to remove contaminants and insoluble components. C2C12 cells were mixed into the GelMA solution at a cell density of 12.5 million cells per mL before adding 0.01% ascorbic acid (Sigma Aldrich), a free-radical scavenger, and 2 mM LAP, a photoinitiator.

The cell-laden hydrogel solution was injected into the fluidics device with a syringe. A transparency photomask containing a capsule pattern was placed onto the fluorescence microscope as described previously. The device was mounted on the photomask and manually positioned to locate two pillars within the capsule shape using the microscope eyepiece under brightfield illumination. This region was exposed to UV light for 12–15 seconds to photopolymerize the GelMA solution containing the C2C12 cells (Fig. 1D and E). This process was repeated several times within one device to obtain up to 10 samples. Unreacted monomer solution and cells were washed away with sterile PBS. Thus, the 3D skeletal muscle-on-a-chip with cells patterned between and around anchoring pillars was created.

The samples were cultured in growth media for 24 hours, then switched to differentiation media, composed of Dulbecco’s Modified Eagle’s high glucose medium (Hyclone) supplemented with 2% horse serum (HS, Omega Scientific) and 2% penicillin/streptomycin (Gibco), to induce cell differentiation and fusion. Media was supplied to the cells within the device through a syringe pump (Harvard Apparatus) at a constant flow rate of 40 μL per hour in an incubator set at 37 °C and 10% CO₂. This flow rate was used based on our previous study which showed that, for samples in our device, a steady-state concentration can be achieved within 1000 seconds at a flow rate of 40 μL per hour.⁴³

Immunofluorescence staining of muscle tissues

The tissues were washed with PBS three times, fixed with 4% paraformaldehyde (PFA, Sigma Aldrich) solution for 15 minutes at room temperature, followed by several PBS washes to remove excess PFA. Next, a blocking buffer composed of 3% bovine serum albumin (BSA, Sigma Aldrich) and 0.5% Triton-X 100 (Fisher Scientific) was added and incubated for 1 hour in 4 °C to prevent non-specific binding of antibodies. Mouse monoclonal antibody for myosin heavy chain (MF20, Developmental Studies Hybridoma Bank) was diluted 1 : 100 in blocking buffer and perfused into the device overnight at 4 °C. The primary antibody was removed with several PBS washes. A solution containing the following was prepared: AlexaFluor 488 goat anti-mouse secondary antibody (Cat. No. A-11001, ThermoFisher Scientific) diluted 1 : 100 in blocking buffer, rhodamine-conjugated phalloidin (Cat. No. R415, ThermoFisher Scientific) diluted 1 : 100 in blocking buffer, and Hoechst 33342 dye (Cat. No. H3570, ThermoFisher Scientific) diluted to 1× in blocking buffer. The muscle strips were incubated in this solution overnight at 4 °C, then washed away with excess PBS prior to imaging.

Microscopy for imaging acellular samples and staining samples

A laser scanning confocal microscope (Olympus FV1000) was used to obtain Z-stack images of acellular 3D samples of the PAm hydrogel layers, PAm pillars, and patterned GelMA hydrogels. Each component was doped with 1% (v/v) 200 nm fluorescent microspheres that emit at various wavelengths, including yellow-green (505/515 nm), orange (540/560 nm), and dark red (660/680 nm). Samples were imaged at 10× magnification, with a z-step size of 1.0 μm.

A spinning disk confocal microscope (Perkin Elmer Ultraview) was used for Z-stack imaging of tissues stained for myosin heavy chain (green), F-actin (red), and nuclei (blue). Samples were imaged with a 40× oil immersion objective lens, with a z-step size of 0.5 μm. Single layer images of fluorescent particles for quantification of bead displacements and subsequent strains were also captured with the spinning disk confocal.

A Keyence BZ-X710 fluorescence microscope was used to obtain videos of acellular samples under perfusion at varying flow rates (40 μL h⁻¹, 100 μL h⁻¹, 400 μL h⁻¹) to ensure that the GelMA hydrogel and PAm pillars were attached to the top and bottom PAm hydrogel layers. To improve visualization, the fluid was doped with far-red (200 nm; magenta color) particles. Samples were imaged at 10× and 20× objective lens.

Quantification of alignment score and fusion index

Z-stack images obtained from the confocal microscope were processed in ImageJ (NIH) for quantification. Alignment score was assessed as the deviation of multinucleated myotubes with three or more nuclei from the major axis. The major axis for each sample was drawn as the line connecting the centroids of the two pillars. The angular deviation was noted from ImageJ in 10° intervals and plotted as a histogram. Fusion index was calculated as the number of nuclei within multinucleated myotubes containing three or more nuclei out of the total number of nuclei within the sample, as a percentage.⁴⁴ A grid was overlayed on a merged stack of MF20 staining and nuclei counterstain, helping to facilitate the analysis. As a note, the tissue on the outer rims of the pillars was not considered in these calculations as the tissue in these regions is not unidirectionally-aligned and functions primarily to anchor the engineered microtissue in place. Data is presented as mean ± standard deviation, and the comparison between the groups was carried out by using one-way ANOVA with Tukey’s multiple comparison test, where P-values < 0.1 were considered statistically significant. For both alignment and fusion, n = 3–5 samples per group from 3 different chips were used. Data is presented using GraphPad Prism software.

Calculation of elastic modulus of PAm hydrogel

PAm hydrogels with a radius and height of 3.5 and 3 mm, respectively, were fabricated and incubated in PBS overnight to reach equilibrium prior to compression tests.⁴⁵ The tests were performed on an Instron 3342 Universal Testing System equipped with Model 2519–104 force transducer. The maximum force load was set to 250 N and the samples were compressed at a rate of 0.3 mm min⁻¹. The Young’s modulus was determined by calculating the slope of a linear region of stress–strain curve.

Quantification of strains

Fluorescent particles embedded within the PAm hydrogels were imaged using a confocal microscope at days 0, 2, 4, 8, and 12. The 2D images of the fluorescent particles embedded in the PAm hydrogels was recorded before C2C12 encapsulation (reference state) and at various post-encapsulation time points, up to 12 days (deformed state). The deformation of the PAm hydrogel surface was calculated by analyzing the 2D bead displacement using particle image velocimetry (PIV) to compare the reference state images to the deformed state images, yielding a displacement vector field, u and v. The corresponding strains were calculated using infinitesimal strain approximation given by ε_ij = 1/2 * (u_ij + v_ji). The mean of the absolute value of the individual components of the strain tensor was calculated at different x-positions to examine the changes in the cell-generated forces as a function of culture time.

Comparison of empirical strain distribution with theoretical strain distribution

A finite element model of a cylinder with a height of 70 μm and diameter of 100 μm tethered to a rectangular prism of length 350 μm was created using COMSOL Version 4.2. Here, the cylindrical structure and the rectangular prism was used to model the hydrogel pillar and the underlying PAm hydrogel, respectively. A displacement boundary condition was applied at the periphery of the cylinder along the x-axis while a symmetric condition was imposed at the top surface of the cylinder. The rectangular prism was tethered in all directions at the bottom surface while all other surfaces were considered stress free. These boundary conditions were used to generate a theoretical strain field resulting from the cylindrical structure being displaced 5 μm along the x-axis. This displacement value was equal to the average displacement of three samples found experimentally by comparing the reference state images to the deformed state images. The theoretical strain field from FEM model was compared to the strain field resulting from the displacement field obtained via PIV.

Calculation of passive tension

The tissue samples were cultured for 12 days prior to analyzing the displacement of the pillars to which they are tethered. The values for the pillar displacement determined experimentally from individual microtissues were used as the displacement boundary conditions within the COMSOL based finite element model described previously. Here, the resultant stress tensor component, τ_xz, was integrated under the pillar area and multiplied by 2 to approximate the passive tension existing within the muscle fiber.

Assessing pillar bending

To assess the potential bending of the PAm pillars, finite element analysis was carried out on the domain depicted in Fig. 6A. A traction boundary condition was applied to the surface of the pillar in the x-direction to simulate the contractile forces generated by the cells. Stress values of 0, 115, 230, and 450 Pa were used, which corresponds to passive tensions of 0, 5, 10, and 20 μN over the lateral surface area of the pillar. These passive tensions were used in the FEA because they span the entire range of the tension generated by the muscle tissues (Fig. 6E). Boundary conditions applied on the upper and lower surfaces were obtained from FEM analysis of pillar displacements. The displacements of the pillar in the x-direction were plotted to examine the presence of bending.

Fig. 6.

Quantification of passive tension generated by the engineered muscle using COMSOL. (A) 3D rendering of the finite element domain used for simulating the deformations in the PAm hydrogel caused by pillar displacement. (B) The magnitude of the displacement vectors shown as a heat map on the finite element domain. (C) The strain values for ε_xx, ε_yy and ε_xy on the surface of the PAm hydrogels obtained from finite element simulations (theoretical, top row) and empirically (experimental, bottom row). (D) Stress tensor component, τ_xz, and traction stress vector obtained from the finite element simulations shown as a heat map and vector field, respectively. (E) Histogram showing the distribution of the magnitudes of passive tension generated by 30 microtissues.

Cardiotoxin-induced structural disruption of the engineered tissue

As a proof-of-concept validation of the potential application of the skeletal-muscle-on-a-chip platform as a screening molecule, we have examined cardiotoxin-induced changes of the engineered skeletal muscle tissue. To this end, day 12 engineered muscle tissue strips were exposed to cardiotoxin from Naja mossambica mossambica (Sigma, C9759) at concentrations of 0 μM, 0.1 μM, and 0.5 μM diluted in differentiation medium (2% horse serum in DMEM). The compound was supplied to the tissues in the microfluidic chip under continuous flow at 40 μL h⁻¹. Structural changes of the tissue were examined after 24 hours of cardiotoxin administration, where samples were fixed with PFA and stained for F-actin and nuclei. Changes in passive tension were assessed over a 3 day period of cardiotoxin administration. The passive tension was quantified every 24 hours for 3 days by analyzing the displacement of the left and right pillar as compared to the reference day 0 pillar positions in COMSOL, as described previously. Data is presented as mean ± standard deviation, where n = 4–5 samples per group from 3 different chips. Data is presented using GraphPad Prism software.

Results

Device fabrication and characterization

To develop aligned 3D skeletal muscle tissues and calculate the strain profile and passive tension within the tissue, we created a microfluidic device containing a central chamber with multiple hydrogel structures. Specifically, a cell-laden gelatin network, confined around two PAm pillars, was sandwiched between two PAm hydrogel layers. The acellular PAm hydrogel structures were designed to serve different functions: (1) PAm hydrogel pillars acted as anchoring sites, which induce uniaxial alignment of the cells/tissues, (2) top and bottom hydrogel layers spatially confined cell-laden gelatin networks and underwent quantifiable elastic deformations necessary to quantify the cell and tissue generated strains and forces.

Fig. 1 and S1† illustrate the device fabrication and subsequent cell encapsulation procedures. Following the initial fabrication of the device, we used a previously described 3D photo-patterning method to generate PAm hydrogel pillars between the top and bottom PAm hydrogel planar layers (Fig. 1A–C and S2A†).⁴² With all the necessary components in place, we next used the same photo-patterning technique to form a cell-laden gelatin methacrylate (GelMA) hydrogel around the PAm pillars (Fig. 1D and E). While any shape can be patterned, we found the capsule shape to be most optimal in order to position cells between and around the anchoring pillars. To depict this setup, an acellular sample was constructed, with each hydrogel containing 200 nm diameter fluorescent particles of different colors. Using a confocal microscope, the sample was imaged to visualize these structures within the device. The side view, represented by the X–Z projection, clearly shows the PAm hydrogel pillars in green and the GelMA hydrogel capsule in red placed between the planar PAm hydrogel layers in violet (Fig. 2A). The X–Y projections, depicting a top view at different Z planes (Fig. 2B), and a 3D rendering of each component along with a 3D representation of the composite structure (Fig. 2C), are also shown. The thicknesses of the middle layer (comprised of PAm pillars and GelMA hydrogel) and the planar hydrogels on the top and bottom were measured to be approximately 70 and 40 μm, respectively.

Fig. 2.

Characterization of various hydrogel structures within flow chamber. Z-stack images of the hydrogels, loaded with fluorescent microparticles, were obtained using a laser scanning confocal microscope (green: PAm pillars; red: GelMA hydrogel; magenta: PAm planar hydrogels). (A) X–Z cross-section and (B) X–Y planes at the specified Z locations are shown. (C) 3D renderings of each component and the composite structure are shown. Scale bars: (A) horizontal: 100 μm; vertical: 30 μm; (B) 100 μm.

To ensure that the GelMA hydrogel and PAm pillars were fixed in place, acellular samples were analyzed to show that these hydrogel structures would not detach from the top and bottom PAm hydrogel layers in response to flow. Evidence that the GelMA hydrogel and PAm pillars are attached to the PAm hydrogel layer can be clearly observed in Videos S1–S5.† As seen from Videos S1–S3,† in all flow conditions, the GelMA hydrogel and PAm pillars remain stationary and do not dislodge, even at the highest flow rate of 400 μL h⁻¹, which is ten times the flow rate that was used during muscle tissue culture. Videos S4 and S5† further demonstrate the strong adhesion of the GelMA hydrogel and PAm pillars to the underlying PAm hydrogel. Video S4,† which displays the GelMA structure and PAm pillar at position Z2 (see Fig. 2A), clearly shows the fluid flowing around the periphery of the GelMA hydrogel under perfusion. No such fluid flow is observed at the interface of the GelMA-PAm hydrogels (Video S5,† which shows the interface between the underlying PAm hydrogel layer and both the GelMA hydrogel and PAm pillar at position Z3; see Fig. 2A). The absence of fluid flow at the GelMA-PAm hydrogel layer interface further suggests that the hydrogel layers are adhered to each other strongly.

Formation of 3D skeletal muscle micro tissues

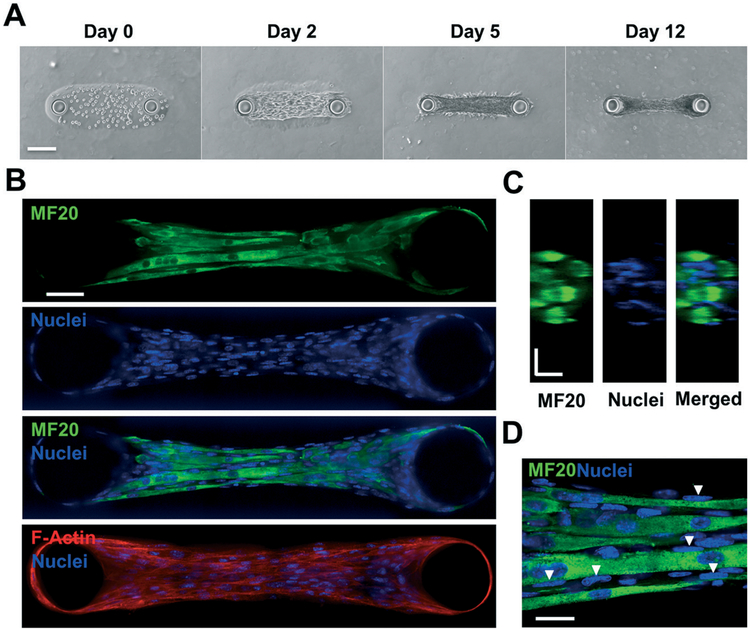
Skeletal muscle microtissues were formed using C2C12 murine myoblasts encapsulated in a GelMA hydrogel, where gelatin is a collagen-derived matrix with inherent cell adhesive sites. Using photo-polymerization, the cells were encapsulated within a GelMA hydrogel surrounding the two PAm pillars and sandwiched between two acellular polyacrylamide hydrogel layers. Up to ten of these structures were formed within one microfluidic chip, spatially separated from one another by a minimum of 800 μm in all directions. Following the initial encapsulation, the chip was perfused with PBS to wash away un-encapsulated cells and un-reacted reagents. The cells were cultured in growth medium for 24 hours to equilibrate with the new environment, and then maintained in low-serum differentiation medium for the remainder of the culture to induce differentiation, cell fusion, and the formation of multinucleated myotubes. The cell-laden GelMA hydrogel was monitored for tissue formation and remodeling for up to 12 days (Fig. 3A). Brightfield images at various time points in Fig. 3A show that cell–cell attachment and alignment were evident by day 2, formation of a dense microtissue by day 5, and further compaction of the muscle tissue strip by day 12.

Fig. 3.

Muscle tissue growth and characterization. (A) Brightfield images depict cell growth, attachment, and hydrogel compaction as a function of days in culture. (B) Immunofluorescent staining images taken from a spinning disk confocal microscope of day 12 samples for myosin heavy chain (MF20) (green), nuclei (blue), and the merged composite. This result suggests a highly matured muscle tissue composed of several multinucleated myotubes. F-actin staining (red) depicts cytoskeletal alignment (bottom). (C) Y–Z confocal sections of a microtissue stained for MF20 (green) and nuclei (blue) illustrate the three-dimensional, cylindrical morphology and fascicular structure of the engineered muscle tissue. (D) High magnification (100×) images of MF20 and nuclei depict the arrangement of nuclei on the periphery of myotubes (white arrows). Scale bars: (A) 150 μm; (B) 50 μm; (C) and (D) 20 μm.

To assess the need for the PAm hydrogel pillars-induced uniaxial cell alignment on skeletal muscle tissue formation, cell-laden GelMA hydrogels of identical geometries were fabricated within the device without the pillar support and compared against those cultured under identical conditions but in presence of pillars (Fig. S2B†). By day 5, cells cultured in the absence of pillars collapsed inwards into a ball of cells while those cultured in presence of pillars formed intact, aligned muscle strips. Thus, due to cell-mediated degradation of the GelMA hydrogel and contraction of the myoblasts, the anchoring function of the pillars was necessary to generate muscle tissue strips.

Effect of pillar diameter and inter-pillar distance on micro-tissue formation

Having established that 3D skeletal muscle microtissues can be successfully generated within a microfluidic device, we next evaluated the effect of varying the pillar diameters and inter-pillar distances on tissue differentiation and maturation. To do so, we quantified two well-known characteristics of multinucleated myotubes, fusion index and alignment score, at day 12 of the culture. The selected region of the engineered organoid outlined by the “box” in Fig. S3A,† hereafter termed as characteristic tissue volume, was used to calculate fusion index and alignment score. Note that the figure only shows a single slice of the tissues but the analyses was performed for the entire 3D tissue.

First, the inter-pillar distance was kept constant at 500 μm while the pillar diameters were varied at 100 μm, 200 μm, and 300 μm. The aspect ratios of the resulting characteristic tissue volumes were 1 : 5, 2 : 5, and 3 : 5. In the second set of experiments, the pillar diameter was fixed at 100 μm, while the inter-pillar distances were varied at 500 μm, 1000 μm, and 1500 μm. The aspect ratios of the resulting characteristic tissue volumes were 1 : 5, 1 : 10, and 1 : 15. Together the experiments allowed us to determine the effect of aspect ratio on tissue formation. Initial observations suggested that groups with an aspect ratio of 1 : 10 and 1 : 15 were found to be more susceptible to rupture, while groups with an aspect ratio of 2 : 5 and 3 : 5 remodeled and compacted the GelMA hydrogel to a lesser degree compared to those in 1 : 5 aspect ratio.

Samples were cultured for 12 days and immunostained for myosin heavy chain, a marker for differentiated muscle cells, and counterstained for the nuclei. The presence of cells expressing myosin heavy chain and containing multiple nuclei indicated the formation of multinucleated myotubes. As seen in Fig. 4A over 90% of myotubes in the groups with aspect ratios 1 : 5, 1 : 10, and 1 : 15 were aligned within 10° of the major axis, and almost 100% were within 20°. On the other hand, for the groups with aspect ratios of 2 : 5 and 3 : 5, there was a significantly larger variation in alignment relative to the major axis, with some myotubes having up to 60–70° deviation from the major axis, indicating more random orientation and less alignment. Furthermore, from Fig. 4B, the fusion indices for the groups with aspect ratios of 1 : 15, 1 : 10, 2 : 5, and 3 : 5 were in the range of 14–15%, while that of the 1 : 5 group was approximately 32%. The fusion index for the group with an aspect ratio of 1 : 5 is more than two-folds greater than that of the other groups. The corresponding images for all aspect ratios are shown in Fig. S3B.† Together the data suggests that the microtissues with an aspect ratio of 1 : 5 had the highest efficiency for myotube formation, thus we utilized the tissues with this ratio for all further analyses.

Fig. 4.

Myotube alignment and muscle cell fusion. (A) Alignment score showing the deviation of the longitudinal myotube axis from the mean orientation axis for 5 experimental groups (1 : 15, 1 : 10, 1 : 5, 2 : 5, and 3 : 5) after 12 days of culture. Values are calculated as a percent of total myotubes per sample. 3–5 samples from 3 different chips were used per group. For each group, the plot illustrates the mean value along with standard deviation. (B) Fusion indices, calculated as the percentage of the total number of nuclei within myotubes relative to the total number of nuclei in the sample, for each experimental group, analyzed from confocal z-stacks of immunofluorescence staining for myosin heavy chain (MF20) and nuclei counterstain. 2000 nuclei from 3–5 samples examined from 3 different chips were used for each group. The plot shows the mean value alone with standard deviation. One-way ANOVA with Tukey’s multiple comparison test was used to assess statistical significance (*p < 0.1, **p < 0.01, ***p < 0.001).

Characterization of muscle tissue morphology and differentiation

Engineered muscle tissue strips with the aspect ratio of 1 : 5 were further characterized. Samples cultured for 12 days were stained for myosin heavy chain, F-actin (to assess cytoskeletal alignment and cellular organization within the microtissue), and the nuclei. Images of a representative z-slice obtained from a spinning disk confocal microscope show multiple horizontally-aligned multinucleated myotubes parallel to one another within each organoid, suggesting the formation of muscle tissue bundles (Fig. 3B). Further, the unidirectional alignment of all cells along the major axis throughout the microtissue, including those not expressing myosin heavy chain, was clearly seen in images of F-actin staining. Y–Z cross-sectional images of myotubes and nuclei illustrate a three-dimensional, cylindrical muscle bundle densely packed with several myotubes of approximately 10–15 μm in diameter, with nuclei dotting the periphery (Fig. 3C). This closely resembles the fascicular morphology of native skeletal muscle tissue.⁴⁶ The corresponding high-magnification image clearly depicts elongated nuclei that are primarily present on the periphery of the myotubes, as indicated by the white triangles (Fig. 3D). These hallmarks of skeletal muscle tissue provide further confidence that our engineered muscle organoids mimic several structural features of native skeletal muscle.

Calculation of strains during tissue morphogenesis

We next examined the strains that are exhibited by the C2C12 cells as they differentiate, organize, and fuse to form multinucleated myotubes and 3D tissues. Since the GelMA degrades and remodels with tissue formation, the stress transduced to the underlying PAm hydrogel layer was used for the strain calculations. We examined the deformation of the PAm planar hydrogel and quantified the 2-dimensional strain field ε_xx, ε_yy, ε_xy as a function of culture time (days 2, 4, 8, and 12). The strains are shown within a mask of the perimeter of the microtissue (dotted lines in Fig. 5A) to illustrate their precise location. While the strains ε_xx were present throughout the tissue early in tissue formation (at days 2 and 4), as the cells differentiate, fuse, and remodel the surrounding matrix to form a muscle strip, the strains were localized to the pillars, yielding almost no deformation in the region between the pillars (Fig. 5A). A similar trend was also evident in ε_xx and ε_xy directions (Fig. S4A and S5A†). Time-dependent immunofluorescence staining further corroborated these strain patterns. At day 4, most cells remain as undifferentiated single cells, while at day 12, cells have fused to form a continuous 3D tissue composed of several multinucleated myotubes (Fig. S6†).

Fig. 5.

Quantification of cell generated strains on the PAm hydrogel with culture time. (A) Heat map of tensile strain values, ε_xx, calculated from the deformations observed on the PAm hydrogel layer at culture days 2, 4, 8, and 12. The dotted lines display the contour of the cell-laden GelMA hydrogel. Negative and positive values indicate contraction and extension of the hydrogel. (B) Bar graph of binned values of ε_xx along the long axis of cell-laden GelMA hydrogel. The locations of the bin centers are indicated in the x-axis of the plot and are shown pictorially in the inset containing the Brightfield image of the microtissue. (C) An overlay of X–Y confocal sections of fluorescent particles embedded in the PAm hydrogel surface at day 0 (green) and day 2 (red) in the left panel and at day 0 (green) and day 12 (red) in the right panel. The lack of overlap between green and red beads in the right panel indicates the inward shift of the two pillars at day 12 suggesting the contraction of the microtissue. Scale bars: 50 μm.

Furthermore, we quantified the strain magnitudes along the tissue length by binning several x-positions over the length of the tissue to confirm the strain pattern in Fig. 5A. As evidenced in Fig. 5B, by day 12, the strain magnitudes of ε_xx were highest at the pillars and minimal elsewhere throughout the construct area. Furthermore, the magnitudes of ε_xx were approximately two-fold greater than those of ε_yy and ε_xy, indicating that the strain in the x-direction is dominant (Fig. S4B and S5B†). Considering also the cylindrical geometry of the muscle bundle from Fig. 3C, these results could be attributed to the muscle strip detaching from the underlying hydrogel layer after day 4 and forming a tense hanging rope as the cells fuse to each other to form multi-nucleated tubes and remodel the GelMA. The formation of such a tissue rope anchored to the PAm pillars resulted in the localization of cellular forces around the two PAm pillars.

We also examined the displacement of the pillars at day 2 and day 12 of tissue development. Fig. 5C shows confocal images of the fluorescent particles embedded in the PAm hydrogel underneath the muscle strip, overlaying day 0 (green) with either day 2 (red, left) or day 12 (red, right). The circles are the rims of the PAm pillars, which are highlighted by the presence of fluorescent beads. Note that there are no beads visible within the outline of the pillars due to imaging constraints. At day 2, when the tissue was nascent, the beads appeared as yellow, indicating a strong overlap of green (day 0) and red beads (day 2), which in turn suggested no noticeable pillar displacement. On the contrary, at day 12, there was a distinct shift and measureable inward displacement of the beads compared to day 0, indicating that the cellular forces exerted by the fused muscle strip shifted the pillars.

Calculation of passive tension

Since the cells were simply pulling the pillars inwards along the major axis without rotations, we used finite element analysis to calculate the passive tensile forces generated by the microtissues. We compared the experimentally determined strain field on the top surface of the PAm hydrogel layer with that of a theoretical strain field resulting from purely displacing the PAm pillars along a single dimension. The experimentally determined elastic modulus of the PAm hydro-gels, 11.85 ± 1.31 kPa, was used in determining the theoretical strain field (Fig. S7†). The theoretical strain field was obtained using finite element analysis where the depiction of the domain with a simulated displacement of a single pillar is given in Fig. 6A. The resultant displacement field of the PAm pillar (on the PAm hydrogel layer) is shown as a heat map in Fig. 6B. The comparison of the experimentally determined strains with those from the theoretical calculations is given in Fig. 6C. Note that the region of the heat map immediately around the pillars, given by a dark red and blue circular shape, was error due to a poor signal-to-noise ratio. However, outside of this region, there was a strong overlap in the patterns of the strain fields for ε_xx, ε_yy and ε_xy. This pattern suggested that the muscle tissue strip displaces the PAm pillars towards the center of the microtissues and the resultant force could be obtained using the loading configuration that was simulated using the finite element model. To this end, we first generated the shear stresses, τ_xz, resulting from the engineered muscle strip at a single pillar with displacement arrows overlaid (Fig. 6D). The summation of these stresses over the area of each pillar yielded the passive tension. Fig. 6E presents a distribution of the passive tension of over 30 engineered skeletal muscle microtissues (6–8 different chips), where the mean tension is 8.16 μN ± 3.41 μN. As a result, the system developed in this study can be used to engineer mature skeletal muscle tissue mimics as well as quantify passive tension generated by the tissue.

Cardiotoxin-induced structural disruption of the engineered tissue

To assess the potential application of the skeletal muscle-on-a-chip platform as a screening tool, we performed a proof-of-concept study to evaluate cardiotoxin-induced structural changes of the engineered tissue and the accompanying changes in the passive tension. Cardiotoxin (CTX) is a toxin found in snake venom that is known to prompt myotube depolarization and disrupt the muscle cytoskeleton and is commonly used in experiments to induce skeletal muscle injury in animal models. We evaluated the response of the engineered muscle microtissues to CTX by applying 0 μM (control), 0.1 μM, or 0.5 μM CTX to day 12 engineered muscle tissues. As seen in Fig. 7, our results show a dose-dependent response to cardiotoxin. After 24 hours of exposure to CTX, the control samples and samples exposed to 0.1 μM had an intact or mostly-intact cytoskeleton, respectively; however, those exposed to 0.5 μM cardiotoxin exhibited a severely disrupted and fragmented cytoskeleton (Fig. 7A). The changes in passive tension for these three groups reflect the cardiotoxin-induced structural damages of the engineered tissue. The passive tension of the control samples remained constant over a 3 day experimental period, whereas the tissues exposed to 0.1 μM cardiotoxin incurred a gradual decrease in passive tension and 0.5 μM samples incurred a sharp and immediate drop in passive tension (Fig. 7B). Most of the samples exposed to 0.5 μM cardiotoxin showed a complete cytoskeletal rupture of the tissues. This proof-of-concept study highlights the practical application of our platform by assessing both the tissue structural changes and the associated changes in passive tension in response to a small molecule.

Fig. 7.

Dose-dependent response of engineered muscle strips to cardiotoxin (CTX). (A) F-actin and brightfield images of muscle strips subjected to 0 μM, 0.1 μM, and 0.5 μM CTX for 24 hours. (B) CTX administration results in a dose-dependent drop in passive tension due to cytoskeletal disruption.

Discussion

Organ-on-a-chip systems have been touted as the next generation of in vitro tissue-specific models for studying tissue development and disease causation, and for use in drug discovery and development. Such systems have many advantages as a perfusion system surpasses the limitations associated with static 3D cultures as it continuously provides fresh nutrients and removes wastes and metabolic byproducts, while minimizing the usage of reagents and compounds. Further, current organ-on-a-chip platforms have been able to mimic the native cellular and tissue responses to various mechanical or chemical perturbations.^11,12,34 In this study, we have utilized a previously described 3D photo-patterning technology to additively form acellular and cell-laden hydrogel structures to generate skeletal muscle tissues within a microfluidics device.⁴²

The immunofluorescence images show that the engineered tissues displayed the hallmarks of skeletal muscle tissue – cylindrical fascicular morphology, multinucleated myotubes, nuclei elongation, and nuclei on myotube periphery. The GelMA hydrogel used to encapsulate the cells facilitated the formation of multinucleated myotubes to create 3D tissues. GelMA, which supports initial attachment of cells to the surrounding biomaterial via inherent cell-adhesive sites, further promotes cell fusion as it actively degrades and remodels in the presence of cells. These properties of GelMA support multinucleated myotube formation, cellular alignment, and matrix remodeling to form a compact muscle tissue bundle.

Moreover, we have developed a method to calculate the passive tension generated by the muscle tissue bundle based on the real-time strain profile. Since the cell-mediated degradation of the GelMA hydrogel results in a change in its material properties over time, it is inaccurate to utilize traction stress measurements from GelMA to quantify the contractile stresses and strains associated with the engineered tissue. Hence, we used a “far-field” approach in which we used stress transduction from the cell-laden GelMA to the underlying PAm hydrogel.¹⁹ The PAm is a bioinert, non-degrading material that exhibits constant linear elastic material properties throughout the course of the experiments. The deformation of PAm hydrogels due to the contractile stresses generated by the cells embedded within the GelMA layer was quantified by tracking the fluorescent particles in real-time. The material deformations allowed us to calculate the strain patterns of the developing tissue as a function of time to evaluate muscle tissue formation and, subsequently, obtain the passive tensile forces.

An inherent limitation of far field measurements is the decay of stresses as a function of distance between the stress-generating cells and the underlying elastic material (“sensor”) under deformation. To minimize the effect of decay on stress transduction, only the fluorescent particles on the surface of the PAm layer immediately adjacent to the cell-laden GelMA hydrogel were imaged during data acquisition. Furthermore, cell-laden GelMA hydrogels were packed with high cell density to ensure the presence of cells throughout the structure. The degradation of the GelMA hydrogel with culture time could have an effect on the strain profile; however, the degradation-mediated changes in the strain profile will be negligible as the encapsulated myoblasts fuse to form multinucleated muscle tissues suspended by the PAm pillars. The strain profile gathered at the later culture time is mostly due to the PAm pillar displacement which is caused by the muscle tissues pulling inwards.

We first showed that our engineered muscle bundle forms a three-dimensional free-hanging rope-like structure by comparing the immunofluorescence images from Fig. 2B and C with the strain distribution heat map from Fig. 4B. Noting the cylindrical morphology of the muscle strip, along with the day 12 strain profile indicating that the strains are localized entirely at the pillars, we deduced that the engineered muscle has released from the hydrogel surfaces and stays as a suspended rope-like structure. As a result, the tensile force could be calculated directly from the pillar displacement. The displacement of the pillars formed the boundary conditions for the finite element model of a linearly elastic isotropic material to determine the stresses generated at each pillar, which summed to yield the value of the tension. Since the top and bottom PAm hydrogels were of similar thickness and rigidity, the displacement of the pillar was considered to be uniform and thus only the fluorescent particles in the bottom PAm layer were tracked. Further, the significant distance of 800 μm between each engineered tissue ensured that the measured displacements belonged only to the respective sample, and that the deformation of the PAm surface due to one muscle tissue would have negligible effects on the readouts of the adjacent samples. In fact, the value for the mean tension, 8.16 μN, is similar to the average static tension of 10.8 μN found by Sakar, et al., in their engineered muscle micro-tissues.²⁹ In native skeletal muscle tissue, the passive tension is associated with the myofibrillar structure (and hence the tissue architecture).⁴⁷ Exposure to cardiotoxin incurred structural disruption of the engineered skeletal muscle tissues. Concomitant with the structural changes, the engineered tissues exhibited a corresponding drop in passive tension, underlying the structure–function relationship.

We performed bending analysis along the length of the pillar shaft to evaluate the bending of the pillars caused by the tension generated by the microtissues. By applying a load perpendicular to the shaft, our analyses show bending of the pillars, where the amount of bending increases with increasing tension applied (Fig. S8†). Since all displacements were measured in presence of fluid flow any bending of the pillars observed could be due to the suspended microtissues and hence should not have any effect on the passive tension calculations. Moreover, the bending does not disrupt the force transmitted from the PAm pillars to the PAm hydrogel layers.

Taken together, the PAm hydrogel layers, the degradable nature of GelMA, and the PAm support pillars allowed for the remodeling of the extracellular matrix and the alignment and fusion of single cells into multinucleated myotubes to form compact skeletal muscle tissue bundles. In addition to serving as a “force sensor”, the PAm hydrogel layers on the top and bottom of the device performed two critical functions. First, PAm is a bioinert hydrogel that prevents cell attachment, thus cells are spatially confined and prevented from attaching to any region outside the patterned space. Secondly, the PAm hydrogel allows for GelMA and PAm to entangle with its meshwork during gelation. Due to the molecular miscibility of monomers, the GelMA and acrylamide monomers diffuse into the PAm hydrogel network, and subsequently create physical entanglements with the underlying PAm. This not only maintains the structural integrity of the cell-laden GelMA hydrogels, but also supports attachment of the PAm pillars to the polyacrylamide hydrogel layers on the top and bottom surfaces of the central chamber of the device following photo-polymerization. This PAm-layer-PAm-pillar attachment was critical to the successful quantification of the passive tension generated by the tissues.

The strength of our platform is the ability to quantify tension during tissue culture in real-time without destroying the engineered muscle tissues. Also, the design described in this study yields three-dimensional (3D) muscle strips. Our platform is amenable to both light and fluorescence microscopy. This sets up our system for future studies, where we can incorporate electrical or optical stimulation to induce the active contraction of the tissues and measure the twitch and tetanic forces that are generated. One could also envision varying the mechanical properties of the pillars and hydrogels to mimic the mechanical properties of the extracellular environment. For example, we can modify the stiffness of the pillars to force these tissues to contract against larger or smaller loads, and thus measure the fatigue induced by working the muscle. However, our system also has some limitations. For example, length-tension relationships are typically determined by shortening or lengthening the construct. As our skeletal muscle construct is engineered in a closed system, it cannot be accessed by any micromanipulators and as such cannot be shortened or lengthened, making it difficult to measure the length-tension relationship.

Conclusion

In summary, we have created a 3D skeletal muscle-on-a-chip platform and described a method to calculate the passive tension generated by the engineered muscle tissues. Our approach utilizes the tissue anchoring sites, which induce uniaxial alignment, to obtain the strain profile and force measurements. We have demonstrated that the multi-layered hydrogel system supports tissue growth for long-term cultures and we have also characterized the resulting tissue structure and morphology. Our proof-of-concept toxicity study illustrates the ability of this platform to recapitulate expected changes in the skeletal muscle tissue structure and function in response to a small molecule. Further, the skeletal muscle-on-a-chip detailed here provides a platform to study stimuli-induced changes in cell fusion and myotube size and relate this to the associated functional force measurements. Moving forward, using both healthy and disease-specific human induced pluripotent stem cells (hiPSCs), such as those with Duchenne’s muscular dystrophy (DMD), will allow us to build human- and patient-specific skeletal muscle platforms that improve upon the complexity of existing in vitro disease models.⁴⁸ Ultimately, we hope to investigate the effects of novel pharmaceutical and cell-based therapeutics on the structure and function of human skeletal muscle tissues from both toxicity and efficacy standpoints.