An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing

Abstract

Ocean color measured from satellites provides daily global, synoptic views of spectral waterleaving reflectances that can be used to generate estimates of marine inherent optical properties (IOPs). These reflectances, namely the ratio of spectral upwelled radiances to spectral downwelled irradiances, describe the light exiting a water mass that defines its color. IOPs are the spectral absorption and scattering characteristics of ocean water and its dissolved and particulate constituents. Because of their dependence on the concentration and composition of marine constituents, IOPs can be used to describe the contents of the upper ocean mixed layer. This information is critical to further our scientific understanding of biogeochemical oceanic processes, such as organic carbon production and export, phytoplankton dynamics, and responses to climatic disturbances. Given their importance, the international ocean color community has invested significant effort in improving the quality of satellite-derived IOP products, both regionally and globally. Recognizing the current influx of data products into the community and the need to improve current algorithms in anticipation of new satellite instruments (e.g., the global, hyperspectral spectroradiometer of the NASA Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission), we present a synopsis of the current state of the art in the retrieval of these core optical properties. Contemporary approaches for obtaining IOPs from satellite ocean color are reviewed and, for clarity, separated based their inversion methodology or the type of IOPs sought. Summaries of known uncertainties associated with each approach are provided, as well as common performance metrics used to evaluate them. We discuss current knowledge gaps and make recommendations for future investment for upcoming missions whose instrument characteristics diverge sufficiently from heritage and existing sensors to warrant reassessing current approaches.

1. Introduction

Understanding oceanic response to the Earth’s changing climate, the ocean’s role in land-oceanatmosphere carbon cycles, regional marine ecosystems’ responses to hazards, variations across systems, and the health of aquatic fisheries and other critical habitats – to name only a few – requires access to substantial volumes of marine biogeochemical information (IOCCG, 2008; IOCCG, 2009). Ocean color satellite instruments not only collect data on temporal and spatial scales that cannot currently be achieved by conventional in situ or aircraft sampling platforms, but also provide data records that allow retrospective analyses of spatiotemporal trends. These instruments provide estimates of spectral water-leaving radiances – the light exiting a water mass that defines its color, leading to the colloquial discipline name ocean color. The scientific community has invested significant effort in the development of algorithms to derive marine biogeochemical and optical quantities from satellite measurements of ocean color (IOCCG, 2006; IOCCG, 2014). With these algorithms, ocean color data records provide invaluable resources to study global and large-scale regional (e.g., Southern Ocean and North Atlantic) carbon stocks (Allison et al., 2010; Duforet-Gaurier et al., 2010; Gardner et al., 2006; Loisel et al., 2002; Siegel et al., 2014; Siegel et al., 2005; Stramska, 2009; Stramska & Stramski, 2005), phytoplankton population diversity and succession (IOCCG, 2014), phytoplankton physiology (Westberry et al., 2016; Westberry & Siegel, 2006), and oceanic productivity (Antoine et al., 1996; Behrenfeld et al., 2005; Saba et al., 2011; Uitz et al., 2010).

The continuous global data record from polar orbiting ocean color satellites in low Earth orbit (LEO) now spans twenty years and includes, but is not limited to, data collected by the following instruments: the NASA Sea-viewing Wide Field of View Sensor (SeaWiFS; 1997–2010), the NASA Moderate Resolution Imaging Spectroradiometers onboard Terra (MODIST; 1999present) and Aqua (MODISA; 2002-present), the ESA Medium Resolution Imaging Spectrometer (MERIS; 2002–2012), the NASA-NOAA Suomi National Polar-orbiting Partnership Visible Infrared Imaging Radiometer Suite (VIIRS; 2012-present), and the ESA Ocean and Land Colour Instrument (OLCI; 2016-present). Over this time span, the number of derived data products increased substantially given improvements in computing power, better and more diverse in situ measurements, improved knowledge of ocean optics, unlimited access to the data records, and the varied instrument characteristics of the satellite missions (e.g., their spectral, spatial, and temporal resolutions). The interest in using satellite data records to support coupled hydrodynamic-biological modeling efforts (Dutkiewicz et al., 2015; Gnanadesikan et al., 2010; Mannino et al., 2016; Rousseaux & Gregg, 2015) and management and decision making activities (Schaeffer et al., 2015) has also grown. Looking forward, upcoming instruments, such as the spectrometer to be flown as part of the NASA Plankton, Aerosol, Cloud, ocean Ecosystem mission (PACE; launch planned for 2022), will extend current ocean color records and will provide improved sensing systems, including increased spectral resolution (and, possibly, polarization information from a second instrument) that will undoubtedly expand interest in ocean color data records and stimulate derived product development activities.

Recognizing the current influx of data products into the community and the forthcoming need to develop enhanced approaches that exploit the characteristics of new instruments, we present a synopsis of the current state of the art in the retrieval of a core suite of properties used in studying ocean biogeochemistry, namely spectral marine inherent optical properties (IOPs). IOPs are insensitive to changes in the light field and encompass the absorption and scattering properties of seawater and its particulate and dissolved constituents. Ocean color satellite instruments measure the spectral radiance emanating from the top of the atmosphere, L_t(λ) (μW cm^-2 nm^-1 sr^-1) at, at least, discrete visible (VIS; 400–700 nm) and near-infrared (NIR; 700–1000 nm) wavelengths. Generally speaking, two approaches exist to retrieve IOPs from satellite measurements of ocean color. The first approach, used in standard agency processing (e.g., NASA, NOAA, and ESA), applies atmospheric correction (AC) algorithms to remove the contribution of the atmosphere from the total signal at the top of the atmosphere and produce estimates of remote-sensing reflectances, R_rs(λ) (sr^-1), the light exiting the water normalized to a hypothetical condition of an overhead Sun and no atmosphere (Gordon & Clark, 1980; Gordon & Wang, 1994) (paths 1 → 2 → 4 or 1 → 2 → 3 → 4 in Fig. 1). In the field, R_rs(λ) is calculated as the ratio of water-leaving radiance, L_w(λ) (μW cm^-2 nm^-1 sr^-1), to downwelling irradiance just above the air-sea interface, E_s(λ) (μW cm^-2 nm^-1). Since R_rs(λ) is an apparent optical property, that is, it is dependent upon the details of the light field, field measurements are generally made as close to the time of the local satellite overpass(es) as possible. Algorithms are then applied to the R_rs(λ) to produce estimates of geophysical properties, such as IOPs (IOCCG, 2006; Werdell et al., 2013a). The second approach relates L_t(λ) directly to IOPs or an optical proxy for a biogeochemical stock (Hu, 2009; Matthews et al., 2012; Wynne et al., 2013), circumventing the need for AC that can sometimes be confounded by absorbing aerosols and optically complex water masses (path 1 → 4 in Fig. 1).

Figure 1:

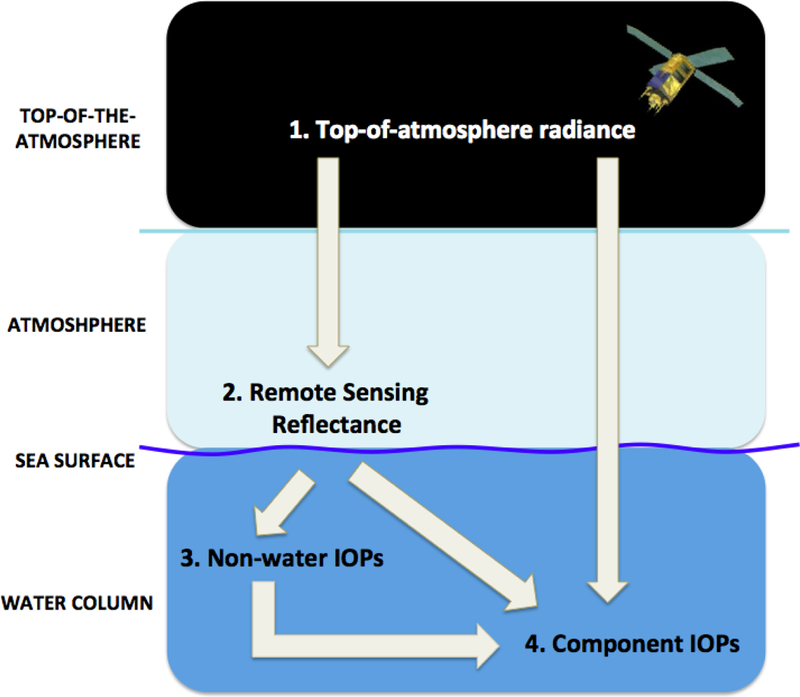
Schematic of inversion methods pathways. Component IOPs can be derived from topof-atmosphere radiance, remote-sensing reflectance, or non-water IOPs. Each of these approaches requires a different numbers of explicit steps as described in the text.

Algorithms for quantifying IOPs from ocean color adopt numerous forms and are used to generate varied optical data products to serve diverse purposes. The total IOPs, those that result from additive contributions of all water constituents with optical signatures, determine the propagation of light within an aquatic medium and, hence, the changes in the magnitude and spectral composition of the light field throughout the water column. They are the major determinants of R_rs(λ) and thereby play a critical role in the interpretation of ultraviolet-to-near infrared remote-sensing data. The component IOPs associated with specific types of water constituents, such as phytoplankton, non-algal particles (NAP), and colored dissolved organic matter (CDOM), carry information about ocean properties and processes that have specific biological and biogeochemical significance, including standing stocks and rate processes of aquatic carbon pools. For example, spectral absorption coefficients of phytoplankton provide essential parameters for quantifying primary production (Bannister, 1974; Kiefer & Mitchell, 1983; Lee et al., 1996b; Marra et al., 2007). Phytoplankton absorption coefficients arguably also provide the single best parameters for optically-based assessments of phytoplankton community composition that is typically described in terms of community size structure and pigment composition (Bracher et al., 2017; Brewin et al., 2011; Bricaud et al., 2007; Ciotti et al., 2002; Devred et al., 2011; Hirata et al., 2008; Hoepffner & Sathyendranath, 1993; Lohrenz et al., 2003; Moisan et al., 2011; Organelli et al., 2013; Sathyendranath et al., 2001; Sathyendranath et al., 2005; Uitz et al., 2015). Likewise, spectral absorption coefficients of CDOM provide biogeochemically useful proxies of aquatic dissolved organic carbon (DOC) (Fichot & Benner, 2011; Mannino et al., 2008; Matsuoka et al., 2012; Vantrepotte et al., 2015; Vodacek et al., 1997), allowing the estimation of this carbon pool from optical measurements in some aquatic environments.

The flow of this paper is as follows. First, we review the state of the art in approaches for obtaining IOPs from satellite ocean color. We separate the approaches based on common methods in either inversion methodology or the type of IOPs sought. We next provide summaries of known uncertainties associated with the approaches and common performance metrics. Both of the latter merit (and could fill) full reviews, but doing so exceeds the scope of this review, so only synopses are provided. We then discuss knowledge gaps and recommendations for future investment and conclude with a discussion of recommendations for the upcoming missions, including PACE, whose instrument characteristics diverge sufficiently from heritage and existing sensors such that novel and/or refined approaches will be required to best exploit and take advantage of these characteristics.

2. Heritage algorithmic approaches

2.1. Equations and assumptions

2.1.1. Relating R_rs(λ) to IOPs

Considerable effort has focused on the development of analytical frameworks for deriving unknown marine IOPs from sensor-observed R_rs(λ), recognizing that these frameworks cannot be exactly reduced to an analytical equation or expression (IOCCG, 2006). Mathematically, deriving IOPs requires solution of an inverse problem that can be solved by developing an appropriate forward model, F, that explicitly relates the observed quantity (in this case, R_rs(λ) to a set of unknown variables-of-interest (IOPs):

$$R_{rs}(\lambda )=F\left[IO{P}_S(\lambda )\right]$$ (1)

Given that R_rs(λ) is an apparent optical property (AOP) that depends on the geometry of the light field, F must explicitly or implicitly account for angular variations associated with illumination conditions. Once a suitable forward model has been developed, it is often possible to derive IOPs from sensor-observed R_rs(λ) using an inverse solution method:

$$IOPs(\lambda )=F^{-1}\left[R_{rs}(\lambda )\right]$$ (2)

The inverse solution method is often mathematically ill-posed, however, as different combinations of IOPs can result in the same R_rs(λ) spectrum in the visible (VIS) domain (DefoinPlatel & Chami, 2007; Sydor et al., 2004; Twomey, 1977). This is particularly the case when the number of independent observations (i.e. number of sensor VIS wavelengths) is small compared to the number of unknown IOP variables, or when uncertainty in the observed R_rs(λ) is high. Historically, two distinct forward modeling approaches have been routinely used to develop the relationship between R_rs and IOPs: (1) scalar radiative transfer (RT) simulations; and (2) approximation to the RT such as the quasi-single scattering approximation (QSSA). RT simulations comprehensively quantify the fate of the incident downwelling photon flux as it interacts with optically significant constituent matter. The QSSA is a simplified analytical model that approximates R_rs(λ) as a function of spectral IOPs. Note that statistical and neural network approaches also exist that directly relate measured R_rs(λ) and IOPs, thus simplifying Eq. (1) further. We review these methods in Section 2.2.3.

Many RT codes have been developed that compute R_rs(λ) from user-input IOPs and other key environmental parameters (e.g. sea surface state, atmospheric transmittance, solar geometry, viewing geometry, and water column depth). Historically, hydrological RT codes have been either Monte Carlo ray tracing-based methods (Boynton & Gordon, 2002; Gordon & Boynton, 1998; Kattawar & Adams, 1989; Zhai et al., 2008) or direct solutions to the RT equation (Mobley et al., 1993), with the latter being most common in recent ocean optics studies. A substantial benefit of hydrologic RT codes is they can capture the effects of multiple scattering, inelastic radiative processes, and vertical water-column structure. In addition, hydrologic and atmospheric RT codes can be coupled to simulate sensor-observed L_t(λ). Note, however, that RT simulations can be computationally intensive, are conceptually complex, rely on accurate user inputs (e.g., IOP measurements or models), and can be limited by any assumptions associated with measurement gaps, including bio-optical models that may be used to parameterize input IOPs (Gordon et al. 1988). In addition, most RT codes in use are scalar and do not account for polarization. Including polarization may result in significantly different (≤50%) values relative to heritage scalar results (Harmel et al., 2012; Mobley, 2015), opening the door for retrieval of more information about atmospheric and oceanic particles.

The QSSA was first derived for ocean color applications by Gordon (1973). Essentially, the QSSA assumes most scattering occurs in the forward direction and, accordingly, that the color and shape of the upward propagating light field is primarily determined by absorption and singlescattering at large angles (rather than multiple scattering at small angles), respectively (Gordon, 1993). Using this assumption, several analytical expressions have been developed that approximate the sub-surface remote-sensing reflectance, r_rs(λ) (sr^-1) as a function of total absorption, a(λ) (m^-1), and backscattering, b_b(λ) (m^-1) coefficients (Gordon et al., 1988; Morel, 1988; Morel & Prieur, 1977). Alternatively, the QSSA can be used to model subsurface irradiance reflectance, R(λ) (unitless), defined as the ratio of subsurface upwelling irradiance, E_u^-(λ), to subsurface downwelling irradiance, E_d^-(λ), (both with units of μW cm^-2 nm^-1). Other models have additionally included explicit dependencies on the volume scattering function (VSF) (Jerlov, 1976; Zaneveld, 1982; Zaneveld, 1995). The major benefit of QSSA models is the provision of an explicit analytical relation between IOPs and r_rs(λ). Establishing this relationship, however, requires various assumptions of boundary conditions, such as an infinitely deep and a homogeneous water column. Furthermore, QSSAs cannot capture extreme multiple scattering effects, require an additional module to consider inelastic processes, do not account for the polarization, and are not as accurate as RT codes. Some formulations exist that address bottom reflectance (Lee et al., 1994; Lee et al., 1998a; Philpot, 1987; Sathyendranath & Platt, 1988), but we do not discuss them in detail in this review.

2.1.2. Common QSSA equations

Most contemporary ocean color applications employ QSSA models that express r_rs(λ) as a function of IOPs. In these cases, it is necessary to convert the R_rs(λ) observed by the satellite instrument to r_rs(λ) using a relationship such as Lee et al. (2002):

$$r_{rs}(\lambda )=\frac{R_{rs}(\lambda )}{0.52+1.7R_{rs}(\lambda )}$$ (3)

Note that in conventional NASA processing, the input R_rs(λ) includes “exact” normalization to account for bidirectional reflectance distribution function (BRDF) effects (Morel et al., 2002). We assume R_rs(λ) to be normalized as such in this review, which effectively removes most of the effects of the Sun being off-zenith. The most commonly employed relationships to express r_rs(λ) as a function of IOPs can be represented in the expression developed by (Gordon et al., 1988):

$$r_{rs}(\lambda )={\sum }_{i=1}^2{G}_i(\lambda ){[u(\lambda )]}^i$$ (4)

where the G(λ) coefficients represent the combined influence of illumination conditions and geometry, sea surface properties, and the shape of the marine VSF and , u(λ) is described as:

$$u(\lambda )=\frac{b_b(\lambda )}{a(\lambda )+b_b(\lambda )}$$ (5)

as obtained from the QSSA approximation. Eq. (4) has a unique positive solution for u(λ) when r_rs(λ) and G(λ) are all positive. Common methods for estimating the G(λ) functions include Gordon et al. (1988), where G₁(λ) and G₂(λ) are spectrally fixed as 0.0949 and 0.0794 (see Lee et al. (2002) and Lee et al. (2011) for alternative coefficients) and the tabulated results of Morel et al. (2002), where G₁(λ) is estimated for given solar and sensor geometries and chlorophyll-a concentrations (C_a; mg m^-3) and G₂(λ) is set to 0. Appendix A provides an alternate list of expressions for Eq. (4). In current practice, these methods for estimating G(λ) cannot represent all illumination conditions and geometries, sea surface properties, and shapes of the particle VSF. Alternative representations of G(λ) within a QSSA have emerged to address the uncertainties associated with these specific effects being poorly defined (see Section 5.3).

2.1.3. Common IOP component definitions and equations

The total spectral absorption coefficient is a conservative property and thus, by definition, can be expressed as the sum of all individual absorbing constituents:

$$a(\lambda )={\sum }_{i=1}^2{a}_i(\lambda )$$ (6)

where index i indicates the i^th of N total individual absorbing constituents. Practically, similar constituents are grouped into components (Roesler et al., 1989; Stramski et al., 2001):

$$a(\lambda )=a_w(\lambda )+{\sum }_{i=1}^{N_{ph}}{a}_{ph,i}(\lambda )+{\sum }_{i=1}^{N_{nap}}{a}_{nap,i}(\lambda )+{\sum }_{i=1}^{N_{cdom}}{a}_{cdom,i}(\lambda )$$ (7)

where the subscripts w, ph, nap, and cdom indicate contributions by water, phytoplankton, NAP, and CDOM and the index i may indicate a number of individual constituents (i.e., phytoplankton cells) or sub-components (i.e., multiple phytoplankton communities) enumerated as N_ph. Similarly, N_nap and N_cdom are the number of different types of NAP and CDOM present. Further, each absorbing component can be expressed as the product of its normalized spectral absorption coefficient (shape; a*) and its magnitude (A):

$$a(\lambda )=a_w(\lambda )+{\sum }_{i=1}^{N_{ph}}{A}_{ph,i}{a}_{ph,i}^{*}(\lambda )+{\sum }_{i=1}^{N_{nap}}{A}_{nap,i}{a}_{\text{ nap}.}^{*}(\lambda )+{\sum }_{i=1}^{N_{cdom}}{A}_{cdom,i}{a}_{cdom,i}^{*}(\lambda )$$ (8)

where the term “normalized” is used here to describe the process of obtaining a representation of absorption spectral shape. Multiple approaches have been adopted (Bricaud et al., 1995; Bricaud et al., 1998; Roesler et al., 1989), as expanded upon in Section 2.1.4, and the units of A and a* depend upon the choice of normalization. For example, when the phytoplankton component absorption spectrum is scaled to the chlorophyll-a concentration, the term A_ph,i is equivalent to the chlorophyll-a concentration (mg m^-3) and a*_ph,i(λ) is the chlorophyll-a specific absorption coefficient (m² mg^-1) associated with the i^th phytoplankton type present. The shapes of a_nap(λ) and a_cdom(λ) are spectrally similar, and for simplicity, or when the degrees of freedom are low, they are often treated in combination:

$$a_{dg}(\lambda )=a_{nap}(\lambda )+a_{cdom}(\lambda )$$ (9)

where a_dg is a heritage term, namely absorption by detrital particulate matter and gelbstoff, although NAP encompasses more than detrital particulate matter (i.e., living and detrital particulate organic matter, exclusive of in vivo phytoplankton pigments, as well as inorganic particulates) and CDOM operationally includes sub-micron particles. The term A_dg,i (m^-1) is accordingly introduced for scaling the magnitude of the i^th normalized CDOM + NAP coefficient, a_dg*(λ) (unitless). The total absorption coefficient from Eq. (8) now becomes:

$$a(\lambda )=a_w(\lambda )+{\sum }_{i=1}^{N_{ph}}{A}_{ph,i}{a}_{ph,i}^{*}(\lambda )+{\sum }_{i=1}^{N_{dg}}{A}_{dg,i}{a}_{dg,i}^{*}(\lambda )$$ (10)

Note, however, that this simplification is not ubiquitous and several algorithms derive the a_cdom(λ) and a_nap(λ) components separately from one another, as described in Section 2.1.4.

The total spectral backscattering coefficient can be similarly expanded as (Stavn & Richter, 2008; Stramski et al., 2001):

$$b_b(\lambda )=b_{bw}(\lambda )+{\sum }_{i=1}^{N_{\mathrm{ph}}}{b}_{bph,i}(\lambda )+{\sum }_{i=1}^{N_{\mathrm{nap}}}{b}_{bnap,i}(\lambda ).$$ (11)

As for absorption, we can express each constituent within the components of b_b(λ) as the product of a normalized backscattering spectrum (shape; b*) and its magnitude (B). The total backscattering coefficient can thus be expressed as:

$$b_b(\lambda )=b_{bw}(\lambda )+{\sum }_{i=1}^{N_{ph}}{B}_{bph,i}{b}_{bph,i}^{*}(\lambda )+{\sum }_{i=1}^{N_{nap}}{B}_{bnap,i}{b}_{bnap,i}^{*}(\lambda ).$$ (12)

As the two non-water backscattering components are considered spectrally similar, Eq. (12) is often reduced to:

$$b_b(\lambda )=b_{bw}(\lambda )+{\sum }_{i=1}^{N_p}{B}_{bp,i}{b}_{bp,i}^{*}(\lambda ).$$ (13)

For the inversion problem to be well-posed, the number of unknown IOP variables must not exceed the number of observed independent variables (spectral bands). Contemporary oceancolor sensors are multi-spectral, having between 5 and 8 VIS bands suitable for use in inversion algorithms. We note, however, that the number of unknown parameters one can actually solve for may be significantly less than the number of bands available depending on the uncertainties in the measured input reflectances and the amount of un-correlated information within them (e.g. Twomey 1977). We expect that for future missions with hyperspectral spectrometers from the ultraviolet (UV; ~350 nm) to the NIR (~900 nm), such as PACE, the number of retrievable parameters will be much fewer than the number of wavebands, but the uncertainty in the retrieved parameters will be much lower. In the simplest formulation described by Eqs. (4), (5), (10) and (13) and with N_p=N_ph=1, only three normalized spectral shapes are required (a*_ph(λ), a*_dg(λ), and b*_bp(λ)) and three unknown IOP magnitudes, (A_ph, A_dg and B_p), are retrieved. Methods used to partition a(λ) and b_b(λ) into additional subcomponents and mathematical solution methods to invert IOPs from r_rs(λ) are described in Sections 2.1.4 and 2.2, respectively.

2.1.4. Approaches to Retrieving Component IOPs from Reflectance

Broadly speaking, many variants of several approaches exist to invert R_rs(λ) or r_rs(λ) to IOPs, all of which require varied degrees of knowledge of IOP component spectral shapes. Methods for assigning spectral shapes or partitioning total IOPs into their components, however, are not often mutually exclusive from the inverse solution method. Next, we present IOP spectral shape parameterization and partitioning approaches. A detailed discussion of solution methods is presented separately in Section 2.2. For the purposes of this section, it is convenient and necessary to introduce two solution concepts for deriving component IOPs: (A) a simultaneous solution of b_bp(λ), a_ph(λ), and a_dg(λ) (or, a_cdom(λ) and a_nap(λ)) (path 2→4 in Fig. 1); and (B) a two-part solution where first b_bp(λ) and a(λ) are determined, then a(λ) is subsequently decomposed into its components (path 2→3→4 in Fig. 1);. For reference, these two concepts map most directly to the solution methods presented in Sections 2.2.1 and 2.2.2.

2.1.4.1. Seawater absorption and backscattering

A number of values for a_w(λ) have been estimated from laboratory measurements of pure water samples (Pope & Fry, 1997) or modeled using in situ samples collected from hyper-oligotrophic regions of the ocean (Lee et al., 2015; Morel et al., 2007; Smith & Baker, 1981). Several sets of spectral b_bw(λ) have been derived previously from theory (Buiteveld et al., 1994; Morel, 1974; Shifrin, 1988). Theoretical values from Zhang and Hu (2009) and Zhang et al. (2009) are considered the current state of the art, agreeing to within 2% on average with the only pure water scattering measurements made by Morel (1968). The vibrational states and thermodynamic properties of seawater, and hence its optical properties, vary with changes in temperature (T) and/or salinity (S) in specific spectral regions. Accordingly, recent efforts have focused on modeling the spectral shapes of a_w(λ) (Pegau et al., 1997; Röttgers et al., 2014; Sullivan et al., 2006; Twardowski et al., 1999) and b_bw(λ) (Pegau et al., 1997; Röttgers et al., 2014; Zhang et al., 2009) as functions of T and S. Satellite observations of sea surface temperature (SST; Kilpatrick et al. (2001) and sea surface salinity (SSS; Lagerloef et al. (2008), as well as climatological values (Antonov et al., 2010; Reynolds et al., 2002), have made it possible to implement T-S dependent b_bw(λ) within inverse algorithms (Werdell et al., 2013b).

2.1.4.2. Phytoplankton, NAP, and CDOM absorption

Partitioning total absorption, a(λ), into several broadly-defined components associated with CDOM, phytoplankton, and NAP is possible because of the availability of routine experimental methodologies for determinations of a_cdom(λ), a_ph(λ), a_nap(λ), and a_p(λ) (= a_nap(λ) + a_ph(λ)) (Bricaud et al., 1981; Bricaud & Stramski, 1990; Ferrari & Tassan, 1999; Kishino et al., 1985; Miller et al., 2002; Mitchell et al., 2003; Mitchell & Holm-Hansen, 1991; Pegau et al., 2003; Röttgers & Doerffer, 2007; Röttgers et al., 2007; Stramski et al., 2015; Twardowski et al., 1999), with the understanding that interpretation of these components remains constrained by their operational definitions and measurement protocols. For example, whereas a_cdom(λ) is defined by the 0.2 μm pore size of the filter used to establish the dissolved fraction of the sample, a_p(λ) is typically measured with a filter-pad method by collecting particles on GF/F glass-fiber filters (Mitchell et al., 2003). Thus, the filter-pad method does not account for a certain fraction of particulate absorption associated with submicron particles (Stramski, 1990) and closure in the nominal size range 0.2 μm to 0.7 μm is lacking unless the missing fraction is measured (Simeon et al., 2003). Note that partitioning a(λ) in the actual methodological sense is practically equivalent to partitioning of the non-water absorption coefficient, a_nw(λ) = a(λ) - a_w(λ), because a_w(λ) is assumed to be known (see above).

2.1.4.2.1. Simultaneous partitioning methodology

Most heritage IOP models pursue a simultaneous solution (path 2→4 in Fig. 1), which requires assumptions about the spectral shapes of a_ph(λ) and a_dg(λ). These approaches often parameterize a single spectral shape for a*_ph(λ) based on in situ measurements (Garver & Siegel, 1997; Maritorena et al., 2002; Roesler & Perry, 1995; Sathyendranath et al., 1989), multiple a*_ph(λ) spectra associated with different pigment-based taxonomic groups (Roesler & Boss, 2003; Roesler et al., 2004; Werdell et al., 2014), or as empirically-derived Gaussian-based approximations to measurements (Hoge & Lyon, 1996; Lee et al., 1996a). Spectral variations in a*_ph(λ) do exist, however, due to the types and relative concentrations of phytoplankton present and their physiological responses to growth conditions including light, nutrient availability, and temperature. This leads to temporal, spatial and depth variations in the spectral shapes of a*_ph(λ) that are encountered in the ocean. During pixel-by-pixel processing a*_ph(λ) is either treated as a spectral constant or a bio-optical model is used in an attempt to capture its variability. Commonly used approaches for parameterizing a*_ph(λ) are summarized in Table 1.

Table 1:

Example methods for deriving normalized a_ph(λ).

Reference	Uses measured data (Y/N)	Input data required	Description
Prieur and Sathyendranath (1981)	Y	Ca	Single a*ph(λ) vector
Roesler et al. (1989)	Y	Ca	Single a*ph(λ) shape
Lee et al. (1996)	N	Ca	Blends two Gaussian basis vectors
Bricaud et al. (1995)	Y	Ca	Blends two basis vectors
Bricaud et al. (1998)	Y	Ca	Blends two basis vectors
Hoge and Lyon (1996)	N	Ca	Single Gaussian basis vector (Hoepffner and Sathyendranath 1993)
Sathyendranath et al. (2001)	Y	Ca	Blends a*ph(λ) basis vectors for two phytoplankton populations
Ciotti et al. (2002)	Y	Size parameter, Sf	Blends a*ph(λ) basis vectors for micro- and picophytoplankton

A fixed shape for a*_dg(λ) is typically modeled with the exponential function:

$$a_{dg}^{*}(\lambda )=\exp (-S_{dg}\lambda ),$$ (14)

where the exponential decay coefficient, S_dg, which typically varies between 0.01 and 0.02 nm^-1 (Roesler et al., 1989), is assigned as a constant value (Hoge & Lyon, 1996; Maritorena et al., 2002; Roesler & Perry, 1995). The choice of S_dg is sometimes based on region-specific in situ measurements (Brando et al., 2012), global in situ datasets (Lee et al., 2009), or by optimally tuning the inverse algorithm’s bio-optical parameters with a training dataset (Maritorena et al., 2002). Alternatively, the approach of Lee et al. (2009) estimates S_dg dynamically from an empirical dependence on the blue to green reflectance ratio:

$$S_{dg}=0.015+\frac{0.002}{0.6+r_{rs}(443)/r_{rs}(55x)’}$$ (15)

where the reference wavelength, 55x, is centered on the greenest wavelength of the satellite instrument (e.g. 555 nm for SeaWiFS and 547 nm for MODIS). This method does not permit S_dg to fall below 0.015 nm^-1 and predicts a decrease in S_dg as water becomes clearer (through an increasing 443–55x ratio), which has not been ubiquitously observed, particularly in the presence of photobleaching. Generally speaking, the magnitudes of S_dg (or S_g) and a_dg(440) (or a_g(440) share an inverse relationship (Bricaud et al. 2012), a model parameterization explored in Brewin et al. (2015a). Twardowski et al. (2004) suggested that exponential relationships do not accurately represent the spectral shape of CDOM, offering power-laws as the alternative and demonstrating that S_dg values will vary dependent on specified spectral range used to compute it (see also Nelson and Siegel (2002). Most recently, Cael and Boss (2017) demonstrated that a stretched exponential provides a better model than Eq. (14) or a power-law for a_dg(λ).

2.1.4.2.2. Two-step partitioning methodology

Many emerging IOP models pursue a two-step solution (path 2→3→4 in Fig. 1) for partitioning a(λ) into its subcomponents. One pathway begins with decomposing of a_nw(λ) into a_p(λ) and a_cdom(λ) and then subsequently subdividing a_p(λ) into a_ph(λ) and a_nap(λ). (Bricaud & Stramski, 1990; Cleveland & Perry, 1994; Hoepffner & Sathyendranath, 1993; Lin et al., 2013; Morrow et al., 1989; Roesler et al., 1989; Wang et al., 2008; Zheng & Stramski, 2013a). This multiple-step approach has had limited applicability within the remote sensing context, primarily because of difficulties in directly estimating a_p(λ) and a_cdom(λ) from ocean color measurements. Currently, the most common pathway involves partitioning of a_nw(λ) into a_ph(λ) and a_dg(λ) (Eq. (10); for examples of partitioning methods in this category see Table 2.

Table 2:

Example approaches for partitioning a(λ) into a_ph(λ) and a_dg(λ).

Reference	Method and assumptions for parameterizing aph(λ) and adg(λ)	Additional input data	Applied to ocean color data? (Y/N)
Roesler et al. (1989)	• adg(λ) has fixed exponential slope, Sdg • aph(λ) blue-to-red absorption peak defined using pigment data • Solves for adg(λ) and aph(λ)	• Ca • Phaeophytin-a concentration	N
Lee et al. (2002)	• adg(λ) has fixed exponential slope, Sdg • Empirical relationship uses rrs(λ) to parameterize band ratio of aph(λ) • Solves for adg(λ) and aph(λ)	• None	Y
Ciotti and Bricaud (2006) Method 1	• adg(λ) assumed to be exponential • Empirical relationships uses Ca to parameterize band ratios of aph(λ) • Solves for Mdg, Sdg, adg(λ), and aph(λ) algebraically (Bricaud and Stramski 1990)	• Ca	Y
Ciotti and Bricaud (2006) Method 2	• adg(λ) assumed to be exponential • aph(λ) parameterized through mixing of pico- and microphytoplankton contributions (Ciotti et al. 2002) • Solves for Mdg, Sdg, Mph, and the size parameter of phytoplankton (Sf) via nonlinear optimization	• Ca	Y
Zheng and Stramski (2013b)	• adg(λ) assumed to be exponential • aph(λ) shape expressed through band ratios of 412:443 and 510:490 • Searches multiple speculative (feasible) solutions of Mdg, Sdg, adg(λ), and aph(λ) (Bricaud and Stramski 1990) • Computes candidate and selects optimal solution for adg(λ) and aph(λ) using stacked inequality contstraints	• Pre-determined bounds of inequality constraints	Y
Zhang et al. (2015)	• adg(λ) assumed to be exponential • aph(λ) parameterized as the sum of mixing of pico-, nano-, and microphytoplankton contributions • Solves for Mdg, Sdg, adg(λ), and aph(λ) including contributions of pico-, nano-, and microphytoplankton using constrained least-squares optimization	• Ca-specific a*ph(λ) for pico-, nano-, and microphytoplankton	N

Despite its convenience within the remote-sensing paradigm, combining a_nap(λ) and a_cdom(λ) into one term, a_dg(λ), has disadvantages when linking IOPs to ocean biogeochemical processes. NAP and CDOM can originate from different sources, are affected by different physical and biogeochemical processes and are associated with different pools and residence times in the ocean. In addition, NAP is assumed to contribute to scattering significantly while CDOM’s contribution is assumed negligible. As such, they cannot always be expected to demonstrate strong covariation in coastal or open ocean waters. Furthermore, while NAP and CDOM both show an exponential decrease in absorption with increasing wavelength, their spectral slopes are typically considerably different, with S_nap and S_cdom encompassing 0.005–0.015 nm^-1 and 0.01–0.03 nm^-1, respectively (Babin et al., 2003; Roesler et al., 1989; Tzortziou et al., 2007). Ultimately, retrieving S_cdom from satellite observations is desirable as it provides a reliable indicator of the source, molecular size, aromatic content and extent of photochemical versus microbial degradation of organic matter in aquatic environments (e.g. Blough & Green, 1995; Chin et al., 1994; Helms et al., 2008; Tzortziou et al., 2011). Similarly, retrieving S_nap may enable the relative proportions of mineral and organic matter to be determined (Babin et al., 2003). As such, effort has focused on the development of partitioning approaches to derive a_ph(λ) and separate a_dg(λ) into a_nap(λ) and a_cdom(λ) (Chang & Dickey, 1999; Claustre et al., 2000; Dong et al., 2013; Gallegos & Neale, 2002; Lin et al., 2013; Schofield et al., 2004; Zheng et al., 2015).

Similar to other categories of absorption partitioning models, methods developed to partition a(λ) into a_ph(λ), a_nap(λ), and a_cdom(λ) typically carry significant limitations associated with restrictive assumptions about model outputs, the use of ancillary input data, and region-specific parameterizations. Several models employ a single spectral shape or a linear combination of a small number of predefined spectral shapes for a*_ph(λ) (Devred et al., 2011; Gallegos & Neale, 2002; Schofield et al., 2004). Nearly all assume an exponential function for the spectral shapes of both a*_nap(λ) and a*_cdom(λ), in some cases with a fixed value for one of the two (Dong et al., 2013). Many use empirical parameterizations requiring input ancillary data, such as C_a (Claustre et al., 2000), R_rs(λ) and/or b_b (λ) (Dong et al., 2013), or even direct measurements of a_cdom(λ) (Chang & Dickey, 1999). Furthermore, most models in this category have features or parameterizations that reflect intended applicability only to specific regions or in situ measurements taken with specific instruments (Chang & Dickey, 1999; Claustre et al., 2000; Gallegos & Neale, 2002; Schofield et al., 2004; Zheng et al., 2015).

2.1.4.3. Particulate backscattering

The total backscattering coefficient of seawater, b_b(λ), is most commonly represented as a sum of only two components, the pure seawater backscattering coefficient free from particulate matter, b_bw(λ), and the particulate backscattering coefficient, b_bp(λ) (Eq. (13). The pure seawater component is assumed to be known a priori or predictable as described previously. Particulate backscattering is typically assumed to include the contributions from all kinds of suspended particles pooled together into a single particulate component, b_bp(λ). In some models, the particulate component has been further partitioned into two components such as organic and inorganic particle components (Bukata et al., 1995), large-sized and small-sized particle components (Roesler & Perry, 1995), and phytoplankton and NAP components (Brando et al., 2012) (Eq. (11).

Many IOP models adopt a power-law to describe the spectral shape of b*_bp(λ) (Gordon & Morel,1983; Morel & Prieur, 1977):

$$b_{bp}^{*}(\lambda )={\lambda }^{-S_{bp}},$$ (16)

where S_bp typically varies between 0 and 3, largely driven by varying proportions of large and small particles (Reynolds et al., 2016; Sathyendranath et al., 1989; Stramska et al., 2003). Note, this relationship is not exhaustively based on in situ or laboratory measurements and deserves systematic evaluation in the future. Stramska et al. (2003) and Reynolds et al. (2016) show in situ determinations of backscattering versus wavelength and the power function for these data. Based on b_bp(λ) values from 394 to 852 nm collected in the Arctic, Reynolds et al. (2016) reported the range of S_bp from 0.13 to 3.01 with the majority of data (80%) between 0.5 and 1.5, a median value of 1, and a mean value of 1.5. In some inverse models, the value of S_bp is treated as constant based on in situ measurements with values of 0.5 used in coastal waters and values of 1.0 for oceanic waters (Mobley, 1994). When r_rs(λ) are known, methods to estimate S_bp from r_rs(λ) or C_a also exist (Table 3). Roesler and Boss (2003) proposed an alternative approach that does not assume a power-law spectra for particulate backscattering, but rather assumes a spectrally constant particulate back-scattering ratio, $\tilde{b}(\lambda )=b_{bp}(\lambda )/b_p(\lambda )$ and a power-law spectral dependence for particulate beam attenuation, S_c (which is consistent with measurements):

$$b_{bp}(\lambda )=\tilde{b}(\lambda )\left[c_p\left({\lambda }_0\right){\left(\frac{\lambda }{{\lambda }_0}\right)}^{-S_c}-a_p(\lambda )\right]$$ (17)

where, λ₀ is a reference wavelength and c_p(λ)₀) is the particulate beam attenuation coefficient at λ₀. For a_p(λ), a priori assumptions about the spectral shape of the model output of particulate backscattering components can be highly restrictive, especially for application at arbitrary time and location within the global ocean. Loisel and Stramski (2000) developed an approach that does not require a priori assumptions about the spectral shape of output IOPs by providing solutions for b_b(λ) and a(λ) at different light wavelengths independently. The particulate component b_bp(λ) is calculated from b_b(λ) by subtracting the known or assumed values of b_bw(λ). Similarly, a_nw(λ) is calculated by subtracting the known or assumed values of a_w(λ) from a(λ). Loisel and Stramski (2000) provides one example where absorption components must be retrieved in a second step from the derived a_nw(λ), as described above.

Table 3:

Example methods for deriving normalized S_bp.

Method	Uses measured data (Y/N)	Input data required	Description
Morel and Maritorena (2001)	Y	Ca	• Sbp defined in terms of $\tilde{b}$
Gordon et al. (1988)	N	Ca	• Defines bp(λ) from Ca • Assumes $\tilde{b}$ = F(Ca)
Ciotti et al. (1999)	Y	Ca	• Logarithmic function from −2 where Ca = 0.05 mg m−3 to 0 where Ca = 20 mg m−3
Lee et al. (2002)	Y	rrs(λ)	• Empirical relationship
Roesler and Boss (2003)	N	$\tilde{b}$(λ), cp(λ), ap(λ)	• Solves for for bbp(λ) and Sc
Antoine et al. (2011)	Y	Ca or bb(555)	• Empirical relationship
Brewin et al. (2012)	N	Ca	• Empirical relationship for bbp(λ)

2.2. Solution methods

2.2.1. Semi-analytical inversion approaches

Semi-analytical inversion algorithms (SAAs) estimate marine IOPs from sensor-observed R_rs(λ) using a combination of empiricism and radiative transfer theory. SAAs attempt to simultaneously estimate the magnitudes of a_ph(λ), a_dg(λ), and b_bp(λ) (Brando et al., 2012; Brewin et al., 2015a; Bukata et al., 1995; Devred et al., 2006; Garver & Siegel, 1997; Hoge & Lyon, 1996; IOCCG, 2006; Maritorena et al., 2002; Roesler & Perry, 1995; Wang et al., 2005; Werdell et al., 2013a). These SAAs generally assign constant spectral values for a_w(λ) and b_bw(λ), parameterize the spectral dependency of the IOPs of non-water constituents (a*_ph(λ), a*_dg(λ), and b*_bp(λ) for all sensor bands in the VIS part of the spectrum, or at a few specific bands, and retrieve the magnitudes of these constituents (A_ph, A_dg, and B_bp). They primarily differ only in the assumptions employed to define component IOP spectral shapes (see Sections 2.1.4), the inverse relation between r_rs(λ) and IOPs (see Section 2.1.2), and the mathematical method applied to calculate the magnitude of the component IOPs.

Generally speaking, SAAs fall into four broad classes based on their solution method: (i) nonlinear spectral optimization, (ii) direct linear inversion, (iii) spectral deconvolution, and (iv) bulk inversion (Table 4). SAA methods (i) and (ii) use R_rs(λ) and normalized spectral shapes as inputs and estimate the amplitudes for absorption and backscattering components via linear or nonlinear least squares inversion of Eqs. (4) and (5). Roesler and Perry (1995), for example, used the nonlinear least-squares Levenberg-Marquardt optimization scheme. Hoge and Lyon (1996) later showed the problem could be linearized and, thus, directly solved by simple linear matrix inversion (single solution). The system is over-determined when the number of input R_rs(λ) wavelengths exceeds the number of unknowns, in which case the single solution obtained is the best in the least-square sense (Wang et al., 2005). These two classes best represent the simultaneous solution described as concept (A) in Section 2.1.4.

Table 4:

Example of semi-analytical solution classes used in ocean-color algorithms.

Class	Methodology	Example usage
Non-linear spectral optimization	Levenberg Marquardt	Roesler and Perry (1995) Garver and Siegel (1997) Maritorena et al. (2002)
	Nelder-Mead	Evers-King et al. (2014)
	Particle swarm	Slade et al. (2004)
	Genetic algorithm	Haigang et al. (2003)
	Simulated annealing	Salinas et al. (2007)
Direct linear inversion	Linear matrix inversion	Hoge and Lyon (1996) Wang et al. (2005)
Spectral deconvolution	Step-wise algebraic	Lee et al. (2002) Smyth et al. (2006) Pinkerton et al. (2006)
Bulk inversion	Step-wise algebraic solving for each wavelength independently	Loisel and Stramski (2000)
Ensemble inversion	Adaptive linear matrix inversion	Brando et al. (2012)

SAA method (iii), spectral deconvolution, assigns spectral shapes for some components and proceeds in a step-wise fashion to sequentially determine the component IOPs, unlike methods (i) and (ii) that iteratively run the forward model to find the optimal solution of the amplitudes. Examples of class (iii) are described in Lee et al. (2002) and Smyth et al. (2006). Note that SAAs in this class first determine total absorption and backscattering (unlike spectral optimization approaches) and, therefore, can be employed to explore multiple approaches to decompose a(λ) and b_bp(λ) into their component parts (for reference, path 2→3→4 in Fig. 1). A key difference between the spectral deconvolution and the other methods is that there is no residual difference between input and output R_rs(λ) spectra in the bulk inversion scheme, whereas residual differences between input and output R_rs(λ) spectra are inherent to the other inversion schemes (with the residuals used as performance metrics, see Section 4, or to assign spectral variations to retrieved absorption constituents not captured by input spectral shapes (Roesler & Perry, 1995). Accordingly, spectral deconvolution approaches are inherently sensitive to biases in sensorobserved R_rs(λ) data due to sensor miscalibration and/or sub-optimal AC.

Finally, SAAs in method class (iv), bulk inversions, do not assign shape-components – that is, they do not predefine spectral shapes for the absorption or backscattering coefficients when deriving the total absorption coefficients. The approach introduced in Loisel and Stramski (2000) is a widely used example. In practice, SAAs in this class determine IOPs at each wavelength independently and, therefore, can be used to calculate spectral shape functions (e.g., S_bp) dynamically. These SAAs, however, require additional assumptions and/or intermediate products, such as spectral diffuse attenuation coefficients of downwelling irradiance (K_d(λ); m^-1). Appendix A of Werdell et al. (2013a) provides a detailed discussion of these broad SAA classes.

An emerging generation of SAAs adopts ensemble approaches, employing either ranges of shape-components (Brando et al., 2012; Wang et al., 2005) or on-the-fly identification of optical water types, which can conceptually be used to assign corresponding shape-components (Moore et al., 2009; Vantrepotte et al., 2012). In the former, ranges of shape-components for unknown parameters are applied iteratively. The final unknown parameters are either calculated as the median of all valid values retrieved during the iteration, or selected from a range of retrievals based on threshold and/or best-fit metrics. In the latter, shape-components are dynamically assigned for each satellite pixel based on an environmental classification metric, thus minimizing assumptions that singular shape-components represent all water types and conditions at all times.

2.2.2. Look-up-table approaches

Look-up table (LUT) solution methods first use a forward model to generate a database of R_rs(λ) and/or L_t(λ). Each R_rs(λ) or L_t(λ) spectrum in the LUT corresponds to a unique combination of water column properties (IOPs and, if relevant, depth and seafloor reflectance) and atmospheric properties (if relevant, cloud cover, surface conditions, and sun geometry). The LUT is constructed by running a forward model (QSSA or RT) for each combination of parameters to be considered (Hedley et al., 2009; Liu & Miller, 2008; Mobley et al., 2005). The IOPs used in the forward modeling arise from either in situ datasets or are generated with bio-optical models using constituent-specific parameterizations, such as mass-specific properties at reference wavelengths and associated spectral shape functions (see Sections 2.1.3 and 2.1.4).

To derive IOPs, the sensor-observed R_rs(λ) or L_t(λ) for a given image pixel is compared with the spectra stored in the LUT. The LUT is searched until an entry or suite of entries is found that best match the sensor-observed spectrum. A best match is determined once the cost function (distance measure) achieves a pre-defined threshold, in a manner similar to spectral optimization. The returned IOP solution is defined as that which corresponds to the closest-matching forwardmodeled R_rs(λ) or L_t(λ) in the LUT. If the search returns a solution set – all spectra within a prescribed uncertainty tolerance, ε, of the measured spectrum – the solution might be computed as the average of all associated parameters consistent with the retrieved spectra. An advantage to this approach is that ε can be defined as a function of known sources of uncertainty, such as those associated with the remote sensor and data/parameterizations used to generate the database, and the divergence of the various consistent solutions can provide a measure of the uncertainty in retrieved IOPs. The cost function can be spectrally weighted to account for band-specific instrument noise and sensitivity to constituent variability.

Mobley et al. (2005) and Liu and Miller (2008) constructed RT-based LUTs using the commercial software HydroLight (Mobley & Sundman, 2008). Mobley et al. (2005) generated a LUT containing 41,591 spectra for various combinations of water constituent IOPs, bottom type reflectance, water depth, sun angle, wind speed, and sky conditions from their study region . The approach was developed for inverting airborne-based hyperspectral R_rs(λ) imagery to derive IOPs, seafloor type, and water-column depth without the need for in situ ancillary data. Liu and Miller (2008) used a C_a-based bio-optical model to parameterize IOPs and included inelastic scattering effects, resulting in a LUT with 22,575 individual spectra. Their LUT-derived IOPs compared well with both in situ and model-simulated hyperspectral data.

The LUT methodology offers several useful features. It does not require uniqueness of solution and can return a suite of solutions with which an estimate of uncertainty can be derived for each retrieved parameter. Inelastic processes can be easily incorporated in forward models, such as C_a and CDOM fluorescence if robust quantum efficiencies are well described. LUTs can be easily tuned to a region of interest based on known environmental conditions, thus reducing the required search space. While it is typical to assume vertical homogeneity within the water column, vertical structure can, in principle, be included. The LUT methodology also includes a number of limitations. The utility of the LUT requires accurate characterization of the IOPs and because limited analytic or empirical models (e.g., C_a-based IOP models) are used, the internal dependences may not reflect natural sources of variability and non-covariability. Generating the LUT with RT code can be computationally expensive, although this is generally an infrequent investment. Searching for solutions can also be computationally expensive. Even with limited sets of IOPs (e.g., ten a*(λ) or b*(λ), the number of spectra in the LUT database will be 100^m, where m is the number of different constituents. This burden can be eased somewhat using suitable LUT search algorithms and with improved computational power. Hedley et al. (2009), for example, dynamically constructed a LUT by adaptively constraining model runs to reduce the LUT size. Each sensor-observed R_rs(λ) is projected onto principle component space and passed through a binary decision tree until it is optimally matched with similar spectra. Hedley et al. (2009) found this approach to be computationally comparable to spectrum matching approaches (c.f. SAA class (i) methods), such as Levenberg-Marquardt nonlinear optimization.

2.2.3. Empirical approaches

Empirical algorithms derive IOPs from some predictor variable(s), typically sensor-observed R_rs(λ) or derived parameters (e.g. C_a), using a large data set derived from in situ observations or AOP/IOP datasets synthesized using RT modeling. Most approaches follow statistical methods including, but not limited to, univariate polynomial regression (Lee et al., 1998b), multiple linear regression (MLR) (Mannino et al., 2014), principal component regression (PCR) (Craig et al., 2012), and machine learning algorithms (Chang, 2015; Doerffer & Schiller, 2007; Ioannou et al., 2011; Jamet et al., 2012). While these approaches diverge from the RT and QSSA methods and spectral shape parameterizations presented to this point, their inclusion in this review remains relevant as they provide viable methods for deriving IOPs from satellite ocean color radiometry.

Several univariate empirical models relate an IOP to C_a using both linear and non-linear regression methods (Bricaud et al., 1995; Gordon & Morel, 1983; Huot et al., 2008; Loisel & Morel, 1998; Morel, 1988). While these methods are useful for oceanic waters where phytoplankton dominate the in-water optical field, they can be confounded in optically complex waters with elevated CDOM and high inorganic particle loads. Univariate methods also exist that predict IOPs as a function of R_rs(λ) (Lee et al., 1998b; Stramska et al., 2003; Stramski et al., 1999). The empirical model developed by Lee et al. (1998b), for example, relates the total absorption coefficient at a green or red reference wavelength to a r_rs(λ) band ratio via polynomial regression. This model initiates the quasi-analytical algorithm (QAA, the SAA class (iii) inversion scheme of Lee et al. (2002). It is important to recognize that such empirical relationships often form the base of the spectral shape parameterizations presented in Section 2.1.4, such as Eq. (15) and the contents of Tables 1 and 3, and thereby inherently reside within the some of the SAA and LUT inversion methods reviewed above.

MLR models allow IOPs to be derived from sets of multiple predictors, for example, absolute R_rs(λ) values, R_rs(λ) differences, and/or R_rs(λ) ratios. Mannino et al. (2014) and Cao et al. (2018), for example, demonstrated an MLR that effectively derived a_cdom(λ) and S_cdom from R_rs(λ). MLRs, however, become unstable when the set of predictor variables exhibits co-linearity (that is, one or more of the predictor variables are highly correlated). To address this, a data reduction method is often employed to decrease the number of variables used in the model. Mannino et al. (2014) used a stepwise backward approach and reduced the number of input R_rs(λ) from five to two. Other approaches, such as principal component analysis (PCA; an orthogonal linear transform, also known as empirical orthogonal function (EOF) analysis (Preisendorfer & Mobley, 1988), can also be used to reduce dimensionality of the predictor variable set without an appreciable loss of information (Barnes et al., 2014; Craig et al., 2012; Soja-Woźniak et al., 2017).

Using principal component regression (PCR; a combination of PCA and MLR), Craig et al. (2012) developed an algorithm for deriving C_a and a_ph(λ) from R_rs(λ) in optically complex waters. The first four PCs were used in an MLR model as they cumulatively explained over 99% of variance in the R_rs(λ) predictor dataset. Similarly, Fichot et al. (2008) and Cao et al. (2014) used a PCR model to retrieve K_d(λ) in the range 320–490 nm from multi-spectral R_rs(λ) for a variety of water bodies ranging from oligotrophic to turbid estuarine systems. Barnes et al. (2014) used PCR to derive K_d(λ) in the UV from satellite-observed R_rs(λ) in optically shallow reef waters. Thus far, the limitation of PCA-based approaches appears to be reliance on training with region-specific data in order to perform optimally. One might also argue that PCR approaches are not mechanistic. Careful interpretation of the spectral behavior of the principal component (PC) loadings, however, can reveal coherent features that are clearly related to absorption, fluorescence, and scattering processes (Craig et al., 2012; Fichot et al., 2008; Soja-Woźniak et al., 2017). Barnes et al. (2014) noted that PCs that cumulatively explain the bulk of the variance in the predictor dataset do not always serve as the best predictor variables but they can be used to identify important physical or biological driving forces a posteriori. They proposed that consideration of all PCs during MLR development and their reduction through suitable variable selection procedures (for example, stepwise forward addition) may be more robust.

Advanced machine learning methods exist to derive IOPs, including artificial neural networks (D'Alimonte et al., 2012; Doerffer & Schiller, 2007; Ioannou et al., 2011; Ioannou et al., 2013; Tanaka et al., 2004) and gene expression programming (Chang, 2015). Artificial neural networks (ANNs) have shown promise for retrieving K_d(λ), constituent matter concentrations (C_a and NAP), and a_cdom(λ) (Chen et al., 2014a; D'Alimonte et al., 2012; Doerffer & Schiller, 2007; Dzwonkowski & Yan, 2005; Schiller & Doerffer, 1999; Tanaka et al., 2004)). ANN approaches also exist solely for deriving IOPs (Chen et al., 2014b; Chen et al., 2015; Ioannou et al., 2011; Ioannou et al., 2013). Krasnopolsky and Schiller (2003) recommended training two ANNs that act as forward and inverse models, respectively. By employing the forward and inverse ANNs in concert, an ANN-based algorithm can then dynamically assess its retrieval skill and flag poor quality values (Doerffer & Schiller, 2007). Ioannou et al. (2011) demonstrated an ANN-based approach using independent validation data and benchmarking with the SAAs of Lee et al. (2002) and Maritorena et al. (2002). They also demonstrated ANN handling of noise (10–20%) in the input R_rs(λ) dataset without compromised performance. Like all empirical approaches, however, machine learning methods require a large R_rs(λ)/IOP training dataset (order of 1,000 records per Ioannou et al. (2011) and order of 100,000 records per Doerffer and Schiller (2007) that spans a wide range of optical conditions. Accordingly, ANN approaches are often tuned and applied regionally (D'Alimonte et al., 2012; Doerffer & Schiller, 2007); however, through the appropriate use of RT modeling and/or in situ datasets, the development of globally-applicable ANN-based algorithms has been demonstrated (Chen et al., 2014b; Ioannou et al., 2011).

3. Sources and derivation of uncertainties

3.1. IOP measurement uncertainties

In situ and laboratory measurements of IOPs are used to develop and refine algorithms and to assess their performance. For algorithm development, IOP measurement uncertainties, and any associated assumptions required where IOP measurements are lacking, propagate directly into the algorithms. For performance assessment, IOP measurement uncertainties must be considered to isolate satellite instrument performance, along with uncertainties in the radiometric measurements serving as algorithm input. This section briefly summarizes known uncertainties in and limitations of relevant IOP measurements and their potential impacts on remote-sensing algorithms and products. The NASA Ocean Optics Protocol series (https://oceancolor.gsfc.nasa.gov/docs/technical) has far greater detail on this subject. In general, availability of more than one technology to measure a parameter (e.g. instrumental closure) may improve estimates of the true uncertainty associated with a parameter of interest.

3.1.1. In situ absorption, attenuation, and total scattering measurements

The community standard approach for measuring in situ a(λ) and c(λ) for the last twenty years has been WET Labs ac meters (Twardowski et al., 1999; Zaneveld et al., 1992). These instruments have two flow tubes, typically 0.25 m in length, with the a(λ) tube having a reflective quartz sleeve and the c(λ) tube having a non-reflective matt black finish. Total scattering is then calculated as $b(\lambda )=c(\lambda )-a(\lambda )$. Measurements made with ac meters have associated uncertainties due to their inability to measure exactly these parameters (e.g., finite acceptance angle, inability to collect all the scattered light), the effect of flow in and around each flow tube that possibly disrupts/disaggregates and reorients particles, random electronic noise, and bias errors due to factors such as calibration uncertainty.

All ac meters require periodic calibration to some reference medium, typically purified water, to track drift. With careful attention to instrument protocols and repetition in calibrations, uncertainties of 0.005 to 0.01 m^-1 and 0.01 to 0.015 m^-1 are achievable for absorption and attenuation, respectively. Note that these values vary spectrally, with the largest uncertainties near 400 nm. Instrument drift remains of particular concern when working in clear waters, where calibrations are carried out daily to ensure data quality. Absorption and attenuation measurements also require correction for the dependence of pure water absorption on T and S in the NIR (Pegau et al., 1997; Sullivan et al., 2006). Because these corrections can be significant, associated uncertainties in a(λ) and c(λ) are expected to be greater in the NIR relative to the VIS.

An ongoing area of research focuses on quantifying the correction for the reflective flow tube for a(λ) that does not direct all scattered light towards a diffuse director, and can be of order 30–50% of the derived absorption coefficient (Stockley et al. 2017). Zaneveld et al. (1994) suggested several approaches for this scattering correction, all with assumptions and associated uncertainties. Their baseline correction, traditionally applied to bench-top spectrophotometers, subtracts the NIR offset, which assumes that scattering does not vary spectrally. Their proportional correction incorporates the observed spectral scattering variability and assumes a spectrally constant ratio of the scattering correction to an approximation of total scattering. Both corrections also assume null absorption in the NIR, which does not follow many recent observations in areas where NAP concentrations are significant (Babin & Stramski, 2004; Bowers & Binding, 2006; McKee et al., 2013; Rottgers et al., 2014; Röttgers & Gehnke, 2012; Stramski et al. 2004b; Stramski et al., 2007;Tassan & Ferrari, 1995; Tassan & Ferrari, 2003) leading to approaches that assume some fraction of the NIR signal is due to absorption.

3.1.2. Laboratory absorption measurements

Absorption measurement of discrete samples is performed using bench-top spectrophotometers. These instruments typically lack the sophisticated optics of the ac meters (i.e., collimated beams, reflective tubes, detector-side diffusers) and have 10-cm maximal cuvette pathlengths. In dilute ocean waters, this necessitates concentration of particulate matter, while in more complex waters, scattering by suspended particulates leads to substantially overestimated absorption estimates. Since the 1980s, the traditional approach has been to concentrate the particulate matter onto filters and measure directly in the spectrophotometer in transmission mode (Kiefer & SooHoo, 1982). The advantage of filtering samples, aside from concentrating particulate matter, is the separation of the absorbing components. The filtration separates CDOM from the particulate matter. CDOM absorption can be accurately measured in a cuvette due to the negligible scattering. Particulate matter absorption can be measured directly on the filter.

Glass fiber filters are the standard as they have a small nominal pore size (0.7 μm for Whatman GF/F, the recommended brand and model) and a relatively spectrally flat spectrophotometric signature, with relatively low uncertainty (Roesler, 1998; Stramski et al., 2015). The highly scattering glass fibers significantly increase the optical pathlength, increasing substantially the signal to noise. This effect can be corrected using a pathlength amplification factor, β, determined using a variety of empirical approaches based upon paired measurements in suspensions and on filters (Allali et al., 1997; Arbones et al., 1996; Bricaud & Stramski, 1990; Cleveland & Weidemann, 1993; Finkel & Irwin, 2001; Lohrenz, 2000; Mitchell, 1990; Moore et al., 1995; Nelson et al., 1998; Stramska et al., 2003; Tassan & Ferrari, 1995). The lack of consensus in β results from the suspension measurements used to construct the correction being prone themselves to scattering errors similar to those in the ac meters, but with less information for correction. Recent progress has been made to better constrain β (Lefering et al., 2016; Röttgers & Gehnke, 2012; Stramski et al., 2015). Stramski et al. (2015), for example, provide a protocol for measuring absorption by placing the filter inside a large diameter commerciallyavailable integrating sphere (Labsphere, Inc), which optimizes the collection of scattered light by the glass fiber filter over the traditional transmission mode measurements. The dual beam configuration allows the absorption by the directly transmitted beam to be separated from the absorption by beams scattered by the sphere. At present, β remains quantified for the VIS range only, and preliminary analysis of the UV region suggests large uncertainties due to the combination of one or more of the following: weak lamp strength, weak detection capabilities, and strong absorption by the integrating sphere itself and the glass fiber filters, as well as possible instability of the particulate absorption signal in the UV over short temporal scales. The analysis in the UV remains an active area of investigation.

The filter pad approach also offers a capability for separating the particulate absorption into contributions by phytoplankton and NAP. Kishino et al. (1985) proposed the method of measuring the particulate sample, then returning the filter pad to the filtration cup and gently adding methanol to extract the pigments from the cell, filtering the methanol through and rinsing gently with filtered seawater to remove the methanol. The remaining material is the nonpigmented particulate matter, NAP, which is then scanned again. After correction for pathlength amplification (which will be different for the particulate and NAP scans), the phytoplankton absorption is calculated by difference. The more accurate description of this component is the absorption by phytoplankton pigments in vivo as the NAP does include the non-pigmented phytoplankton cellular material. Samples with phycobilipigments such as phycoerithrin require an additional treatment with hot water or phosphate buffer (Roesler & Perry, 1995) or buffered Milli-Q water (Sobiechowska-Sasim et al., 2014) to extract the water-soluble pigments. Oxidation with bleach is another approach (Doucha & Kubin, 1976; Ferrari & Tassan, 1999; Röttgers & Gehnke, 2012), although rather than removing the pigments from the sample, the oxidized pigment molecules remain on the filter and their absorption shifts to the far blue and UV portion of the spectrum, and thus should be used with caution. Some investigators have also explored the separation of the NAP into organic and inorganic components using combustion or chemical oxidation (Estapa & Mayer, 2010; Werdell & Roesler, 2003). The efficacy remains elusive because the treatment impacts the absorbing material and because the inorganic particles often have an organic coating. When that coating is removed, the underlying mineral absorption properties are revealed but, in this case, the sum of the components is not conserved.

Uncertainties associated with the spectrophotometric approach vary between instruments, but for a quality dual beam benchtop model, absorbance resolution is of order 10^-4, which translates into a signal to noise ratio of about 10³. To avoid self-shading and multiple scattering, target absorbances should fall between ~0.1 and ~0.4 (van de Hulst, 1957), which may require the use of multiple cuvette pathlengths or filter volumes over the UV-VIS range. Generally speaking, filters should not be overloaded such that absorbance exceeds 0.4 to avoid artifacts associated with self-shading (and additional enhancement of multiple scattering). In contrast, with regard to spectrophotometric measurements on suspension, absorbances measured in the beam attenuation configuration should remain generally below ~0.13 to keep the optical thickness (the product of beam attenuation and pathlength) below 0.3 (i.e., the single scattering regime) (Mitchell et al., 2003). The variability associated with the filter pad measurement includes filter-to-filter variations, pathlength amplification uncertainties, and sample handling uncertainties. Furthermore, the associated uncertainties for replicate samples far exceed the instrument resolution and are typically of order a few percent. It should also be noted that the sample condition can yield higher uncertainties due to uneven distribution of material on the filter. This is often due to gelatinous or polysaccharides in the sample. In such cases, multiple readings per filter and replicate filters are required to reduce uncertainties.

3.1.3. VSF and backscattering measurements

The coefficients b(λ) and b_b(λ) can be computed from VSF measurements via straightforward integration, however, only several prototype sensors capable of VSF measurements over broad angular ranges exist (e.g. Chami et al., 2014; Harmel et al., 2016; Lee & Lewis, 2003; Twardowski et al., 2012). The Multi Angle Scattering Optical Tool (MASCOT), calibrated with NIST-traceable micro spherical beads and measuring the VSF in 10° increments from 10° to 170° relative to the incident beam, has demonstrated uncertainties of ≤2% at each angle and ~1% for integrated b_b(λ) (Sullivan et al., 2013; Twardowski et al., 2012). The Multispectral Volume Scattering Meter (MVSM) (Berthon et al., 2007; Lee & Lewis, 2003; Zhang et al., 2012) measures the VSF with an angular resolution of 0.25° from 0.5 to 179° at eight wavelengths. The MVSM and the MASCOT can be used with the Sequoia Scientific LISST-100X that measures the VSF at 532 nm from 0.07° to 13.9° (e.g. Slade & Boss, 2006). The combination of the measurements by these two instrument forms a more complete angular resolution of the VSF at 532 nm and inter-instrument comparisons shows agreement to within 10% in both forward and backward angles (Zhang & Gray, 2015). At the time of this writing, the new Sequoia Scientific LISST-VSF had not been fully characterized.

The WET Labs ECO-BB and HOBI Labs Hydroscat instruments provide commercially available spectral backscattering sensors that make a VSF measurement with broad angular weighting at a single fixed geometry (the ECO-BB has a centroid angle of 124° and the Hydroscat has a centroid angle of 140°). In addition, WET Labs ECO-VSF sensors make a VSF measurement at several fixed geometries (centroid angles at 104°, 131°, and 150°). Estimation of b_b(λ) from these instruments requires a conversion coefficient, χ, that is specific to each angular measurement geometry (Sullivan et al., 2013). Historical χ factors have been based on both modeled and/or measured VSF shape analyses that effectively assume a single constant, representative shape for natural waters (Berthon et al., 2007; Boss & Pegau, 2001; Chami et al., 2006; Maffione & Dana, 1997; Oishi, 1990; Sullivan & Twardowski, 2009; Zhang et al., 2014). Typically, derivations of χ adopt a spectrally independent VSF shape in the backward direction. This assumption has been examined both theoretically and experimentally, where in many cases, the shape has been found to be spectrally independent within measurement uncertainties (e.g. Berthon et al., 2007; Boss & Pegau, 2001; Maffione & Dana, 1997; Mobley et al., 2002; Twardowski et al., 2001; Ulloa et al., 1994; Vaillancourt et al., 2004; Whitmire et al., 2007; Whitmire et al., 2010). That said, the conditions for applicability of this assumption remain under active investigation (Chami et al., 2006; Harmel et al., 2016; Jonasz & Fournier, 2007; Sullivan & Twardowski, 2009; Zhang et al., 2014; Zhang et al., 2017). Current estimation of uncertainties associated with applying χ to derive b_b(λ) range from 1–2% when the geometry of the VSF measurement is well known and the centroid of the measurement is near 120° (Sullivan et al., 2013). After calibration with NIST-traceable micro-spherical beads and analytical derivation of angular weighting functions, WET Labs ECO sensors show total estimated uncertainties of ≤5% (Sullivan et al., 2013), whereas HOBI Labs (Bellevue, WA) Hydroscat sensors are calibrated using a Spectralon plaque and with similar estimated uncertainties. Instrumental closure between a Hydroscat and a Wet Labs ECO-VSF showed differences < 2% (Boss et al., 2004). A recent comparison of three WET Labs single angle backscattering sensors (ECO-FLBB, ECO-BB and MCOMS) deployed on hundreds of profiling floats, however, found consistent differences of up to 30%, which is inconsistent with the above discussion (Poteau et al., 2017). At the time of this writing, this discrepancy results from the manufacturer applying the wrong calibration constant, with steps underway to provide a remedy (A. Barnard, WET Labs, personal communication).

All scattering sensors suffer from attenuation along the path. A correction is typically warranted when the pathlength between source, sample volume, and receiver exceeds several cm (Sullivan et al., 2013; Twardowski et al., 2012). For WET Labs ECO sensors, this correction is <1% when absorption (including water) is <0.5 m^-1. For the Hydroscat, which has a pathlength of 0.15 m, the correction is ~50% when c is 1 m^-1. Doxaran et al. (2016) provides additional analysis of this problem and improved correction methods.

3.1.4. Pure seawater measurements

Backscattering by pure seawater is often considered to be constant and well-known in remote sensing algorithms (IOCCG, 2006) and common practice for several decades has been to use a constant pure seawater backscattering spectra originating from Morel (1974). As described in Section 2.1.4.1, Zhang et al. (2009) provides the most recent theoretical description of pure seawater scattering as a function of the physical properties of water with variables of T, S, and pressure. The physical constants in the calculations are all known with excellent precision (<0.1%), with the exception of the depolarization ratio. The currently recommended value for this parameter is 0.039 from measurements by Farinato and Rowell (1976). Pure water scattering in the blue decreases by more than 10% when using a value of 0.039 relative to the value of 0.09 used by Morel (1974). The Zhang and Hu (2009) computations of pure water scattering with a value of 0.039 produce volume scattering functions that match experimental measurements by Morel (1968) within 2% (Jonasz & Fournier, 2007). Nonetheless, this important parameter deserves additional experimental evaluation to further reduce uncertainties in pure water scattering values.

To date, Mason et al. (2016) provides the most recent laboratory measurements of pure water absorption in the UV and VIS domain. These values are much lower than previously measured in the UV (Pope & Fry, 1997; Smith & Baker, 1981). Lee et al. (2015) derived higher values for seawater in the UV, which possibly result from contributing UV absorption by dissolved inorganic constituents in seawater. Lee et al. (2015) derived their values via analytical inversion of a remote sensing reflectance inversion model, in lieu of direct experimental measurement. Given the lack of closure amongst the varied methods, additional research is necessary to understand the effects of dissolved inorganic substances in the UV and associated uncertainties.

3.1.5. In situ sampling

Assessment of how well in situ observations compare with remotely sensed observations must include uncertainties associated with sampling a dynamic environment with multiple scales of variability. Temporally, it is rare for in situ observations to be made simultaneously with remote measurements. Following, any temporal offset must at least consider the time scales of environmental change to address how conditions imaged at time t_a compare with the water mass that was observed at time t_b when t_a ≠ t_b. In dynamic coastal environments, uncertainties can grow rapidly as Δt=t_b-t_a increases and will scale with both advective velocities and spatial variability. Likewise, uncertainties are also associated with observations made at dissimilar spatial scales, both horizontally and vertically. Horizontally, discrete water samples and in situ optical measurements may represent conditions at a point location representing O(1 m²) (depending how long the water was sampled and advective velocities), whereas sensor-observed R_rs(λ), even if measured simultaneously, is a vertically integrated value averaged laterally across the ground sampling distance (GSD) of the system (1 km², for example, in the cases of SeaWIFS and PACE). Vertically, discrete samples of IOPs, C_a, or parameters related to phytoplankton community composition collected at only one or few depths in the upper optical depth prohibit reconstruction and true representation of the full optically-weighted signal observed by the satellite (Gordon & Clark, 1980; Smith, 1981; Zaneveld, 1995). Optical depths vary spectrally such that satellite retrieved spectral absorption comes from different optical depths – and, thus, phytoplankton and particle populations – suggesting that satellite algorithm development and data product validation activities benefit from (and are better informed by) continuous depth resolved measurements (Werdell & Bailey, 2005; Werdell et al., 2014).

Temporal scales of variability in the open ocean are dominated by biological dynamics (e.g., phytoplankton production and loss processes), as well as physical dynamics (e.g. mixed-layer dynamics, horizontal stretching, folding, and mixing). During the day, when passive remote sensing is possible, near-surface C_a, a(λ), and b_b(λ) can change by as much as a factor of two (Siegel et al., 1989; Dickey et al., 1991). Within shallow coastal waters where R_rs(λ) is often dominated by non-living, organic and inorganic particles, temporal scales of variability in these biological and optical properties are typically minutes to hours as the result of advection by changing tidal currents, suspension of bottom sediments by waves and currents, and land-ocean exchanges of optically-important materials. In the vertical direction, stratification in the concentration and composition of near-surface optical constituents with depth is common within shallow coastal waters in association with current and wave suspension of bottom sediments, thin, sub-surface biological layers, and buoyant plumes. If the gradients are large enough and close enough to the surface, they affect R_rs(λ) as observed by ocean color sensors (Andre, 2002; Petrenko et al., 1998; Yang et al., 2013).

While it is impossible to remove all sampling uncertainty, uncertainties can be minimized with sampling approaches devised with understanding of the sources and magnitudes of environmental variability. Understanding the statistics of the underlying parameter (e.g. its probability distribution) in space and time can provide guidance as to how uncertainties are reduced when aggregating independent matchups (e.g. can the simple 1/N^1/2 decrease in the standard error of the mean apply, with N being the number of independent match-ups). Knowledge of such variability suggests that minimizing sampling uncertainty requires collection of in situ observations as close to the time of the remote observations as possible and at spatial scales that resolve sub-pixel variability and depth scales to resolve the exponentially-weighted IOPs over spectrally varying optical depths. Acknowledging that temporal and spatial variability are correlated through advection, spatial uncertainty associated with sub-pixel variability can be reduced by increasing the number of sub-pixel observations in space or time (Moses et al., 2016; Werdell et al., 2013b).

3.1.6. Closure between measured IOPs and R_rs(λ)

Understanding the quality of measured IOPs and AOPs is often accomplished through RT-in situ closure experiments. These closure experiments are conducted by using in situ IOPs as input into a RT model that simulates AOPs. RT-modeled AOPs are then compared to in situ AOPs to see how well they agree. The degree of agreement in closure exercises is typically quantified using metrics such as the coefficient of determination, root mean square difference, absolute difference and root mean square relative difference at a few wavelengths (Tonizzo et al., 2017). All components of the closure exercise have uncertainties – the IOPs and AOPs suffer from measurement error (as described above), while the RT model has assumptions, typically regarding IOPs not directly measured (e.g., VSF), horizontal homogeneity, inelastic scattering contributions, sky/sun models, the air-sea interface, and polarization effects (as described in Section 2.1). Despite these caveats, when performing careful measurements and understanding the impacts of various assumptions, it remains possible to obtain closure (often within 20–30%) and use such an exercise to evaluate biases introduced by different measurement methods (Lefering et al., 2016; Mobley et al., 2002; Tonizzo et al., 2017; Tzortziou et al., 2006; Werdell et al., 2014).

3.2. Uncertainties in derived IOPs

Characterization of errors and uncertainties associated with ocean color products allows endusers to determine if the derived product is fit-for-purpose. Uncertainty estimates are key to interpretation of higher level modeling efforts that incorporate ocean color products (e.g., primary production and data assimilation in ecosystem or biogeochemical models) (Gould et al., 2014; Sheng et al., 2014). This requires complete documentation of uncertainties associated with an IOP product and their method of determination on a pixel-by-pixel basis. Satellite-to-in situ analyses provide one suitable way to characterize the uncertainty of derived IOP products (Bailey & Werdell, 2006). These matchup analyses, however, provide only a general estimate of IOP algorithm uncertainty, remain limited to coverage by the existing at-sea optics sampling platforms (ships of opportunity, buoys, floats, and gliders), and do not adequately resolve variability in either time or space (Valente et al., 2016; Werdell & Bailey, 2005).

Errors and uncertainties in derived IOP products mainly result from three sources: (i) uncertainties in input R_rs(λ) data due to sensor noise and atmospheric correction error; (ii) the forward model used, its general formulation and parameterization, and the assumptions and approximations it carries; and, (iii) the inverse solution method used (IOCCG, 2006; Werdell et al., 2013a). In theory, these factors should be collectively considered when deriving error estimates, but it is generally difficult to do so in practice. Several approaches exist for generating uncertainty estimates for various ocean color products, including IOPs (Mélin & Franz, 2014; Salama et al., 2012). Algebraic error propagation analysis provides one way to assess model sensitivity and quantify uncertainties in IOPs (Lee et al., 2010; Neukermans et al., 2014; Neukermans et al., 2009). Lee et al. (2010), for example, estimated how uncertainty in an early stage of the QAA algebraic algorithm propagates to IOP components derived in subsequent steps of the algorithm, thereby assessing how uncertainties in specific model parameters (e.g., S_bp and S_dg) influence the accuracy of derived absorption components. Conceptually, the propagation of radiometric uncertainty could be accomplished analytically for ocean color AC as well, however, this requires the difficult characterization of uncertainties in ancillary input data and for all of the major steps of data processing (Mobley et al., 2016).

Spectral matching inversion models often provide uncertainties estimated from gradient-based methods. Non-linear least squares inversions use matrix algebra to combine information about how small changes in the best-fit retrieved IOP parameters affect the forward modeled R_rs(λ) and ultimately derive the standard error of the retrieved products from the covariance matrix (Bates & Watts, 1988; Press et al., 1992). This gradient-based approach is used in several ocean color SAAs that derive IOPs (Maritorena et al., 2010; Maritorena & Siegel, 2005; Salama et al., 2009; Van Der Woerd & Pasterkamp, 2008; Werdell et al., 2013a). In addition, Salama et al. (2011) developed a gradient-based approach for estimating uncertainties associated with varying the inverse model parameterization without the need for performing an inversion. Some non-linear curve fitting techniques can also account for the uncertainties in the observed reflectance (if known; see Maritorena et al. (2010). It is important to recognize that uncertainty estimates from non-linear least square generally rely on the difference between observed and modeled reflectance and are thus influenced by the forward reflectance model approximations and parameterization. Gradient-based methods do not handle uncertainties due to sensor noise and/or AC error (Salama et al., 2011). It has also been shown that gradient-based uncertainty estimates tend to be proportional to the magnitude of the retrieved variables (Maritorena & Siegel, 2005; Salama et al., 2009).

Ensemble-type methods (e.g., Monte Carlo) provide another technique for estimating IOP uncertainties. In this approach, each AOP input and/or the inverse model parameterization is perturbed m times, with a set of m candidate IOP solutions returned. The IOP solution and its uncertainty are derived from the distribution of candidates. Using this approach, Wang et al. (2005) computed the absolute uncertainty of IOPs apportioned to noise in the input R_rs(λ) data. Median IOPs and their associated uncertainties were then computed from a subset of the ensemble capable of reproducing the input R_rs(λ) throughout the spectrum within a defined range. Similarly, Schiller and Doerffer (1999) and Salama (2012) used ensemble-based approaches to quantify IOP uncertainties in ANNs and stochastic inverse IOP models, respectively. While a powerful tool for estimating uncertainties in derived IOPs, ensemble methods are computationally expensive, often requiring thousands of perturbations per pixel, and often do not account for correlative errors between variables. Ensemble-based approaches also make assumptions about noise characteristics of sensor-observed R_rs(λ) (e.g., ranges, statistical distributions, and spectral correlations) that may not always be appropriate for all conditions at all times.

Other approaches have been developed for estimating uncertainties in R_rs(λ) and/or C_a that could be extended to IOP retrieval models (Frouin & Pelletier, 2015; Mélin et al., 2010; Mélin et al., 2016; Moore et al., 2009; Moore et al., 2015). The approach of Moore et al. (2009) can be used to assign an uncertainty value to each pixel of a product (e.g., C_a) derived from R_rs(λ). For each R_rs(λ) spectra, a fuzzy classification scheme assigns a fractional membership corresponding to each of the predefined optical classes that allows for non-discrete uncertainty estimates when the matchup statistics are applied. This method is model-independent and can be applied to virtually any ocean color product; however, it is limited by the quantity and representativeness of matchup data available. Frouin and Pelletier (2015) used a Bayesian approach to predict R_rs(λ) from L_t(λ), which can conceptually be extended to IOPs. A Bayesian inverse modeling approach allows the definition of a confidence domain of the predicted quantity and as such, in the particular case of ocean color remote sensing, can provide a measure of its uncertainty at each pixel. Uncertainties associated with C_a or R_rs(λ) have also been assessed by comparing the coincident daily data records from pairs of sensors (Mélin et al., 2010; Mélin et al., 2016). This co-location approach characterizes uncertainties associated with random effects and can be used either with a particular sensor serving as the reference or by treating each sensor equally. The approach enables IOP uncertainties to be spatially resolved for pairs of sensors, but has not yet been applied to evaluate its ability to assess temporal variations of uncertainties, particularly over short time scales for which only few satellite-to-in situ pairs are available.

4. Performance Metrics

Recognizing the current influx of algorithms into the community, the forthcoming need to develop enhanced approaches that exploit new instruments’ characteristics, and the varied portabilities of globally parameterized algorithms to specific regions, development and implementation of rigorous metrics to assess algorithm performance is essential. Broadly speaking, the choice of algorithm often depends on: (i) precision and dynamic range requirements that dictate the repeatability and distributions of desired retrievals; (ii) biases, imposed most often by the applicability of algorithm parameterizations and training data sets (and their sizes and broad representativeness) to specific regions of interest; (iii) robustness, defined by spatial and temporal stability, frequency of invalid retrievals and uncertainty requirements; and, (iv) the computational efficiency of an algorithm and computational resources available. Deep discussions related to algorithm selection for particular applications or specific statistical metrics for use in algorithm comparisons exceed the scope of this review (we refer the reader to Brewin et al. (2015b); however, several features of contemporary inverse IOP models that are typically overlooked or minimized in algorithm evaluation activities merit presentation in the context of this review. They include algorithm internal consistency metrics, internallyapplied geophysical restraints, and data transformations.

Internal consistency verifications exist to assess the quality of derived IOPs once an algorithm returns a solution. Comparisons of model-derived remote-sensing reflectances, R_rs^mod(λ) – those remote-sensing reflectances calculated using the forward model with the derived IOPs as inputs – with the sensor-observed remote-sensing reflectances, R_rs^obs(λ), provide a similarity metric that is commonly embedded within an algorithm. When the computed distance measure falls below some predefined tolerance, the R_rs^mod(λ) and R_rs^obs(λ) are deemed suitably similar and the algorithm reports the computed IOPs. This process is akin to in situ closure experiments, discussed in Section 3.1.6. Boss and Roesler (2006) and Werdell et al. (2013a) assessed algorithm closure in this manner by computing their absolute percent relative difference:

$$\Delta R_{rs}(\lambda )=100\%\frac{\left|R_{rs}^{mod}(\lambda )-R_{rs}^{obs}(\lambda )\right|}{R_{rs}^{obs}(\lambda )}$$ (18)

These authors considered internal consistency achieved when the ΔR_rs fell below a predefined value over a predefined wavelength range. Boss and Roesler (2006) used 10% for any band within the wavelength range 400–555 nm and Werdell et al. (2013a) used 33% for the average ΔR_rs for all wavelengths within 400–670 nm (the current NASA implementation of Werdell et al. (2013a) uses 400–600 nm). These algorithms return a non-solution when the value of ΔR_rs exceeds their threshold values. Note that several alternatively suitable distance measures exist, including the Euclidean distance, Chi square distance, root mean square error, and relative root mean squared error (Brando et al., 2012; Brewin et al., 2015b; Hedley et al., 2009). In general, errors result from residual biases, not normally distributed random error, so non-parametric metrics should also be explored. They are also, in general, less sensitive to outliers compared to parametric distance measures and do not assume a probability distribution of R_rs. Note also that internal consistency verification does not directly apply to, nor is possible for, all algorithms, such as Lee et al. (2002) and others in the spectral deconvolution class defined in Section 2.2.1.

Standard satellite data processing provides another series of internal verifications through quality flags, such as the l2_flags product reported by the NASA SeaWiFS Data Analysis System (SeaDAS; https://seadas.gsfc.nasa.gov). During routine processing, a pixel is considered of poor quality if one or more key flags are activated by algorithm failure or the presence of, for example, clouds, ice, land, saturated radiances, or straylight (Robinson et al., 2003).

Even with suitable internal algorithm closure, IOPs with unrealistic or non-physical values may be returned as a solution given that the inversion is mathematically ill-posed. Inspection of derived IOP ranges counters this to ensure they fall within a suitably realistic range that is consistent with known natural variability. Werdell et al. (2013a), for example, applied a series of inequality constraints after the non-water IOP solutions have been derived, specifically:

$$\begin{array}{l}-0.05b_{bw}(\lambda )<b_{bp}(\lambda )<0.05\left[m^{-1}\right]\\ -0.05a_w(\lambda )<a_{ph}(\lambda )<5.0\left[m^{-1}\right]\\ -0.05a_w(\lambda )<a_{dg}(\lambda )<5.0\left[m^{-1}\right]\end{array}$$ (19)

In this case, when one or more of the derived IOPs fall outside the defined range, the algorithm returns a non-solution. We note that the inequality constraints in Eq. (19) allow for slightly negative solutions. This should be allowed given uncertainties in the in situ measurements (if it is not allowed, the match-up statistics will be biased high). As an alternative to using inequality constraints to check the validity of derived IOPs, it is possible to constrain the solution method such that the solution space search is limited to a predefined range (Garcia et al., 2014; McKinna et al., 2015). Constrained solution methods, however, can potentially interfere with the mathematical mechanism for searching multi-parameter solution space and can result in IOP solutions that sit on the edge of the solution space (Garcia et al., 2014; Huang et al., 2013).

Characterization of bias and uncertainties for ocean constituents occasionally benefit from data transformations. Satellite C_a, for example, are nearly log-normally distributed in space (Campbell, 1995), as confirmed when viewing frequency distributions of untransformed and logtransformed SeaWiFS chlorophyll data for May 1998 (Fig. 2). As normally distributed data are required for parametric statistical tests to retain their meaning, interpretations of statistical results can be misleading if non-normally distributed data are used for characterization. In application of log-transformed SeaWiFS chlorophyll comparisons, Gregg and Casey (2004) derived an RMS log error of 31.0%. In this case, 76% of the comparisons fell below this error level, which is reasonably close to the definition of the RMS. When using untransformed data, the RMS contained 95% of the data, which deviates significantly from the expected 67%, strongly suggesting erroneous application of the RMS due to a non-normal data set (Fig. 2). The extent to which other optical constituents or IOPs possess spatial or temporal deviations that differ significantly from normal (Gaussian) distributions remains understudied and non-parametric descriptors of uncertainty and bias should be explored. Frequency diagrams demonstrate the nature of the distributions and may guide the choice of statistical applications and transforms. Means and medians should also be computed – medians are less sensitive to data distribution, such that it is likely that the data are not normally distributed when the median differs substantially from the mean. Comparison between frequency distributions of derived products and those measured in situ (e.g., in databases) are critical to assess the applicability of the specific dataset to derive inversion algorithms on global scales, as a non-representative dataset is likely to bias the global algorithm (Werdell et al., 2009; Werdell et al., 2013a). Care should be applied to subsample the dataset to be spatially (and if possible temporally) representative of the variability of the full domain of interest.

Figure 2:

(a.) SeaWiFS chlorophyll-a concentration for May 1998. Subplots (b.) and (c.) show how global chlorophyll-a concentration for May 1998 is nearly log-normally distributed.

5. Looking forward

In the following sections, we briefly overview new and upcoming missions, knowledge gaps in IOP bio-optical models and measurements, and the future of inverse methods, uncertainty considerations, and methods for algorithm assessment. A number of recent and soon-to-launch ocean color missions will carry novel sensor payloads with unprecedented observing capabilities (Table 5). It is useful to briefly contextualize these missions to consider existing knowledge gaps in IOP retrieval methodologies and recommend paths forward. Furthermore, building upon Section 2.2 where heritage algorithmic approaches were reviewed, it is important to identify knowledge and measurement gaps that require attention to further improve upon inverse IOP modeling efforts in the PACE era. In particular, we discuss gaps in absorption and backscattering coefficients, additional data needed to improve algorithms, non-conventional approaches, and future machine learning approaches.

Table 5:

A sample of recent or soon-to-launch Earth observing satellite missions capable of ocean color observations.

Mission	Agency	Sensor	Launch	Bands†	Nadir pixel size (m)	Other Specifications
High spatial resolution missions: O(100 km) swath
Landsat-8 Landsat-9	USGS/ NASA	OLI OLI-II	2013 2020	• 4 VIS	• 30	• 16 day revisit
Sentinel 2A Sentinel 2B	ESA	MSI	2015 2017	• 4 VIS	• 10	• 10 day revisit • 5 day revisit in constellation
HySpiri	NASA	VSWIR	TBD	• UV-SWIR • Contiguous (10 nm)	• 60	• 19 day revisit
EnMAP	DLR	EnMAP	2017	• UV-SWIR • Contiguous (6.5 nm)	• 30	• 4 day revisit
Geostationary missions
Geo-Kompsat 2B	KIOST	GOCI-II	2019	• 1 UV • 8 VIS	• 250 local • 1000 global	• Geostationary over NE Asia
Medium spatial resolution missions: O(1000 km) wide swath
Sentinel 3A Sentinel 3B	ESA	OLCI	2016 2018	• 8 VIS	• 300 coast • 1000 ocean	• 4 day global coverage • 2 day global coverage in constellation
Oceansat-3	ISRO	OCM-3	2018	• 8 VIS	• 360	• 2 day global coverage
Suomi-NPP JPSS-1	NOAA/ NASA	VIIRS	2011 2017	• 5 VIS	• 360	• 1 day global coverage
GCOM-C	JAXA	SGLI	2018	• 1 UV • 6 VIS	• 250 coast • 1000 ocean	• 3 angle polarimetry • 2 day global coverage
PACE	NASA	OCI/ polarimter	2022	• 350–900 nm • Contiguous (5 nm)	• 1000	• Multi-angle polarimetry • 2 day global coverage

^†For comparative purposes, SeaWiFS sensor launched in 1997 had six VIS bands

5.1. Future sensing technologies

Future technologies suitable for IOP remote sensing can roughly be split into three categories: (i) high spatial O(10 m) pixel sensor instruments in low Earth orbits (LEO), (ii) sensors in geostationary Earth orbits (GEO) with moderate resolution O(1 km) pixels, and (iii) moderate spatial O(1 km) pixel resolution LEO sensors. These three categories clearly demonstrate the tradeoffs required for remote sensing – there is only so much radiant energy emanating from the ocean and each sensor optimizes on spatial resolution at the expense of spectral and/or temporal resolution and vice versa. A summary of recently launched and soon-to-be launched sensors applicable to retrieving IOPs is given in Table 5.

High spatial resolution sensors have recently provided remarkable insights into sub-mesoscale processes in coastal regions (Franz et al., 2015; Vanhellemont & Ruddick, 2014). However, as current instruments with high spatial resolution (OLI and MSI) were primarily designed for terrestrial observations, they have limited and relatively wide bands sets (typically four VIS bands) and signal-to-noise characteristic not ideal for remote sensing dark ocean targets. Nonetheless, much work is underway to improve the radiometric quality of high spatial resolution data and AC correction, to support heritage IOP methodologies (Franz et al., 2015; Pahlevan et al., 2014; Pahlevan et al., 2017; Vanhellemont & Ruddick, 2015; Vanhellemont & Ruddick, 2016). A present limitation of high spatial resolution sensors is their swath width, which is typically O(100 km), their repeat time O(10 days), and the fact they are typically not tasked to image the open ocean away from coastlines. Collectively, this means that existing high resolution sensors in LEO are not conducive to providing near-daily basin-scale measurements of oceanic IOPs.

The capabilities of GEO satellites have recently been demonstrated using meteorological satellites (Murakami, 2016; Neukermans et al., 2009; Neukermans et al., 2012) and with the Geostationary Ocean Color Imager (GOCI) (Choi et al., 2012). GEO sensors offer the ability to observe diurnal marine processes by capturing multiple images of a region throughout the day. With better temporal resolution compared to LEO, GEO sensors can resolve dynamic marine processes such as suspended sediment plumes (Choi et al., 2013) and diurnal variability in phytoplankton blooms (Lou & Hu, 2014). In addition, multiple GEO images can provide more spatially complete daily snapshots of a region when averaged together. However, like high resolution LEO sensors, GEO sensors do not provide near-daily global coverage and are multispectral with band sets similar to heritage ocean color missions such as SeaWiFS. We note, however, potential synergies between high radiometric quality LEO sensor data and high temporal frequency GEO sensor data have recently been considered, specifically approaches for combining the two data types for the purpose of producing improved temporally-rich ocean color data suitable for observing coastal waters (Peschoud et al., 2017; Vanhellemont et al., 2014).

Moderate spatial resolution sensors have been, and continue to be, used for deriving near-daily global IOP data products. They are well-calibrated sensors with dynamic ranges and signal-tonoise characteristics necessary for observing ocean properties (Hu et al., 2012). These polar orbiting LEO sensors completely image the Earth’s surface in O(1 day) and are the critical for climate-quality synoptic-scale observations of marine biogeochemical processes. Most inverse IOP methods detailed in Section 2.2 were developed for application to moderate spatial resolution LEO sensors with measured success. We note that the number of spectral bands observed by existing (MODIS, OLCI, VIIRS) and most future (SGLI, OCM-3) moderate spatial resolution LEO sensors are only slightly better than historical instruments (e.g. SeaWiFS, MERIS, OCM-1, OCM-2) with the exception of the primary PACE instrument, which will be a hyperspectral sensor. We discuss the capabilities of the PACE mission in the following section.

5.1.1. The PACE Mission

The PACE mission spacecraft will carry its primary instrument, the Ocean Color Imager (OCI), in a polar LEO providing global coverage every two days. The OCI spectroradiometer will have higher spectral resolution (~5 nm contiguous bands) than historical and contemporary satellite sensors (see Table 5), ranging from the UV (~350 nm) to NIR (~900 nm), and will potentially be flown with a multi-angle polarimeter as a second instrument in its payload. Accordingly, it is prudent to pursue inverse IOP methods that take maximal advantage of these new features.

The PACE spectroradiometer has the potential to discriminate optical constituent matter in ways previously impracticable with multispectral data. High-resolution spectral capabilities can better inform SAA approaches such as those presented above (Vandermeulen et al., 2017; Wolanin et al., 2016) and also allow common spectroscopy approaches, such as derivative analysis, to be utilized (Bracher et al., 2009). It is also expected that R_rs(UV) measurements will enable improved separation of a_cdom(λ) and a_nap(λ), as S_cdom exceeds S_nap and hence typically a_cdom(λ) > a_nap(λ) in the UV. The PACE spectrometer also has the potential to improve estimates of phytoplankton community composition through its continuous measurements of spectral features aligned with accessory pigment absorption (Bracher et al., 2017; Torrecilla et al., 2011; Vandermeulen et al., 2017). For example, existing ocean color sensors lack appropriately placed yellow/orange spectral bands (560–650 nm) needed to detect phycobilipigments, such as phycocyanin, indicative of cyanobacteria (McKinna, 2015).

Finally, measurements of polarized R_rs(λ) (or reflectance) show sensitivity to microphysical properties of hydrosols (marine particles), such as their composition (e.g., refractive index), size,and shape (Chowdhary et al., 2012; Kattawar, 2013; Lotsberg & Stamnes, 2010). Loisel et al. (2008), for example, demonstrated the use of polarized radiometry to distinguish organic and inorganic particles near the mouth of the Amazon River. Accordingly, it is anticipated that polarimetric remote sensing will provide additional information for inverse IOP methods (Harmel, 2016; Ibrahim et al., 2016) that can, in principle, lead to improved methods for determining pigment concentrations, particles sizes, and phytoplankton taxonomy.

5.2. IOP theoretical models and measurements

5.2.1. Knowledge gaps in absorption

Particulate absorption measurements from UV to NIR may still have significant biases that need to be addressed. In situ measurements, currently made largely using WET Labs ac meters, still suffer from large uncertainties due to the necessity to scatter correct the measurements as discussed in section 3.1.1. This issue appears most acute in coastal environments where particulate absorption cannot be assumed to be vanishingly small at NIR wavelengths, an assumption that may be reasonable in clear open ocean conditions. Improved scattering corrections have been proposed, but they require companion measurements collected using a VSF sensor to independently calculate the scattering error to derive uncertainties (McKee et al., 2013; Tonizzo et al., 2017; Stockley et al. 2017). We note, however, that these corrections have not been widely adopted as they do not seem to merge with offshore solutions. Integrating cavity absorption sensors have recently been commercialized (e.g., the Turner Design Integrating Cavity Absorption Meter (ICAM) and the Trios Online hyperSpectral integrating Cavity Absorption meteR (OSCAR), which theoretically collect all, or nearly all, scattered light, and can potentially derive absorption with reduced uncertainties. These sensors, however, are only now being fully characterized, including considerations for inelastic scattering.

For pure seawater absorption, there is a clear need for research to better understand the role of absorption by dissolved inorganics in the UV such as oxygen, NO₃, Br^-, and other salt ions comprising sea salts that have significant absorption in the UV (Armstrong & Boalch, 1961; Copin-Montegut et al., 1971; Johnson & Coletti, 2002; Lenoble, 1956; Ogura & Hanya, 1966; Shifrin, 1988). These effects have received scarce attention in recent literature. At 230 nm, these constituents all maintain more than an order of magnitude higher absorption than the values of pure water absorption, with steeply increasing absorption at shorter UV wavelengths. How substantially these constituents absorb at wavelengths longer than 300 nm remains unresolved, as the tail absorption effects have typically not been studied with high accuracy. Even relatively small contributions could be significant since pure water absorption is very low, particularly in the 320 to 420 nm range (< 0.01 m^-1). Armstrong and Boalch (1961) found significant effects of sea salt absorption out to 400 nm, but rigorous purification steps were not taken, so it is unclear if their additions of artificial sea salts introduced organic contaminants.

For inverse IOP methods, such as SAAs, there is no generalized bio-optical model that can parameterize the spectral shape a*_ph(λ) in the UV. Additional characterization of UV phytoplankton absorption, including contributions of absorbing compounds such as mycosporine-like amino acids (MAAs) is essential to resolve this gap. Given that phytoplankton community structure varies with environmental conditions, however, additional review of how measurements of T, S, nutrients, and light can better inform or constrain a*_ph(λ) within the context of remote sensing will also improve the skill of IOP inversions. We note, however, that while laboratory absorption techniques in the VIS have become significantly more robust (Stramski et al., 2015), accurate quantification of UV absorption with a filter-pad method remains a challenge, particularly because the absorption signal in this spectral region may exhibit significant drift on relatively short time scales comparable with the duration of spectral scan. Additionally, commercially-available in situ UV absorption meters do not currently exist.

5.2.2. Knowledge gaps in backscattering

Successfully partitioning of b_bp(λ) into multiple components is currently limited by insufficient knowledge about natural variability in particle backscattering properties in the ocean. Whereas technological and methodological capabilities to derive total b_bp(λ) in situ exist, and there are inversion approaches to derive particulate scattering components from VSF measurements (Twardowski et al., 2012; Zhang et al., 2012; Zhang et al., 2014; Zhang et al., 2011), there is a lack of routine experimental methodologies for directly determining particle type-specific backscattering data for multiple particulate backscattering components (e.g., b_ph(λ) and b_nap(λ). A continued need for further advancements in understanding of particulate backscattering, such as the roles of different particle types, remains an important challenge (Stramski et al., 2004a). Furthermore, in support of upcoming missions with expanded spectral ranges, investing in the development of hyperspectral backscattering instruments that span UV-NIR should be pursued. Current commercially-available sensors (WET Labs ECO-BB and HOBI Labs HydroScat) measure b_bp(λ) at a finite number of wavelengths (3–9 channels). Additional gaps are associated with how the spectral shape of the particulate backscattering coefficient is parameterized. For example, the appropriateness of its assignment as a power-law (Eq. 16) and under what circumstances the particulate backscattering ratio can be assumed to be spectrally constant (Eq. 17) (Gordon et al., 2009).

As reviewed in Sections 2.1.4.1 and 3.1.4, Zhang and Hu (2009) and Zhang et al. (2009) describe the physical relationships to derive the currently recommended values for b_bw(λ). The largest remaining uncertainty is the depolarization ratio. As mentioned, we recommend a δ value 0.039 at this time, however uncertainty in this parameter is at least 50% based on the range in values measured by Farinato and Rowell (1976), the only set of experimental measurements we are aware of in the last 50 years. Additional research is required to improve the accuracy of δ,, and to ascertain any associated dependencies (e.g., spectral, T, S).

5.3. Inverse models

5.3.1. Inverting AOPs to IOPs with additional optical information

In addition to the widely applied QSSA of Gordon et al. (1988), other approximations with potential value for IOP inverse models exist that have not widely been adopted in standard ocean color data processing schemes (Appendix A). Zaneveld (1982; 1989; 1995), for example, derived an analytical expression for r_rs(λ) that explicitly includes treatment of the VSF (in lieu of relying on average parameterizations such as the G_i(λ) in Eq. 4) (Appendix B). From a remote-sensing perspective, such an expression enables application of algorithms that explicitly contain the shape of the VSF. By doing so, it also merges two separate, disconnected steps in current QSSA algorithm work: (i) the BRDF correction of input R_rs(λ) based on tables from Morel et al. (2002) (see Section 2.1.2), and (ii) the subsequent inverse model. Combining these steps in a single, rigorous relationship allows explicit assessment of errors in component variables. In the current two-step approach, errors associated with, for example, the VSF are dispersed in several poorly defined parameters that are empirically tuned. Furthermore, approximations that retain as much of the functional form of the RT equation as possible presumably remain inherently more stable. Zaneveld (1989) provided an inversion approach for his analytical expression that would benefit from renewed assessment by the community.

Only a subset of contemporary inversion methods explicitly includes inelastic processes, such as Raman scattering or fluorescence (e.g. Lee et al., 1994; Loisel & Stramski, 2000; Sathyendranath et al., 2001), although generalized methods for their inclusion now exist (Lee et al., 2013; McKinna et al., 2016; Westberry et al., 2013). To date, no treatment of Raman scattering accounts for T and S effects, although implementing T and S corrections within an inversion algorithm has been demonstrated (Werdell et al., 2013b). Walrafen (1967), Walrafen et al. (1986) and Becucci et al. (1999) all provide information on the temperature dependence of Raman scattering. Becucci et al. (1999) provides information on the salinity dependence of Raman scattering (through the use of synthetic seawater). On average, the observed effects were on the order of 20% from 10 to 30°C and 10% from 0 to 26 ppt. In contrast, Bartlett et al. (1998) found no evidence for a salinity effect on Raman in seawater samples, which suggests that further review is necessary. Broadly speaking, neither C_a or CDOM fluorescence are considered in IOP inversions (for an exception, see Lee et al. 1994). Given observed variability in C_a and CDOM fluorescence (Del Castillo et al., 2001; Falkowski & Kolber, 1995; Green & Blough, 1994; Hoge et al., 1993), further study is needed to assess how to best parameterize these inelastic scattering processes within inverse IOP methods.

5.3.2. Optically shallow waters

Interest has steadily increased in utilizing ocean color data to monitor ecosystem health in optically shallow shelf waters (Devlin et al., 2015; Hedley et al., 2016). However, most inverse IOP methods used to process global datasets were designed for optically deep oceanic waters with some exceptions (Lee et al., 2001; Lee et al., 1999). These algorithms are easily confounded by light reflected off the seafloor in clear, shallow waters resulting in biased IOP retrievals (Barnes et al., 2013; McKinna et al., 2015). A number of SAAs have been developed for remote sensing shallow waters using either multi- or hyperspectral airborne spectroradiometric data (Dekker et al., 2011), however, historical approaches have focused more on bathymetry and seafloor mapping rather than deriving water-column properties (Brando et al., 2009; Werdell & Roesler, 2003). Dedicated optically shallow ocean color algorithms have started to become available for deriving IOPs (Barnes et al., 2017; Barnes et al., 2013; McKinna et al., 2015). It is challenging, however, to incorporate these approaches into global data processing, as optically shallow waters make up only a small fraction of overall pixels and no robust mechanism currently exists to adequately flag their location during routine processing. In the approach of McKinna et al. (2015), for example, ancillary bathymetry and benthic albedo datasets are needed to help to constrain the dimensionality of the solution space to three unknowns (A_ph, A_dg, B_p). The need for large region-specific ancillary benthic albedo and bathymetry datasets can be alleviated, however, through the recently-developed algorithm of (Barnes et al., 2017); an approach that would be well-suited to spectrally-rich ocean color data collected by missions such as PACE.

As described in Section 3.1.4, coastal waters are often optically heterogeneous, making validation of algorithms difficult. This is compounded in optically shallow regions where withinpixel seafloor and bathymetric variability and stray light from adjacent features (e.g. sand cays and breaking waves) further complicate algorithm validation efforts. Not only are appropriate sampling protocols and methodologies required, but also a publicly accessible archive of in situ AOP/IOP data for algorithm development and validation. To that end, it is likely that the recently initiated NASA-funded COral Reef Airborne Laboratory (CORAL; https://coral.jpl.nasa.gov/) project will contribute greatly to the afore-mentioned knowledge gaps.

5.3.3. Non-conventional approaches for estimating IOPs from ocean color

Methods that relate L_t(λ) to IOPs have recently emerged and will benefit from further review and development (path 1→4 in Fig. 1). These approaches circumvent the need for AC (path 1→2 in Fig. 1) that can sometimes be confounded by absorbing aerosols and optically complex water masses. Two broad classes of approaches exist, specifically empirical models and coupled atmosphere-ocean algorithms models. Common empirical methods for deriving IOPs from R_rs(λ) were described in Section 2.2.3. Coupled atmosphere-ocean approaches operate similarly to the methods described in Sections 2.2.1 and 2.2.2, but solve for both atmospheric and marine variables simultaneously (e.g. Chomko & Gordon, 1998; Chomko et al., 2003; Gordon et al., 1997; Kuchinke et al., 2009a; Kuchinke et al., 2009b; Li et al., 2008; Spurr et al., 2007; Stamnes et al., 2003; Steinmetz et al., 2011). In general, this approach involves the combination of a model that accounts for aerosol properties and a model to express hydrosol (i.e. water components) via IOPs and/or other constituents, such as C_a. The number of unknown variables in coupled models exceeds typical SAAs due to the combination of aerosol and marine expressions and, as such, coupled models generally require more spectral observations (bands) than traditional SAAs. When applied to data from current ocean color instruments, coupled models use L_t(λ) from both the VIS and NIR bands. The retrieval of the aerosol and hydrosol variables then reduces to a classic inverse problem where modeled L_t(λ) is fitted to match sensor-observed L_t(λ). Both non-linear and linearization techniques have been developed to solve for the aerosol and marine parameters.

The main benefits of a coupled atmosphere-ocean approach lie in its potential to better identify and account for absorbing aerosols and non-negligible NIR radiances, both of which require special consideration in the classic decoupled AC scheme. Nonetheless, the ability of a coupled model to perform well under a wide variety of atmospheric and oceanic conditions remains dependent upon the general formulation of the aerosol and marine components, which unavoidably include inherent limitations and uncertainties. Furthermore, coupled oceanatmosphere approaches are historically computationally demanding and often require retrievals to be constrained to avoid unrealistic or unambiguous solutions.

5.3.4. Improved computational capabilities and statistical methods

Computational processing capabilities have historically driven the design and implementation of remote sensing algorithms. Most LUT, ANN, and coupled ocean-atmosphere approaches require additional computation capabilities relative to SAAs and, as such, have received less attention in operational ocean color processing environments with near-real-time data delivery requirements. We expect these limitations to be progressively alleviated as computing power continues to grow and new hardware accelerator technologies such as graphic processing units (GPUs) are utilized. Furthermore, with the spectrally rich data expected from PACE, we anticipate the ocean color community will benefit from pursuing integration into the realm of computer (data) science, following the path of the terrestrial remote sensing (Verrelst et al., 2015) and medical imaging (Jiang et al., 2010) communities.

Statistical methods with large(r) computational requirements, such as random forests and support vector machines, have only recently been explored for IOP inverse modeling, several of which have been shown to be effective for deriving constituent matter concentrations (Camps-Valls et al., 2006; Chang, 2015; Kim et al., 2014). Clustering methods are used to partition marine waters into distinct optical types (Mélin & Vantrepotte, 2015; Moore et al., 2009; Neukermans et al., 2016). Those that provide weighted water types per satellite pixel allow blending of multiple algorithms that have been tuned to specific water types (Moore et al., 2001; Moore et al., 2014; Woźniak et al., 2010). Statistical methods have also been shown to be highly effective in reducing solution spaces or finding a solution neighborhood, thereby speeding up the search for an optimal solution (De Noia et al., 2015; Hedley et al., 2009). In addition, as the capabilities of modern computers continue to expand alongside improvements in RT code and innovative machine learning tools, such as TensorFlow (Abadi et al., 2016), the burden of simulating large synthetized datasets to enable development of advanced empirical algorithms will also diminish.

5.4. Uncertainties

While the term uncertainty is used in virtually all of the studies mentioned in Section 3.2, the actual values presented often represent different mathematical constructs that are not always comparable. This may be due to the lack of consensus on the type and characteristics of the uncertainties required by space agencies or by the user-community. For space agencies, uncertainty metrics are useful for quality assurance and product assessment, while for ocean modelers, uncertainties are useful during data assimilation and when performing modelobservation comparisons. Additional work is necessary to define uncertainties and recommend their computation. The IOCCG Working Group on Uncertainties in Ocean Color Remote Sensing (http://ioccg.org/group/uncertainties/) provides additional guidance on the subject.

Furthermore, it remains critical for measurement technology to continue to improve (thereby reducing measurement uncertainties) to ensure our ability to perform closure and validate remotely sensed products. Looking towards PACE, for example, hyperspectral measurements that extend into the UV will be critical. Specific technology gaps exist in: (i) in situ spectral b_b(λ) and VSF measurements – commercial or prototypical hyperspectral backscattering sensors do not yet exist; (ii) in situ absorption measurements with significantly reduced uncertainties associated with scattering correction and extension to the UV – emerging commercial instrumentation do not require such a correction but, these instruments are only recently being validated; and, (iii) polarized IOPs that report the 12 and 22 elements of the Mueller Matrix (at least) to better model the polarized underwater light field –instrumentation that provides more accurate estimates of polarized IOPs will reduce uncertainties in AOP-IOP closure. In addition, methods for closing the scale gap between in situ and satellite measurements when matched up (see Section 3.1.5) must be explored. This might be accomplished through increased spatial resolution of satellites, particularly in coastal areas (Moses et al., 2016), as well as through the use of moving in situ platforms (e.g., gliders and flow-through systems) that travel significant distances in a relatively short time periods to provide information on and quantify satellite subpixel variability (e.g., Werdell et al., 2013c).

5.5. Performance metrics

Varied validation methods exist to evaluate derived IOPs using independent measurements designated to be truth. Generally speaking, the most common encompass comparisons of IOPs derived from synthesized R_rs(λ) with synthesized IOPs (IOCCG, 2006; Werdell et al., 2014) and IOPs derived from in situ or satellite-observed R_rs(λ) with coincident in situ IOPs (Brewin et al., 2015b; IOCCG, 2006; Werdell et al., 2013a). Other emerging approaches include, but are not limited to, simulating R_rs(λ) from the derived IOPs using the forward model or an alternative RT model for comparison with independent in situ measurements of R_rs(λ) (Tonizzo et al., 2017) and time-series and population statistical analyses when sufficient volumes of in situ data exist (Kostadinov et al., 2007; Werdell et al., 2009). With the exception of the latter, most validation methods ultimately rely on interpretation of regression results and one-to-one scatter plots to quantitatively assess algorithm performance.

Broadly speaking, the community has not achieved absolute consensus on the best statistical metrics for assessing algorithm performance and, as previously stated, we do not make recommendations here, other than to request further study. While r-squared values (r²), regression slopes and intercepts, biases, absolute and relative percent differences, RMS, and biased and unbiased root mean square errors have evolved as the most popular to determine how closely derived IOPs represent the truth measurements, many of these metrics overlap in their meaning and interpretation and other metrics exist (Brewin et al., 2015b; Willmott et al., 2017). Multi-dimensional tools have also shown promise and merit increased consideration, including Taylor and Target plots (Jolliff et al., 2009; Taylor, 2001), as do population statistics such as temporal and spatial frequency distributions, cumulative distribution functions, and long-term time series when sufficient truth data can be accumulated. Since different IOPs are related in nature in ways that may not be parametrized in a specific inversion schemes, these relationships can also be used to test the skill of an inversion (e.g., verifying that distributions of retrieved a_nap(λ) / a_ph(λ) achieve consistency with in situ observations).

For satellite applications, we also encourage the consideration of temporal and spatial variability and stability (e.g., rates of failures and appearances of outliers and anomalies). Other topics for future consideration include evaluation of regional versus global performance, additional comparisons of multiple satellite instruments with varied spectral bands that may impart inherent differences in IOP retrievals, and, in the coming hyperspectral era of NASA’s PACE mission, development of decision support metrics to drive execution of validation activities on all available wavelengths versus a subset of identified key wavelengths.

6. Summary and recommendations

We have presented the current state of the art in approaches to obtain IOPs from ocean color remote sensing, as well as outlined the areas where uncertainties and knowledge gaps remain. As an increasing number of space-based instruments measure ocean color simultaneously, uncertainties in L_t(λ) and R_rs(λ) are expected to become better constrained through sensor intercomparisons and growth of the invested community. As computing power continues to increase, computationally expensive methods such as ANN and LUTs are likely to be used routinely and comparisons between IOPs generated from all the methods outlined above will increase, resulting in more robust ensemble results, such as those derived from ensembles of weather prediction models. Significantly more in situ data needs to be collected using community adopted measurement protocols to assess the performance and utility of the different methods across space and time, and sub-pixel variability and uncertainties in the in situ measurements need to be better characterized. These measurements will become the basis for international databases for novel algorithm refinement and developments. Below we provide a set of recommendations that could help improve IOP inversion algorithm further.

Data and measurements

We recommend:

• Development of new, commercially available instrumentation for measuring a(λ), c(λ), b(λ), b_b(λ) and the VSF(λ) from UV to NIR at high spectral resolution (~5 nm);

• Development of instrumentation and methods to measure the polarized scattering elements of the Mueller matrix and radiance fields in situ;

• Additional research into UV absorption of dissolved inorganic constituents of seawater;

• Additional research into the depolarization ratio for pure water scattering;

• Assembly of additional publicly-available in situ and simulated hyperspectral datasets for algorithm development and testing, with attention to the temporal, spatial, and biogeochemical representativeness of these datasets; and,

• Continued collection, assembly, and public dissemination of key biogeochemical variables that can be directly inferred from IOPs including, but not limited to: particle size distributions, phytoplankton pigment concentrations, phytoplankton classes and metrics of community composition, and particulate and dissolved organic carbon.

Algorithm and radiative transfer codes

We recommend:

• Sharing of algorithm code (e.g., open-source distribution) to encourage maximization of knowledge transfer and testing/vetting of novel approaches;

• Development and distribution of vector RT codes for application in aquatic environments to study the effects of polarization on R_rs(λ);

• Evaluation of the use of additional environmental information (e.g., T, S, and distance from shore) to help inform and constrain IOP inversion algorithms; and,

• Assessment of the increase in information that multi-angle polarimetry introduces to inform and better constrain IOP inversions and prepare for future missions (e.g., PACE) where polarimeter and radiometer may observe the Earth simultaneously.

System uncertainty

We recommend:

• Increased assessment and quantification of uncertainty budgets, including those associated with the satellite instrument, sub-pixel variability, atmospheric correction algorithms, bidirectional reflectance characterizations and simplified AOP-IOP relationships, in-water algorithms, and in situ and laboratory measurements, so that efforts can target reduction of the largest sources of uncertainty.

Table 6:

Historical recommendations for the depolarization ratio, δ, of pure water.

δ (unitless)	Reference
0.108	Kratohvil et al. (1965)
0.091	Morel (1974b), Shifrin (1988a)
0.051	Buiteveld et al. (1994a)
0.039	Jonasz and Fournier (2007)

Highlights.

• Ocean color algorithms for obtaining marine inherent optical properties are reviewed

• Known uncertainties associated with each approach and knowledge gaps are discussed

• Common performance metrics used to evaluate the satellite retrievals are provided

• Recommendations for future investment for upcoming satellite missions are presented

Abbreviations

AC

atmospheric correction

ANN

artificial neural network

AOP

apparent optical property

BRDF

bidirection reflectance distribution function

Ca

chlorophyll-a

CDOM

colored dissolved organic matter

CORAL

COral Reef Airborne Laboratory

DLR

German Aerospace Center

DOC

dissolved organic matter

EnMAP

Environmental Mapping and Analysis Program

EOF

empirical orthogonal function

ESA

European Space Agency

GEO

geostationary Earth orbit

GSD

ground sampling distance

GOCI

Geostationary Ocean Color Imager

IOCCG

International Ocean Colour Coordinating Group

IOPs

Inherent Optical Properties

ISRO

Indian Space Research Organisation

JAXA

Japanese Aerospace Exploration Agency

KIOST

Korean Institute of Ocean Science and Technology

LEO

low Earth orbit

LUT

look-up-table

MAAs

mycosporine-like amino acids

MASCOT

Multi Angle Scattering Optical Tool

MERIS

Medium Resolution Imaging Spectroradiometer

MLR

multiple linear regression

MODISA

Moderate Resolution Imaging Spectroradiometer aboard the Aqua spacecraft

MODIST

Moderate Resolution Imaging Spectroradiometer aboard the Terra spacecraft

MSI

MultiSpectral Instrument

MVSM

Multispectral Volume Scattering Meter

NAP

non-algal particles

NASA

National Aeronautics and Space Administration

NIR

near-infrared

NOAA

National Oceanic and Atmospheric Administration

OCI

Ocean Color Instrument

OCM

Ocean Color Monitor

OCTS

Ocean Color Temperature Scanner

OLCI

Ocean and Land Colour Instrument

OLI

Operational Land Imager

PACE

Plankton, Aerosol, Cloud, ocean, Ecosystem mission

PC

principal component

PCA

principal component analysis

PCR

principal component regression

RT

radiative transfer

QSSA

quasi single scattering approximation

S

salinity

SAAs

semi-analytical inversion algorithms

SeaWiFS

Sea-viewing Wide-Field-of-view Sensor

SGLI

Second-generation Global Imager

SSS

sea surface salinity

SST

sea surface temperature

T

temperature

USGS

United States Geological Survey

UV

ultraviolet

VIIRS

Visible Infrared Imaging Radiometer Suite

VIS

visible

VSF

volume scattering function

VSWIR

Visible ShortWave InfraRed sensor

Appendix A

In addition to the widely applied radiative transfer approximation of Gordon et al. (1988), other numerical approximations exist to relate R_rs(λ) or r_rs(λ) to IOPs. This appendix serves to provide a brief summary of several common alternatives, all of which can be used in place of Eq. (4).

Jerome et al. (1996) suggests that nadir-viewing r_rs(λ) can be expressed as:

$$r_{rs}(\lambda )=-0.00042+0.112\frac{b_b(\lambda )}{a(\lambda )}-0.0455{\left(\frac{b_b(\lambda )}{a(\lambda )}\right)}^2$$

Morel and Gentili (1993) expresses r_rs(λ) as:

$$r_{rs}(\lambda )=\frac{f(\lambda )}{Q(\lambda )}\frac{b_b(\lambda )}{a(\lambda )}$$

where f(λ) represents the combined influence of illumination conditions and geometry and sea surface properties and Q(λ) defines the ratio of upwelling irradiance to upwelling radiance. Morel et al. (2002) provides a LUT for f(λ) / Q(λ) for various sensor-viewing and solar zenith angles, tabulated at seven wavelengths [412.5, 442.5, 490, 510, 560, 620, and 660 nm] and for six C_a [0.03, 0.1, 0.3, 1, 3, and 10 mg m^-3].

Albert and Mobley (2003) generated the following expression for r_rs(λ) using Hydrolight:

$$r_{rs}(\lambda )=p_{1}u(\lambda )\left(1+p_{2}u(\lambda )+p_{3}u{(\lambda )}^2+p_{4}u{(\lambda )}^3\right)\left(1+p_5\frac{1}{\cos \left({\theta }_s\right)}\right)\left(1+p_{6}W\right)\left(1+p_7\frac{1}{\cos \left({\theta }_{\nu }\right)}\right)$$

where p_1…7 = [0.0512, 4.6659, -7.8387, 5.4571, 0.1098, -0.0044, 0.4021], W is wind speed, θ_s is solar zenith angle, and θ_v is the sensor-viewing angle.

Lee et al. (2004) explicitly account for the phase function effect of molecular and particulate scattering (Morel & Loisel, 1998) and express r_rs(λ) as:

$$r_{rs}(\lambda )=g_w\frac{b_{bw}(\lambda )}{a(\lambda )+b_{b(\lambda )}(\lambda )}+g_p(\lambda )\frac{b_{bp}(\lambda )}{a(\lambda )+b_b(\lambda )}$$

Using Hydrolight, they defined g_w as 0.113 and g_p(λ) as:

$$g_p(\lambda )=0.197\left[1-0.636\exp \left(-2.552\frac{b_{bp}(\lambda )}{a(\lambda )+b_b(\lambda )}\right)\right]$$

Park and Ruddick (2005) parameterized R_rs(λ) as follows using Hydrolight:

$$R_{rs}(\lambda )=\sum _{i=1}^4{G}_{i}u{(\lambda )}^i$$

with G_i tabulated in a LUT for various θs_, θ_v, relative azimuth angles, and ratios of b_bp(λ) / b_b(λ).

Appendix B

In addition to the widely applied radiative transfer approximation of Gordon et al. (1988) (Eq. 4), there are other approximations that may additionally have value in AOP-IOP inversions. In particular, Zaneveld (1982; 1989; 1995) derived analytically from the radiative transfer equation an expression of remote sensing reflectance r_rs(θ,φ):

$$r_{rS}(\theta ,\varphi )=\frac{1}{{\mu }_d}\frac{f_b(\theta ,\varphi )\frac{b_b}{2\pi }}{K_{Lu}(\theta ,\varphi )\left|\cos \theta \right|+a+b_b-\left(f_L(\theta ,\varphi )-1\right)b_f}$$ (B1)

For brevity in this Appendix, spectral dependence is implied, but not denoted. In Eq. (B1), μ_d is the average cosine of downwelling irradiance, K_Lu is the diffuse attenuation coefficient of the upwelling nadir radiance L_u(θ, ϕ), b_f is the forward scattering coefficient,

$$f_b(\theta ,\varphi )=\frac{{\int }_0^{2\pi }{\int }_0^{\pi /2}\beta \left(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime }\right)L\left({\theta }^{\prime },{\varphi }^{\prime }\right)\sin {\theta }^{\prime }d{\theta }^{\prime }d{\varphi }^{\prime }}{E_{od}{b}_b/2\pi }$$ (B2)

$$f_L(\theta ,\varphi )=\frac{{\int }_0^{2\pi }{\int }_{\pi /2}^{\pi }\beta \left(\theta ,\varphi \cdot {\theta }^{\prime }\cdot {\varphi }^{\prime }\right)L\left({\theta }^{\prime },{\varphi }^{\prime }\right)\sin {\theta }^{\prime }d{\theta }^{\prime }d{\varphi }^{\prime }}{b_f{L}_u(\theta ,\varphi )}$$ (B3)

In Eq. (B2), the shape factor f_b represents the ratio of the light actually scattered into the direction (θ,ϕ) by scattering of downwelling radiance to the light that would be received if the VSF was constant and equal to b_b/2π. In Eq. (B3), f_L represents the ratio of the light actually scattered into the direction (θ,ϕ) by scattering of upwelling radiance to the light that would be received if the upwelling radiance were isotropic and equal to L_u(θ,ϕ) and if the VSF was constant and equal to b_f/2π. Assuming the volume scattering function and the radiance distribution are continuous within their respective angular ranges, the shape factor f_b can be rewritten as:

$$f_b(\theta ,\varphi )=\frac{\beta \left({\gamma }_m\right){\int }_0^{2\pi }{\int }_0^{\pi /2}L\left({\theta }^{\prime },{\varphi }^{\prime }\right)\sin {\theta }^{\prime }d{\theta }^{\prime }d{\varphi }^{\prime }}{E_{od}{b}_b/2\pi }=\frac{2\pi \beta \left({\gamma }_m\right)}{b_b}$$ (B4)

where β(γ_m) represents the downwelling radiance distribution less the weighted mean volume scattering function and γ_m the corresponding scattering angle. Inserting Eq. (B4) into Eq. (B1), we have:

$$r_{rs}(\theta ,\varphi )=\frac{1}{{\mu }_d}\frac{\beta \left({\gamma }_m\right)}{K_{Lu}(\theta ,\varphi )\left|\cos \theta \right|+a+b_b-\left(f_L(\theta ,\varphi )-1\right)b_f}$$ (B5)

Note that Eq. (B5) explicitly includes the VSF in defining the remote sensing reflectance. Zaneveld (1989) provided an inversion for Eq. (B5) that has not been rigorously assessed by the community to date. It is important to note that inelastic processes such as Raman scattering are not included in the above relationships.

Eq. (B5) has several attractive aspects from a remote sensing algorithm perspective.First, it would seem desirable to develop algorithms that explicitly contain the shape of the VSF. As Morel and Gentili (1993) point out, the BRDF which describes the shape of the upwelling radiance distribution, “… is essentially controlled by the shape of the VSF…” Exclusively using integrated coefficients such as b_b must introduce some approximate error. Second, using a relationship such as Eq. (B5) merges two separate, disconnected steps in current QSSA algorithm work – recall that in current NASA processing, for example, R_rs(λ) are first “exactly” normalized following Morel et al. (2002) to account for varied solar geometry, then the IOP inversion is executed. Combining these steps in a single, rigorous relationship allows explicit assessment of errors in component variables. In the current two-step approach, errors associated with, for example, the VSF are dispersed in several poorly defined parameters that are empirically tuned. Finally, approximations that retain as much of the functional form of the RT equation as possible would seem to be inherently more stable.