Abstract
Heavy metal biosorption is an efficient technology for the decontamination of metal from industrial waste water. The present study focused on exploration of Aspergillus niger towards removal of Cr(VI) from aqueous solution. The influence of different experimental parameters—initial pH, adsorbent dose, initial concentration, contact time, shaking speed, temperature, and their combined effect during Cr(VI) adsorption—was investigated by means of response surface methodology based on four factorial Box–Behnken experimental design. Optimized values of initial Cr(VI) concentration, pH, adsorbent dose, and contact time were found as 33.33 mg/L, 4.6, 1.0 g/L, and 48.45 min, respectively. A. niger showed the highest adsorption capacity 11.792 mg/g at initial pH 2.0. Equilibrium data fitted well to the Temkin and Freundlich isotherms. Cr(VI) biosorption showed Pseudo-second order rate kinetics. The activation energy of the adsorption was estimated as 2.9 × 10−3 kJ/mol. Thermodynamics properties of the Cr(VI) biosorption was spontaneous in nature. Desorption study showed that nearly 94% of the Cr(VI) adsorbed on A. niger could be desorbed using 0.5 M EDTA.
Keywords: Chromium (VI), Aspergillus niger, Biosorption, Optimization, Isotherms, Kinetics
1. Introduction
Heavy metal pollution in both aquatic and terrestrial ecosystem is a major threat. Therefore recovery of heavy metals from aqueous medium is a prime priority among the scientists. However, metal decontamination is not an easy task because all the extraction techniques are neither economically nor environmentally friendly [27]. Therefore, scientists are constantly searching for a viable economic method that is eco-friendly also. Among the different heavy metals (Cu, Ni, Zn, Pb, Hg, Cd, and Cr) chromium is considered as dangerous one and has become a serious health hazard [22]. Chromium generally discharges into the environment through various industrial wastes including electroplating, tanning, steel industry, textile dyeing, manufacturing of pigments, refractory materials, etc. [1]. Among different oxidation states of chromium (−2 to +6), only Cr(III) and Cr(VI) are available in the environmental samples, and in comparison Cr(VI) is highly oxidizing in nature. Probably because of this Cr(VI) is considered as a cancer causing agent [29]. However, Cr(VI) does not interact directly with DNA, it shows intercellular reduction to Cr(III) via reactive intermediates [30].
Research also highlighted that under normal physiological conditions, Cr(VI) crosses the membrane and spontaneously reacts with intracellular reductants like ascorbate and glutathione and subsequently converts to short-lined intermediates (e.g. Cr(V) or Cr(IV)) and free radicals which ultimately give stable product Cr(III) [23].
To overcome these toxic effects of Cr(VI) from environmental samples, many environmental methods are available such as ion exchange, electrochemical treatment, chemical reduction, etc. But above mentioned methods are ineffective when metal concentration in the effluent is higher than 100 mg/m3 [34]. In contrast to the above mentioned method adsorption technology is considered the only viable method [18] where various low cost adsorbents were used such as non-living biomass of Alligator weed [35], [5], Citrus Limetta peel [26], fungal biomass [1], alfalfa biomass [8], activated carbon [28]. But none of the above adsorbents showed good performance towards removal of Cr(VI) except fungal biomass.
The most widely used adsorption technology was conducted by changing one variable, while keeping other variables constant. However, this conventional method consumes huge time and also requires a large number of experiments to determine the optimal levels. Moreover, output of this experiment is sometime unreliable. To overcome these problems an optimization procedure by means of statistical model known as response surface methodology (RSM) is introduced [12]. The experimental data were fitted in a second order polynomial equation and finally it was validated by performing analysis of variance and lack of fit. RSM is basically a computational statistical technique which mainly screens out the optimal operational conditions for a particular system [20].
Keeping in mind the above fact, the present study was conducted through batch mode for removal of Cr(VI) from aqueous solution using biomass of Aspergillus niger. The operating variables such as pH, initial concentration, contact time, adsorbent dose, stirring rate and temperature were considered for the present study. Finally, adsorption isotherm, kinetic thermodynamics studies were conducted to find out the best condition and feasibility of adsorption process.
2. Materials and methods
2.1. Biosorbent preparation
2.1.1. Preparation of dead fungal biomass
Species of Aspergillus was chosen as test fungi i.e. A. niger. This species was cultivated in the medium containing sterilized boiled water and mashed potato 250 g and dextrose 20 g and incubated at 30 ± 2 °C. After 7 days of incubation, the live fungi were killed by boiling them in 0.5 N NaOH solutions for 15 min and then thoroughly washing with excess double distilled water till the pH of the eluent reached neutral. After washing, the biomass was dehydrated at 5 °C for 24 h and powdered. The dried biomass was stored in a desiccator and used for subsequent experiments.
2.1.2. Preparation of stock solution
Cr(VI) stock solution (10 mg/L) was prepared by dissolving K2Cr2O7 in double distilled water which was diluted to desired concentrations (5–60 mg/L).
2.1.3. Biosorption of Cr(VI)
The biosorption of Cr(VI) experiments (except the experiment on the effect of temperature) was conducted at a fixed temperature of 35 ± 2 °C. 2.828 g of K2Cr2O7 was dissolved in 1 L of distilled water to obtain a stock solution having 1000 mg/L of Cr(VI). The stock solution was then diluted to obtain test solutions of desired strength.
2.1.4. Chromium analysis and uptake capacity
Cr(VI) was analysed spectrophotometrically after forming a colour compound of Cr(VI) with 1,5-diphenylcarbazide. Absorbance was recorded at 540 nm, using Perkin Elmer (Lamda 35, UV–VIS) spectrophotometer using standard method [7]. The amount of Cr(VI) biosorbed at equilibrium, qe (mg/g), which represents the metal uptake and it was evaluated by the following Eq. (1):
| (1) |
where V is the volume of Cr(VI) solution (l), Ci and Ce are the initial and final concentrations of hexavalent chromium in solution (mg/L−1), respectively, and m is the mass of dry biosorbent (g).
2.1.5. FTIR and SEM studies
In order to understand the chemical nature of the adsorbent surface, before and after adsorption of Cr(VI) onto A. niger was examined by Fourier Transform Infrared Spectrometer (FTIR GX 2000, Perkin-Elmer). For the FTIR analysis, 30 mg of finely ground biomass was pelleted with 300 mg of KBr (Sigma) in order to prepare translucent sample discs. The surface morphology of the biosorbent was evaluated by scanning electron microscopy (SEM) (HITACHI, S-530, Scanning Electron Microscope and ELKO Engineering) at an accelerating voltage of 20.0 kV. Unloaded and metal-loaded A. niger biomass samples were mounted on aluminium stab sequenced by coating with a thin layer of gold under vacuum to increase the electron conduction and to improve the quality of the micrographs.
2.2. Isotherm, kinetics and thermodynamics study
2.2.1. Adsorption isotherms
Analysis of data by adsorption isotherms is very important to design of an adsorbent and for calculating the adsorption efficiency of the adsorbent systems. In this study the Langmuir, Freundlich, D-R and Temkin adsorption isotherm models are analysed and mathematical expressions of these models are given in Supp Table 1.
2.2.2. Adsorption kinetics
The rate of fluoride adsorption on fluoride was determined by studying the adsorption kinetics at fixed initial concentration with different time interval and fixed adsorbent dose. The kinetics of fluoride adsorption can be assessed by Pseudo-first-order, Pseudo-second-order kinetics and intraparticle diffusion model and mathematical expressions of these models are given in Supp Table 2.
2.2.3. Activation energy and thermodynamic parameters
The activation energy Ea for fluoride adsorption onto lichen was calculated by the Arrhenius Eq. (2):
| (2) |
where k is the rate constant, A is the Arrhenius constant, Ea is the activation energy (kJ mol−1), R is the gas constant (8.314 J mol−1 K−1) and T is the temperature (K). Ea can be determined from the slope of a plot of ln k versus 1/T. Thermodynamic behaviour of adsorption of fluoride on lichen was evaluated by the thermodynamic parameters – Gibbs free energy change (ΔG°), enthalpy (ΔH°) and entropy (ΔS°). These parameters were calculated using the following Eqs (3), (4), (5):
| (3) |
| (4) |
| (5) |
where KC is the distribution coefficient for adsorption, Ca is the equilibrium fluoride concentration on the adsorbent (mg/L) and Ce is the equilibrium fluoride concentration in solution (mg/L). A plot of ΔG° versus temperature, T will be linear with the slope and intercept giving the values of ΔH° and ΔS°.
2.3. Modelling experiment
The experimental design for optimization of Cr(VI) removal on A. niger involves number of steps as per the statistical methodology. A 24 full factorial experiment design with four independent variables (initial concentration, adsorbent dose, contact time and pH) at two levels was carried out initially. The values represent the levels (coded as −1, 0 and +1) of all selected variables which have profound role in the adsorption process (Table not supplied). The response surface methodology developed a curve surface which represents the relationship between the design variables and the response (Design expert trial 8.0.1.7, State-Ease Inc., Minneapolis, USA). The relationship can be represented by the following Eq. (6).
| (6) |
where Y is response and the design variables xi (i = “1………n”). The symbol ε indicates the random error in Y. In order to make the simplicity, a polynomial to express the function ‘f’ can be generally used. A second order design was built to determine if the response surface could be a plane in the range of the tested factors. The model represented in Eq. (7) includes simple, interaction and quadratic factors. This model was used to predict the response variable and subsequently explore the design surface.
| (7) |
where β0, βi, βij are regression coefficients for the intercept, linear and interactions among factors, respectively, Y is the response vector for qe and % Removal, whereas Xi and Xj are the independent factors in coded units, and ε is the error term [4]. The fitness of regression model was evaluated by calculating coefficient of determination (R2).
2.4. Regeneration study
Desorption studies are extremely helpful for recycling the adsorbent and recovery of adsorbate. To remove the adsorbed Cr(VI), the spent adsorbent was treated with 0.5(M) EDTA, equilibrated for 1.5 h, and filtered. After filtration, the filtrate was removed and analysed spectrophotometrically for Cr(VI).
3. Results and discussion
3.1. Adsorbent characterization
The fungal biomass was dried and powdered for scanning electron analysis. Both before and after adsorption of Cr(VI) by fungal biomass were used for SEM study. The change in the surface morphology was studied for both A. niger.
The surface morphology of the A. niger biomass was examined by SEM (Fig. 1a and b), clearly revealing the mycelia. As seen in Fig. 1a, the adsorbent has some heterogeneity which is suppose to be the active site for metal (Cr(VI) binding. SEM picture also revealed that the surface of fungal biomass (A. niger) is flattened after Cr(VI) adsorption. Apart from that no further significant morphological changes were apparent in the SEM image. The hyphae of fungi were cylindrical, septate, and branched. However, when chromium containing mycelium was applied for SEM, it revealed that chromium was uniformly bound to the fungal mycelium and a higher chromium absorption together with flocculation in mycelium was observed (Fig. 1b). The biosorbed chromium was assumed to be Cr(III), as Cr(VI) is reduced to Cr(III) that is free to bind to these sites and, once bound, acts as a template for further heterogeneous nucleation and crystal growth [22].
Figure 1.
(a) SEM image of biomass before adsorption, (b) SEM image of biomass after adsorption.
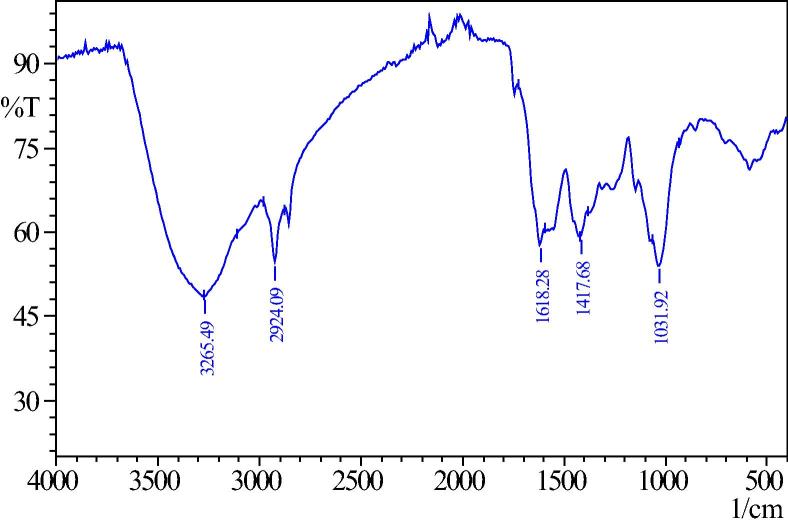
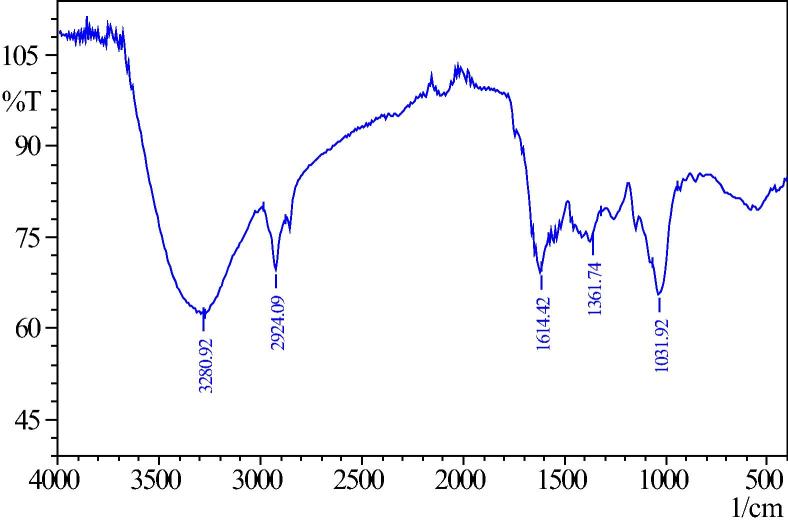
FTIR spectra can provide valuable information about the surface functional groups of the adsorbent. Figure 2a, Figure 2ba and b represent the FTIR of before and after adsorption of Cr(VI) by A. niger. The spectra display variety of stretching frequency indicating the complex nature of the adsorbent. Tharp bands at 3265 cm−1, 1618 cm−1, 1417 cm−1, and 1031 cm−1 can be assigned to alcoholic –OH, carboxylic acid –COOH, –C–H, –N–H and amine –C–N stretching of Cr(VI), the bands at 3265 cm−1, 1618 cm−1 and 1417 cm−1 of unloaded A. niger (Fig. 2a) shifted to 3280 cm−1, 1614 cm−1 and 1361 cm−1 whereas the bands at 2924 cm−1 and 1031 cm−1 remain the same (Fig. 2b). This information clearly indicates that the removal of Cr(VI) is mainly due to interaction of majority of the functional groups containing –OH and –N–H ionizing groups. Bai and Abraham [3] suggested in their paper that Cr(VI) anions were presumably interacting strongly with the positively charged amines of A. niger cell wall. Almost a similar finding was reported by Khambhaty et al. [15].
Figure 2a.
Before removal of chromium by Aspergillus niger.
Figure 2b.
After removal of chromium by Aspergillus niger.
3.2. Effect of initial Cr(VI) ion concentration
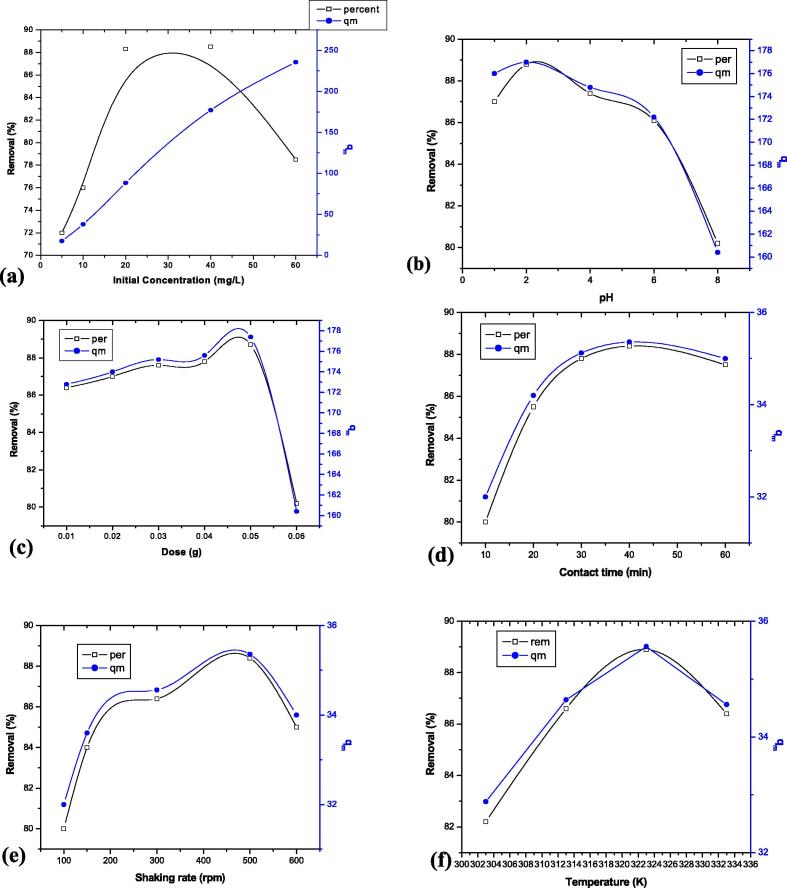
The rate of adsorption is a function of the initial concentration of the adsorbate, which makes it an important factor to be considered for effective adsorption. The effect of different initial Cr(VI) ion concentration on adsorption of Cr(VI) ion onto A. niger biomass is presented in Fig. 3a. The percentage removal of Cr(VI) ion increased with increasing initial Cr(VI) ion concentration. This observation is probably due to gradual saturation of available active centre of fixed amount of adsorbent. Moreover, results also revealed that the adsorption capacity increased with increasing initial concentration of hexavalent chromium. This fact can be attributed that metal ions provide required driving force to exceed the mass transfer resistance of hexavalent chromium between liquid and solid adsorbent. The increase in the initial Cr(VI) ion concentration also enhances the interaction between the Cr(VI) ions in the aqueous phase and the biomass surface. This also leads to enhance the metal uptake capacity of A. niger. Similar results were obtained in the adsorption of Cr(VI) ions by natural plant material. This fact may be attributed to the higher number of active groups available for Cr(VI) adsorption and reduction because of the increased amount of A. niger biomass. Almost a similar result was reported by Aravindhan et al. [2].
Figure 3.
Effect of different operating variables on removal of Cr(VI) by Aspergillus niger biomass (a) initial concentration, (b) pH, (c) adsorbent dose, (d) contact time, (e) shaking rate, (f) temperature.
3.3. Effect of pH
The pH of the solution is one of the most critical parameters in the adsorption process, which affects surface charge of the adsorbent material and the degree of ionization and specification of adsorbate. The effect of pH on the removal efficiency of Cr(VI) ion was studied at different pH values ranging from 1.0 to 6.0, the results are depicted in Fig. 3b. Fig. 3b also suggests that there is sharp decline of Cr(VI) removal when solution pH changes from 1 to 6.0. The maximum adsorption of Cr(VI) ions are obtained at pH 2.0. So, pH 2.0 was selected as optimum pH for Cr(VI) ion adsorption onto A. niger biomass. From the stability diagram, it was evident that the most prevalent form of Cr(VI) in aqueous solution was acid chromate (HCrO4−), chromate (CrO42−), dichromate (Cr2O72−) and other oxyanions of Cr. Dominant form of Cr(VI) at initial pH of 2 is acid chromate (HCrO4−). An increase in pH facilitates the conversion of HCrO4− to other forms, CrO42− and Cr2O72−. The decrease in Cr(VI) ion removal efficiency at higher pH might be due to the competition between OH− and chromate ions (CrO42−), where the former being the dominant species wins the race [31]. This is in agreement with our experimental observations showing a very low removal at pH 8. The effect of pH can be explained by its influence on the protonation of the functional groups on the cell surface [3], [10]. At the pH values 1.5 and 2, functional groups such as amino groups are protonated (NH3+) and chromate ions are in the forms Cr2O72− and HCr2O4−. The negatively charged dichromate ions are electrostatically attracted by the positively charged amino groups. However, earlier researches [22], [23], [9] indicate that at this pH value, Cr(VI) is also rapidly reduced to Cr(III).
3.4. Effect of adsorbent dose
In this study, six different adsorbent dosages were selected ranging from 0.01 to 0.05 g while the Cr(VI) concentration was fixed at 40 mg/L. The results are presented in Fig. 3c. It was observed that removal of hexavalent chromium gradually increased with an increment of A. niger biomass in aqueous medium. Such a trend is mostly attributed to an increase in the absorptive surface area and the availability of more active binding sites on the surface of the adsorbent. However, after a certain point, the equilibrium adsorption capacity decreased. This perhaps is due to reduction of effective active centre available for hexavalent chromium binding through the amount of adsorbate available in the medium [21]. As a matter of fact, aqueous medium does not get chance to attach to the surface of the adsorbent and subsequently qe value decreased with an increase in adsorbent dose. Furthermore, maximum Cr(VI) ion removal (87.8%) was recorded by 0.05 g A. niger biomass and further an increase in adsorbent dose did not significantly change the adsorption yield. This is due to the non-availability of active sites on the adsorbent and establishment of equilibrium between the Cr(VI) ion on the adsorbent and in the solution.
3.5. Effect of contact time
The uptake of Cr(VI) ion as a function of contact time is shown in Fig. 3d. As illustrated in Fig. 3, adsorption of Cr(VI) ion increased with a rise in contact time up to 40 min. Further increase in contact time did not increase the Cr(VI) adsorption process. The equilibrium was nearly reached at 40 min for fixed initial Cr(VI) ion concentration (40 mg/L). Hence, in the present work, 60 min was chosen as the equilibrium time. The higher rate of adsorption at the initial stage is perhaps due to huge active centre available on the surface of A. niger [16]. In the later stage the sorption is likely an attachment-controlled process due to less available sorption sites. The uptake capacity of Cr(VI) against time t curve is absolutely smooth and continuous leading to saturation, indicating the possible monolayer coverage of the Cr(VI) on the surface of A. niger biomass [6]. Similar findings for Cr(VI) adsorption onto other adsorbents have been reported by other investigators [2], [11].
3.6. Effect of shaking rate
The effect of shaking rate on Cr(VI) adsorption is shown in Fig. 3e and it appears that shaking rate has pronounced effect on the amount of Cr(VI) adsorbed. As the shaking rate increased from 100 to 500 rpm, the adsorption capacity increased from 32.00 to 35.36 mg/g. However beyond 500 rpm, the adsorption capacity decreased. The enhancement of adsorption at higher shaking rate is probably due to thinning of boundary layer thickness near the adsorbent surface [6], [13]. Therefore, with increasing shaking rate the concentrations of Cr(VI) ions near the adsorbent surface would be increased. A higher shaking rate also encouraged a better mass transfer of Cr(VI) ions from bulk solution to the surface of the adsorbent and shortened the adsorption equilibrium time. Study result revealed that adsorption of hexavalent chromium increases with increasing agitation speed. However, removal status of Cr(VI) showed almost constant after reaching an optimum speed [14].
3.7. Effect of temperature
Temperature has tremendous role in adsorption chemistry [19]. The percentage of Cr(VI) adsorption was studied as a function of temperature in the range 30–60 °C. The results obtained are shown in Fig. 3f. The Fig. 3f demonstrated that the percentage removal of hexavalent chromium is increased with increasing temperature. That means the interaction between Cr(VI) and A. niger is absolutely endothermic in nature. However, Choudhary et al. [6] reported that Cr(VI) removal decreases with an increase in temperature.
3.8. Adsorption isotherms
Biosorption isotherms describe the relationship between the mass of the adsorbed component per biosorbent mass and the concentration of this component in the solution [17]. The assessment helps to construct better adsorbent for future research. In the present study, the Langmuir, Freundlich, Temkin, Dubinin-Radushkevich (D-R) models were used to evaluate the equilibrium data. The calculated results of the Langmuir, Frendulich, Temkin and D-R isotherm constant are given in Table 1. It is observed that only Freundlich and Temkin isotherms showed good agreement with high R2 value. The Dimensionless constant RL are 0.0613, 0.03162, 0.0213 and 0.0160 which again indicate the overall adsorption process is favourable (Supp Table 3).
Table 1.
Adsorption isotherm constants for adsorption of Cr(VI) onto biomass of Aspergillus niger.
| Adsorption isotherm | Parameters | R2 | |
|---|---|---|---|
| Langmuir isotherm |
qmax, mg/g KL, L/mg |
11.792 0.175 |
0.539 |
| Freundlich isotherm |
KF, mg/g, (L mg−1)1/n n |
23.927 × 104 0.110 |
0.675 |
| Temkin isotherm |
B, mg/g A |
8.0 × 10−4 1.525 |
0.812 |
| D-R isotherm |
qm, mg/g β, mol2 kJ−2 E, kJ mol−1 |
4.344 5822 2.9 × 10−3 |
0.127 |
The D-R constants qm and β were calculated from the linear plots of lnqe versus ε2 and are given in Table 1. The constant β gives an idea about the mean free energy E (kJ/mol) of adsorption per molecule of the adsorbate when it is transferred to the surface of the solid from infinity in the solution and can be calculated from the relationship;
| (8) |
If the magnitude of E is between 8 and 16 kJ mol−1, the sorption process is supposed to proceed via chemisorptions, while for values of E < 8 kJ mol−1, the sorption process is of physical nature. The present study results indicate that Cr(VI) sorption onto A. niger biomass is absolutely physical interaction.
3.9. Adsorption kinetics
The kinetics of the chromium biosorption was evaluated by applying Pseudo first order, Pseudo second order and intraparticle diffusion model. The constants of all the above mentioned kinetics models are determined experimentally by non-linear regression. The value of rate constant is given in Table 2 along with correlation coefficient values. Calculated correlations coefficient is very high for both Pseudo-first-order and Pseudo-second-order kinetics models. Therefore, the biosorption kinetics could well be estimated more favourably by Pseudo first order and Pseudo second order kinetics models rather than intraparticle diffusion model.
Table 2.
Kinetic parameters for adsorption of Cr(VI) onto biomass of Aspergillus niger.
| Adsorption isotherm | Parameters | R2 | |
|---|---|---|---|
| Pseudo-first-order |
qe,exp, mg/g k1, min−1 |
1.156 20.255 |
0.878 |
| Pseudo-second-order |
k2, g/mg−1 min−1 qe,cal, mg/g |
0.022 0.106 |
0.942 |
| Intraparticle diffusion |
Kd, mg/g·min1/2 I |
4.119 298.36 |
0.306 |
3.10. Adsorption thermodynamic
The study of free energy, enthalpy and entropy are important thermodynamic parameters for better understanding the entire adsorption process. For calculating thermodynamic parameters, following equations are follows:
| (9) |
| (10) |
where Ce is the equilibrium concentration in solution in mg/L and CAe is the equilibrium concentration on the sorbent in mg/L and Kc is the equilibrium constant. The Gibbs free energy (ΔG°) for the adsorption of A. niger leaf dust at all temperatures was obtained from Eq. (10) and is presented in Table 3. From Table 3 it is clear that the reaction is spontaneous in nature as G° values are negative at all the temperature studied. The gradual increase in free energy with temperature, suggest that the adsorption is favourable at a higher temperature.
Table 3.
Thermodynamic parameters for adsorption of chromium (VI) by biomass of Aspergillus niger.
| Temperature (K) | ΔG°(kJ/mol) | ΔH° | ΔS° |
|---|---|---|---|
| 303 | −5026.217 | ||
| 313 | −5192.099 | 89.537 | 13.619 |
| 323 | −5205.368 | ||
| 333 | −5470.04 |
3.11. Box–Behnken analysis
Total 29 experiments were performed for four different independent process parameters and their interaction effect on percent removal of Cr(VI). The entire experimental designed along with observed and predicted values are depicted in Supp Table 4. A second-order polynomial equation was developed which represent responses as functions of initial Cr(VI) and pH(D). An empirical relationship between the percent removal and the input test variables in coded units can be expressed by the flowing equation:
| (11) |
In the above Eq. (11) A, B, C and D are independent singular factors, whereas AB, AC, AD, BC and CD are interaction factors and the quadratic terms include A2, B2, C2 and D2.
Table 4 represents the analysis of variance (ANOVA) results of the full factional design using the experimental data. The ANOVA was performed by means of Fisher’s F-test. The model F-value was recorded 52.54 enlightening that the model was significant (p < 0.0001); R2 of 0.9813, and co-efficient of variation is 2.11%. As the model indicates high F-value (52.54) with probability level p < 0.0001, the experiment is accurate and reliable. The prob > F value is the probability of F-statistics value and is used to test the null hypothesis. The parameters having an F-statistics probability value less than 0.05 are said to be significant (Supp Table 5). The adequate precision ratio is 27.725 which measures the signal to noise ratio of this model that is greater than 4, this model can be used to navigate the design space. The ‘Lack of fit F-value ‘of 191.02 implies the lack Fit is significant. There is only a 0.52% chance that a ‘Lack of fit F-value’ this large to occur due to noise (Supp Table 6). On the other hand, a high value adjusted determination co-efficient (R2 = 0.9626) was estimated. This result indicates 96.26% of the total variation on Cr(VI) biosorption data can be describe by the selected model.
Table 4.
Analysis of variance (ANOVA), regression coefficient estimate and test of significance for Cr(VI) removal on Aspergillus niger.
| Source | Sum of squares | df | Mean square | F value | p-value prob > F |
|---|---|---|---|---|---|
| Model | 1923.58 | 14 | 137.40 | 52.54 | <0.0001 |
| A-Initial concentration | 10.09 | 1 | 10.09 | 3.86 | 0.0696 |
| B-Adsorbent dose | 202.67 | 1 | 202.67 | 77.51 | <0.0001 |
| C-pH | 6.00 | 1 | 6.00 | 2.29 | 0.1522 |
| D-contact time | 13.91 | 1 | 13.91 | 5.32 | 0.0369 |
| AB | 147.78 | 1 | 147.78 | 56.51 | <0.0001 |
| AC | 0.67 | 1 | 0.67 | 0.25 | 0.6216 |
| AD | 7.59 | 1 | 7.59 | 2.90 | 0.1106 |
| BC | 41.05 | 1 | 41.05 | 15.70 | 0.0014 |
| BD | 2.65 | 1 | 2.65 | 1.01 | 0.3313 |
| CD | 9.19 | 1 | 9.19 | 3.51 | 0.0819 |
| A2 | 617.87 | 1 | 617.87 | 236.28 | <0.0001 |
| B2 | 4.07 | 1 | 4.07 | 1.56 | 0.2324 |
| C2 | 1.63 | 1 | 1.63 | 0.62 | 0.4432 |
| D2 | 37.05 | 1 | 37.05 | 14.17 | 0.0021 |
| Residual | 36.61 | 14 | 2.61 | ||
| Lack of fit | 36.58 | 12 | 3.05 | 191.02 | 0.0052 |
| Pure error | 0.032 | 2 | 0.016 | ||
| Cor total | 1960.19 | 28 |
In this result B, D, AB, BC, A2 and D2 are significant model terms. The “Lack of fit F value” of 119.02 implies that lack of fit is significant relative to the pure error. There is a 0.52% chance that a “Lack of Fit F value” (Supp Table 6).
Furthermore, Supp Fig. 1a represents the relationship between actual values and predicted values. From the Supp Fig. 1a it is clear that actual values are distributed near the straight line, indicating nice fitness of the model [25]. The assumption of normality can be checked by constructing a normal probability curve of the residuals (Supp Fig. 1b). Again in Supp Fig. 1c, demonstrate the relationship between studentized residuals versus predicted was tested and the residuals were scattered randomly around ±3.00. This was an indication of better fitment of the model with experimental data.
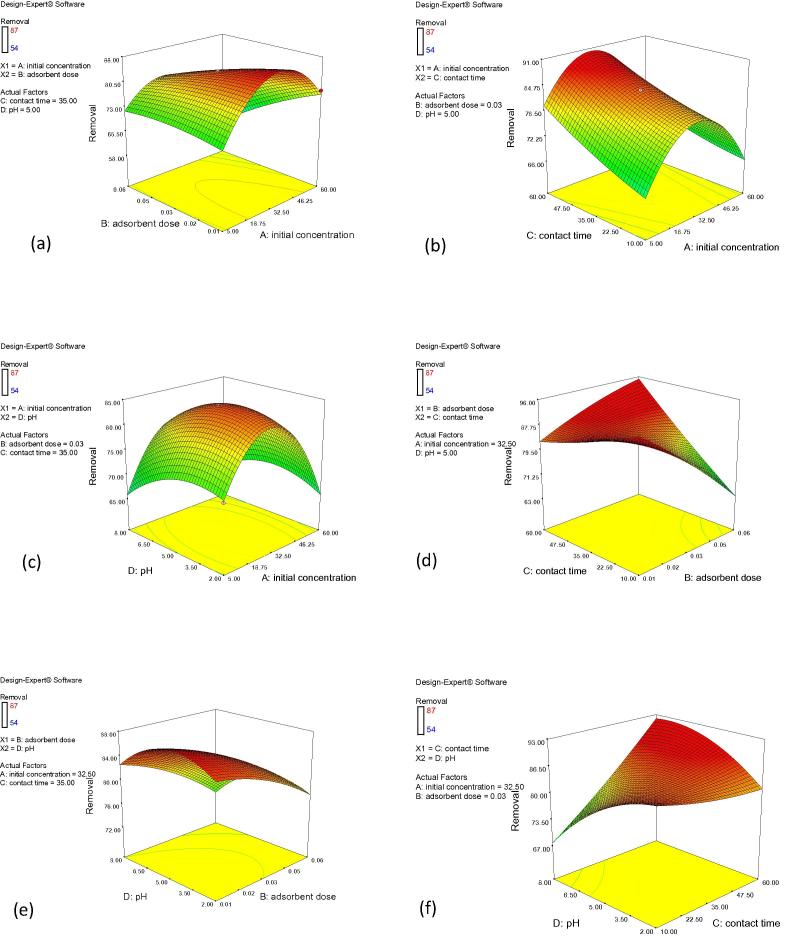
On the other hand, the hierarchical quadratic model was used to represent the response surface in three-dimensional plots and to find the optimal conditions for Cr(VI) adsorption on A. niger. Response surface space was built taking into account with the operating variables (Fig. 4). Fig. 4 shows that the model predicted Cr(VI) adsorption efficiency close to 87.16% onto A. niger. 3D Mesh diagram was obtained from RSM design matrix (Fig. 4a–f) and it is basically used in order to note the point of optimum response as well as to study the effect of each parameter on the biosorption process [33]. Altogether six mesh diagrams were constructed by varying adsorbent dose and initial concentration when contact time pH were kept constant (Fig. 4a). In the similar ways other plots were drawn (Fig. 4b–f).
Figure 4.
(a–f) Response surface plots showing the effect of independent variables on Cr(VI) biosorption onto Aspergillus niger.
3.12. Optimization using desirability functions
The desirability functions are very much important for computing optimization of desired goal for each factor and responses. The possible goals for the present experiment are: maximize, minimize, target, within range, none (for response only) and set to an exact value (factor only). Finally, the overall desirability function can be obtained by combining the desired goals. The optimization of Cr(VI) biosorption was determined at an initial concentration of Cr(VI) 33.33 mg/L, adsorbent dose (A. niger) 1.0 g/L, pH 4.00 and contact time 48.45 min. Under these optimize conditions, maximum Cr(VI) biosorption was recorded as 87.00% with a desirability of 1.00 (Supp Fig. 2). The obtained value of desirability shows that the estimated function may represent the experimental model and desired conditions (Supp Table 7).
3.13. Regeneration study
Reuse of exhausted adsorbent is extremely important for minimization of metal contamination. Moreover, reusability of spent adsorbent can be assessed by its adsorption performance in successive adsorption–desorption operation [32]. Keeping in mind, the above needs, a regeneration study has been done for further use of already exhausted adsorbent. The entire desorption of Cr(VI) was studied by different concentrations (0.05, 0.1, and 0.5 M) of EDTA solution (Supp Fig. 3). From Supp Fig. 3 it is clear that 96.1% of Cr(VI) was effectively desorbed from the biosorbent using 0.5 (M) EDTA solution. Almost similar desorption study of chromium was reported by Reya et al. [24]. They reported that 94% of Cr(VI) can be effectively removed using EDTA.
3.14. Comparative study
The Langmuir adsorption study of various published adsorbent is presented in Table 5. From the table it has been found that maximum adsorption capacity of Rhizopus nigricans was recorded 123.45 mg/g at pH 2, followed by S. obliquus, R. arrhizus and C. vulgaris at same pH of the solution. All other adsorbents showed adsorption capacity ranging from 3.0 to 14.7 mg/g. The present dead A. niger biomass showed adsorption capacity 11.792 at pH 2 which is quite good than any other reported biosorbents.
Table 5.
Biosorption of Cr(VI) ions by different biosorbents.
| Biosorbent | Biosorption capacity (mg/g) | pH | Biosorbent concentration (mg/L) | References |
|---|---|---|---|---|
| Plam flower (acid treated) | 7.13 | 4.5 | 10.0 | Selvi et al. [32] |
| Activated carbon from coconut tree saw dust | 3.46 | 8.0 | 50.0 | Gupta et al. [24] |
| Spirogyra | 14.7 | 2.0 | 5.0 | Kratochvil and Volesky [36] |
| Hazelnut shell | 9.38 | 1.0 | 4.0 | Cimino et al. [37] |
| S. obliquus | 58.8 | 2.0 | 2.0 | Cetinkaya et al. [38] |
| C. vulgaris | 79.3 | 2.0 | 2.0 | Cetinkaya et al. [38] |
| Rhizopus nigricans | 123.45 | 2.0 | 1.0 | Sudha and Abraham [39] |
| Zooglea ramigera | 3.0 | 2.0 | – | Vegliò and Beolcini [40] |
| P. chrysosporium | 11.02 | 4.0 | 0.1 | Singh et al. [41] |
| C. resinae | 10.69 | 5.0 | 0.1 | Singh et al. [41] |
| P. resinae | 10.35 | 4.0 | 0.1 | Singh et al. [41] |
| Rhizopus arrhizus | 78.0 | 2.0 | 100 | Aksu and Balibek [42] |
| Aspergillus sp. | 11.792 | 2.0 | 1.0 | Present study |
4. Conclusion
The present study has revealed that A. niger were effective in removing Cr(VI) from aqueous solution. The sorption of Cr(VI) process was found to depend on pH of the medium, pH 2.0 being the optimum value. Kinetics of the Cr(VI) adsorption data showed that biosorption of Cr(VI) by A. niger followed well the Pseudo-second-order kinetics model. Equilibrium data fitted well with the Langmuir adsorption isotherm. Response surface methodology based on 4-level Box-Behnken design was used to optimize various parameters for Cr(VI) biosorption. According to ANOVA analysis, Cr(VI) removal is highly affected by initial concentration of Cr(VI), and adsorbent dose. The hierarchical quadratic model represents adequately the response surface space based on the adjusted determination coefficient (Radj2 = 0.96) and adequate precision ratio (27.73). Using this model, optimum conditions are pH 4.6, 0.05 g of biomass and contact time 48.45 min. At these conditions, the predicted removal efficiency achieved was nearly 87.11% of Cr(VI) from aqueous solution using A. niger biomass. Regeneration studies suggested that the spent adsorbent can desorb 96.1% of Cr(VI) using 0.5(M) EDTA solution. Based on all results, it can be concluded that A. niger biomass will be an effective and alternative biosorbent for removal of Cr(VI) from aqueous solution because of its easy availability as well as low cost.
Acknowledgements
The authors are thankful to all faculty members and nonteaching staff of the Department of Environmental Science, University of Burdwan, West Bengal, India for providing infrastructural facilities and active moral support towards completion of this work.
Footnotes
Peer review under responsibility of National Research Center, Egypt.
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.jgeb.2017.01.006.
Appendix A. Supplementary data
References
- 1.Ahluwalia S.S., Goyal D. Life Sci. 2010;10(5):480–485. [Google Scholar]
- 2.Aravindhan R., Fathima A., Selvamurugan M., Rao J.R., Balachandran U.N. Clean Technol. Environ. Policy. 2012;14:727–735. [Google Scholar]
- 3.Bai R.T., Abraham E. Bioresour. Technol. 2001;79:73–81. doi: 10.1016/s0960-8524(00)00107-3. [DOI] [PubMed] [Google Scholar]
- 4.Chattoraj S., Mondal N.K., Das B., Roy P., SadhukhanAppl B. Water Sci. 2013 [Google Scholar]
- 5.Chhikara S., Dhankhar R. J. Environ. Biol. 2008;29:773–778. [PubMed] [Google Scholar]
- 6.Choudhary T.R., Amin M.N., Quraishi S.B. Res. J. Eng. Appl. Sci. 2014;3(1):1–6. [Google Scholar]
- 7.J.S. Clesceri, A.E. Grenberg, A.D. Eaton, Twentieth ed., 1998, pp. 3–13.
- 8.K. Dokken, G. Gamez, I. Herrera, K. Tiemann, N.E. Pingitore, R.R. Chianelli, in: Proceedings of the Conference on Hazardous Waste Research, Snowbird, Utah, 1999, pp. 101–113.
- 9.Dupont L., Guillon E. Environ. Sci. Technol. 2003;37:4235–4241. doi: 10.1021/es0342345. [DOI] [PubMed] [Google Scholar]
- 10.D.K. Eaton, L. Kann, S. Kinchen, et al., 55(5) (2005) 1–108. [PubMed]
- 11.C. Escudero, N. Fiol, I. Villaescusa, J-C. Bollinger, 2013 doi: 10.1016/j.arabjc.2013.03.011.
- 12.Ghosh S.B., Baumik R., Mondal N.K. Clean Technol. Environ. Policy. 2016;18:1069–1083. [Google Scholar]
- 13.Hanafiah M.A.K., Zakaria H., Wan Ngah W.S. Water Air Soil Pollut. 2009;201(1-4):43–53. [Google Scholar]
- 14.Hu J., Lo I.M., Chen G. Water Sci. Technol. 2004;50(12):139–146. [PubMed] [Google Scholar]
- 15.Khambhaty Y., Mody K., Basha S., Jha B. World J. Microbiol. Biotechnol. 2009;25:1413–1421. [Google Scholar]
- 16.Makshoof A., Umar F., Sana Z.A., Salman M. Clean Technol. Environ. Policy. 2014;16:579–590. [Google Scholar]
- 17.Mondal N.K., Roy S. Clean Technol. Environ. Policy. 2016;18:429–447. [Google Scholar]
- 18.Mondal N.K., Roy S. Clean Technol. Environ. Policy. 2016;18:429–447. [Google Scholar]
- 19.Mondal N.K., Das K., Das B., Sadhukhan B. Clean Technol. Environ. Policy. 2015 [Google Scholar]
- 20.R.H. Myers, D.C. Montgomery, C.M. Anderson-Cook, third ed., Wiley, New York, 2009.
- 21.Nethaji S., Sivasamy A. Clean Technol. Environ. Policy. 2014;16:361–368. [Google Scholar]
- 22.Park D., Yun Y.S., Park J.M. Process Biochem. 2005;40:2559–2565. [Google Scholar]
- 23.Park D., Yun Y.S., Jo J.H., Park J.M. Water Res. 2005;39:533–540. doi: 10.1016/j.watres.2004.11.002. [DOI] [PubMed] [Google Scholar]
- 24.Reya I.I., Rajamehala M., Lakshmi P.M., Emilin R.R. Int. J. Chem. Tech. Res. 2012;4(4):1708–1719. [Google Scholar]
- 25.Sadhukhan B., Mondal N.K., Chattoraj S. Clean Technol. Environ. Policy. 2014;16(6):1015e1025. [Google Scholar]
- 26.Saha R., Kakali M., Saha I., Ghosh A., Ghosh S.K., Saha B. Res. Chem. Intermed. 2013;39:2245–2257. [Google Scholar]
- 27.Sarkar S., Gupta A. Indian J. Environ. Health. 2003;45:73–82. [PubMed] [Google Scholar]
- 28.Selvi K., Pattabhi S., Kadirvelu K. Bioresour. Technol. 2001;80:87–89. doi: 10.1016/s0960-8524(01)00068-2. [DOI] [PubMed] [Google Scholar]
- 29.Sobol Z., Schiestl R.H. Environ. Mol. Mutagen. 2012;53:94–100. doi: 10.1002/em.20679. [DOI] [PubMed] [Google Scholar]
- 30.Sobol Z., Schiestl R.H. Environ. Mol. Mutagen. 2012;53:94–100. doi: 10.1002/em.20679. [DOI] [PubMed] [Google Scholar]
- 31.Sugashini S., Begum K.M.M.S. Clean Technol. Environ. Policy. 2013;15:293–302. [Google Scholar]
- 32.Sukumar C., Janaki V., Vijayaraghavan K., Kamala-Kannan S., Santhi K. Clean Technol. Environ. Policy. 2016 [Google Scholar]
- 33.Varsihini C.J.S., Das D., Das N. J. Rare Earths. 2014;32(8):745–758. [Google Scholar]
- 34.Vijayaraghavan K., Yun Y.S. Chem. Eng. J. 2008;145:44–49. [Google Scholar]
- 35.Wang X.S., Tang Y.E.P., Tao S.R. Adsorption. 2008;14:823–830. [Google Scholar]
- 36.Kratochvil D., Volesky B., Demopoulos G. Water Res. 1997;31:2327–2339. [Google Scholar]
- 37.Cimino G., Passerini A., Toscano G. Water Res. 2000;34:2955–2962. [Google Scholar]
- 38.Cetinkaya D.G., Aksu Z., Ozturk A., Kutsal T. Process Biochem. 1999;34:885–892. [Google Scholar]
- 39.Sudha B.R., Abraham T.E. Bioresour. Technol. 2001;79:3–81. doi: 10.1016/s0960-8524(00)00107-3. [DOI] [PubMed] [Google Scholar]
- 40.Vegliò F., Beolchini F. Hydrometallurgy. 1997;1997(44):301–316. [Google Scholar]
- 41.Singh U., Singh B.P., Singh K.K. J. Chem. Pharmaceu. Res. 2012;4(6):3063–3072. [Google Scholar]
- 42.Aksu Z., Balibek E. J. Hazard Mater. 2007;145:210–220. doi: 10.1016/j.jhazmat.2006.11.011. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.