Advances in coarse-grained modeling of macromolecular complexes

Abstract

Recent progress in coarse-grained (CG) molecular modeling and simulation has facilitated an influx of computational studies on biological macromolecules and their complexes. Given the large separation of length- and time-scales that dictate macromolecular biophysics, CG modeling and simulation are well-suited to bridge the microscopic and mesoscopic or macroscopic details observed from all-atom molecular simulations and experiments, respectively. In this review, we first summarize recent innovations in the development of CG models, which broadly include structure-based, knowledge-based, and dynamics-based approaches. We then discuss recent applications of different classes of CG models to explore various macromolecular complexes. Finally, we conclude with an outlook for the future in this ever-growing field of biomolecular modeling.

Introduction

Many biological processes rely on macromolecules to serve as building blocks for large-scale complexes, exemplified by viruses, ribosomes, and cytoskeletal filaments [1–3]. These so-called macromolecular complexes often contain many copies of the same macromolecule that collectively aggregate through non-covalent interactions into ordered and functional suprastructures [4]. Furthermore, the lifecycles of these complexes are inherently dynamic, in which configurational transitions act as regulatory signals [5].

Since molecular phenomena at the scale of individual macromolecules translates into emergent and collective macroscopic behavior, it is clear that a fundamental understanding of these intriguing biophysical complexes requires a hierarchical approach. Recent advances in experimental techniques now offer multifaceted insights into these systems. For example, ensemble-averaged atomic structures can be resolved at high-resolution using X-ray crystallography or cryo-electron microscopy [6,7]. For dynamic information, one may use fluorescence techniques [8,9] or nuclear magnetic resonance (NMR) spectroscopy [10,11], albeit with lower spatial resolution. To complement these experimental approaches, theorists may attempt to leverage all-atom (AA) molecular dynamics (MD) simulations to access dynamical phenomena with molecular-scale resolution [12].

Within the space of MD simulation techniques, coarse-grained (CG) modeling and simulation are particularly attractive for the study of macromolecular complexes. By design, CG models are reduced representations of AA models that aim to retain the essential molecular aspects for the biophysical system of interest. As a result, CG simulations have three primary benefits in comparison to AA simulations. First, these models enable simulations of large, biologically-relevant systems by virtue of the reduced number of particles. Second, the removal of highly-fluctuating atomic degrees of freedom facilitates faster configurational sampling, as both larger integration time steps can be used while the underlying free energy surface is smoother. Hence, the combination of these first two benefits may facilitate observation of interesting collective behavior. Finally, the construction of useful CG models grants tacit insight into molecular features (i.e., from CG mappings) and interactions (i.e., from CG parameterizations) that are essential for biophysical function. For these reasons, CG simulations may provide insights and perspectives that would otherwise be inaccessible from AA molecular simulations, which has indeed driven the continued use and development of CG models and methods.

In this review, we summarize recent advances in the development and application of CG models for studying the structure and dynamics of biological macromolecules. In particular, we focus on highly CG models for proteins and nucleic acids, i.e., per-residue resolutions or coarser, which enable large-scale simulations of CG macromolecular complexes. Interested readers may refer to other in-depth reviews that discuss related topics, including higher-resolution CG models and ultra-low-resolution phenomenological models for proteins, membranes, carbohydrates and nucleic acids [13–17]. We first broadly describe the most common methodologies for CG modeling that have been developed over the last five years, with our intention to expand upon previous reviews on this subject, e.g., references [18,19]. We then survey recent uses of these models for macromolecular complexes, for which CG models have provided new insights. We conclude with a brief summary and discussion on the future outlook of the field.

Coarse-Grained Modeling of Large Biomolecules

As CG models have grown in both popularity and utility, so have the strategies for generating CG models of macromolecular complexes. Here, we focus on low-resolution models that have been used extensively; specifically, we refer to CG models that resolve proteins (nucleic acids) at the per-residue (per-backbone/sidechain) level or coarser. All procedures for CG modeling must answer two questions: how do we define the correspondence between atomic and CG degrees of freedom (i.e., mapping) and how do we define the effective interactions between CG sites (i.e., energetics)? Within our scope, we further classify three methodological avenues that have been used to approach these questions. We denote these as structure-based, knowledge-based, and dynamics-based approaches, which are each described below and schematically shown in Figure 1.

Figure 1.

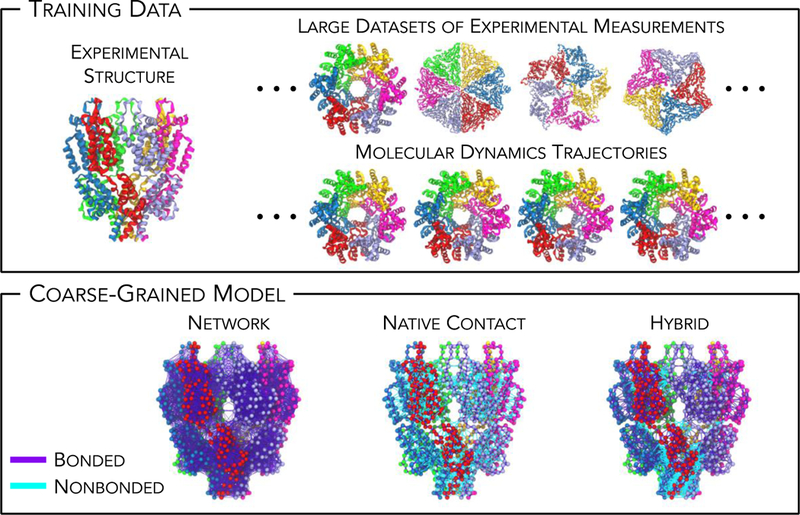
Different avenues of approach for model development of highly coarse-grained (CG) macromolecules, which are broadly classified into structure-based, knowledge-based, and dynamics-based strategies. Here, the capsid and spacer peptide 1 (CA-SP1) domains of the human immunodeficiency virus (HIV) protein is used as a representative example. (Top) Each model class relies on different training datasets and methods; for example, an experimental structure (PDB 5L93), an extended dataset of experimental measurements (PDB 5L93, 3ZX8, 3J37 and 6BVF), or statistics from an all-atom molecular dynamics trajectory (initial structures from PDB 5L93), respectively. (Bottom) Resultant models can be classified as network-based and native-contact-based models (or hybrids thereof); bonded (nonbonded) interactions are depicted by solid purple (cyan) lines while CG sites (per residue) are depicted as spheres.

Structure-based approaches.

As perhaps the most prevalent CG approach in the literature, structure- based methods aim to leverage atomic-resolution experimental data on native structures to construct CG models. An underlying assumption in these models is that conservation of close contacts between residues that are observed in native structures are important for the functional dynamics of these biomolecules. Based on this intuition, mapping is typically prescribed such that each CG site represents a different residue, which, for example, may be based on C-α positions.

Two broad methods exist to describe the energetics of these CG models, i.e., the effective CG interactions. The first strategy is to use so-called network models in which the CG molecule is described by a graph of proximal masses that are connected by springs; by construction, the ground state predicted by network models yields the experimental structure. In the past, several network models have been proposed [20–23], which, when combined with spectral graph analysis techniques (e.g., normal mode or principal component analysis), provide considerable information on the conformational modes of macromolecules. The other strategy is to use so-called (off-lattice) Gō models [24,25], which instead describe native contacts using attractive, non-bonded interactions, while all other (i.e., non-native) interactions are assumed to be purely repulsive. However, in all of these earlier methods, the prescribed energy landscape is funneled such that only states that minimally frustrate the experimental topology are allowed [26]. Consequently, both network and Gō models have limited usability when large conformational transitions or changes in chemical environment (e.g., through mutations or ligand interactions) are of interest.

To address these deficiencies, variants of both network and native-contact models have recently been reported. The ability to investigate large-amplitude changes during conformational transitions, for example, has been enabled by network models [27,28] and Gō models [29–31] that utilize an energy landscape constructed from the mixture of single-state energetics from two or more different conformational states. However, it remains to be seen if physically-relevant transition states and associated pathways can be predicted by these methods, which warrants further investigation. Other proposed variants have suggested the need to go beyond simple harmonic (Lennard-Jones) interactions that are common in network (native-contact) models. For instance, algorithms inspired from graph theory [32,33] have been proposed as a means to differentiate network weights based on chemical fragments to ultimately improve accuracy. In alternative formulations, network bonds have been replaced by local density kernels for flexibility analysis [34]. Native-contact models have undergone a similar treatment. To represent implicit anisotropic interactions (e.g., due to the presence of side chains), which may only be active in certain configurations, virtual binding sites have been introduced [35,36]. The self-organizing polymer (SOP) model has also been suggested as a variant of Gō models with softer bonded and repulsive interactions. This approach ostensibly improves agreement with force-induced folding and unfolding behavior, and has shown empirical success for both proteins and RNA [37–39].

Importantly, many recent CG models have opted to hybridize both network-based and native-contact-based approaches [35,36,40–43]; for example, a network model could represent different intra-protein conformers, while a native-contact model represents inter-protein interfaces. Indeed, this type of approach is well-suited for studies of large-scale macromolecular complexes. However, several aspects of structure-based CG modeling remain open-ended. Mapping of CG sites, for example, is almost entirely decided by chemical intuition, and mostly at the level of C-α atoms. While systematic mapping methods for structure-based CG models are not as prevalent, some promising directions have recently been reported. For instance, graph decimation methods have been shown to generate a hierarchy of network model resolutions, which may be easily extended as a mapping operator [33]. In addition, the ability to discriminate phenomena based on physical chemistry principles remains a challenge. In the next section, we describe knowledge-based CG models which attempt to resolve some of these issues.

Knowledge-based approaches.

Broadly speaking, we define knowledge-based approaches as CG parameterization strategies that leverage the growing collection of different macromolecules (and their conformers) with solved experimental structures or measured macroscopic properties. Here, the goal is to design CG models with greater degrees of transferability and chemical specificity, i.e., a generalized model that can be used to independently describe any given macromolecular assembly of interest. Knowledge-based approaches have been used in the past to propose residue-specific pair interactions, such as in the well-known Miyazama-Jernigan potential [44,45]. Recently, there has been a resurgence of knowledge-based approaches, which have been timely given advances in macromolecular structure characterization and statistical methodologies.

Knowledge-based models that build upon aforementioned structure-based models have been proposed for both protein and nucleic acid CG models. The primary distinction between these methods is the choice of the target observable. For instance, parameter sets for network models have been introduced that delineate different inter-residue coupling forces to reproduce experimental Debye-Waller factors [46]. On the basis of statistical distributions of residue contacts observed in training sets of experimental structures, it is possible to formulate hybrid network/native-contact models that capture pairwise energies [47], vibrational entropies [42,43], relative entropies [48,49], and maintained contacts [50]. In the case of intrinsically disordered proteins, in which native states are largely unknown, large datasets of radius of gyrations were used to parameterize effective CG potentials. Similar approaches have been adopted for RNA, although it appears that more complex CG interactions are needed to also account for base-pair orientation [51,52].

A prime example of knowledge-based models has been for protein structure prediction and homology modeling, e.g., as evaluated by the Critical Assessment of Structure Prediction (CASP) experiments [53]. To this end, one consideration that requires further investigation is the transferability of current knowledge-based models. In practice, training sets are composed of related proteins, and it is unclear if models generated from one set (e.g., globular proteins) can be successful applied toward another set (e.g., intrinsically disordered proteins).

Another promising direction for knowledge-based models is to leverage Bayesian inference techniques, which have previously been applied to calibrate and select optimal force fields for MD simulations [54–56]. Within our scope, the question is how can we infer reference atomic distributions from CG data? Recently, an approach was reported that sought to determine optimal mappings and energetics of individual proteins by the use of a combination of experimental atomic models and low-resolution cryoEM density maps [57,58].

Dynamics-based approaches.

While the previous two approaches are largely dependent on experimental data, dynamics-based approaches instead use systematic algorithms to derive CG mappings and energetics based on molecular-level statistics from AA MD simulations. Mapping procedures, for instance, may determine the optimal clustering of atoms into CG sites to recapitulate the lowest-frequency collective motions [59,60] or to maximize the relative fluctuations between sites [61] for a given number of CG particles. Determination of the optimal number of CG sites is also possible based on scaling laws for the residual thermal fluctuations obtained from CG-mapped AA trajectories [62]. Similarly, methods to parameterize network models to recapitulate fluctuations from MD simulations have been reported [63,64], while generalized extensions of this model have been trained on ensembles of proteins with different force-fields [65,66]. However, while numerous strategies have been developed to systematically parameterize CG interactions [67–74], these methods have found limited use in CG modeling studies of macromolecular complexes. In part, the difficulty is in capturing all of the relevant physics, including many-body effects such as hydrophobicity, in CG models (e.g., due to the use of simple pairwise interactions). We note that this is one aspect of the general CG representability problem [75]. Recent work has demonstrated both the means and utility of increasingly expressive CG interactions, which include CG interactions that are based on order parameters [76,77], such as local densities [78,79]. Furthermore, the general “Ultra-CG” (UCG) machinery enables the systematic mixing of different CG interaction models, which may represent different physical (e.g., conformational changes, ligand binding) or chemical (e.g., hydrolysis, protonation) states [41,77,80,81]; these would be a natural extension to the aforementioned multi-state structure-based CG models. Another general challenge is that CG models based on statistical mechanics formulations may preclude transferability, given their inherent dependence on thermodynamic state [75]. However, empirical evidence on the utility of state-dependent CG potentials for improved transferability has begun to emerge [82,83], and careful analysis on the origins of this behavior may provide new insights into this problem. Finally, dynamics-based approaches can be augmented with knowledge of experimental observables, which has recently been proposed as an integrated framework to generate new classes of CG models [84].

Applications of Coarse-Graining for Macromolecular Complexes

Recent advances in CG models have resulted in new mechanistic insights into large macromolecular complexes and their polymeric or aggregated assemblies. For example, network models are amenable for the exploration of collective motions with large computational efficiency [27,85]. On the other hand, native-contact models have been particularly useful in studying dynamical processes during the lifecycle of macromolecular complexes [15]. Finally, CG models have found additional utility as part of so-called integrative modeling, in which information from different hierarchies of scale (e.g., a continuum from AA to CG descriptions) are leveraged to gain hierarchical insights [86]. Below, we highlight a few recent applications of CG models, e.g., as seen in Figure 2, within these three broad categories.

Figure 2.

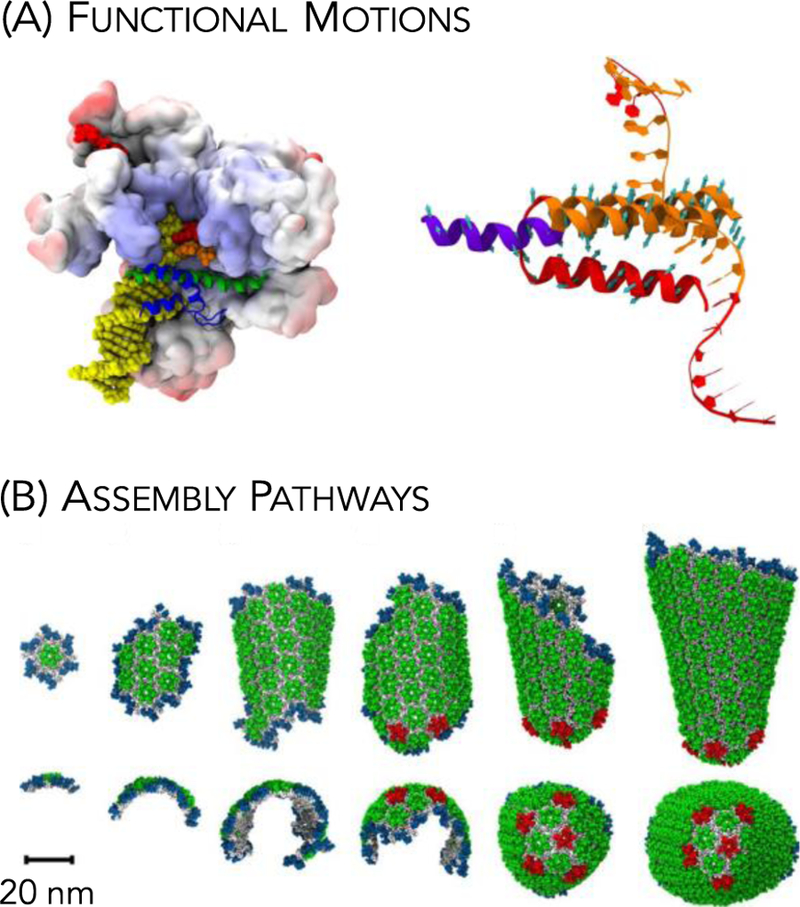
Two representative applications of coarse-grained modeling. (A) Schematic of the closed loop complex of RNA polymerase (colored surface) and RNA (yellow balls) [left] with large-scale collective motions indicated by the teal arrows along the bridge helix [right] (adapted from Ref. [34]). (B) Self-assembly pathway of the human immunodeficiency virus (HIV) CA capsid protein subunits in forming the mature capsid of infectious virions. Identified are CA hexamers (green), pentamers (red) and the growing edge of the conical capsid (blue) (adapted from Ref. [35]).

Large-scale functional motions.

Conformational transitions within macromolecular complexes have been explored using variants of both network and native-contact models. For example, flexibility analysis has revealed the collective motions that contribute to catalysis and translocation of RNA polymerase [34] (see Figure 2A) and to mechanical phenotypes of amyloid fibrils with disease expression [87]. Highly CG multi-state network models have also successfully recapitulated transition paths between the large-scale structural transitions in ribosomal complexes between the initiation and elongation states [33]. Finally, multi-state native-contact models have recently revealed the mechanism of action of motor protein motility, including kinesin [30] and myosin VI [29].

Dynamic assembly/disassembly pathways.

A key attribute of macromolecular complexes is their dynamic ability to assemble from their macromolecular constituents with high fidelity and then disassemble, to recycle, release, or replace components based on regulatory signals. Viruses are a quintessential example as viral cargo must be packaged and transported from host cells and released into newly infected cells. To this end, native-contact models have revealed hierarchical assembly modes during the replication cycle of HIV-1 (see Figure 2B) [35,36,88,89]. Similarly, dynamic de-polymerization responses of microtubules due to either mechanical forces or severing enzymes have been explored using native-contact models [90,91]. Most recently, UCG models of actin filaments under different hydrolysis states have revealed cooperativity effects that regulate polymerization of actin subunits [41].

Role of CG in hierarchical and integrative modeling.

The final aspect of CG modeling that we highlight is its integration in hierarchical modeling frameworks, in which a separation of length-and/or time-scales in the biophysical system of interest requires multiple resolutions of data that can span AA models to experimental data. For instance, CG models can accelerate the sampling of AA statistics. One such example is a multi-resolution approach known as the Adaptive Resolution Scheme (AdResS), which simultaneously models a region of interest in atomic detail within an environment of CG representation. An example would be ligand recognition in lysozymes [92]. An alternative approach is to explicitly use distributions from CG simulations to initiate AA simulations via back-mapping procedures [93] or to construct biased simulations that enhance AA configurational sampling [94]. In the opposite direction, continuum or mesoscopic fields can be applied to CG simulations. For instance, hydrodynamic flow fields, which can affect macromolecule relaxation and aggregation, have been integrated into CG MD simulations using the Lattice Boltzmann technique [95–97].

Conclusions and Future Outlook

Driven by a desire to understand the hierarchical nature of macromolecular complexes and their assemblies with molecular fidelity, the field of coarse-grained (CG) modeling and simulation continues to rapidly evolve. Here, we present recent advances in methodology and application of highly CG models for proteins and nucleic acids. Interestingly, previously classified boundaries between CG models, which broadly contain structure-based, knowledge-based, and dynamics-based approaches, appear to be melding into a unified nexus that blends these various philosophies. Nonetheless, we emphasize two main challenges to be considered for future advances. The first is that many aspects of CG modeling remain heavily reliant on either intuition or arbitrary modeling decisions. The second is that many CG models are inherently prescriptive, thereby limiting their ability to predict new phenomena. To address these issues, we anticipate that new methodological advances to generate CG mappings and energetics, especially those related to statistical inference approaches or based on a deeper understanding of systematic coarse-graining theory, will greatly expand the utility of CG modeling and simulation.

Highlights.

• Coarse-grained models are reduced representations of all-atom models that aim to retain the essential molecular aspects for the biophysical system of interest.

• Coarse-grained simulations may provide insights and perspectives that would otherwise be inaccessible from all-atom molecular simulations.

• Coarse-grained simulations bridge insights between microscopic and mesoscopic or macroscopic phenomena.

• Coarse-grained modeling strategies are discriminated on the basis of their use of experimental structural data, large datasets of experimental observables, or molecular simulations.

• Advances in methodology have enabled models to more expressively capture conformational changes in macromolecular complexes.

• Coarse-grained simulations have been used to elucidate hierarchical and dynamical behavior in complex macromolecular systems.