Abstract
We review mathematical and computational models of the structure, dynamics, and force generation properties of dendritic actin networks. These models have been motivated by the dendritic nucleation model, which provided a mechanistic picture of how the actin cytoskeleton system powers cell motility. We describe how they aimed to explain the self-organization of the branched network into a bimodal distribution of filament orientations peaked at 35° and − 35° with respect to the direction of membrane protrusion, as well as other patterns. Concave and convex force–velocity relationships were derived, depending on network organization, filament, and membrane elasticity and accounting for actin polymerization at the barbed end as a Brownian ratchet. This review also describes models that considered the kinetics and transport of actin and diffuse regulators and mechanical coupling to a substrate, together with explicit modeling of dendritic networks.
Keywords: Actin-based motility, Mathematical modeling, Dendritic network, Lamellipodium
Introduction
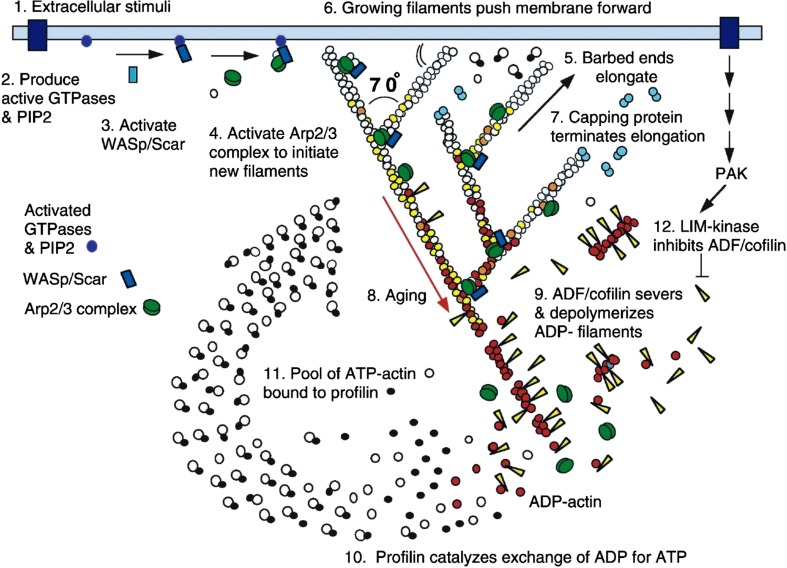
The dendritic nucleation model of actin based cell motility, originally presented by Mullins, Heuser and Pollard (1998) and Pollard, Blanchoin and Mullins (2000), continues to be tremendously influential. It is not only influential in the cytoskeleton field, but more generally in cell biology, biophysics, and quantitative biology. The schematic shown in Fig. 1 from the review by Pollard and Borisy (2003) is one of the most frequently shown figure in talks and presentations at the ASCB annual meetings for nearly two decades. When proposed, the dendritic nucleation model put together the work from numerous prior experimental studies into a mechanistic picture of how actin powers cell motility. According to this mechanism, signals from membrane proteins at the leading edge of motile cells result in activation of the Arp2/3 complex that nucleates new filament ends on the side of mother filaments. The actin filaments polymerize at their barbed end and push at an angle against the leading edge membrane. Filament elongation is controlled by capping proteins while cofilin preferentially severs filaments that age by the process of ATP hydrolysis and phosphate release. The resulting oligomer and monomer fragments diffuse back to the leading edge for polymerization as profilin-actin.
Fig. 1.
The dendritic nucleation/array treadmilling model of leading edge protrusion, reproduced with permission from Pollard and Borisy (2003). Proteins near the membrane activate the Arp2/3 complex which nucleates new barbed ends in the form of branches off of an existing mother filament. Growth from filament barbed end polymerization is terminated by binding of capping proteins. Severing and depolymerization of aged filaments creates oligomers and monomers that diffuse and repolymerize. Forces generated by actin polymerization result in membrane protrusion and/or retrograde flow of the network
The mechanisms and ideas embodied by the dendritic nucleation model drew many physicists, mathematicians, and engineers to the field of actin based motility. As presented, this model provides a process of self-organization where biochemical kinetics, 3D network structure, and mechanics combine to provide biological function. The basic mechanisms are specific enough to motivate models that derive the implications of the underlying processes, explore the phase space of possible kinetic and mechanical behavior, and provide experimental tests. This review highlights in an approximate chronological order some of these modeling contributions. Specifically, we focus on those works that explicitly addressed a characteristic feature of the dendritic nucleation model: the dynamic branched network structure of lamellipodia. This turned out to be a rich system for, still ongoing, theoretical and computational works. We outline the conceptual progress achieved in this area, which indicates the degree to which dendritic network models can be meaningfully compared to experiments. We refer the reader to other reviews for experimental work relevant to and/or motivated by the dendritic nucleation mechanism (Blanchoin et al. 2014; Carlier and Shekhar 2017; Fletcher and Mullins 2010; Nicholson-Dykstra et al. 2005; Pollard 2007; Pollard and Cooper 2009; Rottner and Schaks 2018; Skruber et al. 2018; Watanabe 2010) and for general reviews of models of actin-based motility (Carlsson and Mogilner 2010; Danuser et al. 2013; Pollard and Berro 2009; Ryan et al. 2012).
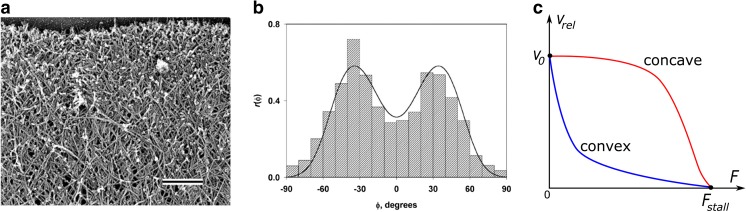
A large number of models of dendritic networks aimed to explain two main features of actin organization in lamellipodia, shown in Fig. 2. One of them is the organization of the branched network with filaments oriented in a bimodal distribution, with orientations peaked at 35° and − 35° with respect to the direction of membrane protrusion (Fig. 2a, b) (Schaub et al. 2007; Svitkina et al. 1997; Vinzenz et al. 2012). Another related aspect is the force–velocity behavior of dendritic nucleation systems. This is the relationship between actin network extension rate with respect to opposing force on the plasma membrane at the leading edge, an obstacle such as the tail of bacterium Listeria monocytogenes (a bacterium that hijacks actin polymerization to propel itself), or beads coated with activators of the Arp2/3 complex. Experiments have shown a large variability in the shape of force-velocity curves: in some cases, they have a convex shape while in other cases a concave shape (Bieling et al. 2016; Heinemann et al. 2011; Marcy et al. 2004; McGrath et al. 2003; Parekh et al. 2005; Prass et al. 2006; Wiesner et al. 2003) (Fig. 2c).
Fig. 2.
Orientation pattern and force of dendritic actin networks. a and b are reproduced with permission from Maly and Borisy (2001) (Copyright (2001) National Academy of Sciences, U.S.A.). a Electron micrograph showing the dendritic network structure of the lamellipodium at the leading edge of a moving Xenopus keratocyte. The cell membrane is at the top of the image. Bar = 0.2 μm. b Histogram of angles between filaments and the normal to the leading edge and theoretical curve. Negative and positive angles indicate deviation to one or the other side from the normal. The region shown in a was approximately one-half the lamellipodial area from which the histogram was generated. The characteristic 35°/−35° filament orientation pattern is observed. c Examples of convex and concave force–velocity relationships. The vertical axis represents the rate of actin network with respect to the load and the horizontal axis the opposing force. Velocity v0 is the free actin filament polymerization speed
An important background paper to the dendritic network models described below is the “elastic Brownian ratchet” model (Mogilner and Oster 1996). This study established a firm link between actin network structure and force generation. A mean field model was used to show that larger forces can be generated when actin filaments polymerize at an angle against the membrane at the leading edge of a motile cell or an obstacle, such as the tail of Listeria monocytogenes. In the original Brownian ratchet model (Peskin et al. 1993), the kinetic mechanism allowing actin polymerization to generate force (Hill and Kirschner 1982) was the thermal fluctuations of the obstacle (or membrane) that allowed for gaps large enough for incorporation of new monomers from the cytoplasm. Mogilner and Oster calculated that bending fluctuations of the actin filament itself can also generate gaps large enough to allow polymerization. Depending on the opposing force, an optimal angle exists that gives the fastest polymerization rate. In lamellipodia, this angle was calculated to be of the order of 48°. At the time, this angle was close to the angle electron microscopy experiments indicated for actin filaments in lamellipodia. In the context of the lamellipodium, the elastic Brownian ratchet polymerization mechanism was predicted to produce a force-velocity curve that is largely concave (Mogilner and Oster 1996) though a convex shape was found in a later extension of the model to account for filament tethering to the surface (Mogilner and Oster 2003).
Models of orientation pattern selection and associated force generation properties
The first to simulate a polymerizing dendritic network was Carlsson (2001) who developed a 3D stochastic model focused on the processes of polymerization, depolymerization, capping, branching, and debranching of filaments against a fluctuating obstacle. In this model of a dendritic network, actin filaments were assumed to be short enough to be considered rigid rods and the concentration of diffuse actin and other regulators were assumed to be uniform (so not considered explicitly). Branching was assumed to occur near the obstacle, corresponding to activation of Arp2/3 complex near the plasma membrane/obstacle. Assuming branching could occur at a 70° angle from a mother filament (corresponding to the Arp2/3 complex branching angle), the simulation showed network structures that qualitatively resembled those seen in electron micrographs of actin filaments in lamellipodia. This occurred as long as there was a bias for branch formation in the growth direction, or barbed-end uncapping effects, or both, an effect that was also described in more detail in subsequent models (see below). The density of the network and orientation pattern was dependent on the rate constants of branching and capping. Uncapping effects caused the structures to have a few very long filaments that were similar to those seen in the “actin comet” tails of pathogenic bacteria. Another aspect that this model highlighted was the interplay between network structure and force generation. By implementing a model of how force slows down polymerization and also accounting for excluded volume interactions among filaments, Carlsson observed a self-regulating effect: as the obstacle force increased, the force per filament remained rather constant as the number of filaments in contact with the obstacle increased. In this limit, the velocity of the obstacle was weakly dependent on external force, as expected for concave force–velocity relationship.
Maly and Borisy (2001), in the same year as Carlsson (2001), discovered that dendritic actin networks (studied in a two-dimensional system assumed to represent the thin and flat lamellipodium) self-organize in distinct patterns of filament orientation. The orientation pattern depended on the relationship between filament elongation velocity vpol and relative extension rate vrel = vmem + vretro, namely the sum of membrane protrusion velocity vmem and rate of actin network retrograde flow vretro, both assumed positive numbers (note: Maly and Borisy assumed vretro = 0 but the same analysis applies to non-zero values). This effect depends on the fact that filaments oriented at angles (with respect to the leading edge) larger than a critical angle ϕ, for which cos(ϕ) = vrel / vpol, lose contact with the membrane since they are not polymerizing quick enough to catch up. Assuming that polymerizing filaments branch when in contact with the leading edge (or close enough to it) and the critical angle is smaller than 70°, the favored pattern is filaments with orientations centered at 35°/−35°. The reason is that the filament population around 35° can generate daughter branches at − 35° and vice versa; thus, the population sustains itself even as individual filaments get capped. By contrast, filaments with orientations close to 0° would generate branches at 70° angles, which would stay behind and cap since they would be above the critical angle. This idea, which was supported by a new analysis of electron micrographs of keratocytes and fibroblasts (Maly and Borisy 2001), provided a mechanism by which the dendritic network can sustain a ± 35° orientation pattern through self-organization rather than unknown molecular mechanisms for precise angle regulation at the location of branch formation. When the critical angle is larger than 70° (small values of vrel / vpol), a 70°/0°/−70° pattern is also stable.
In further support of the self-regulating effect observed in prior studies (Carlsson 2001), Carlsson (2003) used a deterministic rate-equation model to describe the response to force of the orientation distribution of branches. A filament force–velocity relationship was implemented in the “autocatalytic” model (the model in which new filaments were generated by branching). The equations were along the lines of Maly and Borisy, also explicitly considering the filaments leaving the branching region. This model showed that the network growth velocity is approximately independent of the applied opposing force on the network.
Atilgan et al. (2005) performed simulations of dendritic networks with actin filaments treated as rigid rods with volume exclusion, polymerization, depolymerization, branching, and capping. By simulating the dendritic network within the confines of a thin lamellipodium, these authors found that the 35°/−35° pattern observed in prior experiments was reproduced only in the limit where branching by the Arp2/3 complex occurred with an angle restriction along the 2D plane of the lamellipodium. No such pattern was observed if the Arp2/3 complex is assumed to unbind from an activating membrane complex, diffuse after activation, and then binds to actin filaments at any orientation to generate a branch. Similarly, no 35°/−35° orientation pattern was observed if branching occurred at the membrane without any orientation restriction. The authors hypothesized that transmembrane receptors involved in the recruitment of Arp2/3 complex activators, such as the Cdc42/WASP complex, concentrate at the leading edge as a result of an energetic preference to be at curved regions of the plasma membrane. Thus, this study provided a mechanism by which the lamellipodium establishes itself as a flat organelle.
Schaus et al. (2007) introduced the effect of membrane and filament fluctuations to models of dendritic networks, which prior studies considered rigid. They considered a two-dimensional stochastic model that included barbed end polymerization, pointed end depolymerization, capping, uncapping, branching, debranching, and bending energy of filaments along with a membrane surface energy and membrane bending energy. In the reference state, filaments organized in 35°/−35° patterns relative to the leading edge and settled to vrel / vpol = 0.38 and 200 barbed ends per micrometer at the leading edge. The pattern was robust with respect to plasma membrane surface and bending energies, but required sufficiently short branches (of order 50 nm) close to the edge to avoid splaying at large angles, generally consistent with the expectations from Mogilner and Oster (1996). Backward branching was allowed, which produced filaments at 105°/−105°; these were assumed to cap quicker than the forward facing filaments, resulting in short backward facing filaments. This study also supported that the optimal branching angle to rapidly produce a two peak orientation pattern was near 70°, the value realized by the Arp2/3 complex. At low values of vrel, the simulations of Schaus et al. produced the anticipated 70°/0°/−70° pattern. In a follow-up study, Schaus and Borisy (2008) examined the effect of load sharing among branching filaments to conclude that the flexibility of membrane and filaments promotes “work sharing,” which improves response speed to applied force.
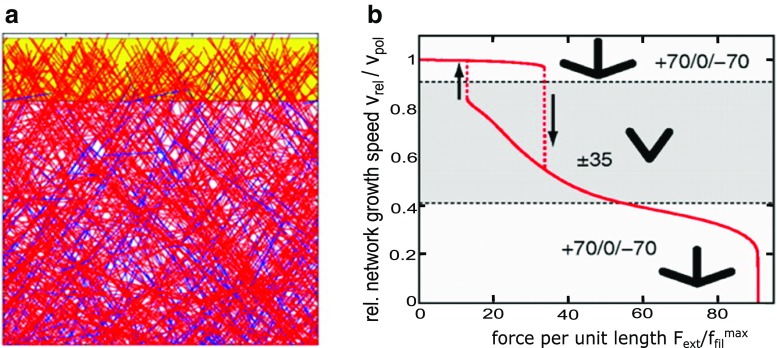
Steady-state filament orientation patterns and the force–velocity relationship were further studied by Weichsel and Schwarz (2010) who provided a comprehensive study of the 2D limit. They used deterministic rate equations similar to prior works (Carlsson 2003; Maly and Borisy 2001) as well as simulations of 2D branching network that included branching near the leading edge, capping, and polymerization. They showed how the steady-state orientation pattern transitions from 70°/0°/−70° to 35°/−35° as the relative protrusion velocity to polymerization rate, vrel / vpol increases past the critical angle corresponding to filaments that can barely catch up with the leading edge when polymerizing at 70° (the transition does not occur precisely at this value due to the finite speed at which filaments exit the branching region). At the very high values of vrel / vpol, the pattern resumes to the 70°/0°/−70° orientation, when the critical angle is past the corresponding angle to 35°. The authors modeled the effect of external force by assuming filaments share the load equally and act as Hookean springs with an angle-dependent elasticity (Mogilner and Oster 1996). The predicted force–velocity dependence showed a rich behavior with history-dependent effects (Fig. 3). The value of vrel was rather weakly dependent on force when the change in force was not large enough to cause a transition of the orientation pattern (as in prior models; Carlsson 2001) with the exception of a rapid decrease to stall at the highest force sustainable. Abrupt velocity transitions were observed in regions where applied force resulted in change of orientation pattern, and hysteresis loops were observed due to the transient competition between the orientation patterns. However, for filaments elongating as simple (Peskin et al. 1993), rather than elastic (Mogilner and Oster 1996), Brownian ratchets, the difference in performance of the two competing orientation patterns was found to be too weak to show significant hysteresis effects and the force–velocity curve was convex. Weichsel and Schwarz described how their model might provide a unifying description on prior experimental observations suggesting hysteresis phenomena (Parekh et al. 2005). In subsequent works, Weichsel et al. (2013) described a common framework that connects the results of models that assumed zeroth versus first order branching kinetics, corresponding to whether branching rate is limited by the reservoir of activated Arp2/3 complex or not. The role of obstacle geometry was also studied using similar approaches (Gong et al. 2017; Weichsel and Schwarz 2013).
Fig. 3.
Snapshot and force–velocity curve from the model of Weichsel and Schwarz, reproduced with permission from Weichsel and Schwarz (2010). a Snapshot of steady-state stochastic simulation in a 35°/− 35° orientation pattern. b Force–velocity relation of protruding actin network shows parts with concave and convex behavior with abrupt transitions upon change of indicated network orientation pattern. A hysteresis-cycle is seen between the fast and intermediate growth phases
Quint and Schwarz (2011) studied 2D deterministic rate equations similar to prior works (Carlsson 2003; Maly and Borisy 2001; Weichsel and Schwarz 2010) and showed that an off-center “suboptimal” −20°/50° and −20°/50° pattern can also exist if the branching rate is proportional to the sine of the angle with respect to the direction of protrusion. In this case, the 70°/0°/−70° pattern never becomes a favorable one to develop. The suboptimal distribution only appeared when the angle corresponding to the Arp2/3 complex branching angle is larger than 60°. These authors speculated that the 70° branching angle might have evolved to be just above 60° to allow a suboptimal orientation distribution that may help to broaden the filament angles and mechanically reinforce the lamellipodium through cross-links to the 35°/−35° pattern.
Smith and Liu (2013) performed 2D simulation of a system of polymerizing, branching, and capping filaments sharing a load. The simulation setup was similar to Weichsel and Schwarz (2010), with some differences such as the assumption that branching can occur in a broader region from the leading edge (of order 54 nm) and that capped filaments do not branch. The most stable pattern was 70°/0°/−70° while the 35°/−35° pattern was observed only when the branching region was very narrow. Under these conditions, it was found that the force–velocity curve can exhibit hysteresis phenomena and convex/concave shapes. Hysteresis was due to change in the number of filaments contacting the load versus time, with short-time behavior giving a convex shape. As the number of filaments contacting the surface changed over time (similar to Carlsson 2003), the long-time behavior could be convex or concave depending on the magnitude of the capping rate constant. A 3D model generalization exhibited similar behavior.
The force–velocity relationship of a rigid branching network (incorporating branching, capping and polymerization and depolymerization at the barbed end) encountering a fluctuating rigid obstacle was considered by Hansda et al. (2014). This study was at the level of a multi-Brownian ratchet stochastic model. It explicitly accounted for unequal sharing of load among filaments as a result of the different distances of each end to the boundary (an effect also considered in a somewhat different setup in the work by Schaus et al. 2007). The force–velocity curve for conditions that corresponded to the 70°/0°/−70° orientation pattern was shown to convert from convex to concave curves as the number of filaments increased. This behavior differs to the convex shape established in models of multi-Brownian-ratchet models of parallel bundles of filaments (Wang and Carlsson 2014).
Experimental results from a recent study combining electron microscopy and methods to control membrane tension (Mueller et al. 2017) recently confirmed one of the basic modeling predictions, namely the ability of dendritic networks to change density and orientation under external force. In these experiments, an increase in membrane tension caused the actin filament density to increase while maintaining a pattern with a predominantly 35°/−35° orientation, consistent with the self-adjustment mechanism (Carlsson 2001; Carlsson 2003; Weichsel and Schwarz 2010). Reduction in tension caused a change from a 35°/−35° orientation pattern at steady state to a pattern with filaments oriented around 0°, consistent with a transition to a 70°/0°/−70° orientation pattern at low load (Weichsel and Schwarz 2010) (Fig. 3). A numerical simulation developed in 2D by Mueller et al. (2017), similar to Weischel and Schwarz (2010) with polymerization, capping, and branching of filaments toward the leading edge, reproduced these results in addition to the transient behavior observed in the experiments.
Models of dendritic networks considering biochemical actin turnover and mechanics
Considering a branching actin network in the context of the diffuse pool of actin monomers and regulators (Arp2/3 complex, capping protein, cofilin, tropomyosin, etc.) as well as the overall mechanical properties of the network has been the topic of several models.
Alberts and Odell (2004) developed a 3D network model in the context of Listeria propulsion. In this model actin filaments could attach to the bacterial surface (as occurs through the Arp2/3 complex activator ActA), branch, and depolymerize. This model further accounted for ATP hydrolysis and phosphate dissociation and was also able to accommodate cofilin binding and severing. Applying force balance equations, the model was able to generate bacterial propulsion with its characteristic actin comet tail. Burroughs and Marenduzzo (2007) also reproduced comet tails and moving beads in a Brownian dynamics simulation that included branching and stored elastic energy in the network.
Liu and coworkers (Banigan et al. 2013; Lee and Liu 2008; Lee and Liu 2009) developed a Brownian dynamics computational model with diffusing actin monomers polymerizing at the ends of filaments near an obstacle that activated Arp2/3-complex-mediated 70° branching at one of its faces. The simulations also included capping, debranching, and depolymerization and showed that motility speed varied non-monotonically with the concentration of Arp2/3 complex, capping rate, and depolymerization rate, as observed in vitro. Under the conditions of these simulations, the force generation mechanism was identified as self-diffusiophoresis, driven by the concentration gradient of polymerized actin around the obstacle and was weakly dependent on filament persistence length (Lee and Liu 2008). This mechanism produced a concave force–velocity curve (Lee and Liu 2009) even in the presence of binding interactions with the obstacle surface (Banigan et al. 2013). The authors suggest that self-diffusiophoresis is contributing as a physical mechanism more generally in actin-based motility. How this mechanism contributes under conditions of a highly cross-linked network of short stiff filaments in lamellipodia remains to be resolved.
Schreiber et al. (2010) created a three-dimensional model that simulated a stochastically growing dendritic network with branching at the leading edge and pushing against a membrane while also introducing adhesion of the network to a substrate, excluded volume interactions among filaments, and accounted for mechanical balance through the network (Fig. 4). The model also included severing of actin filaments in addition to force-dependent growth at the barbed end, depolymerization at the pointed end together with irreversible capping. A hard wall base was used for the substrate boundary with two movable hard walls at the top (opposite substrate) and leading edge. Tension in the membrane was modeled as a force applied to the top of the cell. This model included several key new elements of the dendritic nucleation model such as severing and mechanical coupling. Its results agreed with basic features found in crawling cells, which included a concave-down force–velocity relation and magnitudes of retrograde flow speed, filament concentration, and protrusion speed. The authors pointed out that the shape of the force velocity curve as well as the speed of retrograde flow is significantly influenced by excluded volume interactions. Thus, they speculated that the branched network may provide mechanical strength by hindering filament rotation. It was stated that a 35°/−35° filament orientation pattern was observed; however, it is unclear how this compares to prior studies (Atilgan et al. 2005) that suggested this pattern requires a 2D branch angle orientation restriction.
Fig. 4.
Simulation snapshots from Schreiber et al., reproduced with permission from Schreiber et al. (2010). Top snapshot represents a simulation with branched rods. Representations of individual dendrals from the branched network shown on the bottom. This network produced a concave force–velocity curve
Another series of studies by Hu and Papoian (2010, 2011, 2013) moved the field closer to integrating models of dendritic network structure with the biochemical and mechanical interactions of the full dendritic nucleation system. These studies accounted for concentration gradients of Arp2/3 complex, capping protein, and actin in the cytoplasmic pool. The 3D stochastic simulation accounted for the interactions between a flexible membrane and actin filaments that were considered rigid. The model also considered polymerization/depolymerization, branching/debranching, and capping/uncapping. Branches were formed on the side of parent filaments in a region near the leading edge at an angle chosen from a Gaussian distribution centered around 70°. Hu and Papoian found that concentrations of actin and regulators influence the growth speed and force–velocity response in a complex manner. The protrusion speed and branch nucleation rate increased with actin concentration up to a plateau. In the simulations, fast polymerization could deplete the cytoplasmic Arp2/3 complex concentration while either too high or too low Arp2/3 complex concentrations resulted in slow motion of the membrane: at low Arp2/3 complex concentration the small number of filaments in the network produced a small force while local concentration depletion was limiting at high concentrations. It was also found that there is an optimal concentration of capping protein that promotes actin-based motility. Capping protein not only prevents polymerization of barbed ends which push the membrane forward but also capped filaments increase monomeric actin concentration promoting polymerization on the uncapped barbed ends. It was stated that a filament orientation pattern of 35°/−35° emerged in the simulations. Similar to the results of Schreiber et al. (2010), it is unclear how this compares to prior studies (Atilgan et al. 2005) that suggested the 35°/−35° pattern requires a 2D branch angle orientation restriction.
Razbin et al. (2015) studied the mechanics of a mother and daughter filament in 2D, modeled analytically as worm-like chains. They found that the branch can increase the stiffness of the tilted mother filament by more than a factor of four (depending on its location), while only requiring 1.5 times the length of the mother filament. An ensemble of such structures was found to be about twice as stiff as unbranched networks. The authors estimate the lamellipodium network is likely to be in a parameter regime where filament bending is important in determining elastic behavior and thus excluded volume interactions may be less significant than what was suggested by the network of stiff rods model of Schreiber et al. (2010).
Conclusion and outlook
The results of the models reviewed provided several conditions under which the 35°/−35° and other patterns develop along with mechanisms that can generate concave or convex force–velocity relationships. They demonstrated a non-trivial dependence of filament density and orientation pattern on the location and mechanism of branching and capping. They also suggest that the resulting force generation capabilities are influenced by dendritic network structure. As evidenced by the recent work by Mueller et al. (2017), advances in experimental methods that combine force measurements with actin dynamics and network structure should further help test the precise mechanism of dendritic network structure and force generation.
We can identify a few areas for possible future modeling work. Such work could develop and justify constitutive relationships assumed by models of actin-based motility that start from a more coarse-grained level of description (Barnhart et al. 2017; Campas et al. 2012; Lewalle et al. 2014; Ryan et al. 2017; Zhu and Mogilner 2012). For example, work by Falcke and collaborators described protrusive activity and concave force-velocity behavior of lamellipodia considering the actin network as a cross-linked gel connected to the membrane through a layer of polymerizing semiflexible filaments (Dolati et al. 2018; Enculescu et al. 2010; Zimmermann et al. 2010; Zimmermann and Falcke 2014). In an another example, in the mathematical model of Boujemaa-Paterski et al. (2017), dendritic network growth speed and steering of in vitro motility were modeled in terms of an overall network geometrical factor together with the effects of actin monomer depletion that negatively impacts dendritic network growth.
Connection to modeling in between the molecular and filament level could account for the biophysics of protein complexes that regulate the mechanisms by which filament ends associate with the membrane to polymerize, cap, and branch (Bieling et al. 2018; Dickinson 2008; Risca et al. 2012; Stark et al. 2017) and how they are decorated by side binding proteins for stabilization, severing, or debranching (Christensen et al. 2017; De La Cruz and Sept 2010; Schramm et al. 2017).
Another consideration is related to the turnover and diffusion of actin and regulators in the cytoplasm (Hu and Papoian 2010; Vitriol et al. 2015; Watanabe 2010). Prior models have considered such aspects (Ditlev et al. 2009; McMillen and Vavylonis 2016; Mogilner and Edelstein-Keshet 2002; Novak et al. 2008; Smith et al. 2013; Vitriol et al. 2015), and Huber et al. (2008) considered the effect of filament length distribution without an explicit network model. Experimental evidence for distributed turnover of actin and regulators (Millius et al. 2012; Watanabe and Mitchison 2002) suggests possible regulation of dendritic network structure through severing, debranching and annealing (Miyoshi and Watanabe 2013; Smith et al. 2013). Finally, the results of Schreiber et al. (2010) motivate further models connecting dendritic network structure to interaction with focal adhesions and myosin forces.
The predictive and quantitative system-level descriptions of lamellipodia envisioned by the dendritic nucleation model (Fig. 1) keeps motivating productive interactions among workers in theory and computation, quantitative cell biology, and in vitro reconstitution experiments.
Funding information
This work was supported by NIH grants R01GM114201 to D.V.
Conflict of interest
Danielle Holz declares that she has no conflicts of interest. Dimitrios Vavylonis declares that he has no conflicts of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
References
- Alberts JB, Odell GM. In silico reconstitution of Listeria propulsion exhibits nano-saltation. PLoS Biol. 2004;2:2054–2066. doi: 10.1371/journal.pbio.0020412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atilgan E, Wirtz D, Sun SX. Morphology of the lamellipodium and organization of actin filaments at the leading edge of crawling cells. Biophys J. 2005;89:3589–3602. doi: 10.1529/biophysj.105.065383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banigan EJ, Lee KC, Liu AJ. Control of actin-based motility through localized actin binding. Phys Biol. 2013;10:066004. doi: 10.1088/1478-3975/10/6/066004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnhart EL, Allard J, Lou SS, Theriot JA, Mogilner A. Adhesion-dependent wave generation in crawling cells. Curr Biol. 2017;27:27–38. doi: 10.1016/j.cub.2016.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bieling P, et al. Force feedback controls motor activity and mechanical properties of self-assembling branched actin networks. Cell. 2016;164:115–127. doi: 10.1016/j.cell.2015.11.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bieling P, Hansen SD, Akin O, Li TD, Hayden CC, Fletcher DA, Mullins RD. WH2 and proline-rich domains of WASP-family proteins collaborate to accelerate actin filament elongation. EMBO J. 2018;37:102–121. doi: 10.15252/embj.201797039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanchoin L, Boujemaa-Paterski R, Sykes C, Plastino J. Actin dynamics, architecture, and mechanics in cell motility. Physiol Rev. 2014;94:235–263. doi: 10.1152/physrev.00018.2013. [DOI] [PubMed] [Google Scholar]
- Boujemaa-Paterski R, et al. Network heterogeneity regulates steering in actin-based motility. Nat Commun. 2017;8:655. doi: 10.1038/s41467-017-00455-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burroughs NJ, Marenduzzo D. Nonequilibrium-driven motion in actin networks: comet tails and moving beads. Phys Rev Lett. 2007;98:238302. doi: 10.1103/PhysRevLett.98.238302. [DOI] [PubMed] [Google Scholar]
- Campas O, Mahadevan L, Joanny JF. Actin network growth under load. Biophys J. 2012;102:1049–1058. doi: 10.1016/j.bpj.2012.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlier MF, Shekhar S. Global treadmilling coordinates actin turnover and controls the size of actin networks. Nat Rev Mol Cell Biol. 2017;18:389–401. doi: 10.1038/nrm.2016.172. [DOI] [PubMed] [Google Scholar]
- Carlsson AE. Growth of branched actin networks against obstacles. Biophys J. 2001;81:1907–1923. doi: 10.1016/S0006-3495(01)75842-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlsson AE. Growth velocities of branched actin networks. Biophys J. 2003;84:2907–2918. doi: 10.1016/S0006-3495(03)70018-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlsson AE, Mogilner A. Actin-based motility. Dordrecht: Springer; 2010. Mathematical and physical modeling of actin dynamics in motile cells; pp. 381–412. [Google Scholar]
- Christensen JR, Hocky GM, Homa KE, Morganthaler AN, Hitchcock-DeGregori SE, Voth GA, Kovar DR. Competition between tropomyosin, fimbrin, and ADF/cofilin drives their sorting to distinct actin filament networks. Elife. 2017;6:e23152. doi: 10.7554/eLife.23152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danuser G, Allard J, Mogilner A. Mathematical modeling of eukaryotic cell migration: insights beyond experiments. Annu Rev Cell Dev Biol. 2013;29:501–528. doi: 10.1146/annurev-cellbio-101512-122308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De La Cruz EM, Sept D. The kinetics of cooperative cofilin binding reveals two states of the cofilin-actin filament. Biophys J. 2010;98:1893–1901. doi: 10.1016/j.bpj.2010.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickinson RB. A multi-scale mechanistic model for actin-propelled bacteria. Cell Mol Bioeng. 2008;1:110–121. doi: 10.1007/s12195-008-0027-5. [DOI] [Google Scholar]
- Ditlev JA, Vacanti NM, Novak IL, Loew LM. An open model of actin dendritic nucleation. Biophys J. 2009;96:3529–3542. doi: 10.1016/j.bpj.2009.01.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolati S et al (2018) On the relation between filament density, force generation and protrusion rate in mesenchymal cell motility. Mol Biol Cell mbcE18020082. 10.1091/mbc.E18-02-0082 [DOI] [PMC free article] [PubMed]
- Enculescu M, Sabouri-Ghomi M, Danuser G, Falcke M. Modeling of protrusion phenotypes driven by the actin-membrane interaction. Biophys J. 2010;98:1571–1581. doi: 10.1016/j.bpj.2009.12.4311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher DA, Mullins RD. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–492. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong B, Lin J, Qian J. Growing actin networks regulated by obstacle size and shape. Acta Mech Sinica-Prc. 2017;33:222–233. doi: 10.1007/s10409-016-0628-5. [DOI] [Google Scholar]
- Hansda DK, Sen S, Padinhateeri R. Branching influences force-velocity curves and length fluctuations in actin networks. Phys Rev E. 2014;90:062718. doi: 10.1103/PhysRevE.90.062718. [DOI] [PubMed] [Google Scholar]
- Heinemann F, Doschke H, Radmacher M. Keratocyte lamellipodial protrusion is characterized by a concave force-velocity relation. Biophys J. 2011;100:1420–1427. doi: 10.1016/j.bpj.2011.01.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill TL, Kirschner MW. Bioenergetics and kinetics of microtubule and actin filament assembly-disassembly. Int Rev Cytol. 1982;78:1–125. doi: 10.1016/S0074-7696(08)60105-9. [DOI] [PubMed] [Google Scholar]
- Hu L, Papoian GA. Mechano-chemical feedbacks regulate actin mesh growth in lamellipodial protrusions. Biophys J. 2010;98:1375–1384. doi: 10.1016/j.bpj.2009.11.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu L, Papoian GA. How does the antagonism between capping and anti-capping proteins affect actin network dynamics? J Phys Condens Matter. 2011;23:374101. doi: 10.1088/0953-8984/23/37/374101. [DOI] [PubMed] [Google Scholar]
- Hu LH, Papoian GA. Molecular transport modulates the adaptive response of branched actin networks to an external force. J Phys Chem B. 2013;117:13388–13396. doi: 10.1021/jp405179e. [DOI] [PubMed] [Google Scholar]
- Huber F, Käs J, Stuhrmann B. Growing actin networks form lamellipodium and lamellum by self-assembly. Biophys J. 2008;95:5508–5523. doi: 10.1529/biophysj.108.134817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee KC, Liu AJ. New proposed mechanism of actin-polymerization-driven motility. Biophys J. 2008;95:4529–4539. doi: 10.1529/biophysj.108.134783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee KC, Liu AJ. Force-velocity relation for actin-polymerization-driven motility from Brownian dynamics simulations. Biophys J. 2009;97:1295–1304. doi: 10.1016/j.bpj.2009.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewalle A, Fritzsche M, Wilson K, Thorogate R, Duke T, Charras G. A phenomenological density-scaling approach to lamellipodial actin dynamics. Interface focus. 2014;4:20140006. doi: 10.1098/rsfs.2014.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maly IV, Borisy GG. Self-organization of a propulsive actin network as an evolutionary process. Proc Natl Acad Sci U S A. 2001;98:11324–11329. doi: 10.1073/pnas.181338798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcy Y, Prost J, Carlier MF, Sykes C. Forces generated during actin-based propulsion: a direct measurement by micromanipulation. Proc Natl Acad Sci U S A. 2004;101:5992–5997. doi: 10.1073/pnas.0307704101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGrath JL, Eungdamrong NJ, Fisher CI, Peng F, Mahadevan L, Mitchison TJ, Kuo SC. The force-velocity relationship for the actin-based motility of Listeria monocytogenes. Curr Biol. 2003;13:329–332. doi: 10.1016/S0960-9822(03)00051-4. [DOI] [PubMed] [Google Scholar]
- McMillen LM, Vavylonis D. Model of turnover kinetics in the lamellipodium: implications of slow- and fast- diffusing capping protein and Arp2/3 complex. Phys Biol. 2016;13:066009. doi: 10.1088/1478-3975/13/6/066009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millius A, Watanabe N, Weiner OD. Diffusion, capture and recycling of SCAR/WAVE and Arp2/3 complexes observed in cells by single-molecule imaging. J Cell Sci. 2012;125:1165–1176. doi: 10.1242/jcs.091157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyoshi T, Watanabe N. Can filament treadmilling alone account for the F-actin turnover in lamellipodia? Cytoskeleton (Hoboken) 2013;70:179–190. doi: 10.1002/cm.21098. [DOI] [PubMed] [Google Scholar]
- Mogilner A, Edelstein-Keshet L. Regulation of actin dynamics in rapidly moving cells: a quantitative analysis. Biophys J. 2002;83:1237–1258. doi: 10.1016/S0006-3495(02)73897-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A, Oster G. Cell motility driven by actin polymerization. Biophys J. 1996;71:3030–3045. doi: 10.1016/S0006-3495(96)79496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A, Oster G. Force generation by actin polymerization II: the elastic ratchet and tethered filaments. Biophys J. 2003;84:1591–1605. doi: 10.1016/S0006-3495(03)74969-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller J, et al. Load Adaptation of Lamellipodial Actin Networks. Cell. 2017;171:188–200. doi: 10.1016/j.cell.2017.07.051. [DOI] [PubMed] [Google Scholar]
- Mullins RD, Heuser JA, Pollard TD. The interaction of Arp2/3 complex with actin: nucleation, high affinity pointed end capping, and formation of branching networks of filaments. Proc Natl Acad Sci U S A. 1998;95:6181–6186. doi: 10.1073/pnas.95.11.6181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson-Dykstra S, Higgs HN, Harris ES. Actin dynamics: growth from dendritic branches. Curr Biol. 2005;15:R346–R357. doi: 10.1016/j.cub.2005.04.029. [DOI] [PubMed] [Google Scholar]
- Novak IL, Slepchenko BM, Mogilner A. Quantitative analysis of G-actin transport in motile cells. Biophys J. 2008;95:1627–1638. doi: 10.1529/biophysj.108.130096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parekh SH, Chaudhuri O, Theriot JA, Fletcher DA. Loading history determines the velocity of actin-network growth. Nat Cell Biol. 2005;7:1219–1223. doi: 10.1038/ncb1336. [DOI] [PubMed] [Google Scholar]
- Peskin CS, Odell GM, Oster GF. Cellular motions and thermal fluctuations: the Brownian ratchet. Biophys J. 1993;65:316–324. doi: 10.1016/S0006-3495(93)81035-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard TD. Regulation of actin filament assembly by Arp2/3 complex and formins. Annu Rev Biophys Biomol Struct. 2007;36:451–477. doi: 10.1146/annurev.biophys.35.040405.101936. [DOI] [PubMed] [Google Scholar]
- Pollard TD, Berro J. Mathematical models and simulations of cellular processes based on actin filaments. J Biol Chem. 2009;284:5433–5437. doi: 10.1074/jbc.R800043200. [DOI] [PubMed] [Google Scholar]
- Pollard TD, Borisy GG. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112:453–465. doi: 10.1016/S0092-8674(03)00120-X. [DOI] [PubMed] [Google Scholar]
- Pollard TD, Cooper JA. Actin, a central player in cell shape and movement. Science. 2009;326:1208–1212. doi: 10.1126/science.1175862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard TD, Blanchoin L, Mullins RD. Molecular mechanisms controlling actin filament dynamics in nonmuscle cells. Annu Rev Biophys Biomol Struct. 2000;29:545–576. doi: 10.1146/annurev.biophys.29.1.545. [DOI] [PubMed] [Google Scholar]
- Prass M, Jacobson K, Mogilner A, Radmacher M. Direct measurement of the lamellipodial protrusive force in a migrating cell. J Cell Biol. 2006;174:767–772. doi: 10.1083/jcb.200601159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quint DA, Schwarz JM. Optimal orientation in branched cytoskeletal networks. J Math Biol. 2011;63:735–755. doi: 10.1007/s00285-010-0389-x. [DOI] [PubMed] [Google Scholar]
- Razbin M, Falcke M, Benetatos P, Zippelius A. Mechanical properties of branched actin filaments. Phys Biol. 2015;12:046007. doi: 10.1088/1478-3975/12/4/046007. [DOI] [PubMed] [Google Scholar]
- Risca VI, Wang EB, Chaudhuri O, Chia JJ, Geissler PL, Fletcher DA. Actin filament curvature biases branching direction. Proc Natl Acad Sci U S A. 2012;109:2913–2918. doi: 10.1073/pnas.1114292109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rottner K, Schaks M. Assembling actin filaments for protrusion. Curr Opin Cell Biol. 2018;56:53–63. doi: 10.1016/j.ceb.2018.09.004. [DOI] [PubMed] [Google Scholar]
- Ryan GL, Watanabe N, Vavylonis D. A review of models of fluctuating protrusion and retraction patterns at the leading edge of motile cells. Cytoskeleton (Hoboken) 2012;69:195–206. doi: 10.1002/cm.21017. [DOI] [PubMed] [Google Scholar]
- Ryan GL, Holz D, Yamashiro S, Taniguchi D, Watanabe N, Vavylonis D. Cell protrusion and retraction driven by fluctuations in actin polymerization: a two-dimensional model. Cytoskeleton (Hoboken) 2017;74:490–503. doi: 10.1002/cm.21389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaub S, Meister JJ, Verkhovsky AB. Analysis of actin filament network organization in lamellipodia by comparing experimental and simulated images. J Cell Sci. 2007;120:1491–1500. doi: 10.1242/jcs.03379. [DOI] [PubMed] [Google Scholar]
- Schaus TE, Borisy GG. Performance of a population of independent filaments in lamellipodial protrusion. Biophys J. 2008;95:1393–1411. doi: 10.1529/biophysj.107.125005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaus TE, Taylor EW, Borisy GG. Self-organization of actin filament orientation in the dendritic-nucleation/array-treadmilling model. Proc Natl Acad Sci U S A. 2007;104:7086–7091. doi: 10.1073/pnas.0701943104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schramm AC, Hocky GM, Voth GA, Blanchoin L, Martiel JL, De La Cruz EM. Actin filament strain promotes severing and cofilin dissociation. Biophys J. 2017;112:2624–2633. doi: 10.1016/j.bpj.2017.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber CH, Stewart M, Duke T. Simulation of cell motility that reproduces the force-velocity relationship. Proc Natl Acad Sci U S A. 2010;107:9141–9146. doi: 10.1073/pnas.1002538107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skruber K, Read TA, Vitriol EA (2018) Reconsidering an active role for G-actin in cytoskeletal regulation. J Cell Sci 131. 10.1242/jcs.203760 [DOI] [PMC free article] [PubMed]
- Smith DB, Liu J (2013) Branching and capping determine the force-velocity relationships of branching actin networks. Phys Biol 10:016004 [DOI] [PMC free article] [PubMed]
- Smith MB, Kiuchi T, Watanabe N, Vavylonis D. Distributed actin turnover in the lamellipodium and FRAP kinetics. Biophys J. 2013;104:247–257. doi: 10.1016/j.bpj.2012.11.3819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark BC, Lanier MH, Cooper JA. CARMIL family proteins as multidomain regulators of actin-based motility. Mol Biol Cell. 2017;28:1713–1723. doi: 10.1091/mbc.E17-01-0019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svitkina TM, Verkhovsky AB, McQuade KM, Borisy GG. Analysis of the actin-myosin II system in fish epidermal keratocytes: mechanism of cell body translocation. J Cell Biol. 1997;139:397–415. doi: 10.1083/jcb.139.2.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinzenz M, et al. Actin branching in the initiation and maintenance of lamellipodia. J Cell Sci. 2012;125:2775–2785. doi: 10.1242/jcs.107623. [DOI] [PubMed] [Google Scholar]
- Vitriol EA, McMillen LM, Kapustina M, Gomez SM, Vavylonis D, Zheng JQ. Two functionally distinct sources of actin monomers supply the leading edge of lamellipodia. Cell Rep. 2015;11:433–445. doi: 10.1016/j.celrep.2015.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R, Carlsson AE. Load sharing in the growth of bundled biopolymers. New J Phys. 2014;16:113047. doi: 10.1088/1367-2630/16/11/113047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe N. Inside view of cell locomotion through single-molecule: fast F-/G-actin cycle and G-actin regulation of polymer restoration. Proceedings of the Japan Academy, Series B. 2010;86:62–83. doi: 10.2183/pjab.86.62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe N, Mitchison TJ. Single-molecule speckle analysis of actin filament turnover in lamellipodia. Science. 2002;295:1083–1086. doi: 10.1126/science.1067470. [DOI] [PubMed] [Google Scholar]
- Weichsel J, Schwarz US. Two competing orientation patterns explain experimentally observed anomalies in growing actin networks. Proc Natl Acad Sci U S A. 2010;107:6304–6309. doi: 10.1073/pnas.0913730107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weichsel J, Schwarz US. Mesoscopic model for filament orientation in growing actin networks: the role of obstacle geometry. New J Phys. 2013;15:035006. doi: 10.1088/1367-2630/15/3/035006. [DOI] [Google Scholar]
- Weichsel J, Baczynski K, Schwarz US. Unifying autocatalytic and zeroth-order branching models for growing actin networks. Phys Rev E Stat Nonlinear Soft Matter Phys. 2013;87:040701. doi: 10.1103/PhysRevE.87.040701. [DOI] [PubMed] [Google Scholar]
- Wiesner S, Helfer E, Didry D, Ducouret G, Lafuma F, Carlier MF, Pantaloni D. A biomimetic motility assay provides insight into the mechanism of actin-based motility. J Cell Biol. 2003;160:387–398. doi: 10.1083/jcb.200207148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J, Mogilner A. Mesoscopic model of actin-based propulsion. PLoS Comput Biol. 2012;8:e1002764. doi: 10.1371/journal.pcbi.1002764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmermann J, Falcke M. Formation of transient lamellipodia. PLoS One. 2014;9:e87638. doi: 10.1371/journal.pone.0087638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmermann J, Enculescu M, Falcke M. Leading-edge-gel coupling in lamellipodium motion. Phys Rev E Stat Nonlinear Soft Matter Phys. 2010;82:051925. doi: 10.1103/PhysRevE.82.051925. [DOI] [PubMed] [Google Scholar]