From solution to surface to filament: actin flux into branched networks

Abstract

The actin cytoskeleton comprises a set of filament networks that perform essential functions in eukaryotic cells. The idea that actin filaments incorporate monomers directly from solution forms both the “textbook picture” of filament elongation and a conventional starting point for quantitative modeling of cellular actin dynamics. Recent work, however, reveals that filaments created by two major regulators, the formins and the Arp2/3 complex, incorporate monomers delivered by nearby proteins. Specifically, actin enters Arp2/3-generated networks via binding sites on nucleation-promoting factors clustered on membrane surfaces. Here, we describe three functions of this surface-associated actin monomer pool: (1) regulating network density via product inhibition of the Arp2/3 complex, (2) accelerating filament elongation as a distributive polymerase, and (3) converting profilin-actin into a substrate for the Arp2/3 complex. These linked functions control the architecture of branched networks and explain how capping protein enhances their growth.

Introduction

The main job of the actin cytoskeleton is to shape, support, and move membranes, and so most actin filaments nucleate and grow in close proximity to membrane surfaces. The growth of a branched actin network against a membrane generates a pushing force (Mogilner and Oster 1996) that drives many cellular processes, including pseudopod protrusion at the leading edge of crawling cells (Bisi et al. 2013), healing of membrane ruptures (Clark et al. 2009), assembly of autophagosomes (Kast et al. 2015), endocytosis (Mooren et al. 2012), phagocytosis (Insall and Machesky 2009), cell fusion (Richardson et al. 2007), and cell-cell adhesion (Efimova and Svitkina 2018). These force-generating, branched actin networks are created by the coordinated activity of a set of conserved components working together to form a spatially distributed motor. This motor, driven by the free energy of polymer elongation, differs fundamentally from conventional molecular motors, such as myosins, kinesins, and dyneins, which harness conformational changes to move along preexisting polymers.

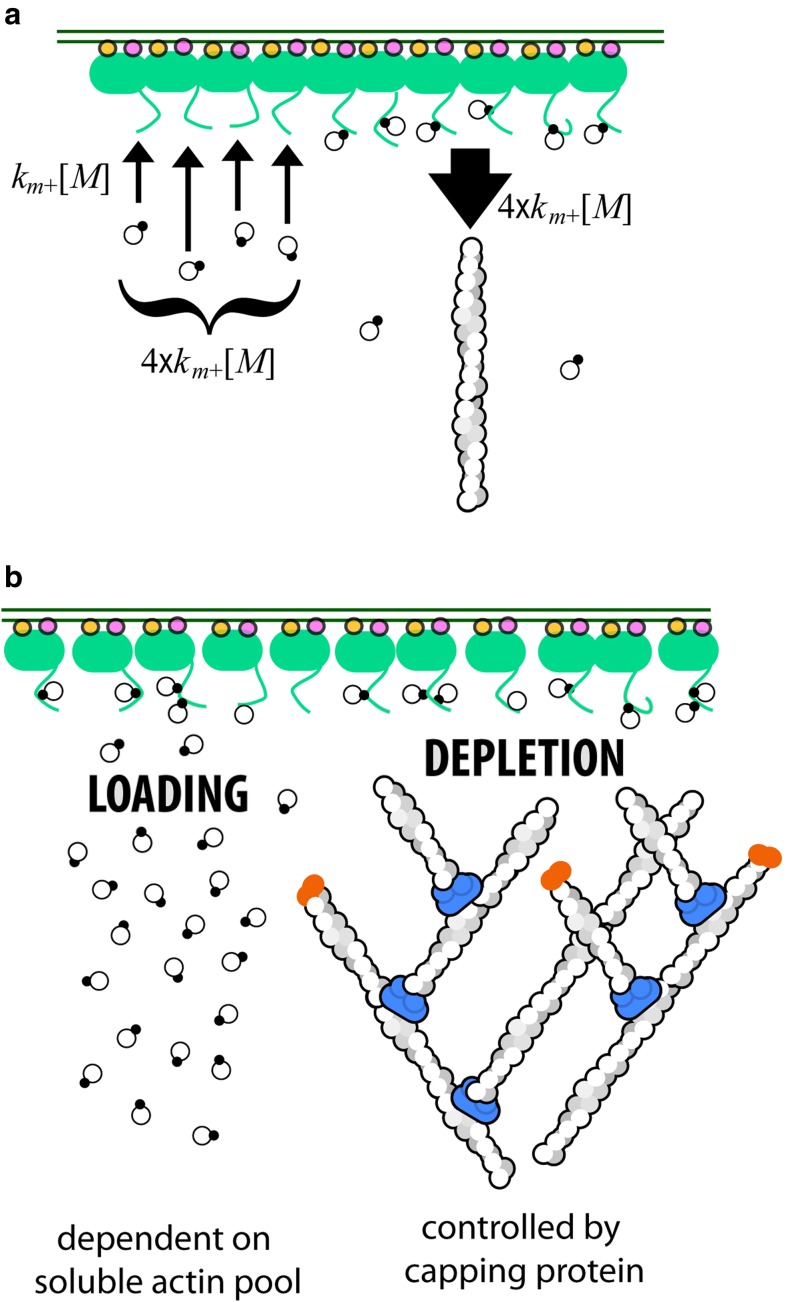
In this review, we synthesize results from more than 20 years of work on core components of the branched network motor to produce a quantitative description of how actin flows from solution onto membrane surfaces and then into branched filament networks. This route of actin incorporation contrasts sharply with the diffusion-limited growth of actin filaments from soluble monomers (Drenckhahn and Pollard 1986; Pollard 1986). Due to its simplicity, monomer incorporation directly from solution (Fig. 1a) has become the textbook picture of filament growth (e.g., found in Alberts et al. 2015 and Pollard et al. 2017) and a key assumption of many mathematical models of branched actin network assembly (e.g., Schaus et al. 2007; Berro et al. 2010; Raz-Ben Aroush et al. 2017). It turns out, however, that membranes are not passive platforms for the accumulation of signaling molecules; they are active surfaces that accumulate monomeric actin and feed it into growing networks. Here, we show that surface-mediated actin filament growth (Fig. 1b) explains many features of branched network architecture and function that are not easily accounted for under the assumption that filaments grow by interacting with soluble actin and/or profilin/actin complexes. Specifically, we discuss how actin monomers bound to nucleation-promoting factors (NPFs) mediate product inhibition of the Arp2/3 complex and thereby control actin network density. We also describe how Wiskott-Aldrich Syndrome Protein (WASP) family proteins function as distributive actin polymerases, and we explain the mechanism by which capping protein accelerates the growth of some filaments by terminating the growth of others. The latter effect arises from a phenomenon we call branch competition.

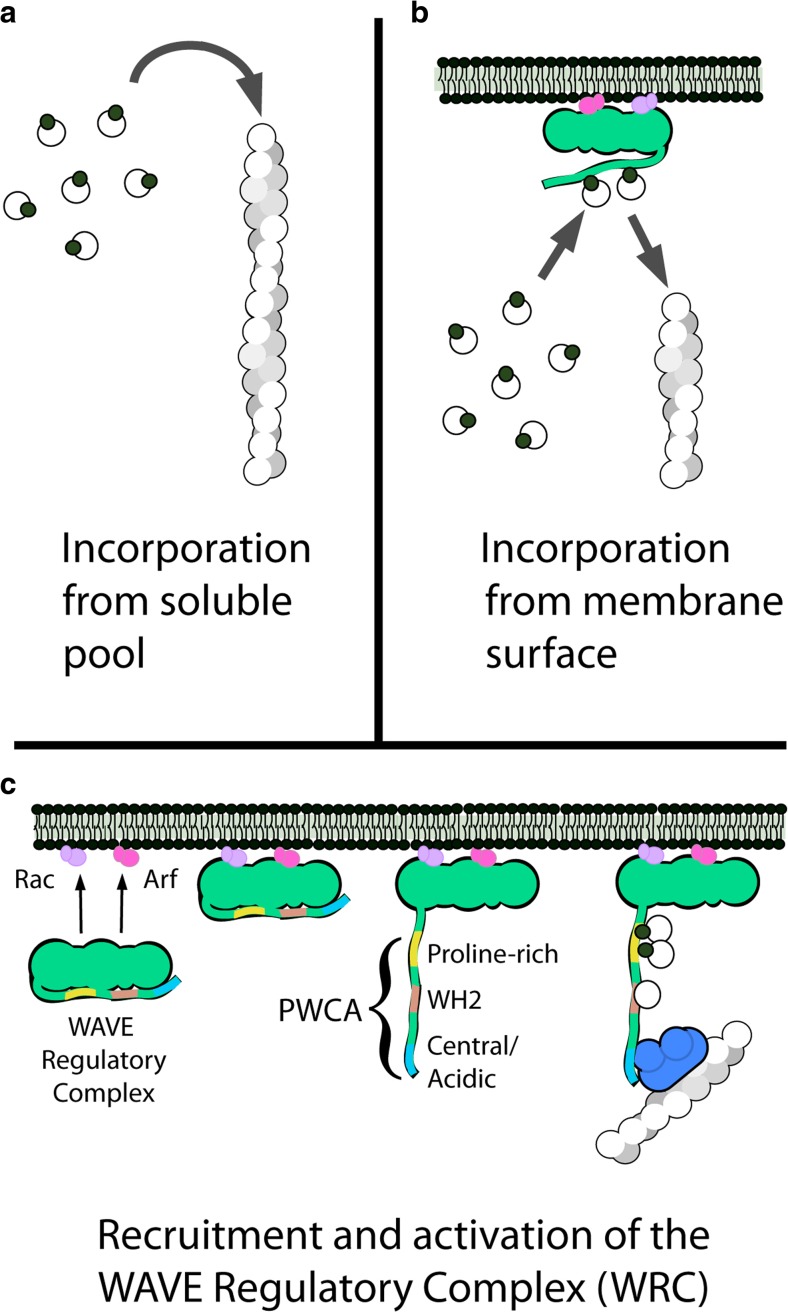
Fig. 1.

Actin filament assembly and the surface-associated monomer pool. a In vitro, an actin filament (helical structure on right) can elongate by incorporation of monomers and/or profilin-actin complexes (linked filled and empty circles) directly from solution. b The filaments in a branched actin network grow by incorporating monomers from membrane-associated nucleation-promoting factors such as the WAVE Regulatory Complex (green). c Recruitment and activation of the WAVE Regulatory Complex. Two small, membrane-associated G proteins (Rac and/or Arf) bind a WAVE Regulatory complex and induce a conformational change that releases a natively unstructured region, called a PWCA domain. PWCA sequences, which are found in all WASP-family nucleation-promoting factors, comprise a proline-rich sequence (P) that binds profilin and profilin-actin complexes, a WH2 domain (W) that binds monomeric actin, and a central/acidic region (CA) that interacts with the Arp2/3 complex

Note that understanding how actin flows through the membrane-associated pool requires some mathematical analysis. To improve readability, however, we follow the example of Mogilner and Oster (1996) and the advice of Fawcett and Higginson (2012), by placing all mathematical derivations in separate appendices (see Appendix 1 for definitions of parameters and dynamical variables).

Features and functions of a branched actin network

In addition to monomeric actin and/or profilin-actin complexes, three components are required to construct a force-generating, branched actin network: (1) the Arp2/3 complex, which creates new filaments that branch from the sides of preexisting filaments (Mullins et al. 1998); (2) nucleation-promoting factors, which both activate the Arp2/3 complex (Machesky et al. 1999) and accelerate filament elongation (Bieling et al. 2018); and (3) capping protein, which terminates barbed-end elongation of actin filaments (Isenberg et al. 1980) but also promotes rapid, polarized growth of branched actin networks (Loisel et al. 1999; Akin and Mullins 2008).

The Arp2/3 complex creates new actin filaments that are linked and entangled into branched networks, but it is the nucleation-promoting factors that determine the location, architecture, and function of these networks. Network construction begins with the accumulation of active NPFs on a membrane surface. These localized NPFs promote Arp2/3-dependent nucleation and rapid filament elongation in a narrow zone adjacent to the membrane, producing an anisotropic network in which the growing end of most filaments points toward the membrane (Small et al. 1995; Cameron et al. 2001). The most well-studied class of nucleation-promoting factors are members of the WASP family, including WASP itself (Derry et al. 1994), WAVE/Scar (Machesky et al. 1999), N-WASP (Rohatgi et al. 1999), WHAMM (Campellone et al. 2008), WASH (Liu et al. 2009), and JMY (Zuchero et al. 2009). Each of these actin regulators responds to a different set of signals and creates actin networks that contribute to different cellular processes (Campellone and Welch 2010). Isoforms of WAVE, for example, assemble branched actin networks in leading-edge lamellipodia and are recruited to the membrane surface as part of a large WAVE Regulatory Complex (Fig. 1c). Membrane localization of the WAVE Regulatory Complex is driven by its interaction with two small, membrane-associated G proteins (Koronakis et al. 2011; Chen et al. 2017).

All WASP family nucleation-promoting factors bind directly to profilin, actin, and the Arp2/3 complex via a core set of conserved sequences, collectively known as a PWCA motif (Fig. 1c). The arrangement of binding sites within a PWCA sequence is conserved across orthologous and paralogous proteins, strongly suggesting that they function together as a unit. Starting from the C-terminal end of the sequence: the central/acidic (CA) region binds to the Arp2/3 complex (Marchand et al. 2001) and promotes a conformational change required for dendritic nucleation activity (Espinoza-Sanchez et al. 2018). The WASP homology 2 (WH2 or W) sequence binds monomeric actin (Dominguez 2007) and promotes filament formation by delivering its bound actin to an Arp2/3 complex on the adjacent CA sequence (Marchand et al. 2001; Dayel and Mullins 2004). Efficient filament formation requires simultaneous binding of two WCA sequences (Padrick et al. 2011) and a preexisting (mother) filament to an Arp2/3 complex (Mullins et al. 1998; Machesky et al. 1999). Requiring the Arp2/3 complex to bind a preexisting filament makes the process of filament formation autocatalytic. Finally, the proline-rich region (P) binds profilin-actin complexes and delivers actin monomers to growing filament ends and to adjacent WH2 domains (Bieling et al. 2018). This collection of activities makes the PWCA motif the central conduit through which actin flows into branched networks.

WH2 domains form a polymerase and a feedback controller

In addition to providing actin monomers required by the Arp2/3 complex (Dayel and Mullins 2004), WH2 domains also transfer monomers to the fast-growing, barbed end of an actin filament (Higgs et al. 1999). When a large number of actin-loaded WH2 domains are clustered on a surface, they act collectively to accelerate the assembly of nearby filaments and networks (Bieling et al. 2018). Interestingly, this polymerase activity likely explains previous reports of an Arp2/3-independent component in the polymerization-driven movement of the intracellular pathogen Listeria monocytogenes (Brieher et al. 2004).

In addition to functioning as a polymerase, monomer transfer from WH2 domains to nearby filaments enables the number of growing filaments to control the rate at which new filaments are formed by the Arp2/3 complex (Akin and Mullins 2008). This is similar to what engineers call a “feedback controller,” a device that measures the output of a system and then adjusts the input to achieve a desired result, and it has a profound effect on network architecture. A mathematical model helps us see the importance of this negative feedback (Appendices 2 and 3). Without negative feedback, Arp2/3-dependent filament formation would be a simple autocatalytic reaction (Fig. 2a), meaning that every new filament becomes a new substrate for the Apr2/3 complex, and accelerates creation of additional filaments (Pantaloni et al. 2000; Zalevsky et al. 2001; Achard et al. 2010). This autocatalytic mechanism predicts that the density of growing filament ends near the membrane, E (with units of μm⁻²), will almost always grow or decay exponentially (see Appendix 2 for details):

$$E\left(t\right)=E_{0}e\left(k_N{W}_{\mathit{tot}}^2-k_C\right)t$$ 1

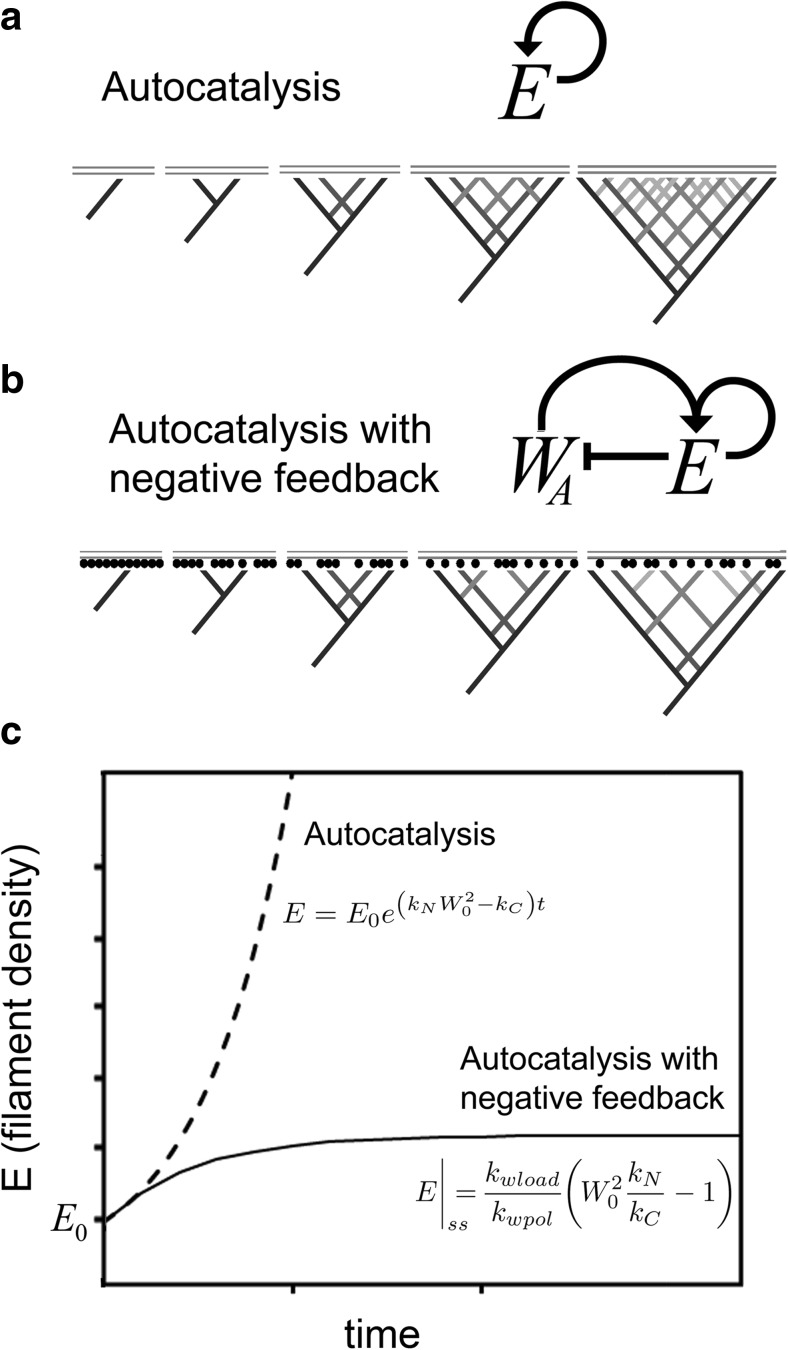
Fig. 2.

Autocatalytic filament formation with and without negative feedback. Nucleation of new actin filaments by the Arp2/3 complex is autocatalytic, because the product of the reaction—a “daughter” filament—is also a substrate—an additional “mother” filament. a If autocatalysis were unregulated, filaments would beget filaments and the network density would grow exponentially. b In reality, however, the activity of the Arp2/3 complex is product inhibited, because growing filaments leech actin monomers away from WASP family proteins on the membrane surface, thus slowing the rate of nucleation. c Time evolution of filament density predicted by simple autocatalysis (Eq. 1, top curve) and autocatalysis with negative feedback (bottom curve)

Where E₀ is the initial density of free filament ends near the membrane (in μm⁻²), W_tot is the surface density of WASP family proteins (also in μm⁻²), and k_N and k_C are rate constants that describe filament nucleation and capping (Appendix 1). This model produces a non-zero, steady-state filament density only when nucleation exactly balances capping (i.e., when k_NW_tot² = k_C). Whenever the surface density of WASP family proteins is high enough to drive nucleation faster than capping (i.e., when k_NW_tot² > k_C), the exponent in Eq. 1 will be positive, and any filaments present at the beginning of the reaction (E₀) will spark unbounded, exponential growth (Fig. 2c).

Obviously, filament density cannot grow without bound, since only a finite number of actin molecules can be packed into a given volume. The densities of real branched networks, observed in vivo and in vitro, have stable, steady-state values that are much lower than the physical limit imposed by packing. Furthermore, the effects of NPF surface density and capping protein concentration on network architecture (Bernheim-Groswasser et al. 2002; Akin and Mullins 2008) argue that steady-state density is determined primarily by kinetic rather than steric effects.

Branched actin network density is controlled by WH2-mediated product inhibition of the Arp2/3 complex. It works like this: when a WASP family protein transfers its bound actin to an Arp2/3 complex or a nearby filament, it becomes temporarily inactive and must be “recharged” with another actin monomer. As actin filaments accumulate to higher and higher densities near the membrane, they leech actin monomers away from WASP family proteins at higher and higher rates. This monomer leeching decreases the steady-state density of actin-charged WASP family proteins and reduces the rate of nucleation (Fig. 2b). Here we have a negative feedback loop that tames explosive, autocatalytic nucleation by the Arp2/3 complex and creates a homeostatic mechanism for controlling branched network density. With negative feedback, whenever nucleation outpaces capping, the filament density rises, but the increasing filament density acts to slow the rate of nucleation until it is eventually balanced by capping. Note that, without capping, this negative feedback would cause the rate of nucleation to continue falling toward zero. This is one way that capping protein promotes branched network formation, which we called monomer gating (Akin and Mullins 2008).

To gain more quantitative insight into the effect of negative feedback on network density, we can introduce into our mathematical model a requirement that WH2 motifs in a PWCA motor domain must bind actin to activate the Arp2/3 complex. Under these conditions, we see that the density of filament ends in proximity to the membrane now has a stable, steady-state solution (see Appendix 3):

$${\left.E\right|}_{\mathit{ss}}=\frac{k_{\mathit{\text{wload}}}}{k_{\mathit{\text{wpol}}}}\left(W_{\mathit{tot}}^2\frac{k_N}{k_C}-1\right)$$ 2

In Eq. 2 above, steady-state filament density depends on (1) the square of the NPF surface density, (2) the ratio of nucleation and capping rates (k_N/k_C), and (3) the ratio of how fast actin is loaded onto WH2 domains to how fast it is drained away by polymerase activity toward nearby barbed ends (k_wload/k_wpol). Note that steady-state filament density no longer depends on the starting density, E₀ (Fig. 2c).

The PRD accelerates filament growth and also loads actin onto WH2 domains

All WASP family nucleation-promoting factors contain a proline-rich domain (PRD), which sits on the N-terminal side of the Arp2/3-activating, WCA motif. The strings of proline residues in this region bind either SH3-containing adaptor proteins or the actin monomer-binding protein profilin (Perelroizen et al. 1994; Petrella et al. 1996). The proline-rich region of mammalian WAVE1, for example, can bind six profilin molecules, with varying affinities (Bieling et al. 2018). Profilin can bind both actin and poly-proline simultaneously, so in the cytoplasm, where most monomeric actin is bound to profilin, the PRD will be occupied by profilin-actin complexes. Similar to actin transfer from WH2 domains described above, the transfer of profilin-actin complexes from proline-rich domains onto nearby barbed ends promotes filament elongation and, when multiple PRD-containing proteins are clustered on a surface, this process can increase elongation velocity several fold (Bieling et al. 2018).

Actin can also transfer from profilin-actin complexes on the proline-rich domain to an adjacent WH2 domain (Fig. 3). The binding sites for profilin and WH2 domains overlap, and in solution, profilin-actin complexes do not have a detectable affinity for WH2 domains (Higgs et al. 1999). Resonance energy transfer experiments reveal, however, that profilin-actin complexes bound to a PRD can form short-lived ternary complexes with adjacent WH2 domains (Bieling et al. 2018). This configuration, similar to one observed in a profilin-actin-VASP complex (Ferron et al. 2007), can promote loading of the WH2 domain with monomeric actin, which accounts for the synergistic polymerase activity of linked proline-rich and WH2 domains using profilin-actin as a substrate (Bieling et al. 2018; Hansen and Mullins 2010). Transfer of actin from the PRD to the WH2 domain also facilitates activation of the Arp2/3 complex in the presence of profilin, which normally inhibits actin-binding to WH2 domains (Higgs et al. 1999). Without this ability to load WH2 domains with actin from profilin-actin complexes, profilin strongly inhibits Arp2/3-dependent nucleation (Machesky and Insall 1998) and poisons network formation.

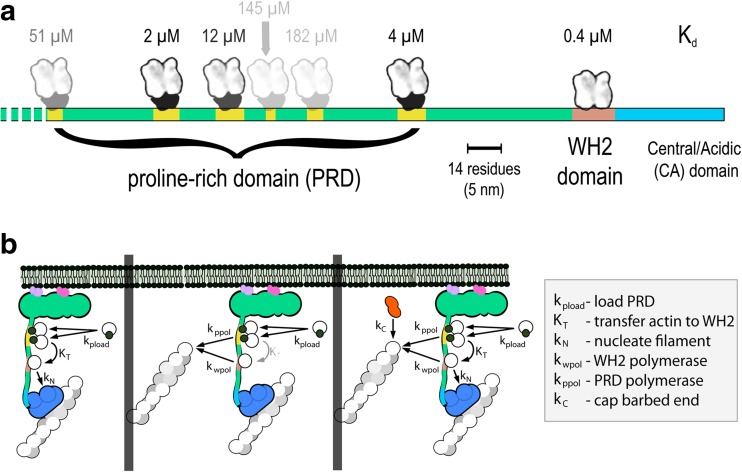
Fig. 3.

Layout of the WAVE1 PWCA domain and flux of actin and profilin-actin through the proline-rich and WH2 domains. a Linear model of the PWCA domain from WAVE1, consisting of amino acids 277–559. Profilin-binding sites in the proline-rich domain are marked in yellow, the actin-binding WH2 domain is red, and the central/acidic region is blue. Actin monomers and profilin-actin complexes are shown on the same scale as the linear extent of the PWCA polypeptide (note scale bar). The affinity (dissociation equilibrium constant) of each profilin or actin-binding site is marked above in micromolar. b Pathways by which actin flows through surface-associated WASP family proteins and into growing filament networks. Left: poly-proline sequences bind profilin-actin complexes and can transfer monomeric actin onto the WH2 domain. From there, the actin can be used to activate the Arp2/3 complex and create a new filament, branching from the side of a preexisting filament. Middle: Actin can be transferred from the WH2 domain and poly-proline sequences onto the ends of nearby filaments. Decreased transfer from the poly-proline sequences and increased depletion by nearby filaments decreases the occupancy of the WH2 domain and slows the rate of nucleation. Right: capping protein decreases the number of growing filaments and increases the steady-state occupancy of both the WH2 domain and the poly-proline sequences

How PWCA motor domains deliver actin monomers to filament ends

Together, the WH2 and proline-rich regions of a PWCA domain create an effective polymerase that accepts both actin monomers and profilin-actin complexes as substrates. Significantly, the proline-rich regions of formin FH1 domains also accelerate filament elongation by collecting profilin-actin complexes and transferring them to nearby filament ends. Although the same biochemical mechanisms underlie profilin-actin transfer from FH1 and PWCA domains (see below), the polymerase activities they support are quite different. In formin-mediated polymerization, two FH1 domains serve a single actin filament attached to an adjacent dimer of FH2 domains. This combination creates a highly processive polymerase that remains attached to one filament for many cycles of monomer addition (Higashida et al. 2004; Kovar and Pollard 2004). In contrast, the polymerase activity of PWCA domains is highly distributive, because enhanced filament growth depends on multiple, short-lived interactions between a filament end and a cluster of PWCA domains. We know that individual filament-PWCA interactions are short-lived because a single filament can grow laterally across a lawn of immobilized PWCA domains at a velocity proportional to the PWCA density (Bieling et al. 2018). This activity also contrasts sharply with “actoclampin” models of filament growth (Dickinson and Purich 2002; Dickinson 2009), in which a filament remains “clamped” to a surface-associated polymerase. A distinguishing feature of distributive PWCA polymerase activity is that filament elongation rate depends on how many filaments share the same PWCA cluster.

The distributive polymerase activity of PWCA clusters relies on a convenient set of biochemical properties shared by both profilin and the WH2 domain. Specifically, both actin-binding factors (1) permit association of bound monomers with filament barbed ends, (2) bind monomeric actin with high affinity, and (3) bind filament ends with much lower affinity. This suite of properties was first described for profilin by Pollard and Cooper (1984), who recognized that the shift from high-affinity monomer-binding to low-affinity barbed end binding must be coupled to a free energy change in the profilin-monomer-filament complex, most likely a polymerization-driven conformational change in the monomer. Some studies linked this free energy change to ATP hydrolysis on the bound actin (Romero et al. 2004; Romero et al. 2007), but multiple lines of biochemical and biophysical evidence have effectively ruled out a requirement for ATP hydrolysis (Blanchoin and Pollard 2002; Jégou et al. 2011). Higgs et al. (1999) discovered that the WH2 domain also supports polarized filament assembly and must have a profilin-like, differential affinity for monomers versus barbed ends. Profilin and the WH2 domain do not behave identically, however, because in the absence of monomeric actin, the WH2 domain can remain tightly attached to filament ends, tethering them to membrane surfaces (Co et al. 2007). Structural studies have identified polymerization-associated conformational changes in actin (von der Ecken et al. 2015), and these may be sufficient to explain the thermodynamic landscape of profilin-monomer-filament interaction (Kinosian et al. 2002; Courtemanche and Pollard 2013).

In solution, neither profilin nor the WH2 domain promotes rapid filament elongation. It is only when clustered at high density on a surface that their differential affinity for monomers versus barbed ends can be exploited to create an effective polymerase. In vivo, interactions between signaling molecules produce some of this clustering, but the assembly of a branched actin network also inherently drives high-density clustering of associated PWCA domains (Co et al. 2007) and strongly favors polymerase activity. Monomer transfer from a loaded PWCA domain can begin when a bound profilin-actin complex attaches to the barbed end of a nearby filament (Fig. 4a). Here is the point at which the terminal actin monomer probably undergoes a conformational change that promotes rapid profilin dissociation (Fig. 4a, step 3); otherwise, the attached profilin would interfere with continued filament elongation. Kinetic and thermodynamic studies suggest a > 200-fold difference in profilin’s affinity for monomers versus barbed ends (Kinosian et al. 2002; Courtemanche and Pollard 2013). When uncomplexed profilin dissociates from the proline-rich region, high concentrations of profilin and actin in the cytoplasm ensure that it will almost always be replaced by a profilin-actin complex. A similar sequence of events underlies transfer of actin from the WH2 domain to the end of a nearby filament (Fig. 4b). Effective polymerase activity requires that the switch from high to low affinity be very fast and that the local density of PWCA domains be high enough to support frequent monomer transfer events. Under these conditions, a surface-proximal filament can elongate faster than the “diffusion limit,” simply because it encounters surface-associated monomers more frequently than soluble monomers. In other words, the effective concentration of surface-associated actin that is available to the filament is higher than the concentration of monomers in solution.

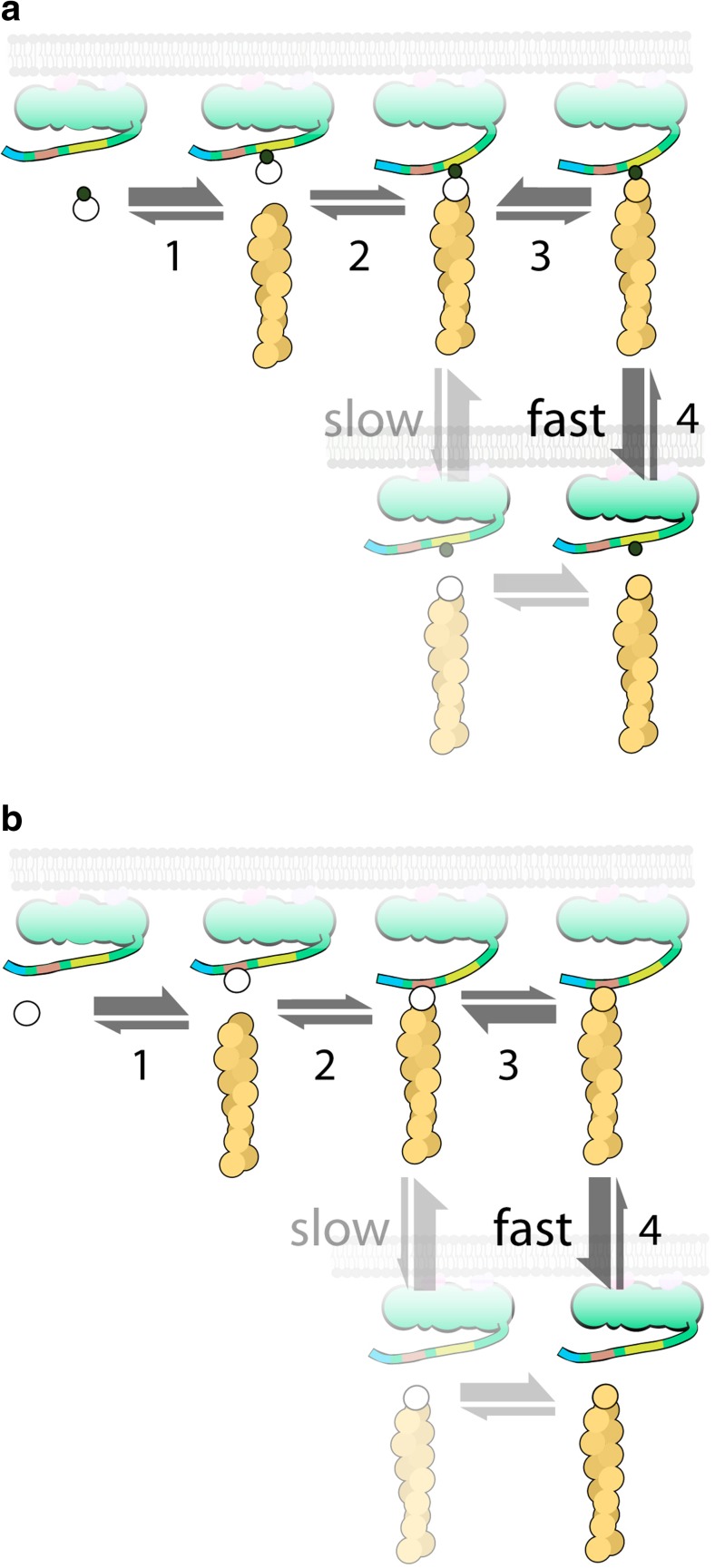
Fig. 4.

Sequence of steps in the transfer of actin from a proline-rich (a) or WH2 (b) domain of a membrane-associated nucleation-promoting factor onto the end of an actin filament. a A profilin-actin complex (linked circles) binds to the proline-rich (yellow) region (step 1), the bound profilin-actin complex attaches to the barbed end of an actin filament (step 2), the terminal actin monomer undergoes a rapid conformational change (step 3), and the profilin-poly-proline complex dissociates from the barbed end of the filament (step 4). In the absence of a conformational change in the terminal actin subunit, dissociation of the profilin is slow. b Monomeric actin (open circle) binds to the WH2 (red) sequence (step 1), the WH2-bound actin monomer attaches to the barbed end of a nearby filament (step 2), the terminal actin monomer undergoes a rapid conformational change (step 3), and the WH2 domain rapidly dissociates from the filament barbed end (step 4). Effective polymerase activity requires that the local density of PWCA domains be high enough to support frequent monomer transfer events

A PWCA cluster can sustain fast filament elongation because it acts as a “kinetic funnel” that accumulates actin and profilin-actin complexes from solution and feeds them to growing filaments faster than the filaments could gather those soluble building blocks on their own. Note that, even though the surface-associated actin pool is saturable, it can be replenished from solution much faster than an actin filament can grow from soluble monomers. To see how this works, consider a simple system with a cluster of 10 PWCA domains and one membrane-proximal actin filament (Fig. 5a). We will assume that each PWCA domain binds a single profilin-actin complex from solution, which dissociates only when the actin is transferred to the growing filament end. For simplicity, we will also assume that soluble profilin-actin complexes bind with the same kinetics to a PWCA domain and the end of a filament, namely at a rate of k_m+[M], where k_m+ is a simple, second-order rate constant and [M] is the concentration of soluble profilin-actin. At steady-state, the rate at which the PWCA actin pool is replenished from solution depends on the number of unoccupied PWCA domains. For example, if the steady-state occupancy of the pool is six actin monomers, four PWCA domains will be unoccupied and flux into the membrane-associated pool will be 4 × k_m+[M]. Since the system is at steady-state, the cluster must also be delivering actin to the filament end at a rate of 4 × k_m+[M], that is, four times faster than the filament could grow on its own by interacting with soluble monomers. If steady-state filament growth were slower, occupancy of the pool would be higher, causing the rate of replenishment to be proportionally lower.

Fig. 5.

The steady-state occupancy of actin-binding sites on the membrane surface depends on the rates at which they are loaded and depleted. The WH2 and proline-rich domains are loaded by the binding of soluble actin monomers or profilin-actin complexes (left). These sites are depleted primarily by interactions between the bound actin and growing filament ends close to the membrane (right). Loading depends primarily on the concentration of soluble actin and profilin-actin, while depletion is proportional to the number of growing filament ends in proximity to the membrane. By capping fast-growing barbed ends, capping protein lowers the rate of depletion and increases the steady-state occupancy of surface actin pool

Estimating how much actin enters a network from the surface-associated pool

Experiments in which branched networks grow faster than can be explained by diffusion-limited incorporation of monomers from solution provide a basis for estimating the fraction of actin that enters the network from the surface-associated pool. For example, in Bieling et al. (2018), we observed branched actin networks grow from surfaces coated with ~ 1800 WAVE1 molecules/μm² in 5 μM profilin-actin at a rate approximately fourfold faster than single filaments in 5 μM profilin-actin. In a separate set of experiments, we compared single filaments growing across uncoated surfaces and surfaces coated with ~ 1800 WAVE1 molecules/μm². Filaments on WAVE1-coated surfaces elongated sixfold faster than those on uncoated surfaces. If most of the filaments in our branched network grow at approximately the same rate, we can say that more than 90% of the actin in the network comes from the surface-associated pool and less than 10% comes from solution (see Appendix 4).

What happens inside living cells? In Schizosaccharomyces pombe, for example, the soluble actin concentration is ~ 32 μM (Wu and Pollard 2005), which is sixfold higher than in the experiments described above. The surface density of WASP family proteins at a site of branched network assembly inside S. pombe is ~ 25,000/μm² (Arasada and Pollard 2011) or about 14-fold higher than in the experiments described above. Contributions from the soluble pool to filament elongation should increase linearly with the concentration of soluble actin, while contributions from the surface-associated actin pool will increase linearly with surface density of PWCA-containing proteins. So based on the available numbers, we expect the distributive polymerase activity of PWCA clusters to dominate network assembly in vivo even more than we observe in vitro.

How capping protein accelerates branched network growth

Extending our mathematical description of branched network formation to include the combined polymerase activities of the WH2 and proline-rich domains (see Appendix 5), we can calculate the steady-state elongation rate (dL/dt) of filaments in proximity to surfaces coated with PWCA motor domains.

$$\frac{\mathit{dL}}{\mathit{dt}}=\mathit{\text{kwpol}}\frac{k_C}{k_N{W}_{\mathit{tot}}}\left(1+\frac{\mathit{\text{kpload}}}{\mathit{\text{kwload}}}\right)$$ 3

According to Eq. 3, filament growth velocity depends on the WH2 polymerase rate constant (k_wpol) and on how quickly the proline-rich and WH2 domains can be loaded with their respective substrates: profilin-actin complexes and actin monomers (k_pload and k_wload). Note also that a faster rate of nucleation (~k_NW_tot) actually decreases the elongation velocity because it produces a higher density of free barbed ends, which compete with each other for a limited resource: PWCA-bound actin monomers. The filament elongation velocity increases linearly with capping rate (k_C) for the same reason.

The effect of capping protein on elongation is one of the most significant implications of Eq. 3 and warrants further discussion. Heuristically, capping decreases the steady-state density of free filament ends (E) in proximity to the membrane surface (Eq. 2), slowing the rate of actin depletion. As a consequence, the steady-state occupancy of both the WH2 and proline-rich domains (W_A and P_A) increases, fueling faster filament assembly via their combined distributive polymerase activity (Fig. 5b). We call this phenomenon branch competition, because all the growing filament ends in a given branched network compete for actin flowing through the same cluster of surface-associated binding sites. The surface-associated actin pool, therefore, forms a limited capacity channel, and the more filaments compete for the actin flowing through this channel, the slower each filament grows. Importantly, this effect occurs entirely at the PWCA-coated surface and does not require changes in the concentration of soluble actin or profilin-actin complexes.

The effect of filament capping on the distributive polymerase activity of PWCA domains partially accounts for previous reports that capping protein promotes branched network assembly, both in vivo and in vitro. These reports include evidence that decreasing capping protein in live cells shuts down branched network assembly (Iwasa and Mullins 2007) and can cause leading-edge morphology to switch from lamellipodial to filopodial (Mejillano et al. 2004; Edwards et al. 2015). Conversely, increasing cellular activity of capping protein can accelerate actin network growth and leading-edge membrane protrusion (Hug et al. 1995; Sun et al. 1995; Jung et al. 2016). In vitro, capping protein is absolutely required for reconstitution of polarized, force-generating branched actin networks (Loisel et al. 1999) and increasing the capping protein concentration linearly increases the rate of network growth (Akin and Mullins 2008).

Conclusions and implications

Since its discovery, much attention has focused on the Arp2/3 complex and the mechanism by which it creates new actin filaments from the sides of preexisting ones. It turns out, however, that the Arp2/3 complex is only one cog in a more complex machine for making polarized actin networks that push against membrane surfaces. The other components of this self-assembling machine—nucleation-promoting factors and capping protein—contribute to network formation in non-intuitive ways that require quantitative analysis to fully understand. Note that the mathematical models we use here simply illustrate how well-established protein-protein interactions can account for higher-order network behavior. By simply keeping track of actin flux into the network, we derive equations that describe two fundamental features of a branched network: density (Eq. 2) and velocity (Eq. 3).

We suggest that the conserved requirement for WH2-dependent actin delivery to the Arp2/3 complex reflects the importance of product inhibition in controlling branched network architecture (Fig. 3). WASP-family proteins across eukaryotic phyla contain WH2 domains (Fritz-Laylin et al. 2017), but there is no a priori reason why a nucleation factor should require WH2-bound actin to create a new filament. Formin-family proteins, for example, have no similar requirement, and the Arp2/3 complex could almost certainly have evolved without it. Arp2 and Arp3 can form a surface similar to the barbed end of an actin filament (Kelleher et al. 1995), so in principle a simple conformational change in the complex could have been sufficient to create a new filament. Requiring a WH2-bound monomer to nucleate a new filament, however, applies the brakes to autocatalytic nucleation at high filament densities and creates a stable, steady-state network.

Interestingly, members of the Ena/VASP family of actin regulators share elements of domain architecture, monomer transfer, and polymerase activity with WASP family proteins. Specifically, Ena/VASP proteins contain the PW section of a PWCA motor domain: a profilin-binding, proline-rich domain located on the N-terminal side of an actin-binding, WH2-like sequence. The Dominguez lab demonstrated the potential of these proline-rich sequences to transfer actin from profilin-actin complexes to adjacent WH2-like sequences by solving the atomic structure of a ternary complex between profilin, actin, and the WH2-like domain of VASP (Ferron et al. 2007). As with WASP family proteins, both the proline-rich and WH2-like sequences of VASP can deliver actin to free barbed ends of nearby filaments, together forming an effective polymerase that accelerates filament elongation in both the absence and presence of profilin (Breitsprecher et al. 2008; Hansen and Mullins 2010). Ena/VASP proteins accumulate in many of the same places as WASP family proteins, including leading-edge lamellipodia, but their functions have often been contrasted (Mejillano et al. 2004; Svitkina et al. 2003). Based on their similar polymerase activities, WASP and VASP family proteins should cooperate to form surfaces that actively promote filament assembly. The biologically relevant differences between WASP and VASP family proteins may be more of degree than kind. Specifically, Ena/VASP proteins are tetrameric, which makes their polymerase activity more processive than that of WASP family proteins (Hansen and Mullins 2010). The greater processivity of VASP and its ability to form tight clusters are likely the unique features that enable it to promote filopodia formation on membranes populated with many similar polymerases (Svitkina et al. 2003).

Understanding how capping protein modulates actin network assembly is important for two reasons. Firstly, it provides deeper insight into the biophysical mechanisms that underlie branched network motor activity and explains why capping protein forms an integral part of this motor. Secondly, we can begin to make sense of how and why cells regulate the localization and activity of capping protein. Until recently, the orthodox view of actin regulation held that capping protein is not regulated at all and that it diffuses freely through the cytoplasm in its active form (Pollard and Borisy 2003). We now know of two widely conserved factors that bind capping protein and regulate its activity in space and time. The first is V-1/myotrophin, which binds and completely inactivates capping protein. In mouse and Dictyostelium cells, V-1 is present in sufficient concentrations to sequester the majority of capping protein in inactive complexes, and knocking down endogenous V-1 expression has a similar effect to overexpressing capping protein (Jung et al. 2016). The second capping regulator is Capping protein, ARp2/3, and Myosin I Linker (CARMIL), which reduces capping protein’s affinity for filament ends but does not abolish capping activity altogether. In a beautiful study, combining biochemistry and cell biology, Fujiwara et al. (2014) showed that CARMIL promotes V-1 dissociation from capping protein, which is then capable of binding filament ends. These authors also showed that CARMIL can localize to leading-edge lamellipodia, where capping protein activity is absolutely required for branched actin network formation.

Carlier previously proposed an explanation for the growth-enhancing effects of capping protein, called the funneling hypothesis (Carlier and Pantaloni 1997; Carlier 1998; Carlier and Pantaloni 2007). Briefly, the funneling hypothesis is based on an analysis of steady-state actin treadmilling, and it assumes that filament disassembly occurs primarily via slow depolymerization from the pointed end. For this slow process to fuel rapid filament growth at the barbed end, actin from a large number of depolymerizing filament ends must be funneled into a small number of growing filament ends by the activity of capping protein. Importantly, the funneling model requires that actin filaments elongate by incorporating monomers directly from solution, and it assumes that changes in filament elongation rate are driven by changes in the concentration of soluble actin (Carlier and Pantaloni 1997). In addition, this model predicts a highly non-linear dependence of filament growth velocity on capping, with low concentrations of capping protein having very little effect.

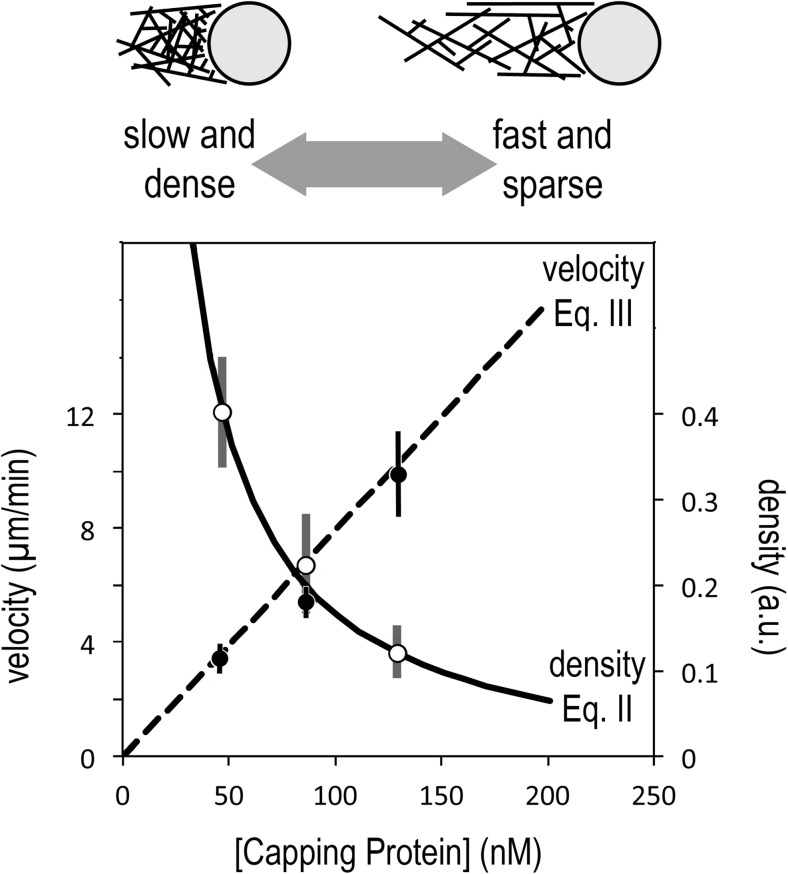
We previously demonstrated, however, that the growth rate of Arp2/3-generated actin networks increases linearly with capping protein concentration, even when the soluble pool of monomeric actin remains constant (Akin and Mullins 2008). Moreover, when we adjust the capping protein concentration to account for mechanical effects, Eqs. 2 and 3 provide an excellent description of the effects of capping on both density and velocity of branched actin networks from the earlier in vitro study (Fig. 6). We can see from both the data and the equations that branch competition links filament density in a reciprocal relationship to growth velocity. When capping activity is low, the networks are slow-moving and dense, but as capping increases, the networks become faster and sparser (Fig. 6). We can multiply the filament density and growth rate (Eqs. 2 and 3) together to compute the overall rate of polymer formation. Interestingly, the reciprocal dependences of these two quantities on capping ensure that their product is almost invariant to changes in capping protein concentration. This recapitulates another experimental result reported by Akin and Mullins (2008). More recently, we showed that capping protein can accelerate growth of branched actin networks to velocities higher than can be explained by incorporation of monomers from solution (Bieling et al. 2018). The results of both Akin and Mullins (2008) and Bieling et al. (2018) are consistent with Carlier’s general idea that actin filaments compete for a limited pool of polymerization-competent monomers, but obviously, they cannot be explained by the original funneling hypothesis (Carlier and Pantaloni 1997). Funneling à la Carlier requires filaments to compete for soluble actin monomers, pulled from a pool whose size is set by the balance between slow filament depolymerization and fast filament assembly. Branch competition, on the other hand, reflects competition between filaments for surface-bound monomers, and the size of this pool can change independently of the soluble actin concentration.

Fig. 6.

The antagonistic relationship between elongation and nucleation of filaments in a branched actin network means that the velocity and density have reciprocal responses to capping protein. Low rates of capping create networks that are denser but slower, while high rates of capping produce networks that are sparser but faster (top). This effect is described quantitatively by Eqs. 2 and 3 (bottom), which predict a linear increase in network velocity with capping protein concentration (Eq. 3, dashed line), and an inverse relationship between network density and capping (Eq. 2, solid line). Data points are taken from Fig. 2c, d of Akin (2008) and represent velocity and density of polarized, branched actin networks assembled from purified components by nucleation-promoting factors immobilized on polystyrene microspheres. Density (right axis) is expressed in arbitrary units based on intensity of fluorescently labeled actin (for more experimental details, see Akin, 2008). To account for mechanical effects associated with propulsion of spherical particles coated with immobile nucleation-promoting factors, we have adjusted the data points by subtracting the capping protein concentration required for the actin network to break symmetry and begin moving

Finally, the ability of profilin to inhibit WCA-stimulated actin assembly (i.e., in the absence of a proline-rich domain) has been interpreted as evidence that profilin generally antagonizes Arp2/3-dependent nucleation and acts in vivo to shunt actin away from branched networks (Rotty et al. 2015; Suarez et al. 2015; Suarez and Kovar 2016). By loading WH2 domains with actin, however, the proline-rich region converts profilin-actin into a perfectly good substrate that the Arp2/3 complex can use to create new filaments. In addition, the polymerase activity of proline-rich regions enables profilin to actually accelerate rather than inhibit branched network growth. Interestingly, the earliest reconstitution of Arp2/3-dependent Listeria motility in cell extracts (Theriot et al. 1994) demonstrated that profilin not only localizes to the growing surface of the actin network but is also required for network formation and growth. Subsequently, Yarar et al. (2002) showed that the proline-rich domains of endogenous NPFs, WASP, and WAVE1 enhance branched actin network formation in cell extracts by recruiting profilin-actin. Intriguingly, Mouneimne et al. (2012) found that some effects of profilin are isoform specific, with profilin-1 promoting membrane protrusion and cell migration. Given profilin’s active participation in the two major aspects of branched network assembly, nucleation and elongation, questions remaining to be answered include (1) how do critical features of network architecture (e.g., density, velocity, mechanics) respond to changes in total profilin concentration and (2) how do different profilin isoforms collaborate with the various WASP family proteins to promote different types of network growth.

Appendix 1. Definition of key parameters and dynamical variables

Models discussed in this work assume that the concentrations of all soluble components—actin, profilin-actin, capping protein, and the Arp2/3 complex—are approximately constant. For this reason, they have been combined with the appropriate n-th order rate constants to form pseudo (n-1)-th order rate constants. Note that, since the dynamical variables in our model are surface densities (expressed in μm⁻²) rather than concentrations (expressed in μM), the values of rate constants determined in solution must be corrected (typically by a factor < 4) before the results can be compared to experimental data.

Dynamical variables

E

is the density of free barbed ends of actin filaments proximal to the membrane surface. The proximity requirement is defined as the distance within which the filaments can productively interact with membrane-associated WASP family nucleation-promoting factors. This variable is treated as a surface density (in μm⁻²).

W_A

is the surface density (in μm⁻²) of WH2 domains that are bound to monomeric actin.

P_A

is the surface density (in μm⁻²) of poly-proline domains that are bound to profilin-actin complexes.

Parameters

E₀

is the initial density (in μm⁻²) of free barbed ends of actin filaments in proximity to the membrane.

W_tot

is the total surface density (in μm⁻²) of WASP family proteins associated with the membrane.

k_N

is a pseudo third-order rate constant (in μm⁴ s⁻¹) that describes Arp2/3-dependent filament nucleation. This parameter is the product of a fourth-order rate constant, k_n+ (in μM⁻¹ μm⁴ s⁻¹), with the solution concentration of the Arp2/3 complex, [Arp2/3], which is assumed to remain constant. For low concentrations of the Arp2/3 complex, this parameter can be approximated by k_n+[Arp2/3]. Because this is a high-order reaction that requires formation of a multi-component complex, however, the range over which this approximation holds is unclear.

k_C

is a pseudo first-order rate constant (in s⁻¹) that describes filament capping. This parameter is the product of the second-order rate constant for capping protein binding to free barbed ends, k_c+ (in μM⁻¹ s⁻¹), with the solution concentration of capping protein [C], which is assumed to remain constant. This can also be expressed as: k_c+[C].

k_wload and k_pload

are pseudo first-order rate constants (in sec⁻¹) that describe, respectively, the binding of actin to WH2 domains and the binding of profilin-actin complexes to poly-proline sequences. These parameters are products of second-order rate constants for protein-protein interaction, k_wa+ and k_ppa+ (in μM⁻¹ s⁻¹), with the solution concentrations of monomeric actin [A] and profilin-actin complexes [PA], which are assumed to remain constant. These parameters can also be expressed as: k_wa+[A] and k_ppa+[PA].

k_wd and k_pd

are first-order rate constants (in s⁻¹) that describe, respectively, dissociation of actin from a WH2 domain and dissociation of a profilin-actin complex from a poly-proline sequence.

k_wpol and k_ppol

are second-order rate constants (in μm⁻² s⁻¹) that describe, respectively, the transfer of actin from WH2 domains and profilin-actin complexes on poly-proline sequences to the ends of nearby actin filaments.

K_trans

is the rate (in μm⁻² s⁻¹) of intramolecular transfer of an actin monomer from a profilin-actin complex bound to a proline-rich domain to an adjacent, empty WH2 domain.

Appendix 2. Simple autocatalytic activation of the Arp2/3 complex

We assume that (1) the availability of soluble Arp2/3 complexes is not rate limiting and (2) the nucleation reaction is fast enough that the density of WASP family proteins available to interact with Arp2/3 complexes is approximately equal to the total surface density, W_tot. We can then write the rate of nucleation as k_NW_tot²E, where E is the number density of growing filaments near the NPF-coated surface and k_N is a nucleation rate constant. Strictly speaking, the nucleation rate depends on the density of filamentous polymer near the surface (F) rather than the density of free barbed ends (E). For a branched actin network growing against a surface, however, the density of polymer in proximity to the surface is proportional to E and inversely proportional to the cosine of the average angle (θ) between the filaments and a vector normal to the surface. We can, therefore, define the nucleation rate constant (k_N) to account for the difference between E and P.

The density W_tot is squared to account for the fact that two WASP family proteins are required to activate an Arp2/3 complex. In growing networks, capped filaments rapidly lose contact with NPF-coated surfaces and cease contributing to the nucleation reaction, so the change in filament number depends on both nucleation and capping:

$$\frac{\mathit{dE}}{\mathit{dt}}=k_N{W}_{\mathit{tot}}^{2}E-k_{C}E$$ 4

Here, k_C is a pseudo-first-order capping rate constant that assumes capping protein concentration (2) does not change. Note that this equation has steady-state solutions only when k_NW_tot² ≤ k_C.

$$E\left(t\right)=E_0{e}^{\left(k_N{W}_{\mathit{tot}}^2-k_C\right)t}$$ 5

For k_NW_tot² < k_C capping outpaces nucleation and the density of the network monotonically decreases with time, from its initial value (E₀) toward zero. When k_NW_tot² > k_C, the exponent is positive and any filaments present at the beginning of the reaction (E₀) will spark unbounded, exponential growth. Finally, when k_NW_tot² = k_C (i.e. when W_tot = [k_C/k_N]^1/2), capping and nucleation are balanced, and filament density remains constant at E₀. This is not a stable steady-state, however, and tiny fluctuations in nucleation or capping will cause the filament density to either collapse or to grow without bound.

Appendix 3. The effect of WH2 polymerase activity on Arp2/3 activation

A stable steady-state solution to Eq. (4) requires some sort of negative feedback by which an increase in the number of growing filaments could decrease the rate of new filament formation. The nucleation reaction itself provides some negative feedback, as recognized by Weichsel et al. (2017). These authors suggested that nucleation uses up “active” nucleation-promoting factors which much be “re-activated.” Although they did not elaborate on the putative “active” and “inactive” states, we know from previous work (Machesky, 1999; Zalevsky, 2001; Dayel, 2004) that NPFs with monomeric actin bound to their WH2 domains can activate the Arp2/3 complex while NPFs lacking actin cannot. We can rewrite Eq. (4), taking into account the fact that at least one of the WASP-family proteins that activates an Arp2/3 complex must be charged with actin.

$$\frac{\mathit{dE}}{\mathit{dt}}=k_N{W}_{\mathit{tot}}{W}_{A}E-k_{C}E$$ 6

When a nucleation-promoting factor transfers actin to the Arp2/3 complex or to the end of a nearby filament, it becomes temporarily inactive until “recharged” with actin. We must, therefore, also take account of the charging and depletion of WH2 domains, which can be (4) described by the following equation:

$$\frac{d{W}_A}{\mathit{dt}}=k_{\mathit{\text{wload}}}\left(W_{\mathit{tot}}-W_A\right)-k_{\mathit{wd}}{W}_A-k_{N}E{W}_{\mathit{tot}}{W}_A-k_{\mathit{\text{wpol}}}E{W}_A$$ 7

Equation 7 assumes (1) that the concentration of soluble actin monomers remains relatively constant and (2) that the total surface density of nucleation-promoting factors (W_tot) is simply the sum of the densities of actin-charged (W_A) and actin-depleted (W) molecules. In addition to nucleation and capping, we introduce rate constants for association and dissociation of actin and WH2 domains (k_wload and k_wd) and a rate constant for the polymerase activity of the WH2 domain (k_wpol).

We can now set the rates of change in Eqs. 6 and 4 equal to zero and solve for both the steady-state occupancy of the WH2 domain by monomeric actin, W_A, and the density of free barbed ends. The steady-state occupancy of WH2 domains turns out to be:

According to this equation, WH2 occupancy decreases with nucleation and increases with capping, reflecting the fact that free barbed ends in the actin network leech away bound actin.

$${\left.W_A\right|}_{\mathit{SS}}=\frac{k_C}{k_N{W}_{\mathit{tot}}}$$ 8

Note that this equation is physically meaningful over a limited range of parameter values. If the nucleation or capping rates are zero, no stable network forms. We can also show (see below) that no network forms when k_C is equal to greater than k_NW₀². Satisfyingly, when k_C is exactly equal to k_NW₀², and the steady-state filament density is zero, occupancy of the WH2 domain is simply W_tot, the total surface density of WASP family proteins.

Similarly, we find that the steady-state density of free barbed ends is given by:

$${\left.E\right|}_{\mathit{ss}}=\frac{k_{\mathit{\text{wload}}}{W}_{\mathit{tot}}^2\frac{k_N}{k_C}-\left(k_{\mathit{\text{wload}}}+k_{\mathit{wd}}\right)}{k_N{W}_{\mathit{tot}}+k_{\mathit{\text{wpol}}}}$$

Activation of the Arp2/3 complex may leech some bound actin from nucleation-promoting factors, but this reaction is limited by a slow, first-order step (Zalevsky, 2001; Marchand, 2001). This slow step makes nucleation much slower than transfer of actin from WH2 domains to free barbed ends (Bieling et al. 2018). From the measured rates of these reactions, we estimate that, given identical local densities of barbed ends and Arp2/3 complexes, the rate of actin flow from WH2 domains into filament elongation will be almost two orders of magnitude greater than that caused by nucleation. Neglecting the effects of nucleation and dissociation on the availability of actin-charged WH2 domains yields a simpler equation.

$${\left.E\right|}_{\mathit{ss}}=\frac{k_{\mathit{\text{wload}}}}{k_{\mathit{\text{wpol}}}}\left(W_{\mathit{tot}}^2\frac{k_N}{k_C}-1\right)$$ 9

The parenthetical expression in Eq. 6 defines a fundamental stability criterion for formation of an actin network in contact with a surface. Our physical interpretation is that, when this expression is less than or equal to zero, no network forms. The condition that must be satisfied for network formation is, therefore:

$$W_{\mathit{tot}}>\sqrt{\frac{k_C}{k_N}}$$

In other words, the surface density of WASP family proteins required to generate a stable actin network scales as the square root of the ratio of capping and nucleation rates. This relationship likely explains failure of network formation at high concentrations of capping protein or low concentrations of the Arp2/3 complex (e.g., Akin, 2008).

Appendix 4. Estimating actin contributed by the surface-associated monomer pool

We assume that monomers from solution add to filaments at a rate of K_soln while surface-associated actin incorporates at a rate of K_surf. The composite rate of elongation is, therefore, given by:

$$K_{\mathit{\text{comp}}}=f{K}_{\mathit{\text{surf}}}+\left(1-f\right)K_{\mathit{so}ln}$$

where f is the fraction of monomers incorporated from the surface. If we express the overall filament growth rate and the surface-mediated component of elongation in terms of the diffusion-limited growth from soluble monomers, we can rewrite the above equation as:

$$\alpha K_{\mathit{so}ln}=f\left(\beta K_{\mathit{so}ln}\right)+\left(1-f\right)K_{\mathit{so}ln}$$

where α and β are the ratios of the composite and surface-driven elongation rates to the diffusion-limited growth rate. Solving for f, the fraction of monomers that incorporate from the PWCA-coated surface yields:

$$f=\left(\frac{\alpha -1}{\beta -1}\right)$$

At PWCA surface densities of ~ 1800 μm⁻², which are more than an order of magnitude lower than those estimated for PWCA-coated membranes in living cells, Bieling et al. (2018) placed a upper bound on β of ~ 6 and a lower bound on α of ~ 4. Substituting these values into the equation for f indicates that, under these conditions, more than 60% of the actin in a branched network enters from the surface, and less than 40% enters from solution. Note that the filaments in a branched network are not all aligned with the direction of motion, and if the average angle between filaments and the direction of motion is φ then our estimate for β decreases by cosφ, increasing the lower bound on f. Under most conditions φ ~ 35°, so a more accurate estimate for the fraction of actin incorporated from these PWCA-coated surfaces is > 75%. Finally, the bounds on α and β provided by Bieling et al. (2018) were measured at different profilin-actin concentrations, 5 and 1 μM, respectively. Correcting the value of β for the differences in elongation rate and surface occupancy at the two different concentrations pushes the estimate of the surface contribution up even further, to > 90%.

Appendix 5. The effect of profilin-actin bound to proline-rich domains

In the presence of profilin and actin, the composite motor activity of branched actin networks can be described by three state equations: one for free barbed ends (E), a second for actin-charged WH2 domains (W_A), and a third describing occupancy of poly-l-proline sequences by profilin-actin complexes (P_A). For simplicity, we will assume that the proline-rich domain contains only one profilin-binding site.

$$\frac{\mathit{dE}}{\mathit{dt}}=k_N{W}_{\mathit{tot}}{W}_{A}E-k_{C}E$$ 10

$$\frac{d{W}_A}{\mathit{dt}}=K_{\mathit{\text{trans}}}+k_{\mathit{\text{wload}}}\left(W_{\mathit{tot}}-W_A\right)-k_{\mathit{wd}}{W}_A-k_{\mathit{\text{wpol}}}E{W}_A-k_{N}E{W}_{\mathit{tot}}{W}_A$$ 11

$$\frac{d{P}_A}{\mathit{dt}}=-K_{\mathit{\text{trans}}}+k_{\mathit{\text{pload}}}\left(W_{\mathit{tot}}-\mathit{PA}\right)-k_{\mathit{pd}}\mathit{PA}-k_{\mathit{\text{ppol}}}E{P}_A$$ 12

The above expressions for E and W_A come from Eqs. 6 and 7 of Appendix 3, with one additional term (K_trans) added to Eq. 7 to account for the transfer of actin onto the WH2 domain from profilin-actin complexes bound to the proline-rich region. We call this modified expression Eq. 11. In the expression for P_A (Eq. 12) the rate constants, k_pload and k_pd, govern binding and dissociation of profilin-actin and the proline-rich region. As usual, k_pload is a pseudo first-order rate constant that assumes the concentration of soluble profilin-actin complexes does not change. The second-order rate constant, k_ppol, governs polymerase activity, in which profilin-actin is transferred from the poly-proline sequence to the end of a nearby filament.

To better understand the connection between kinetics and network architecture, we can set all three differential equations above to zero and solve for the steady-state values of E, W_A, and P_A. To simplify the math, we assume that soluble actin monomers and profilin-actin complexes are both present at high enough concentrations so that loading WH2 and proline-rich domains from solution is much faster than transfer of actin between these sites. Given these assumptions, E|_ss and W_A|_ss, are given by Eqs. 8 and 9 (see Appendix 3), and the steady-state value of P_A is given by:

$${\left.\mathit{PA}\right|}_{\mathit{ss}}=W_{\mathit{tot}}\left(\frac{k_{\mathit{\text{pload}}}}{k_{\mathit{\text{ppol}}}}\right)\frac{k_C{k}_{\mathit{\text{wpol}}}}{k_C\left[k_{\mathit{\text{wpol}}}\left(\frac{k_{\mathit{\text{pload}}}}{k_{\mathit{\text{ppol}}}}\right)-k_{\mathit{\text{wload}}}\right]+k_{\mathit{\text{wload}}}{k}_N{W}_{\mathit{tot}}^2}$$ 13

This equation reveals that P_A|_ss has a hyperbolic dependence on capping rate. We can see this more easily by lumping the other parameters into three composites: α, β, and γ.

$${\left.\mathit{PA}\right|}_{\mathit{ss}}=\frac{\alpha k_C}{\beta k_C+\mathrm{\gamma }}$$

At low capping rates (i.e., low concentrations of capping protein), the occupancy of the proline-rich domain increases linearly with capping rate, but at higher capping rates, PRD occupancy begins to saturate. It is important to note that this equation is valid only over a limited range of capping rates. When the capping rate matches the maximum possible nucleation rate, W_tot²k_N, Eq. 9 (see Appendix 3) says that the steady-state density of free barbed ends will fall to zero and Eq. 13 says that the proline-rich domains will be maximally occupied by profilin-actin complexes (i.e., P_A|_ss = W_tot). If we limit ourselves to the biologically relevant regime of Eq. 13, where the capping rate is low enough to permit formation of a stable, branched actin network, we can simplify the expression significantly:

$${\left.P_A\right|}_{\mathit{ss}}=\frac{k_C}{W_{\mathit{tot}}{k}_N}\left(\frac{k_{\mathit{\text{pload}}}}{k_{\mathit{\text{ppol}}}}\right)\left(\frac{k_{\mathit{\text{wpol}}}}{k_{\mathit{\text{wload}}}}\right)$$ 14

To assess the overall polymerase activity of surface-associated PWCA domains, we must combine contributions from both WH2 and proline-rich regions. The rate at which a filament in proximity to a PWCA-coated surface elongates is the sum of the WH2 and proline-rich domain occupancies multiplied by their respective polymerase rate constants:

$$\frac{\mathit{dL}}{\mathit{dt}}=k_{\mathit{\text{wpol}}}{W}_A{\left|{}_{\mathit{ss}}+k_{\mathit{\text{ppol}}}{P}_A\right|}_{\mathit{ss}}$$

Substituting from Eqs. 8 (see Appendix 3) and 14, we obtain:

$$\frac{\mathit{dL}}{\mathit{dt}}=k_{\mathit{\text{wpol}}}\frac{k_C}{k_N{W}_{\mathit{tot}}}\left(1+\frac{k_{\mathit{\text{pload}}}}{k_{\mathit{\text{wload}}}}\right)$$ 15

Conflict of interest

R. Dyche Mullins declares that he has no conflict of interest. Peter Bieling declares that he has no conflict of interest. Daniel Fletcher declares that he has no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.