Real-Time, Image-Based Slice-to-Volume Registration for Ultrasound-Guided Spinal Intervention

Abstract

purpose:

Real-time fusion of magnetic resonance (MR) and ultrasound (US) images could facilitate safe and accurate needle placement in spinal interventions. We develop an entirely image-based registration method (independent of or complementary to surgical trackers) that includes an efficient US probe pose initialization algorithm. The registration enables the simultaneous display of 2D ultrasound image slices relative to 3D pre-procedure MR images for navigation.

Methods:

A dictionary-based 3D-2D pose initialization algorithm was developed in which likely probe positions are predefined in a dictionary with feature encoding by Haar wavelet filters. Feature vectors representing the 2D US image are computed by scaling and translating multiple Haar basis filters to capture scale, location, and relative intensity patterns of distinct anatomical features. Following pose initialization, fast 3D-2D registration was performed by optimizing normalized cross-correlation between intra- and pre-procedure images using Powell’s method. Experiments were performed using a lumbar puncture phantom and a fresh cadaver specimen presenting realistic image quality in spinal US imaging. Accuracy was quantified by comparing registration transforms to ground truth motion imparted by a computer-controlled motion system and calculating target registration error (TRE) in anatomical landmarks.

Results:

Initialization using a 315-length feature vector yielded median translation accuracy of 2.7 mm (3.4 mm interquartile range, IQR) in the phantom and 2.1 mm (2.5 mm IQR) in the cadaver. By comparison, storing the entire image set in the dictionary and optimizing correlation yielded a comparable median accuracy of 2.1 mm (2.8 mm IQR) in the phantom and 2.9 mm (3.5 mm IQR) in the cadaver. However, the dictionary-based method reduced memory requirements by 47× compared to storing the entire image set. The overall 3D error after registration measured using 3D landmarks was 3.2 mm (1.8 mm IQR) mm in the phantom and 3.0 mm (2.3 mm IQR) mm in the cadaver. The system was implemented in a 3D Slicer interface to facilitate translation to clinical studies.

Conclusion:

Haar feature based initialization provided accuracy and robustness at a level that was sufficient for real-time registration using an entirely image-based method for ultrasound navigation. Such an approach could improve the accuracy and safety of spinal interventions in broad utilization, since it is entirely software-based and can operate free from the cost and workflow requirements of surgical trackers.

A. Introduction

Needle placement in spinal interventions is commonly performed in the management and treatment of chronic back pain,(Manchikanti et al n.d.) with increased efforts in recent years to improve accuracy and better identify the basic mechanisms underlying effective pain management(Tompkins et al 2017). During such procedures, the needle position relative to nerve bundles and other surrounding anatomy is visualized via intra-procedure imaging. Fluoroscopy is the standard image guidance method in a subset of these procedures, providing intermittent visualization of the needle location. However, fluoroscopic guidance can be costly in an outpatient setting, and the associated radiation risk to the patient and personnel has been a growing concern(Straus 2002) (average fluoroscopy time in discography > 146 s)(Zhou et al 2005). Moreover, challenges in visualizing nerve bundles and soft tissue regions in fluoroscopic imaging limits the accuracy of needle targeting. Ultrasound (US) image guidance could be a valuable alternative for these procedures, carrying advantages in cost, radiation exposure, and real-time guidance. However, its widespread utilization has been limited due to challenges in clearly visualizing bone structures of the spine. Furthermore, pre-procedure magnetic resonance imaging (MRI) has become increasingly common as a diagnostic modality with superior visibility of nerves and soft tissues(Dagenais et al 2010). Real-time registration of intra-procedure US imaging with pre-procedure MRI could provide a low-cost, safe, and accurate method for needle targeting by displaying co-registered diagnostic-quality MRI slices along with US. Thus, the overall objective of this work is to develop a real-time 3D-2D image registration technique to align live intra-procedure 2D US images with pre-procedure MRI and facilitate accurate needle targeting in spine pain interventions.

Existing ultrasound guidance solutions(Bax et al 2008, Fenster et al 2014, Kadoury et al 2010, Khallaghi et al 2015, Hummel et al 2008) developed for a variety of clinical applications commonly use hardware tracking (e.g., optical, electromagnetic, or mechanical tracking) to compute the correspondence between 2D intra-procedure imaging and 3D pre-procedure imaging. In addition to the cost and complexity of such hardware and geometric calibration within routine clinical workflow, tracking typically ignores internal organ motion or deformation of the patient during the procedure. Intra-procedure organ motion is a common scenario in many ultrasound-guided needle insertion procedures when the patient is awake under local anesthesia(De Silva et al 2013a). To compensate for tracking errors due to intra-procedure organ motion, image-based registration methods have been previously developed to align live intra-procedure images to the pre-procedure images using the anatomical information contained in the images(Gillies et al 2017).

Such registration needs to be performed quickly and accurately, and previous solutions have initialized the registration with an initialization pose obtained from a hardware tracking system(Khallaghi et al 2015, Xu et al 2008). The local optimization methods for fast 3D-2D registration require initialization to be sufficiently proximal to the global optimum(Powell 1965, Shewchuk 1994). Robust optimization techniques that increase capture range and overcome local optima by way of redundancy (e.g., multi-start CMA-ES(Otake et al 2013), evolutionary optimizers(Hansen and Ostermeier 1997)) may not be suitable for applications requiring fast, real-time performance, thus necessitating hardware-based initialization to perform robust image registration. An accurate, fast software-based pose initialization obviates the need for hardware tracking equipment and could further reduce the cost and improve the usability of ultrasound guidance solutions. To achieve this objective, we propose an ultrasound guidance system with image-based registration that includes a software-based algorithm for automatic initialization.

In the context of spine needle interventions, there have been multiple attempts to develop ultrasound-guided solutions. Some systems have relied upon external hardware tracking to estimate ultrasound probe pose as mentioned above. For example, Chen et al.(Chen et al 2010) proposed an ultrasound guided spine needle injection system with real-time electromagnetic (EM) tracking to estimate probe pose and identify corresponding pre-procedure CT image slices. In addition to 3D-2D mapping via EM tracking, image-based 3D-3D registration between CT and US has been performed using a biomechanical model. Another clinical pilot study(Sartoris et al 2017) evaluated the feasibility of EM tracking in MR-US fusion in a costly setup in which both MR and US modalities were available within the interventional suite.

Several image-based registration solutions have also been reported(Yan et al 2012, Hacihaliloglu et al 2014, Winter et al 2008, Barratt et al 2006) to register pre-procedure CT images to intra-procedure 3D ultrasound of the spinal anatomy. While such work demonstrated the feasibility of image-based registration methods to align bone structures visible in 3D ultrasound images with a pre-procedure imaging modality, such registration only enables the information from the pre-procedure image to be mapped to a static, intermittent intra-procedure 3D US image. Slice-to-volume registration could provide real-time guidance by mapping the live 2D US image sequence to the 3D pre-procedure image space, though achieving real-time performance without latency introduced by the registration computation remains a challenging problem.

Toward this objective, Brudfors et al.(Brudfors et al 2015, A. et al 2015) proposed a system for intra-procedure guidance without external hardware tracking systems, whereby volumetric US images were acquired in near real-time while performing a statistical model-to-volume registration to determine the probe pose. This work demonstrated the feasibility of a software-based tracking solution and warranted further investigation to validate the utility and robustness for clinical translation.

Model-to-volume registration methods have also been extended to MR-US registration(Behnami et al 2017). Pesteie et al.(Pesteie et al 2015) described a real-time ultrasound image classification method to estimate the desired probe pose during spine needle interventions using local directional Hadamard features. Such features can be computed efficiently (within as little as 20 ms) and demonstrated the capability of feature encoding methods in compactly representing information embedded in ultrasound images. In this work we propose a solution that efficiently encodes features in a similar manner (Haar features), and we leverage the resulting fast, robust initialization as a basis for fast 3D-2D registration without hardware tracking. The utility of an automatic, robust initialization method using anatomical feature extraction via segmentation and edge matching has been previously demonstrated by aligning pre-procedure CT and intraoperative 3D US in liver interventions.(Nam et al 2011)

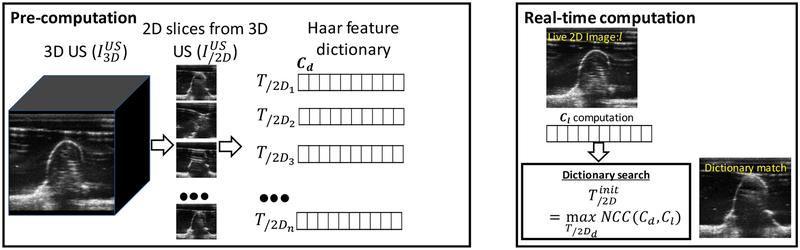
In our approach, the approximate pose of the ultrasound probe is computed by storing commonly encountered probe poses in the form of a feature dictionary. A dictionary of commonly encountered poses or image regions has recently been used in image registration(Afzali et al 2016, Avidar et al 2017), and restricting the probable poses to a finite set is practical and relevant in the context of ultrasound guidance since the physician often relies upon standard anatomical views (e.g., axial and sagittal views of the spine), and in some cases access to the anatomical site permit only certain types of probe motion (e.g., longitudinal translation along the spine). Thus, slices pertaining to typical probe motion patterns are extracted from a pre-procedure 3D ultrasound image to construct a dictionary. Live 2D ultrasound images are matched against the dictionary to find the closest matching probe pose.

For compact feature extraction and representation of anatomy in 2D US images, we propose to use Haar wavelet-based coefficients. Haar features are efficient to compute and possess superior image encoding properties compared to other neighborhood feature descriptors.(Heinrich et al 2012, Dalal and Triggs 2005) Prior applications in fingerprint compression and JPEG image compression(Montoya Zegarra et al 2009, Tico et al n.d., Cheung et al 2006) have demonstrated their capacity in representing image information with a very few number of wavelet coefficients. Haar features have also been used in real-time object detection tasks for their fast performance and ability to distinguish between different object classes when multiple Haar basis functions are used in cascade(Viola and Jones 2001). Such characteristics are desirable to differentiate between dictionary entries and robustly finding the match for a given probe pose. Utilizing these characteristics, we investigated methods to efficiently represent anatomical details in spine ultrasound images using Haar wavelet coefficients and propose a solution to find the initialization pose of the ultrasound probe in real-time. This image-based initialization is subsequently used in a slice-to-volume registration framework. In addition to slice-to-volume registration, a multi-modality registration between 3D US and pre-procedure MRI enables the geometric mapping between live 2D US and its corresponding MRI slice.

In this work, we present a 3D-2D registration solution that is fully image- and software-based and obviates the need for hardware tracking systems from the workflow. The solution consists of two major components. First, an efficient feature representation and matching to determine initialization pose in 3D-2D registration. Second, a fast rigid, image-based 3D-2D registration algorithm following the initialization to estimate the rigid pose of the 2D ultrasound image in 3D space. The work was validated in experiments performed using a lumbar puncture spine phantom and a fresh cadaver specimen that exhibited realistic ultrasound and MR image quality/artifacts.

B. Methods

B.1. Image Based MR-US Registration

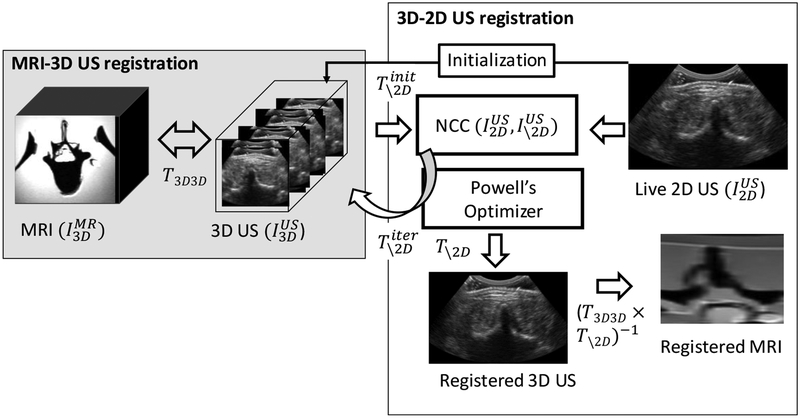
The overall objective of the proposed MR-US registration system is to achieve real-time alignment of live 2D US slices to the 3D pre-procedure MR image. Live 2D US $\left(I_{2D}^{US}\right)$ images are registered to pre-procedure MRI $\left(I_{3D}^{MR}\right)$ via an intermediary 3D US image $\left(I_{3D}^{US}\right)$ acquired at the beginning of the case as shown in Figure 1. Registration between $I_{3D}^{MR}$ and $I_{3D}^{US}$ is performed as a one-time step using a multi-modality 3D-3D registration technique that is outside the registration methods presented in this work. The mismatch of image-intensities in multi-modality 3D-3D registration has been previously addressed using robust image similarity metrics(Sun et al 2015, Fuerst et al 2014) and imaging physics-based US wave propagation models that simulated US image intensities from the other modality(Wein et al 2008). The methods and experiments described below focus on the mono-modality 3D-2D registration step to achieve fast and accurate registration between $I_{3D}^{US}$ and $I_{2D}^{US}$. Such registration permits real time 3D pose estimation of the US probe relative to the anatomy during the intervention.

Figure 1:

Image-based registration framework to align live 2D US images and pre-procedure 3D MRI in real-time. 3D-2D registration algorithm (white box) includes a software-based method for pose initialization and 6 degree-of-freedom search optimizing normalized cross-correlation using Powell’s method. MRI-3D US registration is performed prior to the intervention using multi-modality registration (gray box) that yields the registered MRI slice to the live 2D US image.

B.2. Haar Wavelet-Based Initialization

Initialization is an important step in the 3D-2D registration process. Small capture ranges, non-convex objective functions, and local optimization methods demand that initialization is sufficiently proximal to the global optimum for robust registration performance. A dictionary-based method was implemented in the solution described below to obtain the initialization pose of the US probe via an efficient feature representation and matching mechanism. 2D slices $\left(I_{/2D}^{US}\right)$ from likely US probe poses during the procedure (e.g., axial and/or sagittal US slices) are extracted from $I_{3D}^{US}$ to construct the dictionary. The dictionary can then be searched to find the closest matching image for a given live 2D image $\left(I_{2D}^{US}\right)$. Storing entire images in the dictionary and then assessing the similarity between dictionary images and the live 2D image is an exhaustive implementation that is computationally intensive; furthermore, the number of poses that can be stored in the dictionary is limited by memory.

To efficiently encode and compactly represent image features, we compute Haar wavelet coefficients and construct a feature vector depicting each image. The Haar basis filter φ_j,k(t) is defined with scaling (j) and translation (k) parameters as:

$${\phi }_{j,k}(t)=\phi \left(2^{j}t-k\right)$$ (1)

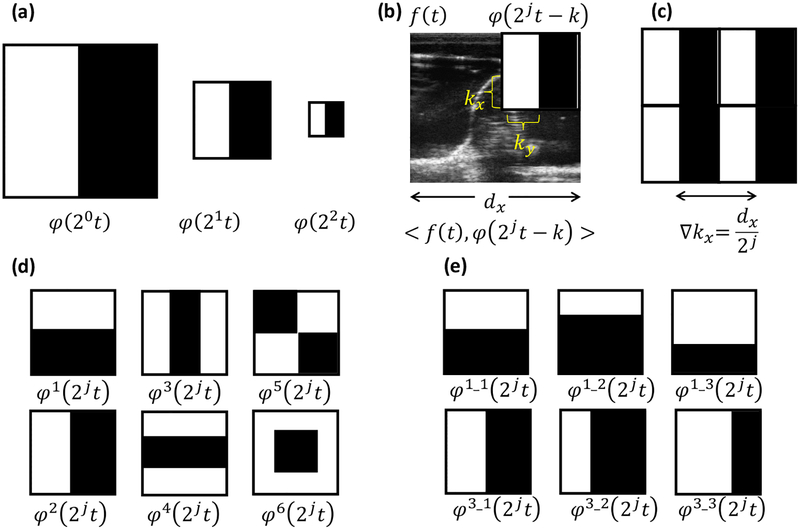
where t = (t_x, t_y ) and k = (k_x, k_y) are vectors with spatial x and y components. A basis filter captures relative intensity patterns in the image that likely exist in ultrasound images due to anatomy-US interactions including reflections and shadowing. A filter with small scaling j is sensitive to large anatomical variation patterns in images, whereas the filters become responsive to fine anatomical structures with increasing j as shown in Figure 2. The translation parameter k encodes the spatial location of the filter. The number of coefficients to represent an image increases exponentially with j. However, our expectation is that coarse scales capture specular reflection patterns to achieve reliable distinguishability with a small number of coefficients.

Figure 2:

Haar basis functions and computation of Haar filter responses. Responses are computed by subtracting the cumulative sum of the image intensities within black and white regions. (a) Varying the scale of the basis filter function to capture fine-scale anatomical features. (b) Computing the response of a single Haar basis filter by translating the filer across the image. (c) Multiple filter responses resulting from basis filter translations at ∇k intervals. (d) Different types of Haar basis functions investigated. (e) Basis filter variations by changing black/white region proportions. φ¹ and φ² basis filters are given as examples where variation filters were obtained for all 6 basis filter types in (d).

At a given scale j, the filter is translated to multiple locations to generate a series of filter responses. The number of translation locations within a scale is 2^2j and they are spaced $\Delta k_x=\frac{d_x}{2j}$, $\Delta k_y=\frac{d_y}{2^j}$ distance apart, where (d_x, d_y) are image dimensions in the x and y directions. The number of elements as scale j is determined by 2^2j, and for a given representation total number of elements is determined by N_j = ∑_j 2^2j. The compactness and the efficiency of the feature encoding could be dependent on the type of wavelet basis function. In wavelet analysis, multiple basis functions have been investigated(Li et al 2011, Singh and Tiwari 2006). Among previously proposed wavelet basis functions, Haar basis functions have demonstrated computational advantages to obtain fast performance. Within the domain of Haar basis functions, we investigated whether a combination of multiple Haar basis functions would yield an efficient feature representation. The various types of Haar basis functions being investigated and denoted as ${\phi }_{j,k}^b(t)$ are shown in figure 2d. Variations within a certain type of basis function are also explored by changing the filter parameters as shown in figure 2e. Filter responses, C (j, k), are computed via the dot product of the 2D image, f (t) and the basis filter function, φ_j,k(t), as shown in Equation 2 using the integral image(Viola and Jones 2001) for fast and efficient computation.

$$C(j,k)=<f(t),{\phi }_{j,k}(t)>$$ (2)

Thus, filter responses at different scales, translation, and basis function types are combined to form a feature vector representing the image. Multiple Haar filter responses from different basis functions are combined at each level. The total number of elements per vector representation is calculated as N_T = ∑_j 2^2j × N_b. The dictionary is constructed by computing a feature vector for 2D images sampled at different transformations – for example, longitudinal translation of the probe along the spine. Transformation feature vector tuples (T_/2Di, Cd) are stored to form a dictionary. For a live 2D image, the approximate initialization pose, $T_{/2D}^{init}$, is found by comparing the feature vector of the live 2D image to the dictionary. Normalized cross correlation (NCC) between the live 2D vector and a dictionary vector was calculated according to Equation 3 as:

$$T_{/2D}^{init}=\underset{\left\{T_{/2D_d}\right\}}{\text{argmax}}\frac{1}{N_j}\sum _{j=1}^{N_j}NCC\left(C_d(j),C_l(j)\right)$$ (3)

where C_d(j) is the Haar filter response from the dictionary, and C_l(j) is the Haar filter response for the live 2D image. N_j is the number of filter coefficients at the scale j. Averaging the estimates of NCC at each scale normalized the effect due to large number of elements in fine scales.

B.3. 3D-2D Registration

Registration between live 2D and pre-procedure 3D images is performed using the initialization transformation, $T_{/2D}^{init}$, described in section B.2. Note that the accuracy of the initialization step is limited to the dictionary transformation spacing, whereas this subsequent registration step estimates the residual error by aligning all 6 degrees-of-freedom (DOF) simultaneously in the 3D-2D registration framework. During registration iterations, 3D US image was transformed using $T_{/2D}^{iter}$ in the 3D (6 DOF) space and the slice, $I_{/2D}^{US}$, was obtained as the overlapping plane between transformed 3D US image and live 2D US image. The NCC between the live 2D US image $\left(I_{2D}^{US}\right)$ and the overlapping slice $\left(I_{/2D}^{US}\right)$ from the 3D US image was chosen as the objective function according to Equation 4.

$$T_{/2D}=\underset{\left\{T_{/2D}^{iter}\right\}}{\text{argmax}}NCC\left(I_{2D}^{US},I_{/2D}^{US}\right)$$ (4)

Calculation of NCC is parallelizable, allowing fast performance, and it is robust to intensity scaling differences – e.g., due to variable acoustic coupling at the probe-skin interface. While we did not perform any image pre-processing steps to save computation time, edge-preserving noise reduction has been shown to mitigate the effects of speckle in similar work. (De Silva et al 2013b). The optimization was performed using Powell’s method(Powell 1965) that exhibits second-order, quadratic convergence, a property that is desirable for fast performance. Second order, quadratically converging algorithms such as Newton’s method, conjugate gradient method, BFGS method leverage speed improvements compared to linear optimization techniques such as gradient descent, simplex method. When compared with other second order algorithms, Powell’s method has the additional benefit of being derivative-free which further helps in computational speed. Translations and rotations with different physical units were normalized in a 6D cartesian coordinate system by applying a rescale factor (=0.01) such that a 0.01° rotation results in a distance equivalent to 1 mm translation in the optimization search space. Termination criteria for the optimization algorithm were step size tolerance (=0.0001), metric value tolerance (=0.00001), and maximum number of iterations (=500).

B.4. Experiments

Images were acquired using an E-Cube 12R ultrasound imaging system (Alpinion Medical Systems, Seoul, Korea) with a mechanical 3D US probe (4DSCA01). Experiments were performed using a lumbar puncture phantom (CIRS, Norfolk, VA) and a fresh cadaver specimen (Figure 4) that exhibited realistic spine image quality, including shadowing of bone structures in the spine. A computer-controlled motion stage was used to impart known translations to the probe. In a single 3D image acquisition, mechanical sweep of the 3D US probe acquired 60 2D US images with an angular span of 72° with 1.2° angular spacing. The set of 2D images were linearly interpolated in a 3D grid of 224×149×149 with 0.6 mm isotropic spacing to construct a single 3D image. The baseline 3D US image needs to cover a sufficient region for live 2D images to be fully contained in the 3D image and facilitate subsequent 3D-2D image-based registration. Therefore, multiple single 3D images with overlapping regions were acquired while translating the US probe along the spine to construct a stitched 3D US image covering a substantial anatomical region of at least 6 cm in length. Thus, single 3D US images were acquired at 1 cm intervals in a span of 6 cm in the phantom and 8 cm in the cadaver, respectively, capturing approximately three vertebrae. Adjacent images were registered pairwise and mapped to a common 3D coordinate system. The 3D-3D registration was also solved using NCC similarity optimized using Powell’s method. The resulting images were transformed and interpolated to construct the 3D image $I_{3D}^{US}$ capturing a wide region in anatomy. The accuracy of 3D volume construction via image stitching was measured by comparing registered images to the imparted translation by the motion stage.

Figure 4:

Experimental setup for translating the US probe using a motion stage (a) lumbar puncture phantom and (b) cadaver experiments. Probe was rigidly attached to the motion stage, which imparted known translations to the probe providing a basis for validating the registration algorithm.

2D images were acquired at 1 mm intervals with 0.15 mm isotropic spacing and resampled to image with 0.6 mm spacing and 224×149 dimensions. Each resampled 2D US image was registered to the baseline 3D US image using Haar-based initialization methods described in this work. The dictionary was constructed to comprise ~13,000 ultrasound probe poses in three translation directions covering a 140-mm span (0.6 mm spacing) in the longitudinal translation direction and 10 mm span (1.2 mm spacing) in the lateral and probe-axial translation directions (in-plane translations along the axial 2D US plane).

During image acquisition, the US probe axis was only approximately orthogonal to the translation direction of the motion stage and the non-planar, curved surface of the phantom and the cadaver cause additional irregularities to the simple 1D translational motion. Thus, 2D US images were not perfectly correlated with the axial slices extracted from the baseline 3D US image. In-plane translations (within the 10 mm span) within the axial 2D US plane in the dictionary facilitated the retrieval of an approximate pose in the presence of such irregularities. To analyze the efficiency of Haar-based initialization, the accuracy was measured after constructing dictionaries with different (N_j, N_b) configurations. The number of scales (N_j) was varied from (1–4), and the number of Haar basis filters (N_b) was varied from 1 to 5, 10, 30, and 60. The basis filters were selected from a pool of 60 different basis filters constructed from six different types shown in Figure 2d and 10 variations for each type obtained according to Figure 2e.

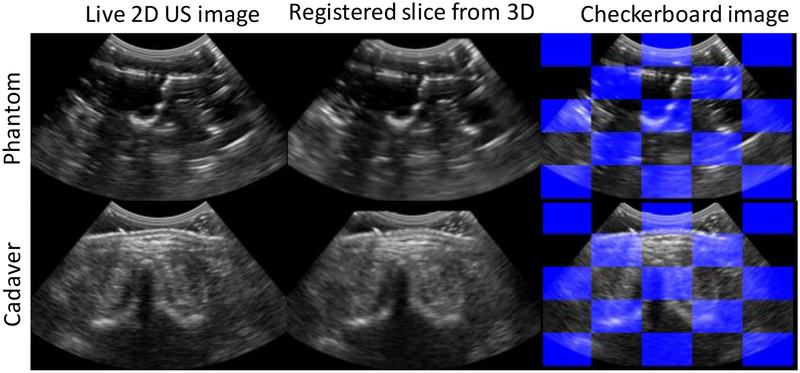
Figure 10:

Alignment of registered images in phantom and cadaver experiments. Left column shows the live 2D US image, right column shows the corresponding slice from the baseline 3D US image after registration, and checkerboard image shows alternating image patches from both the images.

Accuracy was evaluated for the initialization step by comparing the Haar-based initialization to the translation imparted by the motion stage. As a control experiment, the entire 2D image set was stored in the dictionary, and the initialization pose was selected by optimal NCC between the live 2D image and the dictionary image. After initialization, 3D-2D registration was performed in the 6 DOF continuous search space without being limited to the discrete poses stored in the dictionary. To assess the necessity of a good initialization method, 3D-2D registration was also performed after the straightforward method of initializing at the center of the 3D image.

Registration validation by comparing to the motion stage translations as the ground truth quantified the translational accuracy against the probe displacements. However, it did not account for any possible motion in other rotational degrees of freedom. To quantify the overall 3D error, accuracy was also measured using manually-identified corresponding landmark locations in the 2D and 3D US images. Target registration error (TRE) was calculated as the point-based 3D error of the corresponding anatomical landmarks after registration using 19 landmark pairs in the phantom and 24 landmark pairs in the cadaver. The capture range of the 3D-2D registration process was measured by varying the initialization ± 15 mm from the ground truth in 1 mm increments and repeatedly performing registrations. Analysis of capture range of the registration framework provides a basis to evaluate the level of initialization accuracy required to achieve robust 3D-2D registration.

C. Results

C.1. Haar Filter Responses

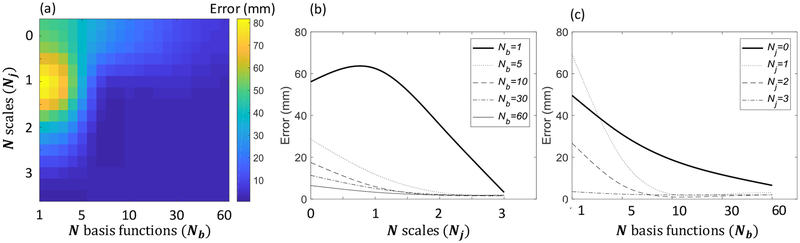
Figure 5a shows the accuracy of the initialization method as a function of the number of scales, N_j and the number of basis functions, N_b, used when constructing the Haar feature vectors in the dictionary. The results show a variety of combinations (N_j, N_b) that yield acceptable initialization accuracy for robust registration. Initialization accuracy improved steeply as a function of N_j and N_b as shown in Figure 5b and 5c. When using a single basis function (N_b =1), a large number of scales (N_j ≥ 3) was needed to achieve reliable initialization accuracy. However, when multiple basis functions were combined, reliable initialization accuracy was achieved with a smaller number of scales (for example, when N_b = 30, N_j =2 yielded satisfactory performance). This is a desirable property, since the length of the feature vector (N_T) increases linearly with N_b; however, it increases exponentially with N_j. Thus, in terms of efficiency in feature representation, combination of multiple basis functions without increasing the scale is helpful to build a large dictionary.

Figure 5:

Initialization accuracy as a function of variable number of scales and number of basis functions. (a) Error for different combinations of number of scales and number of basis functions (N_j,N_b). (b) Error for variable number of scales, N_j with the number of basis functions, N_b, fixed. (c) Error for variable number of basis functions, N_b with the number of scales, N_j, fixed.

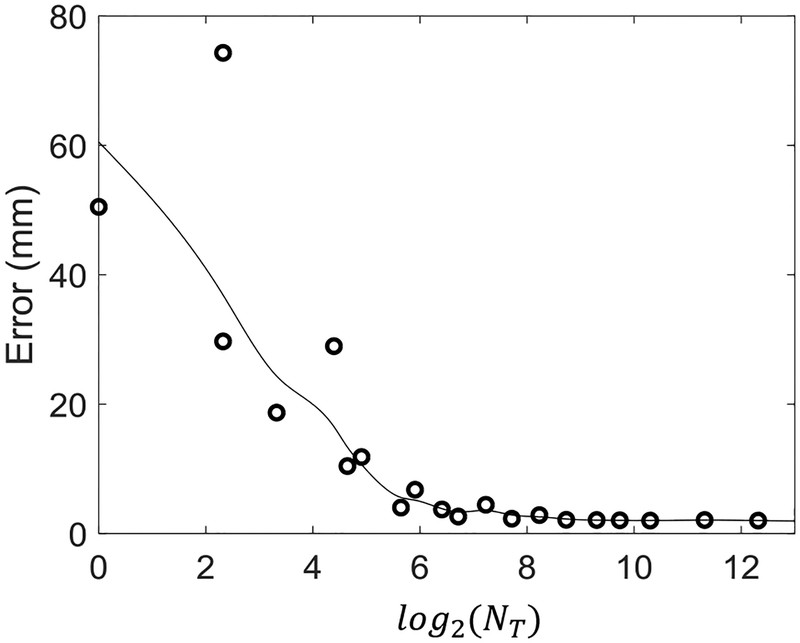
Figure 6 shows the initialization accuracy as a function of feature vector length N_T, demonstrating a rapid decrease in error with increasing N_T. Accuracy < 5 mm was found with an 85-length feature vector, and accuracy < 3 mm was achieved with a 315-length feature vector. The input 2D image size (after down-sampling) in these experiments was 14,000. Thus, the dictionary storage requirements decrease by approximately 217× and 47×, respectively, to achieve the same levels of initialization accuracy. We also investigated the effect of the type of Haar basis function used in constructing the feature vector and the initialization accuracy. Different basis functions performed comparably with no statistically significant difference between the distributions in initialization accuracy. However, certain basis filter types were more robust to outliers, and finding the optimal basis filter combination is an open question that could be empirically investigated using machine learning methods or other approaches in future work.

Figure 6:

Initialization accuracy as a function of the number of elements (N_T) in the Haar feature vector representation.

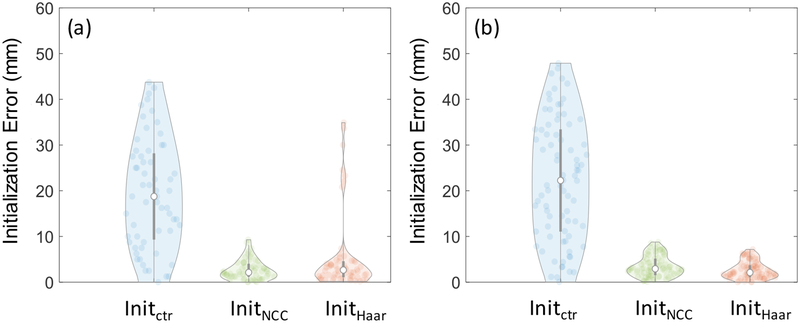
Figure 7 shows the initialization error distributions with Haar-filter based initialization in comparison to two other methods for initialization. Init_ctr initialized at the center of the image, whereas Init_NCC stored and compared entire 2D images in the dictionary. Values of N_b = 15 and N_j = 2 were used for Haar-based initialization, constituting a 315-length feature vector. In the lumbar puncture phantom experiments, the initialization accuracy of the Haar dictionary-based method was 2.7 (median) and 3.4 (interquartile range - IQR) mm, and that of the NCC dictionary-based method using the entire image was 2.1 mm (2.8 mm IQR). In the cadaver experiments, the Haar-based method achieved accuracy of 2.1 mm (2.5 mm IQR), whereas the NCC method achieved 2.9 mm (3.5 mm IQR). Comparable performance was achieved with both dictionary-based methods, substantially improving the initialization when compared to Init_ctr. In the phantom experiments Haar-based initialization exhibited some outliers due to a similar view in an adjacent vertebra, attributable to the homogeneity of the phantom. Such was not observed in the more realistic context of the cadaver. Overall, Haar-based initialization demonstrated comparable performance to the exhaustive approach of storing the entire 2D images.

Figure 7:

Initialization accuracy prior to 3D-2D registration step for (a) phantom and (b) cadaver experiments presented as violin plots. The circle in each violin plot denotes the median, and the gray bar marks the interquartile range. The violin thickness is proportional to the data density at different error (vertical axis), values and it presents each data point that contributed to the distribution as a pale circle in the distribution. Init_ctr represents a reference method where the 2D slice was initialized at the center of the 3D image. Init_NCC stored entire 2D images in the dictionary and searched for the entry with the optimal NCC and Init_Haar demonstrates the performance with the methods proposed in this work.

C.2. 3D-2D Registration

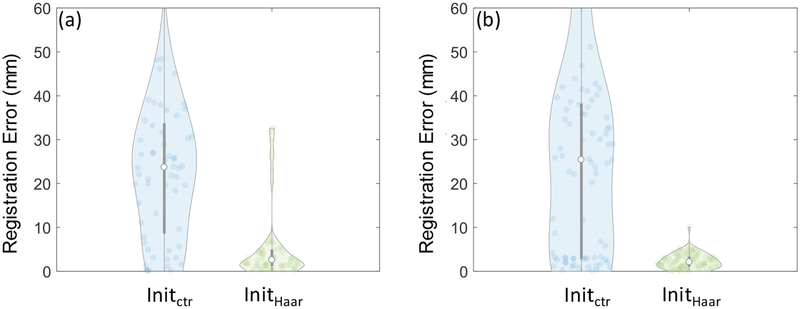
Figure 8 shows the overall 3D-2D registration accuracy with and without Haar-based initialization. In the phantom experiments, the median accuracy was improved from 23.7 mm (25.1 mm IQR) with center initialization to 2.6 mm (3.7 mm IQR) with Haar-based initialization. In the cadaver experiments, the accuracy was improved from 25.4 mm (35.3 mm IQR) to 2.3 mm (2.6 mm IQR). Thus, initialization was a necessary step to accurately perform the registration, and Haar-based initialization achieved a level of accuracy sufficient to facilitate fast, robust 3D-2D registration. The current implementation required 1.1 ± 0.8 (mean ± std) s in Intel Xeon 1.7 GHz CPU with 12 GB memory.

Figure 8:

3D-2D image registration accuracy with different initialization methods for (a) phantom and (b) cadaver experiments. The accuracy was measure using the translation from the motion stage as the ground truth.

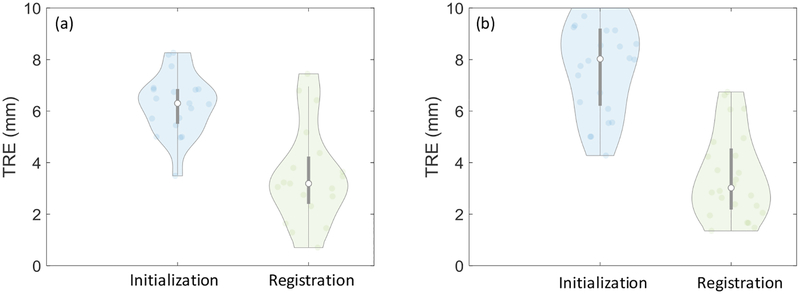
When validated using the translation from the motion stage as the ground truth, 3D-2D registration step did not exhibit substantial improvement from the initialization accuracy achieved of the proposed method. However, Figure 9 shows the improvement after the 3D-2D registration step when validated using manually identified fiducials that incorporated motion in all 6 DoF. 3D-2D registration improved the 3D error by compensating for residual errors in directions that were not used in constructing the feature dictionary. The overall 3D error was 3.2 mm (1.8 mm IQR) in the phantom studies and 3.0 mm (2.3 mm IQR) in the cadaver studies.

Figure 9:

TRE distributions after initialization of the Haar-dictionary method and after 3D-2D registration step for (a) phantom and (b) cadaver. The accuracy was quantified using manually identified anatomical landmarks.

Figure 10 shows the alignment achieved in 3D and 2D US images after registration in phantom and cadaver, qualitatively demonstrating a reasonable level of registration for purposes of needle targeting.

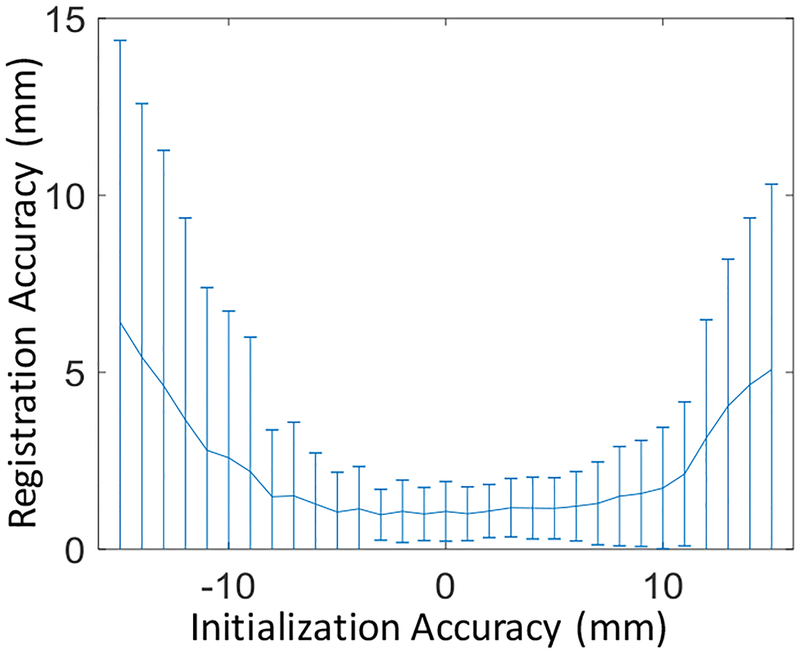
Figure 11 shows the capture range for 3D-2D registrations, indicating that registration could be performed successfully when the accuracy of initialization was within ± 8 mm. While Haar-based initialization achieved this requirement, it could also be a useful parameter in determining the spacing between slices extracted from 3D US images to construct the dictionary.

Figure 11:

Capture range for 3D-2D registration demonstrating the required initialization accuracy to achieve reliable registration performance.

The accuracy of 3D-3D registration between ultrasound volumes was validated using known translations imparted by the motion stage, found to be 1.0 ± 0.2 (mean ± std) mm. In the stitched US volume, the continuity of anatomical structures was consistent in qualitative observations, and such image quality is essential in subsequent image registrations when pre-procedure 3D US volume acts as an intermediary between live 2D ultrasound and 3D MR imaging.

D. Discussion and Conclusions

In this work, we reported a fully image-based, slice-to-volume registration solution that could facilitate guidance for ultrasound needle interventions in the spine. Such an approach obviates the need for hardware-based tracking equipment for ultrasound probe pose estimation and could decrease the cost, ease workflow, and enhance portability of accurate image guidance in common practice. Our approach to provide a software-based initialization utilizes the fact that the physicians typically rely upon certain patterns of probe motion during an interventional procedure, and the discrete set of poses related to the patterns can be efficiently stored in the form of a dictionary for real-time retrieval and matching. Probe motion patterns likely exist in many other ultrasound-guided clinical interventions such as prostate biopsy where the transrectal access limits only certain types of probe motion, cervical brachytherapy procedures and liver focal ablation procedures where the probe is positioned transabdominally to acquire a limited set of views of pertinent anatomy. Thus, a dictionary-based method for registration initialization could be feasible and directly translated to many other ultrasound guided interventions. In our experiments, we observed a ~47× improvement in memory efficiency in image feature representation, an improvement factor commensurate with the compression ratio observed in the Haar wavelet coefficients in image compression applications(Nashat and Hassan 2016). Efficiency in image representation is critical in constructing a large dictionary of ultrasound probe poses.

A dictionary-based approach discretizes the continuous range of probe poses observed in interventions to facilitate a fairly close initialization to 3D-2D registration. Unique representation of the discrete set of poses is an essential property to differentiate between dictionary elements when matching against a live 2D US image. In our experiments with a dictionary element size = 315 (computed as responses to 315 Haar filters), the method yielded all unique responses in terms of the match score calculated according to equation 3. The match score differences between the best matching element and the remaining dictionary elements were within a range (0.35–0.55×10⁻⁴). Similar match scores indicate similarity in appearance to the 2D image being probed, and the second closest matching score (within 0.35×10⁻⁴ of the best match) corresponded to a probe pose 1.0 mm away from the best match. Overall mean ± std match score differences between the best matching element and the remaining dictionary elements was 0.06 ± 0.05. Anatomical homogeneity is a factor to consider when building a dictionary that uniquely represents different elements. In our experience, despite the structural similarity of different vertebrae, inhomogeneity within and adjacent to the vertebrae resulted in US image features that could be uniquely represented and identified with 315-length feature vector. If a certain patient has homogeneous anatomy that results in closely resembling images at a coarse level, increasing the feature vector size could embed more granular anatomical detail to achieve uniqueness at the cost of memory.

In the experiments, the intermediary 3D US image was acquired using a mechanically swept 3D US probe. To obtain a sufficient span of the spinal anatomy, we stitched multiple 3D US images to construct the baseline 3D image. However, the methods described do not depend on the specific 3D US acquisition/construction method or the use of a 3D US imaging system. Multiple techniques(Fenster et al 2001) that are available to construct a 3D US volume using a standard 2D US probe could be used alternatively. Such capability extends the methods presented in this work to a form compatible with standard ultrasound imaging systems already commonly available in outpatient clinics.

The registration methods were validated using a computer-controlled motion system. The current experiments also introduced a small degree of rotational variability due to non-planar skin interface in both the phantom and the cadaver. Both the initialization and the final registration achieved robust performance in the presence of these rotational errors (even though the rotations were not considered when building the dictionary). The robust registration performance observed warrants more clinical investigation after introducing rotational/angular motion of the probe. Validation was performed both via measuring the motion recorded by the motorized stage and manually identifying fiducials. While the motion stage imparted a known set of translations to the probe in a controlled setting, the measured accuracy could be limited if the probe tilted while moving along the phantom and the cadaver. On the other hand, manually identified fiducials allow for measurement error due to both translation and rotation errors; however, the corresponding landmarks identified in 2D slices and 3D images could be subject to observer variability and suffer from large fiducial localization errors. Thus, these factors challenge the assessment of error, and the actual error of the registration process could be even lower than that reported in this paper.

The required needle targeting accuracy of the system is governed in part by the smallest clinically relevant anatomical structures targeted during intervention. For spine needle injections in the lumbar region, the measured registration accuracy <3 mm is comparable to that previously shown for electromagnetic and vision-based tracking systems (e.g., 2.9–3.8 mm reported in the context of ultrasound needle interventions in the spine) (Sartoris et al 2017, Stolka et al 2014) and should provide relevant anatomical visualization from MRI in reaching the intended target while avoiding surrounding critical structures. Patient motion during the procedure present an additional potential source of error that was not represented in the phantom and cadaver experiments in this work. However, the presented algorithm successfully corrected for US probe motion relative to a stationary patient. Therefore, fast, near real-time registration can in principle compensate for intra-procedure patient motion relative to the probe (De Silva et al 2013b) (i.e., performing registration every 1 s causes errors due to patient motion within a 1 s interval). Thus, further improvement in speed could strengthen the algorithm in compensating for continuous patient motion such as that caused by respiration.

The Haar-feature based initialization method and subsequent 3D-2D registration step provide a fully software-based solution (i.e., free from additional tracking hardware) for guidance in needle interventions. Registration can be performed continuously as a background process and/or immediately prior to needle insertion to verify needle position relative to the anatomy using information available in the corresponding MRI slice. Future work includes measuring the overall needle targeting accuracy of the system by combining 3D US-2D US registration and the offline / one-time 3D US-MRI registration. Testing in a clinical setting and assessment of needle targeting accuracy will follow after incorporating all patterns of probe motion encountered in clinical procedures within the dictionary. The resulting image-based method for needle guidance and navigation could improve the accuracy and safety of spinal interventions, enable broader utilization of navigation, and reduce confounding geometric factors underlying patient outcomes in pain management.

Figure 3:

Computing the approximate initialization pose using a Haar filter dictionary. The dictionary is pre-computed from 2D slices extracted from the 3D US image acquired prior to the procedure. During the procedure Haar coefficients computed from the live 2D image are matched against the dictionary to find the closest matching US probe pose.