Nanomagnetic properties of the meteorite cloudy zone

Significance

The cloudy zone is naturally occurring nanocomposite found in Fe–Ni metal-bearing meteorites. It not only is a potent carrier of paleomagnetic information from the early solar system but also shows promise as a sustainable alternative to rare earth-based permanent magnets. Here we explain how the remarkable magnetic properties of the cloudy zone are linked to its 3D chemical, crystallographic, and magnetic architecture, using a state-of-the-art combination of nanometer to subnanometer resolution tomography and micromagnetic simulations. We discover the mechanism by which paleomagnetic information becomes encoded into the cloudy zone and, inspired by our findings, point toward potential pathways to optimize synthetic analogues of the cloudy zone for industrial applications.

Abstract

Meteorites contain a record of their thermal and magnetic history, written in the intergrowths of iron-rich and nickel-rich phases that formed during slow cooling. Of intense interest from a magnetic perspective is the “cloudy zone,” a nanoscale intergrowth containing tetrataenite—a naturally occurring hard ferromagnetic mineral that has potential applications as a sustainable alternative to rare-earth permanent magnets. Here we use a combination of high-resolution electron diffraction, electron tomography, atom probe tomography (APT), and micromagnetic simulations to reveal the 3D architecture of the cloudy zone with subnanometer spatial resolution and model the mechanism of remanence acquisition during slow cooling on the meteorite parent body. Isolated islands of tetrataenite are embedded in a matrix of an ordered superstructure. The islands are arranged in clusters of three crystallographic variants, which control how magnetic information is encoded into the nanostructure. The cloudy zone acquires paleomagnetic remanence via a sequence of magnetic domain state transformations (vortex to two domain to single domain), driven by Fe–Ni ordering at 320 °C. Rather than remanence being recorded at different times at different positions throughout the cloudy zone, each subregion of the cloudy zone records a coherent snapshot of the magnetic field that was present at 320 °C. Only the coarse and intermediate regions of the cloudy zone are found to be suitable for paleomagnetic applications. The fine regions, on the other hand, have properties similar to those of rare-earth permanent magnets, providing potential routes to synthetic tetrataenite-based magnetic materials.

Meteorites are fragments of asteroids—the remnants of planetesimals that formed during the first few million years of the solar system. Magnetic minerals in meteorites, such as Fe–Ni alloy, preserve evidence that magnetic fields were generated by the liquid iron cores of differentiated planetesimals shortly after their formation, much like the magnetic field of the Earth is generated by its liquid iron core today (1). Slow cooling ($\sim 10^{-1}$ to $\sim 10^3$ °C/My) of meteoritic Fe–Ni alloy gives rise to distinctive metallurgical features spanning a range of length scales, from the familiar centimeter-scale Widmanstätten intergrowth of kamacite (bcc Fe–Ni) and taenite (fcc Fe–Ni) to a nanometer-scale intergrowth of tetrataenite islands (ordered ${\text{Fe}}_{0.5}{\text{Ni}}_{0.5}$) in an Fe-rich fcc or bcc matrix, known as the “cloudy zone” (Fig. 1). The cloudy zone forms at T $<$ 450 °C by a process of spinodal decomposition (2). Islands of tetrataenite can vary in diameter from over 500 nm to less than 10 nm, depending on the cooling rate and the local Ni content. Small island sizes promote uniformly magnetized (i.e., single-domain) states, while the L10 ordered tetragonal symmetry of tetrataenite generates high magnetic coercivity (up to 2 T). These two properties combine to make the cloudy zone a potent carrier of paleomagnetic information in meteorites as well as a potential sustainable replacement for rare-earth permanent magnet materials (3, 4). As islands of tetrataenite form in the presence of the meteorite parent body’s internally generated magnetic field, it has been proposed that the cloudy zone preserves a record of the field’s intensity and polarity (5, 6). The ability to extract this paleomagnetic information only recently became possible with the advent of high-resolution X-ray magnetic imaging methods, which are capable of quantifying the magnetic state of the cloudy zone on submicrometer-length scales (7). Despite notable successes of this new “nanopaleomagnetic” approach (8–11), precisely how paleomagnetic information is recorded by the cloudy zone remains unknown, and further questions about the timing of primary remanence acquisition during cooling, and the susceptibility of the cloudy zone to acquire secondary remanence postcooling, remain open. Providing answers to these questions is an essential step in the quest to develop a quantitative theory linking the magnetic state of the cloudy zone to the intensity of the parent-body magnetic field.

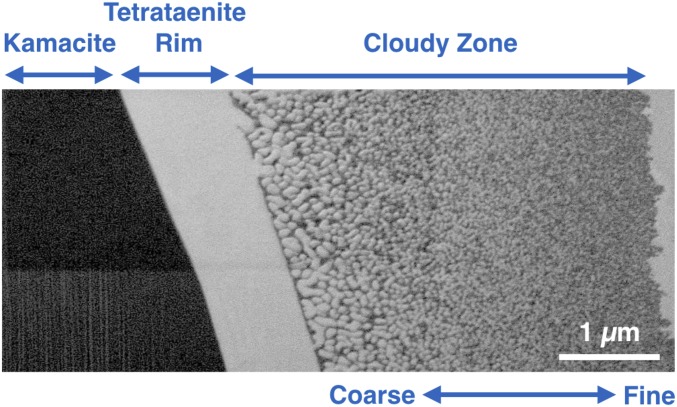
Fig. 1.

FIB-secondary electron micrograph of the interface region between kamacite (bcc iron) and taenite (fcc Fe–Ni), which forms part of the Widmanstätten intergrowth in the Tazewell meteorite. Kamacite (Left) is followed by a rim of pure tetrataenite (Center), which then gives way to the cloudy zone (Right), a nanoscale intergrowth of tetrataenite islands surrounded by an Fe-rich matrix. The cloudy zone transitions from coarse tetrataenite particles ($>$150 nm) to fine tetrataenite particles ($<$50 nm) with increasing distance from the tetrataenite rim. The matrix phase (dark in the image) percolates throughout the entire cloudy zone.

Here, we begin to address these issues by performing a combined tomographic and micromagnetic study of the cloudy zone in the Tazewell IAB sLH iron meteorite, which cooled at a rate that is conducive to the preservation of nanopaleomagnetic remanence. Cooling rate affects both the size of the tetrataenite islands and the degree of Fe–Ni ordering within them (5). Alternating (002) planes of Ni and Fe, in nearly equal ratios, are required to form the ordered tetragonal structure of tetrataenite, with the magnetic easy axis aligning along the crystallographic c-axis. If the cooling rate is too fast, insufficient time is available for the Fe–Ni ordering to take place, and the soft ferromagnetic phase taenite is retained that is unsuitable for nanopaleomagnetic analysis. The quickly cooled Bishop Canon IVA meteorite ($\sim$2,500 °C/My) demonstrates such soft magnetic behavior, characterized by the presence of large, meandering magnetic domains throughout the cloudy zone, consistent with the absence of tetrataenite (10). If the cooling rate is too slow ($<$0.5 °C/My), the tetrataenite islands grow to such size that they develop multiple magnetic domains. In addition, the coarse length scale of the cloudy zone in slowly cooled meteorites leads to the conversion of the metastable, paramagnetic, fcc matrix phase to a more stable, soft ferromagnetic, bcc martensite phase, which further degrades and complicates the paleomagnetic properties. Both phenomena are observed in the slowly cooled mesosiderites (12), making them unsuitable for nanopaleomagnetic study. A “Goldilock’s zone” for cooling rates exists, whereby cooling is slow enough to enable tetrataenite formation yet fast enough to prevent the tetrataenite islands growing to sizes that are beyond their single-domain threshold and to maintain the metastable, paramagnetic, fcc structure of the matrix phase. These considerations constrain usable meteorite samples to those which have experienced parent body cooling rates between $\sim$0.5 °C/My and $\sim$150 °C/My (12). With a cooling rate of $\sim$20.8 °C/My at 500 to 600 °C (13), the Tazewell IAB sLH meteorite displays a well-preserved cloudy zone that has not been affected by shock and is well within the desired cooling-rate window for nanopaelomagnetic studies. We present a multiscale, multidimensional study of the cloudy zone in the Tazewell meteorite, yielding structural, crystallographic, and chemical information across the entire cloudy zone, in three dimensions and at nanometer to subnanometer spatial resolution. This information provides the input for micromagnetic simulations of both individual tetrataenite islands and small clusters of islands, which have far-reaching implications for nanopaleomagnetic studies of planetesimals as well as for our understanding of the thermodynamic and structural behavior of possible replacements for rare-earth permanent magnet materials.

Results

A 3D Structure of the Cloudy Zone.

A 2D cross-section through the interface region of the Widmansätten intergrowth in the Tazewell meteorite is shown in Fig. 1. A region of kamacite (far left) is followed by a $\sim 1\mu \text{m}$-thick rim of tetrataenite, which is then followed by the island/matrix nanostructure of the cloudy zone. The size of the tetrataenite islands (bright regions) decreases systematically from 150 nm adjacent to the rim to less than 10 nm at a distance of several microns away from the rim. This change from “coarse” to “fine” island sizes is caused by a decrease in the local Ni concentration with increasing distance from the rim, which in turn lowers the temperature at which spinodal decomposition initiates during cooling (thereby reducing the diffusion length and time available for coarsening of the islands). The matrix phase (dark regions) appears to percolate throughout the entire cloudy zone. We reveal the true 3D structure of the cloudy zone through the complementary approaches of 3D Energy Dispersive Spectroscopy (3D-EDS) and APT (see Materials and Methods).

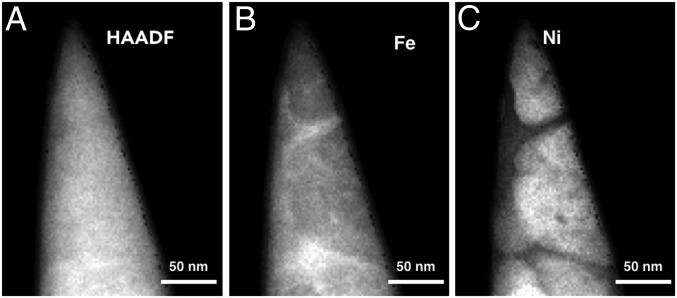
Due to the similarity in mean atomic number between the two different Fe–Ni alloy phases, conventional scanning transmission electron microscopy (STEM) using the high-angle annular dark-field (HAADF) signal does not resolve the internal microstructure in the cloudy zone (Fig. 2A). The Fe-rich matrix (Fig. 2B) and the Ni-rich tetrataenite islands (Fig. 2C) are clearly resolved through the acquisition of an EDS chemical map at each angle of a tilt series. The spectral signals are denoised using principal component analysis (PCA), and the total intensity associated with the Fe_Kα peak (Fig. 2B) and the Ni_Kα peaks (Fig. 2C) are integrated. The resulting tilt series of chemical maps are reconstructed to form a quantitative 3D volume of Fe and Ni concentrations using a compressive sensing (CS) algorithm (14, 15).

Fig. 2.

(A) STEM HAADF micrograph of the coarse cloudy zone. (B) Iron concentration map collected with 3D-EDS. (C) Nickel concentration map collected with 3D-EDS.

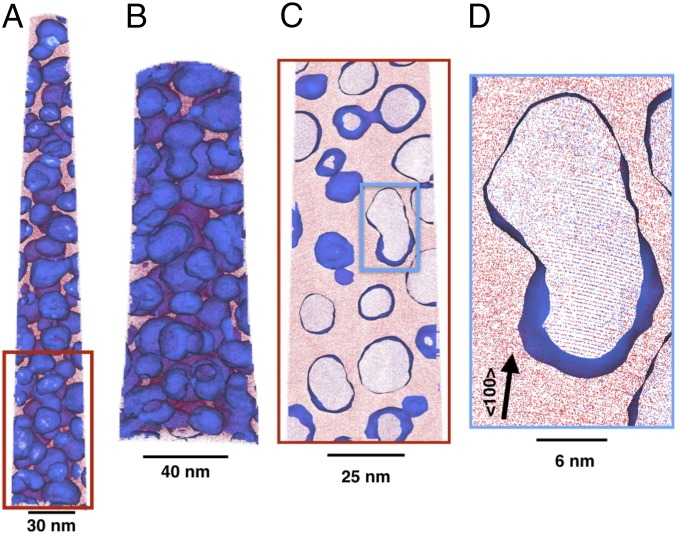
In the coarse cloudy zone (Fig. 3A and SI Appendix, Movie S1), we observe two large tetrataenite islands (blue). The sample volume is shown as reconstructed by STEM-EDS tilt-series tomography and visualized as surfaces of constant intensity, termed “isosurfaces.” The intensities defining the isosurfaces were defined by the strong contrast between the two phases in the Ni maps to reveal the morphology of the matrix and tetrataenite phases. In the coarse cloudy zone (Fig. 3A), the tetrataenite islands contain continuous threads of matrix phase (yellow) running through them. The matrix threads form a mostly continuous network of 10 to 30 nm-diameter structures, with occasional small isolated patches of matrix contained within the tetrataenite islands.

Fig. 3.

(A–C) 3D visualizations of tomographic reconstructions from STEM-EDS tilt series using the characteristic Ni K X-ray emission lines. In A and B, surfaces of constant intensity, termed isosurfaces, are shown. A rectangular subvolume (“corner cut”) has been removed to enhance the visibility of small features, with the tetrataenite particles depicted in blue and the Fe-rich matrix phase in yellow for (A) the coarse and (B) the medium cloudy zones. (C) A single plane or “orthoslice” from the center of the reconstruction volume of the medium cloudy zone.

Fig. 3B and SI Appendix, Movie S2 show a region of the intermediate-fine cloudy zone. With smaller island sizes, the full 3D shape of some of the tetrataenite islands in this tomographic volume are recovered. We use best-fit ellipsoids as a representative metric for island size within the tomographic volume (16, 17). In the intermediate region of the cloudy zone, we find the major axis diameter to range from 18 nm up to 100 nm. Comparison of the major, intermediate, and minor ellipsoid axes yields a prolate tri-axial symmetry with the ratio of major/intermediate and intermediate/minor axes ranging from $\sim$1 to $\sim$2, with an average of $\sim$1.2 (we caution, however, that the small number of complete particles observed means that these values may not be representative).

The 3D nature of a fine region of the cloudy zone was explored through the use of APT (Fig. 4 and SI Appendix, Movies S3–S5). Fig. 4 A and B show APT data from the fine cloudy zone (tetrataenite particles with long diameter of 30 nm or less). These are two datasets collected from the same needle (additional APT studies of other parts of the cloudy zone are provided in SI Appendix). Isosurfaces defined by a Ni content of 32.5% identify 260 tetrataenite islands within the APT needle; of these, only 8 of these volumes are fully contained in the tip shown in Fig. 4A. For these particles, we estimate the major axis of the best fitting ellipse at 20 nm, based on the extent of the isosurface. In general, the islands measured in the volume seen here possess an oblate spheroid aspect ratio. It should be noted that particle geometry is poorly constrained by APT, as this is highly sensitive to assumptions made during the reconstruction process. However, these reconstruction artifacts do not affect the robustly determined chemistry or absolute volume fraction of the two phases. For this reason, 3D-EDS provides the most reliable geometrical information about the cloudy zone. In Fig. 4D, we are able to observe the atomic planes in the tetrataenite particle, demonstrating that the needle was aligned close to $⟨100⟩$.

Fig. 4.

(A and B) APT reconstruction of two datasets of same needle from the fine cloudy zone showing the 32.5% Ni isosurface. Red dots indicate Fe atoms; blue dots are Ni. (C) A 1 nm othroslice from the region highlighted in A. (D) Zoomed-in detail of the tetrataenite particle highlighted in C. Atomic planes along a $<100>$ can be resolved in the interior of the 32.5% Ni isosurface.

Chemical Composition of the Cloudy Zone.

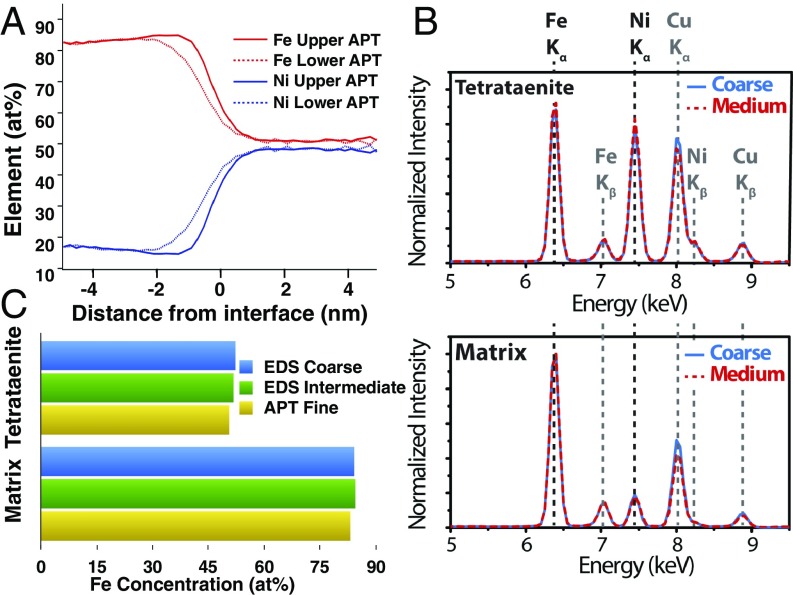
The composition of tetrataenite islands and the matrix phase in coarse, medium, and fine regions of the cloudy zone was measured using APT (Fig. 4 A and B and SI Appendix). The transition from tetrataenite to matrix corresponds to a sharp compositional gradient that is just 2 nm wide, as seen in the proxigrams in Fig. 5A. The average composition of tetrataenite particles is found to be 49.61 $\pm$ 0.16% Fe, 50.00 $\pm$ 0.16% Ni, and 0.39 $\pm$ 0.02% Co. The matrix phase is found to be 81.95 $\pm$ 0.15% Fe, 17.69 $\pm$ 0.16% Ni, and 0.36 $\pm$ 0.02% Co. The error presented is equal to 2 SD based on counting statistics. The chemical composition information contained in the 3D-EDS datasets was also examined (see Materials and Methods) and agrees very well with APT measurements (albeit with significantly greater uncertainties). Our quantification of the 3D-EDS measurements produces an average spectrum for each phase, as seen in Fig. 5B. Cliff–Lorimer quantification of the average spectra gives the composition of coarse cloudy zone phases as tetrataenite at 52 $\pm$ 2% Fe, 48 $\pm$ 2% Ni, and the matrix at 84 $\pm$ 2% Fe, 16 $\pm$ 2% Ni (errors reflect uncertainties in X-ray counting statistics). Likewise for the medium cloudy zone, we observe the tetrataenite composition to be 52 $\pm$ 2% Fe and 48 $\pm$ 2% Ni, with the matrix phase measured at 85 $\pm$ 2% Fe and 15 $\pm$ 2% Ni. The elemental compositions of islands and matrix do not change significantly between the coarse, medium, and fine regions (Fig. 5C). Instead, the variations in both APT and 3D-EDS datasets correspond to the uncertainties in the quantification methods. Ultimately, APT provides us with the most accurate chemical picture of the cloudy zone, whereas 3D-EDS provides us with the most accurate geometric information.

Fig. 5.

(A) Proxigrams for the two APT datasets in Fig. 4 A and B reveal a sharp interface between the tetrataenite and matrix phases. (B) The thickness map-derived spectra for the two 3D-EDS studies presented. (C) Comparison of Fe composition quantification results by APT and EDS for the tetrataenite and matrix phases. APT analyses revealed the average composition of tetrataenite in the fine cloudy zone to be 48.4 $\pm$ 0.4% Fe to 51.1 $\pm$ 0.4% Ni and the matrix phase in the fine region to be 81.8 $\pm$ 0.2% Fe and 17.8 $\pm$ 0.2% Ni. EDS quantification yielded a composition of 52.1 $\pm$ 2% Fe and 47.9 $\pm$ 2% Ni for the tetrataenite islands and 84.4 $\pm$ 2% Fe and 15.6 $\pm$ 2% Ni for the matrix.

Crystallographic Analysis of the Cloudy Zone.

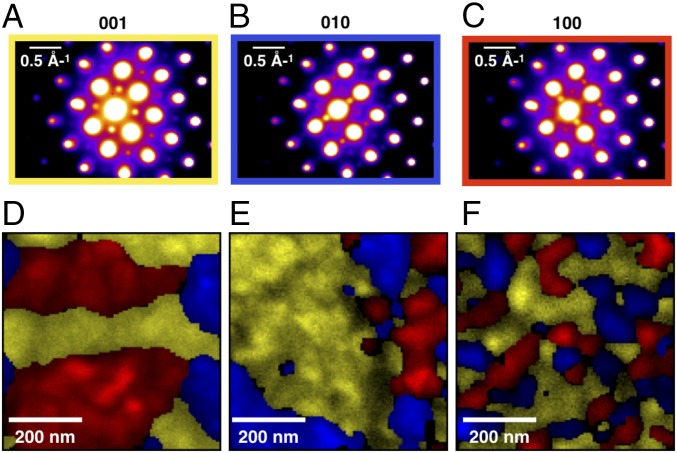
Scanning precession electron diffraction (SPED) allows a 2D array of electron diffraction patterns to be recorded with a step size of 5 nm, while minimizing dynamical scattering effects and increasing the recorded area of the Ewald sphere. SPED experiments produce a series of diffraction patterns, used to map out the distribution of tetrataenite c-axis orientations as well as to identify an ordered superstructure in the matrix phase. Recording a diffraction pattern at every pixel results in a statistically dense dataset, to which we applied machine learning strategies to deconvolve signals arising from overlapping features and noise. Our approach relies on first denoising the data using PCA. The processed maps are then analyzed using a cluster analysis scheme, to isolate and identify regions that are most self-similar (see Materials and Methods).

A $⟨110⟩$ lamella was tilted parallel to $⟨100⟩$ for the collection of SPED data. The effective lamella thickness at this tilt angle inevitably leads to the overlap of multiple islands in the recorded data, requiring statistical unmixing postacquisition. Cluster analysis identifies three ${⟨100⟩}_{\text{tet}}$ diffraction patterns, each containing a distinct set of superlattice peaks corresponding to one of the three choices of c-axis orientation for tetrataenite (Fig. 6 A–C). The orientation maps for the coarse, medium, and fine regions of the cloudy zone (Fig. 6 D–F) show groups of neighboring islands with a uniform c-axis orientation. Variations in the proportions of different easy axes in the cloudy zone are thought to reflect the strength and direction of magnetic field present during cooling (see SI Appendix, Table S2). Due to the limited field of view, however, it is not possible to extract meaningful paleomagnetic information from these data. Due to the projection thickness at this high tilt angle, a unique matrix diffraction pattern could not be determined from this lamella.

Fig. 6.

SPED cluster analysis results along the [001] direction of the cloudy zone. (A–C) The three dominant cluster centers for the three different {100} tetrataenite orientations. (D–F) Cluster loading maps, showing how the three different orientations group in the (D) coarse, (E) intermediate, and (F) fine regions of the cloudy zone.

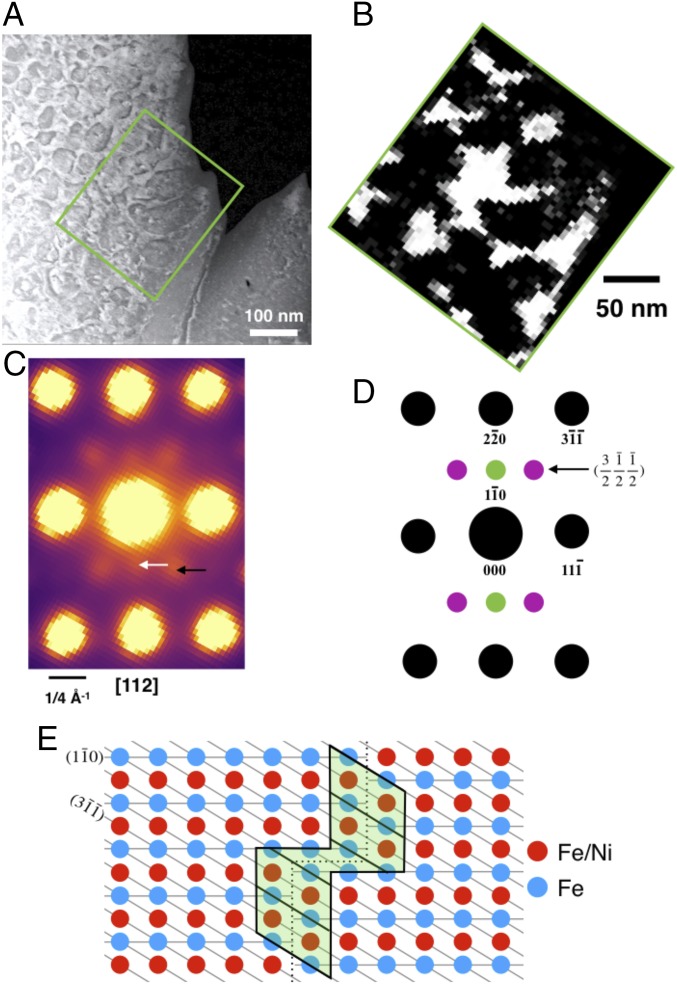
To isolate the crystal structure of the matrix phase, a second lamella was fabricated with a surface normal approximately parallel to the [112] zone axis of the parent taenite crystal structure. In the field of view studied, we observed mainly [211] and [121] orientations of tetrataenite islands, both of which lack superlattice peaks associated with their ordered structure. In contrast, a superstructure in the matrix becomes apparent, leading to a stronger overall diffraction condition, as seen in the STEM annular dark field image (Fig. 7A). Application of the cluster analysis of these SPED data reveals the presence of a diffraction pattern (Fig. 7C) unique to the matrix phase (Fig. 7B). The representative pattern contains strong reflections associated with the cubic lattice and additional superlattice reflections, which arise due to the chemical ordering of the matrix phase.

Fig. 7.

(A) STEM-HAADF of cloudy zone along the [112] direction. Tetrataenite particles are dark against the bright Fe-rich matrix. (B) Cluster analysis loading map associated with the cluster center diffraction pattern shown in C. (C) Cluster center for the matrix phase. Misalignment of superlatice reflections highlighted with white and black arrows. (D) Schematic diffraction pattern along [112] based on the proposed ordered structure. Black and green spots are in line with kinematic simulations of ${\mathrm{F}\mathrm{e}}_3$Ni. Purple spots are added based on experimental results. (E) Model for the matrix phase when viewed down the [112] with an antiphase boundary highlighted in green.

Bryson et al. (6) proposed an ordered matrix phase, based on the presence of superlattice peaks in [001] diffraction patterns collected from island/matrix regions containing only one or two out of the possible three tetrataenite orientations. When combined with EDS analysis, their observations were most consistent with a ${\text{Fe}}_3\text{Ni}$ cubic primitive structure. The (cluster center) diffraction pattern in Fig. 7C contains $\left(1\overline{1}0\right)$ superlattice peaks that are consistent with such an ordering of the matrix phase (green spots in Fig. 7D). However, the presence of the $\left(\frac{3}{2},\frac{\overline{1}}{2},\frac{\overline{1}}{2}\right)$ (purple spots in Fig. 7D) requires an additional doubling of the spacing of the $\left(3\overline{1}\overline{1}\right)$ planes that is not consistent with the ${\text{Fe}}_3\text{Ni}$ structure. Furthermore, the arrows in Fig. 7C indicate that the $\left(\frac{3}{2},\frac{\overline{1}}{2},\frac{\overline{1}}{2}\right)$ and (110) superlattice peaks are not exactly aligned. Close examination of these peaks (in both the raw data and cluster-based results) reveals that their relative positions change as the beam position is rastered across the sample. While these observations demonstrate unequivocally that the matrix phase is an ordered structure, the precise nature of the ordered structure is clearly more complex than the pure ${\text{Fe}}_3\text{Ni}$ structure proposed by Bryson et al. (6).

Micromagnetic State of the Cloudy Zone.

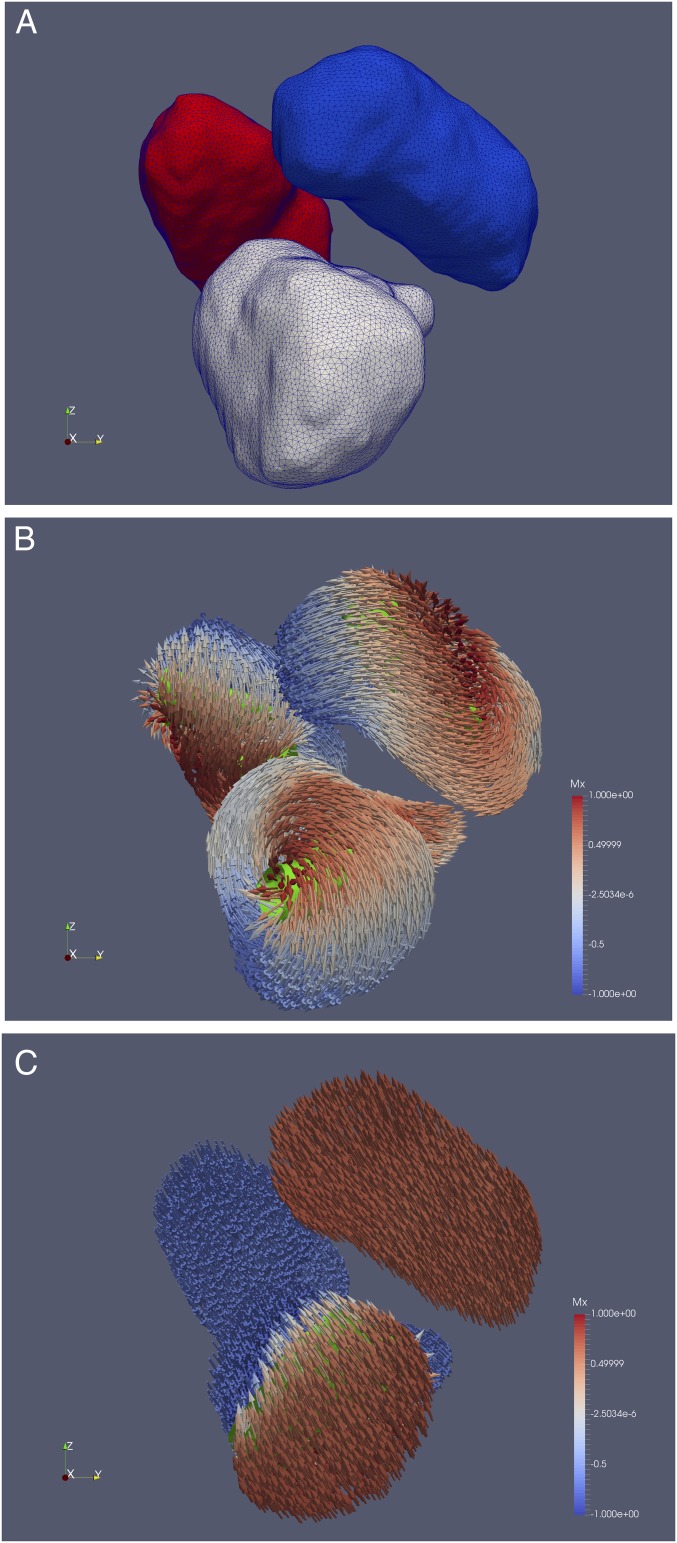
Three neighboring tetrataenite islands were extracted from the tomography stack of the intermediate cloudy zone and converted to tetrahedral volume meshes (Fig. 8A). Two of the islands are approximately prolate ellipsoids, with major axis diameters of $\sim$80 to 90 nm and minor axis diameters of $\sim$40 to 50 nm. The third island is similar in size but has an L-shaped geometry (Fig. 3C), possibly resulting from a merger of two smaller islands. Finite-element micromagnetic simulations were performed initially using room-temperature micromagnetic parameters appropriate to cubic disordered ${\text{Fe}}_{0.5}{\text{Ni}}_{0.5}$ ($M_s$ = 1,273 kA/m, $K_1$ = 1 kJ/${\text{m}}^3$, $A_{ex}$ = 1.13 ×$10^{-11}\text{J/m}$), which is a soft ferromagnet below its Curie temperature of $\sim$450 °C (18, 19). The matrix phase is not included in the micromagnetic models, since Mössbauer spectroscopy demonstrates that the matrix phase is paramagnetic in the bulk cloudy zone (20, 21). All three islands adopted either single- or double-vortex states at remanence (Fig. 8B), regardless of whether simulations were performed for each island separately or whether all three islands were simulated together (including, thereby, the effects of magnetostatic interactions between the islands). Magnetostatic interactions were sufficiently large to change significantly the values of vortex nucleation, switching, and annihilation fields during hysteresis cycles and also to influence the sense of vortex rotation and core magnetization adopted at remanence. The strength of interactions was not sufficient, however, to force the islands into a single-domain state. “High-temperature” simulations were performed by rescaling the micromagnetic parameters. $M_s$ was reduced by a factor of 2, $A_{ex}$ was reduced by a factor of 4, and $K_1$ was reduced to 0, corresponding to a normalized temperature of T/$T_c$ = 0.9. The remanence states observed at room temperature were all retained at high temperature, indicating that above 320 °C (the critical temperature for Fe–Ni ordering in tetrataenite) the cloudy zone can best be considered as an ensemble of weakly to moderately interacting single- or double-vortex states.

Fig. 8.

(A) Finite-element meshes of three neighboring islands extracted from the 3D-EDS tomography reconstruction of the intermediate cloudy zone. Average mesh element size is 1.6 nm. Best-fitting ellipsoids yield island sizes of (red) 82 × 48 × 38 nm, (white) 92 × 61 × 40 nm, and (blue) 92 × 47 × 41 nm. The white island has a distinct L shape due to coalescence of two smaller islands. (B) Remanent micromagnetic state for interacting islands of taenite, representing the likely magnetic state of the cloudy zone above 320 °C. Islands adopt predominantly single (occasionally double) vortex states. Green isosurfaces outline the approximate position of the vortex core. (C) Remanent micromagnetic state for interacting islands of tetrataenite, representing the likely magnetic state of the cloudy zone below 320 °C. The tetrataenite easy axis for all three islands is parallel to the long axis of the red island in A. Two islands show ideal single-domain states. The third island adopts a two-domain state with a sharp domain wall at the intersection of the two coalesced islands.

The effect of Fe–Ni ordering below 320 °C was explored in a series of simulations in which the uniaxial anisotropy was increased from $K_u$ = 0 to $K_u$ = 1370 kJ/${\text{m}}^3$ [the room-temperature value for pure tetrataenite (22)] in increments of 10 kJ/${\text{m}}^3$. This procedure approximates the effect of a continuous and homogeneous increase in Fe–Ni ordering throughout the system. The orientation of the uniaxial easy axis was chosen to lie along either the long, intermediate, or short axis of the islands (see SI Appendix, Movies S6–S9). When simulating a cluster of three islands, the c-axis of all three islands was oriented in the same direction, thereby mimicking the small clusters of islands with equal c-axis observed using SPED (Fig. 6). For isolated islands, placing the uniaxial easy axis along the long axis of the island leads to a transition to a stable single-domain state. Placing the easy axis along either the intermediate or short axes leads to the formation of a two-domain state, consisting of two equal and oppositely magnetized domains separated by a central domain wall. When magnetostatic interactions between the islands were included, however, there was a greater tendency for single-domain states to be adopted, as the interaction field caused walls to displace and eventually annihilate at the boundary of the islands (Fig. 8C). The vortex to two-domain to single-domain transition represents a complete rearrangement of the magnetic state of the system; there is no obvious relation between either the intensity or direction of remanence before and after the transition (see SI Appendix, Movies S10 and S11).

Discussion

The Chemical and Structural and State of Cloudy Zone.

The combination of TEM and APT has yielded the most comprehensive picture of the cloudy zone to date. Chemically, a rather simple picture emerges: Well-defined and constant compositions for the islands at 49.6% Fe:50.0% Ni, and matrix 82.0% Fe:17.7% Ni are observed throughout the entire cloudy zone, with the two phases separated by a sharp ($<$2 nm wide) chemical gradient. This observation implies that the chemical equilibrium between the islands and matrix was maintained at least down to the temperature of formation of the fine cloudy zone. The chemistry of the islands is consistent with tetrataenite, as expected. However, the chemical composition of the matrix is revealed to be much richer in Fe than has been suggested in some previous studies (2, 6, 23–26) and inconsistent with the proposal that the matrix is pure ordered ${\text{Fe}}_3\text{Ni}$ (6). The improvement in chemical analysis is explained by the more sophisticated methods of 3D-EDS quantification used here, combined with the enhanced capability to isolate signals from each phase through the use of high-resolution APT. This brings our composition data into agreement with the work of Miller et al. (27), who examined meteorites with a similar cooling history. Our results contrast with the APT results of Rout et al. (26), who examined a more rapidly cooled IVA meteorite. This suggests that the composition of the matrix phase is a function of the cooling rate, with slower cooling rates leading to a more Fe-rich matrix, consistent with expectations based on the low-temperature phase diagram (2).

Morphologically, we observe distinct characteristics in the coarse, intermediate, and fine cloudy zones. In the coarse cloudy zone, islands contain multiple threads of fine-scale matrix material, forming a network that connects back to the main matrix on either side of an island. We interpret this network of threads as relics of matrix material that became trapped as smaller islands grew and coalesced during the process of coarsening while the parent body cooled (SI Appendix, Fig. S13). Tetrataenite particles are often observed to be composed of two particles intersecting at 90° (Figs. 1 and 3C). In the intermediate cloudy zone, tetrataenite islands contain more isolated regions of matrix, which appear like secondary precipitates, but may also be simple relics of the coarsening process. Intermediate islands have a range of sizes and shapes but are, on average, classified as prolate ellipsoids. A weak $\left\{100\right\}$ texture is observable, providing the first hint that there is crystallographic control of the shape and elongation direction of the tetrataenite islands. We speculate that there is a preference for the elongation direction of an island to align with one of the $⟨100⟩$ directions of the cubic parent phase and that this elongation direction is parallel to the c-axis of tetrataenite. Islands in the fine zone show few, if any, secondary precipitates, indicating that the fine zone has undergone less coarsening.

Crystallographically, we have demonstrated that nearby tetrataenite islands are able to adopt different c-axis orientations, thereby confirming one of the fundamental assumptions of nanopaleomagnetic studies of the cloudy zone. The distribution of c-axis orientations is not random but consists of $\sim$50 to 500 nm clusters of islands with uniform c-axis orientation. Clustering was first predicted by Bryson et al. (7) to explain the unexpectedly large size of magnetic domains observed in the coarse and intermediate cloudy zone of the Tazewell meteorite using XPEEM. The close match between the shape and size of the c-axis clusters observed with SPED and the shape and size of magnetic domains observed with XPEEM confirms that the magnetic state of the cloudy zone is controlled by the underlying crystallography and clustering of the islands. This is most evident in the fine zone, which typically displays a strong and uniform magnetization with localized deviations in magnetization direction causing a fine-scale mottling in both electron holography and XPEEM images. A high degree of c-axis alignment is required to explain these observations. The origin of this enhanced c-axis alignment in not well understood, but various possibilities are considered below.

The electron diffraction pattern for the matrix phase (Fig. 7) contains two distinct sets of superlattice reflections. The first set of reflections (110 type; green spots in Fig. 7D) are consistent with one of the three possible tetrataenite orientations as well as Fe₃Ni when viewed along the [112]. The application of data clustering to the scanning diffraction data, however, spatially localizes this diffraction pattern to the matrix region. Additionally, the cluster center presented in Fig. 7C contains a second set of reflections that are incompatible with either Fe₃Ni or tetrataenite (pink spots in Fig. 7D). These reflections require a further doubling of the lattice periodicity. Although such a doubling could, in principle, be explained by an ordered structure of the Fe₇Ni type, this structure does not provide a good fit to the intensities of superlattice peaks, nor does it explain the observation that the row of superlattice spots are clearly misaligned with respect to each other. We propose an alternative model, whereby the approximate doubling of lattice periodicity occurs inside antiphase boundaries created by incommensurate ordering of Fe and Ni (Fig. 7E). Local doubling of the periodicity of $\left(3\overline{1}\overline{1}\right)$ planes occurs within the antiphase boundary regions. The presence of antiphase boundaries also provides a mechanism for short-range chemical segregation, enabling the incorporation of additional Fe into the structure needed to match the experimentally observed composition of the matrix (note that excess Fe is found in the central part of the kinked antiphase boundary in Fig. 7E). Such incommensurate ordering, creating high densities of antiphase boundaries and local chemical segregation, is well known in off-stoichiometry A₃B alloys (28, 29), which create similar patterns of superlattice reflections. Conventional Fe–Ni systems in this composition range usually undergo a martensitic transformation upon cooling. However, it appears that, in this case, the high degree of lattice coherency within the intergrowth, and the relatively small volume of the matrix phase, provides a sufficiently large barrier to this transformation, allowing the newly identified ordered phase to exist metastably.

Compositionally, the matrix lies in between Fe₃Ni and Fe₇Ni. The magnetic ground state of Fe₃Ni is predicted to be ferromagnetic at 0 K, with a moment of 2.066 ${\mu }_B$ per atom (compared with the 2.2 ${\mu }_B$ per atom for Fe in kamacite) (30). The magnetic ground state of Fe₇Ni is predicted to be ferrimagnetic with a moment of 0.942 ${\mu }_B$ (30). We can speculate that the magnetic ground state of the matrix lies somewhere between these two cases. The matrix is paramagnetic at room temperature due to its combination of high Fe content and fcc structure, which is incompatible with strong ferromagnetism (31). This property matches the proposed properties of antitaenite, a low-moment phase of taenite that is the most widely accepted explanation for the matrix phase. It is tempting, therefore, to state that antitaenite and the Fe-enriched, incommensurate ordered structure identified here are one and the same thing, although this statement would have to be corroborated by further studies involving a wider range of Fe–Ni meteorites.

The Mechanism of Remanence Acquisition in the Cloudy Zone.

Magnetically, we have demonstrated that the coarse to intermediate cloudy zone adopts vortex states for T $>$ 320 °C. Weak to moderate magnetostatic interactions between taenite islands have no effect on their domain state, so vortex states will dominate in all regions containing islands larger than the single-domain threshold (22.5 nm diameter for spherical particles; 65 nm long axis for a prolate ellipsoid with aspect ratio 2:1; see Materials and Methods). Below 320 °C, ordering of Fe and Ni atoms to form tetrataenite leads to a dramatic increase in uniaxial anisotropy and a transition from vortex to single-domain states, via an intermediate two-domain state. A two-domain state is preserved in isolated islands when the c-axis is chosen to be perpendicular to the elongation direction of the island or at the intersection of two coalescing islands. However, the presence of an externally applied field, as well as magnetostatic interactions between neighboring islands, plays an important role, causing the domain wall to displace to the island boundary, where it annihilates to produce a single domain. Once a single-domain state has been achieved, the field needed to renucleate the domain wall is very high (of the order of 1 T). This means that the magnetization state of each island becomes effectively fixed once the domain wall annihilates—that is, this is the blocking point for the acquisition of paleomagnetic remanence. This mechanism of blocking is very different from the thermal blocking process envisaged in previous models (32). We predict a fundamental difference in the mechanism of remanence acquisition within the coarse/intermediate cloudy zones versus the fine cloudy zone, caused by the presence of vortex states in the former and single-domain states in the latter. The domain state transition from a single-vortex to a single-domain state, via an intermediate two-domain state, driven by the phase transformation from taenite to tetrataenite, provides an effective mechanism for an ancient field to influence the paleomagnetic state of the cloudy zone by biasing the movement of domain walls during the transition. Once remanence is blocked, by annihilation of the domain wall, the high domain wall nucleation field prevents remagnetization, explaining the apparent lack of secondary magnetization in the cloudy zone. In the fine cloudy zone, the influence of magnetostatic interactions between uniformly magnetized islands is likely to be dominant. Further work is now needed to explore these complexities, such as extending the simulations to include much larger numbers of interacting islands and also investigating the quantitative relationship between the final remanence state and the intensity of the ancient magnetic field present on the meteorite parent body.

Both the intensity and direction of remanence change dramatically as a result of the transition to tetrataenite, suggesting that the final remanence is recorded during this ordering process, potentially erasing any memory of remanence that may already have been recorded above 320 °C. This statement has profound implications for the concept of time-resolved paleomagnetic information recorded throughout the cloudy zone. If all remanence is recorded at 320 °C, rather than at the temperature of spinodal decomposition, then all regions record their remanence at the same instance in time, rather than at sequentially different times according to the local Ni content. While this destroys the concept of time resolution as originally postulated by Bryson et al. (7), in which sequential subregions of the cloudy zone record remanence at different times, time-resolved records of dynamo activity can still be derived by studying several meteorites from a single parent body that cooled to 320 °C at different rates. For this reason, Bryson et al.’s observation of strong and weak magnetization in the Imilac and Esquel meteorites, representing the early and late stages of core solidification on the pallasite parent body, respectively, still stands. Their approach was subsequently extended by Nichols et al. (9) to observe the predicted quiescent period of dynamo activity on the pallise parent body that preceded core solidification. Simulations containing much larger ensembles of interacting islands are now necessary to determine whether any fraction of preexisting remanence can survive the transition, thereby preserving a time-resolved paleomagnetic record. In addition, regions of the cloudy zone containing islands below the single-domain threshold size may have significantly enhanced the capacity to retain a memory of a preexisting remanence, since the choice of c-axis orientation during the transition to tetrataenite is likely to be strongly influenced by the direction of uniform magnetization in the parent taenite island. This case would apply, for example, to some rapidly cooled IVA meteorites, which preserve evidence of a time-varying magnetic field generated by their parent body (10).

The Origin of Optimal Hard Magnetic Properties in the Fine Cloudy Zone.

The high degree of magnetic alignment observed in the fine cloudy zone may have several possible origins. Previous suggestions that this effect was due to exchange coupling between islands via the matrix are contingent on the matrix phase being ferromagnetic (6, 7). High-resolution Mössbauer spectroscopy measurements have since shown that the matrix is paramagnetic in the bulk phase and only appears ferromagnetic at surfaces and in thin films (21). With a paramagnetic matrix, magnetostatic interactions between islands provide an alternative mechanism leading to strong alignment. Smaller islands in the fine cloudy zone mean that single-domain states, rather than vortex states, are likely to dominate both above and below 320 °C. Taenite islands with uniform magnetization will generate larger magnetostatic interaction fields, which may cause higher degrees of c-axis alignment (and, as suggested above, increase the chances of remanence being inherited through the taenite to tetrataenite transition). Second, the finest islands form in regions with lowest average Ni content. According to the most commonly used phase diagram for the Fe–Ni system (2), spinodal decomposition in these regions will initiate below 320 °C, in which case islands will grow already within the tetrataenite stability field. The ability of magnetostatic interactions to influence the choice of c-axis orientation may be dramatically enhanced under these conditions, leading to the high degree of alignment through a process of self-organization.

A Pathway to Sustainable Rare Earth-Free Permanent Magnets.

Synthetic rare-earth permanent magnets possess a wide range of applications. However, the scarcity and environmental impact of extracting rare earth elements, combined with the increasing demand for permanent magnets in the transport and renewable energy industries, means that sustainable alternatives need to be developed. Recently, a low-temperature nitrogen insertion and topotactic extraction (NITE) process has been developed to produce gram quantities of well-ordered tetrataenite on short (i.e., laboratory) time scales (4), opening up the possibility of creating bulk synthetic tetrataenite for industrial use. Unfortunately, the magnetic coercivity of the material produced so far is below that needed to become a viable competitor to rare earth magnets (3). We observe much higher coercivity in localized regions of the meteorite cloudy zone, suggesting that there is a scope to learn valuable lessons from nature as we strive to optimize the properties of synthetic tetrataenite (3, 33). The fine cloudy zone provides a suitable template for a sustainable permanent magnetic material. To achieve the maximum energy product, it is necessary to maximize both the saturation magnetization and the coercivity, both of which are observed using electron holography and XPEEM measurements in the fine cloudy zone (6, 7). The results of the present study suggest that these optimal conditions are achieved through a two-phase intergrowth, where fully isolated islands of single-domain tetrataenite, with highly aligned c-axes, are coherently intergrown with a metastable, partially ordered fcc paramagnetic matrix phase. Adapting the NITE process to produce a synthetic equivalent of the ordered matrix phase may be achievable by simple modification of the chemical composition of the precursor Fe–Ni alloy. Mechanical mixing of synthetic tetrataenite and matrix nanoparticles, followed by low-temperature/high-pressure sintering in the presence of a strong magnetic field, would then provide a potential route to fabricating the same two-phase nanocomposite of tetrataenite and matrix phase in the laboratory that nature took tens of millions of years to achieve on the meteorite parent body.

Materials and Methods

Sample Preparation.

A section of the Tazewell meteorite was acquired from the Sedgwick Museum of Earth Sciences, University of Cambridge, sample no. 16269. The same sample has previously been studied using electron holography, XPEEM, and Mössbauer spectroscopy. Focused Ion Beam (FIB) milling with in situ lift-out was used to prepare samples for SPED, 3D-EDS, and APT study, using an FEI Helios Dual-Beam FIB located in the Department of Materials Science and Metallurgy, University of Cambridge. Planar lamellae were prepared for SPED analysis using a basic in situ TEM lamella preparation strategy. Final thinning and low kilovolt cleaning were performed using a simplified version of the process outlined by Schaffer et al. (34). Tomography needle samples were fabricated using the block lift-out approach described by Thompson et al. (35). For 3D-EDS and APT studies, blocks of the cloudy zone were lifted out and mounted in situ onto tomography posts. For 3D-EDS, Cu tomography pins specifically designed to work with the Fischione Instruments 2050 full-tilt tomography sample holder were used. APT needles were mounted on a Cameca silicon lift-out coupon with 36 posts. After welding with FIB-induced Pt deposition, needle geometries were formed using the procedure described by Larson et al. (36). Amorphous damage and Ga⁺ implantation were removed using a 2 kV, 100 pA polishing step. Several APT samples were fabricated with the tip axis parallel to either the [001] and [110] directions.

3D-EDS.

Tomographic elemental mapping of the cloudy zone was performed using EDS on an FEI Tecnai Osiris 80-200, operating at an accelerating voltage of 200 kV. The high density of the Fe–Ni phase in the cloudy zone coupled with the variable thickness of a tomography needle geometry means that electron energy loss spectroscopy would suffer from multiple scattering events, leading to nonquantitative results. Additionally, the four-detector geometry of the Osiris instrument allows for rapid mapping of the sample, minimizing drift during the tilt series collection. Needle samples were loaded into the microscope using the Fischione full-tilt tomography holder. The EDS tilt series was collected every 5° from −70° to +75°. Elemental maps were collected in a 246 nm × 327 nm region of interest on each of the tomography needles studied. With a pixel size of 2.46 nm, this resulted in the collection of 348,000 spectra.

EDS Structural and Chemical Quantification.

The EDS tilt series collected produces a statistically dense spectral dataset. Integrated Fe and Ni spectral peak intensities were extracted from the EDS tilt series using spectral and machine-learning tools in the open source Python library, Hyperspy (37). The spectra were denoised using PCA and background-subtracted before performing the intensity integration on the two respective elemental peaks. Intensity integration produces a grayscale tilt series for each element, where the peak intensity is proportional to the quantity of iron or nickel present in each pixel. The tilt series are aligned using TomoJ (38) and then reconstructed using an in-house CS algorithm (14, 15). The two resulting volumes were individually segmented using a random walker algorithm (39), and the resulting volumes were then compared with the structural morphologies for tetrataenite and matrix phases seen in Figs. 2 and 3. Morphological analysis was performed on the segmented Ni maps, as these provided a stronger contrast between tetrataenite particles and the Fe₃Ni matrix.

CS reconstruction preserves the boundaries and physical morphologies of features found in the tilt series. However, the resulting grayscale values in the reconstruction are not linearly preserved. This results in uncertainty for the use of the reconstructed grayscale information for EDS quantification. We addressed this uncertainty by developing an alternative method for the quantification of 3D chemical data. First, the CS reconstruction volume was segmented to label voxels as either Ni-rich or Fe-rich. These chemical phase-specific subvolumes were then reprojected, using a discrete Radon transform in Sci-Kit Image (Python), giving a phase-specific thickness map at each tilt angle (40, 41). These thickness maps were registered to the raw EDS spectra using image-processing routines in Matlab. The reconstruction problem was then recast as a system of linear equations, assuming the observed spectra were a linear combination of signals arising from the island and matrix phases. At each energy channel, the 348,000 simultaneous equations provided for an overdetermined problem to recover the coefficients corresponding to the intensity at each energy channel for each of the two phases. Across the entire spectrum, this analysis determined the characteristic EDS spectra of the island and matrix phases based on the physically segmented tomography volume (Fig. 3A). Cliff–Lorimer methods were used to quantify the Fe–Ni ratio from the resulting EDS spectra. We estimate the relative uncertainty in the ratio to be at 2% based on counting statistics. Errors associated with the first principles-derived k-factors provided by the instrument manufacturer have been reported at approximately 8% using the Co-K and Pt-L lines (42). However, calculated Fe and Ni k-factors for K lines are known to have particularly low errors (1% to 2%) (43) and are systematic and of similar small magnitudes for Fe and Ni (and will therefore be substantially reduced in relative composition). As such, we report 2% errors for EDS quantification in line with the X-ray counting statistics.

APT.

APT experiments were carried out on a LEAP 3000X-HR instrument (University of Oxford), running in laser mode with a 532 nm beam operating at 0.4 nJ. A small subset of samples were also run in voltage mode, to confirm the accuracy of composition data, although the data yield was lower from these. The specimen stage temperature was kept at 55 K for all experiments. Data were reconstructed using IVAS software (3.6.12). The composition of the islands and matrix was obtained by placing numerous cylindrical regions of interest at least 1 nm away from the nearest interface, in order avoid sampling neighboring phases (SI Appendix, Fig. S3). The atoms inside multiple cylinders across multiple datasets were summed to produce the average compositions quoted. The compositional variations of either phase between different APT datasets were not statistically significant.

SPED.

SPED allows for detailed crystallographic mapping of a sample by precessing the electron beam about a small angle. This results in diffraction patterns where the dynamical effects of scattering are minimized and we are able to record a larger region of the Ewald sphere (44). Here, the electron probe is also scanned across the region of interest to map out the crystallography of the sample. We use a Phillips CM300 FEGTEM equipped with a Nanomegas ASTAR precession system. Using 300 kV spot 7, we collect diffraction patterns every 5 nm in the region of interest. For the sample oriented along the [100] direction, we collected three sets of maps, one from the coarse, medium, and fine regions of the cloudy zone (Fig. 6). Each [100] map collected was 600 nm × 600 nm. For the lamella oriented along the [112] zone axis of the parent taenite crystal structure, a single map of 220 nm × 235 nm was collected (Fig. 7). Once the data were collected, the maps were then analyzed using cluster analysis, to determine the dominant diffraction patterns (45). This allows for physical diffraction patterns to be analyzed and orientation maps to be produced.

Cluster Analysis.

Cluster analysis is the unsupervised (or semisupervised) identification and classification of groups of points that lie close together in space (46). In the context of SPED, for a highly coherent crystal structure such as that reported here, statistical decomposition methods such as PCA and Nonnegative Matrix Factorization (NMF) can be misleading, because so many of the reflections are common to all of the diffraction patterns in the scan. As a result, the common reflections tend to be grouped into one significant component and variations in the structure (often limited to a small number of weak reflections) are associated with the higher components. For clustering, each diffraction pattern is assigned a position in high-dimensional space according to how much of each component is associated with it. Clusters are formed by grouping points in this space that are “close together,” and the average diffraction pattern for each signal is calculated from that point in space. Although it is common to define distances using a Euclidean metric, custom metrics can be used as well. The key advantage here is that the component corresponding to the common reflections can and will be included in the cluster representations, leading to meaningful diffraction patterns that nevertheless highlight the key structural differences between the different phases in the microstructure.

For Fig. 7, initial decomposition was performed using NMF retaining 6 components. Clustering was performed using the Gustafson–Kessel variation of the probabilistic fuzzy c-means algorithm, searching for five clusters within the data. For Fig. 6, a custom distance metric was used, based on the identification of peaks and their cumulative distance from those in other patterns. The distances themselves form clusters; these were used to derive the localization maps. The representative patterns were derived as the weighted means of the patterns in those areas.

Micromagnetic Modeling.

The Finite Element Method/Boundary Element Method (FEM-BEM) micromagnetics package MERRILL (Micromagnetic Earth Related Rapid Interpreted Language Laboratory) was used to solve for the magnetic scalar potential inside each particle and thereby calculate the demagnetizing energy of the system (47, 48). This approach avoids the need to discretize the nonmagnetic volume outside the particle. Tetrahedral meshes of average 1.6 nm spacing were used for modeling magnetic behavior of the particles to ensure that exchange interactions were being accounted for appropriately. Simulations were performed using an Apple iMac with a 3.4 GHz Intel i7 processor and 24 GB of RAM. Each particle was initialized with a random magnetization state. Simulations then minimized the total micromagnetic energy at each applied field and/or anisotropy value, using a conjugate gradient method adapted to micromagnetic problems. The total micromagnetic energy consists of summing the exchange, cubic anisotropy (in the case of taenite), uniaxial anisotropy (in the case of tetrataenite), magnetostatic, and demagnetizing energies. Material parameters used were appropriate for taenite at room temperature: saturation magnetization $M_s$ = 1,273 kA/m, exchange constant $A_{ex}$ = 1.13 ×$10^{-11}\text{J/m}$, and cubic anisotropy with $K_1$ = 1 kJ/${\text{m}}^3$ (18, 19). Similarly, for tetrataenite, the room temperature parameters were saturation magnetization $M_s$ = 1,390 kA/m, exchange constant $A_{ex}$ = 1.13 ×$10^{-11}$ J/m, and cubic anisotropy with $K_u$ = 1,370 kJ/${\text{m}}^3$ (22). For simulations performed on individual islands, the anisotropy vector was set to be parallel to either the long, intermediate, or short axis found for the best-fit ellipsoid for each island. For simulations performed on all three interacting islands, the anisotropy vector was set to be parallel to either the long, intermediate, or short axis found for just one of the islands. To simulate the transition from taenite to tetrataenite, the cubic anisotropy was set to zero and the uniaxial anisotropy was increased from $K_u$ = 0 to $K_u$ = 1,370 kJ/${\text{m}}^3$ in increments of 10 kJ/${\text{m}}^3$. The converged solution at each step was used as the starting configuration for the next step. The room-temperature single-domain threshold for a spherical particle of taenite was calculated using the size-scaling method of ref. 47. A spherical mesh of 25 nm diameter and 1 nm element size was used, with size scaling factors varying from 0.5 to 3 and back again in steps of 0.1. The threshold for a prolate ellipsoid particle with aspect ratio 2:1 was calculated using an initial mesh of diameter 50 × 25 nm and 1 nm element size. Quoted values are the lower limit obtained during the decreasing-size portion of the size hysteresis loop.