Probabilistic control of HIV latency and transactivation by the Tat gene circuit

Significance

The reservoir of HIV latently infected cells is the major obstacle for complete eradication of HIV infection. Latency and its transactivation in HIV-infected cells are controlled by the intracellular HIV Tat gene circuit. By reconstructing the probability landscape of the circuit through exact solution of the underlying chemical master equation we examined the detailed mechanism of probabilistic intracellular control of latency and transactivation. We show that while the Tat circuit lacks deterministic bistability its probability landscape exhibits bimodality. Moreover, by exploring changes in the probability landscapes under different perturbations, our study suggests effective therapeutic targets for strategies of “shock and kill” to eliminate latently infected cells and “block and lock” to enforce deep latency.

Abstract

The reservoir of HIV latently infected cells is the major obstacle for eradication of HIV infection. The “shock-and-kill” strategy proposed earlier aims to reduce the reservoir by activating cells out of latency. While the intracellular HIV Tat gene circuit is known to play important roles in controlling latency and its transactivation in HIV-infected cells, the detailed control mechanisms are not well understood. Here we study the mechanism of probabilistic control of the latent and the transactivated cell phenotypes of HIV-infected cells. We reconstructed the probability landscape, which is the probability distribution of the Tat gene circuit states, by directly computing the exact solution of the underlying chemical master equation. Results show that the Tat circuit exhibits a clear bimodal probability landscape (i.e., there are two distinct probability peaks, one associated with the latent cell phenotype and the other with the transactivated cell phenotype). We explore potential modifications to reactions in the Tat gene circuit for more effective transactivation of latent cells (i.e., the shock-and-kill strategy). Our results suggest that enhancing Tat acetylation can dramatically increase Tat and viral production, while increasing the Tat–transactivation response binding affinity can transactivate latent cells more rapidly than other manipulations. Our results further explored the “block and lock” strategy toward a functional cure for HIV. Overall, our study demonstrates a general approach toward discovery of effective therapeutic strategies and druggable targets by examining control mechanisms of cell phenotype switching via exactly computed probability landscapes of reaction networks.

HIV infection is a global epidemic and currently over 36 million people worldwide live with the virus (1). Present antiretroviral therapies (ARTs) can effectively suppress HIV viral replication by disrupting the viral life cycle at multiple stages. However, they do not eradicate HIV infection. The major barrier for complete eradication of HIV from the host is the reservoir of latently infected CD4⁺ T cells. These cells are not recognized by the immune system and their persistence is not affected by ART. Latency transactivation is the process of transition from the latent state, in which HIV gene transcription is largely inactive, to the transactivated state with active HIV gene transcription and viral replication. Latent cells can stochastically transactivate to actively produce new virions, resulting in viral rebound once ART is interrupted. To eradicate HIV from the host, the latent reservoir must be eliminated.

The HIV latent reservoir is extremely stable, with an estimated half-life of ∼44 mo (2–4). Given the large number (>10⁶) of latently infected cells within a host, it would take ∼70 y for the loss of all latent cells, even if no new latently infected cells were generated due to the administration of ART (2, 3). The “shock-and-kill” strategy was proposed to eradicate the latent reservoir by activating latently infected cells using latency reversing agents (LRAs) (5–8), so they can be eliminated either by the immune system or by viral cytopathic cell death. However, recent clinical trials and experiments with histone deacetylase inhibitor (HDACi)-based LRAs did not show effective reductions in the latent reservoir (5–8). Novel LRAs are needed for more effective activation and killing of latently infected cells.

To eliminate the HIV latent reservoir, it is important to understand the mechanisms that control the stability of HIV latency, so strategies can be designed to destabilize latency and thereby help eliminate the latent reservoir. The latency of HIV-infected cells and their transactivation are stochastically controlled by the HIV Tat gene circuit (9–11). Tat, the transactivator of transcription, is a critical regulatory protein encoded in the HIV genome and is under the control of a single HIV promoter, the LTR. The Tat gene circuit was experimentally found to be sufficient to generate bimodal phenotypes of latency and transactivation independent of the CD4⁺ T cell resting state (9, 12). While circuits of genetic switches with bimodal control have been extensively studied in systems such as Escherichia coli (13) and phage lambda (14–17), the HIV Tat gene circuit is different. The Tat circuit consists of a single positive feedback loop and does not contain any double-negative feedbacks (9, 12). In addition, it exhibits no cooperativity (9, 12). Mathematical models have shown that simple positive feedback loops without cooperativity cannot maintain a stable off-state and therefore do not have deterministic bistability (18–20). However, it is well known that bistability can be induced by stochasticity in small-volume systems, such as cells, (21–23) or by stochastic gene regulatory networks (9, 12, 20, 24–27), contrary to what is predicted by corresponding deterministic models (e.g., based on mass action). How the bimodality of latency and transactivation is controlled through the Tat gene circuit and which reactions are the controlling ones remain unanswered questions.

Cell phenotypes are controlled by intracellular reaction networks that are intrinsically stochastic. Understanding the regulatory mechanism of cell phenotypes relies on effective models and efficient algorithms to predict the correct cell behavior from the underlying reaction networks. Accurate characterization of the probability landscape of intracellular reaction networks provides a powerful approach to study the probabilistic control and switching of cell phenotypes, and significant progress has been made in this field (14, 28–33). Here we systematically investigate the stochastic control of HIV latency and transactivation by characterizing the full probability landscape of the Tat circuit under different conditions. This is achieved by directly solving the underlying chemical master equation (CME) using the accurate CME (ACME) method (14, 31–33). By taking advantage of the strong coupling among reactions, the ACME method can dramatically reduce the size of the required state space and therefore allows exact computation of the probability landscapes with mathematically derived error bounds (32, 33) for many stochastic networks that were otherwise infeasible (14, 31–33). Importantly, the rate of HIV phenotype switching between latency and transactivation can be accurately calculated using the ACME method (32, 33).

In this study, we first characterize the full probability landscape of the wild-type HIV Tat circuit at steady state and then compute the landscapes with different model parameters to investigate the stability and regulatory mechanisms that control the latency phenotype. We further identify potential therapeutic targets based on probability landscapes and compute phenotype switching rates for effectively reversing the latent state of HIV-infected cells and thereby facilitating depletion of the HIV latent reservoir.

Materials and Methods

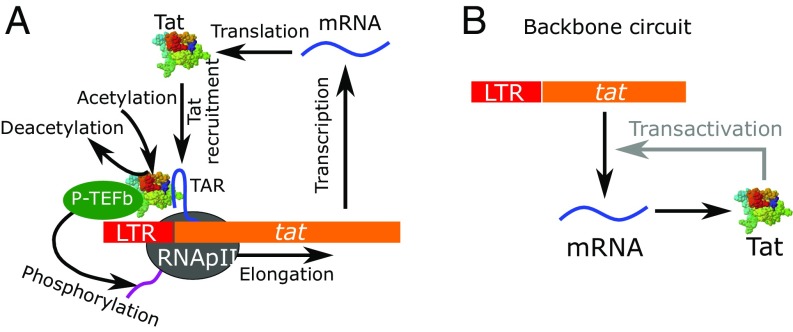
The reaction scheme of the HIV Tat gene circuit used in this study is shown in Fig. 1A (9, 11, 12, 34–36). The detailed reactions are listed in SI Appendix, Table S1. Among proteins encoded by the HIV genome, the Tat protein is essential for HIV production (11). In the absence of Tat, the basal transcription of HIV genes, including tat, can initiate from the LTR region but cannot elongate efficiently. Upon initiation, the RNA polymerase II transcription complex pauses at the promoter proximal location (11, 37–40). Further elongation only occurs at an extremely low basal transcription rate ($k_{b0}$). The premature HIV mRNA fragment generated from the initiated transcription forms the HIV transactivation response (TAR) element, which is a highly stable RNA stem–loop structure (41). When Tat is available, it binds the TAR element in the paused transcription complex at binding rate $k_b$ to recruit the positive transcription elongation factor (P-TEFb), an essential host transcription regulator in eukaryotes, to the paused transcription complex to form the Tat–TAR–P-TEFb (TTP) complex. The Tat protein in the TTP complex can be acetylated at lysines 25, 50, and 51 (42, 43) at rate $k_a$ and represented as acTTP (SI Appendix, Table S1). After Tat acetylation, the P-TEFb complex is released to hyperphosphorylate the C-terminal domain of the RNA polymerase II (44), so that the paused transcription complex can transition to productive elongation and a mature HIV mRNA can be synthesized at a transactivated rate $k_f$. Tat is then released from the complex after elongation and is available for another cycle of transactivation. By recruiting P-TEFb to speed up transcription, the HIV Tat gene circuit forms a Tat-dependent positive feedback loop in the transactivation of HIV (Fig. 1B). In this circuit, Tat can be produced from two different modes: either from slow Tat-independent basal production or from rapid Tat-dependent transactivated production. These two modes have substantially different production rates of Tat, and implicitly of other HIV proteins. Values of parameters for the Tat circuit (SI Appendix, Table S1) were obtained from the literature. For those parameters with no accurate experimental measurements, we used values from previous modeling studies (9, 12, 24, 36) and complemented them with detailed exploration of the sensitivity of our results to the choice of these parameter values. Additional justifications for parameter choices and details of the ACME method can be found in SI Appendix.

Fig. 1.

The HIV Tat circuit. (A) Detailed molecular interactions in the Tat gene circuit (SI Appendix, Table S1). (B) The backbone positive feedback logic in the Tat circuit.

Results

HIV Tat Circuit Exhibits Stochastic Bimodality of Latency and Activation.

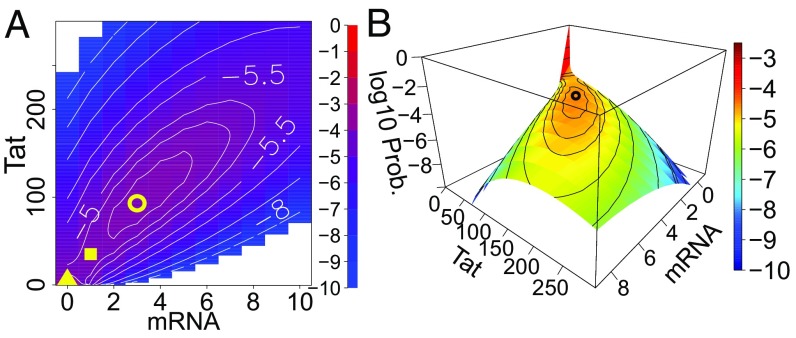
We computed the steady-state probability landscape of the HIV Tat circuit and projected it onto the 2D space of Tat mRNA and Tat protein (Fig. 2A, top view and Fig. 2B, side view). Our results show that the Tat circuit exhibits bimodality (i.e., has two distinct probability peaks) (Fig. 2). The first peak, which corresponds to latency, is located at zero copies of both Tat mRNA and Tat protein with a maximum probability of 0.98 (Fig. 2). The second peak located at 3 copies of mRNA and 93 copies of Tat protein, with a small peak probability of $3.2\times {10}^{-5}$ (Fig. 2), corresponds to the transactivated cell phenotype. We define the stochastic separatrix state as the state with the lowest probability between the two probability peaks. For the wild-type Tat circuit, the separatrix state has 1 copy of Tat mRNA and 34 copies of Tat protein (Fig. 2A, yellow square). For easier comparison, we further project the probability landscape onto the 1D space of Tat protein copy number (SI Appendix, Fig. S1A), in which the separatrix state is at 16 copies of Tat protein (SI Appendix, Fig. S1A, dashed red line). The latency probability peak is high, sharp, and narrow (Fig. 2B and SI Appendix, Fig. S1A), which explains the high stability of HIV latency. That is, once a cell is in latency, it is difficult to become spontaneously reactivated. In contrast, the peak of transactivation is very broad and shallow (Fig. 2A and SI Appendix, Fig. S1A); the variance-to-mean ratio for Tat copy number in transactivated cells with greater than 16 copies of Tat protein is calculated to be 29.

Fig. 2.

Bimodal steady-state probability landscape of HIV Tat circuit. (A) Top view of the 2D steady-state landscape. The contour lines show the probability in log scale. The yellow triangle indicates the location of probability peak of latency, the yellow circle indicates the location of the probability peak of activation, and the yellow square indicates the stochastic separatrix state. (B) Perspective view of the 2D steady-state landscape. The yellow triangle in the bottom left corner of A corresponds the high peak of latency shown in red in B.

Positive Feedback Is Essential for Transactivation.

To study the contribution of the positive feedback loop in the control of HIV latency and transactivation, we first disrupted the positive feedback by blocking Tat–TAR binding, that is, by setting $k_b=0$ in the model, and found that the probability peak of transactivation disappears (SI Appendix, Figs. S1B and S2A). Although a small probability shoulder remains at around 20 copies of Tat protein, which suggests that it is still possible to transactivate from the latent state, however it may not be able to efficiently sustain transactivation events, where a large copy number of Tat protein may be required (SI Appendix, Figs. S1B and S2A). This unimodal probability landscape suggests that upon inhibition of Tat–TAR binding, latency is the only stable cell phenotype (SI Appendix, Figs. S1B and S2A). The effect of disrupting the positive feedback through blocking Tat acetylation (by setting $k_a=0$) yields a probability landscape that exhibits the same qualitative behavior (SI Appendix, Fig. S2B).

To further characterize the role of the positive feedback loop in the Tat circuit, we compare the behavior of the wild-type and the two differently perturbed circuits by examining their rates of transactivation from latency, rates of returning to latency from the activated state and their 95 percentile amplitudes of Tat copy number in activated cells. Detailed procedures for obtaining the phenotype switching rates are described in SI Appendix. While the Tat circuit is modeled in single cells, its steady-state probability landscape is the distribution of all possible cell phenotypes in a population of cells carrying the identical Tat circuit. Therefore, the computed rates correspond to the transition rates between the latent reservoir and the transactivated cell population.

The computed transactivation rate with the wild-type Tat circuit is $4.5\times {10}^{-4}\hspace{0.17em}{\text{d}}^{-1}$ (SI Appendix, Table S2). For a population of latently infected cells with identical parameters, this corresponds to a half-life of 51 mo (SI Appendix, Table S2). The rate corresponds to the occurrence of 450 independent Tat circuit transactivation events per day from a latent reservoir of size ${10}^6$. The rate of returning to latency is computed to be 0.065 per day (SI Appendix, Table S2), which is 1,400-fold larger than the latency transactivation rate and shows the low stability of the transactivated state. The rates are shown in SI Appendix, Table S1. The number of Tat circuit transactivation events per day not only depends on the transactivation rate but also on the size of the latent reservoir (SI Appendix, Table S1).

Compared with the wild-type Tat circuit, a Tat circuit without positive feedback would have much smaller latency transactivation rates (3.4 × 10⁵ d⁻¹, roughly 10-fold smaller than the wild-type Tat circuit, SI Appendix, Table S2) with extremely long latent reservoir half-lives (SI Appendix, Table S2). The circuits also have a much higher rate of returning to latency and much smaller Tat copy numbers in transactivated cells (SI Appendix, Table S2). Overall, these results show that the positive feedback is essential in transactivating the Tat circuit in latently infected cells. Without positive feedback, the Tat circuit in latently infected cells cannot be effectively transactivated.

Tat Acetylation and Tat–TAR Binding Control Bimodal Phenotype.

Depending on parameters, the Tat circuit can exhibit three different types of probability landscapes at steady state: (i) unimodality at latency, which has a single probability peak at zero copies of Tat mRNA and protein, (ii) unimodality at transactivation, which has a single probability peak at nonzero copies of Tat mRNA and protein, and (iii) stochastic bimodality, which has two probability peaks, one at zero Tat copy number and the other at high Tat copy number. We study the effect of changing the rates of different reactions in the Tat circuit that may be potential drug targets to disrupt the bimodality and induce transactivation. We perturb the basal transcription rate ($k_{b0}$), the nuclear import and export rates ($k_e$ and $k_i$), the Tat–TAR binding and unbinding rates ($k_b$ and $k_u$), and the Tat acetylation and deacetylation rates ($k_a$ and $k_d$). We examine the effect of perturbations of these reactions on the steady-state probability landscape. Since perturbing the basal transcription rate does not eliminate the transactivation peak (SI Appendix, Fig. S3) and perturbing Tat mRNA export and Tat protein import does not eliminate the latency peak (SI Appendix, Figs. S4 and S5), we focus on the perturbations of Tat acetylation/deacetylation rates and Tat–TAR binding/unbinding rates. The results are summarized in SI Appendix, Table S3.

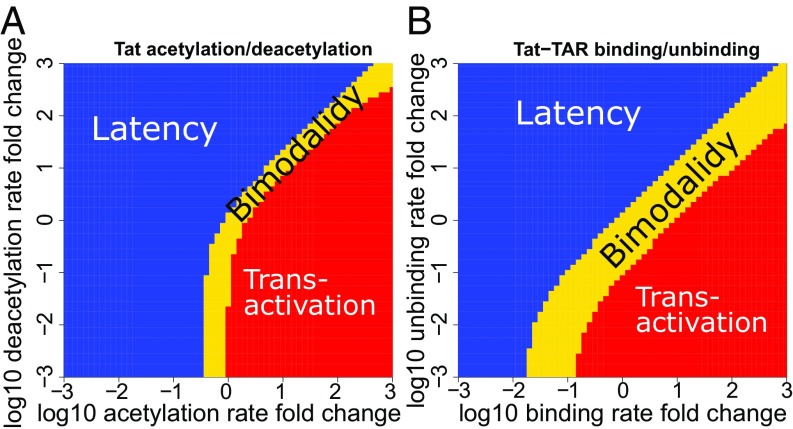
Perturbations of Tat acetylation/deacetylation rates and Tat–TAR binding/unbinding rates dramatically disrupt the bimodal probability landscape (SI Appendix, Figs. S6 and S7). When the Tat acetylation rate, $k_a$, is large, or the deacetylation rate, $k_d$, is small, the Tat circuit exhibits only one probability peak at the transactivation state (red region in Fig. 3A and SI Appendix, Fig. S6). When the acetylation rate is small and the deacetylation is large, the Tat circuit exhibits only one probability peak at latency (blue region in Fig. 3A and SI Appendix, Fig. S6). Interestingly, between the regions of unimodal latency and unimodal transactivation there is a narrow region in which the Tat circuit exhibits bimodality (yellow region in Fig. 3A) with the presence of probability peaks corresponding to latency and transactivation (SI Appendix, Fig. S6). That is, both phenotypes are possible under conditions defined by this narrow region. Perturbing the Tat–TAR binding and unbinding rates have similar effects (SI Appendix, Fig. S7), but with a wider region of bimodality (Fig. 3B). In addition, perturbations in reactions can also change the shape of the probability landscapes. Increasing the Tat acetylation rate can dramatically shift the peak of transactivation to a much higher Tat copy number (SI Appendix, Fig. S6), while perturbing other parameters has little effect on the mode of the transactivation peak (SI Appendix, Figs. S3, S4, and S7).

Fig. 3.

Phase diagrams of cell phenotypes when perturbing the Tat acetylation/deacetylation rates and the Tat–TAR binding/unbinding rates. Distribution of unimodal and bimodal cell phenotypes in the Tat acetylation and deacetylation parameter space (A) and in the Tat–TAR binding and unbinding parameter space (B). Blue region: unimodality at latency. Red region: unimodality at transactivation. Yellow region: stochastic bimodality with both latent and transactivated cell phenotypes possible.

Tat Acetylation and Tat–TAR Binding Control Intracellular Tat Copy Number and Transactivation Rate.

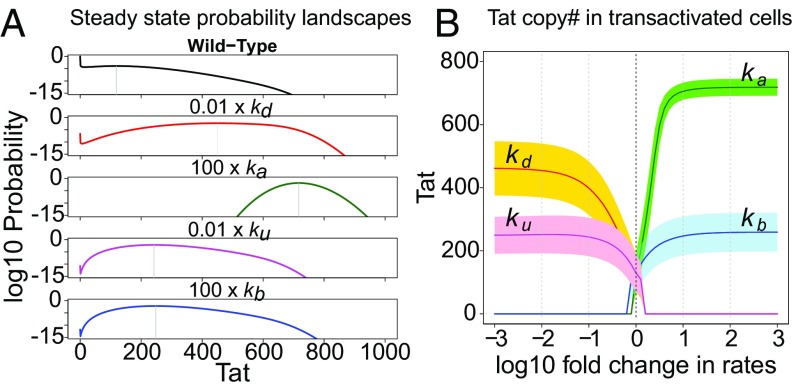
We examined how Tat acetylation/deacetylation and Tat–TAR binding/unbinding affect the production of Tat protein during latency transactivation. We first identified the peak of transactivation, which is separated from the peak of latency in the steady-state probability landscape by the stochastic separatrix (e.g., red dashed line in SI Appendix, Fig. S1A). The mean and variance of the Tat copy number in the transactivation peak were calculated at different model conditions. Results show that altering the Tat acetylation and deacetylation rates will result in a significantly larger mean copy number of Tat protein than altering the Tat–TAR binding/unbinding rates (Fig. 4 and SI Appendix, Table S4), while both are larger than the wild-type Tat circuit. The variance of the Tat copy number at the transactivation peak is also altered.

Fig. 4.

Effects of individual perturbations of four parameters to transactivate the Tat circuit: Tat acetylation/deacetylation and Tat–TAR binding/unbinding. (A) The steady-state probability landscapes of the Tat circuit for wild-type parameters and the four perturbations. (B) The steady-state Tat protein mean copy number and SD (shaded area) in transactivated cells when perturbing the four parameters.

The rate of latency transactivation and the rate of returning to latency can be significantly impacted by the rates of Tat acetylation/deacetylation and Tat–TAR binding/unbinding. In comparison, decreasing the Tat deacetylation rate is less effective in increasing the latency transactivation rate than increasing the Tat–TAR binding rate. A 100-fold decrease in the Tat deacetylation rate only increases latency transactivation by 1.4-fold and reduces the half-life of the latent reservoir by 31% (SI Appendix, Fig. S8 and Table S4), whereas a 100-fold increase of the Tat–TAR binding rate can increase the rate of latency transactivation by about 1.8-fold and it reduces the half-life of the latent reservoir by 45% (SI Appendix, Fig. S8 and Table S4). Additionally, the rate of returning to latency is dramatically reduced by all four reaction perturbations, which makes latency transactivation almost irreversible (SI Appendix, Table S4).

Discussion and Conclusions

Current ART can effectively suppress within-host HIV replication, but it does not eradicate HIV infection. The long-term persistence of the HIV latent reservoir forms the major barrier for the complete eradication of HIV. Latency transactivation is the process of transition from the latent state, in which HIV gene transcription is largely inactive, to the transactivated state with active HIV gene transcription and viral replication. In the transactivated state latently infected cells can be killed by viral cytopathic effects or be recognized and killed by immune system effector cells. While the shock-and-kill strategy has been proposed to reduce the size of the latent reservoir, a shock using HDACi-based LRAs has so far failed to reduce the latent reservoir (5, 7, 8, 45, 46).

The intracellular Tat circuit is known to play an important role in controlling latency and its transactivation in HIV-infected cells (9–12, 47). However, it has not been targeted for latency reversal. In this study, we characterized the maintenance and the transition kinetics between the cellular phenotypes of latency and transactivation through computational modeling of the HIV Tat circuit. Using this model, we further identified potential targets in the Tat circuit for therapeutic interventions toward latency reversal. To simplify the model, we only consider spontaneous transactivation of latently infected cells and not transactivation due to antigen stimulation. We also assume latently infected cells have quiescent HIV transcription and thus do not express HIV epitopes that can lead to their recognition and death by immune-mediated mechanisms. As the transitions from latency to the activated state are rare events, for which simulation methods such as the Gillespie algorithm (48) are not effective, quantifying the probabilistic behavior of the Tat circuit is technically challenging. In this study, we directly computed the probability landscapes of the Tat circuit and the rate of latency transactivation using the ACME method (14, 31–33).

Our results revealed the probabilistic bimodal control mechanism of HIV latency and transactivation. Our results showed that the steady-state probability landscape of HIV-infected cells controlled by the Tat circuit can simultaneously exhibit two distinct probability peaks corresponding to latent and transactivated cell phenotypes. The latency peak is high and narrow, indicating a stable latent state. The transactivation peak is low and broad, indicating a less-stable state with a highly fluctuating copy number of Tat protein in transactivated cells. This high level of Tat fluctuation likely contributes to the observed large variability in the amount of HIV produced from activated cells (49). The stability of the latent state in the wild-type HIV Tat circuit is maintained by both the slow transition from the latent state to the transactivated state and the faster transition from the transactivated state back to the latent state (SI Appendix, Table S2).

Based on the computed latency transactivation rate, the computed 51-mo half-life of latent reservoir with identical wild-type Tat circuit parameters is close to the current estimate of ∼44 mo based on clinical data (3, 4). Hill et al. (50) estimated the frequency of successful transactivation from latent reservoir that lead to viral rebound after cessation of ART to be approximately four per day, whereas Pinkevych et al. (51) estimated the frequency to be one in every 5–8 d. Assuming ${10}^6$ latently infected cells in the latent reservoir, that is, a total of ${10}^{11}$ CD4⁺ T cells in a HIV-1–infected individual with 10 in a million being latently infected, our model predicts 450 independent Tat circuit transactivations per day. The size of the latent reservoir can vary by orders of magnitude among patients and the frequency of predicted transactivation events will then also vary (52). Following Tat circuit transactivation many other events need to occur before viremia would be observed. An activated cell might die before producing any virus or the virus released may be cleared before infecting another cell. Our model does not predict the frequency of successful transactivation events as in Hill et al. (50) and Pinkevych et al. (51); rather, it only predicts the number of events in which the Tat copy number exceeds a predefined threshold needed for transactivation. Therefore, the predicted Tat circuit transactivation frequency of 450 ${\text{d}}^{-1}$ is necessarily greater than the frequency of successful transactivation that eventually led to viral rebound.

The transactivation rate was computed based on the transactivation events from the wild-type Tat circuit without taking into consideration other factors, such as necessary host factors (53, 54), the organization and structure of chromatin (55–57), epigenetics and DNA and chromatin modification (56), and the metabolic state of the host cell (58). These factors are required but may not be available in latently infected resting memory CD4⁺ T cells for successful transactivation and viral replication. Thus, the actual rate of transactivation may be lower and the reservoir half-life longer than we estimated above. Moreover, antigen-induced activation of latently infected CD4⁺ T cells would be expected to shorten the half-life. Since these factors may affect the half-life of latent reservoir, a computation of half-life based solely on the Tat circuit may be inaccurate but is a necessary first step in gaining insight into the required processes and their kinetics.

We identified potential targets for therapeutic interventions toward reversing latency. While transactivation events occur in a probabilistic fashion, exact quantification of the probability landscape of the Tat circuit enables prediction of the effects of possible circuit modifications on the overall expected behavior of the cell. We set out to identify specific reactions in the circuit whose alteration can tilt the probability landscape in such a way that the HIV latent reservoir can be depleted more effectively.

Our results showed that perturbing Tat acetylation/deacetylation and the Tat–TAR binding/unbinding can effectively eliminate latency or suppress the transactivation. To compare the effectiveness of manipulating these different reactions, we compared the mean intracellular Tat copy number in transactivated cells and the rate of latency transactivation at the same levels of change in the reaction rate. Our results suggest that both manipulations of Tat–TAR binding/unbinding and Tat acetylation/deacetylation can induce higher intracellular copy number of Tat protein than the wild-type Tat circuit in transactivated cells. However, the intracellular Tat copy number when manipulating Tat acetylation/deacetylation can be much higher than when manipulating Tat–TAR binding/unbinding. Due to the role of Tat in transactivating HIV replication, higher intracellular Tat may lead to higher production of HIV proteins, which can help immune cells to target and destroy infected cells. However, high intracellular Tat may also induce higher production of HIV virions, which can further lead to reseeding of the HIV latent reservoir and compromise the effect of reservoir depletion, unless potent ART is given that can suppress nearly all de novo viral infection (59). While the intracellular Tat copy number is higher with Tat acetylation/deacetylation manipulations than with Tat–TAR binding/unbinding manipulations, we found surprisingly that the latency transactivation rate with manipulations of Tat–TAR binding/unbinding is faster than with manipulation of Tat acetylation/deacetylation. However, the lower intracellular Tat protein level in Tat–TAR binding/unbinding manipulation may result in weaker immune response and cell killing rate in a shock-and-kill strategy. Therapies based on a combination of increase in Tat acetylation and Tat–TAR binding rates are likely to be more effective.

HDACis, such as vorinostat (60, 61), panobinostat (6), and romidepsin (62), have been tried as LRAs, though unsuccessful clinically (5, 7, 8, 62), due to their effects on opening chromatin structure and exposing HIV genes for active transcription. Since deacetylation of Tat is a critical step in the Tat circuit, deacetylase inhibitors can potentially affect Tat deacetylation (43, 63) and therefore directly interfere with Tat-mediated transactivation. Overall, to activate latently infected cells for shock and kill, our model suggests that if agents can be found to effectively and specifically increase Tat acetylation rate and Tat–TAR binding rate to the same level as HDAC inhibitors do for the deacetylation rate they might be more effective LRAs than HDACis.

In addition to shock and kill, our results can also help evaluate the strategy toward a functional cure. The ability of long-term viral suppression after termination of ART provides an important treatment strategy alternative to eradication. Our model showed that transactivation of the Tat circuit can be strongly suppressed by disrupting the Tat positive feedback loop through inhibition of Tat acetylation or Tat–TAR binding to the degree that the activated cells are forced back into a “deep latent” state with a diminished transactivation rate. According to our model, the positive feedback loop is essential for the bimodal phenotype and effective transactivation. Several recently discovered small molecules might be able to block the positive feedback. For example, didehydro-cortistatin A (dCA) can strongly inhibit Tat–TAR binding (64–66). Neomycin can also inhibit Tat–TAR binding and increase the unbinding rate (67). A synthetic oligonucleotide complementary to the HIV-1 TAR RNA apical stem–loop was also found to strongly inhibit Tat–TAR interaction (68). Our results showed that although complete removal of the positive feedback eliminates the distinct probability peak of transactivation from the probability landscape, the residual tail probability at large Tat copy number (SI Appendix, Fig. S1) may still support transactivation with low probability. Based on the probability landscapes, the model predicted the removal of positive feedback reduces the latent cell transactivation rate by roughly 10-fold. For a host with a large (∼10⁶) latent reservoir, a 10-fold reduction may not effectively suppress activation from latency. Hence, our model suggests one ought to be cautious about the effectiveness of “block and lock.”

Our study on the Tat circuit behavior in individual cells provides important insights into understanding the intracellular probabilistic control of HIV latency. However, there are many factors beyond the Tat circuit that are not currently incorporated in this model. First, since we do not model intercellular interactions, such as new infections and viral replication; the current model only explains the behavior of an HIV latent reservoir with identical Tat circuit parameters in an ART-suppressed patient. Second, the toggling of the ON and OFF state of HIV promoter may also play a role in controlling the latency–transactivation bimodality (12, 24). Without explicitly modeling the ON/OFF toggling of HIV promoter, the interpretations of our model are bound to assumptions that either the HIV promoter is constantly turned on, or the slow promoter ON/OFF toggling is implicitly encoded in the slow basal transcription rate. Third, our model does not incorporate the constraining factors in resting memory CD4⁺ T cells for maintaining the state of latency, which might be important since a large fraction of latently infected cells are resting memory CD4⁺ T cells (2, 69). Finally, the immune response against infected cells forms an additional layer of complexity for strategies such as shock and kill (70–72). These mechanisms all likely have important roles in the control of viral latency and transactivation. Incorporating these mechanisms in future modeling studies will lead to improved understanding of HIV latency and transactivation control.

Overall, our results showed that by studying the detailed intracellular transcriptional control of HIV latency and transactivation one can discover more effective therapeutic targets from the underlying reaction network for HIV latency reversal. This approach can also be used to explore alternative strategies for an HIV cure, such as a functional cure based on the block-and-lock strategy (66) that attempts to enforce a state of “deep latency.” The ACME method provides a powerful approach for accurately studying the probabilistic behavior of cell phenotypes controlled by the underlying stochastic gene regulatory networks.