Regularization-Free Strain Mapping in Three Dimensions, With Application to Cardiac Ultrasound

Abstract

Quantifying dynamic strain fields from time-resolved volumetric medical imaging and microscopy stacks is a pressing need for radiology and mechanobiology. A critical limitation of all existing techniques is regularization: because these volumetric images are inherently noisy, the current strain mapping techniques must impose either displacement regularization and smoothing that sacrifices spatial resolution, or material property assumptions that presuppose a material model, as in hyperelastic warping. Here, we present, validate, and apply the first three-dimensional (3D) method for estimating mechanical strain directly from raw 3D image stacks without either regularization or assumptions about material behavior. We apply the method to high-frequency ultrasound images of mouse hearts to diagnose myocardial infarction. We also apply the method to present the first ever in vivo quantification of elevated strain fields in the heart wall associated with the insertion of the chordae tendinae. The method shows promise for broad application to dynamic medical imaging modalities, including high-frequency ultrasound, tagged magnetic resonance imaging, and confocal fluorescence microscopy.

Introduction

Quantifying deformation from medical imaging stacks holds potential for improving diagnosis of pathologies in load-bearing and load-producing biologic tissues. For example, myocardial infarction leads to local changes in myocardial tissue stiffness and loss of heart function. However, quantifying these abnormalities for medical diagnosis is often impossible because of the limited precision and accuracy of the existing tools for estimating strain fields from medical imaging scans. State-of-the-art digital image correlation techniques, which match patterned features between pairs of images to estimate displacement fields over time, are accurate only when displacement fields are two dimensional (2D), with all displacement and deformation occurring in the plane of the original image [1–8]. Accuracy suffers when three-dimensional (3D) motion causes image features to move into or out of the imaging plane, as it occurs commonly with static medical imaging equipment [9–11]. As a consequence, 2D methods applied to 3D medical image stacks have limited clinical application.

Digital volume correlation (DVC) techniques can overcome this challenge by tracking displacement in 3D, but these, too, suffer from limitations on accuracy and precision. DVC techniques typically estimate displacement fields over time via a volumetric cross correlation (3D-XCOR) approach that maximizes the similarity between groups of voxels in initial “reference” imaging volumes and subsequent “deformed” imaging volumes. Strain fields calculated from the gradient of these estimated displacement fields suffer from the well-known challenge of taking numerical gradients of noisy data: numerical differentiation magnifies small errors in displacement tracking. This problem is exacerbated for DVC relative to 2D digital image correlation because modern imaging stacks typically have higher resolution within each imaging plane or “slice” than between slices. The existing techniques, therefore, have to impose regularization, either by smoothing or by making guesses about the mechanical properties of the tissue being imaged [4,6]. Even advanced regularization techniques, such as diffeomorphic smoothing [12,13], hyperelastic warping [14–16], or finite element based methods [8,17–19], have limitations. These either do not warp reference volumes when searching for their counterparts in deformed imaged volumes [12,13]; require imposition of strain compatibility upon averaged fields [7]; or require imposition of an assumed material model [8,13–16,19–21]. Overcoming all of these limitations currently requires post hoc regularization that tends to mask strain concentrations [6,8,22,23]. However, many of these limitations can be overcome using modern tools of computer vision [23].

We therefore developed an unconstrained 3D strain estimation algorithm for full volumetric data sets which reliably determines strains within tissue volumes without material assumptions or regularization. The method, which we term 3D “direct deformation estimation” (3D-DDE), estimates deformation gradient fields directly from a new warping function that maps targeted regions in the reference image volumes to their counterparts in deformed image volumes without consideration of displacement fields, analogous to an earlier 2D implementation [10].

To benchmark 3D-DDE, we compared it not only to standard 3D-XCOR, but also to a hybrid method that we term “3D-LSF.” As described in the supplemental methods which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection, 3D-LSF estimates strains from displacement fields estimated from Lucas–Kanade warping of reference image to the deformed image.

We began by validating 3D-DDE on volumetric images deformed in silico with deformation fields from exact solutions of continuum mechanics, including deformation fields that are difficult to analyze with current state-of-the-art techniques. We then demonstrated the utility of 3D-DDE on real world data by performing the first full thickness strain mapping of a mouse heart wall and showed spatial variations of strain associated with both anatomical features and myocardial infarction. 3D-DDE yielded superior accuracy, noise-insensitivity, and precision compared to the existing displacement-based methods and furthermore identified regions of tissue with high strain gradients. These features of 3D-DDE suggest promise for enabling quantitative diagnosis using dynamic and noninvasive technologies such as ultrasound.

Methods

Strain Mapping Methods.

3D-DDE strain mapping was performed using a custom code written in the MATLAB environment (The Mathworks, Natick, MA). As described in detail in the supplemental text which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection, strain mapping proceeded by first finding the spatially varying warping function W_3D that best maps a single region in the template volumetric image to a single region in a deformed volumetric image. For each search region i in the reference configuration, with local coordinates X⁽ⁱ⁾, vector of parameters p⁽ⁱ⁾ were fit by optimally warping, using a Newtonian Descent algorithm [24], to match voxel intensities of the template volume into the best fit of the deformed volume

$${\mathbf{W}}_{3D}^{(i)}({\mathbf{X}}^{(i)};{\mathbf{p}}^{(i)})={\mathbf{A}}^{(i)}({\mathbf{p}}^{(i)}){[{\mathbf{X}}^{(i)}1]}^{\mathrm{T}}$$ (1)

where ${\mathbf{A}}^{\left(i\right)}\left({\mathbf{p}}^{\left(i\right)}\right)$ is chosen to be an affine transformation with parameters ${\mathbf{p}}^{\left(i\right)}$

$${\mathbf{A}}^{(i)}({\mathbf{p}}^{(i)})=\left[\begin{array}{cccc}1+p_1^{(i)}& p_4^{(i)}& p_7^{(i)}& p_{10}^{(i)}\\ p_2^{(i)}& 1+p_5^{(i)}& p_8^{(i)}& p_{11}^{(i)}\\ p_3^{(i)}& p_6^{(i)}& 1+p_9^{(i)}& p_{12}^{(i)}\\ 0& 0& 0& 1\end{array}\right]$$ (2)

The warping function in Eq. (1) then returns deformed image coordinates x⁽ⁱ⁾

$${[{\mathbf{x}}^{(i)}1]}^{\mathrm{T}}={\mathbf{A}}^{(i)}({\mathbf{p}}^{(i)}){[{\mathbf{X}}^{(i)}1]}^{\mathrm{T}}$$ (3)

This specific form of the warping function was chosen to be analogous to the deformation gradient tensor so that it could be directly estimated during voxel intensity mapping. The deformation gradient tensor $\mathbf{F}$ is an affine transformation that relates the infinitesimal vector $d\mathbf{X}$ in a reference configuration to a corresponding infinitesimal vector $d\mathbf{x}$ in a deformed configuration, Eq. (3) is analogous to the equation for the deformation gradient tensor

$$d\mathbf{x}=\mathbf{F}d\mathbf{X}$$ (4)

Since they are analogous, $\mathbf{F}$ can be directly extracted from ${\mathbf{A}}^{\left(i\right)}\left({\mathbf{p}}^{\left(i\right)}\right)$ by ignoring the displacement parameters $p_{10}^{\left(i\right)}$, $p_{11}^{\left(i\right)}$, and $p_{12}^{\left(i\right)}$ and removing the final row

$${\mathbf{F}}_{3\mathrm{D}}^{(i)}=\left[\begin{array}{ccc}1+p_1^{(i)}& p_4^{(i)}& p_7^{(i)}\\ p_2^{(i)}& 1+p_5^{(i)}& p_8^{(i)}\\ p_3^{(i)}& p_6^{(i)}& 1+p_9^{(i)}\end{array}\right]$$ (5)

To compute a full deformation field, rather than a single measure of the deformation gradient tensor at a single location, the reference image is divided into multiple search regions. Considering multiple search regions across the reference image, each with a centroid Y⁽ⁱ⁾ in the coordinate system of the reference volumetric image and each at acquired at a time t_j, we obtain an expression for the full deformation field over space and time

$${\mathbf{F}}_{3\mathrm{D}}^{(i,j)}({\mathbf{Y}}^{(i)},t_j)=\left[\begin{array}{ccc}1+p_1^{(i,j)}& p_4^{(i,j)}& p_7^{(i,j)}\\ p_2^{(i,j)}& 1+p_5^{(i,j)}& p_8^{(i,j)}\\ p_3^{(i,j)}& p_6^{(i,j)}& 1+p_9^{(i,j)}\end{array}\right]$$ (6)

Similar to our prior work in two dimensions [10], the deformation field is then known by ${\mathbf{F}}_{3\mathrm{D}}^{(i,j)}$ without regularization, least squared estimation of the displacement field, or numerical derivatives of displacement estimates (Fig. 1, Supplemental Fig. S1, Supplemental Theory which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). Briefly, all strain measures can be derived from the deformation gradient tensor, including the Green–Lagrange strain tensor: ${\mathbf{E}}^{\left(\mathit{i},\mathit{j}\right)}\left({\mathbf{Y}}^{\left(i\right)},t_j\right)=\frac{1}{2}\left({\left({\mathbf{F}}_{3D}^{\left(i,j\right)}\left({\mathbf{Y}}^{\left(i\right)},t_j\right)\right)}^{\mathrm{T}}\left({\mathbf{F}}_{3D}^{\left(i,j\right)}\left({\mathbf{Y}}^{\left(i\right)},t_j\right)\right)-\mathbf{1}\right)$ in which 1 is the identity tensor [25].

Fig. 1.

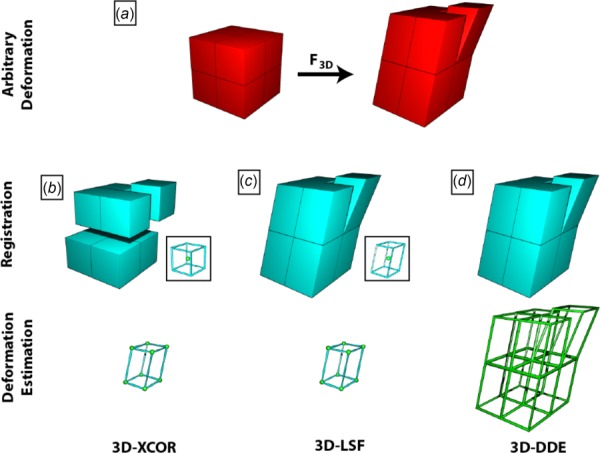
Schematic representation of how 3D-XCOR, 3D-LSF, and 3D-DDE calculate 3D deformation gradient tensors. (a) Representation of a volumetric image divided into eight volumes with original undeformed image (left) and deformed configuration (right). (b) 3D-XCOR estimates how each reference volume maps to an equal number of voxels in the deformed image. Considering the centroid of each region (spheres, inset and vertices of bottom), 3D-XCOR finds a best fit displacement. (c) The 3D-LSF method improves on 3D-XCOR by warping the reference regions before finding the best match in the deformed image. Like 3D-XCOR, it considers the displacements of the centroids of these regions when calculating deformation (inset and bottom row). (d) 3D-DDE accurately calculates the deformation of all eight regions independently (outlines, bottom row), directly from the warping function that maps the undeformed volumes to the deformed volumes.

We compared 3D-DDE to the previously established methods using computer-generated volumetric images. We provided these with texture by superimposing randomly placed three-dimensional Gaussian functions of varying intensity over the baseline intensity of the volumetric image. We warped these textured volumetric images using techniques described in Supplemental Methods which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection, and explored both the accuracy of the methods and their sensitivity to image noise.

Experimental Methods.

Ultrasound images of a beating heart were acquired in vivo from both healthy (n = 2) and infarcted (n = 2) adult male C57BL/6 wild-type mice using a high-frequency small animal ultrasound system (Vevo2100, FUJIFILM VisualSonics Inc., Toronto, ON, Canada). Prior to ultrasound imaging, each mouse was anesthetized with 3.0% isoflurane and room air at 1.5 L/min. After removing hair from the left ventral thorax using a depilatory cream, mice were positioned supine on a heat-modulated imaging stage (FUJIFILM VisualSonics Inc., Toronto, ON, Canada). Forelimb and hindlimb paws were secured to gold-plated stage electrodes to monitor electrocardiography (ECG) and respiration signals and to prevent unwanted motion. Ophthalmic ointment was applied to the eyes to prevent drying of the corneas. Throughout imaging, each mouse's body temperature was monitored closely using a rectal temperature probe and maintained between 34 and 37 °C. Isoflurane levels were adjusted around 2.0% to keep respiration rates above 50 breaths per minute and maintain a stable heart rate. The Purdue Animal Care and Use Committee approved all studies.

Both cardiac and respiratory gating were employed to acquire 4D cardiac ultrasound data using a previously established method [16,17]. To summarize the imaging method briefly, a series of spatially dependent 2D cine loops of the heart were acquired using a 40 MHz linear array ultrasound probe (MS550D) attached to a linearly translating step motor (3D acquisition motor). The transducer was oriented perpendicular to the base-apex axis of the heart to acquire cross-sectional views of the left ventricle.

A MATLAB script was then used to translate the transducer with a 180 μm step size starting from the apex to the base of the heart, acquiring cine loops at each sequential location and at a known Z-position. To minimize respiration artifacts, ultrasound data were only acquired in-between breaths by gating for respiration signal. At each spatial position, ECG-gated ultrasound images were sampled across several hundred cardiac cycles at successive 1 ms delays between R–R peaks. On average, a single 2D cineloop sampled at 1000 Hz took 25–30 s to acquire. The sampled images were then sorted in reference to the identified R-peaks to reconstruct a representative 2D cine loop of a beating heart. Spatially adjacent cine loops from known Z-positions were then imported into MATLAB and temporally matched to digitally reconstruct a volumetric mouse heart dataset. Bilinear interpolation was used to resample the ultrasound data from its native voxel resolution (40 μm × 90 μm × 193 μm; axial × lateral × elevational) to isotropic 60 μm voxels. The method was highly reproducible and no motion artifacts were observed. These preprocessed volumetric data were then used for the strain calculation methods.

In preparation for myocardial infarction induction surgery, the mice were ventilated via endotracheal intubation and connected to a small animal ventilator (SomnoSuite, Kent Scientific Inc., Litchfield, CT). The ventilator supplied air to the lungs with a target inspiratory pressure between 16 and 18 cm H₂O and a minimum peak-end expiratory pressure between 3 and 5 cm H₂O to prevent pneumothorax during surgery. The mice were subjected to a left mini-thoracotomy by making a small incision between the second and third ribs. Once the incision was made, a rib cage retractor was used to carefully expose the left ventricle without damaging the left lung. The pericardium was then dissected and excess pericardial fat removed to visualize the left anterior coronary artery. Once the coronary artery was clearly visualized, an 8-0 suture was looped around the artery, and the two ends of the suture were tightened to permanently occlude the vessel to induce ischemia. The rib cage and the skin were then sutured separately, and the mice remained connected to the ventilator until they regained their natural breathing pattern and were mobile. Buprenorphine (0.05–0.2 mg/kg) was administered subcutaneously prior to and periodically for 48 h after surgery. The mice were then allowed to recover for two weeks before ultrasound images of the remodeled heart were acquired.

Results

Comparison to State-of-the-Art Methods Showed That Three-Dimensional Direct Deformation Estimation Was More Accurate and Precise Than Displacement-Based Methods.

To test 3D-DDE in silico, we first resolved nonuniform strain fields arising in an artificial image volume from a spatially and temporally varying deformation gradient tensor, F, in an orthogonal Cartesian (X, Y, Z) frame defined relative to the reference image volume

$$\mathbf{F}\left(X,t\right)=\mathbf{I}+At{X}^2\mathbf{e}\otimes \mathbf{e}$$ (7)

where A is the controlled amplitude, time t ranged from 0 to 1, I is the second-order identity tensor, and e is a unit vector in the X-direction. This spatially quadratic field was chosen as a best-case scenario for competing XCOR methods because, under these conditions, XCOR's imposition of displacement compatibility on strain fields can converge to the exact strain fields [10]. When a random 3D texture was deformed according to Eq. (7) (see Supplemental Methods which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection), 3D-DDE was more accurate and more precise than both standard 3D-XCOR and displacement-based tracking (3D-LSF) for all parameter choices (Fig. 2). Although displacement-based approaches were just as accurate as 3D-DDE for uniform strain fields (see Supplemental Data which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection), 3D-DDE was superior for all cases involving strain gradients (Fig. 2, Supplemental Data which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection).

Fig. 2.

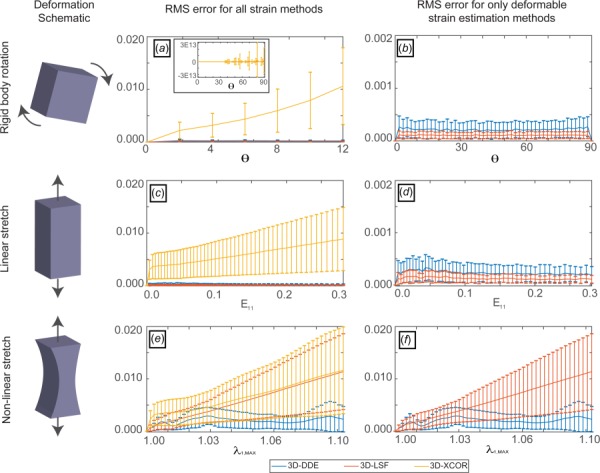
Accuracy and precision of 3D-DDE relative to other regularization-free strain mapping techniques. 3D-DDE was over an order of magnitude more accurate and substantially more precise than other methods for estimating spatially varying strain fields in artificial images. (a) For a 3D rigid body rotated an angle Θ in one plane, 3D-XCOR failed to correctly predict the strain field, with error that was nearly unbounded for large rotation angles (inset). (b) 3D-LSF and 3D-DDE had negligible errors for rigid body rotations. (c) RMS error for a uniaxial stretch E₁₁ scaled with strain for 3D-XCOR. (d) 3D-LSF and 3D-DDE had negligible error for linear, uniform straining. (e) RMS error increased with stretch level λ for both 3D-XCOR and 3D-LSF in a 3D body undergoing nonlinear stretch given by Eq. (1). (f) However, 3D-DDE again estimated strains with minimal error for these nonlinear, nonuniform strain fields. Note that panels (b), (d), and (f) contain data from panels (a), (c), and (e), respectively, zoomed in to focus on results comparing only 3D-LSF and 3D-XCOR.

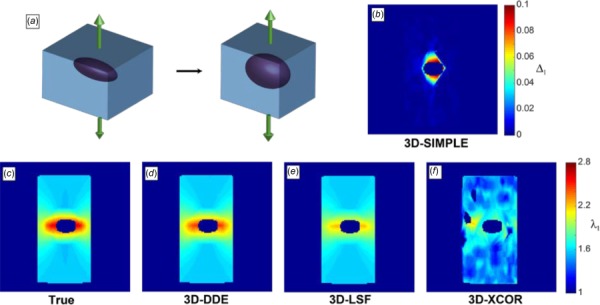
Three-Dimensional Direct Deformation Estimation Accurately Estimated Strains in Representative Three-Dimensional Strain Fields.

Next, to benchmark 3D-DDE against other methods on representative data for which the true strain fields were known, displacement fields of an Eshelby inclusion were used to nonlinearly warp a volumetric image in silico. Using closed form solutions for a full field 3D Eshelby inclusion, true values of deformation were known a priori at every location in time and space for this problem (Fig. 3(a)) (see Supplemental Methods which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection) [26]. 3D-DDE was accurate and precise, with 3D-LSF and 3D-XCOR each performing successively worse (Figs. 3(c)–3(f), Supplemental Video 1 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). The challenge of distinguishing tracking errors from true regions of elevated strain was overcome through 3D-SIMPLE (Supplemental Methods which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection), which identified the regions of high strain gradient and elevated strain surrounding the inclusion (Fig. 3(b), Supplemental Video 1 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection).

Fig. 3.

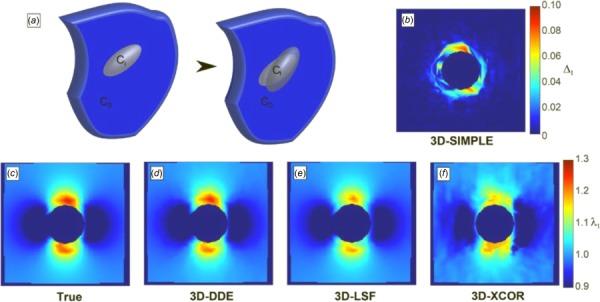
Principal stretch ratio estimations around image volumes of a contracting Eshelby inclusion, generated in silico. (a) Schematic of the Eshelby problem. (b) 3D-SIMPLE detected strain elevation surrounding the inclusion. (c) True values of the stretch ratio in the z-direction matched (d) the 3D-DDE estimated values, while (e) 3D-LSF and (f) 3D-XCOR estimates were successively worse.

Three-Dimensional Direct Deformation Estimation and 3D-SIMPLE Identified and Characterized Singular Strain Fields.

To benchmark 3D-DDE against other methods on a more complicated strain field for which the exact solutions were known, displacement fields surrounding a penny-shaped crack were used to nonlinearly warp a volumetric image in silico following the procedures used for the Eshelby solution (Fig. 3(a), Supplemental Methods which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection) [27]. During loading, the crack, initially ellipsoidal due to a preload, extended into a more spherical ellipsoid. Again, 3D-DDE identified the input strain field faithfully, with 3D-LSF and 3D-XCOR performing successively worse (Figs. 4(c)–4(f), Supplemental Video 2 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). 3D-SIMPLE identified regions of elevated strain and high strain gradient, including both the singular crack tips and the displacing fracture surfaces (Fig. 4(b), Supplemental Video which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection 2 ).

Fig. 4.

Principal stretch ratios for image volumes of a preloaded, penny-shaped crack generated in silico. (a) Schematic, (b) 3D-SIMPLE detected the developing crack, ((c) and (d)) 3D-DDE estimates matched the actual fields, while 3D-LSF (e) and 3D-XCOR (f) were successively less accurate.

In Vivo Ultrasound of a Beating Murine Heart Revealed the Mechanics of the Deforming Papillary Muscles.

3D-DDE identified strain fields from the noisy in vivo volumetric imaging data acquired by high-frequency ultrasound imaging of a murine heart. Volumes assembled from 2D ultrasound slices were synchronized to an ECG signal using postprocessing techniques [28], allowing for the estimation of full 3D strain fields (Fig. 5, Supplemental Videos 3–9 which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection, top row). Taking end diastole as a reference configuration, the papillary muscle was manually segmented from the heart. In the supplemental videos which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection, the maximum principal strain was overlaid atop the 3D volume images. Large Green–Lagrange strains evolved throughout systole, gradually relaxing to the reference state during diastolic filling (Figs. 5(c)–5(g), Supplemental Video 3 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). These features were not visible using prior techniques such as 3D-XCOR (Supplemental Video 10 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection, first column). Note that the tensile strains shown correspond to radial strains in the myocardium.

Fig. 5.

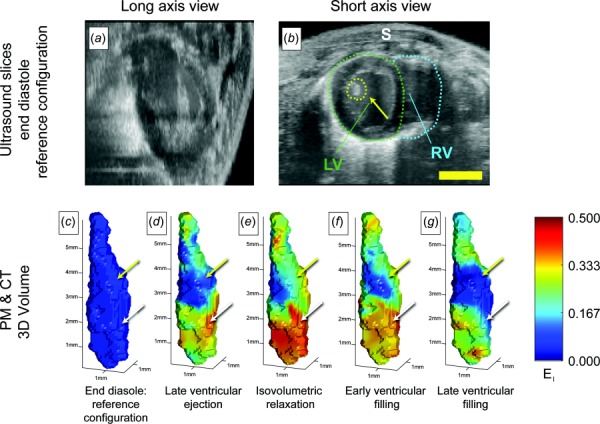
Peak principal strain fields estimated from high frequency ultrasound imaging of a beating mouse heart, showing spatial variations associated with the structure of the heart. ((a) and (b)) Volumetric ultrasound data were acquired over several cycles of a beating mouse heart, then analyzed using 3D-DDE to detect spatial variations in Green–Lagrange strain fields. (c)–(g) These strain fields were segmented to reveal 3D strains in the left ventricle papillary muscle and to track how the myocardial first principal component of the 3D strain fields varied near the insertions of the chordae tendinae. (c) End diastole was taken as a reference configuration. (d) The heart developed strains in the left ventricle as it contracted and blood was ejected from the heart, while the papillary muscles remained unstretched. (e) As the heart cycle reached peak systole and entered isovolumetric relaxation, principal strains in the heart wall reached maximum levels on the order of 0.5. (f) As the heart relaxed during early ventricular filling, strain levels reduced, approaching baseline levels after (g) late ventricular filling. Throughout the cardiac cycle, strains in the papillary muscles (upper arrows yellow online) were lower than those in the surrounding myocardium in the apex (white, lower arrows). LV: left ventricle, RV: right ventricle, and S: skin. Scale bars: 3 mm.

The papillary muscles, which assist in the opening and closing of the atrioventricular valves, underwent high strains (arrows, Fig. 5). However, the chordae tendineae, which connect the papillary muscle to the atrioventricular valves, showed much lower straining over the course of a cardiac cycle. In the vicinity of the chordae tendineae to papillary muscle insertion site, a substantial change in strain was noted, with a transition from the highest to the lowest tensile principal strains evident (Fig. 4, Supplemental Video 3 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection).

In Vivo Ultrasound of Post Myocardial Infarction Hearts Revealed Dramatic Differences in Wall Strain When Compared to Controls.

3D-DDE provided a robust quantification of differences between healthy and 2 week post-myocardial infarction (PMI) murine hearts. Again combining 2D slices synchronized to an ECG signal, we estimated full 3D field strain fields in healthy control and PMI murine hearts. Regions of myocardial infarction were estimated from a combination on MR images (not shown) and prior knowledge of where the infarction was induced.

Radial strains, represented by the peak principal strains, were dramatically reduced in magnitude in the infarcted region of the heart wall in PMI hearts; these regions of attenuated strain were not evident in control hearts (Figs. 6(d)–6(g), Supplementary Videos 4 and 10, which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). Peak 3D principal Green–Lagrange strain was attenuated by approximately 90% in these regions during systole compared to control hearts (Figs. 6(h) and 6(i), Supplementary Videos 4 and 10 which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). Average strains were also lower in PMI hearts. In addition to this absolute measure of stiffening from infarction, a relative measure was evident, with strains in the infarct regions disproportionately lower than those in the surrounding healthy tissue.

Fig. 6.

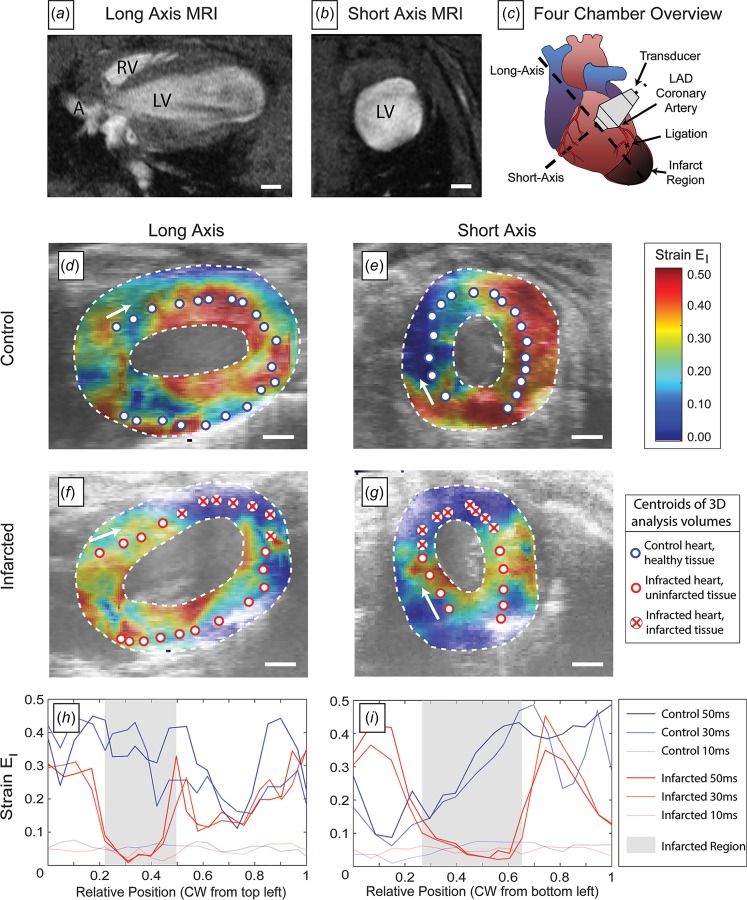
Strain patterns in control versus postmyocardial infarction hearts, demonstrating dramatically reduced strains in infarcted heart tissue. ((a) and (b)) Magnetic resonance images of mouse hearts showing the anatomical planes studied using 3D-DDE of ultrasound imaging volumes. (c) A schematic of the heart demonstrating the orientation of the short and long axis as well as the location of the infarction. ((d) and (e)) Peak principal strain at a specific timepoint in control hearts. ((f) and (g)) Peak principal strain at this same timepoint in hearts following myocardial infarction, showing distinctly different strain patterns in both the long and short axis views. (h) Strain as a function of position along the midline of the long-axis view of the heart, showing strain attenuation in the infarcted tissue. Line corresponds to different times; position is measured from the base of the arrow in panel (f). (i) Strain as a function of position along the midline of the short-axis view of the heart, showing strain attenuation in the infarcted tissue, and elevated strain in the tissue surrounding the infarct region. Lines again correspond to different times; position is measured from the base of the arrow in panel (g). Scale bars: 1 mm.

These features were consistent in two control and two infarcted hearts (Supplementary Videos 4 and 10, which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection) and were consistent when the analysis was imitated with a reference configuration at isovolumetric relaxation rather than end diastole (Supplementary Video 11, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). These features were evident when hearts were analyzed with prior techniques such as 3D-LSF, however, not pronounced and not well-defined above noise (Supplementary Videos 12 and 13, which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). Finally, when analyzed with 3D-XCOR, features were not evident above noise (Supplementary Videos 14 and 15, which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection).

Discussion

Three-dimensional direct deformation estimation provided accurate and precise local estimates of complex, nonuniform strain fields. The algorithm was insensitive to noise compared not only to 3D-XCOR but also to a hybrid method that used displacement fields estimated using optimal warping of reference volumes (3D-LSF). Although other technologies could be tailored through regularization, smoothing, or imposition of a hyperelastic constitutive law, 3D-DDE provided accuracy and precision without such without ad hoc constraints or post hoc regularization. The method outperformed state-of-the-art techniques when strain concentrations and gradients existed.

The key features of 3D-DDE that enabled this are unique from other cross-correlation techniques: (1) optimal 3D warping of undeformed images prior to cross-correlation using the established Lucas–Kanade algorithm [24] and (2) direct calculation of the deformation gradient without taking numerical gradients of a displacement field. The latter factor enabled robust identification of strain concentrations and strain gradients. 3D-SIMPLE, a metric of the error from displacement-based approaches associated with artificially enforcing compatibility, enabled the first fully automated detection of strain concentrations in 3D volumetric images, both at the poles of a contracting ellipsoidal inclusion and in the vicinity of a stressed penny-shaped crack.

Out-of-plane motion and deformation are challenges for all 2D and 3D imaging modalities. In 2D, such motion and deformation is impossible to track in the absence of additional information such as a rigorous model of behavior or images from additional cameras. In 3D, the reduced resolution in the out-of-plane direction leads to reduced resolution in displacements in that direction, and in general, leads to increased error in strain estimation when gradients of these displacement fields are taken to estimate strains [3,4,7,8,12–23,29,30]. By eliminating the need for these numerical derivatives, the current method eliminates this latter source of error.

The noise-insensitivity of 3D-DDE enabled analysis of a sequence of noisy, volumetric, high-frequency ultrasound images of a beating mouse heart, resolving for the first time the local strain patterns during the cardiac cycle without resorting to post hoc regularization schemes. The peak principal strains, which in general corresponded to radial strains fields, were on the order of those reported in a recent meta study [31].

The current study presented the first analysis of strain fields associated with the insertion of the chordae tendineae into the papillary muscle of the myocardial wall was measured. This is a compelling application because no other technology exists for assessing risk of chordae tendinae rupture, which is usually lethal [32]. The low principal strains values of the chordae tendineae obtained in vivo from the 3D-DDE method yielded similar results to a previous ex vivo study, which reported a maximum strain of 4% in a porcine chordae tendineae under physiological loading [33]. Because the chordae tendineae are more than an order of magnitude stiffer than papillary muscle [20,30], this insertion site is susceptible to elevated strains. Indeed, the most common site of papillary muscle rupture observed clinically in the setting of acute myocardial infarction is the site where we observed a substantial transition from highest to lowest strain [34].

Three-dimensional direct deformation estimation also quantified differences between healthy and infarcted myocardium, with infarcted scar regions presenting significantly attenuated strain magnitudes relative to healthy controls. These attenuated strain fields indicated that the local remodeling following myocardial infraction [22–25] produced scar tissue that was significantly stiffer than either surrounding healthy tissue or tissue in healthy controls: the noncontractile scar tissue was relatively resistant to extension as the surrounding healthy tissue contracted. Interestingly, these areas of very low strain were abutted by regions of elevated strain compared to controls. This might indicate an adaptive, compliant interface; in other tissue interfaces, such compliant zones have been shown to relieve stress concentrations between healthy and infarcted tissues (cf., see Refs. [28] and [35]). Standard techniques such as 3D-XCOR could not resolve these features. We note that the choice of reference configuration would affect the magnitudes of strains but not the qualitative trends, as the deformation gradients calculated using any reference configuration over the cardiac cycle can be calculated as a linear transformation of those calculated here [36]. The current study demonstrates that responses to myocardial infarction can be quantified noninvasively and support the use of high-frequency ultrasound as a diagnostic tool.

Results provided the first glimpse into the mechanical structure of key connections between stiff and compliant tissues in the heart. Although no gold standard estimation of strain fields exists for comparison, those measured by 3D-DDE are qualitatively as expected. High strains in the ventricular wall correlated with ventricular ejection, and relatively small strains were observed in the stiff chordae tendineae. These results were expected due to the high stiffness mismatch of the chordae tendineae and the more compliant myocardium.

More broadly, results showed that, as in other severe material mismatches in physiology and nature (e.g., see Refs. [26], [27], and [31]), mechanisms appear to be in place to limit elevations of strain at the insertion of chordae tendineae into the papillary muscle in the wall of the heart. The absence of local strain concentrations at the points of insertion, where gross wall strains change substantially, suggests a future target for mechanically based diagnosis of structural pathologies related to valve function. This exercise demonstrated that our technique could readily resolve small structural differences effectively.

Although the results demonstrated dynamic and regularization-free 3D strain analysis of tissue structures in vivo, the method has several shortcomings that bear mention. Acquisition of volumetric images remains challenging. We found a kernel size of 15 × 15 × 15 voxels to be the minimum for reliable strain estimation and the sampling rate of current commercial 3D ultrasound probes to be inadequate for identifying subtle features within a strain field. We overcame this limitation by taking advantage of the periodicity and reproducibility of a heart beat to construct 3D volumes from 2D slices, yielding a much higher resolution volumetric time series of composite heartbeats. Our experiments required specialized apparatus not typically available in a clinical ultrasound suite, although others have overcome this limitation by focusing on nearly quasi-static images (e.g., see Ref. [37]). As in cine MRI, the 4D ultrasound technique used ECG gating to compile a representative cardiac cycle at each spatial location. Although this has proved effective in the previous work [38], this does come with the assumption that the heart has a normal rhythm throughout the imaging procedure. In a cohort of healthy hearts, we expect the kinematics of the myocardial wall and papillary muscles to be conserved across multiple animals. Although our sample size here was small, the qualitative features observed in the treatment group were similar. However, further study is needed to determine how and whether the postinfarct changes observed in this small dataset vary depending on coronary anatomy, postinfarction remodeling phase, and degree of the infarct.

Direct deformation estimation is a gradient descent-like algorithm and is, therefore, susceptible to all associated shortcomings. These algorithms require an initial guess of parameters. An initial guess is in the vicinity of a local minimum rather than the global minimum that can cause the optimization to return an incorrect solution or fail to converge. This has implications for both spatial and temporal resolution. In terms of spatial resolution, intensity features should be on the order of but smaller than the search region size. We found that the smallest reliable search region size is about 1000 total voxels, corresponding to a 10 × 10 × 10 voxel search region. If features are too large, the solution will be overdefined and the optimization will not converge. However, this can be alleviated by downsampling. In terms of temporal resolution, the changes between successive volumetric images must be sufficiently small that the optimal parameters do not change from the parameters of the previous time increment—used as an initial parameter guess—do not end up in the vicinity of a local minimum. In practice, we found that displacements between successive volumetric images cannot be much larger than 20% of the search region size in any dimension. For deformation, we found that exceeding 10% deformation between frames also fails to reliably find global minima and accurate solutions. These issues could be alleviated with techniques such as preregistration; however, this was not explored in the current manuscript.

Three-Dimensional direct deformation estimation holds promise beyond purely biomedical applications. The potential to identify cracks and strain concentrations is of potential value in applications such as earthquake fault analysis with ground-penetrating radar (e.g., see Ref. [39]) and inspection of aerospace composites [34,40,41]. The method is also of potential value to efforts to extend current 2D strain analysis of brain motion to from working with image slices to fully volumetric data sets, where a major unmet challenge is to identify the origins of strain concentrations near attachment points (e.g., see Refs. [11] and [42–55]). In all such applications, we believe that the accuracy and precision of 3D-DDE and the reliability check afforded by 3D-SIMPLE will improve our ability to interpret the distribution of strains on the interior of biological and engineered structures.

Funding Data

• American Heart Association (14SDG18220010).

• National Heart, Lung, and Blood Institute (R01HL109505).

• National Institute of Biomedical Imaging and Bioengineering (U01EB016422).

• National Institute of Diabetes and Digestive and Kidney Diseases (DK101001-01).

• National Science Foundation (CMMI-1548571).

Author Contributions

J.J.B., R.B.P., S.T., and G.M.G. developed the strain analysis tools. A.S., F.D., A.K., and C.J.G. designed the ultrasound data acquisition methods and animal studies. J.J.B., R.A.R., R.B.P., S.T., and G.M.G. performed the testing of the strain analysis methods. J.J.B., S.T., and G.M.G. wrote the manuscript. All authors edited the manuscript.

Nomenclature

$A$ =

controlled amplitude

${\mathbf{A}}^{\left(i\right)}$ =

affine transformation function

$d\mathbf{x}$ =

infinitesimal vector of coordinates in deformed configuration

$d\mathbf{X}$ =

infinitesimal vector of coordinates in reference configuration

$\mathbf{e}$ =

unit vector in the X-direction

$\mathbf{F}$ =

deformation gradient tensor

${\mathbf{F}}_{3\mathrm{D}}^{\left(i\right)}$ =

three-dimensional deformation gradient tensor for the ith search region

${\mathbf{F}}_{3\mathrm{D}}^{(i,j)}$ =

three-dimensional deformation gradient tensor for the ith search region at time j

$\mathbf{I}$ =

identity tensor

p⁽ⁱ⁾ =

vector of parameters in the ith search region

t_j =

time j

W_3D =

three-dimensional warping function

X⁽ⁱ⁾ =

vectorized local coordinates in the ith search region

Y⁽ⁱ⁾ =

centroid in the coordinate system of the reference volumetric image

Abbreviations

DVC =

digital volume correlation

ECG =

electrocardiography

2D =

two-dimensional

3D =

three-dimensional

3D-DDE =

three-dimensional direct deformation estimation

3D-LSF =

three-dimensional least squared fit

3D-XCOR =

three-dimensional normalized cross correlation