Abstract
Although the underlying mechanisms of pelvic organ prolapse (POP) remain unknown, disruption of elastic fiber metabolism within the vaginal wall extracellular matrix (ECM) has been highly implicated. It has been hypothesized that elastic fiber fragmentation correlates to decreased structural integrity and increased risk of prolapse; however, the mechanisms by which elastic fiber damage may contribute to prolapse are poorly understood. Furthermore, the role of elastic fibers in normal vaginal wall mechanics has not been fully ascertained. Therefore, the objective of this study is to investigate the contribution of elastic fibers to murine vaginal wall mechanics. Vaginal tissue from C57BL/6 female mice was mechanically tested using biaxial extension–inflation protocols before and after intraluminal exposure to elastase. Elastase digestion induced marked changes in the vaginal geometry, and biaxial mechanical properties, suggesting that elastic fibers may play an important role in vaginal wall mechanical function. Additionally, a constitutive model that considered two diagonal families of collagen fibers with a slight preference toward the circumferential direction described the data reasonably well before and after digestion. The present findings may be important to determine the underlying structural and mechanical mechanisms of POP, and aid in the development of growth and remodeling models for improved assessment and prediction of changes in structure–function relationships with prolapse development.
Keywords: vaginal wall, women's health, mechanical testing, pelvic floor disorders, elastic fibers
1. Introduction
The descent of the female pelvic organs due to the loss of structural support, known as pelvic organ prolapse (POP), is a prevalent disorder. Each year, an estimated 225,000–280,000 women undergo surgery for POP in the U. S. with another 120,000 requiring reoperations [1]. POP corrective surgery costs the U.S. more than $1 billion per year [2], a number that is likely to increase in the next 10 years as the demographics shift to an increasingly elderly and obese population. Additionally, patients typically develop POP between the ages of 50 and 70. Therefore, without adequate treatment, many women could potentially be dealing with issues such as incomplete bladder emptying, defecatory dysfunction, sexual dysfunction, discomfort, poor self-image, limitations in physical activity, and a reduced quality of living [3] in the later portion of their lives [1].
Progress toward understanding the underlying mechanisms of POP has been limited, in part, due to a lack of knowledge of the basic science of the vaginal wall and the surrounding pelvic support structures [4]. In particular, limited information is available on the microstructural composition and structure–function relationships within the vaginal wall. Four distinct layers comprise the vaginal wall: the epithelium, subepithelium, muscularis, and adventitia [5–7]. The epithelium is the innermost layer and consists of stratified squamous epithelial cells [7]. The outermost layer, the adventitia, is composed of loose connective tissue. The subepithelium and muscularis, which together form a fibromuscular layer between the epithelium and adventitia, provide most of the vaginal wall support, both longitudinal and central [7]. The muscularis contains an inner, circumferentially oriented and an outer, longitudinally oriented sheet of smooth muscle [8] and provides active support to the vagina [5]. The subepithelium is a dense connective tissue layer composed primarily of collagen and elastic fibers, and provides a large degree of passive mechanical support [5,6]. Thus, collagen and elastic fibers are two of the main load-bearing constituents in the vaginal wall. Their quality and quantity are dependent upon a precise equilibrium between synthesis, maturation, and degradation, subjecting the tissue to a constant remodeling [7]. Further, studies in other soft tissues suggest that the two constituents are functionally linked, and that a loss of elastic fibers decreases collagen fiber undulation and subsequently alters tissue stiffness [9–11]. The homeostatic maintenance of these constituents is essential for normal pelvic support; however, the organization and orientation and interactions between collagen and elastin within the vaginal wall remain unknown.
Pelvic support is maintained by the levator ani muscles, as well as the vagina and its connective tissue attachments. While levator ani injury is well established as a potential mechanism of POP [12,13], a large proportion of prolapse cases exhibit no evidence of muscle injury [14]. Furthermore, weakness or failure of the vaginal wall and certain ligaments of the uterus has been associated with POP, specifically, the cardinal and uterosacral ligaments, which are heavily involved in providing level-I support that is often absent in cases of prolapse [4,15–19]. Tissue weakness arises following a disruption in matrix protein metabolism, such as altered collagen and elastic fiber turnover [20–22]. Disruption of elastic fiber metabolism within the vaginal wall extracellular matrix (ECM) has been highly implicated in POP pathogenesis [23–28]. Several studies have demonstrated that elastopathic knockout mice (i.e., mice missing genes crucial for production and maintenance of elastic fibers) readily develop prolapse [24,29–31]. Additionally, increased levels of matrix metalloprotease activity have been observed in the vaginal wall of prolapsed mice [30–33]. Compromised elastic fiber integrity may lead to an increase in matrix metalloprotease activity within the vaginal wall extracellular matrix, which may increase the degradation of collagen fibers and compromise vaginal wall mechanical integrity [25]. In addition to the aforementioned biochemical role, elastic fibers may also contribute to vaginal wall mechanical integrity by providing tissue resilience and recoil as observed in other soft tissues [25,26,34]. Hence, the combined effect of elastic fiber alteration and collagen turnover may affect the biomechanical properties of the vaginal wall and contribute to the development of POP [25]. The role of elastic fibers in normal vaginal wall mechanics, however, is not fully understood [24,25,27,35].
Elastic fibers are composed of elastin and fibrillin microfibrils, and are major components of several soft tissues including skin, lungs, and vasculature [36–38]. Elastin is the primary component of mature elastic fibers (90% elastin), while the microfibrils are primarily located within the outer mantle [39]. Elastin enables tissues to store energy and deform under physiologic loads, and subsequently use that energy to recoil back to a reference state. Loss of elastin has been implicated in a variety of soft tissue diseases including vascular disease [37], altered lung function [40], skin pathologies [41,42], and premature cervical remodeling [43–45] in addition to POP. Hence, elastase treatment has commonly been used to degrade elastin in soft tissues in order to quantify its mechanical and structural role including studies in arteries, tendons, ligaments, intervertebral disks, esophagus, and lungs [9,10,46–53]. To date, these studies have yielded important insights regarding the role of elastin in tissue recoil, resistance to deformation in the low-stretch regime or “toe-region,” as well as its potential role in stabilizing collagen fiber undulation cf. [9,10,36–38,47]. Few studies to date, however, have quantified the effect of elastase digestion on tissue undergoing biaxial loading [9,54–57], whereas biaxial mechanical tests—particularly inflation–extension tests are important as they preserve the tissue's native geometry and mimic physiologic loading conditions [58,59]. The effect of elastase digestion on the vagina, however, is currently unknown. Therefore, the objective of this study is to assess the contribution of elastic fibers to the biaxial mechanical properties of the murine vaginal wall via elastase digestion.
2. Methods
2.1. Specimen Preparation.
All animal care and handling protocols were approved by the Tulane University Institutional Animal Care and Use Committee. Female C57BL/6 mice (4–6 months old) were monitored in accordance with Institutional Animal Care and Use Committee guidelines, sacrificed while in estrus, and stored in a freezer at −20 °C. Note that Rubod et al. identified no significant effect of freezing on vaginal wall passive mechanical behavior [60]. Following one freeze-thaw cycle, the reproductive tract was excised, and the vaginal tissue was separated from the rest of the reproductive system by a cut made at the border between the cervix and vagina. Upon excision from the body cavity, the vagina retracted (shortened). Thus, the extent of this retraction was estimated by measuring the in situ to ex vivo change in length between stain lines placed during dissection [61]. This measurement will henceforth be referred to as the estimated physiologic (i.e., in vivo) axial stretch ().
2.2. Mechanical Testing.
To assess biaxial mechanical properties while maintaining native tissue geometry, inflation–extension testing was performed [62,63]. Geometrically intact specimens were cannulated in Hank's Balanced Saline Solution (HBSS) within a pressure myograph system (Danish Myo Technology, Aarhus, Denmark). Tissues were secured to the ridged cannulas using two 6-0 silk sutures per cannula. The unloaded length was identified by discerning the point at which the tissue began to buckle and was then recorded using a hand-held digital micrometer [62]. Vaginal samples frequently collapsed at 0 mmHg; hence, the outer diameter at 4 mmHg was selected as the unloaded diameter and was recorded using an Eclipse TS100 video-microscope (Nikon, Melville, NY) [62]. As described previously [62], the axial force was zeroed while the tissue was in the unloaded configuration, and the tissue length was adjusted based on the estimated physiologic axial stretch. Samples underwent five cycles of pressure–diameter (P–d) preconditioning (P = 0–25 mmHg) while axial length was held constant at the estimated physiologic axial stretch, and five cycles of force–length (F–l) preconditioning ( = 4% below to 4% above the estimated physiologic axial stretch), while pressure was held constant at 8 mmHg (≈1/3 of the max pressure [61]). Since the vagina recoiled following extraction, previously published methods were utilized to identify and then test the tissue at the physiologic axial length [63,64]. From the P–d tests, the physiologic axial stretch was estimated (control: 1.14 ± 0.01; treatment: 1.15 ± 0.01) by identifying the axial stretch at which the transducer-measured force remained constant for increasing values of intraluminal pressure (Fig. 1(a)) [61,63]. To theoretically confirm the experimentally estimated physiologic axial stretch as described by van Loon [65], F–l tests ( = 4% below to 4% above the estimated physiologic axial stretch) at four different pressures (2, 8, 17, and 25 mmHg) were performed (Fig. 1(b)) [61,63]. The axial stretch ratio at which the force–axial stretch response for all or most of the four pressures intersect is the confirmed physiologic (i.e., in vivo) axial stretch (). Following another five cycles of P–d conditioning, the tissue was allowed to equilibrate for 15 min at 8 mmHg at the physiologic axial stretch. Specimens then underwent P–d tests (P = 0–25 mmHg) at the confirmed physiologic axial stretch, and at 4% above and below. Required elastase concentration and treatment duration were determined experimentally via pilot studies, and treatment with 15 U of porcine pancreatic elastase (Worthington Biochemical, Lakewood, NJ) for 45 min was found to induce the largest change in mechanical properties consistently and repeatedly. Longer incubation times resulted in tissue damage and leakage during pressurization. Thus, following mechanical testing of control tissues, specimens (n = 8) were intraluminally treated with 15 U of elastase for 45 min [9]. Post-treatment, tissues were flushed with HBSS; the reference configuration was established by re-estimating the unloaded length and the physiologic axial stretch, and the preconditioning and mechanical testing protocols were repeated.
Fig. 1.

Estimation of the physiologic, in vivo axial stretch ratio for representative sample #4 in Table 1: (a) the nearly constant transducer-measured axial force occurs at the estimated physiologic (in vivo) axial stretch ratio and (b) the point of intersection of force–length (extension) tests performed at constant, multiple luminal pressures further confirms the estimated in vivo axial stretch ratio. The dashed vertical line represents the estimated in vivo axial stretch.
2.3. Mechanical Test Data Analysis.
P–d and F–l test data were taken from the last loading cycle of the tests and processed by averaging over intervals of pressure and axial stretch, respectively, using a custom matlab code (MathWorks, Natick, MA) [61]. Vaginal wall-average circumferential and axial Cauchy stresses were then calculated, respectively, as [66]
| (1) |
| (2) |
where intraluminal pressure, , and the transducer-measured force, , are measured on-line; deformed outer radius, is calculated from on-line measurements of the outer diameter; and deformed inner radius, is obtained by assuming conservation of volume (i.e., incompressibility)
| (3) |
| (4) |
where and are the undeformed and deformed outer radii, respectively. and are the undeformed and deformed inner radii, respectively. is calculated from the unloaded wall thickness determined during opening angle experiments (Sec. 2.5). and are the unloaded and loaded axial lengths, respectively, and is the mean volume. Circumferential (), axial (), and radial () stretches were calculated as follows:
| (5) |
| (6) |
| (7) |
where and represent the deformed and undeformed midwall (average) radii, respectively. Following the approach of Le et al. [67], vaginal tissue average compliance was computed as the change in diameter divided by the corresponding change in luminal pressure. This was computed at pressure values of 2.5, 5, 10, 15, and 20 mmHg pre- and postdigestion.
2.4. Constitutive Modeling: Two Fiber-Family Holzapfel–Gasser–Ogden Model.
The use of hyperelastic theory in modeling of soft tissues has been instrumental to the elucidation of structure–function relationships in healthy and diseased states [9,54,68]. Particularly, microstructurally motivated strain energy functions have been insightful, as they allow for the delineation of the unique roles of structural ECM components—elastic and collagen fibers. Hence, after a pilot study, the two fiber-family Holzapfel–Gasser–Ogden (HGO) strain energy function was selected [69,70]
| (8) |
The first term is the neo-Hookean function for the isotropic ground substance (refers to the noncollagenous substances such as: glycoproteins, proteoglycans, glycosaminoglycans, and amorphous elastin), and the second term quantifies the behavior of two symmetric, diagonally oriented families of collagen fibers with similar model properties (i.e., ). is the shear modulus of the ground substance when isolated in the reference configuration, is a modulus-like material parameter, and is a dimensionless parameter. and are related to the collagen fiber stiffening in the small and large strain regimes, respectively [71]. The strain energy function was implemented in a transversely isotropic framework for [72]
| (9) |
where is the Cauchy stress, is the Lagrange multiplier, , and are the first and fourth invariants of the right Cauchy-Green strain tensor , respectively. is the left Cauchy-Green strain tensor, and is the deformation gradient tensor. is the preferred direction of the collagen fiber family in the reference configuration, and is the average orientation of the family of collagen fibers from the long axis of the vagina, hence, . The theoretical expression for the luminal pressure is obtained via the integration of the radial component of the linear momentum equilibrium equation while enforcing radial boundary condition at the inner radius (i.e., ), assuming zero pressure at the outer radius [63,66]. The optimal objective function chosen [73] to be minimized provides a good fit compromise between low and high strains [63]
| (10) |
where the superscripts and denote theoretical and experimental, respectively. is the total number of data points per sample.
To evaluate changes induced by elastase digestion, data from all three P–d tests performed were simultaneously fitted for the control and elastase groups, respectively. Data from P–d tests conducted at 4% below the estimated physiologic axial stretch, however, were frequently negative in both the control and elastase groups indicating buckling [54]. Pilot modeling results indicated the HGO model did not yield acceptable descriptive capability when data for the P–d tests conducted at 4% above were included, due, in part, to the relatively high axial force values observed (140 mN) (Supplemental Fig. 1, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). From these observations, one may infer that tests at ± 4% above the estimated in vivo axial stretch might be outside of the physiologic range [74]. Hence, constitutive modeling was used to describe vaginal behavior from the P–d test conducted at the estimated in vivo stretch only, before and after digestion.
2.5. Parameter Fitting and Sensitivity Analysis.
Within a custom Python program, the differential evolution algorithm for global optimization was employed to minimize the objective function (i.e., Eq. (10)) [75]. Differential evolution is a stochastic optimizer which samples the objective function at multiple, randomly chosen points within the domain resulting from the parameter bounds provided to create an initial solution population. Mutation and recombination are performed to arrive at the best solution [76]. The algorithm was run multiple times to ensure repeatability of optimized values, thereby ascertaining the uniqueness of parameter values obtained. Lower and upper bounds for the model parameters were set at values that yielded best-fit parameter values. The following constraints were placed on the parameters: , , and . Along with the coefficient of determination , the root-mean-square error (RMSE) was used to assess the goodness-of-fit of the model
| (11) |
To assess the model's sensitivity to its parameters and the associated treatment-induced changes, local sensitivity analysis was performed about the optimized average model parameter values by computing nondimensional local sensitivity indices [77] as follows:
| (12) |
where , and are the components of the Cauchy stress tensor.
2.6. Opening Angle Measurement.
Since each sample was treated as a control, then with elastase and tested postdigestion, opening angle experiments could be performed only on the treated samples following mechanical assessment. Hence, additional samples from C57BL/6 mice at estrus were used for opening angle control test. In order to ensure that the lack of treatment was the only variable, these control samples were also subjected to the same extension–inflation test protocol [62]. For the elastase treated samples, of the eight samples tested mechanically postdigestion, opening angle tests were performed on six, the other two were used for pilot study relating to microstructural analysis. Following inflation–extension testing, a ring ( thick) was excised from the center of the tissue, at the point at which the outer diameter was tracked. Following a 30-min equilibration in HBSS, the ring was imaged with a Moticam 580 microscope camera (Motic, Richmond, BC, Canada). A radial cut was introduced to the anterior section of the ring, and following another 30-min equilibration, the near-zero stress state was imaged. The opening angle (a measure of residual stress) was measured from the midpoint of the inner wall to the outer edges on either side of the cut using the angle tool in ImageJ (NIH, Bethesda, MD) [66,78].
2.7. Constituent Area Fraction.
Specimens were fixed in 10% formalin and embedded in paraffin. Sections (thickness 4 ) were cut circumferentially and then stained with Masson's trichrome (MTC), Picrosirius red (PSR), and Hart's elastin stains to detect smooth muscle, collagen, and elastin, respectively (for each stain: n = 6 for control, n = 5 for elastase-treated). All images were obtained using an Olympus BX51 microscope with a DP27 camera (Olympus, Tokyo, Japan). Area fraction calculations did not incorporate values from the epithelium, which is considered to be a non load-bearing layer [66]. To quantify the ratio of type-I to type-III collagen before and after elastase digestion, PSR images were analyzed using a custom matlab code (Mathworks) that calculates the area fraction by determining the ratio of red and orange (type-I), and green and yellow (type-III) pixels to the total pixel count [68,79]. MTC images were analyzed using Image J's color deconvolution plugin to isolate specific colors based on pixel values, resulting in composite red (smooth muscle) and blue (collagen) images [78,80]. Next, gnu image manipulation program was used to calculate total pixels and area fractions of each constituent, utilizing a grayscale threshold to eliminate residual staining and normalize pixel values. Similarly, in analysis of Hart's stained samples, a representative elastic fiber was selected. Then using gnu image manipulation programs select-by-color tool, all pixels of similar values were selected. The ratio of these stained pixels to total pixel count in the ring was computed to be the area fraction of elastic fibers.
2.8. Statistical Analyses.
To evaluate the effect of elastase treatment on the geometry of the vaginal tissues, Student's t-tests were performed on unloaded geometrical parameters: outer diameter (paired), and length (paired), which were measured during the mechanical tests, and thickness (unpaired), which was measured during opening angle experiment. Similarly, an unpaired Student's t-test was performed on opening angle values to evaluate treatment effect on residual strain. Paired Student's t-tests were performed on the estimated circumferential and axial physiologic (in vivo) stretches. To assess the treatment's impact on the mechanical contribution of the extracellular matrix (ECM) components and on their organization, paired Student's t-tests were performed on optimized model parameters and on the average compliance values. To assess histological changes, pre- and post-treatment constituent area fractions were compared via unpaired Student's t-tests. All statistical analyses were performed in R [81]. Statistical significance level was set at , and statistical trend at . Results are presented as mean ± standard error of the mean (SEM).
3. Results
3.1. Experimental Findings From Biaxial Mechanical Tests.
Intraluminal exposure to elastase for 45 min induced marked changes in tissue geometry. A trend toward significant increase () in the unloaded outer diameter ( to ) was observed postdigestion. After treatment, the unloaded thickness exhibited statistical trend () toward decrease ( to ). While the opening angle increased ( to ), it exhibited neither statistical significance nor trend (). While no statistically significant change () was detected in the estimated in vivo (i.e., physiologic) circumferential stretch ratio (), the in vivo axial stretch ratio () exhibited statistical trend () toward a significant increase postdigestion (Table 1).
Table 1.
Optimized parameter values for the HGO model with measures of goodness-of-fit for murine vaginal samples (paired) pre- and postelastase digestion
| Sample | (kPa) | (kPa) | (deg) | RMSE | ||||
|---|---|---|---|---|---|---|---|---|
| Control | ||||||||
| Sample #1 | 2.51 | 0.28 | 19 | 54.3 | 0.98 | 0.10 | 1.13 | 1.21 |
| Sample #2 | 2.11 | 0.22 | 48 | 54.9 | 0.97 | 0.15 | 1.10 | 1.15 |
| Sample #3 | 0.81 | 0.66 | 55 | 55.1 | 0.99 | 0.10 | 1.08 | 1.13 |
| Sample #4 | 1.90 | 0.12 | 40 | 54.0 | 0.98 | 0.16 | 1.13 | 1.14 |
| Sample #5 | 4.73 | 0.01 | 359 | 56.1 | 0.91 | 0.18 | 1.04 | 1.12 |
| Sample #6 | 3.06 | 5.28 | 110 | 56.1 | 0.98 | 0.10 | 1.02 | 1.11 |
| Sample #7 | 5.45 | 0.01 | 162 | 54.3 | 0.96 | 0.16 | 1.06 | 1.14 |
| Sample #8 | 2.63 | 0.36 | 73 | 55.0 | 0.98 | 0.13 | 1.07 | 1.12 |
| Mean | 2.90 | 0.87 | 108 | 55.0 | 0.97 | 0.13 | 1.08 | 1.14 |
| SEM | 0.54 | 0.63 | 39 | 0.3 | 0.01 | 0.01 | 0.01 | 0.01 |
| Treatment | ||||||||
| Sample #1 | 1.17 | 0.02 | 129 | 56.4 | 0.97 | 0.12 | 1.06 | 1.20 |
| Sample #2 | 1.10 | 1.04 | 93 | 56.5 | 0.98 | 0.11 | 1.05 | 1.15 |
| Sample #3 | 0.28 | 2.88 | 108 | 57.5 | 0.99 | 0.11 | 1.03 | 1.15 |
| Sample #4 | 0.91 | 0.02 | 107 | 56.5 | 0.92 | 0.22 | 1.09 | 1.17 |
| Sample #5 | 5.59 | 0.09 | 253 | 56.3 | 0.93 | 0.16 | 1.03 | 1.12 |
| Sample #6 | 3.16 | 0.65 | 122 | 55.6 | 0.98 | 0.11 | 1.05 | 1.11 |
| Sample #7 | 5.65 | 0.003 | 105 | 53.8 | 0.93 | 0.19 | 1.10 | 1.16 |
| Sample #8 | 2.69 | 0.18 | 55 | 53.8 | 0.97 | 0.15 | 1.11 | 1.12 |
| Mean | 2.57 | 0.61 | 121 | 55.8 | 0.96 | 0.15 | 1.06 | 1.15 |
| SEM | 0.74 | 0.35 | 20 | 0.5 | 0.01 | 0.01 | 0.01 | 0.01 |
3.2. Computational Findings From Biaxial Mechanical Tests.
The HGO model exhibited reasonable fits to the biaxial experimental data (Fig. 2). The coefficients of determination () values, were and pre- and postdigestion, respectively. The best-fit model parameters are listed in Table 1. While changes in the optimized pre- and post-treatment model parameters were not statistically significant, the average ground substance shear modulus () and collagen-associated, modulus-like () parameters decreased post-treatment by 19% and 28%, respectively (Table 1). However, the average collagen-associated, dimensionless parameter () increased post-treatment by 60% (Table 1). Post-treatment, the mean orientation/alignment angle () of the collagen fiber families was nearly unchanged (2% increase) and indicated a bias toward the circumferential direction (pre: 55.0±0.3 deg and post: , as measured from the longitudinal axis) (Table 1).
Fig. 2.

Fits of the HGO model to experimental (pre- and post-treatment with elastase) data (, n = 8, paired): (a) intraluminal pressure versus outer diameter: a rightward shift was observed post-treatment, indicating dilatation of the vagina, (b) wall-averaged circumferential Cauchy stress versus circumferential stretch ratio: a rise was observed post-treatment, indicating increased structural stiffness circumferentially, (c) wall-averaged axial Cauchy stress versus circumferential stretch ratio, (d) wall-averaged axial Cauchy stress versus axial stretch ratio, (e) the transducer-measured axial force versus pressure, which remained nearly constant with increasing pressure, and (f) the sum of transducer-measured force and force due to increasing intraluminal pressure versus pressure: the increased separation at higher pressures is attributable to dilated lumen (increased inner radius) of the elastase-treated vagina
Pre- and postdigestion, local sensitivity plots show that the biaxial mechanical response of the tissue was mostly influenced by and (Fig. 3). Postdigestion, biaxially, the influence of both parameters increased the most, relative to control (Fig. 3).
Fig. 3.

Holzapfel–Gasser–Ogden model sensitivity in the (a) circumferential and (b) axial directions, pre-elastase (solid lines) and postelastase (dashed lines) treatment. Pre- and post-treatment, the model was most sensitive to the collagen-associated nondimensional parameter— and the alignment angle-. Relative to control, post-treatment, the influence of the two parameters increased the most in both directions. Sensitivity indices were computed using optimized model parameters for averaged data (n = 8/group, for control and elastase).
Post-treatment, a statistically significant decrease in average compliance was observed at 5 and 10 mmHg; however, average compliance was not statistically significant outside of this pressure range (Fig. 4). Finally, having found the HGO model to have reasonable descriptive capability for the modeled P–d test data, its predictive capability [66] was assessed by fitting the model to the F–l test data at constant pressures (Supplemental Fig. 2, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection).
Fig. 4.

Vaginal tissue average compliance as a function of intraluminal pressure, data = . Statistically significant (*p < 0.05) decrease was observed at 5 and 10 mmHg.
3.3. Constituent Area Fraction.
No statistically significant changes in type-I and type-III collagen area fractions were identified for samples pre- (45%, 29%) and post- (48%, 26%) elastase treatment (Figs. 5(a)–5(d)). Smooth muscle area fractions of 7.7% and 6.8% were identified pre- and post-treatment (Figs. 5(e)–5(h)). A statistically significant (p < 0.03) lower elastic fiber area fraction was observed after treatment (before: 2.4%, after: 0.9%). Additionally, stained tissue ring images revealed observably fewer elastic fibers in the elastase-digested samples, along with an apparent decrease in organization and orientation (Figs. 5(i)–5(l)), and Supplemental Figs. 3(a)–3(b)), which are available under the “Supplemental Data” tab for this paper on the ASME Digital Collection.
Fig. 5.
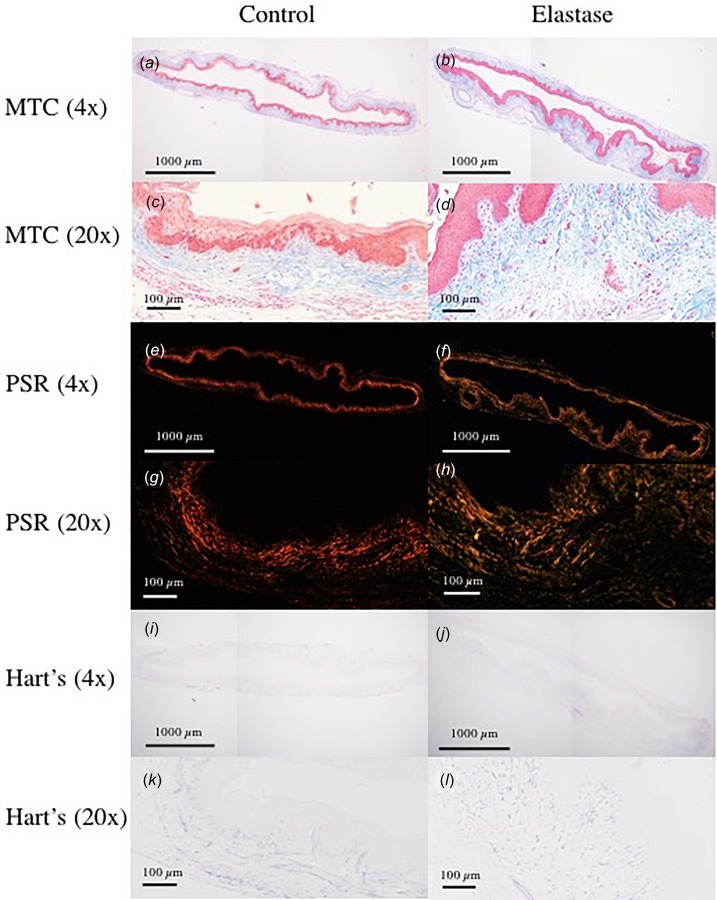
Histological section samples stained with: (a)–(d) PSR,(e)–(h) MTC, and (i)–(l) Hart's elastin stain. Elastic fiber area fraction exhibited statistically significant decrease post-treatment. For all stains, area fraction analysis was performed using images acquired at 4× objective. In the 20× and 40× (Supplemental Fig. 3, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection) objective images of Hart's stained section, a decrease in population and organization of elastic fibers is observable.
4. Discussion
In this study, intraluminal exposure of murine vaginal tissue to elastase for 45 min induced significant changes in the geometry and biaxial mechanical behavior of the murine vaginal wall, similar to those seen in murine arteries [9,54]. As expected, albeit not statistically significant, elastase treatment resulted in decreased tissue thickness, which is consistent with the observed treatment-induced loss in tissue constituents, change in structure, or both (Figs. 5(i)–5(l)). Post-treatment, the increase in the unloaded outer diameter (Table 1) and the corresponding rightward shift in the pressure–diameter curve (Fig. 2(a)) indicated treatment-induced dilatation of the vaginal caliber. In addition, the post-treatment rise in the circumferential stress-stretch curve (Fig. 2(b)) was indicative of a treatment-induced decrease in vaginal distensibility. Similar trends have been observed in murine, canine, and rabbit carotid arteries [9,10,54,83], as well as, in human arteries [82], and hamster lungs [83], which demonstrated a marked loss of distensibility in the low-strain regime following digestion. Loss of distensibility herein may stem from the substantial dilation of the vaginal caliber following digestion, which then results in earlier engagement of collagen fibers at lower pressures (i.e., loss of crimp/undulation) similar to postulated mechanisms in arteries, e.g., [9,10,82]. Specifically, elastic fibers in vasculature are thought to be deposited and assembled within the prenatal period, and then stretched as the tissue grows during postnatal development [84]. Thus, the elastic fibers are taut and engaged at low physiologic loads, while the collagen remains highly undulated; therefore, contributing to the gradual stiffening behavior observed in most soft tissues as the collagen fibers are engaged at higher stretches [61]. Loss of elastin is thus assumed to decrease the initial undulation of collagen fibers, resulting in loss of compliance in the low-strain regime. Supporting this, Ferruzzi et al. identified a significant loss of collagen fiber undulation following the removal of elastic fibers in murine carotid arteries, consistent with a marked increase in stiffness [9]. Also, in porcine aorta, the loss of elastin evidenced by multiphoton images resulted in rapid recruitment of collagen fibers [57]. Similarly, Grant et al. observed significant reduction of collagen crimp in rat tail tendons following elastase treatment [46]; and lengthening of porcine medial collateral ligament postelastase treatment resulted from loss of prestress and stabilization of collagen crimp by elastic fibers [47]. While the collagen fiber undulation of the vagina before and after elastase digestion remains to be imaged, the experimental and modeling findings herein support published studies suggesting that elastin and collagen fibers may interact via stabilizing collagen undulation, thus contributing to vaginal compliance in the low-strain regime. Specifically, the post-treatment changes observed in the sensitivity plots of the HGO model support the postulated earlier recruitment of collagen fibers due to loss of crimp. The loss of crimp was best indicated by the rise in the influence of postdigestion (i.e., earlier stiffening) (Figs. 3(a) and 3(b)) observed herein.
The microstructurally motivated model used herein identified decreases in model parameters— and . These parameters are associated with the low strain regime/toe region, where elastic fibers are postulated to dominate the mechanical response of soft-tissues [71]. The decrease in these parameters may indicate loss of elastic fiber and reduced collagen crimp as supported by studies in arteries [9,54]. Note, however, that the decrease in the parameter observed in this study were moderate compared to those observed in studies in the murine carotid artery and aorta [9,54]. This may be due, in part, to differences in elastic fiber architecture between arteries and the vaginal wall. In arteries, the elastic fibers are organized in the medial layer in an interconnecting fenestrated network and compose ∼70% of the arterial wall [85–87]. Detailed organizational information on vaginal wall microstructure is currently lacking [4]; however, the elastin composition is significantly lower (∼2%). Further, vaginal elastic fibers are regarded to be randomly oriented in the subepithelium along with collagen fibers, and the adventitia contains circular bundles of elastic fibers [4]. Therefore, the lack of an interconnected elastic fiber network in the vagina may contribute to the discrepancies in tissue behavior between the vagina and arteries with elastase digestion. Future work is necessary to rigorously quantify vaginal elastic fiber volume, organization, and interactions with collagen fibers, in order to further delineate structure–function relationships in the vagina.
Additionally, model parameters, and , increased following elastase digestion. These parameters are associated with the high strain regime/linear region, where collagen fibers are fully recruited and dominate the mechanical response of the soft tissues [71]. Increases in the and parameters were also observed in prior studies in vasculature, which utilized the four-fiber family HGO model [9,54]. Further, the increase in in this study supports the hypothesis that postdigestion, collagen fibers are engaged earlier. Noting, however, that tensile modulus decreased following elastase digestion in human annulus fibrosis [88] and rat lung [50]. Additionally, a reduction in stress was reported in the human supraspinatus tendon [89] and rat tail tendons demonstrated no changes in linear modulus [46]. These differences may be attributable to variations in mechanical testing techniques (e.g., uniaxial tensile test versus extension–inflation test) or differences in tissue reference configurations. However, they may also indicate that the structural interactions between elastin and collagen fibers differ across soft tissues and merit further investigation. Additionally, the sensitivity analysis identified an increase in the influence of model parameters and (Fig. 3), which may be attributed to the postulated decreased collagen fiber undulation—evidenced by the earlier rise in their influence at lower stretch values, and corresponding increased stiffness of the overall tissue due to elastic fiber fragmentation. The increased sensitivity to collagen fiber alignment angle, (Fig. 3) exhibited by the model may be attributed, in part, to the 2% increase in following elastase digestion (Table 1).
Although the changes in mechanical behavior postelastase digestion observed herein show similar trends to that of vasculature, they differ from previous findings in vaginal tissue. For example, Rahn et al.'s stress–strain plot of the nonprolapsed fibulin-5 knockout mice revealed an opposite shift relative to that of the nonpregnant wild-type control. Statistically significant differences in estimated biomechanical properties (failure load, maximum stress, distension, and strain), however, were not observed in the mechanical behavior of the elastase-digested samples reported therein [25]. However, among other differences in methods, variation in mechanical testing protocols, as well as in elastic fiber removal strategy may account for this discrepancy. For example, Rahn et al. conducted uniaxial tests in which rings of midvaginal tissue were mounted between stainless steel wires, as opposed to the biaxial extension–inflation protocols on geometrically intact whole vaginal tissue performed herein [25]. Additionally, the use of a genetically compromised mouse model of elastic fiber deficiency versus elastase digestion in healthy tissues may contribute to variations in mechanical response.
In addition to computational approach, opening angle experiments are also capable of providing potential insight into fiber undulation and elastic–collagen fiber interactions. Opening angles are thought to arise from residual stress within a tissue, due to difference in deposition stretches of elastic and collagen fibers. In arteries, elastic fibers are produced only during the prenatal period. Thus, elastic fibers undergo extensive deformations during developmental growth and are in tension while in the in vivo state. Collagen, on the other hand, undergoes continuous turnover throughout aging and thus exists at a lower prestretch in vivo than elastic fibers. The differences in undulation between these two load-bearing constituents lead to residual stress within a tissue [84], which is often measured via opening angle experiments. Opening angles have been shown to significantly decrease postelastase digestion in murine carotid arteries [9,10]; however, in this study, we report the opposite for vaginal tissue. Contrary to vasculature, the reproductive tract is suggested to be uniquely posed to produce elastic fibers postdevelopment [7,90]. Continuous turnover of elastic fibers may impact their prestretch and thus the overall residual stress within the vaginal wall. Characteristics of elastic fiber turnover within the vaginal wall ECM, however, remain unknown. Thus, there is a pressing need to identify elastic fiber deposition time course and prestretch, as well as the effect of these characteristics on collagen fiber undulation and organization [27,84]. Understanding these dynamics of elastic fiber metabolism within the vaginal wall may be crucial to understanding the etiology of POP. Additionally, it may provide important insights into the effectiveness of surgical intervention strategies, particularly in understanding the microstructural environment in which meshes are implanted and how tissue composition may affect tissue remodeling postsurgical intervention [91,92].
This study is not without limitations; we modeled murine vaginal wall mechanics using a two-dimensional membrane approach. While this is an important first step in understanding vaginal wall structure–function relationships, a more comprehensive three-dimensional approach representing the vagina as a thick-walled vessel and incorporating the residual stress throughout the wall is required for a more robust representation of vaginal wall mechanics and future work of developing growth and remodeling models [93]. Additionally, while the HGO model utilized herein reasonably described the P–d test data, the model did not robustly predict the F–l test data at constant pressures (Supplemental Fig. 2, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). This is not unexpected as the model parameters were fitted to P–d data. However, this brings up an important issue that while the model yielded reasonable descriptive capability for the P–d tests, the predictive capability with regard to the F–l tests is lacking and additional efforts are necessary to refine the functional form of the constitutive model to appropriately represent the mechanical behavior of the vagina. Regardless, the study herein provides an initial step toward developing microstructurally motivated models to describe vaginal multiaxial behavior. Rynkevic et al. regarded the comfort zone of operation of the ovine vagina as within 10–20% of the total elongation experienced during uniaxial load to failure test [74]. Considering this and our observations from the tests performed herein at 4% above and below the estimated physiologic axial stretch, tests performed within 1–2% range of the estimated physiologic axial stretch might be more physiologically relevant. Additionally, the elastase concentration and incubation time were selected following a pilot study to delineate the treatment, which decreased mechanical properties while maintaining consistent and repeatable testing conditions. Noticeably from the imaged stained sections, while a statistically significant decrease in elastin area fraction was observed, some elastin components remain in the tissue following digestion; thus, it is not completely removed from the tissue.
5. Conclusion
This study investigated the role of elastic fibers in murine vaginal wall mechanics using an experimental methodology, which mimics physiologic loading conditions and preserves the vagina's idealized cylindrical geometry. Elastase digestion induced marked changes in biaxial mechanical response, suggesting that elastic fibers may play an important role in vaginal wall mechanical function. Modeling results suggest that a constitutive model considering two diagonal families of collagen fibers reasonably describes biaxial vaginal wall mechanical response. Furthermore, our results suggest that elastic–collagen fiber interactions may be important for vaginal mechanical homeostasis. The present findings may help to understand the underlying mechanisms of POP and aid in the development of growth and remodeling models for improved assessment and prediction of changes in structure–function relationships with prolapse development and progression.
Supplementary Material
Acknowledgment
The authors would like to thank Steve Abramowitch for thoughtful discussion.
Contributor Information
Akinjide R. Akintunde, Department of Biomedical Engineering, , Lindy Boggs Center Suite 500, , Tulane University, , New Orleans, LA 70118 , e-mail: aakintun@tulane.edu
Kathryn M. Robison, Mem. ASME , Department of Biomedical Engineering, , Lindy Boggs Center Suite 500, , Tulane University, , New Orleans, LA 70118 , e-mail: krobison@tulane.edu
Daniel J. Capone, Department of Biomedical Engineering, , Lindy Boggs Center Suite 500, , Tulane University, , New Orleans, LA 70118 , e-mail: dcapone@tulane.edu
Laurephile Desrosiers, Department of Female Pelvic Medicine , and Reconstructive Surgery, , UQ Ochsner Clinical School, , 1514 Jefferson Highway, , New Orleans, LA 70121 , e-mail: laurephile.desrosiers@ochsner.org.
Leise R. Knoepp, Department of Female Pelvic Medicine , and Reconstructive Surgery, , UQ Ochsner Clinical School, , 1514 Jefferson Highway, , New Orleans, LA 70121 , e-mail: lknoepp@ochsner.org
Kristin S. Miller, Mem. ASME , Department of Biomedical Engineering, , Lindy Boggs Center Suite 500, , Tulane University, , New Orleans, LA 70118 , e-mail: kmille11@tulane.edu.
Funding Data
Division of Civil, Mechanical, and Manufacturing Innovation (Early CAREER Development Award CMMI-1751050, Funder ID. 10.13039/100000147).
National Institute of General Medical Sciences (P20GM103629, Funder ID. 10.13039/100000057).
Tulane University (Newcomb College Institute Faculty Grant, Funder ID. 10.13039/100007875)
References
- [1]. DeLancey, J. O. , 2005, “ The Hidden Epidemic of Pelvic Floor Dysfunction: Achievable Goals for Improved Prevention and Treatment,” Am. J. Obstet. Gynecol., 192(5), pp. 1488–1495. 10.1016/j.ajog.2005.02.028 [DOI] [PubMed] [Google Scholar]
- [2]. Subak, L. L. , Waetjen, L. E. , van den Eeden, S. , Thom, D. H. , Vittinghoff, E. , and Brown, J. S. , 2001, “ Cost of Pelvic Organ Prolapse Surgery in the United States,” Obstet. Gynecol., 98(4), pp. 646–651. 10.1016/S0029-7844(01)01472-7 [DOI] [PubMed] [Google Scholar]
- [3]. Pizarro-Berdichevsky, J. , Clifton, M. M. , and Goldman, H. B. , 2015, “ Evaluation and Management of Pelvic Organ Prolapse in Elderly Women,” Clin. Geriatr. Med., 31(4), pp. 507–521. 10.1016/j.cger.2015.06.008 [DOI] [PubMed] [Google Scholar]
- [4]. Baah-Dwomoh, A. , McGuire, J. , Tan, T. , and De Vita, R. , 2016, “ Mechanical Properties of Female Reproductive Organs and Supporting Connective Tissues: A Review of the Current State of Knowledge,” ASME Appl. Mech. Rev., 68(6), p. 060801. 10.1115/1.4034442 [DOI] [Google Scholar]
- [5]. Abramowitch, S. D. , Feola, A. , Jallah, Z. , and Moalli, P. A. , 2009, “ Tissue Mechanics, Animal Models, and Pelvic Organ Prolapse: A Review,” Eur. J. Obstetr. Gynecol., 144, pp. S146–S158. 10.1016/j.ejogrb.2009.02.022 [DOI] [PubMed] [Google Scholar]
- [6]. Alperin, A. M. , and Moalli, A. P. , 2006, “ Remodeling of Vaginal Connective Tissue in Patients With Prolapse,” Curr. Opin. Obstetr. Gynecol., 18(5), pp. 544–550. 10.1097/01.gco.0000242958.25244.ff [DOI] [PubMed] [Google Scholar]
- [7]. Kerkhof, M. H. , Hendriks, L. , and Brölmann, H. A. , 2009, “ Changes in Connective Tissue in Patients With Pelvic Organ Prolapse—A Review of the Current Literature,” Int. Urogynecol. J. Pelvic. Floor Dysfunct., 20(4), pp. 461–474. 10.1007/s00192-008-0737-1 [DOI] [PubMed] [Google Scholar]
- [8]. Skoczylas, L. C. , Jallah, Z. , Sugino, Y. , Stein, S. E. , Feola, A. , Yoshimura, N. , and Moalli, P. , 2013, “ Regional Differences in Rat Vaginal Smooth Muscle Contractility and Morphology,” Reprod. Sci., 20(4), pp. 382–390. 10.1177/1933719112472733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Ferruzzi, J. , Collins, M. J. , Yeh, A. T. , and Humphrey, J. D. , 2011, “ Mechanical Assessment of Elastin Integrity in Fibrillin-1-Deficient Carotid Arteries: Implications for Marfan Syndrome,” Cardiovasc. Res., 92(2), pp. 287–295. 10.1093/cvr/cvr195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Fonck, E. , Prod'hom, G. , Roy, S. , Augsburger, L. , Rüfenacht, D. A. , and Stergiopulos, N. , 2007, “ Effect of Elastin Degradation on Carotid Wall Mechanics as Assessed by a Constituent-Based Biomechanical Model,” Am. J. Physiol. Heart Circ. Physiol., 292(6), pp. H2754–H2763. 10.1152/ajpheart.01108.2006 [DOI] [PubMed] [Google Scholar]
- [11]. Henninger, H. B. , Underwood, C. J. , Romney, S. J. , Davis, G. L. , and Weiss, J. A. , 2013, “ Effect of Elastin Digestion on the Quasi‐Static Tensile Response of Medial Collateral Ligament,” J. Orthop. Res., 31(8), pp. 1226–1233. 10.1002/jor.22352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. DeLancey, J. O. , and Starr, R. A. , 1990, “ Histology of the Connection Between the Vagina and Levator Ani Muscles. Implications for Urinary Tract Function,” J. Reprod. Med., 35(8), pp. 765–771.https://www.ncbi.nlm.nih.gov/pubmed/2213737 [PubMed] [Google Scholar]
- [13]. Tracy, P. V. , DeLancey, J. O. , and Ashton-Miller, J. A. , 2016, “ A Geometric Capacity-Demand Analysis of Maternal Levator Muscle Stretch Required for Vaginal Delivery,” ASME J. Biomech. Eng., 138(2), p. 021001. 10.1115/1.4032424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. DeLancey, J. O. , Morgan, D. M. , Fenner, D. E. , Kearney, R. , Guire, K. , Miller, J. M. , Hussain, H. , Umek, W. , Hsu, Y. , and Ashton-Miller, J. A. , 2007, “ Comparison of Levator Ani Muscle Defects and Function in Women With and Without Pelvic Organ Prolapse,” Obstet. Gynecol., 109(2), pp. 295–302. 10.1097/01.AOG.0000250901.57095.ba [DOI] [PubMed] [Google Scholar]
- [15]. Miklos, J. R. , Moore, R. D. , and Kohli, N. , 2002, “ Laparoscopic Surgery for Pelvic Support Defects,” Curr. Opin. Obstetr. Gynecol., 14(4), pp. 387–395. 10.1097/00001703-200208000-00005 [DOI] [PubMed] [Google Scholar]
- [16]. DeLancey, J. , 1992, “ Anatomic Aspects of Vaginal Eversion After Hysterectomy,” Am. J. Obstetr. Gynecol., 166(6), pp. 1717–1724. 10.1016/0002-9378(92)91562-O [DOI] [PubMed] [Google Scholar]
- [17]. Becker, W. R. , and De Vita, R. , 2015, “ Biaxial Mechanical Properties of Swine Uterosacral and Cardinal Ligaments,” Biomech. Model. Mechanobiol., 14(3), pp. 549–560. 10.1007/s10237-014-0621-5 [DOI] [PubMed] [Google Scholar]
- [18]. Tan, T. , Cholewa, N. , Case, S. , and De Vita, R. , 2016, “ Micro-Structural and Biaxial Creep Properties of the Swine Uterosacral–Cardinal Ligament Complex,” J. Biomed. Eng. Soc., 44(11), pp. 3225–3237.https://link.springer.com/article/10.1007%2Fs10439-016-1661-z [DOI] [PubMed] [Google Scholar]
- [19]. Baah-Dwomoh, A. , and De Vita, R. , 2017, “ Effects of Repeated Biaxial Loads on the Creep Properties of Cardinal Ligaments,” J. Mech. Behav. Biomed. Mater., 74, pp. 128–141. 10.1016/j.jmbbm.2017.05.038 [DOI] [PubMed] [Google Scholar]
- [20]. Rivaux, G. , Rubod, C. , Dedet, B. , Brieu, M. , Gabriel, B. , De Landscheere, L. , Devos, P. , Delmas, V. , and Cosson, M. , 2011, “ Biomechanical Characterisation of Uterine Ligaments. Implications for the Pelvic Floor,” Pelvi-Perineologie, 6(2), pp. 67–74. 10.1007/s11608-010-0348-4 [DOI] [Google Scholar]
- [21]. Rivaux, G. , Rubod, C. , Dedet, B. , Brieu, M. , Gabriel, B. , and Cosson, M. , 2013, “ Comparative Analysis of Pelvic Ligaments: A Biomechanics Study,” Int. Urogynecol. J., 24(1), pp. 135–139. 10.1007/s00192-012-1861-5 [DOI] [PubMed] [Google Scholar]
- [22]. Rubod, C. , Brieu, M. , Cosson, M. , Rivaux, G. , Clay, J.-C. , de Landsheere, L. , and Gabriel, B. , 2012, “ Biomechanical Properties of Human Pelvic Organs,” Urology, 79(4), pp. 968.e917–968.e922. 10.1016/j.urology.2011.11.010 [DOI] [PubMed] [Google Scholar]
- [23]. Kerkhof, M. H. , Ruiz-Zapata, A. M. , Bril, H. , Bleeker, M. C. , Belien, J. A. , Stoop, R. , and Helder, M. N. , 2014, “ Changes in Tissue Composition of the Vaginal Wall of Premenopausal Women With Prolapse,” Am. J. Obstet. Gynecol., 210(2), pp. 168.e161–168.e169. 10.1016/j.ajog.2013.10.881 [DOI] [PubMed] [Google Scholar]
- [24]. Drewes, P. G. , Yanagisawa, H. , Starcher, B. , Hornstra, I. , Csiszar, K. , Marinis, S. I. , Keller, P. , and Word, R. A. , 2007, “ Pelvic Organ Prolapse in Fibulin-5 Knockout Mice—Pregnancy-Induced Changes in Elastic Fiber Homeostasis in Mouse Vagina,” Am. J. Pathol., 170(2), pp. 578–589. 10.2353/ajpath.2007.060662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Rahn, D. D. , Ruff, M. D. , Brown, S. A. , Tibbals, H. F. , and Word, R. A. , 2008, “ Biomechanical Properties of the Vaginal Wall: Effect of Pregnancy, Elastic Fiber Deficiency, and Pelvic Organ Prolapse,” Am. J. Obstet. Gynecol., 198(5), pp. 590.e591–590.e596. 10.1016/j.ajog.2008.02.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Rahn, D. D. , Acevedo, J. F. , and Word, R. A. , 2008, “ Effect of Vaginal Distention on Elastic Fiber Synthesis and Matrix Degradation in the Vaginal Wall: Potential Role in the Pathogenesis of Pelvic Organ Prolapse,” Am. J. Physiol. Regul. Integr. Comp. Physiol., 295(4), pp. R1351–R1358. 10.1152/ajpregu.90447.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Downing, K. T. , Billah, M. , Raparia, E. , Shah, A. , Silverstein, M. C. , Ahmad, A. , and Boutis, G. S. , 2014, “ The Role of Mode of Delivery on Elastic Fiber Architecture and Vaginal Vault Elasticity: A Rodent Model Study,” J. Mech. Behav. Biomed. Mater., 29, pp. 190–198. 10.1016/j.jmbbm.2013.08.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Chen, B. , Wen, Y. , and Polan, M. L. , 2004, “ Elastolytic Activity in Women With Stress Urinary Incontinence and Pelvic Organ Prolapse,” Neurourol. Urodynam., 23(2), pp. 119–126. 10.1002/nau.20012 [DOI] [PubMed] [Google Scholar]
- [29]. Liu, X. , Zhao, Y. , Pawlyk, B. , Damaser, M. , and Li, T. , 2006, “ Failure of Elastic Fiber Homeostasis Leads to Pelvic Floor Disorders,” Am. J. Pathol., 168(2), pp. 519–528. 10.2353/ajpath.2006.050399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Wieslander, C. K. , Marinis, S. I. , Drewes, P. G. , Keller, P. W. , Acevedo, J. F. , and Word, R. A. , 2008, “ Regulation of Elastolytic Proteases in the Mouse Vagina During Pregnancy, Parturition, and Puerperium,” Biol. Reprod., 78(3), pp. 521–528. 10.1095/biolreprod.107.063024 [DOI] [PubMed] [Google Scholar]
- [31]. Rahn, D. , Acevedo, J. , Roshanravan, S. , Keller, P. , Davis, E. , Marmorstein, L. , and Word, R. , 2009, “ Failure of Pelvic Organ Support in Mice Deficient in Fibulin-3,” Am. J. Pathol., 174(1), pp. 206–215. 10.2353/ajpath.2009.080212 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Moalli, P. A. , Shand, S. H. , Zyczynski, H. M. , Gordy, S. C. , and Meyn, L. A. , 2005, “ Remodeling of Vaginal Connective Tissue in Patients With Prolapse,” Obstet. Gynecol., 106(5), pp. 953–963. 10.1097/01.AOG.0000182584.15087.dd [DOI] [PubMed] [Google Scholar]
- [33]. Budatha, M. , Roshanravan, S. , Zheng, Q. , Weislander, C. , Chapman, S. L. , Davis, E. C. , Starcher, B. , Word, R. A. , and Yanagisawa, H. , 2011, “ Extracellular Matrix Proteases Contribute to Progression of Pelvic Organ Prolapse in Mice and Humans,” J. Clin. Invest., 121(5), pp. 2048–2059. 10.1172/JCI45636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Gosline, J. , Lillie, M. , Carrington, E. , Guerette, P. , Ortlepp, C. , and Savage, K. , 2002, “ Elastic Proteins: Biological Roles and Mechanical Properties,” Philos. Trans.: Biol. Sci., 357(1418), pp. 121–132. 10.1098/rstb.2001.1022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. De Landsheere, L. , Munaut, C. , Nusgens, B. , Maillard, C. , Rubod, C. , Nisolle, M. , Cosson, M. , and Foidart, J. , 2013, “ Histology of the Vaginal Wall in Women With Pelvic Organ Prolapse: A Literature Review,” Int. Urogynecol. J., (12), pp. 2011–2020. 10.1007/s00192-013-2111-1 [DOI] [PubMed] [Google Scholar]
- [36]. Oxlund, H. , Manschot, J. , and Viidik, A. , 1988, “ The Role of Elastin in the Mechanical Properties of Skin,” J. Biomech., 21(3), pp. 213–218. 10.1016/0021-9290(88)90172-8 [DOI] [PubMed] [Google Scholar]
- [37]. Wagenseil, J. , and Mecham, R. , 2012, “ Elastin in Large Artery Stiffness and Hypertension,” J. Cardiovasc. Transl. Res., 5(3), pp. 264–273. 10.1007/s12265-012-9349-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Starcher, B. C. , 1986, “ Elastin and the Lung,” Thorax, 41(8), pp. 577–585. 10.1136/thx.41.8.577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Peter, D. Y. , Robert, P. M. , and David, E. B. , 1994, Extracellular Matrix Assembly and Structure, Elsevier Science, Cambridge, MA. [Google Scholar]
- [40]. Mecham, R. P. , 2018, “ Elastin in Lung Development and Disease Pathogenesis,” Matrix Biol., 73, pp. 6–20. 10.1016/j.matbio.2018.01.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Frances, C. , and Robert, L. , 1984, “ Elastin and Elastic Fibers in Normal and Pathologic Skin,” Int. J. Dermatol., 23(3), pp. 166–179. 10.1111/j.1365-4362.1984.tb04506.x [DOI] [PubMed] [Google Scholar]
- [42]. Echenne, P. B. , Barneon, G. G. , Pages, G. M. , Caillens, G. J. , Guibal, G. C. , Jarrousse, G. Y. , Dimeglio, G. A. , and Pous, G. J. , 1988, “ Skin Elastic Fiber Pathology and Idiopathic Scoliosis,” J. Pediatr. Orthop., 8(5), pp. 522–528. 10.1097/01241398-198809000-00004 [DOI] [PubMed] [Google Scholar]
- [43]. Leppert, P. C. , Yu, S. Y. , Keller, S. , Cerreta, J. , and Mandl, I. , 1987, “ Decreased Elastic Fibers and Desmosine Content in Incompetent Cervix,” Am. J. Obstetr. Gynecol., 157(5), pp. 1134–1139. 10.1016/S0002-9378(87)80277-6 [DOI] [PubMed] [Google Scholar]
- [44]. Jayyosi, C. , Lee, N. , Willcockson, A. , Nallasamy, S. , Mahendroo, M. , and Myers, K. , 2018, “ The Mechanical Response of the Mouse Cervix to Tensile Cyclic Loading in Term and Preterm Pregnancy,” Acta Biomater., 78, pp. 308–319. 10.1016/j.actbio.2018.07.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45]. Nallasamy, S. , Yoshida, K. , Akins, M. , Myers, K. , Iozzo, R. , and Mahendroo, M. , 2017, “ Steroid Hormones are Key Modulators of Tissue Mechanical Function Via Regulation of Collagen and Elastic Fibers,” Endocrinology, 158(4), pp. 950–962. 10.1210/en.2016-1930 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46]. Grant, T. M. , Yapp, C. , Chen, Q. , Czernuszka, J. T. , and Thompson, M. S. , 2015, “ The Mechanical, Structural, and Compositional Changes of Tendon Exposed to Elastase,” Ann. Biomed. Eng., 43(10), pp. 2477–2486. 10.1007/s10439-015-1308-5 [DOI] [PubMed] [Google Scholar]
- [47]. Henninger, H. B. , Valdez, W. R. , Scott, S. A. , and Weiss, J. A. , 2015, “ Elastin Governs the Mechanical Response of Medial Collateral Ligament Under Shear and Transverse Tensile Loading,” Acta Biomater., 25, pp. 304–312. 10.1016/j.actbio.2015.07.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Yuan, H. , Kononov, S. , Cavalcante, F. , and Lutchen, K. , 2000, “ Effects of Collagenase and Elastase on the Mechanical Properties of Lung Tissue Strips,” J. Appl. Physiol., 89(1), pp. 3–14. 10.1152/jappl.2000.89.1.3 [DOI] [PubMed] [Google Scholar]
- [49]. Jesudason, R. , Black, L. , Majumdar, A. , Stone, P. , and Suki, B. , 2007, “ Differential Effects of Static and Cyclic Stretching During Elastase Digestion on the Mechanical Properties of Extracellular Matrices,” J. Appl. Physiol., 103(3), pp. 803–811. 10.1152/japplphysiol.00057.2007 [DOI] [PubMed] [Google Scholar]
- [50]. López-Aguilar, J. , and Romero, P. V. , 1998, “ Effect of Elastase Pretreatment on Rat Lung Strip Induced Constriction,” Respir. Physiol., 113(3), pp. 239–246. 10.1016/S0034-5687(98)00054-1 [DOI] [PubMed] [Google Scholar]
- [51]. Moretto, A. , Dallaire, M. , Romero, P. , and Ludwig, M. , 1994, “ Effect of Elastase on Oscillation Mechanics of Lung Parenchymal Strips,” J. Appl. Physiol., 77(4), pp. 1623–1629. 10.1152/jappl.1994.77.4.1623 [DOI] [PubMed] [Google Scholar]
- [52]. Barbir, A. , Michalek, A. J. , Abbott, R. D. , and Iatridis, J. C. , 2010, “ Effects of Enzymatic Digestion on Compressive Properties of Rat Intervertebral Discs,” J. Biomech., 43(6), pp. 1067–1073. 10.1016/j.jbiomech.2009.12.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53]. Fan, Y. , Zhao, J. , Liao, D. , and Gregersen, H. , 2005, “ The Effect of Digestion of Collagen and Elastin on Histomorphometry and the Zero-Stress State in Rat Esophagus,” Dig. Dis. Sci., 50(8), pp. 1497–1505. 10.1007/s10620-005-2868-2 [DOI] [PubMed] [Google Scholar]
- [54]. Collins, M. , Eberth, J. , Wilson, E. , and Humphrey, J. , 2012, “ Acute Mechanical Effects of Elastase on the Infrarenal Mouse Aorta: Implications for Models of Aneurysms,” J. Biomech., 45(4), pp. 660–665. 10.1016/j.jbiomech.2011.12.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55]. Gundiah, N. , Babu, A. R. , and Pruitt, L. A. , 2013, “ Effects of Elastase and Collagenase on the Nonlinearity and Anisotropy of Porcine Aorta,” Physiol. Meas., 34(12), pp. 1657–1673. 10.1088/0967-3334/34/12/1657 [DOI] [PubMed] [Google Scholar]
- [56]. Bloksgaard, M. , Leurgans, T. M. , Spronek, B. , Heusinkveld, M. H. G. , Thorsted, B. , Rosenstand, K. , Nissen, I. , Hansen, U. M. , Brewer, J. R. , Bagatolli, L. A. , Rasniussen, L. M. , Irmukhamedov, A. , Reesink, K. D. , and De Mey, J. G. R. , 2017, “ Imaging and Modeling of Acute Pressure-Induced Changes of Collagen and Elastin Microarchitectures in Pig and Human Resistance Arteries,” Am. J. Physiol., 313(1), pp. H164–H178. 10.1152/ajpheart.00110.2017 [DOI] [PubMed] [Google Scholar]
- [57]. Zeinali-Davarani, S. , Chow, M.-J. , Turcotte, R. , and Zhang, Y. , 2013, “ Characterization of Biaxial Mechanical Behavior of Porcine Aorta Under Gradual Elastin Degradation,” J. Biomed. Eng. Soc., 41(7), pp. 1528–1538. 10.1007/s10439-012-0733-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58]. Humphrey, J. , Kang, T. , Sakarda, P. , and Anjanappa, M. , 1993, “ Computer-Aided Vascular Experimentation: A New Electromechanical Test System,” Ann. Biomed. Eng., 21(1), pp. 33–43. 10.1007/BF02368162 [DOI] [PubMed] [Google Scholar]
- [59]. Macrae, R. A. , Miller, K. , and Doyle, B. J. , 2016, “ Methods in Mechanical Testing of Arterial Tissue: A Review,” Strain, 52(5), pp. 380–399. 10.1111/str.12183 [DOI] [Google Scholar]
- [60]. Rubod, C. , Boukerrou, M. , Brieu, M. , Dubois, P. , and Cosson, M. , 2007, “ Biomechanical Properties of Vaginal Tissue. Part 1: New Experimental Protocol,” J. Urol., 178(1), pp. 320–325. 10.1016/j.juro.2007.03.040 [DOI] [PubMed] [Google Scholar]
- [61]. Amin, M. , Le, V. P. , and Wagenseil, J. E. , 2012, “ Mechanical Testing of Mouse Carotid Arteries: From Newborn to Adult,” J. Vis. Exp., (60), p. 3733. 10.3791/3733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62]. Robison, K. M. , Conway, C. K. , Desrosiers, L. , Knoepp, L. R. , and Miller, K. S. , 2017, “ Biaxial Mechanical Assessment of the Murine Vaginal Wall Using Extension-Inflation Testing,” ASME J. Biomech. Eng., 139(10), p. 104504. 10.1115/1.4037559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63]. Ferruzzi, J. , Bersi, M. , and Humphrey, J. , 2013, “ Biomechanical Phenotyping of Central Arteries in Health and Disease: Advantages of and Methods for Murine Models,” Ann. Biomed. Eng., 41(7), pp. 1311–1330. 10.1007/s10439-013-0799-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64]. Cox, R. H. , 1974, “ Three-Dimensional Mechanics of Arterial Segments In Vitro: Methods,” J. Appl. Physiol., 36(3), pp. 381–384. 10.1152/jappl.1974.36.3.381 [DOI] [PubMed] [Google Scholar]
- [65]. Van Loon, P. , 1977, “ Length-Force and Volume-Pressure Relationships of Arteries,” Biorheology, 14(4), pp. 181–201. 10.3233/BIR-1977-14405 [DOI] [PubMed] [Google Scholar]
- [66]. Humphrey, J. D. , 2002, Cardiovascular Solid Mechanics: Cells, Tissues, and Organs, Springer Science & Business Media, New York. [Google Scholar]
- [67]. Le, V. , Yamashiro, Y. , Yanagisawa, H. , and Wagenseil, J. , 2014, “ Measuring, Reversing, and Modeling the Mechanical Changes Due to the Absence of Fibulin-4 in Mouse Arteries,” Biomech. Model. Mechanobiol., 13(5), pp. 1081–1095. 10.1007/s10237-014-0556-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68]. Bersi, M. R. , Collins, M. J. , Wilson, E. , and Humphrey, J. D. , 2013, “ Disparate Changes in the Mechanical Properties of Murine Carotid Arteries and Aorta in Response to Chronic Infusion of Angiotensin-II,” Int. J. Adv. Eng. Sci. Appl. Math., 4(4), pp. 228–240. 10.1007/s12572-012-0052-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69]. Holzapfel, G. A. , Gasser, T. C. , and Ogden, R. W. , 2000, “ A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models,” J. Elasticity Phys. Sci. Solids, 61(1/3), pp. 1–48. 10.1023/A:1010835316564 [DOI] [Google Scholar]
- [70]. Holzapfel, G. A. , and Ogden, R. W. , 2010, “ Constitutive Modelling of Arteries,” Proc. R. Soc. A: Math., Phys. Eng. Sci., 466(2118), pp. 1551–1597. 10.1098/rspa.2010.0058 [DOI] [Google Scholar]
- [71]. Ni Annaidh, A. , Bruyere, K. , Destrade, M. , Gilchrist, M. D. , Maurini, C. , Ottenio, M. , and Saccomandi, G. , 2012, “ Automated Estimation of Collagen Fibre Dispersion in the Dermis and Its Contribution to the Anisotropic Behaviour of Skin,” Ann. Biomed. Eng., 40(8), pp. 1666–1678. 10.1007/s10439-012-0542-3 [DOI] [PubMed] [Google Scholar]
- [72]. Ogden, R. W. , 2003, “ Nonlinear Elasticity, Anisotropy, Material Stability and Residual Stresses in Soft Tissue,” Biomechanics of Soft Tissue in Cardiovascular Systems, Holzapfel G. A. and Ogden R. W., eds., Springer, Vienna, Austria, pp. 65–108. [Google Scholar]
- [73]. Gleason, R. L. , Dye, W. W. , Wilson, E. , and Humphrey, J. D. , 2008, “ Quantification of the Mechanical Behavior of Carotid Arteries From Wild-Type, Dystrophin-Deficient, and Sarcoglycan-Delta Knockout Mice,” J. Biomech., 41(15), pp. 3213–3218. 10.1016/j.jbiomech.2008.08.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74]. Rynkevic, R. , Martins, P. , Hympanova, L. , Almeida, H. , Fernandes, A. A. , and Deprest, J. , 2017, “ Biomechanical and Morphological Properties of the Multiparous Ovine Vagina and Effect of Subsequent Pregnancy,” J. Biomech., 57, pp. 94–102. 10.1016/j.jbiomech.2017.03.023 [DOI] [PubMed] [Google Scholar]
- [75]. Storn, R. , and Price, K. , 1997, “ Differential Evolution—A Simple and Efficient Heuristic for Global Optimization Over Continuous Spaces,” J. Global Optim., 11(4), pp. 341–359. 10.1023/A:1008202821328 [DOI] [Google Scholar]
- [76]. Price, K. V. , 2005, “ Differential Evolution a Practical Approach to Global Optimization,” Global Optimization, Storn R. M. and Lampinen J. A., eds., Springer, Berlin. [Google Scholar]
- [77]. Akintunde, A. , and Miller, K. , 2018, “ Evaluation of Microstructurally Motivated Constitutive Models to Describe Age-Dependent Tendon Healing,” Biomech. Model. Mechanobiol., 17(3), pp. 793–814. 10.1007/s10237-017-0993-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78]. Schneider, C. A. , Rasband, W. S. , and Eliceiri, K. W. , 2012, “ NIH Image to ImageJ: 25 Years of Image Analysis,” Nat. Methods, 9(7), pp. 671–675. 10.1038/nmeth.2089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79]. Udelsman, B. V. , Khosravi, R. , Miller, K. S. , Dean, E. W. , Bersi, M. R. , Rocco, K. , Yi, T. , Humphrey, J. D. , and Breuer, C. K. , 2014, “ Characterization of Evolving Biomechanical Properties of Tissue Engineered Vascular Grafts in the Arterial Circulation,” J. Biomech., 47(9), pp. 2070–2079. 10.1016/j.jbiomech.2014.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80]. Ruifrok, A. C. , and Johnston, D. A. , 2001, “ Quantification of Histochemical Staining by Color Deconvolution,” Anal. Quant. Cytol. Histol., 23(4), pp. 291–299.https://www.ncbi.nlm.nih.gov/pubmed/11531144 [PubMed] [Google Scholar]
- [81]. Team, R. C. , 2016, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- [82]. Dobrin, P. B. , Baker, W. H. , and Gley, W. C. , 1984, “ Elastolytic and Collagenolytic Studies of Arteries. Implications for the Mechanical Properties of Aneurysms,” Arch. Surg., 119(4), pp. 405–409. 10.1001/archsurg.1984.01390160041009 [DOI] [PubMed] [Google Scholar]
- [83]. Karlinsky, J. B. , Catanese, A. , Honeychurch, C. , Sherter, C. B. , Hoppin, F. G. , and Snider, G. L. , 1976, “ In Vitro Effects of Elastase and Collagenase on Mechanical Properties of Hamster Lungs,” Chest, 69(2 Suppl), pp. 275–276. 10.1378/chest.69.2_Supplement.275 [DOI] [PubMed] [Google Scholar]
- [84]. Cardamone, L. , Valentin, A. , Eberth, J. , and Humphrey, J. , 2009, “ Origin of Axial Prestretch and Residual Stress in Arteries,” Biomech. Model. Mechanobiol., 8(6), pp. 431–446. 10.1007/s10237-008-0146-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85]. Lee, T. C. , Midura, R. J. , Hascall, V. C. , and Vesely, I. , 2001, “ The Effect of Elastin Damage on the Mechanics of the Aortic Valve,” J. Biomech., 34(2), pp. 203–210. 10.1016/S0021-9290(00)00187-1 [DOI] [PubMed] [Google Scholar]
- [86]. Miskolczi, L. , Guterman, L. R. , Flaherty, J. D. , Szikora, I. , and Hopkins, L. N. , 1997, “ Rapid Saccular Aneurysm Induction by Elastase Application In Vitro,” Neurosurgery, 41(1), pp. 220–228. 10.1097/00006123-199707000-00034 [DOI] [PubMed] [Google Scholar]
- [87]. Greenwald, S. E. , Moore, J. E., Jr., Rachev , A., Kane, T. P. C. , and Meister, J. J. , 1997, “ Experimental Investigation of the Distribution of Residual Strains in the Artery Wall,” ASME J. Biomech. Eng., 119(4), pp. 438–444. 10.1115/1.2798291 [DOI] [PubMed] [Google Scholar]
- [88]. Smith, L. , Byers, S. , Costi, J. , and Fazzalari, N. , 2008, “ Elastic Fibers Enhance the Mechanical Integrity of the Human Lumbar Anulus Fibrosus in the Radial Direction,” J. Biomed. Eng. Soc., 36(2), pp. 214–223. 10.1007/s10439-007-9421-8 [DOI] [PubMed] [Google Scholar]
- [89]. Fang, F. , and Lake, S. P. , 2016, “ Multiscale Mechanical Integrity of Human Supraspinatus Tendon in Shear After Elastin Depletion,” J. Mech. Behav. Biomed. Mater., 63, pp. 443–455. 10.1016/j.jmbbm.2016.06.032 [DOI] [PubMed] [Google Scholar]
- [90]. Woessner, J. , 1963, “ Formation and Breakdown of Collagen and Elastin in the Human Uterus During Pregnancy and Post-Partum Involution,” Biochem. J., 89(1), pp. 75–82. 10.1042/bj0890075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91]. Liang, R. , Abramowitch, S. , Knight, K. , Palcsey, S. , Nolfi, A. , Feola, A. , Stein, S. , and Moalli, P. A. , 2013, “ Vaginal Degeneration Following Implantation of Synthetic Mesh With Increased Stiffness,” BJOG, 120(2), pp. 233–243. 10.1111/1471-0528.12085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92]. Jallah, Z. , Liang, R. , Feola, A. , Barone, W. , Palcsey, S. , Abramowitch, S. D. , Yoshimura, N. , and Moalli, P. , 2015, “ The Impact of Prolapse Mesh on Vaginal Smooth Muscle Structure and Function,” BJOG, 123(7), pp. 1076–1085. 10.1111/1471-0528.13514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93]. Alford, P. , Humphrey, J. , and Taber, L. , 2008, “ Growth and Remodeling in a Thick-Walled Artery Model: Effects of Spatial Variations in Wall Constituents,” Biomech. Model. Mechanobiol., 7(4), pp. 245–262. 10.1007/s10237-007-0101-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


